Hierarchical Terrain Classification Based on Multilayer Bayesian Network and Conditional Random Field
Abstract
:1. Introduction
1.1. SAR Images Classification
1.2. Motivation and Contributions
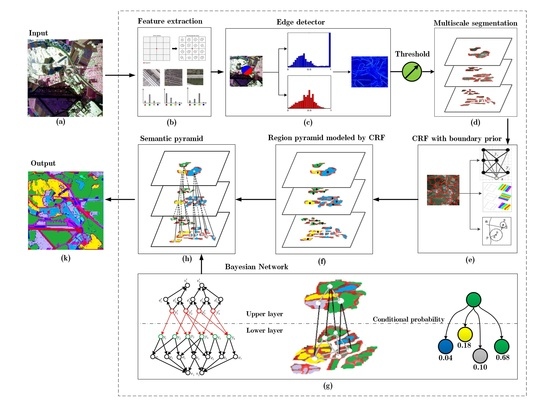
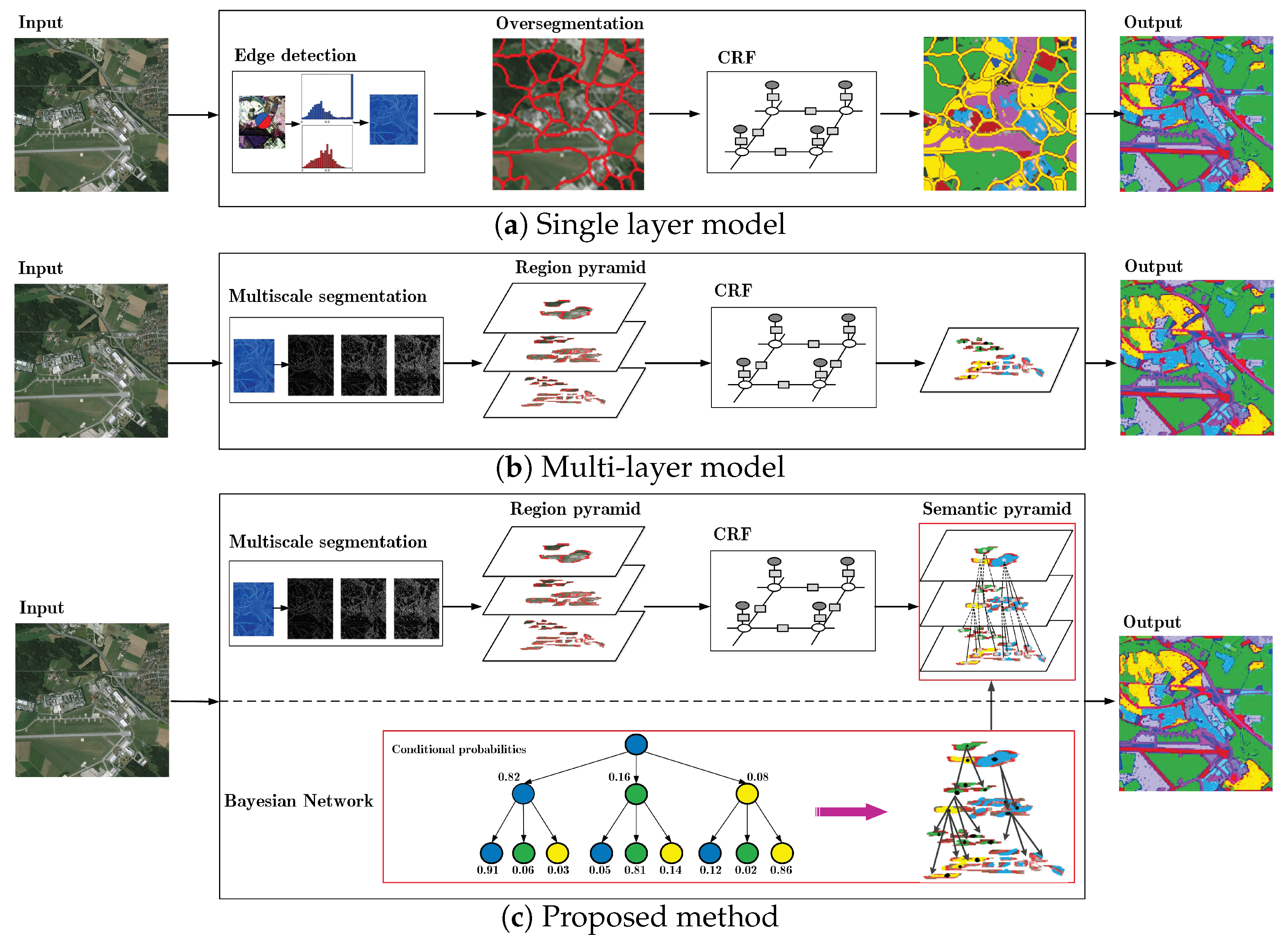
2. Overview of the Framework
3. Multiscale Segmentation
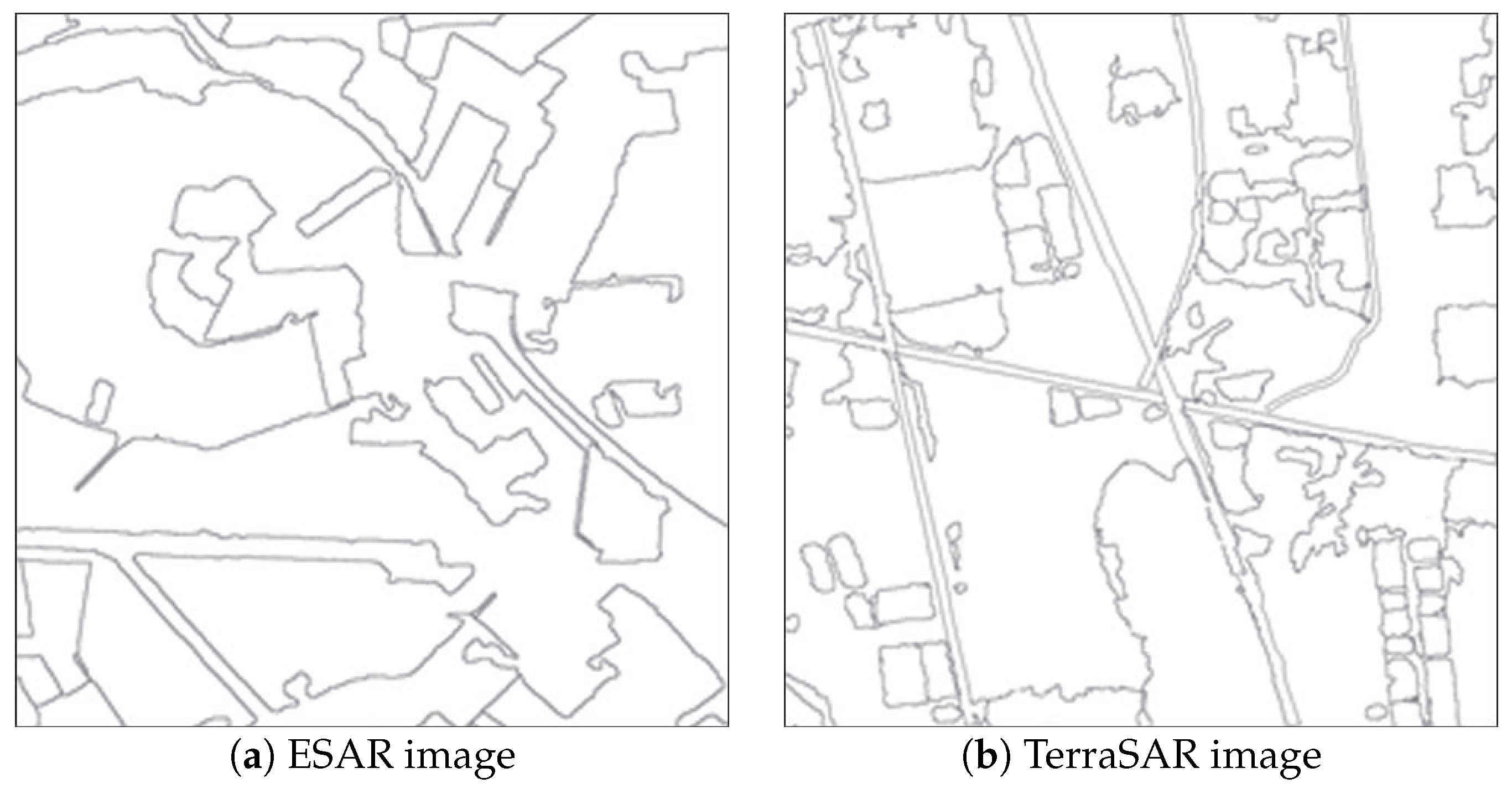
3.1. Edge Detection
3.2. Region Pyramid Construction
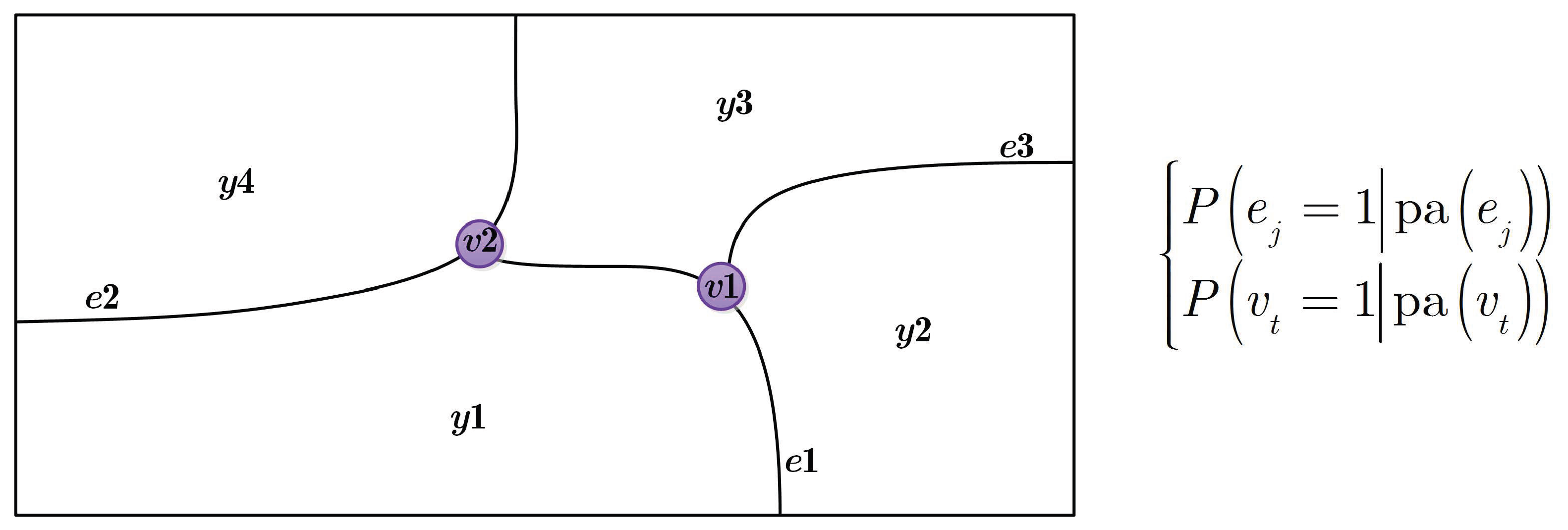
4. Semantic Pyramid Construction by CRF and BN
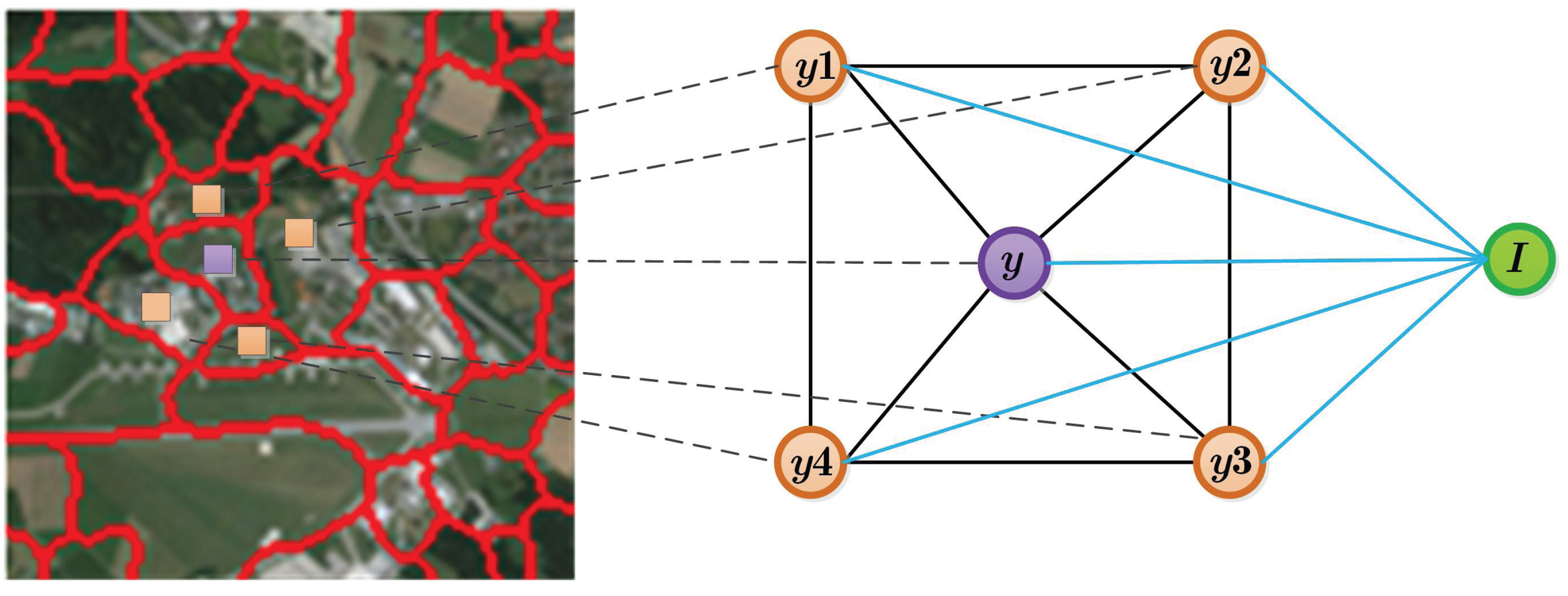
4.1. CRF with Boundary Prior Knowledge
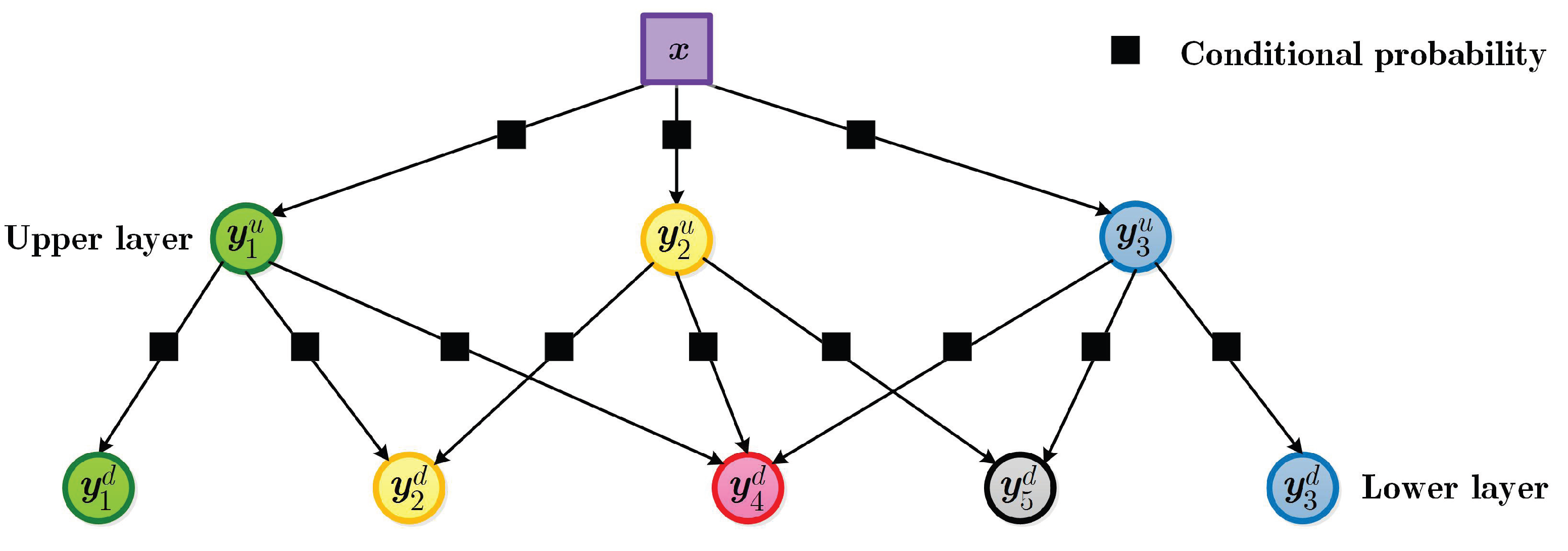
4.2. Multi-Layer Bayesian Network
4.3. Unified Inference Model for CRF and BN
5. Experiment
5.1. Experiment Data
5.2. Experiment Settings
5.3. Results and Analysis
- (1)
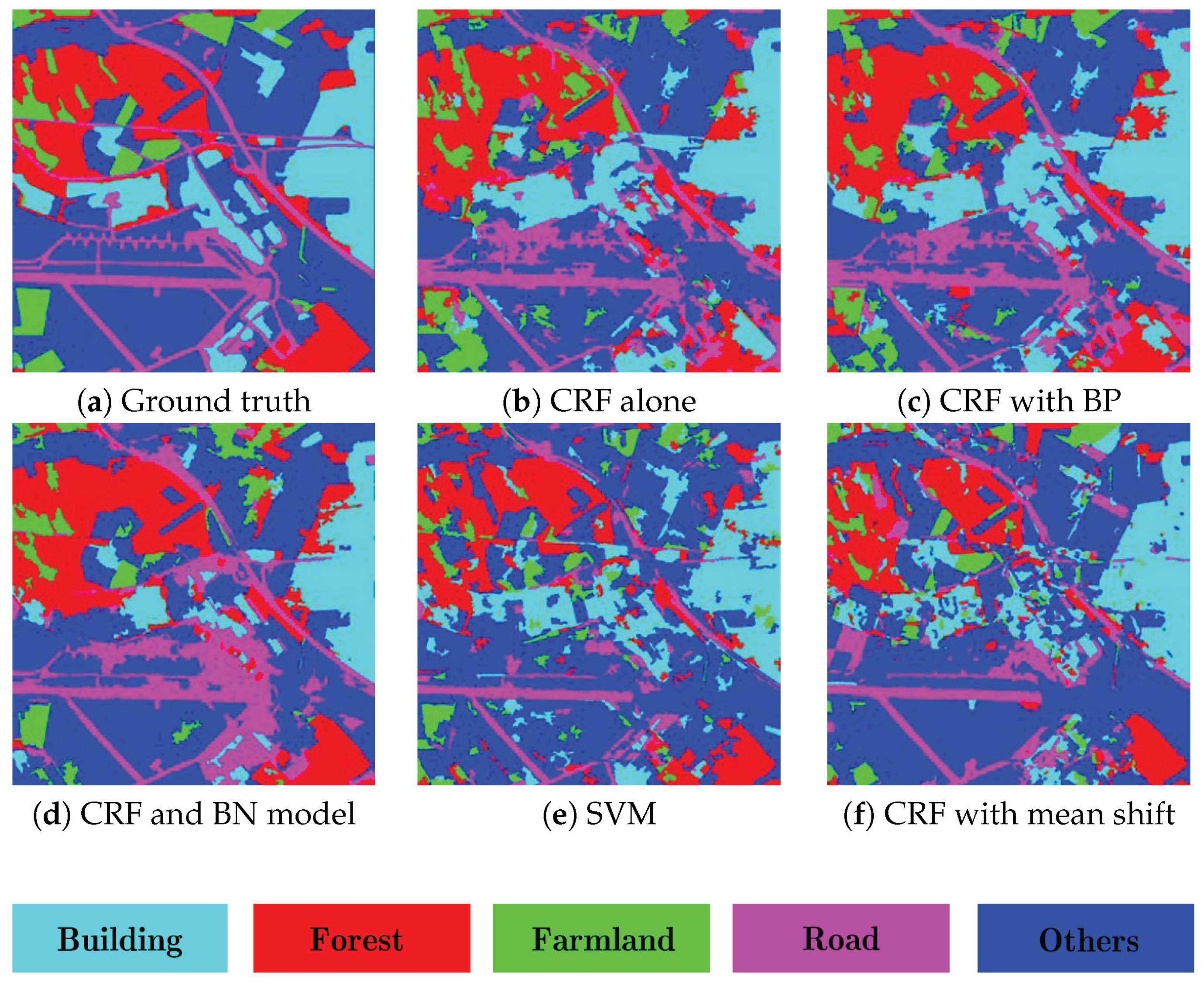
- For the ESAR data, the average classification accuracy of CRF model alone [36] is about 70.7%, as shown in Figure 9b. When the boundary prior knowledge is incorporated into CRF model, the average accuracy is up to 72.8%, the classification performance is improved about 2%, especially those areas around the boundary, as shown in Figure 9c. The performance of the proposed method is more promising, as shown in Figure 9d. Compared with the CRF model alone and CRF with boundary prior approaches, the accuracy is improved about 6% and 3.8%, respectively. This is because of the additional contextual knowledge, namely the causal dependencies between adjacent layers are integrated into the proposed classification framework. Figure 9e,f presents the results of SVM [34] and the CRF model based on mean shift [35]; the comparable performance demonstrates the effectiveness of the segmentation algorithm used in this paper.
- (2)
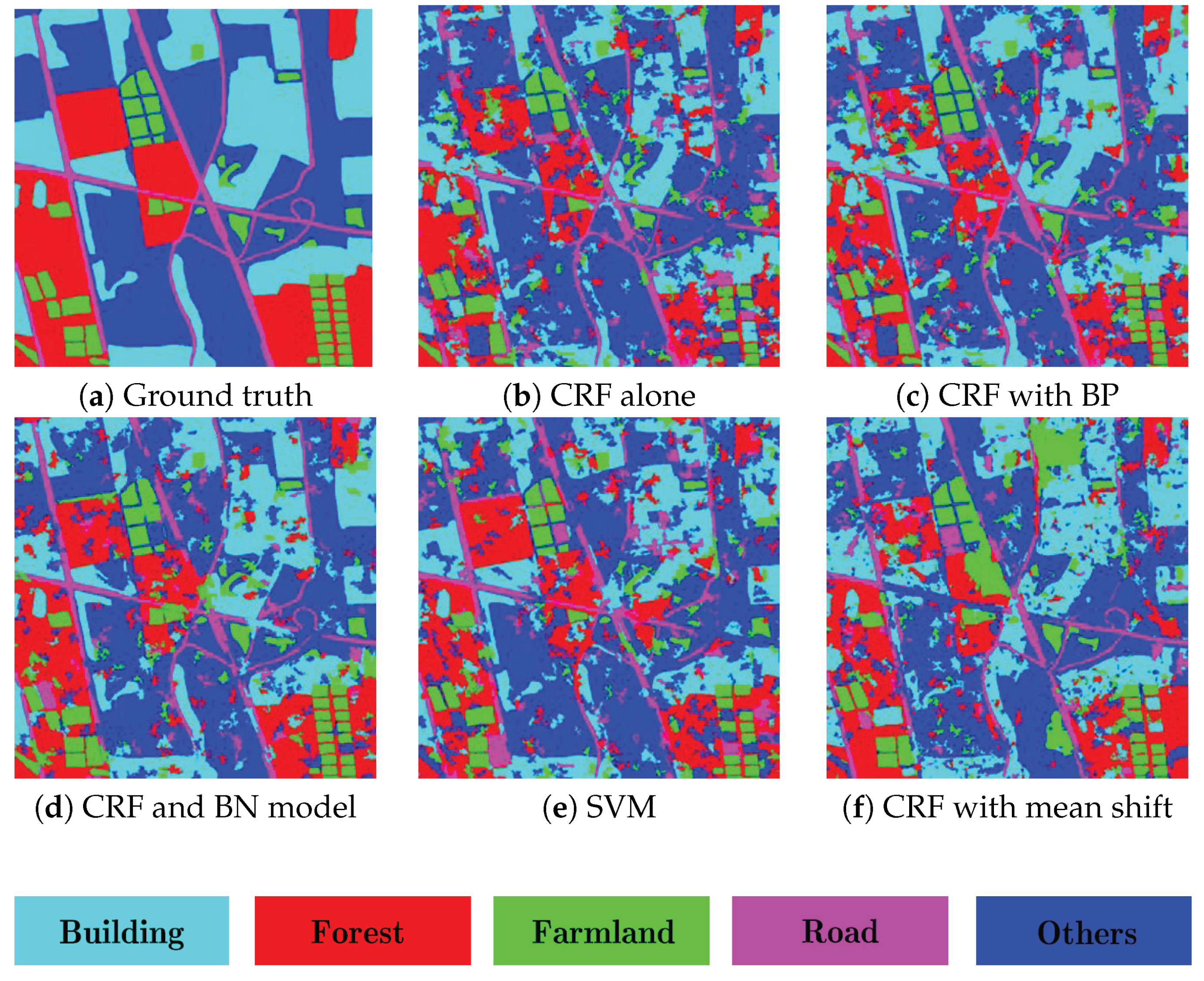
- Figure 10 displays the results on the TerraSAR image. The average classification accuracy of the proposed method is about 81.2%, which is better than the CRF model alone, 73.0%, and CRF with boundary prior, 76.1%. These experimental results also demonstrate that the incorporation of additional prior knowledge, namely the causal connections modeled by BN, is a benefit to the enhancement of classification performance. Moreover, note that the accuracy of CRF with boundary prior knowledge is improved about 3% compared with the CRF model alone, and the recognition ability on those sub-regions, e.g., forest, buildings, is improved effectively, which verifies the effectiveness of the incorporation of the boundary prior knowledge.
- (3)
- Since the causal relationships between adjacent layers, as well as the boundary prior knowledge are integrated into the proposed method, the computational cost of our method is relatively higher than those methods used for comparison purposes.
6. Discussion
- (1)
- The number of layers for constructing a region pyramid plays an important role in performance enhancement, and how to select the optimal number of layers is an issue that should be further studied. In theory, the more layers we select, the higher the accuracy that will be achieved. However, an optimum selection is intractable because we should ensure the existence of the classification probabilities of those sub-regions conditioned on their parents’ regions in the upper layer. Therefore, this issue should be further studied for the enhancement of the performance.
- (2)
- There are several hyperparameters in the process of oversegmentation, e.g., the scale for the extraction of local edges, etc. These hyperparameters, which like the concept of receptive field in the deep learning community, have some impact on the classification performance. However, how to select an optimum setting still needs to be addressed.
- (3)
- Since there are several parameters that should be learned in our proposed method, a higher computational cost should be paid. Consequently, we should make a tradeoff between the computational cost and classification accuracy, especially for the selection of the number of layers in forming a region pyramid.
- (4)
- Combining more prior knowledge with the image data itself is a benefit to the accuracy improvement. Therefore, more prior knowledge is encouraged to be incorporated into this classification framework to further performance enhancement.
- (5)
- The overfitting problem should also be considered in the case of insufficient training samples. In this paper, a uniform distribution is used to model the prior probability. To further improve the generalization, other strategies, like the solution in [37], should be taken into account.
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| BN | Bayesian Network |
| CPT | Conditional Probability Table |
| CRF | Conditional Random Field |
| FG | Factor Graph |
| MRF | Markov Random Field |
| MPE | Most Probable Explanation |
| OWT | Oriented Watershed Transformation |
| SAR | Synthetic Aperture Radar |
| SLS | Stochastic Local Search |
| SVM | Support Vector Machine |
| UCM | Ultrametric Contour Map |
References
- Moreira, A.; Prats-Iraola, P.; Younis, M.; Krieger, G.; Hajnsek, I.; Papathanassiou, K.P. A tutorial on synthetic aperture radar. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–43. [Google Scholar] [CrossRef]
- Huynen, J.R. Phenomenological theory of radar targets. In Electromagnetic Scattering; Academic Press: New York, NY, USA, 1970; pp. 653–712. [Google Scholar]
- Cloude, S. Group theory and polarisation algebra. Optik 1986, 75, 26–36. [Google Scholar]
- Krogager, E. New decomposition of the radar target scattering matrix. Electron. Lett. 1990, 26, 1525–1527. [Google Scholar] [CrossRef]
- Freeman, A.; Durden, S.L. A three-component scattering model for polarimetric SAR data. IEEE Trans. Geosci. Remote Sens. 1998, 36, 963–973. [Google Scholar] [CrossRef]
- Yamaguchi, Y.; Moriyama, T.; Ishido, M.; Yamada, H. Four-component scattering model for polarimetric SAR image decomposition. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1699–1706. [Google Scholar] [CrossRef]
- Touzi, R. Target Scattering Decomposition in Terms of Roll-Invariant Target Parameters. IEEE Trans. Geosci. Remote Sens. 2007, 45, 73–84. [Google Scholar] [CrossRef]
- An, W.; Cui, Y.; Yang, J. Three-Component Model-Based Decomposition for Polarimetric SAR Data. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2732–2739. [Google Scholar]
- Sato, A.; Yamaguchi, Y.; Singh, G.; Park, S.E. Four-Component Scattering Power Decomposition with Extended Volume Scattering Model. IEEE Geosci. Remote Sens. Lett. 2012, 9, 166–170. [Google Scholar] [CrossRef]
- He, C.; Li, S.; Liao, Z.X.; Liao, M.S. Texture classification of PolSAR data based on sparse coding of wavelet polarization textons. IEEE Geosci. Remote Sens. 2013, 8, 4576–4590. [Google Scholar] [CrossRef]
- Kandaswamy, U.; Adjeroh, D.A.; Lee, M.C. Efficient Texture Analysis of SAR Imagery. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2075–2083. [Google Scholar] [CrossRef]
- Akbarizadeh, G. A New Statistical-Based Kurtosis Wavelet Energy Feature for Texture Recognition of SAR Images. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4358–4368. [Google Scholar] [CrossRef]
- Planinsic, P.; Singh, J.; Gleich, D. SAR Image Categorization Using Parametric and Nonparametric Approaches Within a Dual Tree CWT. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1757–1761. [Google Scholar] [CrossRef]
- Dekker, R.J. Texture analysis and classification of ERS SAR images for map updating of urban areas in The Netherlands. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1950–1958. [Google Scholar] [CrossRef]
- Dai, D.; Yang, W.; Sun, H. Multilevel Local Pattern Histogram for SAR Image Classification. IEEE Geosci. Remote Sens. Lett. 2011, 8, 225–229. [Google Scholar] [CrossRef]
- Deng, Q.; Chen, Y.; Zhang, W.; Yang, J. Colorization for Polarimetric SAR Image Based on Scattering Mechanisms. In Proceedings of the 2008 Congress on Image and Signal Processing, Sanya, China, 27–30 May 2008; pp. 697–701.
- Turner, D.; Woodhouse, I.H. An Icon-Based Synoptic Visualization of Fully Polarimetric Radar Data. Remote Sens. 2012, 4, 648–660. [Google Scholar] [CrossRef]
- Uhlmann, S.; Kiranyaz, S. Integrating Color Features in Polarimetric SAR Image Classification. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2197–2216. [Google Scholar] [CrossRef]
- Golparvar-Fard, M.; Balali, V.; de la Garza, J.M. Segmentation and recognition of highway assets using image-based 3D point clouds and semantic Texton forests. J. Comput. Civ. Eng. 2012, 29, 04014023. [Google Scholar] [CrossRef]
- Balali, V.; Golparvar-Fard, M. Segmentation and recognition of roadway assets from car-mounted camera video streams using a scalable non-parametric image parsing method. Autom. Constr. 2015, 49, 27–39. [Google Scholar] [CrossRef]
- Li, S.Z. Markov Random Field Modeling in Image Analysis; Springer Science & Business Media: Berlin, Germany, 2009. [Google Scholar]
- Lafferty, J.D.; Mccallum, A.; Pereira, F.C.N. Conditional Random Fields: Probabilistic Models for Segmenting and Labeling Sequence Data. In Proceedings of the Eighteenth International Conference on Machine Learning (ICML), Williamstown, MA, USA, 28 June–1 July 2001; pp. 282–289.
- Nielsen, T.D.; Jensen, F.V. Bayesian Networks and Decision Graphs; Springer Science & Business Media: Berlin, Germany, 2009. [Google Scholar]
- D’Elia, C.; Ruscino, S.; Abbate, M.; Aiazzi, B.; Baronti, S.; Alparone, L. SAR Image Classification Through Information-Theoretic Textural Features, MRF Segmentation, and Object-Oriented Learning Vector Quantization. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1116–1126. [Google Scholar] [CrossRef]
- Voisin, A.; Krylov, V.A.; Moser, G.; Serpico, S.B.; Zerubia, J. Classification of Very High Resolution SAR Images of Urban Areas Using Copulas and Texture in a Hierarchical Markov Random Field Model. IEEE Geosci. Remote Sens. Lett. 2013, 10, 96–100. [Google Scholar] [CrossRef]
- Su, X.; He, C.; Feng, Q.; Deng, X.; Sun, H. A Supervised Classification Method Based on Conditional Random Fields With Multiscale Region Connection Calculus Model for SAR Image. IEEE Geosci. Remote Sens. Lett. 2011, 8, 497–501. [Google Scholar] [CrossRef]
- Zhang, G.; Jia, X. Simplified Conditional Random Fields with Class Boundary Constraint for Spectral-Spatial Based Remote Sensing Image Classification. IEEE Geosci. Remote Sens. Lett. 2012, 9, 856–860. [Google Scholar] [CrossRef]
- Ding, Y.; Li, Y.; Yu, W. SAR Image Classification Based on CRFs with Integration of Local Label Context and Pairwise Label Compatibility. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 300–306. [Google Scholar] [CrossRef]
- Mortensen, E.N.; Jia, J. Real-Time Semi-Automatic Segmentation Using a Bayesian Network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, New York, NY, USA, 17–22 June 2006; pp. 1007–1014.
- Arbelaez, P.; Maire, M.; Fowlkes, C.; Malik, J. Contour Detection and Hierarchical Image Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 898–916. [Google Scholar] [CrossRef] [PubMed]
- Arbelaez, P. Boundary Extraction in Natural Images Using Ultrametric Contour Maps. In Proceedings of the Conference on Computer Vision and Pattern Recognition Workshop, New York, NY, USA, 17–22 June 2006; p. 182.
- Hutter, F.; Hoos, H.H.; Stutzle, T. Efficient stochastic local search for MPE solving. In Proceedings of the Nineteenth International Joint Conference on Artificial Intelligence, Edinburgh, UK, 30 July–5 August 2005; pp. 169–174.
- Liu, D.C.; Nocedal, J. On the limited memory BFGS method for large scale optimization. Math. Program. 1989, 45, 503–528. [Google Scholar] [CrossRef]
- Maghsoudi, Y.; Collins, M.J.; Leckie, D.G. Radarsat-2 Polarimetric SAR Data for Boreal Forest Classification Using SVM and a Wrapper Feature Selector. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 1531–1538. [Google Scholar] [CrossRef]
- Comaniciu, D.; Meer, P. Mean shift: A robust approach toward feature space analysis. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 603–619. [Google Scholar] [CrossRef]
- Zhang, P.; Li, M.; Wu, Y.; Li, H. Hierarchical Conditional Random Fields Model for Semisupervised SAR Image Segmentation. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4933–4951. [Google Scholar] [CrossRef]
- Salazar, A.; Safont, G.; Vergara, L. Surrogate techniques for testing fraud detection algorithms in credit card operations. In Proceedings of the 2014 IEEE International Carnahan Conference on Security Technology (ICCST), Rome, Italy, 13–16 October 2014; pp. 1–6.



| Attribute | Feature Type | Dimension |
|---|---|---|
| Intensity | Haar | 7 |
| Grey | 16 | |
| Polarization | Pauli | 3 |
| SDH | 9 | |
| Huynen | 3 | |
| Texture | Gaussian filters | 17 |
| Classes | ESAR Data | TerraSAR Data | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 1 | 2 | 3 | 4 | 5 | |
| 1 | 0.71 | 0.12 | 0.04 | 0.05 | 0.08 | 0.7 | 0.08 | 0.07 | 0.05 | 0.1 |
| 2 | 0.1 | 0.7 | 0.15 | 0.02 | 0.03 | 0.07 | 0.7 | 0.15 | 0.02 | 0.06 |
| 3 | 0.02 | 0.15 | 0.7 | 0.04 | 0.09 | 0.03 | 0.1 | 0.75 | 0.04 | 0.08 |
| 4 | 0.05 | 0.02 | 0.03 | 0.82 | 0.08 | 0.1 | 0.04 | 0.03 | 0.8 | 0.03 |
| 5 | 0.08 | 0.06 | 0.06 | 0.1 | 0.7 | 0.1 | 0.08 | 0.04 | 0.1 | 0.68 |
| Method | Category | Building | Forest | Farmland | Road | Others | Average |
|---|---|---|---|---|---|---|---|
| Building | 0.7305 | 0.1505 | 0.0034 | 0.0296 | 0.086 | ||
| Forest | 0.1374 | 0.7203 | 0.0732 | 0.041 | 0.0282 | ||
| Experiment 1 | Farmland | 0.0118 | 0.1966 | 0.581 | 0.0146 | 0.196 | 0.7066 |
| Road | 0.0887 | 0.0706 | 0.0034 | 0.6302 | 0.2071 | ||
| Others | 0.0487 | 0.0341 | 0.0649 | 0.1193 | 0.733 | ||
| Building | 0.8164 | 0.1083 | 0.0047 | 0.0214 | 0.0493 | ||
| Forest | 0.1007 | 0.802 | 0.0419 | 0.0182 | 0.0372 | ||
| Experiment 3 | Farmland | 0.0136 | 0.2423 | 0.5156 | 0.014 | 0.2145 | 0.7284 |
| Road | 0.0964 | 0.0578 | 0.0084 | 0.6258 | 0.2116 | ||
| Others | 0.0623 | 0.0428 | 0.0544 | 0.1125 | 0.728 | ||
| Building | 0.6613 | 0.1522 | 0.0076 | 0.1025 | 0.0763 | ||
| Forest | 0.0274 | 0.8329 | 0.0468 | 0.033 | 0.0598 | ||
| Experiment 5 | Farmland | 0.0028 | 0.1201 | 0.6069 | 0.0092 | 0.261 | 0.7669 |
| Road | 0.0197 | 0.0495 | 0.0031 | 0.7602 | 0.1675 | ||
| Others | 0.0165 | 0.0266 | 0.0299 | 0.1251 | 0.802 | ||
| Building | 0.7728 | 0.0666 | 0.0255 | 0.0166 | 0.1185 | ||
| Forest | 0.0693 | 0.7109 | 0.0179 | 0.0043 | 0.1975 | ||
| Experiment 4 | Farmland | 0.0461 | 0.1376 | 0.4655 | 0.0057 | 0.3451 | 0.7127 |
| Road | 0.063 | 0.049 | 0.0286 | 0.4049 | 0.4545 | ||
| Others | 0.0664 | 0.0379 | 0.037 | 0.0429 | 0.8158 | ||
| Building | 0.7884 | 0.0356 | 0.0294 | 0.0321 | 0.1246 | ||
| Forest | 0.0841 | 0.6325 | 0.0296 | 0.0455 | 0.2083 | ||
| Experiment 2 | Farmland | 0.0329 | 0.1685 | 0.4345 | 0.0362 | 0.3297 | 0.7218 |
| Road | 0.0698 | 0.0463 | 0.0255 | 0.5104 | 0.3479 | ||
| Others | 0.0458 | 0.0201 | 0.0268 | 0.0624 | 0.8449 |
| Method | Category | Building | Forest | Farmland | Road | Others | Average |
|---|---|---|---|---|---|---|---|
| Building | 0.673 | 0.0513 | 0.0369 | 0.0436 | 0.1952 | ||
| Forest | 0.0927 | 0.6679 | 0.0321 | 0.0355 | 0.1718 | ||
| Experiment 1 | Farmland | 0.0725 | 0.011 | 0.6573 | 0.0494 | 0.2099 | 0.7295 |
| Road | 0.1005 | 0.053 | 0.0419 | 0.6891 | 0.1155 | ||
| Others | 0.0497 | 0.0471 | 0.0394 | 0.0359 | 0.8278 | ||
| Building | 0.7706 | 0.0363 | 0.0419 | 0.0316 | 0.1196 | ||
| Forest | 0.088 | 0.665 | 0.043 | 0.0377 | 0.1663 | ||
| Experiment 3 | Farmland | 0.0623 | 0.0372 | 0.7486 | 0.0284 | 0.1235 | 0.7607 |
| Road | 0.0945 | 0.0373 | 0.0317 | 0.7699 | 0.0666 | ||
| Others | 0.0595 | 0.0481 | 0.0423 | 0.0422 | 0.8079 | ||
| Building | 0.8005 | 0.0454 | 0.0371 | 0.0145 | 0.1025 | ||
| Forest | 0.0315 | 0.7984 | 0.0413 | 0.0241 | 0.1047 | ||
| Experiment 5 | Farmland | 0.0328 | 0.0309 | 0.8383 | 0.0433 | 0.0546 | 0.8117 |
| Road | 0.0554 | 0.02 | 0.0347 | 0.7905 | 0.0993 | ||
| Others | 0.0517 | 0.0434 | 0.0309 | 0.0284 | 0.8455 | ||
| Building | 0.7069 | 0.0649 | 0.0403 | 0.039 | 0.1489 | ||
| Forest | 0.0546 | 0.714 | 0.04 | 0.0326 | 0.1587 | ||
| Experiment 4 | Farmland | 0.0151 | 0.0621 | 0.7112 | 0.0965 | 0.1151 | 0.7422 |
| Road | 0.0729 | 0.0663 | 0.0529 | 0.6292 | 0.1787 | ||
| Others | 0.0573 | 0.0553 | 0.0323 | 0.0421 | 0.813 | ||
| Building | 0.764 | 0.0381 | 0.0391 | 0.0316 | 0.1272 | ||
| Forest | 0.0697 | 0.7035 | 0.0794 | 0.0236 | 0.1238 | ||
| Experiment 2 | Farmland | 0.0911 | 0.0567 | 0.7054 | 0.0746 | 0.0722 | 0.7403 |
| Road | 0.0617 | 0.0323 | 0.0365 | 0.6317 | 0.2379 | ||
| Others | 0.0766 | 0.0392 | 0.0912 | 0.0204 | 0.7726 |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, C.; Liu, X.; Feng, D.; Shi, B.; Luo, B.; Liao, M. Hierarchical Terrain Classification Based on Multilayer Bayesian Network and Conditional Random Field. Remote Sens. 2017, 9, 96. https://doi.org/10.3390/rs9010096
He C, Liu X, Feng D, Shi B, Luo B, Liao M. Hierarchical Terrain Classification Based on Multilayer Bayesian Network and Conditional Random Field. Remote Sensing. 2017; 9(1):96. https://doi.org/10.3390/rs9010096
Chicago/Turabian StyleHe, Chu, Xinlong Liu, Di Feng, Bo Shi, Bin Luo, and Mingsheng Liao. 2017. "Hierarchical Terrain Classification Based on Multilayer Bayesian Network and Conditional Random Field" Remote Sensing 9, no. 1: 96. https://doi.org/10.3390/rs9010096
APA StyleHe, C., Liu, X., Feng, D., Shi, B., Luo, B., & Liao, M. (2017). Hierarchical Terrain Classification Based on Multilayer Bayesian Network and Conditional Random Field. Remote Sensing, 9(1), 96. https://doi.org/10.3390/rs9010096