1. Introduction
The estimation of land surface temperature (LST) from acquisitions of medium-resolution sensors has a long tradition. Data from the AVHRR (Advanced Very High Resolution Radiometer) sensors flown on NOAA-satellites is operationally available since the early 80s with 1 km spatial resolution at nadir. Given that the data has been archived, the generation of long time series is possible. This paper focuses on a comparison of different mono- and split-window algorithms to derive LST from AVHRR top of atmosphere (TOA) data under clear sky conditions. The comparison is performed against the background of future generation of long time series and their analysis. Included is not only a careful selection of algorithms based on their suitability for time series generation, but also a straightforward specification of related errors and sensitivities.
One way to estimate LST is to remove the attenuation effects of the atmosphere from TOA brightness temperatures. These effects are thereby determined quantitatively using radiative transfer models (RTMs) and assumptions of the composition of the atmosphere. Given that the atmosphere is well characterized, this method can be very accurate. However, main constraint of such approaches is the high CPU usage of the RTMs, which makes them unsuitable for the processing of extensive time series with pixel-based approaches. More straightforward is the application of methods, which are based on pre-computed functions and coefficients. These allow an effective data processing. A selection of such methods is described in this article specifically for the case of AVHRR bands. A more complete overview of methods is given for example in [
1]. Another fast option to retrieve LST are neural networks as described for example in [
2].
The estimation of LST from AVHRR/2, AVHRR/3 (13 sensors on the NOAA satellites and now AVHRR/3 on Metop-A and Metop-B), as well as AVHRR-heritage sensors, can be accomplished taking advantage of the splitting of the thermal domain into two channels. The two channels are in wavelength ranges with different absorption features of mainly water vapour. As such, the difference of the two channels can be used to eliminate these atmospheric effects in the data. The two channels are usually located around 11 and 12 µm. Measured brightness temperatures of these two channels can be directly used with the respective surface emissivities to deduct LST. The split-window technique is simple and robust [
3] and therefore favoured by many researchers and also operational providers of LST (e.g., Land Surface Analysis Satellite Applications Facility (LSA SAF) [
4], Copernicus Land [
5], NASA MODIS LST [
6]). AVHRR/1 however carries only one band in the thermal domain, only mono-window algorithms are applicable here. These algorithms are missing any measured information about atmospheric absorption; correction procedures are fully dependent on external data. Due to reduction to one band the accuracy of mono-band algorithms is expected to be lower than split-window algorithms [
7]. Nevertheless, [
8] reported accuracies for mono-window algorithms which are comparable to what was found for split-window algorithms.
Early developments of mono-window algorithms were undertaken by [
9], also [
10] suggests in his review paper a single channel algorithm. Further work was presented by [
11,
12]. A more recent overview is given by [
1] who address the mono-window algorithms as single-channel methods. The work of [
8] complements the overview with an additional statistical mono-window algorithm. All these methods are based on precomputed coefficients and functions, which can vary for different states of the atmosphere.
In the literature, numerous split-window algorithms have been published, starting as early as 1970, when first studies were published about the estimation of Sea Surface Temperatures [
13]. The studies were based on modelled and on measured data. A good overview is given in [
1]. The authors divide the split-window algorithms into linear and non-linear split-window algorithms. Both these algorithms use the information of one of the two brightness temperatures as a general offset, as well as the difference between the two brightness temperatures to express the magnitude of absorption in the atmosphere. All algorithms come with a range of coefficients, which are determined empirically and reflect the influence of the emissivity, the difference of the emissivities of the two bands, the water vapour in the atmosphere and the sensor view angle. As such, expressions have been developed to empirically deduct the coefficients from these variables in a linear or also non-linear way (e.g., [
9,
14,
15,
16,
17,
18]). Another way of incorporating the influence of water vapour, the longer atmospheric path determined by the view angle, and also temperature itself to the expression, is to use different sets of coefficients for subranges of each variable. This approach was followed for example by [
16,
19], who simulated band brightness temperatures using a radiative transfer model for a variety of atmospheric conditions and a range of sensor view angles. The atmospheric conditions thereby covered given ranges of atmospheric water vapour, and initial guess LST or T
air broad enough, to reflect the most possible atmospheric conditions. The coefficients are then derived for subranges of atmospheric water vapour and initial guess LST or T
air from the modelled brightness temperatures and the input LST into the radiative transfer runs. As the band brightness temperatures usually are modelled using the sensors spectral response, the resulting coefficients are sensor-specific and cannot be transferred from one to another sensor without loss of accuracy. There have been studies comparing different split-window algorithms ([
3,
20,
21,
22]), highlighting the advances and drawbacks of single algorithms and their implementation at that time. As pointed out by [
8], the approach of creating sets of coefficients does also apply for mono-window algorithms.
Nowadays, the availability of long term time series of medium resolution data of sensors such as AVHRR enables researchers to investigate climate relevant trends in this multi-decadal Earth Observation data. This study therefore investigates the suitability of a variety of selected algorithms to long time series processing in the framework of the TIMELINE project at the Earth Observation Center (EOC) of the German Aerospace Center (DLR). The project aims in creating long and homogeneous time series from AVHRR/1, AVHRR/2 and AVHRR/3 starting in the early 80s. Most of the proposed split-window algorithms have been developed a few years back. This is why the accompanying coefficient sets are usually given only for one or more of the older AVHRR sensors. These coefficient sets might match perfectly to the one AVHRR sensor or to the set of sensors, but fail to give similar accuracies using the coefficients on all available AVHRR data, as each sensor features its unique spectral response curve. As such, the generation of a longer time series with coefficients from literature are prone to larger errors, which might introduce artificial anomalies like sudden steps in the time series. It is, therefore, of utmost importance to use updated coefficients. Nowadays, the focus of satellite product analysis is more and more shifted towards time series analysis. As such, LST products should be consistent and fit to the concept of climate data records (CDR) [
3]. This work therefore includes the generation of new coefficient sets for each of the AVHRR sensor, to enable analyses that focus on time series applications. The generation of the coefficients follows the development of e.g., [
16], by generating different coefficient sets for different ranges of columnar water vapour, temperature, mean band emissivity and—if applicable—the difference of the two band emissivities.
The focus of our analysis not only emphasises on the performance, as expressed by accuracy and precision measures, of the split-window algorithms themselves, but also on the sensitivity of the split-window algorithms to their input data (e.g., columnar water vapour). Performance assessments provide information on the magnitude of variation that can be expected from using one or the other split-window approach. The sensitivity analysis highlights the influence of the input variables into the split-window algorithms. This is important mainly in cases where the quality of an input variable is of varying quality. In such cases, reduced quality of input data caused by systematic and/or random effects is propagated to the LST generation—depending on its sensitivity. Both, the performance and the sensitivity measures can be further used for uncertainty and quality estimation of a final LST AVHRR time series product which relate product quality to state of the art user requirements (accuracy better than 1 K as given for example by GCOS ([
23]). Current data providers of LST, which aim for long time series with high accuracy, are for example the LSA SAF, which will soon provide consistent Meteosat LST in a joint effort with CM SAF [
24]. In addition, the Copernicus Land Programme provides LST from MeteoSat data ([
4,
5]). Furthermore, the GlobTemperature Project using (Advanced) Along-Track Scanning Radiometer (A)ATSR data ([
25]), and NASA’s MODIS LST product [
26] provide LST time series. The latter product was used in the study for a comparison with one of the proposed algorithms to confirm the soundness and validity of the approach.
2. Data
This assessment was specifically designed for AVHRR. The AVHRR sensors (AVHRR/1, 2, and 3) are mounted on the NOAA-series of satellites, since 2006 AVHRR/3 is also onboard of the MetOp series. AVHRRs carries one band in the red (band 1), one in the near infrared (band 2), and one in the shortwave infrared (band 3) domain. Since AVHRR/3, band 3 can also contain acquired radiation in the mid infrared wavelength. Main bands for LST estimation are however the bands in the thermal infrared. AVHRR/2 and 3 contain two channels in the thermal infrared, while AVHRR/1 features only one band in this domain (
Table 1).
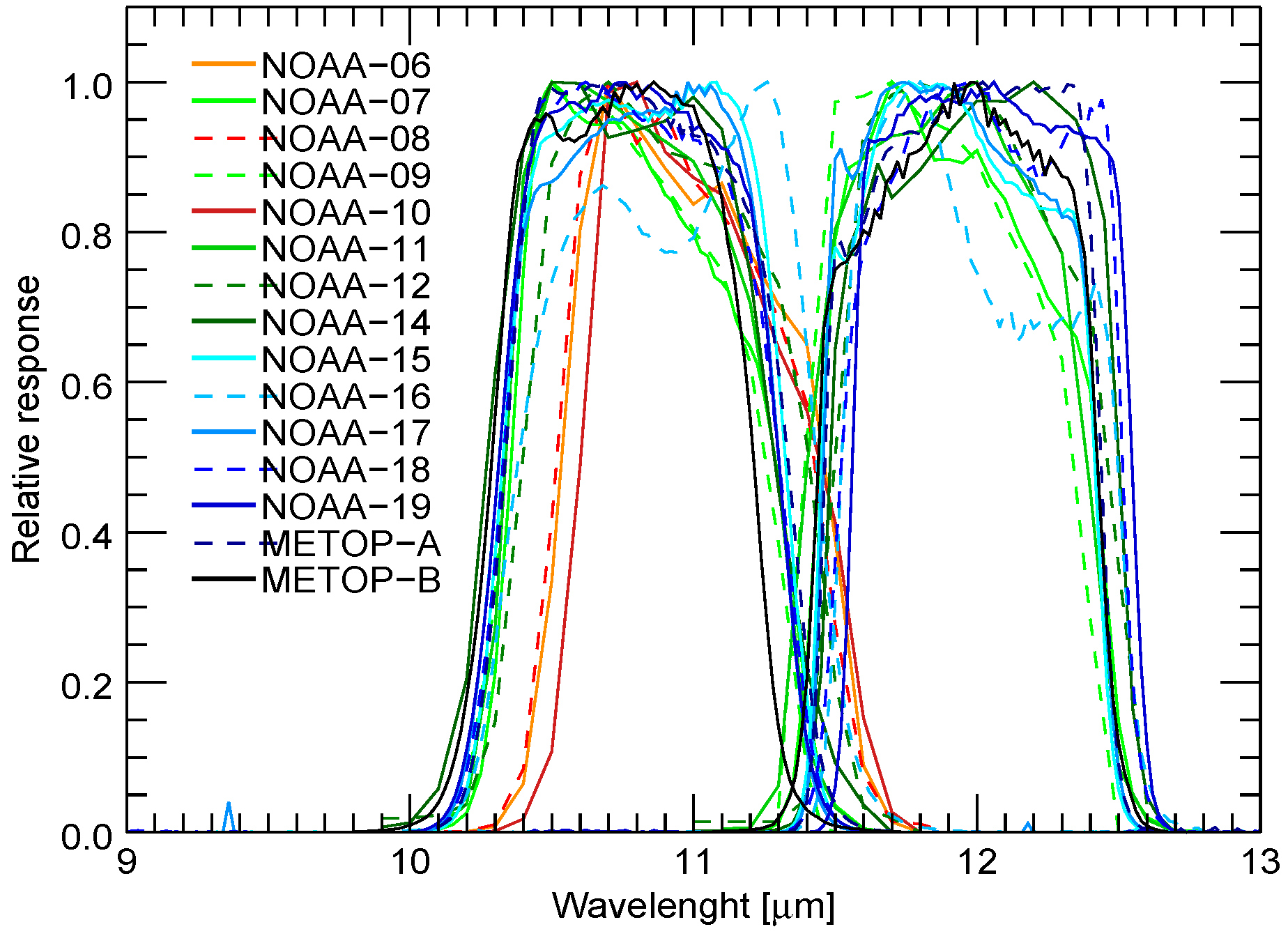
Although the different AVHRR sensors measure in the same bands, their spectral responses are not identical, as each sensor is a unique instrument, which is subject to some form of degradation. The degradation of a sensor and therewith possible overall changes in the spectral responses are accounted for by calibration. However, no information about possible changes in the spectral form is available after lunch [
27].
Figure 1 shows the spectral response curves of band 4 and band 5 of the different sensors. The response curves may differ substantially not only between the different models, but also within one model (especially AVHRR/3).
For the method development of this assessment, it was necessary to compile a dataset of atmospheric profiles. For this, a selection of a training database of global profiles (called SeeBor Version 5.0) was used [
28]. This database consists of 15.704 global profiles of temperature, moisture and ozone at 101 pressure levels—all for clear sky conditions. The profiles were all quality checked and a surface temperature was assigned to each profile based on a physically based scheme. The profiles of the database are compiled from five different existing databases (NOAA-88, ECMWF 60L training set, TIGR-3, ozone sondes from 8 NOAA Climate Monitoring and Diagnostics Laboratory sites, and radiosondes from 2004 in the Sahara Desert) [
28]. From this database a selection was made for this assessment, which ensured having profiles in all ranges of surface temperature and columnar water vapour (see
Table 2), as well as from as many land cover types (referring to the International Geosphere-Biosphere Programme (IGBP)) as possible. Due to the uneven distribution of land cover classes in the profile database, the number of profiles for each land cover class differs. A total of 2662 profiles were selected, featuring the following characteristics: 811 profiles are taken from TIGR-3, 317 profiles from Radiosondes, 479 profiles from Ozonesondes, and 1055 profiles are taken from ECMWF. The profiles were taken in a range of different land cover classes as defined in
Table 3.
Further, a land use classification [
29] was used to retrieve emissivity values for the application of the algorithm on real AVHRR data. The emissivity estimation was done using the Vegetation Cover Method (VCM) from [
30].
For the comparison with MODIS data, the MOD11A1 V6 Land Surface Temperature and Emissivity product (MOD11A1) was used. The data was retrieved from the USGS HTTP-Server [
26]. The MODIS data, as well as the AVHRR data, were projected to a common 1 km lat/lon grid. The MODIS LST product is already cloud screened. FOR AVHRR we used the APOLLO (AVHRR Processing scheme over cLouds, Land and Ocean) tests. APOLLO is an algorithm that was designed in the late 1980s and continuously improved and extended afterwards [
31,
32]. Additionally, a buffer was laid around all clouds, as some border pixels were not detected by the algorithm.
3. Methods
Ten mono- and split-window approaches were tested to their suitability of long-term processing of LST from AVHRR data.
Table 4 presents all the approaches tested and compared during this study. General to all algorithms is that new coefficients were generated for each of them. As such, only the approach was tested, but not the original published expression.
3.1. Coefficients Generation
The coefficients for the mono- and the split-window algorithms were all retrieved in the same manner. The first step consists of the selection of profiles from the SeeBor V5 database, as described
Section 2. MODTRAN 5.3 was then run using the selected profiles. Thereby, each profile was used multiple times with varying surface characteristics. First of all, the already existing LST values of each profile [
28] were tripled as [LST – 5 K, LST, LST + 5 K] to increase the simulated LST variability. Then, the sensor view angle was set to the values [0, 20, 40, 60], the mean band emissivity to values of [0.89, 0.92, 0.96, 0.99] and the difference of the band emissivities to [−0.02, −0.01, 0.00, 0.015]. MODTRAN 5.3 was run for each combination of these values and for each band. Resulting radiances were saved in a database. In a subsequent step, the radiances were convolved over the spectral response of each of the AVHRR sensors and converted to brightness temperatures using Planck’s radiation equation as described in the NOAA Polar Orbiter Data [
34] User’s Guide for AVHRR/1 and AVHRR/2 and NOAA KLM User’s Guide for AVHRR/3 [
35]. One half of the brightness temperatures were then used together with the associated input LST values for the coefficient estimation of the six split-window equations using least squares minimization. The other half was reserved for accuracy analysis.
The coefficient estimation was done for three different kinds of input cases, whenever possible:
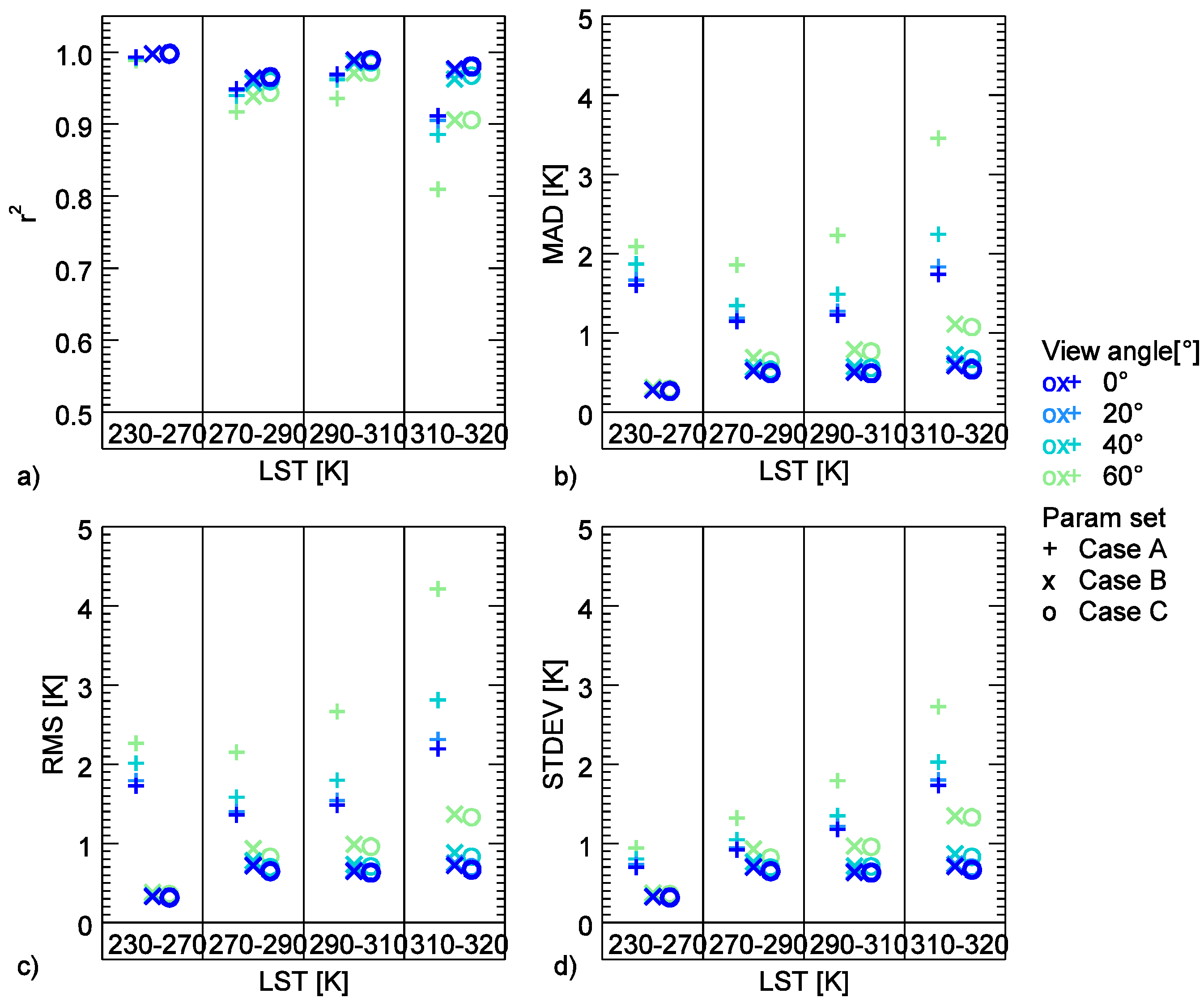
Case A: The coefficients were retrieved for each class of sensor view angle (VA).
Case B: The coefficients were retrieved for each class of sensor view angle, as well as for 8 ranges of columnar water vapor (VA/CWV).
Case C: The coefficients were retrieved for each class of sensor view angle, for 8 ranges of columnar water vapor and for 4 classes of surface temperature (VA/CWV/LST). Using the Jiménez-Muñoz and Sobrino 2008 algorithm and Qin et al., 2001 algorithm, the coefficients were retrieved for sensor view angle and surface temperature (VA/LST). The Yu et al., 2008 algorithm uses ranges of columnar water vapour and surface temperature only (CWV/LST). Case C has for each algorithm the maximal surface ranges necessary.
The hypotesis is that Case C will give the highest accuracies, while Case A shows the highest errors. Due to the large range of columnar water vapor and LST, not all possible combinations in Case C could be filled using the data from the selected profiles. In operational processing of LST therefore, also Case B and Case A might be of interest. Therefore Case A, B, and C were analysed.
According to [
3,
36], the temperature lapse rate influences the accuracy and precision of the split-window retrieval. They found, that the final accuracy decreases with increasing lapse rate and brightness temperature difference. As a consequence, the different set of coefficients were retrieved for daytime (LST − T
air > −2 K) and night-time (LST − T
air < 2 K) conditions, selecting only the appropriate profiles. As the conditions have an overlap of 4 K, the profiles also have a proper subset. It should be noted that the criteria for day and night discrimination are violated for example in case of advection of air masses. The discrimination between day and night conditions could have been expanded to the definition of different LST − T
air subranges. However, the present profile database does not provide enough samples to add this extra dimension. Additionally, accurate information about the skin temperature-T
air relation must be available before application of the algorithm to real data, which might be critial—especially for the past decades.
Figure 2 shows a schematic overview over the coefficient retrieval.
3.2. Performance and Sensitivity Assessment
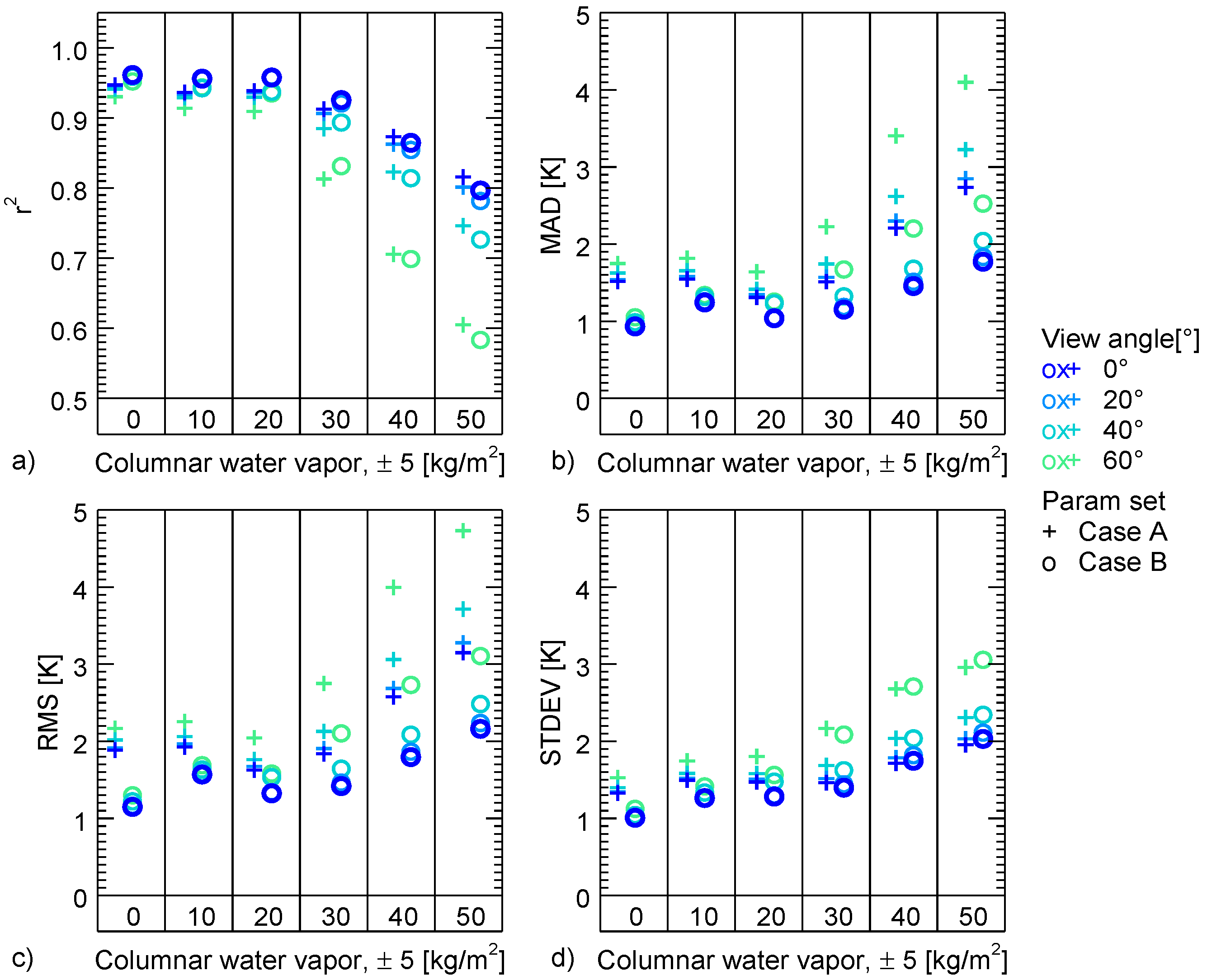
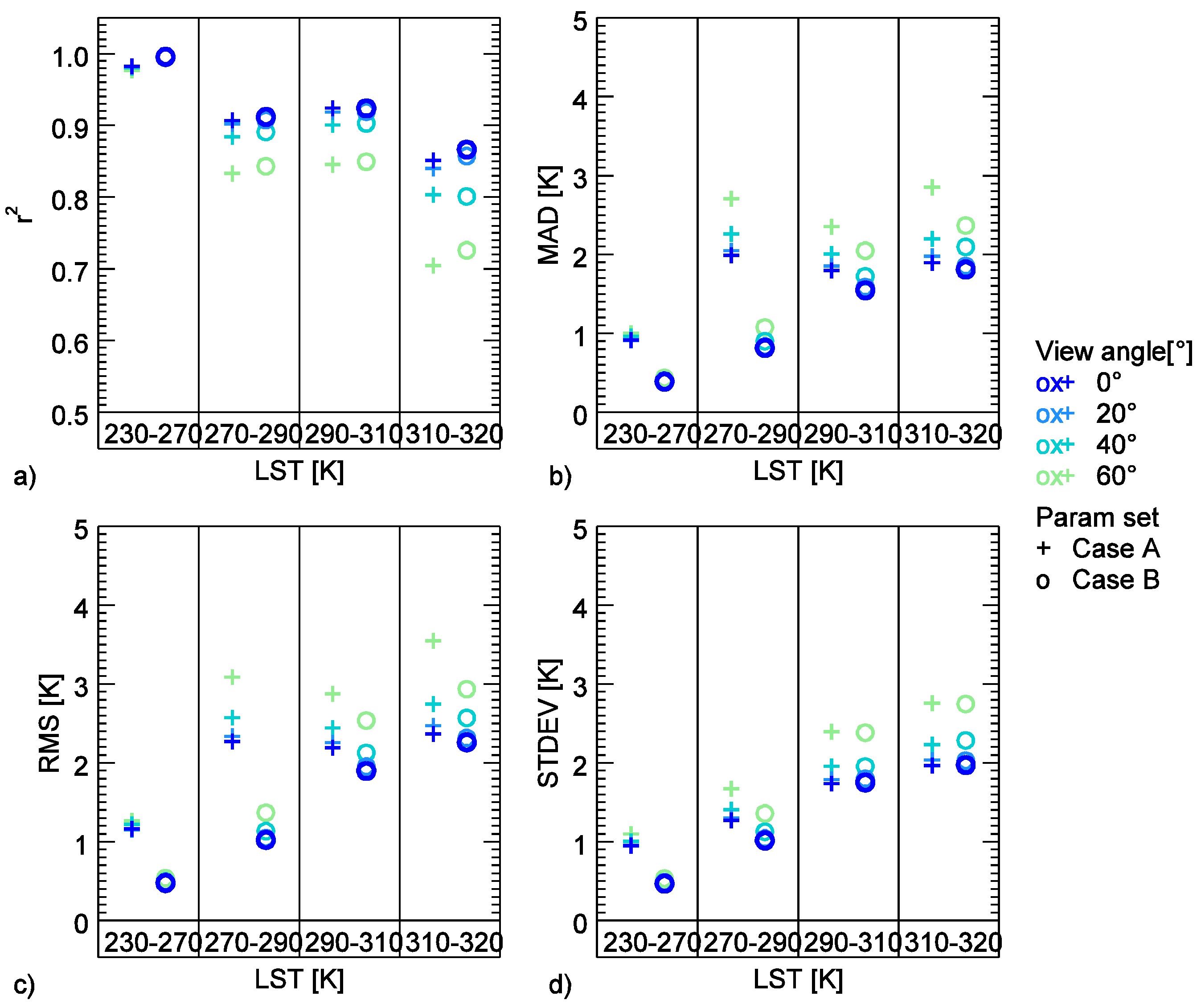
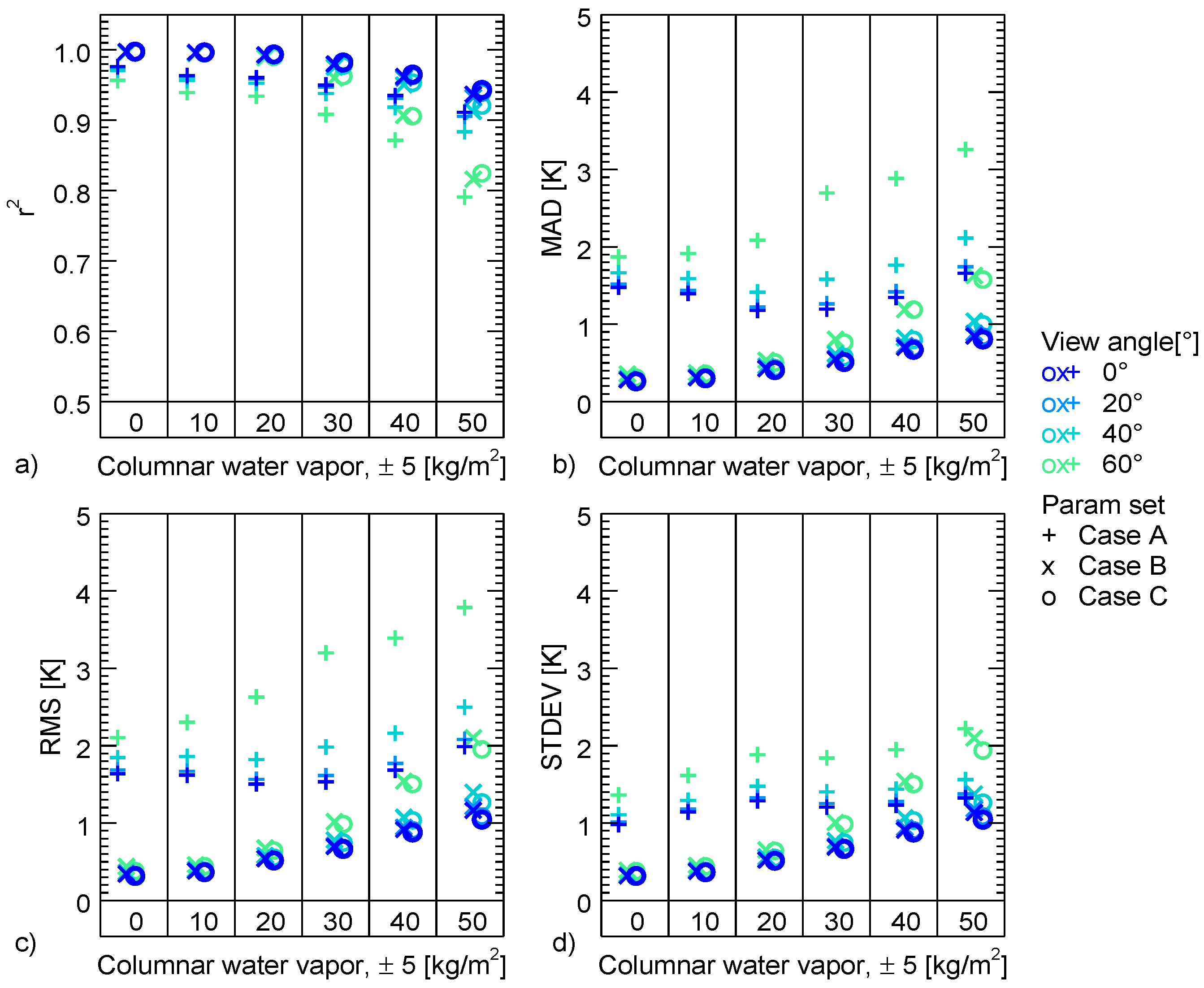
Performance, as expressed by accuracy and precision, was measured using the reserved second half of the modelled brightness temperature values from the coefficient retrieval. Thereby, for each profile and view angle, LST was calculated using the algorithms on the basis of the brightness temperature, and the atmospheric information from the profiles for parameter class selection (columnar water vapour and initial guess LST). Statistics was summarized for each class of view angle, initial guess LST, and columnar water vapour by comparing the initial LST and the output LST from the split-window algorithms. Such, the difference between the initial LST and the output LST from the split-window algorithms for each class was calculated. From these differences then statistical values were derived. The comparison was performed in form of mean absolute difference (MAD), root mean square (RMS), standard deviation (STDEV), and correlation coefficient (r2).
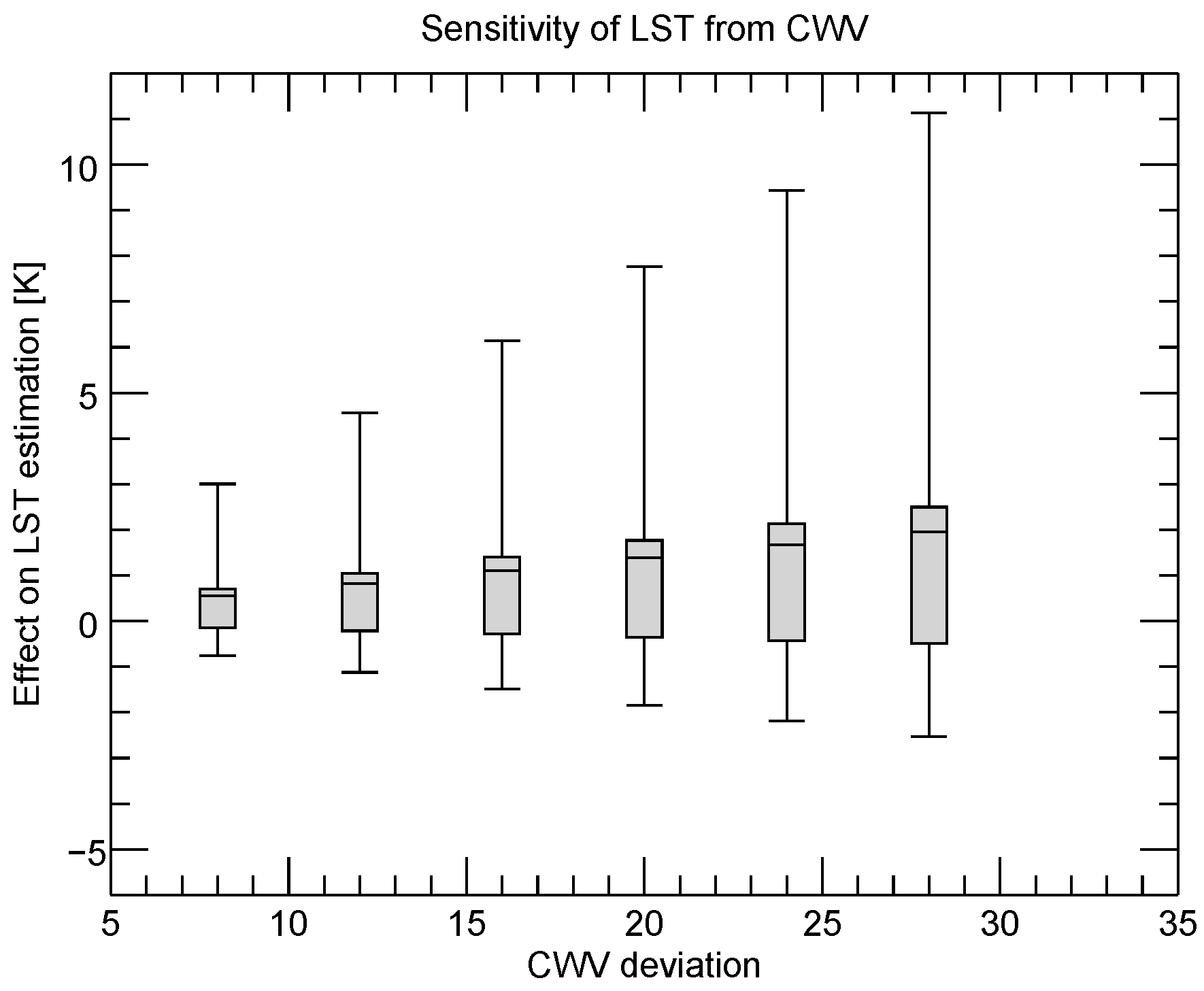
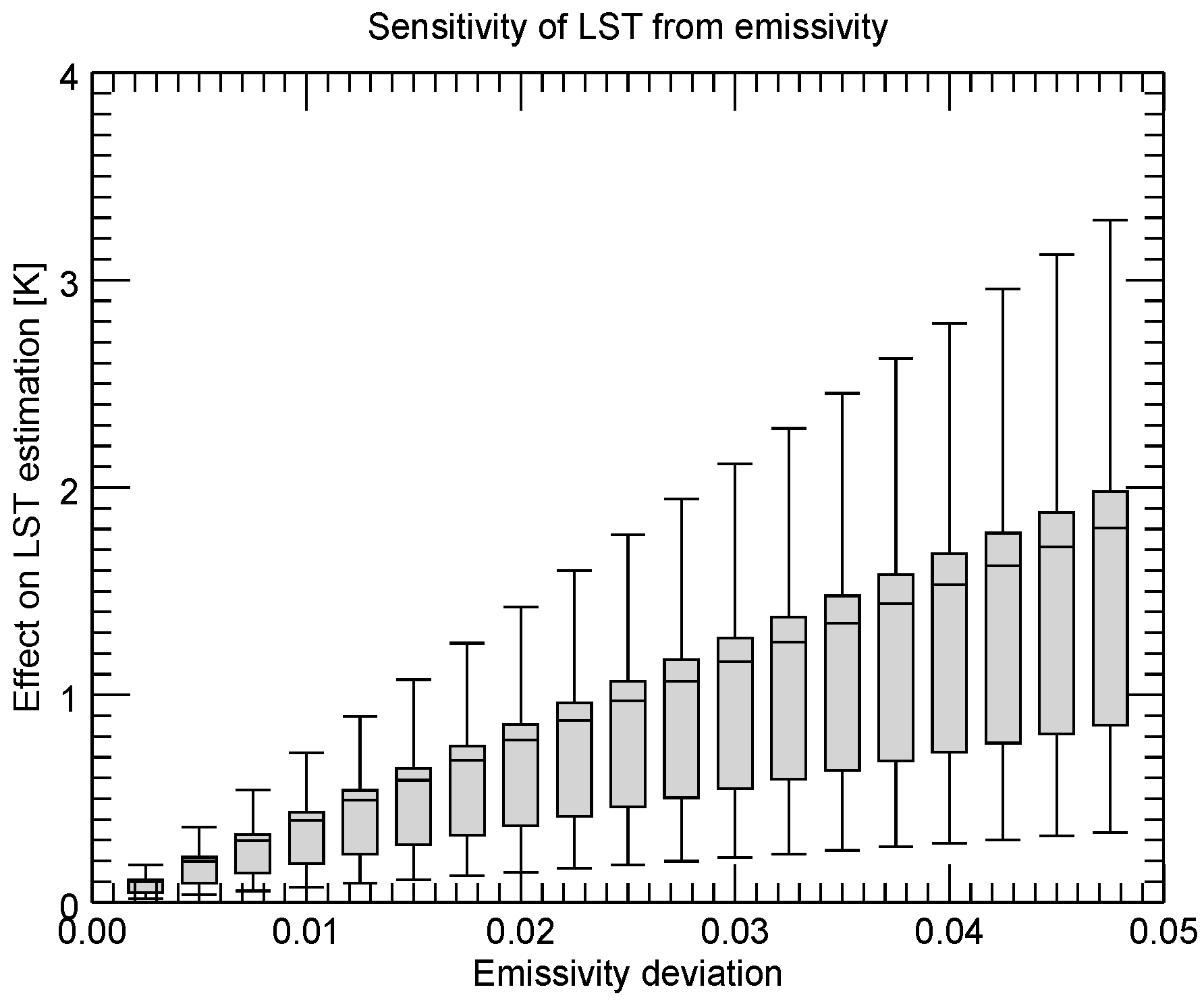
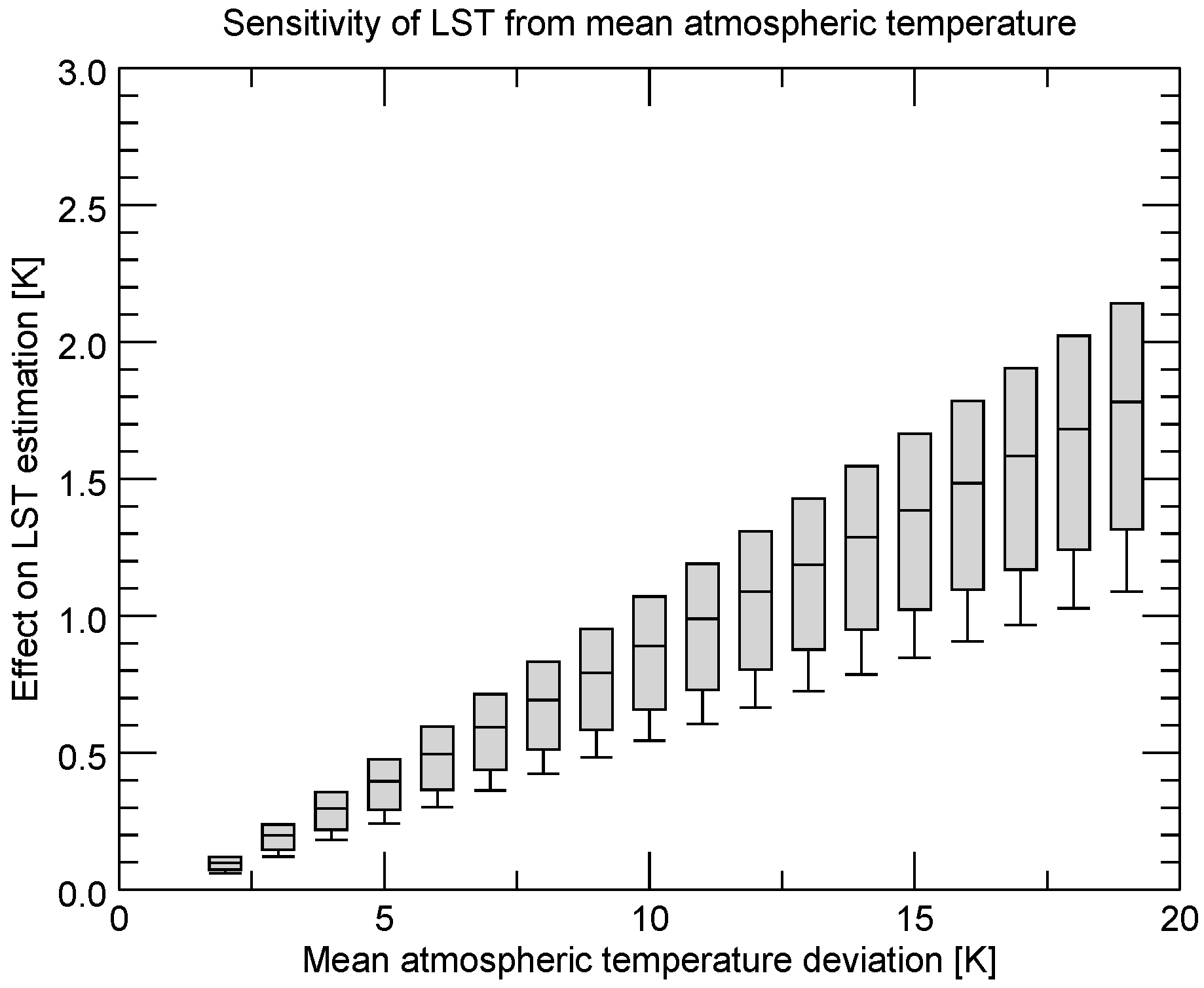
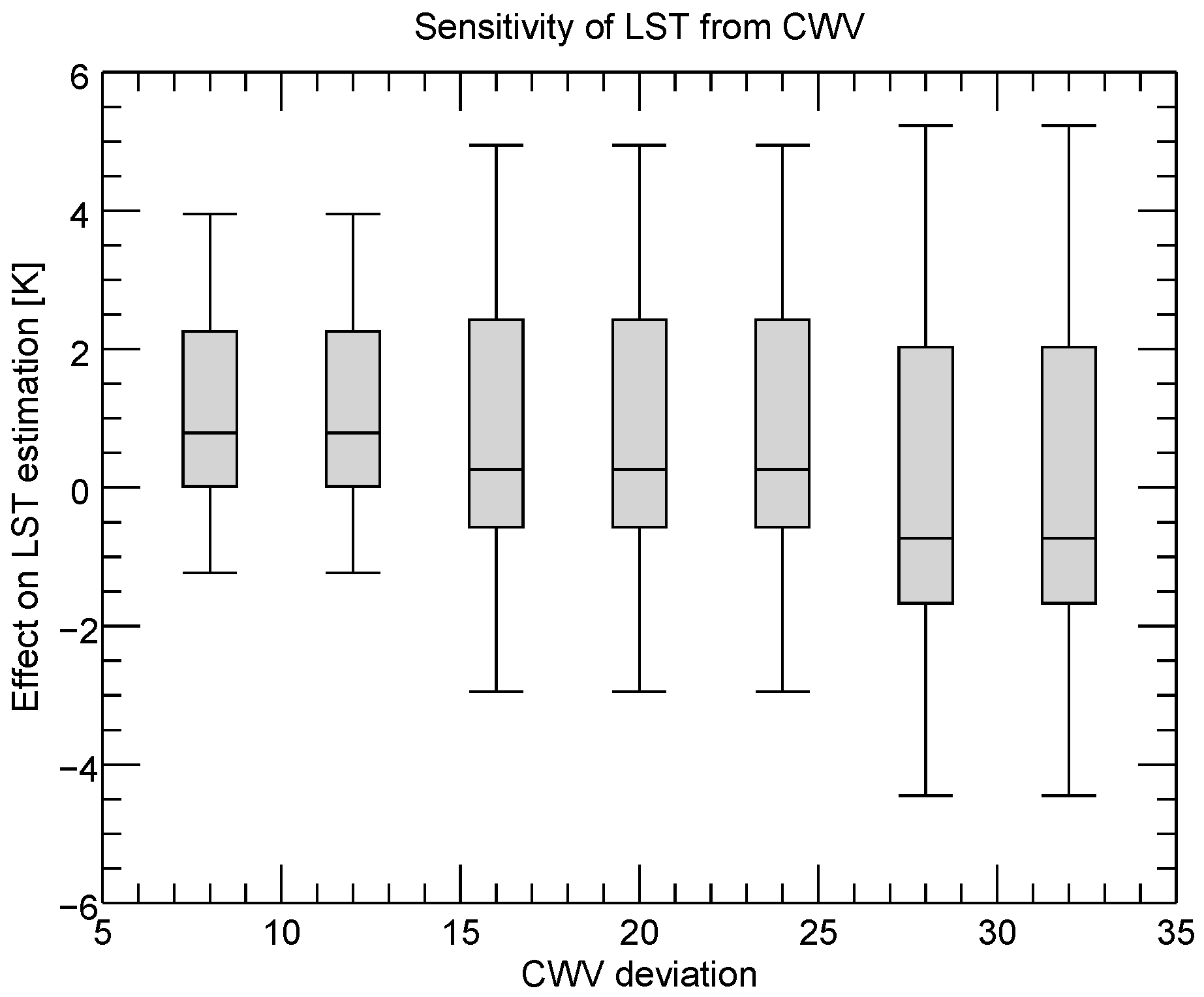
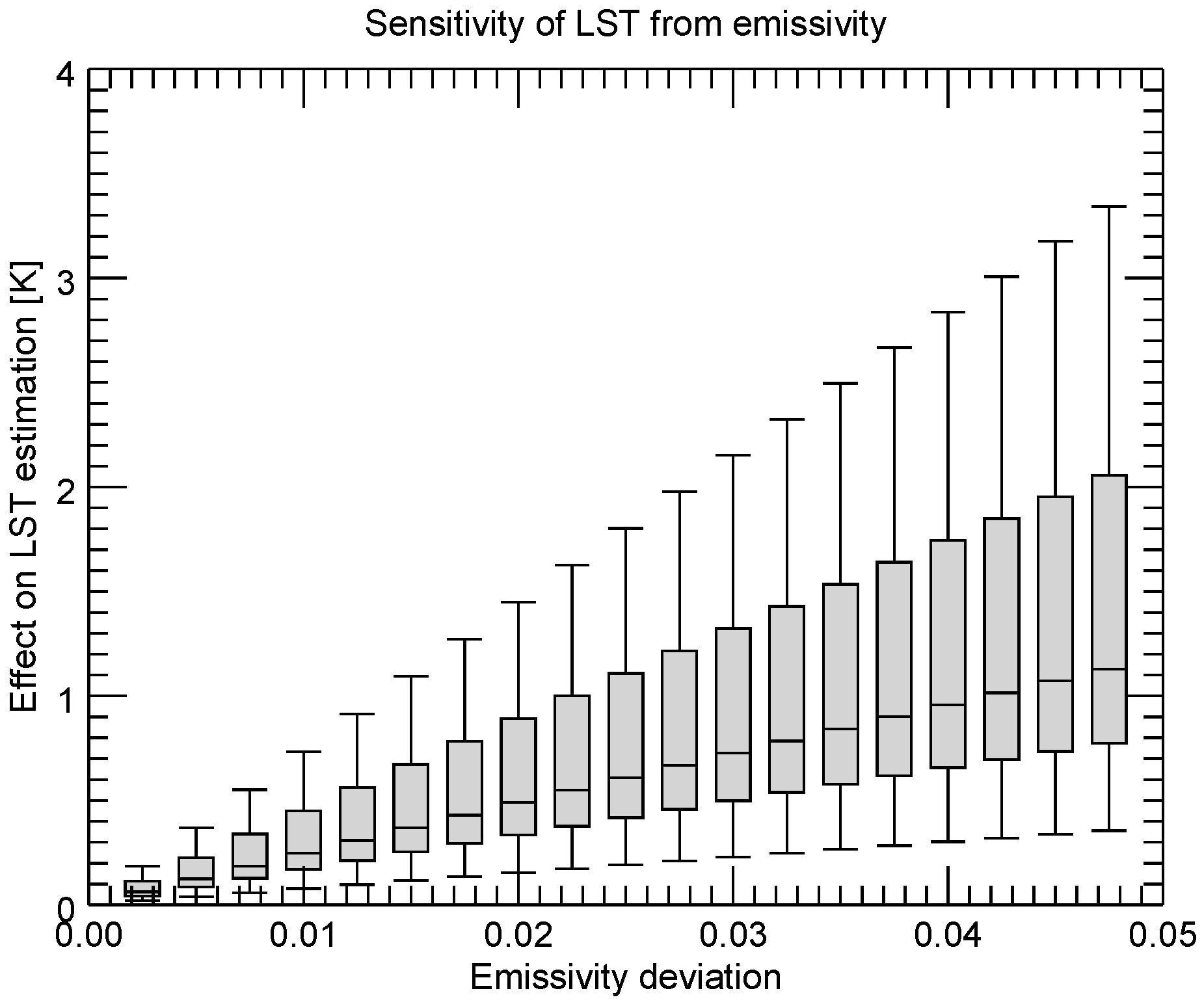
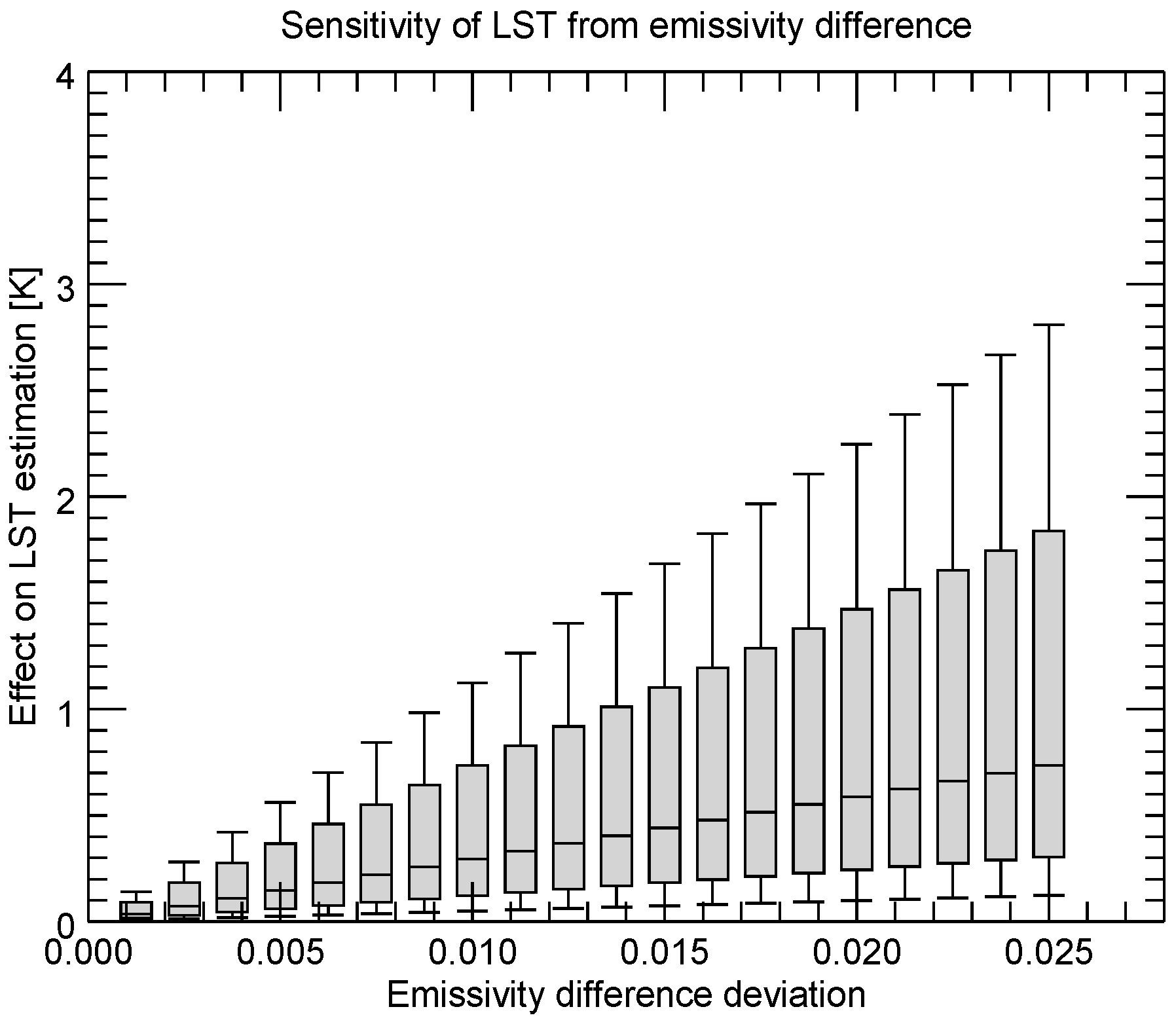
The sensitivity analysis was undertaken by artificially altering the input parameters columnar water vapour, initial guess LST, mean band emissivity, and difference of band emissivity. In case of the columnar water vapour and the initial guess LST, the wrong input values affect the choice of the parameter class and led therefore to a lower accuracy of LST. In case of wrong mean emissivity and wrong differences of band emissivity, the correct parameter classes are chosen, but the algorithm does not foresee such wrong values and therefore renders incorrect LST values. The magnitude of the over- or underestimation of LST is expressed in boxplot figures. Furthermore, total sensitivity is given for each algorithm.
3.3. Emissivity Estimation
To estimate LST using mono- or split-window algorithms, emissivity must be known a priori. For the comparison with MODIS data, the emissivity was estimated using the
Vegetation cover method (VCM) from [
30]. The VCM method was proposed for AATSR data. Due to the spectral similarity of the thermal bands of AVHRR and AATSR, the method could be employed for this study.
with
k = 4, 5 is the emissivity of band 4 resp. 5,
is the emissivity of vegetation,
is the emissivity of the ground below the vegetation,
is the maximum cavity term, and FVC is the fractional vegetation cover. The coefficients
,
and
are dependent on land surface cover and the spectral band. Additionally, to the estimation of band emissivity, the method of [
30] offers the possibility to estimate the related uncertainty of the emissivity. It should be noted that this expression does not account for the anisotropy of emissivity. As pointed out by [
37] on the example of inorganic soils, this can lead to systematic errors in LST ranging between 0.4 K and 1.3 K for dry atmospheres.
5. Comparison with MODIS Data
To check the validity of the approach, AVHRR LST calculated with the Becker and Li 1990 algorithm combined with the Vegetation Cover Method (VCM) from [
30] was compared with the MODIS V005 LST product (MOD11A1/MYD11A1) and the results of using the original Becker and Li 1990 coefficients and the NDVI approach of [
40]. The comparison was done for the year 2001 and NOAA-16. For the calculation of the new AVHRR LST, preferably Case C (consideration of ranges for view angle, columnar water vapour and first guess LST) coefficients were used. In case where no coefficients were available due to missing coefficients in the database, case B or even case A might have been used. This could happen in rare extreme situations (e.g., very cold and humid), where the database would not provide enough profiles to calculate coefficients. The direct application of the coefficients provided for discrete ranges leads to discontinuities in the resulting LST images. To counteract this, actual LST values are weighted means from different parameter classes using trilinear interpolation.
For the comparison, the data was filtered in several ways. Firstly, all pixels which were marked as cloud cover in either the AVHRR or the MODIS product were removed. Second, each cloud-free pixel was checked for its spatial homogeneity. If the standard deviation in a window of 3 × 3 pixels would exceed 0.5 K, the middle pixel would be removed. This resulted in a 55% reduction of the data. This filtering was necessary to reduce noise effects due to inaccurate geometric alignment. The view angle difference between AVHRR and MODIS was allowed to be maximal 20°; the difference between acquisition times was set to maximal 10 min. The minimum number of pixel per tile was set to 50. Statistical measures were then calculated for different geographical subsets as defined by the MODIS tiles. Such, overall MAD between these filtered AVHRR and MODIS is 1.8 K, overall standard deviation is 1.4 K. Using the same collection of pixels, the MAD between AVHRR and MODIS using the original approach [
40] is 3.3 K.
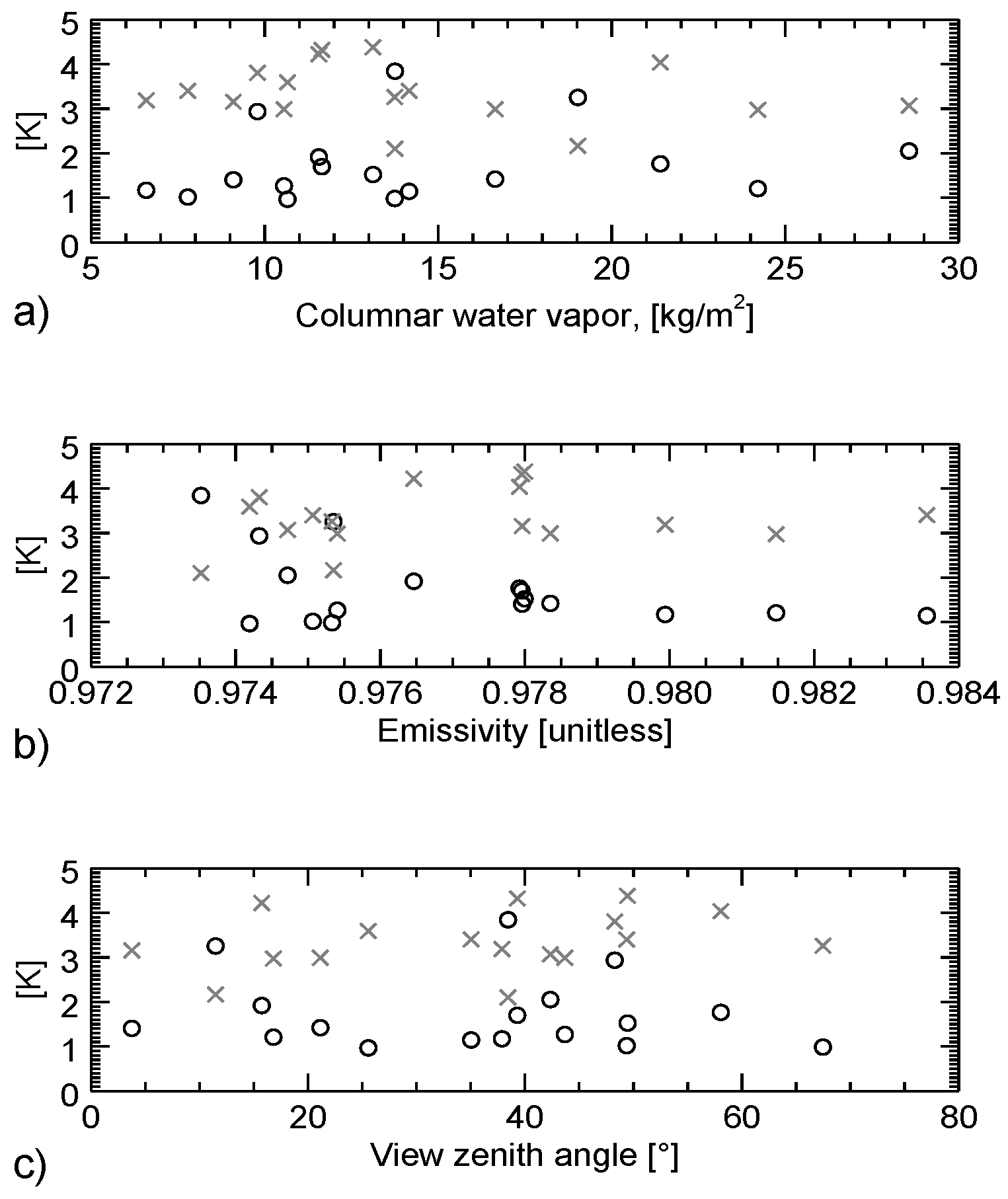
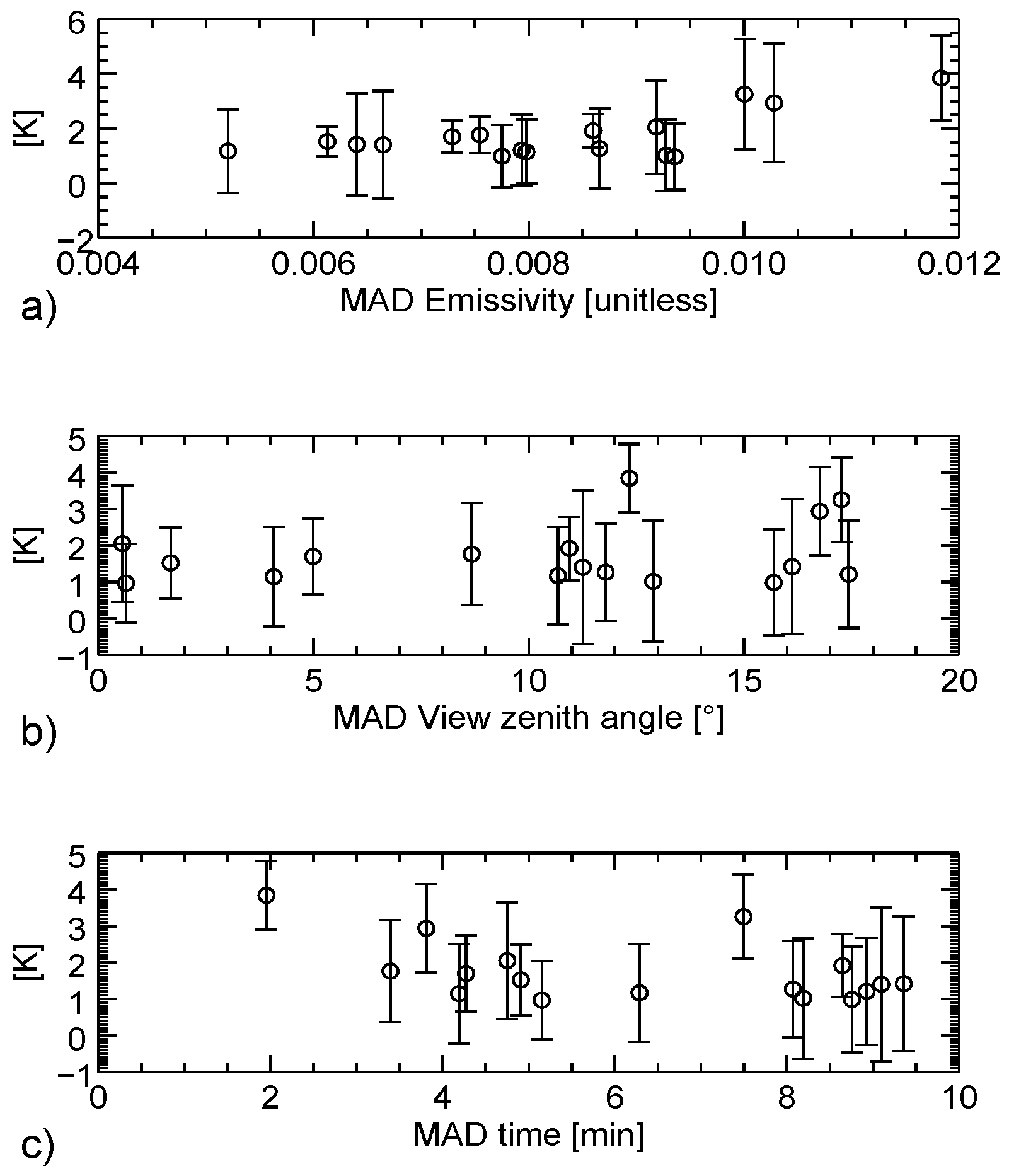
Figure 17 shows the MAD per MODIS tile and date in relation to mean total column water vapour, mean emissivity, and mean zenith view angle. The MAD values are given for the original (grey) and the newly calculated (black) coefficients. The figures do not reveal a relation between the MAD magnitudes with any of the other variables; the error seems to be distributed randomly.
Figure 18 shows the same MADs as in
Figure 17, but this time in relation to the difference of mean emissivities, mean absolute zenith angle and time difference, each between AVHRR and MODIS. To each MAD value its associated standard deviation is plotted. The MAD increase slightly with increasing MADs of emissivity and view zenith angle. Time differences (acquisition times around noon) hardly show an influence.
Table 6 shows more statistical values in tabular form together with the number of available pixels per tile. In 13 out of 17 tiles, the MAD is below 2 K. In many cases, the AVHRR LST shows negative offset compared to the MODIS LST resulting in negative mean differences. It should be noted that the magnitude of the dataset should be enlarged for a more thorough validation. Nevertheless, the statistical values of this chapter may serve as indication of the validity the LST approach. Unfortunately, the data is, despite of application of the cloud masks and an additional cloud border buffer, not fully cleared of cloud contaminated pixels, which leads to higher MADs in some cases (e.g., Tile Nr. 16 in
Table 6—data not shown).
6. Discussion
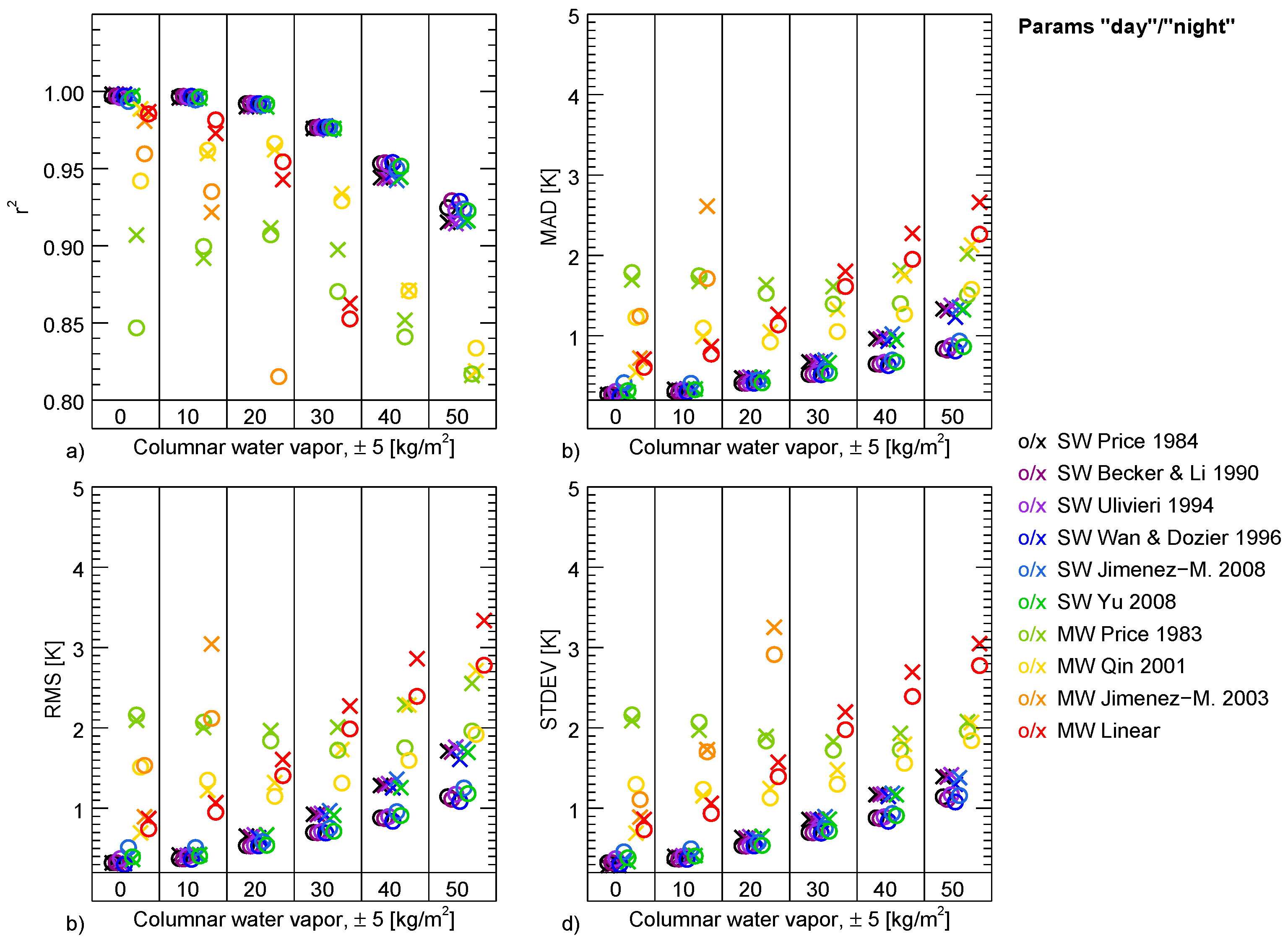
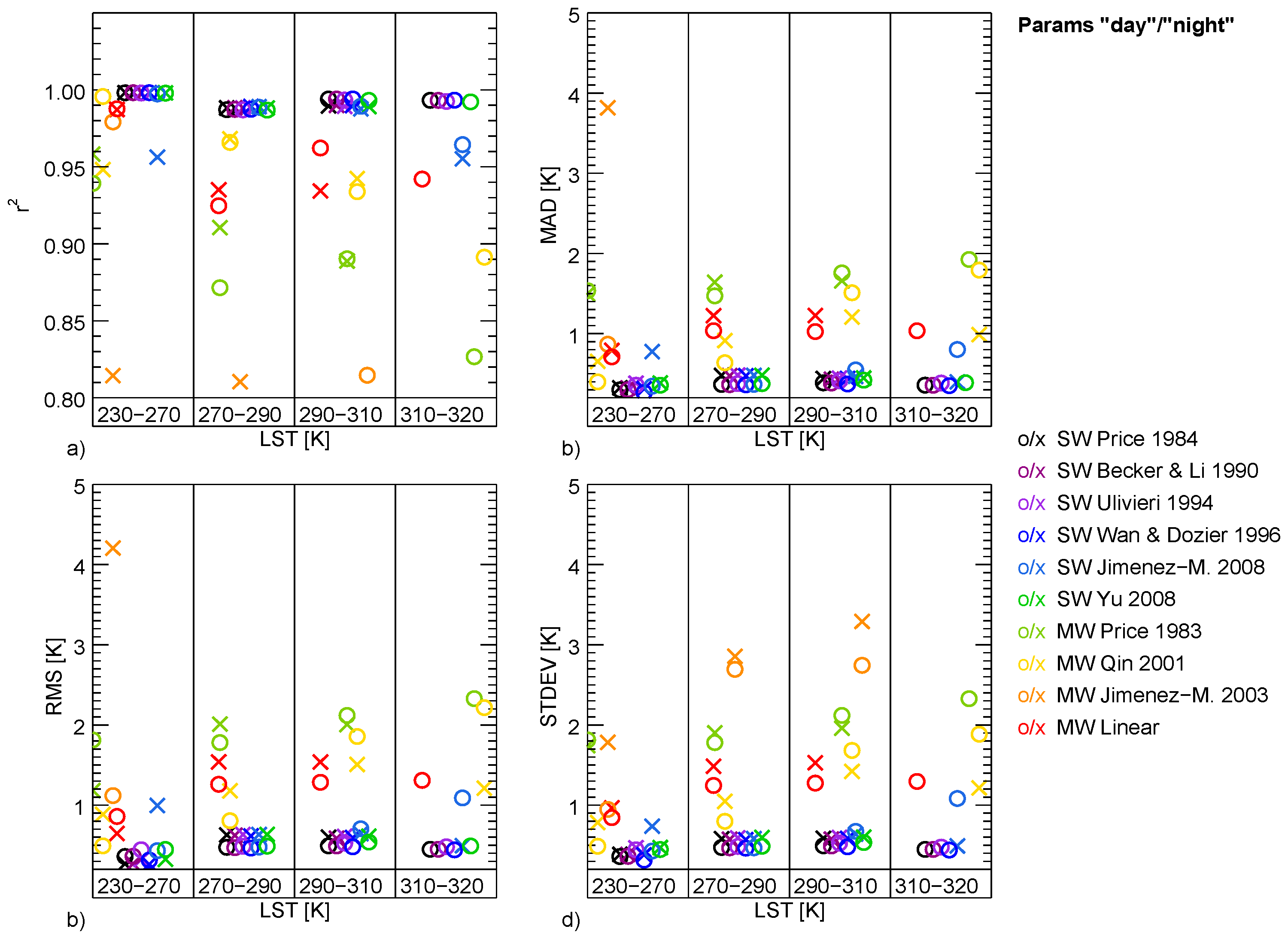
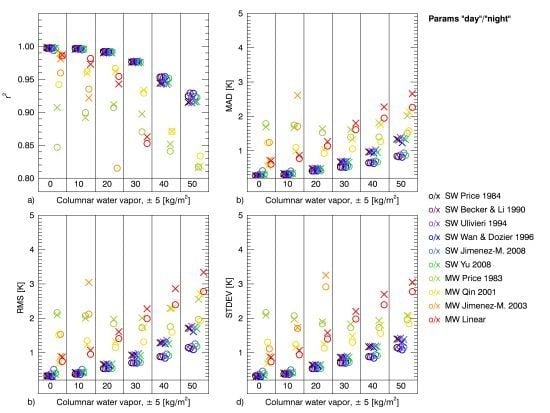
In this work, four mono-window and six split-window algorithms were analysed in terms of their suitability for long time series processing of AVHRR data. To make the algorithms comparable, new coefficients were calculated for all algorithms in the same simulated data framework. It was found that the performance of the split-window algorithms were very similar in all cases. The MAD stays below 0.4 K in non-humid atmospheres. From the analysis of performance all six split-window algorithms could be recommended. The performance of the mono-window algorithms differed considerably amongst the algorithms. The Qin et al. 2001 and the linear method thereby showed the best performance, while the Price 1983 and the Jiménez-Muñoz and Sobrino 2003 algorithm performed less accurate. Due to its best performance, the Qin et al. 2001 algorithm is suggested for long time series processing aiming at climate relevant trends.
Even though the coefficients were calculated for different ranges of columnar water vapour, the accuracy of the algorithms decreases with increasing columnar water vapour. Nevertheless, it is suggested to use humidity dependent coefficients, as the error rises especially in less humid atmospheres in case of coefficients that do not consider humidity dependent ranges (case A). The additional splitting of the coefficients to separate temperature ranges improved the accuracy mainly in very humid conditions. In such cases, the splitting might lower the MAD a few tenth degree. In less-humid conditions, the splitting did not improve the accuracy. The sensor view angle is considered in all cases (A, B, and C), nevertheless, accuracy is still lower in case of higher view angles. As such, view angle, humidity, and first guess LST could serve as proxy for the data quality.
Due to differing spectral response curves, it was assumed that the stability of a long time series of LST from AVHRR data would suffer in case of nonconsideration of the different sensors characteristics. It was shown that the neglecting of the influence of the spectral response curves would produce maximum differences ranging from 0.19 K to 0.71 K in case of the split-window algorithms. Maximum differences ranging from 0.10 K to 1.8 K (36.7 K for Jiménez-Muñoz and Sobrino 2003) in case of the mono-window algorithms would occur. Even if neglecting the case of Jiménez-Muñoz and Sobrino 2003, the numbers suggest using sensor dependent coefficients, as significant additional noise would be introduced to a long time series in case of nonconsideration.
For the processing of long time series data not only the performance of an algorithm is important, but also its sensitivity to its input data. The uncertainty inherent to all input data is an additional source of noise, lowering the overall accuracy of a final LST product. As the availability of input data is non ideal and even poor in case of the early years when AVHRR was flown, algorithms with lower sensitivity to their input data are to be preferred to algorithms with a high sensitivity. It is not always straightforward to know about the associated error in an input dataset. However, some studies might indicate about the magnitude of the error of a certain variable. Ref. [
41] for example compared three land surface broadband emissivity datasets. They found land cover dependent differences and RMSEs between 0.009 and 0.011. If just the error in band emissivity as input to the Qin et al., 2001 or the Becker and Li 1990 would be comparable to the findings of this study, this lead to errors between 0.1 and 0.8 K. Relating this to the GCOS requirement of accuracy better than 1 K [
23], it becomes clear that errors in surface emissivity may substantially lower the quality of a product.
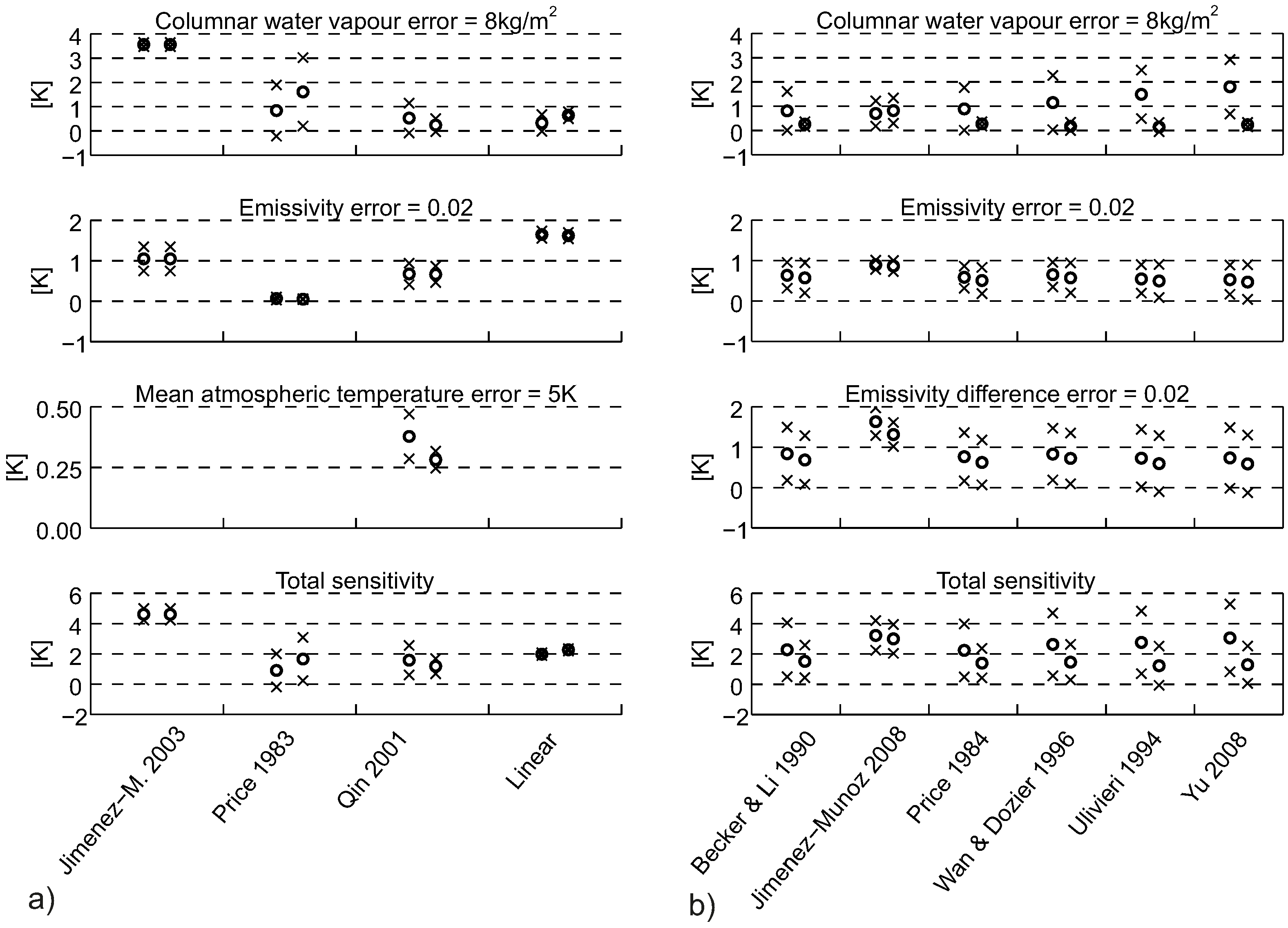
This study has shown that the different sensitivities amongst the split-window algorithms are more similar than the sensitivities of the different mono-window algorithms. In the presented case of
Figure 15 lowest sensitivity is found for the Becker and Li 1990 and the Price 1984 algorithms with a total mean sensitivity of 1.9 K for daytime and nighttime conditions. Highest total sensitivity is found for the Jiménez-Muñoz and Sobrino 2008 algorithm with 3.1 K for same conditions. Lowest sensitivity of the mono-window algorithms is found for the Price 1983 and the Qin et al., 2001 algorithms with a total mean sensitivity of 1.3 K for daytime and nighttime conditions. Highest total sensitivity is found for the Jiménez-Muñoz and Sobrino 2003 algorithm with a total sensitivity of 4.6 K for same conditions. Against the background of long time series and the situation of imperfect input data, the Becker and Li 1990 and the Price 1984 split-window algorithms and the Price 1983 and the Qin et al., 2001 algorithms are best suited for.
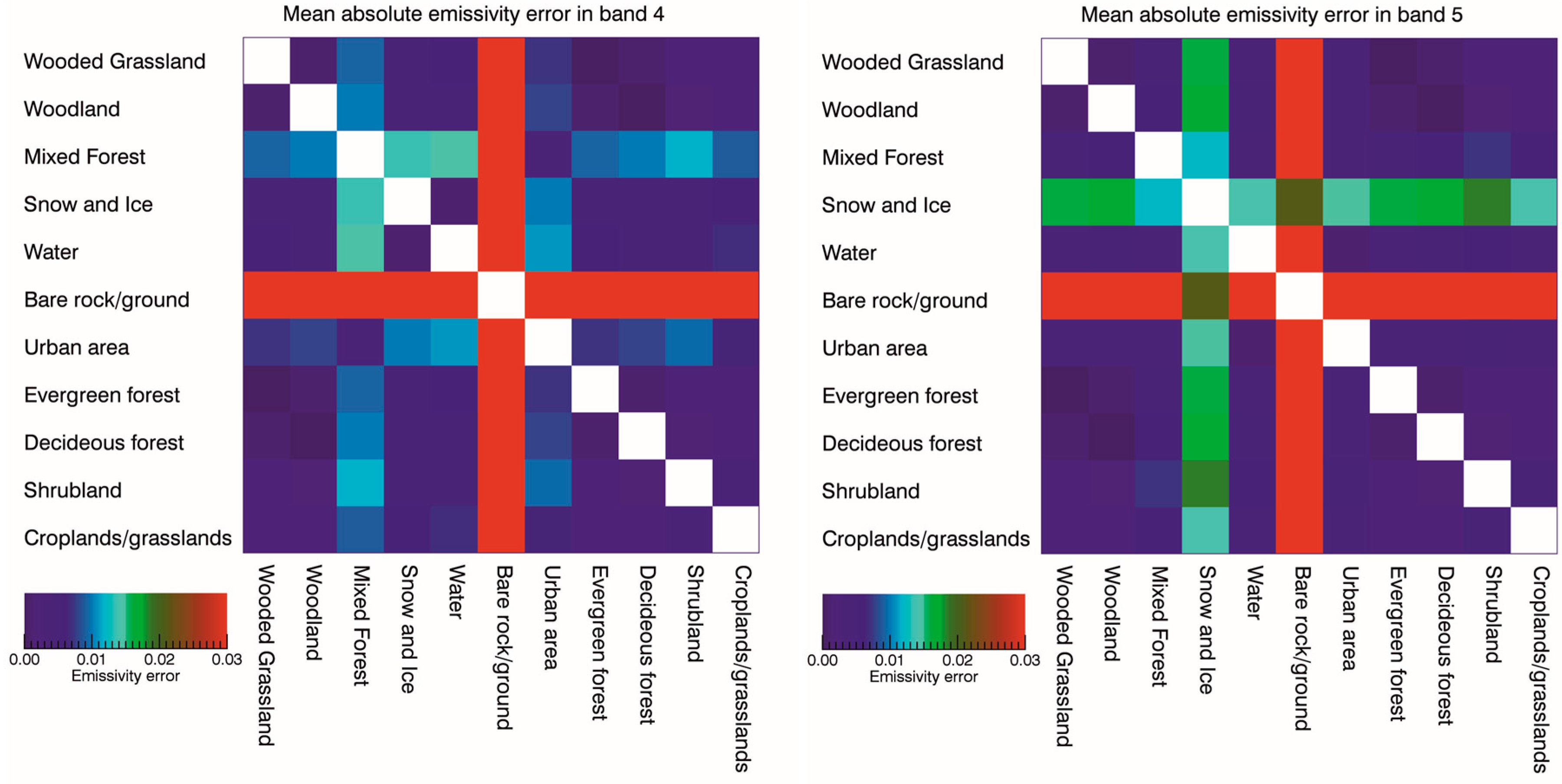
The simulation of the impact of misclassification errors to estimated LST showed that mainly misclassification of bare rock and ground has a significant impact, as well as the class snow and ice in case of band 5. Any misclassification from one to another vegetation class resulted in emissivity errors of less than 0.01, which would result in LST errors of generally less than 0.3 K. To avoid large errors in LST due to misclassification it is suggested to perform an additional check for pixels, which are assigned to the classes bare rock/ground and snow based on classification maps or other procedures.
Regarding the selection of suitable algorithms for time series processing, the synopsis of the performance and the sensitivity analysis following algorithm we suggest: For the mono-window algorithm the Qin et al., 2001 is preferred due to its good performance and low sensitivity results. For the split-window algorithm the Becker and Li 1990 and the Price 1984 algorithm can be suggested showing also good performance and low sensitivity values.
A first comparison with MODIS data using the Becker and Li 1990 approach combined with the Vegetation Cover Method (VCM) from [
30] showed despite of some cloud contaminated pixels a good agreement with an overall MAD between AVHRR and MODIS of 1.8 K [K], and an overall standard deviation of 1.4 [K]. This showed a clear improvement over the original AVHRR LST approach assessed in [
40], which had an overall MAD of 3.3 K.
The processing has been performed by a preference of coefficients of case C (consideration of ranges for view angle, columnar water vapour and first guess LST). In case where no coefficients were available due to missing coefficients in the database, case B or even case A might have been used. This could happen in extreme situations (e.g., very cold and humid), where the database would not provide enough profiles to calculate coefficients. A selection of pixels, where case C is applied only, might improve further the comparison.
Besides the selection of suitable algorithms, the quantitative results are relevant for the assessment of global warming. The IPCC report from 2014 [
42] concludes an average global surface warming of 0.85 K over the period 1880 to 2012, while the period from 1983 to 2012 was likely to be the warmest period of the last 1400 years in the Northern Hemisphere. Warming per decade varied from almost 0 K to more than 0.2 K since 1951. The assessment of performance and sensitivity of AVHRR LST shows that LST derived from AVHRR is feasible under certain conditions only as input to global warming studies. Firstly, the chosen algorithm should be applied using coefficients considering at least various levels of columnar water vapour and view angles. Performance differences between using coefficient set Case A (only view angle considered) and Case C (view angle, total columnar water vapour, and first guess LST considered) could exceed 1 K in case of the Becker and Li 1990 algorithm—which is a multiple of the before mentioned warming per decade. Second, the algorithms should generally show good performance and low sensitivity, as presented in this study. Maximum differences between algorithms in presented total sensitivity was found to be 3.7 K for the mono-window algorithms and 1.6 K for the split-window algorithms. The general level of presented total sensitivities (except Jiménez-Muñoz and Sobrino 2003) of about 2 K is not representative of general LST retrieval, but still points, third, to the importance of the quality of the input data to the LST algorithms. Forth, only LST values carrying a low uncertainty can be used—this would exclude surfaces under very humid atmospheres or surfaces acquired by a large sensor view angle. The performance of even the best ranking algorithms in this study approaches 1 K (RMSD) in case of very humid atmospheres—in case of large view angles even 2 K.
Besides the considerations on performance and sensitivity, data from the AVHRR instruments are influenced by several other factors which complicate direct use of the data [
40]. The orbital drift and the differentiation of the NOAA satellites into morning and afternoon passes for example lead to different acquisition times over the lifespan of a single sensor and the whole AVHRR time series. It follows that AVHRR LST data cannot be directly be used for climate change studies, but should be further processed to match temporal requirements of such analyses. AVHRR LST further forms valuable input as an additional source of information to studies using a multitude of sensors.
7. Conclusions
LST can be retrieved with increasing accuracy and precision, making it a suitable candidate for regional and global assessments of climate variability and change. There are attempts to use LST as a substitute for surface air temperature in areas where in situ measurements are scarce, however, it can also be used directly for change studies. AVHRR has been flown since the early 80ies on a series of platforms. The resulting long time series—35 years—is unique. Although there are some constraints to the direct use of the data (e.g., orbital drift), the resulting time series can be used to generate additional value by extending existing time series of newer sensors with AVHRR back in time or fill gaps of these time series in areas where cloud cover is predominant. As such, AVHRR LST plays an important part in improving climatological databases.
As the number of bands of the AVHRR instrument was not consistent, AVHRR/1 had only one band in the thermal domain, whereas AHVRR/2 and /3 have 2 bands, four different mono-window algorithms and six different split-window algorithms were assessed. For the comparison, new coefficients were generated in the form of a small look up table, accounting for different ranges of columnar water vapour, emissivity, emissivity difference (AVHRR/2 and /3 only) and first guess LST. Such sensor—specific parameters prevent producing artificial anomalies or wrong trends in the data, when processing long time series from AVHRR. For the generation of the coefficients, a radiative transfer model (MODTRAN V5) was used to model top-of-atmosphere brightness temperatures to given LST and the previously mentioned ranges. The least squares method was then used to generate the coefficients and corresponding statistical measures from the database. The statistical measures were used for the performance assessment of the different algorithms. Further, the sensitivity of the single algorithms to their input data was assessed, by simulating ranges of input values. The synopsis of the performance, as expressed by accuracy and precision measures, and sensitivity analysis revealed that the Qin et al., 2001 algorithm is to be preferred amongst the mono-window algorithms due to its good performance and low sensitivity results. Amongst the split-window algorithms the Becker and Li 1990 and the Price 1984 algorithm can be suggested, as both show good performance and low sensitivity values.
A comparison of the application of the Becker and Li 1990 coefficients and the Vegetation Cover Method (VCM) [
30] to AVHRR with the MODIS LST product revealed a good agreement and confirmed the approach to be valid and physically sound.