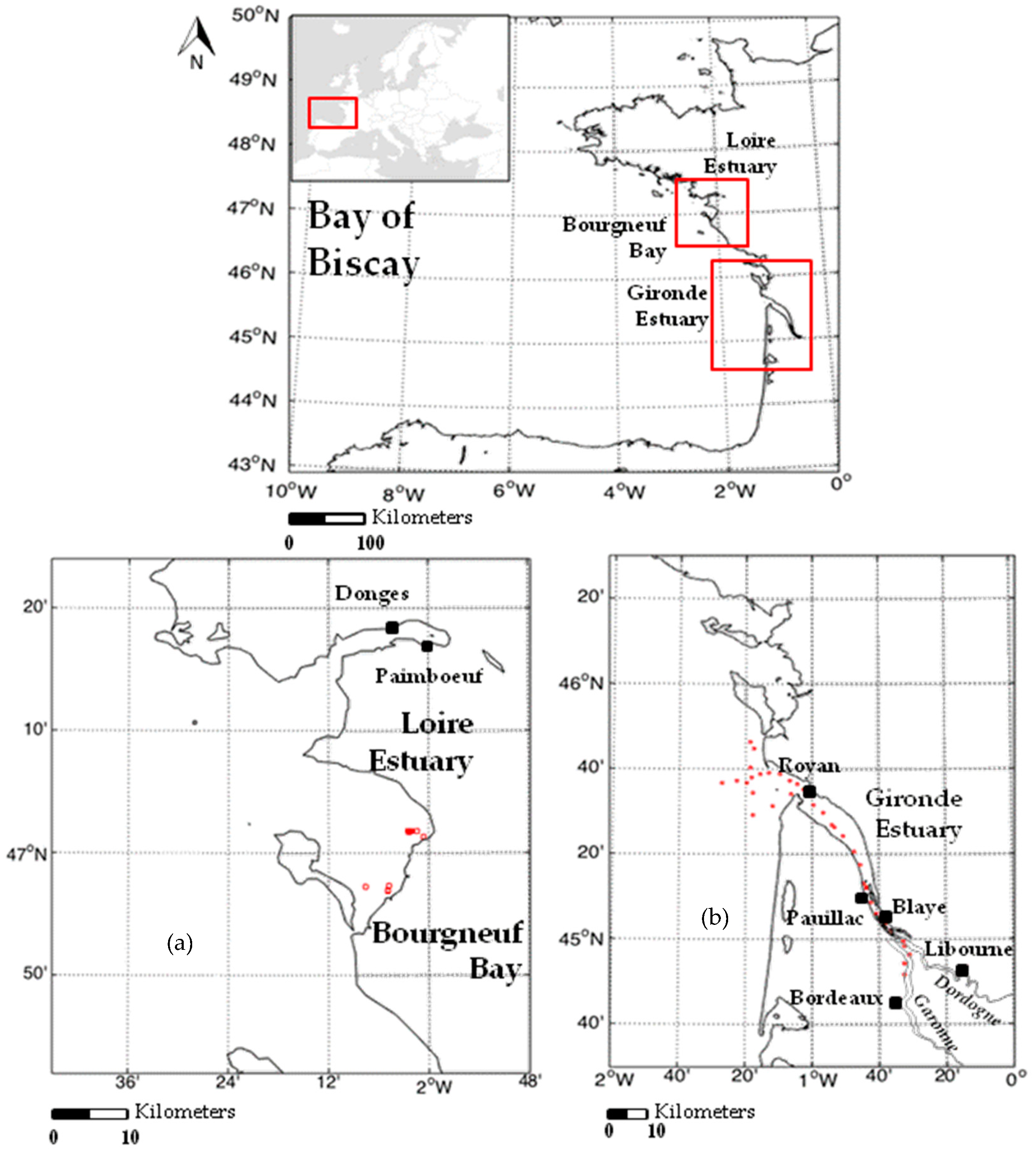
3.1. Atmospheric Corrections
In this section, the ACOLITE NIR and SWIR atmospheric corrections applied to OLI data with fixed scene epsilons are compared. A detailed explanation of these atmospheric corrections can be found in [
19,
51,
57]. Results from ACOLITE are then compared to the MACCS atmospherically corrected products provided by the Theia Data Center. Finally, a comparison is made between OLI and VIIRS water reflectance. This comparison was not conducted for MODIS products as previous studies [
19] have already shown a satisfactory correspondence between the OLI and MODIS Aqua atmospheric corrections in turbid coastal waters.
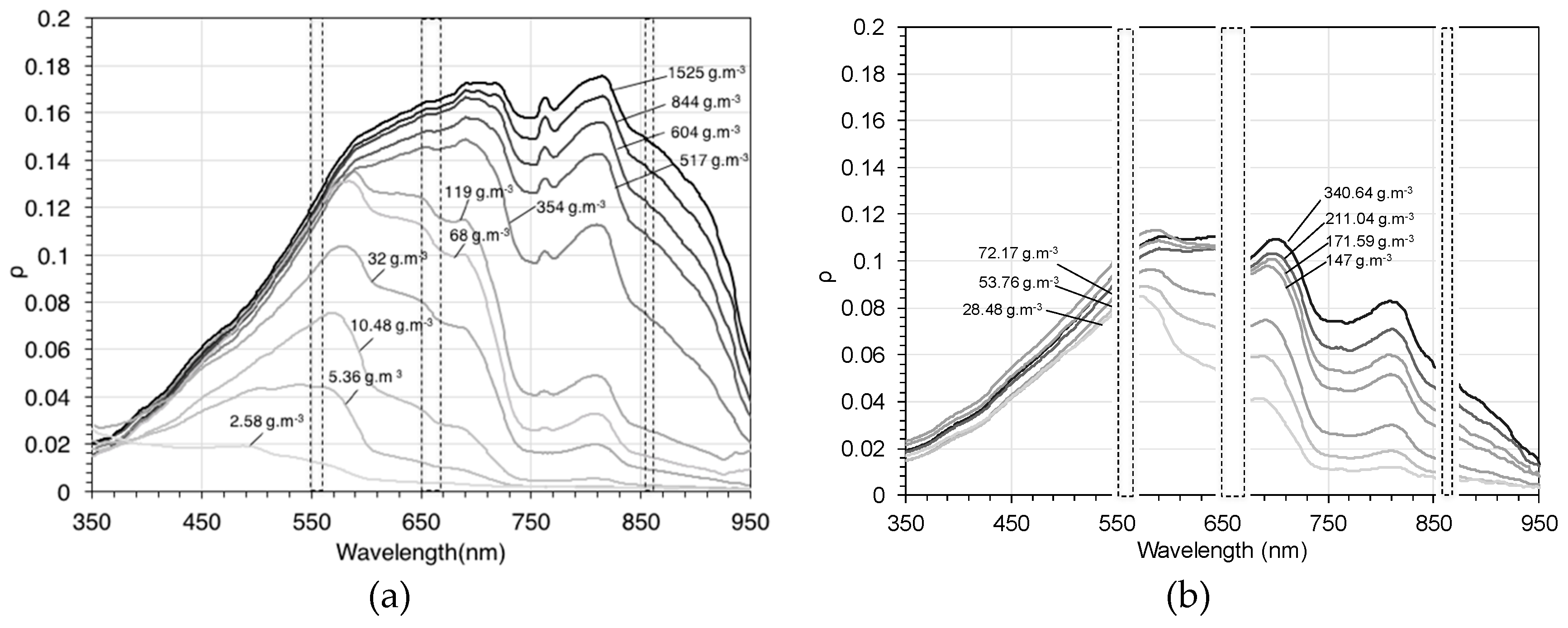
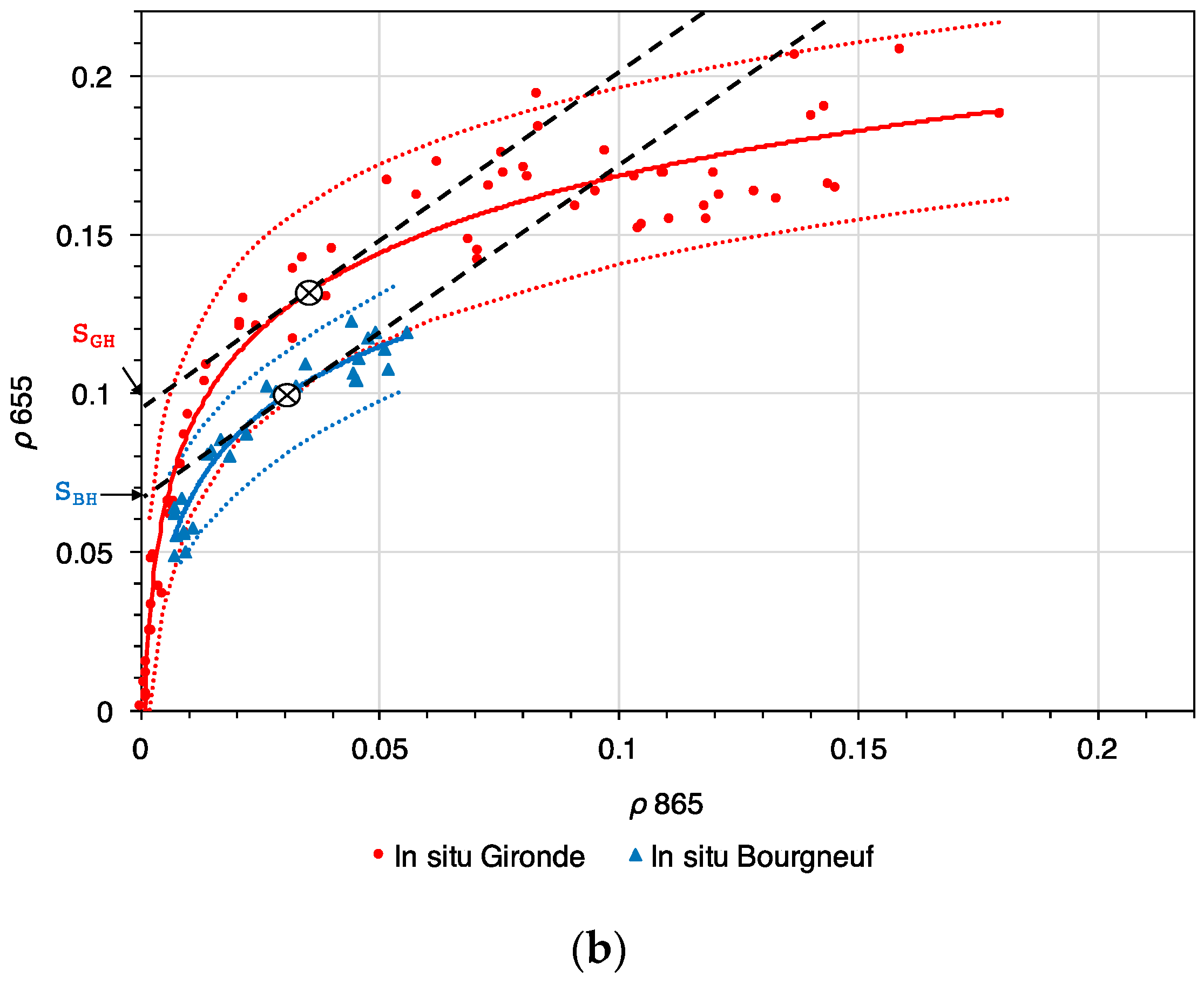
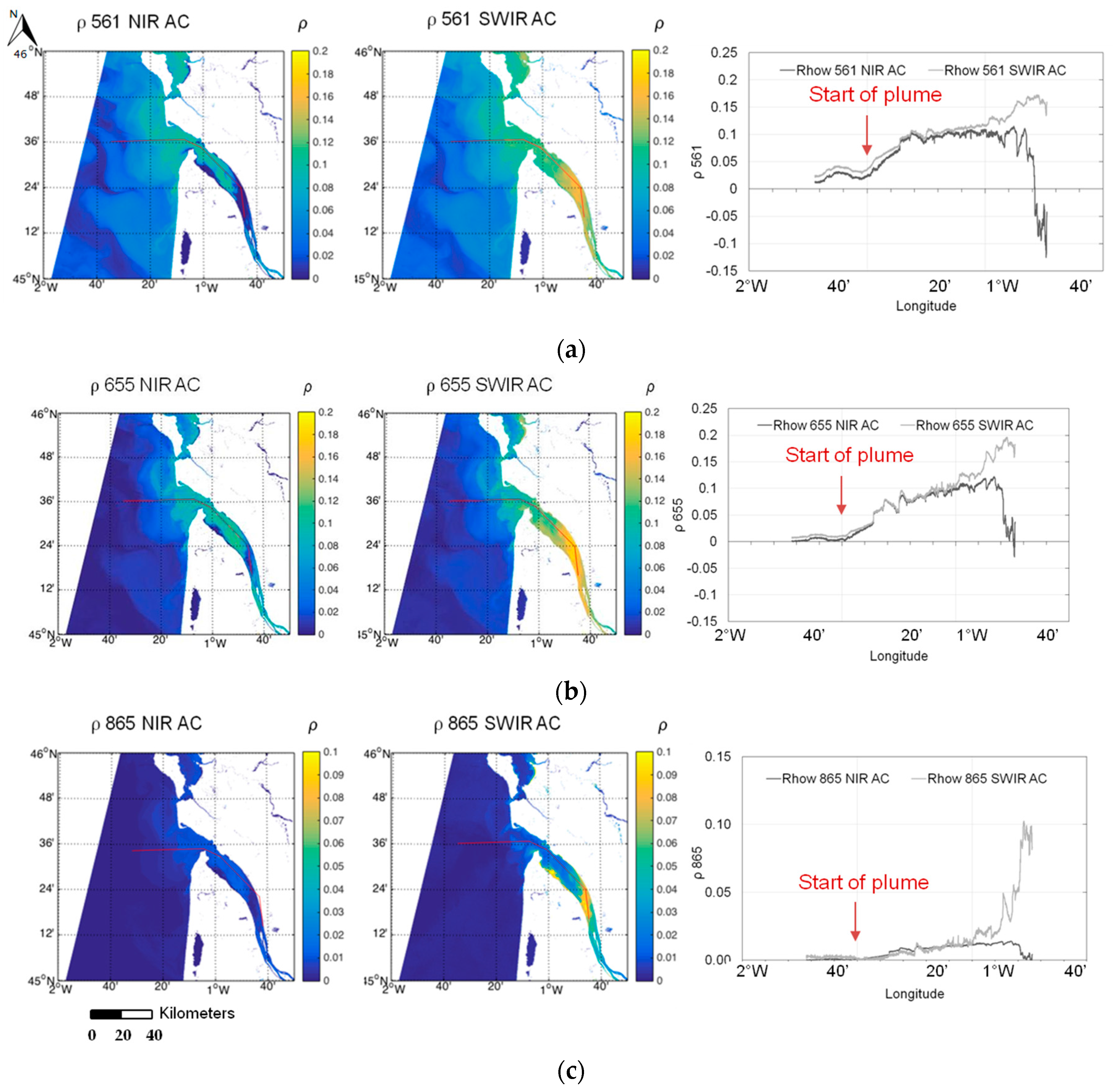
Figure 5 shows the water reflectance values in the OLI green, red and NIR bands obtained applying the ACOLITE-NIR (left column) and ACOLITE-SWIR (right column) atmospheric corrections. The SWIR AC results in water reflectance values at 561 nm 3% (NRMSE) higher than the values obtained applying the NIR AC over the clearest waters (where
ρ 561 < 0.001 and
ρ 655 < 0.005, as defined by Vanhellemont and Ruddick, 2015) of the transect compared. In the 655 nm band, the difference between the values obtained with the two methods is below a 5% difference for
ρ 655 < 0.1. At higher
ρ 655 values, found in the Gironde Estuary where the water is more turbid, the NIR AC fails and provides near-zero and even negative values. The spatial variability was calculated for offshore waters (
ρ 655 < 0.005), estimating the NRMSE (%) of several 8 × 8 pixel boxes, resulting in an average variability of 5% for the SWIR AC, which could be interpreted as noise. Hence, the mean difference between the NIR AC and SWIR AC for all the bands (areas with low levels of water turbidity in low-turbidity offshore waters) was calculated and proved to be lower than the calculated computed spatial variability. As the NIR AC fails for higher water reflectance (
ρ 561 > 0.1,
ρ 655 > 0.1,
ρ 865 > 0.02), the SWIR AC is the most appropriate correction for the selected study areas. These comparisons are conducted for the transect shown in
Figure 5. These results are in accordance with those obtained by [
19], who were the first to show the capabilities of Landsat 8/OLI and the SWIR AC to derive accurate
ρ values in turbid coastal waters.
3.1.1. ACOLITE vs. MACCS Products Comparison
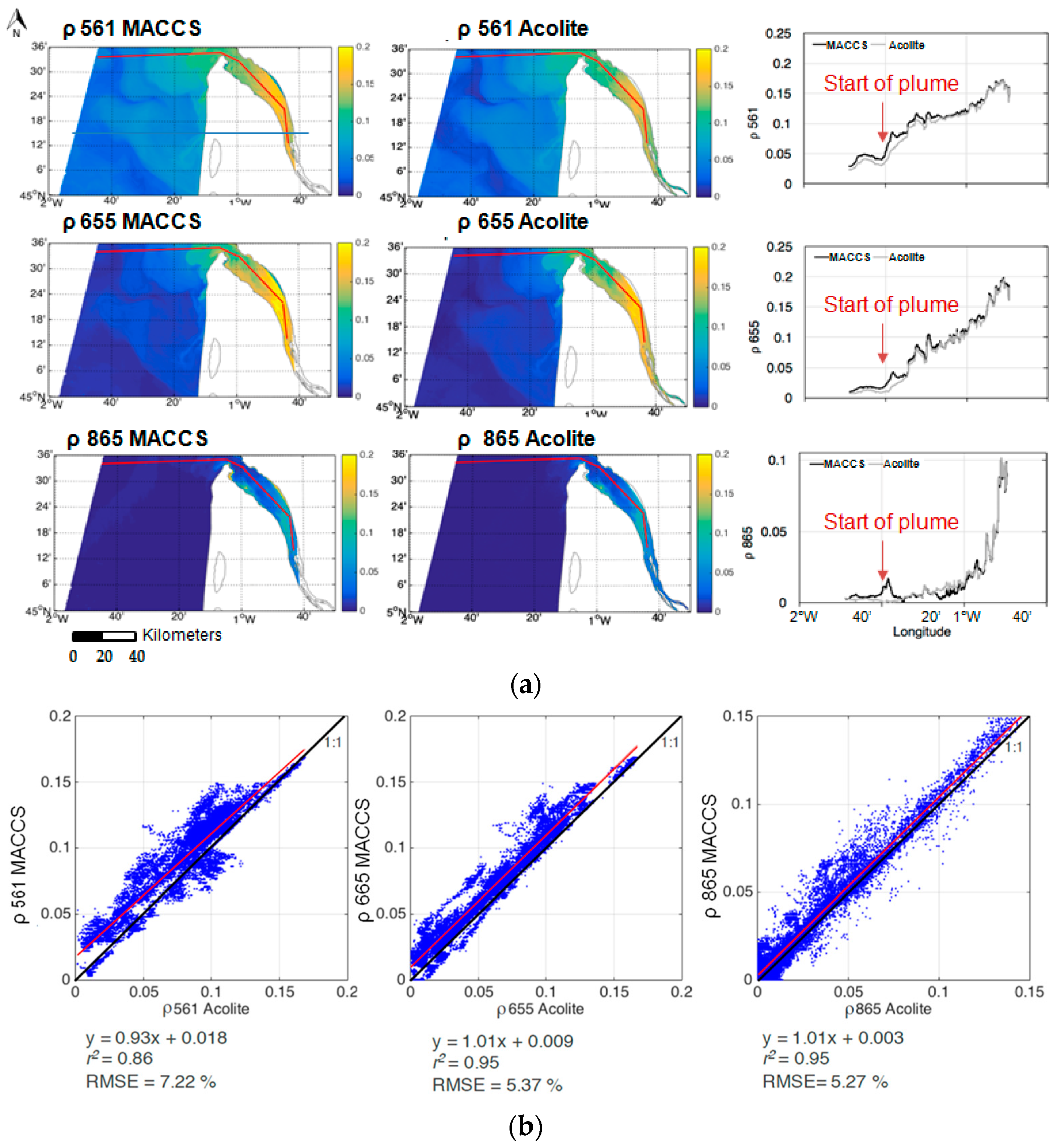
Here, the ACOLITE SWIR AC and Theia Data Center MACCS water reflectance products are compared (
Figure 6). The highest differences were observed over the less turbid waters, but in general a good agreement exists between both products. The flagged (grey) pixels on MACCS maps over the estuary correspond to the limit of the tile provided by the MACCS-Theia Land Data Center (longitude > 0°45′W).
Figure 6b compares
ρ values in the green, red and NIR bands obtained by applying both atmospheric corrections to the selected images (
Table 5). The selected images were acquired at different periods of the year and for different tidal conditions. The best correlations were obtained for the red and the NIR bands with coefficients of determination of 0.95, a slope close to 1 and a NRMSE around 5%. The maximum differences were observed in the green band (NRMSE = ~7%).
The MACCS algorithm is based on land pixels and estimates the aerosol optical thickness combining a multi-spectral assumption, linking the surface reflectance in the red and blue wavebands, and the assumption that multi-temporal observations of a given area should yield similar surface reflectance when separated by a few days. However, this method is not able to estimate the aerosol model and uses a constant model for a given site, which is a disadvantage for regions where the aerosol model is subject to large spatial variations, such as coastal regions. Instead, the ACOLITE AC method estimates the aerosol type using SWIR bands in clear water pixels for each image. In this study, the aerosol type was assumed to be constant over a single OLI tile (170 × 185 km
2), but there is an option provided by the ACOLITE software to allow the type to vary spatially. Research [
19] demonstrated that products from OLI compare well with those of MODIS Aqua and Terra, using the SWIR bands corrected atmospherically with ACOLITE. For this reason, and since the ACOLITE AC uses an ocean color approach, this method is considered more appropriate for the coastal waters of the study regions, even though the MACCS method is proved to provide satisfactory results over the most turbid waters. Another reason explaining the differences between both atmospheric corrections is that the MACCS AC applies a continental model in this area, while it has been demonstrated that the maritime model is dominant in the Gironde area [
58]. The aerosols of maritime origin are almost non-absorbent, so an overestimation of aerosol absorbance is expected when applying a continental model, especially in offshore waters where there is no land aerosol influence. The reason for the green band differences observed is unclear; it could be due to an overestimation caused by the MACCS AC, or an underestimation by the ACOLITE AC caused by a green band overcorrection. However, as the major differences are observed for the lower
ρw values (
Figure 6b), this dissimilarity is probably related to a flawed correction over offshore waters, where low green
ρw values are usually found. Studies found on the use of the MACCS AC over coastal areas did not provide information that could explain the differences observed [
42,
58] other than those already mentioned. Since the green band NRMSE percentage remained low enough (<7%) for the purpose of this study, a deeper analysis on the reasons for these differences was considered out of scope.
3.1.2. Validation of Atmospheric Correction
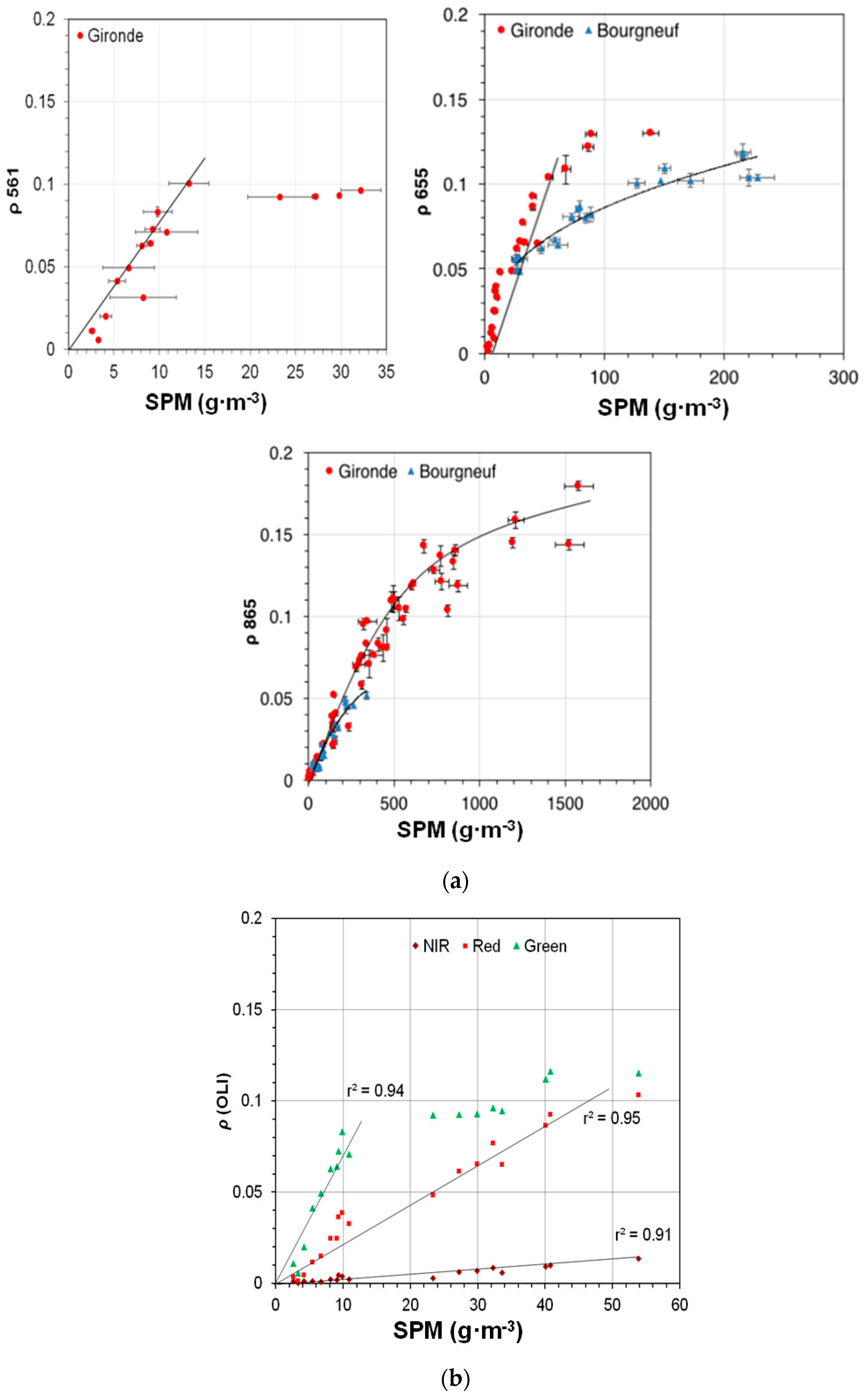
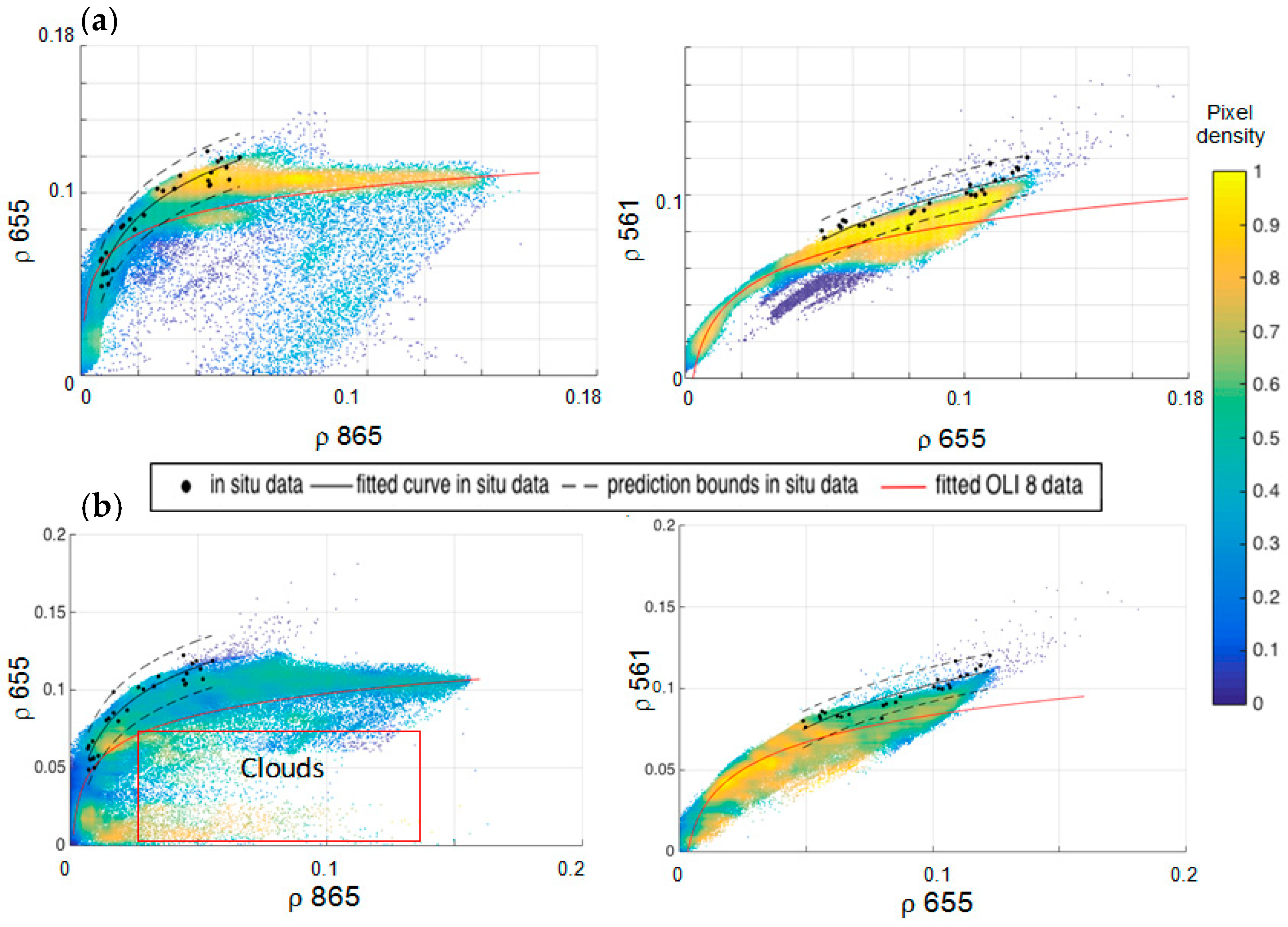
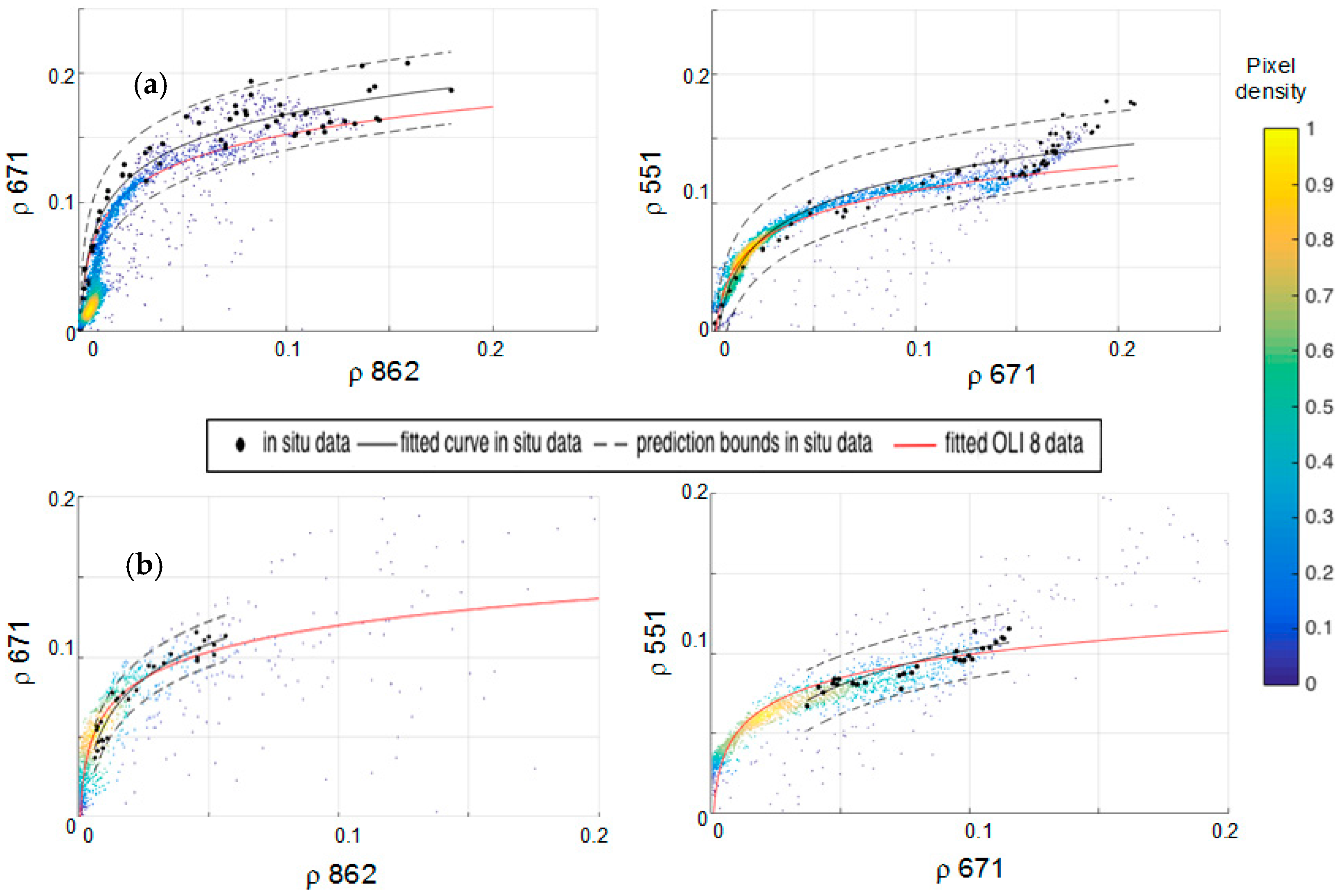
Figure 7a shows the band-to-band
ρ value scatter-plots derived from four OLI satellite images of the Gironde Estuary (a and b) and for the Bourgneuf-Loire area (c and d). The same band-to-band
ρ value scatter-plots derived from in situ measurements are superimposed. In the case of the Gironde area, the in situ values accurately match the OLI-derived reflectance values, and the logarithmic regressions for both datasets follow the same trend. In the case of the Bourgneuf-Loire area, the trend divergence between in situ and satellite datasets is more significant. This is mainly due to the dispersion observed on the satellite dataset caused by the presence of clouds (
Figure 7) on the image acquired on 12 April 2013. The ACOLITE software provides a good mask for clouds, but in some cases cloud shadows or cloud edges are insufficiently masked, introducing significant scatter. Nevertheless, there is a fair overlap between in situ and satellite data for this area as well, taking into account the dataset number difference (in situ stations
n = 29 vs. satellite pixels
n = ~20,000) and the effect of cloud pixels from 12 April 2013. This image was selected because it was acquired on the last day of the field survey carried out in this area, in April 2013.
Similar
ρ band-to-band comparisons were conducted between VIIRS-derived images, and in situ–measured water reflectance at bands centered at 551, 671 and 862 nm (
Figure 8). A fair match is obtained between field and satellite datasets for both the Gironde and the Bourgneuf-Loire areas. As can be observed, the in situ (black line) and satellite (red line) regression curves overlap. This demonstrates that the atmospheric correction applied to the VIIRS images, using the SWIR bands and the Seadas (version 7.3), is appropriate for this type of environment.
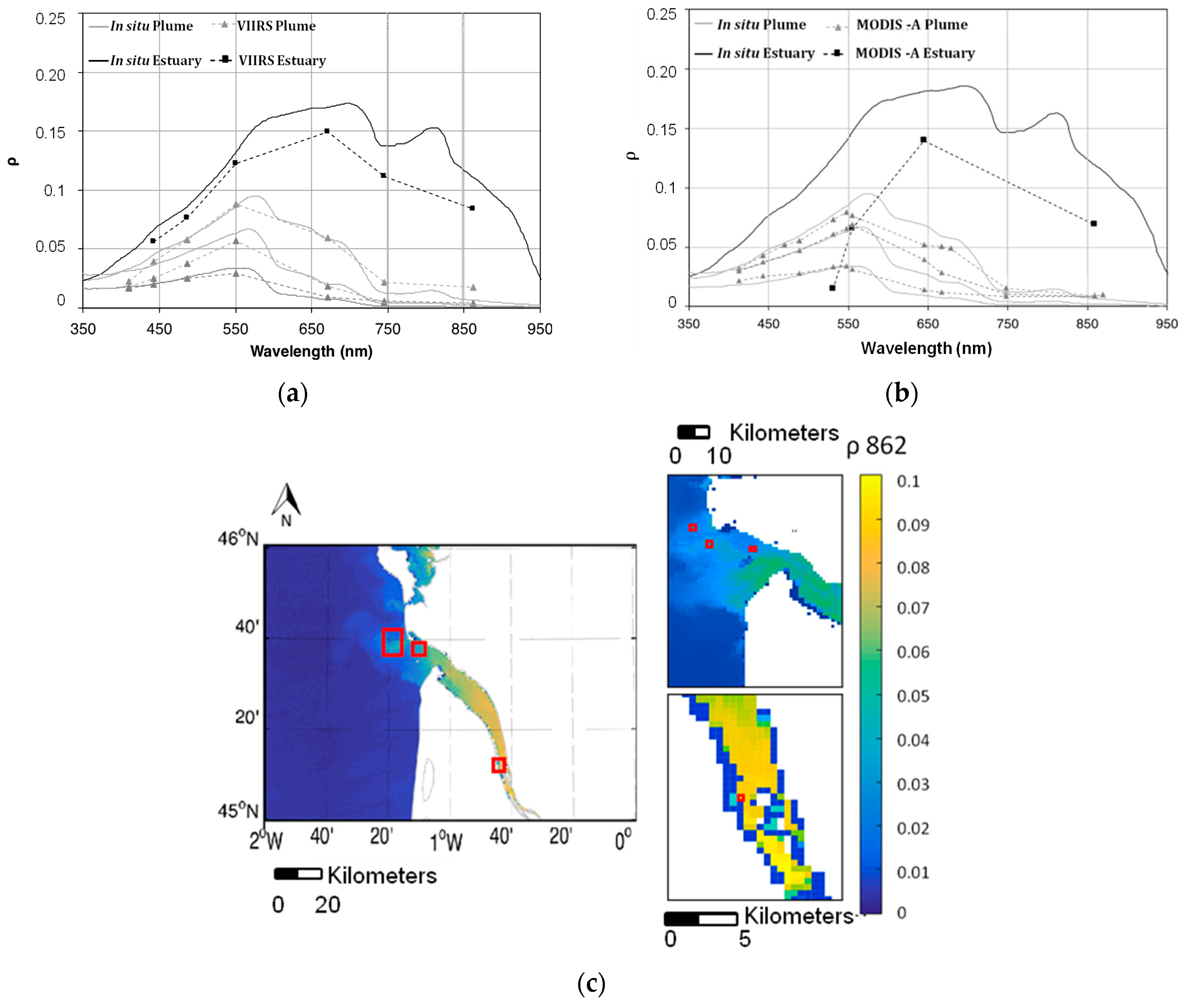
Figure 9 presents a comparison between in situ–measured and satellite-derived reflectance spectra corresponding to VIIRS and MODIS Aqua images acquired on 12 June 2012, 15 July 2014, 16 July 2014. Satellite data were atmospherically corrected using the SWIR option as well. A good match was obtained for the plume area, but in the estuary, the satellite-derived reflectance was systematically lower than values measured in situ at the Pauillac station. This is due to the size sampling differences (satellite vs. in situ) and the effect of the land reflectance in land/water border pixels. Water pixels located near the shore may be contaminated by the land signal, causing erroneous water reflectance estimates. This underestimation in the case of VIIRS (
Figure 9a) is lower than in the case of MODIS, where a particularly sudden decrease is observed for the lower wavelengths. This is caused by the use of the MODIS band B5 (1240 nm), which causes an overcorrection in the shorter wavelength band.
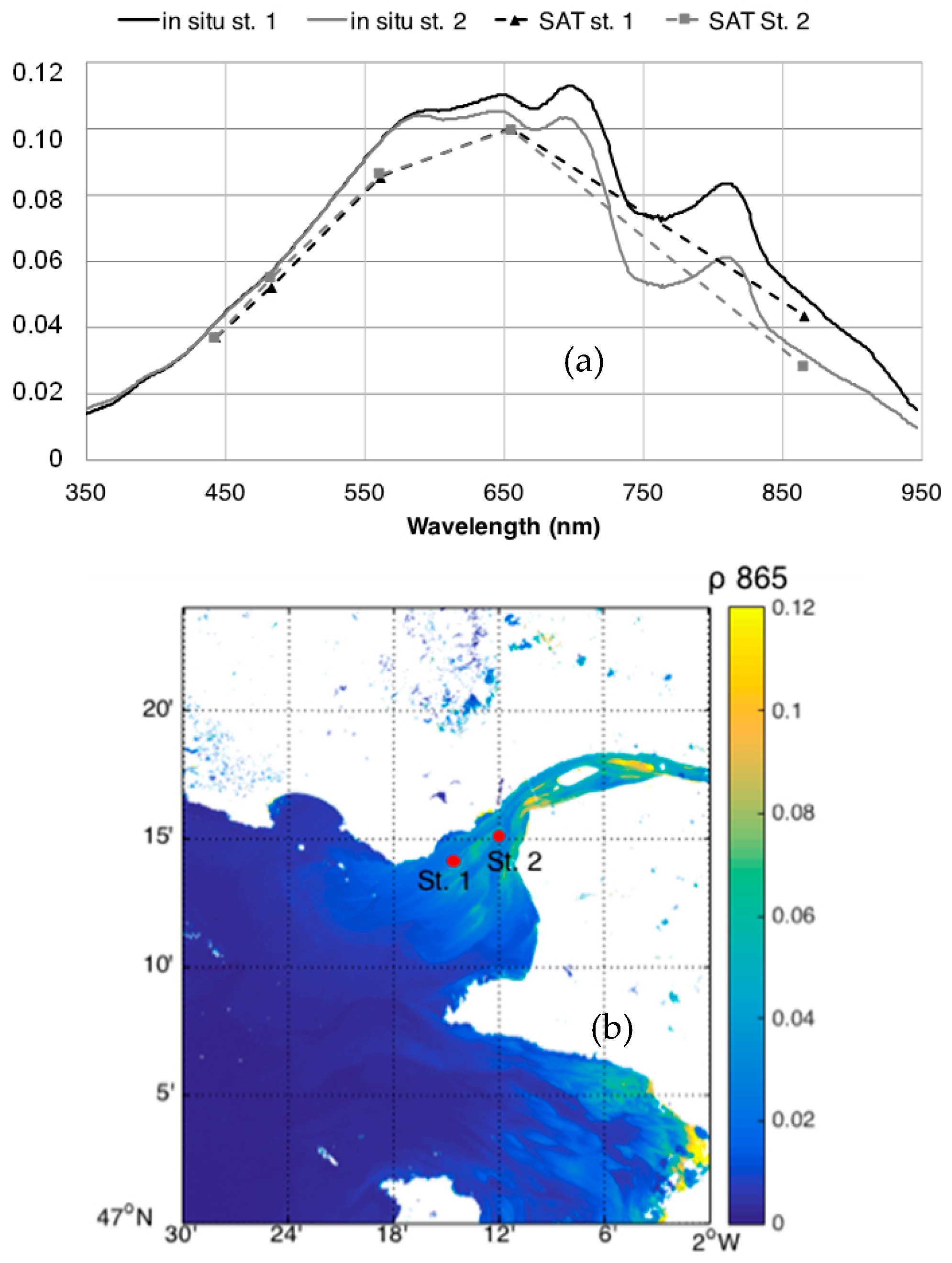
In
Figure 10, the reflectance spectra measured in situ on 11 April 2016 at 10:26 (Station 1) and at 11:16 (Station 2) are compared to the OLI-derived values (image acquired at 10:53). There is a closer match between the water reflectance values measured at Station 2 than at Station 1. This could be due to the lower time difference between the image acquisition and the in situ measurement for Station 2 (23 min) than for Station 1 (27 min), together with the significant small-scale variability of the SPM concentration in this specific area given that measurements were conducted during the ebb tide. In general, satellite products appear to underestimate the ‘true’, i.e., field-measured, water reflectance. Valid match-ups with MODIS and VIIRS were not obtained on the same day.
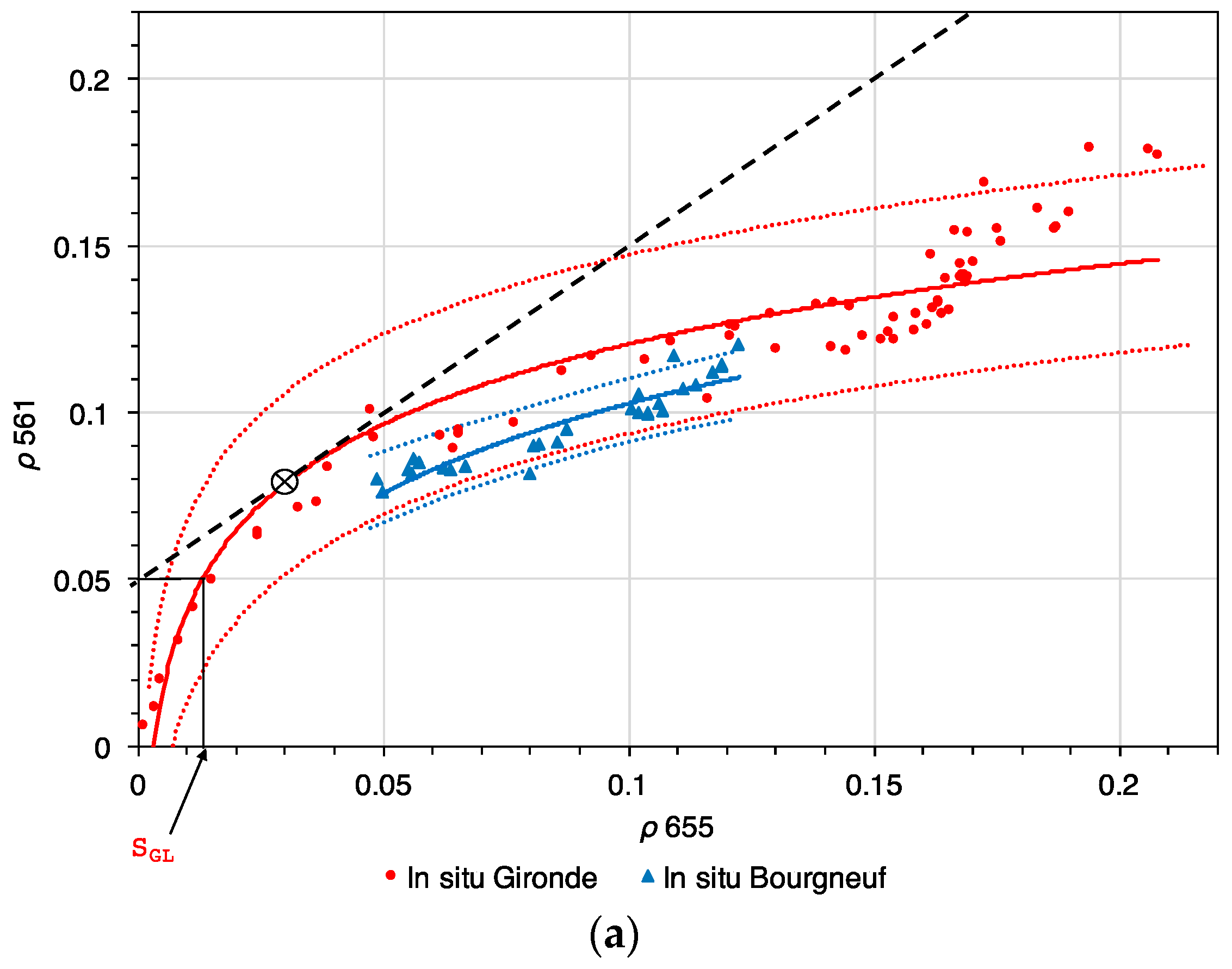
The comparison between in situ and satellite data products resulted in a good match between the green-red and red-NIR bands, with some discrepancies. In general, the trends observed for the satellite data were lower in the higher reflectance values. This is due to the difference in the amount of data (in situ stations
n = 29 vs. satellite pixels
n = ~20,000) and to cloud shadow and land effects on coastal pixels. Regarding the OLI red-green bands’ (655 vs. 561 nm) comparison, a break was observed between the 0–0.15 and the 0.15–0.2 intervals. If the fit would have been made for values of
ρ 655 <0.08, the red and black curves in
Figure 7 and
Figure 8 would have had a better correspondence for the lower reflectance values, so better results would have been obtained if the comparison was achieved by intervals (e.g., 0–0.08, 0.8–0.2). However, showing the entire data range provides a better understanding of the type of data obtained in situ and from satellite remote sensing measurements, and since the in situ data matches the satellite data, the atmospheric correction was considered to provide realistic reflectance results. The switching bounds were determined using field data, so a better match between the two types of data (in situ vs. satellite) would not affect the switching bound values selected.
Differences observed between in situ and satellite data, in
Figure 9 and
Figure 10, could be due to several reasons: (1) an overcorrection of the atmospheric contribution in the SWIR method; (2) the spatial difference between the satellite pixel and field measurements (250/750 m
2 pixel versus ~1 m
2); (3) the near-shore location of the station in the estuary. Option 3 appears to be the most plausible, as the pixel selected for the comparison did not correspond exactly to the location of the Pauillac field station: the next pixel away from the shore was selected to avoid the land effect. Thus, the reflectance values at this location are different to the ones measured in situ at Pauillac. In the case of MODIS (
Figure 9b), there is an obvious overcorrection inside the estuary, due most probably to the low pixel resolution for this area combined with the selection of the 1240 SWIR band. This effect was also observed in the highly turbid waters of the La Plata river by [
52].
3.2. OLI-VIIRS Comparison
Water reflectance values in the green, red and NIR OLI bands (561, 655 and 865 nm) were re-sampled by neighborhood, averaged to a grid of 750 m resolution and then compared to VIIRS-derived values at 551, 671 and 862 nm bands using a common grid. This comparison was achieved for the image acquired on 12 April 2013 (
Table 7). A fair correspondence was found in the Gironde area for this cloud-free image with a large range of water reflectance values, taking into account the significant overpass time difference between both sensors (~3 h) and the large tidal dynamics occurring in this region, as well as the bandwidth differences between the two satellite sensors. The best correspondence was obtained in the green bands (slope = 0.83,
r2 = 0.71), followed by the red bands (slope = 0.66,
r2 = 0.6), and the NIR bands (slope = 0.29,
r2 = 0.38), even though substantial scatter was present. In the case of the Bourgneuf-Loire area, the best correspondence was obtained between red bands (slope = 0.99,
r2 = 0.42), followed by the NIR bands with a better slope, but with more scatter (slope = 0.82,
r2 = 0.1), and the green bands (slope = 0.64,
r2 = 0.67). Differences between both areas were possibly due firstly to the different optical characteristics and dynamics occurring in both areas, and secondly to a failure of the VIIRS atmospheric correction inside the Gironde Estuary. This exercise was not conducted for MODIS images, because comparisons have already been carried out in similarly turbid waters [
19].
Comparisons between OLI and VIIRS products were not found in the literature. However, there is an increasing interest in the exploitation of VIIRS products for coastal studies as this satellite sensor is considered to provide continuity to MODIS. In this study, the VIIRS performance was assessed in highly turbid coastal waters; it showed good results in coastal waters, but the bands’ spatial resolution was too coarse to be used inside the estuary. Nevertheless, the results presented here are promising, as this sensor is still being calibrated, its performance is being tested [
59] and methods are currently being developed to use the high-resolution bands in coastal waters [
60]. The water reflectance values derived from satellite data were slightly lower than the values measured in situ. This is mainly due to the difference in sampling size, as OLI images have a resolution of 30 m, while the water volume sampled in situ was much lower (~10 L). Research [
57] showed good agreement between OLI and in situ spectra in low- to high-turbidity waters. This study confirms their findings in study areas with different SPM characteristics with respect to the North Sea [
21].
In summary, the SWIR atmospheric correction appears to be the most appropriate for the selected study areas, including low- to high-turbidity waters (
Figure 5a). ACOLITE software corrections provided satisfactory water reflectance values for OLI images, in good agreement with MACCS reflectance products (
Figure 6a), as already highlighted in previous studies (e.g., [
42]). In relation to VIIRS, there is a good correspondence between in situ and satellite-derived water reflectance for both study areas (
Figure 8 and
Figure 9,
Table 7), although additional in situ–satellite match-ups would be necessary to draw further conclusions. The problem with the atmospheric corrections of MODIS data is the use of the 1240 nm band, which can provide reflectance values above zero in highly turbid waters, causing an overcorrection to the visible bands [
52,
61].
3.3. Multi-Conditional SPM Algorithm
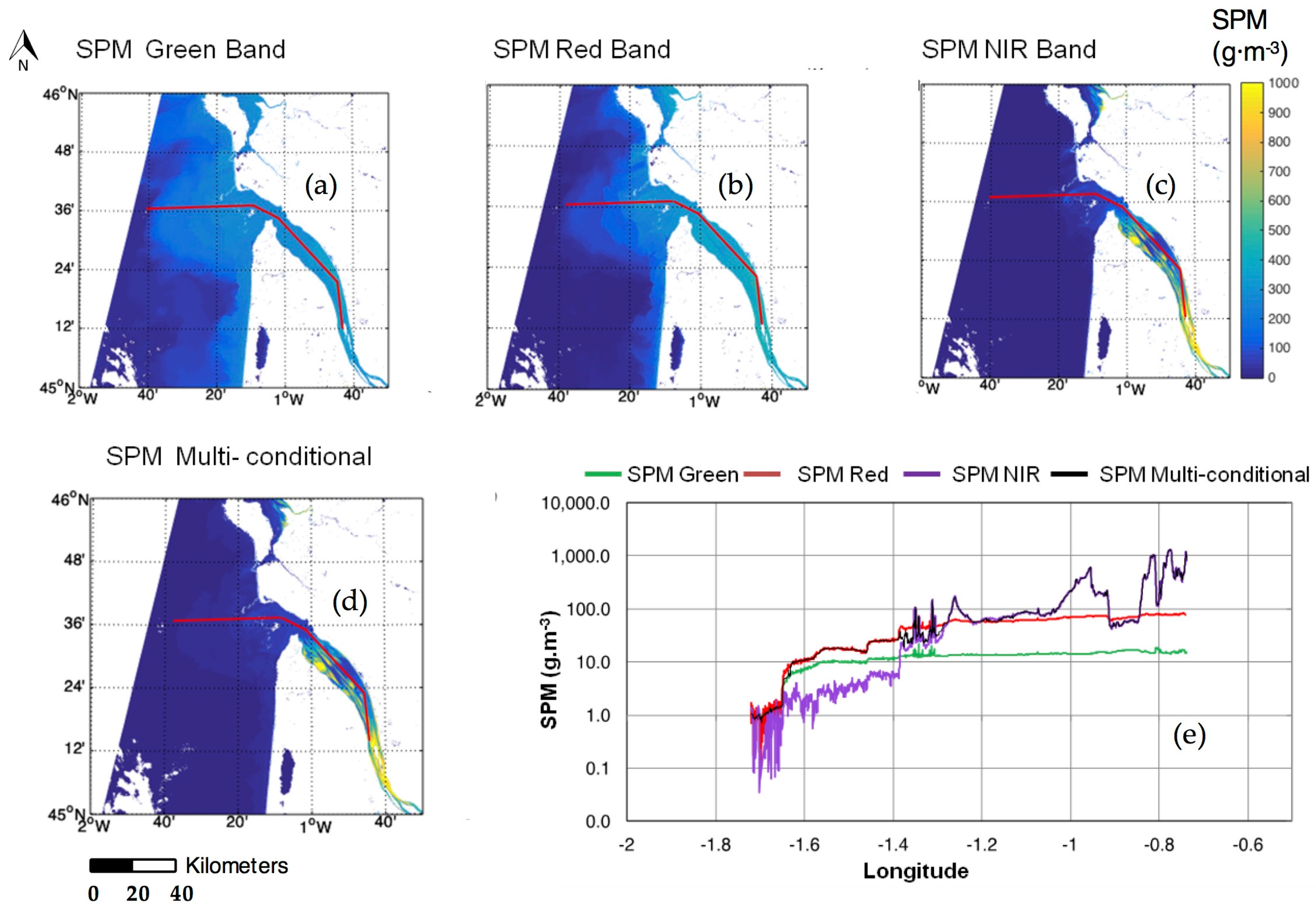
Figure 11 presents the application of the switching SPM model (
Table 2) combined with the smoothing procedure (Equations (3)–(6),
Table 3) to the OLI image of the Gironde Estuary, acquired on 2 February 2015. The transect along the plume and estuarine area proves that the developed switching and smoothing methods allow a smooth transition between the SPM concentration remotely sensed from the offshore low-turbidity waters to the highly turbid waters inside the estuary. Note that the SPM NIR band values are highly noisy for concentrations lower than 50 g·m
−3.
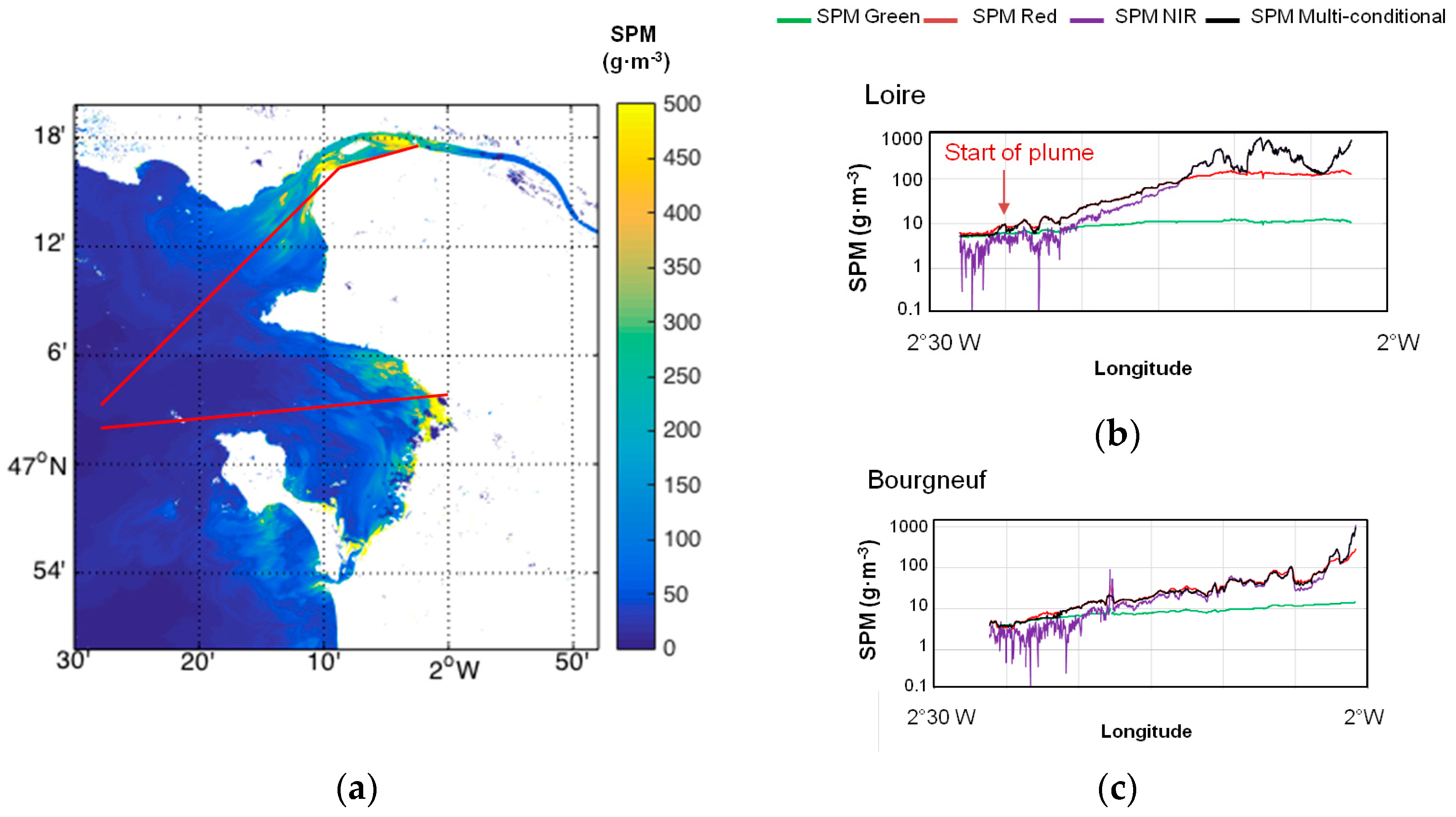
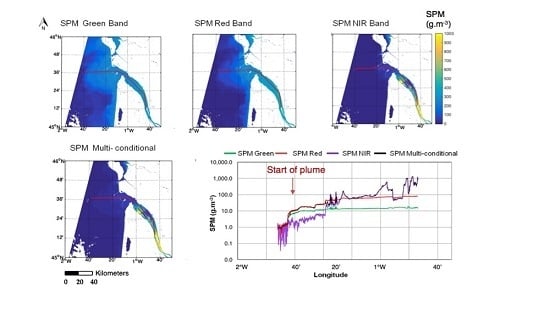
Figure 12 shows the application of the SPM multi-conditional algorithm to a cloud-free image acquired on 12 April 2016 over the Bourgneuf-Loire area using the procedure presented in
Section 2. The smooth transition between the remotely sensed SPM concentration is clearly observed along both the Loire and Bourgneuf transects. As shown in
Figure 12b,c, the SPM multi-conditional algorithm (black line) starts estimating SPM using the green band equation in the clear water area (green line) for both the Loire and Bourgneuf transects. Then, as the SPM concentration increases, due to the river plume in the Loire transect and to the mudflat SPM re-suspension in the Bourgneuf area, the multi-conditional algorithm switches to the red band–estimated SPM (red line). Then, as the red band reflectance increases due to the near-shore SPM concentration increase, the algorithm switches to the SPM calculated with the NIR band equation. The figure clearly shows a high variability in SPM estimation using the NIR band equation (purple line) in clear waters (2°30′W–2°20′W), proving the importance of using equations appropriate for each concentration SPM range.
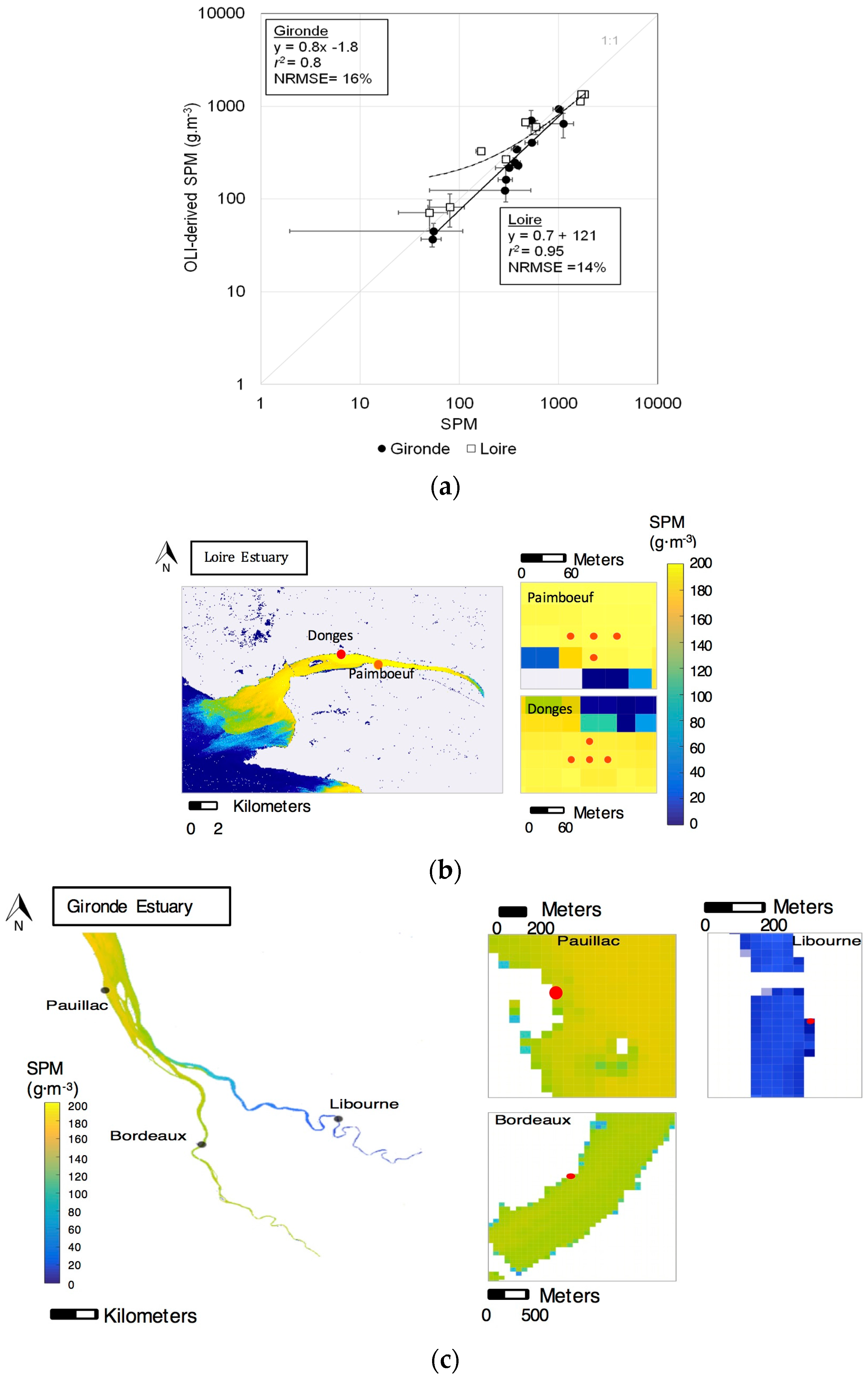
Match-ups between in situ–measured SPM (MAGEST and SYVEL network stations) and OLI-derived SPM concentrations were then analyzed (
Figure 13,
Table 8) to prove that the multi-conditional algorithm provides accurate SPM concentrations. The dates to the OLI images used for satellite—in situ match-ups are shown in
Table 6, together with tidal ranges and tide times (low and high tides) in the Gironde Estuary (Pauillac) and Loire Estuary (Donges) at those dates. The in situ SPM concentrations for the Gironde Estuary were derived from the turbidity measurements (in FNU) at the stations and the turbidity-SPM relationship was established with in situ measurements taken in the Gironde Estuary. In general, OLI provided good SPM estimates at the Pauillac and Libourne stations (
r2 = 0.8 and 0.95, NMRSE = 16% and 14%, respectively, for Gironde and Loire). Previous match-ups using the MAGEST network measurements and SPOT 5 satellite data provided good results with higher pixel resolutions than OLI, showing the capacity of these stations for satellite imagery validation [
42]. Additionally, the SPM concentration calculated using different models (refer to
Table A2 in the
appendix), including the models of [
18,
42], were matched to in situ SPM measurements. The resulting match-ups (
Table 8) show that the multi-conditional algorithm provided, for both the Gironde and the Loire areas, the best of fit (
r2 = 0.8, 0.67) and low error (16%, 14%) combination when compared to SPM estimated using other models. The combination of several models adapted to each concentration range is the main reason for this result, together with the selection of the best-fitted models. As proved by other studies [
35,
36,
37], the selection of a specific model combining different bands is an improvement when estimating the SPM concentration in coastal waters.
Table 8 shows the in situ-satellite match-up results using different SPM models. In the case of the Gironde area, the fit, slope, NRMSE (%) and offset when using the band-ratio and single-band exponential and polynomial regressions were similar. Slightly better results were obtained with the exponential NIR-red band ratio models (
r2 = 0.7, slope = 1.1, NRMSE = 22.3%, offset = 16) compared to the exponential NIR band model (
r2 = 0.8, slope = 0.65, NRMSE = 20%, offset = 66), but the polynomial single-band model performed better when using the single NIR band (
r2 = 0.8, slope = 0.8, NRMSE = 16.4%, offset = −3), compared to the band ratio (
r2 = 0.74, slope = 0.9, NRMSE = 19.8%, offset = 33). The SPM concentration estimates did not improve when using equations published in other studies for the same study areas [
18,
42] providing larger NMRSEs (36.5%, 44.7%) and offsets (−185, −24), compared to the results obtained with the multi-conditional algorithm (slope = 0.8,
r2 = 0.8, NRMSE = 16%, offset = −1.8). In the case of the Bourgneuf-Loire area, the combination of the re-calibrated NIR and red band semi-empirical models from Reference [
16] with the multi-conditional algorithm provided the best fit and lowest error (slope = 0.67,
r2 = 0.95, NRMSE = 14%, offset = 121). In this case, the performance of the algorithm will improve with a re-calibration of the models with additional in situ data.
The configuration of the pixels selected for the match-ups is shown in
Figure 13. OLI-derived SPM estimates provided good match-up results with the in situ measurements. In the case of the Bourgneuf-Loire area, instead of using one pixel for the match-ups, as in the case of Gironde, an average of four pixels was used, as it provided the best results. Vertical error bars show the standard deviation of the four pixels selected, in the case of the Loire area (see
Figure 13b), and of the three nearby pixels in the case of the Gironde area (shown as red rectangles), even if a single pixel was used for the match-ups (red circle) in
Figure 13c. Horizontal error bars correspond to the temporal SPM variability ±10 min from the satellite overpass time. There appears to be an underestimation by the algorithm at SPM concentrations above 100 g·m
−3 and a slight overestimation below 500 g·m
−3 (and above 100 g·m
−3) in the Bourgneuf-Loire area, while the Gironde algorithm seems to overestimate values above 500 g·m
−3. This tendency was also observed by [
42] using SPOT 4 data, where the same pixel configuration was used for the Loire match-ups. The imprecision observed for these match-ups is due to several factors, such as the accuracy of the SPM algorithms, the errors and uncertainties in field measurements, the spatial differences between the sampling station and satellite pixel location, as well as uncertainties related to atmospheric corrections. Different SPM models including band ratios, such as those developed by [
18,
42] for these areas, were applied to the images, but the match-up results did not improve (see
Table 8).
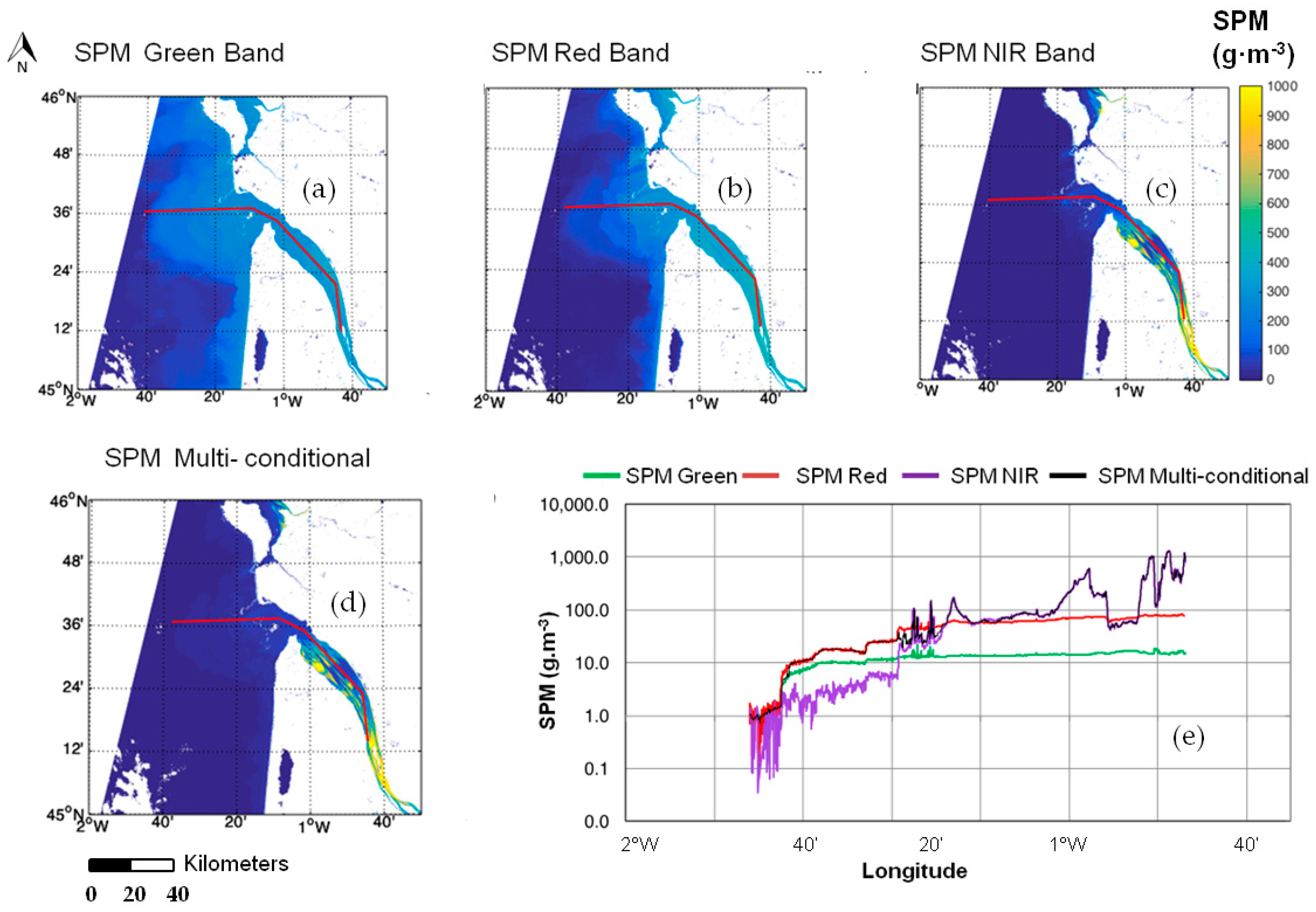
Figure 14 compares the SPM concentrations derived from OLI, VIIRS and MODIS (Aqua) satellite data recorded on the same day over the Gironde Estuary. Water reflectances at 655 (OLI), 671 (VIIRS), 645 nm (MODIS aqua) show a similar trend along the transect. VIIRS products provided higher values than OLI in general, up to the most upstream section of the Estuary, where there was a sharp decrease. It corresponded to a failure of the atmospheric correction, due to the low VIIRS spatial resolution for this particular area. This failure was also observed along the MODIS transect, where the most upstream pixels are missing, resulting in a sudden SPM concentration decrease. Generally, the MODIS and OLI transects overlap up to the most upstream section of the estuary, where SPM concentrations are overestimated by MODIS. This is due to the proximity of the land on the last transect pixels, which, as seen in
Figure 13d, results in a rapid decrease of the SPM concentration. In this particular region, the reflectance at 859 nm showed a fast increase for MODIS, which was not observed in the OLI 865 band. Hence, particular attention needs to be paid to the near-shore pixels, where the atmospheric correction may provide inaccurate water reflectance estimates, resulting in inaccurate SPM retrievals. For practical reasons, the same switching bounds applied to OLI were used for VIIRS and MODIS Aqua. However, the fine adjustment of the switching bounds to each sensor’s spectral bands could provide better results. Despite the fact that the MODIS atmospheric corrections provided underestimated water reflectance values, the transect comparison showed a good match between the three SPM maps.
Overall, the multi-conditional SPM algorithm provides a smooth transition between SPM models for three different sensors over an area that goes from low- to high-turbidity surface waters. The band-switching technique allows keeping the optimal sensitivity of
ρ to SPM variations and avoiding the saturation of
ρ in (highly) turbid waters. The study areas were characterized by a high amount of cloudy days, and taking into account that OLI images are only available every 16 days, it was difficult to obtain numerous cloud-free images to apply the SPM algorithm. Again, the purpose of this study was not to provide the best SPM models for each area, but to develop a method and test it on selected satellite data recorded for optimal conditions (cloud-free, clear atmosphere) representative of a wide range of SPM concentrations in coastal and estuarine waters. Similar methods have already been developed [
35,
36], but the procedure presented in the present study (1) automatically selects the model switching bounds based on in situ measurements; (2) fully applies the method to real satellite data provided by three different sensors; and (3) validates the results based on match-ups with field data.