1. Introduction
The detection of clouds, cirrus, and shadows is among the first processing steps after processing raw instrument measurements to at-sensor radiance or reflectance values. A robust discrimination of cloudy, cirrus-contaminated, and clear sky pixels is crucial for many applications, including the retrieval of surface reflectance within atmospheric correction (e.g., see [
1,
2]) or the co-registration with other images (e.g., see [
3,
4]). The retrieval of surface reflection becomes impossible for optically thick clouds and pixels affected by cirrus and shadows must be treated as individual cases for a physically correct retrieval. Many applications benefit if a detection of snow and water is additionally performed (e.g., see [
5,
6]). In that respect, such a classification is an essential pre-processing step before higher-level algorithms can be applied (e.g., see [
7,
8]). Examples are the application of agriculture-related products which might require clear sky pixels as input (e.g., see [
9,
10]).
Here we describe ready-to-use classification methods which are applicable for the series of Sentinel-2 MSI (Multi-Spectral Imager) [
11,
12,
13] instruments. Ready-to-use methods are in a state where their application by a user requires no further research and only a little work for initial setup. The first Sentinel-2 in a series of at least four was launched in 2015, became operational in early 2016, and the Copernicus program aims at having two operational instruments in orbit at a time until 2020. The MSI offers optimized bands for Earth-observation applications as well as for the detection of visible and sub-visible cirrus clouds for which the so-called cirrus channel B10 at 1.38
m is essential. Such a band is also present it the Operational Land Imager (OLI) [
14,
15,
16] instrument, which is the most recent installment of the NASA Landsat series. OLI and MSI share similar bands such as the SWIR bands at 1.61
m and 2.19
m, but differ in that OLI includes thermal bands while the MSI includes a higher spectral sampling within the red edge. A substantial difference between the two missions is the amount of transmitted data which is caused by higher number of platforms (two vs. one), higher swath (290 km vs. 185 km), higher spectral sampling (13 vs. 11 bands) and higher spatial sampling (
m),
m, and
m vs.
m,
m, and
m). These technical improvements represent a new leap in the total amount of freely available earth observation data and hence calls for fast, and easy to parallelize algorithms to allow the efficient processing and exploitation of the incoming data.
In the past, many detection schemes have been developed to detect clouds, cirrus, shadows, snow/ice, and clear sky observations or a subset or superset of these classes. Such schemes are in general distinct for a particular instrument, although basic physical principles for similar spectral bands hold among instruments. Some examples from the relevant literature can be found in a variety of references [
1,
17,
18,
19,
20,
21,
22,
23,
24,
25,
26,
27,
28]. Cloud detection is the main focus for most of these references, while the aim of this study is the separation of all introduced classes.
A comprehensive overview of the existing literature is beyond the scope of this paper, but existing schemes could be characterized by being local or aware of spatial context, self-contained or dependent on external data, or by being probabilistic or decision-based. Local schemes neglect spatial contexts such as texture (e.g., see [
25,
26,
27]) or objects where for example a cloud shadow could be estimated from the position of a nearby detected cloud, its height, and the given viewing geometry (e.g., see [
22]). Self-contained schemes would only depend on the measured data and already available metadata, where other schemes might be based on a time series for this area (e.g., see [
1]) or on data from numeric weather prediction models (e.g., see [
23]). Probabilistic schemes try to estimate the probability that a given observation belongs to a given class (e.g., see [
23,
24]). Thus for a given set of classes, the user needs to convert the resulting set of class probabilities into a final decision. It depends on the application if this degree of freedom is welcome or just additional burden. In contrast to this, decision-based schemes select a single class for a given measurement (e.g., see [
28]) as the final result. Any probabilistic classification technique can be extended to a decision-based scheme by adding a method which selects a single class from the list of class probabilities as the final result.
Any particular scheme might be a mixture of the discussed approaches or even include strategies not mentioned here. The taken approach will determine not only the classification skill of the algorithm but also the needed effort for implementing and maintaining it as well as the reached processing performance. Although difficult to prove in theory, we assume that local and self-contained approaches are the best choices regarding processing performance and least effort for implementation and maintenance. Such schemes omit the added complexity of processing external dependencies, the computation of spatial metrics and any object recognition and operate only a per-spectrum or per-pixel level. It is of course not guaranteed that such algorithms are inherently fast; e.g., if an online radiative transfer is used for classification. However, this class of algorithms is very well suited for the application of machine learning techniques, which allow rapid development and improvements of algorithms as well as excellent processing speeds. The detection performance of such algorithms can be used to establish a baseline for competing and potentially more sophisticated algorithms to quantitatively assess their potential additional computational costs.
To establish such as baseline, we decided to build up a database of labeled MSI spectra and to apply machine learning techniques to derive ready-to-use classification algorithms. It can serve not only as a valuable tool for algorithm development but also for validation of algorithms. The included spectra should cover much of the natural variability which is seen by MSI while the choice of labels was limited to cloud, cirrus, snow/ice, shadow, water, and clear sky. To our best knowledge, manual classification of images is the most suitable way of setting up such a database for Sentinel-2. To avoid the step of visually inspecting images by a human expert, one could exploit measurements from active instruments such as a LIDAR (e.g., ground-based from EARLINET [
29,
30] or spaceborne from CALIOP [
31]) or cloud radar (e.g., spaceborne from CloudSat [
32]). Such measurements should cover large fractions of MSI’s swath and potential time delays between data acquisitions should be not greater than several minutes. Currently, suitable space-borne options are not available for Sentinel-2A. Ground-based instruments could be used in principle, but their measurements would cover only a small fraction of the occurring viewing geometries as well as natural variability of surface, atmospheric, and meteorological conditions. The database is discussed in
Section 2 and the application of machine learning algorithms is discussed in
Section 3.
We understand that the term scheme or technique describes the general method, while a particular, ready-to-use instance of a method with given parameters is an algorithm. The term decision tree refers to the method, while a given tree with branches and parameters is a particular algorithm. We discuss decision trees with features computed from simple band math formulas (see
Section 3.2) which are one of the most simple and straightforward to understand techniques. These algorithms are simple to implement for any processing chain, can be represented by simple charts, but offer only limited classification skill. This ease of use and simplicity qualifies decision trees as baseline algorithms to judge the performance of other, possibly more complex and computationally more demanding, algorithms.
To improve the classification skill, we present a detection scheme based on classical Bayesian probability estimation which delivers superior results and is made available to the community as open source software (see
Section 3.3). It is a technique that has only recently been used for the detection of clouds [
24] and represents a straightforward and fast technique which is very well suited for the processing of large amounts of data. The database, the presented decision trees, as well as the classical Bayesian detection scheme are available at [
33].
We included a broad range of available standard methods for our study, but focus the discussion on decision trees and the classical Bayesian approach. In
Section 3.4 we discuss these results with regards to other commonly used techniques such as random forests, support vector machines, stochastic gradient descent, and adaptive boosting.
2. Database of Manually Classified Sentinel-2 MSI Data
Sentinel-2 images are selected such that the derived database covers the relevant natural variability of MSI observations. Each included spectrum carries either one of the following labels: cloud, cirrus, snow/ice, shadow, water, and clear sky and is accompanied by the relevant metadata from the Level-1C product. The selection of labels was driven with atmospheric correction of MSI observations in mind, where clear sky, cirrus, and shadow pixels are treated with slightly different approaches. The water class is included for these pixels since remote-sensing-reflectance is a more suitable quantity rather than surface reflectance. Both quantities are products of atmospheric correction algorithms and require different processing steps since for remote-sensing-reflectance the reflection and transmission of the water surface must be corrected. Currently, no external information such as atmospheric fields from numerical weather models like from ERA-interim reanalysis [
34] or products from global networks such as aerosol optical depth from Aeronet [
35] is included in the database. Since time and location for each included spectra are known, it poses no particular difficulty to extend the database.
The broad global distribution of included images ensures that a wide range of inter-class variability is captured within the database. This variability is highlighted in
Figure 1, which depicts histograms of at-sensor reflectances for each MSI channel per class. The figure shows clearly that each of the classes exhibits distinct spectral properties, but also that a classification algorithm has to cope with significant inter- and intra-class variability.
The surface reflectance spectrum and actual atmospheric properties determine spectral shapes of the at-sensor reflectance. This effect can be nicely seen for the so-called cirrus channel B10 at 1380 nm, which shows only small to zero values for most classes other than the cirrus class. The atmosphere is mostly opaque at this wavelength due to the high absorption of water vapor which is mostly concentrated at the first few kilometers above the surface within the planetary boundary layer. Since cirrus clouds typically form well above that height, their scattering properties allow some reflected light to reach the sensor. A different distinct atmospheric band is B9, which is centered at a weaker water vapor absorption band and is used for atmospheric correction. The variability here is caused by surface reflectance and variations in water vapor concentration, which a classification algorithm needs to separate. The reflectance of the snow class decreases substantially for the shortwave infrared channels 11 and 12, while this is not so much the case for the cloud class which shows a mostly flat reflectance spectra in the visible. Also, the increase of surface reflectance at the so-called red edge can be nicely seen in the clear sky class which contains green vegetation.
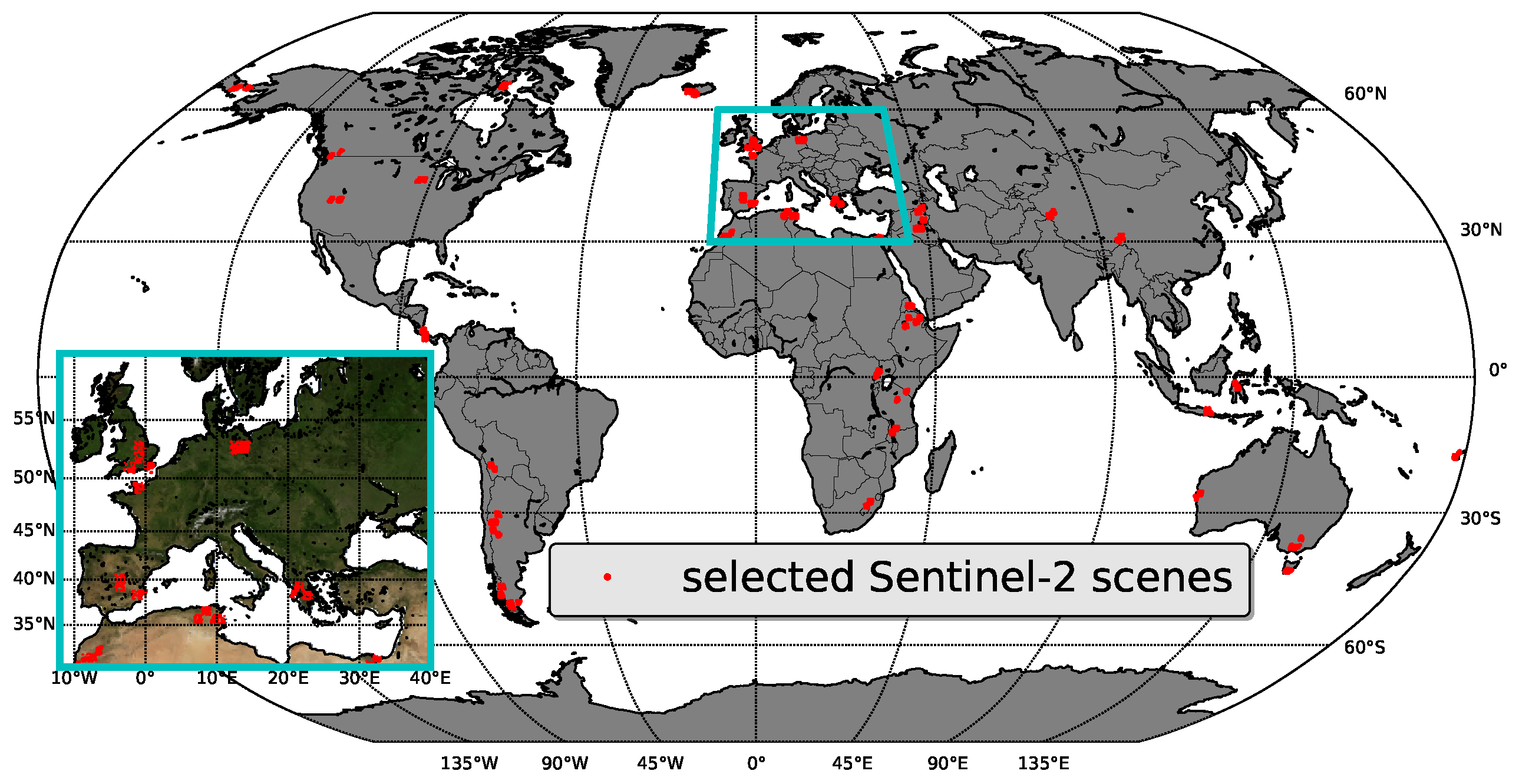
The database is based on images acquired over the full globe, and their global distribution is illustrated in
Figure 2. All spectral bands of the Level-1C products were spatially resampled to 20 m to allow multispectral analysis. The selected scenes are distributed such that a wide range of surface types and observational geometries are included. Multiple false-color RGB views of a scene and it’s spatial context is used to label areas with manually drawn polygons. We want to emphasize, that the spatial context of a scene is crucial for its correct manual classification. This is especially the case for shadows cast by clouds or barely visible cirrus. One should also note, that shadows can be cast by objects outside the current image. Not all classes can be found in each image, but we took care to distribute classes evenly.
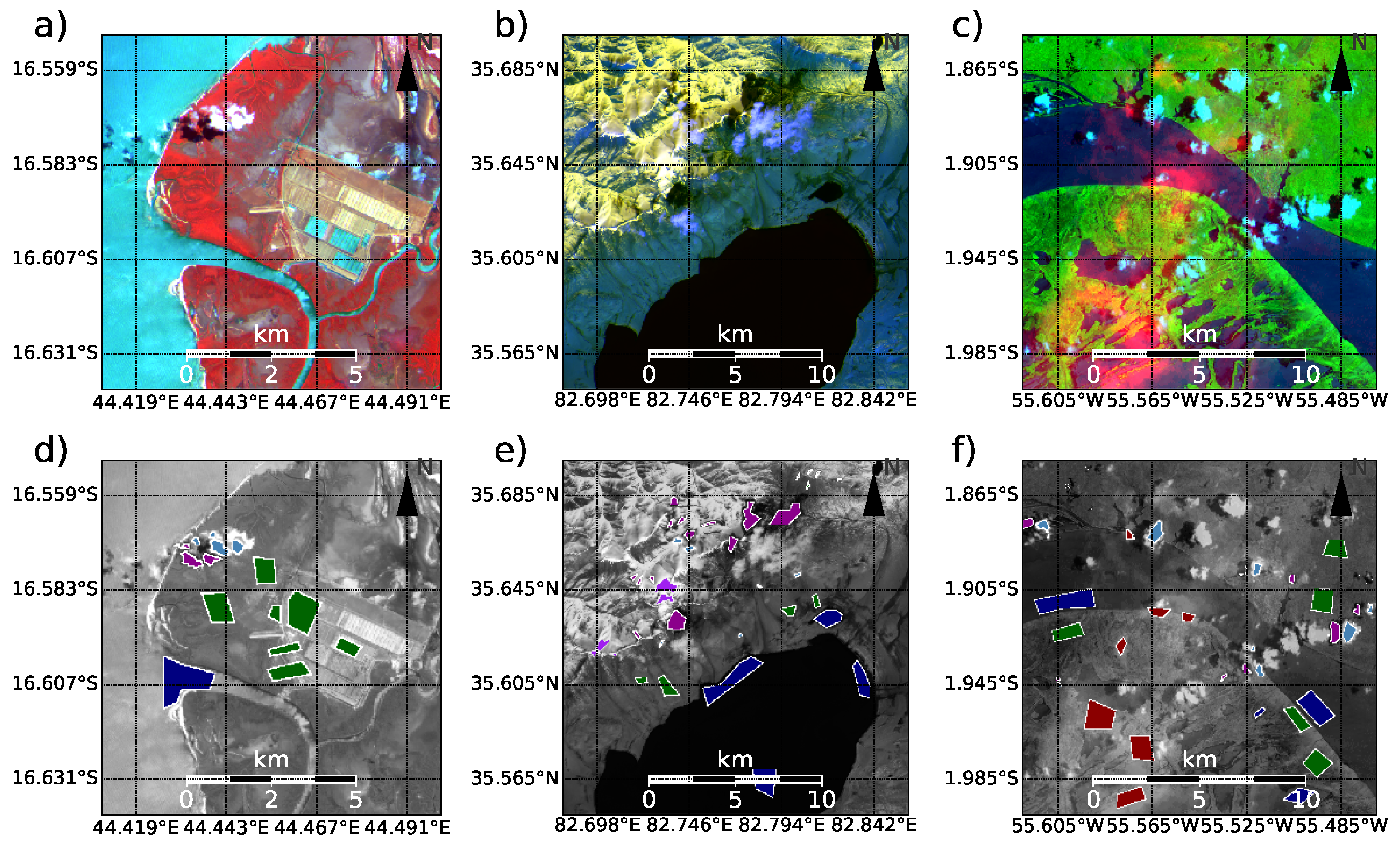
Figure 3 is a showcase for this manual classification approach for three selected scenes. Their actual positions and used channel combinations are shown in
Table 1. It is evident that there is a large degree of freedom on how polygons are placed and which objects are marked. Also, the extent of objects with diffuse boundaries poses a particular burden on the consistency of the manual classification. This merely indicates that a certain degree of subjectivity is inherent in this approach. However, this holds for any other approach when soft objects, such as clouds or shadows, are to be defined by hard boundaries. The effect of the human error is minimized by a two-step approach, where images are initially labeled and revisited some time later to re-evaluate past decisions. Human errors, if present, should lead to unexpected results when comparing labels of the database with classification results from detection algorithms. One example would be prominent misclassification errors between simple-to-distinct classes such as shadow and snow. Next to the spectra itself, the database contains metadata such as the scene-ID, observation time and geographic position, which could be used to establish location-aware algorithms, or to analyze comparison results concerning their location. Currently, metrics for spatial context are not included but could be added with little extra work if needed.
3. Classification Based on Machine Learning
Labeling Sentinel-2 MSI spectra can be understood as a supervised classification problem in machine learning, for which a rich body of literature and many implemented methods exist. This section introduces shortly some aspects of machine learning which are relevant for this paper and the following subsections provide details about the applied methodology and results. Many methods and available implementations have free parameters which have a substantial impact on the classification result, and optimal parameter settings need to be found for each problem at hand. A common optimization strategy for these parameters is applied here which is described in
Section 3.1. This paper is focused on decision trees and classical Bayesian classification, which are discussed in
Section 3.2 and
Section 3.3. Reasons for limiting the study to the two methods is that decision trees are among the most commonly used methods and therefore can establish a baseline and that it is straightforward for both methods to provide algorithms results in a portable way. Portability means that the implementations can run on various hardware and software environments. The classification performance of these two methods is compared with other commonly used methods such as support vector classifiers, random forest, and stochastic gradient descent and results are discussed in
Section 3.4.
Supervised classification describes the mapping of input data, which is called feature space, to a fixed and finite set of labels. Here, the feature space is constructed from single MSI spectra using simple band math functions like a single band, band-differences, band-ratios, or generalized indices which are given in
Table 2. Only the given functions were considered in this paper, and it is assumed that these functions cover large fractions of the regularly used band relationships. Many suitable techniques have free parameters and it is often necessary to optimize their settings to improve classification results.
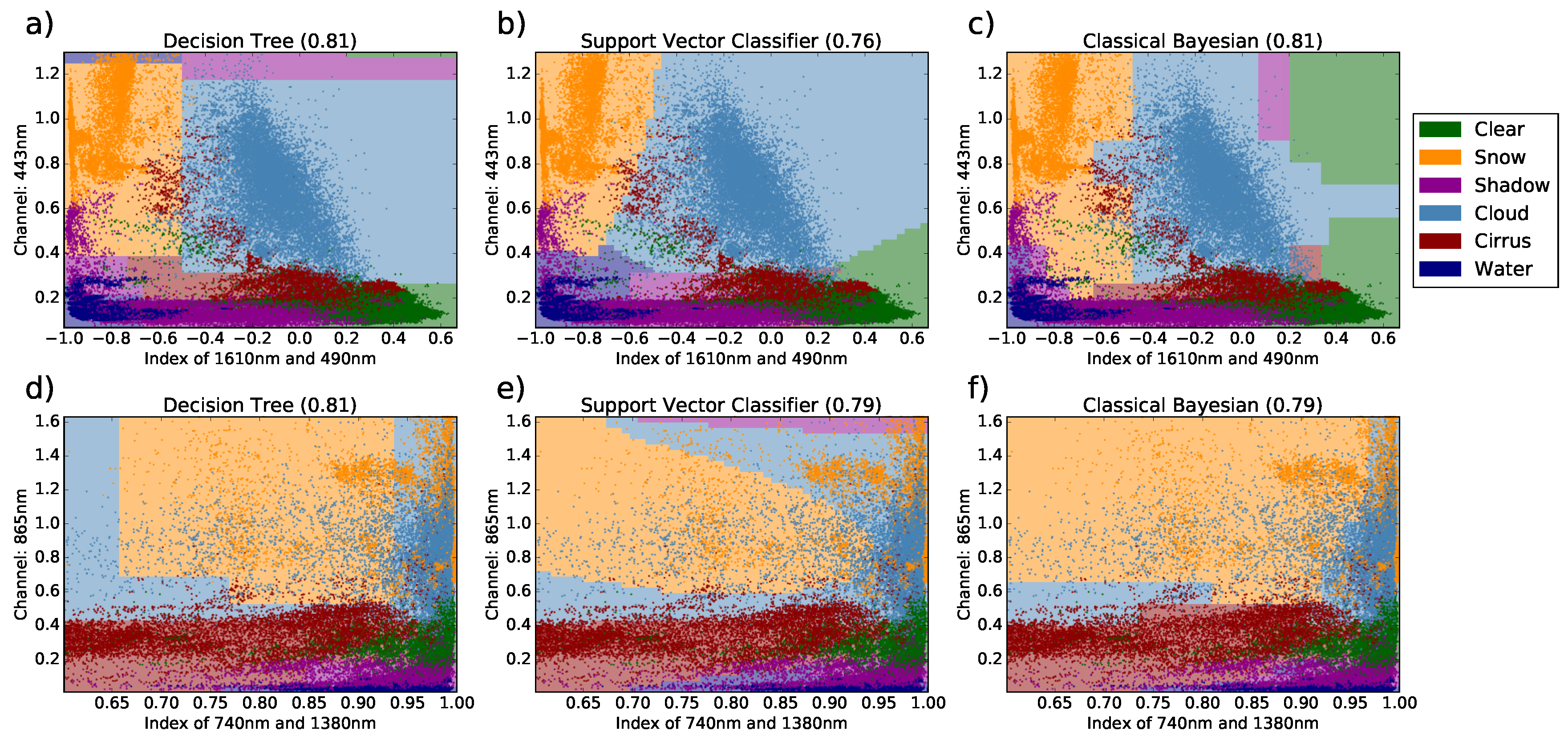
After setup, a classification algorithm can be used as a black box and purely judged by its performance concerning various metrics such as classification skill or needed computational effort. Such an analysis is depicted in
Figure 4 for three selected algorithms and two selected features. The features were optimized such that all three algorithms reach similar classification performance. The first column of the figure illustrates results for decision trees which are in principle limited to a rectangular tiling of the feature space. Ready-to-use examples of decision trees are given in
Section 3.2. The next column shows results for the same set of transformations, but for a support vector classifier (SVC), which has much more freedom for tiling the feature space. The last column depicts results for the classical Bayesian approach for which a ready-to-use algorithm is discussed in
Section 3.3. The separation of the feature space for this algorithm is defined by histograms with respect to a chosen binning scheme and determines the tiling of the feature space. A brief discussion on other possible methods is given in
Section 3.4. For visualization purposes, the feature space was limited to two dimensions and only simple transformations based on band math were allowed.
Those examples were chosen to illustrate the difference between selecting a particular machine learning method and selecting appropriate transformations of the input data. These aspects are well known and comprise almost textbook knowledge, but we included this material to highlight the fact that different transformations on the input data lead to different separation of the discussed classes in the feature space. Then, different algorithms can result in various compartmentations of the feature space for the classes, and both choices affect the final classification skill. These problems might have many multiple solutions, of which many can be approximately equivalent for various metrics. Choosing a particular algorithm from such a set of mostly similar algorithms can be random or subjective, without meaningful impact on the final classification result. Discussing individual aspects of a particular algorithm, e.g., a single threshold for a feature on a branch within a decision tree, could be meaningless.
3.1. Optimization and Validation Strategy
All presented classification algorithms are based on a common optimization strategy. We treat the construction of feature spaces and optimization of classification parameters independently and drive the search using random selection techniques. Each step consists then of a randomly selected set of features, a randomly selected set of parameters, and the constructed algorithm. We want to note that many algorithms can reduce the initially given feature space to a smaller, possibly parameterized, number. Feature spaces are constructed using simple band math formulas which are listed in
Table 2. The included relations depend on one to four bands, such that a space with
n features could depend on up to
bands.
To separate the training and validation, we randomly split the database into mutually exclusive sets for training and validation. This random split is performed on the total level of the database and includes all datasets as shown in
Figure 2. No spectrum which is used for training is therefore used for validation of the algorithm. The classification skill of each algorithm can be evaluated by the ratio of correctly classified cases which naturally varies between zero and one. This score is computed for the training and the validation data set, but only the value of the validation dataset is used for ranking different algorithms. A particular algorithm is excluded if the difference between the two scores becomes too high, which is a simple indication for overfitting.
This understanding of validation is somewhat differently used than in other parts of remote sensing, where validation is usually performed as a comparison of two products (e.g., total column water vapor derived from optical remote sensing measurements and GPS based methods) where one of them is considered as the truth or the product with smaller uncertainty. Here, it is used as confirmation that the machine learning algorithm shows similar results for two separate datasets and that the algorithm doesn’t just remember the training dataset.
All presented classification scores are therefore results for the database and the transfer to Sentinel-2 images is based on the assumption that the database is representative of all images. A high value for the classification skill is only a necessary condition for good classification results. If extensive experience with the results of a particular algorithm shows consistency problematic results for specific circumstances, the database should be updated to make it more representative, and the algorithm should be retrained.
3.2. Ready-to-Use Decision Trees
Decision trees can be best understood as a hierarchy of thresholds on single features. All possible decision paths form a tree with each path being a branch. We use the Python library scikit-learn [
36] which provides the needed functionality with the CART method [
37], which is an optimized version of the C4.5 method [
38,
39]. It returns optimized decision tree algorithms with prescribed depth for a given training data set which was projected to a selected feature space. The method aims to find a global optimum concerning classification skill and is free of additional parameters.
Decision trees could be constructed manually, but this work can be tedious and doesn’t guarantee to deliver better results than automated methods. Both, automated and manual construction aims for a global optimum for given training data and feature space. However, the space of possible decision trees might contain a large number of algorithms with almost equal classification skill near the global optimum. This indicates that the choice of a particular algorithm is certainly not unique and might leave room for discussion. Here, we decided to discuss pragmatically the best trees which we found regarding classification skill for the validation data set. Since the search for optimum feature space is random, we can not guarantee that the global optimum was found, but a long search time was allowed. The search was stopped when after 5000 attempts no better algorithm was found than already known.
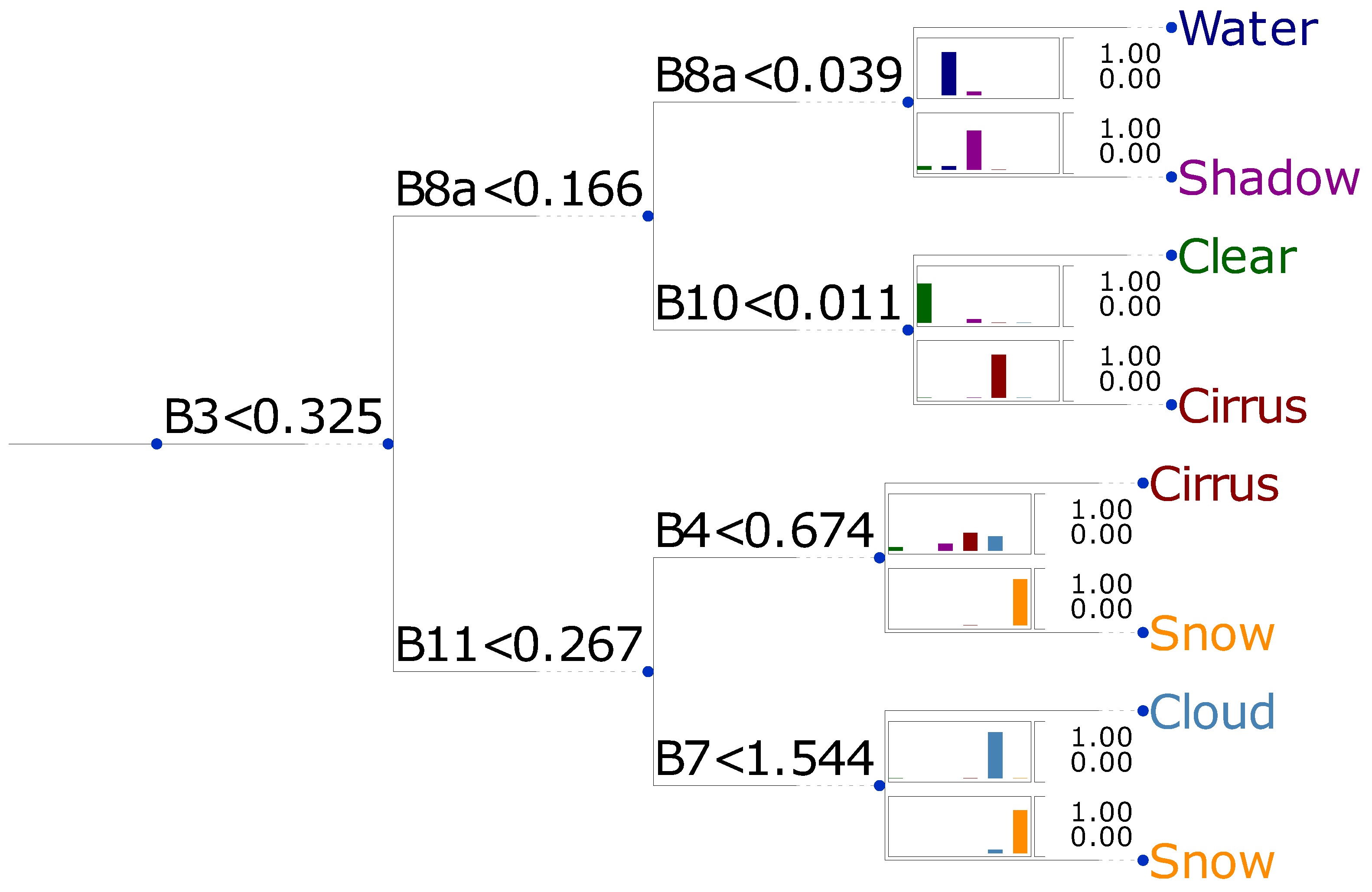
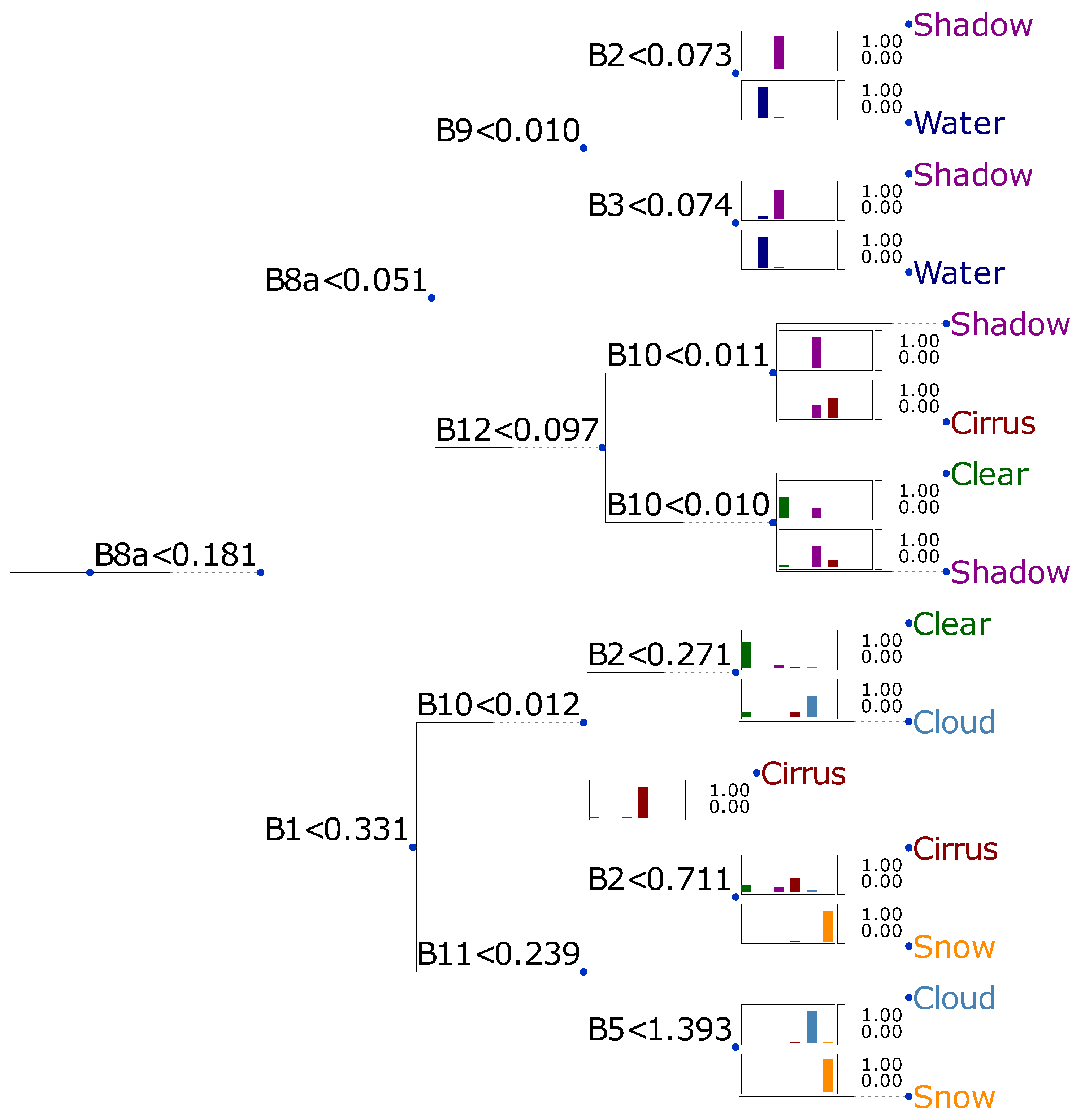
Figure 5 depicts a decision tree schematically with depth three and with a ratio of correctly classified spectra of
. The figure also illustrates the success rate of complete separation at the end of each branch. As an example, the final water class contains still a small fraction of shadows, but negligible remainders of other class members. The feature space of this tree is completely composed of bands, and the units are at-sensor reflectance. The ratio of correctly classified spectra increases slightly to
if band math is allowed within feature space construction.
Figure 6 shows the resulting tree in the same style as the previous figure. Both results illustrate that increasing the space of feature spaces can improve the classification performance, but that the effect is not dramatic when decision trees are concerned. This increase in classification skill requires the additional computation of features from bands which should reduce the computational performance of the algorithm.
These result nicely show, that even with a simple technique, a reasonable separation of the classes can be accomplished. The complexity and to some extent the expected classification skill increases with increasing depth of the trees. One can expect, that the increase in classification skill becomes negligible from a particular depth on and that an increase in depth adds only to the complexity and the risk of overfitting. When increasing the allowed depth to four, the ratio of correctly classified spectra increases to and a further increase to five only results in a value of . This indicates that a reasonable regime for classification trees is reached at a depth of four.
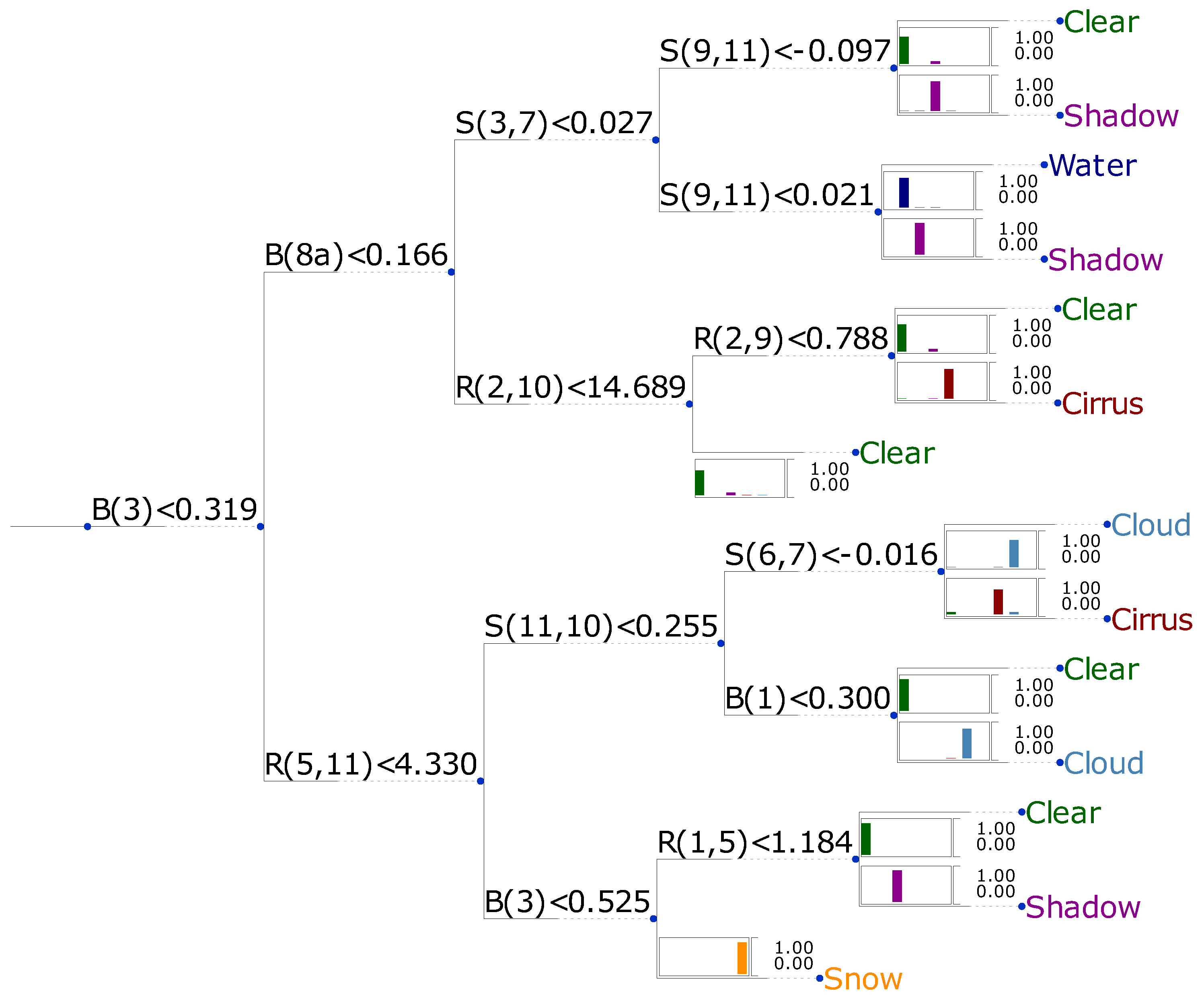
Similar as for the case of depth three, results at a depth of four with a feature space composed of bands only is shown in
Figure 7, while the result for the constructed feature space is shown in
Figure 8. Both algorithms show a similar rate of correctly classified spectra, but the algorithm with the derived feature space shows slightly better results with
vs.
. It is noteworthy that both decision trees have branches which terminate before the maximum allowed depth is reached. The best solution includes only band math functions for selecting a single band (B), the difference between two bands (S), and the ratio of two bands (R). It is beyond the scope of this work to discuss the physical reasons on how these particular algorithms function. Our focus is to present them in a way which makes them ready-to-use for many applications requiring a pixel mask as input. However, these algorithms are somewhat limited in their classification skill, such that more sophisticated methods might be desirable for certain applications. In the next section, we describe a classification system which reaches a much higher ratio of correctly classified spectra.
3.3. Ready-to-Use Classical Bayesian
Classical Bayesian classification is based on Bayes law for inverting joint probabilities. It can be expressed as:
where
expresses the joint occurrence probability of class
C under the condition of the feature
F, with
and
being the global occurrence probabilities of the class
C and the feature
F.
is the joint occurrence probability of the feature
F for the class
C. The term
classical distinguishes this approach from the much more commonly used approach of naive Bayesian classification, where one assumes that features are uncorrelated which allows to expresses the joint probability
as the product of single occurrence probabilities for each feature. Applications to cloud detection can be found in [
23,
40,
41] while an in-depth discussion of the classical Bayesian approach can be found in [
24]. In summary, the joint probability
is derived from a histogram of the database with the dimensionality of the number of used features. Free parameters are the number of histogram bins and a smoothing value. The success of this method is based on the selection of the most suitable feature space which follows the previously discussed random approach. The classification is performed by computing the occurrence probability for each class and selecting the one with the highest probability.
Since this method computes occurrence probabilities for each class, it is straightforward to include a confidence measure for each classification. Such a measure can be of great importance in post processing steps, where one might want to process only clear sky pixels for which the classification algorithm was very certain. The construction of such a measure is certainly not unique. We chose to proceed with a simple form, where the sum of all probabilities is normalized to one and the confidence measure is the relative value of the probability of the selected class and the sum of all other probabilities.
Similar as for the case of decision trees, not a single algorithm was found which represents the global optimum, but rather a whole suite of algorithms with similar classification scores. The est found option reaches a ratio of correctly classified spectra of
for the feature space:
.
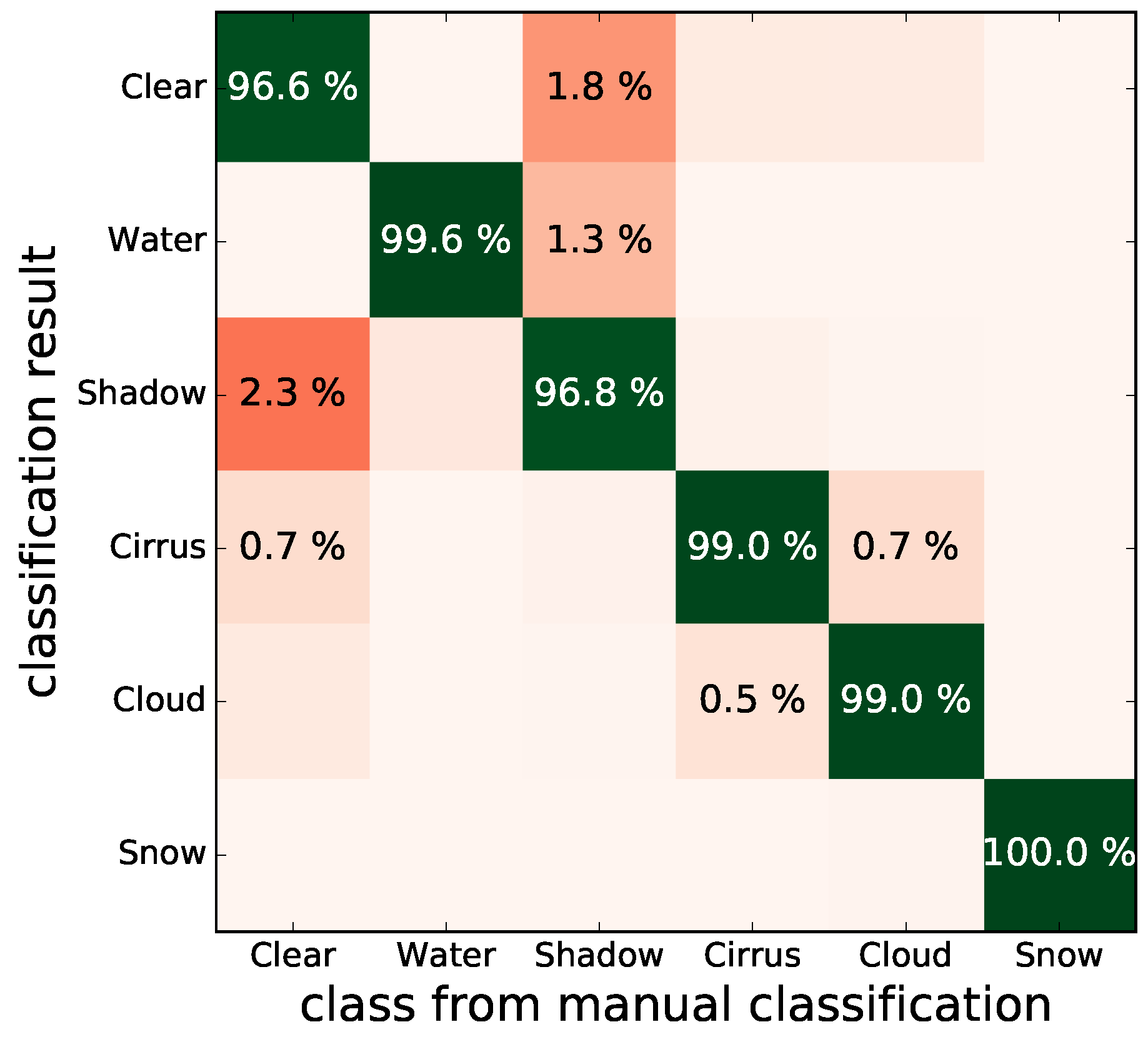
Figure 9 shows the confusion matrix for this algorithm, where off-diagonal elements above
are shown. The confusion matrix was derived from the validation dataset. All classes show excellent values. The largest misclassifications happen between clear sky and shadow and water and shadow classes. This is to be expected for any algorithm since the boundary of the shadow class is diffuse by nature. Also, some smaller confusion between water and shadow should be acceptable since both classes have members who are very dark in all MSI channels.
This figure shows similar information about the classical Bayesian algorithm as the histograms shown for each branch of the discussed decision trees (see
Figure 5,
Figure 6,
Figure 7 and
Figure 8). In contrast to the decision trees, the classification rates are shown for the total classification result and are not broken down for its inner structure. Such an approach is much less straightforward for classical Bayesian algorithms than for decision trees since the exploited features are used at once and are not ordered within an internal hierarchy.
Figure 10 shows RGB images of Sentinel-2 scenes together with the derived mask and the classification confidence. The figure captures diverse areas and includes mountainous regions, green vegetation, snow and ice, as well as clouds and shadows. Especially the mountainous regions show that a separation of ice and shadows is achieved. Many pixels are marked as affected by shadows, which can be useful when atmospheric correction is performed. Only a few spatial patterns from the images are present in the confidence masks which indicates that this measure is mostly independent of the scene. Some larger water bodies and snow-covered areas can be found in the confidence maps as areas of reduced noise, but this only illustrates the homogeneity of the scene itself. The used color scale does not exaggerate small variations of the confidence since these might be hard to interpret. However, depending on the actual application, it can be straightforward to use the confidence value and together with appropriately selected thresholds to filter data for further processing. The dark water bodies in panel b of the figure include some areas which are wrongly classified as shadow. This can be expected from the analysis of the confusion matrix (see
Figure 9). The confidence value for these areas is only slightly reduced.
3.4. Comparison with Commonly Used Techniques
This work focuses on decision trees and classical Bayesian algorithms, but the results from other techniques help to put them into perspective. Commonly used techniques from the domain of machine learning are random forests (RF) [
42,
43,
44], support vector classifiers (SVC) [
45], and stochastic gradient descent (SGD) [
46,
47]. Methods which also compute class probabilities can be combined using adaptive boosting [
48,
49]. We used the implementations of these techniques in scikit-learn to derive additional classification algorithms using the same random search approach as outlined above.
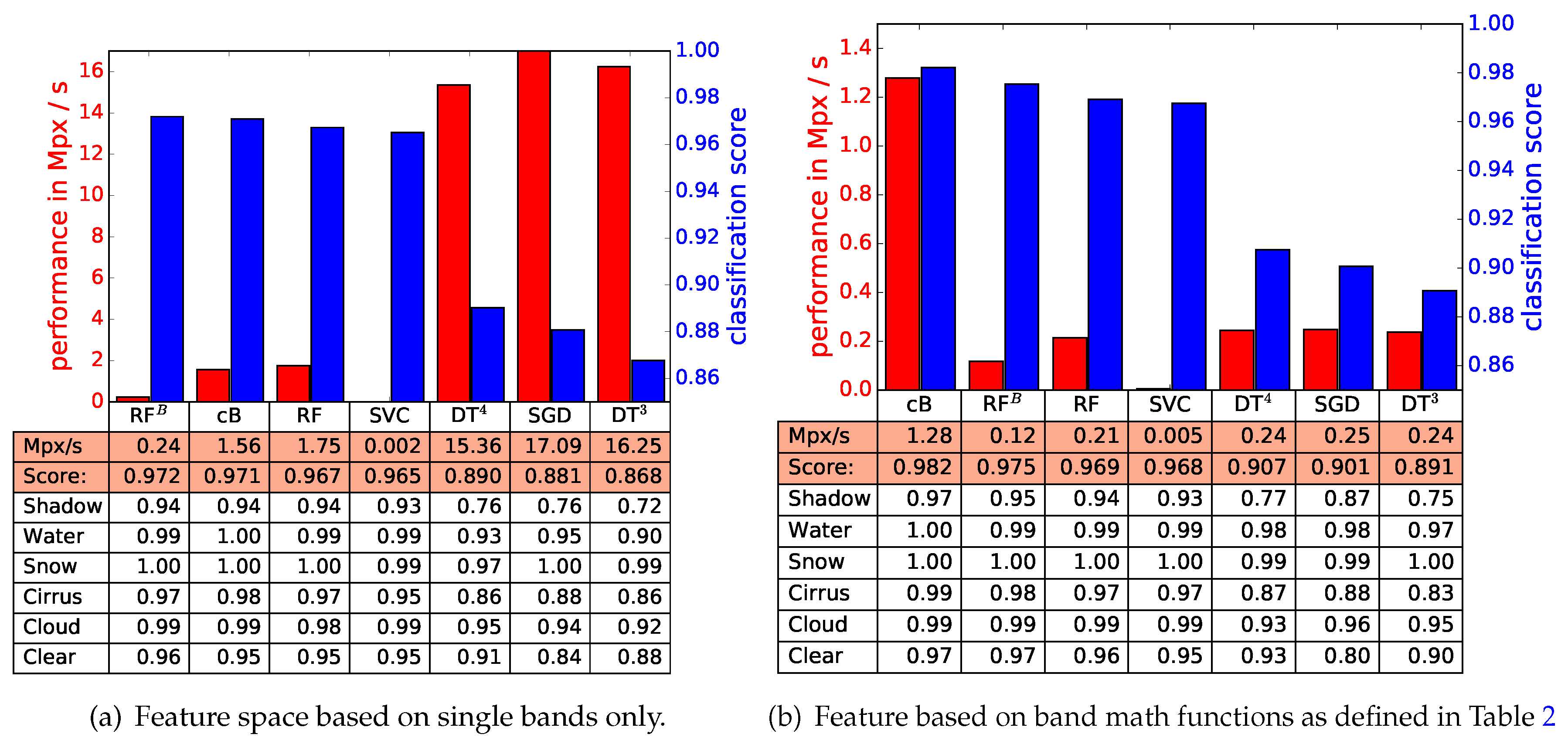
Before presenting the results, we want to emphasize that they represent merely lower boundaries for classification skill and processing speed. The used techniques have free parameters which were sampled by a random search, but experts for particular techniques might be able to use better implementations or find better sets of parameters and hence produce better or faster results than the ones presented here. However, the results might be representative for a typical user who uses an implementation, but is not aware of all possible details. An overview about the numeric experiments is given in
Figure 11. The analysis was separated by the types of allowed feature spaces. The left panel shows results for original bands only, while for the right panel feature spaces based on band math based on
Table 2 were allowed. All presented decision trees from
Figure 5 to
Figure 8 are included as well as the classical Bayesian algorithm which was discussed in
Section 3.3. The classical Bayesian for the single band feature space is based on
. The parameters of the other techniques are not listed here since they depend on a specific implementation and might not be portable among different implementations.
The processing performance in Mega Pixel per second (Mpx/s) is also reported. All computations were performed on an Intel i5-3570 CPU @ 3.40 GHz. These figures depend on the implementation of a particular technique and should only be used to judge a particular implementation and not the technique as such. The classical Bayesian is implemented in the Python language and uses parts of NumPy and SciPy [
50]. It seems obvious that algorithms which use a feature space based purely on bands should have an advantage since the calculation of features can be skipped. This can be nicely seen for the classical Bayesian algorithms, but breaks for the decision trees as well as the stochastic gradient descent, which only shows that even for a single implementation of a technique the real run-times can vary drastically. Possible reasons for this effect might be a change of the used numeric type between the two approaches.
When the classification skill is concerned, random forests, support vector classifiers, and the classical Bayesian show quite similar results and other factors should be discussed when a particular algorithm needs to be selected. Although not impossible, portability of scikit-learn algorithms is currently problematic and only safely possible when the algorithm is retrained on each new computer system. Classical Bayesian algorithms are safely portable among setups which provide a recent python distribution. Also, it shows good processing performance even when implemented in a language which is sometimes referred to as slow.
For the scikit-learn techniques, adaptive boosting was only applied to the random forests since other methods did not provide class probabilities. Only minor improvements are found, which can be expected since random forest already is an ensemble method. The classical Bayesian provides probabilities, and adaptive boosting can be applied. It is not discussed here since it was planned to share the algorithm and a combination with scikit-learn introduces problems with portability.
The classification scores on a per-class level show expected results with the smallest results for shadow and clear sky pixels. This is caused by the diffuse nature of both classes and should not come as a surprise. All in all, the classes show all good scores and the discussion of confusion matrices is not needed.
The classical Bayesian gains little classification skill for feature spaces based on band math. In general, this method is limited to smaller numbers of features and was limited to five for this study. The number of selected features defines the dimensionality of the underlying histograms, and the number of bins sets requirements for needed computer memory as well as the amount of required training data. This indicates that this limit is more practical than theoretical. The stability of the classification skill for both approaches shows that all relevant information for this task can be included within five features.
4. Conclusions
A database of manually labeled spectral from Sentinel-2 MSI was set-up and presented. It contains spectra as well as metadata such as observational geometry and geographic position. The data is labeled with the classes: shadow, snow, cirrus, cloud, water, and clear sky and can be used to create and to validate classification algorithms. The considered classes are crucial for atmospheric correction as well as other methods which rely on pixel masks for the filtering of input data.
The series of Sentinel-2 platforms will deliver unprecedented amounts of Earth observation data which calls for fast and efficient algorithms for data processing. Such algorithms can establish a baseline to quantitatively evaluate the added value of algorithms with a higher demand on computational resources. Machine learning techniques offer straightforward routes for the development of fast algorithms and were applied to derive ready-to-use classification algorithms. Decision trees were discussed since they are simple-to-understand and easy-to-implement and are therefore suitable candidates for baseline algorithms. It was found that trees of depth four show a classification performance as good as trees with higher depth. The ratio of correctly classified spectra reached
, while trees of depth three can reach values of
. Several ready-to-use decision trees were presented in schematic form. Feature spaces based on the bands alone as well as based on band math were tested. For algorithms with the same number of features, those based on the full range of band math formulas gave only slightly better results than those using single bands only. An algorithm based on the classical Bayesian approach was discussed to increase the classification performance to a value of
. A limiting factor in a further increase of the detection skill is the inherent diffuse separation of clear sky and shadow pixels. Smaller effects are caused by a misclassification of dark water and shadow pixels. The discussed database, the presented decision trees, as well as the classical Bayesian approach are available at [
33].
A comparison with other widely used machine learning techniques shows, that similar results can be achieved with random forests and support vector classifiers. Since portability and processing performance can be an issue, the classical Bayesian algorithm is a good candidate for general use and distribution of algorithms.
The presented classification is an essential pre-processing step, which in most workflows will be followed by additional processing or further classification. The derived classification can then be used as input data filter for these steps.
Selecting an actual algorithm should be based on user requirements which diminish the value of general suggestions. If users need full control over the algorithm and are willing to invest labor, the database and one of the suggested machine learning methods can be applied. This approach is of particular value if the detection of a subset of the presented class is required with higher accuracy than others. If only a minimum of extra work can be spent on this task, potential users should choose either the presented implementation based on the classical Bayesian or one of the presented decision trees. Selection of the decision trees depends mainly on the required processing speeds and classification performance. For highest processing speeds, the decision tree of depth three based on single bands should be used (see
Figure 5). If this requirement can be relaxed, the decision tree of depth four based on band math (see
Figure 8) delivers better classification performance with possibly decreased processing speeds. Much better classification performance can be expected from the classical Bayesian implementation which is ready-to-use.