1. Introduction
Remote sensing, especially in the microwave region, has become the most convenient and feasible tool widely applied in deformation mapping. In the Three Gorges Region (TGR), due to the often limited access to Global Positioning System (GPS) measurements, the high costs of skilled labour and instrumentation required, it is difficult to obtain sufficient local geodetic measurements [
1]. The usage of satellite remote sensing data for landslide studies in the TGR can be traced back to the 1980s [
2]. Due to the high humidity caused by the monsoon climate of this region, optical sensors are often limited in obtaining an effective time series of measurements. A Synthetic Aperture Radar (SAR), which is able to work both day and night during all weather conditions and which repeatedly acquires time series of high-resolution images covering large areas, has been recognized as an effective and powerful sensor for landslide monitoring [
1,
3].
The differential Interferometric SAR (DInSAR), which is capable of detecting surface deformation over a large area in the direction of the satellite Line of Sight (LOS) with a centimetre-to-millimetre precision, has been extensively applied to monitor volcanic activities, earthquakes, mining deformations, glacier movement, subsidence and landslides [
4,
5,
6,
7,
8,
9,
10,
11,
12,
13]. Time series algorithms have been developed to extend the use of DInSAR for temporal evolution of ground deformation, which can be essentially divided into two broad categories: the Persistent Scatterer (PS) InSAR [
14,
15,
16] and Small Baseline Subset (SBAS) [
17,
18].
However, the applications of DInSAR/time series DInSAR in the Three Gorges Region are limited by the difficulties arising from steep slopes, dense vegetation cover and high humidity. The experiment using PS-InSAR with ENVISAT data to measure deformation in the TGR area did not find sufficient PS points [
19], which lead to the failure of phase unwrapping [
3]. The attempt of using PS-InSAR with ASAR images to monitor the Shuping landslide failed for the same reason [
1]. Experiments applying the SBAS method on TerraSAR-X (TSX) data in the Three Gorge Region did not find significant dependence upon the perpendicular baseline or dramatic increase of reliable scatterers over time, suggesting the use of SBAS method has limited benefit in this case [
20].
In addition, DInSAR measurements on the Shuping landslide yielded varied results in previous studies. Fu et al. obtained DInSAR measurements on 12 corner reflectors (CRs) (−1–11 cm in 140 days) of the Shuping landslide using five ENVISAT ASAR images spanning from September 2005 to March 2006. The investigated period missed the most active period of the Shuping landslide [
21]. Xia et al. used the same 12 CRs to derive linear displacement rates of 1–11 cm/year from September 2005 to June 2007 [
22], in contradiction with the results of [
21] with a different deformation rate but an overlapping observation period between September 2005 and March 2006. For the period between September 2005 and June 2007, extensometer measurements show 50–70 cm/year displacement with a dramatic increase from May to August 2007 [
23], which is different from the linear trend monitored by PS-InSAR.
It should be noted there is a limitation of DInSAR with regard to the maximum detectable displacement. If no prior knowledge of the deformation is provided, which is usually the case, the implementation of phase unwrapping relies on an assumption that the phase difference between any two neighbouring pixels does not exceed
. This implies the maximum detectable deformation per pixel is half wavelength. In addition, phase gradients larger than 0.5 fringes may cause large-scale unwrapping errors, which means the displacement gradient between two neighbouring pixels is limited to 1/4 wavelength [
24]. Thus, the maximum detectable displacement gradient (DDG) of InSAR measurements is
where
denotes the maximum DDG,
is the wavelength of the SAR sensor and
is the pixel size of the SAR images for classical interferometry, or distance between persistent scatterers for PS techniques. The value of
depends on the satellite. For example, in the case of TerraSAR-X Hi-resolution Spotlight (with wavelength 0.031 m, pixel size 0.456 m) data, the maximum DDG is 0.0059 using a small multi-looking factor of 2. This means that over a ground distance of 1 m (about 1 pixel in the case of TSX Hi Res data), a displacement of 0.59 cm in one revisit cycle (11 days) will be underestimated even when given very high phase coherence. In a real scenario, the coherence is usually lower, especially in densely vegetated areas. The theoretical limit will drop with the coherence leading to further underestimation, which is the case in our study. Many slow-moving landslides (~1.6 m/year as defined in [
25,
26] and cases reported in [
27,
28]) can exceed this threshold of displacement gradient, especially near the landslide boundary.
The sub-pixel Offset Tracking (sPOT) technique (sometimes referred to as Pixel Offset Mapping) has previously been applied to monitor glacier movements, volcanic activities and co-seismic tears in the solid earth resulting from severe earthquakes to address the technical defects and limitations of conventional DInSAR techniques, particularly their sparse coverage and the impact of dense vegetative cover [
29]. In the past, studies on offset tracking techniques to measure slope movements are dominated by using optically sensed imagery from spaceborne or airborne platforms [
30,
31,
32,
33,
34,
35].
For SAR sensors, initially medium resolution SAR imagery were employed in offset tracking for measurements of very large deformation (metres to tens of metres) [
36,
37,
38]. Intensity Tracking (based on Normalized Cross Correlation) was proposed and implemented on a set of ERS-1/2 SAR data acquired from March 1992 to February 1996 in order to estimate the motion of Monacobreen in Northern Svalbard [
36]. It indicated that in the case of various SAR missions (RADARSAT, ERS-2, ENVISAT, ALOS) with a more than 24 day revisit interval, intensity based tracking is the only technique able to correctly measure glacier movement. The work by [
37] proposed a PO-SBAS approach using ENVISAT data to measure large displacements (several metres) occurring in the inner part of the Sierra Negra caldera due to the October 2005 eruption. This PO-SBAS approach attempted to minimize the perpendicular baseline via small baseline combinations of offset pairs. However, the TSX data employed in our study consistently has short baselines ranging from 12 m to 220 m, so the benefit of creating a SBAS network is limited. With the availability of higher resolution SAR data, Manconi et al. obtained post-event deformation maps for emergency evaluation of a large, rapidly-moving (10–20 m) landslide [
39,
40,
41]. The same PO-SBAS approach was applied to ascending and descending pairs of COSMO-SkyMed images to retrieve 3D deformation of the Montescaglioso landslide (Italy) of which the main movement occurred over 15–20 min with an average velocity of about 0.5–1 m per minute.
Sub-Pixel Offset Tracking has recently been employed to derive centimetre-level landslide rates in the Three Gorges Region using 1–3 m resolution space-borne SAR images. Li et al. [
42] used four pairs of TSX HS images to derive 2D (azimuth and slant range) landslide displacement in the Three Gorges Region. The results indicate May–August 2009 was the most active period of the Shuping landslide. However, due to the impact of dense seasonal vegetation cover, some results still show false deformation features in the slant range direction. Singleton et al. [
20] conducted further analysis focusing on the 540,000 m
2 area centred on the landslide blocks. This work focused on the use of previously installed Corner Reflectors (CRs) with offset tracking, to derive a deformation magnitude for each CR in order to plot time series deformation curves, confirming a dramatic increase in landslide rates from May to August in 2009. However, it was pointed out that the errors associated with the corner reflector measurements are an order of magnitude lower than those calculated from densely vegetated terrain. Also, it was pointed out in [
43] using ground-based SAR (GB-SAR) data to measure the displacement from artificial CRss, the main constraint of the offset tracking technique is the need of CRs. This raises a large question for the vast majority of regions where no CRs are available especially in densely vegetated terrain. The question arises: are sPOT techniques able to correctly measure landslide rates? This is the starting point of this study.
As the main objective of this study, the potential of using natural scatterers is assessed on deformation measurements using an offset tracking approach by combining sub-pixel cross-correlation with a time series statistical analysis, which makes a significant difference in that it does not rely on high contrast surface features (e.g., Corner Reflectors). Unlike the scenario of a very large deformation [
36,
37,
38,
44], this study aims to exploit the use of offset tracking with time series high-resolution SAR data covering two years, to derive the temporal evolution and spatial distribution of a slow-moving landslide with an active period of months and accumulative displacement of up to 1 m per year. The study area is characterized by dense vegetation cover on steep slopes, which causes rapid decrease of temporal correlation/low coherence of DInSAR on natural scatterers. Given the deformation velocity, the offsets caused by seasonal changes of vegetation cannot be ignored, which increases the challenge of the use of natural scatterers.
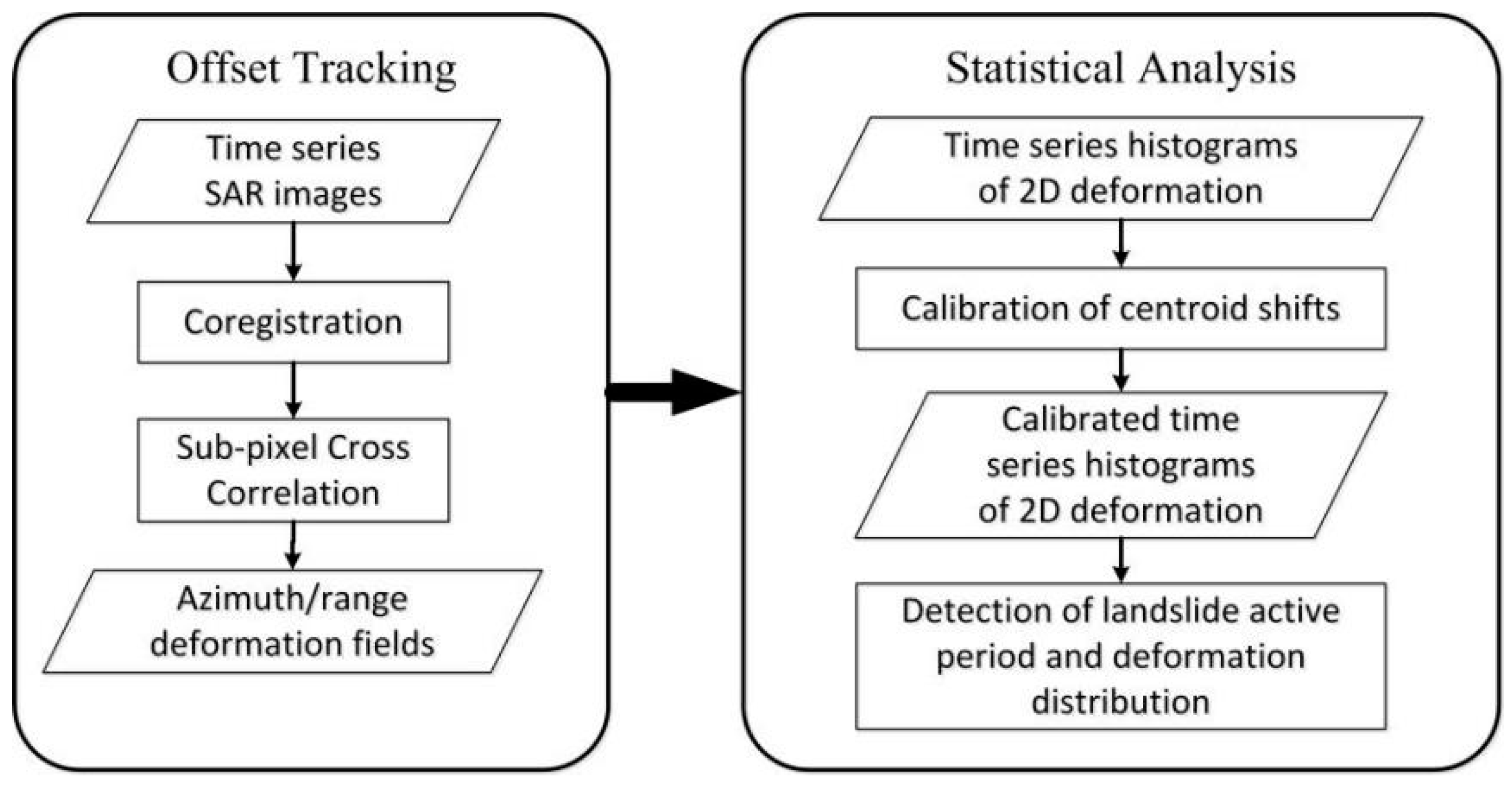
In this paper, sub-Pixel Offset Tracking is applied in monitoring ground deformation in densely vegetated terrain and concentrating on the evaluation of its general application in the vast majority of regions where CRs are not available. Firstly, the landslide displacement rates in the field site, Shuping landslide area, were measured from artificial CRs using the fully available 2 year time series TerraSAR-X (TSX) Hi-resolution Spotlight data acquired from February 2009–April 2010 and January 2012–February 2013. Secondly, the correlation between the landslide displacements and water level variations of the Three Gorges Reservoir were then analysed to infer a possible failure mechanism for the Shuping landslide. Finally, as a key part of this study, the capability of sPOT techniques for measuring ground displacements in densely vegetated areas was assessed by a statistical analysis of deformation magnitudes derived from natural scatterers on the whole landslide body. Based on the above analysis, an approach is proposed to extend the applications of sPOT to densely vegetated terrain without requiring artificial CRs.
2. Study Site
The Three Gorges Region (TGR) of China, which is located between latitude 28°32′N–31°44′N and longitude 105°44′E–111°39′E, is the region directly or indirectly involved in the submersion of the water storage of the Three Gorges Project (TGP). It stretches along the Yangtze River including 16 county-level divisions of the Chongqing municipality and 4 divisions of the Hubei province. The Three Gorges Dam (TGD), located at Sandouping Town to the west of the city of Yichang, China, is one of the world’s largest civil engineering structures, which blocks water to form a 660 km long and ≈1.1 km wide reservoir. The water level of the Yangtze River in the TGD rose from 66 m to 135 m, 156 m and eventually 175 m above sea level during the three impoundments in 2003, 2006 and 2009. The Three Gorges Project (TGP) does a remarkable job of generating a huge amount of electric power as well as controlling floods and improving the shipping capacity of the Yangtze River. However, the construction and operation of Three Gorges Dam resulted in a significant land use change, which altered energy and water budgets, affected the regional weather and climate patterns, and is linked to the dramatically increased geological hazards dominated by landslide activities in the Three Gorges Region [
45,
46,
47]. Numerous landslide activities have occurred in residential areas with high population density, causing a lot of wasted resources and loss of property.
As the construction and operation of the Three Gorges Dam raised major concerns about its environmental impacts, a number of studies have been carried out on several topics, including terrestrial ecosystems, sedimentation, pollution, river discharges, regional climate and induced geological hazards dominated by landslides [
48,
49,
50,
51,
52,
53].
Most of the landslides which occurred in the Three Gorges Region are identified as being triggered by water, with the variations of reservoir water level and seasonal heavy rainfall being the two main factors [
23,
54].
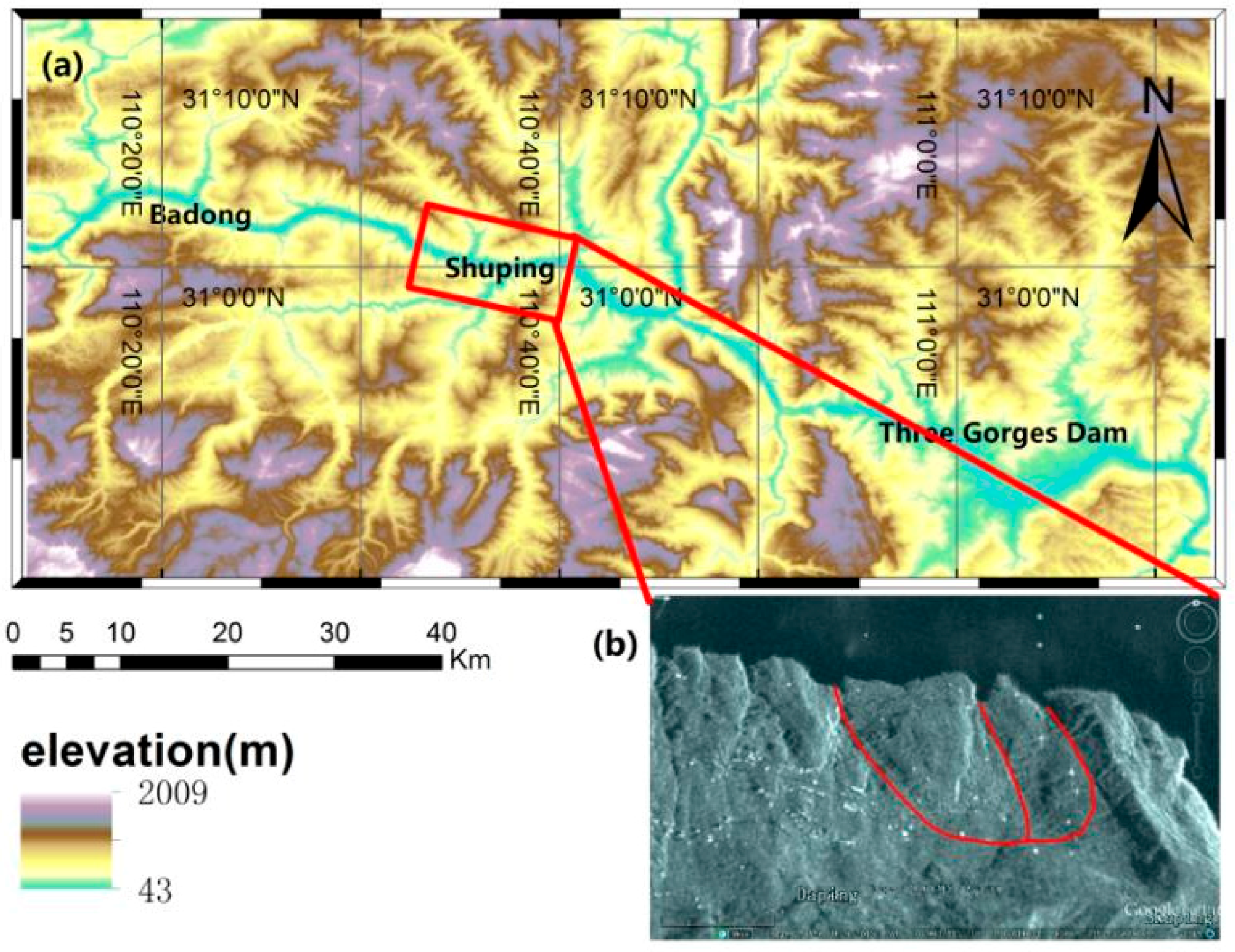
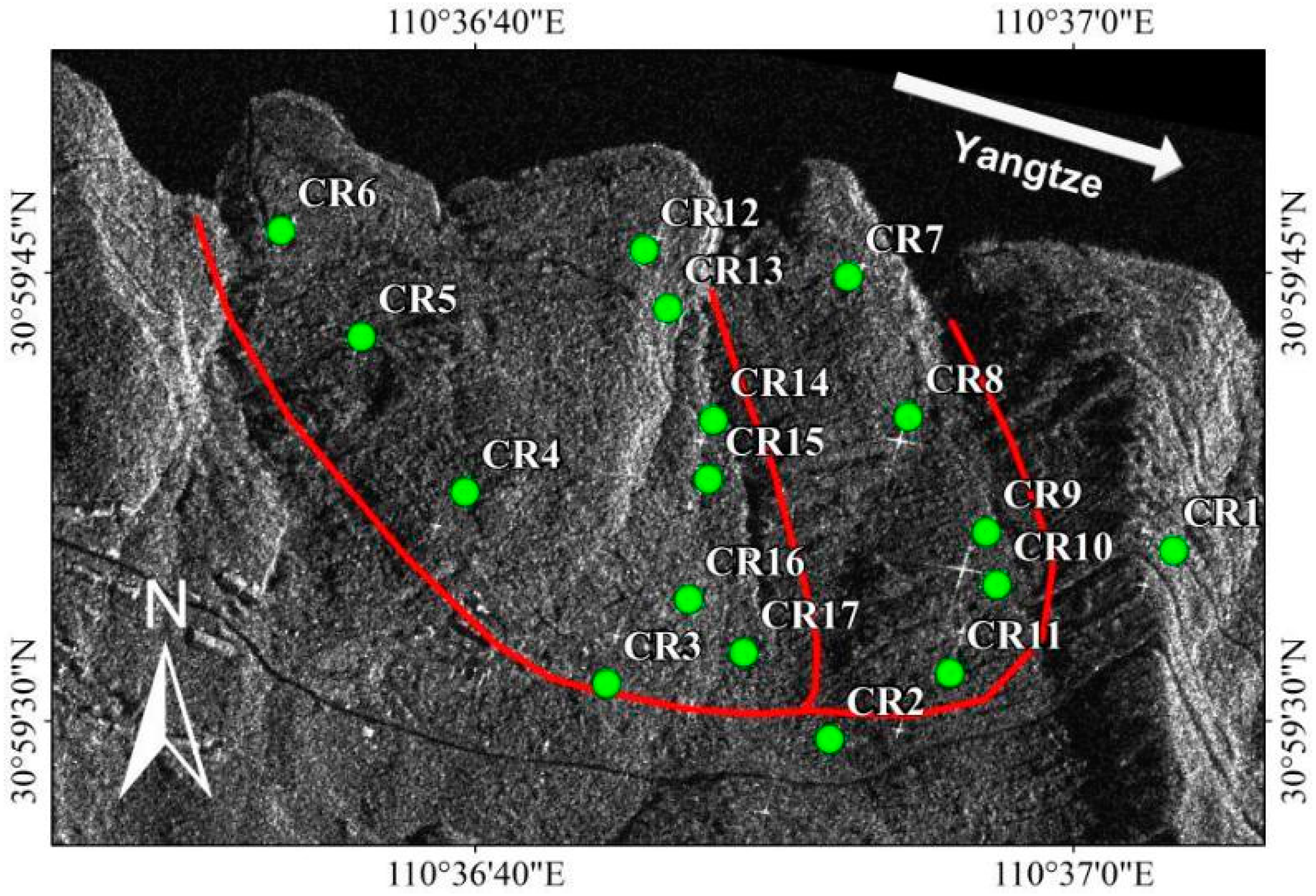
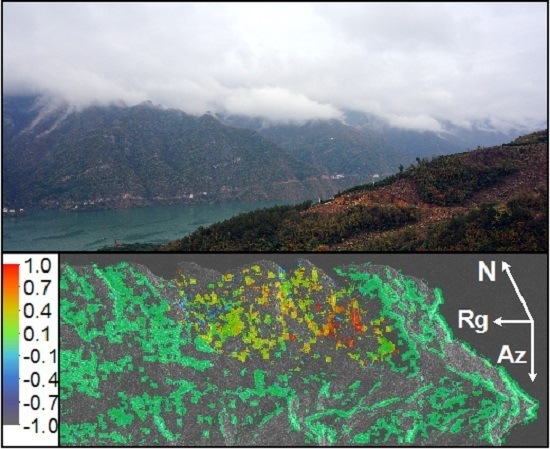
The field site, Shuping landslide area, is located on the south bank of the Yangtze River near Shazhenxi Town, Zigui County with centre coordinates of 30.996°N, 110.609°E as indicated in
Figure 1a. The Shuping landslide was identified as an ancient landslide during the field investigations before the construction of Three Gorges Dam [
55]. This area is underlaid by muddy sandstone and sandy mudstone of the Triassic Badong formation. The landslide is composed of two blocks as marked in
Figure 1b facing the North, with a width of about 650 m, elevation ranging from 65 to 400 m, thickness of 40–70 m, volume of about 20 million m
3 and average slope varying from 22° on the upper part to 35° on the lower part [
54]. The landslide area is characterised by terraced slopes densely covered with orange trees. The landscape photos of the Shuping landslide area in
Figure 2 show cracks on the local infrastructure and one photo of one of the CRs is shown.
The Shuping landslide is a typical slope accumulation landslide where deformation has increased since the water impoundment of the Three Gorges Reservoir in 2003. In June 2003, significant deformation appeared on the slope and it acute from 8 February 2004 on. This serious deformation posed a significant danger to 580 inhabitants and 163 houses directly in its path and most of the inhabitants had moved of the landslide area by May 2004. According to GPS measurements, from January 2004–October 2006, when the reservoir water level varied between 135 and 145 m, the ground deformation of Shuping landslide area was predominantly a combination of squirm and uniform deformation. The accumulative displacement reached 300 mm from August 2004 to August 2006, 250 mm from August 2006 to July 2007, 500 mm from August 2007 to February 2009, and 700 mm from February 2009 to February 2010 according to extensometer measurements along the centre line of eastern block [
23,
54]. Following this for every single year, the deformation magnitude periodically fluctuates with variations in the reservoir water level which also coincides with rainfall periodicity [
56].
5. Discussion
5.1. Performance Assessment of sPOT on Vegetated Surface
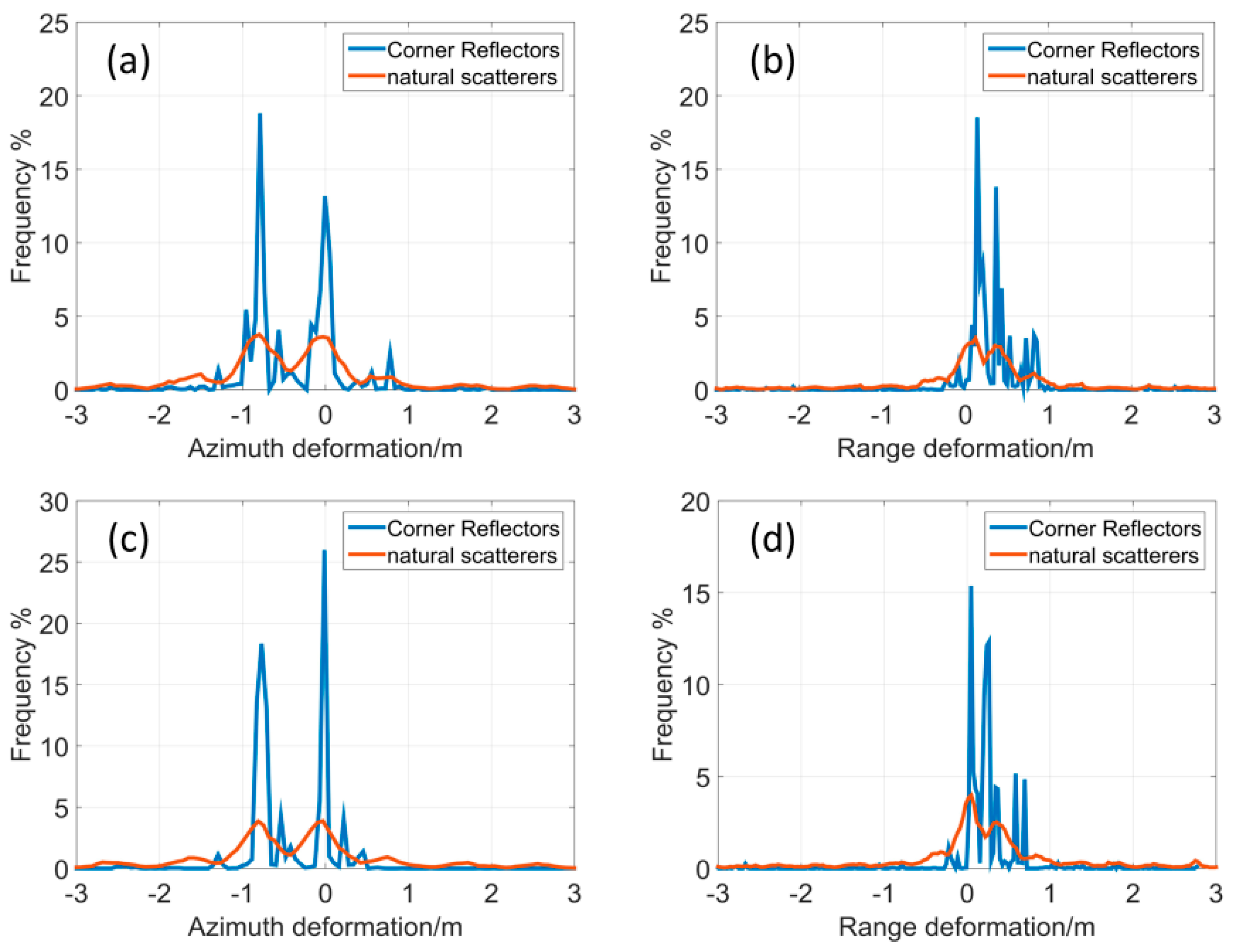
The performance of sPOT in the vegetated areas is assessed by cumulative histograms of azimuth and range offsets [
20,
67] derived from a rectangular area (242,035 m
2) on the stable ground adjacent to the landslide body. In COSI_Corr, the sub-pixel accuracy is achieved by a quadratic polynomial interpolation of the correlation peak instead of oversampling the SAR intensities. Therefore, we only alter the correlation window size in the tests.
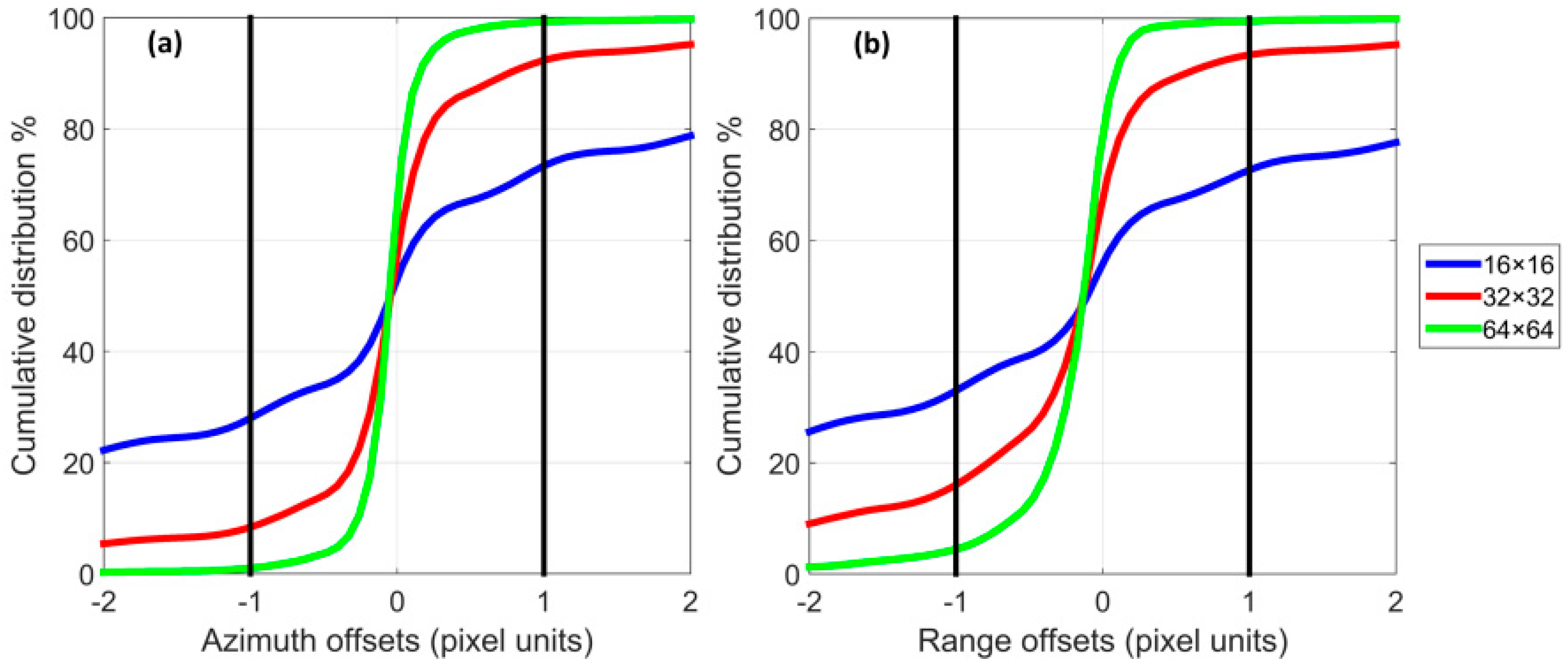
Cumulative Distribution Functions (CDFs) of azimuth/range displacements are plotted for different correlation window sizes, as shown in
Figure 18.
The elapsed time of each parameter setting in a 64 bit Windows 7 system (processor speed: 2.3 GHz, RAM: 8 GB) is listed in
Table 4.
We can see that using a correlation window size of 32 × 32, in the CDFs of both azimuth and range displacements, over 75% of pixels are characterised by displacements around zero and within ±1.0 pixel offset range. A larger window size improves the accuracy but dramatically increases the processing time (detailed in
Table 4). Larger window sizes also increase artifacts and reduce the resolution of the deformation fields [
67]. In the above experiments, it is found that a 32 × 32 correlation window size fulfils the research objectives with a reasonable time consumption and is therefore chosen in the processing for both CRs and vegetated surface.
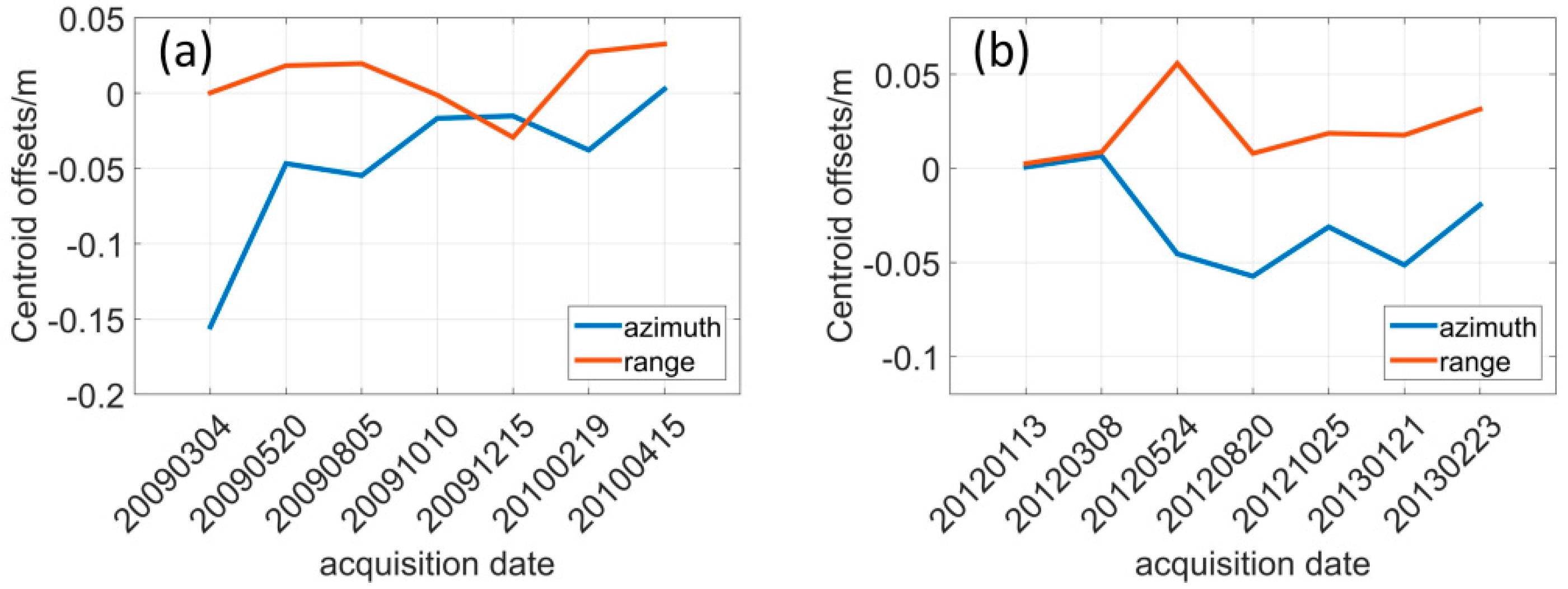
Slight offsets of the centroid are observed from the CDFs of azimuth/range displacements (
Figure 18), which very likely results from the impact of dense vegetative cover. This is also pointed out in
Section 4.3 via the time series histograms of 2D deformation derived from stable ground, which can be corrected by the proposed calibration technique. As long as the majority of the pixels are characterised with deformation around a certain magnitude within a reasonable offset range, the parameters are considered satisfactory to provide sufficient robustness for sPOT method in the vegetated terrain.
5.2. Accuracy Assessment of Sub-Pixel Offset Tracking (sPOT)
The applicability of sPOT techniques to monitor landslides is determined by their accuracy, which consists of image co-registration errors and the uncertainty associated with Cross Correlation. In theory, the uncertainty of Cross Correlation can be calculated as the standard deviation error of the determination of the correlation peak [
68], expressed as follows:
where
is the cross-correlation coefficient;
is the number of independent samples involved in the Cross Correlation, referring to the original image resolution element. The correlation peak is then interpolated using a quadratic polynomial for 1/4 pixel accuracy.
Thus, with a correlation window size of 32 × 32 and a correlation coefficient no less than 0.783 for all CRs, the Cross Correlation has an uncertainty of 0.02 pixels. This is validated by a simulation of cross-correlation using the same parameters with the image acquired on 21 February 2009 as the master and the same image shifted by 5 pixels in slant range direction and 8 pixels in inverse azimuth direction as the slave. The 2D offsets derived by the cross-correlation are analysed and shown in
Table 5. These results are obtained with the correlation coefficients ranging from 0.806 to 0.999, almost the same correlation coefficients measured from CRs.
From
Table 5, we can see that with the correlation coefficients of no less than 0.8, the cross-correlation measures a mean offset of 5 pixels in the range direction and−8 pixels in the azimuth direction, exactly the same offsets as the image shifted prior to the simulation. The standard deviation errors are 0.022 pixels and 0.021 pixels respectively in the range and azimuth directions. This is in alignment with the theoretical uncertainty calculated for CRs (with a correlation coefficient no less than 0.783) using Equation (6). Thus, the calculated uncertainty is believed to be a good estimate of practical errors of cross-correlation.
It is worth noting that the coregistration is not perfect. The residual errors from the coregistration step may lead to uncompensated image offsets which can be mixed in with the investigated displacements [
37]. Thus, the overall errors of offset tracking should consider the coregistration errors with the standard deviation errors of cross-correlation. Taking into account both of the cross-correlation uncertainty and the co-registration errors up to 1/10 pixels, the theoretical accuracy of sPOT comes to 0.12 pixels. Substituting the range pixel spacing of 45.6 cm and azimuth pixel spacing of 86.2 cm of TSX Spotlight data into Equation (6), the accuracy of offsets measured from CRs is 5.5 cm in the range direction and 10.3 cm in the azimuth direction. Thus, the offset tracking technique has sufficient accuracy on CRs to monitor Shuping landslides with regard to the annual displacement rate up to 1 m in the azimuth direction and up to 0.7 m in the range direction.
The corner reflector measurements were compared with the results of the same period presented in [
20], the differences between slant range/azimuth offsets are shown in
Table 6.
As shown in
Table 6, the root mean square error (RMSE) of offset measurements is 0.088 m in azimuth direction and 0.032 m in range direction, both within the expected accuracy of corner reflector measurements, which reaches a good agreement from a statistical standpoint.
The accuracy of the offsets derived from natural scatterers in the vegetated terrain is assessed by simulation using the correlation coefficients of 21 February 2009–15 April 2010 image pair as inputs. The histogram of the correlation coefficients of natural scatterers is plotted in
Figure 19. All contributions from artificial CRs were masked out before analysis.
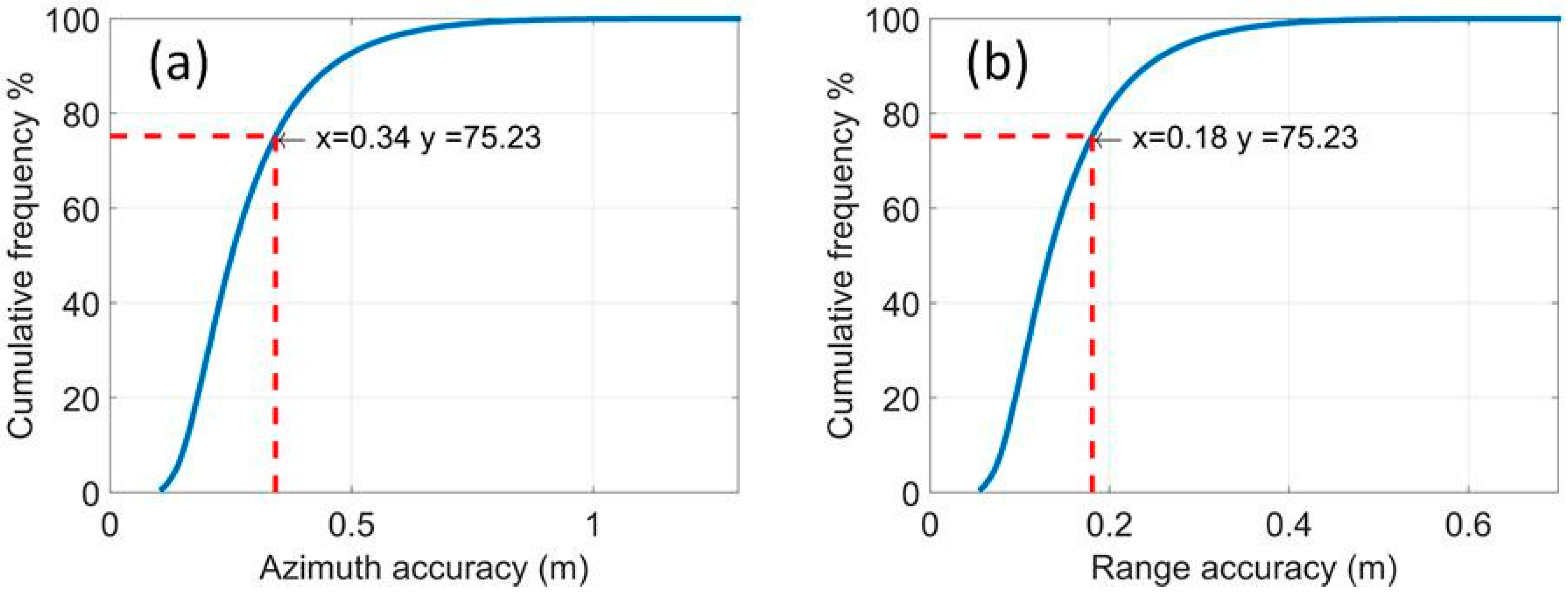
The accuracy consists of the simulated uncertainties using Equation (6) and co-registration errors of 1/10 pixel size. The cumulative distributions of the 2D accuracy are shown in
Figure 20.
From
Figure 20, we can see that over 75% of natural scatterers have improved accuracy rates of 34 cm in the azimuth direction and 18 cm in the range direction. For a typical correlation coefficient of 0.25, the lowest accuracy is 24 cm in the azimuth direction and 13 cm in the range direction. Hence, the accuracy of the natural scatterers is statistically significant in measuring the Shuping landslides with regard to the annual displacement rate up to 1 m in the azimuth direction and 0.7 m in the range direction.
5.3. Validation of Derived Shuping Landslide Rates
Due to the lack of availability of in-situ measurements of CRs in the Shuping landslide area, the offset tracking results are verified by the extensometer measurements presented by Wang et al. [
23] on the eastern block of the Shuping landslide (where CR7-11 is located).
The measured range and azimuth deformation represent the components of the actual displacement projected on the slant range and azimuth directions. The displacement vector measured by extensometers is along the slope surface and centreline of the eastern block [
23], approximately along the gradient of the elevation model. Slope degrees are derived using 1 arc-second SRTM DEM for each elevation value. By the decomposition of the extensometer measurements on to the North, East and Up directions, the azimuth and slant range offsets dr and da can be resolved using the following Equations [
69]:
where
are the Upward, Northward and Eastward displacement,
and
denote the range and azimuth displacement derived from SAR images,
is the antenna incidence angle,
represents the satellite orbit heading (the angle formed between North and azimuth direction).
CR9 in the eastern block is selected for the comparison because its elevation of 277 m is closest to one of the extensometers “SP1-9” crossing the 275 m contour as presented in [
23]. The SP1-9 shows 70 cm increase of displacement from February–August 2009.
With an orientation of 355° (measured in Google Earth using the centreline of the eastern block), slope degrees of 22° (derived from the DEM), accumulative displacement of 0.7 m is decomposed and inversed to the radar geometry using Equations (7) and (8). The inversion obtained −0.62 m of azimuth displacement and 0.33 m of slant range displacement for the period of 1 February–01 August 2009. The accumulative displacements derived by offset tracking on CR7 for 21 February–5 August 2009 are −0.6 m in the azimuth direction and 0.44 m in the range direction. We can see that the azimuth displacement derived by offset tracking is very close to the extensometer measurement with only a difference of 2 cm, while the range displacement has a difference of 11 cm. This is probably because the extensometer only measures the displacement projection along the orientation of the block (355°) approximately to the North and the decomposed range displacement is only part of the projection of actual displacement along the slant range. Overall, the extensometer measurements revealed a consistent pattern of all extensometers with a dramatic increase of the displacement from May to August 2009, which is in alignment with the pattern detected by offset tracking.
5.4. Landslide Mechanism Inferred From This Study
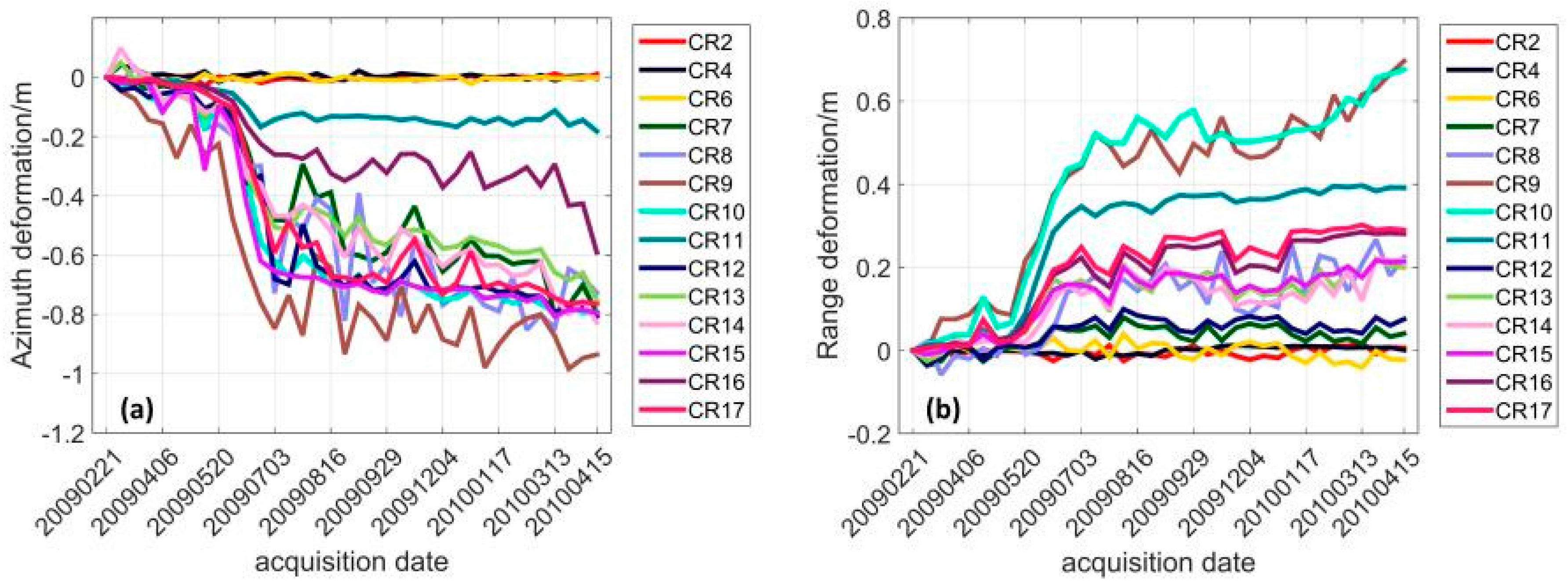
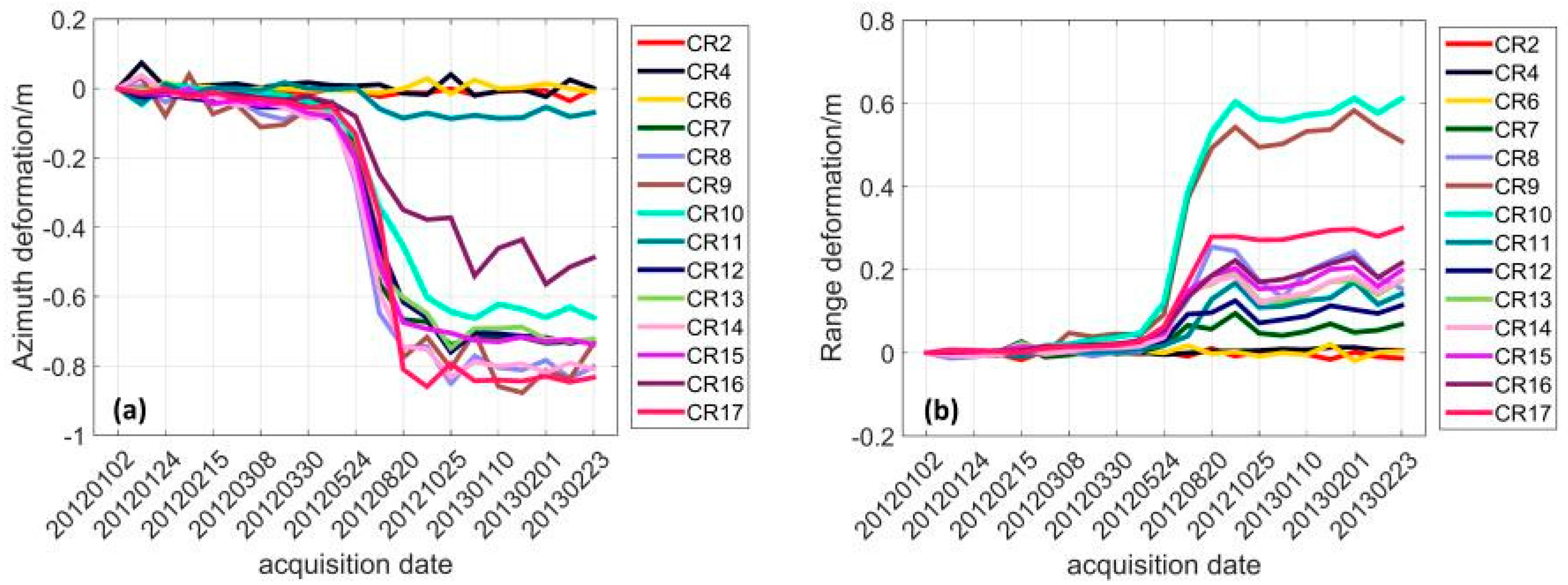
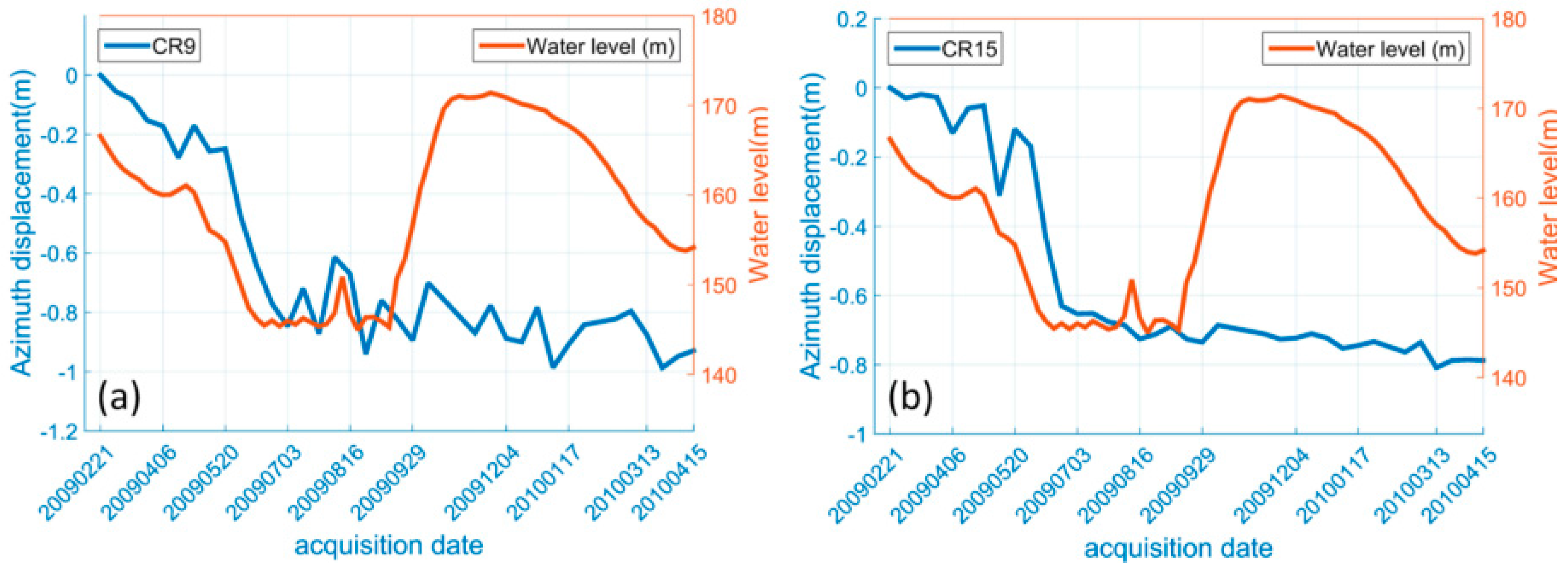
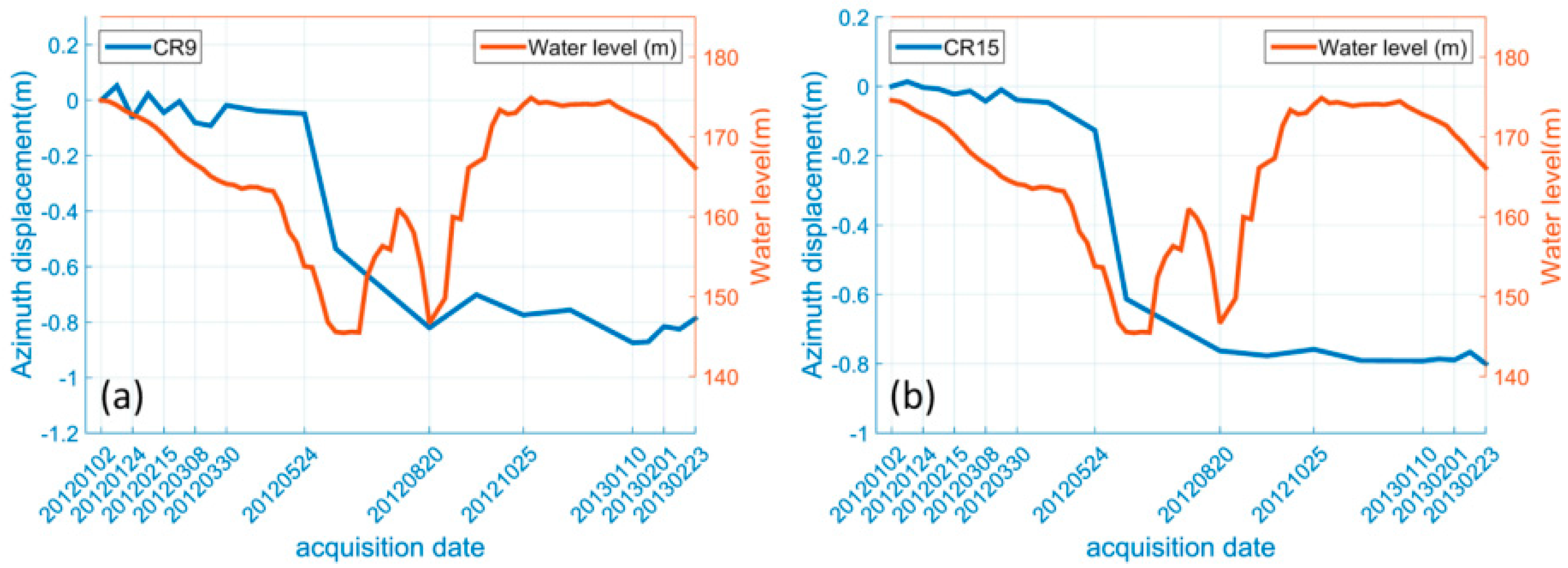
The landslide rates measured from the two annual time series show a consistent seasonal pattern of the deformation magnitude of all CRs located in the landslide blocks, whilst the displacements of CRs on the stable ground fluctuate around zero. The corner reflector measurements inside the landslide boundary show a dramatic increase over the same time period over both observation years (i.e., May to August in 2009 and 2012), which implies that the landslide is likely caused by the same driving factors.
In
Figure 7 and
Figure 8, the measurements of CR9 and CR15 both show a strong correlation with the water level variations of Three Gorges Reservoir in 2009–2010 and 2012–2013 time series observation. It is evident that the landslide active period coincides with the sharp drawdown of the water level of the Three Gorges Dam Reservoir. This suggests a strong connection between the landslide displacements and the operation of the Three Gorges Dam. As there is no deformation observed after the big rise of water level in September, the failure mechanism can be considered as follows: When the reservoir water level increases, the voids of the soil are gradually filled with water during this process. Then the water level reaches its highest level (175 m) and remains in this level for a period. The ground water table gradually reaches a higher elevation and remains in this state. The pressure inside the landslide body balances with the pressure formed by the 175 m water level, which maintains the slope stability. When the water level sharply drops, the ground water content within the landslide body does not drop at the same rate. This results in greater water content inside the landslide body, which forms an outward pressure, leading to the loss of slope stability. However, as the water level drawdown happens synchronously with the seasonal rainfall variations (due to the drawdown being enacted to mitigate against flooding effects form the high seasonal rainfall), a further study is required to differentiate the impacts of these two factors to fully understand the mechanism of the Shuping landslide.
5.5. Potential and Limitations of sPOT to Monitor Landslides in Densely Vegetated Areas
The sub-Pixel Offset Tracking (sPOT) approach only utilizes intensity bands of the satellite imagery to retrieve 2D ground deformation. It is less sensitive to Atmospheric phase screening (APS) and low phase coherence, not requiring phase unwrapping which leads to most of the failures in DInSAR time series approaches due to the low density of Persistent Scatter points. Thus, sPOT techniques potentially has the capability and advantage of measuring the deformation of slope movements with the speed exceeding the maximum detectable displacement of DInSAR or map mass movements in challenging areas such as densely vegetated steep terrain.
The sPOT techniques can be applied in measuring surface deformation when the expected accuracy is sufficient. This is jointly determined by the deformation rates, availability of high-resolution imagery and surface features in the targeted area. Using hi-resolution SAR imagery, sPOT can be used for the monitoring of slow-moving landslides and complement other applications of DInSAR, since sPOT has no limitation on the maximum detectable deformation gradient (DDG) and is still applicable to deformation measurements in the direction perpendicular to satellite LOS.
The deformation rates of the Shuping landslide show that the maximum displacement assumption of DInSAR is not valid in this region, suggesting offset tracking is the only viable alternative method when high resolution imagery is available in order to achieve sufficient accuracy with regard to the displacement rates. Similar to the PSI and SBAS methods, the displacement derived by offset tracking is relative to the stable ground. The constant offsets were removed in the step of centroid shift correction. There can be several sources of the constant offsets, such as the seasonal changes of vegetation cover, the general change of backscatters due to different view angles between passes, etc.
In addition, when there is a lack of ground truth measurements, the results derived from another independent dataset can be utilized in the validation. Thus, for potentially unstable slopes, more than one dataset acquired over the same time period is important for deformation monitoring.
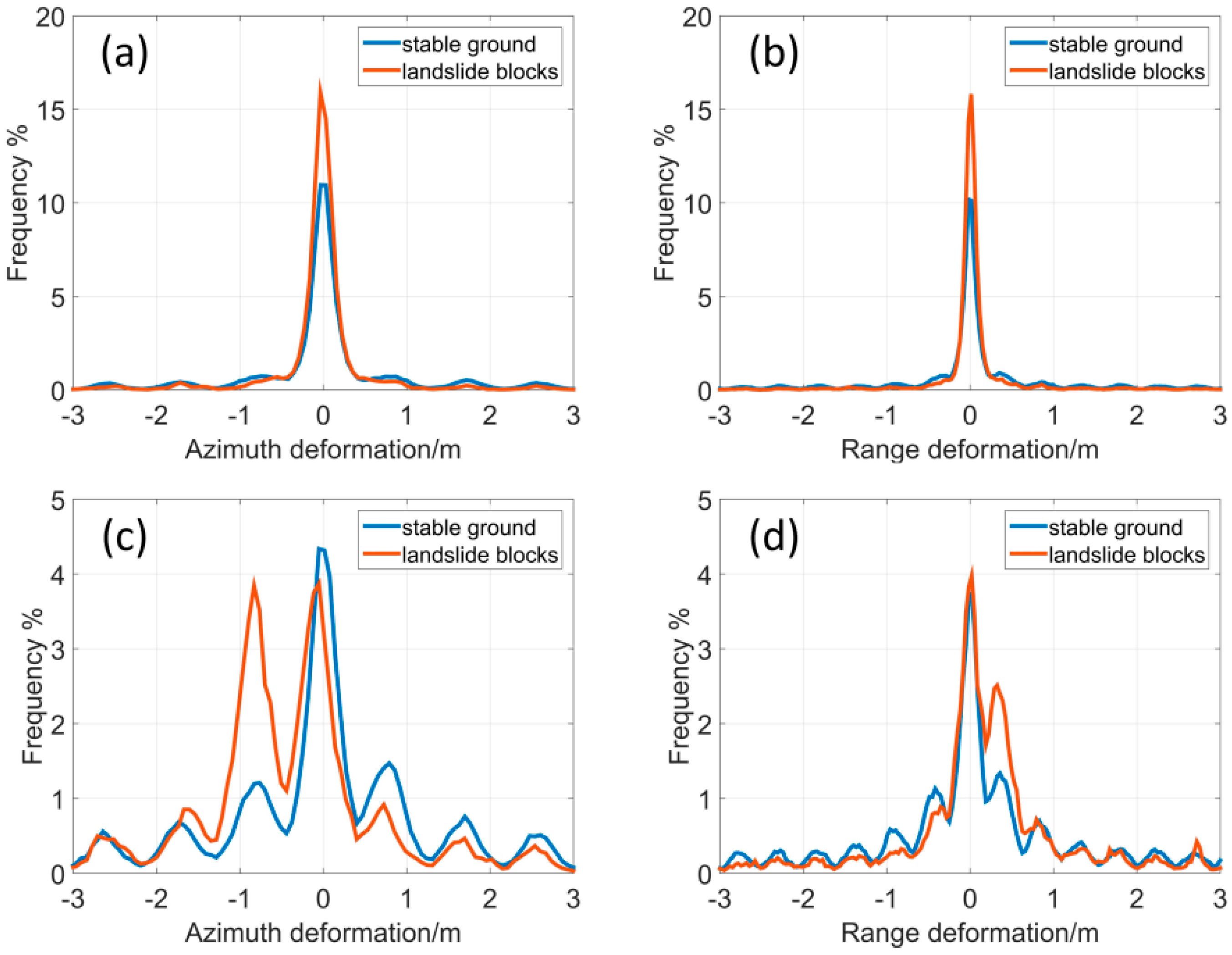
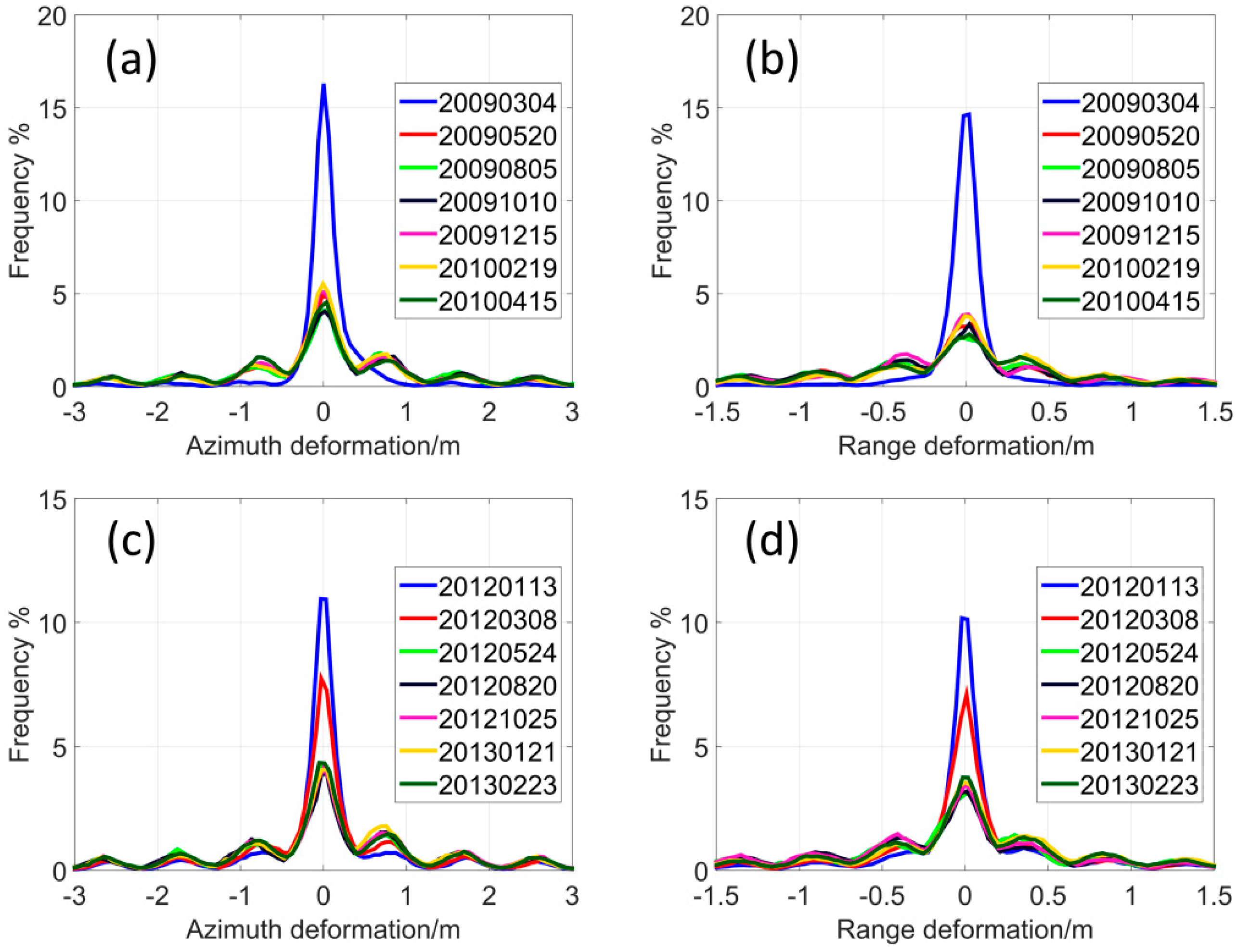
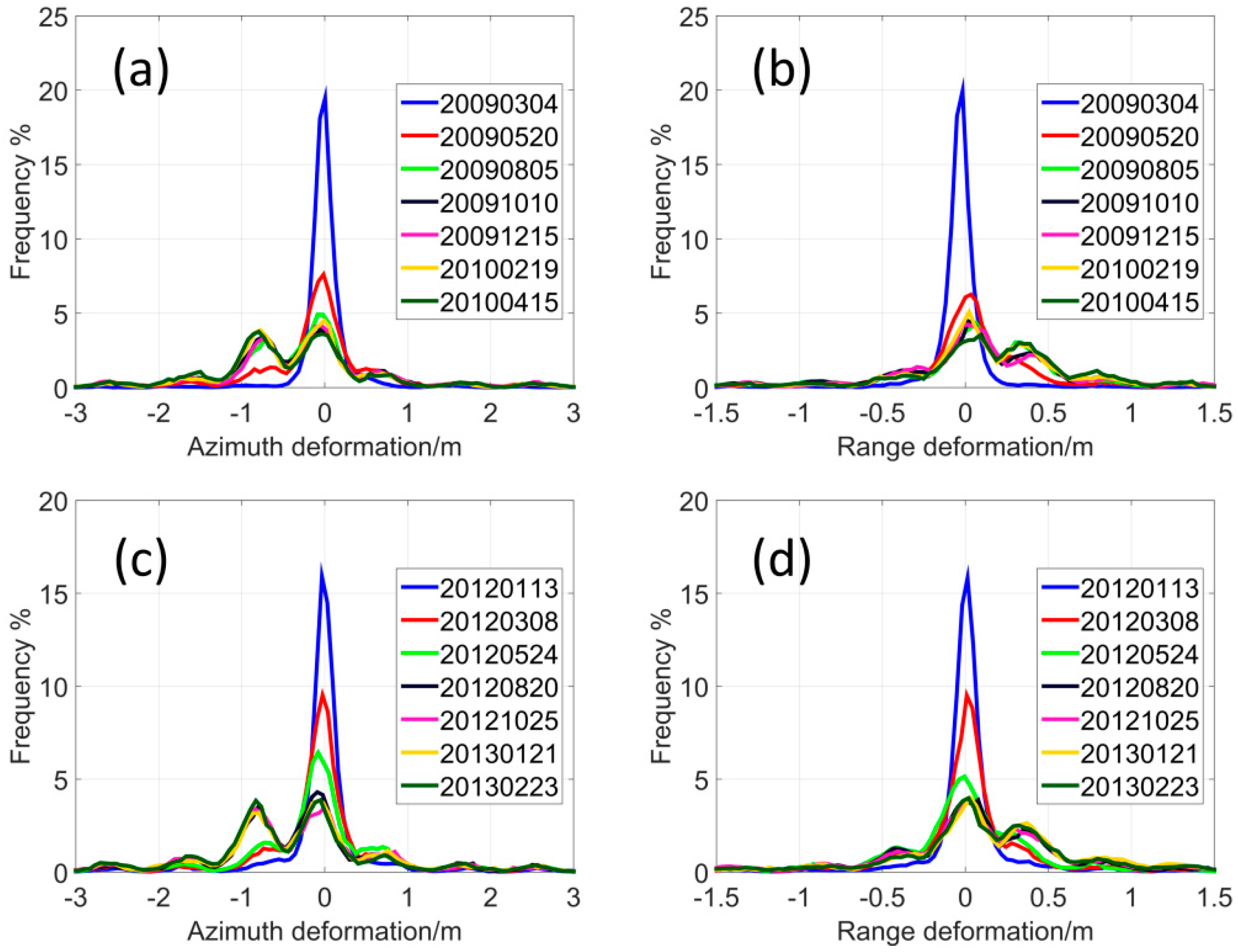
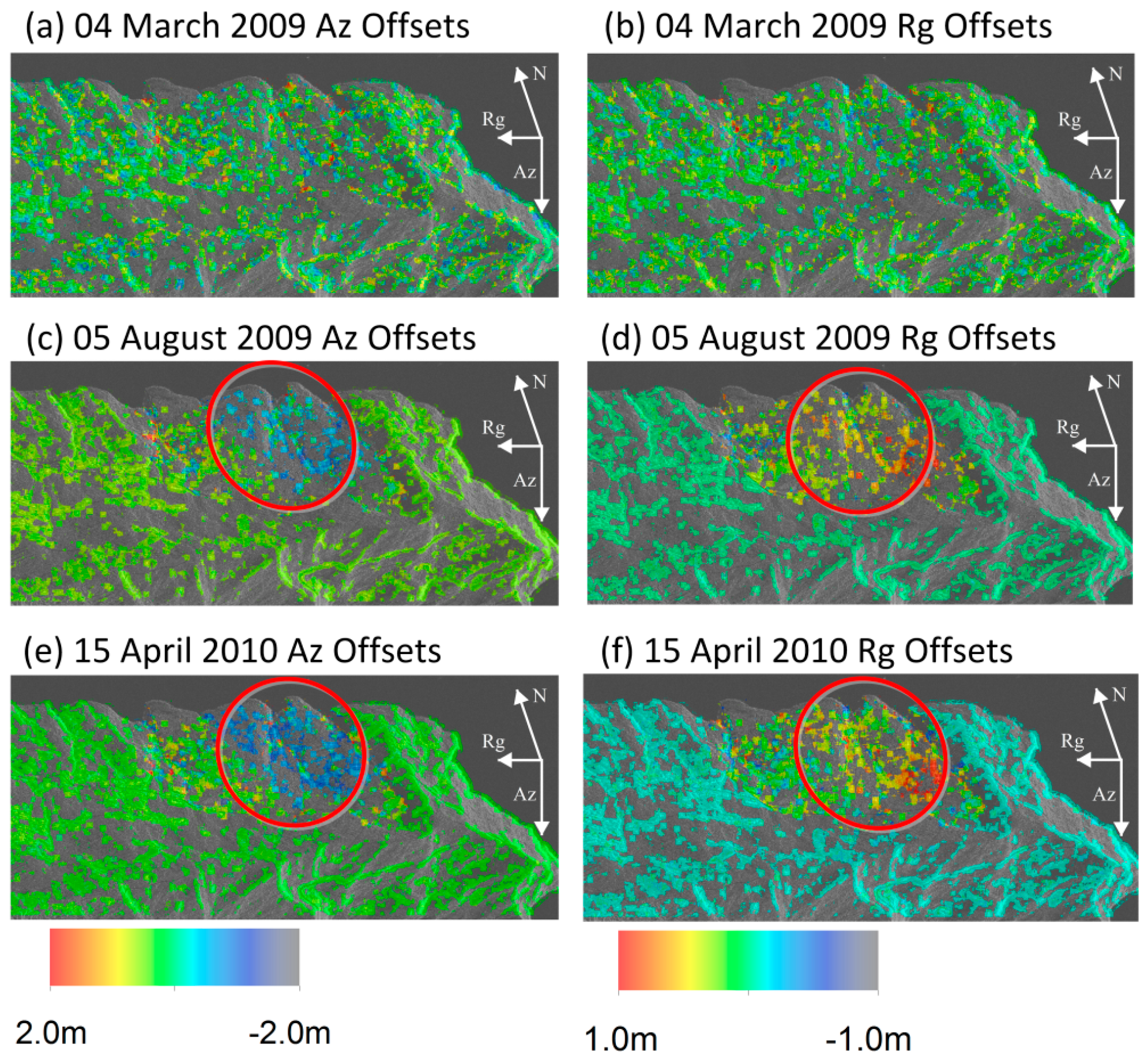
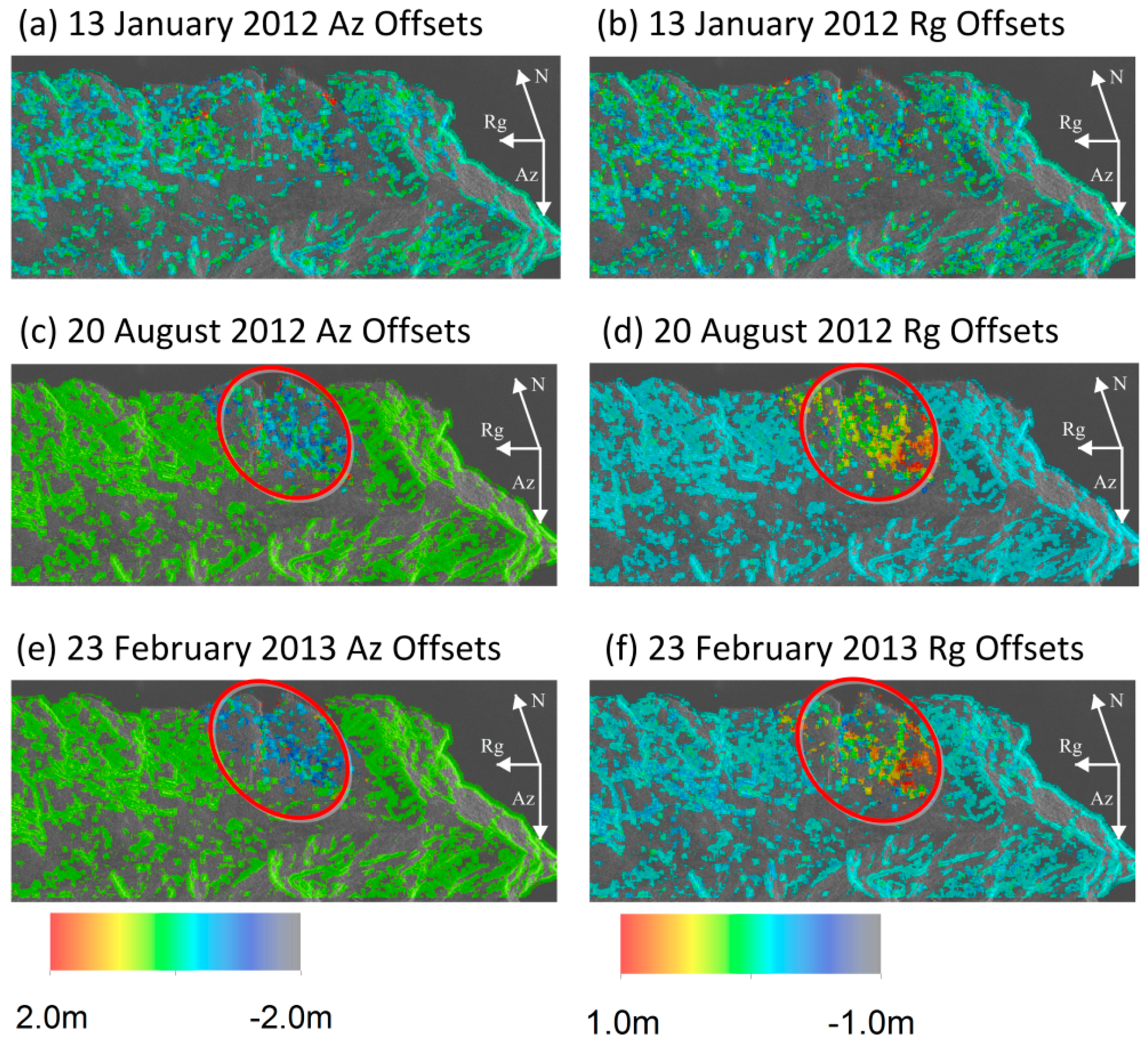
The proposed sPOT approach has been shown of being capable of measuring landslide rates in densely vegetated terrain. Instead of only measuring the deformation magnitude of sparsely distributed 17 CRs, this approach provides a synoptic overview of the deformation fields of all pixels in the landslide area by statistical analysis. From the centroid location changes of every annual time series histograms, the active period of Shuping landslide can be detected. In
Figure 15, for both azimuth and range displacements, we can see the histogram centroid stays the same during from 21 February 2009–20 April 2009 and 2 January 2012–24 May 2012 and then shows a sudden change from May of each annual time series as well as a wider and split distribution of histograms. In the periods during 5 August 2009–15 April 2010 and 20 August 2012–23 February 2013 the centroid rarely moves with slight changes in the envelope shapes. From the statistical analysis, the active period of the Shuping landslide is identified as May to August annually, whilst after August, the slope tends to be relatively stable, which shows an accurate correlation with the corner reflector measurements. Offset maps (
Figure 16 and
Figure 17) show the spatial distribution of the deformation and a distinguishable pattern representing the ongoing landslide.
6. Conclusions
Monitoring of landslides using DInSAR in the Three Gorges Region has received extensive attention over recent years due to the challenges posed in this region. Sub-Pixel Offset Tracking (sPOT) is here shown as an alternative method to address several issues that DInSAR encountered in previous research.
In this study, we demonstrated the capability of sub-Pixel Offset Tracking (sPOT) techniques to monitor relatively fast slope movements in densely vegetated areas with and without the presence of artificial CRs. Although lower accuracy is expected by using sPOT, as long as the accuracy is sufficient with regard to the deformation rates in the study area, sPOT has the advantage of measuring ground displacement perpendicular to the satellite line-of-sight. In addition to DInSAR techniques, sPOT should also be applied to assess if the assumption of DInSAR can be fulfilled. As only SAR amplitude is employed in the processing, sPOT is less sensitive to changes of Atmospheric Phase Screen and low phase coherence. It is not limited by the maximum detectable displacement (MMD) of DInSAR or time series DInSAR as it is not based on any assumption required by phase unwrapping. Artificial CRs can help to achieve higher accuracy for ground deformation measurements made from sPOT measurements in densely vegetated terrain, whist in the vast majority of regions where such high-contrast features are not available, the proposed approach is able to independently measure ground deformation in terms of the detection of the landslide scale, active period and distribution of deformation magnitude of all the scatterers for the whole landslide area.
In this paper, the statistical analysis of landslide rates derived over vegetated surfaces shows a dramatic increase of landslide displacement rates in the time period approximately from May to August in 2009–2010 and 2012–2013. In each annual time series, the landslide active period coincided with a large drawdown of the reservoir water level in the flood season, suggesting that in Shuping there is a strong connection between the formation of landslides and the operation of the Three Gorges Dam.