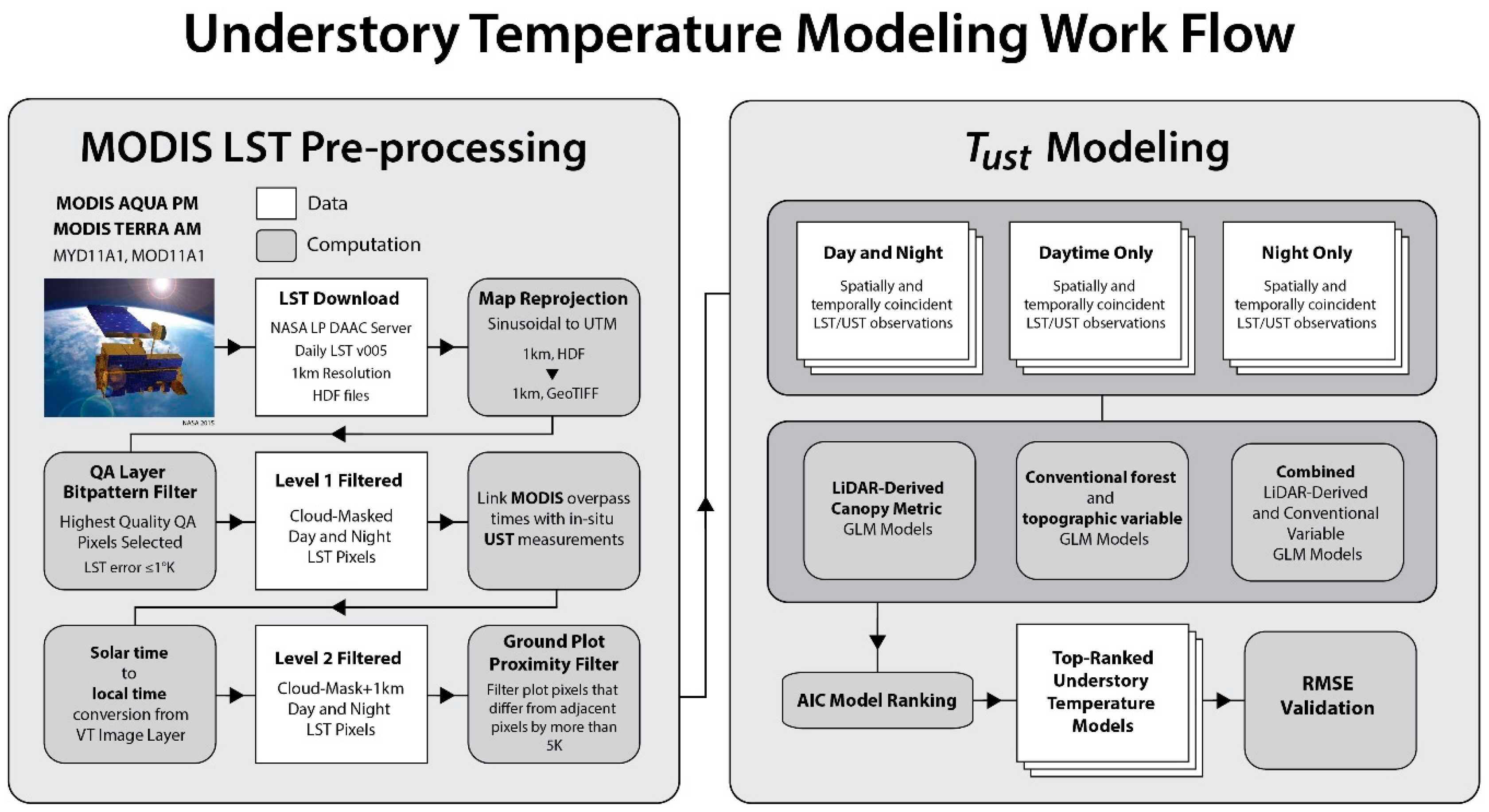
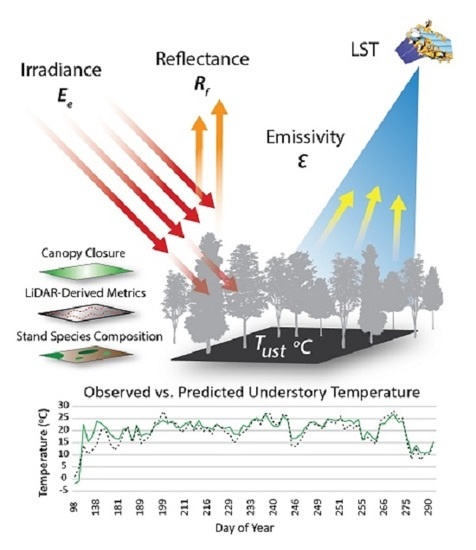
1. Introduction
There is growing interest in using remote sensing for observing Earth’s microclimates in order to acquire a better understanding of ecosystem functions such as vegetation phenology, carbon flux, and the timing of species trophic interactions (e.g., [
1]). Surface air temperature (
Tair) is a critical driver of these environmental processes, especially at high latitudes where seasonal transitions are more highly pronounced [
2]. However, obtaining reliable measurements of
Tair across the landscape is often hindered by missing values due to gaps in the data [
3]. These voids are typically a result of the limited density of meteorological stations distributed across the landscape [
4]. Spatial interpolation of these data is prone to error because of the distance and fine-scale temperature aberrations between stations, especially in mountainous areas where their distribution tends to be even sparser [
5,
6,
7]. Remote sensing of land surface temperature (LST) helps to resolve this issue by providing an inherently spatialized gridded surface that covers even the most remote regions. The Moderate Resolution Imaging Spectroradiometer (MODIS) has proven invaluable for monitoring year-round global temperature in high temporal detail [
8]. MODIS LST data is particularly popular because of its high level of post-processing which produces accuracies of ≤1 °C [
9]. MODIS LST has successfully been used to predict
Tair (e.g., [
10,
11]), however
Tair recordings are commonly made in open areas or high above the forest canopy from eddy covariance flux towers (e.g., [
12,
13]). With observations at heights in excess of 30 m, the relationship between MODIS LST and air temperature in the understory (
Tust) is relatively unknown.
Radiometers do not measure air temperature directly, rather the LST estimations are obtained through a split-window algorithm which translates thermal infrared (TIR) observations into skin temperature of the observable land surfaces (i.e., bare land, urban areas, forest canopy) [
14]. LST is quite different from
Tair and they do not generally correlate well [
15]. This relationship is improved over vegetated areas, since emitted radiance is affected by surface type [
16]. There is a simple and physical relationship between fractional vegetation cover and thermal properties detected by the sensor [
17]. The disparity between LST and
Tair is greater over areas of exposed soil and other surfaces with low emittance [
18]. As a result, the direct relationship between LST and
Tair needs to be determined using a supplementary estimation technique.
Variable forest cover types introduce additional complexities by creating irregularities in the latent heat flux and other radiative exchanges [
19,
20]. The prevalent methodologies used to parameterize
Tair from LST include (i) physical models of the surface energy balance; and (ii) the temperature–vegetation index (TVX) method [
21]. Energy-balance models are based on physical processes, and require large amounts of radiation and latent heat flux data typically not provided by remote-sensing techniques [
15,
22]. The spectral information obtained by the sensor is not able to perceive many of these complex physical variables, such as wind speed and soil moisture [
23].
The challenge in measuring the processes that govern
Tair above vegetation leave most models under-parameterized, and this is the main reason for the development of the temperature–vegetation index (TVX) method [
17]. The premise of the TVX method is an established linear and negative correlation between a remotely-sensed vegetation index, often the normalized difference vegetation index (NDVI), and satellite-derived LST [
24,
25]. The TVX assumes that the radiometric temperature of a fully vegetated canopy is in equilibrium with
Tair [
26]. The premise is that dense vegetation radiates heat so efficiently that it remains close in temperature to the surrounding ambient air [
18]. In effect, the assumption is that the top-of-canopy temperature is the same as the canopy itself [
11]. How this assumption translates to estimating understory temperatures, and the relationship with MODIS LST across different vegetative strata, requires further investigation.
The difference between air temperatures above and below the forest canopy is generally a result of near-surface environmental lapse rates and distance from the ground [
1]. The perspective of forests from a space-borne sensor is of the top of the canopy, and the thermal information beneath is hidden from view due to the relative opacity of the forest itself. The boundary layer separating the emissive properties of the understory and the supracanopy air mass is occupied by different types and densities of canopy vegetation. Therefore estimations of
Tust, without assuming that it is in equilibrium with the canopy, should incorporate physical characteristics of the canopy in addition to MODIS LST. These characteristics can be acquired in a number of ways. Traditionally, forest attributes have been obtained through mensuration techniques developed by the timber industry [
27]. Metrics such as tree height, diameter, and canopy closure are generally used to estimate the volume of harvestable timber in a stand. These methods have since been adapted to characterize forest landscapes for ecosystem management and studies of species ecology (e.g., [
28]). Recently, these conventional mensuration practices have been complemented by the development of airborne laser scanning (LiDAR) data. LiDAR systems procure detailed models of vegetation in three dimensions, with the fundamental benefit of penetrating the canopy to extract additional information from the understory [
29,
30]. Most of the existing literature emphasizes characteristics of the overstory, with relatively few papers using LiDAR to examine the understory within an ecological context [
31,
32,
33]. Nijland et al. [
34] compared LiDAR-derived canopy metrics with more conventional climate and land cover based variables to model the distribution of various understory species with mixed success.
The importance of estimating understory temperature is to increase our understanding of its cause–effect relationship with other natural processes. For example, the timing of phenological events is closely linked to changes in ambient temperature, where the life histories of many species are explicitly adapted to the seasonal environments in which they live [
35]. Monitoring microclimate dynamics provides insight into species sensitivities to weather anomalies and global trends in temperature from climate change [
36,
37]. The MODIS LST imagery offers a mechanism to observe this significant driver of ecosystem dynamics over the broad scale, which in turn provides maps as a basis for species conservation, habitat management, or identifying additional environmental responses to climate change [
38,
39,
40,
41]. The present effort to model
Tust is motivated by our involvement in an ongoing grizzly bear (
Ursus arctos) research program where we are working to monitor critical habitat for this threatened species in Alberta, Canada [
42]. These animals strategically exploit a wide variety of understory plants that provide variable nutrition at differential times of the growing season [
43]. The eventual goal is to model the bears’ response to shifting understory phenology by mapping
Tust accumulations, or growing degree days (GDD) (e.g., [
44,
45,
46]).
The objective of this study is to predict instantaneous measurements of
Tust using daily MODIS LST data and a combination of LiDAR-derived canopy metrics and conventional forest inventory variables. Although MODIS LST has been previously correlated with
Tair [
47,
48,
49], estimating
Tust has not been studied in detail. There is also an absence of in situ meteorological data measured at comparable resolutions to the remotely sensed imagery with which it is correlated [
1]. Using a multivariate statistical approach, we ranked the comparative importance of LiDAR and conventional forest inventory variables in estimating instantaneous
Tust at the MODIS pixel-scale. In situ
Tust measurements were collected over two seasons using a widespread network of meteorological stations distributed throughout the foothills and Rocky Mountains of western Alberta, Canada. Although it is normally assumed that the vegetated canopy is the same temperature as the surrounding ambient air [
18,
26], the understory will experience dissimilar temperatures as a result of the general moderating effect of the canopy [
50]. We hypothesized that based on the interactions between MODIS LST and forest canopies [
16], that supplementary forest canopy and stand variables would significantly improve model predictions of
Tust over those made by LST alone.
3. Results
The quadratic function of Julian day and LST was set as the standard null model, as these two variables were found to explain more than 80% of the variability in
Tust. Julian day explained 20% more variability than LST alone, which is considered good for ecological phenomena [
71]. Using all clear-sky observations, separate baseline model rankings of the two variable types (conventional and LiDAR-derived) was performed to get an overview of their relative importance in predicting
Tust (
Table 3). The delta AIC (Δ
i) is a measure of each model relative to the top-ranked model, where the criterion suggests substantial evidence for models within Δ
i < 2. Values between 3 and 7 indicate that the model has considerably less support, and Δ
i > 10 indicates that the model is very unlikely [
72]. Akaike weights (
wi) can be interpreted as the probability that the top-ranked model is the best in the set of candidate models [
69,
73]. Of the conventional metrics, the best model was explained (in addition to the null) by the interaction between LST and percent conifer, which describes the proportion of coniferous trees within a sample unit. The effect of the interaction term in the model can be interpreted as a linkage between these two variables where the influence of forest composition on
Tust depends on the coincident LST value at the time of observation. Without the interaction, we are simply trying to predict
Tust as solely the unique effect of percent conifer. The top two conventional metric models lead the rankings, each having Akaike weights of 0.50 (percent conifer and the interaction of LST with percent conifer). There was weak support for the addition of elevation, since it is equally ranked with the percent conifer interaction model despite increasing model complexity. By and large, employing conventional variables imparts a major improvement in estimating
Tust over using LST alone, which was ranked very poorly.
There was no observed improvement in the prediction of
Tust using exclusively LiDAR-derived metrics over the null model (
Table 3). The best-performing was skewness, although there is some optimism in the strength of the other LiDAR models since they are all within 2 AIC values of the top ranked model (the null). Any LiDAR-derived metric model containing an interaction term had significantly reduced performance which was reflected by a large increase in AIC value.
The overall top-ranked models from the final groupings (conventional, LiDAR-derived, and both combined) were directly compared to gauge which supplementary variable type best predicts
Tust. This comparison was performed for each overpass dataset (daytime, night, and day–night). The combination of conventional variables and LiDAR-derived metrics clearly produced the best models, regardless of view time, as reflected by the large Akaike weights (
Table 4).
Percent canopy closure (cc) and the LiDAR-derived metric standard deviation of canopy height (stdd) both appear in all of the top-ranked models. They are often in the form of an interaction term with LST, which is a strong indication of an interrelationship with the forest canopy. At night, the standardized coefficients show that for every percent increase in canopy closure, there will be a 0.06 °C increase in
Tust (
Table 5). During the day, for every unit increase in closure,
Tust decreases 0.12 °C. Also in the top daytime models was the percent returns above 1.4 m (pa14) metric, which is the LiDAR-derived equivalent to canopy closure. This metric had a similar negative daytime influence as closure, where an increase in this variable produces a slight drop in
Tust. For both the daytime and day–night models, the interaction term of the LiDAR-derived standard deviation of canopy height was positive, and implies that when LST interacts with increasingly rough canopies,
Tust increases, but very little. At night this relationship is inverted, and a higher standard deviation in height results in a cooling of
Tust. The percent conifer coefficient was negative, suggesting that as the percentage of conifers increases,
Tust will decrease. Overall, canopy closure and the standard deviation of canopy height were the most influential ancillary variables for estimating
Tust.
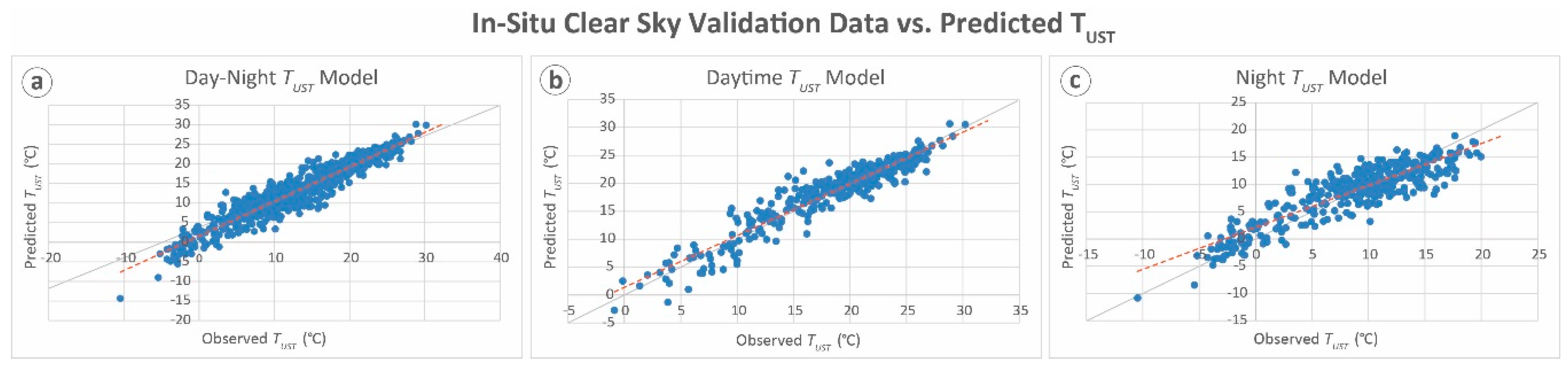
The daytime model was the best performing overall, with a model fit of R
2 = 0.89, and the lowest validation error of mean absolute error (MAE) = 1.4 °C. This prediction accuracy parallels estimations of
Tair [
4,
13,
49], which is noteworthy considering the predictions are of temperatures beneath the forest canopy (
Table 6;
Figure 6).
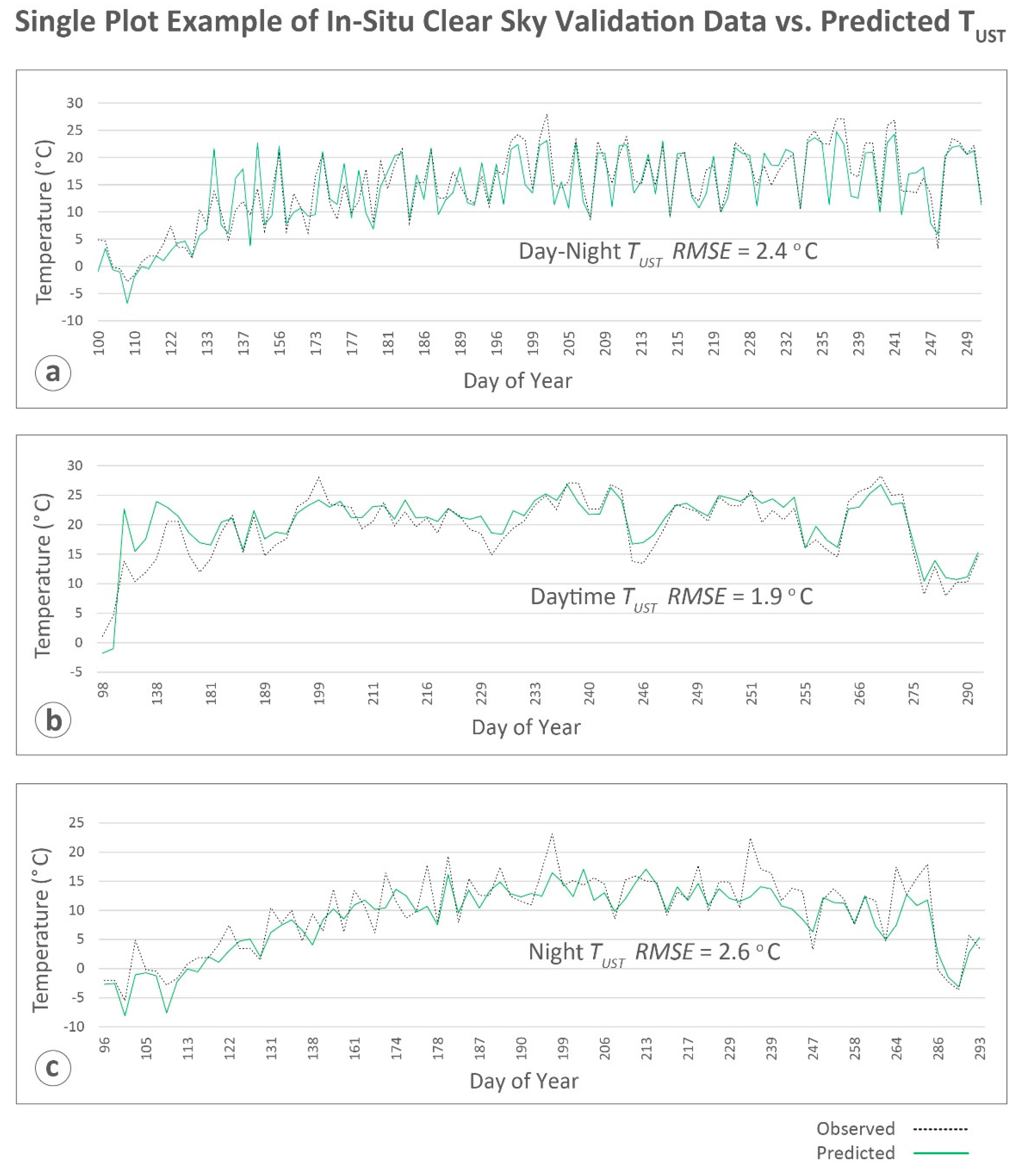
The best day–night model had the same model fit as the daytime model (R
2 = 0.89), but had a 0.5 °C increase in error (MAE of 1.9 °C). Although this model had no overall bias, the validation data show a slight
Tust underprediction in cooler temperatures that occur during the very start and end of the growing season (
Figure 7). The top model derived from night observations had the lowest model fit of the three MODIS view times (R
2 = 0.77) and a small error increase over the daytime model in estimation error (MAE = 2.1 °C). The model appears to underestimate higher temperatures and overestimate colder temperatures which seem to balance out, producing no predictive bias on average.
4. Discussion
Forest type, density, and canopy structure all have an impact on the relationship between MODIS LST and understory air temperature. In this paper, we examined which metrics coupled with MODIS LST improve estimates of
Tust. This is, to our knowledge, the first study of its kind to specifically model air temperatures in the understory using MODIS LST. We statistically predicted instantaneous values of
Tust at a 250 m plot-scale to within MAE 1.4 °C–2.1 °C (depending on the time of day). This is comparable to previous canopy-top
Tair models that had error ranging from 1.3 °C to 3.5 °C and similar model fit [
4,
10,
13,
47]. The fit slightly exceeded that obtained by Hanes and Schwartz [
1], who modeled maximum daily
Tair at the base of a flux tower (1.5 m) (R
2 = 0.86).
The Tust estimates were consistently accurate over a range of forest types and densities. This may be a result of the overall effectiveness of the model variables at representing the forest canopy characteristics. This variability could not be explained by LST alone (null model) as demonstrated in the AIC rankings. Despite the cost of increased model complexity, those which contained canopy metrics consistently ranked higher than the LST null model. A likelihood ratio test was performed to determine if these top-ranked models estimated Tust significantly better than the null. The results found that the addition of canopy metrics produce a significant improvement over the LST null in the day–night combined model (p < 0.001), and marginally significant in the daytime and night models (p = 0.08; p = 0.07).
The improvement of the models through the addition of the canopy metrics implies that there is a distinction between canopy-top (
Tair) and understory temperatures. The difference is likely a result of moderation from the canopy [
50,
74]. Hanes and Schwartz found that as canopy vegetation becomes increasingly dense during spring leaf out, MODIS LST values begin to approach air temperatures at 1.5 m above ground. In areas where canopy density is reduced, the influence of the overlying forest is diminished and therefore LST should deviate from
Tair. However, the
Tust estimates across the study area are consistently accurate despite the broad range of forest densities in the plots (10%–70% closure). This finding implies that, unlike
Tair, the relationship between LST and
Tust is likely consistent regardless of canopy closure.
Modeling day and night LST as separate datasets highlighted daytime as the optimal diurnal period to observe
Tust. The daytime model was best overall, with a 10% increase in model fit and 0.7 °C lower error than at night. The majority of previous
Tair studies (e.g., [
12]) have found increased accuracy during the night, which is attributed to less interference from reflected daytime radiation [
75]. The improved daytime accuracy in the
Tust models may be owed to modeling entirely within forested sites and the inherent difference of estimating
Tust as opposed to
Tair. Essentially, the radiative exchanges in the understory are sufficiently unique to those above the canopy resulting in improved daytime
Tust observations. In addition, the predominance of conifer trees in the study area may have augmented the performance of the daytime model, since low albedo coniferous canopy absorbs and emits energy more effectively than deciduous [
76]; green-needle forest is considered a near-perfect emitter of thermal radiation [
77]. This is supported in a daytime model by the positive interaction between LST and percent conifer. This same interaction term is not present in the night model, perhaps because there is no potential for interaction with sunlight.
Conifer forests are also drier than deciduous, ultimately affecting the latent heat flux between them throughout the diurnal cycle. Williamson et al. [
48] and Niclòs et al. [
4] found that soil moisture was a significant predictor of
Tair as it affects surface emissivity. Considering at-site soil moisture was not measured in this study, GIS-derived variables could have been used as proxies for moisture such as a wet area map [
34]. Cresswell et al. [
78] explain that since the Earth’s skin surface temperature is generally higher than
Tair during the day and cooler at night, this will lead to overestimation and underestimation of air temperature in diurnal
Tair models, respectively. However, this estimation bias was not observed between the
Tust models, perhaps from the moderating effect of the canopy. At night, there was a positive LST interaction with canopy closure which in turn increased
Tust. During the day, this relationship was negative and for every percent increase in closure,
Tust decreased 0.12 °C. These results corroborate that the canopy shades the understory during the day and insulates it at night [
33,
79]. This also implies that the understory microclimate is unique to the overlying canopy and therefore emphasizes the distinction between
Tair and
Tust.
Regarding the performance of the LiDAR-derived metrics, they contributed to all of the top-ranked models, indicating some overall utility. The standard deviation of canopy height was the most predictive either as a solitary variable (at night) or interacting with LST (daytime). It would be more intuitive that average height or canopy density (percent returns above 1.4 m) should explain more variability in
Tust; rather it was the roughness of the forest as expressed by the standard deviation of height [
33]. During the daytime
Tust rises when forest structure becomes increasingly rough, while at night the opposite occurs, where a higher standard deviation results in lower
Tust. A rough surface would be characteristic of forest with a strong variation in age structure or disturbance patterns such as trails or cut lines. Although not in the top-ranked models, LiDAR-derived skewness in the distribution of tree heights appeared strongly in many of the models, having a significant yet subtle influence on
Tust. Skewness is a similar metric to standard deviation and signifies canopy complexities resulting from variable age structure or directional trends in height across the plot due to soil conditions or slope [
80]. The correlation of this metric with
Tust was at all times negative, suggesting that as skewness in height increases,
Tust drops slightly. The relative contribution to model improvement using the LiDAR metrics raises the question of the advantage of these data over the conventional and GIS-derived variables. Ultimately, it depends on the scale and objectives of the research; in this
Tust analysis, the benefits of the LiDAR metrics were not as substantial as the conventional variables. Conversely, the cost of traditional ground measurements are considerably more than LiDAR surveys [
81], especially in contrast to the increasing availability of LiDAR technology and platforms such as unmanned aerial systems [
82,
83].
Downscaling the 2-pulse-per-meter LiDAR metrics to the 250 m plot-scale could have impacted their effectiveness as explanatory variables of
Tust. This was done to match the areal unit scale of the observation plots, however it is unlikely that the effect was significant as averaging would only remove the extreme and outlying values. Tompalski et al. [
84] compared stand-level LiDAR estimates of tree volume to individual volume measurements and found them to be very similar. The areal scale of 250 m was conceivably an improvement over point-source temperature measurements made by lone meteorological stations or flux towers. The relatively low root mean square error (RMSE) in the
Tust models may be indicative of measuring in situ temperature at a broader 250 m scale instead of discrete points on the landscape. The observation plots were located in the center of more expansive areas of homogeneous forest as a solution to the disparity between the resolutions of the larger MODIS LST pixel and the
Tust plots. Olsson and Jonsson [
85] found that different scales of gridded temperature source-data (e.g., MODIS LST) had no significant influence on the accuracy of their forest phenology models.
For this mitigation approach to operate effectively, it was assumed that temperature across the broader homogenous stand was uniform. This assumption was validated over two seasons, by recording in situ air temperature within a 250 m plot placed at the center of a broad expanse (2700 km
2) of perfectly homogenous land cover (native grassland). Employing the identical methodologies as in the forested plots, these data were used to train the LST null model. Air temperature estimates in the validation plot had an average RMSE increase of 2 °C over the equivalent null model estimates in the forested plots. Theoretically, the error should have been lower since the validation plot had completely uniform land cover relative to the principal observation plots. However, this result substantiates that forest cover improves statistical estimates of air temperature using LST [
22].
The tiled and projected M*D11A1 products were chosen for this study based on their ease of use and successful application in previous models (e.g., [
6,
46]). The lower-level LST swath data are less modified and unaffected by projection error or temporal adjustments. However, opting for the higher-level product was a tradeoff between these errors versus the benefit of having the obvious cloud-contaminated LST values removed. During pre-processing the LST imagery selected for this study was reprojected and resampled, which introduces geometric error: chiefly the potential to alter the LST pixel value with values from adjacent cover types. We attempted to mitigate this issue by working in forest stands that were much larger than the plots in which observations were made. Some error may have originated from intrinsic uncertainties in the radiometric or geometric precision of the original MODIS LST data [
6], yet this was mitigated by using only the highest quality QA filtered pixels for the analysis. The local time correction made during pre-processing produced times that were truly instantaneous or within 30 min of a MODIS overpass. It is unlikely that this period was sufficient to allow any significant change in temperature on the ground, but it cannot be ruled out completely.
Terrain complexity within the study area introduced an assortment topographic and microclimatic factors, but these had little effect on the model results. This was expected since this study was a within-pixel analysis with no broader spatial interpolation. Observation plots with limited topography were intentionally selected as “targets” for MODIS in an attempt to constrain the variability of
Tust solely to forest type and structure. Elevation was the only significant topographic variable in the models because small differences in elevation produce considerable changes in the environmental lapse rate (e.g., [
7]). The use of aspirated solar radiation shields worked to limit in situ
Tust measurement bias. However, variability in canopy cover between plots may have exposed some sensors to slightly more radiation than others, potentially altering the results [
86].
Clear-sky overpasses occurred predominantly during the summer and autumn months, however a considerable proportion occurred in autumn. The canopy is mostly intact for the first half of September, but leaf senescence may have introduced some bias in the small proportion of plots that were deciduous. Given the enduring issue of cloud over the mountains, there was a tradeoff between increased observations during a reliably clear time of year and the transition in canopy attributes. An extended observation period was required to observe the full phenological progression of the understory and to obtain a range of seasonal temperatures. Other sources of model uncertainty most likely occurred during exceedingly cold times of year. The MODIS LST product is accurate to ±1 °C between the temperatures of −10 °C and 50 °C [
9], there were early and late season temperatures during the study period that were approximately −20 °C potentially reducing model accuracy. This evidence of seasonal variability affecting model estimates is substantiated by Hanes and Schwartz [
1] who found that differences between
Tair and MODIS LST are increasingly divergent during colder parts of the year in temperate climates, mainly due to snow cover. However, for the purposes of using
Tust for monitoring vegetation phenology, the accuracy of
Tust models is not critical during these colder periods since the plants are still dormant and GDD accumulations have not yet begun.
Overall, the models demonstrate that estimates of
Tust using MODIS LST can be refined with additional variables which characterize the interface between the top of the forest canopy and the understory. These results facilitate the next step in this research to monitor understory phenology over the entire study area. This requires spatially extending the models beyond the observation plots across the gridded MODIS LST surface to produce maps of daily
Tust. GDD maps derived from
Tust should provide improved accuracy in predictions of understory plant phenology than those derived from canopy-top
Tair. Hanes and Schwartz [
1] found that top-of-flux tower GDD accumulations underpredicted plant phenology opposed to measurements made closer to the ground since lapse rates produce cooler temperatures at height. The instantaneous
Tust models derived in this study will ultimately facilitate the development of improved land surface phenology maps.