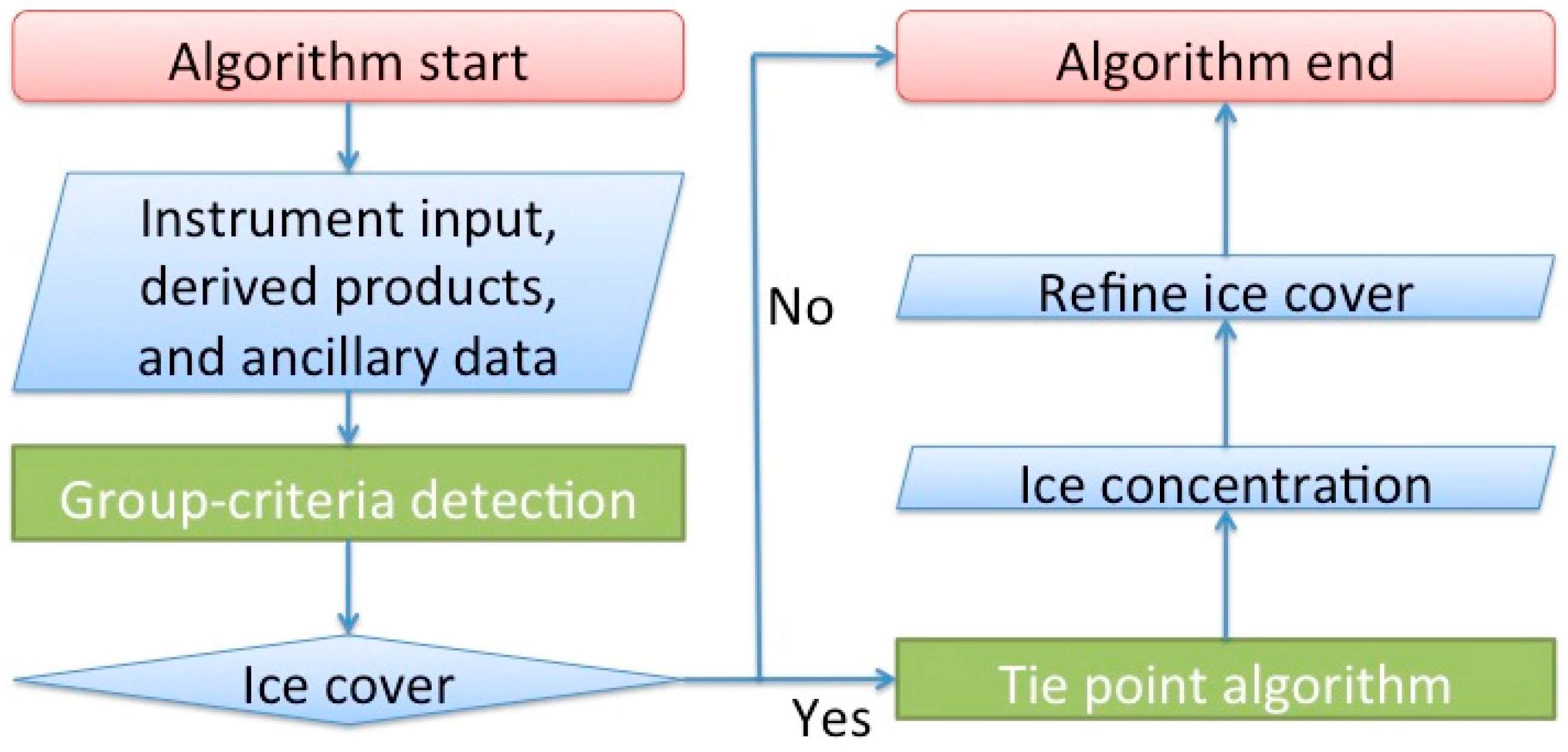
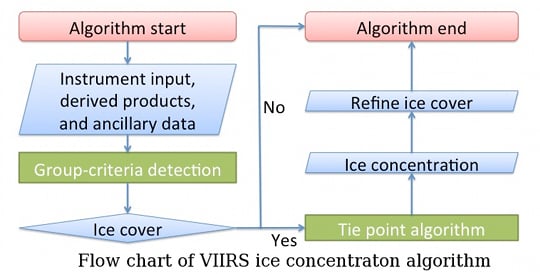
The purpose of this algorithm is to detect ice and to estimate ice concentration, i.e., the fraction of a satellite field-of-view that is covered by ice. Ice is first detected by a group-criteria method. Then ice concentration is retrieved after the visible band reflectance and ice surface temperature of pure ice are determined through a tie point algorithm. The ice cover mask is then further refined based on the retrieved ice concentration. This algorithm has a solid physical foundation and is capable of identifying ice cover mask and retrieving ice concentration in both day (sunlight) and night (dark) conditions. It runs automatically and can be applied globally. Because the surface is obscured by clouds in the visible and infrared observations, the ice cover mask and concentration can only be determined in clear-sky areas.
The accuracy of the algorithm is therefore influenced by the quality of the cloud mask. Pixels that are clear but identified as cloud do not introduce errors in the ice concentration estimates, as these pixels are excluded from the retrieval. In contrast, pixels that are cloudy but identified as clear, called “leakage”, do contribute to errors in ice concentration, as they may be labeled as ice due to their high visible reflectance and/or low temperature. The leakage rate is not known for sea ice scenes, but tests over Greenland show a leakage rate of up to 2.4% with the original VIIRS cloud detection algorithm, and as low as 0 with more recent improvements [
36]. How this impacts errors in ice concentration is difficult to determine, as it depends on the proportions of ice and clouds in any given scene as well as the actually ice concentration under the pixels that were misidentified as clear. The performance of cloud mask in the polar regions in daytime is generally better than that during nighttime due to more available spectral information in daytime. This difference can lead to cloud mask discontinuity in regions that include the terminator, the boundary between the sunlit and dark portions of the earth, and hence a discontinuity in the ice cover mask and ice concentration retrievals.
2.2.1. Ice Detection
On the microphysical scale, surface albedo depends strongly on the internal structure of ice, such as brine pockets and air bubbles in the near surface layers [
40]. These internal structures change with season, the state of the near surface layers, and the age of ice. Absorption and scattering in the snow and ice are determined by their internal inhomogeneities [
40,
41]. Sea ice and snow albedo are very high at visible wavelengths and are low at wavelengths longer than 1.4 micrometers in both Arctic and Antarctic due to stronger absorption and less backscattering in the shortwave infrared, with higher visible albedo for snow surface, as shown in Figures 9 and 10 in [
41], and Figures 1 and 2 in [
42]. This feature is shared by lake ice and snow-covered lake ice in both theoretical simulations and observations, as shown in Figures 2–5 in [
43], and Figure 12 in [
44]. Surface albedo is much lower for surfaces with melting ice and surfaces with melt ponds, with a maximum albedo in the 0.4–0.5 micrometer region and a steep decrease between 0.5 and 0.8 micrometers [
41,
45]. Some ice types, such as clear lake ice, grease ice, and sea ice with melt ponds, can be difficult to detect due to the very low contrast with open water [
41,
43].
In the absence of sunlight, we have to rely on temperature to distinguish ice from liquid water. Surface skin (radiating) temperatures over ice are lower than the melting point (273.15 K for fresh water and around 271.35 K for salt water), when the sea ice/its snow cover is not melting.
Traditionally, the Normalized Difference Snow Index (NDSI) is used to detect snow and ice. NDSI is defined as
where
R1 is the visible channel reflectance (e.g., 0.55 μm, 0.67 μm, or 0.86 μm) and
R2 is the reflectance in a shortwave infrared channel (e.g., 1.6 μm or 2.2 μm). Ice is identified when NDSI is larger than some threshold. In this algorithm, 0.86 μm and 1.6 μm are used for
R1 and
R2, which are VIIRS bands M7 and M10. One advantage of 0.86 μm over 0.55 μm is that NDSI calculated with the 0.55 μm reflectance is high for water that is high in green pigment, causing a false snow/ice detection, while NDSI from 0.86 μm is not.
In the daytime, defined here as solar zenith angles lower than 85°, a pixel is identified as ice covered if the NDSI value is larger than 0.45, the reflectance at 0.865 μm is higher than 0.08 [
46,
47,
48], and the surface temperature is lower than 275.0 K over both freshwater and ocean water. The reason for not using the melting temperature is that ice-covered pixels with some liquid water (leads, melt ponds, or near the ice edge) may have temperatures above the melting point. At night, defined here as solar zenith angles of 85° and higher, a pixel is identified as ice covered if the surface temperature is lower than 275.0 K over lakes, rivers (fresh water), and oceans (salt water).
Over melting ice and melt ponds, the surface albedo is low between 0.5 and 0.8 micrometers, which may cause the NDSI to misidentify melting ice and melt pond as water. When the ice is melting or very thin, the ice surface temperature is close to the melting point, which can lead to errors in the ice/no ice identification. Meanwhile, the uncertainties in the derived ice surface temperature and VIIRS reflectances can also lead to errors in the ice/no ice identification.
2.2.2. Tie Point Algorithm
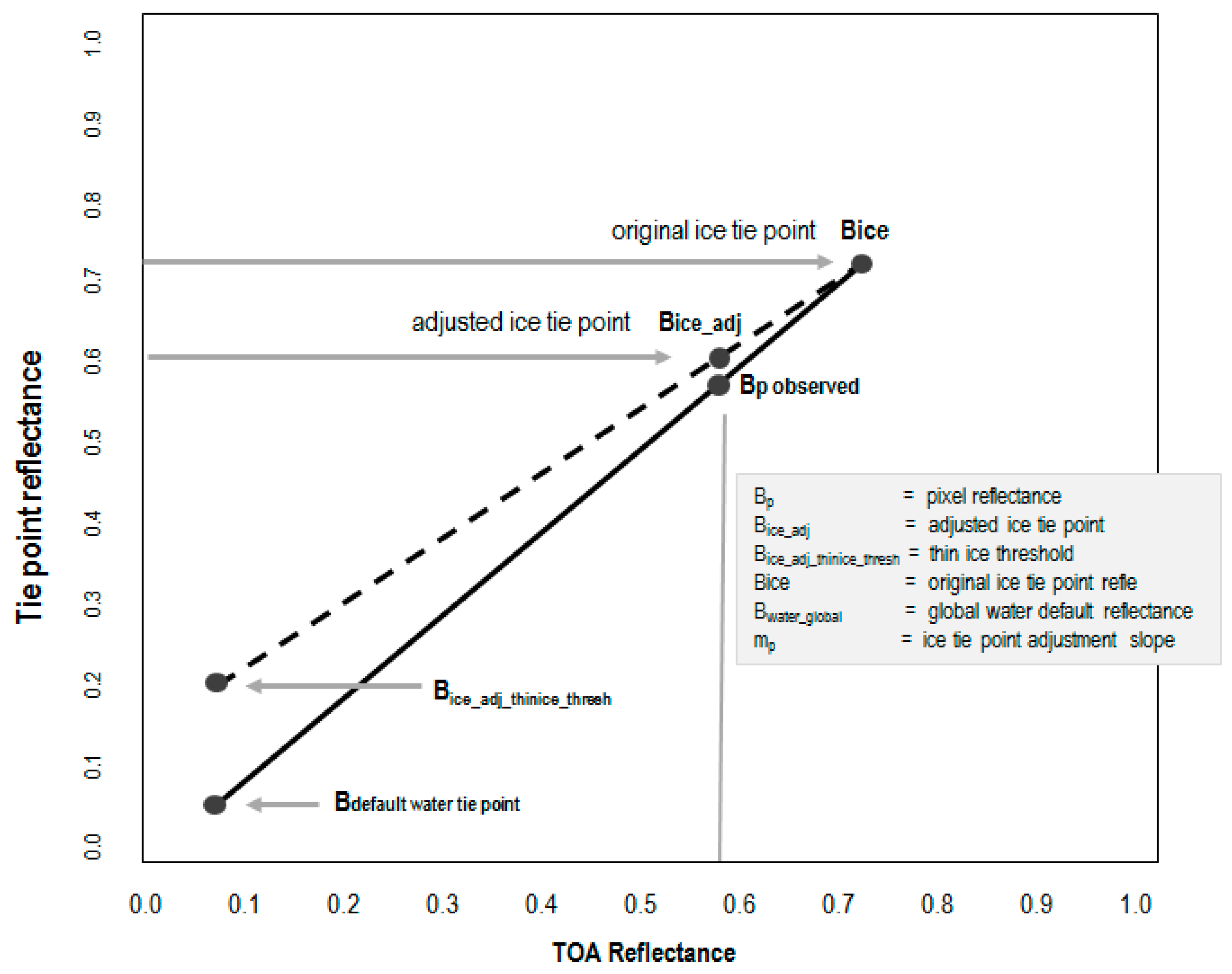
The ice concentration (fraction) in any given pixel is calculated as Equation (4). Reflectances and brightness temperatures of 100% ice and 100% water are needed. These are referred to as “tie points”. However, ice characteristics can vary considerably over space and time so it is not possible to specify fixed reflectance and temperature tie points for ice. While the spectral properties of ice vary with illumination and viewing geometry, air temperature, and the physical characteristics of ice, the main reason for variability within an image is the variation in ice concentration. Therefore, the methodology is to use a search window around each pixel and build histograms of reflectance and brightness temperature in order to identify pixels that are 100% ice. The water tie point is parameterized, as described later.
If an ice tie point can be found, then ice concentration for a pixel,
Cp, at the location is calculated by
where
Bwater is the reflectance or temperature of pure water pixels,
Bice is the reflectance or temperature of pure ice pixels (tie point reflectance or temperature), and
Bp is the observed reflectance or temperature of the pixel. The reflectance in the visible band at 0.67 μm is used because it gives excellent spectral separation between ice (or snow on ice) and open water. In this algorithm, the visible reflectance is used during the day, and ice surface temperature is used at night.
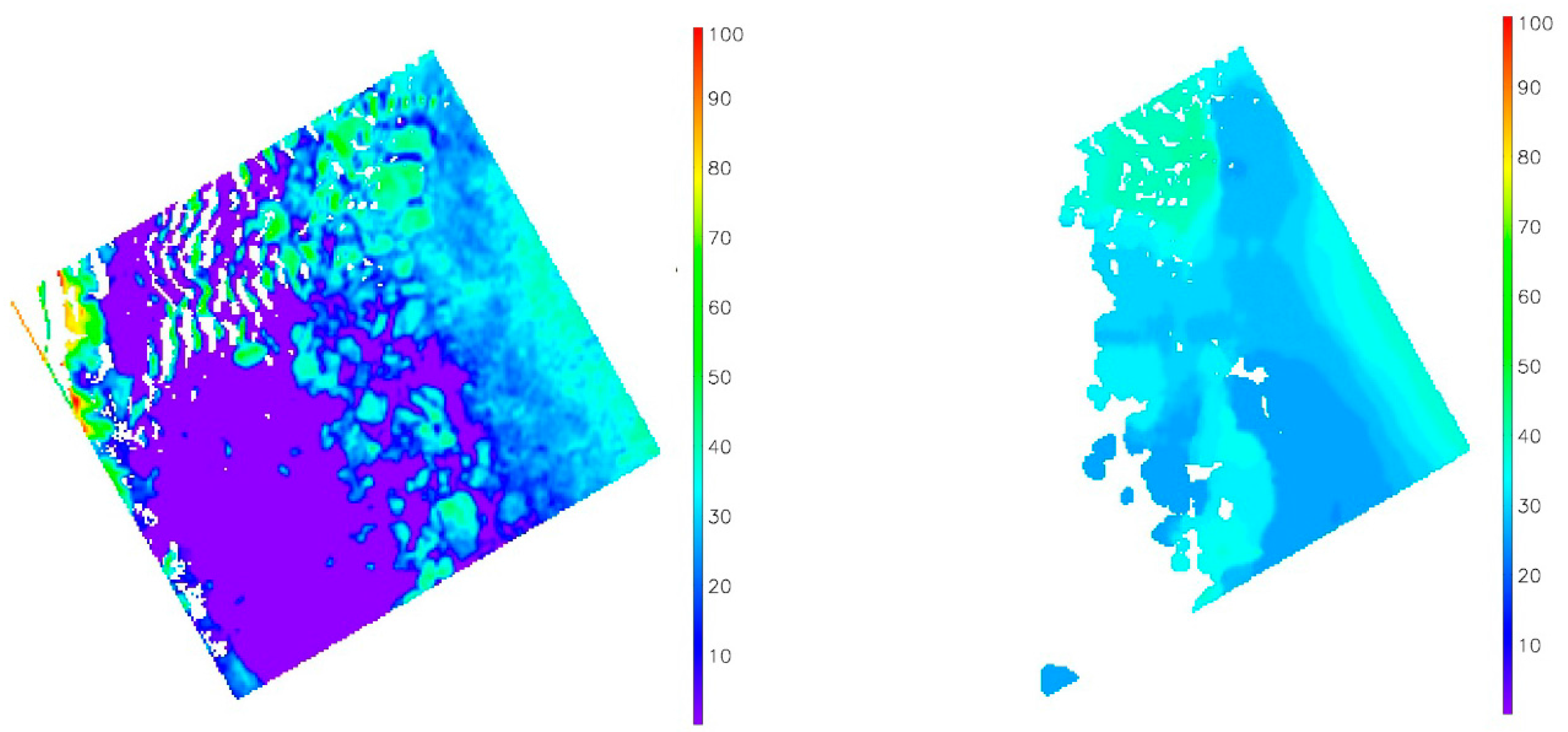
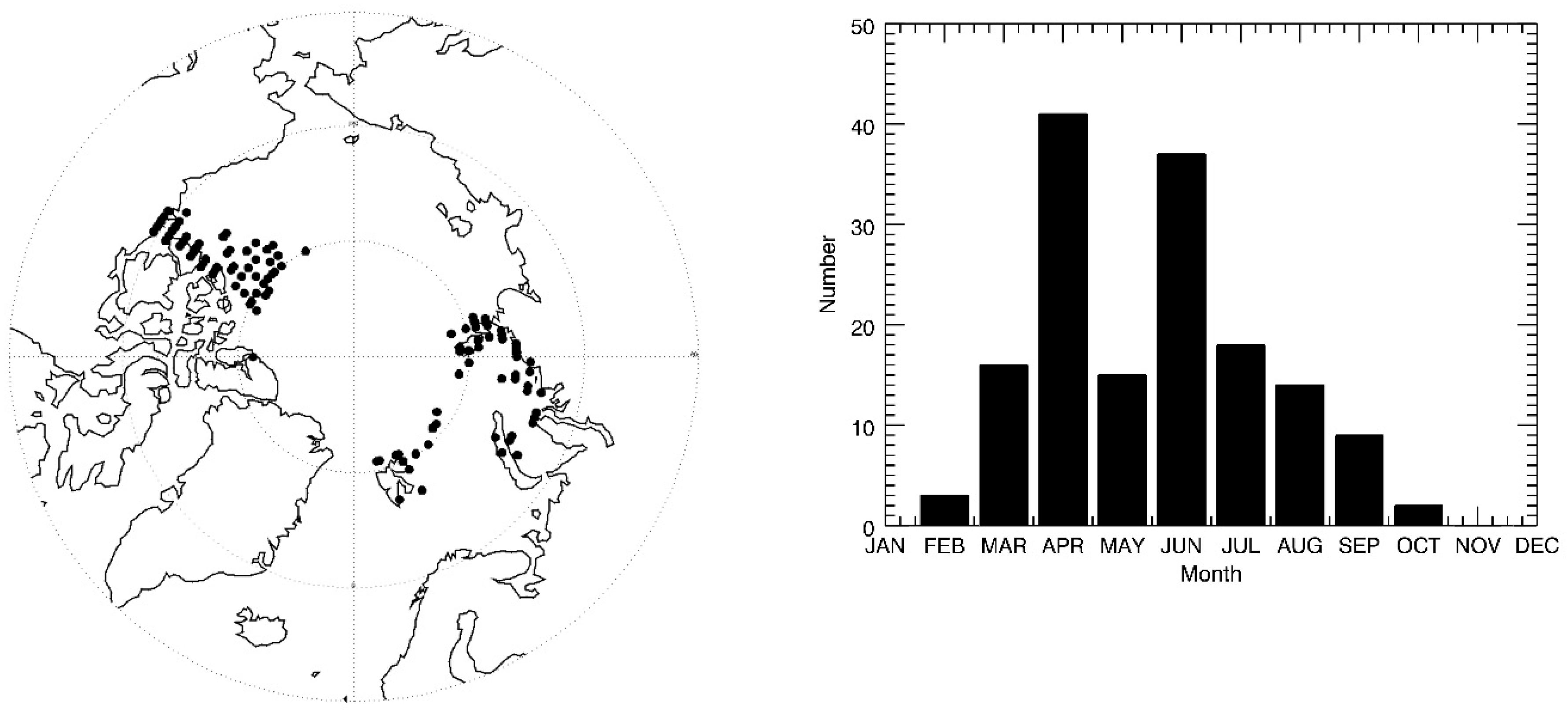
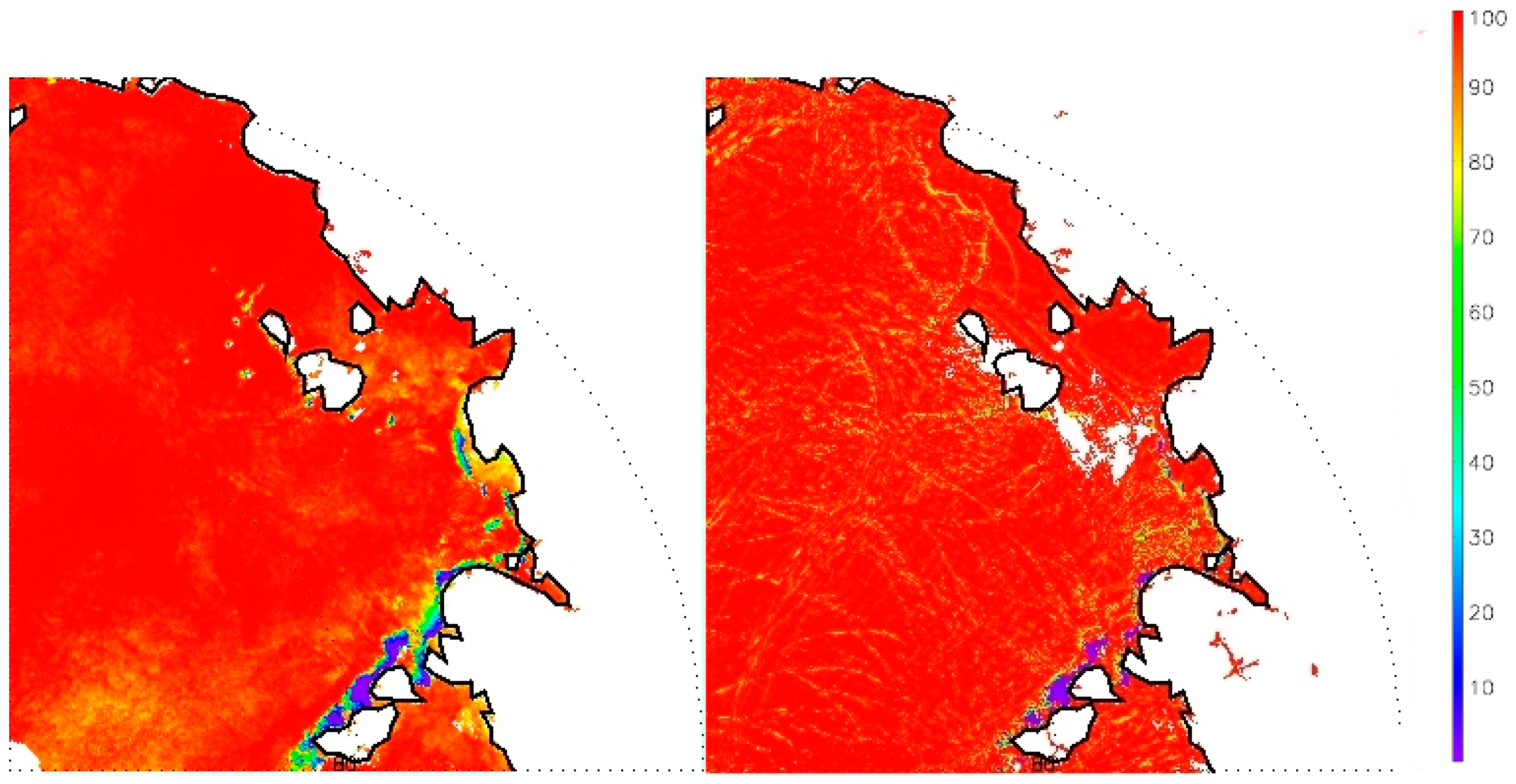
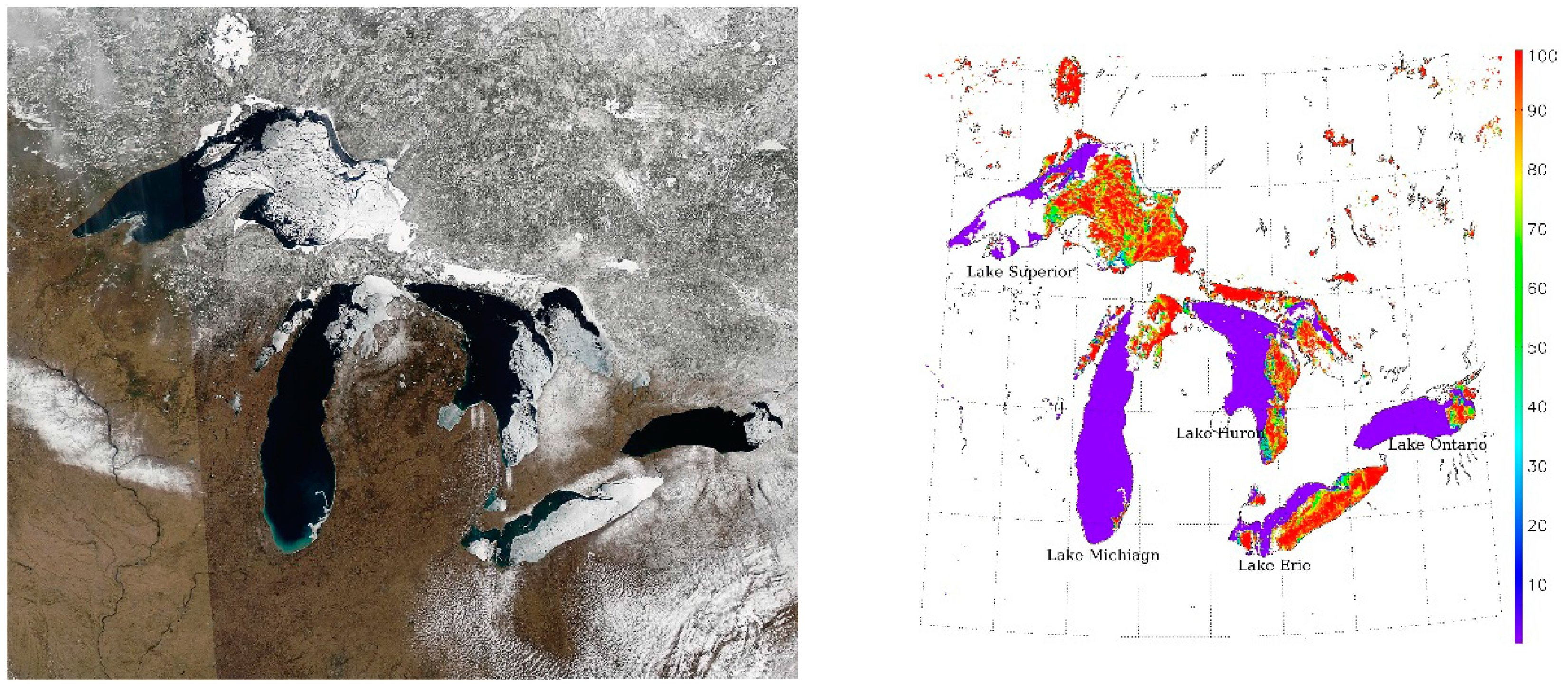
Figure 2 is an RGB (red-green-blue) image from the Landsat 8 Operational Land Imager (OLI) and VIIRS over the Kara Sea just east of Novaya Zemlya. The original spatial resolutions of the Landsat 8 OLI and VIIRS are 30 m and 750 m, which are remapped to 50 m and 1 km using the Equal-Area Scalable Earth (EASE)-Grid using the MODIS Swath-to-Grid Toolbox (MS2GT) (
http://nsidc.org/data/modis/ms2gt/index.html). This scene shows pixels that are open (unfrozen) water, partially ice-covered, and fully ice-covered.
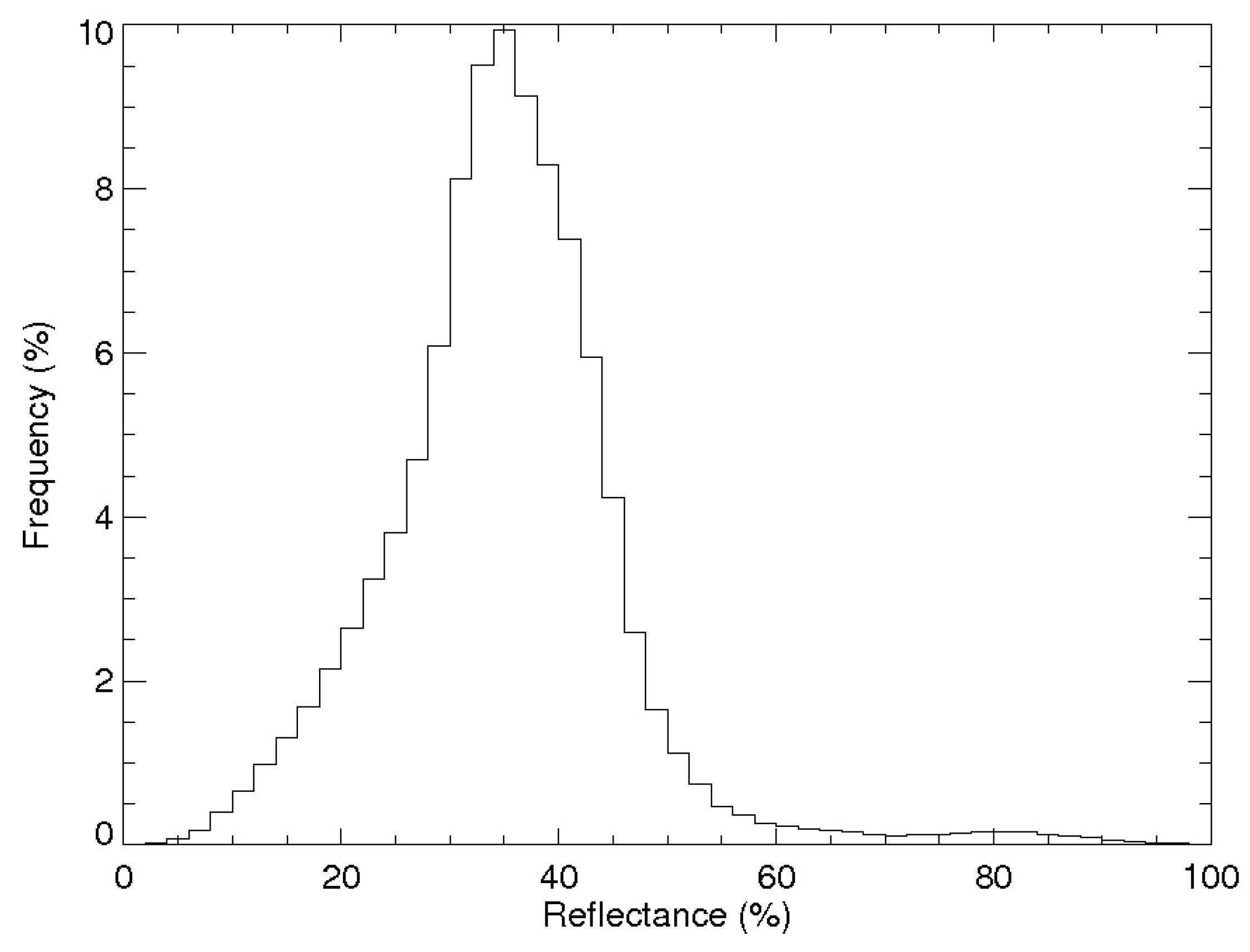
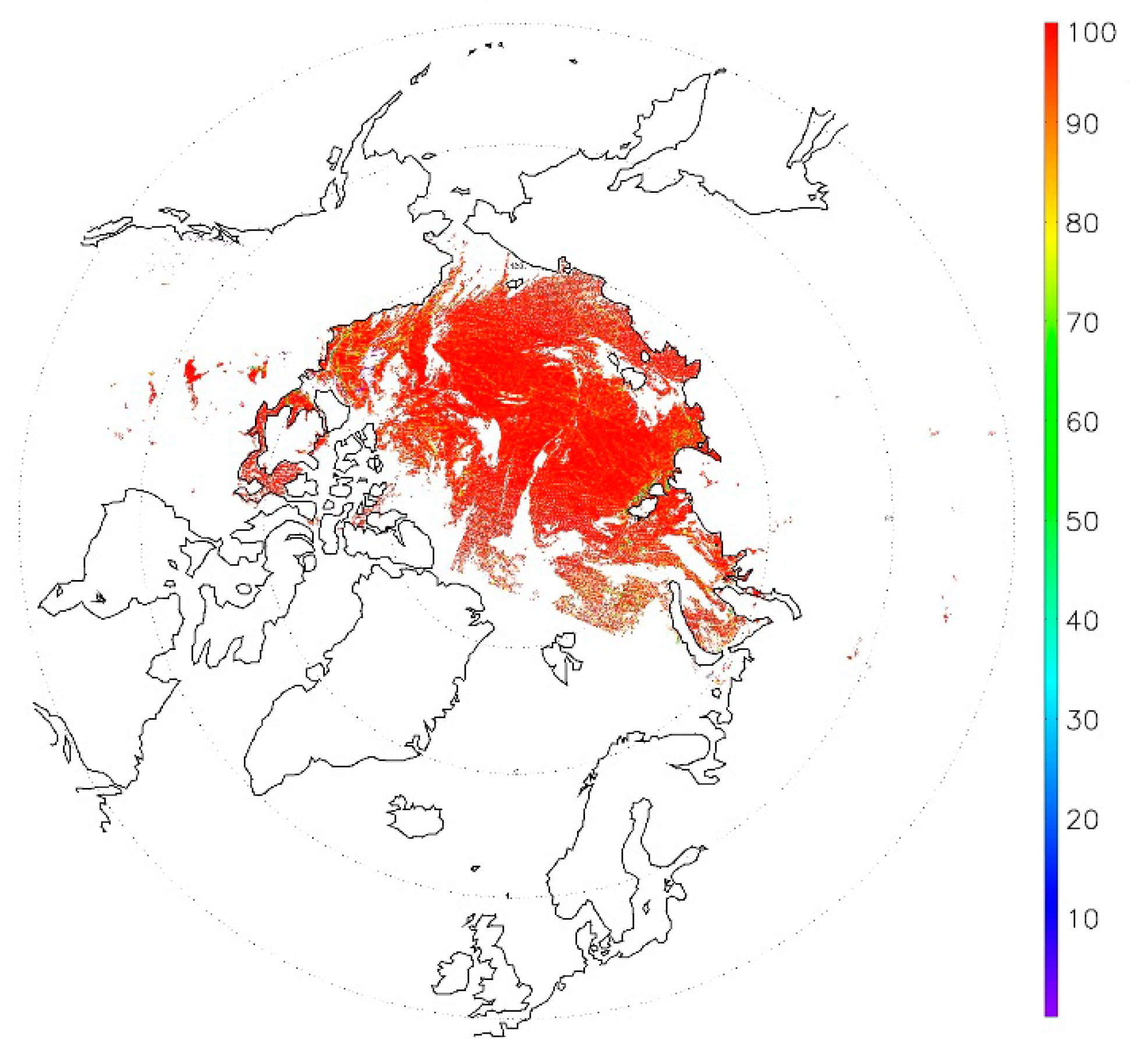
Determining the reflectance/temperature ice tie point at a location is the key to calculating the ice concentration. In a square, sliding search window with a size of N × N original VIIRS M band pixels, the ice reflectance/temperature probability density function (PDF) is calculated using all ice-covered pixels identified by the methodology in the previous section. N is set to 51 with the location of interest at the center. Retrieved tie point values are found to be insensitive to N for 31 < N < 51. This PDF is presented as a histogram;
i.e., it is visualized as a relative frequency histogram. For temperature, the minimum central bin value is 215 K with a bin width of 0.5 K, and a total number of bins of 121. For reflectance, the minimum central bin value is 0.0 with bin width of 0.02; the total number of bins is also 121 to be consistent with temperature. The PDF is then smoothed using a boxcar filter with a width of 5 bins, in which a sliding integral is calculated over the original PDF.
Figure 3 shows the PDF of reflectance of all the ice-covered pixels of the scene in
Figure 2.
The PDF in individual search windows resembles the PDF shown in
Figure 3, with narrower distributions. The ice reflectance/temperature tie point in a search window is the reflectance/temperature with the maximum probability density in the smoothed PDF,
i.e., the maximum sliding integral. The ice reflectance/temperature tie point is assigned to the central pixel. It should be noted that the tie point algorithm is run only under the constraint that at least 10% of the pixels in a search window are clear-sky ice-covered pixels, and the central pixel is ice covered. The sliding search window moves 1 pixel each time to determine the tie point at each every pixel in a scene.
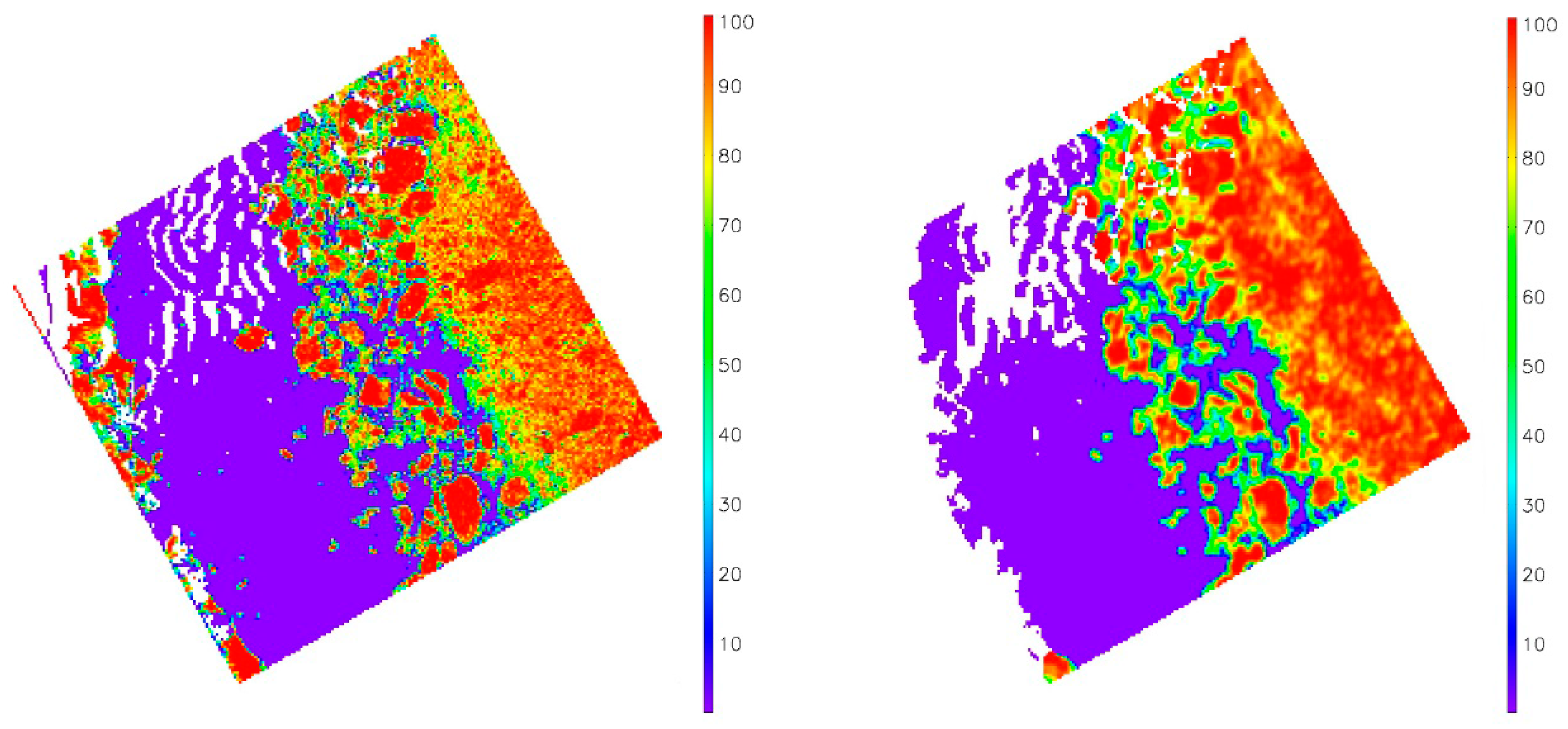
Figure 4 shows the reflectance at 0.67 μm and the derived tie points. This tie point algorithm is adapted from a similar algorithm in [
49], with the assumption that 100% ice concentration occupies enough of all the available clear-sky ice-covered pixels in a search window that an ice tie point can be derived, and ice characteristics in the search window are homogeneous. When these assumptions are not satisfied, the ice concentration can have large uncertainties in regions like the marginal ice zone, and transition zones between melt pond covered and melt pond free sea ice. Due to the constraints on the available clear-sky ice-covered pixels, this tie point algorithm does not work on very small bodies of water.
While the tie point of open water could be obtained dynamically in the same way as the ice tie point, the reflectance and temperature of water within or near the ice pack does not vary as much as ice of varying thicknesses. Therefore, the water reflectance tie point is simply parameterized as a function of solar zenith angle, with a value of 0.05 for solar zenith angles less than 65°, and 0.07 for solar zenith angles greater than or equal to 65° and less than 85°. The water temperature tie point changes with the water salinity, being 273.15 K for freshwater and 271.35 K for salt water.
After the reflectance/temperature ice tie point is determined, ice concentration is calculated following Equation (4), where ice concentration is 100% if the observed reflectance is higher or the temperature is lower than the tie point, or 0% if it is lower (reflectance)/higher (temperature) than the water tie point.
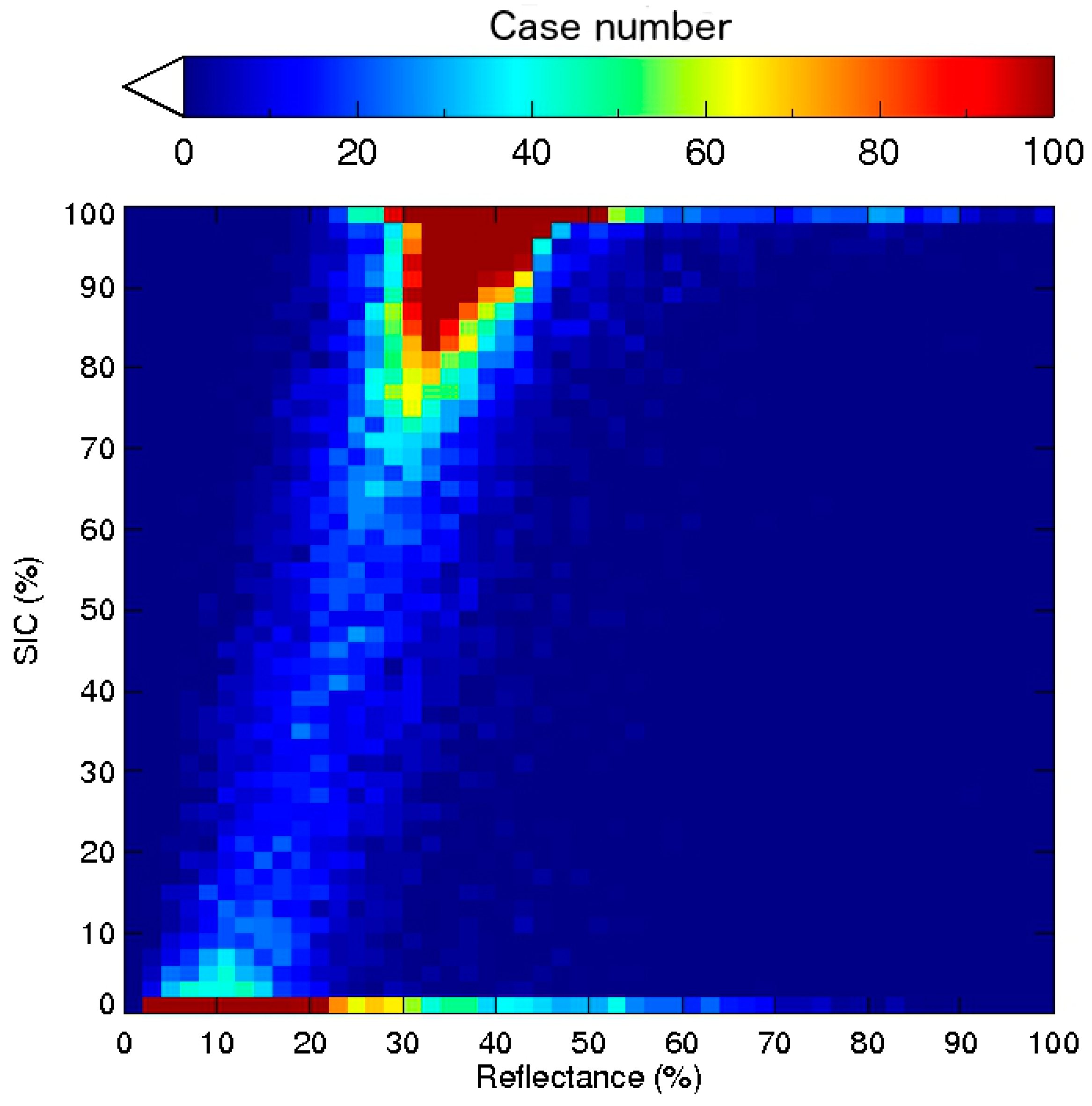
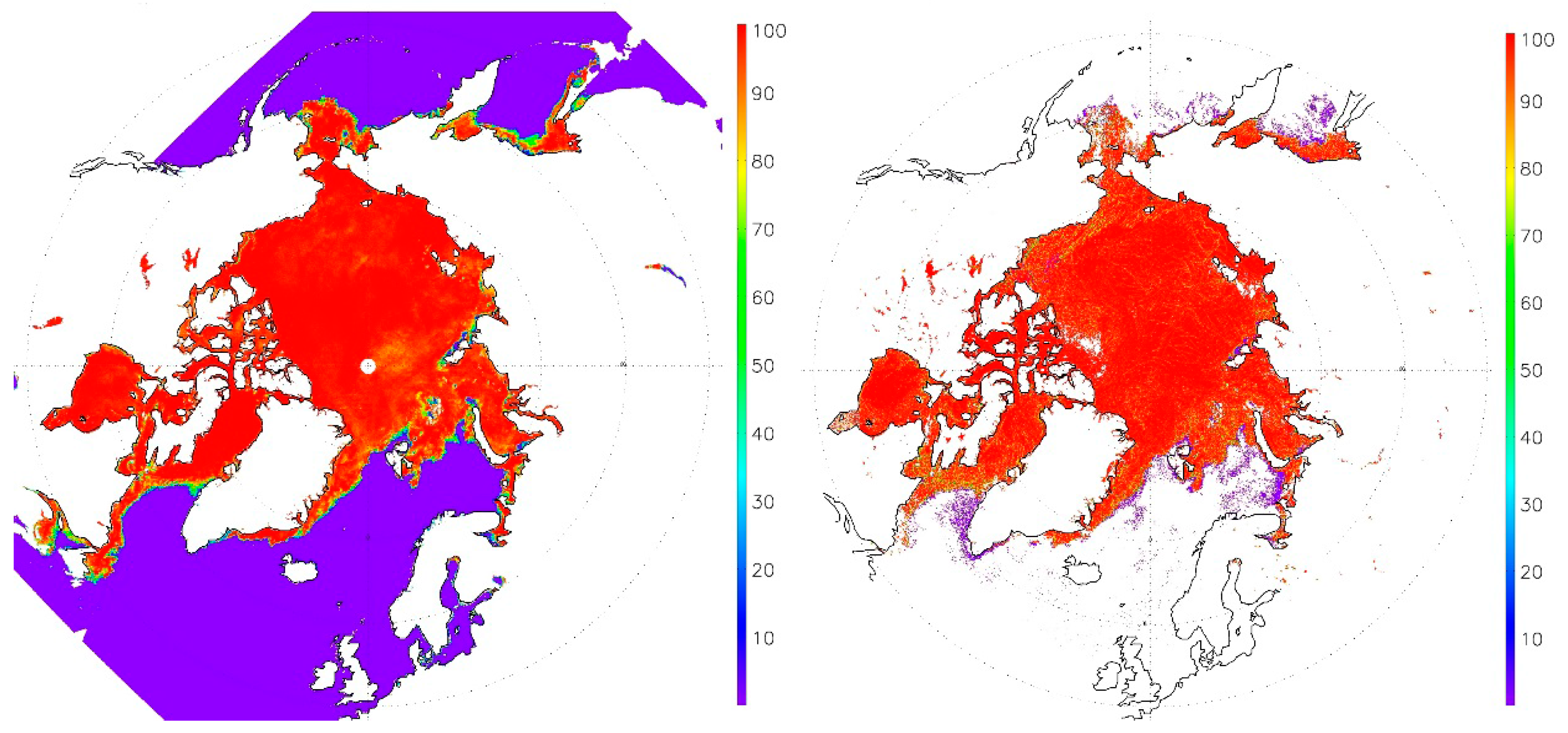
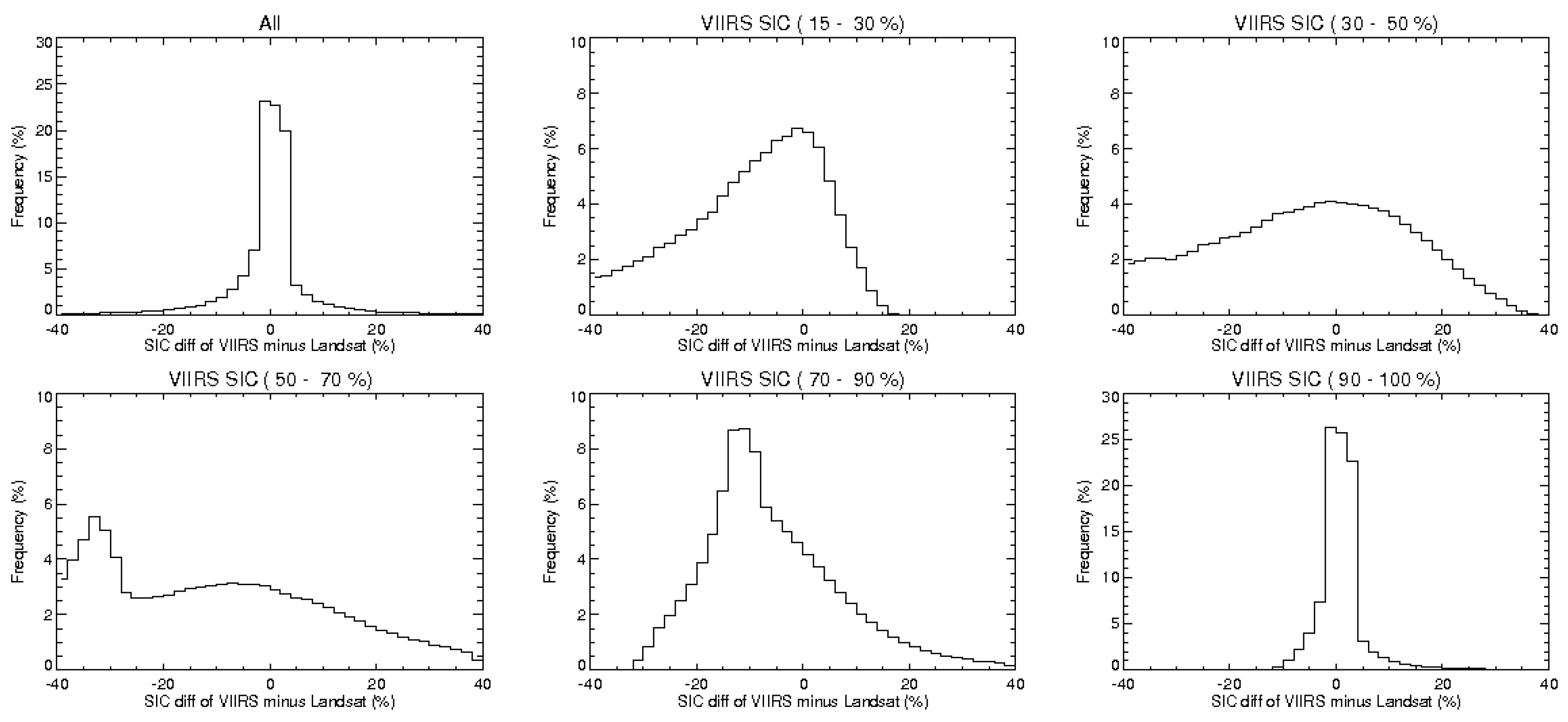
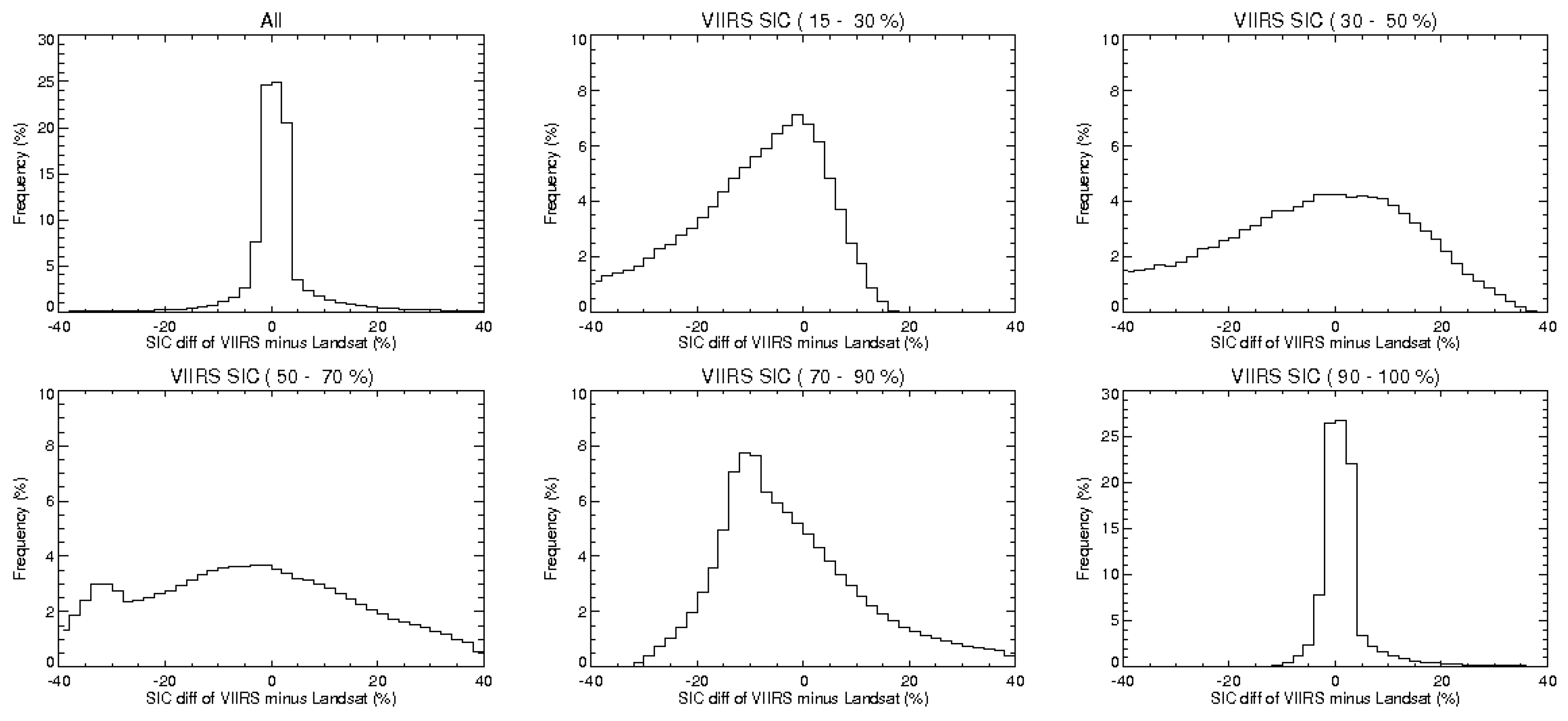
Figure 5 shows the linear relationship of the 0.64 μm reflectance and ice concentration derived from Landsat 8, which demonstrates that using Equation (4) to calculate the ice concentration is a valid approach. The large spread of 0.64 μm reflectances for ice concentrations near 0% may be due to cloud contamination, errors in the land cover data, and/or geo-location errors. Details of the Landsat 8 ice concentration calculation are given in the next section.
As the last step, the ice cover mask from the ice identification step is refined as the final ice cover mask. If the retrieved ice concentration is below 15%, the pixel is relabeled as water in the ice cover mask. This is done because the uncertainty of the estimates for low ice concentrations is 15%–20% (see next section), and to be consistent with passive microwave ice concentration products, which traditionally use the same criterion.