Time Series MODIS and in Situ Data Analysis for Mongolia Drought
Abstract
:1. Introduction
2. Study Area and Data Used
2.1. Study Area
2.2. Data Used
2.2.1. MODIS Products
2.2.2. In Situ Measurement Data
3. Methodology
3.1. Anomaly of MDSI Description
3.2. Anomaly of Climatological Variables Description
3.3. Relationship between MDSI Anomaly and Climatological Variables
4. Results and Discussion
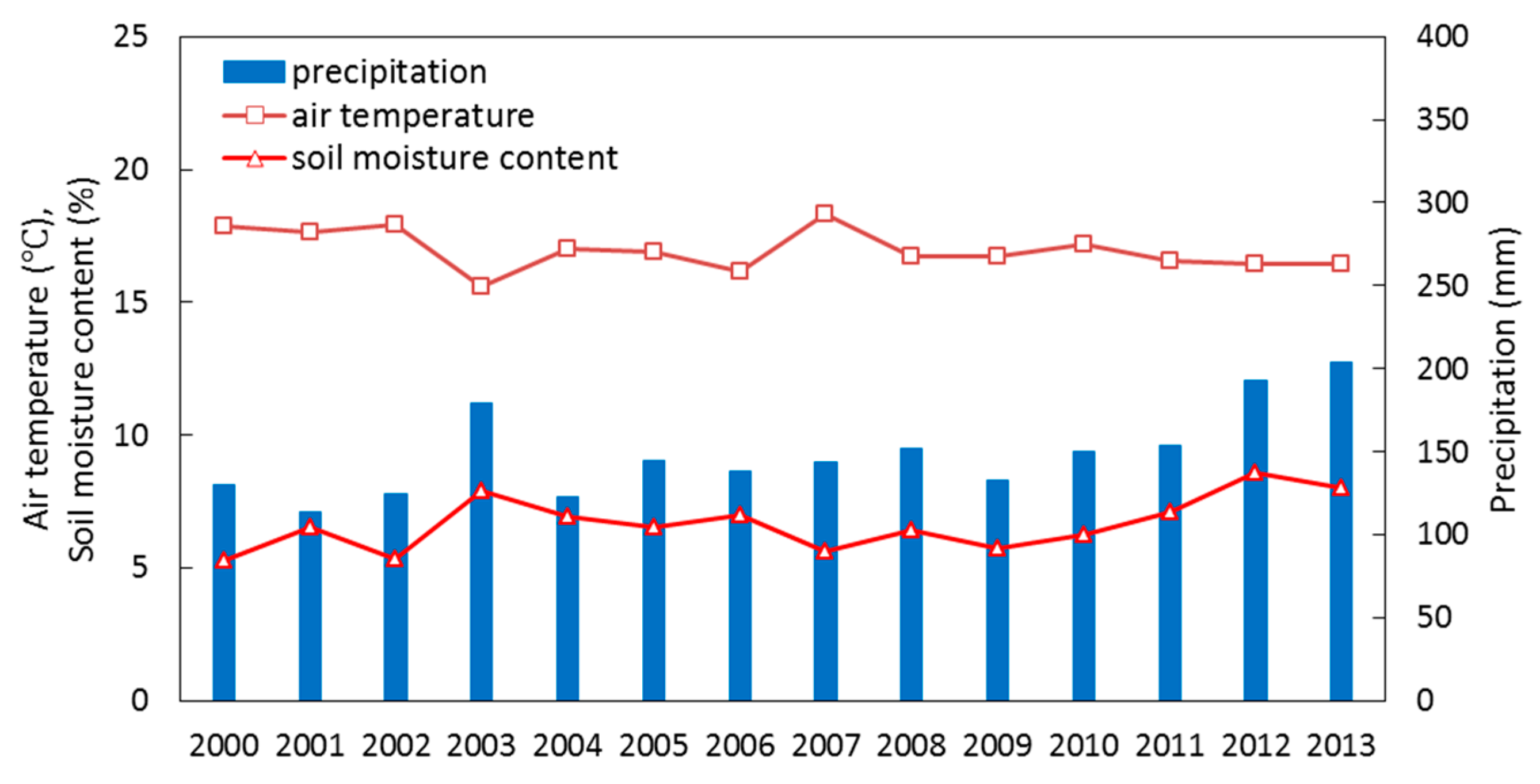
4.1. Climatological Variables among Stations
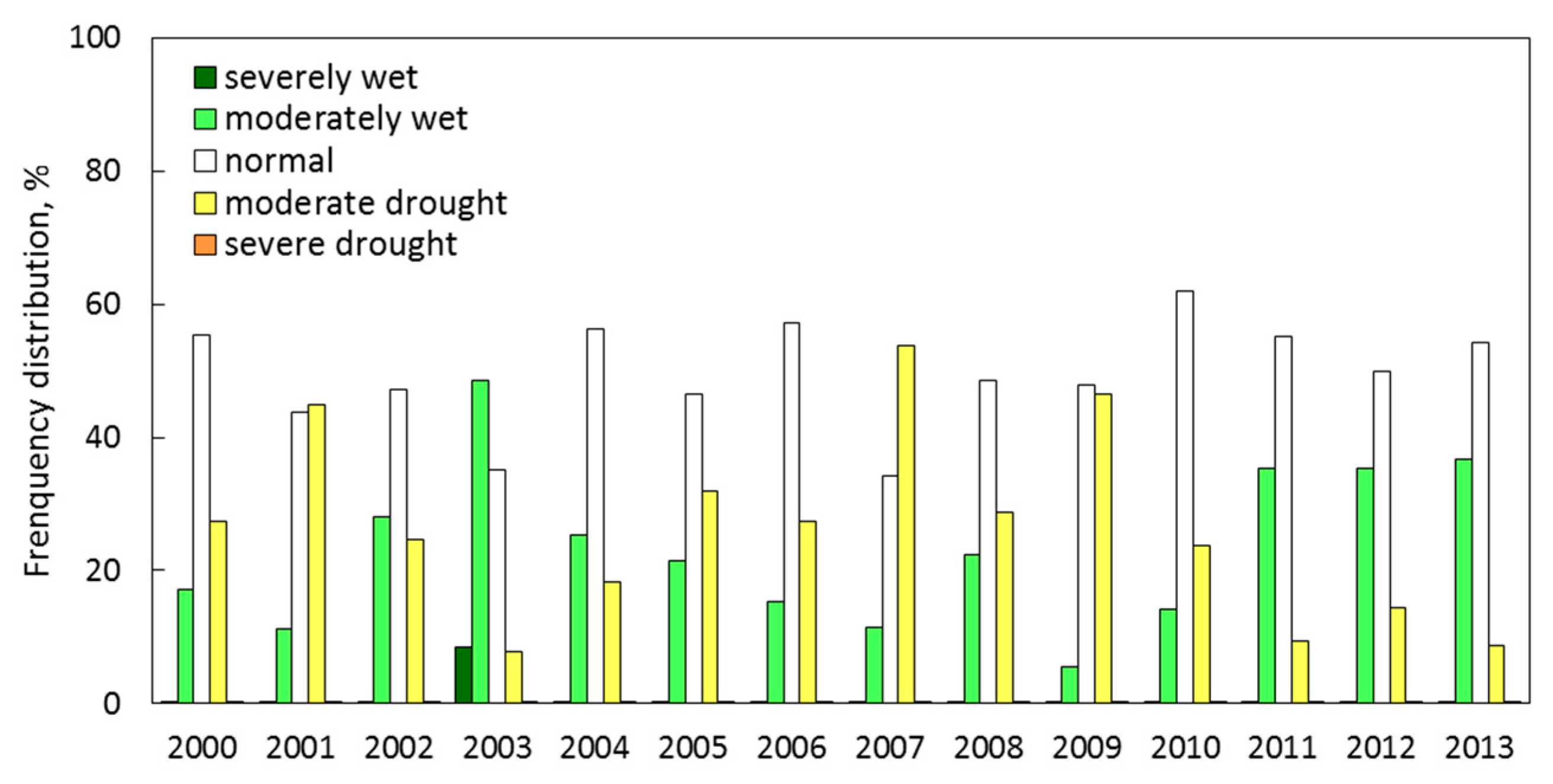
4.2. Anomaly of MDSI Variations
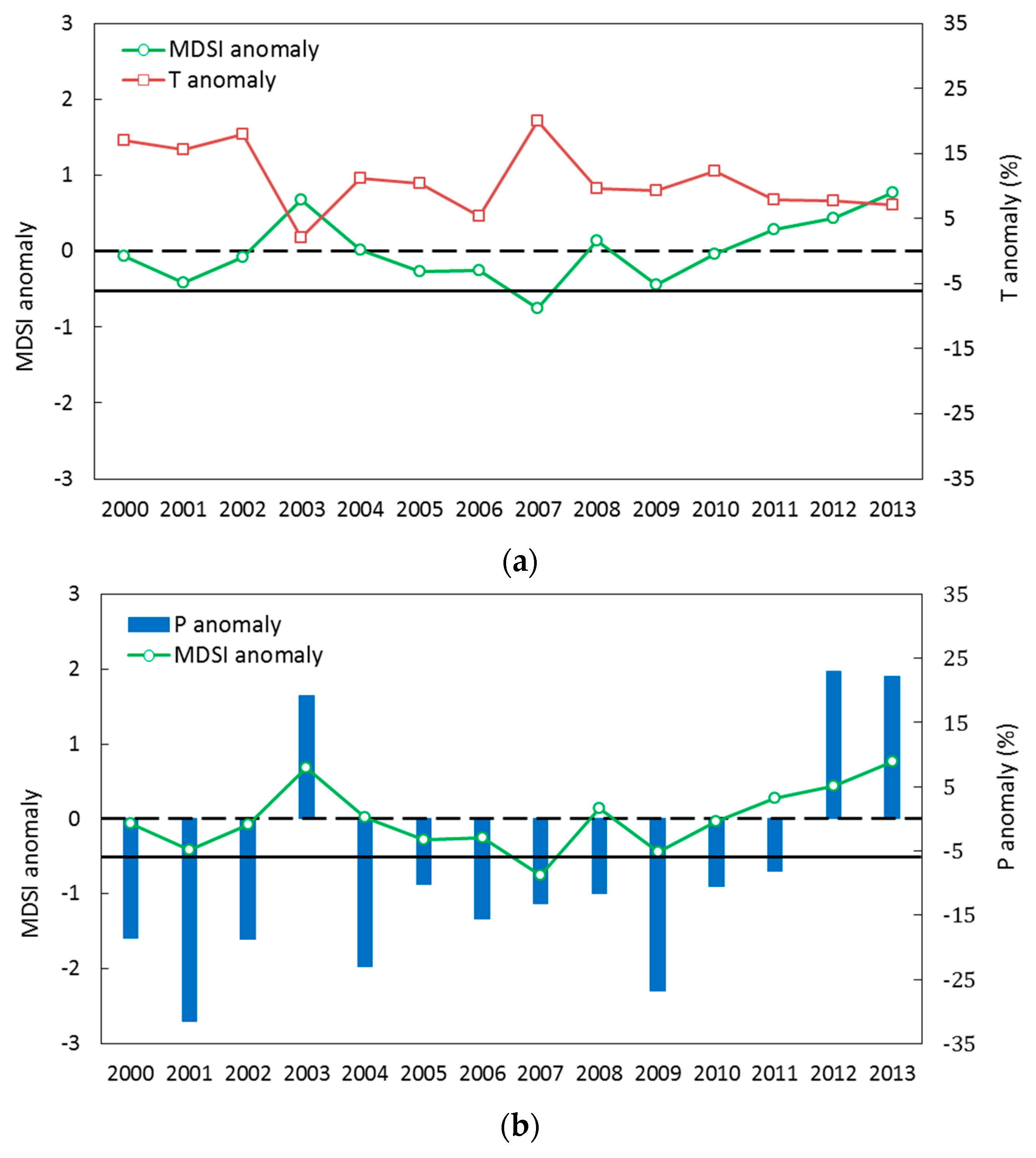
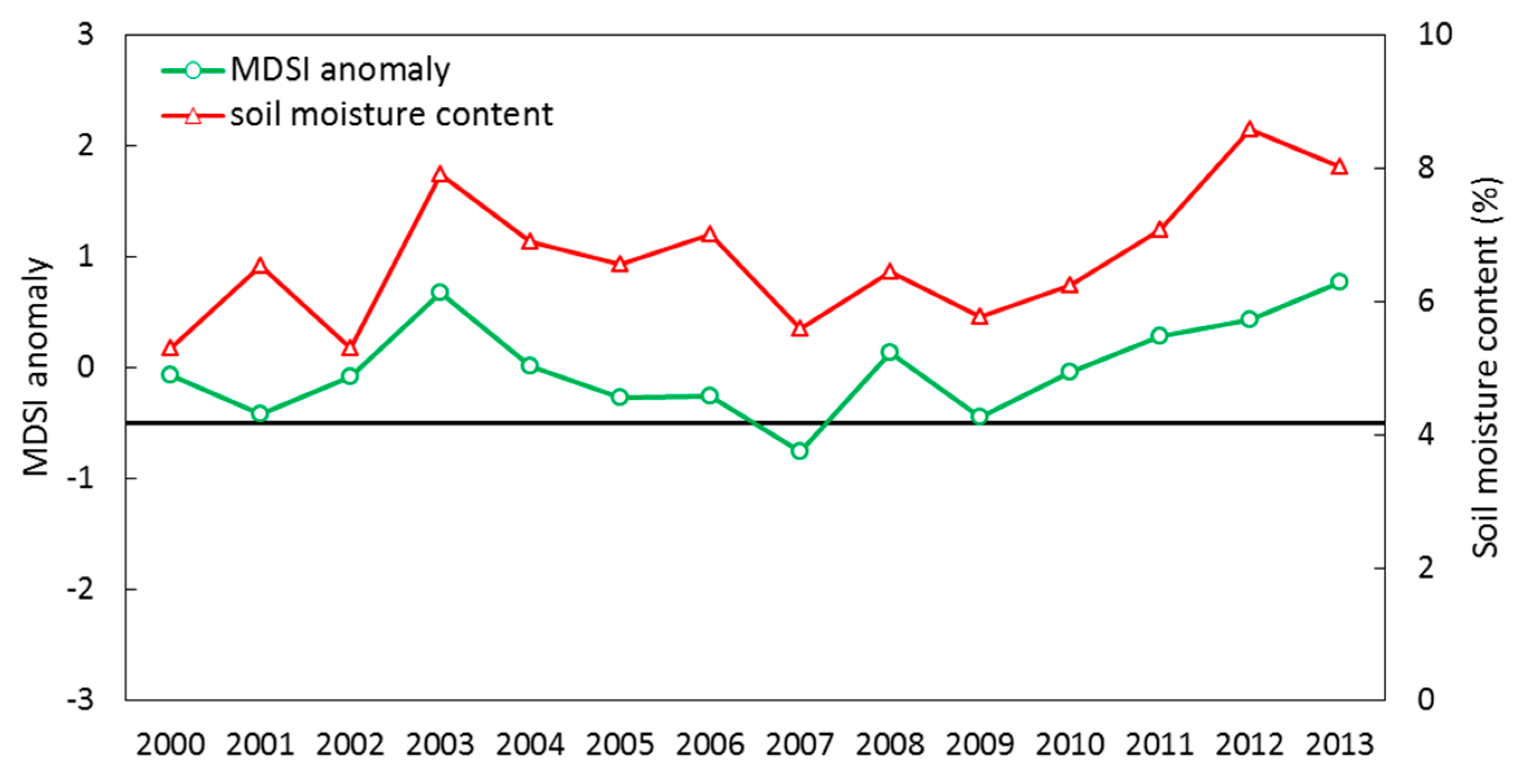
4.3. Anomaly of MDSI and Climatological Variable Variations
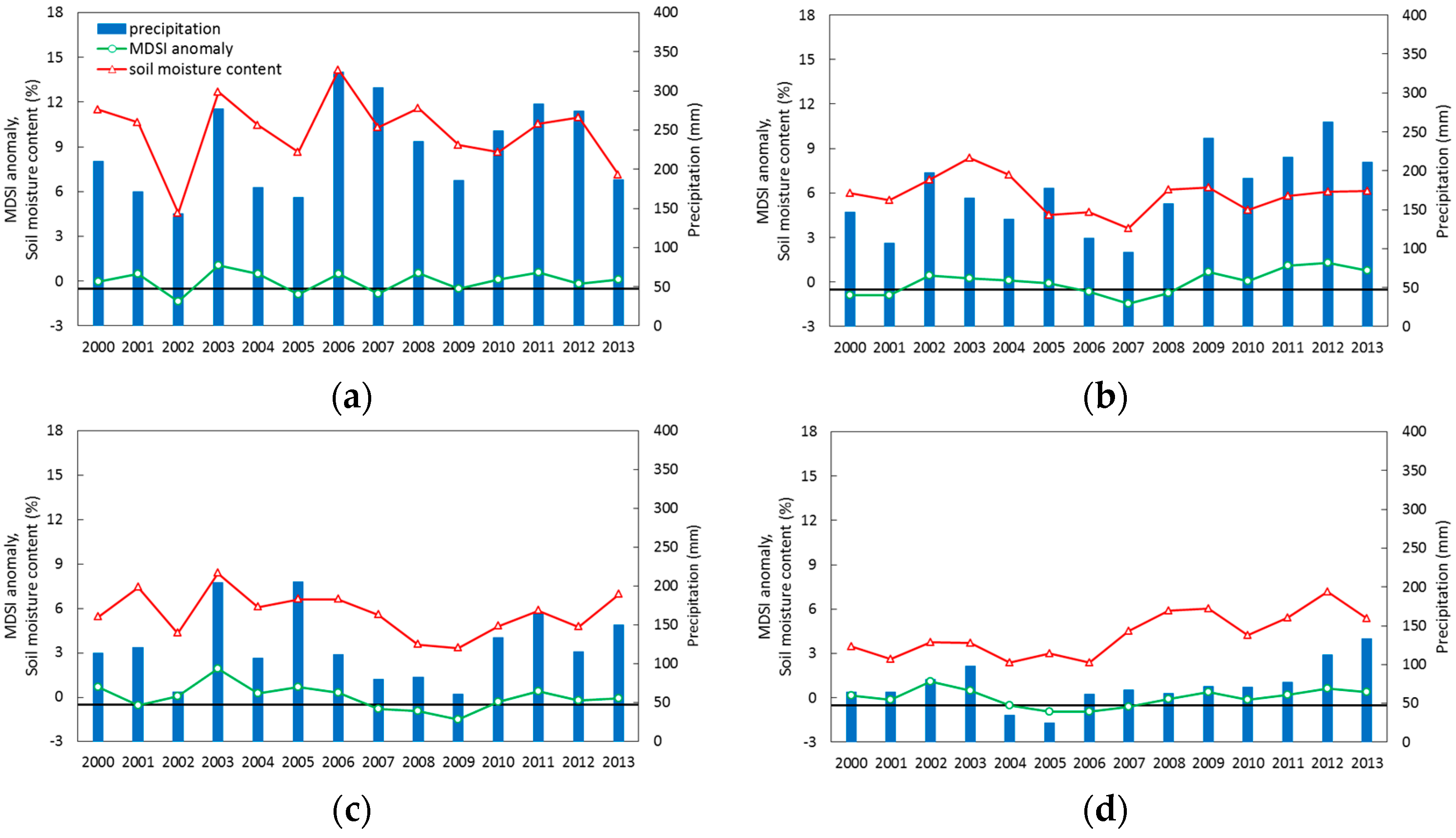
4.4. Anomalies among Different Land Use Areas
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Dagvadorj, D.; Natsagdorj, L.; Dorjpurev, J.; Namkhainyam, B. Mongolia Assessment Report on Climate Change 2009; Ministry of Environment, Nature and Tourism, Mongolia: Ulaanbaatar, Mongolia, 2009. [Google Scholar]
- Morinaga, Y.; Bayarbaatar, L.; Erdenetsetseg, D.; Shinoda, M. Zoo-meteorological study of cow weight change in a forest steppe region of Mongolia. In Proceedings of the Sixth International Workshop on Climate Change in Arid and Semi-Arid Region of Asia, Ulaanbaatar, Mongolia, 25–26 August 2004; pp. 100–108.
- Narasimhan, B.; Srinivasan, R. Development and evaluation of soil moisture deficit index (SMDI) and evapotranspiration deficit index (ETDI) for agricultural drought monitoring. Agric. For. Meteor. 2005, 133, 69–88. [Google Scholar] [CrossRef]
- Yang, X.; Wu, J.J.; Yan, F.; Zhang, J. Assessment of regional soil moisture status based on characteristics of surface temperature/vegetation index space. Acta Ecol. Sin. 2009, 29, 1205–1216. [Google Scholar]
- Justice, C.O.; Townshend, J.R.G.; Vermote, E.F.; Masuoka, E.; Wolfe, R.E.; Saleous, N.; Roy, D.P.; Morisette, J.T. An overview of MODIS Land data processing and product status. Remote Sens. Environ. 2002, 83, 3–15. [Google Scholar] [CrossRef]
- Tucker, C.J.; Choudhury, B.J. Satellite remote sensing of drought conditions. Remote Sens. Environ. 1987, 23, 243–251. [Google Scholar] [CrossRef]
- Tucker, C.J. Comparing SMMR and AVHRR data for drought monitoring. Int. J. Remote Sens. 1989, 10, 1663–1672. [Google Scholar] [CrossRef]
- Nicholson, S.E.; Tucker, C.J.; Ba, M.B. Desertification, drought and surface vegetation: An example from the west African Sahel. Bull. Am. Meteorol. Soc. 1998, 79, 815–829. [Google Scholar] [CrossRef]
- Gonzalez-Alonso, F.; Cuevas, J.M.; Casanova, J.L.; Calle, A.; Illera, P. Drought monitoring in Spain using satellite remote sensing. In Sensors and Environmental Applications of Remote Sensing; Askne, J., Ed.; Taylor & Francis: Abingdon, UK, 1995; pp. 87–90. [Google Scholar]
- Gonzalez-Alonso, F.; Calle, A.; Casanova, J.L.; Vazquez, A.; Cuevas, J.M. Operational monitoring of drought in Spain using NOAA-AVHRR satellite images. In Proceedings of the 28th International Symposium on Remote Sensing of Environment, Cape Town, South Africa, 27–31 March 2000.
- Liu, W.T.; Negron-Juarez, R.I. ENSO drought onset prediction in northeast Brazil using NDVI. Int. J. Remote Sens. 2001, 22, 3483–3501. [Google Scholar] [CrossRef]
- Peters, A.J.; Walter-Shea, E.A.; Ji, L.; Vina, A.; Hayes, M.; Svoboda, M.D. Drought monitoring with NDVI-based standardized vegetation index. Photogramm. Eng. Remote Sens. 2002, 68, 71–75. [Google Scholar]
- Ji, L.; Peters, A. Assessing vegetation response to drought in the northern Great Plains using vegetation and drought indices. Remote Sens. Environ. 2003, 87, 85–98. [Google Scholar] [CrossRef]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Gao, X.; Huete, A.R.; Ni, W.; Miura, T. Optical-biophysical relationships of vegetation spectra without background contamination. Remote Sens. Environ. 2000, 74, 609–620. [Google Scholar] [CrossRef]
- Jiang, Z.; Huete, A.R.; Didan, K.; Miura, T. Development of a two-band enhanced vegetation index without a blue band. Remote Sens. Environ. 2008, 112, 3833–3845. [Google Scholar] [CrossRef]
- Wu, C.; Munger, J.W.; Niu, Z.; Kuang, D. Comparison of multiple models for estimating gross primary production using MODIS and eddy covariance data in Harvard Forest. Remote Sens. Environ. 2010, 114, 2925–2939. [Google Scholar] [CrossRef]
- Tucker, C.J.; Pinzon, J.E.; Brown, M.E.; Slayback, D.; Pak, E.W.; Mahoney, R.; Vermote, E.; Saleous, N. An extended AVHRR 8-km NDVI data set compatible with MODIS and SPOT vegetation NDVI data. Int. J. Remote Sens. 2005, 26, 4485–4498. [Google Scholar] [CrossRef]
- Sellers, P.J. Canopy reflectance, photosynthesis and transpiration. Int. J. Remote Sens. 1985, 6, 1335–1372. [Google Scholar] [CrossRef]
- Tucker, C.J.; Townsend, J.R.G.; Goff, T.E. African land cover classification using satellite data. J. Sci. 1985, 227, 369–375. [Google Scholar] [CrossRef] [PubMed]
- Goward, N.S. Satellite bioclimatology. J. Clim. 1989, 2, 710–720. [Google Scholar] [CrossRef]
- Zhang, X.; Friedl, M.A.; Schaaf, C.B.; Strahler, A.H.; Hodges, J.C.F.; Gao, F.; Reed, B.C.; Huete, A.R. Monitoring vegetation phenology using MODIS. Remote Sens. Environ. 2003, 84, 471–475. [Google Scholar] [CrossRef]
- Guindin-Garcia, N.; Gitelson, A.A.; Arkebauer, T.J.; Shanahan, J.; Weiss, A. An evaluation of MODIS 8- and 16-day composite products for monitoring maize green leaf area index. Agric. For. Meteorol. 2012, 161, 15–25. [Google Scholar] [CrossRef]
- Chang, T.-Y.; Liou, Y.-A.; Lin, C.-Y.; Liu, C.-S.; Wang, Y.-C. Evaluation of surface heat fluxes in Chiayi plain of Taiwan by remotely sensed data. Int. J. Remote Sens. 2010, 31, 3885–3898. [Google Scholar] [CrossRef]
- Liou, Y.-A.; Kar, S.K. Evapotranspiration estimation with remote sensing and various surface energy balance algorithms—A review. Energies 2014, 7, 2821–2849. [Google Scholar] [CrossRef]
- Dao, P.D.; Liou, Y.-A. Object-based Flood Mapping and Affected Rice Field Estimation with Landsat 8 OLI and MODIS Data. Remote Sens. 2015, 7, 5077–5097. [Google Scholar] [CrossRef]
- Liou, Y.-A.; Sha, H.-C.; Chen, T.-M.; Wang, T.-S.; Li, Y.-T.; Lai, Y.-C.; Chiang, M.-H.; Lu, L.-T. Assessment of disaster losses in rice field and yield after tsunami induced by the 2011 Great East Japan earthquake. J. Mar. Sci. Technol. 2012, 20, 618–623. [Google Scholar]
- Nguyen, K.A.; Liou, Y.-A.; Li, M.-H.; Tran, A.T. Zoning eco-environmental vulnerability for environmental management and protection. Ecol. Indic. 2016, 69, 100–117. [Google Scholar] [CrossRef]
- Huete, A.R.; Tucker, C.J. Investigation of soil influences on AVHRR red and near-infrared vegetation index imagery. Int. J. Remote Sens. 1991, 12, 1223–1242. [Google Scholar] [CrossRef]
- Karnieli, A.; Shachak, M.; Tsoar, H.; Zaady, E.; Kaufman, Y.; Danin, A.; Porter, W. The effect of microphytes on the spectral reflectance of vegetation in semi-arid regions. Remote Sens. Environ. 1996, 57, 88–96. [Google Scholar] [CrossRef]
- Huete, A.R.; Liu, H.Q.; Batchily, K.; van Leeuwen, W.J.D. A comparison of vegetation indices over a global set of TM images for EOS-MODIS. Remote Sens. Environ. 1997, 59, 440–451. [Google Scholar] [CrossRef]
- Huete, A.R.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Kim, Y.; Huete, A.R.; Miura, T.; Jiang, Z. Spectral compatibility of vegetation indices across sensors: Band decomposition analysis with Hyperion data. J. Appl. Remote Sens. 2010, 4, 043520. [Google Scholar] [CrossRef]
- Yao, Y.; Liang, S.; Qin, Q.; Wang, K. Monitoring drought over the conterminous United States using MODIS and NCEP Reanalysis-2 data. J. Appl. Meteor. Climatol. 2010, 49, 1665–1680. [Google Scholar] [CrossRef]
- Mu, Q.; Heinsch, F.A.; Zhao, M.; Running, S.W. Development of a global evapotranspiration algorithm based on MODIS and global meteorology data. Remote Sens. Environ. 2007, 111, 519–536. [Google Scholar] [CrossRef]
- Mu, Q.; Jones, L.A.; Kimball, J.S.; McDonald, K.C.; Running, S.W. Satellite assessment of land surface evapotranspiration for the pan-Arctic domain. Water Resour. Res. 2009, 45, W09420. [Google Scholar] [CrossRef]
- Mu, Q.; Zhao, M.; Running, S.W. Evolution of hydrological and carbon cycles under a changing climate. Part III: Global change impacts on landscape scale evapotranspiration. Hydrol. Processes. 2011, 25, 4093–4102. [Google Scholar] [CrossRef]
- Mu, Q.; Zhao, M.; Running, S.W. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Remote Sens. Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
- Mu, Q.; Zhao, M.; Kimball, J.S.; McDowell, N.G.; Running, S.W. A remotely sensed global terrestrial drought severity index. Bull. Am. Meteorol. Soc. 2013, 94, 83–98. [Google Scholar] [CrossRef]
- Bolortsetseg, B.; Bayasgalan, Sh.; Dorj, B.; Natsagdorj, L.; Tuvaansuren, G. Impact on agriculture. In Climate Change and Its Impacts in Mongolia; Batima, P., Dagvadorj, D., Eds.; JEMR Publishing: Ulaanbaatar, Mongolia, 2000; pp. 96–198. [Google Scholar]
- Batima, P.; Dagvadorj, D. Climate Change and Its Impacts in Mongolia; NAMHEM JEMR Publishing: Ulaanbaatar, Mongolia, 2000. [Google Scholar]
- Shiirevdamba, T. Biological Diversity in Mongolia: First National Report; Ministry for Nature and the Environment of Mongolia; Admon Printing House: Ulaanbaatar, Mongolia, 1998; p. 106. [Google Scholar]
- Natsagdorj, L. Climate Change: Pasture and Animal Husbandry; Batima, P., Ed.; Institute of Meteorology and Hydrology of Mongolia: Ulaanbaatar, Mongolia, 2003. [Google Scholar]
- Batima, P.; Bat, B.; Tserendash, S.; Myagmarjab, B. Adapting to drought, zud and climate change in Mongolia’s rangelands. In Climate Change and Adaptation; Neil, L., Ian, B., Adejuwon, J., Barros, V., Lasco, R., Eds.; Earthscan: London, UK, 2008. [Google Scholar]
- Mu, Q.; Zhao, M.; Running, S.W. MODIS Global Terrestrial Evapotranspiration (ET) Product (NASA MOD16A2/A3); Algorithm Theoretical Basis Document, Collection 5; NASA HQ, Numerical Terradynamic Simulation Group, University of Montana: Missoula, MT, USA, 2013. [Google Scholar]
- Solano, R.; Didan, K.; Jacobson, A.; Huete, A. MODIS Vegetation Index User’s Guide (MOD13 Series); Version 2.00, May 2010 (Collection 5); Vegetation Index and Phenology Lab, The University of Arizona: Tucson, AZ, USA, 2010. [Google Scholar]
- LPDAAC. NASA Land Data Products and Services. Available online: https://lpdaac.usgs.gov/ (accessed on 23 March 2016).
- Huete, A.R.; Justice, C.O.; van Leeuwen, W. MODIS Vegetation Index (MOD 13) Algorithm Theoretical Basis Document. Available online: http://modis.gsfc.nasa.gov/data/atbd/atbd_mod13.pdf (accessed on 24 June 2010).
- Wang, Z.; Liu, C.; Huete, A.R. From AVHRR-NDVI to MODIS EVI: Advances in vegetation index research. Acta Ecol. Sin. 2003, 23, 979–987. [Google Scholar]
- Huete, A.R.; Justice, C.O.; Liu, H. Development of vegetation and soil indices for MODIS-EOS. Remote Sens. Environ. 1994, 49, 224–234. [Google Scholar] [CrossRef]
- Information and Research Institute of Meteorology, Hydrology and Environment (IRIMHE), Mongolia 2016. Available online: http://www.icc.mn/ (accessed on 25 March2016).
- Dhar, O.N.; Rakhecha, P.R.; Kolkarni, A.K. Rainfall study of severe drought years of India. Proc. Int. Symp. Hydrol. Aspect Drought. 1979, 1, 28–36. [Google Scholar]
- Loik, M.E.; Breshears, D.D.; Lauenroth, W.K.; Belnap, J. A multi-scale perspective of water pulses in dryland ecosystems: Climatology and ecohydrology of the western USA. Oecologia 2004, 141, 269–281. [Google Scholar] [CrossRef] [PubMed]
- Palmer, W.C. Meteorological Drought. U.S. Weather Bureau Research Paper. Available online: https://www.ncdc.noaa.gov/temp-and-precip/drought/docs/palmer.pdf (accessed on 25 March2016).
- Kim, D.; Byun, H.R.; Choi, K.S. Evaluation, modification, and application of the Effective Drought Index to 200-year drought climatology of Seoul, Korea. J. Hydrol. 2009, 378, 1–12. [Google Scholar] [CrossRef]
- Cheng, C.-H.; Nnadi, F.; Liou, Y.-A. A regional land use drought index for Florida. Remote Sens. 2015, 7, 17149–17167. [Google Scholar] [CrossRef]
- Byun, H.R.; Lee, S.J.; Morid, S.; Choi, K.S.; Lee, S.M.; Kim, D.W. A study on the periodicities of droughts in Korea. Asia Pac. J. Atmos. Sci. 2008, 44, 417–441. [Google Scholar]
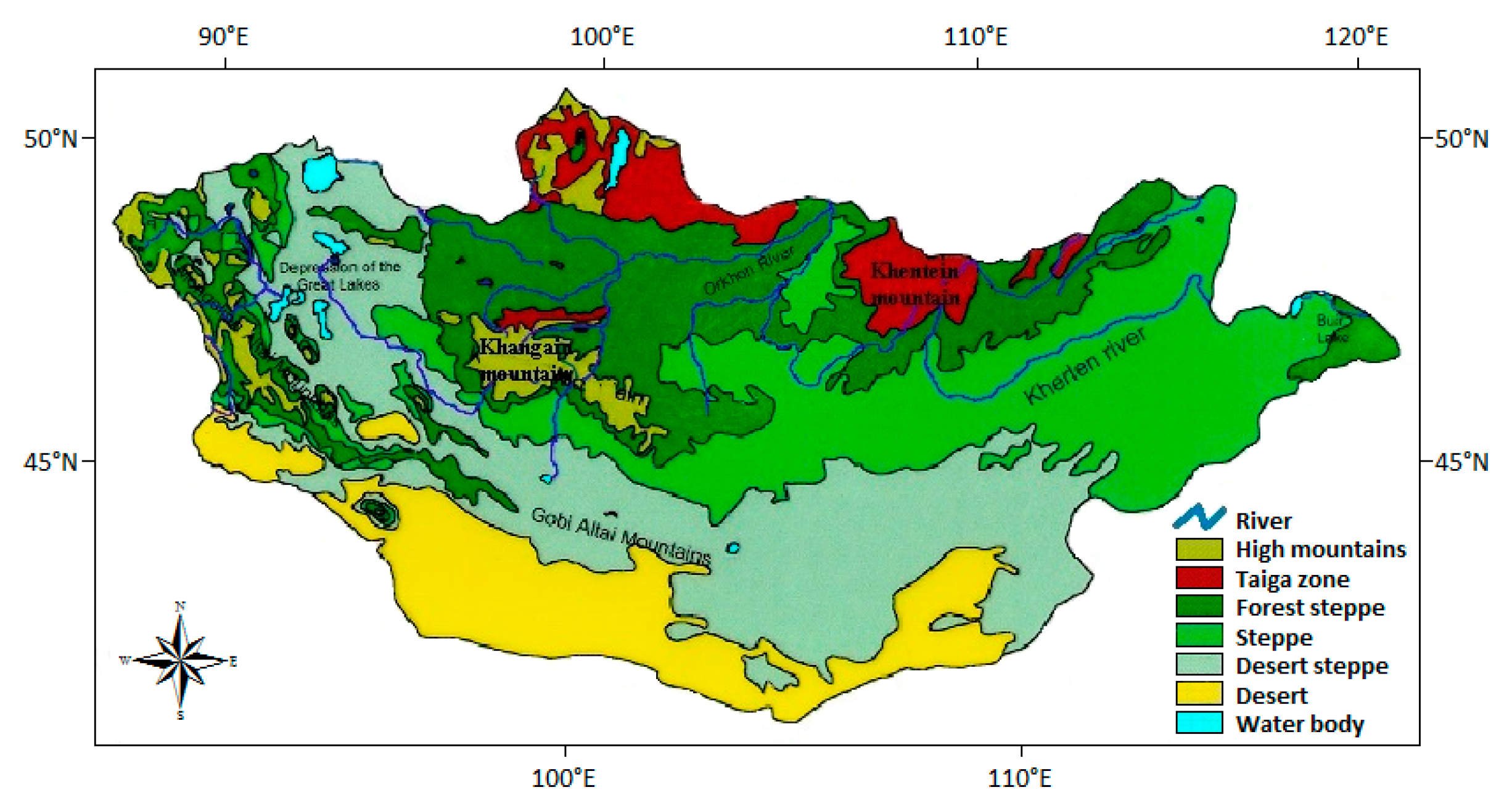
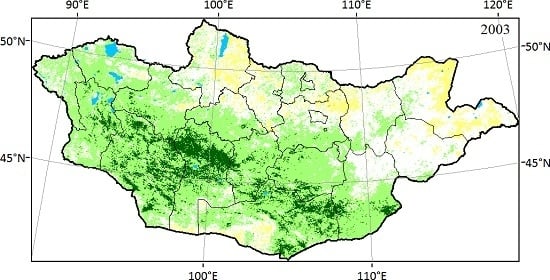
| Station Name | Lat. (°N) | Long. (°E) | Elev. (m) | Various Land Use Areas |
|---|---|---|---|---|
| Ulgii | 48.97 | 89.97 | 1714 | High mountains |
| Khovd | 48.02 | 91.65 | 1405 | High mountains |
| Altai | 46.40 | 96.25 | 2147 | High mountains |
| Tsetserleg | 47.45 | 101.47 | 1695 | Forest steppe |
| Tarialan | 49.61 | 101.99 | 1230 | Forest steppe |
| Bulgan | 48.80 | 103.55 | 1210 | Forest steppe |
| Baruunkharaa | 48.91 | 106.08 | 814 | Forest steppe |
| Undurkhaan | 47.32 | 110.67 | 1028 | Steppe |
| Choibalsan | 48.07 | 114.60 | 759 | Steppe |
| Bayankhongor | 46.13 | 100.68 | 1860 | High mountains |
| Arvaikheer | 46.27 | 102.78 | 1831 | Steppe |
| Baruun-Urt | 46.68 | 113.28 | 986 | Steppe |
| Mandalgobi | 45.77 | 106.28 | 1398 | Desert steppe |
| Sainshand | 44.90 | 110.12 | 915 | Desert steppe |
| Dalanzadgad | 43.58 | 104.42 | 1469 | Desert steppe |
| Saikhan | 44.08 | 103.55 | 1302 | Desert steppe |
| Land Use Areas | Numbers of Station | Air Temperature (°C) | Precipitation (mm) | Soil Moisture Content (%) | |||
|---|---|---|---|---|---|---|---|
| Average | SD | Average | SD | Average | SD | ||
| Over Mongolia | 16 | 17.0 | 0.7 | 149 | 26 | 6.7 | 1.0 |
| Forest Steppe | 4 | 15.4 | 0.9 | 234 | 38 | 10.8 | 2.2 |
| Steppe | 4 | 17.3 | 0.9 | 163 | 48 | 6.8 | 1.5 |
| High Mountains | 4 | 15.3 | 0.8 | 110 | 36 | 4.2 | 1.0 |
| Desert Steppe | 4 | 19.9 | 0.7 | 88 | 28 | 4.8 | 1.3 |
| Climate Parameters | Air Temperature | Precipitation | Soil Moisture Content |
|---|---|---|---|
| Air temperature | 1 | ||
| Precipitation | −0.66 | 1 | |
| Soil moisture content | −0.77 | 0.78 | 1 |
| Category | Description | MDSI | Category | Description | MDSI |
|---|---|---|---|---|---|
| W2 | severely wet | 2.00 or greater | D1 | moderate drought | −0.50 to −1.99 |
| W1 | moderately wet | 0.50 to 1.99 | D2 | severe drought | −2.00 or less |
| WD | normal | 0.49 to −0.49 |
| Land Use Areas | Numbers of Station | MDSI vs. T Anomalies | MDSI vs. P Anomalies | MDSI Anomalies vs. Soil Moisture Content |
|---|---|---|---|---|
| Over Mongolia | 16 | −0.66 ** | 0.81 *** | 0.74 ** |
| Forest Steppe | 4 | −0.67 ** | 0.34 | 0.63 ** |
| Steppe | 4 | −0.65 * | 0.83 *** | 0.39 |
| High Mountains | 4 | −0.52 * | 0.67 ** | 0.64 ** |
| Desert Steppe | 4 | −0.45 | 0.70 ** | 0.72 ** |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dorjsuren, M.; Liou, Y.-A.; Cheng, C.-H. Time Series MODIS and in Situ Data Analysis for Mongolia Drought. Remote Sens. 2016, 8, 509. https://doi.org/10.3390/rs8060509
Dorjsuren M, Liou Y-A, Cheng C-H. Time Series MODIS and in Situ Data Analysis for Mongolia Drought. Remote Sensing. 2016; 8(6):509. https://doi.org/10.3390/rs8060509
Chicago/Turabian StyleDorjsuren, Munkhzul, Yuei-An Liou, and Chi-Han Cheng. 2016. "Time Series MODIS and in Situ Data Analysis for Mongolia Drought" Remote Sensing 8, no. 6: 509. https://doi.org/10.3390/rs8060509
APA StyleDorjsuren, M., Liou, Y.-A., & Cheng, C.-H. (2016). Time Series MODIS and in Situ Data Analysis for Mongolia Drought. Remote Sensing, 8(6), 509. https://doi.org/10.3390/rs8060509