Filling the Polar Data Gap in Sea Ice Concentration Fields Using Partial Differential Equations
Abstract
:1. Introduction
2. Data
3. Method
3.1. Formulation of Data Fill Model
3.2. Stochastic Term Ω
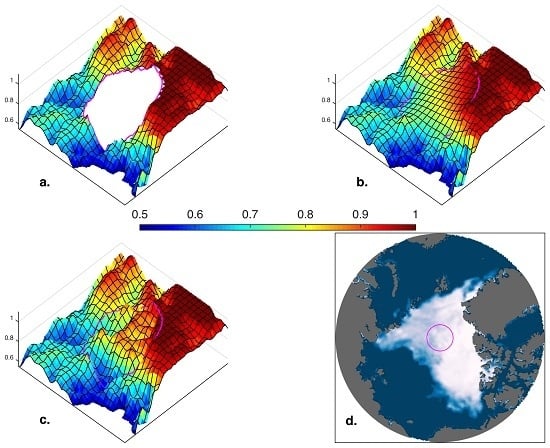
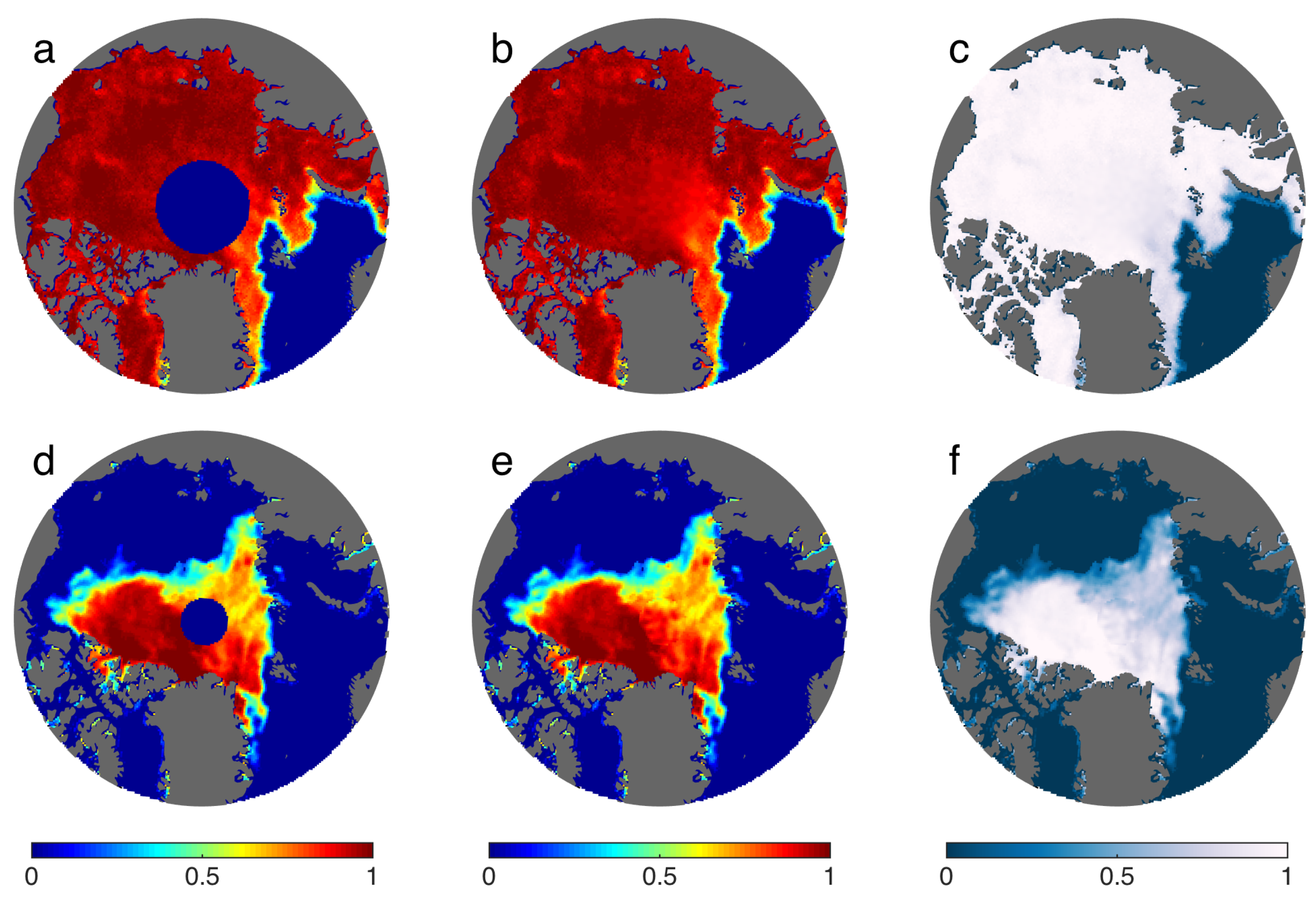
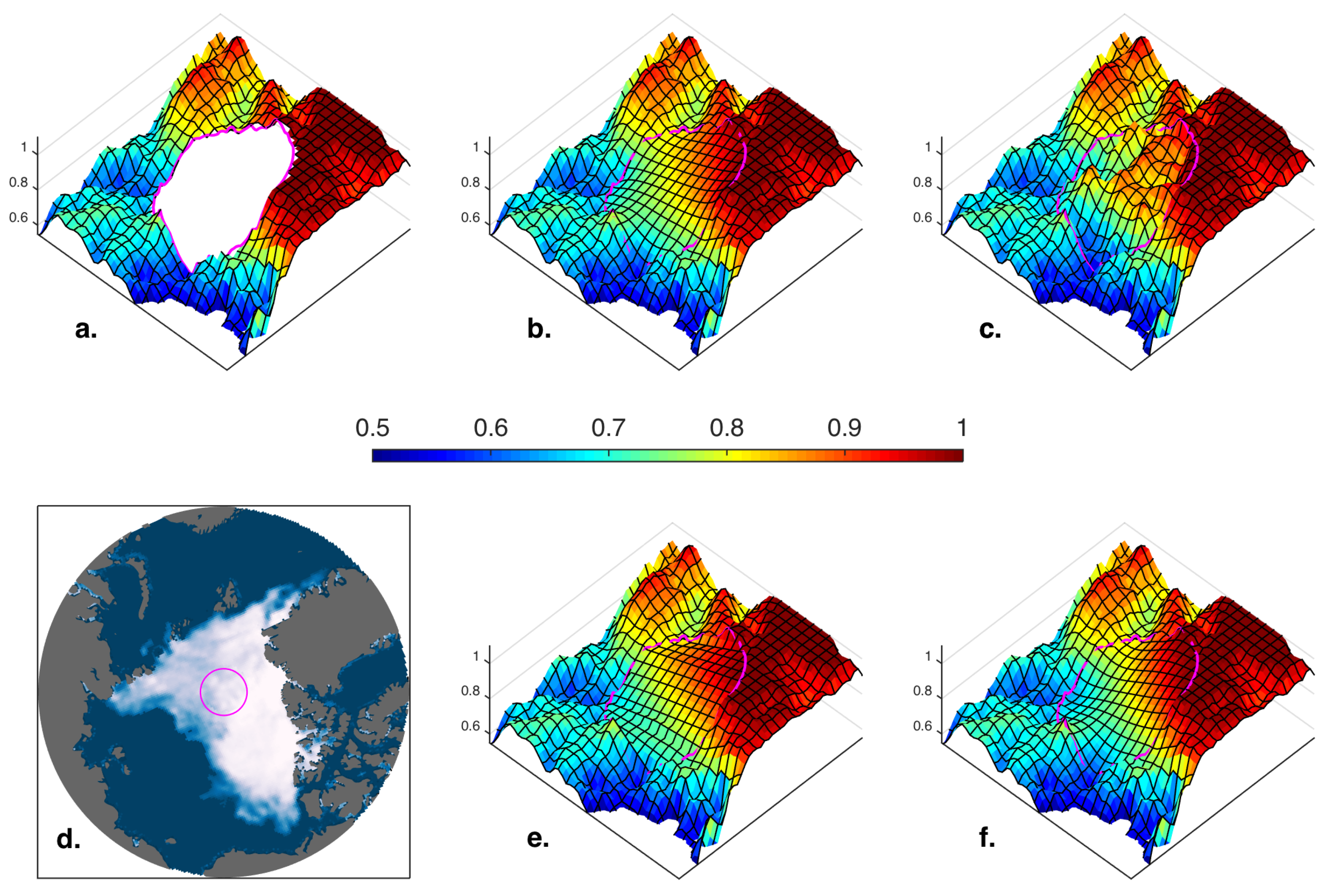
4. Results
4.1. Illustrative Examples
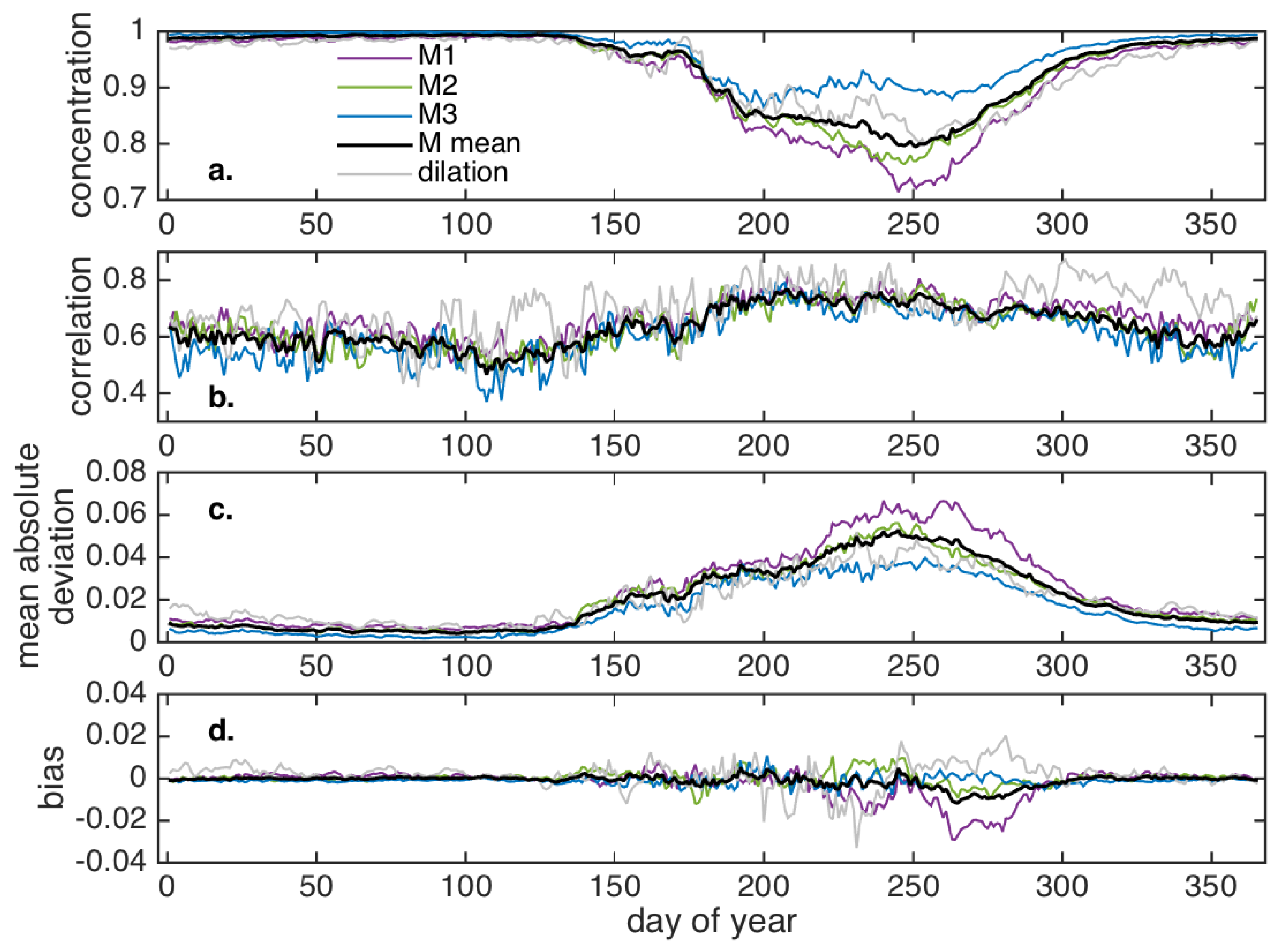
4.2. Validation and Performance Assessment
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Cavalieri, D.J.; Parkinson, C.L. Arctic sea ice variability and trends, 1979–2010. Cryosphere 2012, 6, 881–889. [Google Scholar] [CrossRef]
- Simmonds, I. Comparing and contrasting the behavior of Arctic and Antarctic sea ice over the 35 year period 1979–2013. Ann. Glaciol. 2015, 56, 18–28. [Google Scholar] [CrossRef]
- Cavalieri, D.; Parkinson, C.; Gloersen, P.; Zwally, H.J. Sea Ice Concentrations from Nimbus-7 SMMR and DMSP SSM/I Passive Microwave Data; National Snow and Ice Data Center: Boulder, CO, USA, 1996. [Google Scholar]
- Meier, W.; Fetterer, F.; Savoie, M.; Mallory, S.; Duerr, R.; Stroeve, J. NOAA/NSIDC Climate Data Record of Passive Microwave Sea Ice Concentration; National Snow and Ice Data Center: Boulder, CO, USA, 2011. [Google Scholar]
- Comiso, J.C. Characteristics of arctic winter sea ice from satellite multispectral microwave observations. J. Geophys. Res. 1986, 91, 975–994. [Google Scholar] [CrossRef]
- Cavalieri, D.J.; Gloersen, P.; Campbell, W.J. Determination of sea ice parameters with the NIMBUS 7 SMMR. J. Geophys. Res. 1984, 89, 5355–5369. [Google Scholar] [CrossRef]
- Notz, D. Sea-ice extent and its trend provide limited metrics of model performance. Cryosphere 2014, 8, 229–243. [Google Scholar] [CrossRef]
- Strong, C.; Rigor, I.G. Arctic marginal ice zone trending wider in summer and narrower in winter. Geophys. Res. Lett. 2013, 40, 4864–4868. [Google Scholar] [CrossRef]
- Duchon, J. Splines minimizing rotation-invariant semi-norms in Sobolev spaces. In Constructive Theory of Functions of Several Variables; Springer: Berlin, Germany; Heidelberg, Germany, 1977; Volume 571, pp. 85–100. [Google Scholar]
- Cavoretto, R.; De Rossi, A. Fast and accurate interpolation of large scattered data sets on the sphere. J. Comput. Appl. Math. 2010, 234, 1505–1521. [Google Scholar] [CrossRef]
- Pottmann, H.; Eck, M. Modified multiquadric methods for scattered data interpolation over a sphere. Computer Aided Geometr. Des. 1990, 7, 313–321. [Google Scholar] [CrossRef]
- Arias, P.; Facciolo, G.; Caselles, V.; Sapiro, G. A Variational Framework for Exemplar-Based Image Inpainting. Int. J. Computer Vis. 2011, 93, 319–347. [Google Scholar] [CrossRef]
- Gilbert, J.R.; Moler, C.; Schreiber, R. Sparse Matrices in MATLAB: Design and Implementation. SIAM J. Matrix Anal. Appl. 1992, 13, 333–356. [Google Scholar] [CrossRef]
- Carsey, F.D. Microwave Remote Sensing of Sea Ice; American Geophysical Union: Washington, DC, USA, 1992; p. 462. [Google Scholar]
- Garcia, N.; Stoll, E. Monte Carlo Calculation for Electromagnetic-Wave Scattering from Random Rough Surfaces. Phys. Rev. Lett. 1984, 52, 1798–1801. [Google Scholar] [CrossRef]


| Platform | Radius (km) | Latitude (N) | Time Period |
|---|---|---|---|
| SMMR | 611 | 84.50 | November 1978–June 1987 |
| SSM/I | 311 | 87.20 | July 1987–December 2007 |
| SSMIS | 94 | 89.18 | January 2008–present |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Strong, C.; Golden, K.M. Filling the Polar Data Gap in Sea Ice Concentration Fields Using Partial Differential Equations. Remote Sens. 2016, 8, 442. https://doi.org/10.3390/rs8060442
Strong C, Golden KM. Filling the Polar Data Gap in Sea Ice Concentration Fields Using Partial Differential Equations. Remote Sensing. 2016; 8(6):442. https://doi.org/10.3390/rs8060442
Chicago/Turabian StyleStrong, Courtenay, and Kenneth M. Golden. 2016. "Filling the Polar Data Gap in Sea Ice Concentration Fields Using Partial Differential Equations" Remote Sensing 8, no. 6: 442. https://doi.org/10.3390/rs8060442
APA StyleStrong, C., & Golden, K. M. (2016). Filling the Polar Data Gap in Sea Ice Concentration Fields Using Partial Differential Equations. Remote Sensing, 8(6), 442. https://doi.org/10.3390/rs8060442