A Comparison of Multiple Datasets for Monitoring Thermal Time in Urban Areas over the U.S. Upper Midwest
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Region
2.2. Data
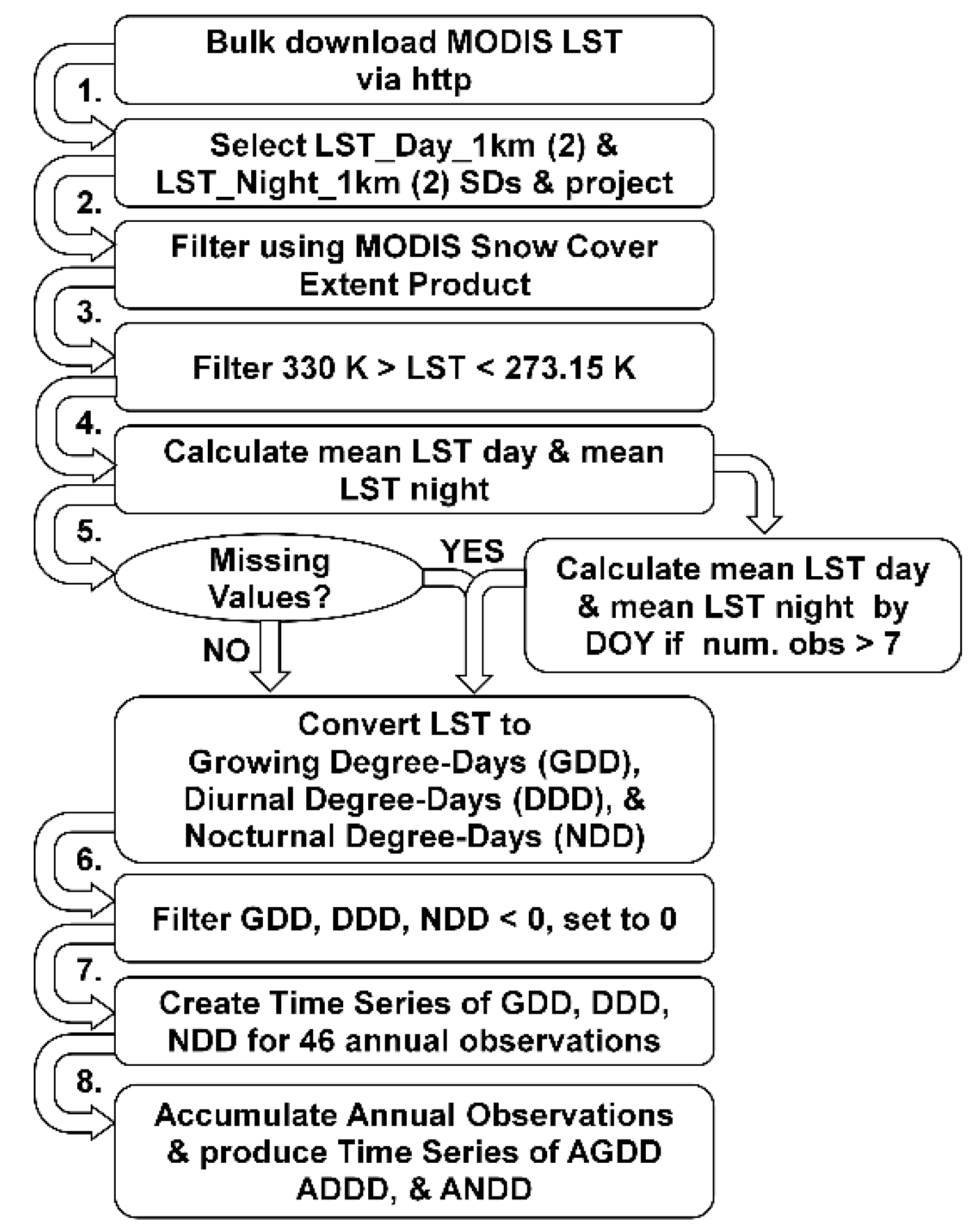
2.2.1. MODIS Land Surface Temperature
2.2.2. Daymet Modeled Air Temperature
2.2.3. Global Historical Climatology Network
2.3. Methods
2.3.1. Thermal Time
2.3.2. Dataset Comparison
3. Results
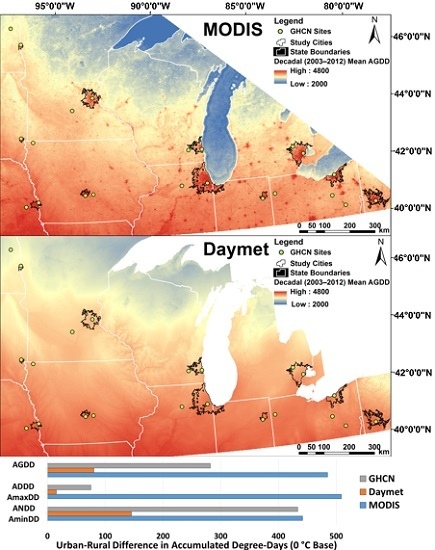
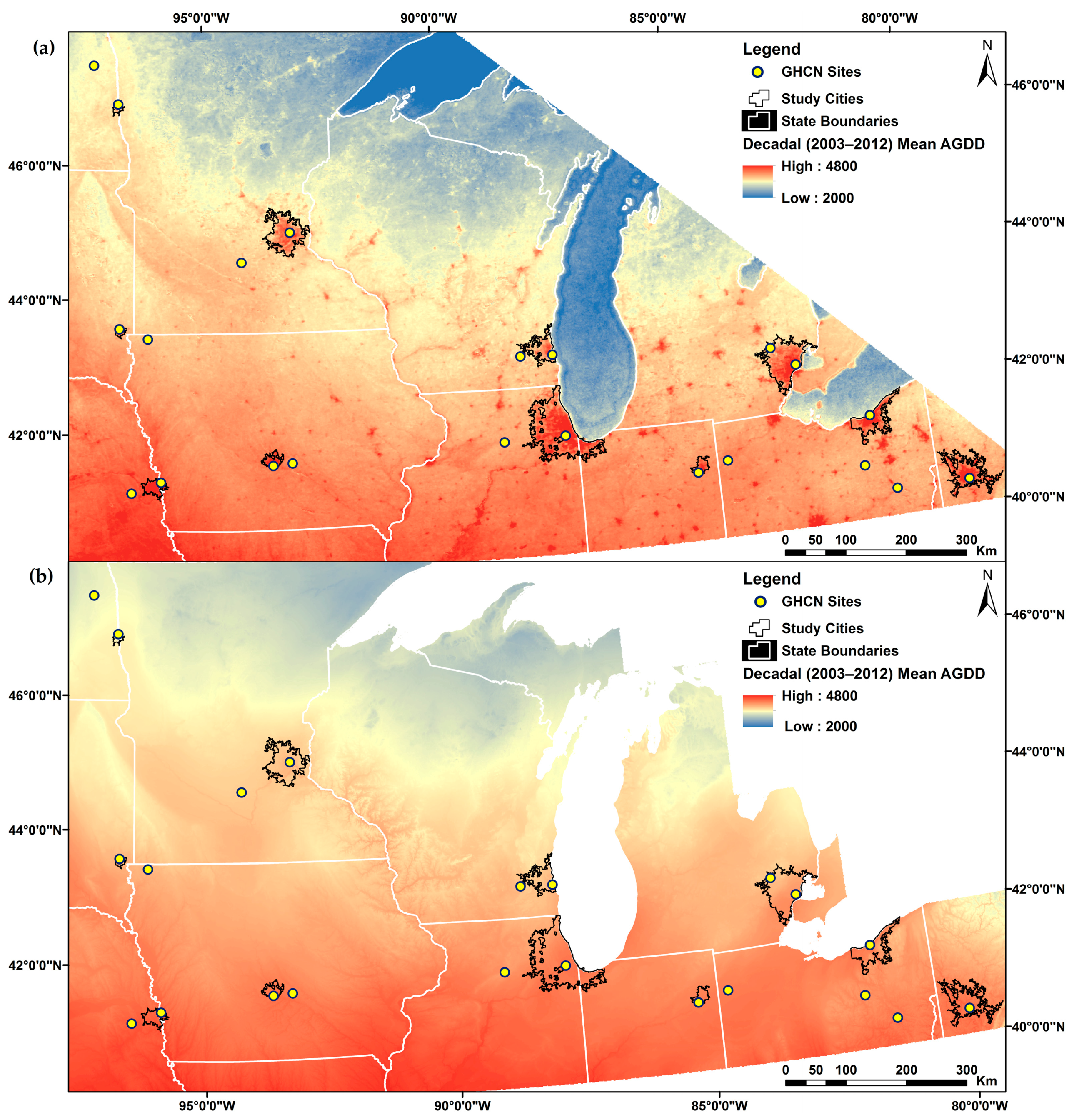
3.1. Regional Characterization of Thermal Regimes
3.1.1. AGDD
3.1.2. ADDD and AmaxDD
3.1.3. ANDD and AminDD
3.2. Urban/Rural Differences and Dataset Comparison
3.2.1. Urban/Rural Differences in Thermal Time
3.2.2. Urban/Rural Differences in Accumulated Thermal Time
3.2.3. Seasonal Progression of Urban/Rural Differences in Accumulated Thermal Time
3.2.4. Thermal Time versus Accumulated Thermal Time
3.2.5. Latitudinal Effects
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| ADDD | Accumulated Diurnal Degree-Day |
| AGDD | Accumulated Growing Degree-Day |
| AmaxDD | Accumulated maximum Degree-Day |
| AminDD | Accumulated minimum Degree-Day |
| ANCOVA | Analysis of Covariance |
| ANDD | Accumulated Nocturnal Degree-Day |
| DD | Degree-Day |
| DDD | Diurnal Degree-Day |
| DOY | Day of Year |
| ENVI | Environment for Visualizing Images |
| GDD | Growing Degree-Day |
| GHCN | Global Historical Climatology Network |
| ha | Hectare |
| Intl. | International |
| Lat | Latitude |
| Lon | Longitude |
| LST | Land Surface Temperature |
| m | Meter |
| M | Million |
| maxDD | Maximum Degree-Day |
| minDD | Minimum Degree-Day |
| MODIS | Moderate Resolution Imaging Spectroradiometer |
| NASA | National Aeronautics and Space Administration |
| NDD | Nocturnal Degree-Day |
| pop | Population |
| R | Rural |
| r2 | Coefficient of Determination |
| RMSD | Root Mean Square Difference |
| SUHI | Surface Urban Heat Island |
| Tbase | Base Temperature |
| TIR | Thermal Infrared |
| Tmax | Maximum Temperature |
| Tmin | Minimum Temperature |
| U | Urban |
| UHI | Urban Heat Island |
References
- United Nations. World Urbanization Prospects: The 2014 Revision, Highlights. Department of Economic and Social Affairs, Population Division 2014, (ST/ESA/SER.A/352). Available online: http://esa.un.org/unpd/wup/highlights/wup2014-highlights.pdf (accessed on 20 January 2016).
- Seto, K.C.; Fragkias, M.; Güneralp, B.; Reilly, M.K. A meta-analysis of global urban land expansion. PLOS ONE 2011, 6, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Angel, S.; Parent, J.; Civco, D.L.; Blei, A.M. Making Room for a Planet of Cities; Lincoln Inst. of Land Policy: Cambridge, MA, USA, 2011. [Google Scholar]
- Seto, K.C. Global urban issues: A primer. In Global Mapping of Human Settlement: Experiences, Datasets, and Prospect; Gamba, P., Herold, M., Eds.; Taylor and Francis Group: CRC Press: Boca Raton, FL, USA, 2009; pp. 3–9. [Google Scholar]
- Arnfield, J. Two decades of urban climate research: A review of turbulence exchanges of energy and water, and the urban heat island. Int. J. Clim. 2003, 80, 386–395. [Google Scholar] [CrossRef]
- Oke, T.R. Boundary Layer Climates, 2nd ed.; Methuen & Co.: London, UK, 1987. [Google Scholar]
- Voogt, J.A. Urban heat island. In Encyclopedia of Global Environmental Change; John Wiley & Sons: New York, NY, USA, 2002; pp. 660–666. [Google Scholar]
- McCarthy, M.P.; Best, M.J.; Betts, R.A. Climate change in cities due to global warming and urban effects. Geophys. Res. Lett. 2010, 37, 1–5. [Google Scholar] [CrossRef]
- Changnon, S.A.; Kunkel, K.E.; Reinke, B.C. Impacts and responses to the 1995 heat wave: A call to action. Bull. Am. Meteorol. Soc. 1996, 77, 1497–1506. [Google Scholar] [CrossRef]
- Patz, J.A.; Campbell, D.; Holloway, T.; Foley, J.A. Impact of regional climate change on human health. Nature 2005, 438, 310–317. [Google Scholar] [CrossRef] [PubMed]
- Oke, T.R. The energetic basis of the urban heat island. Q. J. R. Meteorol. Soc. 1982, 108, 1–24. [Google Scholar] [CrossRef]
- Avissar, M. The effects of urban patterns on ecosystem function. Int. Regional Sci. Rev. 2005, 28, 168–192. [Google Scholar]
- Lo, C.P.; Quattrochi, D.A. Land-use and land-cover change, urban heat island phenomenon, and health implications: A remote sensing approach. Photogramm. Eng. Remote Sens. 2003, 69, 1053–1063. [Google Scholar] [CrossRef]
- Chen, X.; Zhao, H.; Li, P.; Yin, Z. Remote sensing image-based analysis of the relationship between urban heat island and land use/cover changes. Remote Sens. Environ. 2006, 104, 133–146. [Google Scholar] [CrossRef]
- Hartmann, D.L.; Klein Tank, A.M.G.; Rusticucci, M.; Alexander, L.V.; Brönnimann, S.; Charabi, Y.; Dentener, F.J.; Dlugokencky, E.J.; Easterling, D.R.; Kaplan, A.; et al. Observations: Atmosphere and Surface. In Climate Change 2013: The Physical Science Basis, Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; pp. 161–218. [Google Scholar]
- Oke, T.R.; Johnson, G.T.; Steyn, D.G.; Watson, I.D. Simulation of nocturnal surface urban heat islands under “ideal” conditions: Part 2. Diagnosis of causation. Boundary-Layer Meteorol. 1991, 56, 339–358. [Google Scholar] [CrossRef]
- Jackson, T.L.; Feddema, J.J.; Oleson, K.W.; Bonan, G.B.; Bauer, J.T. Parameterization of urban characteristics for global climate modeling. Ann. Assoc. Am. Geogr. 2010, 100, 848–865. [Google Scholar] [CrossRef]
- Deosthali, V. Impact of rapid urban growth on heat and moisture islands in Pune City, India. Atmos. Environ. 2000, 34, 2745–2754. [Google Scholar] [CrossRef]
- Imhoff, M.L.; Zhang, P.; Wolfe, R.E.; Bounoua, L. Remote sensing of the urban heat island effect across biomes in the continental USA. Remote Sens. Environ. 2010, 114, 504–513. [Google Scholar] [CrossRef]
- Kim, Y.H.; Baik, J.J. Maximum urban heat island intensity in Seoul. J. Appl. Meteorol. 2002, 41, 651–653. [Google Scholar] [CrossRef]
- Howard, L. The Climate of London; Harvey and Darton: London, UK, 1833; Volume I–III. [Google Scholar]
- Balchin, W.G.V.; Pye, N. A micro-climatological investigation of bath and the surrounding district. Q. J. R. Meteorol. Soc. 1947, 73, 297–323. [Google Scholar] [CrossRef]
- Oke, T.R. City size and the urban heat island. Atmos. Environ. Pergamon. Press 1973, 7, 769–779. [Google Scholar] [CrossRef]
- Bornstein, R.D. Observations of the urban heat island effect in New York City. J. Appl. Meteorol. 1968, 7, 575–582. [Google Scholar] [CrossRef]
- Kopec, R.J. Further observations of the urban heat island in a small city. Bull. Am. Meteorol. Soc. 1970, 51, 602–606. [Google Scholar] [CrossRef]
- Chandler, T.J. Urban climatology and its relevance to urban design. World Meteorol. Org. 1976, 438, 1–80. Available online: http://ac.ciifen.org/omm-biblioteca/CCI_TECH/WMO-438.pdf (accessed on 8 January 2016). [Google Scholar]
- Landsberg, H.E. The Urban Climate; Academic Press: New York, NY, USA, 1981. [Google Scholar]
- Rao, P.K. Remote sensing of urban heat islands from an environmental satellite. Bull. Am. Meteorol. Soc. 1972, 53, 647. [Google Scholar]
- Streutker, D.R. Satellite-measure growth of the urban heat island of Houston, Texas. Remote Sens. Environ. 2003, 85, 282–289. [Google Scholar] [CrossRef]
- Tomlinson, C.J.; Chapman, L.; Thornes, J.E.; Baker, C.J. Derivation of Birmingham’s summer surface urban heat island from MODIS satellite images. Int. J. Clim. 2012, 32, 214–224. [Google Scholar] [CrossRef]
- Hu, L.; Brunsell, N.A. The impact of temporal aggregation of land surface temperature data for surface urban heat island (SUHI) monitoring. Remote Sens. Environ. 2013, 134, 162–174. [Google Scholar] [CrossRef]
- Roth, M.; Oke, T.R.; Emery, W.J. Satellite-derived urban heat islands from three coastal cities and the utilization of such data in urban climatology. Int. J. Remote Sens. 1989, 10, 1699–1720. [Google Scholar] [CrossRef]
- Voogt, J.A.; Oke, T.R. Thermal remote sensing of urban climates. Remote Sens. Environ. 2003, 86, 370–384. [Google Scholar] [CrossRef]
- Nichol, J. High-resolution surface temperature patterns related to urban morphology in a tropical city: A satellite-based study. J. Appl. Meteorol. 1996, 35, 135–146. [Google Scholar] [CrossRef]
- Streutker, D.R. A remote sensing study of urban heat island of Houston, Texas. Int. J. Remote Sens. 2002, 23, 2595–2608. [Google Scholar] [CrossRef]
- Bounoua, L.; Zhang, P.; Mostoyoy, G.; Thorne, K.; Masek, J.; Imhoff, M.; Shepherd, M.; Quattrochi, D.; Santanello, J.; Silva, J.; et al. Impact of urbanization on US surface climate. Environ. Res. Lett. 2015, 10, 084010. [Google Scholar] [CrossRef]
- Bureau of Economic Analysis. Regional Economic Accounts. US Department of Commerce, 2011. Available online: http://bea.gov/regional/index.htm (accessed on 8 January 2016). [Google Scholar]
- Jin, S.; Yang, L.; Danielson, P.; Homer, C.; Fry, J.; Xian, G. A comprehensive change detection method for updating the National Land Cover Database to circa 2011. Remote Sens. Environ. 2013, 132, 159–175. [Google Scholar] [CrossRef]
- Xian, G.; Homer, C.; Dewitz, J.; Fry, J.; Hossain, N.; Wickham, J. The change of impervious surface area between 2001 and 2006 in the conterminous United States. Photogramm. Eng. Remote Sens. 2011, 77, 758–762. [Google Scholar]
- Maccherone, B.; Frazier, S. About MODIS. NASA, 2015. Available online: http://modis.gsfc.nasa.gov/about/ (accessed on 24 September 2015). [Google Scholar]
- Parkinson, C.L. Aqua: An earth-observing satellite mission to examine water and other climate variables. IEEE Trans. Geosci. Remote Sens. 2003, 41, 173–183. [Google Scholar] [CrossRef]
- NASA LP DAAC. MODIS Level 3. USGS/EROS: Sioux Falls, SD, USA, 2001. Available online: https://lpdaac.usgs.gov/ (accessed on 22 September 2015). [Google Scholar]
- Hubanks, P.A.; King, M.D.; Platnick, S.; Pincus, R. MODIS Atmosphere L3 Gridded Product Algorithm Theoretical Basis Document. NASA, 2008. Available online: http://modis-atmos.gsfc.nasa.gov/_docs/MOD08MYD08%20ATBD%20C005.pdf (accessed on 24 September 2015). [Google Scholar]
- Hall, D.K.; Riggs, G.A.; Salomonson, V.V. MODIS/Terra Snow Cover 8-day L3 Global 500 m Grid V005. National Snow and Ice Data Center: Boulder, CO, USA, 2006. updated weekly. Available online: http://nsidc.org/data (accessed on 15 October 2015).
- Thornton, P.E.; Running, S.W.; White, M.A. Generating surfaces of daily meteorology variables over large reions of complex terrain. J. Hydrol. 1997, 190, 214–251. [Google Scholar] [CrossRef]
- Thornton, P.E.; Thornton, M.M.; Mayer, B.W.; Wilhelmi, N.; Wei, Y.; Devarakonda, R.; Cook, R.B. Daymet: Daily Surface Weather Data on a 1-km Grid for North America, Version 2; ORNL DAAC: Oak Ridge, TN, USA.
- Menne, M.J.; Durre, I.; Vose, R.S.; Gleason, B.E.; Houston, T.G. An overview of the Global Historical Climatology Network-Daily Database. J. Atmos. Oceanic Technol. 2012, 29, 897–910. [Google Scholar] [CrossRef]
- Menne, M.J.; Durre, I.; Korzeniewski, B.; McNeal, S.; Thomas, K.; Yin, X.; Anthony, S.; Ray, R.; Vose, R.S.; Gleason, B.E.; et al. Global Historical Climatology Network—Daily (GHCN-Daily), Verson 3. [2003–01–01 to 2012–12–31]; NOAA National Climatic Data Center: Asheville, NC, USA, 2015. [CrossRef]
- Henebry, G.M. Phenologies of North American Grasslands and Grasses. In Phenology: An Integrative Environmental Science, 2nd ed.; Schwartz, M.D., Ed.; Springer: New York, NY, USA, 2013; Chapter 11; pp. 197–210. [Google Scholar]
- Vancutsem, C.; Ceccato, P.; Dinku, T.; Connor, S.J. Evaluation of MODIS land surface temperature data to estimate air temperature in different ecosystems over Africa. Remote Sens. Environ. 2010, 114, 449–465. [Google Scholar] [CrossRef]
- Krehbiel, C.P.; Jackson, T.; Henebry, G.M. Web-Enabled Landsat data time series for monitoring urban heat island impacts on land surface phenology. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 1–8. [Google Scholar] [CrossRef]
- Anniballe, R.; Bonafoni, S.; Pichierri, M. Spatial and temporal trends of the surface and air heat island over Milan using MODIS data. Remote Sens. Environ. 2014, 150, 163–171. [Google Scholar] [CrossRef]
- Buyantuyev, A.; Wu, J. Urban heat islands and landscape heterogeneity: Linking spatiotemporal variations in surface temperatures to land-cover and socioeconomic patterns. Landsc. Ecol. 2010, 25, 17–33. [Google Scholar] [CrossRef]
- Jochner, S.C.; Sparks, T.H.; Estrella, N.; Menzel, A. The influence of altitude and urbanization on trends and mean dates in phenology (1980–2009). Int. J. Biometeorol. 2012, 56, 387–394. [Google Scholar] [CrossRef] [PubMed]
- Franken, E. Der beginn der forsythienbluete in Hamburg 1955. Meteorol. Rundsch. 1955, 8, 113–115. [Google Scholar]
- Weng, Q.; Lu, D. Subpixel analysis of urban landscapes. In Urban Remote Sensing; Weng, Q., Quattrochi, D.A., Eds.; Taylor and Francis Group, CRC Press: Boca Raton, FL, USA, 2007; pp. 71–90. [Google Scholar]
- Bechtel, B.; Zakšek, K.; Hoshyaripour, G. Downscaling of land surface temperature in an urban area: A case study for Hamburg, Germany. Remote Sens. 2012, 4, 3184–3200. [Google Scholar] [CrossRef]
- Mills, G.; Ching, J.; See, L.; Bechtel, B.; Foley, M. An introduction to the WUDAPT project. In Proceedings of the 9th International Conference on Urban Climate, Toulouse, France, 20–24 July 2015; Available online: http://www.wudapt.org/wp-content/uploads/2015/05/Mills_etal_ICUC9.pdf (accessed on 9 January 2016).
- Krehbiel, C. Impacts of Urban Areas on Vegetation Development along Rural-Urban Gradients in the Upper Midwest: 2003–2012. Master’s. Thesis, South Dakota State University, Brookings, SD, USA, 2015. [Google Scholar]
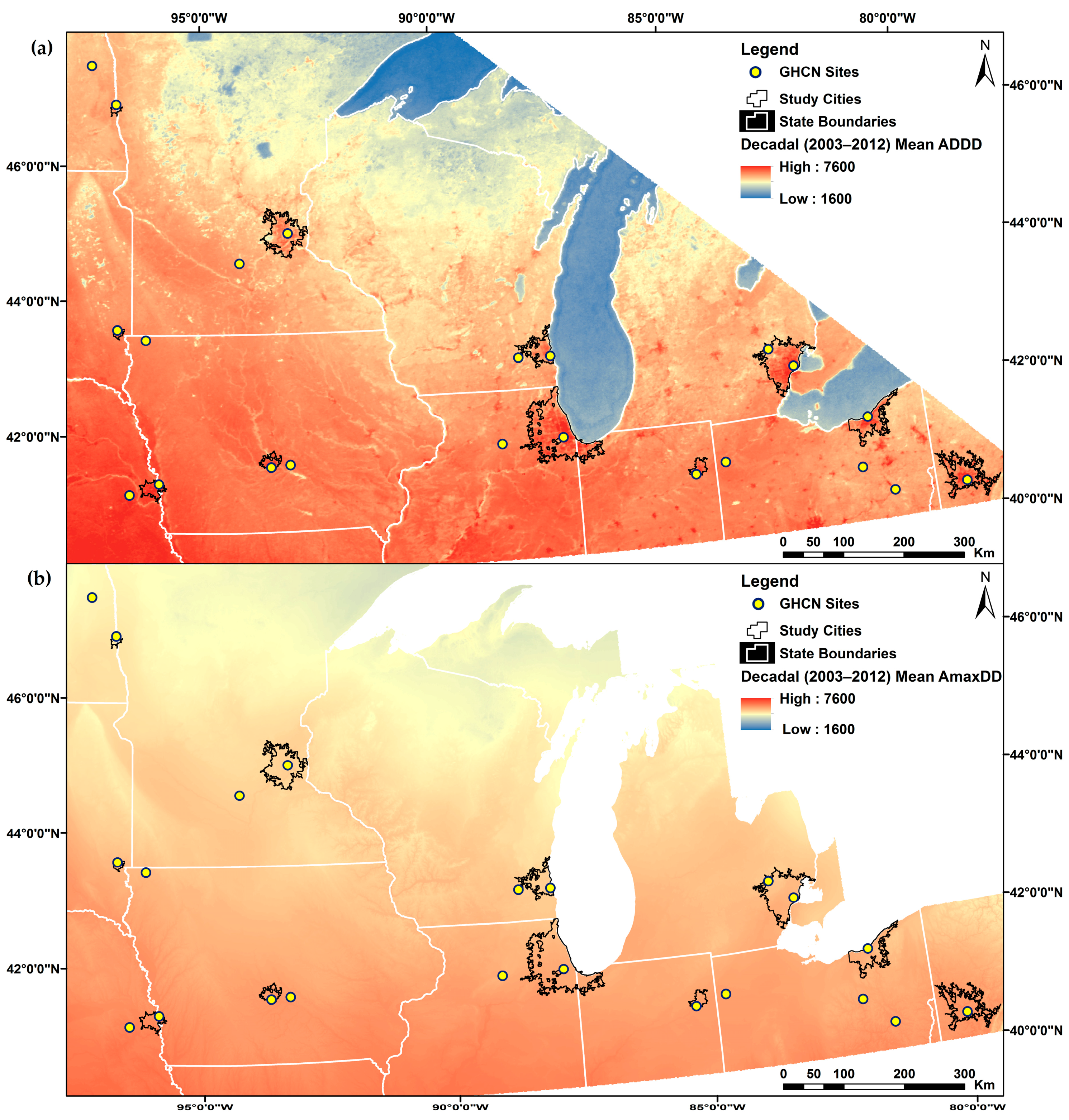
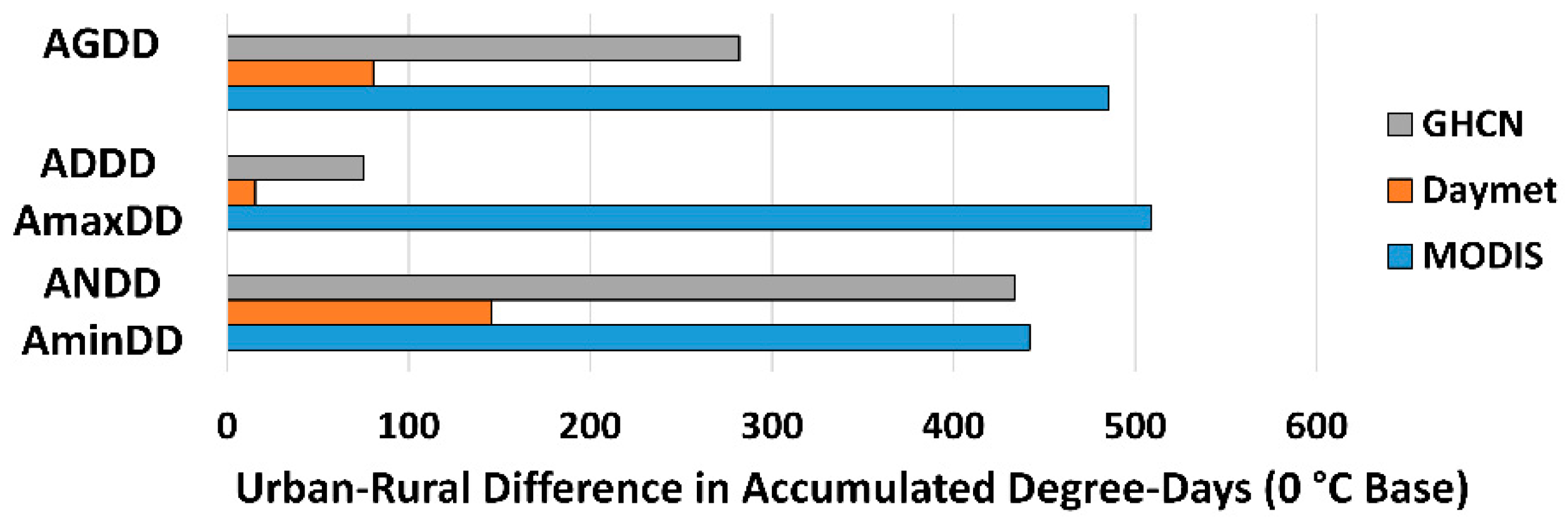

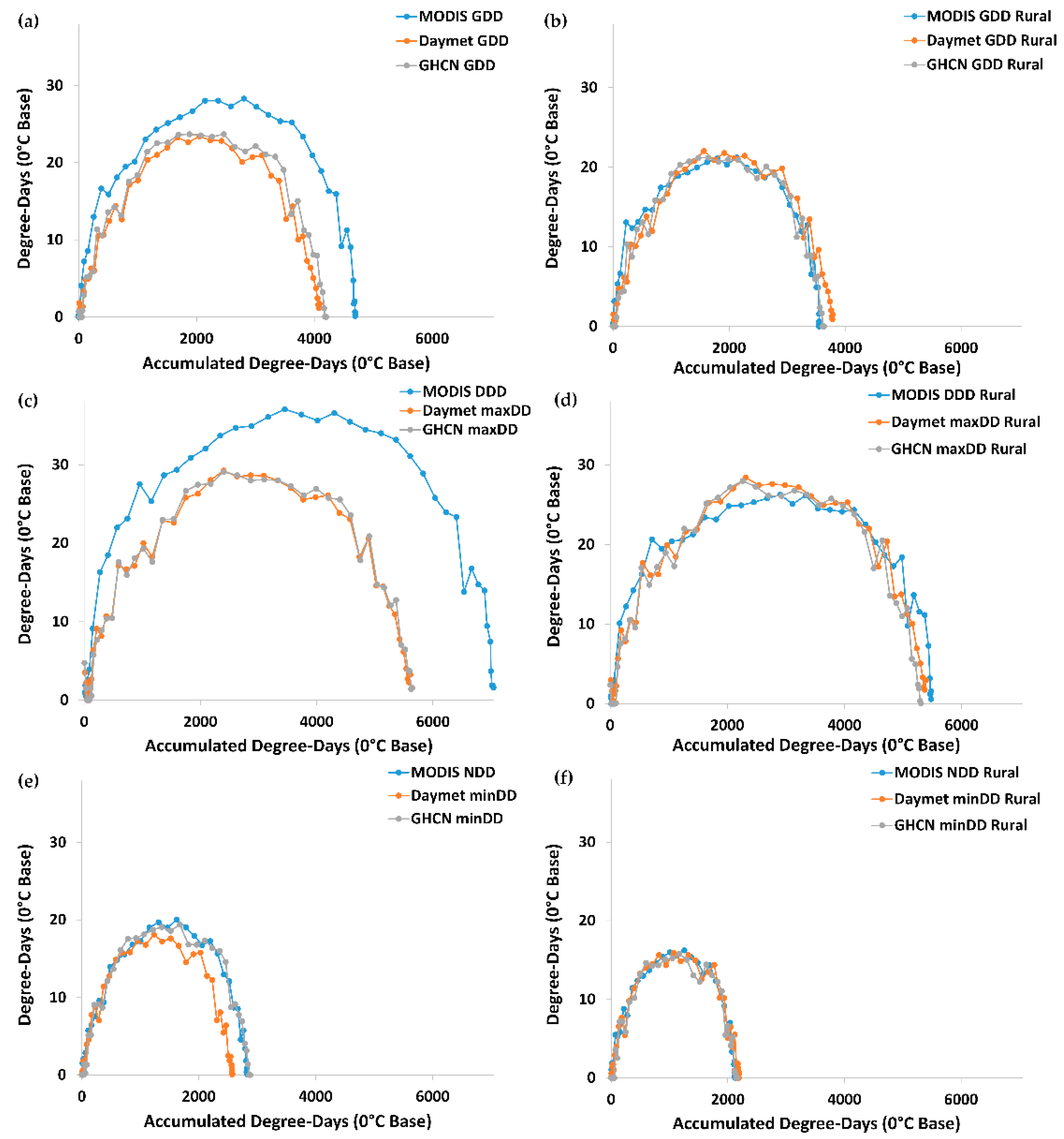

| City | 2011 Population (Total) | 2011 Urban Extent (ha) | 2011 Density (pop/ha) |
|---|---|---|---|
| Chicago | 9,491,283 | 274,465 | 34.6 |
| Detroit | 4,287,556 | 152,077 | 28.2 |
| Minneapolis-St. Paul | 3,388,716 | 113,889 | 29.8 |
| Pittsburgh | 2,359,783 | 77,432 | 30.5 |
| Cleveland | 2,068,606 | 59,608 | 34.7 |
| Milwaukee | 1,561,108 | 47,261 | 33.0 |
| Omaha | 876,836 | 37,280 | 23.5 |
| Des Moines | 580,779 | 22,366 | 26.0 |
| Fort Wayne | 419,609 | 15,848 | 26.5 |
| Sioux Falls | 232,553 | 9468 | 24.6 |
| Fargo | 212,695 | 11,392 | 18.7 |
| ID | City | Type | Station Name | Station ID | Lat | Lon | Elevation (m) |
|---|---|---|---|---|---|---|---|
| 1 | Fargo | U | Fargo Hector Intl. Airport | W00014914 | 46.9 | −96.8 | 274 |
| 2 | Fargo | R | Mayville | C00325660 | 47.5 | −97.4 | 288 |
| 3 | Sioux Falls | U | Sioux Falls Foss Field | W00014944 | 43.6 | −96.8 | 435 |
| 4 | Sioux Falls | R | Rock Rapids | C00137147 | 43.4 | −96.2 | 412 |
| 5 | Omaha | U | Omaha Eppley Airfield | W00014942 | 41.3 | −95.9 | 299 |
| 6 | Omaha | R | Mead 6 S | C00255362 | 41.1 | −96.5 | 352 |
| 7 | Minneapolis-St. Paul | U | University of Minn St. Paul | C00218450 | 45.0 | −93.2 | 296 |
| 8 | Minneapolis-St. Paul | R | Gaylord | C00213076 | 44.6 | −94.2 | 310 |
| 9 | Des Moines | U | Des Moines Intl. Airport | W00014933 | 41.5 | −93.7 | 292 |
| 10 | Des Moines | R | Neal Smith Iowa | R0000INEA | 41.6 | −93.3 | 274 |
| 11 | Milwaukee | U | Milwaukee Mitchell Intl. Airport | W00014839 | 43.0 | −87.9 | 204 |
| 12 | Milwaukee | R | Milwaukee WSFO Dousman | C00478316 | 43.0 | −88.5 | 284 |
| 13 | Chicago | U | Chicago Midway Airport 3 SW | C00111577 | 41.7 | −87.8 | 189 |
| 14 | Chicago | R | Paw Paw 2 S | C00116661 | 41.7 | −89.0 | 290 |
| 15 | Fort Wayne | U | Fort Wayne Intl. Airport | W00014827 | 41.0 | −85.2 | 252 |
| 16 | Fort Wayne | R | Paulding | C00336465 | 41.1 | −84.6 | 221 |
| 17 | Detroit | U | Detroit City Airport | W00014822 | 42.4 | −83.0 | 191 |
| 18 | Detroit | R | White Lake 4 E | C00208941 | 42.7 | −83.5 | 321 |
| 19 | Cleveland | U | Cleveland Burke Lakefront Airport | W00004853 | 41.5 | −81.7 | 178 |
| 20 | Cleveland | R | Wooster Experimental Station | C00339312 | 40.8 | −81.9 | 311 |
| 21 | Pittsburgh | U | Pittsburgh Allegheny Co Airport | W00014762 | 40.4 | −79.9 | 380 |
| 22 | Pittsburgh | R | Dennison Water Works | C00332160 | 40.4 | −81.3 | 262 |
| X | Y | RMSD | Spearman Coefficient |
|---|---|---|---|
| Daymet GDD Rural | Daymet GDD | 0.31 | 0.997 |
| Daymet NDD Rural | Daymet NDD | 0.37 | 0.995 |
| Daymet DDD Rural | Daymet DDD | 0.41 | 0.997 |
| GHCN GDD | Daymet GDD | 0.70 | 0.987 |
| MODIS NDD Rural | MODIS NDD | 0.71 | 0.986 |
| GHCN DDD | Daymet DDD | 0.72 | 0.992 |
| GHCN NDD | Daymet NDD | 0.73 | 0.975 |
| GHCN GDD Rural | GHCN GDD | 0.79 | 0.993 |
| Daymet NDD Rural | MODIS NDD Rural | 0.82 | 0.980 |
| GHCN NDD Rural | Daymet NDD Rural | 0.84 | 0.961 |
| GHCN NDD Rural | GHCN NDD | 0.90 | 0.983 |
| Daymet NDD | MODIS NDD | 0.93 | 0.983 |
| GHCN GDD Rural | Daymet GDD Rural | 0.94 | 0.983 |
| GHCN NDD Rural | MODIS NDD Rural | 0.97 | 0.961 |
| GHCN NDD | MODIS NDD | 1.01 | 0.974 |
| GHCN DDD Rural | GHCN DDD | 1.07 | 0.989 |
| GHCN DDD Rural | Daymet DDD Rural | 1.13 | 0.986 |
| MODIS GDD Rural | MODIS GDD | 1.20 | 0.982 |
| GHCN GDD | MODIS GDD | 1.66 | 0.982 |
| Daymet GDD | MODIS GDD | 1.70 | 0.978 |
| MODIS DDD Rural | MODIS DDD | 1.73 | 0.968 |
| Daymet GDD Rural | MODIS GDD Rural | 1.85 | 0.971 |
| GHCN GDD Rural | MODIS GDD Rural | 1.90 | 0.970 |
| Daymet DDD | MODIS DDD | 2.62 | 0.967 |
| GHCN DDD | MODIS DDD | 2.68 | 0.965 |
| Daymet DDD Rural | MODIS DDD Rural | 3.03 | 0.935 |
| GHCN DDD Rural | MODIS DDD Rural | 3.21 | 0.927 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krehbiel, C.; Henebry, G.M. A Comparison of Multiple Datasets for Monitoring Thermal Time in Urban Areas over the U.S. Upper Midwest. Remote Sens. 2016, 8, 297. https://doi.org/10.3390/rs8040297
Krehbiel C, Henebry GM. A Comparison of Multiple Datasets for Monitoring Thermal Time in Urban Areas over the U.S. Upper Midwest. Remote Sensing. 2016; 8(4):297. https://doi.org/10.3390/rs8040297
Chicago/Turabian StyleKrehbiel, Cole, and Geoffrey M. Henebry. 2016. "A Comparison of Multiple Datasets for Monitoring Thermal Time in Urban Areas over the U.S. Upper Midwest" Remote Sensing 8, no. 4: 297. https://doi.org/10.3390/rs8040297
APA StyleKrehbiel, C., & Henebry, G. M. (2016). A Comparison of Multiple Datasets for Monitoring Thermal Time in Urban Areas over the U.S. Upper Midwest. Remote Sensing, 8(4), 297. https://doi.org/10.3390/rs8040297