Monitoring Grassland Seasonal Carbon Dynamics, by Integrating MODIS NDVI, Proximal Optical Sampling, and Eddy Covariance Measurements
Abstract
:1. Introduction
- assess the seasonal patterns of CO2 exchange, above-ground biomass accumulation, and optical properties of a prairie grassland ecosystem comparing different optical sampling techniques (NDVI680,800 from field spectrometer measurements, proxy NDVI measurements from automated sensors on an “optical phenology station,” and MODIS NDVI measurements);
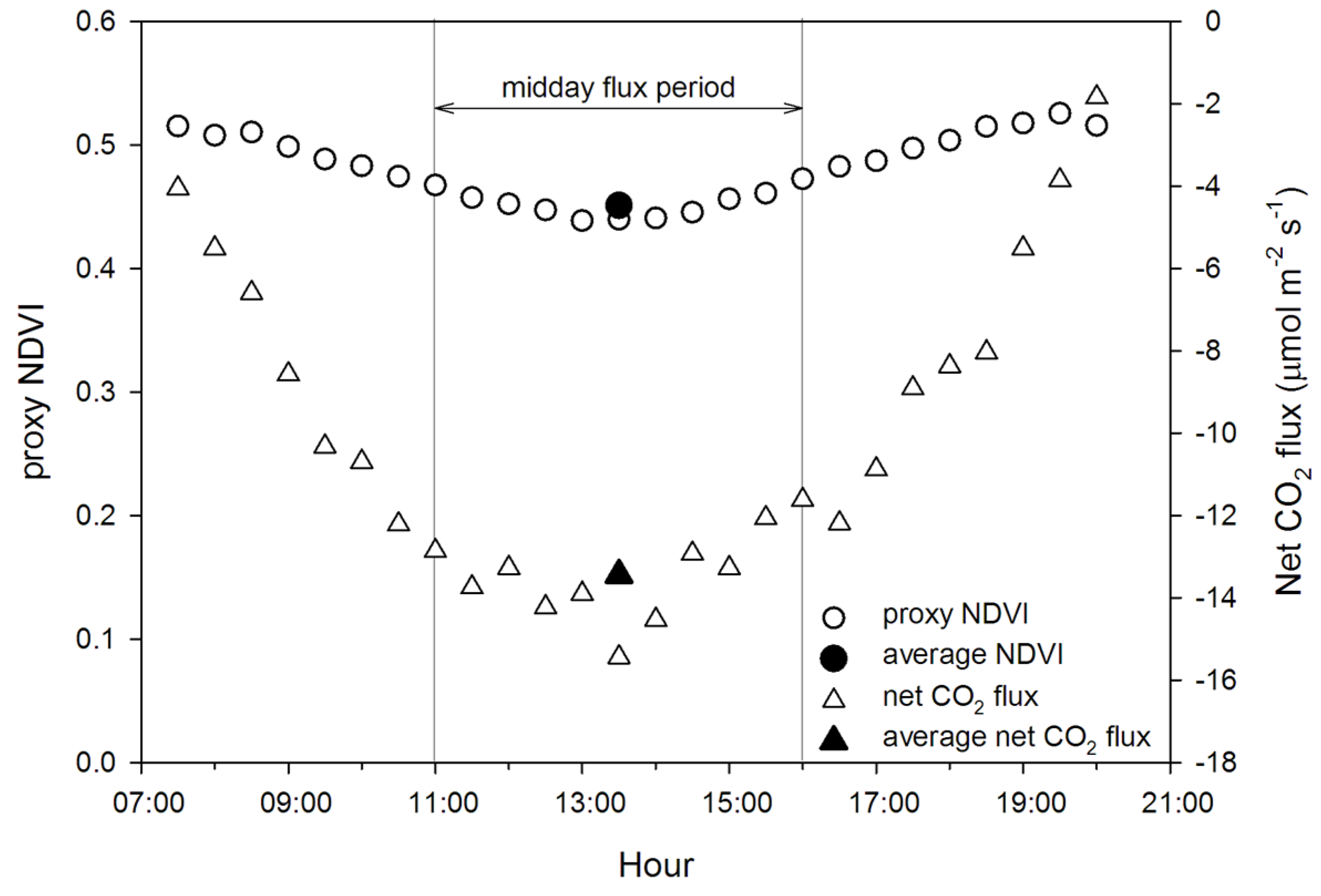
- compare midday data aggregation periods for accurate prediction of fluxes from optical data;
- test different NDVI inputs and related biophysical parameters (fAPARgreen and APARgreen) from both satellite and ground measurements as proxies for flux measurements using the LUE model;
- test the hypothesis of constant ε over the entire season in grassland ecosystem; and
- illustrate the potential of optical data to gap-fill eddy covariance measurements.
2. Materials and Methods
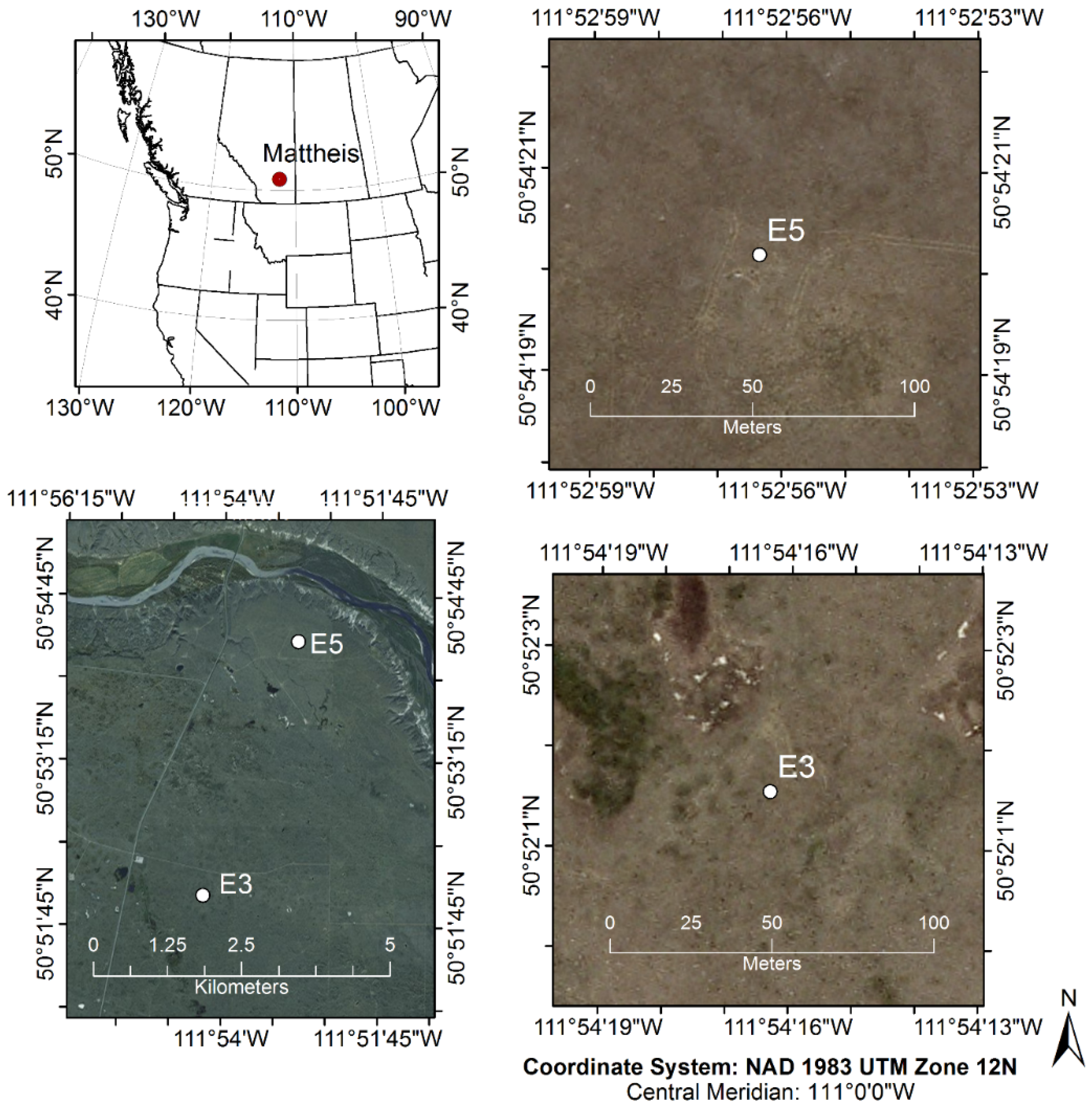
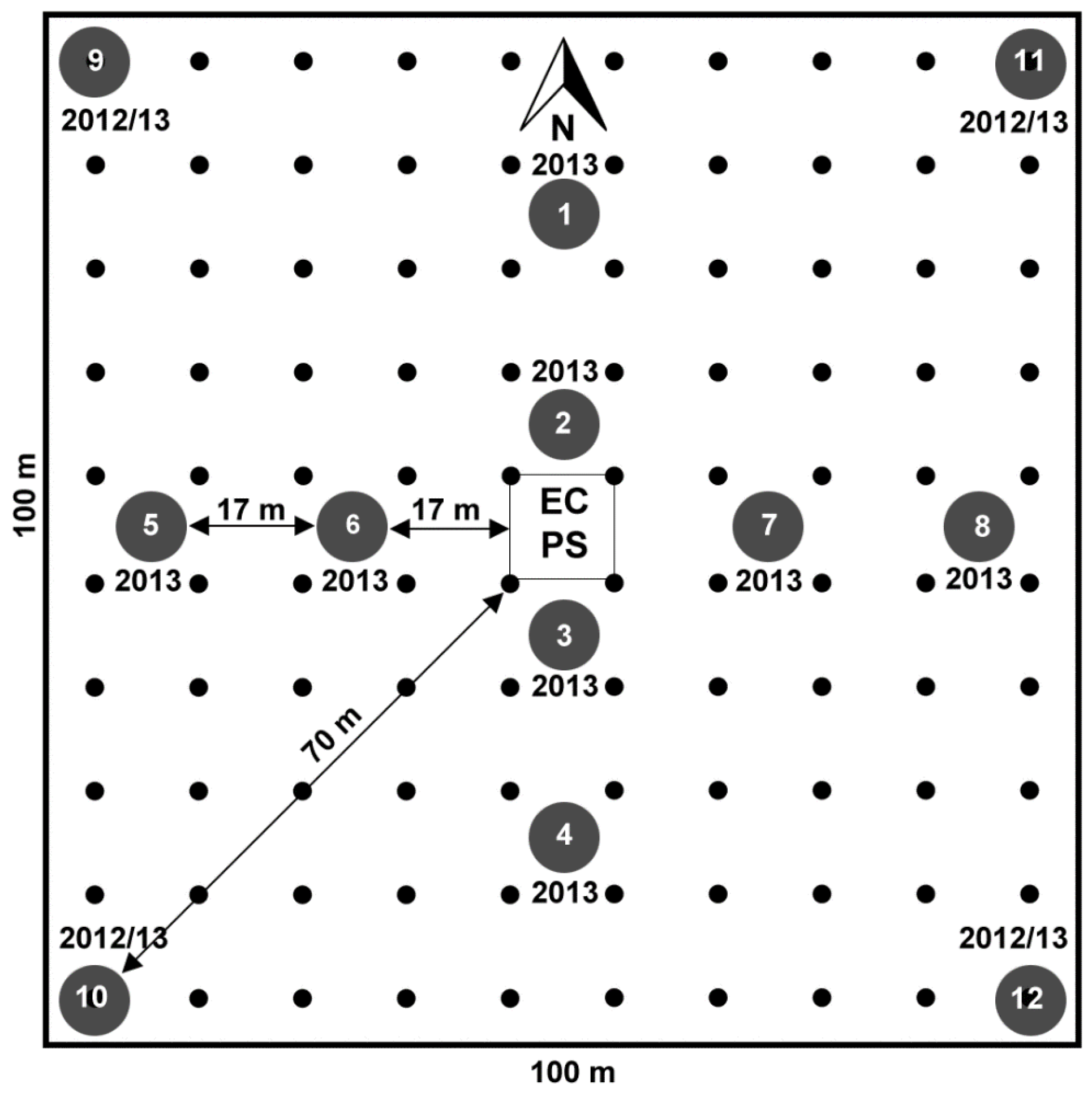
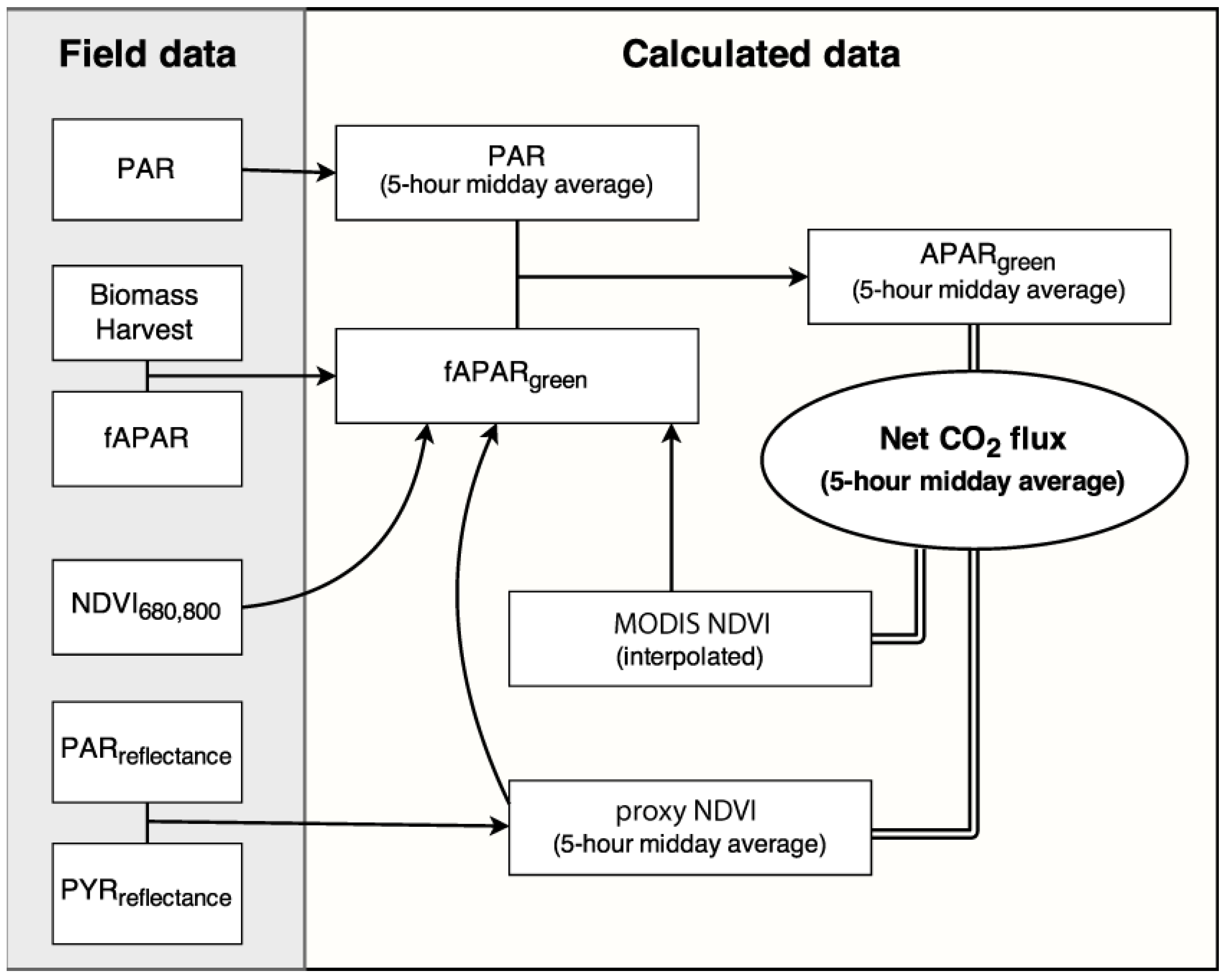
2.1. Study Site and Experimental Design
- -
- CO2 flux measurements from eddy covariance at the E3 and E5 sites,
- -
- -
- aboveground biomass samples from a 1 ha area around each flux tower site periodically collected following the sampling scheme reported in Figure 2,
- -
- NDVI680,800 measurements using a field spectrometer collected at regular intervals in the same area (1 ha) using a 10 m grid spacing (Figure 2),
- -
- incident and reflected incoming PAR measurements at each calibration point (numbered circles, Figure 2), and
- -
- MODIS satellite NDVI data downloaded for the study areas.
2.2. Biomass Estimation
2.3. fAPARgreen and APARgreen Calibration
2.4. NDVI Measurements
2.4.1. NDVI680,800
2.4.2. Proxy NDVI Measurements
2.4.3. MODIS NDVI Measurements
2.5. CO2 Flux Measurements
2.6. Filtering and Averaging Process
2.7. Gap Filling
3. Results
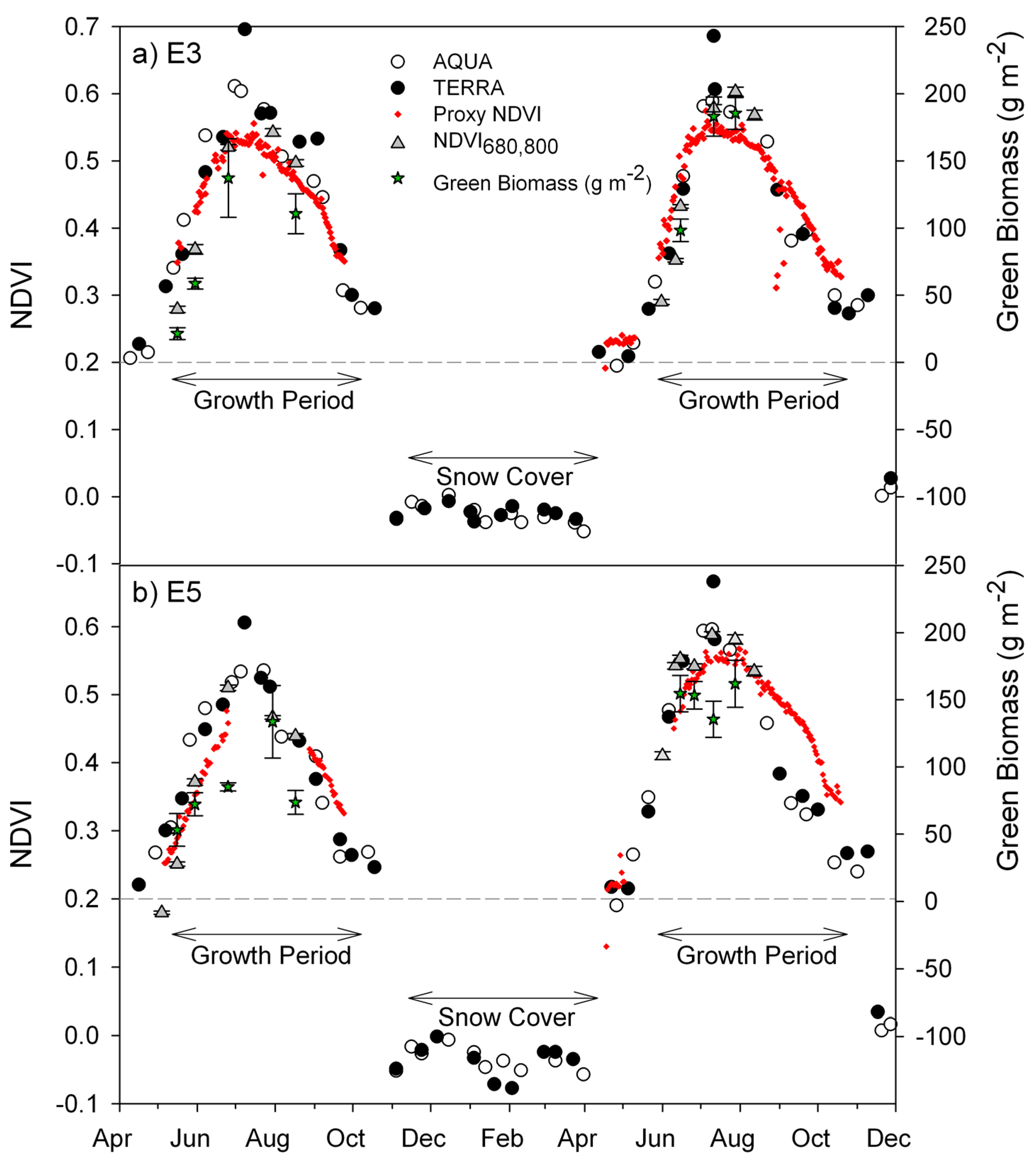
3.1. Seasonal Patterns of CO2 Exchange, Above-Ground Biomass, and NDVI Measurements
3.2. Green Biomass Estimation Using Different NDVI Formulations
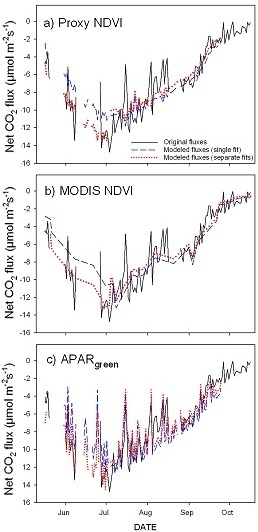
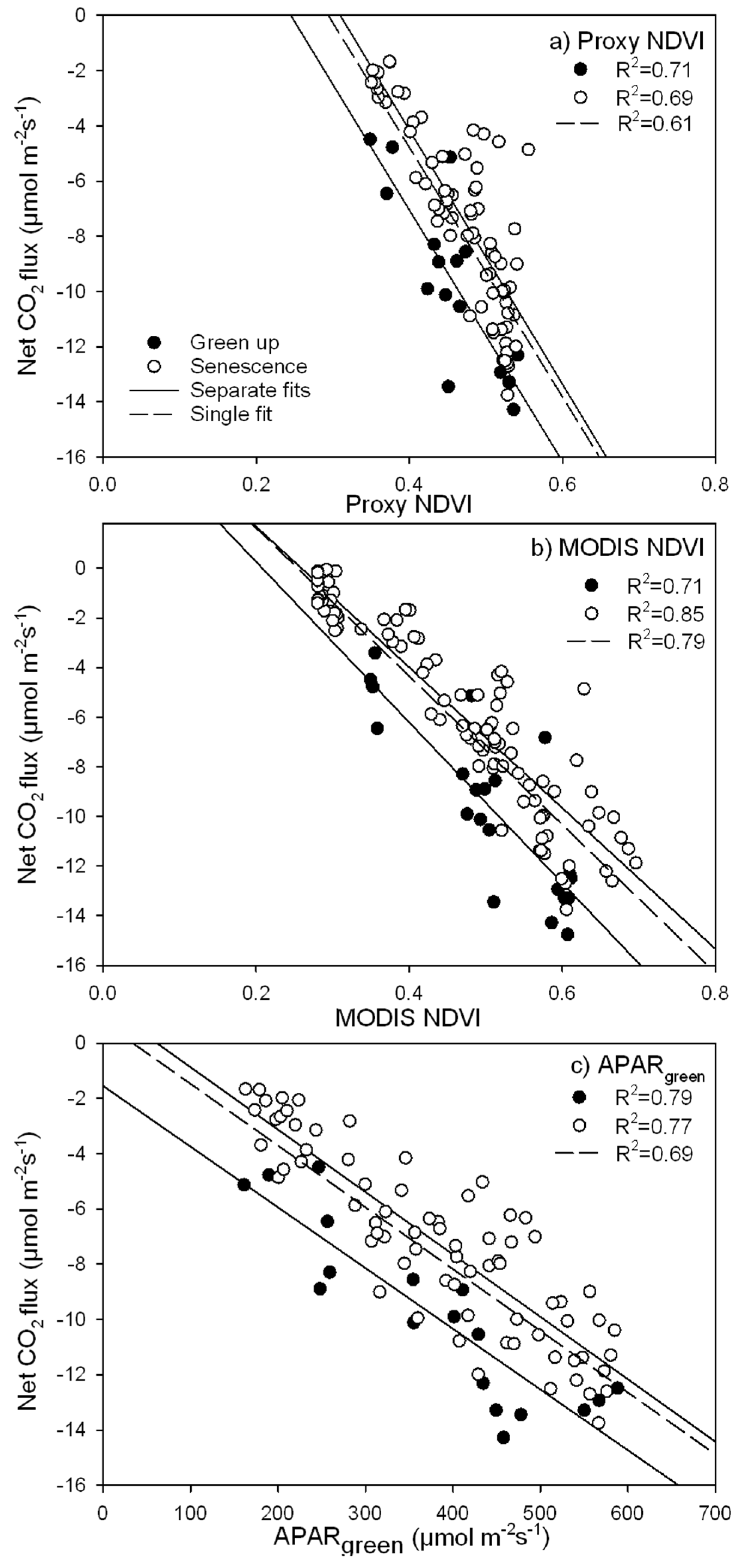
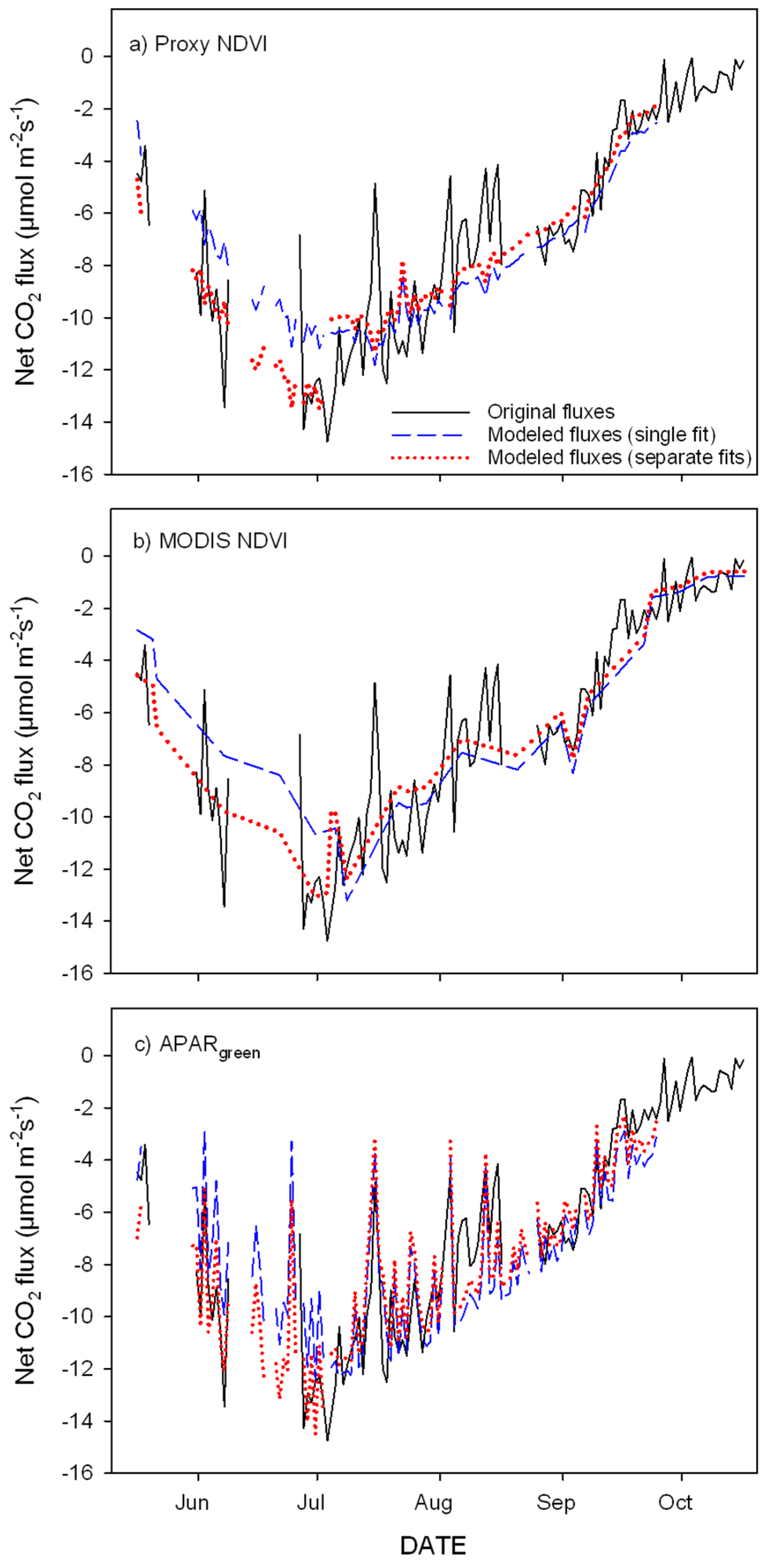
3.3. Parameterization of the LUE Model Using Proxy NDVI, MODIS NDVI and APARgreen
4. Discussion
5. Conclusions
- -
- optical inputs to a simple empirical LUE model closely track seasonal carbon fluxes and provide a simple proxy to fill gaps in the eddy covariance datasets;
- -
- the three NDVI methods give slightly different results depending on different band formulations, footprints and temporal sampling periods; however, low cost sensor (proxy NDVI) can be adopted for monitoring CO2 fluxes;
- -
- proper temporal aggregation improves model accuracy, and further analyses are needed to evaluate the quantitative impact of each aggregation method and period for different sites;
- -
- due to hysteresis and possible stress in the late season, the hypothesis of a constant ε for our ecosystem seems violated over the entire season (May–October), but holds for half season periods;
- -
- greening and senescence phases of the growing season are best captured using separate model fits and give the most accurate carbon flux estimates (model based on APARgreen; R2 = 0.69 for whole season, R2 = 0.79 for green-up phase and R2 = 0.77 for senescence phase);
- -
- this approach is able to distinguish different levels of productivity in the two landscapes sampled, demonstrating the ability to distinguish different levels of carbon uptake.
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Running, S.W. Climate change—Ecosystem disturbance, carbon, and climate. Science 2008, 321, 652–653. [Google Scholar] [CrossRef] [PubMed]
- Fang, C.; Moncrieff, J.B. The dependence of soil CO2 efflux on temperature. Soil Biol. Biochem. 2001, 33, 155–165. [Google Scholar] [CrossRef]
- Lynch, D.H.; Cohen, R.D.H.; Fredeen, A.; Patterson, G.; Martin, R.C. Management of Canadian prairie region grazed grasslands: Soil C sequestration, livestock productivity and profitability. Can. J. Soil Sci. 2005, 85, 183–192. [Google Scholar] [CrossRef]
- Bonan, G.B. Forests and climate change: Forcings, feedbacks, and the climate benefits of forests. Science 2008, 320, 1444–1449. [Google Scholar] [CrossRef] [PubMed]
- Friedel, M.H.; Laycock, W.A.; Bastin, G.N. Assessing rangeland condition and trend. In Field Laboratory Methods for Grassland and Animal Production Research; CABI International: Wallingford, UK, 2000; pp. 227–262. [Google Scholar]
- Adams, B.; Ehlert, G.; Stone, C.; Lawrence, D.; Alexander, M.; Willoughby, M.; Hincz, C.; Moisey, D.; Burkinshaw, A.; Carlson, J. Rangeland Health Assessment for Grassland, Forest and Tame Pasture; Rangeland Management Branch, Public Lands & Forests Division, Alberta Sustainable Resource Development: Edmonton, AB, Canada, 2005. [Google Scholar]
- Allen, V.G.; Batello, C.; Berretta, E.J.; Hodgson, J.; Kothmann, M.; Li, X.; McLvor, J.; Milne, J.; Morris, C.; Peeters, A.; et al. An international terminology for grazing lands and grazing animals. Grass Forage Sci. 2011, 66, 2–28. [Google Scholar] [CrossRef]
- Downing, D.J.; Pettapiece, W.W. Natural Regions and Subregions of Alberta; Government of Alberta: Edmonton, AB, Canada, 2006.
- Adams, B.W.; Poulin-Klein, L.; Moisey, D.; McNeil, R.L. Rangeland Plant Communities and Range Health Assessment Guidelines for the Dry Mixedgrass Natural Subregion of Alberta; Rangeland Management Branch, Public Lands Division, Alberta Sustainable Resource Development: Lethbridge, AB, Canada, 2005. [Google Scholar]
- Conant, R.T. Challenges and opportunities for carbon sequestration in grassland systems: A technical report on grassland management and climate change mitigation. In Integrated Crop Management; Food and Agriculture Organization: Rome, Italy, 2010; Volume 9, pp. 1–57. [Google Scholar]
- Solomon, A.M.; Prentice, I.C.; Leemans, R.; Cramer, W.P. The interaction of climate and land-use in future terrestrial carbon storage and release. Water Air Soil Pollut. 1993, 70, 595–614. [Google Scholar] [CrossRef]
- Wehlage, D.C. Monitoring Year-to-Year Variability in Dry Mixed-Grass Prairie Yield Using Multi-Sensor Remote Sensing. Master’s Thesis, University of Alberta, Edmonton, AB, Canada, 2012. [Google Scholar]
- Frank, D.A. Drought effects on above- and belowground production of a grazed temperate grassland ecosystem. Oecologia 2007, 152, 131–139. [Google Scholar] [CrossRef] [PubMed]
- Hovenden, M.J.; Newton, P.C.D.; Wills, K.E. Seasonal not annual rainfall determines grassland biomass response to carbon dioxide. Nature 2014, 511, 583–586. [Google Scholar] [CrossRef] [PubMed]
- Brookshire, E.N.J.; Weaver, T. Long-term decline in grassland productivity driven by increasing dryness. Nat. Commun. 2015, 6. [Google Scholar] [CrossRef] [PubMed]
- Stohlgren, T.J.; Bull, K.A.; Otsuki, Y. Comparison of rangeland vegetation sampling techniques in the central grasslands. J. Range Manag. 1998, 51, 164–172. [Google Scholar] [CrossRef]
- Lieth, H. Modeling the primary productivity of the world. In Primary Productivity of the Biosphere; Lieth, H., Whittaker, R.H., Eds.; Springer-Verlag: New York, NY, USA; Heidelberg, Germany, 1975; Volume 14, pp. 237–263. [Google Scholar]
- Wu, C.; Munger, J.W.; Niu, Z.; Kuang, D. Comparison of multiple models for estimating gross primary production using MODIS and eddy covariance data in Harvard Forest. Remote Sens. Environ. 2010, 114, 2925–2939. [Google Scholar] [CrossRef]
- Schimel, D.S.; Braswell, B.H.; Holland, E.A.; McKeown, R.; Ojima, D.S.; Painter, T.H.; Parton, W.J.; Townsend, A.R. Climatic, edaphic, and biotic controls over storage and turnover of carbon in soils. Glob. Biogeochem. Cycles 1994, 8, 279–293. [Google Scholar] [CrossRef]
- Ramoelo, A.; Skidmore, A.K.; Schlerf, M.; Heitkonig, I.M.A.; Mathieu, R.; Cho, M.A. Savanna grass nitrogen to phosphorous ratio estimation using field spectroscopy and the potential for estimation with imaging spectroscopy. Int. J. Appl. Earth Obs. Geoinf. 2013, 23, 334–343. [Google Scholar] [CrossRef]
- Baldocchi, D.D.; Hicks, B.B.; Meyers, T.P. Measuring biosphere-atmosphere exchanges of biologically related gases with micrometeorological methods. Ecology 1988, 69, 1331–1340. [Google Scholar] [CrossRef]
- Valentini, R.; Gamon, J.A.; Field, C.B. Ecosystem gas exchange in a California grassland: Seasonal patterns and implications for scaling. Ecology 1995, 76, 1940–1952. [Google Scholar] [CrossRef]
- Soussana, J.F.; Allard, V.; Pilegaard, K.; Ambus, P.; Amman, C.; Campbell, C.; Ceschia, E.; Clifton-Brown, J.; Czobel, S.; Domingues, R.; et al. Full accounting of the greenhouse gas (CO2, N2O, CH4) budget of nine European grassland sites. Agric. Ecosyst. Environ. 2007, 121, 121–134. [Google Scholar] [CrossRef]
- Running, S.W.; Nemani, R.R.; Heinsch, F.A.; Zhao, M.S.; Reeves, M.; Hashimoto, H. A continuous satellite-derived measure of global terrestrial primary production. Bioscience 2004, 54, 547–560. [Google Scholar] [CrossRef]
- Huemmrich, K.F.; Gamon, J.A.; Tweedie, C.E.; Campbell, P.K.E.; Landis, D.R.; Middleton, E.M. Arctic tundra vegetation functional types based on photosynthetic physiology and optical properties. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 265–275. [Google Scholar] [CrossRef]
- Gamon, J.A.; Rahman, A.F.; Dungan, J.L.; Schildhauer, M.; Huemmrich, K.F. Spectral network (SpecNet)—what is it and why do we need it? Remote Sens. Environ. 2006, 103, 227–235. [Google Scholar] [CrossRef]
- Gamon, J.A.; Coburn, C.; Flanagan, L.B.; Huemmrich, K.F.; Kiddle, C.; Sanchez-Azofeifa, G.A.; Thayer, D.R.; Vescovo, L.; Gianelle, D.; Sims, D.A.; et al. SpecNet revisited: Bridging flux and remote sensing communities. Can. J. Remote Sens. 2010, 36, S376–S390. [Google Scholar] [CrossRef]
- Balzarolo, M.; Anderson, K.; Nichol, C.; Rossini, M.; Vescovo, L.; Arriga, N.; Wohlfahrt, G.; Calvet, J.-C.; Carrara, A.; Cerasoli, S.; et al. Ground-based optical measurements at European flux sites: A review of methods, instruments and current controversies. Sensors 2011, 11, 7954–7981. [Google Scholar] [CrossRef] [PubMed]
- Monteith, J.L. Solar-radiation and productivity in tropical ecosystems. J. Appl. Ecol. 1972, 9, 747–766. [Google Scholar] [CrossRef]
- Monteith, J.L. Climate and efficiency of crop production in Britain. Philos. Trans. R. Soc. B Biol. Sci. 1977, 281, 277–294. [Google Scholar] [CrossRef]
- Heinsch, F.A.; Zhao, M.; Running, S.W.; Kimball, J.S.; Nemani, R.R.; Davis, K.J.; Bolstad, P.V.; Cook, B.D.; Desai, A.R.; Ricciuto, D.M.; et al. Evaluation of remote sensing based terrestrial productivity from MODIS using regional tower eddy flux network observations. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1908–1925. [Google Scholar] [CrossRef]
- Damm, A.; Guanter, L.; Paul-Limoges, E.; van der Tol, C.; Hueni, A.; Buchmann, N.; Eugster, W.; Ammann, C.; Schaepman, M.E. Far-red sun-induced chlorophyll fluorescence shows ecosystem-specific relationships to gross primary production: An assessment based on observational and modeling approaches. Remote Sens. Environ. 2015, 166, 91–105. [Google Scholar] [CrossRef]
- Rossini, M.; Meroni, M.; Migliavacca, M.; Manca, G.; Cogliati, S.; Busetto, L.; Picchi, V.; Cescatti, A.; Seufert, G.; Colombo, R. High resolution field spectroscopy measurements for estimating gross ecosystem production in a rice field. Agric. For. Meteorol. 2010, 150, 1283–1296. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Gamon, J.A. The need for a common basis for defining light-use efficiency: Implications for productivity estimation. Remote Sens. Environ. 2015, 156, 196–201. [Google Scholar] [CrossRef]
- Gamon, J.A. Reviews and syntheses: Optical sampling of the flux tower footprint. Biogeosciences 2015, 12, 4509–4523. [Google Scholar] [CrossRef]
- Lobell, D.B.; Asner, G.P.; Ortiz-Monasterio, J.I.; Benning, T.L. Remote sensing of regional crop production in the Yaqui valley, Mexico: Estimates and uncertainties. Agric. Ecosyst. Environ. 2003, 94, 205–220. [Google Scholar] [CrossRef]
- Gamon, J.A.; Field, C.B.; Goulden, M.L.; Griffin, K.L.; Hartley, A.E.; Joel, G.; Penuelas, J.; Valentini, R. Relationships between NDVI, canopy structure, and photosynthesis in three Californian vegetation types. Ecol. Appl. 1995, 5, 28–41. [Google Scholar] [CrossRef]
- Hilker, T.; Coops, N.C.; Wulder, M.A.; Black, T.A.; Guy, R.D. The use of remote sensing in light use efficiency based models of gross primary production: A review of current status and future requirements. Sci. Total Environ. 2008, 404, 411–423. [Google Scholar] [CrossRef] [PubMed]
- Peñuelas, J.; Garbulsky, M.F.; Filella, I. Photochemical reflectance index (PRI) and remote sensing of plant CO2 uptake. New Phytol. 2011, 191, 596–599. [Google Scholar] [CrossRef] [PubMed]
- Myneni, R.B.; Williams, D.L. On the relationship between fAPAR and NDVI. Remote Sens. Environ. 1994, 49, 200–211. [Google Scholar] [CrossRef]
- Wang, R.; Gamon, J.A.; Emmerton, C.A.; Li, H.; Nestola, E.; Pastorello, G.Z.; Menzer, O. Integrated analysis of productivity and biodiversity in a southern Alberta prairie. Remote Sens. 2016, 8, 214. [Google Scholar] [CrossRef]
- Becker, S. Mattheis Ranch Vegetation and Soil Inventory; Rangelands Research Institute, University of Alberta: Edmonton, AB, USA, 2013. [Google Scholar]
- Huemmrich, K.F.; Black, T.A.; Jarvis, P.G.; McCaughey, J.H.; Hall, F.G. High temporal resolution NDVI phenology from micrometeorological radiation sensors. J. Geophys. Res. 1999, 104, 27935–27944. [Google Scholar] [CrossRef]
- Nassar, J.M.; Rodríguez, J.P.; Sánchez-Azofeifa, A.; Garvin, T.; Quesada, M. Manual of methods: Human, Ecological and Biophysical Dimensions of Tropical Dry Forests; Instituto Venezolano de Investigaciones Científicas (IVIC): Caracas, Venezuela, 2008. [Google Scholar]
- Gamon, J.A.; Cheng, Y.F.; Claudio, H.; MacKinney, L.; Sims, D.A. A mobile tram system for systematic sampling of ecosystem optical properties. Remote Sens. Environ. 2006, 103, 246–254. [Google Scholar] [CrossRef]
- Webb, E.K.; Pearman, G.I.; Leuning, R. Correction of flux measurements for density effects due to heat and water-vapor transfer. Q. J. R. Meteorol. Soc. 1980, 106, 85–100. [Google Scholar] [CrossRef]
- Moncrieff, J.; Clement, R.; Finnigan, J.; Meyers, T. Averaging, detrending, and filtering of eddy covariance time series. In Handbook of Micrometeorology: A Guide for Surface Flux Measurement and Analysis; Springer Netherlands: Dordrecht, The Netherlands, 2004; Volume 29, pp. 7–31. [Google Scholar]
- Ibrom, A.; Dellwik, E.; Flyvbjerg, H.; Jensen, N.O.; Pilegaard, K. Strong low-pass filtering effects on water vapour flux measurements with closed-path eddy correlation systems. Agric. For. Meteorol. 2007, 147, 140–156. [Google Scholar] [CrossRef]
- Wille, C.; Kutzbach, L.; Sachs, T.; Wagner, D.; Pfeiffer, E.-M. Methane emission from Siberian arctic polygonal tundra: Eddy covariance measurements and modeling. Glob. Chang. Biol. 2008, 14, 1395–1408. [Google Scholar] [CrossRef]
- Mauder, M.; Foken, T. Impact of post-field data processing on eddy covariance flux estimates and energy balance closure. Meteorol. Z. 2006, 15, 597–609. [Google Scholar] [CrossRef]
- Cheng, Y.F.; Gamon, J.A.; Fuentes, D.A.; Mao, Z.Y.; Sims, D.A.; Qiu, H.L.; Claudio, H.; Huete, A.; Rahman, A.F. A multi-scale analysis of dynamic optical signals in a southern California chaparral ecosystem: A comparison of field, AVIRIS and MODIS data. Remote Sens. Environ. 2006, 103, 369–378. [Google Scholar] [CrossRef]
- Falge, E.; Baldocchi, D.; Tenhunen, J.; Aubinet, M.; Bakwin, P.; Berbigier, P.; Bernhofer, C.; Burba, G.; Clement, R.; Davis, K.J.; et al. Seasonality of ecosystem respiration and gross primary production as derived from fluxnet measurements. Agric. For. Meteorol. 2002, 113, 53–74. [Google Scholar] [CrossRef]
- Moffat, A.M.; Papale, D.; Reichstein, M.; Hollinger, D.Y.; Richardson, A.D.; Barr, A.G.; Beckstein, C.; Braswell, B.H.; Churkina, G.; Desai, A.R.; et al. Comprehensive comparison of gap-filling techniques for eddy covariance net carbon fluxes. Agric. For. Meteorol. 2007, 147, 209–232. [Google Scholar] [CrossRef]
- Wohlfahrt, G.; Pilloni, S.; Hoertnagl, L.; Hammerle, A. Estimating carbon dioxide fluxes from temperate mountain grasslands using broad-band vegetation indices. Biogeosciences 2010, 7, 683–694. [Google Scholar] [CrossRef] [PubMed]
- Running, S.W. Estimating terrestrial primary productivity by combining remote sensing and ecosystem simulation. In Ecological Studies Analysis and Synthesis; Hobbs, R.J., Mooney, H.A., Eds.; Springer-Verlag New York, Inc.: Secaucus, NJ, USA; Berlin, Germany, 1990; Volume 79, pp. 65–86. [Google Scholar]
- Myneni, R.B.; Hall, F.G.; Sellers, P.J.; Marshak, A.L. The interpretation of spectral vegetation indexes. IEEE Trans. Geosci. Remote Sens. 1995, 33, 481–486. [Google Scholar] [CrossRef]
- Pettorelli, N.; Vik, J.O.; Mysterud, A.; Gaillard, J.M.; Tucker, C.J.; Stenseth, N.C. Using the satellite-derived NDVI to assess ecological responses to environmental change. Trends Ecol. Evol. 2005, 20, 503–510. [Google Scholar] [CrossRef] [PubMed]
- Gamon, J.A.; Huemmrich, K.F.; Stone, R.S.; Tweedie, C.E. Spatial and temporal variation in primary productivity (NDVI) of coastal Alaskan tundra: Decreased vegetation growth following earlier snowmelt. Remote Sens. Environ. 2013, 129, 144–153. [Google Scholar] [CrossRef]
- Peng, Y.; Gitelson, A.A.; Keydan, G.; Rundquist, D.C.; Moses, W. Remote estimation of gross primary production in maize and support for a new paradigm based on total crop chlorophyll content. Remote Sens. Environ. 2011, 115, 978–989. [Google Scholar] [CrossRef]
- Rossini, M.; Cogliati, S.; Meroni, M.; Migliavacca, M.; Galvagno, M.; Busetto, L.; Cremonese, E.; Julitta, T.; Siniscalco, C.; di Cella, U.M.; et al. Remote sensing-based estimation of gross primary production in a subalpine grassland. Biogeosciences 2012, 9, 2565–2584. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Peng, Y.; Arkebauer, T.J.; Schepers, J. Relationships between gross primary production, green LAI, and canopy chlorophyll content in maize: Implications for remote sensing of primary production. Remote Sens. Environ. 2014, 144, 65–72. [Google Scholar] [CrossRef]
- Gamon, J.A.; Field, C.B.; Roberts, D.A.; Ustin, S.L.; Valentini, R. Functional patterns in an annual grassland during an aviris overflight. Remote Sens. Environ. 1993, 44, 239–253. [Google Scholar] [CrossRef]
- Balzarolo, M.; Vescovo, L.; Hammerle, A.; Gianelle, D.; Papale, D.; Tomelleri, E.; Wohlfahrt, G. On the relationship between ecosystem-scale hyperspectral reflectance and CO2 exchange in European mountain grasslands. Biogeosciences 2015, 12, 3089–3108. [Google Scholar] [CrossRef]
- Sakowska, K.; Vescovo, L.; Marcolla, B.; Juszczak, R.; Olejnik, J.; Gianelle, D. Monitoring of carbon dioxide fluxes in a subalpine grassland ecosystem of the Italian Alps using a multispectral sensor. Biogeosciences 2014, 11, 4695–4712. [Google Scholar] [CrossRef]
- Field, C.B.; Randerson, J.T.; Malmstrom, C.M. Global net primary production—Combining ecology and remote-sensing. Remote Sens. Environ. 1995, 51, 74–88. [Google Scholar] [CrossRef]
- Zhang, Q.; Cheng, Y.-B.; Lyapustin, A.I.; Wang, Y.; Zhang, X.; Suyker, A.; Verma, S.; Shuai, Y.; Middleton, E.M. Estimation of crop gross primary production (GPP): II. Do scaled MODIS vegetation indices improve performance? Agric. For. Meteorol. 2015, 200, 1–8. [Google Scholar] [CrossRef]
- Turner, D.P.; Ritts, W.D.; Cohen, W.B.; Maeirsperger, T.K.; Gower, S.T.; Kirschbaum, A.A.; Running, S.W.; Zhao, M.S.; Wofsy, S.C.; Dunn, A.L.; et al. Site-level evaluation of satellite-based global terrestrial gross primary production and net primary production monitoring. Glob. Chang. Biol. 2005, 11, 666–684. [Google Scholar] [CrossRef]
- Turner, D.P.; Ritts, W.D.; Cohen, W.B.; Gower, S.T.; Running, S.W.; Zhao, M.S.; Costa, M.H.; Kirschbaum, A.A.; Ham, J.M.; Saleska, S.R.; et al. Evaluation of MODIS NPP and GPP products across multiple biomes. Remote Sens. Environ. 2006, 102, 282–292. [Google Scholar] [CrossRef]
- McCallum, I.; Wagner, W.; Schmullius, C.; Shvidenko, A.; Obersteiner, M.; Fritz, S.; Nilsson, S. Satellite-based terrestrial production efficiency modeling. Carbon Balance Manag. 2009, 4, 8. [Google Scholar] [CrossRef] [PubMed]
- Song, C.; Dannenberg, M.P.; Hwang, T. Optical remote sensing of terrestrial ecosystem primary productivity. Prog. Phys. Geogr. 2013, 37, 834–854. [Google Scholar] [CrossRef]
- Wu, C.Y.; Niu, Z.; Tang, Q.; Huang, W.J.; Rivard, B.; Feng, J.L. Remote estimation of gross primary production in wheat using chlorophyll-related vegetation indices. Agric. For. Meteorol. 2009, 149, 1015–1021. [Google Scholar] [CrossRef]
- Ardö, J. Comparison between remote sensing and a dynamic vegetation model for estimating terrestrial primary production of Africa. Carbon Balance Manag. 2015, 10, 8. [Google Scholar] [CrossRef] [PubMed]
- Ruimy, A.; Saugier, B.; Dedieu, G. Methodology for the estimation of terrestrial net primary production from remotely sensed data. J. Geophys. Res. 1994, 99, 5263–5283. [Google Scholar] [CrossRef]
- Garbulsky, M.F.; Penuelas, J.; Gamon, J.; Inoue, Y.; Filella, I. The photochemical reflectance index (PRI) and the remote sensing of leaf, canopy and ecosystem radiation use efficiencies a review and meta-analysis. Remote Sens. Environ. 2011, 115, 281–297. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Peng, Y.; Masek, J.G.; Rundquist, D.C.; Verma, S.; Suyker, A.; Baker, J.M.; Hatfield, J.L.; Meyers, T. Remote estimation of crop gross primary production with Landsat data. Remote Sens. Environ. 2012, 121, 404–414. [Google Scholar] [CrossRef]
- Garbulsky, M.F.; Penuelas, J.; Papale, D.; Ardo, J.; Goulden, M.L.; Kiely, G.; Richardson, A.D.; Rotenberg, E.; Veenendaal, E.M.; Filella, I. Patterns and controls of the variability of radiation use efficiency and primary productivity across terrestrial ecosystems. Glob. Ecol. Biogeogr. 2010, 19, 253–267. [Google Scholar] [CrossRef]
- Gilmanov, T.G.; Baker, J.M.; Bernacchi, C.J.; Billesbach, D.P.; Burba, G.G.; Castro, S.; Chen, J.; Eugster, W.; Fischer, M.L.; Gamon, J.A.; et al. Productivity and carbon dioxide exchange of leguminous crops: Estimates from flux tower measurements. Agron. J. 2014, 106, 545–559. [Google Scholar] [CrossRef]
- Flanagan, L.B.; Sharp, E.J.; Gamon, J.A. Application of the photosynthetic light-use efficiency model in a northern Great Plains grassland. Remote Sens. Environ. 2015, 168, 239–251. [Google Scholar] [CrossRef]
- Nouvellon, Y.; Seen, D.L.; Rambal, S.; Begue, A.; Moran, M.S.; Kerr, Y.; Qi, J.G. Time course of radiation use efficiency in a shortgrass ecosystem: Consequences for remotely sensed estimation of primary production. Remote Sens. Environ. 2000, 71, 43–55. [Google Scholar] [CrossRef]
- Bradford, J.B.; Hicke, J.A.; Lauenroth, W.K. The relative importance of light-use efficiency modifications from environmental conditions and cultivation for estimation of large-scale net primary productivity. Remote Sens. Environ. 2005, 96, 246–255. [Google Scholar] [CrossRef]
- Yuan, W.; Liu, S.; Zhou, G.; Zhou, G.; Tieszen, L.L.; Baldocchi, D.; Bernhofer, C.; Gholz, H.; Goldstein, A.H.; Goulden, M.L.; et al. Deriving a light use efficiency model from eddy covariance flux data for predicting daily gross primary production across biomes. Agric. For. Meteorol. 2007, 143, 189–207. [Google Scholar] [CrossRef]
- Polley, H.W.; Phillips, R.L.; Frank, A.B.; Bradford, J.A.; Sims, P.L.; Morgan, J.A.; Kiniry, J.R. Variability in light-use efficiency for gross primary productivity on great plains grasslands. Ecosystems 2011, 14, 15–27. [Google Scholar] [CrossRef]
- Hilker, T.; Nesic, Z.; Coops, N.C.; Lessard, D. A new, automated, multiangular radiometer instrument for tower-based observations of canopy reflectance (AMSPEC II). Instrum. Sci. Technol. 2010, 38, 319–340. [Google Scholar] [CrossRef]
- Schmid, H.P. Footprint modeling for vegetation atmosphere exchange studies: A review and perspective. Agric. For. Meteorol. 2002, 113, 159–183. [Google Scholar] [CrossRef]

| Peak NDVI Values | 2012 | 2013 | ||||||
|---|---|---|---|---|---|---|---|---|
| E3 | σ | E5 | σ | E3 | σ | E5 | σ | |
| NDVI680,800 | 0.54 | 0.09 | 0.51 | 0.06 | 0.60 | 0.09 | 0.59 | 0.06 |
| Proxy NDVI | 0.56 | 0.01 | 0.47 * | 0.03 | 0.58 | 0.02 | 0.59 | 0.02 |
| MODIS NDVI-Terra | 0.69 | - | 0.60 | - | 0.68 | - | 0.66 | - |
| MODIS NDVI-Aqua | 0.61 | - | 0.53 | - | 0.58 | - | 0.59 | - |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nestola, E.; Calfapietra, C.; Emmerton, C.A.; Wong, C.Y.S.; Thayer, D.R.; Gamon, J.A. Monitoring Grassland Seasonal Carbon Dynamics, by Integrating MODIS NDVI, Proximal Optical Sampling, and Eddy Covariance Measurements. Remote Sens. 2016, 8, 260. https://doi.org/10.3390/rs8030260
Nestola E, Calfapietra C, Emmerton CA, Wong CYS, Thayer DR, Gamon JA. Monitoring Grassland Seasonal Carbon Dynamics, by Integrating MODIS NDVI, Proximal Optical Sampling, and Eddy Covariance Measurements. Remote Sensing. 2016; 8(3):260. https://doi.org/10.3390/rs8030260
Chicago/Turabian StyleNestola, Enrica, Carlo Calfapietra, Craig A. Emmerton, Christopher Y.S. Wong, Donnette R. Thayer, and John A. Gamon. 2016. "Monitoring Grassland Seasonal Carbon Dynamics, by Integrating MODIS NDVI, Proximal Optical Sampling, and Eddy Covariance Measurements" Remote Sensing 8, no. 3: 260. https://doi.org/10.3390/rs8030260
APA StyleNestola, E., Calfapietra, C., Emmerton, C. A., Wong, C. Y. S., Thayer, D. R., & Gamon, J. A. (2016). Monitoring Grassland Seasonal Carbon Dynamics, by Integrating MODIS NDVI, Proximal Optical Sampling, and Eddy Covariance Measurements. Remote Sensing, 8(3), 260. https://doi.org/10.3390/rs8030260