Regional Scale Rain-Forest Height Mapping Using Regression-Kriging of Spaceborne and Airborne LiDAR Data: Application on French Guiana
Abstract
:1. Introduction
2. Study Area and Datasets
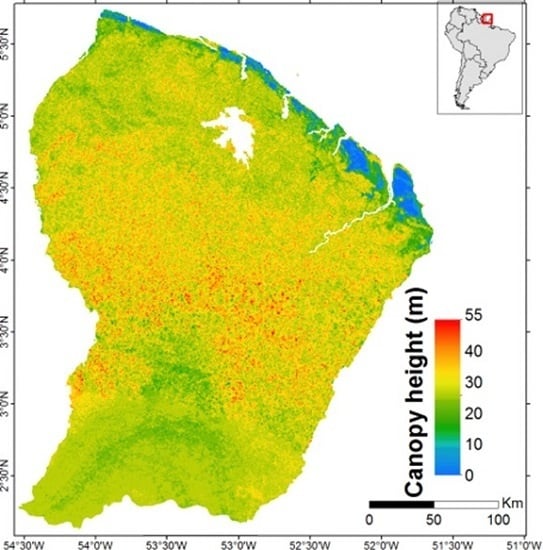
2.1. Study Area
2.2. Datasets Description
2.2.1. Spaceborne LiDAR Dataset
2.2.2. Airborne LiDAR Dataset
Small Footprint Low Density LiDAR Dataset
Small Footprint High Density LiDAR Dataset
2.2.3. Ancillary Datasets
MODerate-Resolution IMAGING Spectroradiometer (MODIS) Data
SRTM Digital Elevation Model Data
Geological Map
Forest Landscape Types Map
- (1)
- LT8 represents dense closed-canopy forest with small crowns of the same canopy height and small gaps mixed with regular canopies with well-developed crowns of almost the same canopy height without large gaps interlaced with flooded savannas (10%).
- (2)
- LT9 is a closed canopy forest dominated by well-developed crowns of almost the same canopy height without large gaps.
- (3)
- LT10 is an irregular and disrupted-canopy forest where the trees have very different heights and different crown diameters with large gaps mixed with closed-canopy forest dominated by well-developed crowns at almost the same elevation without large gaps. LT10 is also interlaced with liana forests.
- (4)
- LT11 is similar to LT10 with more liana forest and non-forest land covers.
- (5)
- LT12 is an open forest associated with wetlands and bamboo thickets. The LT dataset was chosen for its correlation with canopy heights. Indeed, in Fayad et al. [24], the difference between SRTM and canopy top elevations from ICESat were found to be correlated with different LTs as well as different canopy heights.
Average Rainfall Map
3. Canopy Height Estimation Methods
3.1. Canopy Height Trend Mapping Using Random Forest Regressions
3.2. Canopy Height Mapping Using Regression-Kriging
3.3. Ordinary Krigging of Regression Residuals
3.4. Effects of LiDAR Sampling Density on Precision of the Mapped Canopy Heights
4. Results
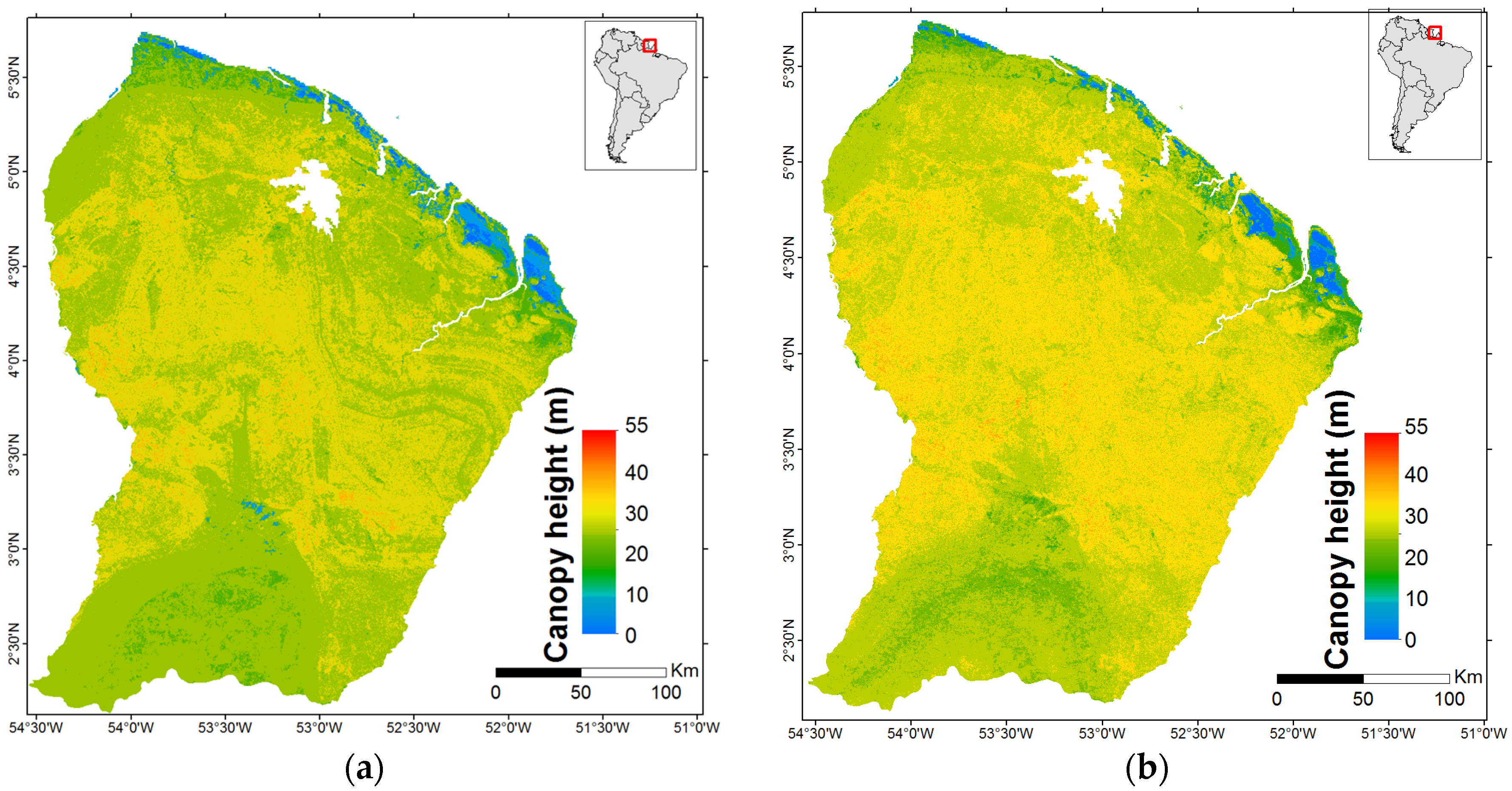
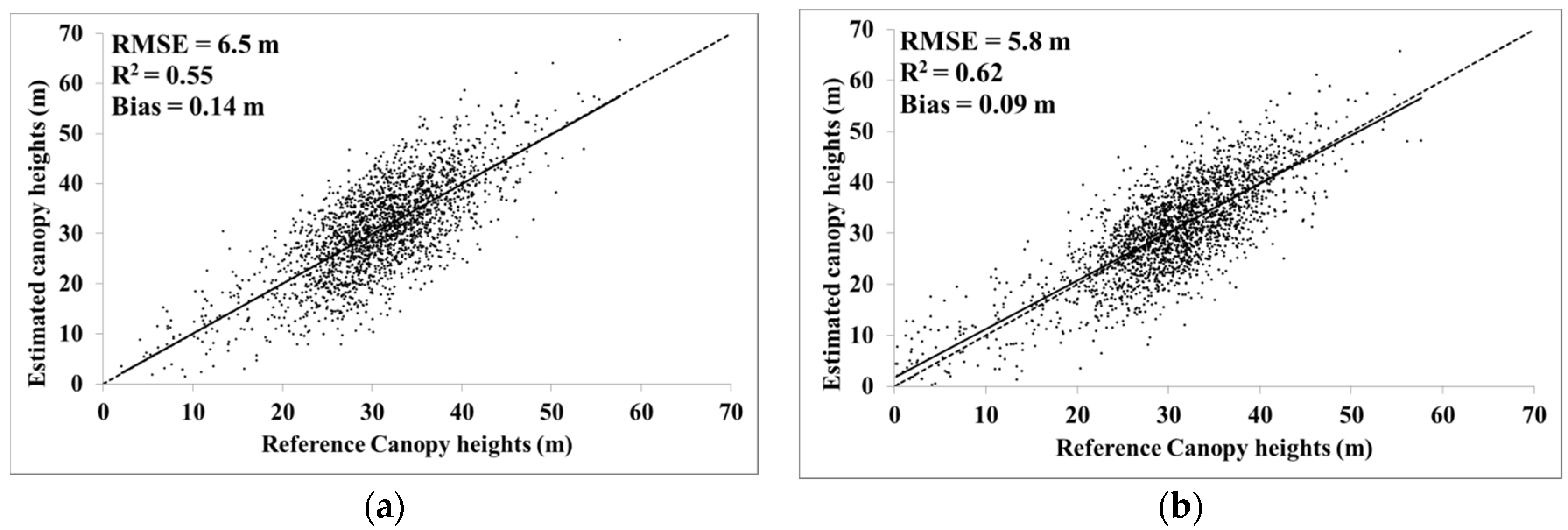
4.1. Canopy Height Trend Mapping Using Random Forest Regressions
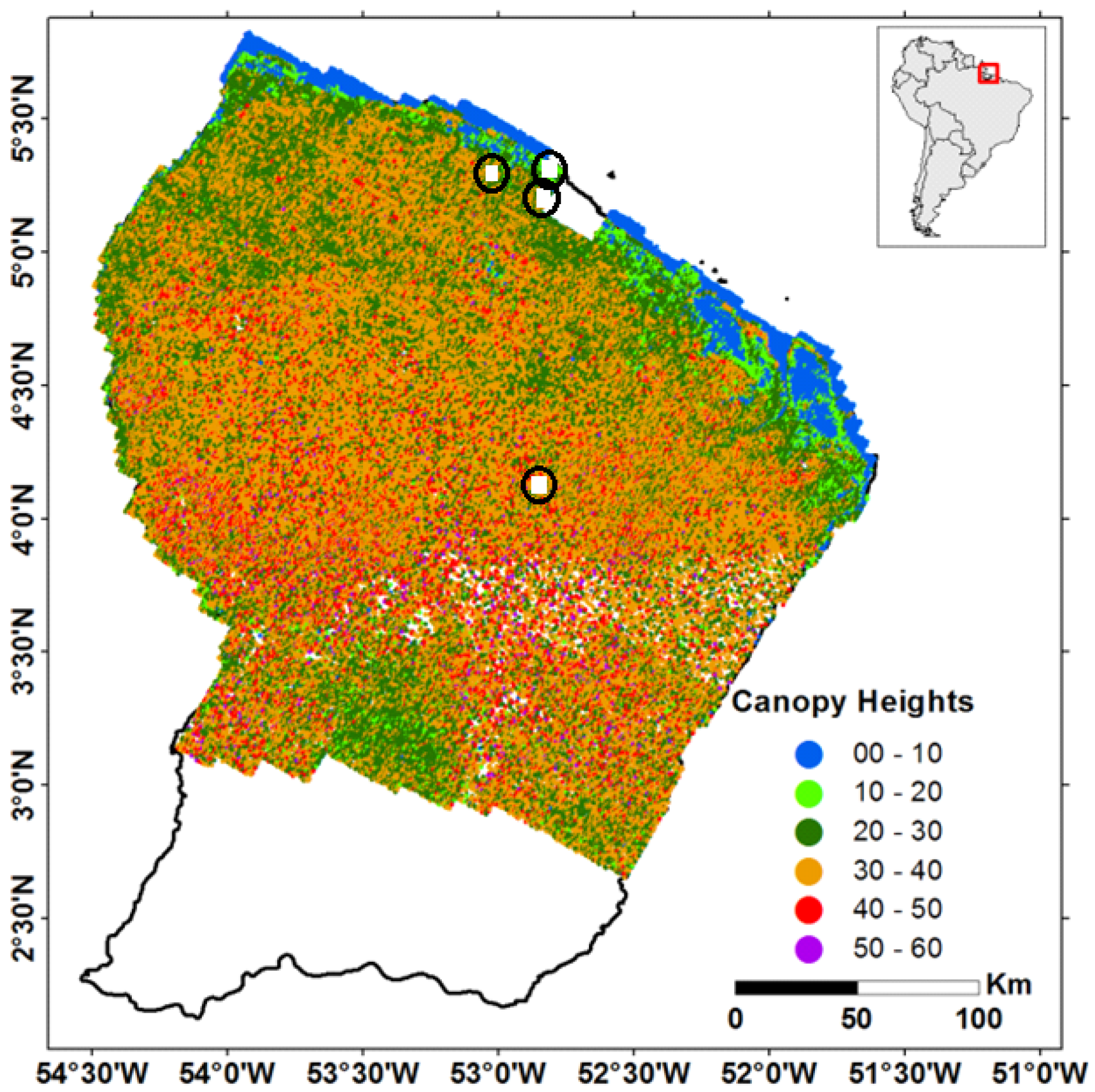
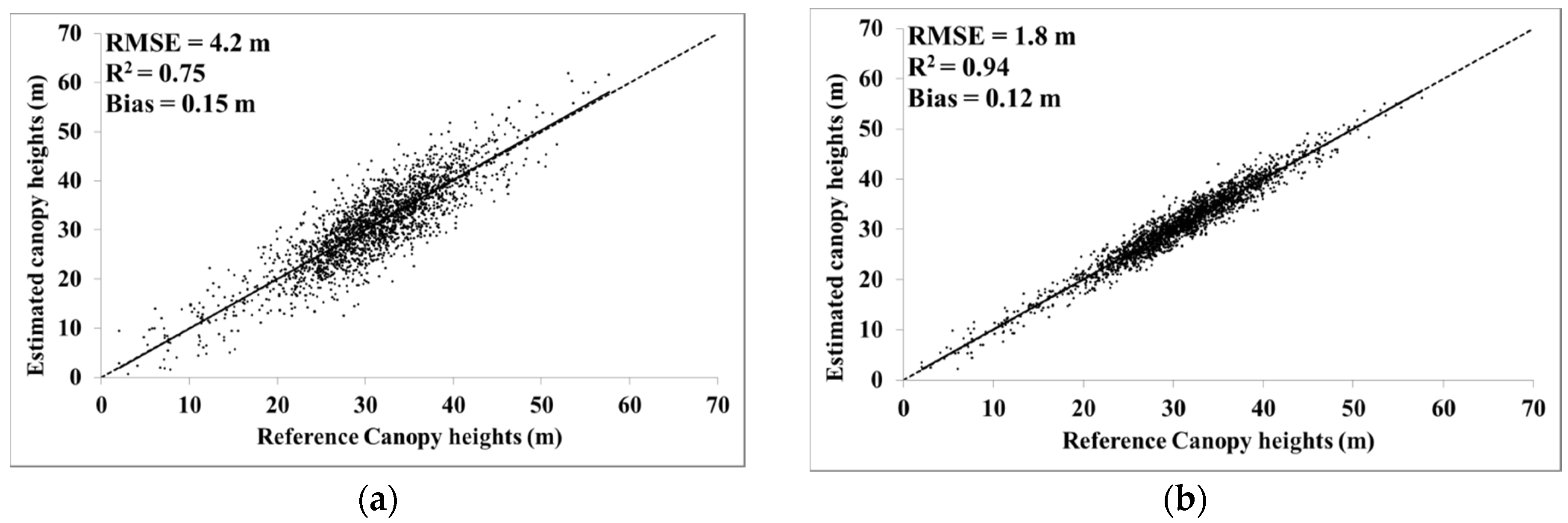
4.2. Canopy Height Estimation Using Regression-Kriging
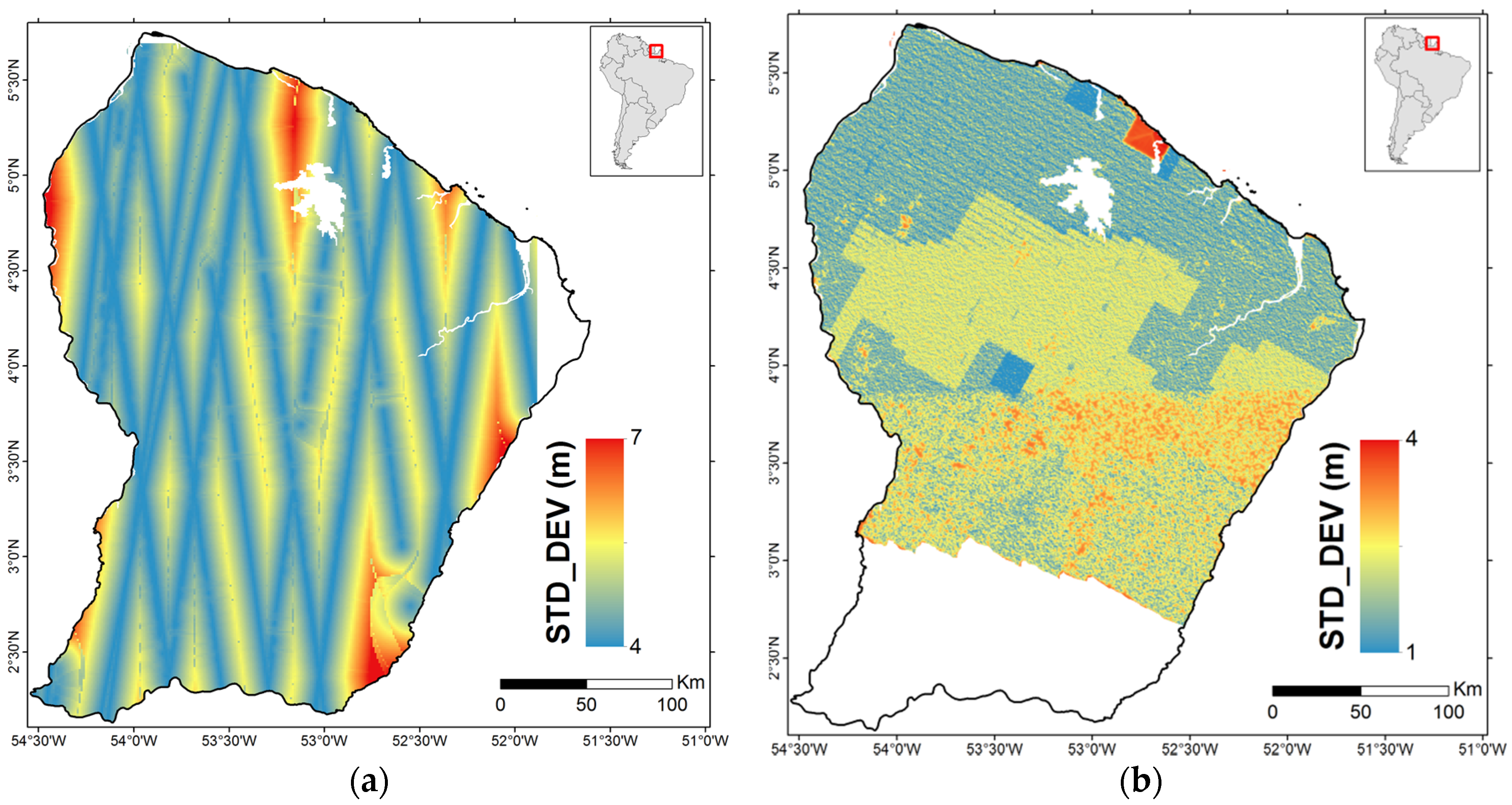
4.3. Relationship between LiDAR Flight Lines Spacing and the Precision on the Kriged Canopy Height
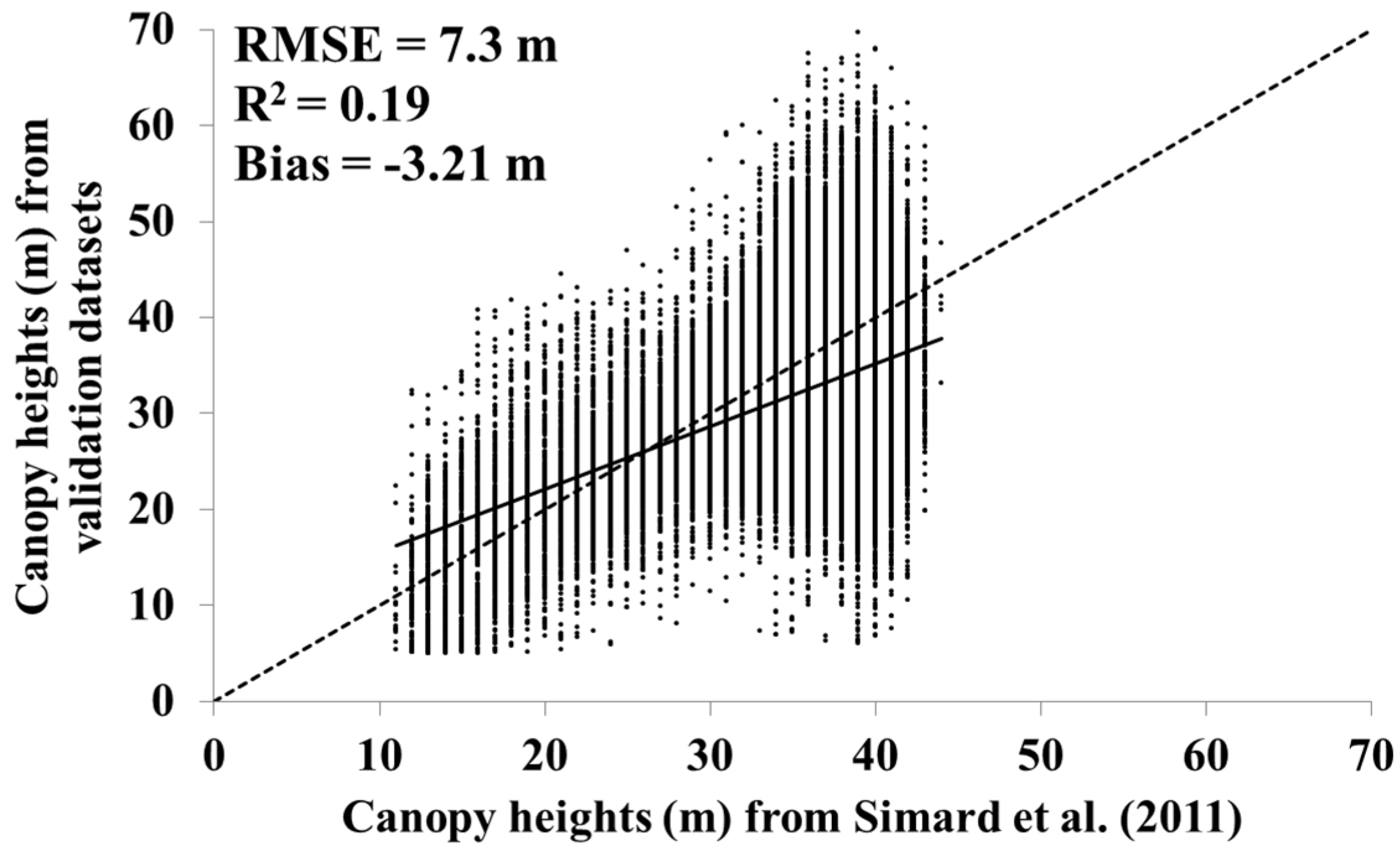
5. Discussion
6. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Drake, J.B.; Robert, G.K.; Ralph, O.D.; David, B.C.; Richard, C.; Bryan, B.J.; Michelle, H. Above-ground biomass estimation in closed canopy neotropical forests using lidar remote sensing: Factors affecting the generality of relationships. Glob. Ecol. Biogeogr. 2003, 12, 147–159. [Google Scholar] [CrossRef]
- Chave, J.; Andalo, C.; Brown, S.; Cairns, M.A.; Chambers, J.Q.; Eamus, D.; Fölster, H. Tree allometry and improved estimation of carbon stocks and balance in tropical forests. Oecologia 2005, 145, 87–99. [Google Scholar] [CrossRef] [PubMed]
- Asner, G.P.; Mascaro, J. Mapping tropical forest carbon: Calibrating plot estimates to a simple LiDAR metric. Remote Sens. Environ. 2014, 140, 614–624. [Google Scholar] [CrossRef]
- Zolkos, S.G.; Goetz, S.J.; Dubayah, R. A meta-analysis of terrestrial aboveground biomass estimation using lidar remote sensing. Remote Sens. Environ. 2013, 128, 289–298. [Google Scholar] [CrossRef]
- Feldpaush, T.R.; Lloyd, J.; Lewis, S.L.; Brienen, R.J.W.; Gloor, M.; Mendoza, A.M.; Lopez-Gonzalez, G.; Banin, L.; Salim, K.A.; Affum-Baffoe, K.; et al. Tree height integrated into pantropical forest biomass estimates. Biogeosciences 2012, 9, 3381–3403. [Google Scholar] [CrossRef]
- Mitchard, E.T.A.; Saatchi, S.S.; White, L.J.T.; Abernethy, K.A.; Jeffery, K.J.; Lewis, S.L.; Collins, M. Mapping tropical forest biomass with radar and spaceborne LiDAR in Lopé National Park, Gabon: Overcoming problems of high biomass and persistent cloud. Biogeosciences 2012, 9, 179–191. [Google Scholar] [CrossRef]
- Lefsky, M.A.; David, H.J.; Michael, K.; Warren, B.C.; Claudia, C.C.; Fernando Del Bom, H.E.-S.; Maria, O.; Raimundo, D.O. Estimates of forest canopy height and aboveground biomass using ICESat. Geophys. Res. Lett. 2005, 32, L22S02. [Google Scholar] [CrossRef]
- Boudreau, J.; Ross, F.N.; Hank, A.M.; André, G.; Luc, B.; Daniel, S.K. Regional aboveground forest biomass using airborne and spaceborne LiDAR in Québec. Remote Sens. Environ. 2008, 112, 3876–3890. [Google Scholar] [CrossRef]
- Saatchi, S.S.; Nancy, L.H.; Sandra, B.; Michael, L.; Edward, T.A.M.; William, S.; Brian, R.Z. Benchmark map of forest carbon stocks in tropical regions across three continents. Proc. Natl. Acad. Sci. USA 2011, 108, 9899–9904. [Google Scholar] [CrossRef] [PubMed]
- Simard, P.M.; Naiara, F.J.B.; Alessandro, B. Mapping forest canopy height globally with spaceborne lidar. J. Geophys. Res. 2011, 116, G04021. [Google Scholar] [CrossRef]
- Baghdadi, N.; le Maire, G.; Fayad, I.; Bailly, J.S.; Nouvellon, Y.; Lemos, C.; Hakamada, R. Testing different methods of forest height and aboveground biomass estimations from ICESat/GLAS data in Eucalyptus plantations in Brazil. IEEE (JSTARS) 2014, 7, 290–299. [Google Scholar] [CrossRef]
- Næsset, E. Predicting forest stand charactersitics with airborne scanning laser using a practical two-stage procedure and field data. Remote Sens. Environ. 2002, 80, 88–99. [Google Scholar] [CrossRef]
- Lee, S.; Ni-Meister, W.; Yang, W.; Chen, Q. Physically based vertical vegetation structure retrieval from ICESat data: Validation using LVIS in White Mountain National Forest, New Hampshire, USA. Remote Sens. Environ. 2011, 115, 2776–2785. [Google Scholar] [CrossRef]
- Hilbert, C.; Schmullius, C. Influence of surface topography on ICESat/GLAS forest height estimation and waveform shape. Remote Sens. 2012, 4, 2210–2235. [Google Scholar] [CrossRef]
- Pang, Y.; Michael, L.; Hans-Erik, A.; Ellen, M.M.; Kirk, S. Validation of the ICEsat vegetation product using crown-area-weighted mean height derived using crown delineation with discrete return lidar data. Can. J. Remote Sens. 2008, 34, S471–S484. [Google Scholar] [CrossRef]
- Enßle, F.; Heinzel, J.; Koch, B. Accuracy of vegetation height and terrain elevation derived from ICESat/GLAS in forested areas. Int. J. Appl. Earth Obs. Geoinf. 2014, 31, 37–44. [Google Scholar] [CrossRef]
- Gwenzi, D.; Lefsky, M.A. Modeling canopy height in a savanna ecosystem using spaceborne lidar waveforms. Remote Sens. Environ. 2014, 154, 338–344. [Google Scholar] [CrossRef]
- Montesano, P.M.; Sun, G.; Dubayah, R.; Ranson, K.J. The Uncertainty of Plot-Scale Forest Height Estimates from Complementary Spaceborne Observations in the Taiga-Tundra Ecotone. Remote Sens. 2014, 6, 10070–10088. [Google Scholar] [CrossRef]
- Peterson, B.; Nelson, K.J. Mapping Forest Height in Alaska Using GLAS, Landsat Composites, and Airborne LiDAR. Remote Sens. 2014, 6, 12409–12426. [Google Scholar] [CrossRef]
- Lefsky, M.A. A global forest canopy height map from the moderate resolution imaging spectroradiometer and the geoscience laser altimeter system. Geophys. Res. Lett. 2010, 37, L15401. [Google Scholar] [CrossRef]
- Houghton, R.A.; Hall, F.; Goetz, S.J. Importance of biomass in the global carbon cycle. J. Geophys. Res. 2009, 114, G00E0. [Google Scholar] [CrossRef]
- Hall, F.G.; Bergen, K.; Blair, J.B.; Dubayah, R.; Houghton, R.; Hurtt, G.; Kellndorfer, J.; Lefsky, M.; Ranson, J.; Saatchi, S.; et al. Characterizing 3D vegetation structure from space: Mission requirements. Remote Sens. Environ. 2011, 115, 2753–2775. [Google Scholar] [CrossRef]
- Carabajal, C.C.; Harding, D.J. SRTM C-band and ICESat laser altimetry elevation comparisons as a function of tree cover and relief. Photogram. Eng. Remote Sens. 2006, 72, 287–298. [Google Scholar] [CrossRef]
- Fayad, N.; Baghdadi, J.-S.; Bailly, N.; Barbier, V.; Gond, M.; Hajj, E.L.; Fabre, F.; Bourgine, B. Canopy Height Estimation in French Guiana with LiDAR ICESat/GLAS Data Using Principal Component Analysis and Random Forest Regressions. Remote Sens. 2014, 6, 11883–11914. [Google Scholar] [CrossRef]
- Harding, D.J.; Carabajal, C.C. ICESat waveform measurements of within-footprint topographic relief and vegetation vertical structure. Geophys. Res. Lett. 2005, 32, L21S10. [Google Scholar] [CrossRef]
- Chen, Q. Retrieving vegetation height of forests and woodlands over mountainous areas in the Pacific Coast region using satellite laser altimetry. Remote Sens. Environ. 2010, 114, 1610–1627. [Google Scholar] [CrossRef]
- Delor, C.; Lahondère, D.; Egal, E.; Marteau, P. Carte Géologique de la France à 1/500 000. Département de la Guyan, 2nd ed.; BRGM, Service Géologique National: Orléans, France, 2001. [Google Scholar]
- Gond, V.; Freycon, V.; Molino, J.-F.; Brunaux, O.; Ingrassia, F.; Joubert, P.; Pekel, J.-F.; Prévost, M.-F. Broad-scale spatial pattern of forest landscape types in the Guiana Shield. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 357–367. [Google Scholar] [CrossRef]
- Freitas, S.R.; Mello, M.C.; Cruz, C.B. Relationships between forest structure and vegetationindices in Atlantic Rainforest. For. Ecol. Manag. 2005, 218, 353–362. [Google Scholar] [CrossRef]
- Pascual, C.; Garcia-Abril, A.; Cohen, W.; Martin-Fernandez, S. Relationship between LiDAR-derived forest canopy height and Landsat images. Int. J. Remote Sens. 2010, 31, 1261–1280. [Google Scholar] [CrossRef]
- Bourgine, B.; Baghdadi, N. Assessment of C-band SRTM DEM in a dense equatorial forest zone. C. R. Geosci. 2005, 337, 1225–1234. [Google Scholar] [CrossRef]
- Givnish, T.; Wong, S.; Stuart-Williams, H.; Holloway-Phillips, M.; Farquhar, G. Determinants of maximum tree height in Eucalyptus species along a rainfall gradient in Victoria, Australia. Ecology 2014, 95, 2991–3007. [Google Scholar] [CrossRef]
- Baccini, A.; Laporte, N.; Goetz, S.J.; Sun, M.; Dong, H. A first map of tropical Africa’s above-ground biomass derived from satellite imagery. Environ. Res. Lett. 2008, 3, 049001. [Google Scholar] [CrossRef]
- Powell, S.L.; Cohen, W.B.; Healy, S.P.; Kennedy, R.E.; Moisen, G.G.; Pierce, K.B.; Ohmann, J.L. Quantification of live aboveground forest biomass dynamics with Landsat time-series and field inventory data: A comparison of empirical modeling approaches. Remote Sens. Environ. 2010, 114, 1053–1068. [Google Scholar] [CrossRef]
- Hengl, T.; Heuvelink, G.B.; Stein, A. A generic framework for spatial prediction of soil variables based on regression-kriging. Geoderma 2004, 120, 75–93. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Ota, T.; Ahmed, O.; Franklin, S.; Wulder, M.; Kajisa, T.; Mizoue, N.; Yoshida, S.; Takao, G.; Hirata, Y.; Furuya, N.; et al. Estimation of Airborne Lidar-Derived Tropical Forest Canopy. Remote Sens. 2014, 6, 10750–10772. [Google Scholar] [CrossRef]
- Baghdadi, N.; le Maire, G.; Osé, K.; Nouvellon, Y.; Mehrez, Z.; Lemos, C.; Hakamada, R. Evaluation of ALOS/PALSAR L-band data for the estimation of Eucalyptus plantations aboveground biomass in Brazil. IEEE JSTARS 2014, 8, 3802–3811. [Google Scholar] [CrossRef]
- Genuer, R.; Poggi, J.-M.; Tuleau-Malot, C. Variable selection using Random Forests. Pattern Recognit. Lett. 2010, 31, 2225–2236. [Google Scholar] [CrossRef]
- Sun, W.; Minasny, B.; McBratney, A. Analysis and prediction of soil properties using local regression-kriging. Geoderma 2012, 171, 16–23. [Google Scholar] [CrossRef]
- Odeh, I.O.A.; McBratney, A.B.; Chittleborough, D.J. Further results on prediction of soil properties from terrain attributes: Heterotopic cokriging and regression-kriging. Geoderma 1995, 67, 215–226. [Google Scholar] [CrossRef]
- Goovaerts, P. Geostatistics for Natural Resources Evaluation; Oxford University Press: New York, NY, USA, 1997. [Google Scholar]


| Short Name | Full Name | Source | Resolution |
|---|---|---|---|
| MIN_EVI | Minimum value of EVI time series data | MODIS | 250 m |
| MEAN_EVI | Mean value of EVI time series data | ||
| MAX_EVI | Maximum value of EVI time series data | ||
| PC1 | 1st principal component of EVI time series data | ||
| PC2 | 2nd principal component of EVI time series data | ||
| PC3 | 3rd principal component of EVI time series data | ||
| Slope | Terrain slope in 3 × 3 cells | SRTM | 90 m |
| Roughness | Terrain roughness in 3 × 3 cells | ||
| ln_drain | Log of drainage surface | ||
| GEOL | Geological map (no units, arbitrary shapes) | [27] | Vector |
| LTs | Forest landscape type (no units, arbitrary shapes) | [28] | 1 km (Vector) |
| Rain | mean value of rainfall | TRMM | 8 km |
| Using RF Only | Using Regression Kriging | |||||
|---|---|---|---|---|---|---|
| Dataset | Bias (m) | RMSE (m) | R² | Bias (m) | RMSE (m) | R² |
| GLAS | 0.14 | 6.5 | 0.55 | 0.09 | 4.2 | 0.75 |
| LD_cal | 0.15 | 5.8 | 0.62 | 0.12 | 1.8 | 0.94 |
| LD_5 | 0.06 | 5.7 | 0.65 | 0.12 | 1.8 | 0.94 |
| LD_20 | 0.09 | 6.0 | 0.63 | 0.14 | 3.3 | 0.75 |
| LD_30 | 0.14 | 6.2 | 0.60 | 0.05 | 3.9 | 0.75 |
| LD_40 | 0.11 | 6.1 | 0.62 | 0.09 | 3.9 | 0.74 |
| LD_50 | 0.07 | 6.2 | 0.60 | 0.13 | 4.8 | 0.66 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fayad, I.; Baghdadi, N.; Bailly, J.-S.; Barbier, N.; Gond, V.; Hérault, B.; El Hajj, M.; Fabre, F.; Perrin, J. Regional Scale Rain-Forest Height Mapping Using Regression-Kriging of Spaceborne and Airborne LiDAR Data: Application on French Guiana. Remote Sens. 2016, 8, 240. https://doi.org/10.3390/rs8030240
Fayad I, Baghdadi N, Bailly J-S, Barbier N, Gond V, Hérault B, El Hajj M, Fabre F, Perrin J. Regional Scale Rain-Forest Height Mapping Using Regression-Kriging of Spaceborne and Airborne LiDAR Data: Application on French Guiana. Remote Sensing. 2016; 8(3):240. https://doi.org/10.3390/rs8030240
Chicago/Turabian StyleFayad, Ibrahim, Nicolas Baghdadi, Jean-Stéphane Bailly, Nicolas Barbier, Valéry Gond, Bruno Hérault, Mahmoud El Hajj, Frédéric Fabre, and José Perrin. 2016. "Regional Scale Rain-Forest Height Mapping Using Regression-Kriging of Spaceborne and Airborne LiDAR Data: Application on French Guiana" Remote Sensing 8, no. 3: 240. https://doi.org/10.3390/rs8030240
APA StyleFayad, I., Baghdadi, N., Bailly, J.-S., Barbier, N., Gond, V., Hérault, B., El Hajj, M., Fabre, F., & Perrin, J. (2016). Regional Scale Rain-Forest Height Mapping Using Regression-Kriging of Spaceborne and Airborne LiDAR Data: Application on French Guiana. Remote Sensing, 8(3), 240. https://doi.org/10.3390/rs8030240