Next Article in Journal
Mapping Complex Urban Land Cover from Spaceborne Imagery: The Influence of Spatial Resolution, Spectral Band Set and Classification Approach
Next Article in Special Issue
Seasonal Variation in the NDVI–Species Richness Relationship in a Prairie Grassland Experiment (Cedar Creek)
Previous Article in Journal
Assessment of S-NPP VIIRS On-Orbit Radiometric Calibration and Performance
Previous Article in Special Issue
Using Remotely-Sensed Land Cover and Distribution Modeling to Estimate Tree Species Migration in the Pacific Northwest Region of North America
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 8
Issue 2
10.3390/rs8020087
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Organismic-Scale Remote Sensing of Canopy Foliar Traits in Lowland Tropical Forests

by
K. Dana Chadwick
1,2,* and
Gregory P. Asner
1
1
Department of Global Ecology, Carnegie Institution for Science, Stanford, CA 94305, USA
2
Department of Earth System Science, Stanford University, Stanford, CA 94305, USA
*
Author to whom correspondence should be addressed.
Remote Sens. 2016, 8(2), 87; https://doi.org/10.3390/rs8020087
Submission received: 5 December 2015 / Revised: 9 January 2016 / Accepted: 14 January 2016 / Published: 23 January 2016
(This article belongs to the Special Issue Remote Sensing of Biodiversity)
Browse Figures
Versions Notes

Abstract

:
Airborne high fidelity imaging spectroscopy (HiFIS) holds great promise for bridging the gap between field studies of functional diversity, which are spatially limited, and satellite detection of ecosystem properties, which lacks resolution to understand within landscape dynamics. We use Carnegie Airborne Observatory HiFIS data combined with field collected foliar trait data to develop quantitative prediction models of foliar traits at the tree-crown level across over 1000 ha of humid tropical forest. We predicted foliar leaf mass per area (LMA) as well as foliar concentrations of nitrogen, phosphorus, calcium, magnesium and potassium for canopy emergent trees (R2: 0.45–0.67, relative RMSE: 11%–14%). Correlations between remotely sensed model coefficients for these foliar traits are similar to those found in laboratory studies, suggesting that the detection of these mineral nutrients is possible through their biochemical stoichiometry. Maps derived from HiFIS provide quantitative foliar trait information across a tropical forest landscape at fine spatial resolution, and along environmental gradients. Multi-nutrient maps implemented at the fine organismic scale will subsequently provide new insight to the functional biogeography and biological diversity of tropical forest ecosystems.

1. Introduction

Determining the spatial distributions and assemblages of plant functional traits is a key goal of functional biogeography and is necessary to understand current, and predict future, ecosystem functioning [1]. The need for spatially explicit understanding of functional trait distributions is especially pressing in humid tropical rainforests. These ecosystems are notoriously difficult to study because of their high biodiversity, low accessibility, and large spatial extent. However, it is essential that we understand their functioning because they provide a wealth of global ecosystem services, including sequestering and storing carbon as well as playing an integral role in both hydrological and biogeochemical cycles [2,3]. Establishing distributions of functional diversity in lowland tropical forests will provide insight into their current functioning and an ability to consider how they might respond in the face of changing climate.
To develop this spatially-explicit, regional understanding of functional diversity and ecosystem processes, we need to overcome the challenges of measuring functional traits at fine spatial resolutions over landscape scales [4]. High Fidelity Imaging Spectroscopy (HiFIS) is an emerging technology that utilizes high spectral resolution remotely sensed reflectance data to estimate foliar or canopy characteristics [5,6]. Utilizing reflectance data from the visible to shortwave infrared (400–2500 nm), HiFIS has been used to successfully predict foliar traits from tropical trees at the leaf scale [7,8,9,10]. In addition, it has recently been demonstrated that, in the tropics, community-scale canopy functional traits can be estimated at the hectare level using airborne HiFIS [11,12]. While this is an impressive step forward, hectare-scale resolution may be too coarse to detect changes in foliar traits across local topo-edaphic gradients. In this study we seek to develop statistical models to quantitatively predict foliar traits at the scale of individual canopies, which would greatly improve our ability to utilize imaging spectroscopy data in fine scale, high resolution studies of ecosystem function.
We focus on several foliar traits that support a variety of canopy functional processes; leaf mass per area (LMA), nitrogen (N), phosphorus (P), calcium (Ca), potassium (K) and magnesium (Mg). Leaf mass per area (LMA) is correlated with increased leaf longevity [13,14]. N and P are utilized in carbon capture and storage, information transfer, protein synthesis and cell growth. Ca is used in cell wall development and rigidity, in addition to signal transduction and enzyme activation [15,16]. K and Mg are involved with cellular metabolism and signaling, and Mg is a component of the chlorophyll molecule. P, Ca, Mg, and K are rock-derived nutrients (RDN), which lack a gaseous phase to their biogeochemical cycles, making them of special interest in humid tropical ecosystems. On old substrates with low fertility soils in the humid tropics, RDN have been found to be in low supply relative to biologic demand and can act to limit ecosystem processes [17,18,19,20,21]. Foliar concentrations of RDN, as well as the ratios between N and RDN can be used to assess what nutrients are in low supply relative to their ecosystem demand [22,23]. The ability to determine these characteristics across the landscape would allow us to map the canopy response to varying substrate fertility conditions. This spatially-explicit understanding of RDN limitation to plant growth could inform our understanding of the potential for forests to absorb atmospheric CO2 via net primary production in the face of increasing greenhouse gas concentrations.
Here we utilize the Carnegie Airborne Observatory—Airborne Taxonomic Mapping System (CAO-AToMS) to ask the following questions: (i) Can we predict canopy LMA and foliar RDN at the organismic (e.g., tree-crown) scale using airborne reflectance spectra from the visible through the shortwave infrared? (ii) How do correlations between the remote sensing models for different foliar traits relate to the correlations between traits found in laboratory-assayed samples?

2. Materials and Methods

2.1. Study Area

This study was conducted in the southern lowland Peruvian Amazon at the Los Amigos Conservation Concession (LACC), located at the confluence of the Rio Madre de Dios and the Rio Los Amigos (Figure 1). The study area is a broadleaf tropical forest, with a mean annual precipitation of 2650 mm [24] and a mean annual temperature of 25.5 °C [25]. The landscape at the site is composed of floodplain forests in the south and east that exist on young substrates and receive nutrient inputs from modern rivers; and terra firme forests in the northwest that are older, depleted in rock-derived nutrients, and elevated above the modern floodplain [12,24].

2.2. Foliar Sampling and Analysis

Foliar samples were collected from 254 canopy trees using the Spectranomics methodology [26], which has been extensively documented [27,28,29], the relevant portions of which are briefly described here. Foliar samples were collected at LACC in August 2013 from mature, sun-lit leaves, then sealed in polyethylene bags, and stored in coolers for transport to the field station for processing within 3 h. A global positioning system (GPS) point was collected for each tree sampled and the canopy was identified in the HiFIS imagery (Figure 1). For LMA determination of each tree, a random selection of fresh, fully expanded leaves was scanned to determine area and weighed in the field. These leaves were dried at 70 °C and reweighed to determine dry mass per area, as well as water content. Additional leaves were selected for drying at 70 °C and were transported in this stable state to the Carnegie Institution for analysis. RDN concentrations were determined by microwave digestion of dried sample in nitric acid solution and subsequent analysis on an inductively coupled plasma optical emission spectrometer (ICP-OES; Thermo Scientific ICAP 6300 Duo View Spectrometer) in the environmental measurements facility at Stanford University [30]. Total N concentration was determined with a combustion autoanalyzer (Costec Analytical Technologies Inc. Valencia, CA, USA).
Figure 1. Map of the sampling area within the Los Amigos Conservation Concession (LACC) study region in the lowland Peruvian Amazon basin. The crowns sampled on landscape are shown in red, but they are not to scale for visualization purposes. Inset shows the location of study area in Peru.
Figure 1. Map of the sampling area within the Los Amigos Conservation Concession (LACC) study region in the lowland Peruvian Amazon basin. The crowns sampled on landscape are shown in red, but they are not to scale for visualization purposes. Inset shows the location of study area in Peru.

2.3. Remotely Sensed Data

CAO-AToMS completed two overflights of LACC in August-September 2013, in concert with the field measurement effort, collecting both Visible-to-Shortwave Infrared (VSWIR) imaging spectrometer and light detection and ranging (LiDAR) data. The CAO-AToMS has been well documented elsewhere [12,31]; a summary of the relevant components is briefly provided here. The VSWIR imaging spectrometer measures spectral radiance in 427 channels across a wavelength range of 380 nm to 2510 nm in 5 nm increments with nominally 6 nm spectral response function (full-width at half-maximum) [31]. Additional detector rows are used to monitor the instrument dark signal levels. One overflight of LACC was conducted at 2000 m a.g.l., yielding a 2 m pixel size (low resolution), and the second was conducted at 1000 m a.g.l., yielding a 1 m pixel size (high resolution).
In order to mask VSWIR data that is not suitable for foliar chemical detection due to intra-crown shadowing, canopy gaps, or regions of water and exposed soil [32], the VSWIR data were ortho-geolocated using the LiDAR data. To achieve this, the three dimensional geolocations of the laser returns were determined by combining the laser ranges with the embedded high resolution GPS-Inertial Measurement Unit (GPS-IMU), producing a “cloud” of LiDAR data. Lowest elevation last returns were used to generate a raster digital terrain model (DTM) of the ground surface elevation across the study area. A raster digital surface model (DSM) was generated based on the interpolation of all LiDAR first-return points. A raster digital canopy model (DCM), which quantifies vegetation height, was generated by computing the vertical distance between the DTM and DSM.
The VSWIR data were converted to radiance (W·sr−1·m−2) with a flat-field correction, laboratory collected data informed radiometric calibration coefficients and spectral calibration. The VSWIR data were co-located to the LiDAR, and a camera model generated a model of image geometry and data on solar and viewing geometry for each VSWIR pixel. The VSWIR imagery was atmospherically corrected using the ACORN-5 model with these inputs (Imspec LLC, Glendale, CA, USA). We iteratively ran the ACORN-5 model with different visibilities until the reflectance at 420 nm (which is relatively constant for vegetated pixels) was 1%, to optimize the aerosol correction. Finally, the VSWIR reflectance imagery was orthorectified to the LiDAR DCM. The mask of shaded pixels and vegetation height was developed using a ray tracing model that utilizes the solar and viewing geometry data, combined with the DCM, to determine pixels that were shaded during the time of overflight; as well as any regions where the vegetation height was less than 2 m [31,32,33]. A mask was also applied to remove any pixels with an NDVI < 0.8 to remove leafless canopies and areas with low leaf area. Masked pixels were excluded from all further analysis, including model development and application [11,32]. VSWIR reflectance values were trimmed at the upper and lower bounds of detection and in regions dominated by atmospheric water vapor, the resulting input bands spanned the wavelengths 440–1330 nm, 1480–1770 nm, and 2040–2440 nm. Lastly, all spectra were brightness normalized to improve their consistency and account for spectral variation associated with structure and viewing angle, which may not have been captured in the preceding processing steps. Brightness normalization his has been found to improve the quality of trait prediction models under scenarios that mirror natural viewing conditions in tropical forests, including within-crown shading that may not be identified as shaded in the LiDAR derived shade mask, variations in LAI, and varying viewing angle and sun angle that can change during the course of collection or between days [9]. These processing steps have allowed us to control for a variety of structural characteristics which would have the potential to interfere with detection and prediction of foliar traits and, in a study of scaling from leaf to canopy scale it was shown that canopy foliar traits are detectable despite any residual structural variability after these filters have been applied [32].

2.4. Model Development

Crown delineations from the field were used to extract HiFIS pixels from each canopy sampled for foliar traits. Tree crowns were selected for inclusion in the model calibration process if they had >15 unmasked pixels from the 2 m resolution VSWIR dataset, this yielded 96 trees to be included in the model development. Figure 2 shows the reflectance and brightness normalized spectra for the crowns selected for model development. The foliar trait values were not transformed using natural logarithm or other transformation prior to model development in the version of the models presented in the primary text, though the analysis was also done using the natural log transformed trait values; those results are presented in Appendix A.
Partial least squares regression (PLSR) is a method of linear regression, frequently used in chemometrics, that is appropriate for use when model input variables have multicollinearity and the number of input variables may exceed the number of observations [32]. For each foliar trait, a PLSR model was fit by first selecting 70% of the model development crowns (n = 66). For these individuals, five pixels were selected from their crowns from each of the two VSWIR datasets. These data were used to build a PLSR model for each foliar trait with parameters selected through a jackknifing backward selection procedure based on variable significance using the autopls package in R [35,36]. Models were validated using 10-fold cross-validation, the statistics from this model testing will be referred to as model validation. In addition, the model for each trait was tested against five pixels randomly selected from the 30% of model development crowns that were left entirely out of the model fitting using the autopls function, the statistics from this model assessment will be referred to as model testing. For each trait, this process of model development was iterated 1000 times. The runtime to generate these iterations ranged from 138 to 200 core-hours per foliar trait. The models that had the best performance in foliar trait prediction during model validation (validation R2 greater than the mean R2 for the 1000 iterations and validation RMSE less than the mean RMSE for the 1000 iterations) were averaged to generate the final model for application.
Figure 2. Range of spectra for canopies used in calibration of the partial least squares regression (PLSR) model: (a) the range of reflectance values before brightness normalization; (b) is the range of brightness normalized reflectance values.
Figure 2. Range of spectra for canopies used in calibration of the partial least squares regression (PLSR) model: (a) the range of reflectance values before brightness normalization; (b) is the range of brightness normalized reflectance values.

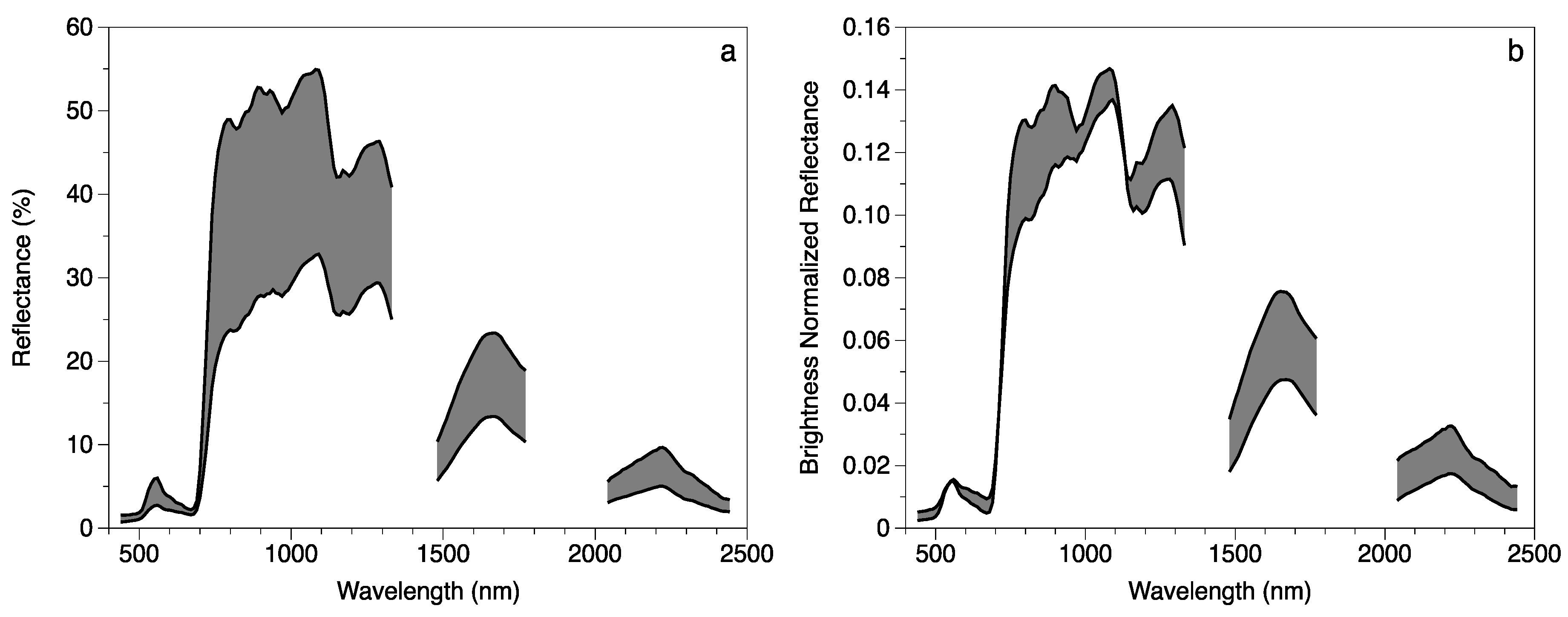
2.5. Model Application and Assessment

The final model for each foliar trait was applied across the full extent of the masked, 2 m resolution VSWIR image. This provided us with a map of predicted values for each foliar trait across the full study landscape. From these images, we extracted all pixels for each crown that was sampled in the field and had at least 9 unmasked pixels in the image with predicted trait values. The trait values for a crown were averaged to determine the crown-level predicted trait value. This yielded 185 crowns; summary statistics for the foliar traits of these crowns are provided in Table 1. The remotely sensed values were averaged for all pixels in the canopy, and the canopy-level predictions were then regressed against the laboratory determined foliar trait for that canopy [37]. We analyzed the slope, intercept, and statistics for these regressions to assess model quality.
Table 1. Summary statistics of foliar traits measured from laboratory analyses for canopies included in the model calibration and validation (n = 185).
Table 1. Summary statistics of foliar traits measured from laboratory analyses for canopies included in the model calibration and validation (n = 185).
Foliar TraitMeanStd. Dev.
LMA (g·m−2)104.426.6
N (%)2.380.68
P (%)0.120.05
Ca (%)0.910.83
K (%)0.640.31
Mg (%)0.220.13
Finally, we considered the relationship between the prediction coefficients of different foliar traits. For each pair of foliar traits, we compared the PLSR coefficients of their respective models at each wavelength to determine the covariance between the models. We also performed a pairwise comparison of the laboratory-determined foliar traits across all foliar samples to determine the correlation between foliar traits due to underlying relationships in foliar biochemistry (for example, the inverse relationship between LMA and N content which is described as part of the leaf economic spectrum [14]). We then assessed if the correlations from the pairwise comparisons of the model coefficients were similar to those found via the comparison of the correlation between laboratory-analyzed foliar traits. Because we are utilizing spectra spanning the visible to the shortwave infrared range, we are detecting elemental concentration of mineral nutrients by proxy through other biochemical constituents of canopy foliage rather than detecting atomic concentrations directly. Therefore, we would expect foliar nutrient concentrations that are correlated within leaves would also have correlated regression coefficients, because the remote detection of these concentrations is achieved through the constellation of biochemicals that are correlated with these nutrients and detectable in the VSWIR spectral range by HiFIS.

3. Results

3.1. Model Fitting and Selection

The mean summary statistics for the 1000 iterations of PLSR model fits for each foliar trait are provided in Table 2. Ca and Mg have the highest average R2 values in the validation and testing sets, followed by N and P, and then K and LMA. However, the normalized RMSE values are relatively consistent across all foliar traits. In addition, the models for all traits had a mean of nine latent vectors.
Table 2. Average statistics from the 1000 models generated for each foliar trait. Model calibration statistics (Cal) are for the pixels that were included in the calibration set of the cross validation for a given iteration. Model validation statistics (Val) are for the pixels withheld for cross validation for that iteration. Model testing statistics (Test) are for the external test against pixels from crowns used at no stage in the calibration or validation steps. Normalized RMSE (nRMSE) is calculated as the RMSE divided by the range of that foliar trait.
Table 2. Average statistics from the 1000 models generated for each foliar trait. Model calibration statistics (Cal) are for the pixels that were included in the calibration set of the cross validation for a given iteration. Model validation statistics (Val) are for the pixels withheld for cross validation for that iteration. Model testing statistics (Test) are for the external test against pixels from crowns used at no stage in the calibration or validation steps. Normalized RMSE (nRMSE) is calculated as the RMSE divided by the range of that foliar trait.
Foliar TraitR2Cal RMSEnRMSER2Val RMSEnRMSELV *R2Test RMSEnRMSE
LMA0.4618.690.120.4319.250.1290.2614.710.10
N0.560.450.120.530.470.1390.360.380.10
P0.530.030.140.500.040.1490.360.030.11
Ca0.660.520.120.640.530.1390.560.470.11
K0.510.200.110.480.210.1190.270.170.09
Mg0.690.060.080.670.060.0890.570.060.08
* Latent Vector.
The models for each trait that had greater than the mean R2 and less than the mean RMSE during model validation were selected for aggregation into the final model. This resulted in the final model having the averaged coefficients of 363, 313, 327, 296, 326, and 335 models for LMA, N, P, Ca, K, and Mg, respectively. The coefficients for the final, aggregated PLSR model for each foliar trait are presented in Figure 3. The models that were arrived at for the untransformed foliar traits (Figure 3), show almost identical trends in their coefficients to those that were developed for the natural log transformed traits (Figure A1), the primary difference being the magnitude of the coefficient values. For the base cation nutrients (Ca, Mg, and K), as well as N and LMA, the shortwave infrared region of the reflectance spectrum, especially the portion between 2040 and 2440 nm, provides significant information for the prediction of these traits. This is an important result because while many imaging spectrometers do not include the shortwave infrared in their spectral range, this region provides significant information about foliar characteristics.
Figure 3. Plots of the PLSR coefficients for each foliar trait being considered. Shaded regions indicate the 95% confidence interval of the mean coefficient value for the aggregated model.
Figure 3. Plots of the PLSR coefficients for each foliar trait being considered. Shaded regions indicate the 95% confidence interval of the mean coefficient value for the aggregated model.

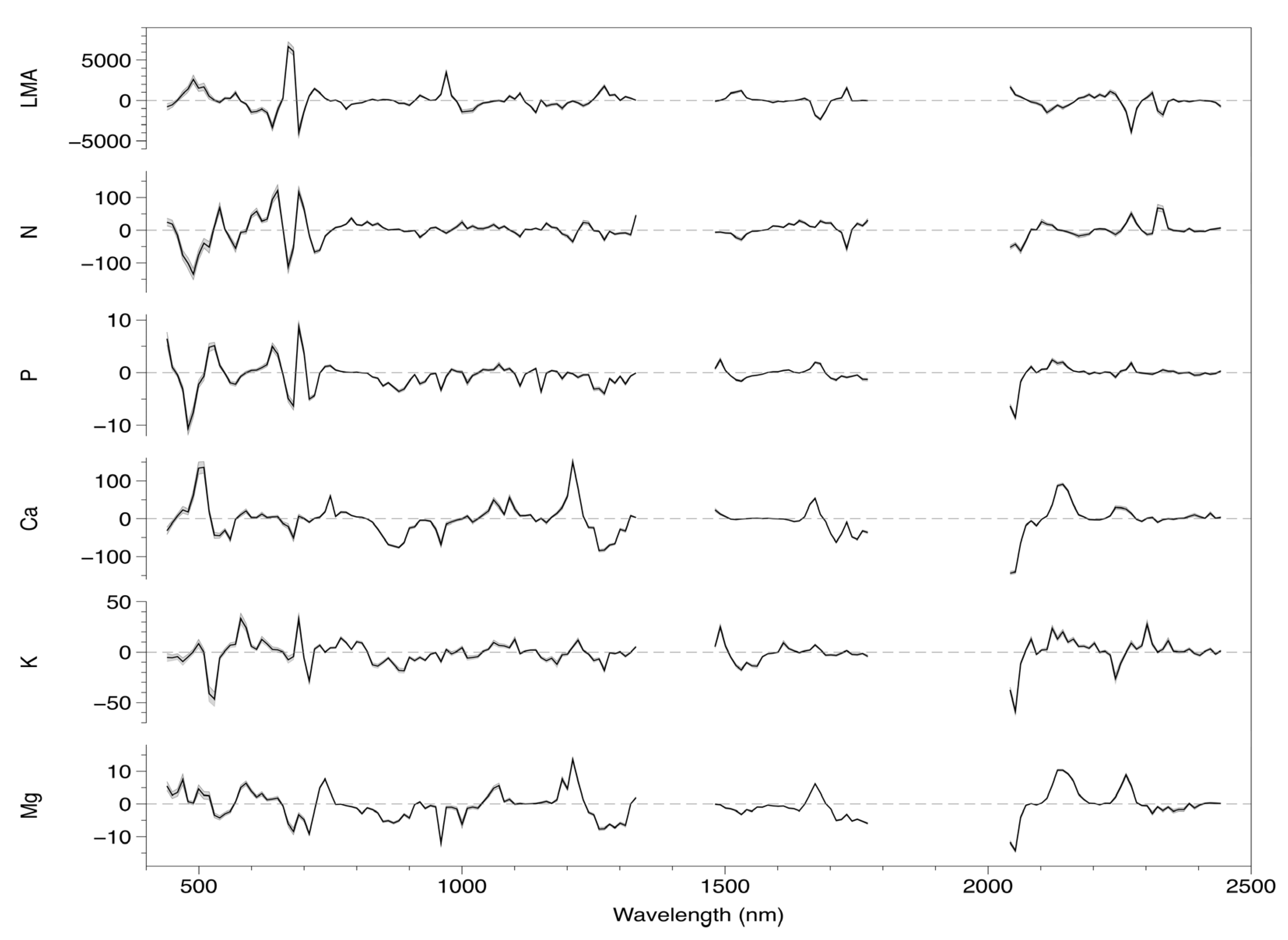
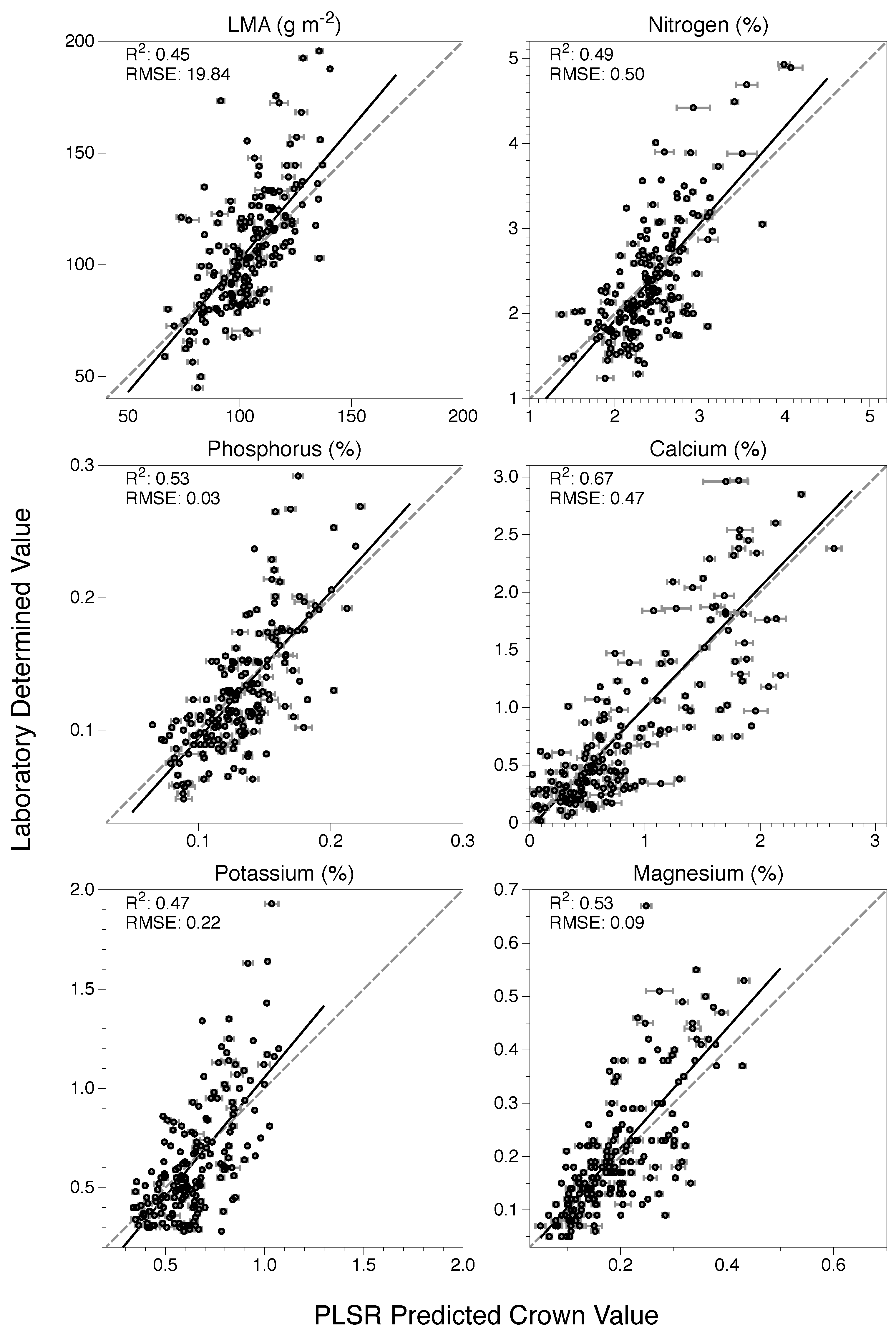
3.2. Model Application and Evaluation

The aggregated models were then applied to the HiFIS data for the full extent of the study area (Figure 4). The 2-m VSWIR data for the study area is comprised of imagery from four flight lines, but these maps do not display visual artifacts that might be expected with varying viewing angles throughout the mosaicked image. In addition, these maps show tradeoffs in foliar traits that are consistent with known relationships, i.e., areas with low predicted LMA tend to have higher predicted N.
The crown level average predictions of each foliar trait were compared against the value of the trait determined from field sampling and laboratory analysis (Figure 5, Table 2 and Table 3). The regressions of the observed versus the predicted values for all traits, except K content, have intercepts that are not significantly different from zero and slopes that are not significantly different from one (p > 0.05; Table 3). This indicates that, with the exception of K, these models have good consistency (slope ~ 1) and are unbiased (intercept ~ 0) [37]. In addition, all of these models explain over 45% of the variance in foliar traits at the crown level (Figure 5, Table 3).
Table 3. The value and 95% confidence interval (CI) for the intercepts and slopes of the regressions that are displayed in Figure 5. If, for the intercept, the CI encompasses 0, then the regression is not statistically significantly biased (p > 0.05, italicized). For the slope, if the CI encompasses 1, then the regression slope does not significantly differ from that of the 1:1 line (p > 0.05, italicized). R2, RMSE, and the RMSE normalized to the range of values are reported.
Table 3. The value and 95% confidence interval (CI) for the intercepts and slopes of the regressions that are displayed in Figure 5. If, for the intercept, the CI encompasses 0, then the regression is not statistically significantly biased (p > 0.05, italicized). For the slope, if the CI encompasses 1, then the regression slope does not significantly differ from that of the 1:1 line (p > 0.05, italicized). R2, RMSE, and the RMSE normalized to the range of values are reported.
TraitIntercept (95% CI)Slope (95% CI)R2RMSEnRMSE
LMA−16.12 (−36.2, 3.97)1.18 (0.99, 1.37)0.4519.80.13
N−0.35 (−0.77, 0.06)1.14 (0.97, 1.31)0.490.500.14
P−0.02 (−0.04, 0.003)1.11 (0.96, 1.26)0.530.030.12
Ca−0.05 (−0.16, 0.07)1.05 (0.94, 1.15)0.670.470.11
K−0.14 (−0.27, −0.02)1.2 (1.02, 1.39)0.470.220.12
Mg−0.01 (−0.04, 0.02)1.12 (0.97, 1.28)0.530.090.13
Figure 4. Maps of foliar trait prediction equations applied to the study area. The foliar traits displayed are specified in the top left of each map. The units of the predicted chemical values are as follows: Leaf mass per area (LMA): g·m−2; N, P, Ca, K, and Mg: %. The color scales are linear and do not indicate the full range of predicted values, values greater than the high value will be displayed in yellow, below the low value will be displayed in black. Areas specified by i–iv are discussed in the text.
Figure 4. Maps of foliar trait prediction equations applied to the study area. The foliar traits displayed are specified in the top left of each map. The units of the predicted chemical values are as follows: Leaf mass per area (LMA): g·m−2; N, P, Ca, K, and Mg: %. The color scales are linear and do not indicate the full range of predicted values, values greater than the high value will be displayed in yellow, below the low value will be displayed in black. Areas specified by i–iv are discussed in the text.
Figure 5. Scatter plots of the crown averaged predicted foliar traits versus the foliar trait data from field sampling and laboratory analysis. Error bars show the standard error about the mean trait value when aggregating pixels to the crown level. The dashed gray line is 1:1; the liner regression fit of observed versus predicted is shown in black (n = 185).
Figure 5. Scatter plots of the crown averaged predicted foliar traits versus the foliar trait data from field sampling and laboratory analysis. Error bars show the standard error about the mean trait value when aggregating pixels to the crown level. The dashed gray line is 1:1; the liner regression fit of observed versus predicted is shown in black (n = 185).

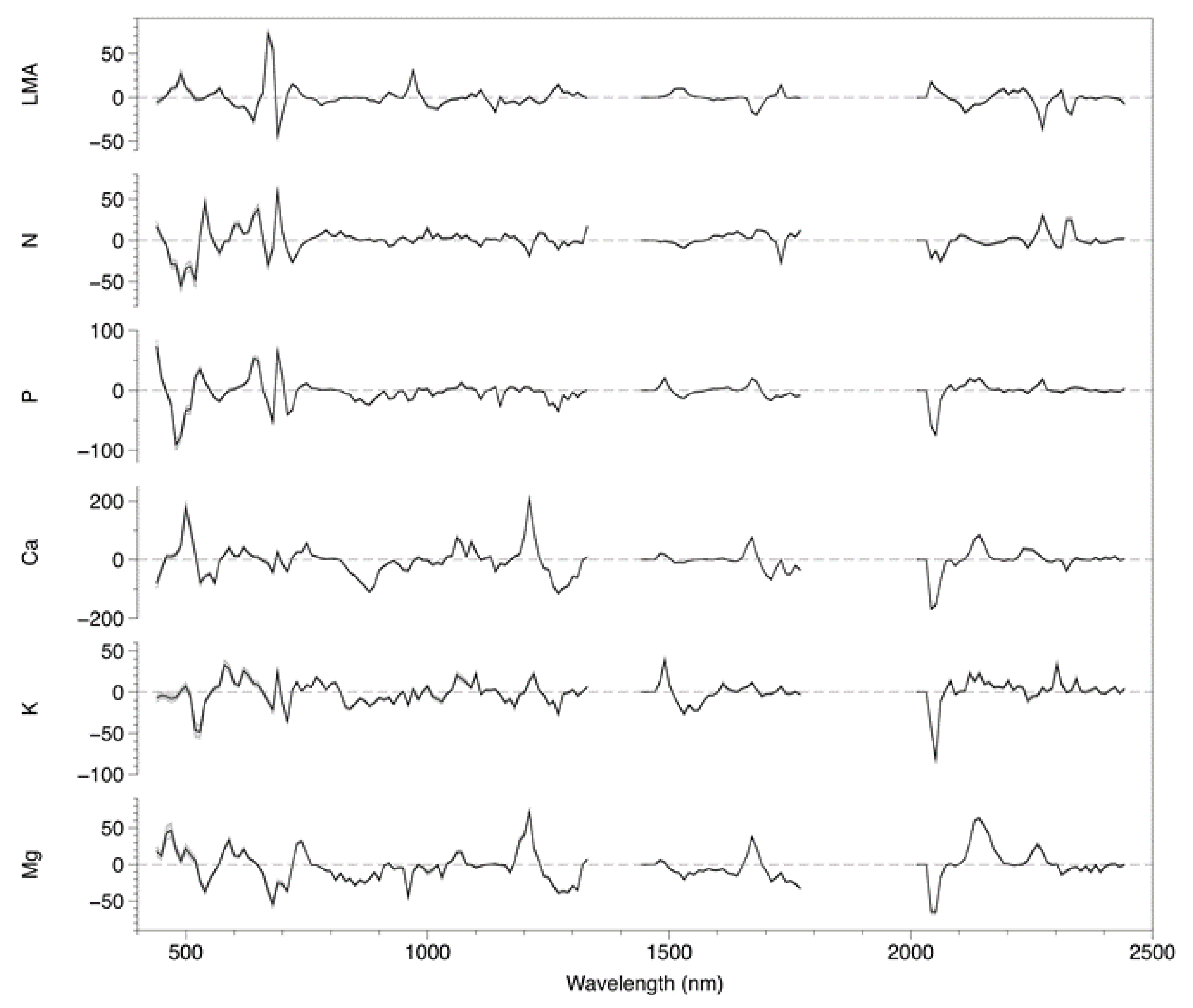
3.3. Coefficient and Trait Correlations

Figure 6a shows the scatter plots of the coefficient value at each wavelength for the aggregate model of one trait against the coefficient value at the same wavelength for the aggregate model of the opposing trait. These scatterplots indicate the level to which the model for one trait is associated with the same spectral regions and features as another trait. We find that 11 of the pairwise comparisons yield correlations of R < |0.5| while four; LMA:N, LMA:P, N:P, and Ca:Mg; have R > |0.5|.
Figure 6. (a) Scatterplots of PLSR coefficients values by wavelength for each foliar trait plotted against one another to assess the correlation of the coefficients between different models. Coefficient values are unitless; (b) scatterplots of foliar chemical values for all trees sampled at CICRA to assess the presence of correlations between the foliar traits measured (LMA is in g·m−2, all nutrient values in %). Correlation values are displayed on each scatterplot in panels a and b; (c) shows the R value for the relationship between pairwise foliar chemical traits against the R value for the relationship between pairwise PLSR regression coefficients for predicting foliar traits (some of the locations have been shifted slightly for visibility; R2 is calculated on correlation values displayed in (a,b)).
Figure 6. (a) Scatterplots of PLSR coefficients values by wavelength for each foliar trait plotted against one another to assess the correlation of the coefficients between different models. Coefficient values are unitless; (b) scatterplots of foliar chemical values for all trees sampled at CICRA to assess the presence of correlations between the foliar traits measured (LMA is in g·m−2, all nutrient values in %). Correlation values are displayed on each scatterplot in panels a and b; (c) shows the R value for the relationship between pairwise foliar chemical traits against the R value for the relationship between pairwise PLSR regression coefficients for predicting foliar traits (some of the locations have been shifted slightly for visibility; R2 is calculated on correlation values displayed in (a,b)).
Figure 6b shows the scatterplots of the relationships between traits that are present in the crowns sampled at LACC. These also have 11 comparisons with R < |0.5| and four; LMA:N, LMA:P, Ca:Mg, and K:Mg; with R > |0.5|. In all cases, when comparing the correlation values of a pairwise comparison of the model coefficients for two traits, and the relationship of those traits found in the foliar samples, the sign of the correlation is the same (Figure 6c). The relationships between the correlation of the coefficients and the correlation of the foliar traits for a given pairwise comparison are quite consistent for all trait comparisons (Figure 6c). Regressing these against one another yields an R2 of 0.94.

4. Discussion

4.1. Mapped Canopy Traits

In addition to the good agreement between field-collected foliar data and the airborne HiFIS-predicted canopy traits (Figure 5), examining the maps of the predicted trait values across the landscape (Figure 4) allows us to assess if they conform to our understanding of trait distributions based on ecosystem processes. The leaf economic spectrum suggests that there is a tradeoff between LMA and mineral nutrient content, specifically N and P [14], where fast growing species have lower LMA and higher foliar nutrient content. In successional areas, we would therefore expect high N and P, and low LMA; this is what we observe in the predicted foliar traits in the locations indicated by (i) in Figure 4. These are areas where river meandering has caused point bar accretions of sediment and led to the development of successional ecosystems, which are composed of plants with fast growth strategies [38,39].
There are also areas of disturbance at LACC that have bamboo (Guadua angustifolia) and other grasses in the canopy (Figure 4 ii). The upper left region is an abandoned landing strip that has bamboo growth along the western side, and the bottom right is a series of bamboo patches that are likely to be the result of disturbance from selective logging or a mining camp in the area prior to 2000 [40]. These regions have high N, P and K concentrations, but low LMA, Ca and Mg trait values, which is consistent with foliar trait distributions found in bamboo. Samples of Guadua angustifolia collected from a different region and analyzed by the Spectranomics program in 2010 were found to have the following chemical values; LMA: 56 g·m−2, N: 3.4%, P: 0.17%, Ca: 0.37%, K: 1.55%, and Mg: 0.16%. This is encouraging because no samples of Guadua were used at any stage in the development of these models.
Within the study area there are two different landforms, which support different types of forest ecosystems. In the northwest of the study area (Figure 4 iii) there is a largely flat, old terrace formation that supports terra firme forest, and the south and east is a region of active floodplain. This is a subsection of the “CICRA” landscape that was considered by Asner et al. [12]. The terra firme soils at this site are highly depleted in RDN, especially Ca and Mg [41], and this is reflected in the strong gradient of low to high foliar concentrations of Ca and Mg when moving from floodplain (iii) to terra firme (iv) in Figure 4. There is a similar but less stark pattern of foliar P and K depletion in terra firme forests, and enrichment in the floodplain. These results are consistent with patterns found from foliar sampling within terrace and floodplain forests in this region [27,42], as well as hectare-scale estimation of community foliar trait composition at this site [12].

4.2. Foliar Trait and Canopy Reflectance Interrelationships

Utilizing airborne HiFIS to estimate the foliar elemental composition of canopies is an indirect measurement, it is the constellation of biochemicals and structural traits that are associated with a nutrient that allows us to detect it using VSWIR spectroscopy [6]. As a result, we would expect that correlation between model coefficients used to predict foliar traits would be similar to the correlation found between the foliar traits themselves resulting from the molecular biology of plants. This is what we see in Figure 6c, and supports the understanding that we are detecting spectral signatures related to biochemistry [43], and not simply structural aspects of the canopy [44].

4.3. Future Research Directions

The models developed here perform well for predicting this set of foliar traits at LACC. Future research will seek to validate these models at other study sites in the Peruvian Amazon to understand the applicability of these models across the region. In addition, the foliar trait maps that have been generated through this study can be used to analyze the diversity of foliar traits for all canopy emergent trees across topoedaphic gradients present in this study region. Patterns of foliar RDN concentrations in particular could inform our understanding of the geographic distribution of both functional and species diversity, as these have been found to be strongly controlled, and responsive to, soil RDN gradients in the Amazon basin [27,42,45]. This type of analysis would provide unprecedented insight into distributions of these traits at the landscape scale, and the ability to examine functional diversity at the level of individuals.

5. Conclusions

We have demonstrated that it is possible to quantitatively predict foliar traits at the scale of individual tree-crowns using airborne HiFIS in a highly diverse lowland tropical forest. The development of statistical models to quantitatively predict foliar RDN content in humid tropical landscapes at fine resolutions has long been a goal of imaging spectroscopy for ecological applications and greatly increases its utility for functional diversity and biogeochemical studies. The ability to predict foliar RDN content at this scale promises to be instrumental in assessing species and community responses to environmental gradients. Understanding patterns and drivers of functional diversity both contributes to our understanding of, and acts as a proxy for, biological diversity in these landscapes [46]. In fact, an understanding of biodiversity via diversity of functional traits is likely to have a greater utility to both understanding ecosystem services and making strategic conservation decisions. This work represents a significant step forward in the goal of understanding the functional diversity of humid tropical forests within and across landscapes.

Acknowledgments

We thank Roberta Martin, Christopher Anderson, Raul Tupayachi, Felipe Sinca, David Knapp, Philip Brodrick and the rest of the Carnegie Airborne Observatory team for assistance with data collection, processing and analysis. CAO data collection and processing, and this study, were funded by the John D. and Catherine T. MacArthur Foundation. K. D. Chadwick was supported by NASA Headquarters under the NASA Earth and Space Science Fellowship Program—Grant 15-EARTH14F-48. The Carnegie Airborne Observatory is made possible by the Avatar Alliance Foundation, John D. and Catherine T. MacArthur Foundation, Gordon and Betty Moore Foundation, Grantham Foundation for the Protection of the Environment, W. M. Keck Foundation, Margaret A. Cargill Foundation, Mary Anne Nyburg Baker and G. Leonard Baker Jr., and William R. Hearst III.

Author Contributions

K.D.C. and G.P.A. conceived and designed the experiments; K.D.C. performed the experiments; K.D.C. analyzed the data; G.P.A. contributed CAO imagery/crown locations/foliar chemical data/computing resources; K.D.C. wrote the paper.

Conflicts of Interest

The authors declare no conflict of interest. The funding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.

Abbreviations

The following abbreviations are used in this manuscript:
CAO-AToMS
Carnegie Airborne Observatory—Airborne Taxonomic Mapping System
DCM
Digital canopy model
DSM
Digital surface model
DTM
Digital terrain model
GPS
Global positioning system
HiFIS
High Fidelity Imaging Spectroscopy
ICP-OES
inductively coupled plasma optical emission spectrometer
IMU
Inertial measurement unit
LACC
Los Amigos Conservation Concession
LiDAR
Light detection and ranging
LMA
Leaf mass per area
NDVI
Normalized difference vegetation index
PLSR
Partial least squares regression
RDN
Rock derived nutrients
RMSE
Root mean square error
VSWIR
Visible to shortwave infrared

Appendix A

Below are figures and a table that follow the analyses that were completed in the main text, but on natural log transformed trait values.
Table A1. The value and 95% confidence interval (CI) for the intercepts and slopes of the regressions displayed in Figure A2. If, for the intercept, the CI encompasses 0, then the regression is not statistically significantly biased (p > 0.05, italicized and bolded). For the slope, if the CI encompasses 1, then the regression slope does not significantly differ from that of the 1:1 line (p > 0.05, italicized and bolded). This table mirrors Table 3 in the main text, except that the analysis has been done for the natural log transformed foliar trait values and predictions, as well as the back transformed trait data and predictions. When back transformed to predict the foliar trait values that we are interested in, any of these models are biased or inconsistent in their predictions.
Table A1. The value and 95% confidence interval (CI) for the intercepts and slopes of the regressions displayed in Figure A2. If, for the intercept, the CI encompasses 0, then the regression is not statistically significantly biased (p > 0.05, italicized and bolded). For the slope, if the CI encompasses 1, then the regression slope does not significantly differ from that of the 1:1 line (p > 0.05, italicized and bolded). This table mirrors Table 3 in the main text, except that the analysis has been done for the natural log transformed foliar trait values and predictions, as well as the back transformed trait data and predictions. When back transformed to predict the foliar trait values that we are interested in, any of these models are biased or inconsistent in their predictions.
TraitNatural Log TransformedBack Transformed
Intercept (95% CI)Slope (95% CI)Intercept (95% CI)Slope (95% CI)
LMA−0.56 (−1.37, 0.25)1.13 (0.95, 1.3)−11.71 (−30.75, 7.33)1.15 (0.97, 1.34)
N−0.14 (−0.3, 0.01)1.16 (0.98, 1.34)−0.53 (−0.95, −0.11)1.24 (1.06, 1.41)
P0.37 (0.04, 0.706)1.19 (1.03, 1.35)−0.03 (−0.05, −0.005)1.22 (1.05, 1.38)
Ca0.12 (0.01, 0.23)1.05 (0.94, 1.16)0.16 (0.06, 0.27)0.95 (0.85, 1.06)
K0.05 (−0.06, 0.15)1.16 (0.97, 1.35)−0.16 (−0.29, −0.04)1.29 (1.09, 1.49)
Mg0.16 (−0.09, 0.41)1.05 (0.91, 1.18)0.01 (−0.02, 0.04)1.09 (0.93, 1.24)
Figure A1. Plots of the PLSR model coefficients for each foliar trait being predicted, in natural log transformed space. Shaded regions indicate the 95% confidence interval of the mean coefficient value that was selected for the aggregated model.
Figure A1. Plots of the PLSR model coefficients for each foliar trait being predicted, in natural log transformed space. Shaded regions indicate the 95% confidence interval of the mean coefficient value that was selected for the aggregated model.
Figure A2. Scatter plots of the crown averaged foliar traits predicted with the models developed using natural log transformed data, versus the foliar chemical data from field sampling and laboratory analysis. The top row is the natural log transformed values and the bottom row is the back transformed values. Error bars show the standard error about the mean trait value when aggregating pixels to the crown level. The dashed gray line is 1:1; the liner regression fit of observed versus predicted is shown in black (n = 185).
Figure A2. Scatter plots of the crown averaged foliar traits predicted with the models developed using natural log transformed data, versus the foliar chemical data from field sampling and laboratory analysis. The top row is the natural log transformed values and the bottom row is the back transformed values. Error bars show the standard error about the mean trait value when aggregating pixels to the crown level. The dashed gray line is 1:1; the liner regression fit of observed versus predicted is shown in black (n = 185).

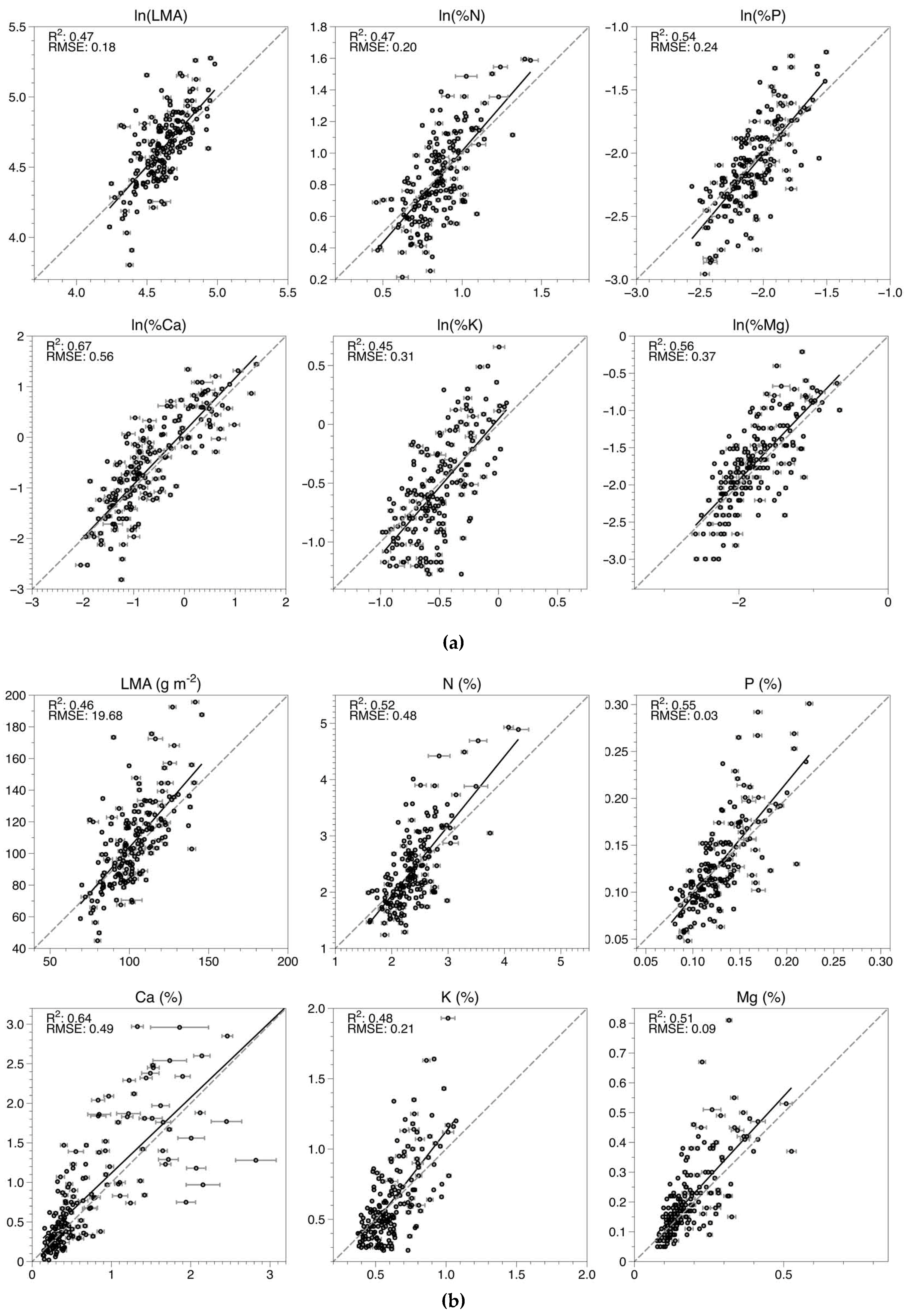
References

  1. Violle, C.; Reich, P.B.; Pacala, S.W.; Enquist, B.J.; Kattge, J. The emergence and promise of functional biogeography. Proc. Natl. Acad. Sci. USA 2014, 111, 13690–13696. [Google Scholar] [CrossRef] [PubMed]
  2. Malhi, Y.; Grace, J. Tropical forests and atmospheric carbon dioxide. Trends Ecol. Evol. 2000, 15, 332–337. [Google Scholar] [CrossRef]
  3. Schimel, D.; Stephens, B.B.; Fisher, J.B. Effect of increasing CO2 on the terrestrial carbon cycle. Proc. Natl. Acad. Sci. USA 2015, 112, 436–441. [Google Scholar] [CrossRef] [PubMed]
  4. Townsend, A.R.; Asner, G.P.; Cleveland, C.C. The biogeochemical heterogeneity of tropical forests. Trends Ecol. Evol. 2008, 23, 424–431. [Google Scholar] [CrossRef] [PubMed]
  5. Kokaly, R.F.; Asner, G.P.; Ollinger, S.V.; Martin, M.E.; Wessman, C.A. Characterizing canopy biochemistry from imaging spectroscopy and its application to ecosystem studies. Remote Sens. Environ. 2009, 113, S78–S91. [Google Scholar] [CrossRef]
  6. Ollinger, S.V. Sources of variability in canopy reflectance and the convergent properties of plants. New Phytol. 2011, 189, 375–394. [Google Scholar] [CrossRef] [PubMed]
  7. Asner, G.P.; Martin, R.E.; Knapp, D.E.; Tupayachi, R.; Anderson, C.; Carranza, L.; Martinez, P.; Houcheime, M.; Sinca, F.; Weiss, P. Spectroscopy of canopy chemicals in humid tropical forests. Remote Sens. Environ. 2011, 115, 3587–3598. [Google Scholar] [CrossRef]
  8. Asner, G.P.; Martin, R.E.; Tupayachi, R.; Emerson, R.; Martinez, P.; Sinca, F.; Powell, G.V.N.; Wright, S.J.; Lugo, A.E. Taxonomy and remote sensing of leaf mass per area (LMA) in humid tropical forests. Ecol. Appl. 2011, 21, 85–98. [Google Scholar] [CrossRef] [PubMed]
  9. Feilhauer, H.; Asner, G.P.; Martin, R.E.; Schmidtlein, S. Brightness-normalized Partial Least Squares Regression for hyperspectral data. J. Quant. Spectrosc. Radiat. Transf. 2010, 111, 1947–1957. [Google Scholar] [CrossRef]
  10. Feilhauer, H.; Asner, G.P.; Martin, R.E. Multi-method ensemble selection of spectral bands related to leaf biochemistry. Remote Sens. Environ. 2015, 164, 57–65. [Google Scholar] [CrossRef]
  11. Asner, G.P.; Martin, R.E.; Anderson, C.B.; Knapp, D.E. Quantifying forest canopy traits: Imaging spectroscopy versus field survey. Remote Sens. Environ. 2015, 158, 15–27. [Google Scholar] [CrossRef]
  12. Asner, G.P.; Anderson, C.B.; Martin, R.E.; Tupayachi, R.; Knapp, D.E.; Sinca, F. Landscape biogeochemistry reflected in shifting distributions of chemical traits in the Amazon forest canopy. Nat. Geosci. 2015, 8, 567–573. [Google Scholar] [CrossRef]
  13. Reich, P.B.; Walters, M.B.; Ellsworth, D.S. Leaf life-span in relation to leaf, plant, and stand characteristics among diverse ecosystems. Ecol. Monogr. 1992, 62, 365–392. [Google Scholar] [CrossRef]
  14. Wright, I.J.; Reich, P.B.; Westoby, M.; Ackerly, D.D.; Baruch, Z.; Bongers, F.; Cavender-Bares, J.; Chapin, T.; Cornelissen, J.H.C.; Diemer, M.; et al. The worldwide leaf economics spectrum. Nature 2004, 428, 821–827. [Google Scholar] [CrossRef] [PubMed]
  15. Demarty, M.; Morvan, C.; Thellier, M. Calcium and the cell wall. Plant Cell Environ. 1984, 7, 441–448. [Google Scholar] [CrossRef]
  16. McLaughlin, S.B.; Wimmer, R. Calcium physiology and terrestrial ecosystem processes. New Phytol. 1999, 142, 373–417. [Google Scholar] [CrossRef]
  17. Vitousek, P.M. Litterfall, nutrient cycling, and nutrient limitation in tropical forests. Ecology 1984, 65, 285–298. [Google Scholar] [CrossRef]
  18. Cuevas, E.; Medina, E. Nutrient dynamics within Amazonian forests. Oecologia 1988, 76, 222–235. [Google Scholar] [CrossRef]
  19. Kaspari, M.; Garcia, M.; Harms, K. Multiple nutrients limit litterfall and decomposition in a tropical forest. Ecology 2008, 11, 35–43. [Google Scholar] [CrossRef] [PubMed]
  20. Townsend, A.R.; Cleveland, C.C.; Houlton, B.Z.; Alden, C.B.; White, J.W. Multi-element regulation of the tropical forest carbon cycle. Front. Ecol. Environ. 2011, 9, 9–17. [Google Scholar] [CrossRef]
  21. Wright, S.J.; Yavitt, J.B.; Wurzburger, N.; Turner, B.L.; Tanner, E.V.J.; Sayer, E.J.; Santiago, L.S.; Kaspari, M.; Hedin, L.O.; Harms, K.E.; et al. Potassium, phosphorus, or nitrogen limit root allocation, tree growth, or litter production in a lowland tropical forest. Ecology 2011, 92, 1616–1625. [Google Scholar] [CrossRef] [PubMed]
  22. Koerselman, W.; Meuleman, A.F.M. The Vegetation N:P Ratio: A New Tool to Detect the Nature of Nutrient Limitation. J. Appl. Ecol. 1996, 33, 1441–1450. [Google Scholar] [CrossRef]
  23. Güsewell, S. N:P Ratios in Terrestrial Plants: Variation and Functional Significance. New Phytol. 2004, 164, 243–266. [Google Scholar] [CrossRef]
  24. Rigsby, C.A.; Hemric, E.M.E.; Baker, P.A. Late Quaternary Paleohydrology of the Madre de Dios River, southwestern Amazon Basin, Peru. Geomorphology 2009, 113, 158–172. [Google Scholar] [CrossRef]
  25. Osher, L.J.; Buol, S.W. Relationship of soil properties to parent material and landscape position in eastern Madre de Dios, Peru. Geoderma 1998, 83, 143–166. [Google Scholar] [CrossRef]
  26. Asner, G.P.; Martin, R.E. Airborne spectranomics: Mapping canopy chemical and taxonomic diversity in tropical forests. Front. Ecol. Environ. 2009, 7, 269–276. [Google Scholar] [CrossRef]
  27. Asner, G.P.; Martin, R.E. Canopy phylogenetic, chemical and spectral assembly in a lowland Amazonian forest. New Phytol. 2011, 189, 999–1012. [Google Scholar] [CrossRef] [PubMed]
  28. Asner, G.P.; Martin, R.E.; Tupayachi, R.; Anderson, C.B.; Sinca, F.; Carranza-Jimenez, L.; Martinez, P.; Carranza-Jiménez, L.; Martinez, P. Amazonian functional diversity from forest canopy chemical assembly. Proc. Natl. Acad. Sci. USA 2014, 111, 5604–5609. [Google Scholar] [CrossRef] [PubMed]
  29. Carnegie Spectranomics. Available online: http://spectranomics.ciw.edu (accessed on 19 January 2016).
  30. Stanford Environmental Measurements Facility. Available online: http://em1.stanford.edu (accessed on 19 January 2016).
  31. Asner, G.P.; Knapp, D.E.; Boardman, J.; Green, R.O.; Kennedy-Bowdoin, T.; Eastwood, M.; Martin, R.E.; Anderson, C.; Field, C.B. Carnegie Airborne Observatory-2: Increasing science data dimensionality via high-fidelity multi-sensor fusion. Remote Sens. Environ. 2012, 124, 454–465. [Google Scholar] [CrossRef]
  32. Asner, G.; Martin, R. Spectral and chemical analysis of tropical forests: Scaling from leaf to canopy levels. Remote Sens. Environ. 2008, 112, 3958–3970. [Google Scholar] [CrossRef]
  33. Asner, G.P.; Knapp, D.E.; Kennedy-Bowdoin, T.; Jones, M.O.; Martin, R.E.; Boardman, J.; Field, C.B. Carnegie Airborne Observatory: In-flight fusion of hyperspectral imaging and waveform light detection and ranging for three-dimensional studies of ecosystems. J. Appl. Remote Sens. 2007, 1. [Google Scholar] [CrossRef]
  34. Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
  35. RDC Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2012. [Google Scholar]
  36. Schmidtlein, S.; Feilhauer, H.; Bruelheide, H. Mapping plant strategy types using remote sensing. J. Veg. Sci. 2012, 23, 395–405. [Google Scholar] [CrossRef]
  37. Piñeiro, G.; Perelman, S.; Guerschman, J.P.; Paruelo, J.M. How to evaluate models: Observed vs. predicted or predicted vs. observed? Ecol. Model. 2008, 216, 316–322. [Google Scholar] [CrossRef]
  38. Salo, J.S.; Kalliola, R.; Häkkinen, I.; Mäkinen, Y.; Niemelä, P.; Puhakka, M.; Coley, P.D. River dynamics and the diversity of Amazon lowland forest. Nature 1986, 322, 254–258. [Google Scholar] [CrossRef]
  39. Puhakka, M.; Kalliola, R.; Rajasilta, M.; Salo, J. River Types, Site Evolution and Successional Vegetation Patterns in Peruvian Amazonia. J. Biogeogr. 1992, 19, 651–665. [Google Scholar] [CrossRef]
  40. Pitman, N.C.A. An Overview of the Los Amigos Watershed, Madre de Dios, Southeastern Peru; Draft Report; Amazon Conservation Association: Washington, DC, USA, 2010. [Google Scholar]
  41. Chadwick, K.D.; Asner, G.P. Tropical soil nutrient distributions determined by biotic and hillslope processes. Biogeochemistry 2016. [Google Scholar] [CrossRef]
  42. Fyllas, N.M.; Patiño, S.; Baker, T.R.; Nardoto, G.B.; Martinelli, L.A.; Quesada, C.A.; Paiva, R.; Schwarz, M.; Horna, V.; Mercado, L.M.; et al. Basin-wide variations in foliar properties of Amazonian forest: Phylogeny, soils and climate. Biogeosciences 2009, 6, 2677–2708. [Google Scholar] [CrossRef]
  43. Townsend, P.A.; Serbin, S.P.; Kruger, E.L.; Gamon, J.A. Disentangling the contribution of biological and physical properties of leaves and canopies in imaging spectroscopy data. Proc. Natl. Acad. Sci. USA 2013, 110. [Google Scholar] [CrossRef] [PubMed]
  44. Knyazikhin, Y.; Schull, M.A.; Stenberg, P.; Mõttus, M.; Rautiainen, M.; Yang, Y.; Marshak, A.; Latorre Carmona, P.; Kaufmann, R.K.; Lewis, P.; et al. Hyperspectral remote sensing of foliar nitrogen content. Proc. Natl. Acad. Sci. USA 2013, 110. [Google Scholar] [CrossRef] [PubMed]
  45. Phillips, O.L.; Vargas, P.N.; Lorenzo, A.; Cruz, A.P.; Chuspe, M.; Sánchez, W.G.; Yli-halla, M.; Rose, S.A.M. Habitat association among Amazonian tree species: A landscape-scale approach. J. Ecol. 2003, 91, 757–775. [Google Scholar] [CrossRef]
  46. Asner, G.P. Organismic Remote Sensing for Tropical Forest Ecology and Conservation. Ann. Mo. Bot. Gard. 2015, 100, 127–140. [Google Scholar] [CrossRef]

Share and Cite

MDPI and ACS Style

Chadwick, K.D.; Asner, G.P. Organismic-Scale Remote Sensing of Canopy Foliar Traits in Lowland Tropical Forests. Remote Sens. 2016, 8, 87. https://doi.org/10.3390/rs8020087

AMA Style

Chadwick KD, Asner GP. Organismic-Scale Remote Sensing of Canopy Foliar Traits in Lowland Tropical Forests. Remote Sensing. 2016; 8(2):87. https://doi.org/10.3390/rs8020087

Chicago/Turabian Style

Chadwick, K. Dana, and Gregory P. Asner. 2016. "Organismic-Scale Remote Sensing of Canopy Foliar Traits in Lowland Tropical Forests" Remote Sensing 8, no. 2: 87. https://doi.org/10.3390/rs8020087

APA Style

Chadwick, K. D., & Asner, G. P. (2016). Organismic-Scale Remote Sensing of Canopy Foliar Traits in Lowland Tropical Forests. Remote Sensing, 8(2), 87. https://doi.org/10.3390/rs8020087

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop