Daytime Thermal Anisotropy of Urban Neighbourhoods: Morphological Causation
Abstract
:1. Introduction
1.1. Neighbourhood-Scale Thermal Anisotropy
1.2. Observations of Urban Effective Thermal Anisotropy
1.3. Modelling Urban Effective Thermal Anisotropy
1.4. Objectives and Degrees of Freedom
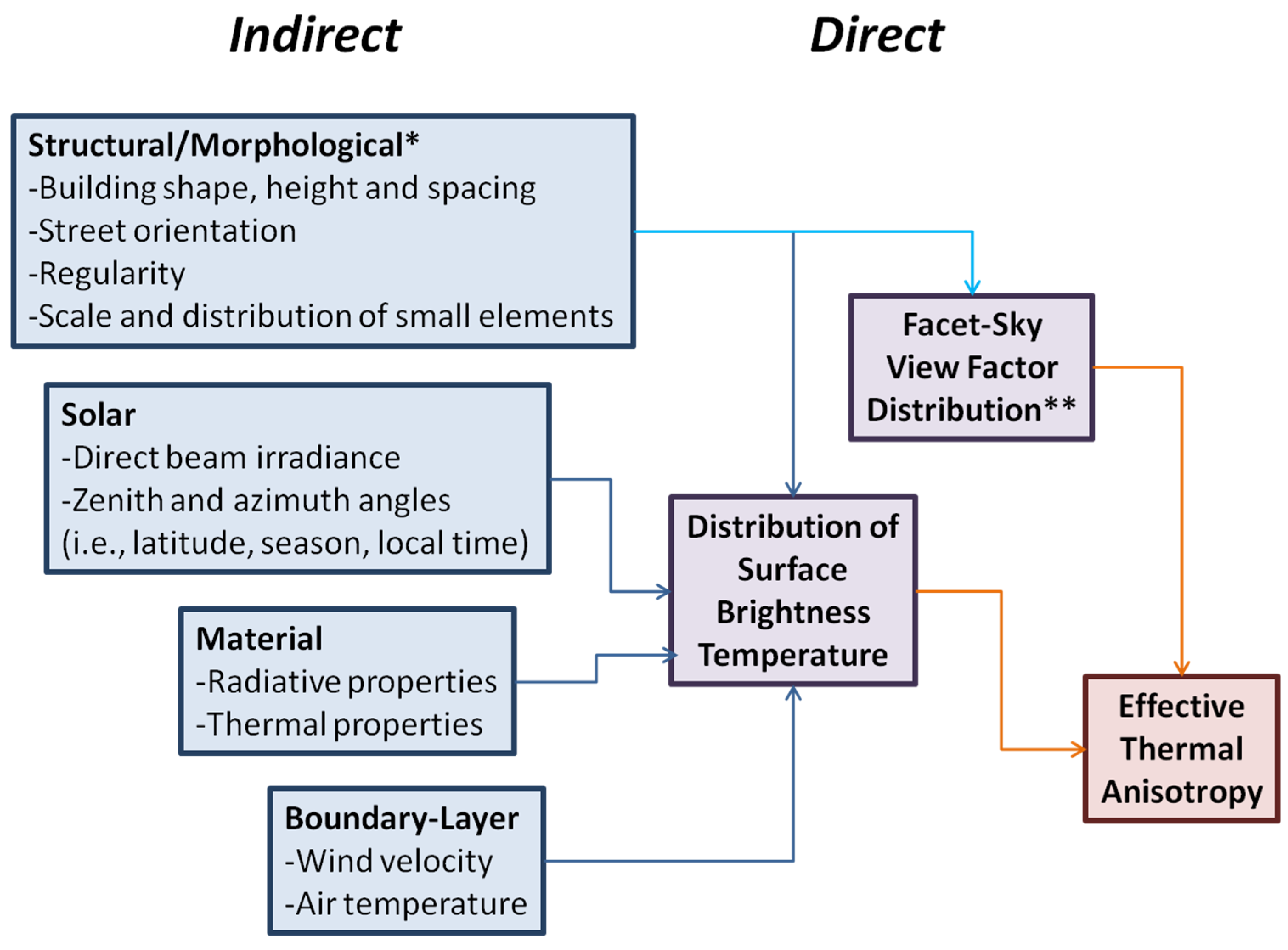
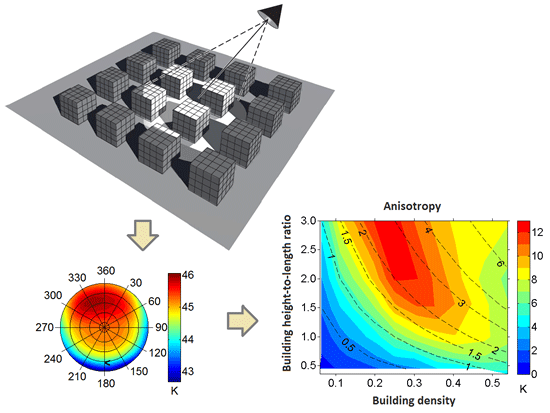
2. Defining Effective Thermal Anisotropy
3. Model Linkage and Evaluation
3.1. Coupling TUF3D and SUM Models
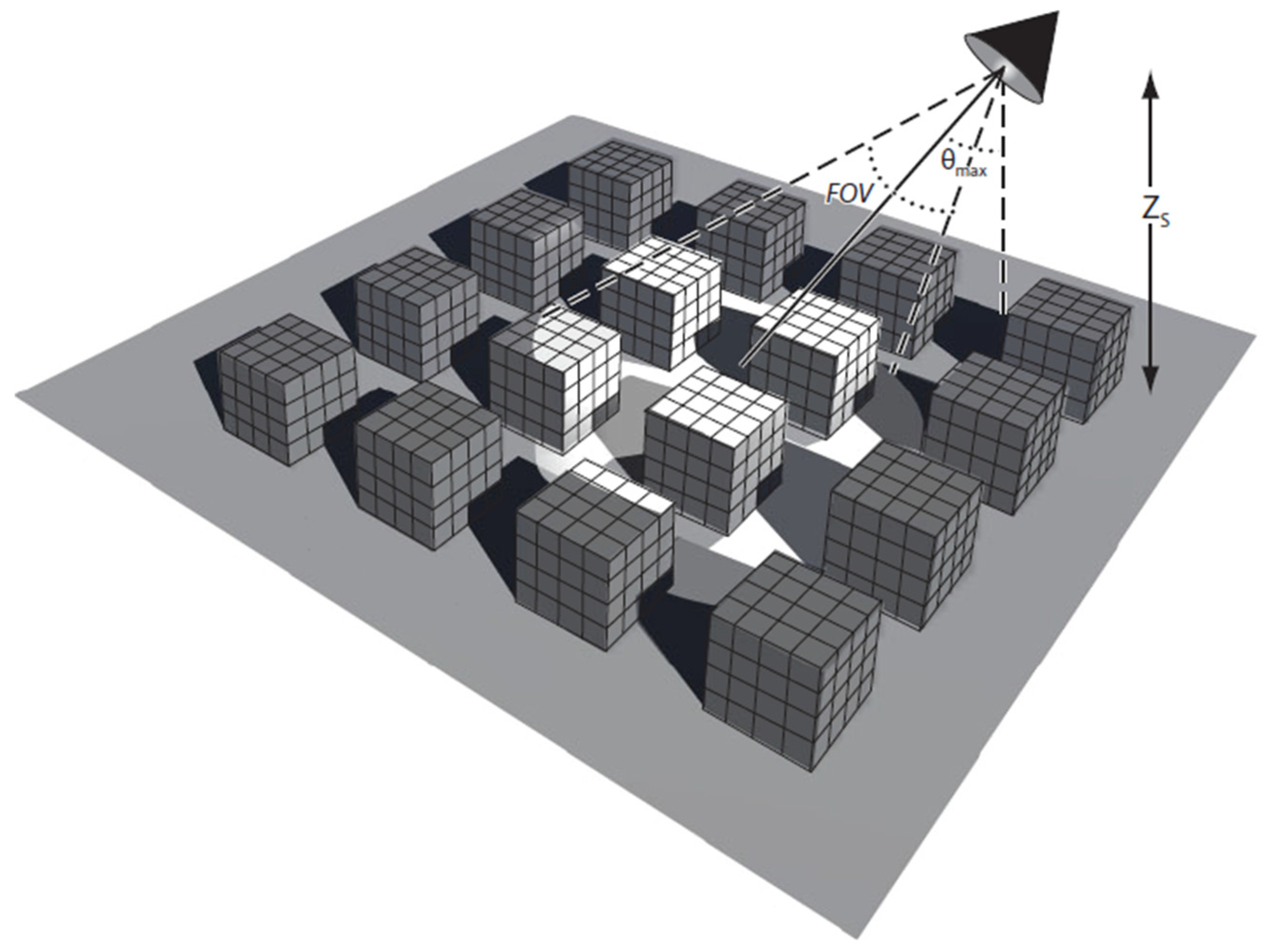
3.2. Sampling the TB Distribution
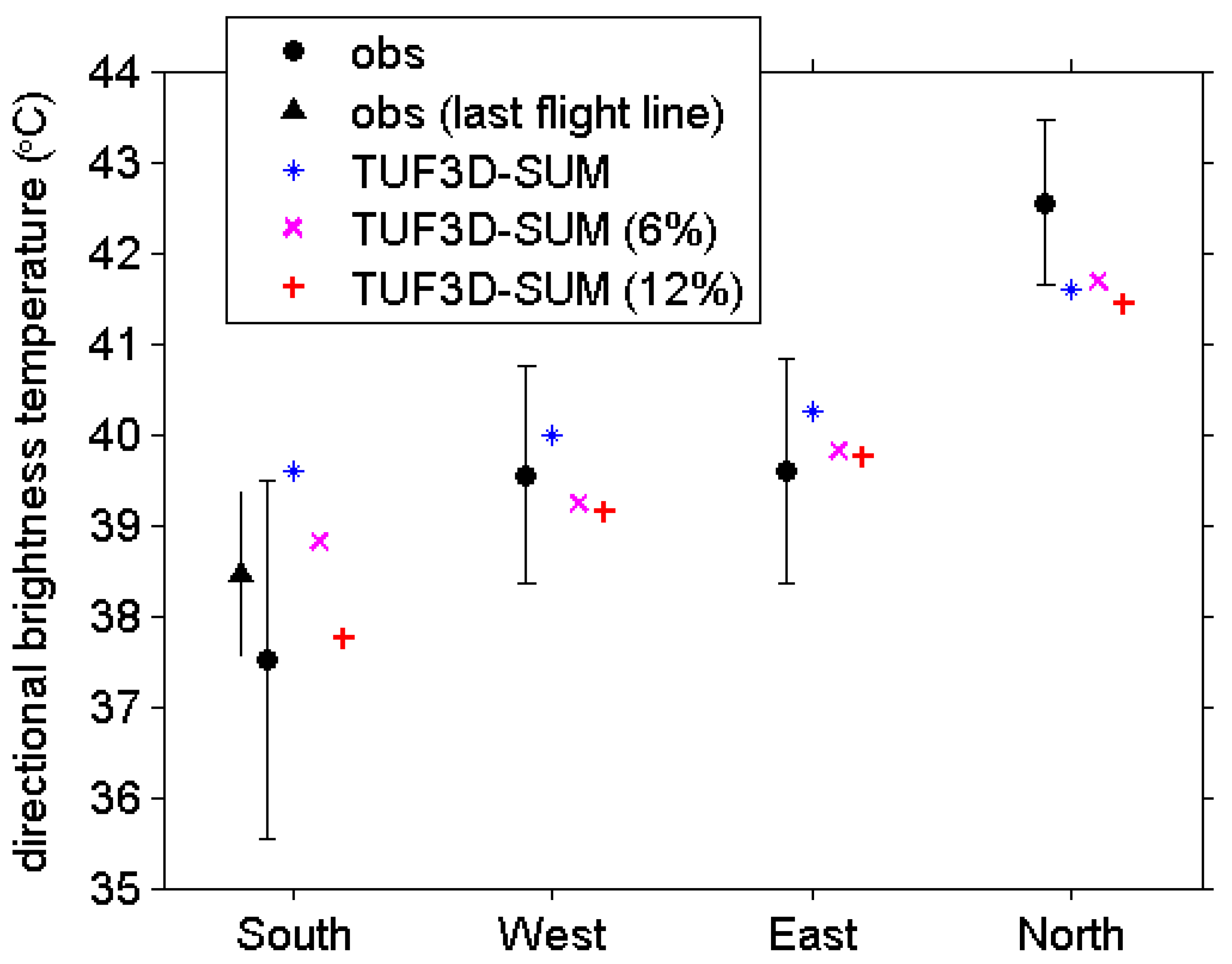
3.3. Model Evaluation: Vancouver Light Industrial Site
4. Effects of Urban Geometry on Anisotropy: Simulation Design
Arrays of Buildings with Square Footprints
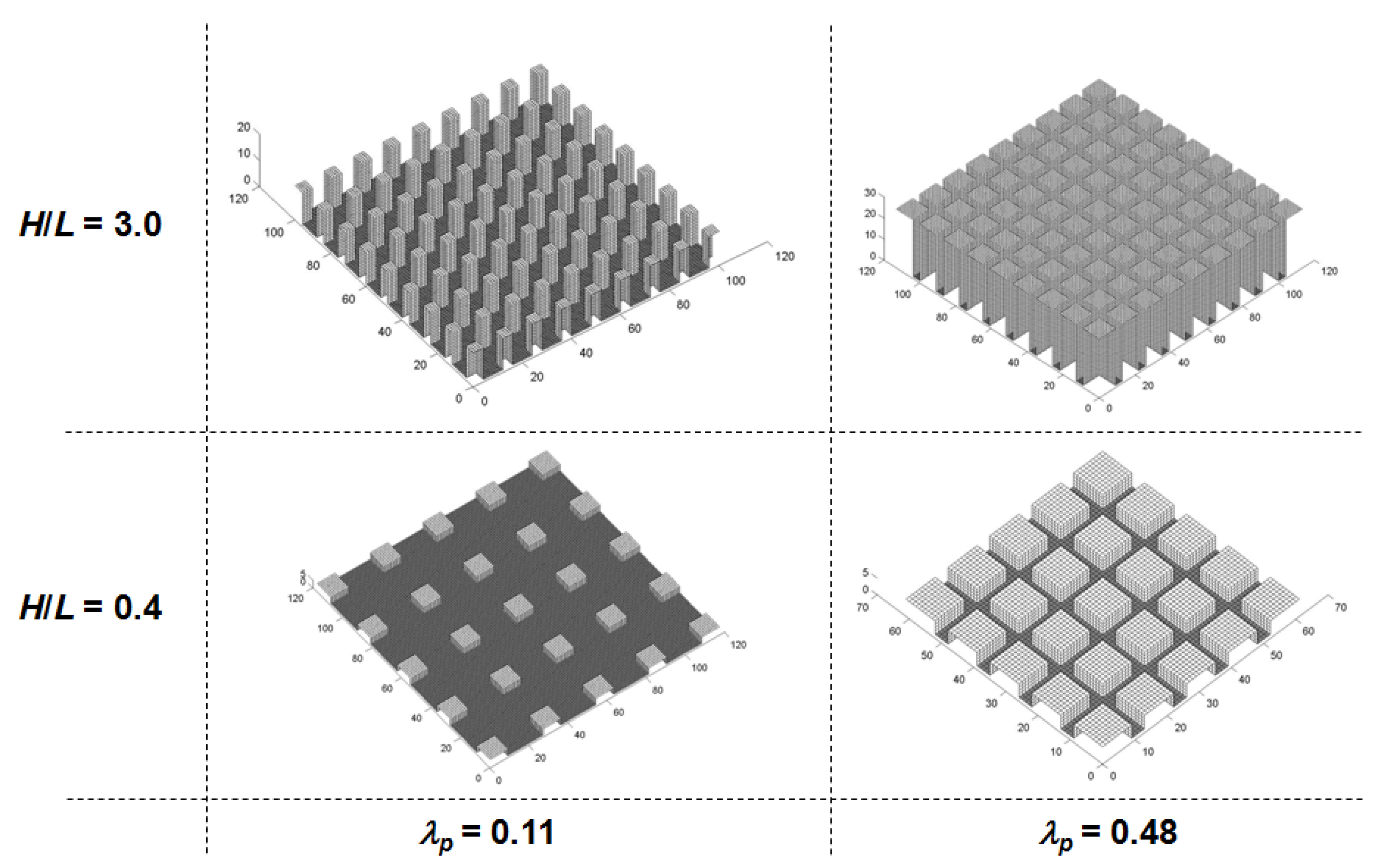
5. Effects of Urban Geometry on Anisotropy: Results and Discussion
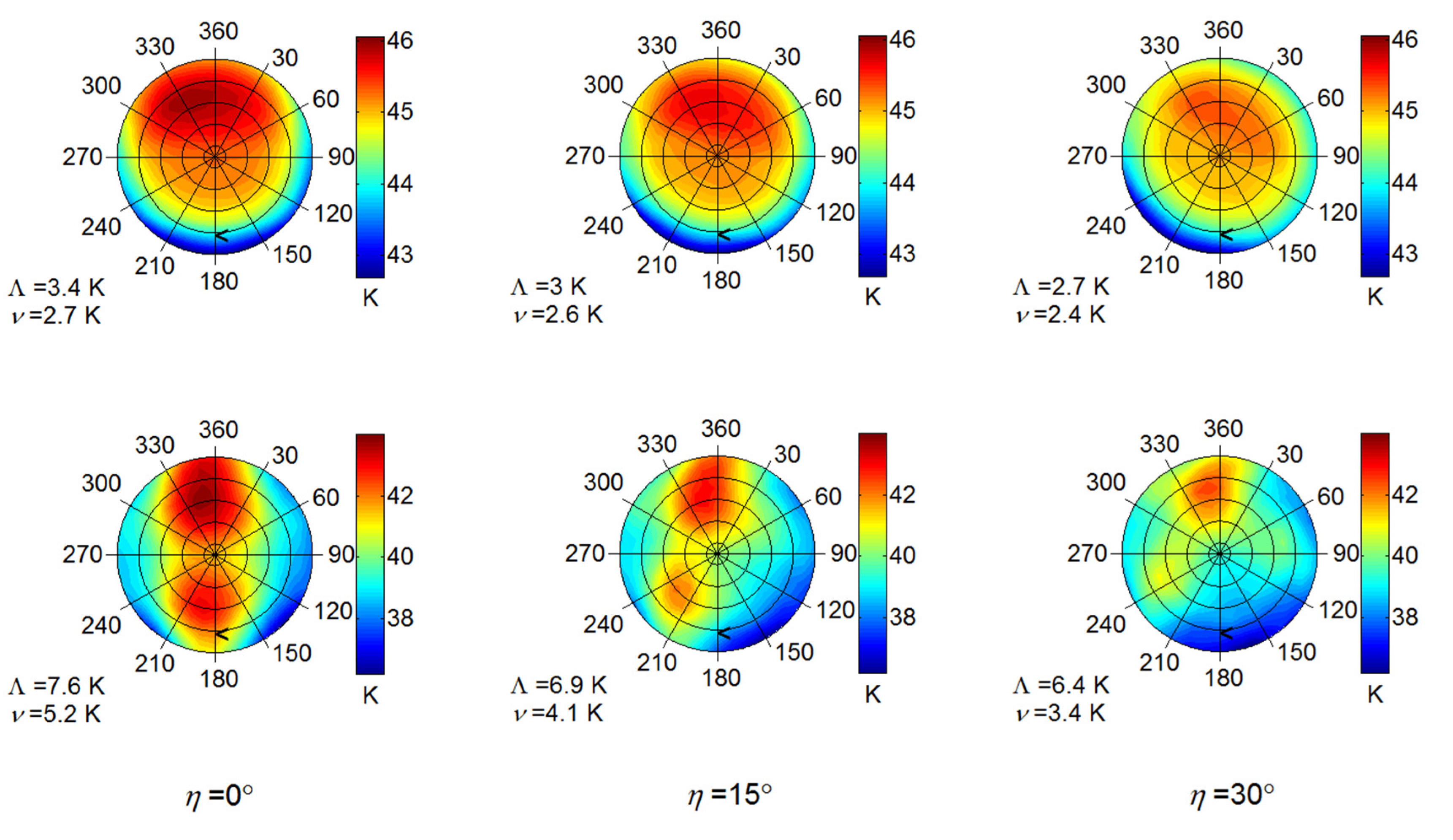
5.1. Variation of Anisotropy With Neighbourhood Geometric Structure
5.2. Geometric Causation of Anisotropy
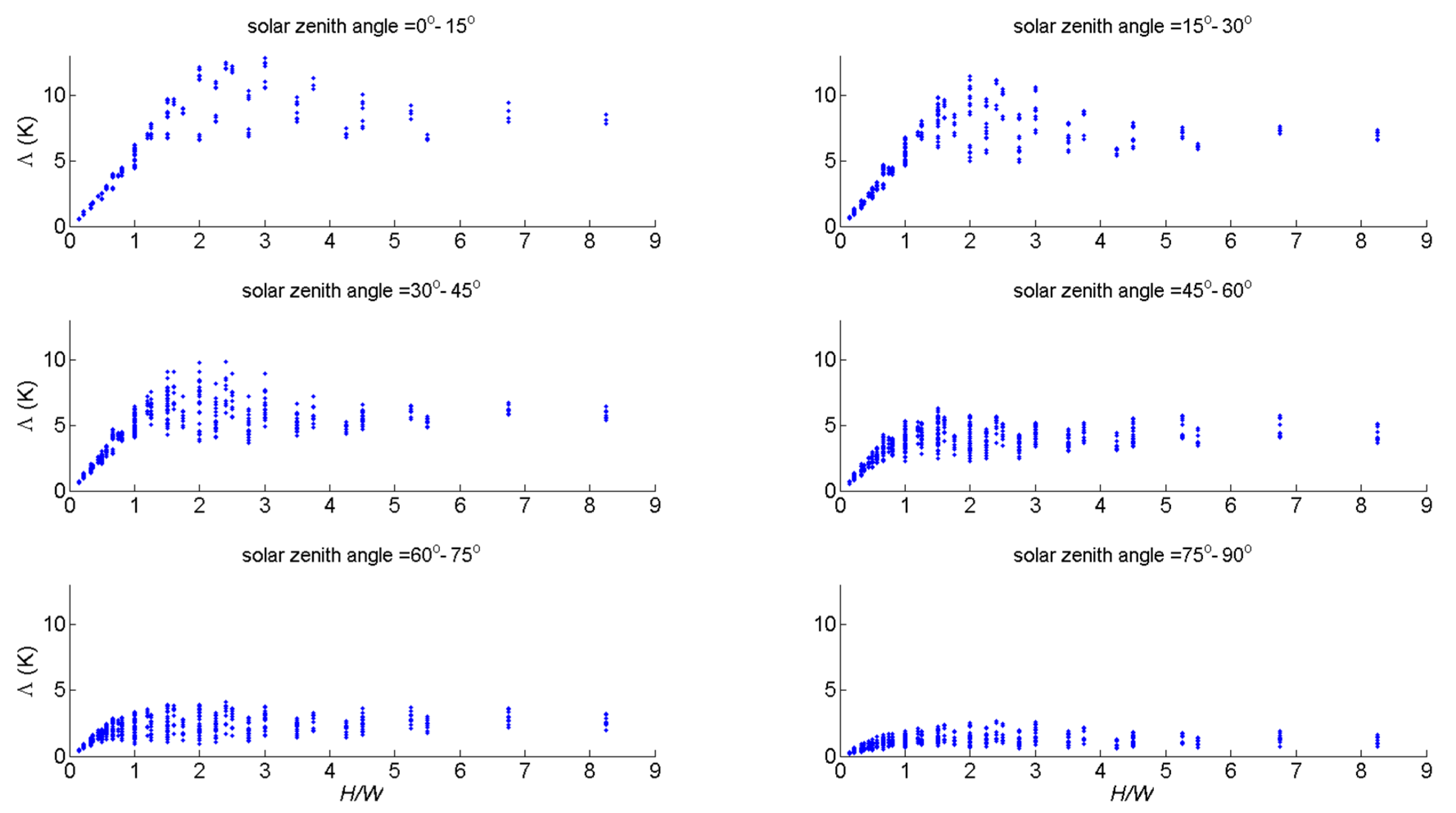
5.2.1. Anisotropy as a Function of Canopy Height-to-Width Ratio
5.2.2. Normalization of Anisotropy Magnitude
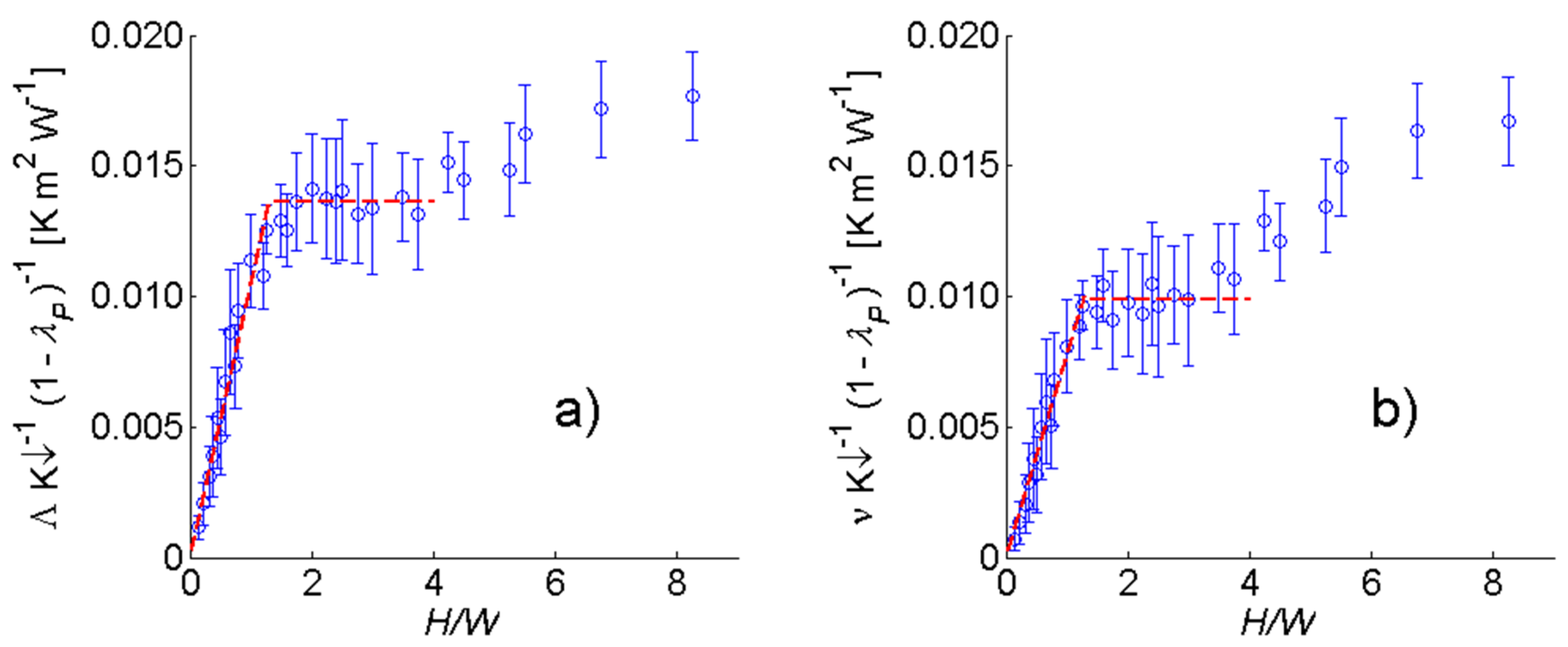
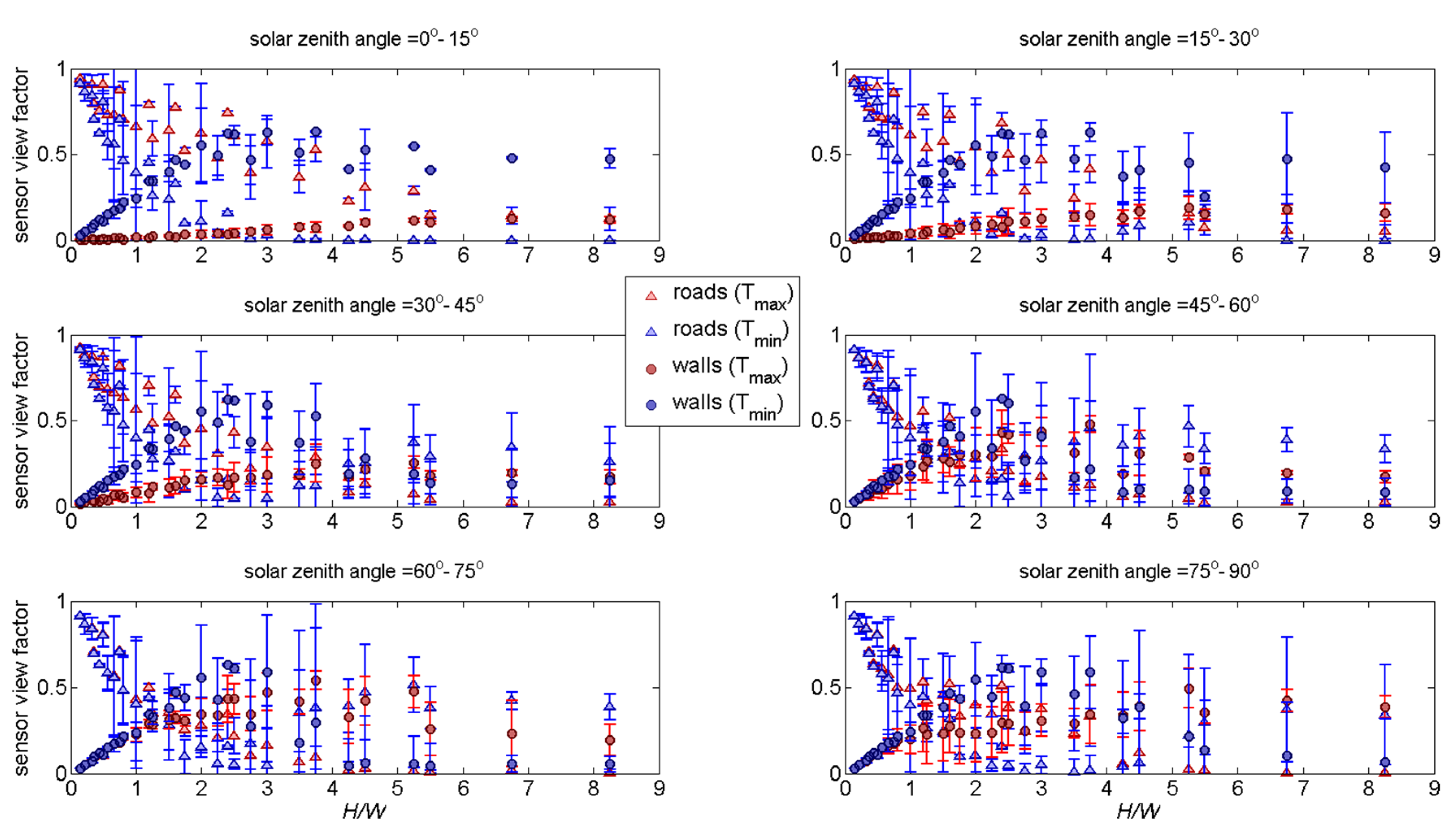
5.2.3. Facets Contributing to Anisotropy
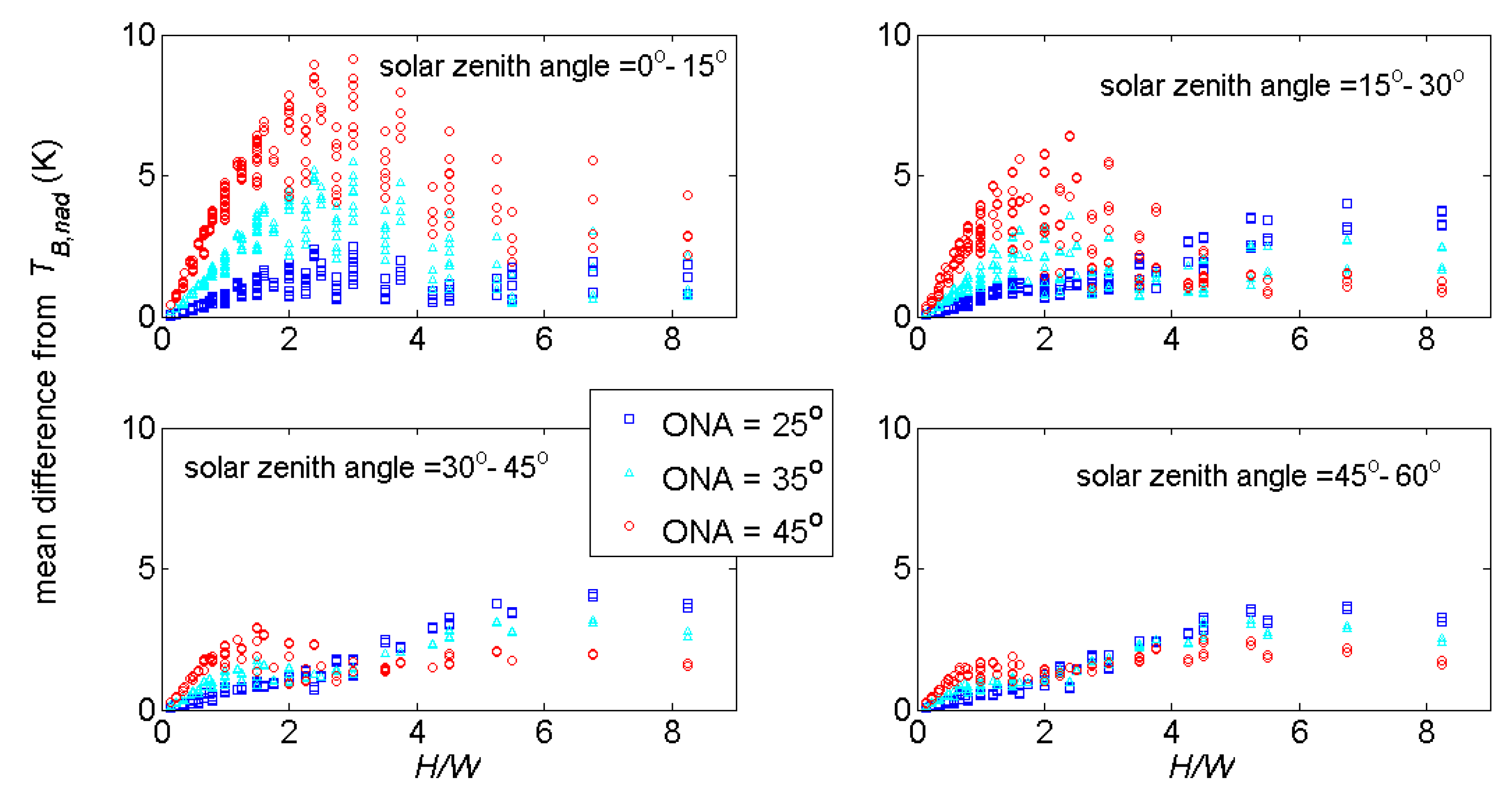
5.3. Sampling Anisotropic Distributions: Maximum Off-Nadir Angle
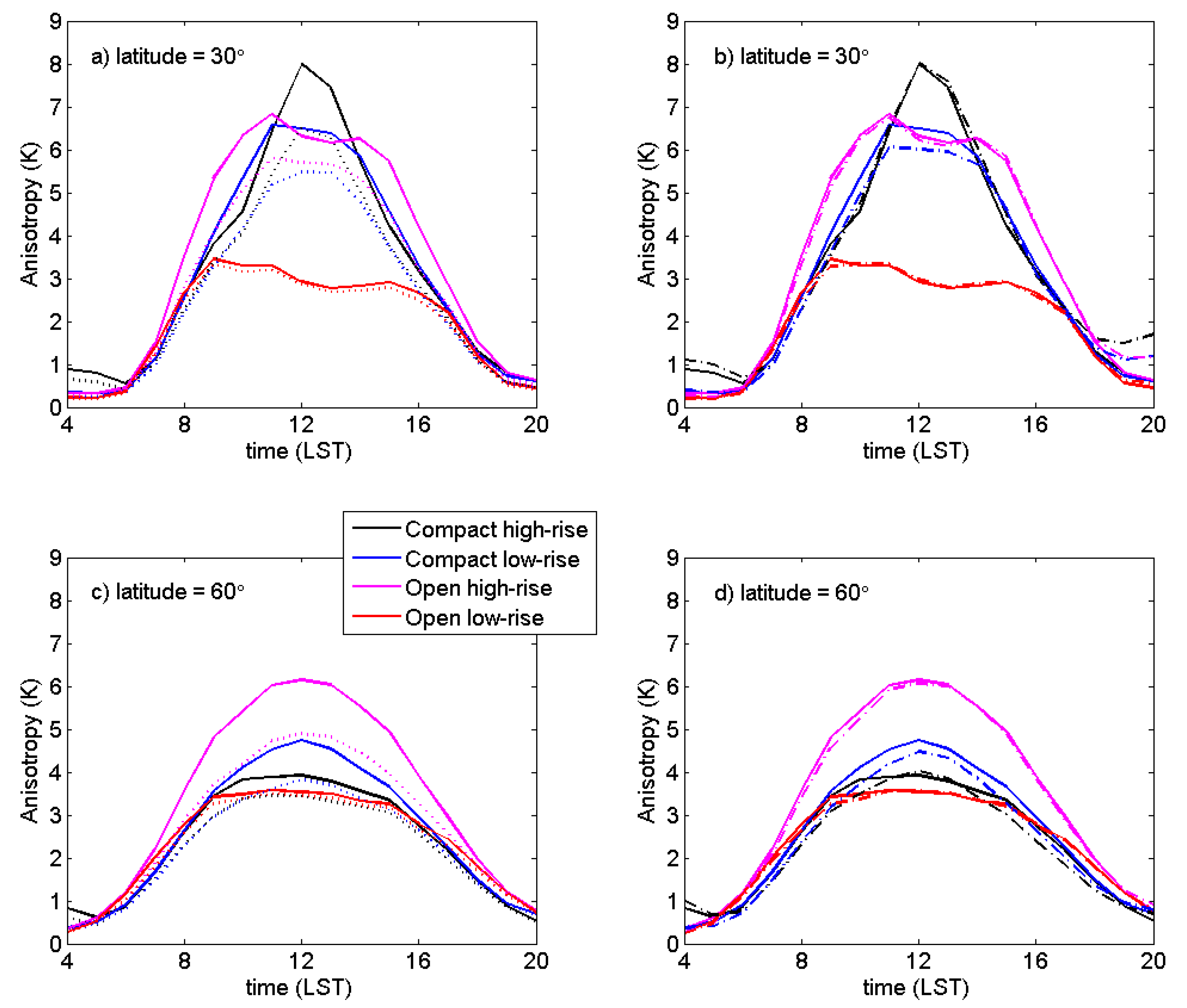
6. Anisotropy of Common Neighbourhoods: Local Climate Zones
6.1. Effects of Neighbourhood Regularity: Street Orientation
6.2. Effects of Material Property Variability
7. Conclusions
- Urban effective anisotropy depends strongly on solar elevation and irradiance. It is increased for smaller solar zenith angle and greater irradiance. When normalized by solar irradiance (or roof surface temperature), anisotropy magnitude is independent of solar zenith angle.
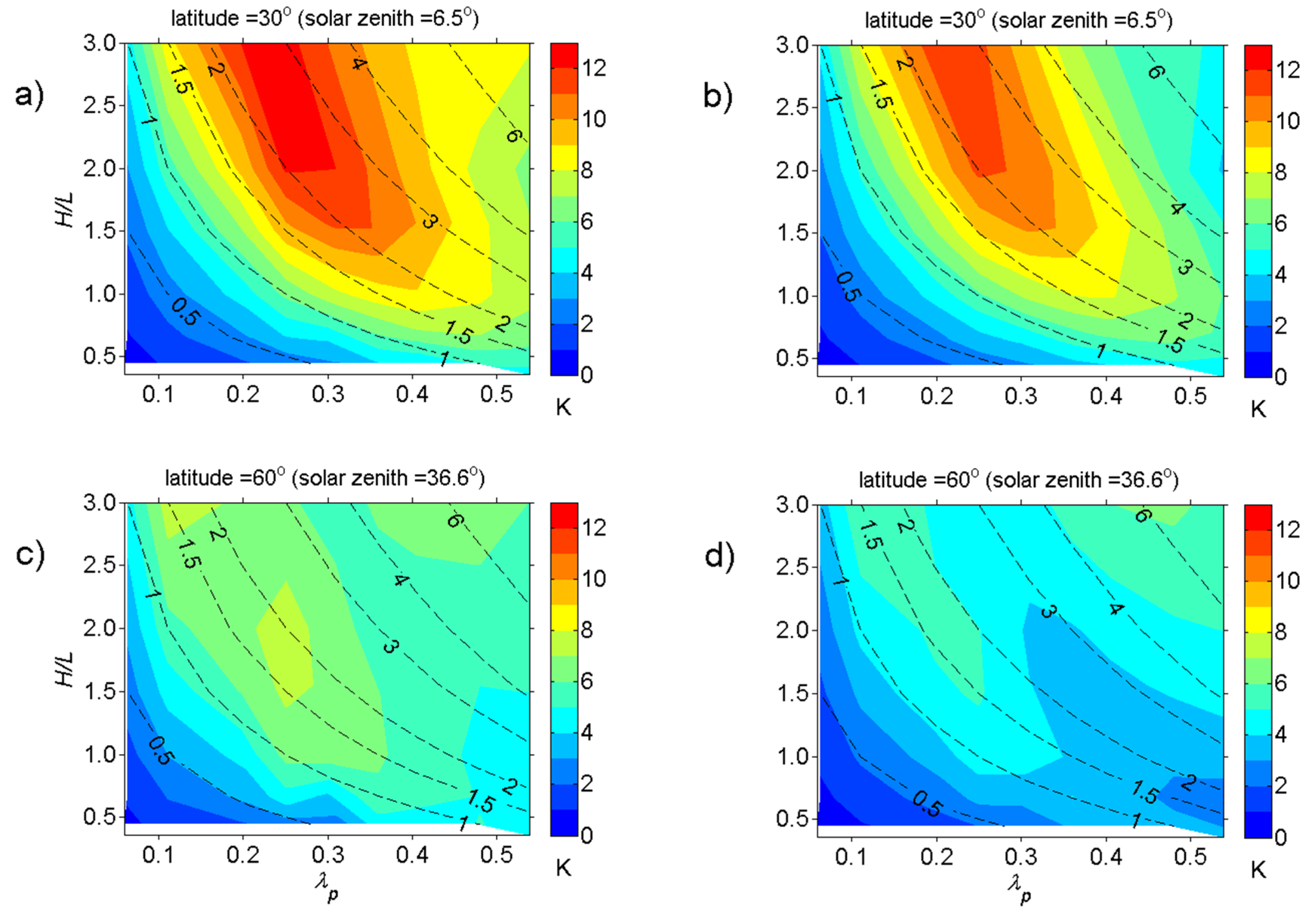
- Urban effective anisotropy depends strongly on urban morphology, in particular, the ratio of building height to street width (H/W). It is maximized for H/W ≈ 1.5–3.0, and within this range it is greater for tall, moderately-spaced buildings than for shorter, closely-spaced buildings. Normalizing anisotropy magnitude by canyon (non-building) plan area (1 – λP) removes this dependence on building shape and spacing, strengthening the relation between anisotropy and H/W.
- Modelled effective thermal anisotropy increases linearly as a function of H/W for H/W < 1.25 (approx.), with a slope that depends on maximum sensor off-nadir angle. For a maximum off-nadir angle of 45°, modeled anisotropy magnitude (in K) is Λ = 0.011 K↓ (1 – λP) H/W over this range of H/W, where K↓ is solar irradiance on a flat surface in W·m−2. This is considered a minimum estimate of anisotropy magnitude for real urban neighbourhoods because small scale structure, tree crowns and other neighbourhood features are neglected.
- Variation of minimum brightness temperature with H/W controls the dependence of anisotropy on H/W more than the corresponding variation of maximum brightness temperature. Cool shaded walls are critical to production of anisotropy for H/W < 3.0.
- Compact and high-rise zones generate greater anisotropy than an “open low-rise” (e.g., suburban) zone. With lower solar elevation angles (i.e., higher latitude), the difference is reduced: the “open low-rise” zone changes little, while the compact and highrise zones’ anisotropy is reduced.
- Regularity of street orientation increases anisotropy. For this limited sample of solar angles and urban geometries, it represents 3%–31% of anisotropy magnitude depending on morphology and time of day (solar elevation).
- Building shape and density, i.e., urban morphology, more strongly modulate anisotropy than material radiative and thermal properties.
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| FOV | Field of view |
| TUF3D | Temperature of Urban Facets in 3-D |
| SUM | Surface–sensor–sun Urban Model |
| AVHRR | Advanced Very High Resolution Radiometer |
| MODIS | Moderate-resolution Imaging Spectroradiometer |
| LST | Local solar time |
| LCZ | Local climate zone |
References
- ReferencesOke, T.R. The urban energy balance. Prog. Phys. Geogr. 1988, 12, 471–508. [Google Scholar]
- Li, Z.-L.; Wu, H.; Wang, N.; Qiu, S.; Sobrino, J.A.; Wan, Z.; Tang, B.-H.; Yan, G. Land surface emissivity retrieval from satellite data. Int. J. Remote Sens. 2013, 34, 3084–3127. [Google Scholar] [CrossRef]
- Voogt, J.A.; Oke, T.R. Thermal remote sensing of urban climates. Remote Sens. Environ. 2003, 86, 370–384. [Google Scholar]
- Weng, Q. Thermal infrared remote sensing for urban climate and environmental studies: Methods, applications, and trends. ISPRS J. Photogram. Remote Sens. 2009, 64, 335–344. [Google Scholar] [CrossRef]
- Li, Z.-L.; Tang, B.-H.; Wu, H.; Ren, H.; Yan, G.; Wan, Z.; Trigo, I.F.; Sobrino, J.A. Satellite-derived land surface temperature: Current status and perspectives. Remote Sens. Environ. 2013, 131, 14–37. [Google Scholar] [CrossRef]
- Norman, J.M.; Divakarla, M.; Goel, N.S. Algorithms for extracting information from remote thermal-IR observations of the Earth’s surface. Remote Sens. Environ. 1995, 51, 157–168. [Google Scholar] [CrossRef]
- Voogt, J.A.; Oke, T.R. Effects of urban surface geometry on remotely-sensed surface temperature. Int. J. Remote Sens. 1998, 19, 895–920. [Google Scholar] [CrossRef]
- Oke, T.R. Boundary Layer Climates; Routledge: London, UK, 1987. [Google Scholar]
- Lagouarde, J.-P.; Kerr, Y.H.; Brunet, Y. An experimental study of angular effects on surface temperature for various plant canopies and bare soils. Agric. For. Meteorol. 1995, 77, 167–190. [Google Scholar] [CrossRef]
- Chehbouni, A.; Nouvellon, Y.; Kerr, Y.H.; Moran, M.S.; Watts, C.; Prevot, L.; Goodrich, D.C.; Rambal, S. Directional effect on radiative surface temperature measurements over a semiarid grassland site. Remote Sens. Environ. 2001, 76, 360–372. [Google Scholar] [CrossRef]
- Menenti, M.; Jia, L.; Li, Z.-L.; Djepa, V.; Wang, J.; Stoll, M.P.; Su, Z.; Rast, M. Estimation of soil and vegetation temperatures with multiangular thermal infrared observations. IMGRASS, HEIFE and SGP 1997 experiments. J. Geophys. Res. 2001, 106, 11997–12010. [Google Scholar] [CrossRef]
- Rasmussen, M.O.; Göttsche, F.; Olesen, F.; Sandholt, I. Directional effects on land surface temperature estimation from Meteosat Second Generation for savanna landscapes. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4458–4468. [Google Scholar] [CrossRef]
- McGuire, M.J.; Balick, L.K.; Smith, J.A.; Hutchison, B.A. Modeling directional thermal radiance from a forest canopy. Remote Sens. Environ. 1989, 29, 169–186. [Google Scholar] [CrossRef]
- Lagouarde, J.-P.; Ballans, H.; Moreau, P.; Guyon, D.; Coraboeuf, D. Experimental study of brightness surface temperature angular variations of Maritime Pine (Pinus pinaster) stands. Remote Sens. Environ. 2000, 72, 17–34. [Google Scholar] [CrossRef]
- Ermida, S.L.; Trigo, I.F.; Dacamara, C.C.; Göttsche, F.M.; Olesen, F.S.; Hulley, G. Validation of remotely sensed surface temperature over an oak woodland landscape—The problem of viewing and illumination geometries. Remote Sens. Environ. 2014, 148, 16–27. [Google Scholar] [CrossRef]
- Lipton, A.E.; Ward, J.M. Satellite-view biases in retrieved surface temperatures in mountain areas. Remote Sens. Environ. 1997, 60, 92–100. [Google Scholar] [CrossRef]
- Minnis, P.; Khaiyer, M.M. Anisotropy of land surface skin temperature derived from satellite data. J. Appl. Meteorol. 2000, 39, 1117–1129. [Google Scholar] [CrossRef]
- Pinheiro, A.C.T.; Privette, J.L.; Mahoney, R.; Tucker, C.J. Directional effects in a daily AVHRR land surface temperature dataset over Africa. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1941–1954. [Google Scholar] [CrossRef]
- Trigo, I.F.; Peres, L.F.; DaCamara, C.C.; Freitas, S.C. Thermal land surface emissivity retrieved from SEVIRI/Meteosat. IEEE Trans. Geosci. Remote Sens. 2008, 46, 307–315. [Google Scholar] [CrossRef]
- Rao, P.K. Remote sensing of urban heat islands from environmental satellite. Bull. Am. Meteorol. Soc. 1972, 53, 647–648. [Google Scholar]
- Roth, M.; Oke, T.R.; Emery, W.J. Satellite-derived urban heat island from three coastal cities and the utilization of such data in urban climatology. Int. J. Rem. Sens. 1989, 10, 1699–1720. [Google Scholar] [CrossRef]
- Iino, A.; Hoyano, A. Development of a method to predict the heat island potential using remote sensing and GIS data. Energy. Build. 1996, 23, 199–205. [Google Scholar] [CrossRef]
- Lagouarde, J.-P.; Moreau, P.; Irvine, M.; Bonnefond, J.M.; Voogt, J.A.; Solliec, F. Airborne experimental measurements of the angular variations in surface temperature over urban areas: Case study of Marseille (France). Remote Sens. Environ. 2004, 93, 443–462. [Google Scholar] [CrossRef]
- Sugawara, H.; Takamura, T. Longwave radiation flux from an urban canopy: Evaluation via measurements of directional radiometric temperature. Remote Sens. Environ. 2006, 104, 226–237. [Google Scholar] [CrossRef]
- Lagouarde, J.P.; Irvine, M. Directional anisotropy in thermal infrared measurements over Toulouse city centre during the CAPITOUL measurement campaigns: First results. Meteorol. Atmos. Phys. 2008, 102, 173–185. [Google Scholar] [CrossRef]
- Lagouarde, J.P.; Hénon, A.; Kurz, B.; Moreau, P.; Irvine, M.; Voogt, J.; Mestayer, P. Modelling daytime thermal infrared directional anisotropy over Toulouse city centre. Remote Sens. Environ. 2010, 114, 87–105. [Google Scholar] [CrossRef]
- Lagouarde, J.P.; Hénon, A.; Irvine, M.; Voogt, J.; Pigeon, G.; Moreau, P.; Masson, V.; Mestayer, P. Experimental characterization and modelling of the nighttime directional anisotropy of thermal infrared measurements over an urban area: Case study of Toulouse (France). Remote Sens. Environ. 2012, 117, 19–33. [Google Scholar] [CrossRef]
- Voogt, J.A.; Soux, C.A. Methods for the assessment of representative urban surface temperatures. In Proceedings of the 3rd Symposium on the Urban Environment (AMS), Davis, CA, USA, 14–18 August 2000; pp. 179–180.
- Adderley, C.; Christen, A.; Voogt, J.A. The effect of radiometer placement and view on inferred directional and hemispheric radiometric temperatures of a urban canopy. Atmos. Meas. Tech. 2015, 8, 1891–1933. [Google Scholar] [CrossRef]
- Nichol, J.E. Visualisation of urban surface temperatures derived from satellite images. Int. J. Remote Sens. 1998, 19, 1639–1649. [Google Scholar] [CrossRef]
- Voogt, J.A.; Oke, T.R. Complete urban surface temperatures. J. Appl. Meteorol. 1997, 36, 1117–1132. [Google Scholar] [CrossRef]
- Voogt, J.A.; Grimmond, C.S.B. Modeling surface sensible heat flux using surface radiative temperatures in a simple urban area. J. Appl. Meteorol. 2000, 39, 1679–1699. [Google Scholar] [CrossRef]
- Chappell, A.; van Pelt, S.; Zobeck, T.; Dong, Z. Estimating aerodynamic resistance of rough surfaces using angular reflectance. Remote Sens. Environ. 2010, 114, 1462–1470. [Google Scholar] [CrossRef]
- Krayenhoff, E.S.; Voogt, J.A. A microscale three-dimensional urban energy balance model for studying surface temperatures. Bound.-Layer Meteorol. 2007, 123, 433–461. [Google Scholar] [CrossRef]
- Soux, A.; Voogt, J.A.; Oke, T.R. A model to calculate what a remote sensor sees of an urban surface. Bound.-Layer Meteorol. 2004, 112, 109–132. [Google Scholar] [CrossRef]
- Krayenhoff, E.S. A Microscale 3-D Urban Energy Balance Model for Studying Surface Temperatures. Master’s Thesis, Department of Geography, Western University, London, ON, Canada, 2005. [Google Scholar]
- Voogt, J.A. Assessment of an urban sensor view model for thermal anisotropy. Remote Sens. Environ. 2008, 112, 482–495. [Google Scholar] [CrossRef]
- Voogt, J.A.; Krayenhoff, E.S. Modeling urban thermal anisotropy. In Proceedings of the 5th International Symposium Remote Sensing of Urban Areas, Phoenix, AZ, USA, 14–16 March 2005.
- Krayenhoff, E.S.; Voogt, J.A. Combining sub-facet scale urban energy balance and sensor-view models to investigate effective thermal anisotropy on city structure. In Proceedings of the 7th Symposium on the Urban Environment, American Meteorological Society, San Diego, CA, USA, 10–13 September 2007.
- Henon, A.; Mestayer, P.G.; Lagouarde, J.-P.; Voogt, J.A. An urban neighborhood temperature and energy study from the CAPITOUL experiment with the SOLENE model. Theor. Appl. Climatol. 2012, 110, 197–208. [Google Scholar] [CrossRef]
- Stewart, I.D.; Oke, T.R. Local climate zones for urban temperature studies. Bull. Am. Meteorol. Soc. 2012, 93, 1879–1900. [Google Scholar] [CrossRef]
- Ashdown, I. Radiosity: A Programmers Perspective; John Wiley & Sons: New York, NY, USA, 1994. [Google Scholar]
- Mills, G.M. An urban canopy-layer climate model. Theor. Appl. Climatol. 1997, 57, 229–244. [Google Scholar] [CrossRef]
- Masson, V.; Grimmond, C.S.B.; Oke, T.R. Evaluation of the town energy balance (TEB) scheme with direct measurements from dry districts in two cities. J. Appl. Meteorol. 2002, 41, 1011–1026. [Google Scholar]
- Kurz, B. Modelisation De L’anisotropie Directionelle de la Temperature de Surface: Application au Cas de Milieu Forestiers et Urbains. Ph.D. Thesis, University of Toulouse, Toulouse, France, 2009. [Google Scholar]
- Rotach, M.W.; Vogt, R.; Bernhofer, C.; Batchvarova, E.; Christen, A.; Clappier, A.; Feddersen, B.; Gryning, S.-E.; Martucci, G.; Mayer, H.; et al. BUBBLE—An urban boundary layer meteorology project. Theor. Appl. Climatol. 2005, 81, 231–261. [Google Scholar] [CrossRef]
- Iqbal, M. An Introduction to Solar Radiation; Academic Press: Toronto, ON, Canada, 1983. [Google Scholar]
- Prata, A.J. A new long-wave formula for estimating downward clear-sky radiation at the surface. Q. J. R. Meteorol. Soc. 1996, 122, 1127–1151. [Google Scholar] [CrossRef]
- Stull, R.B. Meteorology for Scientists and Engineers, 2nd ed.; Brooks/Cole: Pacific Grove, CA, USA, 2000; p. 502. [Google Scholar]
- Oke, T.R. Street design and urban canopy layer climate. Energy Build. 1988, 11, 103–113. [Google Scholar] [CrossRef]
- Huang, H.; Liu, Q.; Qin, W.; Du, Y.; Li, X. Temporal patterns of thermal emission directionality of crop canopies. J. Geophys. Res. 2011, 116, D06114. [Google Scholar] [CrossRef]
- Stewart, I.D.; Oke, T.R.; Krayenhoff, E.S. Evaluation of the local climate zone scheme using temperature observations and model simulations. Int. J. Climatol. 2014, 34, 1062–1080. [Google Scholar] [CrossRef]
- Krayenhoff, E.S.; Voogt, J.A. Impacts of urban albedo increase on local air temperature at daily-annual time scales: Model results and synthesis of previous work. J. Appl. Meteorol. Climatol. 2010, 49, 1634–1648. [Google Scholar] [CrossRef]
- Kimes, D.S. Remote sensing of row crop structure and component temperatures using directional radiometric temperatures and inversion techniques. Remote Sens. Environ. 1983, 13, 33–55. [Google Scholar] [CrossRef]
- Dyce, D.R. A Sensor View Model to Investigate the Influence of Tree Crowns on Effective Urban Thermal Anisotropy. Master’s Thesis, Department of Geography, Western University, London, ON, Canada, 2014. [Google Scholar]
- Dyce, D.R.; Voogt, J.A. The influence of tree crowns on effective urban thermal anisotropy. In Proceedings of the ICUC9—9th International Conference on Urban Climate/12th Symposium on the Urban Environment, Toulouse, France, 20–24 July 2015.
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krayenhoff, E.S.; Voogt, J.A. Daytime Thermal Anisotropy of Urban Neighbourhoods: Morphological Causation. Remote Sens. 2016, 8, 108. https://doi.org/10.3390/rs8020108
Krayenhoff ES, Voogt JA. Daytime Thermal Anisotropy of Urban Neighbourhoods: Morphological Causation. Remote Sensing. 2016; 8(2):108. https://doi.org/10.3390/rs8020108
Chicago/Turabian StyleKrayenhoff, E. Scott, and James A. Voogt. 2016. "Daytime Thermal Anisotropy of Urban Neighbourhoods: Morphological Causation" Remote Sensing 8, no. 2: 108. https://doi.org/10.3390/rs8020108
APA StyleKrayenhoff, E. S., & Voogt, J. A. (2016). Daytime Thermal Anisotropy of Urban Neighbourhoods: Morphological Causation. Remote Sensing, 8(2), 108. https://doi.org/10.3390/rs8020108