A Direct and Fast Methodology for Ship Recognition in Sentinel-2 Multispectral Imagery
Abstract
:1. Introduction
2. Satellite Data and Ship Modeling
2.1. Sentinel-2 Data and Analysis
2.2. Ship Model and Parameters
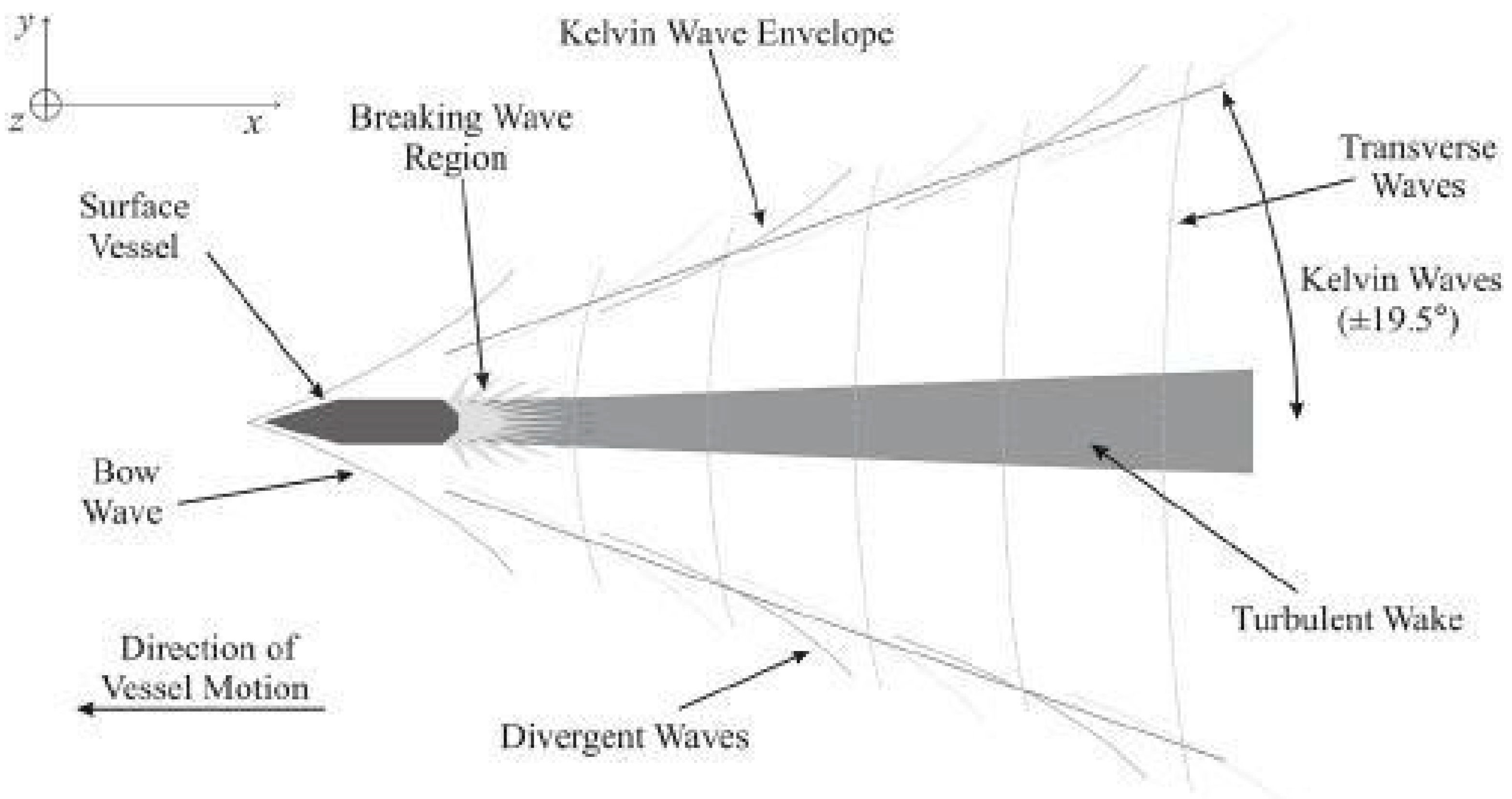
2.3. Turbulent Wakes and Kelvin Waves
3. Results
3.1. Multispectral Signatures
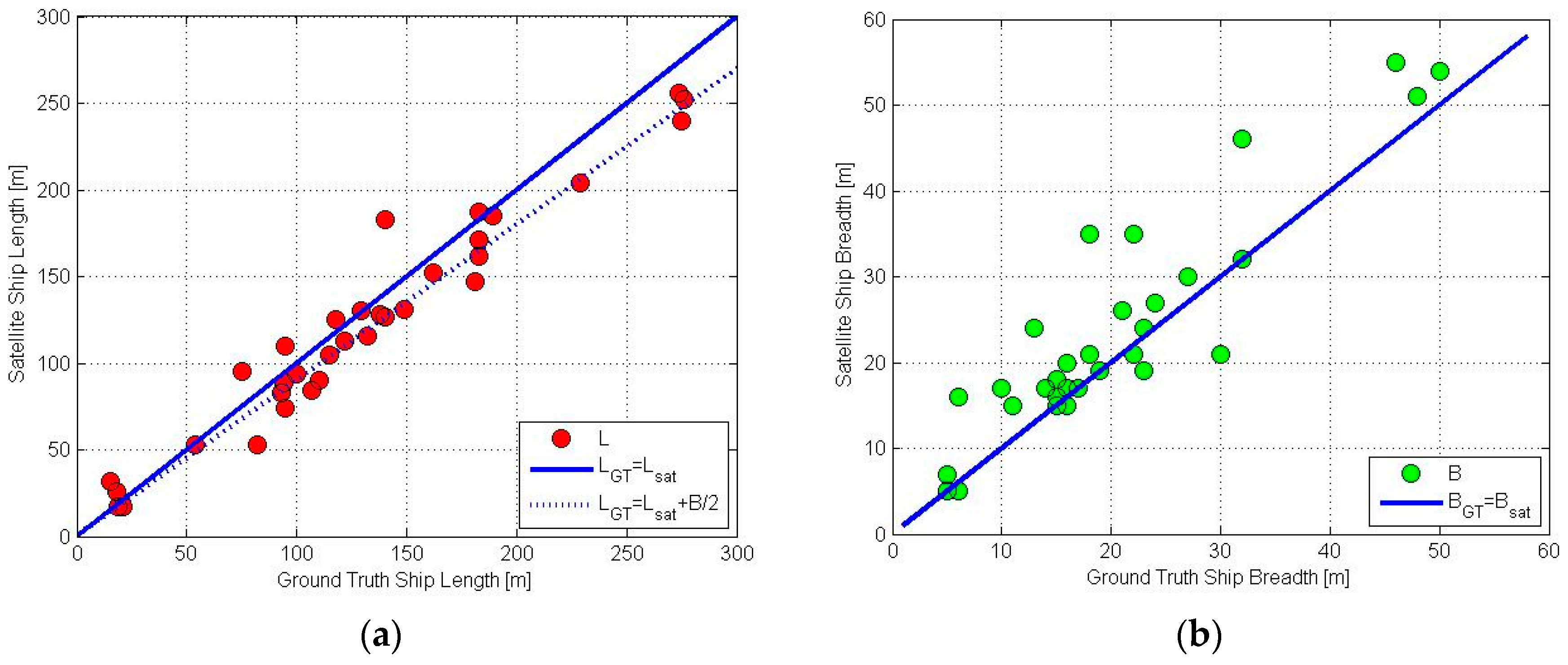
3.2. Ship’s Total Reflectance, Position, Heading, Length, and Breadth
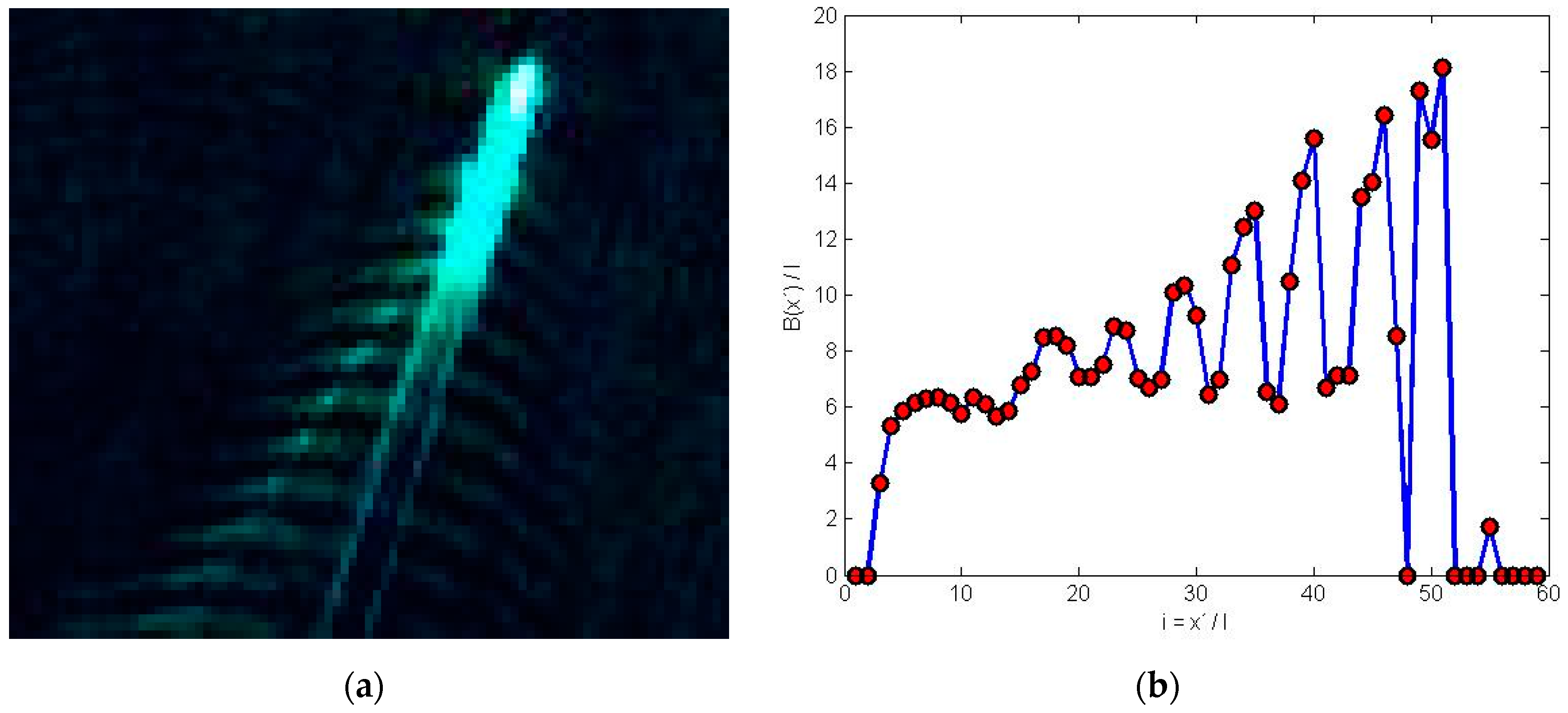
3.3. Wake Removal and Ship Speed
4. Discussion
5. Conclusions and Outlook
Acknowledgments
Conflicts of Interest
Appendix A. Determination of Ship Parameters
References
- ESA Sentinel-2 Delivers First Images. Available online: http://www.esa.int/Our_Activities/Observing_the_Earth/Copernicus/Sentinel-2/Sentinel-2_delivers_first_images (accessed on 7 January 2016).
- Krogager, E.; Heiselberg, H.; Møller, J.G.; von Platen, S. Fusion of SAR and EO imagery for Arctic surveillance. In Proceedings of the NATO IST-SET-128 Specialist Meeting, Norfolk, VA, USA, 4–5 May 2015.
- Brekke, C.; Weydahl, D.J.; Helleren, Ø.; Olsen, R. Ship traffic monitoring using multipolarisation satellite SAR images combined with AIS reports. In Proceedings of the 7th European Conference on Synthetic Aperture Radar (EUSAR), Friedrichshafen, Germany, 2–5 June 2008.
- Daniel, B.; Schaum, A.; Allman, E.; Leathers, R.; Downes, T. Automatic ship detection from commercial multispectral satellite imagery. Proc. SPIE 8743 2013. [Google Scholar] [CrossRef]
- Burgess, D.W. Automatic ship detection in satellite multispectral imagery. Photogramm. Eng. Remote Sens. 1993, 59, 229–237. [Google Scholar]
- Zhu, C.; Zhou, H.; Wang, R.; Guo, J. A novel hierarchical method of ship detection from spaceborne optical image based on shape and texture features. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3446–3456. [Google Scholar] [CrossRef]
- Corbane, C.; Marre, F.; Petit, M. Using SPOT-5 HRG data in panchromatic mode for operational detection of small ships in tropical area. Sensors 2008, 8, 2959–2973. [Google Scholar] [CrossRef] [PubMed]
- Corbane, C.; Najman, L.; Pecoul, E.; Demagistri, L.; Petit, M. A complete processing chain for ship detection using optical satellite imagery. Int. J. Remote Sens. 2010, 31, 5837–5854. [Google Scholar] [CrossRef]
- Tang, J.; Deng, C.; Huang, G.-B.; Zhao, B. Compressed-domain ship detection on spaceborne optical image using deep neural network and extreme learning machine. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1174–1185. [Google Scholar] [CrossRef]
- Gade, M.; Hühnerfuss, H.; Korenowski, G. Marine Surface Films; Springer: Heidelberg, Germany, 2006. [Google Scholar]
- Immitzer, M.; Vuolo, F.; Atzberger, C. First experience with Sentinel-2 data for crop and tree species classifcations in Central Europe. Remote Sens. 2016, 8, 166. [Google Scholar] [CrossRef]
- Eismann, M.T. Hyperspectral Remote Sensing. SPIE 2012, PM210, 748. [Google Scholar]
- Lapierre, F.D.; Borghgraef, A.; Vandewal, M. Statistical real-time model for performance prediction of ship detection from microsatellite electro-optical imagers. EURASIP J. Adv. Signal Process. 2009, 2010, 1–15. [Google Scholar] [CrossRef]
- Golbraikh, E.; Eidelman, A.; Soloviev, A. On the helical behavior of turbulence in the ship wake. J. Hydrodyn. Ser. B 2013, 25, 83–90. [Google Scholar] [CrossRef]
- Bouma, H.; Dekker, R.J.; Schoemaker, R.M.; Mohamoud, A.A. Segmentation and Wake Removal of Seafaring Vessels in Optical Satellite Images. Proc. SPIE 2013, 8897. [Google Scholar] [CrossRef]
- Thomson, W. On ship waves. Proc. Inst. Mech. Eng. 1887, 38, 409–434. [Google Scholar] [CrossRef]
- Selva, M.; Aiazzi, B.; Butera, F.; Chiarantini, L.; Baronti, S. Hyper-sharpening: A first approach on SIM-GA data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3008–3024. [Google Scholar] [CrossRef]

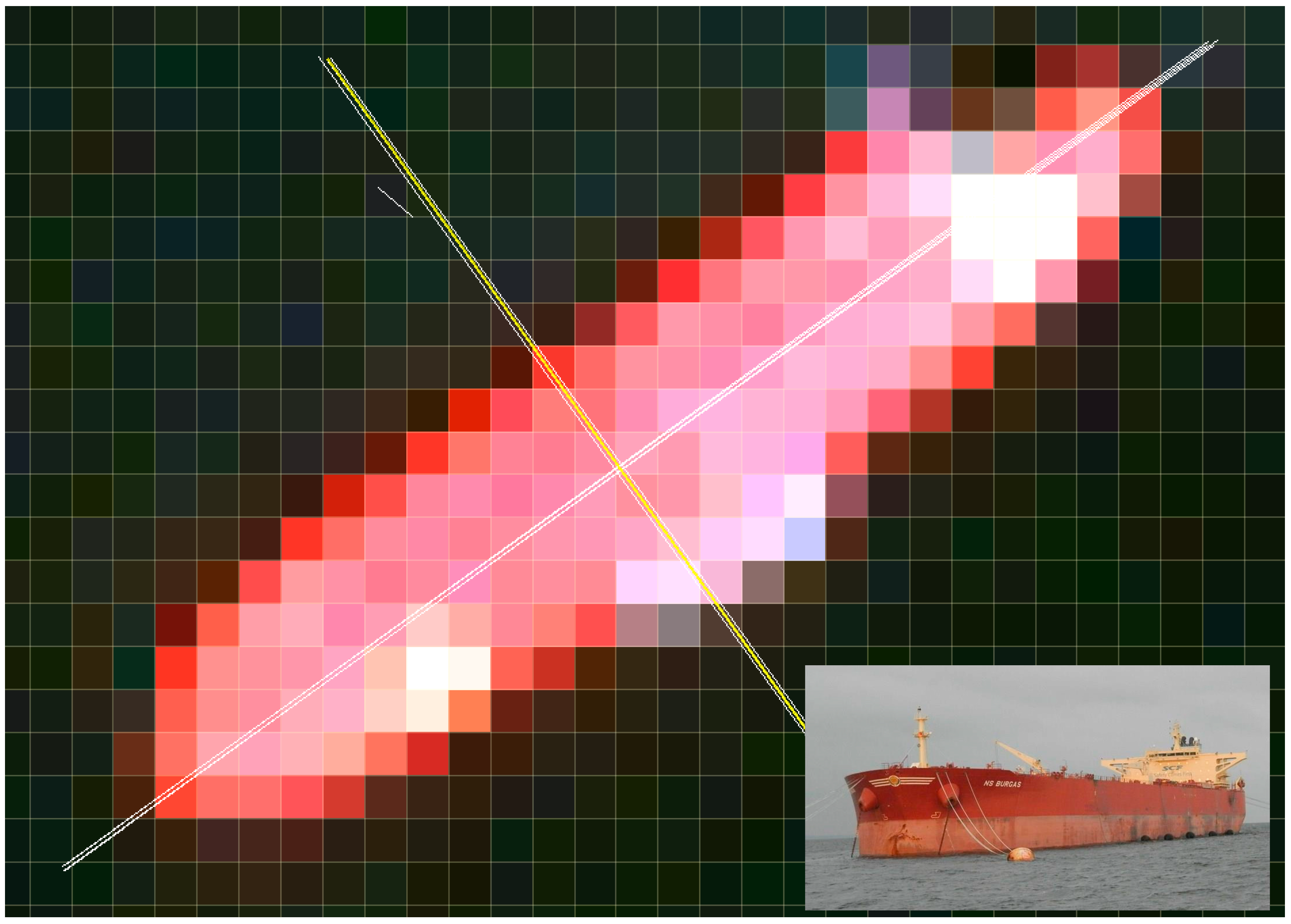
| Ship | I2+3+4 | θ | ε | L (m) | B (m) |
|---|---|---|---|---|---|
| NS Burgas | 26,370 | 33° | 0.913 | 240 (275) | 51 (48) |
| Eagle Barents | 32,976 | 21° | 0.912 | 252 (276) | 55 (46) |
| GijonKnutsen | 9939 | 17° | 0.950 | 187 (183) | 30 (27) |
| MarmaraMariner | 2827 | 4° | 0.968 | 130 (129) | 17 (17) |
| Trade Navigator | 2738 | 11° | 0.963 | 125 (118) | 17 (16) |
| Afines Sky | 8013 | 19° | 0.949 | 152 (162) | 24 (23) |
| Skaw Provider | 818 | 28° | 0.966 | 110 (95) | 15 (15) |
| Loireborg | 2997 | 33° | 0.955 | 113 (122) | 17 (14) |
| Solstraum | 2880 | 23° | 0.899 | 89 (94) | 21 (18) |
| Fjellstraum | 2134 | 1° | 0.950 | 94 (100) | 15 (16) |
| BW Yangtze | 14,530 | 33° | 0.951 | 204 (229) | 32 (32) |
| StenFjell | 4343 | −84° | 0.921 | 131 (149) | 27 (24) |
| SCL Basilia | 4130 | −97° | 0.947 | 127 (140) | 21 (22) |
| Karen Knutsen | 20,809 | −91° | 0.914 | 256 (274) | 54 (50) |
| Edith Kirk | 6208 | −100° | 0.939 | 171 (183) | 30 (27) |
| Grumant | 5256 | −104° | 0.966 | 147 (181) | 19 (23) |
| ChampionTrader | 4223 | −85° | 0.975 | 185 (189) | 21 (30) |
| Wilson Mersin | 1412 | −74° | 0.942 | 84 (107) | 15 (15) |
| Voorneborg | 4590 | −69° | 0.944 | 116 (132) | 20 (16) |
| Coral Monactis | 1765 | −69° | 0.885 | 74 (95) | 18 (15) |
| AtlanticaHav | 358 | −50° | 0.845 | 53 (82) | 15 (11) |
| Coral Obelia | 741 | −49° | 0.930 | 83 (93) | 16 (15) |
| Coral Pearl | 3201 | −60° | 0.934 | 105 (115) | 19 (19) |
| HHL Amur | 8078 | 25° | 0.920 | 128 (138) | 26 (21) |
| HDW Herkules | 1615 | −88° | 0.819 | 53 (54) | 17 (10) |
| Elly Kynde | 165 | 0° | 1 | 17 (19) | ≈5 (5) |
| Gottskar | 434 | 0° | 1 | 17 (21) | ≈5 (6) |
| Frank Maiken | 1081 | 18° | 0.485 | 26 (18) | 16 (6) |
| Haukur 1 | 5366 | −7° | 0.878 | 95 (75) | 24 (13) |
| Ritz Dueodde 1 | 525 | 28° | 0.904 | 32 (15) | 7 (5) |
| Torland 1 | 14,076 | −1° | 0.930 | 183 (140) | 35 (22) |
| Sea Endurance 2 | 4350 | 11° | 0.731 | 90 (110) | 35 (18) |
| Bow Triumph 2 | 11,227 | 2° | 0.852 | 162 (183) | 46 (32) |
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Heiselberg, H. A Direct and Fast Methodology for Ship Recognition in Sentinel-2 Multispectral Imagery. Remote Sens. 2016, 8, 1033. https://doi.org/10.3390/rs8121033
Heiselberg H. A Direct and Fast Methodology for Ship Recognition in Sentinel-2 Multispectral Imagery. Remote Sensing. 2016; 8(12):1033. https://doi.org/10.3390/rs8121033
Chicago/Turabian StyleHeiselberg, Henning. 2016. "A Direct and Fast Methodology for Ship Recognition in Sentinel-2 Multispectral Imagery" Remote Sensing 8, no. 12: 1033. https://doi.org/10.3390/rs8121033
APA StyleHeiselberg, H. (2016). A Direct and Fast Methodology for Ship Recognition in Sentinel-2 Multispectral Imagery. Remote Sensing, 8(12), 1033. https://doi.org/10.3390/rs8121033






