1. Introduction
Unmanned Aerial Vehicles (UAVs) are gaining enormous popularity due to their ability of providing high-quality spatial information in a very flexible manner and at a relatively low cost. Another considerable advantage is the simultaneous acquisition of a photogrammetric point cloud (i.e., a 3D model consisting of a collection of points with X, Y, Z coordinates) and very high-resolution imagery. Due to these reasons, the use of UAVs for a wide range of applications is being analyzed, such as agriculture [
1,
2], forestry [
3], geomorphology [
4], cultural heritage [
5] and damage assessment [
6]. Furthermore, the potential cost savings, improved safety and prospect of enhanced analytics they provide are being increasingly recognized as a competitive advantage from a business perspective [
7].
Similar to traditional aerial photogrammetry, UAV imagery is processed to obtain a dense point cloud, Digital Surface Model (DSM) and orthomosaic. In [
8], the general workflow of utilizing UAVs for mapping applications is described. UAVs are generally mounted with a camera and fly over the study area to obtain individual overlapping images. Flights are planned according to the camera parameters, UAV platform characteristics and user-defined specifications regarding the desired ground sampling distance and image overlap. The acquired images are then processed using photogrammetric methods, for which semi-automatic workflows are currently implemented in various software [
9]. Key tie points are identified in multiple images, and a bundle-block adjustment is applied to simultaneously identify the camera parameters of each image, as well as the location of these tie points in 3D space. Note that this step usually requires the inclusion of external ground control points for an accurate georeferencing. Dense matching algorithms, such as patch-based [
10] or semi-global [
11] approaches, are then applied to obtain a more detailed point cloud. The point cloud is filtered and interpolated to obtain a DSM that provides the height information for the orthomosaic derived from the UAV images. Thus, geospatial applications making use of UAV imagery have access to the information in a point cloud, DSM and orthomosaic for subsequent classification tasks.
Much research regarding the classification of urban areas from aerial imagery still relies on features from either only the imagery or the imagery and DSM. For example, Moranduzzo et al. [
12] divide the orthomosaic into tiles and use Linear Binary Pattern (LBP) texture features to propose class labels that are present in that area. Tokarczk et al. [
13] use Randomized Quasi-Exhaustive (RQE) feature banks to describe texture in UAV orthomosaics for the purpose of classifying impervious surfaces. Feng et al. [
14] use radiometric and Gray-Level Co-Occurrence Matrix (GLCM) texture features to identify inundated areas. The inclusion of elevation data greatly improves image classification results in urban areas [
15,
16]. Indeed, a comparison of building extraction methods using aerial imagery indicates that the integration of image- and DSM-based features obtains high accuracies for (large) buildings [
17]. However, combining the features derived from both the imagery and the point cloud directly (rather than the DSM) has been shown to prove beneficial for classification problems in the fields of damage assessment [
18] and informal settlement mapping [
19].
Combining features from multiple sources or from different feature subsets pertains to the field of multi-view learning [
20]. For example, in this case, point-cloud-based and image-based features could be considered as different views of a study area. Although both are obtained from the same data source (UAV images), the point-cloud represents the geometrical properties of the objects in the scene, whereas the orthoimagery contains reflectance information (i.e., color). Xu et al. [
20] distinguish three types of multi-view learning: co-training, sub-space learning and Multiple Kernel Learning (MKL). Co-training generally consists of training individual models on the different views and then enforcing the consistency of model predictions of unlabeled data. However, such methods require sufficiency, i.e., that each model is independently capable of recognizing all classes. This is not always the case, for example different roof types may be differentiated based on textural features from the imagery, but not geometrically distinguishable in the point cloud. Sub-space learning uses techniques, such as Canonical Correlation Analysis (CCA), to recover the latent subspace behind multiple views. The representation of samples in this subspace can be used for applications such as dimensionality reduction and clustering. MKL can be used in combination with kernel-based analysis and classification methods. Support Vector Machine (SVM) is a successful classification algorithm that utilizes a kernel function to map training sample feature vectors into a higher dimensional space in which the data are linearly separated. As a single mapping function may not be adequate to describe features with different statistical characteristics, MKL defines multiple mapping functions (either on different groups of features or the same group of features, but using different kernel parameters). A number of studies show that MKL achieves higher classification accuracies than single-kernel SVMs [
21]. For example, Gu et al. [
22] demonstrate an MKL algorithm for the integration of heterogeneous features from LiDAR and multispectral satellite for an urban classification problem. Although, as opposed to the integration of LiDAR and satellite imagery, the UAV point cloud and orthoimagery are obtained from a single set of cameras and sensors, we could expect MKL to have a similar beneficial effect.
In this paper, we illustrate how the utilization of classification algorithms that are specifically tailored to the integration of heterogeneous features is more appropriate for exploiting the complementary 2D and 3D information captured by UAVs for challenging classification tasks. The objective of this paper is two-fold. Firstly, we demonstrate the importance of using classification algorithms, such as MKL, which support the integration of heterogeneous features for the classification of UAV data. Secondly, we describe various feature grouping strategies, including a novel automatic grouping strategy, and compare their performances using a number of state-of-the-art MKL algorithms. The methods are compared through a multi-class classification task using UAV imagery of an informal settlement in Kigali, Rwanda.
2. Background
Support Vector Machines (SVMs) are robust classifiers that are particularly suited to high dimensional feature spaces and have proven to obtain high classification accuracies in remote sensing applications [
23]. These discriminative classifiers identify the linear discriminant function that separates a set of
n training samples
representing two classes
based on their respective feature vectors
in a non-linear feature space obtained by a mapping function
:
where
b is a bias term and
w is the vector of weight coefficients, which can be obtained by solving a quadratic optimization problem defined as:
where
C is a regularization parameter representing the relative cost of misclassification,
represent the slack variables associated with training samples, and
q is the dimensionality of the feature space obtained by
. Rather than calculating the mapping function
, the kernel trick can be employed to directly obtain a non-linear similarity measure between each pair of samples
. The optimization function is then solved using the Lagrangian dual formulation as follows:
where
are the Lagrangian multipliers. Various kernel functions are described in the literature, such as the common (Gaussian) Radial Basis Function (RBF) kernel:
The RBF kernel function has one parameter,
(often replaced by
), which represents the bandwidth of the Gaussian function. The bandwidth parameter can be determined by heuristics, such as the median distance between samples [
24] or cross-validation [
22,
25].
Intuitively, one can understand that not all features may be best represented by the same kernel parameters. Instead, Multiple Kernel Learning (MKL) utilizes
P independent input kernels, which allow nonlinear relations between training samples to be described by differing kernel parameters and/or differing input feature combinations. The calculation of the similarity between each pair of training samples using different kernel functions results in
P different kernel matrices
that are then linearly or non-linearly combined into a single kernel
for the SVM classification:
There are a number of advantages of MKL compared to standard SVM methods. Firstly, as it allows kernel parameters to be adapted towards specific feature groups, it may enhance the class separability. Secondly, the combined kernel can be constructed by assigning various weights to the input kernels, thus emphasizing more relevant features. In extreme cases, certain feature kernels may be assigned a weight of zero, thus causing the MKL to act as a feature selection method. Due to these characteristics, MKL is an appropriate classification method for combining features from heterogeneous data sources.
Much of the research regarding MKL for classification focusses on the strategies that are used to combine the input kernels. For example, a fixed rule can be adopted, where each kernel is given an equal weight [
26]. Alternatively, the individual kernel weights could then be determined based on similarity measures between the combined kernel and, for example, an optimal kernel (
), which perfectly partitions the classes. Niazmardi et al. [
27] refer to these as two-stage algorithms, as opposed to single-stage algorithms that optimize the kernel weighting and SVM parameters simultaneously. Although the latter group of methods, including SimpleMKL [
28] and Generalized MKL [
29], are more sophisticated and may potentially achieve higher classification accuracies, they often imply a higher computational complexity.
In fact, a review of MKL methods [
21] suggests that although MKL leads to higher classification accuracies than single-kernel methods, more complex kernel combination strategies do not always lead to better results. Rather, simple linear combination strategies seem to work well for non-linear kernels, such as RBF kernels. Gehler and Nowozin [
30] reached similar conclusions, stating that “baseline methods”, such as averaging or multiplying kernels, reach similar accuracies as more complex algorithms, but at a much lower computational complexity.
Considering that one of the main motivations behind MKL is the ability to adapt kernel parameters for the various features, it is surprising that little work has been done regarding how to divide features into groups so they optimally benefit from the tailored feature mappings. Various MKL studies report different grouping strategies, but none of them seem to compare a wide range of grouping strategies and compare the influence of the grouping strategies on the classification accuracy. Intuitively, such an optimal feature grouping should: (i) group features that are optimally represented by the same kernel parameters; and (ii) group features in a way that allows less or non-relevant features to be suppressed by the kernel weighting strategy. The main difficulty is that measures used to determine the latter, i.e., feature relevance, through non-linear similarity measures often depend on the former, i.e., the chosen kernel parameters. At the same time, the optimal values for these kernel parameters depend on which features are included in the group.
In practice, some studies assign each feature to a unique kernel [
25]. This allows the optimal kernel parameters to be defined per feature and a feature selection to be introduced through MKL methods promoting sparsity. Alternatively, Gu et al. [
22] and Yeh et al. [
31] adopt a multi-scale approach, defining a range of
r bandwidth parameters for each feature
f out of a total of
nf input features to create a total of
r∙nf kernels as the input for the MKL. However, such approaches may fail to describe the complex relations between features and suffer an increased computational complexity due to the presence of more kernels. Another grouping strategy depends on the origins of the image features. In this case, separate kernels are defined for spectral or spatial features, or multi-spectral and radar imagery, and have been shown to outperform assigning features to individual kernels [
25]. In an effort to define the groups automatically, one could consult the literature on view construction for co-training, the first multi-view learning technique. In general, co-training seems to work well when the different views provide complementary information [
20]. This is similar to the observations of Di and Crawford [
32], who found that using the “maximum disagreement” approach to spectral bands performed better than uniform or random sampling for hyperspectral image classification.
However, a direct comparison of different grouping strategies for MKL using heterogeneous features is still lacking. This paper addresses this issue and proposes an automatic algorithm that extracts potential kernel parameters from the training data and performs a backward feature-selection strategy to determine which features should be included in each kernel. It thus simultaneously functions as both a feature grouping and feature selection method.
3. Materials and Methods
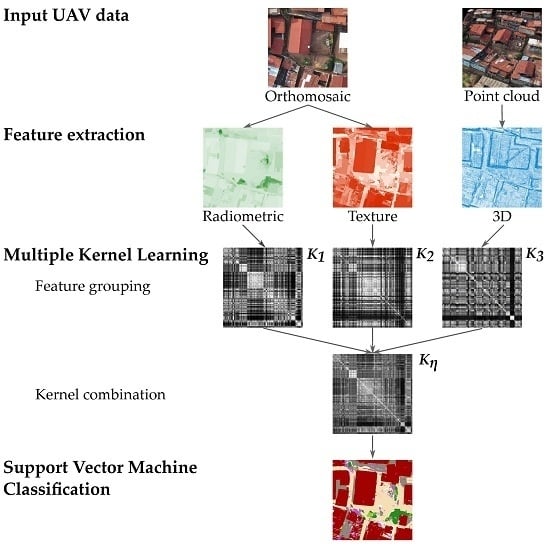
Multiple kernel learning can be applied to UAV data through the workflow presented in
Figure 1. Based on the input data, such as point clouds and imagery, the first step consists of extracting the relevant features from the input data. This may be supplemented by a feature selection strategy if desired. The next step is to divide the features into groups to define the input kernels, which are then combined into a single kernel that is used to define the SVM classifier. Depending on which MKL method is employed, the parameters for kernel weighting and SVM may be optimized jointly or separately. In the following section, we describe the heterogeneous features utilized in this study for the classification (
Section 3.1), various feature grouping strategies (
Section 3.2) and the multiple kernel learning algorithms utilized to classify the data (
Section 3.3).
3.1. Feature Extraction from UAV Data
Four types of features were derived from the orthomosaic and point cloud: 14 image-based radiometric features, 54 image-based texture features, 22 3D features per pixel and 22 3D features averaged over image segments (
Table 1). The image-based radiometric features consist of the original R, G, B color channels of the orthomosaic, their normalized values (r, g, b) and the ExG(2) vegetation index:
[
33], at the pixel-level and averaged over image segments. Here, the segments were obtained through a mean shift segmentation [
34] with a spatial bandwidth of 20 pixels and a spectral bandwidth of five gray values.
The image-based texture features are represented by Local Binary Pattern (LBP) features [
35]. These rotationally-invariant texture features identify uniform patterns, such as edges and corners, based on a defined number of neighboring pixels (
N) at a distance (
R) from the center pixel. The relative presence of each
N + 2 texture pattern in the local neighborhood can be summarized by constructing a normalized histogram for each mean shift segment, where the frequency of each bin is used as a feature.
The third type of features consist of 3D features extracted from the point cloud: spatial binning features, planar segment features and local neighborhood features. Spatial binning features describe the number of 3D points corresponding to each 2D image pixel, as well as the maximal height difference and height standard deviation of these points. Planar segment features are obtained by applying a surface growing algorithm to the point cloud [
36]. The algorithm calculates the planarity of the 10 nearest neighbors for each seed point and adds points within a radius of 1.0 m, which are within a 0.30-m threshold from the detected plane. The latter threshold is relatively high compared to the spatial resolution as in the informal settlement, there are often objects, such as rocks or other clutter, on top of roofs. This could result in non-planar objects, such as low vegetation, being considered as planar. However, such class ambiguities may be rectified through the other features included in our feature set. From each planar segment, four features were extracted: the number of points per segment, average residual to the plane, inclination angle and maximal height difference to the surrounding points. The local neighborhood features are based on the observation that the ratio between the eigenvalues of the covariance matrix of the XYZ coordinates of a point’s nearest neighbors can represent the shape of the local neighborhood [
37]. For example, the relative proportions between these eigenvalues may describe the local neighborhood as being planar, linear or scattered. More specifically, we consider an optimal neighborhood around each 3D point to define the covariance matrix and extract the 3D features described in the framework presented by Weinmann et al. [
38]. To assign 3D features calculated in the point cloud to 2D space, the attributes of the highest point for each pixel in the orthomosaic were assigned to the pixel in question. We thus obtain 3D features (spatial binning, planar segment and neighborhood shape) for each pixel.
The fourth and final type of features consist of averaging these pixel-based 3D features over the image segments. For a more detailed description of how the various features were extracted, the reader is referred to Gevaert et al. [
19]. All feature values are normalized to a scale between 0 and 1 before feature grouping and classification.
3.2. Feature Grouping Strategies
3.2.1. Reference Grouping Strategies
After calculating the input features, each feature
f in the complete set of features
S (
), where
nf indicates the total number of features, must be assigned to a group
Gm,
m = 1,…,
P, where each group will form an individual input kernel
Km. Seven MKL grouping strategies are compared based on: (i) individual kernels; (ii) prior knowledge; (iii) random selection; (iv) feature similarity; (v) feature diversity; (vi) the kernel-based distance between samples; and (vii) a novel multi-scale Markov blanket selection scheme. In Case (i), each feature is assigned to an individual input kernel, so 112 features result in 112 input kernels
Km. The prior knowledge strategy of Case (ii) consists of four kernel groups according to feature provenance: image-based radiometric features, image-based texture features, 3D features per pixel and 3D features averaged over image segments (i.e., the four types of features listed in
Table 1). In Case (iii), the random selection strategy divides the features arbitrarily into a user-defined number of features groups. For Case (iv) the similarity strategy is represented by a kernel k-means clustering [
39] over the feature vectors, thus grouping them into clusters that expose similar patterns in the input data. Di and Crawford [
32] found that such an approach worked better than uniform or random feature grouping for multi-view active learning in hyperspectral image classification tasks.
For Case (v), diverse kernels are obtained by solving the Maximally-Diverse Grouping Problem (MDGP) through a greedy construction approach [
40]. The basic idea of the approach is to iteratively select one unassigned feature, calculate the value of a disparity function considering the assignation of this feature to each feature group
Gm and appoint the feature the group to which its membership would maximize the disparity. To do this, the user first defines the desired number of groups
P, as well as the minimum (
a) and maximum (
b) number of features per group. The population of each group
Gm is started by randomly selecting one of the features in the feature set
S. The remaining features in the set of variables not yet assigned to a group are iteratively assigned to one of the groups
Gm. One feature
fi is selected at random, and the disparity function
(6) is calculated considering its inclusion into each group, which has not yet reached the minimal number of features (i.e., |
Gm| <
a). Once each group has reached the minimal number of features, each group that has not yet reached the maximum (i.e., |
Gm| <
b) is considered. Here, the disparity function describes the normalized sum of the distances between features:
where |
Gm| is the number of elements in group
Gm and the distance
is obtained from the Sample Distance Matrix (SDM). In this case, the SDM is an
nf × nf matrix where the element SDM
i,j gives the
-norm of the difference between features
fi and
fj. In other words, the disparity function is defined as the sum of the Euclidean distance between all of the features within a group over all of the samples divided by the number of features within the group.
Allowing kernel parameters to be set differently for various groups of features has been mentioned as one of the benefits of MKL. Furthermore, the mean distance between training samples is sometimes used as a heuristic for the bandwidth parameter of an RBF kernel [
24]. Therefore, we also analyze the utility of grouping features based on the distance between samples. For Case (vi), we consider using the median (a) within-class vs. (b) between-class distances, as well as (c) a combination of both distances to group the features. To implement this, an SDM is constructed for each single feature. Note that here, the SDM is a
matrix representing the distance between the samples as opposed to the feature distance matrix described in the previous paragraph. The median within-class and between-class distances for each class is obtained by finding the median of the relevant SDM entries and using this median as a feature attribute. For example, the within-class distance of class
u is the median of the SDM entries of all rows and columns representing samples belonging to class
u. Similarly, the between-class distance of class
u is the median of all entries corresponding to rows of samples labeled as
u and columns of all samples not labelled as
u. Note that the median is used instead of the mean to reduce the effect of possible outliers. A classification problem with
Q classes will thus result in
Q feature attributes representing within-class distances, and
Q attributes representing between-class distances. These are simply concatenated to
Q +
Q attributes for the third approach (i.e., within- and between-class distances). These feature attributes are then used as the input for a kernel k-means clustering. Thus, features that have similar (within- or between-class) sample distances and that may thus be best represented by the same bandwidth parameter will be grouped together.
3.2.2. Proposed Feature Grouping Strategy
For the final method (vii), we propose an automatic grouping strategy. Remember that the benefits of applying MKL rather than single-kernel SVM models include feature weighting and the use of different kernel parameters for various feature groups. Regarding the former, MKL allows some feature groups to be given more emphasis; in some cases, it may even assign certain kernels a weight
ηm of zero, thus suppressing noisy or irrelevant feature groups. However, MKL can only suppress certain input kernels and, therefore, can only function as a feature selector if each feature is indeed assigned to a unique kernel, as in Case (i) above. This may fail to account for non-linear relationships that would be identified if features are combined in the same kernel. The second potential benefit of MKL was to allow different kernel mappings for the different feature groups. Gu et al. [
22] even recommended using different bandwidths for the same feature groups, allowing similarities between samples to be recognized along multiple scales. They used pre-defined bandwidth intervals from 0.05 to 2.0 in intervals of 0.05. Yeh et al. [
31] also construct multiple input kernels for each feature by selecting different bandwidth parameters, defining a ‘group’ as the conjunction of different kernel mappings of a single feature. MKL is applied to ensure sparsity amongst features, thus functioning as a feature selection method. Unlike [
22], they select the bandwidth parameters in a data-driven manner based on the standard deviation of the distance between all training samples. Although both methods enable a multi-scale approach to define optimal feature representations using multiple bandwidth parameters, both methods pre-define which features will be grouped together in the input kernels. This could potentially lose non-linear relations between different features.
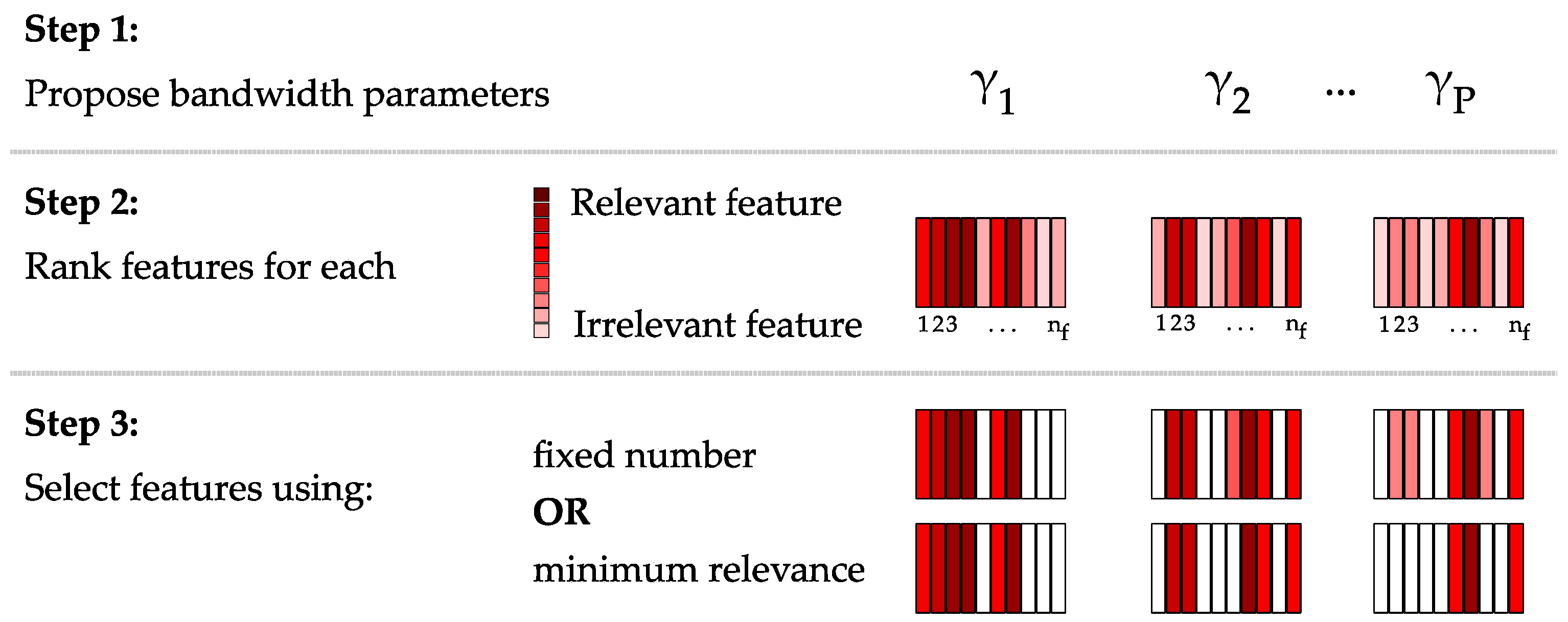
A good feature grouping strategy should therefore remove irrelevant features before kernel construction and allow features to be grouped according to optimal kernel parameters. The novel feature grouping algorithm we propose here does this by first analyzing the dataset to identify candidate bandwidth parameters, performs a feature ranking for each candidate bandwidth and restricts the features within each group according to a pre-defined threshold. The latter can be based on either defining the number of features per kernel or by defining a limit to the cumulative feature relevance. This simultaneous feature grouping and feature selection workflow consists of three steps: (i) selecting candidate bandwidth parameters; (ii) ranking the features using each parameter; and (iii) defining the cut-off criterion that selects the number of features per group (
Figure 2). An additional benefit of the method is that it provides a heuristic for choosing the bandwidth parameter for the RBF kernel.
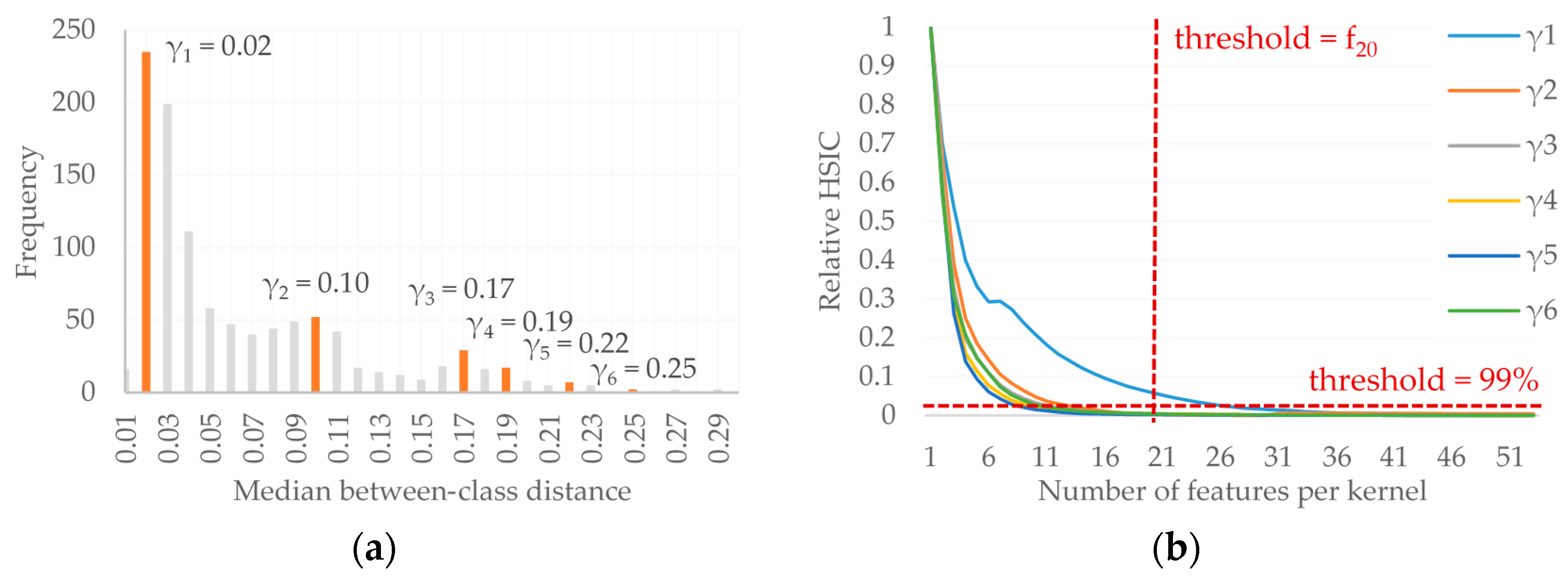
In the first step, potential bandwidth parameters are identified by selecting the median between-class distances for each feature. These between-class distances are obtained by selecting all entries of the SDM that correspond to two samples from different classes. A histogram of these between-class distances is constructed, from which automatic methods can be used to select the potential bandwidth parameters (
Figure 3a). Here, we simply select histogram bins associated with local maxima, i.e., which have a higher frequency than the two neighboring bins. Each of the bins corresponds to a potential bandwidth parameter; thus, different bandwidths are used for the various kernel groups and capturing data patterns at multiple scales. If the histogram does not present local peaks, other strategies could be considered, such as taking regular intervals over the possible between-class distances.
In the second step, a feature selection method based on a kernel-based class separability measure and backwards-elimination [
41] is employed to determine which features to include in each kernel. The idea is to use a supervised strategy to identify the Markov blanket of the class labels [
41]. That is to say, we attempt to identify which features are conditionally independent of the class labels given the remaining features. These conditionally independent features therefore do not influence the class labels and may be removed. By using kernel class separability measures, we can identify non-linear class dependencies in the reproducing kernel Hilbert space. This is implemented by constructing a kernel using all of the features and the candidate bandwidth in question and calculating the class separability measure for an ideal kernel. One by one, the features are removed, and the measure is calculated again. The feature whose removal results in the lowest decrease in class separability is considered to be the least relevant and is removed from the set. The process is repeated until all features are ranked from most to least relevant for each candidate bandwidth. The method would work with any kernel-based class separability measure.
Finally, the user must define the cut-off metric of which features to select in each kernel based on the provided feature ranking for each bandwidth. In this case, the user can choose to either define the maximal number of features per kernel or to use a cumulative relevance metric, such as selecting the number of features that first obtain 99.9% of the maximum cumulative similarity measure provided by the feature ranking (
Figure 3b). It should be noted that this feature grouping strategy also allows for a single feature to be included in various kernels. In theory, this could result in two groups containing identical features, but represented by different bandwidth parameters. The proposed methodology also potentially functions as a feature selection method, as irrelevant or redundant features are likely to be at the bottom of the feature ranking and may therefore not be included in any of the input kernels.
3.3. Kernel Weighting Strategies
3.3.1. Class Separability Measures and Ideal Kernel Definition
Various studies report that there are no large differences in different multiple kernel learning methods in terms of accuracy [
21]. Furthermore, two-stage algorithms that update the combination function parameters independently from the classifier have a lower computational complexity [
27]. Therefore, we hypothesize that the use of kernel class separability measures, or kernel alignment measures, between the individual kernels and an ideal kernel will provide an advantageous trade-off between computational complexity and classification accuracy. The ideal target kernel represents a case of perfect class separability, where kernel values for samples from the same class maximal and samples from different classes have minimal kernel values. Therefore, the similarity of an input kernel
to a target ideal kernel
provides an indication of the class separability given the input kernel. Such measures may be used to optimize kernel parameters or to define the proportional weights of the various feature kernels in the weighted summation. In this case, named class-separability-based MKL (CSMKSVM), the class separability measure
of each individual kernel
and an ideal kernel
is calculated, and then, a proportional weighting is applied as follows:
Qiu and Lane [
42] used a similar heuristic based on the kernel alignment measure [
43]. Here, we compare four class separability measures found in the literature: the square Hilbert-Schmidt norm of the cross-covariance matrix (HSIC) [
44,
45] (8); (ii) Kernel Alignment (KA) [
43] (9); (iii) Centered-Kernel Alignment (CKA) [
46] (10); and (iv) Kernel Class Separability (KCS) [
47] (11).
where
,
being the Kronecker delta and having a value of 1 if
i and
j adhere to the same class and 0 if they have different class labels,
Tr(.) indicates the trace function,
n is the total number of samples,
is the number of samples in the first class,
is the number of samples in class
Q,
and
is an
n × 1 vector of ones.
is any input kernel and could therefore corresponds to either
or
depending on whether the class separability measure is being calculated for the input kernel or combined kernel, respectively.
3.3.2. Comparison to Other MKL Methods
Once the most adequate kernel class separability measure and ideal kernel definition have been selected, the following experiments serve to compare the proposed method to benchmark MKL methods and the influence of the various feature grouping strategies. Six benchmark Multiple Kernel SVM (MKSVM) methods are selected from the MATLAB code provided by Gönen and Alpaydin [
21] (
https://users.ics.aalto.fi/gonen/) and compared to the kernel Class-Separability method (CSMKSVM) described previously. They consist of methods using a Rule-Based linearly-weighted combination of kernels (RBMKSVM), Alignment-Based methods based on the similarity of the weighted summation kernel and an ideal kernel (ABMKSVM) and methods that initiate a linearly (Group Lasso-based MKL (GLMKSVM) and SimpleMKL) or nonlinearly (Generalized MKL (GMKSVM) and Non-Linear MKL (NLMKSVM)) combined kernel and use the dual formation parameters to iteratively update the weight.
The first, RBMKSVM, is a fixed-rule method in which each kernel is given an equal weight
, and the resulting combined kernel is therefore simply the mean of the input kernels. This is followed by CSMKSVM, where the weights are defined by the proportional class separability measure as described in the previous section. The second reference method, ABMKSVM, forgoes the use of a class separability measure, but rather optimizes the difference between the combined kernel and ideal kernel directly. This optimization problem can be solved as follows:
Other methods use the SVM cost term, rather than the distance to an ideal kernel, to update the weights. This can be done by initiating the kernel weights
to obtain a single combined kernel and performing the SVM on this kernel. The results of the SVM are then used to update the kernel weights. For example, recognizing the similarity between the MKL formulation and group lasso [
48], Xu et al. [
49] update the kernel weights according to the
-norm. For GLMKSVM, we use the
-norm, which results in using (13) to update the kernel weights.
Similarly, SimpleMKL [
28] uses a gradient decent on the SVM objective value to iteratively update the kernel weights. The combined kernel is initiated as a linear summation where the weight of each kernel is defined as
. The dual formulation of the MKL SVM is solved (15), and the weights
are optimized using the gradient function provided in (16).
Varma and Babu [
29] use a similar gradient descent method for updating the weights (17), but perform a nonlinear combination of kernels (18), rather than a weighted summation of kernels, as in SimpleMKL.
Here, the regularization function r(∙) is defined as
. NLMKSVM also presents a non-linear combined kernel, namely the quadratic kernel presented in (19); where the weight optimization is defined as a min-max problem [
50] (20) and the weights defined as a
-norm bounded set
(21) with
= 0 and
= 1 in the present implementation.
3.4. Experimental Set-Up
Remote sensing is a valuable tool for providing information regarding the physical status of informal settlements, or slums. Although many studies make use of satellite imagery, even sub-meter imagery may not be sufficient to distinguish between different objects, such as buildings, and to identify their attributes [
51]. This motivates the use of UAVs, which are capable of providing images at a higher spatial resolution, thus enabling improved detection and characterization of objects, as well as more detailed elevation information than is available from satellite imagery. The flexible acquisition capabilities also facilitate the acquisition of recurrent imagery to monitor project implementation, especially in the context of slum upgrading projects. These are some of the incentives that motivate the use of UAVs for informal settlement mapping.
The UAV dataset used for the experiments consists of a point-cloud and RGB orthomosaic of an informal settlement in Kigali, Rwanda, which was acquired using a DJI Phantom 2 Vision + quadcopter in 2015. The UAV acquired images with the standard 14 megapixel fish-eye camera (110° FOV) at an approximate 90% forward- and 70% side-lap. The images were processed using the commercial software Pix4D Mapper (Version 2.0.104). The point cloud densification was performed using the ‘Low (Fast)’ processing option, a matching window size of 7 × 7 pixels and only matching points that are present in at least four images. The DSM was constructed using the Inverse Distance Weighting (IDW) interpolation, with the noise filtering and surface smoothing options enabled. The resulting 8-bit orthomosaic has a spatial resolution of 3 cm. The average density of the utilized point clouds is 1031 points per m
2. This density depends on the data processing parameters, as well as the characteristics of the land cover type. For this application, the point density ranges between 796 and 1843 points per m
2 according to the land cover (see
Table 2).
The study area itself is characterized by small, irregular buildings, narrow footpaths and a steep topography. Ten thematic classes are defined for the classification problem: three different types of building roofs (corrugated iron sheets, galvanized iron with a tile pattern and galvanized iron with a trapezoidal pattern), high vegetation, low vegetation, bare surfaces, impervious surface, lamp posts, free-standing walls and clutter. The latter class may consist of, for example, laundry hung out to dry, the accumulation of solid waste on the streets, passing cars and pedestrians. Reference data were defined by visual interpretation and manually labelling pixels in the orthomosaic (based on the results of the over-segmentation and manually adjusting segment boundaries if necessary).
Ten sets of training data (n = 2000) were extracted from the Kigali dataset. Five sets followed an equal sampling strategy (nc = 200), and five sets followed a stratified sampling strategy, which allows an analysis to be made regarding the sensitivity of kernel class separability measures to unequal class sizes. A set of 5000 samples was extracted for testing. The first set of experiments (Experiment I.A. and Experiment I.B.) compared the class separability measures and ideal kernel definitions using the prior knowledge (Case (ii)) feature grouping. The average Overall Accuracy (OA) for each of the folds, along with the standard deviation, is provided for the equal and stratified sampling training sets separately. In Experiment I.A. the class separability measures are used to define the optimal bandwidth parameter for each input RBF kernel Km. Experiment I.B., on the other hand, uses the class separability measure both to optimize the bandwidth parameter of Km and to perform the proportional kernel weighting in (7) to obtain the kernel weights . In both cases, the search space of the bandwidth parameter was defined by first defining the bandwidth parameter as the mean intra-class -norm and defining a range of as 2−5- to 25-times this mean bandwidth. For these experiments, three different ideal kernel definitions are compared: assigning values of 1, 1/nc and 1/nc2 to samples belonging to the same class, where nc represents the number of samples within that specific class.
The second set of experiments analyzed both the influence of feature grouping and MKL methodology. Regarding the feature grouping strategy, the random-, similarity-, diversity- and class-difference-based methods require the user to define the number of desired kernels. For these experiments, six kernels were defined, as this is the number of kernels identified by the automatic feature grouping method. For the novel feature grouping strategy, we use the results of Experiment I to select the best class separability measure (the HSIC). Furthermore, we report the results of using two different cut-off metrics to define how many features to include in each kernel: we report the results when defining a maximum of 45 features per kernel (HSIC-f
45) and when using the 99.9% cumulative relevance cut-off per kernel (HSIC-99.9%). These thresholds were selected based on the results of the feature ranking (e.g.,
Figure 3b). The minimum (
a) and maximum (
b) number of features per group using the diverse kernel strategy were set to
a = 5 and
b = 70 based on experimental analyses.
MKL was performed on these feature kernels using the seven algorithms described above. Note that the grouping strategy was applied separately for each fold, so the feature groups will not by definition be the same for each training set. Once the groups were identified, the same feature kernels were used as input for each MKL method.
The methods were again compared by computing the mean overall accuracy over each of the 10 folds with reference to the same 5000 sample test set. The error matrix of the CSMKSVM method using the HSIC-f
45 feature grouping strategy is also presented, as well as the correctness (22) and completeness (23) for each of the 10 thematic classes.
where TP indicates the number of true positives per class, FP is the number of false positives and FN is the number of false negatives.
Furthermore, the MKL methods were compared to two baseline classifiers: a standard SVM classifier, implemented in LibSVM [
52], where all features are combined in a single kernel, and a random forest classifier. For the SVM, RBF bandwidth parameter
was defined as described previously, and the regularization parameter
C was optimized through a 5-fold cross-validation between 2
−5 and 2
15. Regarding the random forest classifier, the number of trees was optimized between 100 and 1500 in steps of 100.
In a final step, we provide classification maps of 30 × 30 m subsets of the Kigali dataset. Similar to the other experiments, 2000 labelled pixels were extracted from ten tiles representing the different characteristics of the study area through stratified sampling. These pixels were used to construct a single-kernel SVM, and CSMKSVM using the HSIC-f45 feature grouping strategy. Classification maps of three of the tiles are provided to illustrate the results.
5. Conclusions
In this paper, we demonstrate the suitability of MKL as a classification method for integrating heterogeneous features obtained from UAV data. Utilizing a novel feature grouping strategy and a simple heuristic for weighting the individual input kernels (CSMKSVM), we are able to obtain a classification accuracy of 90.6%, an increase of 5.2% over a standard SVM implementation and 4.1% over a random forest classification model. These improvements are statistically significant with a p-value <0.005, which indicates strong evidence as standard tests use confidence levels of 0.05 or 0.01 to indicate significant differences. A series of experiments reinforces observations by other researchers that complex kernel weighting strategies do not seem to perform significantly better than simple heuristics, such as a proportional weighting based on the HSIC class separability measure.
Furthermore, we observe that much of the literature on MKL classification has focused on ways to weigh the kernels, but not how to group the features appropriately. Experiments demonstrate the importance of the latter to effectively apply MKL. In this application, satisfactory results are obtained when grouping features based on their provenance (i.e., radiometric, texture or 3D features). A novel, automated grouping strategy is also proposed, which consistently obtains high classification accuracies for all seven MKL methods that were tested here. Furthermore, for most MKL methods, the proposed feature grouping strategy performed better than when using individual kernels for each feature. This underlines the importance of proper feature grouping, which not only produces a high and stable overall accuracy, but also reduces the number of input kernels for the MKL and, thus, reduces the computational complexity. These observations support a deeper understanding of MKL for classification tasks. Future applications of classification tasks with heterogeneous features are recommended to start by grouping features according to the proposed automated method and to use CSMKSVM to weight the input kernels for the SVM classification. Finally, this manuscript demonstrates that features extracted from point clouds and orthoimagery derived from UAVs are suitable for land cover classification. Additional research would be needed to analyze to what degree the features are sensitive to the type of UAV, flight parameters and algorithms utilized to produce the point clouds and orthoimagery.