Water Budget Analysis within the Surrounding of Prominent Lakes and Reservoirs from Multi-Sensor Earth Observation Data and Hydrological Models: Case Studies of the Aral Sea and Lake Mead
Abstract
:1. Introduction
- Estimation of the balance of all hydrological fluxes acting vertically and horizontally. The rate of water storage change (ΔS/dt) in a region is the sum of evapotranspiration (ET), precipitation (P) and net surface runoff (ΔR) Equation (1),Based on the applied datasets, two net fluxes are derived from Equation (1). Flux-1 is obtained by combining the Global Precipitation Climatology Centre (GPCC) precipitation data with the WaterGAP Global Hydrological Model (WGHM) ET and in-situ runoff. Flux-2 is obtained by combining the Tropical Rainfall Measuring Mission (TRMM-3B43) precipitation data with the Global Land Data Assimilation System (GLDAS) ET and in-situ runoff.ΔS/dt = P − ET + ΔR
- Estimation of the water storage change (ΔS) in a region is the sum of storages in soil moisture (SM), snow water equivalent (SWE) and surface water (SW) (Equation (2)). Due to the lack of direct measurements, groundwater storage is not considered in the equation.The hybrid storages combine the ΔSW from remote sensing-based reservoir volume estimates with ΔSWE and ΔSM from hydrological model outputs. The WGHM based hybrid storage is referred to as Storage-1, and the GLDAS-based hybrid storage is referred to as Storage-2.ΔS = ΔSM + ΔSWE + ΔSW
- Estimation of total water storage variability (ΔTWS) from time-variable gravity data observed by GRACE. The ΔTWS considers the contribution from the surface (reservoirs, river-network, snow, and ice) and subsurface (soil moisture and groundwater) storage changes. However, GRACE cannot resolve individual flux contributions to ΔTWS and the interactions among them.
2. Study Area
3. Data and Methodology
3.1. Sum of Hydrological Mass Fluxes (ΔS/dt)
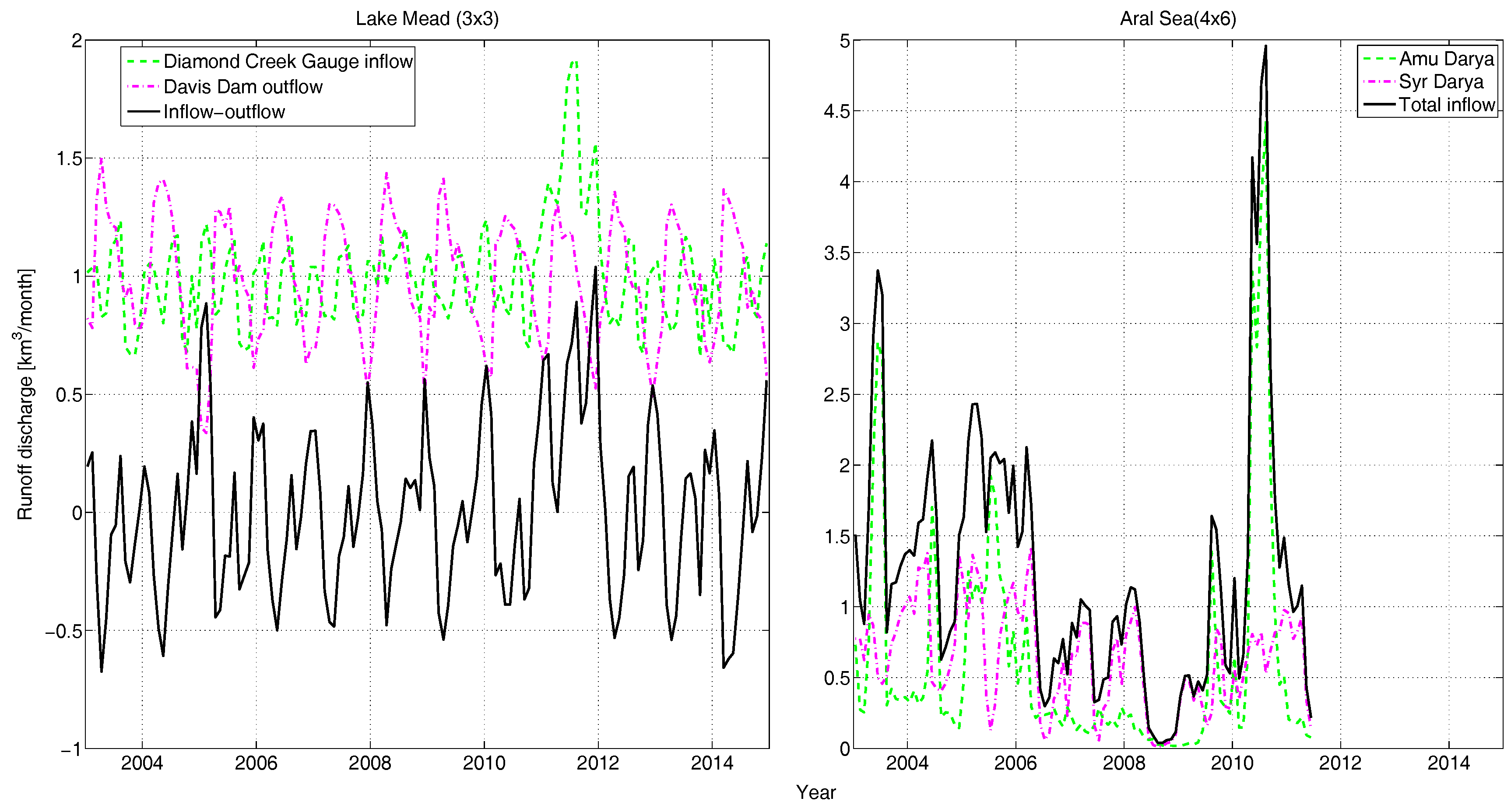
3.1.1. Net Surface Runoff (ΔR)
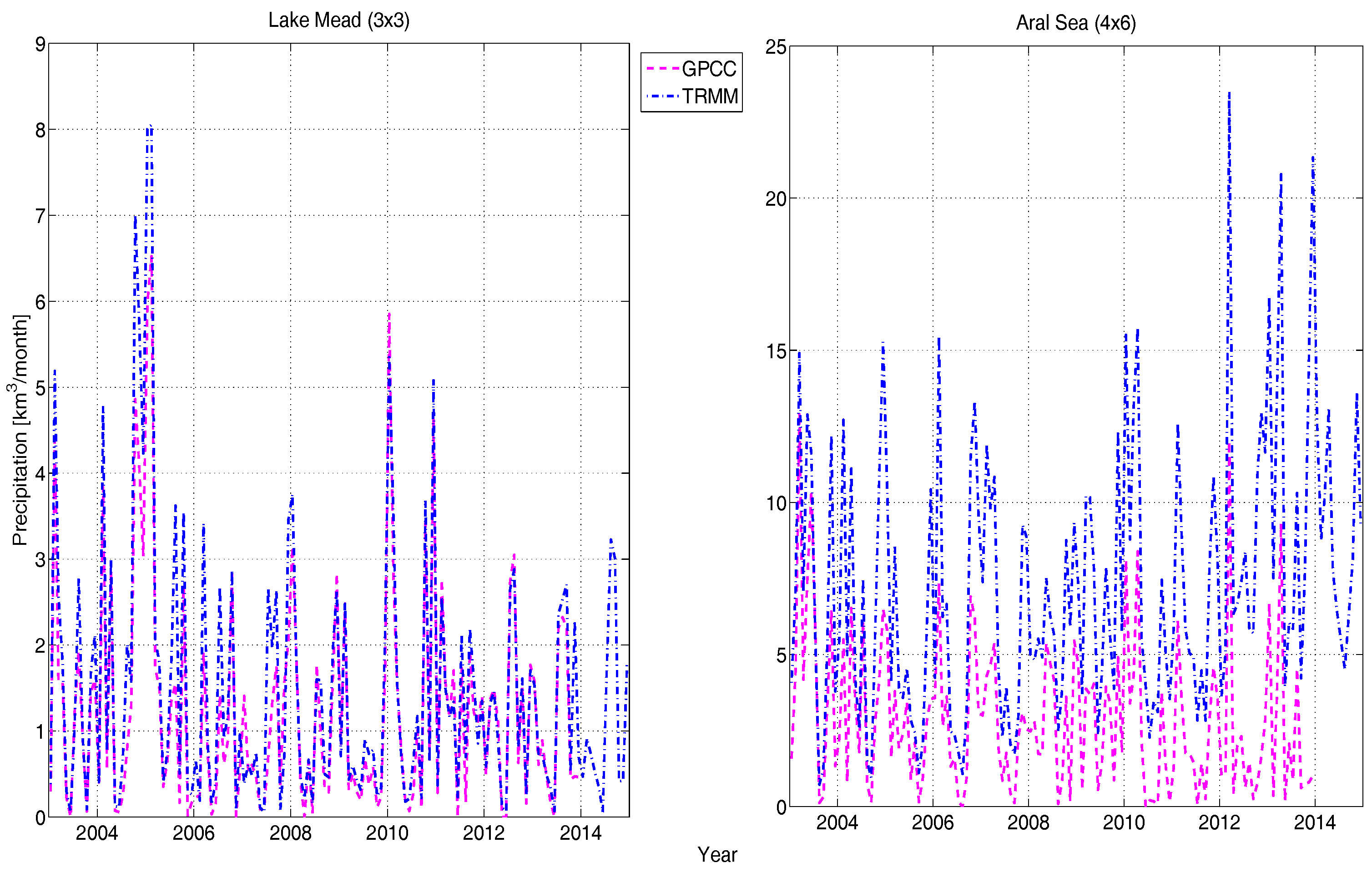
3.1.2. Precipitation (P)
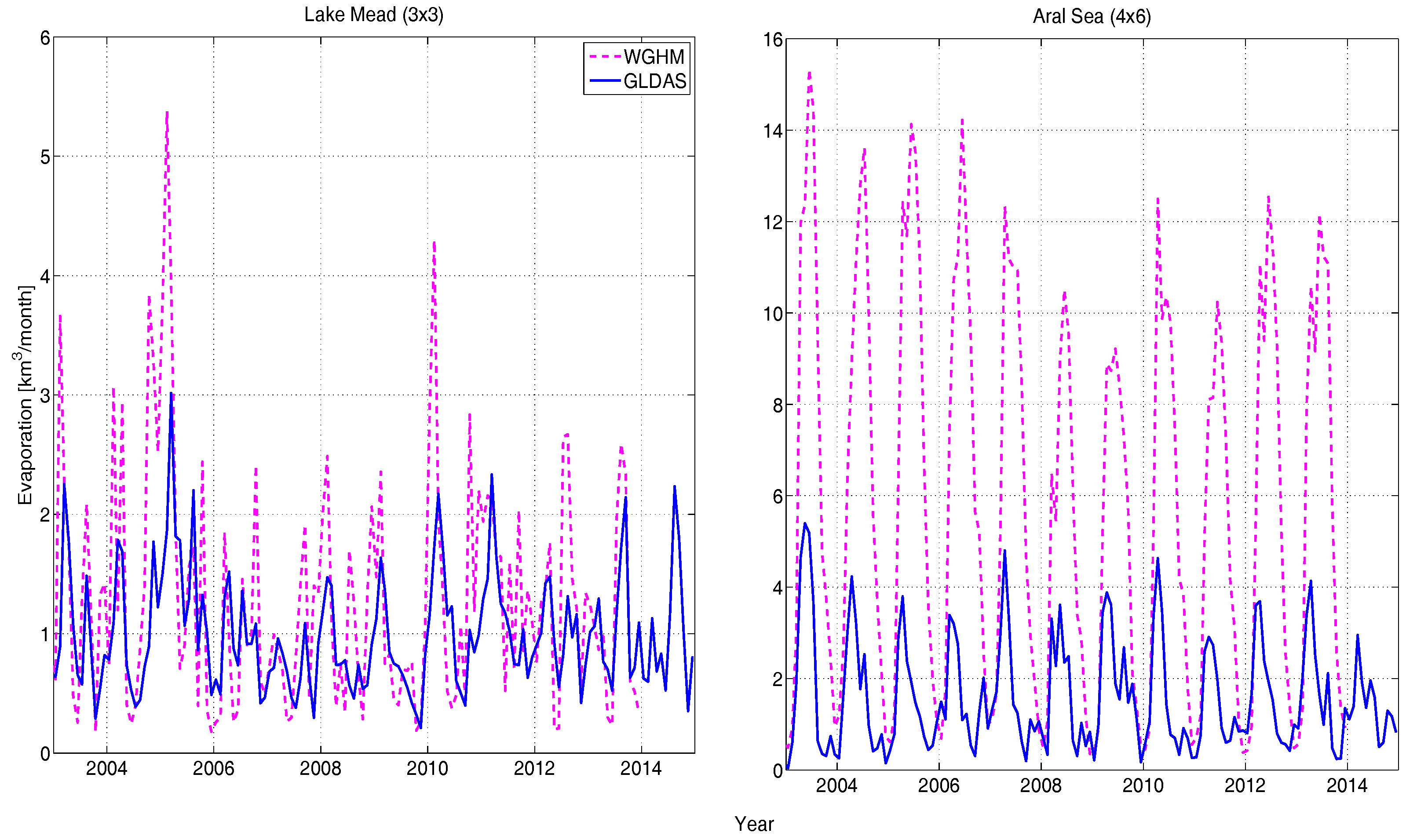
3.1.3. Evapotranspiration (ET)
3.2. Sum of Hydrological Storage Compartments (ΔS)
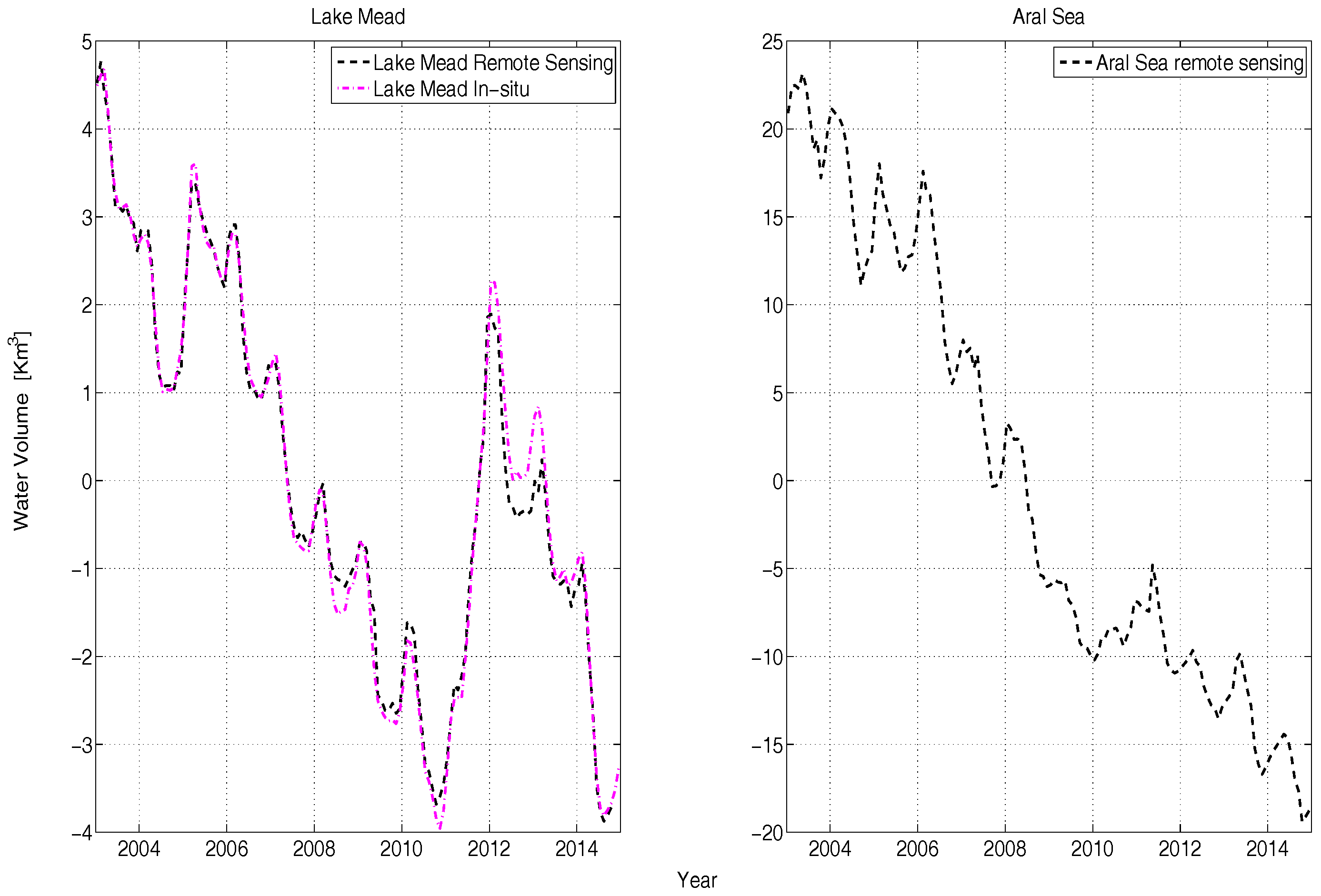
3.2.1. Liquid Surface Water (ΔSW)
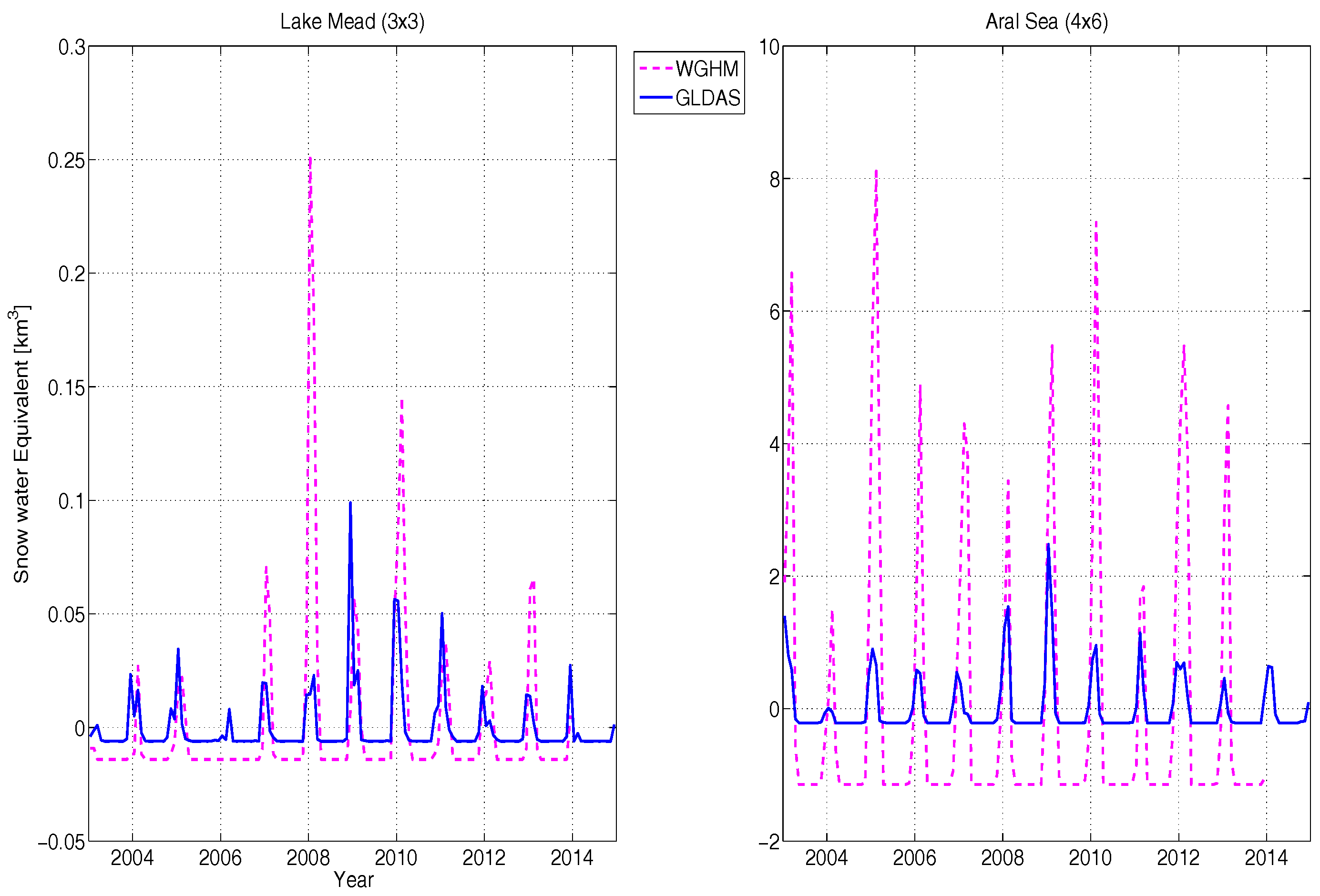
3.2.2. Snow Water Equivalent (ΔSWE)
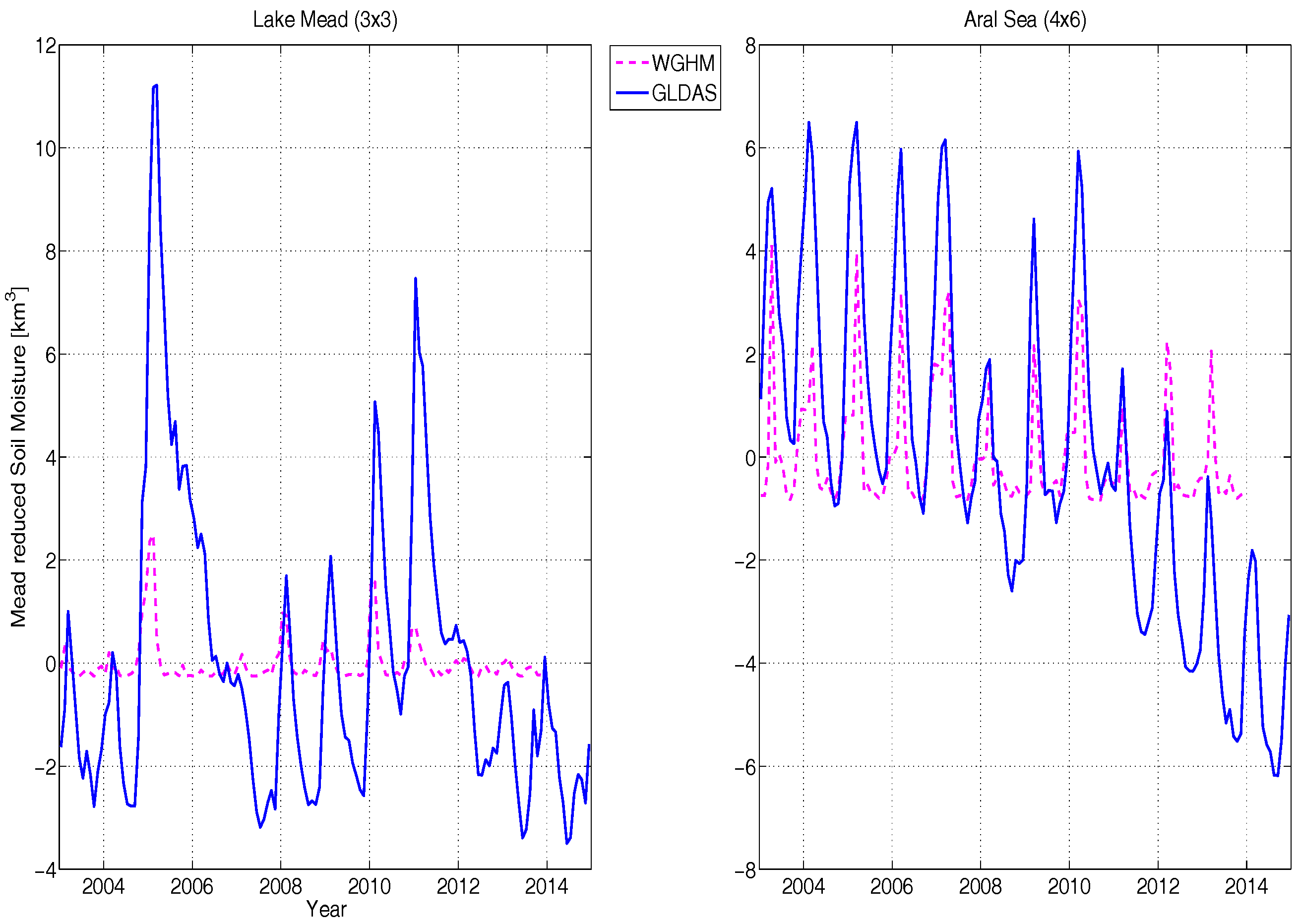
3.2.3. Soil Moisture (Δ SM)
3.3. GRACE-Derived ΔTWS
4. Results
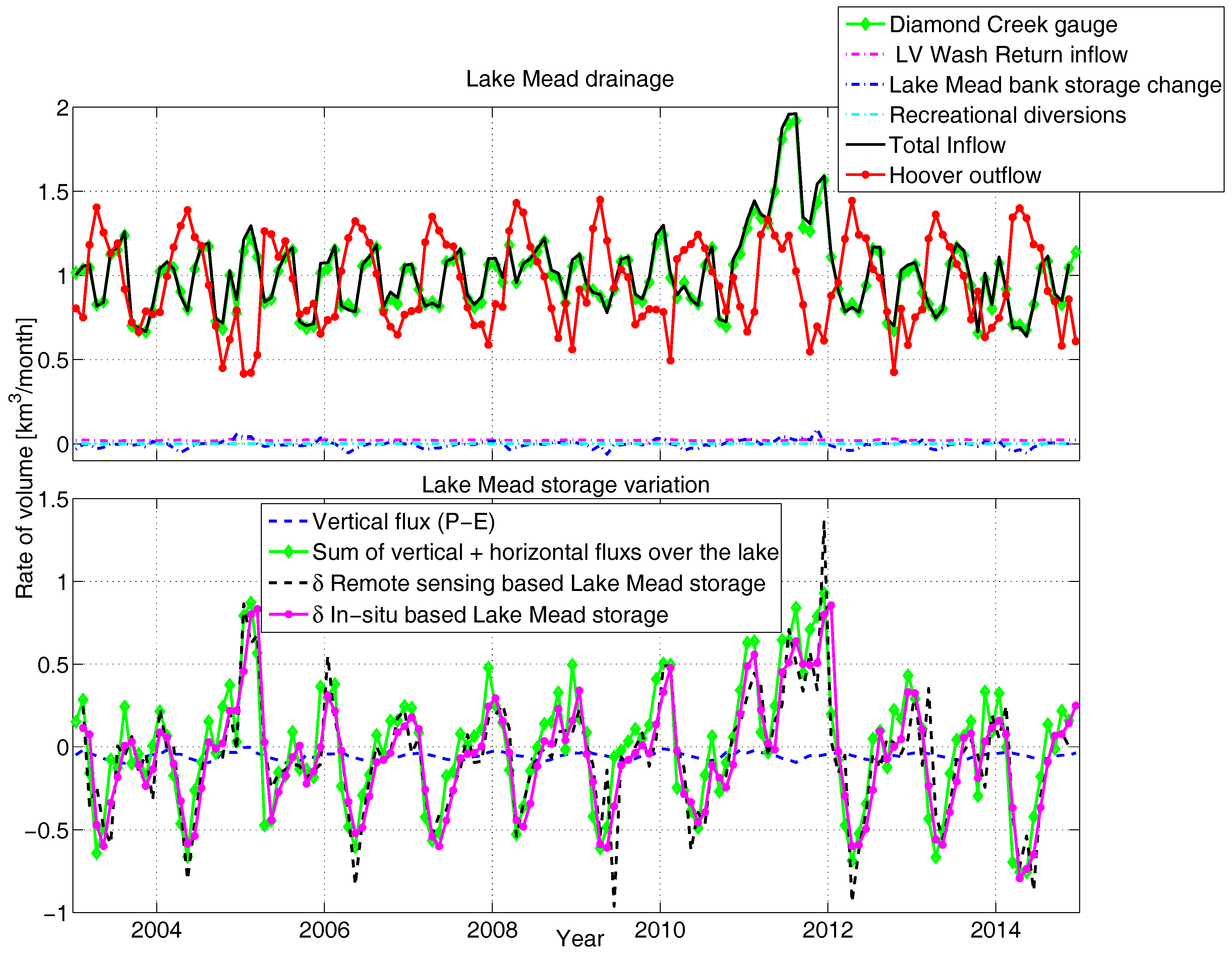
4.1. Lake Mead (Reservoir) Water Budget
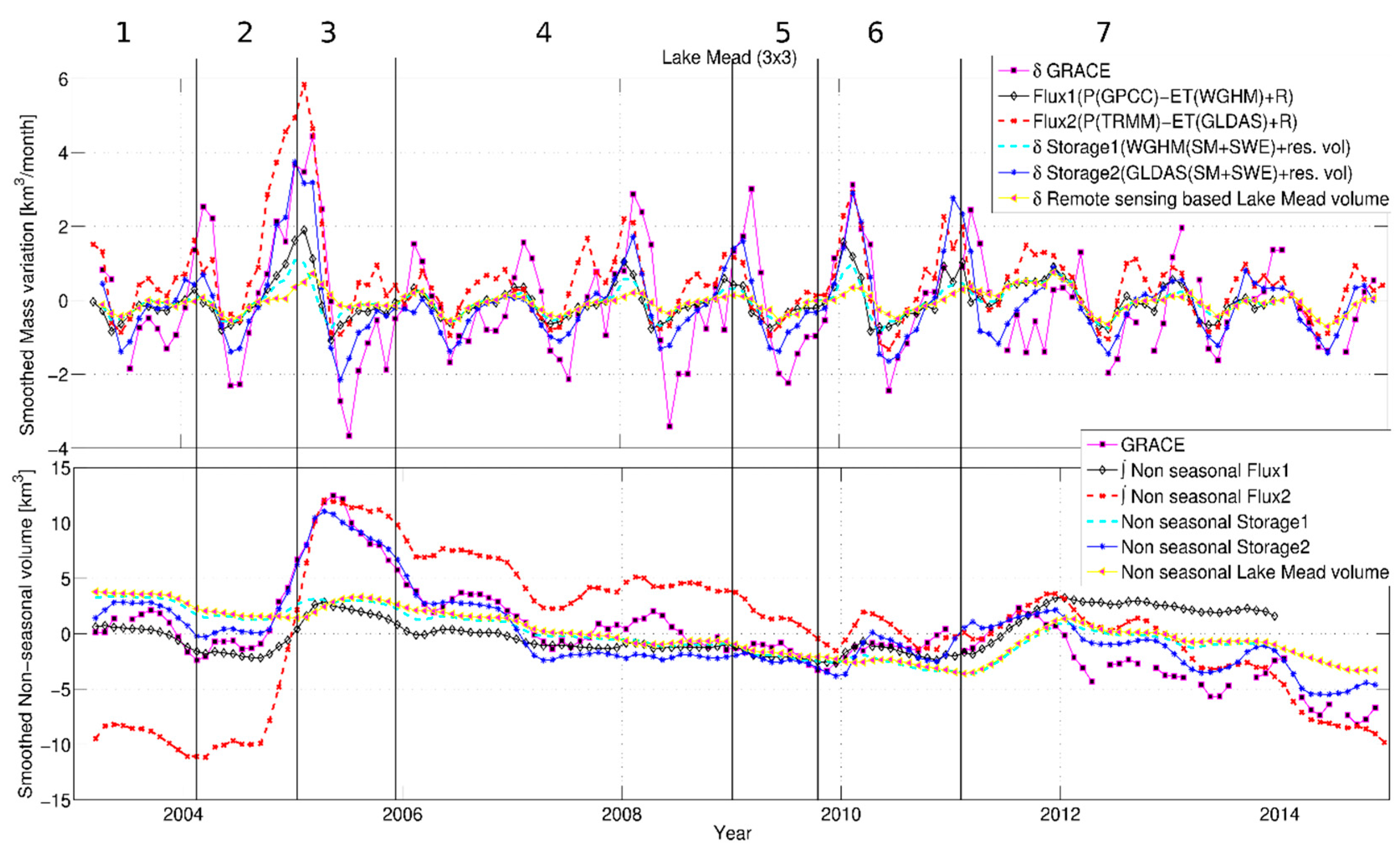
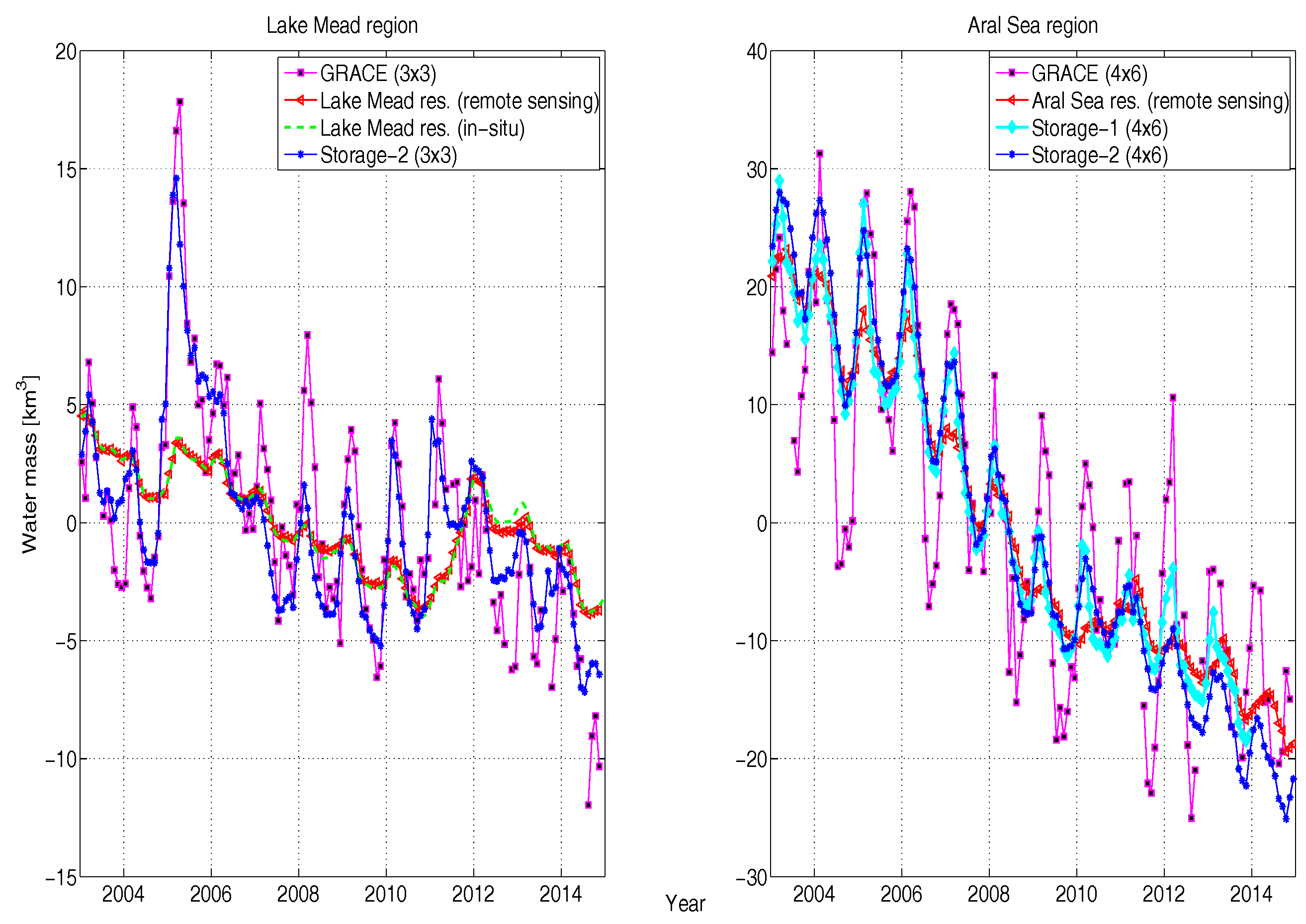
4.2. Lake Mead Region (3° × 3°) Water Budget
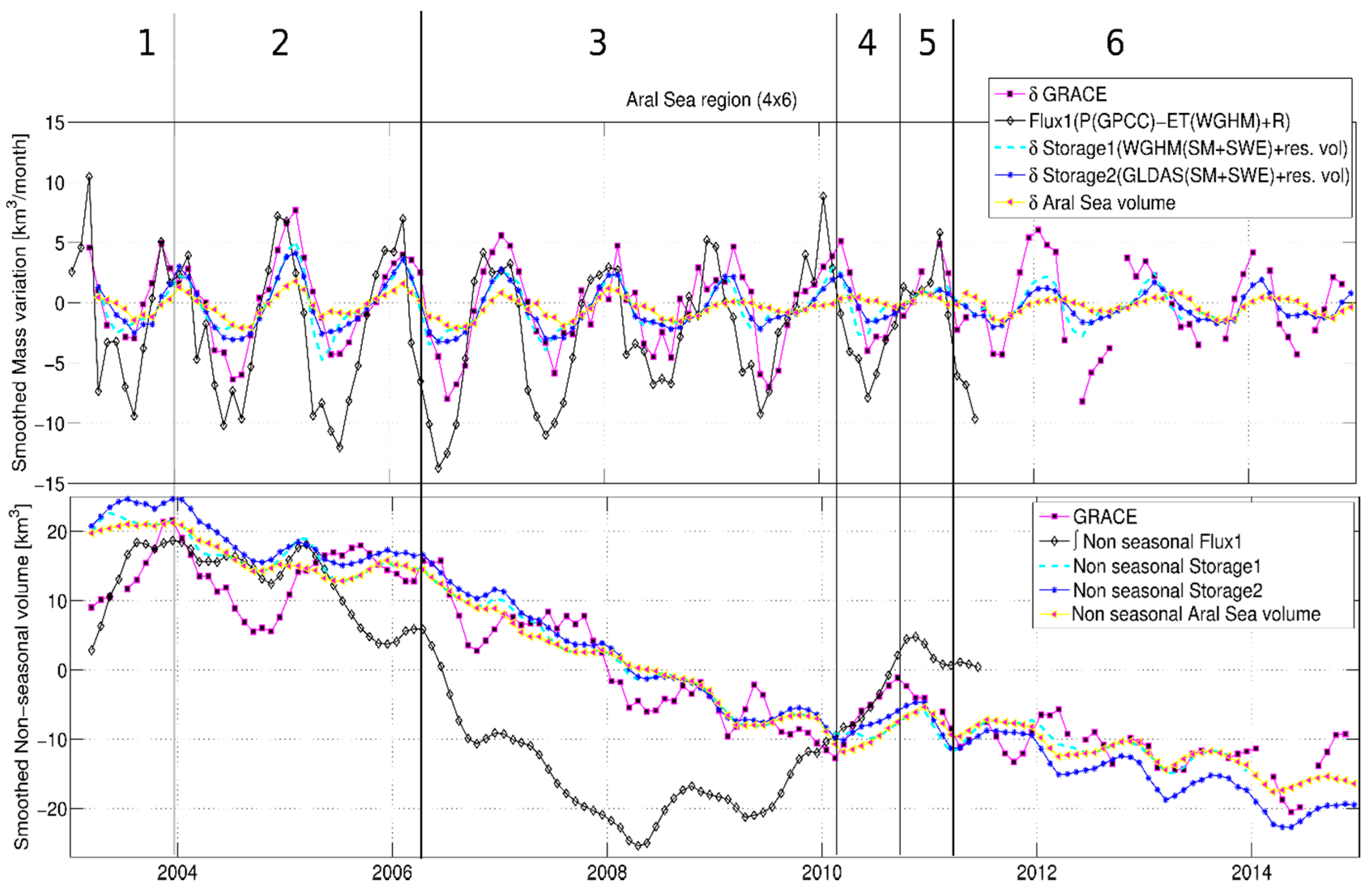
4.3. Aral Sea Region (4° × 6°) Water Budget
5. Discussion
6. Conclusions
- This study showed that the inflow-outflow runoff balance predominately drives the volumetric variations in a moderately sized deep reservoir, such as Lake Mead (where open water surface area is in few hundreds of kilometer square and depth is more than 100 m). While the vertical fluxes acting over the reservoir have negligible contributions (blue and green lines in Figure 10 bottom). Therefore, an accurate estimate of reservoir water volume variability may also help to approximate the runoff estimates at a basin level, especially in rivers connected by reservoirs, such as the Colorado River.
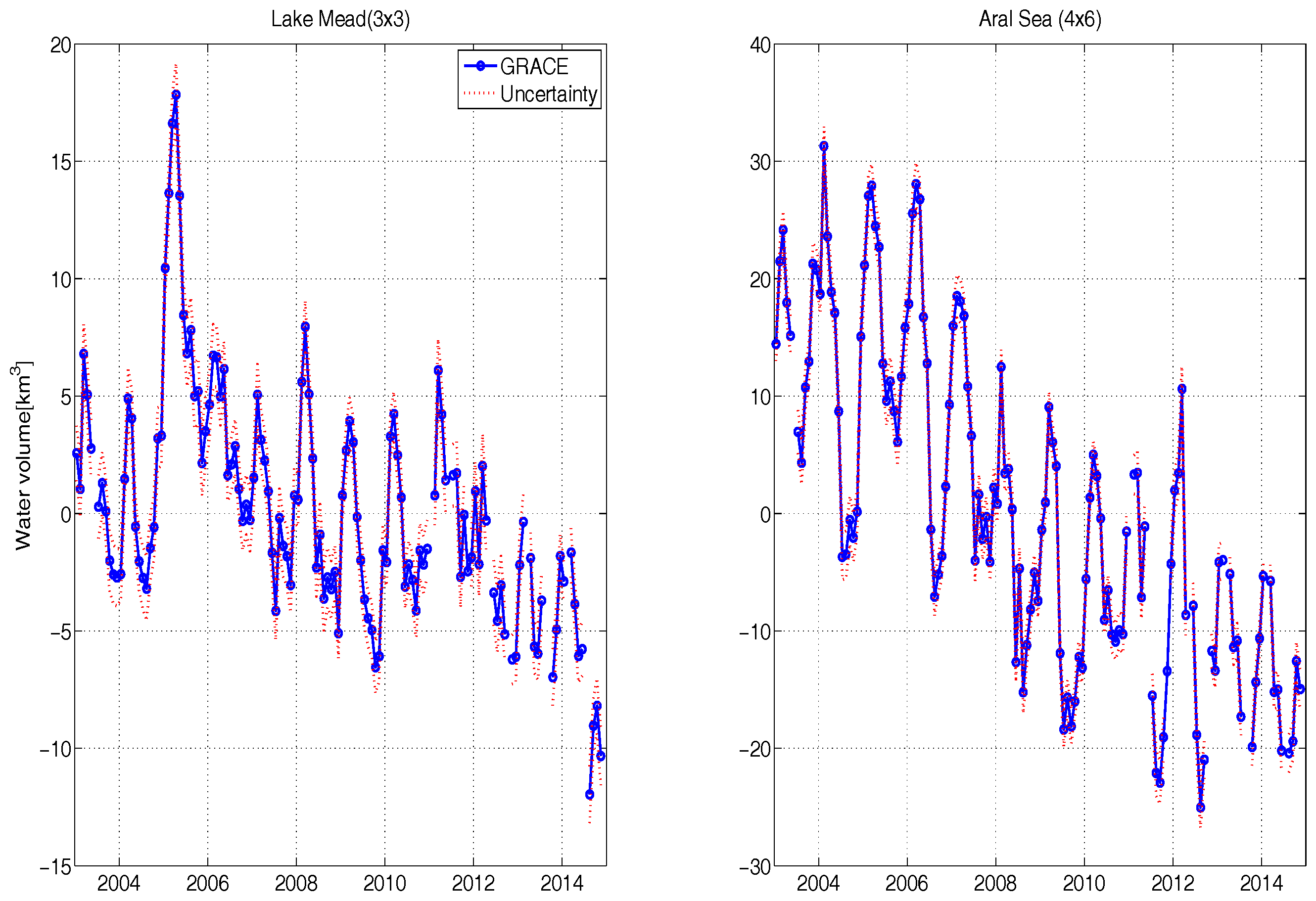
- The regional variability in the hydrological state of Lake Mead is driven by the combination of runoff (Figure 2 left) and precipitation (Figure 3 left). During the study period, the region experienced mass gains twice: the first time occurred during Period-2 (2004–2005) by additional local rainfall, and the second time by the additional inflow from upstream in Period-6 (2011). This lets us conclude that GRACE is sufficiently sensitive to observe mass changes of Lake Mead if the magnitude of change is large.
- In the study, ΔTWS observed by GRACE is compared to the estimated hydrological variations in fluxes and storages within the study area. The study showed that the long-term net flux estimation has a larger uncertainty than the total storage, due to the existing larger uncertainties in the vertical fluxes and error propagation through integration. The hybrid approach combining remote sensing-based reservoir volume estimates with hydrological model outputs provides a better possibility for the estimation of total mass change than hydrological models alone.
- The non-seasonal mass depletion in the Aral Sea region observed by GRACE is mainly driven by the reservoir mass loss because SWE is almost stationary (Figure 6 right) and SM has a limited non-seasonal trend (Figure 7 right). This lets us conclude that the causes of mass variations in the region are not local and are driven by upstream water abstraction. On the other hand, the Lake Mead region features almost similar inter-annual variations in SM, SWE, and the reservoir, allowing us to conclude that most of the mass variations are local (except the 2012 inflow anomaly) and climatically driven.
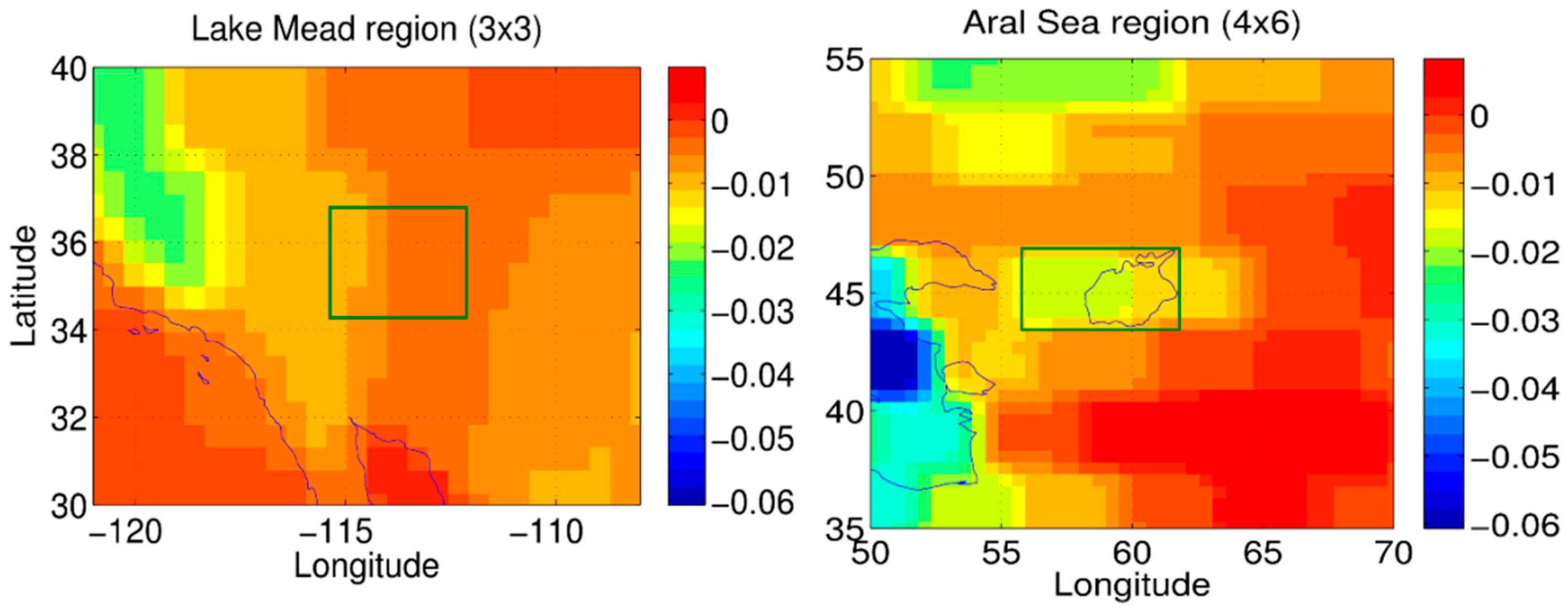
- Since the Aral Sea has changed dramatically in shape and size, the entire hydrological characteristics of the region have been affected. Therefore, for this region, both models inaccurately determine most of the parameters and no reliable in-situ data are available. Hence, for poorly monitored regions such as the Aral Sea, where reliable data is limited, accurate reservoir storage estimates and GRACE-based mass change analysis can greatly improve the understanding of the hydrological state of the region.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Gleick, P.H. Water in Crisis: A Guide to the World’s Fresh Water Resources; Oxford University Press: New York, NY, USA, 1993. [Google Scholar]
- Hall, A.C.; Schumann, G.J.P.; Bamber, J.L.; Bates, P.D. Tracking water level changes of the Amazon Basin with space-borne remote sensing and integration with large scale hydrodynamic modelling: A review. Phys. Chem. Earth Parts ABC 2011, 36, 223–231. [Google Scholar] [CrossRef]
- Duan, Z.; Bastiaanssen, W.G.M. Estimating water volume variations in lakes and reservoirs from four operational satellite altimetry databases and satellite imagery data. Remote Sens. Environ. 2013, 134, 403–416. [Google Scholar] [CrossRef]
- Zhang, J.; Xu, K.; Yang, Y.; Qi, L.; Hayashi, S.; Watanabe, M. Measuring water storage fluctuations in Lake Dongting, China, by Topex/Poseidon satellite altimetry. Environ. Monit. Assess. 2006, 115, 23–37. [Google Scholar] [CrossRef] [PubMed]
- Shiklomanov, A.I.; Lammers, R.B.; Vörösmarty, C.J. Widespread decline in hydrological monitoring threatens Pan-Arctic Research. Eos Trans. Am. Geophys. Union 2002, 83. [Google Scholar] [CrossRef]
- Rodell, M.; Chen, J.; Kato, H.; Famiglietti, J.S.; Nigro, J.; Wilson, C.R. Estimating groundwater storage changes in the Mississippi River basin (USA) using GRACE. Hydrogeol. J. 2006, 15, 159–166. [Google Scholar] [CrossRef]
- Famiglietti, J.S.; Lo, M.; Ho, S.L.; Bethune, J.; Anderson, K.J.; Syed, T.H.; Swenson, S.C.; de Linage, C.R.; Rodell, M. Satellites measure recent rates of groundwater depletion in California’s Central Valley. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- De Paiva, R.C.D.; Buarque, D.C.; Collischonn, W.; Bonnet, M.P.; Frappart, F.; Calmant, S.; Bulhões Mendes, C.A. Large-scale hydrologic and hydrodynamic modeling of the Amazon River basin. Water Resour. Res. 2013, 49, 1226–1243. [Google Scholar] [CrossRef]
- Frappart, F.; Papa, F.; Güntner, A.; Werth, S.; da Silva, J.S.; Tomasella, J.; Seyler, F.; Prigent, C.; Rossow, W.B.; Calmant, S.; et al. Satellite-based estimates of groundwater storage variations in large drainage basins with extensive floodplains. Remote Sens. Environ. 2011, 115, 1588–1594. [Google Scholar] [CrossRef]
- Papa, F.; Frappart, F.; Malbeteau, Y.; Shamsudduha, M.; Vuruputur, V.; Sekhar, M.; Ramillien, G.; Prigent, C.; Aires, F.; Pandey, R.K.; et al. Satellite-derived surface and sub-surface water storage in the Ganges–Brahmaputra River Basin. J. Hydrol. Reg. Stud. 2015, 4, 15–35. [Google Scholar] [CrossRef]
- Singh, A.; Kumar, U.; Seitz, F. Remote sensing of storage fluctuations of poorly gauged reservoirs and state space model (ssm)-based estimation. Remote Sens. 2015, 7, 17113–17134. [Google Scholar] [CrossRef]
- Rosenberg, E.A.; Clark, E.A.; Steinemann, A.C.; Lettenmaier, D.P. On the contribution of groundwater storage to interannual streamflow anomalies in the Colorado River basin. Hydrol. Earth Syst. Sci. 2013, 17, 1475–1491. [Google Scholar] [CrossRef]
- Barsugli, J.J.; Nowak, K.; Rajagopalan, B.; Prairie, J.R.; Harding, B. Comment on “When will Lake Mead go dry?” by T.P. Barnett and D.W. Pierce. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- European Space Agency (ESA) Data User Element. Available online: http://due.esrin.esa.int/page_globcover.php (accessed on 10 May 2016).
- Central Asia (CA) Water Info. Available online: http://www.cawater-info.net/ (accessed on 12 November 2011).
- Rodell, M.; Houser, P.R.; Jambor, U.E.A.; Gottschalck, J. The global land data assimilation system. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef]
- Simple Subset Wizard (SSW): Search for Data Sets. Available online: http://disc.sci.gsfc.nasa.gov/SSW/#keywords= (accessed on 10 November 2016).
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM multisatellite precipitation analysis (TMPA): Quasi-global, multiyear, combined-sensor precipitation estimates at fine scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Döll, P.; Kaspar, F.; Lehner, B. A global hydrological model for deriving water availability indicators: Model tuning and validation. J. Hydrol. 2003, 270, 105–134. [Google Scholar] [CrossRef]
- Müller Schmied, H.; Eisner, S.; Franz, D.; Wattenbach, M.; Portmann, F.T.; Flörke, M.; Döll, P. Sensitivity of simulated global-scale freshwater fluxes and storages to input data, hydrological model structure, human water use and calibration. Hydrol. Earth Syst. Sci. 2014, 18, 3511–3538. [Google Scholar] [CrossRef]
- Small, E.E.; Sloan, L.C.; Hostetler, S.; Giorgi, F. Simulating the water balance of the Aral Sea with a coupled regional climate-lake model. J. Geophys. Res. Atmos. 1999, 104, 6583–6602. [Google Scholar] [CrossRef]
- Small, E.E.; Giorgi, F.; Sloan, L.C.; Hostetler, S. The effects of desiccation and climatic change on the hydrology of the Aral Sea. J. Clim. 2001, 14, 300–322. [Google Scholar] [CrossRef]
- Cretaux, J.F.; Letolle, R.; Bergé-Nguyen, M. History of Aral Sea level variability and current scientific debates. Glob. Planet. Chang. 2013, 110, 99–113. [Google Scholar] [CrossRef]
- Papa, F.; Prigent, C.; Rossow, W.B.; Legresy, B.; Remy, F. Inundated wetland dynamics over boreal regions from remote sensing: The use of Topex-Poseidon Dual-frequency radar altimeter observations. Int. J. Remote Sens. 2006, 27, 4847–4866. [Google Scholar] [CrossRef]
- Seitz, F.; Schmidt, M.; Shum, C.K. Signals of extreme weather conditions in Central Europe in GRACE 4-D hydrological mass variations. Earth Planet. Sci. Lett. 2008, 268, 165–170. [Google Scholar] [CrossRef]
- Forootan, E.; Didova, O.; Kusche, J.; Löcher, A. Comparisons of atmospheric data and reduction methods for the analysis of satellite gravimetry observations. J. Geophys. Res. Solid Earth 2013, 118, 2382–2396. [Google Scholar] [CrossRef]
- Jiang, H.; Feng, M.; Zhu, Y.; Lu, N.; Huang, J.; Xiao, T. An automated method for extracting rivers and lakes from Landsat imagery. Remote Sens. 2014, 6, 5067–5089. [Google Scholar] [CrossRef]
- Eicker, A.; Schumacher, M.; Kusche, J.; Döll, P.; Schmied, H.M. Calibration/data assimilation approach for integrating GRACE data into the WaterGAP Global Hydrology Model (WGHM) using an ensemble Kalman filter: First results. Surv. Geophys. 2014, 35, 1285–1309. [Google Scholar] [CrossRef]
- Schumacher, M.; Eicker, A.; Kusche, J.; Schmied, H.M.; Döll, P. Covariance analysis and sensitivity studies for GRACE assimilation into WGHM. In International Association of Geodesy Symposia; Rizos, C., Ed.; Springer: Berlin/Heidelberg, Germany, 2015; pp. 1–7. [Google Scholar]
- Tangdamrongsub, N.; Steele-Dunne, S.C.; Gunter, B.C.; Ditmar, P.G.; Weerts, A.H. Data assimilation of GRACE terrestrial water storage estimates into a regional hydrological model of the Rhine River basin. Hydrol. Earth Syst. Sci. 2015, 19, 2079–2100. [Google Scholar] [CrossRef]
- Swenson, S.; Yeh, P.J.F.; Wahr, J.; Famiglietti, J. A comparison of terrestrial water storage variations from GRACE with in situ measurements from Illinois. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Swenson, S.; Wahr, J. Monitoring the water balance of Lake Victoria, East Africa, from space. J. Hydrol. 2009, 370, 163–176. [Google Scholar] [CrossRef]
- Strassberg, G.; Scanlon, B.R.; Rodell, M. Comparison of seasonal terrestrial water storage variations from GRACE with groundwater-level measurements from the High Plains Aquifer (USA). Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Becker, M.; LLovel, W.; Cazenave, A.; Güntner, A.; Crétaux, J.F. Recent hydrological behavior of the East African great lakes region inferred from GRACE, satellite altimetry and rainfall observations. C. R. Geosci. 2010, 342, 223–233. [Google Scholar] [CrossRef]
- Singh, A.; Seitz, F.; Schwatke, C. Application of Multi-Sensor satellite data to observe water storage variations. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 1502–1508. [Google Scholar] [CrossRef]
- Forootan, E.; Rietbroek, R.; Kusche, J.; Sharifi, M.A.; Awange, J.L.; Schmidt, M.; Omondi, P.; Famiglietti, J. Separation of large scale water storage patterns over Iran using GRACE, altimetry and hydrological data. Remote Sens. Environ. 2014, 140, 580–595. [Google Scholar] [CrossRef]
- Aus der Beek, T.; Voß, F.; Flörke, M. Modelling the impact of Global Change on the hydrological system of the Aral Sea basin. Phys. Chem. Earth Parts ABC 2011, 36, 684–695. [Google Scholar] [CrossRef]
- Long, D.; Longuevergne, L.; Scanlon, B.R. Global analysis of approaches for deriving total water storage changes from GRACE satellites. Water Resour. Res. 2015, 51, 2574–2594. [Google Scholar] [CrossRef]
- Watkins, M.M.; Wiese, D.N.; Yuan, D.N.; Boening, C.; Landerer, F.W. Improved methods for observing Earth’s time variable mass distribution with GRACE using spherical cap mascons. J. Geophys. Res. Solid Earth 2015, 120, 2648–2671. [Google Scholar] [CrossRef]
- Wiese, D.N. GRACE Monthly Land Water Mass Grids Netcdf Release 5.0|PO.DAAC. Available online: https://podaac.jpl.nasa.gov/dataset/TELLUS_LAND_NC_RL05 (accessed on 31 March 2016).
- Studying Earth’s Gravity. Available online: http://grace.jpl.nasa.gov/ (accessed on 10 November 2016).
- Swenson, S.; Chambers, D.; Wahr, J. Estimating geocenter variations from a combination of GRACE and ocean model output. J. Geophys. Res. Solid Earth 2008, 113. [Google Scholar] [CrossRef]
- Cheng, M.; Tapley, B.D.; Ries, J.C. Deceleration in the Earth’s oblateness. J. Geophys. Res. Solid Earth 2013, 118, 740–747. [Google Scholar] [CrossRef]
- Geruo, A.; Wahr, J.; Zhong, S. Computations of the viscoelastic response of a 3-D compressible Earth to surface loading: An application to Glacial Isostatic Adjustment in Antarctica and Canada. Geophys. J. Int. 2013, 192, 557–572. [Google Scholar]
- Longuevergne, L.; Wilson, C.; Scanlon, B.R.; Crétaux, J.F. GRACE water storage estimates for the Middle East and other regions with significant reservoir and lake storage. Hydrol. Earth Syst. Sci. 2013, 17, 4817–4830. [Google Scholar] [CrossRef]
- Overview—Monthly Mass Grids. Available online: http://grace.jpl.nasa.gov/data/monthly-mass-grids (accessed on 10 October 2016).
- Boulder Canyon Operations Office|Lower Colorado Region|Bureau of Reclamation. Available online: http://www.usbr.gov/lc/region/g4000/wtracct.html (accessed on 10 November 2016).
- United States Geological Survey (USGS) Water Data for the Nation. Available online: http://waterdata.usgs.gov/nwis (accessed on 10 November 2016).
- Rechard, P.A. Determining bank storage of Lake Mead. J. Irrig. Drain. Div. 1965, 91, 141–158. [Google Scholar]
- Lindsey, R. World of Change: Water Level in Lake Powell —Feature Articles. Available online: http://earthobservatory.nasa.gov/Features/WorldOfChange/lake_powell.php (accessed on 19 July 2016).
- Lindsey, R. World of Change: Shrinking Aral Sea —Feature Articles. Available online: http://earthobservatory.nasa.gov/Features/WorldOfChange/aral_sea.php (accessed on 19 July 2016).
- Aladin, N.V.; Plotnikov, I.S.; Micklin, P.; Ballatore, T. The Aral Sea: Water level, salinity and long-term changes in biological communities of an endangered ecosystem-past, present and future. Nat. Resour. Environ. Issues 2009, 15, 177–183. [Google Scholar]
- Abelen, S.; Seitz, F. Relating satellite gravimetry data to global soil moisture products via data harmonization and correlation analysis. Remote Sens. Environ. 2013, 136, 89–98. [Google Scholar] [CrossRef]
- Yin, X.; Gruber, A.; Arkin, P. Comparison of the GPCP and CMAP merged gauge—Satellite monthly precipitation products for the period 1979–2001. J. Hydrometeorol. 2004, 5, 1207–1222. [Google Scholar] [CrossRef]
- Negrón Juárez, R.I.; Li, W.; Fu, R.; Fernandes, K.; de Oliveira Cardoso, A. Comparison of precipitation datasets over the Tropical South American and African continents. J. Hydrometeorol. 2009, 10, 289–299. [Google Scholar] [CrossRef]
- Shin, D.B.; Kim, J.H.; Park, H.J. Agreement between monthly precipitation estimates from TRMM satellite, NCEP reanalysis, and merged gauge-satellite analysis. J. Geophys. Res. Atmospheres 2011, 116. [Google Scholar] [CrossRef]
- Chen, J.; Li, J.; Zhang, Z.; Ni, S. Long-term groundwater variations in Northwest India from satellite gravity measurements. Glob. Planet. Chang. 2014, 116, 130–138. [Google Scholar] [CrossRef]
- Richey, A.S.; Thomas, B.F.; Lo, M.H.; Reager, J.T.; Famiglietti, J.S.; Voss, K.; Swenson, S.; Rodell, M. Quantifying renewable groundwater stress with GRACE. Water Resour. Res. 2015, 51, 5217–5238. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Famigliett, J.S.; Scanlon, B.R.; Rodell, M. Groundwater storage changes: Present status from GRACE observations. Surv. Geophys. 2015, 37, 397–417. [Google Scholar] [CrossRef]
- Castle, S.L.; Thomas, B.F.; Reager, J.T.; Rodell, M.; Swenson, S.C.; Famiglietti, J.S. Groundwater depletion during drought threatens future water security of the Colorado River Basin. Geophys. Res. Lett. 2014, 41, 5904–5911. [Google Scholar] [CrossRef] [PubMed]

| Signals (Including Seasonal Component) | The Lake Mead Region (3 × 3) | The Aral Sea Region (4 × 6) | ||||
|---|---|---|---|---|---|---|
| Correlation | RMSE (km3) | Correlation | RMSE (km3) | |||
| Lag 0 | Lag 1 | Lag 0 | Lag 1 | |||
| δ GRACE-Flux-1 | 0.58 | 0.80 | 1.3 | 0.76 | 0.8 | 4.2 |
| δ GRACE-Flux-2 | 0.63 | 0.76 | 1.3 | - | - | - |
| GRACE-Storage-1 | 0.58 | - | 3.7 | 0.87 | - | 6.5 |
| GRACE-Storage-2 | 0.87 | - | 2.3 | 0.88 | - | 7 |
| GRACE-Reservoir | 0.60 | 4 | 0.82 | - | 7.8 | |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Singh, A.; Seitz, F.; Eicker, A.; Güntner, A. Water Budget Analysis within the Surrounding of Prominent Lakes and Reservoirs from Multi-Sensor Earth Observation Data and Hydrological Models: Case Studies of the Aral Sea and Lake Mead. Remote Sens. 2016, 8, 953. https://doi.org/10.3390/rs8110953
Singh A, Seitz F, Eicker A, Güntner A. Water Budget Analysis within the Surrounding of Prominent Lakes and Reservoirs from Multi-Sensor Earth Observation Data and Hydrological Models: Case Studies of the Aral Sea and Lake Mead. Remote Sensing. 2016; 8(11):953. https://doi.org/10.3390/rs8110953
Chicago/Turabian StyleSingh, Alka, Florian Seitz, Annette Eicker, and Andreas Güntner. 2016. "Water Budget Analysis within the Surrounding of Prominent Lakes and Reservoirs from Multi-Sensor Earth Observation Data and Hydrological Models: Case Studies of the Aral Sea and Lake Mead" Remote Sensing 8, no. 11: 953. https://doi.org/10.3390/rs8110953
APA StyleSingh, A., Seitz, F., Eicker, A., & Güntner, A. (2016). Water Budget Analysis within the Surrounding of Prominent Lakes and Reservoirs from Multi-Sensor Earth Observation Data and Hydrological Models: Case Studies of the Aral Sea and Lake Mead. Remote Sensing, 8(11), 953. https://doi.org/10.3390/rs8110953






