Estimation of Paddy Rice Variables with a Modified Water Cloud Model and Improved Polarimetric Decomposition Using Multi-Temporal RADARSAT-2 Images
Abstract
:1. Introduction
2. Materials and Methods
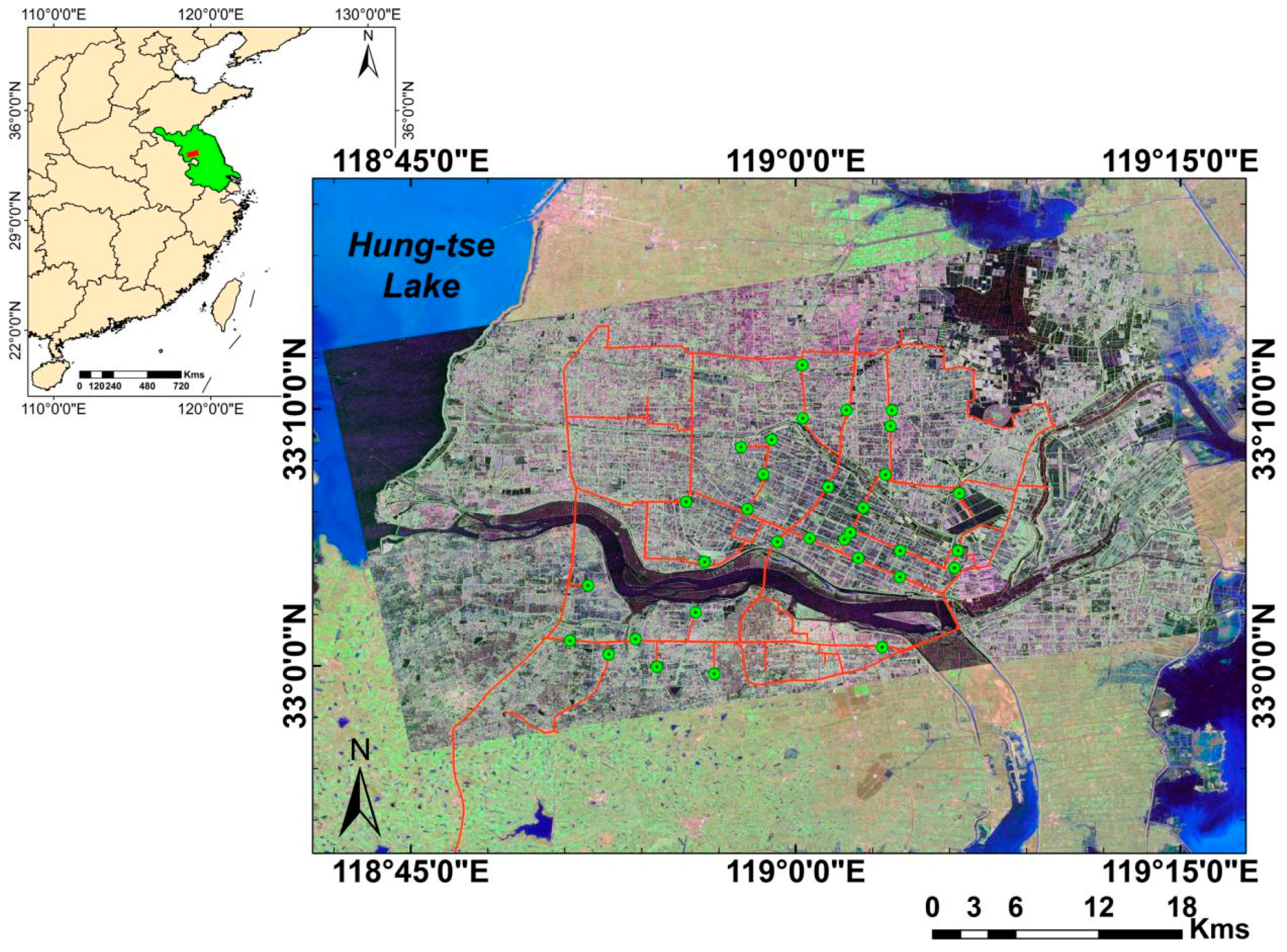
2.1. Study Site
2.2. Acquisition and Processing of RADARSAT-2 Images
2.3. Ground Truth Measurements of Rice Variables
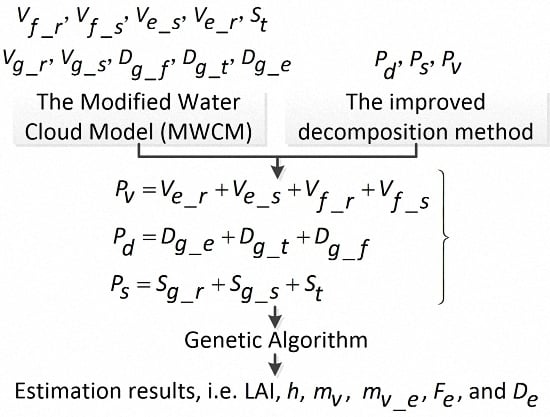
3. Methodology
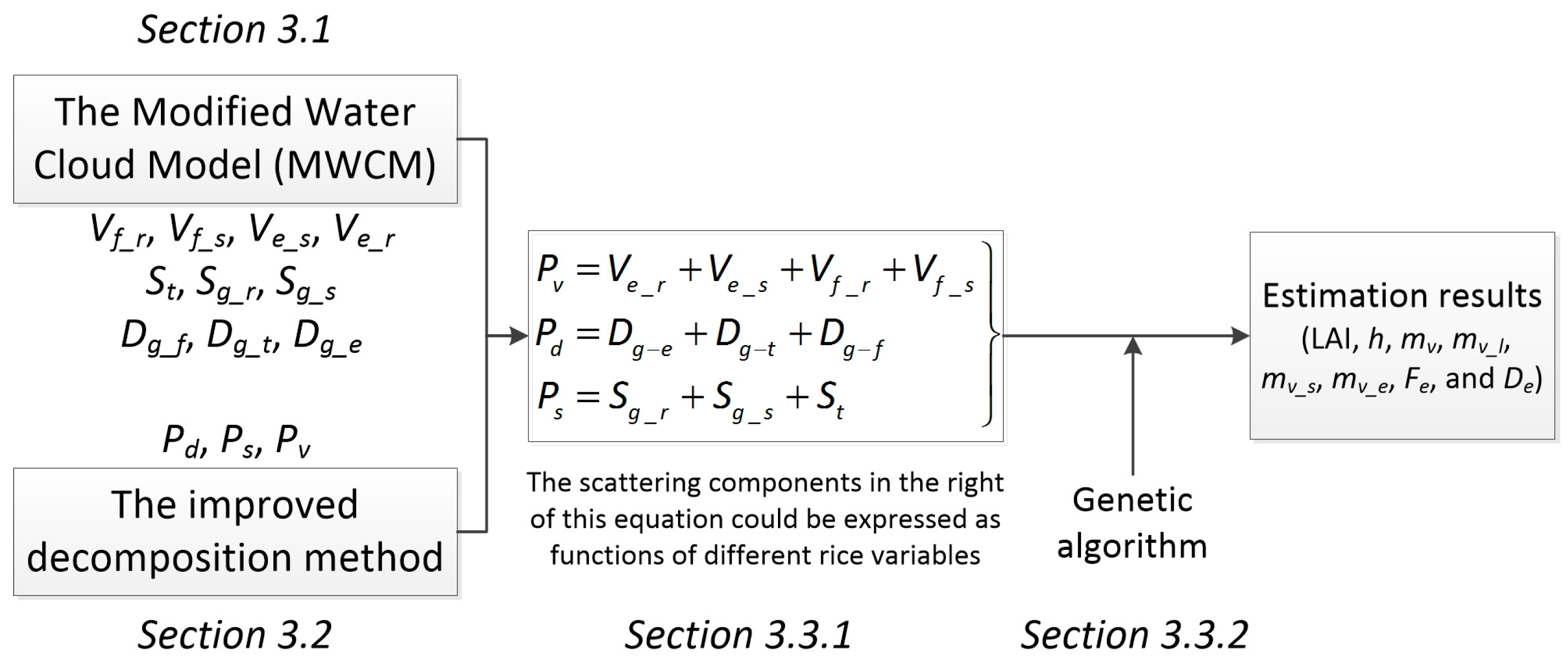
3.1. Modified Water Cloud Model (MWCM)
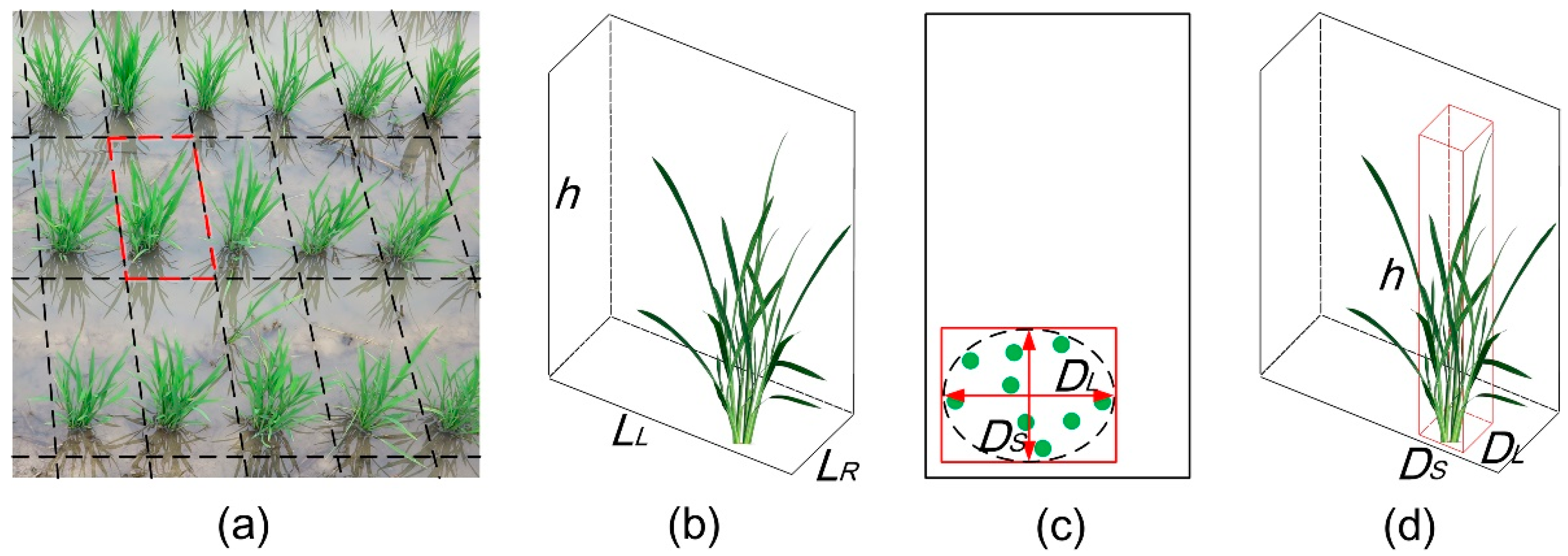
3.1.1. Scattering Cell
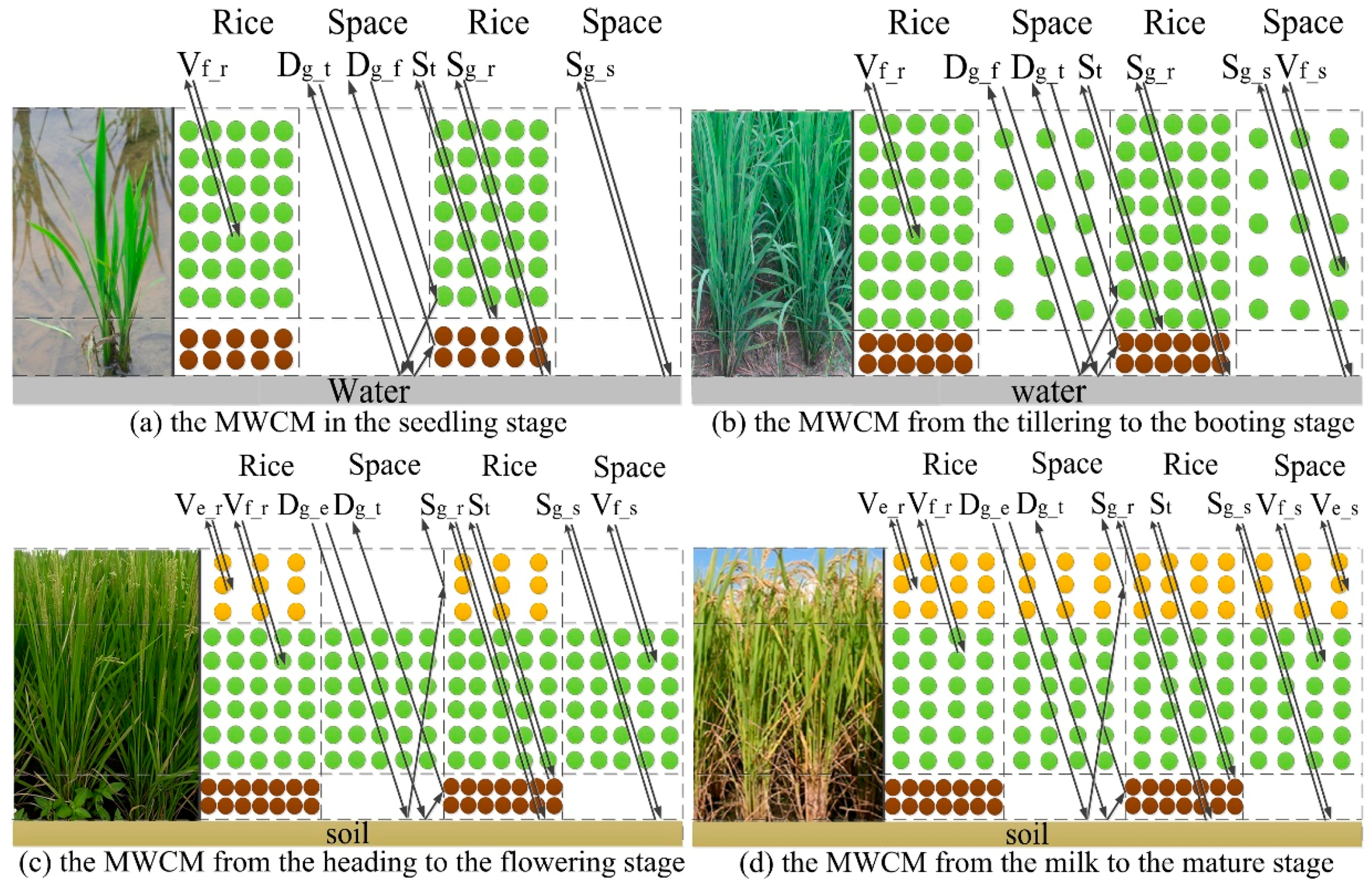
3.1.2. Scattering Components from Multi-Layered Rice Canopy
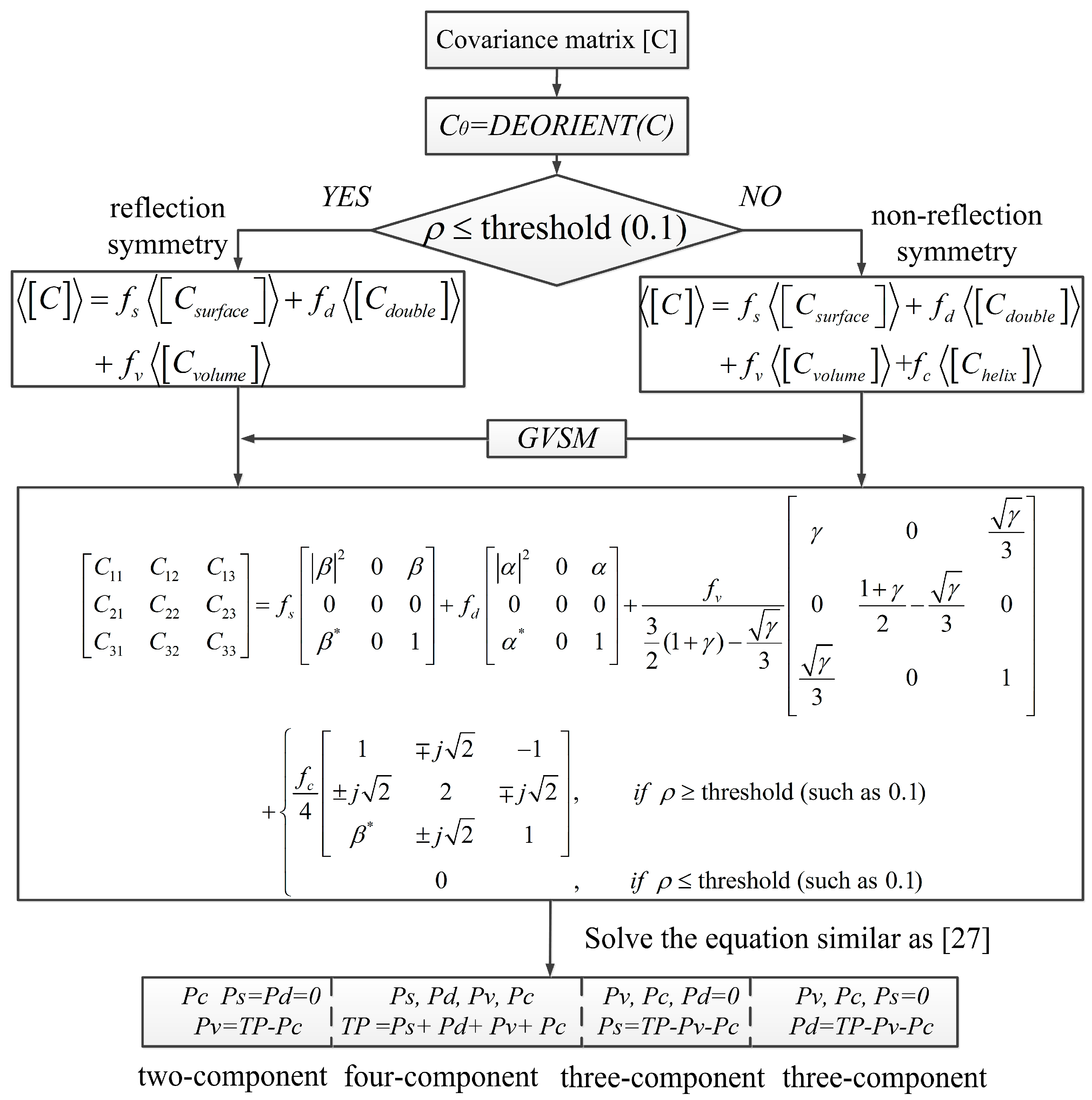
3.2. Improved Polarimetric Decomposition
3.2.1. Deorientation
3.2.2. Distinguish the Reflection Symmetry
3.2.3. Generalized Volume Scattering Model
3.3. Scenario for Estimation of Rice Variables
3.3.1. Different Expressions of Equation (6)
3.3.2. Genetic Algorithm (GA)
3.3.3. Flow Chart for Rice Variable Estimation
4. Results and Discussion
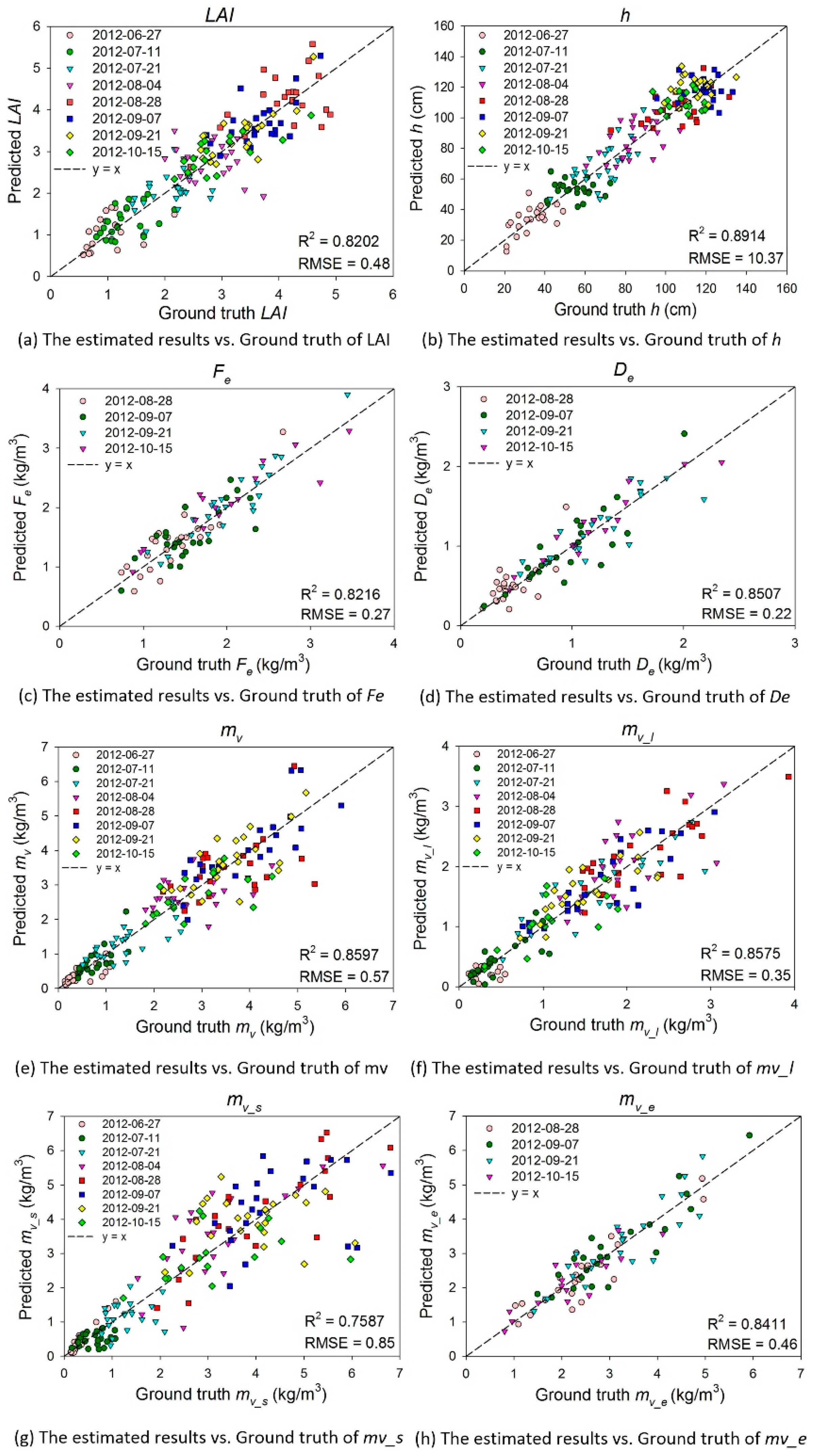
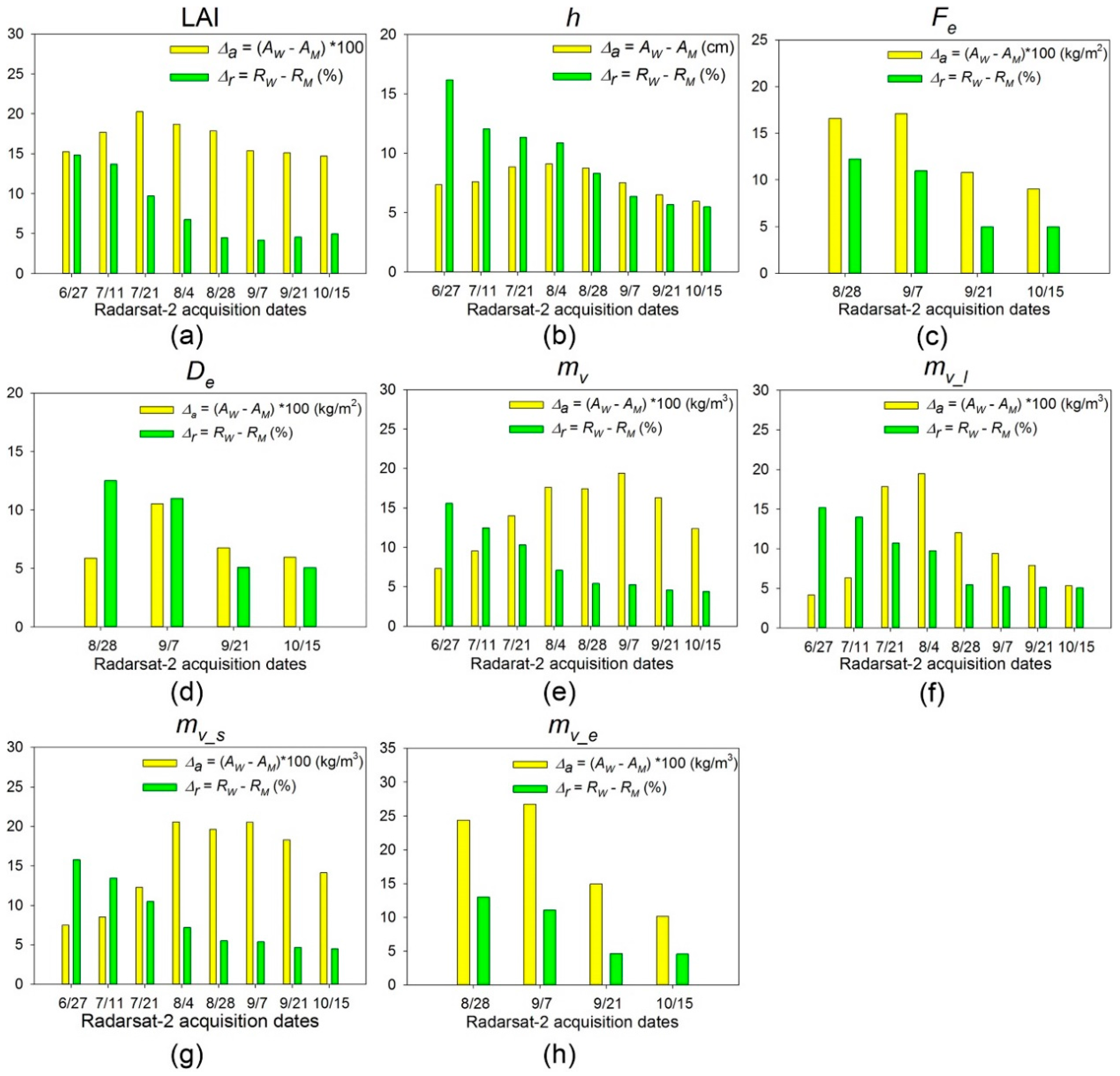
4.1. Estimated Results
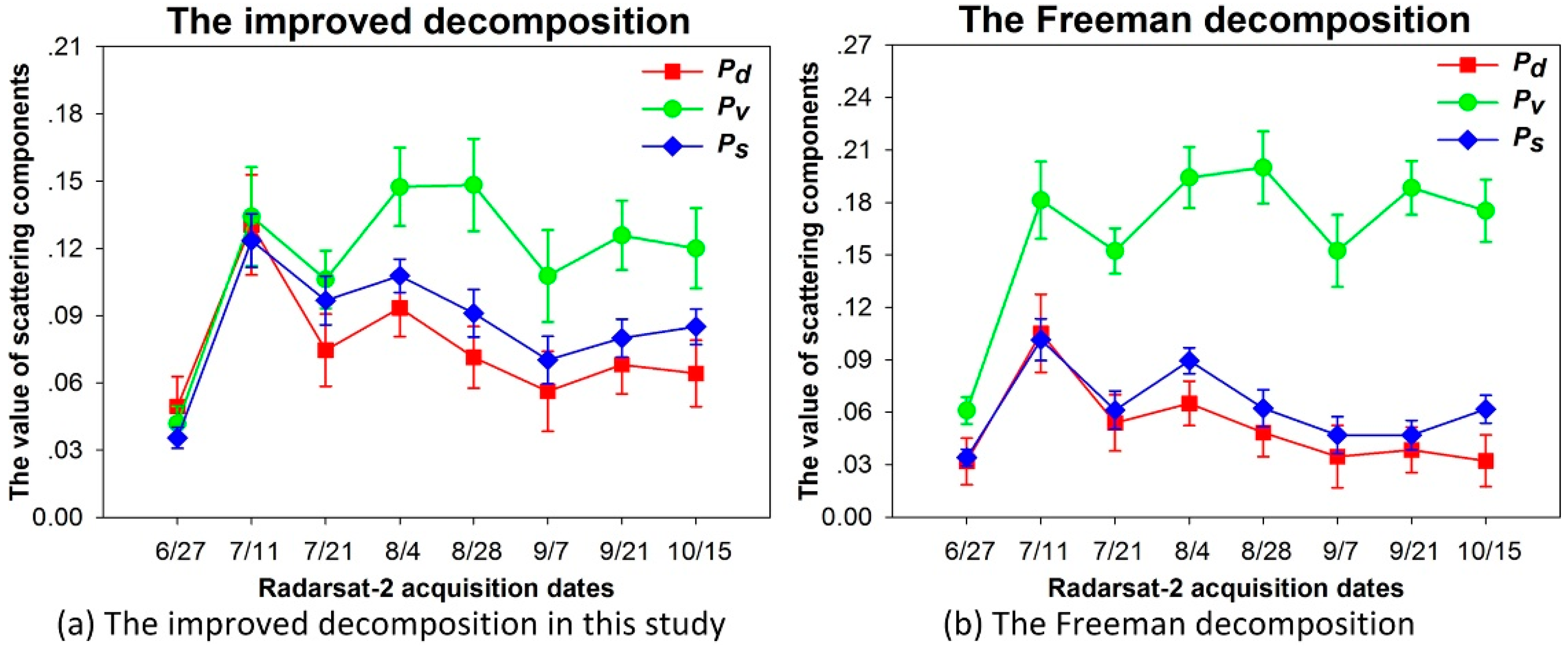
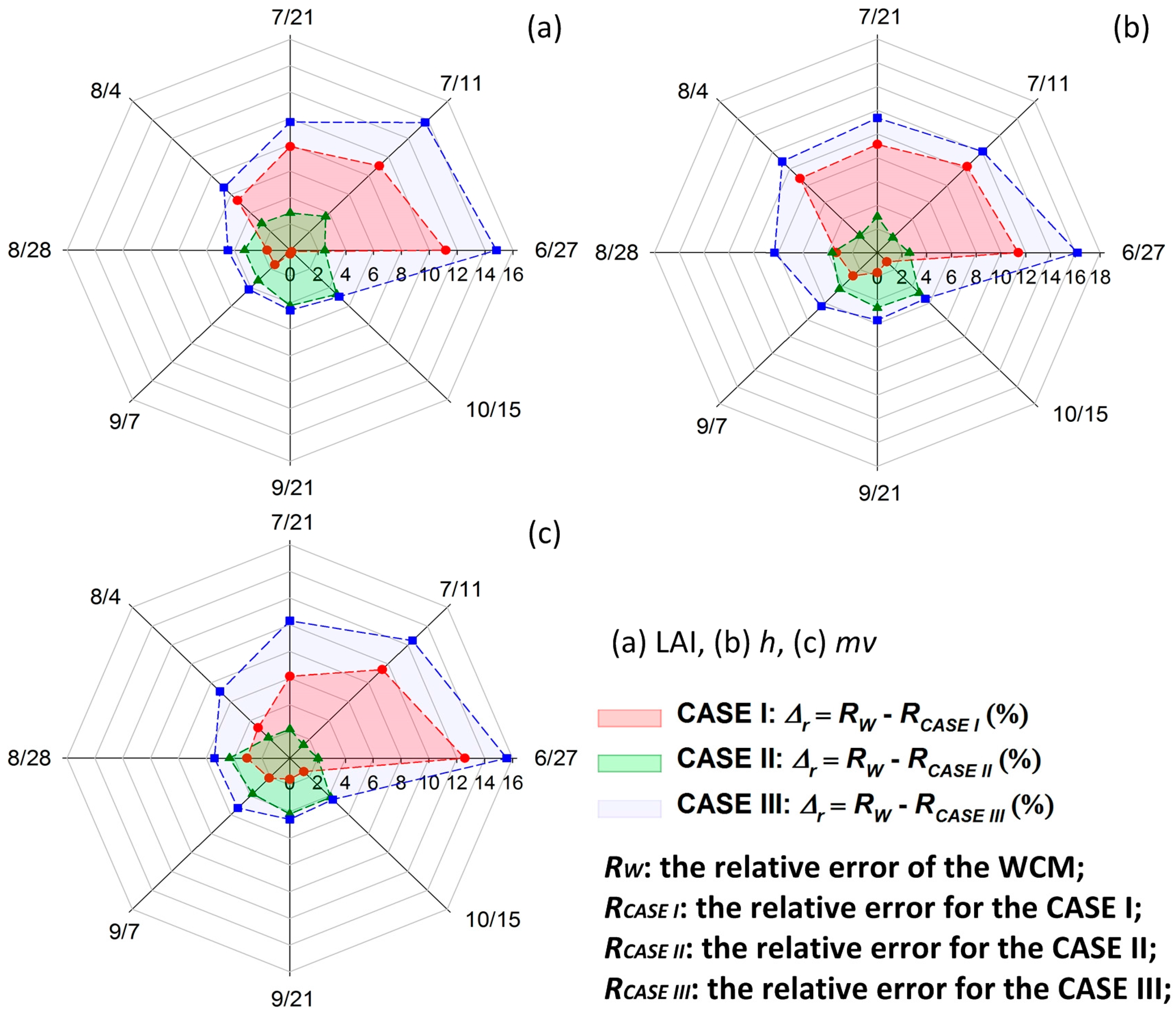
4.2. Comparison with the WCM
4.3. Discussion for the Key Improvements of the MWCM
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kuenzer, C.; Knauer, K. Remote sensing of rice crop areas. Int. J. Remote Sens. 2013, 34, 2101–2139. [Google Scholar] [CrossRef]
- Dong, J.; Xiao, X.; Kou, W.; Qin, Y.; Zhang, G.; Li, L. Tracking the dynamics of paddy rice planting area in 1986–2010 through time series Landsat images and phenology-based algorithms. Remote Sens. Environ. 2015, 160, 99–113. [Google Scholar] [CrossRef]
- Inoue, Y.; Sakaiya, E.; Wang, C. Capability of C-band backscattering coefficients from high-resolution satellite SAR sensors to assess biophysical variables in paddy rice. Remote Sens. Environ. 2014, 140, 257–266. [Google Scholar] [CrossRef]
- Brisco, B. Agricultural applications with radar. In Manual of Remote Sensing: Principles and Applications in Imaging Radar, 3rd ed.; Floyd, M.H., Anthony, J.L., Eds.; American Society of Photogrammetry and Remote Sensing: Washington, DC, USA, 1998; pp. 381–406. [Google Scholar]
- Inoue, Y.; Sakaiya, E.; Wang, C. Potential of X-band images from high-resolution satellite SAR sensors to assess growth and yield in paddy rice. Remote Sens. 2014, 6, 5995–6019. [Google Scholar] [CrossRef]
- Kurosu, T.; Fujita, M.; Chiba, K. Monitoring of rice crop growth from space using the ERS-1 C-band SAR. IEEE Trans. Geosci. Remote Sens. 1995, 33, 1092–1096. [Google Scholar] [CrossRef]
- Lopez-Sanchez, J.M.; Cloude, S.R.; Ballester-Berman, J.D. Rice phenology monitoring by means of SAR polarimetry at X-band. IEEE Trans. Geosci. Remote Sens. 2012, 50, 2695–2709. [Google Scholar] [CrossRef]
- Lopez-Sanchez, J.M.; Vicente-Guijalba, F.; Ballester-Berman, J.D.; Cloude, S.R. Polarimetric response of rice fields at C-band: Analysis and phenology retrieval. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2977–2993. [Google Scholar] [CrossRef]
- Chakraborty, M.; Manjunath, K.; Panigrahy, S.; Kundu, N.; Parihar, J. Rice crop parameter retrieval using multi-temporal, multi-incidence angle Radarsat SAR data. ISPRS J. Photogramm. Remote Sens. 2005, 59, 310–322. [Google Scholar] [CrossRef]
- Shao, Y.; Fan, X.; Liu, H.; Xiao, J.; Ross, S.; Brisco, B.; Staples, G. Rice monitoring and production estimation using multitemporal RADARSAT. Remote Sens. Environ. 2001, 76, 310–325. [Google Scholar] [CrossRef]
- Inoue, Y.; Kurosu, T.; Maeno, H.; Uratsuka, S.; Kozu, T.; Dabrowska-Zielinska, K.; Qi, J. Season-long daily measurements of multifrequency (Ka, Ku, X, C, and L) and full-polarization backscatter signatures over paddy rice field and their relationship with biological variables. Remote Sens. Environ. 2002, 81, 194–204. [Google Scholar] [CrossRef]
- Kumar, V.; Kumari, M.; Saha, S.K. Leaf area index estimation of lowland rice using semi-empirical backscattering model. J. Appl. Remote Sens. 2013, 7, 73474–73474. [Google Scholar] [CrossRef]
- McDonald, K.C.; Dobson, M.C.; Ulaby, F.T. Using MIMICS to model L-band multiangle and multitemporal backscatter from a walnut orchard. IEEE Trans. Geosci. Remote Sens. 1990, 28, 477–491. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, X.; Su, S.; Wang, C. Retrieving canopy height and density of paddy rice from Radarsat-2 images with a canopy scattering model. Int. J. Appl. Earth Obs. Geoinf. 2014, 28, 170–180. [Google Scholar] [CrossRef]
- Graham, A.J.; Harris, R. Extracting biophysical parameters from remotely sensed radar data: A review of the water cloud model. Prog. Phys. Geogr. 2003, 27, 217–229. [Google Scholar] [CrossRef]
- Kumar, K.; Hari Prasad, K.S.; Arora, M.K. Estimation of water cloud model vegetation parameters using a genetic algorithm. Hydrol. Sci. J. 2012, 57, 776–789. [Google Scholar] [CrossRef]
- Attema, E.; Ulaby, F.T. Vegetation modeled as a water cloud. Radio Science 1978, 13, 357–364. [Google Scholar] [CrossRef]
- Beriaux, E.; Lucau-Danila, C.; Auquiere, E.; Defourny, P. Multiyear independent validation of the water cloud model for retrieving maize leaf area index from SAR time series. Int. J. Remote Sens. 2013, 34, 4156–4181. [Google Scholar] [CrossRef]
- Kweon, S.K.; Hwang, J.H.; Oh, Y. COSMO SkyMed AO projects-soil moisture detection for vegetation fields based on a modified water-cloud model using COSMO-SkyMed SAR data. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium(IGARSS), Munich, Germany, 22–27 July 2012.
- Svoray, T.; Shoshany, M. SAR-based estimation of areal aboveground biomass (AAB) of herbaceous vegetation in the semi-arid zone: A modification of the water-cloud model. Int. J. Remote Sens. 2002, 23, 4089–4100. [Google Scholar] [CrossRef]
- Zribi, M.; Chahbi, A.; Lili, Z.; Duchemin, B.; Baghdadi, N.; Amri, R.; Chehbouni, A. Soil surface moisture estimation over a semi-arid region using ENVISAT ASAR radar data for soil evaporation evaluation. Hydrol. Earth Syst. Sci. 2011, 15, 345–358. [Google Scholar] [CrossRef]
- Kweon, S.K.; Oh, Y. A modified water-cloud model with leaf angle parameters for microwave backscattering from agricultural fields. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2802–2809. [Google Scholar] [CrossRef]
- Ulaby, F.; Allen, C.; Eger, G.; Kanemasu, E. Relating the microwave backscattering coefficient to leaf area index. Remote Sens. Environ. 1984, 14, 113–133. [Google Scholar] [CrossRef]
- Prevot, L.; Champion, I.; Guyot, G. Estimating surface soil moisture and leaf area index of a wheat canopy using a dual-frequency (C and X bands) scatterometer. Remote Sens. Environ. 1993, 46, 331–339. [Google Scholar] [CrossRef]
- Van Leeuwen, H.J.C.; Clevers, J.G.P.W. Synergy between optical and microwave remote sensing for crop growth monitoring. In Proceedings of the 6th International Symposium Physical Measurements and Signatures in Remote Sensing, Val D'Isere, France, 17–21 January 1994; pp. 1175–1182.
- Xu, H.; Steven, M.; Jaggard, K. Monitoring leaf area of sugar beet using ERS-1 SAR data. Int. J. Remote Sens. 1996, 17, 3401–3410. [Google Scholar] [CrossRef]
- Bindlish, R.; Barros, A.P. Parameterization of vegetation backscatter in radar-based, soil moisture estimation. Remote Sens. Environ. 2001, 76, 130–137. [Google Scholar] [CrossRef]
- Bolten, J.D.; Lakshmi, V.; Njoku, E.G. Soil moisture retrieval using the passive/active L- and S-band radar/radiometer. IEEE Trans. Geosci. Remote Sens. 2004, 41, 2792–2801. [Google Scholar] [CrossRef]
- Xu, X.O.; Marino, A.; Li, L. Biomass related parameter retrieving from quad-pol images based on freeman-durden decomposition. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011.
- Li, K.; Brisco, B.; Yun, S.; Touzi, R. Polarimetric decomposition with RADARSAT-2 for rice mapping and monitoring. Can. J. Remote Sens. 2012, 38, 169–179. [Google Scholar] [CrossRef]
- Lancashire, P.D.; Bleiholder, H.; Boom, T.; Langelüddeke, P.; Stauss, R.; WEBER, E.; Witzenberger, A. A uniform decimal code for growth stages of crops and weeds. Ann. Appl. Biol. 1991, 119, 561–601. [Google Scholar] [CrossRef]
- Freeman, A.; Durden, S.L. A three-component scattering model for polarimetric SAR data. IEEE Trans. Geosci. Remote Sens. 1998, 36, 963–973. [Google Scholar] [CrossRef]
- Van Zyl, J.J.; Arii, M.; Kim, Y. Model-based decomposition of polarimetric SAR covariance matrices constrained for nonnegative eigenvalues. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1104–1113. [Google Scholar] [CrossRef]
- Yamaguchi, Y.; Sato, A.; Sato, R. Four-component scattering power decomposition with rotation of coherency matrix. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2251–2258. [Google Scholar] [CrossRef]
- Yamaguchi, Y.; Moriyama, T.; Ishido, M.; Yamada, H. Four component scattering model for polarimetric SAR image decomposition. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1699–1706. [Google Scholar] [CrossRef]
- Yajima, Y.; Yamaguchi, Y.; Sato, R.; Yamada, H.; Boerner, W.M. POLSAR image analysis of wetland using a modified four component scattering power decomposition. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1667–1673. [Google Scholar] [CrossRef]
- Sato, A.; Yamaguchi, Y.; Singh, G.; Park, S.E. Four-component scattering power decomposition with extended volume scattering model. IEEE Geosci. Remote Sens. Lett. 2012, 9, 166–170. [Google Scholar] [CrossRef]
- Xu, F.; Jin, Y.Q. Deorientation theory of polarimetric scattering targets and application to terrain surface classification. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2351–2364. [Google Scholar]
- Nghiem, S.V.; Yueh, S.H.; Kwok, R.; Li, F.K. Symmetry properties in polarimetric remote sensing. Radio Sci. 1992, 27, 693–711. [Google Scholar] [CrossRef]
- Antropov, O.; Rauste, Y.; Hame, T. Volume scattering modeling in PolSAR decompositions: Study of ALOS PALSAR data over boreal forest. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3838–3848. [Google Scholar] [CrossRef]
- Golberg, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning; Addison Wesley: Boston, MA, USA, 1989. [Google Scholar]
- Yang, Z.; Li, K.; Liu, L.; Shao, Y.; Brisco, B.; Li, W. Rice growth monitoring using simulated compact polarimetric C band SAR. Radio Sci. 2015, 49, 1300–1315. [Google Scholar] [CrossRef]


| Date | Mode | Incidence Angle(°) | Pixel Spacing (A × R, m) | Phenology |
|---|---|---|---|---|
| 2012-06-27 | FQ20W 1 | 38–41 | 5.2 × 7.6 | Seedling |
| 2012-07-11 | FQ9W | 27–30 | 5.2 × 7.6 | Tillering |
| 2012-07-21 | FQ20W | 38–41 | 5.2 × 7.6 | Elongation |
| 2012-08-04 | FQ9W | 27–30 | 5.2 × 7.6 | Booting |
| 2012-08-28 | FQ9W | 27–30 | 5.2 × 7.6 | Heading |
| 2012-09-07 | FQ20W | 38–41 | 5.2 × 7.6 | Flowering |
| 2012-09-21 | FQ9W | 27–30 | 5.2 × 7.6 | Dough |
| 2012-10-15 | FQ9W | 27–30 | 5.2 × 7.6 | Mature |
| No. of Rice Fields | Total Number of Pixels | Number of Negative Pixels | Percentage of Negative Pixels (%) | ||
|---|---|---|---|---|---|
| Freeman Decomposition | Improved Decomposition | Freeman Decomposition | Improved Decomposition | ||
| (1) | 408 | 31 | 10 | 7.60 | 2.45 |
| (2) | 2238 | 106 | 65 | 4.69 | 2.90 |
| (3) | 1516 | 240 | 80 | 15.83 | 5.28 |
| (4) | 518 | 71 | 32 | 13.90 | 6.18 |
| (5) | 213 | 19 | 8 | 9.39 | 3.76 |
| (6) | 556 | 22 | 13 | 4.14 | 2.34 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.; Li, K.; Shao, Y.; Brisco, B.; Liu, L. Estimation of Paddy Rice Variables with a Modified Water Cloud Model and Improved Polarimetric Decomposition Using Multi-Temporal RADARSAT-2 Images. Remote Sens. 2016, 8, 878. https://doi.org/10.3390/rs8100878
Yang Z, Li K, Shao Y, Brisco B, Liu L. Estimation of Paddy Rice Variables with a Modified Water Cloud Model and Improved Polarimetric Decomposition Using Multi-Temporal RADARSAT-2 Images. Remote Sensing. 2016; 8(10):878. https://doi.org/10.3390/rs8100878
Chicago/Turabian StyleYang, Zhi, Kun Li, Yun Shao, Brian Brisco, and Long Liu. 2016. "Estimation of Paddy Rice Variables with a Modified Water Cloud Model and Improved Polarimetric Decomposition Using Multi-Temporal RADARSAT-2 Images" Remote Sensing 8, no. 10: 878. https://doi.org/10.3390/rs8100878
APA StyleYang, Z., Li, K., Shao, Y., Brisco, B., & Liu, L. (2016). Estimation of Paddy Rice Variables with a Modified Water Cloud Model and Improved Polarimetric Decomposition Using Multi-Temporal RADARSAT-2 Images. Remote Sensing, 8(10), 878. https://doi.org/10.3390/rs8100878