Investigation of Spectral Band Requirements for Improving Retrievals of Phytoplankton Functional Types
Abstract
:1. Introduction
2. Materials and Methods
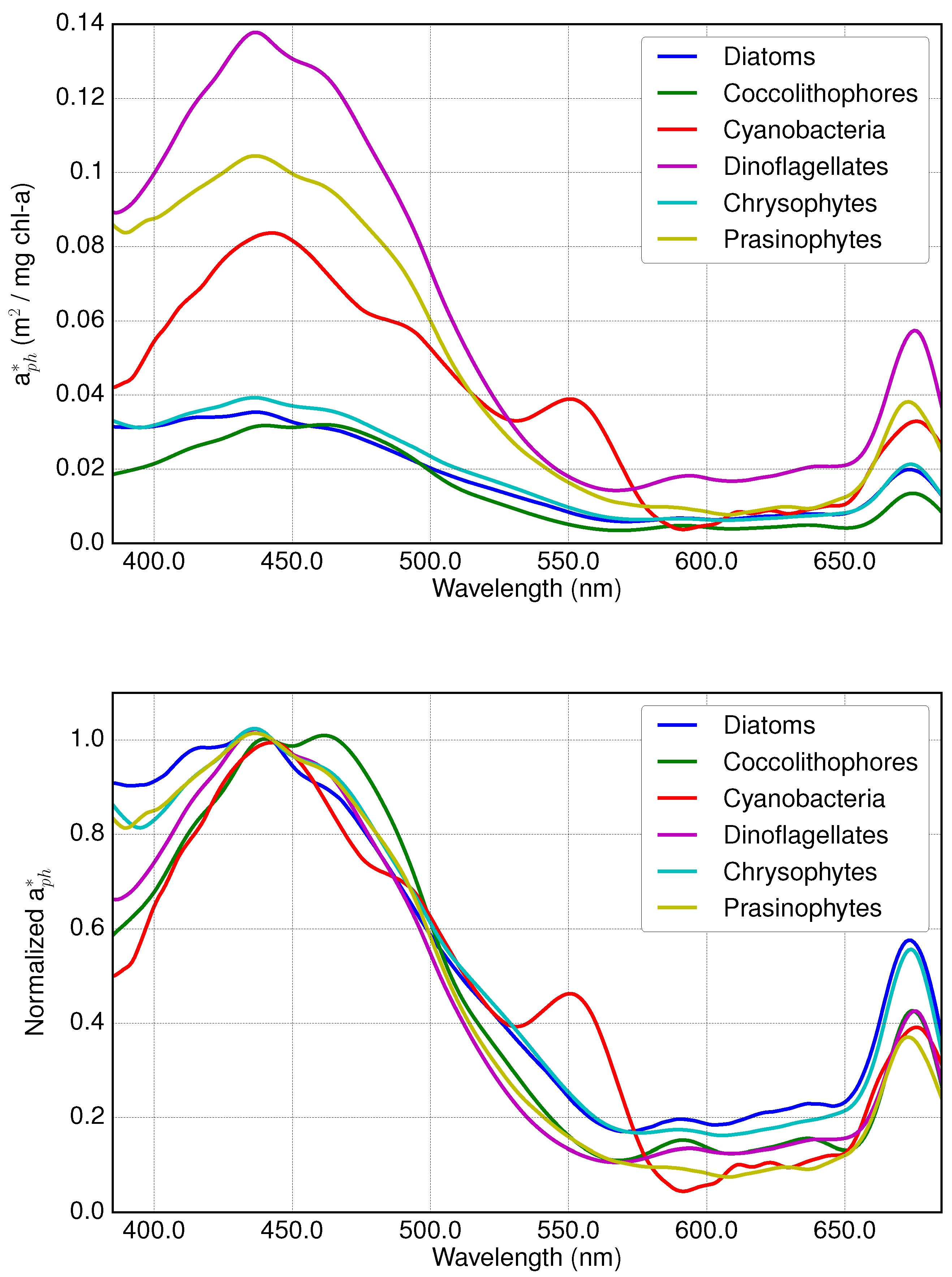
2.1. Absorption Spectra of PFTs
2.2. Forward Modeling of
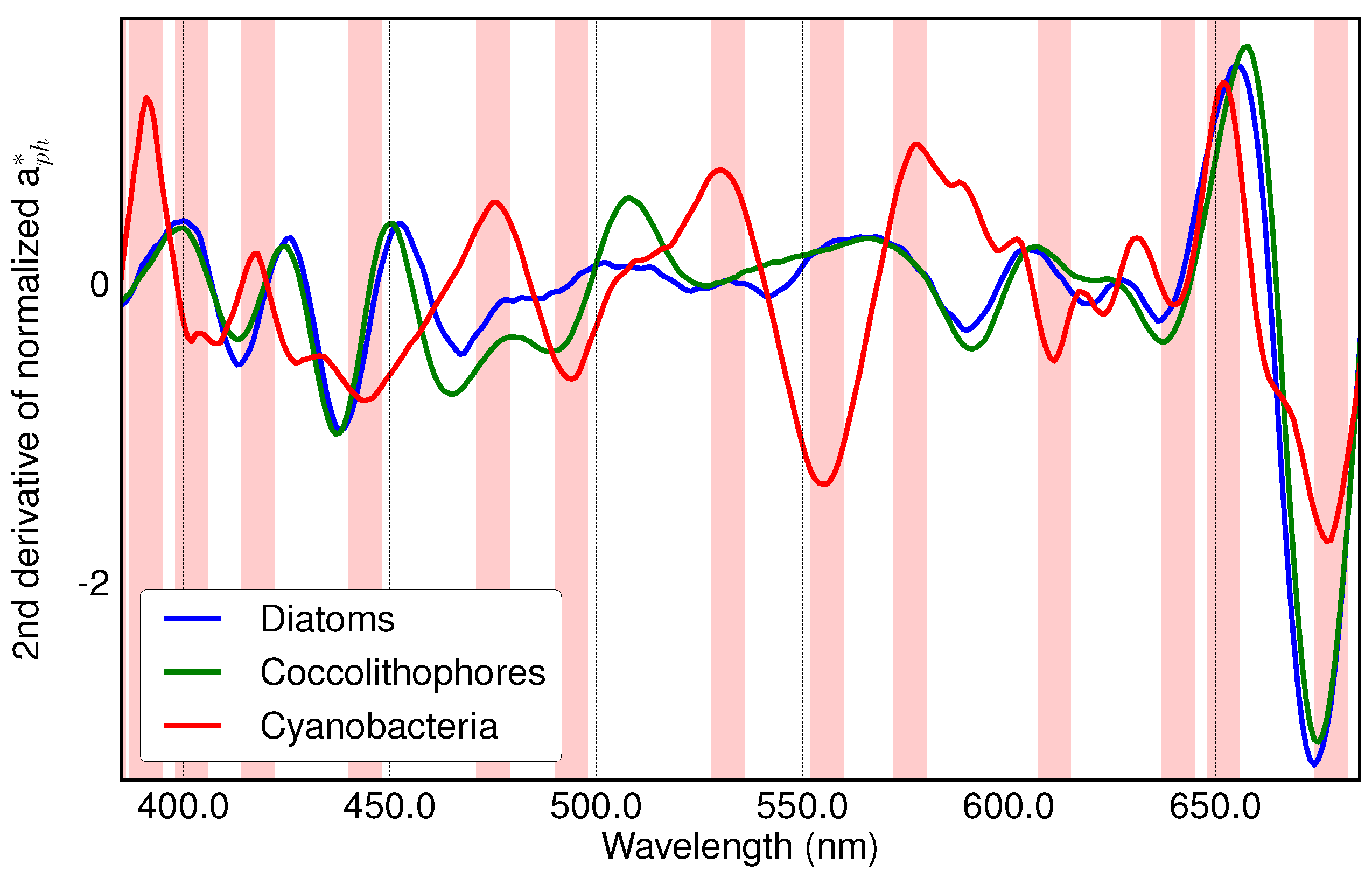
2.3. Derivative Analysis
2.4. Application of Derivative Spectroscopy to Phytoplankton Absorption Spectra for Selection of Spectral Bands (Isada et al., 2015)
2.5. Application of Derivative Spectroscopy to Reflectance Spectra for Selection of Spectral Bands (Lee et al., 2007)
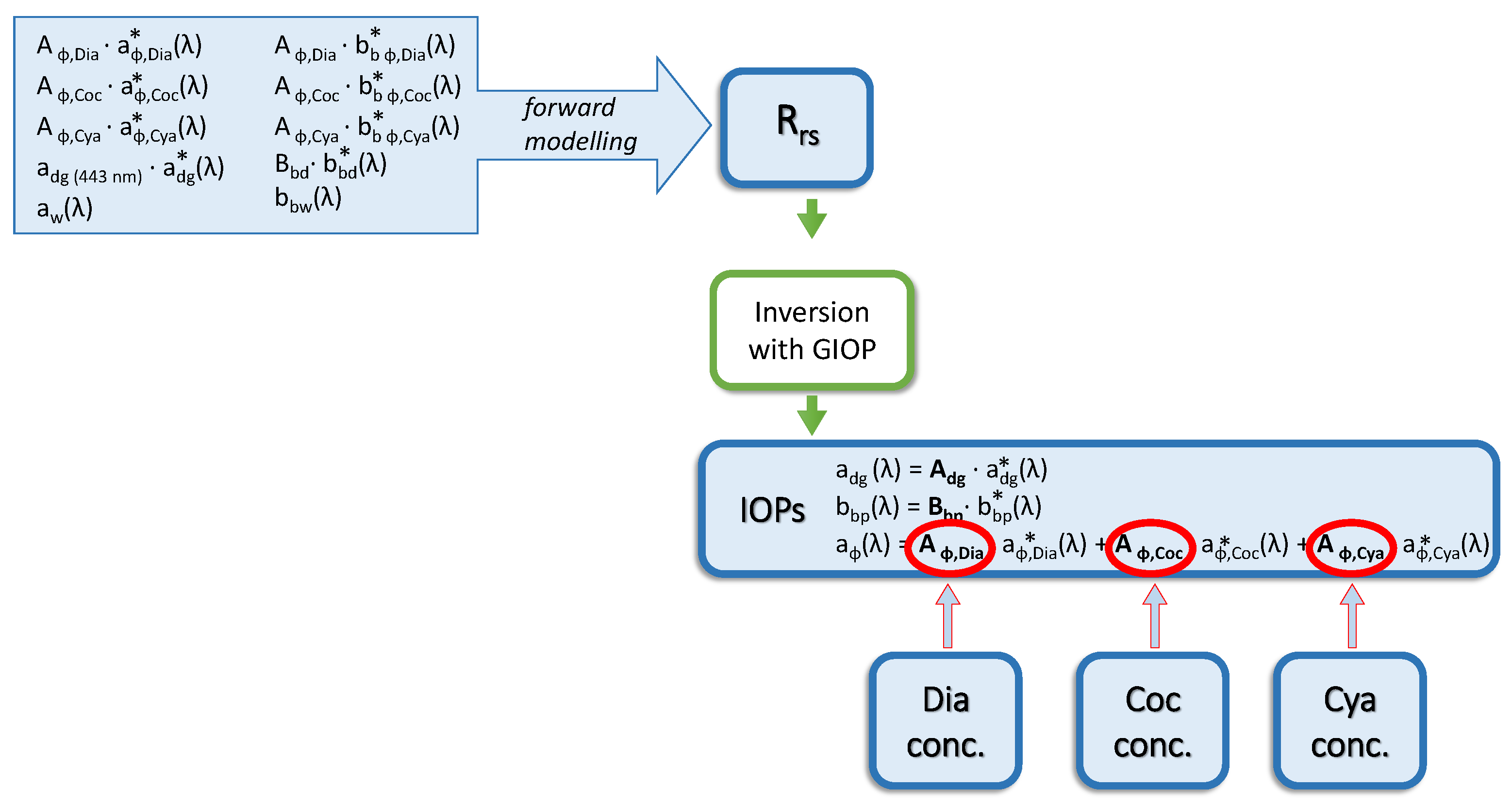
2.6. Ocean Reflectance Inversion with GIOP
3. Results
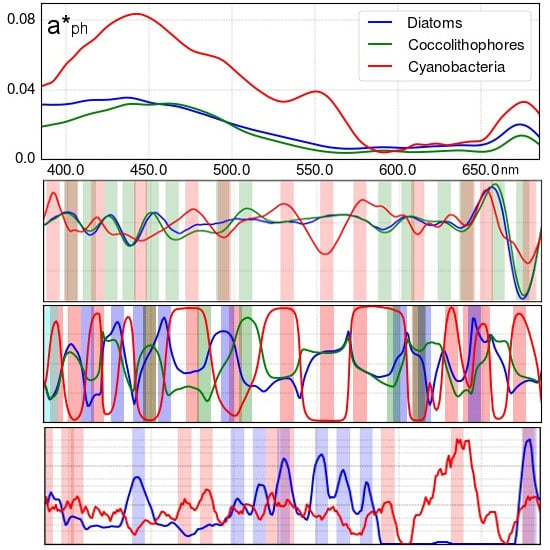
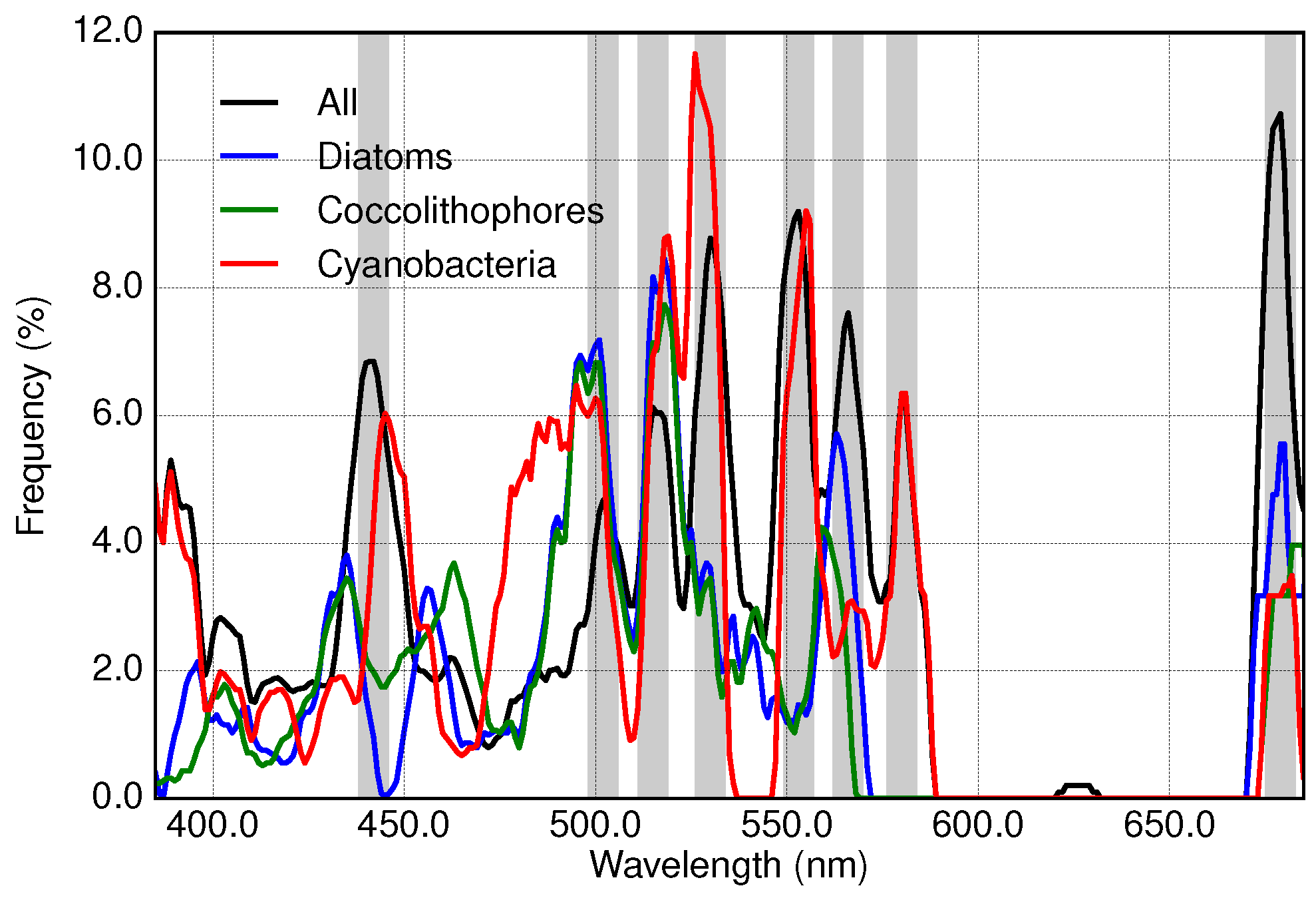
3.1. Analysis of Specific Measured PFT Absorption Spectra of Diatoms, Coccolithophores and Cyanobacteria Using Derivative Analysis
3.2. Results of Applying Derivative Spectroscopy to Mixtures of Phytoplankton Specific Absorption Spectra for the Selection of Spectral Bands, Following Isada et al., 2015
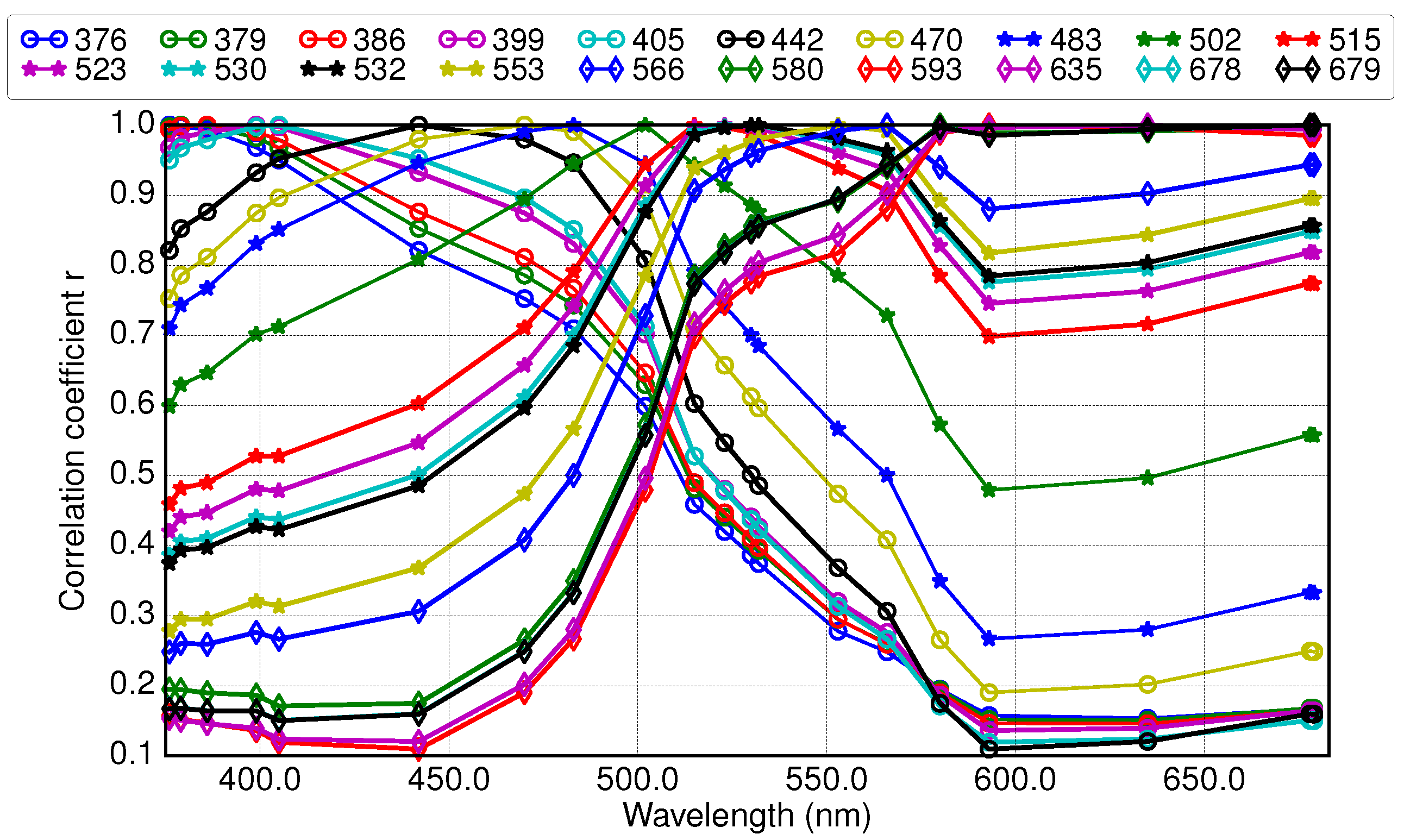
3.3. Results of Applying Derivative Spectroscopy to Reflectance Spectra for Selection of Spectral Bands, Following Lee et al., 2007
3.4. Results of GIOP Retrievals
4. Discussion
4.1. Band Placement Determined with Different Approaches
4.2. Performance of GIOP Retrievals
5. Summary and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Sathyendranath, S.; Aiken, J.; Alvain, S.; Barlow, R.; Bouman, H.; Bracher, A.; Brewin, R.; Bricaud, A.; Brown, C.W.; Ciotti, A.M.; et al. Phytoplankton Functional Types from Space; Reports of the International Ocean Colour Coordinating Group; International Ocean Colour Coordinating Group: Dartmouth, NS, Canada, 2014. [Google Scholar]
- Le Quéré, C.; Harrison, S.P.; Colin Prentice, I.; Buitenhuis, E.T.; Aumont, O.; Bopp, L.; Claustre, H.; Cotrim Da Cunha, L.; Geider, R.; Giraud, X.; et al. Ecosystem dynamics based on plankton functional types for global ocean biogeochemistry models. Glob. Chang. Biol. 2005, 11, 2016–2040. [Google Scholar]
- Hoepffner, N.; Sathyendranath, S. Effect of pigment composition on absorption properties of phytoplankton. Mar. Ecol. Prog. Ser. 1991, 73, l–23. [Google Scholar] [CrossRef]
- Lee, Z.; Carder, K.; Arnone, R.; He, M. Determination of primary spectral bands for remote sensing of aquatic environments. Sensors 2007, 7, 3428–3441. [Google Scholar] [CrossRef]
- Isada, T.; Hirawake, T.; Kobayashi, T.; Nosaka, Y.; Natsuike, M.; Imai, I.; Suzuki, K.; Saitoh, S.I. Hyperspectral optical discrimination of phytoplankton community structure in Funka Bay and its implications for ocean color remote sensing of diatoms. Remote Sens. Environ. 2015, 159, 134–151. [Google Scholar] [CrossRef]
- Guanter, L.; Kaufmann, H.; Segl, K.; Foerster, S.; Rogass, C.; Chabrillat, S.; Kuester, T.; Hollstein, A.; Rossner, G.; Chlebek, C.; et al. The EnMAP spaceborne imaging spectroscopy mission for earth observation. Remote Sens. 2015, 7, 8830–8857. [Google Scholar] [CrossRef]
- Del Castillo, C.E. Pre-Aerosol, Clouds, and ocean Ecosystem (PACE) Mission science definition team report. In Proceedings of the Ocean Carbon and Biogeochemistry Workshop, Woods Hole, MA, USA, 16–19 July 2012.
- Xi, H.; Hieronymi, M.; Röttgers, R.; Krasemann, H.; Qiu, Z. Hyperspectral differentiation of phytoplankton taxonomic groups: A comparison between using remote sensing reflectance and absorption spectra. Remote Sens. 2015, 7, 14781–14805. [Google Scholar] [CrossRef]
- Werdell, P.J.; Roesler, C.S.; Goes, J.I. Discrimination of phytoplankton functional groups using an ocean reflectance inversion model. Appl. Opt. 2014, 53, 4833–4849. [Google Scholar] [CrossRef] [PubMed]
- Werdell, P.J.; Roesler, C.S.; Goes, J.I. Remotely searching for noctiluca miliaris in the Arabian Sea. In Proceedings of the 22th Ocean Optics Conference, Portland, ME, USA, 27–31 October 2014.
- Burrows, J.P.; Hölzle, E.; Goede, A.P.H.; Visser, H.; Fricke, W. SCIAMACHY—Scanning imaging absorption spectrometer for atmospheric chartography. Acta Astronaut. 1995, 35, 445–451. [Google Scholar] [CrossRef]
- Bovensmann, H.; Burrows, J.P.; Buchwitz, M.; Frerick, J.; Noël, S.; Rozanov, V.V.; Chance, K.V.; Goede, A.P.H. SCIAMACHY: Mission objectives and measurement modes. J. Atmos. Sci. 1999, 56, 127–150. [Google Scholar] [CrossRef]
- Bracher, A.; Vountas, M.; Dinter, T.; Burrows, J.P.; Röttgers, R.; Peeken, I. Quantitative observation of cyanobacteria and diatoms from space using PhytoDOAS on SCIAMACHY data. Biogeosciences 2009, 6, 751–764. [Google Scholar] [CrossRef]
- Sadeghi, A.; Dinter, T.; Vountas, M.; Taylor, B.B.; Altenburg-Soppa, M.; Peeken, I.; Bracher, A. Improvement to the PhytoDOAS method for identification of coccolithophores using hyper-spectral satellite data. Ocean Sci. 2012, 8, 1055–1070. [Google Scholar] [CrossRef]
- Dinter, T.; Rozanov, V.V.; Burrows, J.P.; Bracher, A. Retrieving the availability of light in the ocean utilising spectral signatures of vibrational Raman scattering in hyper-spectral satellite measurements. Ocean Sci. 2015, 11, 373–389. [Google Scholar] [CrossRef]
- Wolanin, A.; Rozanov, V.; Dinter, T.; Noël, S.; Vountas, M.; Burrows, J.; Bracher, A. Global retrieval of marine and terrestrial chlorophyll fluorescence at its red peak using hyperspectral top of atmosphere radiance measurements: Feasibility study and first results. Remote Sens. Environ. 2015, 166, 243–261. [Google Scholar] [CrossRef]
- Tyrrell, T.; Merico, A. Overview of fluorescence protocols: Theory, basic concepts, and practice. In Coccolithophores: From Molecular Processes to Global Impact; Thierstein, H.R., Young, J.R., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 75–97. [Google Scholar]
- Röttgers, R.; Schönfeld, W.; Kipp, P.R.; Doerffer, R. Practical test of a point-source integrating cavity absorption meter: the performance of different collector assemblies. Appl. Opt. 2005, 44, 5549–5560. [Google Scholar] [CrossRef] [PubMed]
- Werdell, P.J.; Franz, B.A.; Bailey, S.W.; Feldman, G.C.; Boss, E.; Brando, V.E.; Dowell, M.; Hirata, T.; Lavender, S.J.; Lee, Z.; et al. Generalized ocean color inversion model for retrieving marine inherent optical properties. Appl. Opt. 2013, 52, 2019–2037. [Google Scholar] [CrossRef] [PubMed]
- Gordon, H.R.; Brown, O.B.; Evans, R.H.; Brown, J.W.; Smith, R.C.; Baker, K.S.; Clark, D.K. A semianalytic radiance model of ocean color. J. Geophys. Res. 1988, 93, 10909–10924. [Google Scholar] [CrossRef]
- Lee, Z.; Carder, K.L.; Arnone, R.A. Deriving inherent optical properties from water color: A multiband quasi-analytical algorithm for optically deep waters. Appl. Opt. 2002, 41, 5755–5772. [Google Scholar] [CrossRef] [PubMed]
- Babin, M. Variations in the light absorption coefficients of phytoplankton, nonalgal particles, and dissolved organic matter in coastal waters around Europe. J. Geophys. Res. 2003. [Google Scholar] [CrossRef]
- Pope, R.M.; Fry, E.S. Absorption spectrum (380–700 nm) of pure water. II. Integrating cavity measurements. Appl. Opt. 1997, 36, 8710–8723. [Google Scholar] [CrossRef] [PubMed]
- Smith, R.C.; Baker, K.S. Optical properties of the clearest natural waters (200–800 nm). Appl. Opt. 1981, 20, 177–184. [Google Scholar] [CrossRef] [PubMed]
- Maritorena, S.; Siegel, D.; Peterson, A. Optimization of a semianalytical ocean color model for global-scale applications. Appl. Opt. 2002, 41, 2705–2714. [Google Scholar] [CrossRef] [PubMed]
- Bricaud, A.; Bédhomme, A.L.; Morel, A. Optical properties of diverse phytoplanktonic species: Experimental results and theoretical interpretation. J. Plankton Res. 1988, 10, 851–873. [Google Scholar] [CrossRef]
- Ahn, Y.H.; Bricaud, A.; Morel, A. Light backscattering efficiency and related properties of some phytoplankters. Deep Sea Res. A Oceanogr. Res. Pap. 1992, 39, 1835–1855. [Google Scholar] [CrossRef]
- Brewin, R.J.; Dall’Olmo, G.; Sathyendranath, S.; Hardman-Mountford, N.J. Particle backscattering as a function of chlorophyll and phytoplankton size structure in the open-ocean. Opt. Express 2012, 20, 17632–17652. [Google Scholar] [CrossRef] [PubMed]
- Tsai, F.; Philpot, W. Derivative analysis of hyperspectral data. Remote Sens. Environ. 1998, 66, 41–51. [Google Scholar] [CrossRef]
- Torrecilla, E.; Piera, J.; Vilaseca, M. Derivative analysis of hyperspectral oceanographic data. In Advances in Geoscience and Remote Sensing; Jedlovec, G., Ed.; InTech Open Access Publisher: Rijeka, Croatia, 2009; pp. 597–618. [Google Scholar]
- Torrecilla, E.; Stramski, D.; Reynolds, R.A.; Millán-Núñez, E.; Piera, J. Cluster analysis of hyperspectral optical data for discriminating phytoplankton pigment assemblages in the open ocean. Remote Sens. Environ. 2011, 115, 2578–2593. [Google Scholar] [CrossRef]

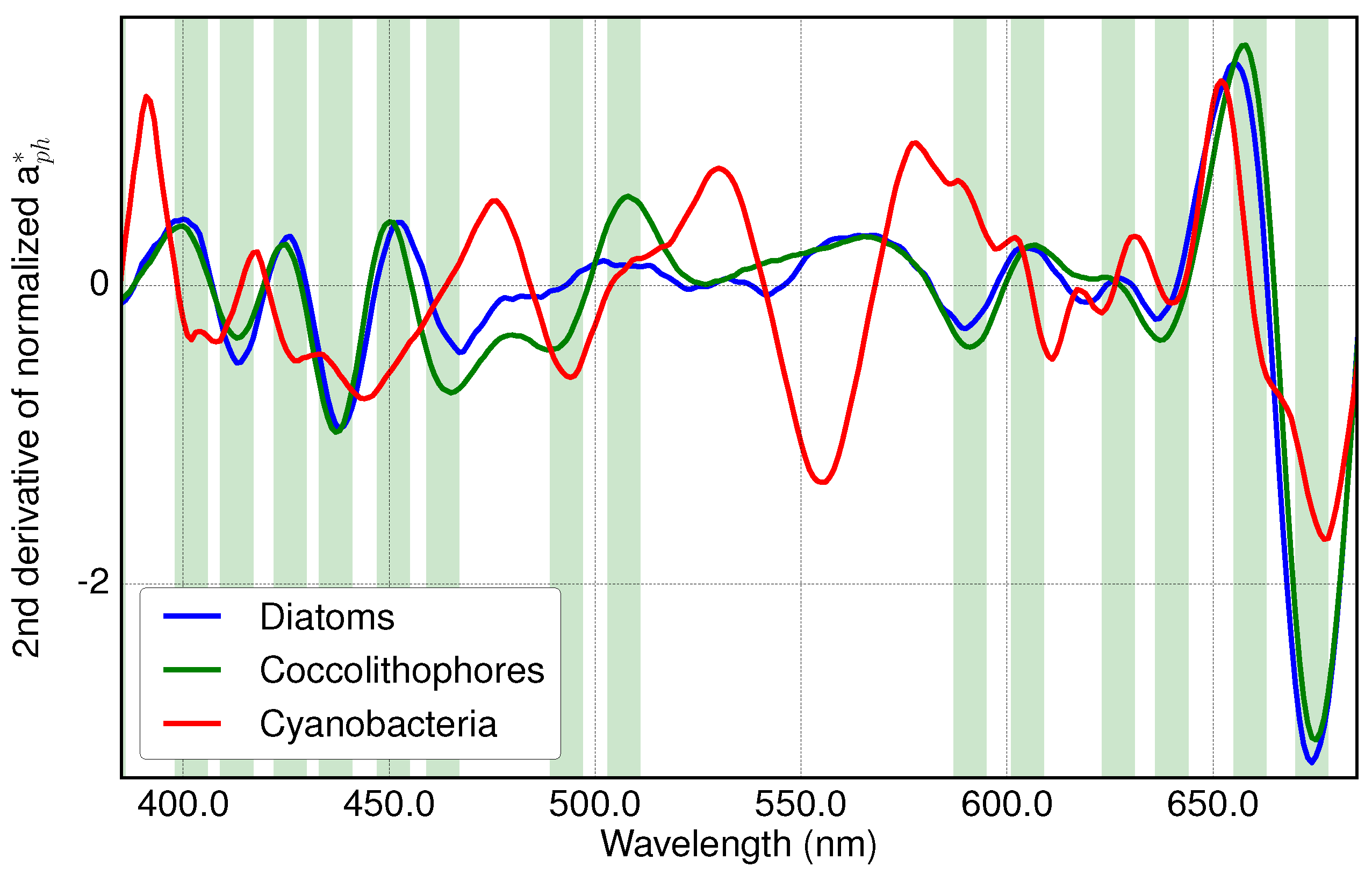
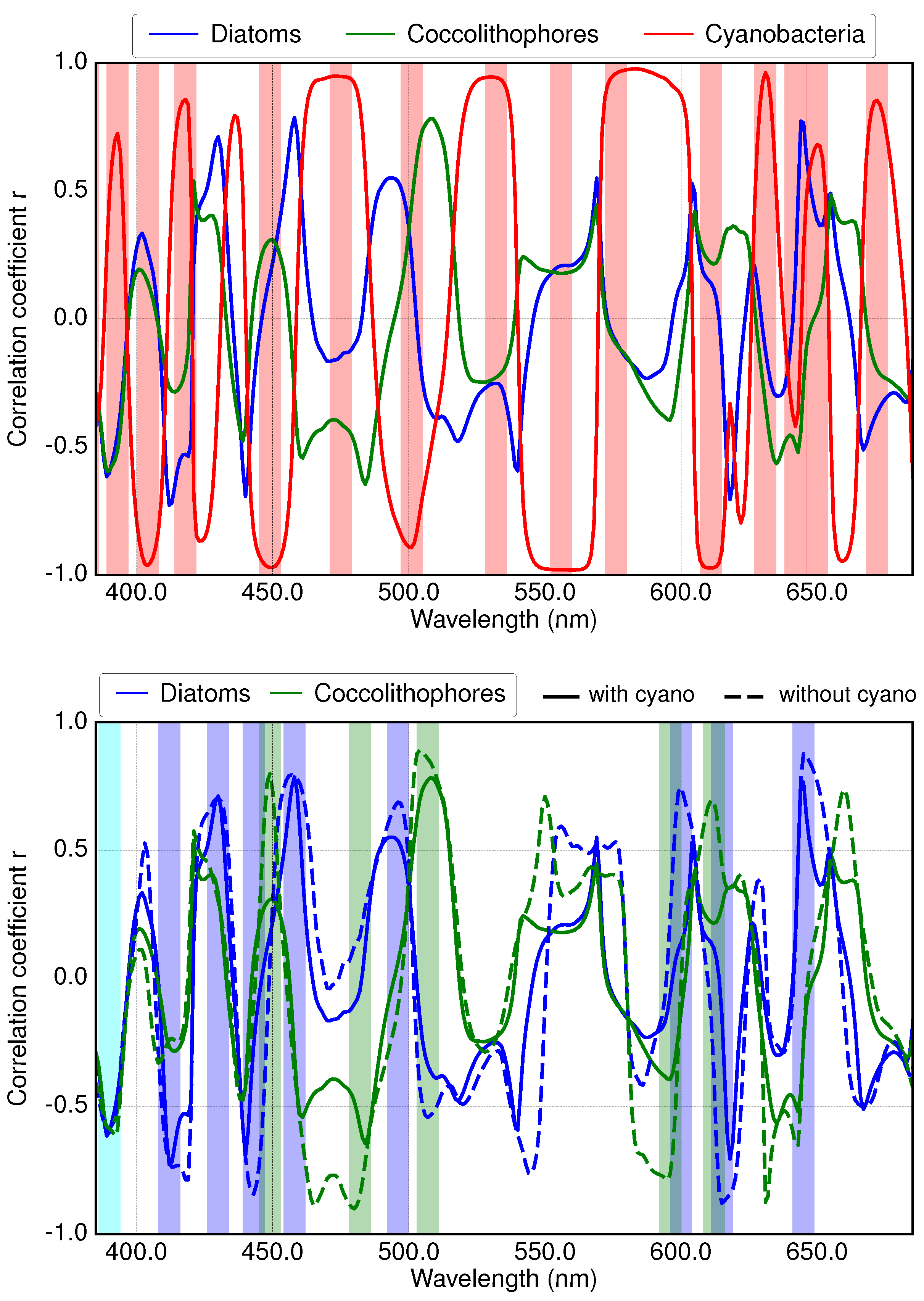
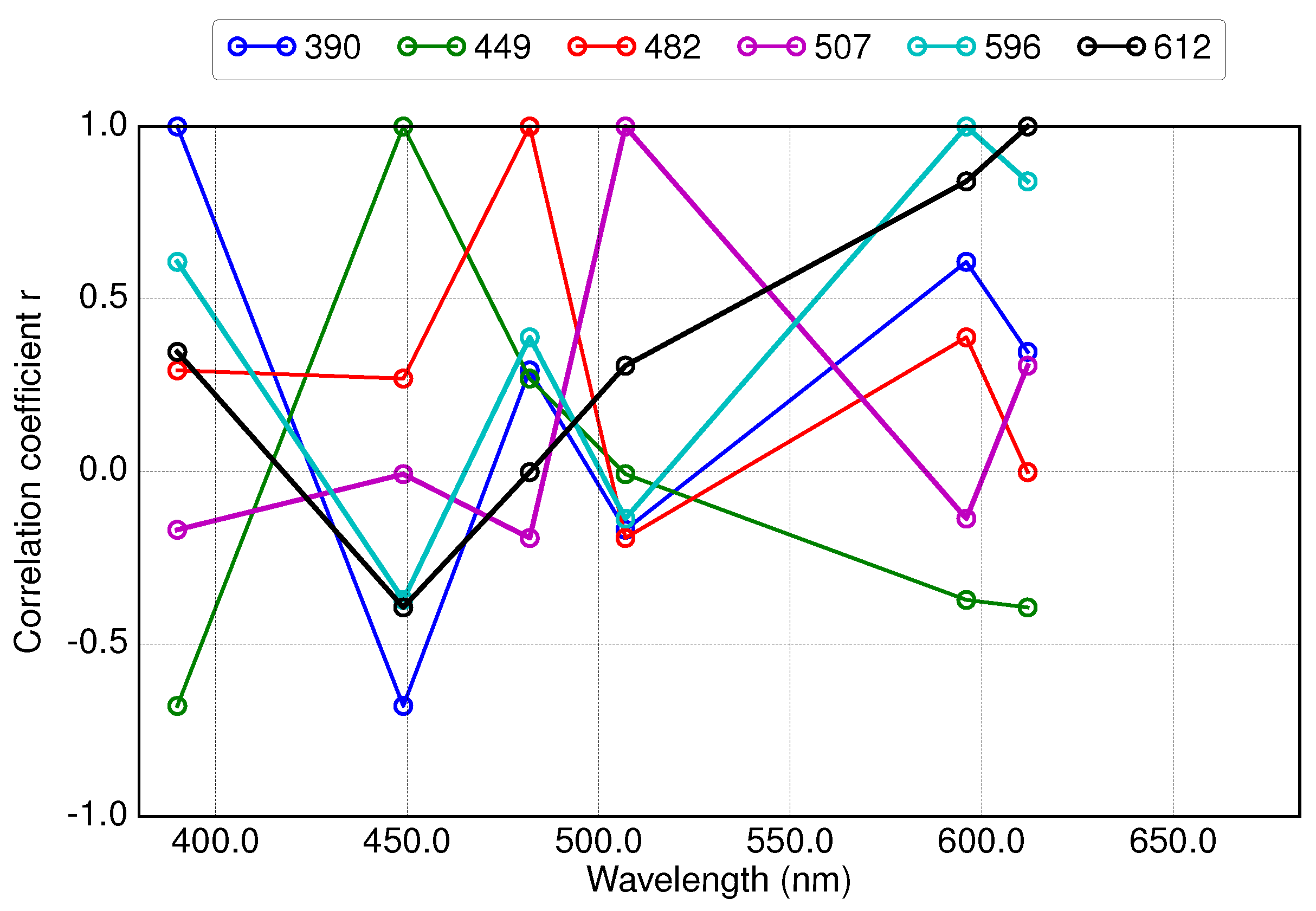
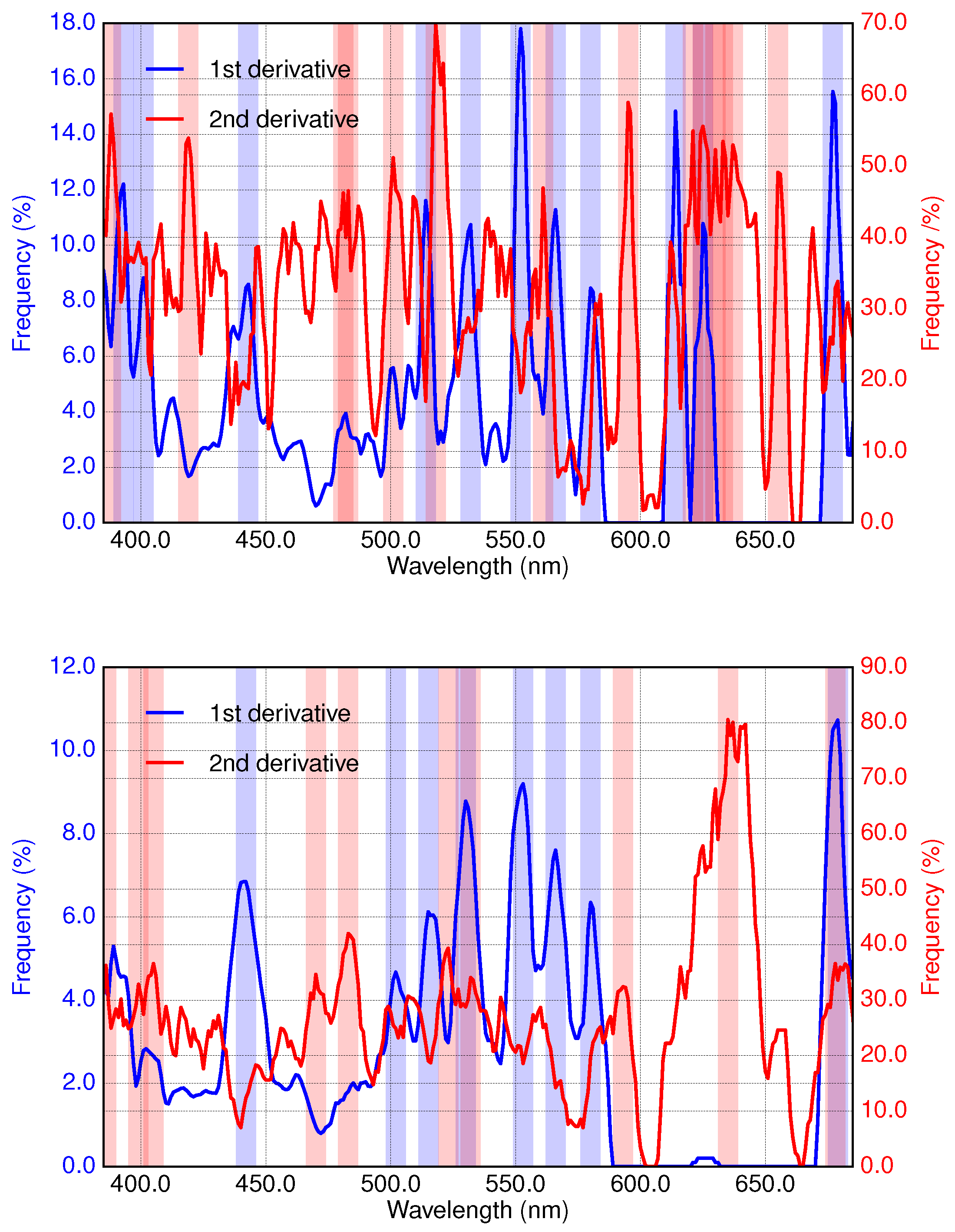
| a Devs | a devs (+red.v.1,2,3) | Freq. 10 nm (+red.) | Mix | MERIS & OLCI | MODIS | SeaWIFS | H&S, 1991 | Isada et al., 2015 | Lee et al., 2007 |
|---|---|---|---|---|---|---|---|---|---|
| 376 | |||||||||
| 382 | 382 | 379 | 381 | ||||||
| 386 | 384 | 385 | |||||||
| 391 | 390 | ||||||||
| 393 | 395 | ||||||||
| 399 | |||||||||
| 402 | 404 | 405 | 404 | 400 | |||||
| 413 | 412 | 412 | 412 | 412 | 413 | 411 | |||
| 418 | 418 | ||||||||
| 426 | 430 | 425 | |||||||
| 437 | 435 | ||||||||
| 444 | 443 | 442 | 443 | 443 | 443 | 443 | 433 | 440 | |
| 451 | 449 | ||||||||
| 463 | 458 | 461 | 458 | 460 | |||||
| 475 | 475 | 470 | 473 | 475 | |||||
| 482 | 483 | ||||||||
| 490 | 488 | 490 | 490 | 488 | 490 | ||||
| 493 | 496 | ||||||||
| 494 | |||||||||
| 501 | 502 | ||||||||
| 507 | 507 | 510 | 510 | 512 | 510 | ||||
| 515 | |||||||||
| 523 | |||||||||
| 530 | 531 | 531 | |||||||
| 532 | 532 | 532 | 532 | 532 | |||||
| 545 | |||||||||
| 556 | 556 | 553 | 555 | 551 | 555 | 556 | |||
| 560 | |||||||||
| 566 | 565 | ||||||||
| 576 | 576 | 580 | 578 | 583 | 585 | 580 | |||
| 591 | 596 | 593 | 594 | 599 | |||||
| 605 | 600 | ||||||||
| 611 | 611 | ||||||||
| 612 | |||||||||
| 615 | 620 | 623 | 615 | 615 | |||||
| 627 | 631 | 635 | 631 | 633 | 635 | ||||
| 640 | |||||||||
| 641 | 642 | ||||||||
| 645 | 644 | 646 | |||||||
| 652 | 650 | 655 | |||||||
| 665 | 667 | 670 | 662 | 665 | |||||
| 674 | 672 | 674 | 674 | ||||||
| 678 | 678 | ||||||||
| 679 | 681 | 678 | 676 | ||||||
| 685 | |||||||||
| 700 | 694 | 710 |
| a Devs | a Devs | a Devs, Reduced v.1 | a Devs, Reduced v.2 | a b Reduced v.3 | Freq. 5 nm | Freq. 5 nm, Reduced | |
|---|---|---|---|---|---|---|---|
| r | 0.83 | 0.85 | 0.82 | 0.86 | 0.87 | 0.90 | 0.86 |
| MAE | 1.25 | 1.10 | 1.05 | 2.23 | 1.80 | 1.02 | 0.77 |
| Freq. 10 nm | Freq. 10 nm, Reduced | Mix | MERIS | MODIS | SeaWiFS | All, 1 nm | All, 5 nm | All, 10 nm | |
|---|---|---|---|---|---|---|---|---|---|
| r | 0.83 | 0.77 | 0.77 | 0.69 | 0.63 | 0.80 | 0.83 | 0.85 | 0.84 |
| MAE | 1.13 | 1.04 | 0.74 | 0.86 | 1.83 | 1.13 | 0.62 | 0.69 | 0.95 |
| a Devs | a Devs | a Devs Reduced v.1 | a Devs, Reduced v.2 | a Devs, Reduced v.3 | Freq. 5 nm | Freq. 5 nm, Reduced | |
|---|---|---|---|---|---|---|---|
| r | 0.89 | 0.90 | 0.91 | 0.91 | 0.93 | 0.92 | 0.91 |
| MAE | 0.91 | 0.90 | 0.92 | 0.98 | 0.71 | 0.72 | 0.80 |
| Freq. 10 nm | Freq. 10 nm, Reduced | Mix | MERIS | MODIS | SeaWiFS | All, 1 nm | All, 5 nm | All, 10 nm | |
|---|---|---|---|---|---|---|---|---|---|
| r | 0.91 | 0.92 | 0.86 | 0.88 | 0.91 | 0.93 | 0.89 | 0.90 | 0.91 |
| MAE | 0.75 | 0.94 | 1.07 | 1.01 | 1.03 | 0.73 | 0.93 | 0.86 | 0.87 |
| a Devs | a Devs | a devs, Reduced v.1 | a Devs, Reduced v.2 | a Devs, Reduced v.3 | Freq. 5 nm | Freq. 5 nm, Reduced | |
|---|---|---|---|---|---|---|---|
| r | 0.99 | 1.00 | 1.00 | 0.99 | 0.99 | 1.00 | 0.99 |
| MAE | 0.13 | 0.15 | 0.15 | 0.41 | 0.35 | 0.13 | 0.13 |
| Freq. 10 nm | Freq. 10 nm, Reduced | Mix | MERIS | MODIS | SeaWiFS | All, 1 nm | All, 5 nm | All, 10 nm | |
|---|---|---|---|---|---|---|---|---|---|
| r | 0.99 | 0.99 | 1.00 | 0.99 | 0.98 | 0.98 | 1.00 | 1.00 | 1.00 |
| MAE | 0.15 | 0.21 | 0.13 | 0.17 | 0.42 | 0.42 | 0.13 | 0.13 | 0.12 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wolanin, A.; Soppa, M.A.; Bracher, A. Investigation of Spectral Band Requirements for Improving Retrievals of Phytoplankton Functional Types. Remote Sens. 2016, 8, 871. https://doi.org/10.3390/rs8100871
Wolanin A, Soppa MA, Bracher A. Investigation of Spectral Band Requirements for Improving Retrievals of Phytoplankton Functional Types. Remote Sensing. 2016; 8(10):871. https://doi.org/10.3390/rs8100871
Chicago/Turabian StyleWolanin, Aleksandra, Mariana A. Soppa, and Astrid Bracher. 2016. "Investigation of Spectral Band Requirements for Improving Retrievals of Phytoplankton Functional Types" Remote Sensing 8, no. 10: 871. https://doi.org/10.3390/rs8100871
APA StyleWolanin, A., Soppa, M. A., & Bracher, A. (2016). Investigation of Spectral Band Requirements for Improving Retrievals of Phytoplankton Functional Types. Remote Sensing, 8(10), 871. https://doi.org/10.3390/rs8100871