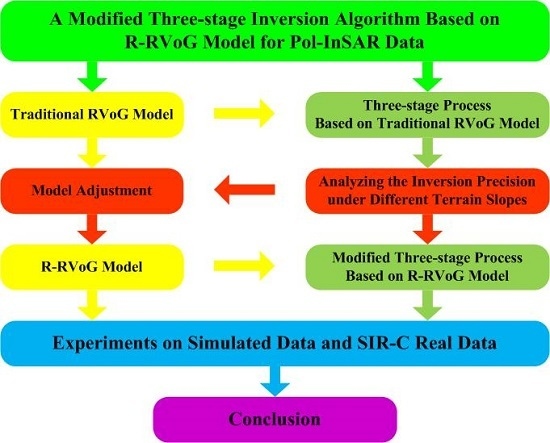
A Modified Three-Stage Inversion Algorithm Based on R-RVoG Model for Pol-InSAR Data
Abstract
:1. Introduction
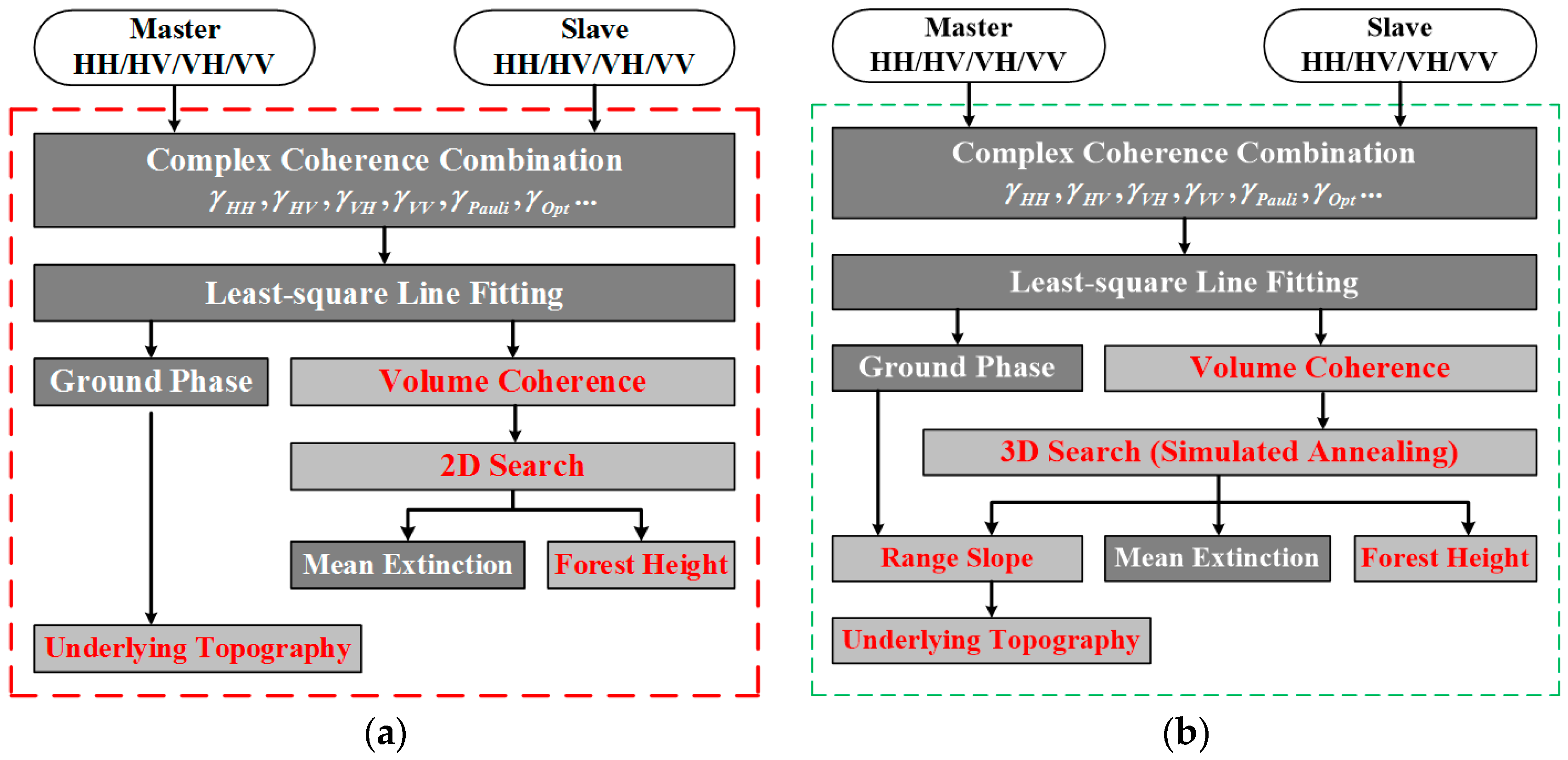
2. Three-Stage Process Based on RVoG Model
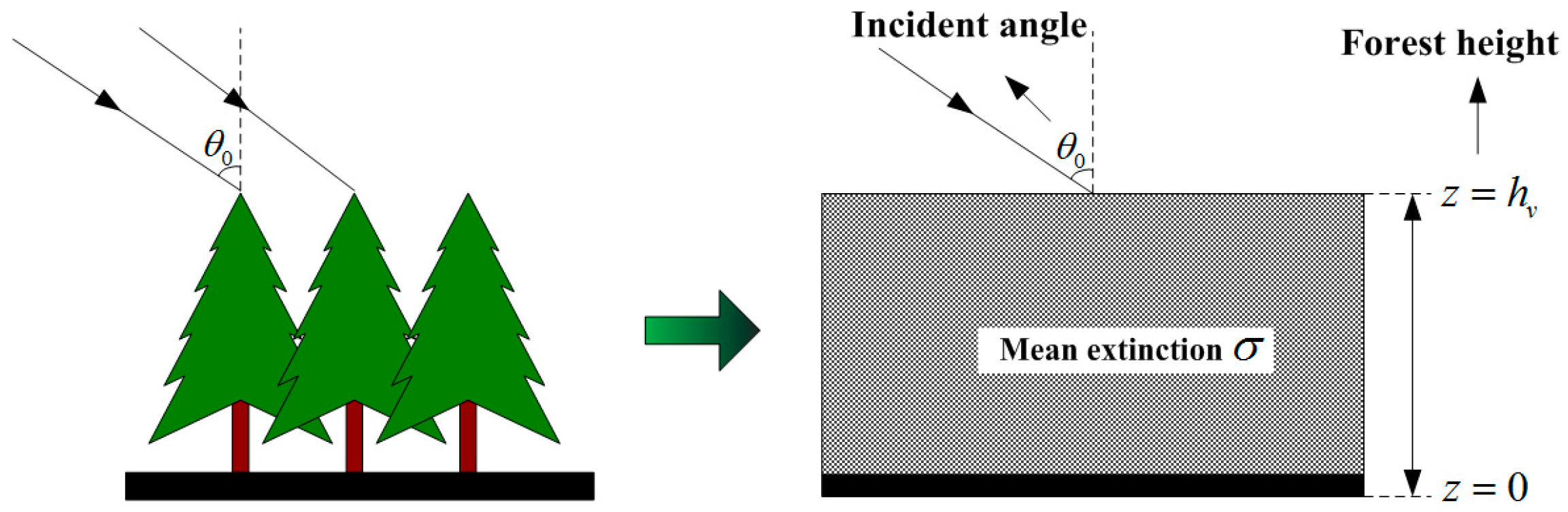
2.1. RVoG Model
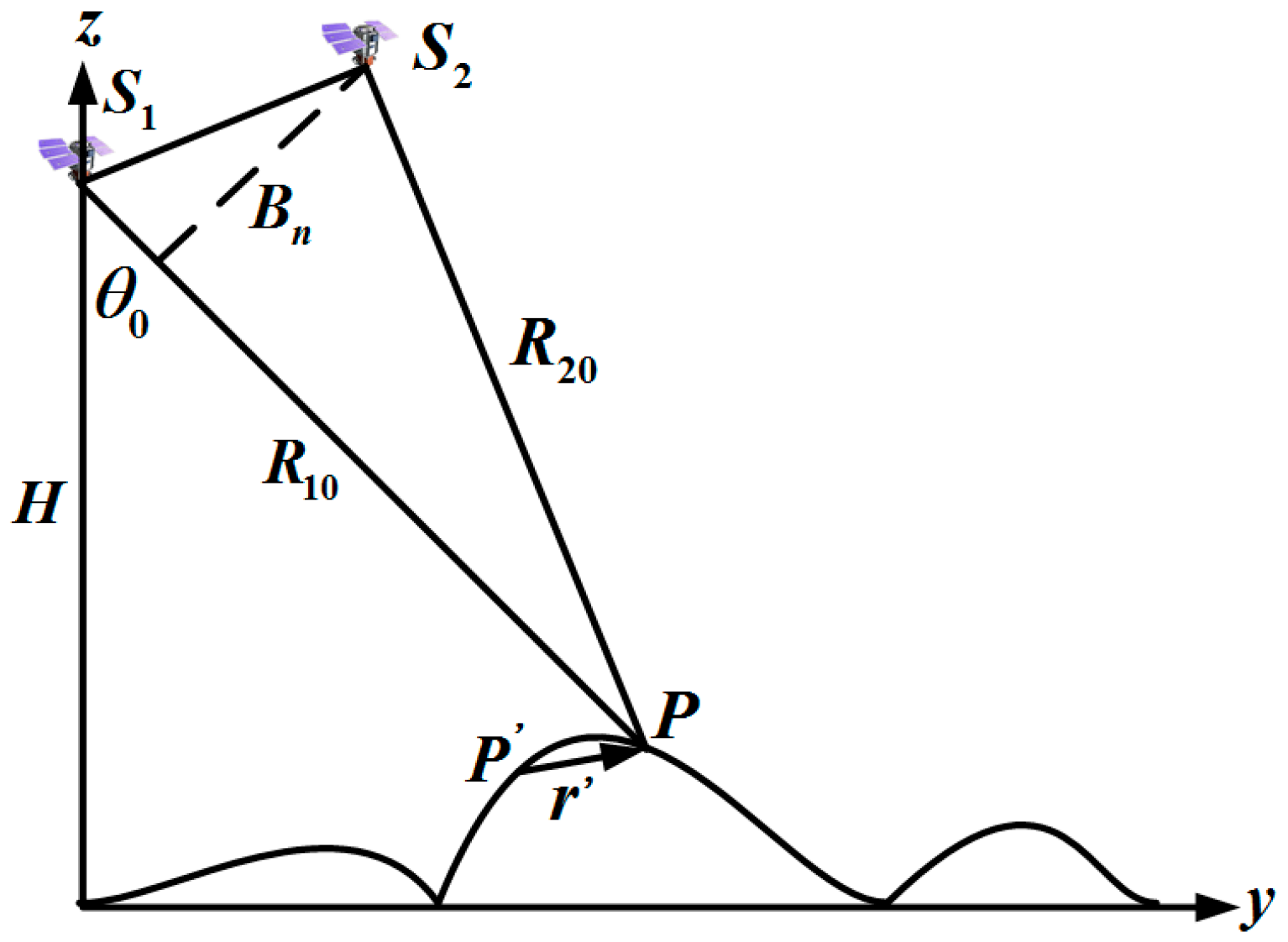
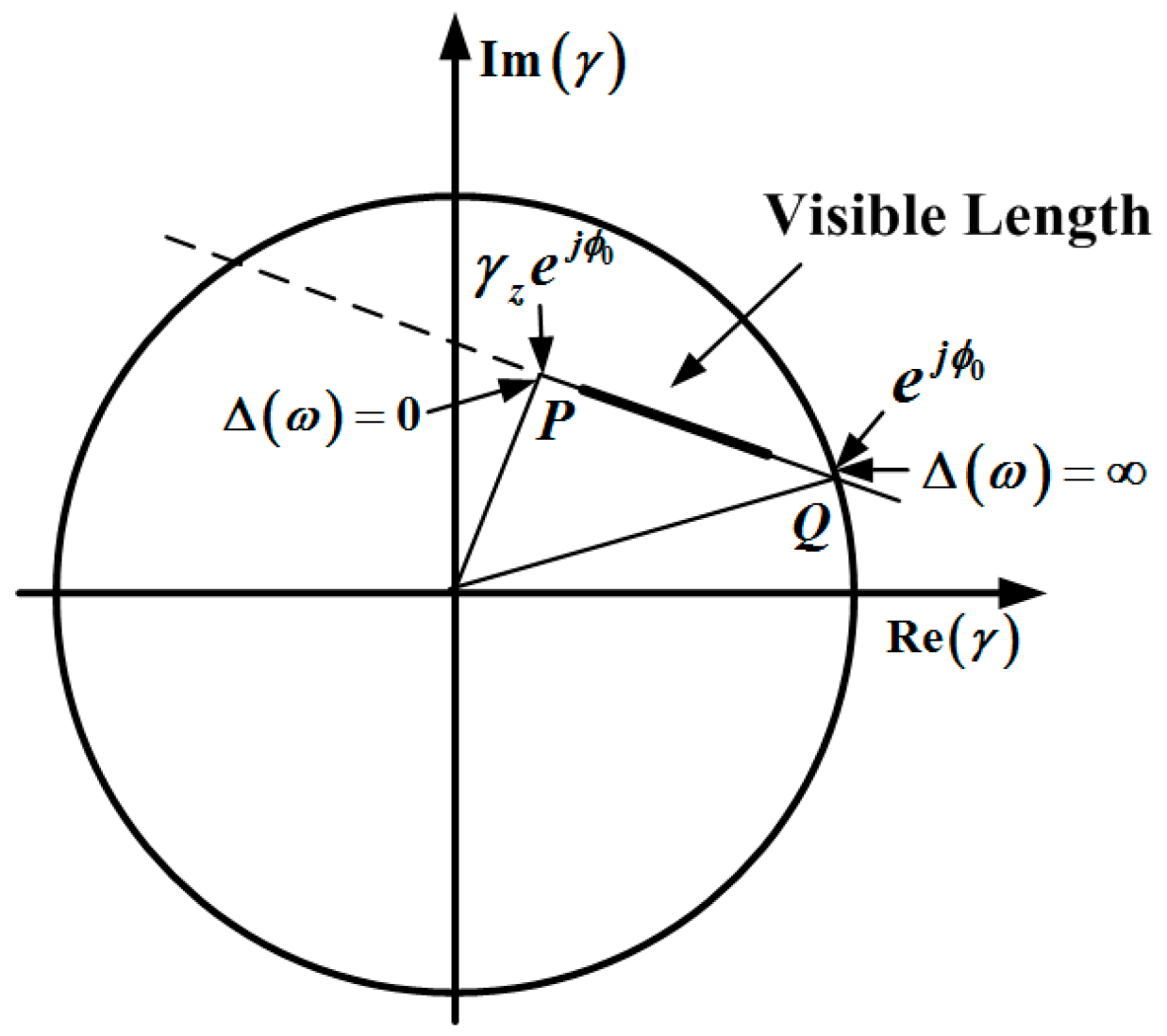
2.2. Three-Stage Processing under Different Range Slopes
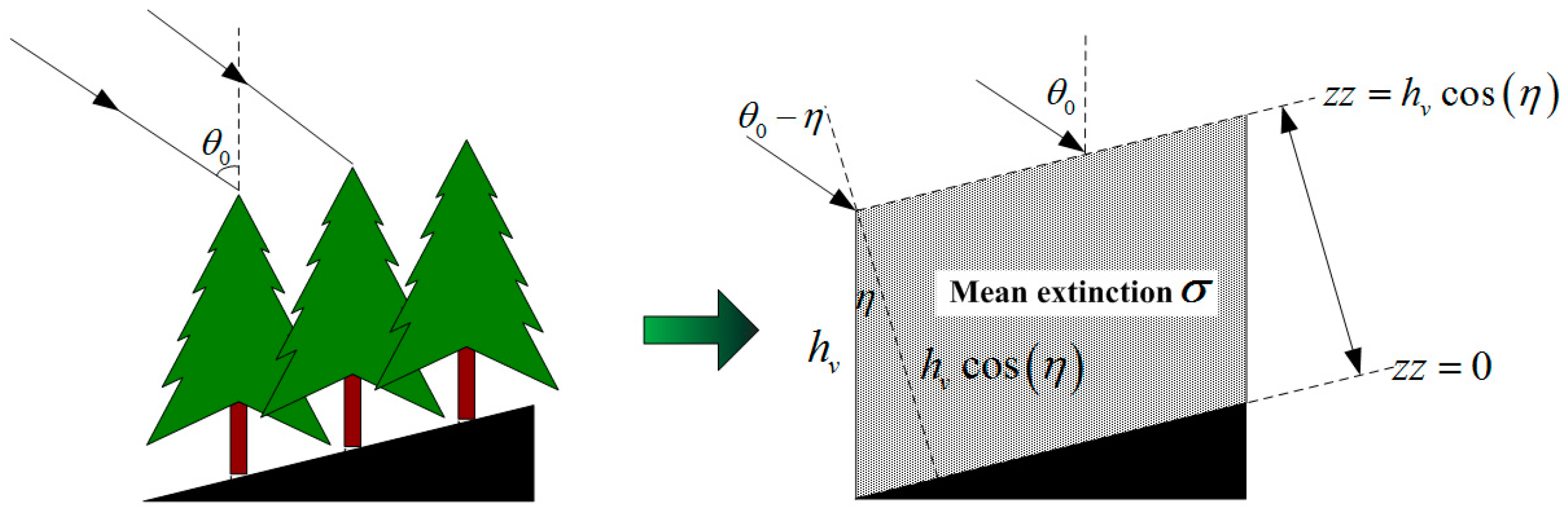
3. R-RVoG Model
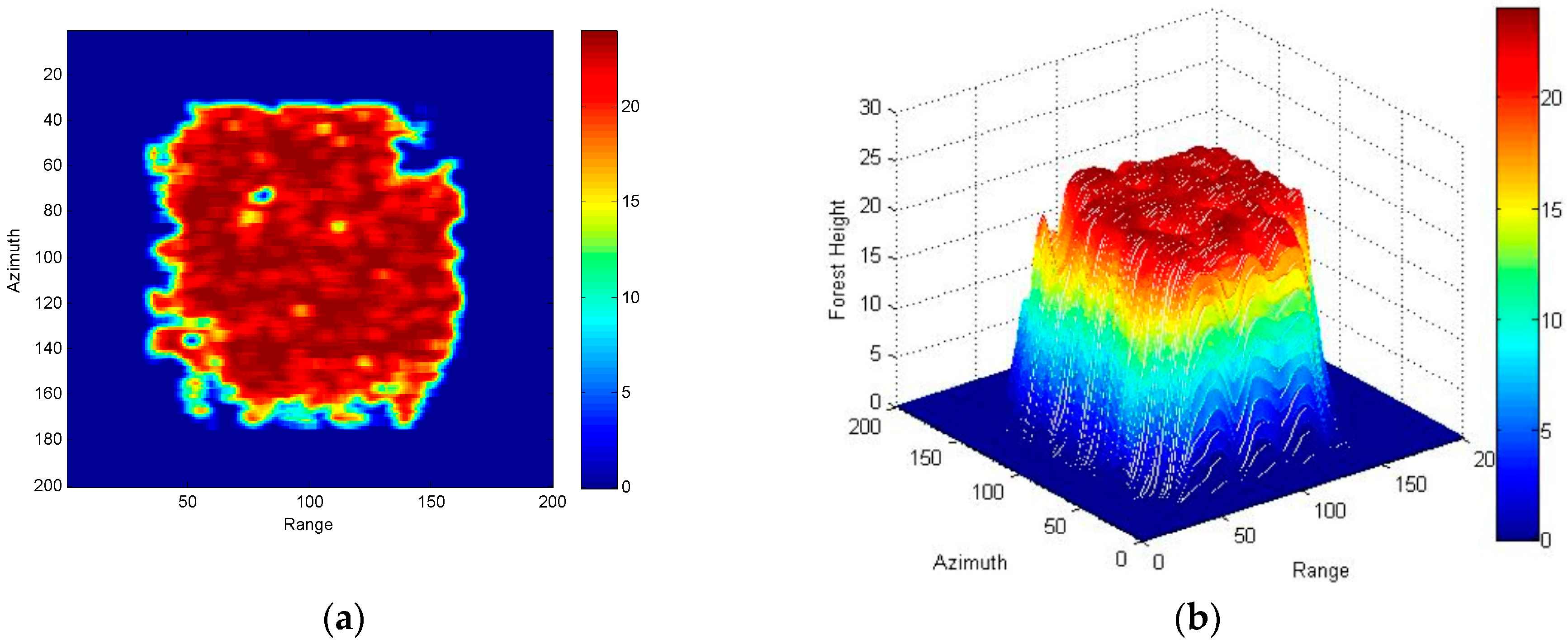
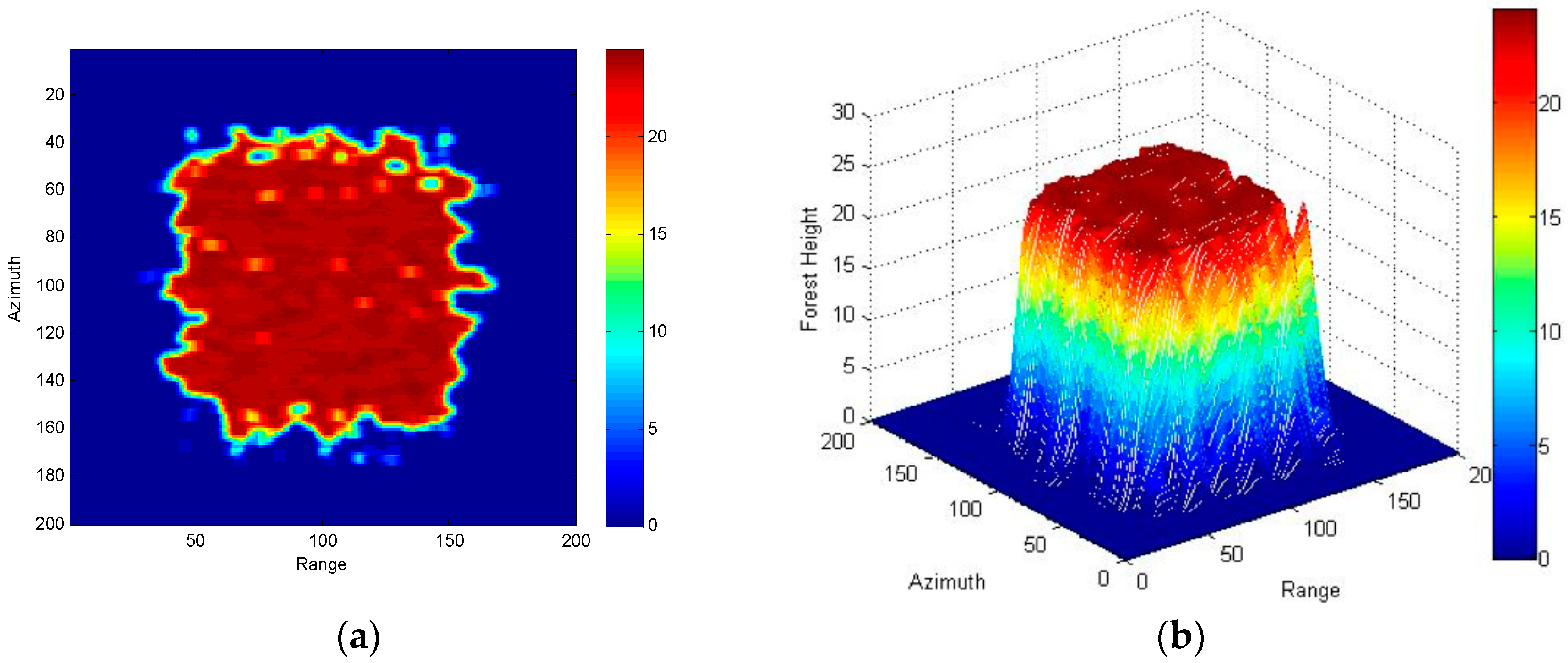
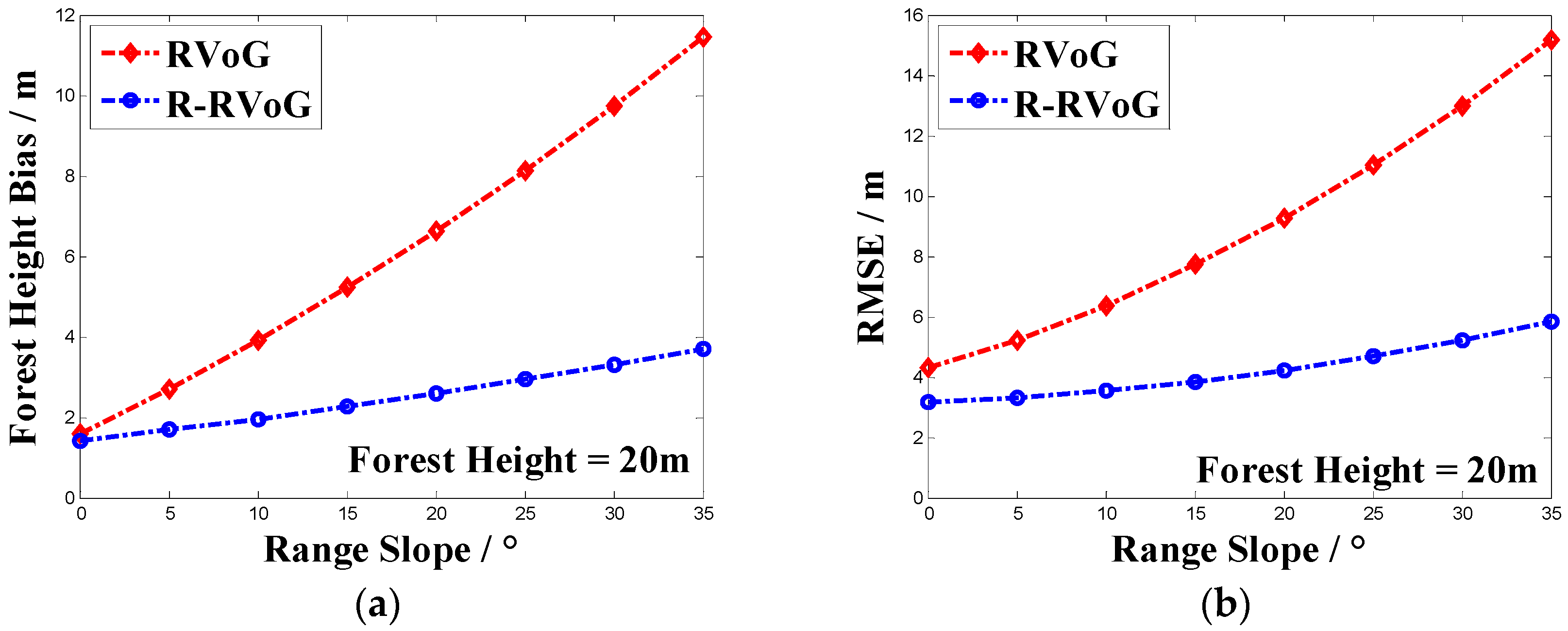
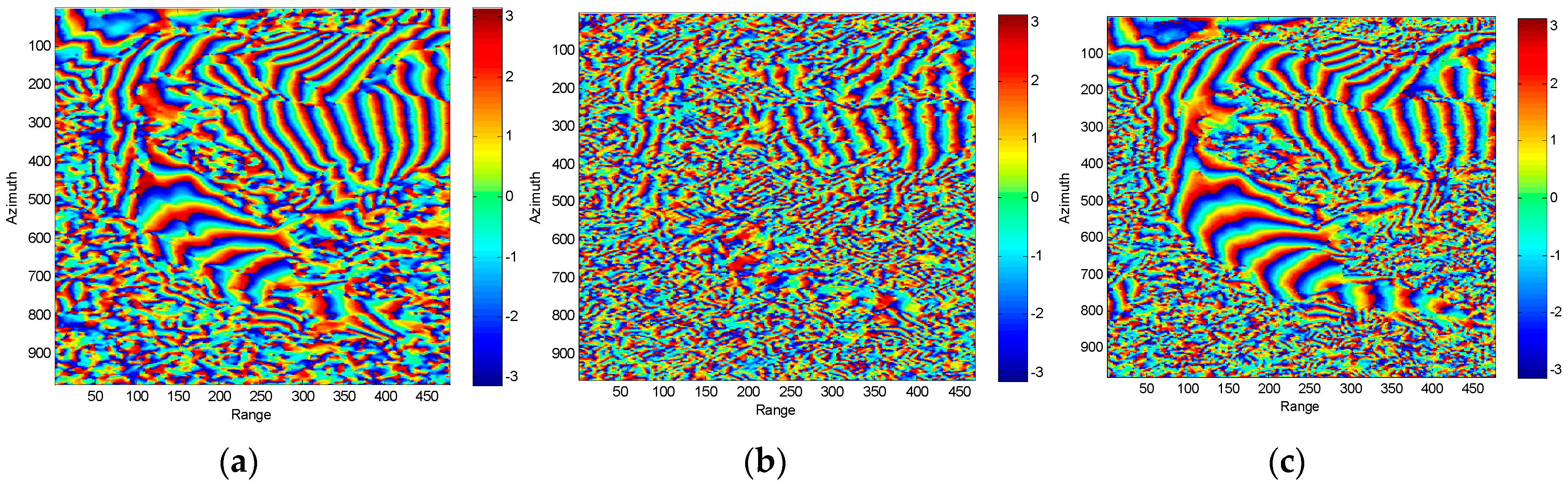
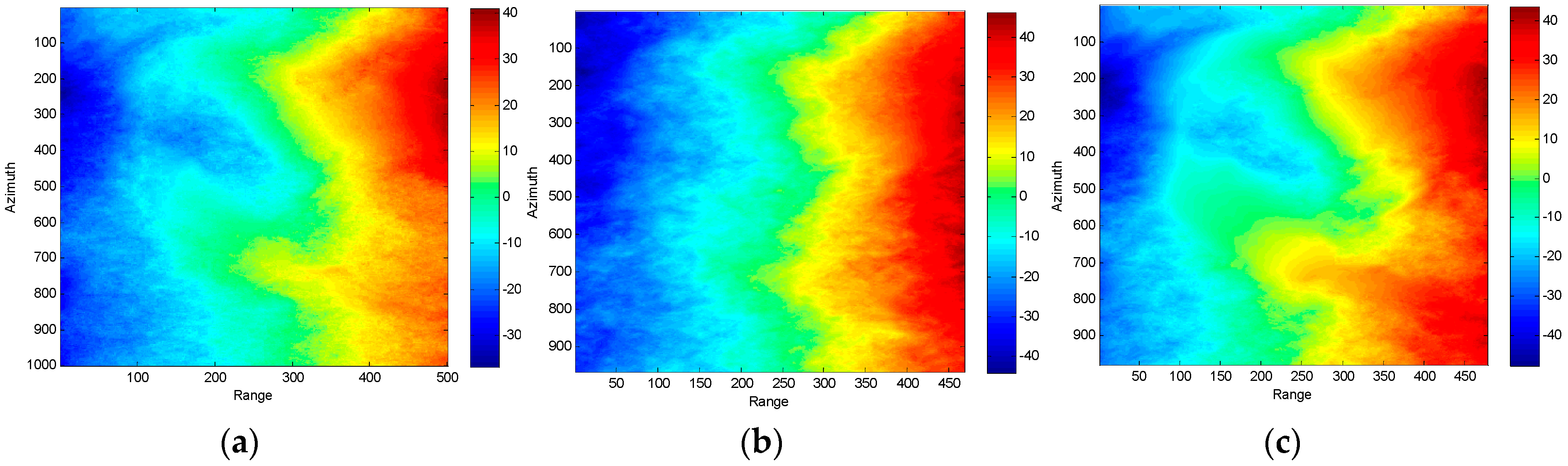
4. Three-Stage Processing of Simulated Data Based on R-RVoG Model
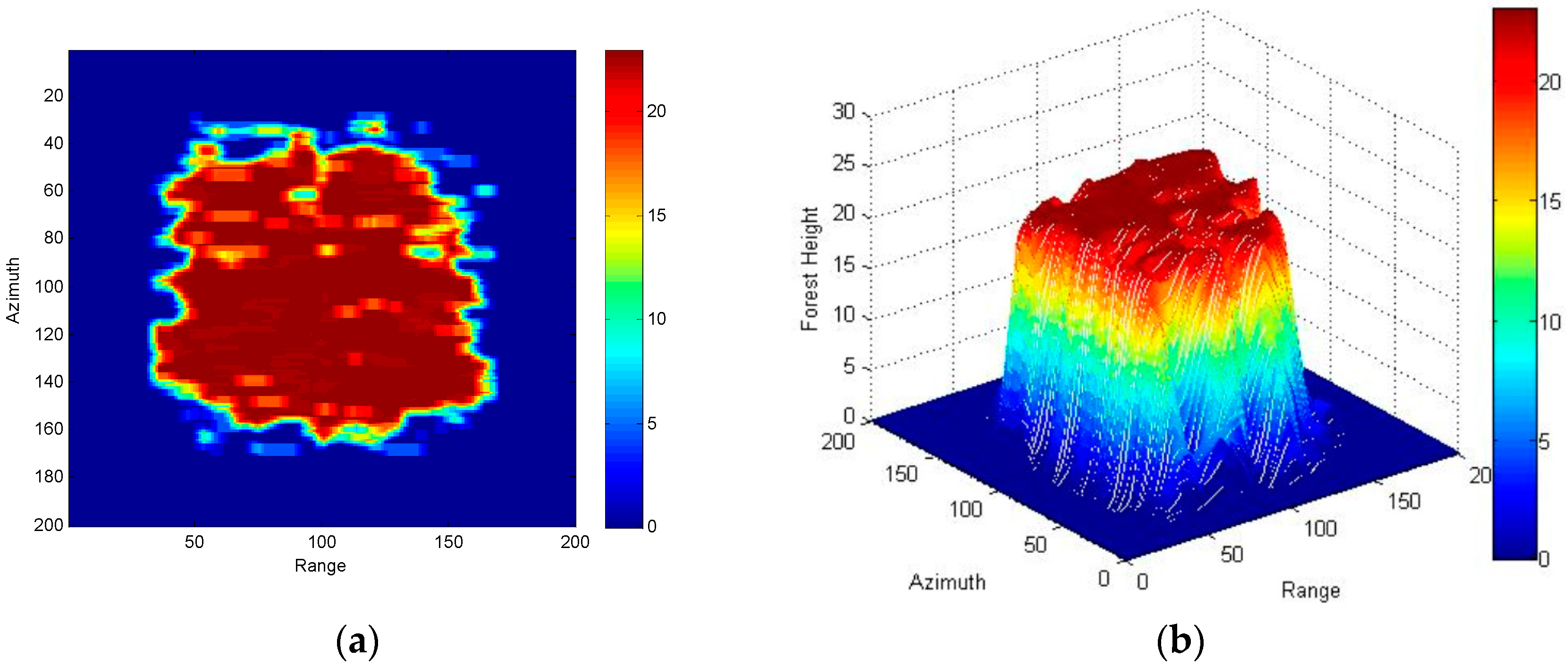
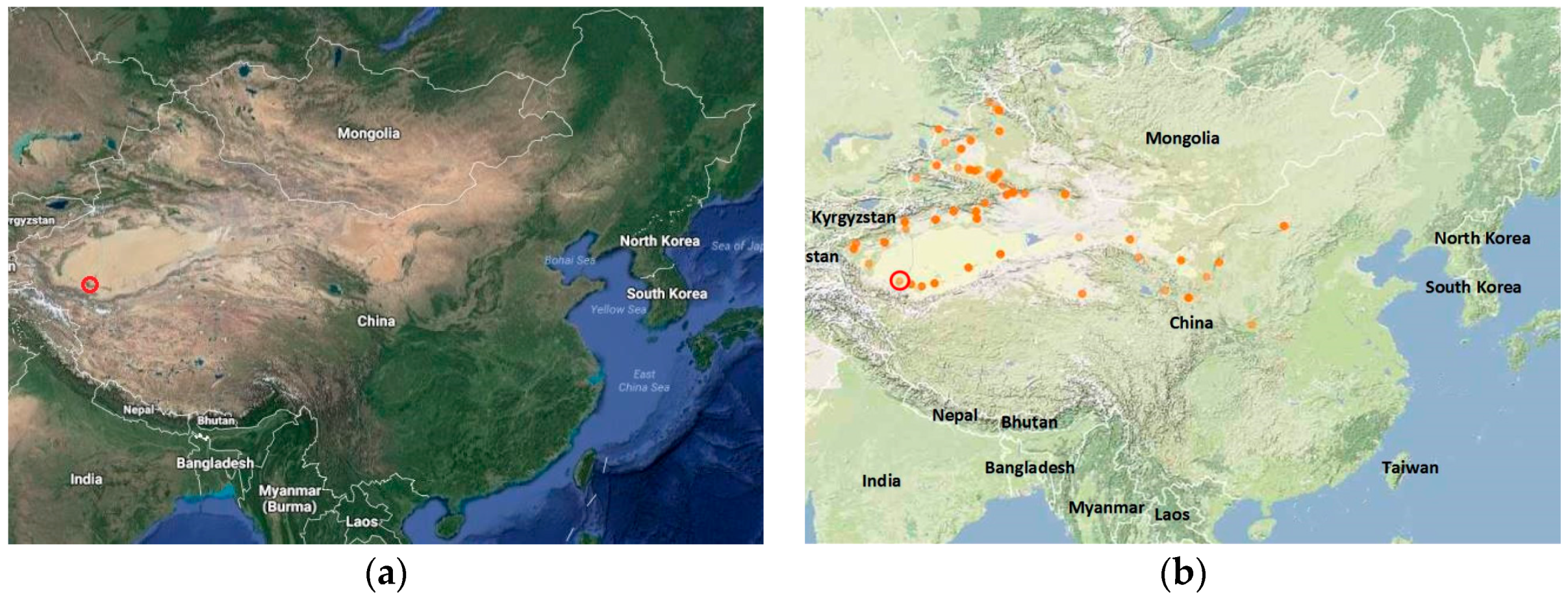
5. Three-Stage Processing of Real Data Based on R-RVoG Model
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Cloude, S.R.; Papathanassiou, K.P. Polarimetric SAR interferometry. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1551–1565. [Google Scholar] [CrossRef]
- Papathanassiou, K.P.; Cloude, S.R. Single-baseline polarimetric SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2352–2363. [Google Scholar] [CrossRef]
- Margarit, G.; Mallorqui, J.J.; Fabregas, X. Single-pass polarimetric SAR interferometry for vessel classification. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3494–3502. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, C.; Liu, Z. Polarimetric SAR interferometry for vegetable vertical structure parameters extraction. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Toronto, ON, Canada, 24–28 June 2002; pp. 2611–2613.
- Carlos, L.; Alberto, A. Assessment and estimation of the RVoG model in polarimetric SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3091–3106. [Google Scholar]
- Philippe, R.; Antoine, R.; Aurelien, A.; Pascale, C.D. Invariant contrast parameters of PolInSAR homogenous RVoG model. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1414–1417. [Google Scholar]
- Carlos, L.; Alberto, A. A study of the RVoG coherent scattering model validity in PolInSAR for forests studies. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Melbourne, Australia, 21–26 July 2013; pp. 2349–2352.
- Bassam, E.H.; Laurent, F. Polarimetric tomography for forest parameters retrieval. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Melbourne, Australia, 21–26 July 2013; pp. 4340–4343.
- Gustavo, H.X.; Karlus, A. Estimating a preliminary terrain model from the X-band InSAR and the RVoG model. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 4089–4092.
- Fu, W.X.; Guo, H.D.; Li, X.W.; Tian, B.S.; Sun, Z.C. Extended three-stage polarimetric SAR interferometry algorithm by dual-polarization data. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2792–2802. [Google Scholar]
- Li, Z.; Guo, M. A new three-stage inversion procedure of forest height with the improved temporal decorrelation RVoG model. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Munich, Germany, 22–27 July 2012; pp. 5141–5144.
- Cloude, S.R.; Papathanassiou, K.P. Three-stage inversion process for polarimetric SAR interferometry. IEE Proc. Radar Sonar Navig. 2003, 150, 125–134. [Google Scholar] [CrossRef]
- Tan, L.L.; Yang, R.L. Investigation on tree height retrieval with polarimetric SAR interferometry. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Boston, MA, USA, 7–11 July 2008; pp. 546–549.
- Treuhaft, R.N.; Madsen, S.; Moghaddam, M.; Van Zyl, J.J. Vegetation characteristics and underlying topography from interferometric data. Radio Sci. 1996, 31, 1449–1485. [Google Scholar] [CrossRef]
- Lee, J.S.; Schuler, D.L.; Ainsworth, T.L.; Krogager, E.; Kasilingam, D.; Boerner, W.M. On the estimation of radar polarization orientation shifts induced by terrain slopes. IEEE Trans. Geosci. Remote Sens. 2002, 40, 30–41. [Google Scholar]
- Moghaddam, M. Effect of medium symmetries in limiting the number of parameters estimated with polarimetric interferometry. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Hamburg, Germany, 28 June–2 July 1999; pp. 2221–2223.
- Schuler, D.L.; Lee, J.S.; Kasilingam, D.; Nesti, G. Surface roughness and slope measurements using polarimetric SAR data. IEEE Trans. Geosci. Remote Sens. 2002, 40, 687–698. [Google Scholar] [CrossRef]
- Lu, H.; Suo, Z.; Guo, R.; Bao, Z. S-RVoG model for forest parameters inversion over underlying topography. Electron. Lett. 2013, 49, 618–620. [Google Scholar] [CrossRef]
- Alberga, V. Volume decorrelation effects in polarimetric SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2467–2478. [Google Scholar] [CrossRef]
- Zhou, Y.S.; Hong, W.; Cao, F. Investigation on the applications of decorrelation analysis in polarimetric SAR Interferometry. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Cape Town, South Africa, 12–17 July 2009; pp. 254–257.
- Irena, H.; Florian, K.; Seung-Kuk, L.; Konstantinos, P.P. Tropical-forest-parameter estimation by means of Pol-InSAR: The INDREX-II campaign. IEEE Trans. Geosci. Remote Sens. 2009, 47, 481–493. [Google Scholar]
- Aurelien, A.; Antoine, R.; Pascale, C.D.; Philippe, R. Vegetation height estimation precision with compact PolInSAR and homogeneous random volume over ground model. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1879–1891. [Google Scholar]
- Florian, K.; Daniel, S.; Irena, H.; Hans, P.; Konstantinos, P.P. TanDEM-X Pol-InSAR performance for forest height estimation. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6404–6422. [Google Scholar]
- Qing, H.X.; Jian, J.Z.; Chang, C.W.; Hai, Q.F. Boreal forest height inversion using E-SAR PolInSAR data based coherence optimization methods and three-stage algorithm. In Proceedings of the Earth Observation and Remote Sensing Applications (EORSA), Changsha, China, 11–14 June 2014; pp. 145–150.
- Quan, X.Y.; Zhang, Z.; Zhang, B.C.; Hong, W.; Wu, Y.R. A study of BP-camp algorithm for SAR imaging. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 4480–4483.
- Maxim, N.; Laurent, F.; Andreas, R. Estimation of Forest Structure, Ground, and Canopy Layer Characteristics from Multi-Baseline Polarimetric Interferometric SAR Data. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1086–1104. [Google Scholar]
- Michele, M.; Benjamin, B.; Gerhard, K. Decorrelation effects in bistatic TanDEM-X data. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Munich, Germany, 22–27 July 2012; pp. 5558–5561.
- Wang, Y.H.; Yan, W.L.; Zhang, G.S. Adaptive simulated annealing for the optimal design of electromagnetic devices. IEEE Trans. Magn. 1996, 32, 1214–1217. [Google Scholar] [CrossRef]
- Soo, Y.L.; Kyung, G.L. Synchronous and asynchronous parallel simulated annealing with multiple Markov chains. IEEE Trans. Parallel Distrib. Syst. 1996, 7, 993–1008. [Google Scholar]
- Kevin, I.S.; Richard, M.E.; Jonathan, E.F.; Chris, M.; Rashmi, M. Dominance-based multiobjective simulated annealing. IEEE Trans. Evol. Comput. 2008, 12, 323–342. [Google Scholar]
- Polulus of China. Available online: http://populus.forestry.gov.cn/hyzyfb.jhtml (accessed on 20 June 2016).
- Hensley, S.; Rosen, P.; Gurrola, E. The SRTM topographic mapping processor. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Honolulu, HI, USA, 24–28 July 2000; pp. 1168–1170.
- Wael, A.J.; Dana, F.; Helmut, R.; Michael, E. Surface elevation changes of glaciers derived from SRTM and TanDEM-X DEM differences. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Melbourne, Australia, 21–26 July 2013; pp. 1893–1896.
- Eric, P.; Laurent, F. PolSARPro V5.0: An ESA educational toolbox used for self-education in the field of PoLSAR and Pol-INSAR data analysis. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Munich, Germany, 22–27 July 2012; pp. 7737–7380.
- Fornaro, G.; Sansosti, E. A two-dimensional region growing least squares phase unwrapping algorithm for interferometric SAR processing. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2215–2226. [Google Scholar] [CrossRef]

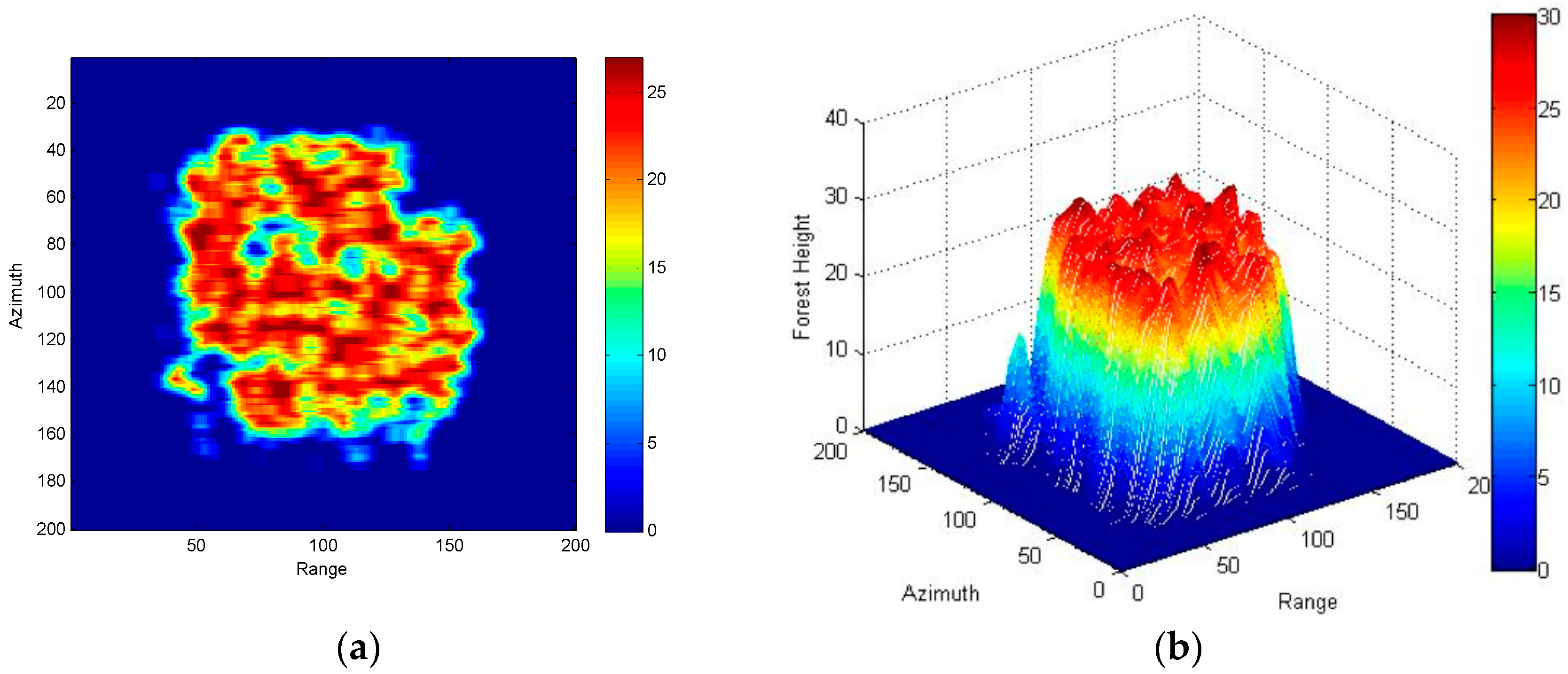
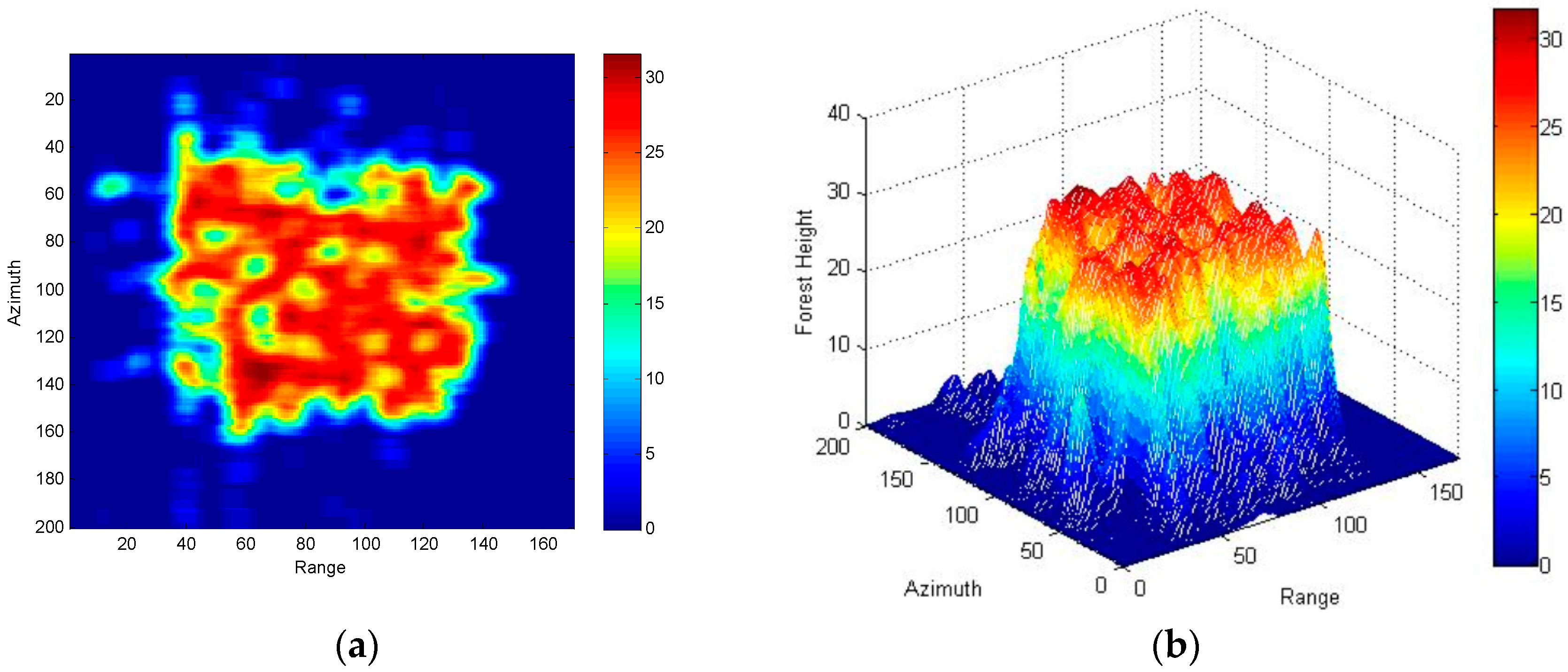
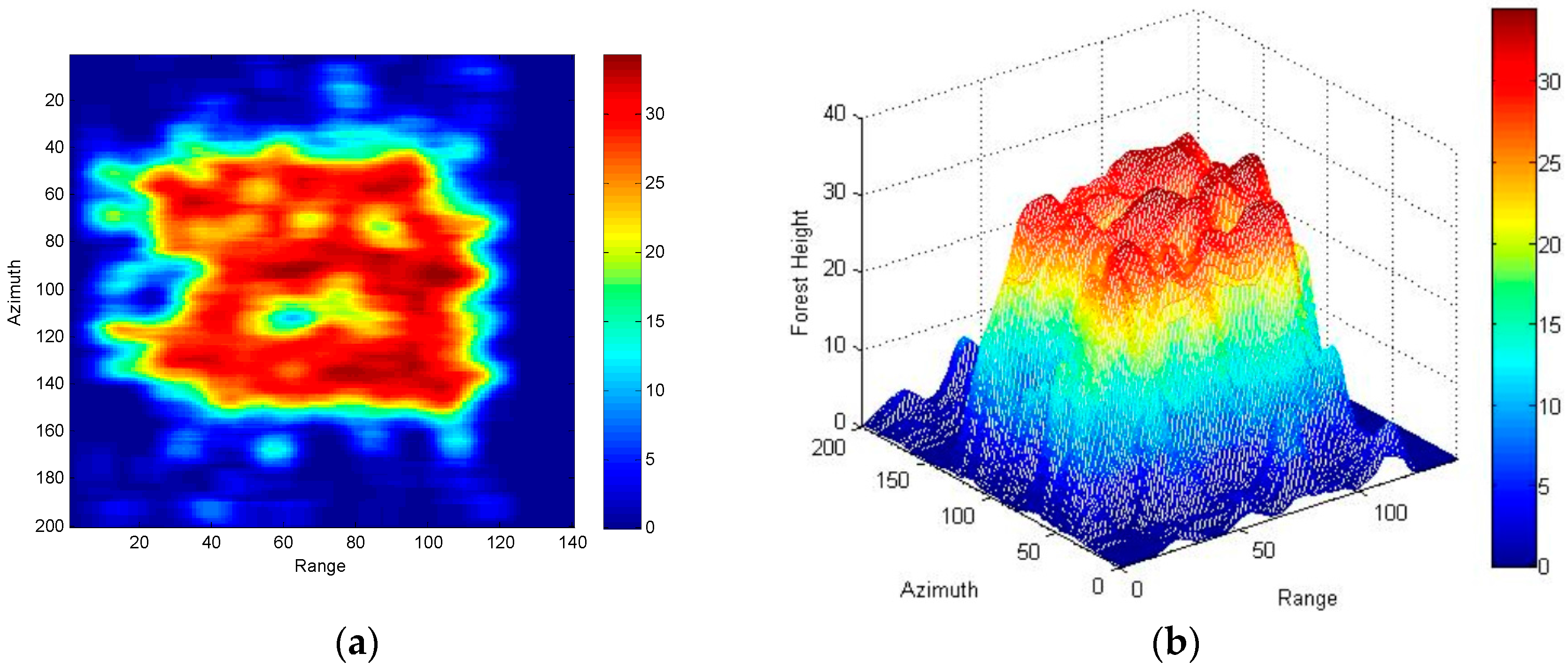
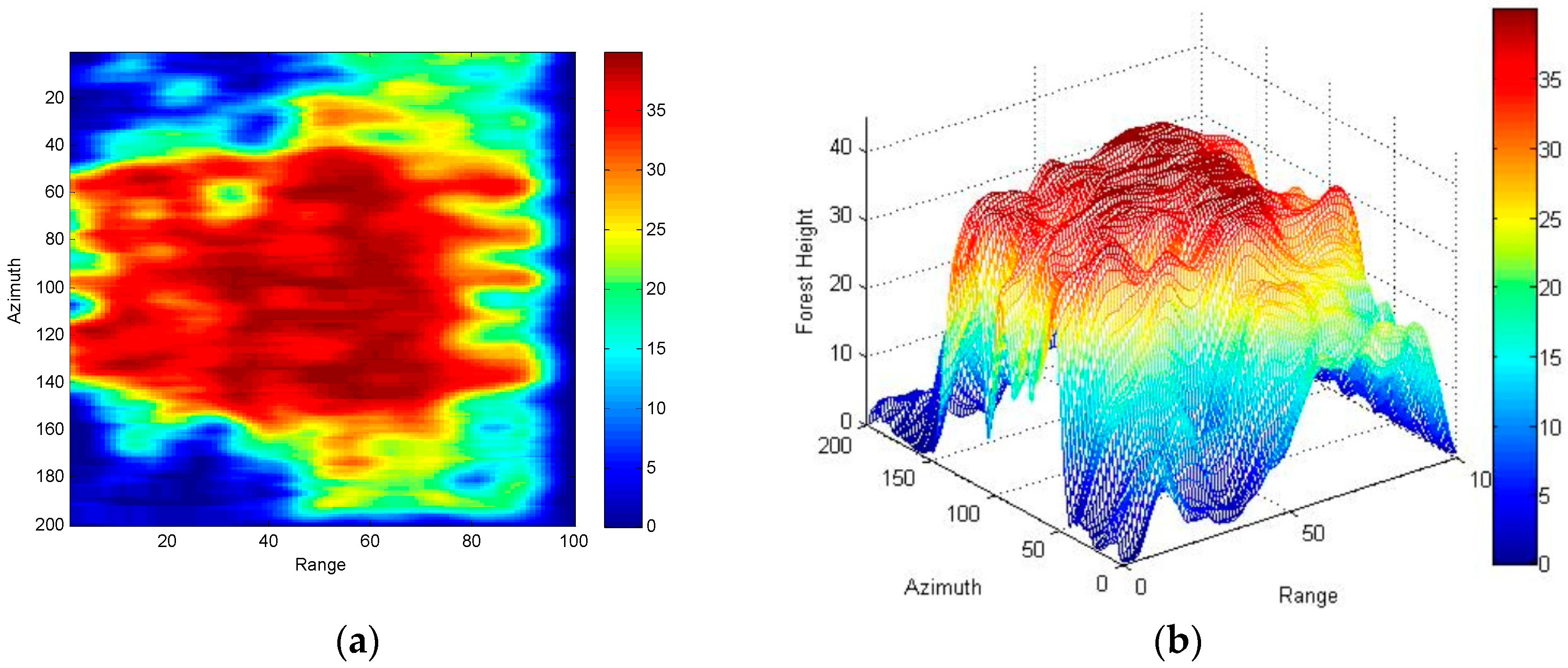
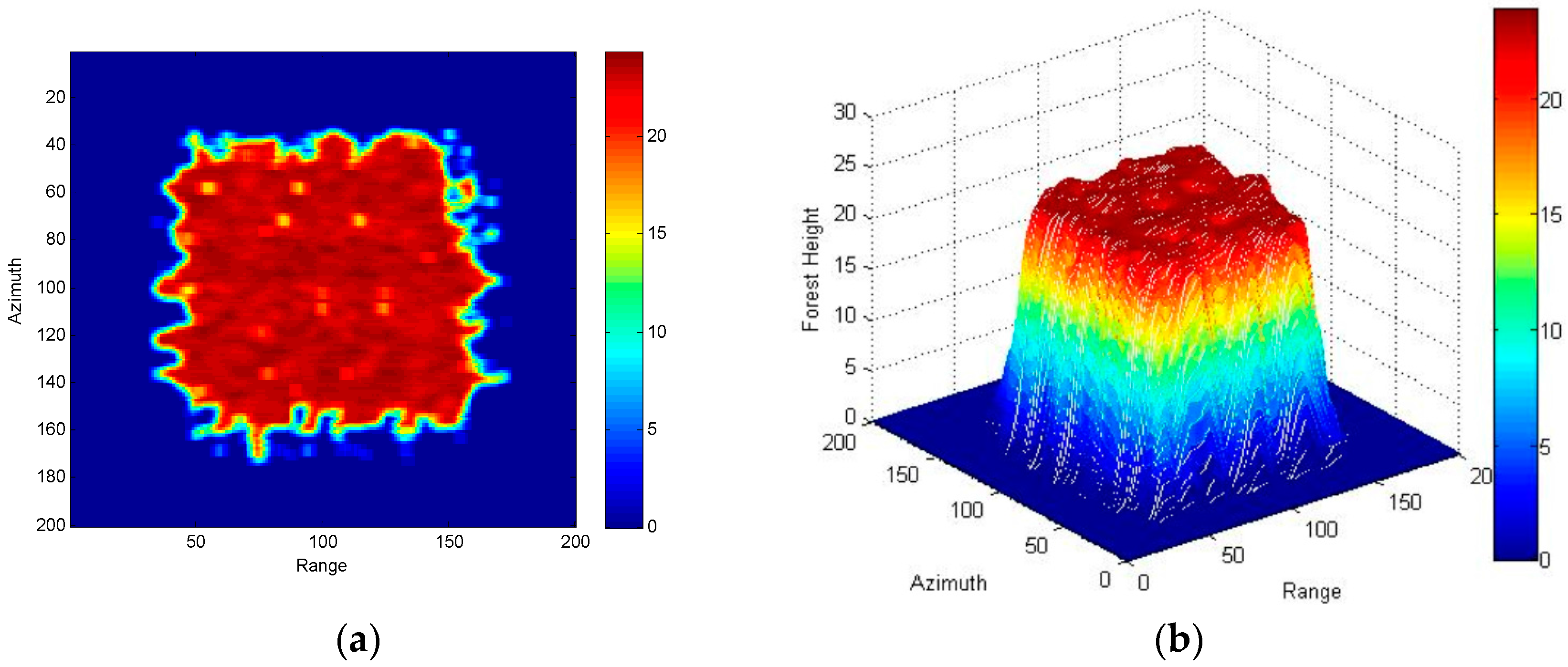
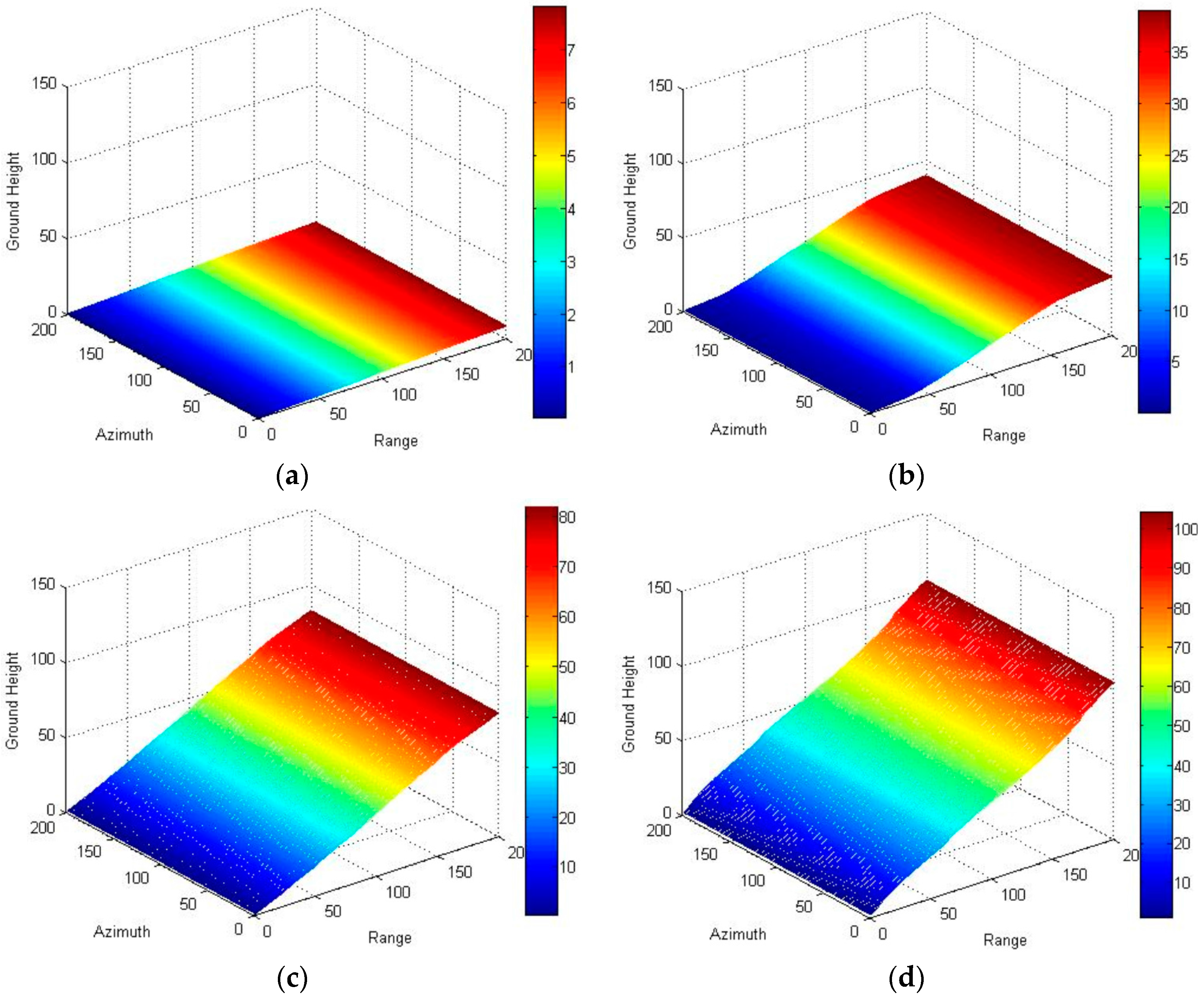


| Satellite Orbit | Scene | ||
|---|---|---|---|
| Semi-major Axis | 6871 km | Range Slope | 0°/10°/20°/30° |
| Angle of Inclination | 97.42° | Azimuth Slope | 0° |
| Eccentricity | 0.0011 | Size of Scene | 200 m × 200 m |
| Argument of Perigee | 90° | Size of Forest | 100 m × 100 m |
| Right Ascension of Ascending Node (RAAN) | 180° | Average Height | 20 m |
| Baseline Length | 800 m | Standard Deviation | 0 m |
| Range Slope | AVG | AVG Bias | SDEV | RMSE |
|---|---|---|---|---|
| 0° | 21.4928 m | 1.4928 m | 3.7126 m | 4.0015 m |
| 10° | 24.6080 m | 4.6080 m | 5.3019 m | 7.0245 m |
| 20° | 26.0583 m | 6.0583 m | 6.3778 m | 8.7965 m |
| 30° | 29.6715 m | 9.6715 m | 8.3581 m | 12.7826 m |
| Range Slope | AVG | AVG Bias | SDEV | RMSE |
|---|---|---|---|---|
| 0° | 21.2126 m | 1.2126 m | 2.7657 m | 3.0198 m |
| 10° | 22.3838 m | 2.3838 m | 2.9972 m | 3.8295 m |
| 20° | 22.7107 m | 2.7107 m | 3.1673 m | 4.1689 m |
| 30° | 22.8127 m | 2.8127 m | 3.3546 m | 4.3777 m |
| Range Slope | Estimated Range Slope | Absolute Biases |
|---|---|---|
| 0° | 2.2341° | 2.2341° |
| 10° | 12.2707° | 2.2707° |
| 20° | 22.4373° | 2.4373° |
| 30° | 32.9703° | 2.9703° |
| Sensor | Scene | ||
|---|---|---|---|
| Semi-major Axis | 6583 km | Central Longtitude | 79.4871979° |
| Angle of Inclination | 57° | Central Latitude | 37.0295486° |
| Eccentricity | 0.00168 | Size of Scene | 18.79 km × 3.735 km |
| Wavelength | 0.24 m | Range Resolution | 18.79 m |
| Incident Angle | 24.373° | Azimuth Resolution | 7.47 m |
| Model | AVG | AVG Bias | SDEV | RMSE |
|---|---|---|---|---|
| True Value | 19.3987 m | 0 m | 2.5564 m | 0 m |
| RVoG | 23.2689 m | 3.8702 m | 2.0548 m | 8.2556 m |
| R-RVoG | 21.5804 m | 2.1817 m | 2.1953 m | 7.2663 m |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Liu, T.; Ding, Z.; Zeng, T.; Long, T. A Modified Three-Stage Inversion Algorithm Based on R-RVoG Model for Pol-InSAR Data. Remote Sens. 2016, 8, 861. https://doi.org/10.3390/rs8100861
Zhang Q, Liu T, Ding Z, Zeng T, Long T. A Modified Three-Stage Inversion Algorithm Based on R-RVoG Model for Pol-InSAR Data. Remote Sensing. 2016; 8(10):861. https://doi.org/10.3390/rs8100861
Chicago/Turabian StyleZhang, Qi, Tiandong Liu, Zegang Ding, Tao Zeng, and Teng Long. 2016. "A Modified Three-Stage Inversion Algorithm Based on R-RVoG Model for Pol-InSAR Data" Remote Sensing 8, no. 10: 861. https://doi.org/10.3390/rs8100861
APA StyleZhang, Q., Liu, T., Ding, Z., Zeng, T., & Long, T. (2016). A Modified Three-Stage Inversion Algorithm Based on R-RVoG Model for Pol-InSAR Data. Remote Sensing, 8(10), 861. https://doi.org/10.3390/rs8100861