Remote Sensing of Particle Cross-Sectional Area in the Bohai Sea and Yellow Sea: Algorithm Development and Application Implications
Abstract
:1. Introduction
2. Materials and Methods
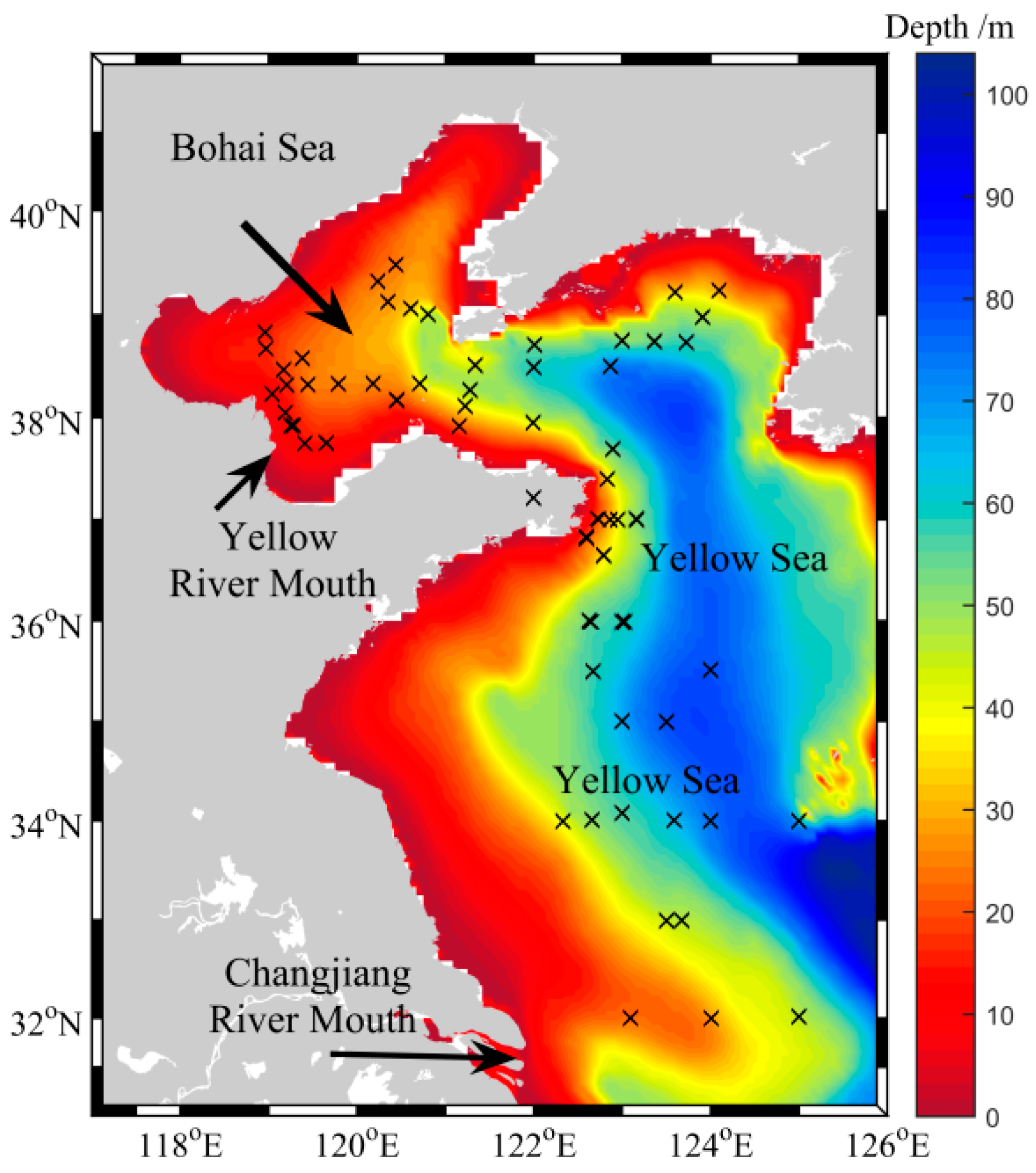
2.1. Study Area and Sampling
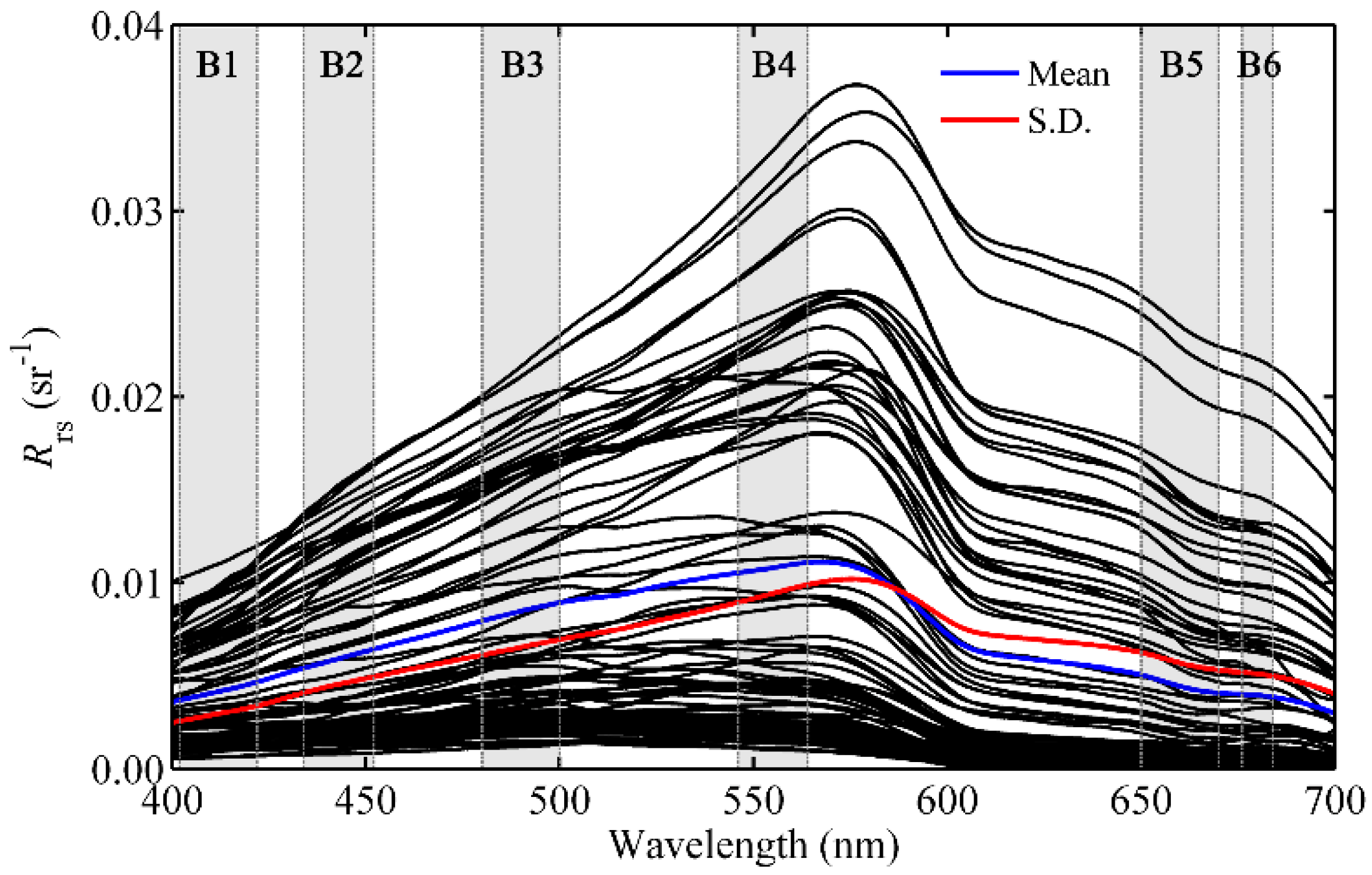
2.2. In Situ Data Measurements
2.3. Satellite Data
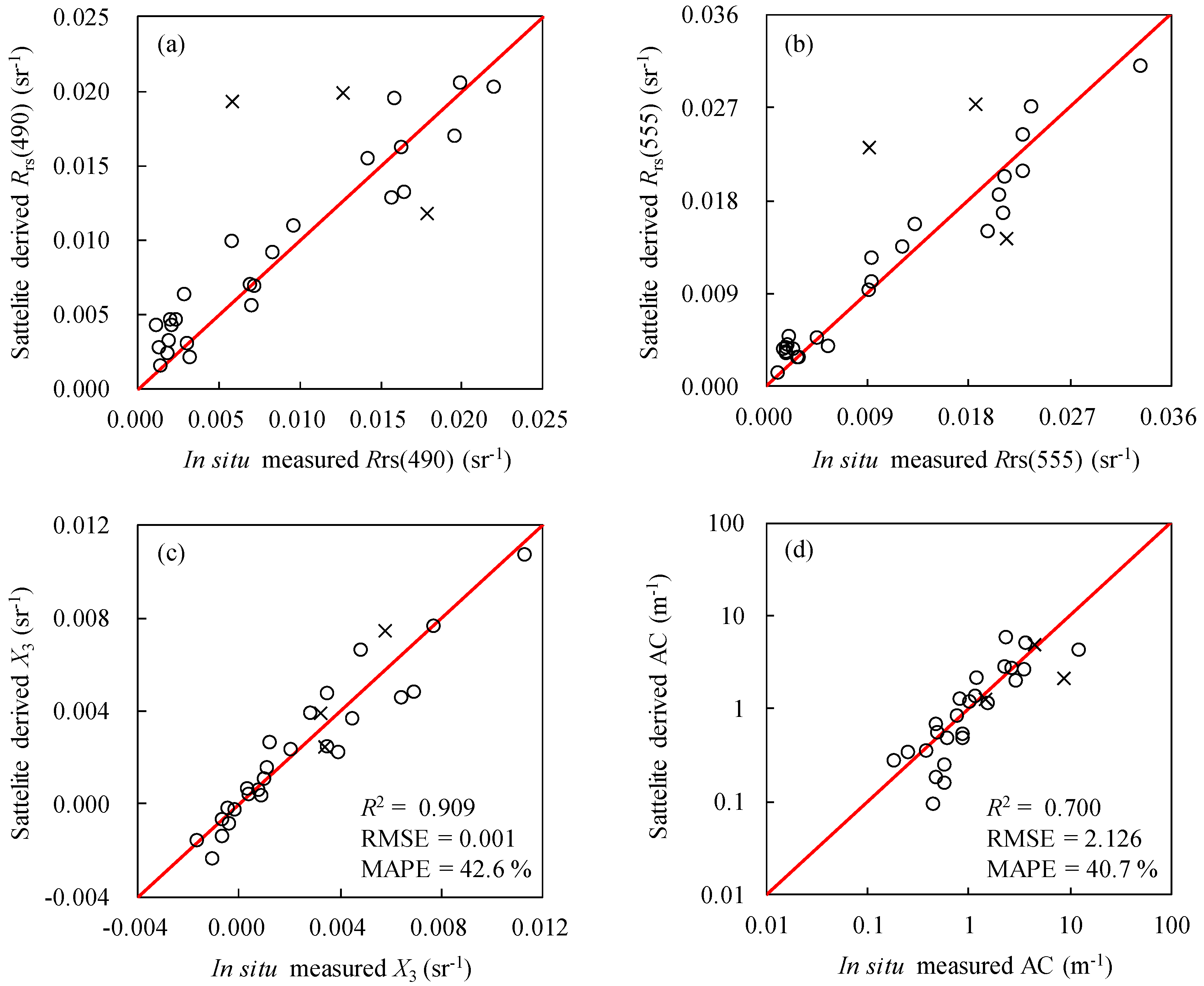
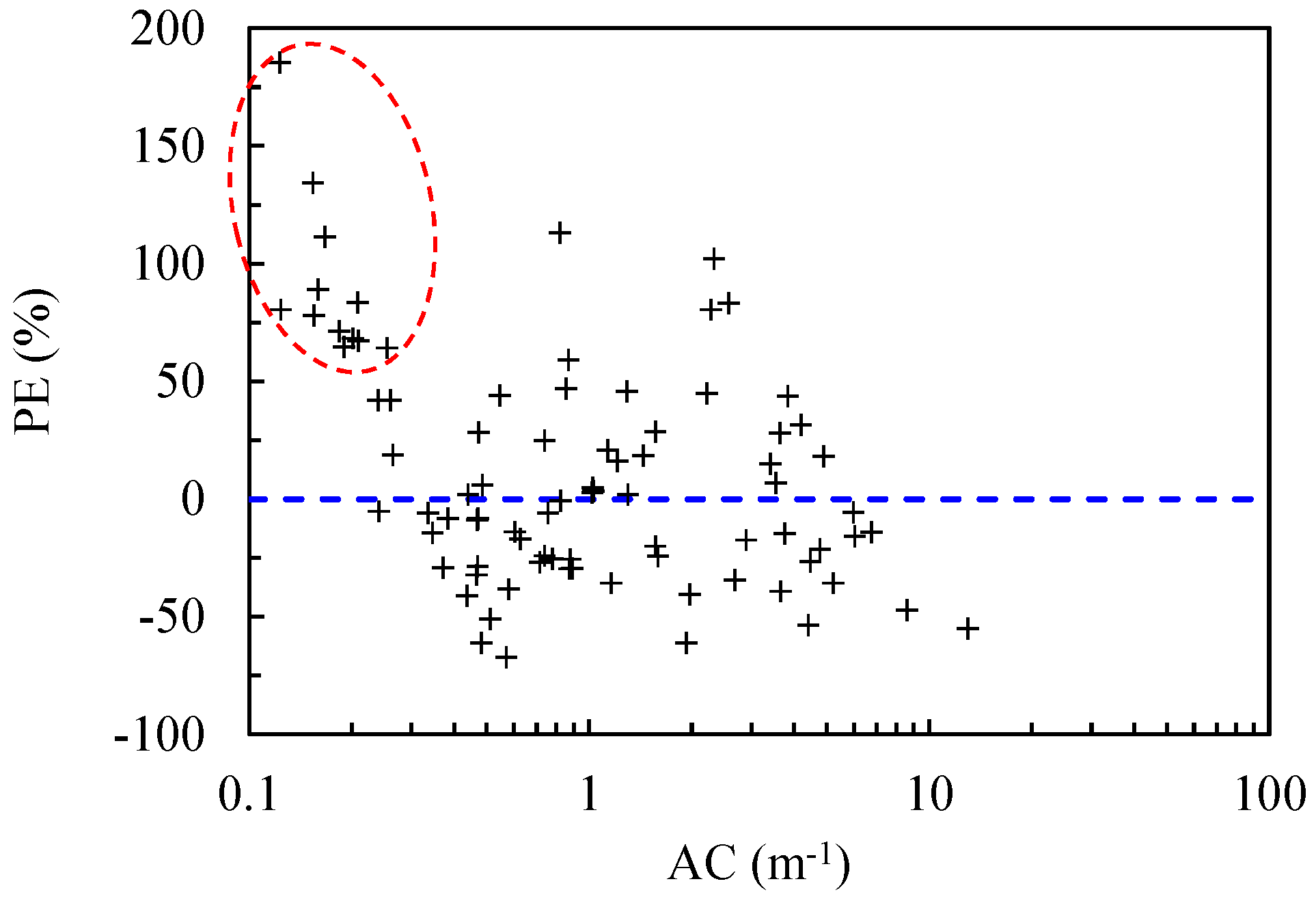
2.4. Accuracy Assessment
3. Results
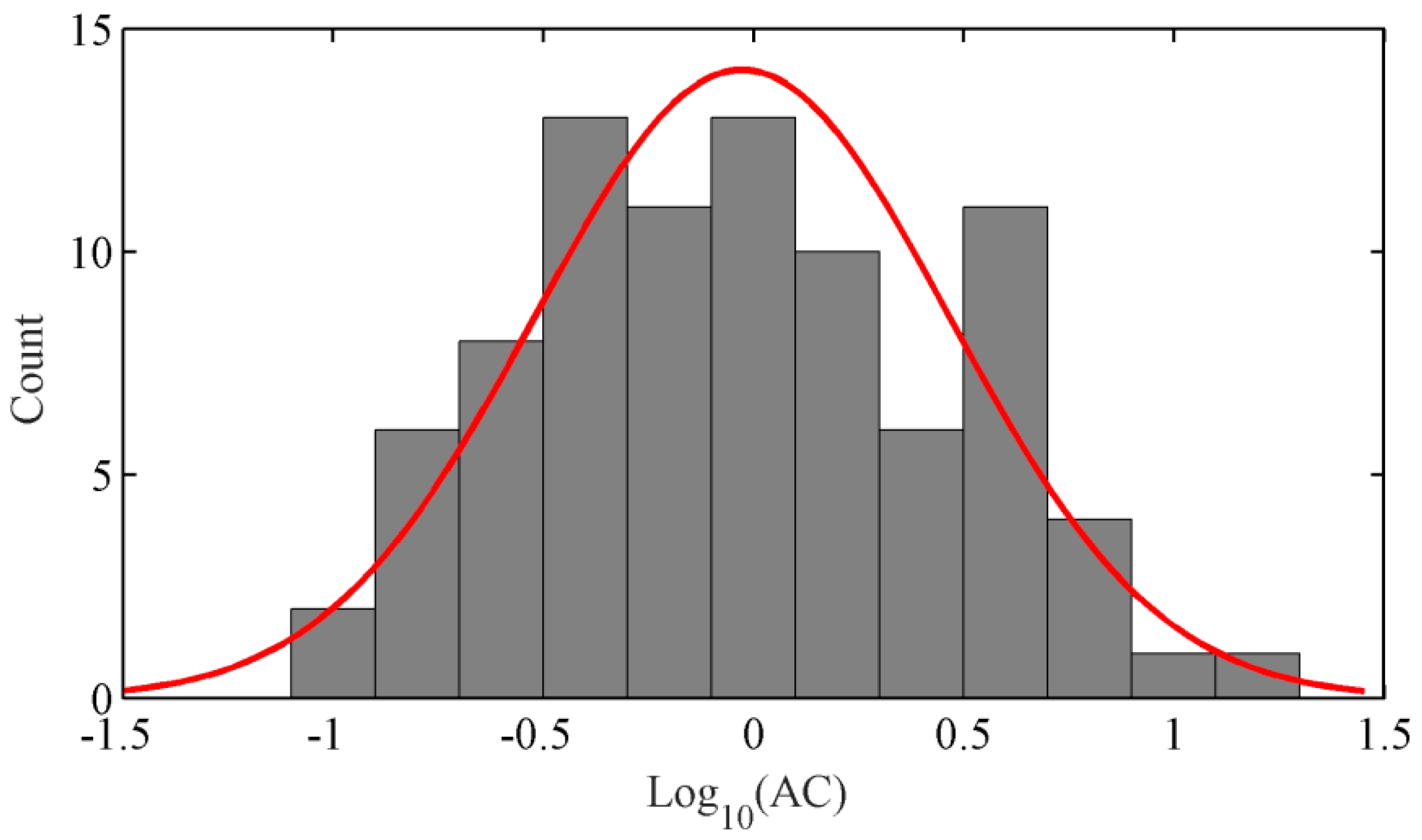
3.1. Data Distributions
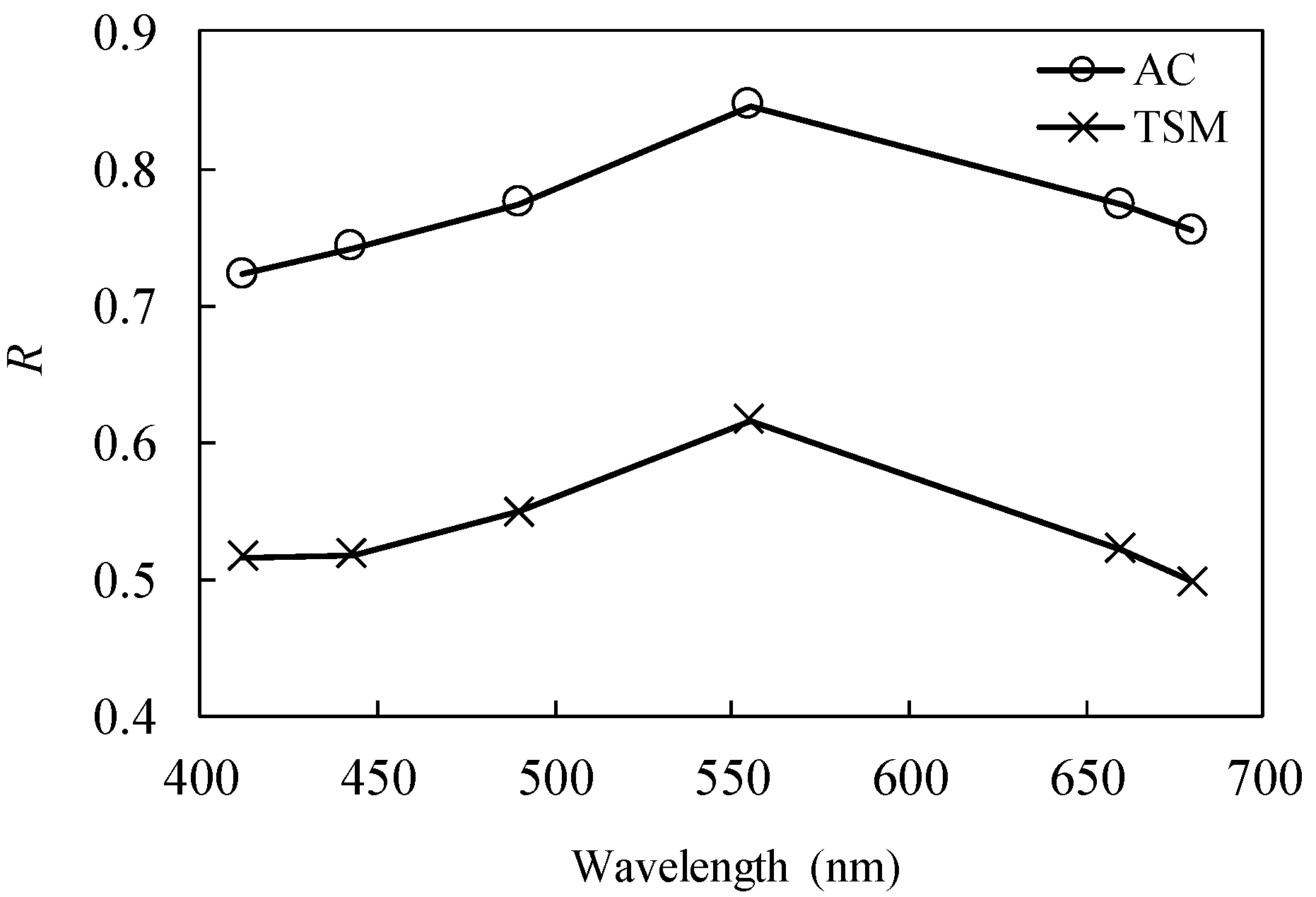
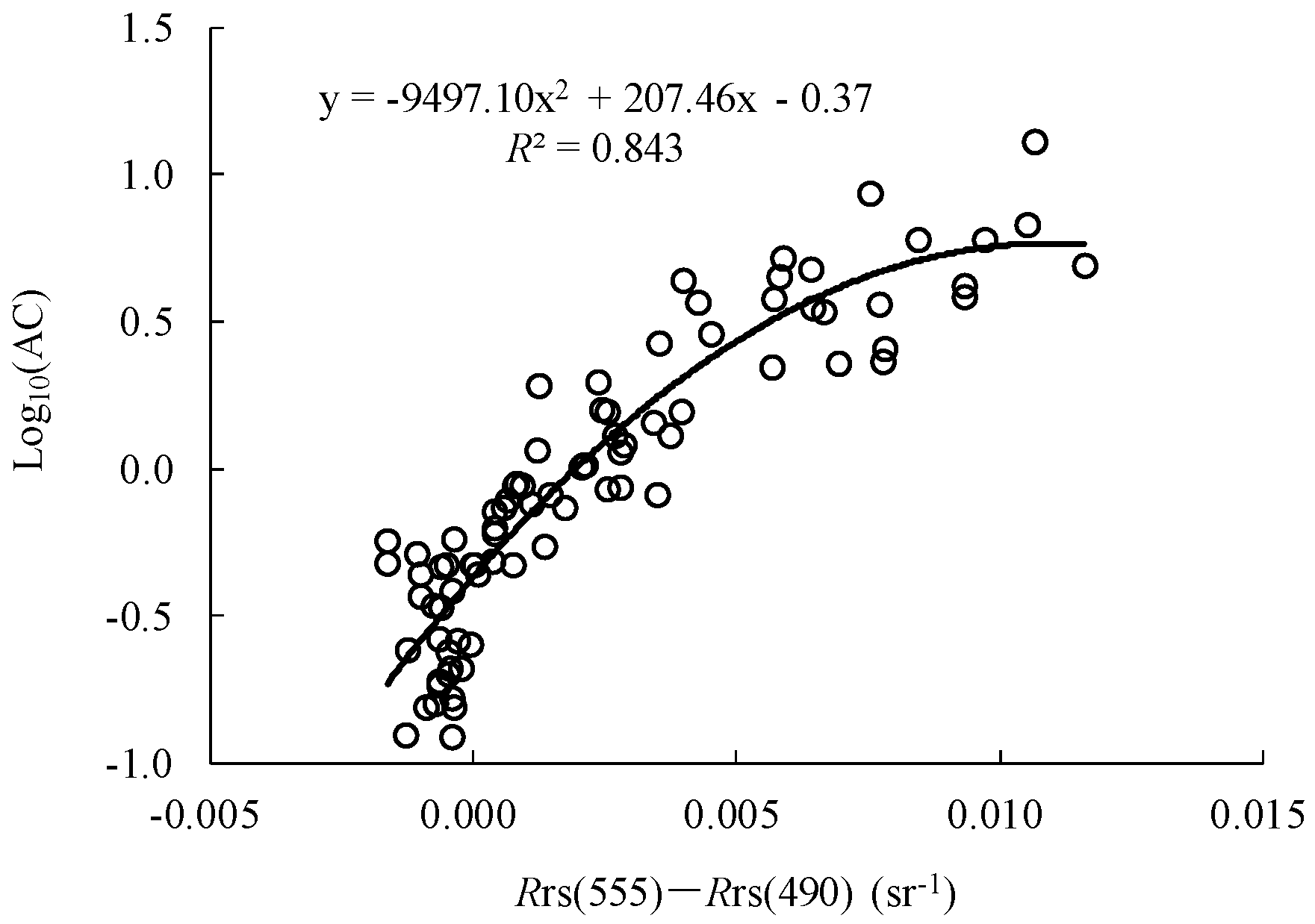
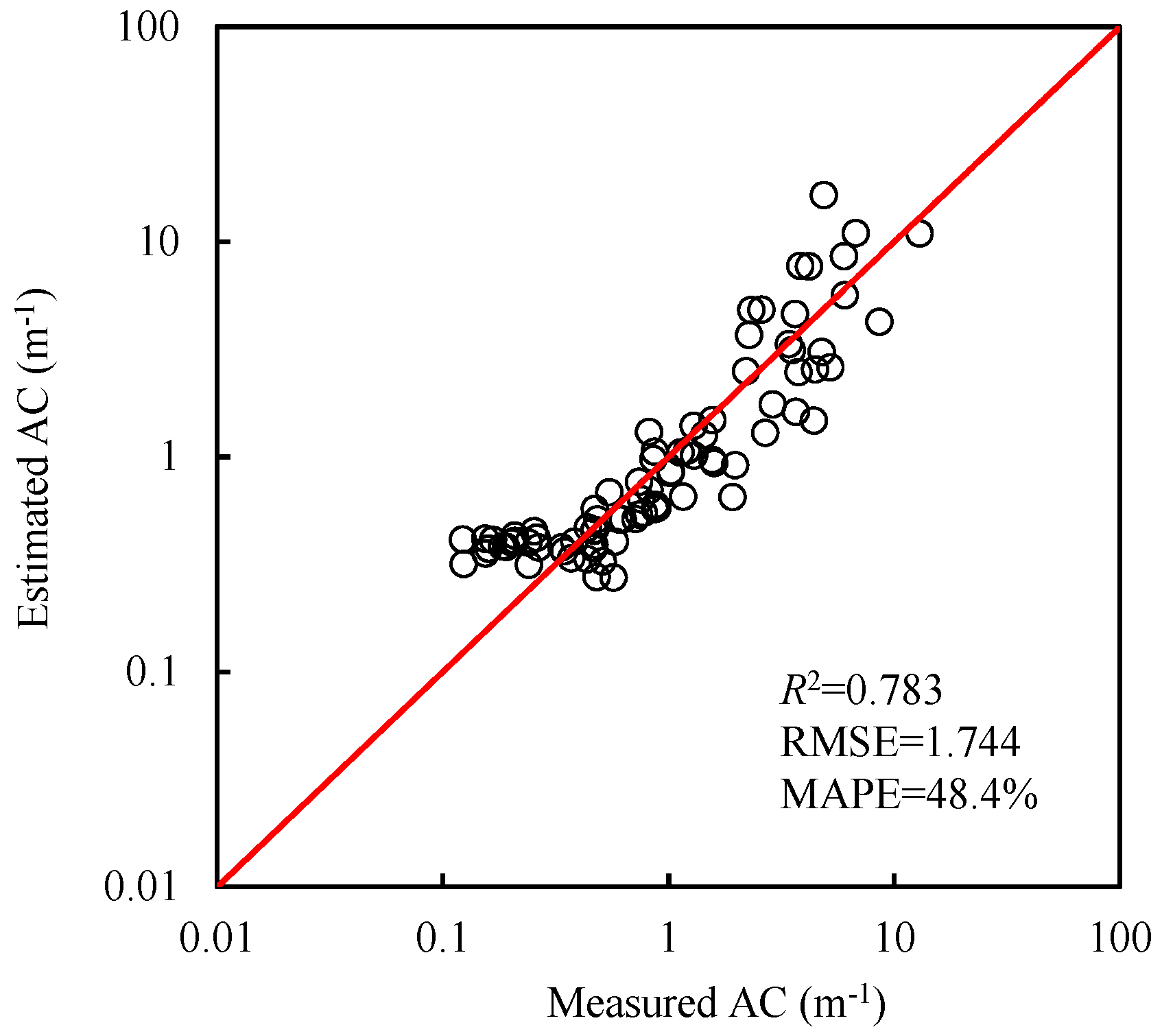
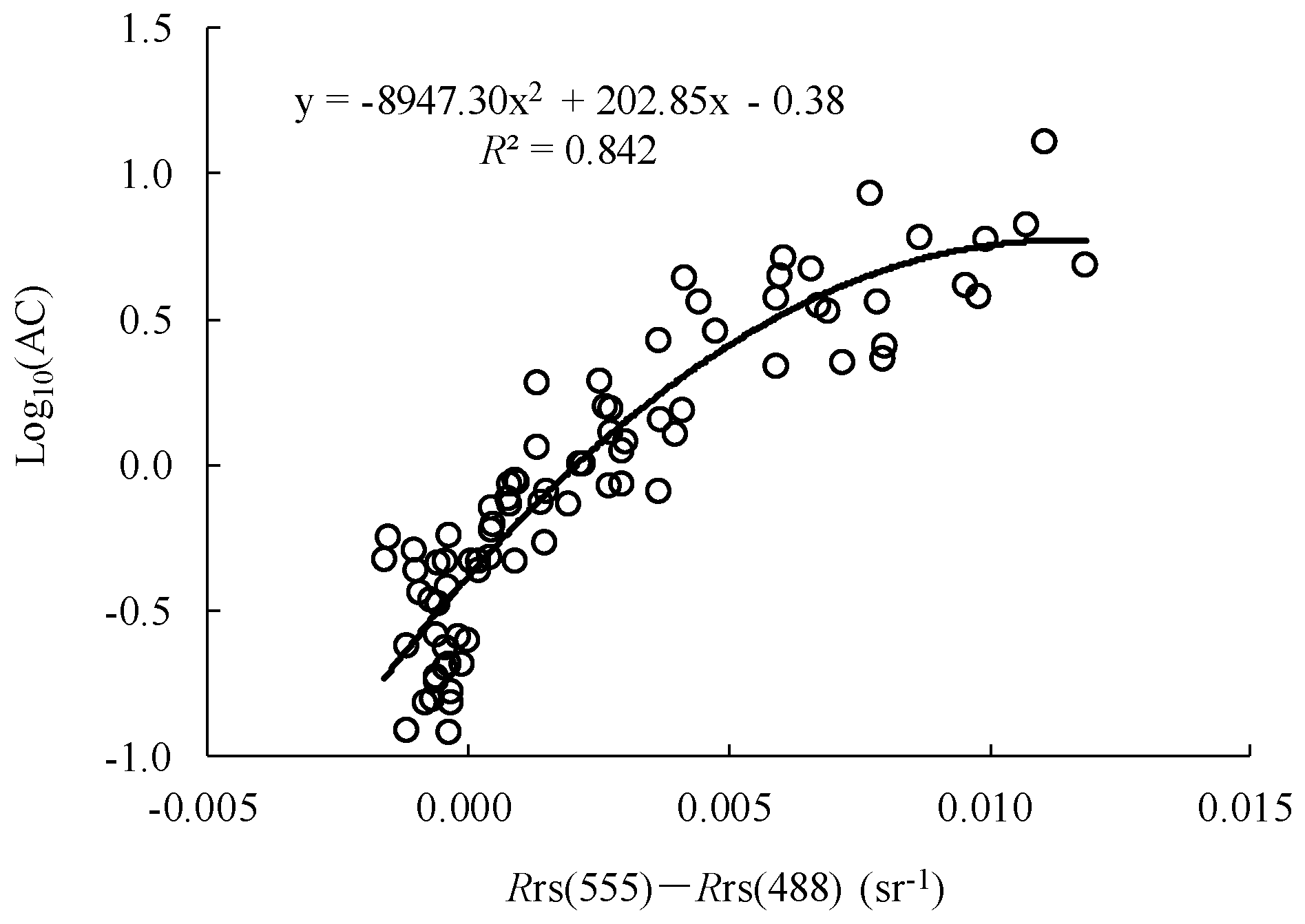
3.2. Development and Performance of AC Retrieval Model
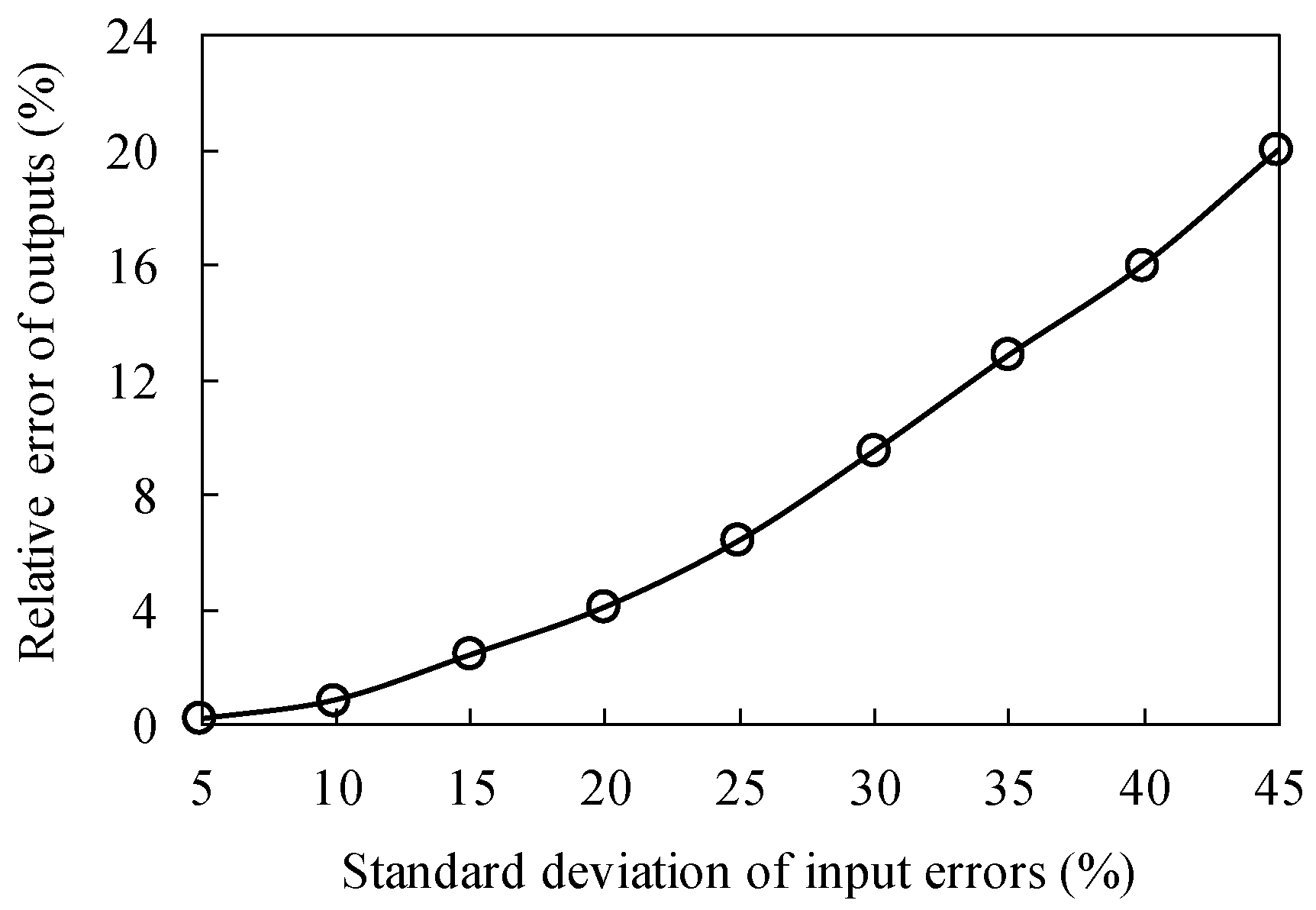
3.3. Model Sensitivity Analysis
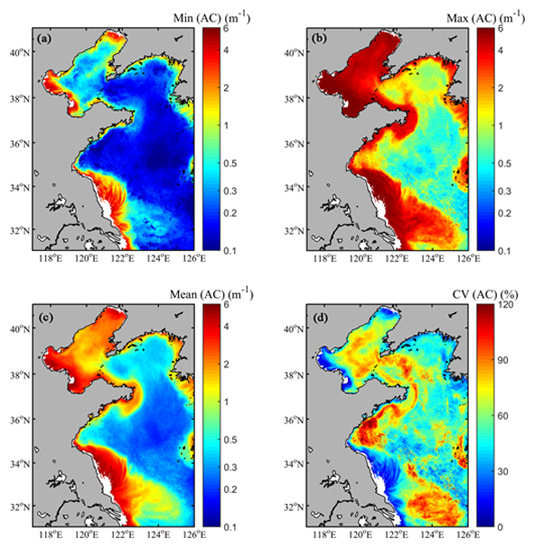
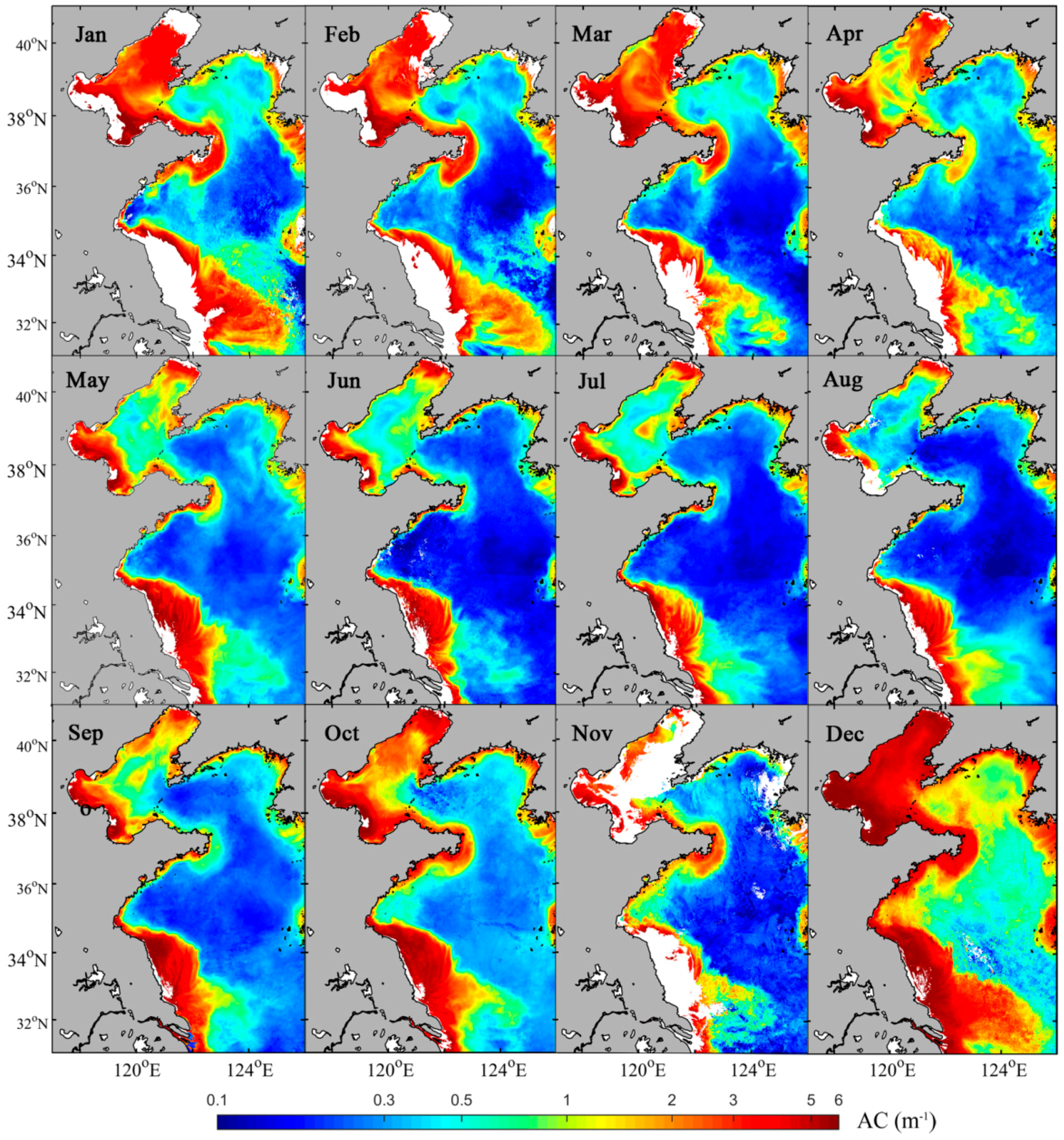
3.4. Model Application to Satellite Data
4. Discussion
4.1. Rationality and Limitation of AC Retrieval Model
4.2. Implications of Remote Sensing Applications of AC
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Doxaran, D.; Froidefond, J.-M.; Castaing, P.; Babin, M. Dynamics of the turbidity maximum zone in a macrotidal estuary (the Gironde, France): Observations from field and MODIS satellite data. Estuar. Coast. Shelf Sci. 2009, 81, 321–332. [Google Scholar] [CrossRef]
- Anderson, R.F.; Hayes, C.T. Characterizing marine particles and their impact on biogeochemical cycles in the geotraces program. Prog. Oceanogr. 2015, 133, 1–5. [Google Scholar] [CrossRef]
- Morel, A. Optics of marine particles and marine optics. In Particle Analysis in Oceanography; Demers, S., Ed.; Springer: Berlin, Germany, 1991; pp. 141–188. [Google Scholar]
- Babin, M.; Morel, A.; Fournier-Sicre, V.; Fell, F.; Stramski, D. Light scattering properties of marine particles in coastal and open ocean waters as related to the particle mass concentration. Limnol. Oceanogr. 2003, 48, 843–859. [Google Scholar] [CrossRef]
- Gordon, H.R.; Morel, A.Y. Remote Assessment of Ocean Color for Interpretation of Satellite Visible Imagery: A Review; Springer: Berlin, Germany, 1983; Volume 4. [Google Scholar]
- Mobley, C.D. Light and Water: Radiative Transfer in Natural Waters; Academic Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Bowers, D.; Braithwaite, K. Evidence that satellites sense the cross-sectional area of suspended particles in shelf seas and estuaries better than their mass. Geo-Mar. Lett. 2012, 32, 165–171. [Google Scholar] [CrossRef]
- Mikkelsen, O.A. Variation in the projected surface area of suspended particles: Implications for remote sensing assessment of TSM. Remote Sens. Environ. 2002, 79, 23–29. [Google Scholar] [CrossRef]
- Neukermans, G.; Loisel, H.; Mériaux, X.; Astoreca, R.; McKee, D. In situ variability of mass-specific beam attenuation and backscattering of marine particles with respect to particle size, density, and composition. Limnol. Oceanogr. 2012, 57, 124–144. [Google Scholar] [CrossRef]
- Agrawal, Y.; Pottsmith, H. Instruments for particle size and settling velocity observations in sediment transport. Mar. Geol. 2000, 168, 89–114. [Google Scholar] [CrossRef]
- Hatcher, A.; Hill, P.; Grant, J. Optical backscatter of marine flocs. J. Sea Res. 2001, 46, 1–12. [Google Scholar] [CrossRef]
- Flory, E.; Hill, P.; Milligan, T.; Grant, J. The relationship between floc area and backscatter during a spring phytoplankton bloom. Deep Sea Res. Part I Oceanogr. Res. Pap. 2004, 51, 213–223. [Google Scholar] [CrossRef]
- Boss, E.; Slade, W.; Hill, P. Effect of particulate aggregation in aquatic environments on the beam attenuation and its utility as a proxy for particulate mass. Opt. Express 2009, 17, 9408–9420. [Google Scholar] [CrossRef] [PubMed]
- Bowers, D.; Braithwaite, K.; Nimmo-Smith, W.; Graham, G. The optical efficiency of flocs in shelf seas and estuaries. Estuar. Coast. Shelf Sci. 2011, 91, 341–350. [Google Scholar] [CrossRef]
- Wang, S.; Qiu, Z.; Sun, D.; Shen, X.; Zhang, H. Light beam attenuation and backscattering properties of particles in the Bohai Sea and Yellow Sea with relation to biogeochemical properties. J. Geophys. Res. Oceans 2016, 121, 3955–3969. [Google Scholar] [CrossRef]
- Bowers, D.; Braithwaite, K.; Nimmo-Smith, W.; Graham, G. Light scattering by particles suspended in the sea: The role of particle size and density. Cont. Shelf Res. 2009, 29, 1748–1755. [Google Scholar] [CrossRef]
- Kostadinov, T.S.; Siegel, D.A.; Maritorena, S. Retrieval of the particle size distribution from satellite ocean color observations. J. Geophys. Res. 2009, 114, C09015. [Google Scholar] [CrossRef]
- Bale, A.; Tocher, M.; Weaver, R.; Hudson, S.; Aiken, J. Laboratory measurements of the spectral properties of estuarine suspended particles. Neth. J. Aquat. Ecol. 1994, 28, 237–244. [Google Scholar] [CrossRef]
- Wei, H.; Sun, J.; Moll, A.; Zhao, L. Phytoplankton dynamics in the Bohai Sea—Observations and modelling. J. Mar. Syst. 2004, 44, 233–251. [Google Scholar] [CrossRef]
- Chen, C.-T.A. Chemical and physical fronts in the Bohai, Yellow and East China Seas. J. Mar. Syst. 2009, 78, 394–410. [Google Scholar] [CrossRef]
- Zhang, M.; Tang, J.; Song, Q.; Dong, Q. Backscattering ratio variation and its implications for studying particle composition: A case study in Yellow and East China Seas. J. Geophys. Res. Oceans 2010, 115. [Google Scholar] [CrossRef]
- Qiu, Z.; Wu, T.; Su, Y. Retrieval of diffuse attenuation coefficient in the china seas from surface reflectance. Opt. Express 2013, 21, 15287–15297. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, Y.; Whitmire, A.; Mikkelsen, O.A.; Pottsmith, H. Light scattering by random shaped particles and consequences on measuring suspended sediments by laser diffraction. J. Geophys. Res. Oceans 2008, 113. [Google Scholar] [CrossRef]
- Traykovski, P.; Latter, R.J.; Irish, J.D. A laboratory evaluation of the laser in situ scattering and transmissometery instrument using natural sediments. Mar. Geol. 1999, 159, 355–367. [Google Scholar] [CrossRef]
- Reynolds, R.; Stramski, D.; Wright, V.; Woźniak, S. Measurements and characterization of particle size distributions in coastal waters. J. Geophys. Res. Oceans 2010, 115. [Google Scholar] [CrossRef]
- De Moraes Rudorff, N.; Frouin, R.; Kampel, M.; Goyens, C.; Meriaux, X.; Schieber, B.; Mitchell, B.G. Ocean-color radiometry across the southern atlantic and southeastern pacific: Accuracy and remote sensing implications. Remote Sens. Environ. 2014, 149, 13–32. [Google Scholar] [CrossRef]
- Miller, R.L.; McKee, B.A. Using MODIS Terra 250 m imagery to map concentrations of total suspended matter in coastal waters. Remote Sens. Environ. 2004, 93, 259–266. [Google Scholar] [CrossRef]
- Stavn, R.H.; Rick, H.J.; Falster, A.V. Correcting the errors from variable sea salt retention and water of hydration in loss on ignition analysis: Implications for studies of estuarine and coastal waters. Estuar. Coast. Shelf Sci. 2009, 81, 575–582. [Google Scholar] [CrossRef]
- Wang, M.; Gordon, H.R. A simple, moderately accurate, atmospheric correction algorithm for SeaWiFS. Remote Sens. Environ. 1994, 50, 231–239. [Google Scholar] [CrossRef]
- Hyde, K.J.; O’Reilly, J.E.; Oviatt, C.A. Validation of SeaWiFS chlorophyll a in Massachusetts Bay. Cont. Shelf Res. 2007, 27, 1677–1691. [Google Scholar] [CrossRef]
- Antoine, D.; d’Ortenzio, F.; Hooker, S.B.; Bécu, G.; Gentili, B.; Tailliez, D.; Scott, A.J. Assessment of uncertainty in the ocean reflectance determined by three satellite ocean color sensors (MERIS, SeaWiFS and MODIS-A) at an offshore site in the mediterranean sea (BOUSSOLE project). J. Geophys. Res. Oceans 2008, 113. [Google Scholar] [CrossRef]
- He, X.; Bai, Y.; Pan, D.; Huang, N.; Dong, X.; Chen, J.; Chen, C.-T.A.; Cui, Q. Using geostationary satellite ocean color data to map the diurnal dynamics of suspended particulate matter in coastal waters. Remote Sens. Environ. 2013, 133, 225–239. [Google Scholar] [CrossRef]
- Sun, D.; Hu, C.; Qiu, Z.; Cannizzaro, J.P.; Barnes, B.B. Influence of a red band-based water classification approach on chlorophyll algorithms for optically complex estuaries. Remote Sens. Environ. 2014, 155, 289–302. [Google Scholar] [CrossRef]
- Tassan, S. Local algorithms using seawifs data for the retrieval of phytoplankton, pigments, suspended sediment, and yellow substance in coastal waters. Appl. Opt. 1994, 33, 2369–2378. [Google Scholar] [CrossRef] [PubMed]
- O’Reilly, J.E.; Maritorena, S.; Mitchell, B.G.; Siegel, D.A.; Carder, K.L.; Garver, S.A.; Kahru, M.; McClain, C. Ocean color chlorophyll algorithms for SeaWiFS. J. Geophys. Res. Oceans 1998, 103, 24937–24953. [Google Scholar] [CrossRef]
- Doxaran, D.; Froidefond, J.-M.; Lavender, S.; Castaing, P. Spectral signature of highly turbid waters: Application with SPOT data to quantify suspended particulate matter concentrations. Remote Sens. Environ. 2002, 81, 149–161. [Google Scholar] [CrossRef]
- Mao, Z.; Chen, J.; Pan, D.; Tao, B.; Zhu, Q. A regional remote sensing algorithm for total suspended matter in the East China Sea. Remote Sens. Environ. 2012, 124, 819–831. [Google Scholar] [CrossRef]
- Siswanto, E.; Tang, J.; Yamaguchi, H.; Ahn, Y.-H.; Ishizaka, J.; Yoo, S.; Kim, S.-W.; Kiyomoto, Y.; Yamada, K.; Chiang, C. Empirical ocean-color algorithms to retrieve chlorophyll-a, total suspended matter, and colored dissolved organic matter absorption coefficient in the Yellow and East China Seas. J. Oceanogr. 2011, 67, 627–650. [Google Scholar] [CrossRef]
- Kohavi, R. A study of cross-validation and bootstrap for accuracy estimation and model selection. In Proceedings of the 14th International Joint Conference on Artificial Intelligence, Montreal, QC, Canada, 20–25 August 1995; Volume 14, pp. 1137–1145.
- Bailey, S.W.; Werdell, P.J. A multi-sensor approach for the on-orbit validation of ocean color satellite data products. Remote Sens. Environ. 2006, 102, 12–23. [Google Scholar] [CrossRef]
- Cui, T.; Zhang, J.; Groom, S.; Sun, L.; Smyth, T.; Sathyendranath, S. Validation of MERIS ocean-color products in the Bohai Sea: A case study for turbid coastal waters. Remote Sens. Environ. 2010, 114, 2326–2336. [Google Scholar] [CrossRef]
- Yang, S.Y.; Jung, H.S.; Lim, D.I.; Li, C.X. A review on the provenance discrimination of sediments in the Yellow Sea. Earth-Sci. Rev. 2003, 63, 93–120. [Google Scholar] [CrossRef]
- Jiang, W.; Pohlmann, T.; Sun, J.; Starke, A. SPM transport in the Bohai Sea: Field experiments and numerical modelling. J. Mar. Syst. 2004, 44, 175–188. [Google Scholar] [CrossRef]
- Xu, Y.; Ishizaka, J.; Yamaguchi, H.; Siswanto, E.; Wang, S. Relationships of interannual variability in SST and phytoplankton blooms with giant jellyfish (Nemopilema nomurai) outbreaks in the Yellow Sea and East China Sea. J. Oceanogr. 2013, 69, 511–526. [Google Scholar] [CrossRef]
- Braithwaite, K.; Bowers, D.; Smith, W.N.; Graham, G.; Agrawal, Y.; Mikkelsen, O. Observations of particle density and scattering in the Tamar Estuary. Mar. Geol. 2010, 277, 1–10. [Google Scholar] [CrossRef]
- Gordon, H.R.; Brown, O.B.; Evans, R.H.; Brown, J.W.; Smith, R.C.; Baker, K.S.; Clark, D.K. A semianalytic radiance model of ocean color. J. Geophys. Res. Atmos. 1988, 93, 10909–10924. [Google Scholar] [CrossRef]
- Risović, D. Effect of suspended particulate-size distribution on the backscattering ratio in the remote sensing of seawater. Appl. Opt. 2002, 41, 7092–7101. [Google Scholar] [CrossRef] [PubMed]
- Bowers, D.; Hill, P.; Braithwaite, K. The effect of particulate organic content on the remote sensing of marine suspended sediments. Remote Sens. Environ. 2014, 144, 172–178. [Google Scholar] [CrossRef]
- Ahn, Y.-H.; Bricaud, A.; Morel, A. Light backscattering efficiency and related properties of some phytoplankters. Deep Sea Res. Part I Oceanogr. Res. Pap. 1992, 39, 1835–1855. [Google Scholar] [CrossRef]
- Vaillancourt, R.D.; Brown, C.W.; Guillard, R.R.; Balch, W.M. Light backscattering properties of marine phytoplankton: Relationships to cell size, chemical composition and taxonomy. J. Plankton Res. 2004, 26, 191–212. [Google Scholar] [CrossRef]
- Peng, F.; Effler, S.W. Characterizations of individual suspended mineral particles in Western Lake Erie: Implications for light scattering and water clarity. J. Gt. Lakes Res. 2010, 36, 686–698. [Google Scholar] [CrossRef]
- Lee, Z.; Carder, K.L.; Arnone, R.A. Deriving inherent optical properties from water color: A multiband quasi-analytical algorithm for optically deep waters. Appl. Opt. 2002, 41, 5755–5772. [Google Scholar] [CrossRef] [PubMed]
- Smyth, T.J.; Moore, G.F.; Hirata, T.; Aiken, J. Semianalytical model for the derivation of ocean color inherent optical properties: Description, implementation, and performance assessment. Appl. Opt. 2006, 45, 8116–8131. [Google Scholar] [CrossRef] [PubMed]
- Binding, C.; Bowers, D.; Mitchelson-Jacob, E. Estimating suspended sediment concentrations from ocean colour measurements in moderately turbid waters; the impact of variable particle scattering properties. Remote Sens. Environ. 2005, 94, 373–383. [Google Scholar] [CrossRef]
- Qiu, Z. A simple optical model to estimate suspended particulate matter in Yellow River Estuary. Opt. Express 2013, 21, 27891–27904. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Cui, T.; Qiu, Z.; Lin, C. A three-band semi-analytical model for deriving total suspended sediment concentration from HJ-1A/CCD data in turbid coastal waters. ISPRS J. Photogramm. 2014, 93, 1–13. [Google Scholar] [CrossRef]
- Kong, J.-L.; Sun, X.-M.; Wong, D.W.; Chen, Y.; Yang, J.; Yan, Y.; Wang, L.-X. A semi-analytical model for remote sensing retrieval of suspended sediment concentration in the gulf of Bohai, China. Remote Sens. 2015, 7, 5373–5397. [Google Scholar] [CrossRef]
- Baker, E.T.; Lavelle, J.W. The effect of particle size on the light attenuation coefficient of natural suspensions. J. Geophys. Res. 1984, 89, 8197–8203. [Google Scholar] [CrossRef]
- Mikkelsen, O.; Pejrup, M. In situ particle size spectra and density of particle aggregates in a dredging plume. Mar. Geol. 2000, 170, 443–459. [Google Scholar] [CrossRef]

| Variable | Band (nm) | Min | Max | Mean | S.D. | CV (%) |
|---|---|---|---|---|---|---|
| TSM (g·m−3) | 0.53 | 43.88 | 7.60 | 7.25 | 95.4 | |
| AC (m−1) | 0.12 | 13.00 | 1.74 | 2.14 | 123.0 | |
| Rrs(λ) (sr−1) | 412 | 0.0006 | 0.0111 | 0.0042 | 0.0030 | 70.7 |
| 443 | 0.0008 | 0.0152 | 0.0060 | 0.0045 | 75.2 | |
| 490 | 0.0012 | 0.0217 | 0.0086 | 0.0066 | 76.0 | |
| 555 | 0.0010 | 0.0333 | 0.0110 | 0.0094 | 85.7 | |
| 660 | 0.0001 | 0.0239 | 0.0045 | 0.0057 | 126.1 | |
| 680 | 0.0001 | 0.0220 | 0.0040 | 0.0051 | 127.8 |
| X | General Form | Best Band (nm) | R2 | RMSE | MAPE (%) |
|---|---|---|---|---|---|
| X1 | Rrs(λ1) | λ1 = 555 | 0.755 | 1.084 | 50.3 |
| X2 | Rrs(λ1)/Rrs(λ2) | λ1 = 660, λ2 = 412 | 0.807 | 1.095 | 44.2 |
| X3 | Rrs(λ1) − Rrs(λ2) | λ1 = 555, λ2 = 490 | 0.843 | 1.145 | 38.9 |
| X4 | λ1 = 555, λ2 = 490, λ3 = 412 | 0.816 | 1.167 | 44.3 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Huan, Y.; Qiu, Z.; Sun, D.; Zhang, H.; Zheng, L.; Xiao, C. Remote Sensing of Particle Cross-Sectional Area in the Bohai Sea and Yellow Sea: Algorithm Development and Application Implications. Remote Sens. 2016, 8, 841. https://doi.org/10.3390/rs8100841
Wang S, Huan Y, Qiu Z, Sun D, Zhang H, Zheng L, Xiao C. Remote Sensing of Particle Cross-Sectional Area in the Bohai Sea and Yellow Sea: Algorithm Development and Application Implications. Remote Sensing. 2016; 8(10):841. https://doi.org/10.3390/rs8100841
Chicago/Turabian StyleWang, Shengqiang, Yu Huan, Zhongfeng Qiu, Deyong Sun, Hailong Zhang, Lufei Zheng, and Cong Xiao. 2016. "Remote Sensing of Particle Cross-Sectional Area in the Bohai Sea and Yellow Sea: Algorithm Development and Application Implications" Remote Sensing 8, no. 10: 841. https://doi.org/10.3390/rs8100841
APA StyleWang, S., Huan, Y., Qiu, Z., Sun, D., Zhang, H., Zheng, L., & Xiao, C. (2016). Remote Sensing of Particle Cross-Sectional Area in the Bohai Sea and Yellow Sea: Algorithm Development and Application Implications. Remote Sensing, 8(10), 841. https://doi.org/10.3390/rs8100841