Next Article in Journal
A Multi-View Dense Image Matching Method for High-Resolution Aerial Imagery Based on a Graph Network
Next Article in Special Issue
Characterization of Active Layer Thickening Rate over the Northern Qinghai-Tibetan Plateau Permafrost Region Using ALOS Interferometric Synthetic Aperture Radar Data, 2007–2009
Previous Article in Journal
Caveats Concerning the Use of SRTM DEM Version 4.1 (CGIAR-CSI)
Previous Article in Special Issue
A GIS-Based Assessment of Vulnerability to Aeolian Desertification in the Source Areas of the Yangtze and Yellow Rivers
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 8
Issue 10
10.3390/rs8100798
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Changes in Mountain Glaciers, Lake Levels, and Snow Coverage in the Tianshan Monitored by GRACE, ICESat, Altimetry, and MODIS

by
Shuang Yi
,
Qiuyu Wang
,
Le Chang
and
Wenke Sun
*
Key Laboratory of Computational Geodynamics, University of Chinese Academy of Sciences, Beijing 100049, China
*
Author to whom correspondence should be addressed.
Remote Sens. 2016, 8(10), 798; https://doi.org/10.3390/rs8100798
Submission received: 7 February 2016 / Revised: 18 September 2016 / Accepted: 20 September 2016 / Published: 26 September 2016
(This article belongs to the Special Issue Remote Sensing in Tibet and Siberia)
Browse Figures
Versions Notes

Abstract

:
The Tianshan mountain range is experiencing a notable environmental change as a result of global warming. In this paper; we adopt multiple remote sensing techniques to examine the diversified geophysical changes in the Tianshan; including glacier changes measured by Gravity Recovery and Climate Experiment (GRACE) and Ice, Cloud, and land Elevation Satellite (ICESat); lake level changes measured by radar altimetry; and snow coverage measured by moderate-resolution imaging spectroradiometer (MODIS). We find a rapid transition from dry years to wet years in 2010 in the western and northern Tianshan for all the geophysical measurements. The transition is likely caused by increasing westerlies and greatly pollutes the gravity signals in the edge of Tianshan. However, glaciers in the central Tianshan are unaffected and have been steadily losing mass at a rate of –4.0 ± 0.7 Gt/year during 2003–2014 according to space gravimetry and –3.4 ± 0.8 Gt/year during 2003–2009 according to laser altimetry. Our results show a weaker declining trend and greater linearity compared with earlier estimates; because we investigate the signal pattern in more detail. Finally; water level records of 60 years in Bosten Lake; China; are presented to show that for areas strongly dependent on meltwater; rising temperature can benefit the water supply in the short run; but cause it to deteriorate in the long run.

1. Introduction

Global climate change has had a profound and lasting effect on the environment [1]. The shrinkage of glacier ice caused by global warming has attracted a large amount of research interest, from the global scale to specific glaciers [2]. Apart from polar ice [3,4], most research is focused on glaciers on the third pole—the Asian high mountains [5,6,7,8,9]. Called the Asian water tower, the Asian high mountains feed several major rivers by widespread glacier melt [10]. Changing glacier mass there will have a far-reaching influence on the water supply of billions of people. Therefore, a good understanding of the glacier mass balance is important for planning and environmental adaptation.
The spatial scope of Asian high mountains mainly includes the Tibetan Plateau and the Tianshan. The Tianshan has some distinct features and is worth studying specifically. First, the Tianshan is the place most distant from the oceans in the Eurasian continent, so the atmospheric water vapor is usually blocked from reaching it [11], and water resources are strongly dependent on meltwater from snow and glaciers; Second, the Tianshan is influenced by the mid-latitude westerly winds, quite different from the Himalayas, which are influenced by the Indian monsoon from the equator [9].
Remote sensing observations are the only feasible approaches to estimating the overall mass balance of mountain glaciers in this region. Widely used techniques include space imagery, digital elevation models (DEMs), laser altimetry, and satellite gravimetry. Space-based imagery only constrains the area change in glaciers [12,13], which is not enough to estimate the mass balance. Recently there have been results from the Pamir and Karakoram differencing two DEMs [14,15]. ICESat, a type of laser altimetry, has a smaller footprint (70 m) compared with radar altimetry (several kilometers), so it is applicable in the estimation of the glacier mass balance. The implementation of ICESat in the Asian high mountains has been a popular method to constrain mass balance [7,16,17,18]. Gravity changes observed by GRACE can directly constrain the overall glacier balance [2,8,19], however, a special method is needed to restore the attenuated signals due to the coarse spatial resolution of GRACE (~300 km).
Recently, there has been a study in the Tianshan using three methods: satellite gravimetry, laser altimetry, and glaciological modeling [6]. However, the mass change time series show great interannual variance (Figure 2a in Farinotti et al. [6]), and the annual trend of glacier change even becomes positive around 2010 (Figure 6 in Farinotti et al. [6]). This suggests that there is a large interannual variation in the glacier changes in the Tianshan. However, we have shown that there is a five-year fluctuation in the Pamirs in an earlier work [19], and the large interannual variation in the Tianshan might be leakage from the signal in the Pamirs. One of the purposes of this work is to determine the spatial range of the large interannual fluctuation and check whether it affects estimates for glaciers in the Tianshan.
The Tianshan is mainly located in Xinjiang Province in western China. In the past decades, western China has been greatly developed as a result of its national policies. The geographical conditions in the Tianshan are diversified and are impacted jointly by climate change and anthropogenic activities. There are glaciers, snow, lakes, and burgeoning residential and agricultural districts in the area. These factors are intricately associated, and a synthetic study will aid in the understanding of the influencing and evolving mechanisms. This work features a systematic and comprehensive study of precipitation, snow, lakes, glaciers, and human activities in the Tianshan. Bosten Lake, a large lake located just at the foot of Tianshan and disturbed by intense anthropogenic activities is specifically discussed.
In the following sections, this work will be arranged in the following structure: First, changes in the total mass, glaciers, and snow coverage will be represented based on multiple data sources; second, we will discuss the spatial features of the large interannual variation introduced above and try to find common characteristics among different data sources; lastly, we will present the record of water level changes in Bosten Lake since 1955 and discuss its relationship with climate change and anthropogenic activies.

2. Data and Methods

2.1. GRACE Data and Processing

The Gravity Recovery and Climate Experiment (GRACE) mission is a twin-satellite system for space gravimetry [20]. The satellites were launched in 2002, and since then models of monthly global gravity models have been released. These are provided at sets of Stokes’ coefficients. The gravity models are estimated by several organizations and have been used in many fields, including mass balance in polar ice sheets [3,4], water balance in basins [21,22,23], and sea level change [24,25]. In this study, we use GRACE data to estimate glacier mass change in the Tianshan. The Release05 solutions over 2003–2014 from the Center for Space Research (CSR) in the University of Texas, GeoForschungsZentrum (GFZ) in Potsdam, and the Jet Propulsion Laboratory (JPL) are adopted [26]. The lowest degrees of the Stokes’ coefficient cannot be determined reliably by GRACE and therefore these are treated in the following way: degree-1 (geocenter motion) coefficients are added back [27], and degree-2 coefficients are replaced by a set of more precise satellite laser ranging observations [28]. Three different filter methods are used to increase the signal-to-noise ratio: a Gaussian filter with a radius of 300 km (hereinafter referred to as G300) [29], a G300 combined with a decorrelation filter from the order m = 6 with a polynomial of order 4 (hereinafter referred to as G300+P4M6) [30], and the anisotropic decorrelation filter DDK4 (hereinafter referred to as DDK4) [31].
The gravity trend observed by GRACE integrates signals from all mass changes, including snow, glaciers, lake, and soil moisture. After the correction of contributions from snow, lakes, and soil moisture in the GRACE observations, we assume the remaining mass variations are due to glacier changes in the Tianshan only. Glacial isostatic adjustment is considered to be negligible here and the changes caused by the elastic response to the ongoing mass changes are corrected for in the processing [19]. Since GRACE solutions lack high-frequency information (truncated at a degree of 60 in this study) and the high-degree of spherical harmonics are further suppressed by the filtering, the observed signals are always broader in space and weaker in strength than the real signals, which is also referred to as the leakage effect. Due to the leakage effect, the negative gravity signal observed by GRACE spans a wider range outside the glacier locations (Figure 1). If signals only within the glacier distributions are summed up, the amount of mass loss in glacier will definitely be underestimated. To correct for the leakage effect and recover the glacier signal, we adopt a spatial domain inversion (SADI) method, which has been explicitly described in Yi and Sun [19].

Description and Demonstration of the Inversion Method

In the SADI method, we first need to define mass concentrations (also termed mascons) that represent the location and shape of signals. We optimize the mass changes in the mascons to best fit the GRACE observations, providing an estimate of the mass change in each mascon. The inversion method can recover the original strength of signal from the smoothed signal observed by GRACE by decreasing the leakage effect, assuming that the spatial extent of the real signal is known.
A regularization factor α is needed in the application of the SADI method to reduce singularities in the inversion. The factor α is determined by the L-curve approach, which chooses an optimal tradeoff between model complexity and data fit [32]. Increasing model complexity results in a better model fit (i.e., a lower post-fit residual). However, there are errors in the observation data, so overfitting will bring these errors into the inversion model making it overly complex. On the other hand, if the inversion model is too simple, the observation data cannot be fit well, and much information will be lost. To sum up, the optimal estimator takes both the model complexity and the observation fit into consideration.
Mascons that represent the location and shape of signals need to be defined to apply the method. There is an apparent negative gravity trend in the Tianshan region. We assume that this is mainly caused by melting glaciers. We define nine mascons according to the glacier distribution (Figure 2a), and information about the glaciers in each mascon can be found in Table 1. The location of glaciers is based on the GLIMS database. The factor α is determined by the L-curve approach (Figure 2b) and the blue star in the corner in Figure 2b is chosen as the optimal factor based on this criterion. The observed signal by GRACE from CSR with 300-km Gaussian smoothing for the optimal is shown in Figure 2c. The estimated mass change is shown in Figure 2e, and its inferred GRACE signal is shown in Figure 2d. The difference between observation and inversion is shown in Figure 2f, which indicates that the negative signal is well fit, but the surrounding signal is nearly unaffected. The negative signal is concentrated in the nine mascons, so the strength significantly increases (the extreme value is amplified by about ten times).
GRACE has a spatial resolution of ~300 km. The Tianshan glaciers have a finer spatial distribution, so we cannot resolve the detailed glacier information theoretically despite the fact that there are as many as 9 mascons here. In fact, our estimated mass distribution in Figure 2e is smoothed by the regularization factor α. In other words, numerous mass distributions could generate the same gravity signals as observed by GRACE, and we cannot tell which one is better because the detailed information is missing. However, all these potential mass distributions must have a similar total amount, which is constrained by the GRACE observation. We are only concerned with the total mass change here, and the mass changes in each individual mascon should not be interpreted.

2.2. ICESat

The Global Land Surface Altimetry Data Version 34 (GLA14) of ICESat production from the U.S. National Snow and Ice Data Center (NSIDC) are used in this study. The product contains date, footprint geospatial location, ellipsoid elevation, geoid, saturation correction, and others. The location of glaciers is based on the Global Land Ice Measurements from Space (GLIMS) [33]. The total area of glaciers in this study is about 11,400 km2, considering a 10% uncertainty. The ICESat footprints on glaciers in our study area are extracted and shown in Figure 1. Due to a large cross-track gap in the mid-latitude region, a reference digital elevation model is needed to correct for topographic differences in the ICESat sampling footprints [34]. The changing rate of elevation of the glacier surface is calculated based on the elevation difference between the IESat and the Shuttle Radar Topography Mission (SRTM). SRTM is a near-global dataset containing the surface topography in 2000 [16]. The density of glacier ice (850 ± 60 kg/m3) is used to convert volume change to mass change [35].

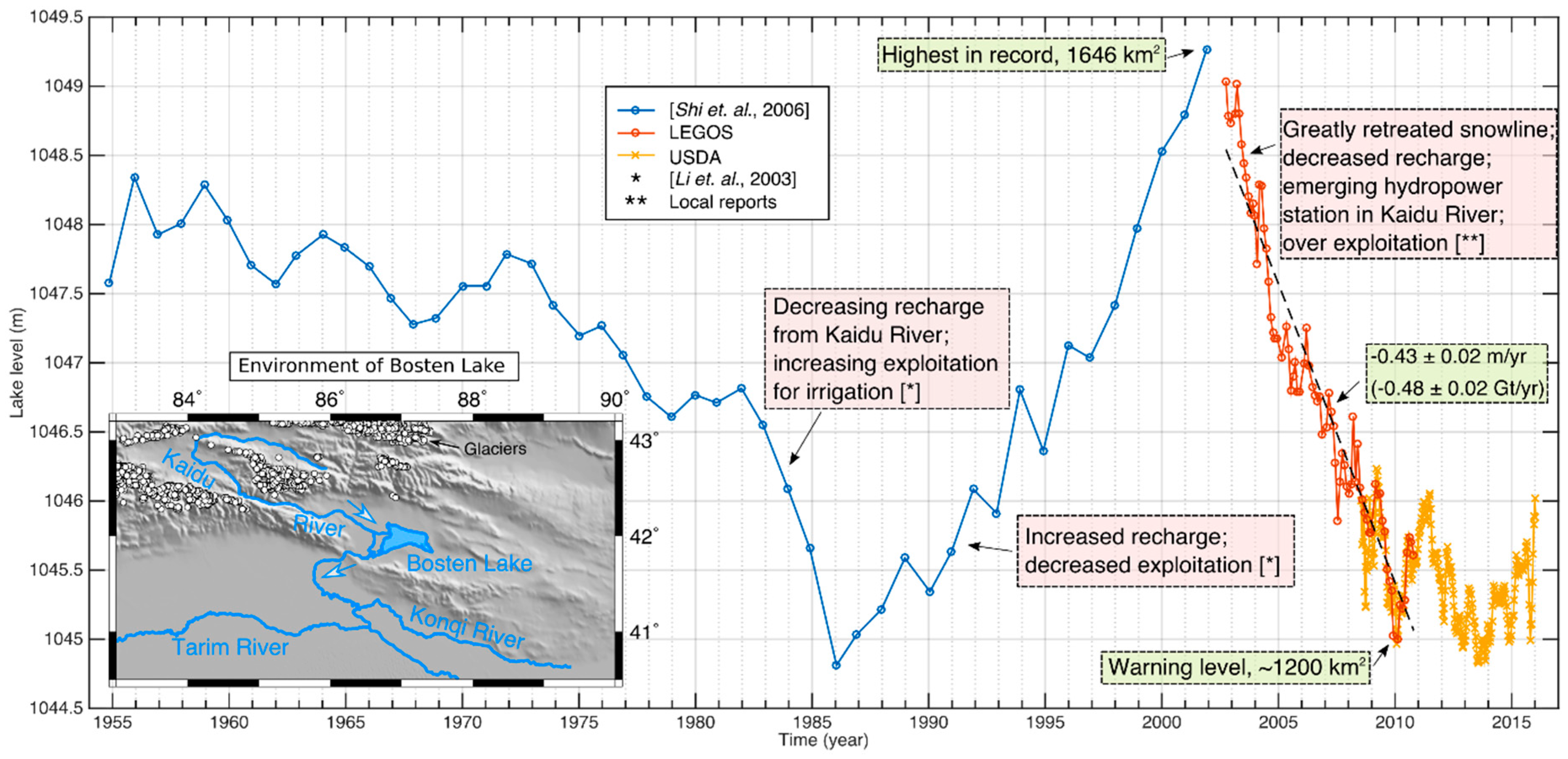
2.3. Lake Level Change

The Tianshan is surrounded by many large lakes, which are fed by precipitation and meltwater and are important water reservoirs in the dry climate condition. Seven large lakes with altimetry observations are studied here, i.e., Balkhash, Issykkul, Kapchagayskoye, Sasykkol, Saysan, Ulungur, and Bosten. The lake level time series shown in this work are processed products from USDA [36] and LEGOS [37]. Bosten Lake is located near a residential area and has site records dating back to 1955, which can be found in Shi et al. [11].

2.4. MODIS

The moderate-resolution imaging spectroradiometer (MODIS) is an important detector loaded on the satellites Terra and Aqua. The multi-band data of MODIS can be used to study the land surface condition and various characteristics concerning cloud, seawater, and atmosphere. The spatial resolution of MODIS data can be as fine as 250 m, and global coverage is obtained every one or two days. There are numerous MODIS derived products, and in this study we use the snow coverage product (with the identifier MOD10) [38]. Although the temporal resolution can be as fine as 1 or 8 days, a resolution of 1 month (with the identifier MOD10CM) is chosen to reduce the influence of cloud shielding, which is very common in this area. The MOD10CM data are provided globally with a resolution of 0.05°. Here, MODIS data from January 2000 to December 2015 are used. The data are obtained from the National Snow and Ice Data Center [39].

2.5. Land Water Model

GLDAS is a global surface modeling system developed by the Goddard Space Flight Center (GSFC) and the National Centers for Environmental Prediction (NCEP) [40]. The model is constrained by both ground and satellites observations and has spatial resolutions from 1° to 0.25° and temporal resolutions from 3 h to 1 month. The outputs concerning water content ranging from the surface down to several meters in depth are adopted here. Four different monthly land surface models of GLDAS are used to estimate the soil moisture: Noah, Mosaic, Community Land Model, and Variable Infiltration Capacity. To be comparable with GRACE data, GLDAS models are expanded into spherical harmonics to a degree of 60 and subtracted from GRACE observation before the inversion method is applied.

2.6. Precipitation

Precipitation is a key factor in the climate system and is a main contributor to lake levels and soil moisture in our study area. Here, the Global Precipitation Climatology Project (GPCP) model [41] is adopted [42]. GPCP incorporates observations from ground stations and satellites to provide a monthly global precipitation dataset with a resolution of 2.5° × 2.5° ever since 1979. In this study, the GPCP data are interpolated by spline interpolation to a finer resolution of 1° × 1°.

2.7. Arctic Oscillation Index (AOI)

The Tianshan is influenced by the westerlies, and the Arctic oscillation index (AOI) is an indicator of the strength of the westerlies [43]. The monthly values of AOI can be obtained from the Climate Prediction Center [44].
All of the datasets are summarized in Table 2.

3. Results

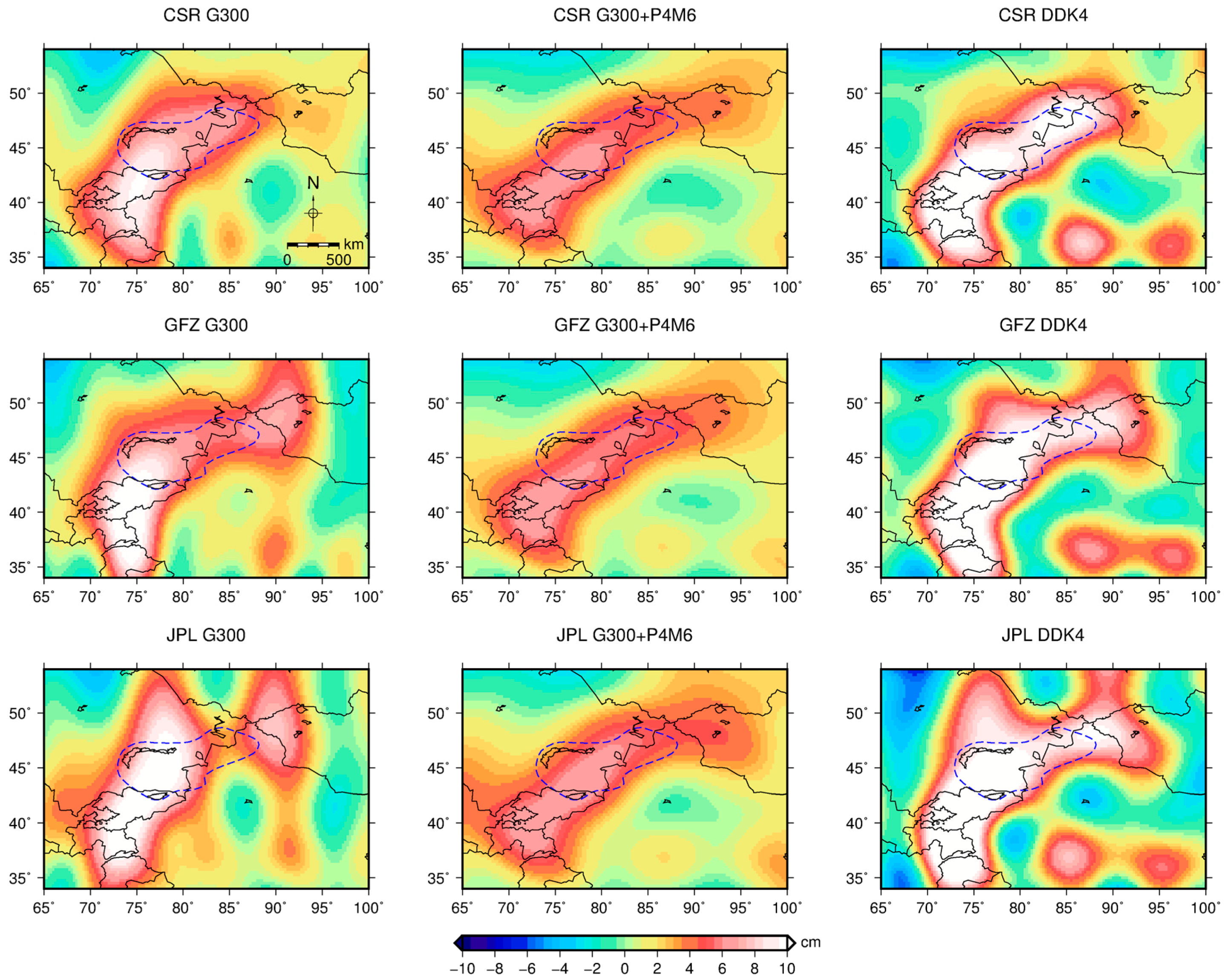
3.1. The Total Mass

The solutions from CSR and the G300 smoothing method are chosen here for a demonstration of the inversion method. By the SADI method, we can obtain the time series of the nine mascons. After summing up the time series of all the mascons, we obtain the total mass change (Figure 3a). It is evident that the interannual variations are large in this region, e.g., there is a rapid jump from 2009 to 2010 as marked by the dashed ellipses. A similar jump could also be found in a recent work by Farinotti et al. [6]. The secular trend based on our result is −6.34 ± 0.65 Gt/year. However, the large variations mean that the trend estimate is sensitive to the time window chosen, and even an increasing trend is possible if a different time period is chosen. The trend from 2003 to 2014 could possibly be biased by variations over a long period ranging from several years (as we can see in the existing observations) to decades (likely to exist but has not confirmed by data).
The time series of each mascon is checked to investigate whether this fluctuation is widespread or limited in spatial range (Figure 3b). The jump only exists in three mascons (5, 6, and 9). Mascon 9 has the largest interannual variation, and is much different from the others. It is influenced by the glacier change in the Pamirs, which displayed a strong five-year fluctuation during 2003–2012 [12]. The three mascons are located in the western or northern edge of the Tianshan region (Figure 2a). Therefore, the central part of Tianshan is less influenced by the interannual fluctuations. The majority of the glacier retreat is located there (Figure 2c). The interannual variation might be caused by the change in the other signal sources (such as soil moisture and lakes) rather than the glaciers, and we will try to confirm this conjecture later. If we sum up the other mascons that have no jump in 2010 (marked with stars in Figure 3b), it is found that the linearity of the time series is much improved, and the trend is −5.43 ± 0.36 Gt/year (Figure 3c). Therefore, in the central Tianshan region, the mass is decreasing more steadily than previously recognized, and the large fluctuations only come from the peripheral regions.

3.2. Glaciers

3.2.1. GRACE

The time series in Figure 3c is the combined effect of all signal sources including glaciers, soil moisture, and the Bosten Lake (the other lakes are out of this region). The soil moisture is estimated by four GLDAS land water models, and the change in the Bosten Lake lake level is derived from altimetry observations. To avoid a potential bias in a specific GRACE dataset or the smoothing method, we adopted solutions from three orgnizations and three smoothing methods, providing a total of nine combinations. After the contributions from soil moisture and the Bosten Lake are corrected, the change in glaciers based on the mean of the nine datasets is shown in Figure 4a (excluding mascons 5, 6, and 9). The change in glaciers is steady without the jump in 2010. The trends of the glaciers from all combinations are shown in Figure 4b, and their mean value is adopted as the final estimation, which is −4.0 ± 0.7 Gt/year. The error bars are estimated based on the post-fit residuals, under the assumption that there is no systematic error in the GRACE solutions. This trend is smaller in absolute value than the previous estimate of −6.6 ± 2.0 Gt/year (one standard deviation) [6]. The main reason is the uncorrected contributions (e.g., from the soil moisture or the snow coverage) that cause the large fluctuations. The end of Farinotti and coworkers’ study period is a trough year, so all the components are varying more intensely than their normal trends. As a result, the uncertainty in each data will be amplified. A large improvement in our estimation is that the large interannual fluctuation is effectively eliminated, so the mass reduction trend of glaciers is better determined. Another reason is that our study region is a little smaller than used by Farinotti, but that will only cause a small difference because the negative gravity trend is mostly located in our study area, and the contribution from the regions we exclude is minute.

3.2.2. ICESat

The estimation based on ICESat is shown in Figure 5. Since we have excluded the western part of the Tianshan region (Mascon 9), we treat it here separately from the eastern part. Footprints in the northern part (Mascons 5 and 6) are too sparse to give a reliable estimation, so they are omitted as well. There are no more than three observation periods (winter, summer, and fall) in each year, so the influence of the annual variation is hard to correct. For this reason, the trends are fitted separately in winter and fall (the summer observations are ignored as there are only three samples). The glacier elevation in the western part has larger fluctuations and a smaller trend than in the eastern part, which is consistent with the GRACE results in the previous section. This confirms that it is reasonable for us to exclude the western part. The changing trend of elevation in the western part is −0.02 ± 0.14 m/year in fall or −0.12 ± 0.11 m/year in winter, which corresponds to a mass change of –0.04 ± 0.28 Gt/year or −0.24 ± 0.22 Gt/year. The changing trend of elevation in the eastern part is −0.44 m/year in both fall and winter (the uncertainties are 0.08 and 0.06 m/year, respectively), which corresponds to a mass change of −3.4 ± 0.8 Gt/year (hereafter we conservatively take the larger one). The counts for each footprint are displayed in the bottom plots in Figure 5. Our trend of −3.4 ± 0.8 Gt/year is quite different from the previous estimation of −5.4 ± 1.5 Gt/year (one standard deviation) by Farinotti et al. [6]. The large difference partly comes from the total area of glaciers: the eastern part has an area of ~8500 km2 and the western part has an area of ~2500 km2, making ~11,000 km2 in total; while Farinotti et al. [6] studied an area of about 13,700 km2, 20% larger. Even if our trend is amplified by 20% (−4.1 Gt/year), it still would be only three-fourths of that of Farinotti et al. [6] (−5.4 Gt/year). It is worth noting that our footprint count is roughly twice as large as that used by Farinotti et al. [6] (e.g., in winter of 2003, our count is about 3000, while theirs is about 1500). This might be caused by a more restrictive filtering stategy on the original data in their method. To sum up, with a narrower study area, albeit twofold more samples, we obtain a smaller glacier trend of −3.4 ± 0.8 Gt/year compared with −5.4 ± 2.9 Gt/year by Farinotti et al. [6].

3.3. Snow Coverage

The annual and seasonal mean of snow coverage from 2000 to 2015 by MODIS is shown in Figure 6. There is a clear annual variation that varies from the highest coverage ratio in winter to the lowest in summer over the entire region. The snow coverage has several features. First, the higher the latitude, the greater the amount of snow preserved in the warmer time period, and in summer, only a small quantity is retained on the mountaintops. Secondly, the snow coverage is obviously greater in the western and northern sides of the mountains, which is the windward side against the westerlies. Thirdly, it is clear that the snow coverage ratio is much higher on the northern side than on the southern side of Tianshan, i.e., there is hardly any snow covering over the entire Tarim basin throughout the year, while vast areas on the northern side of Tianshan have plentiful snowfall in winter. This clearly outlines the influence zone of the westerlies. The monthly variations in the mountain region and the lake area are specially presented in Figure 6. The mountain region has a more moderate annual variation compared with the lake area. Moreover, the peak month in the mountain region is one month later (i.e., February, compared with January in the lake area).
The time series of snow coverage in the Tianshan (only the mountain region is included) is shown in Figure 7. The pattern is dominated by strong annual and interannual variation with an inconspicuous secular trend. There are peak months in 2002 and 2011 and trough months in 2007 and 2013. It is worth noting that MODIS only provides the area change; without the change in thickness, we can not estimate the mass contribution. Assuming the snow has a density of 0.1 g/cm3 and the height change is 10 cm, then a variation of 1 × 105 km2 will cause a mass change of 1 Gt.

3.4. Time Series of All Factors in the Lake Area

Changes in lake level, precipitation, snow coverage, and the total mass of the lake area are shown in Figure 8. Two sets of dry and wet years are identified. Since different physical phenomena have different response speeds, the dry and wet years are shifted/shrunk in different observations. It seems that the AOI is inversely correlated with other phenomena, i.e., a negative AOI corresponds to a mass surplus. Therefore, in wet years, the AOI is negative and vice versa. The AOI, which indicates the variation in the westerlies, is the earliest to show the start of the dry and wet years. The changes in precipitation and snowfall follow this trend and bring the change to the total mass half a year later. The alternation of dry and wet years is also captured by the change in the lakes. There is a synchronous lake level increase in the start of 2010 in all lakes, but some lakes rise one year earlier (e.g., Issykkul and Kapchagayskoye, both of which are located in the western position), implying a faster response to the change in the westerlies.
After checking the AOI records back to 1950, it turns out that its value at the start of 2010 is the strongest in the last 65 years. The evolution of dry and wet years in these five datasets indicates that the westerlies are the cause, and affect the precipitation and snowfall; thus, the lake level and the total mass are subsequently influenced.

3.5. Water Level Change in Bosten Lake over 60 Years

Bosten Lake, the largest freshwater lake in Xinjiang, is located at the foot of Tianshan. Unlike the other lakes in the lake area, Bosten Lake involves intensive human activities, so it is a good example to show the combined influence of climate change and anthropogenic activities. Water level records of the Bosten Lake from three data sources are shown in Figure 9. The change in Bosten Lake level since 1955 can be separated into four stages: an accelerated drop of a total of 3.5 m from 1955 to 1985, a steady uplift of 4.5 m from 1986 to 2001, a rapid drop of 4.5 m from 2002 to 2010, and a fluctuation of 0.5 m around the mean level of 1045.5 m (Figure 9). The first stage is a result of decreasing runoff in Kaidu River along with increasing water consumption, and the condition was greatly exacerbated during 1976–1985 [45]. In the second stage, the exploitation of water resources was strictly curbed, and the contributions from precipitation and meltwater increased over time. At the end of the second stage, the runoff in Kaidu River was about 50% larger than its long-term average, and the water level in the Bosten Lake reached the highest on record with an area of 1646 km2. The third stage coincides with the period of the GRACE mission, which has produced a declining trend of −0.48 ± 0.02 Gt/year during 2003 to 2010, which can not be neglected in the estimated glacier trend of −4.0 Gt/year. The lake level reached the low water level of 1045 m in 1986 and has shown fluctuation ranging from 1045 m to 1046 m ever since.

4. Discussion

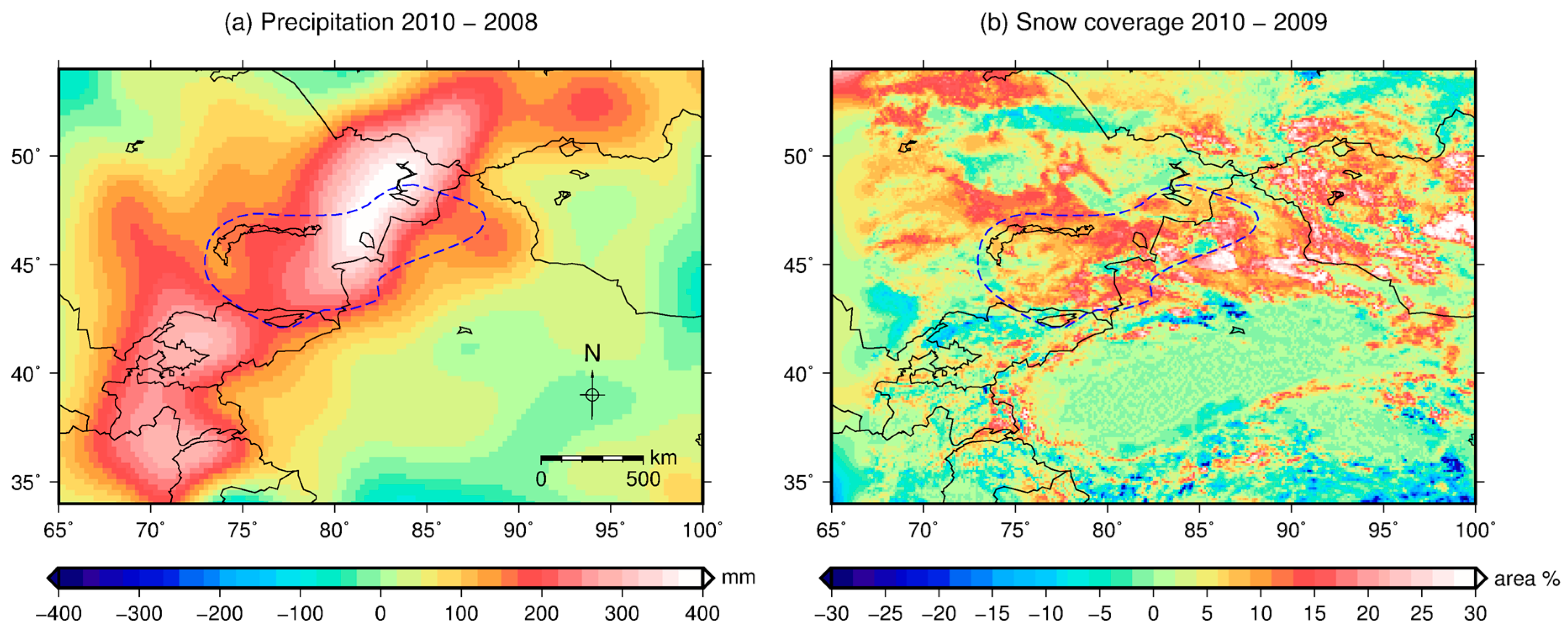
4.1. A Rapid Transition from a Dry Year (2009) to a Wet Year (2010)

4.1.1. Anomaly in the Total Mass

In the lake area, a rapid transition from 2009, a dry year, to 2010, a wet year, has been identified in all records (Figure 8). The difference of total mass between 2009 and 2010 was calculated to investigate the spatial range of the jump in 2010 (Figure 10). The mass is expressed in the format of equivalent water height measured in centimeters [29]. The results from the nine datasets are shown, and they share a high resemblance. Figure 10 also shows that the result is more influenced by the smoothing method than by the solution source. The method of G300+P4M6 is weaker than G300 because of the implementation of the extra decorrelation P4M6. DDK4 has the largest strength, which is likely due to the fact that the nonisostropic filter is more effective in preserving signals in the lower degrees than the Gaussian filter. The spatial range of the anomaly in 2010 coincides with the influence zone of the westerlies: It starts from the Pamir Plateau, spans northward along the Tianshan ridge, and exactly covers the lake areas outlined in this study. From Figure 8e and Figure 10, it is shown that the average jump in the whole lake area is about 7 cm and that the peak value is over 10 cm. It is interesting that the zone only covers the northern side of Tianshan, and the central region of Tianshan is less influenced. It is likely that the high mountain edges block the intrusion of the westerlies and constrain their impact mainly to the northern lower altitudes. If so, the central region of Tianshan is actually protected from the influence of the westerlies. However, the Pamir Plateau, the area in the forward position that blocks the westerlies, is overwhelmed by the westerlies despite its high altitudes. We have reported a five-year fluctuation in this intersection zone of the westerlies from the middle latitude and the Indian monsoon from the Indian Ocean, which is likely to be a combination effect of these two climatic forces [12].

4.1.2. Anomalies in Precipitation and Snowfall

The annual differences in precipitation and snowfall are also examined. Rainfall and snowpack are the main water supplies in our study region and are expected to be quite sensitive to the AOI. The precipitation increased in two steps from 2008 to 2010 (Figure 8c), so the difference between 2008 and 2010 is shown here (Figure 11a). An advance of one year is reasonable because it will take time for the change in precipitation to affect the mass change. We have separately checked the difference between 2009 and 2010 as well as between 2008 and 2009, and the results show that the anomaly zone was first located in the Pamir Plateau during 2008–2009, and is then shifted subsequently to the lake area during 2009–2010 (not shown here). This dynamic change is consistent with the blowing direction of the westerlies. The precipitation anomaly zone is identical to the anomaly zone in the total mass (Figure 10). The annual precipitation in this region is about 1000 mm, and the annual anomalies are generally less than 50 mm (Figure 8c). However, the jump from 2008 to 2010 can reach 400 mm, so this is a major event in the climatic change in this region.
The annual difference in snow coverage between 2009 and 2010 is shown in Figure 11b. The anomaly zone is also located in the lake area. The high altitudes of the Tianshan as well as the Pamir Plateau are less impacted by this snow anomaly. One possible reason is that the snow coverage ratio is already very high in the high altitudes, so further increases are limited. Compared with the anomaly zone of the total mass, the precipitation anomaly has a higher similarity than the snow in the spatial pattern, which implies that precipitation is a primary impact factor.

4.2. Water Level Change in the Bosten Lake and the Glacier Change

Bosten Lake is the end of the Kaidu River and is also the source of the Konqi River (inset in Figure 9). Recharge from the Kaidu River accounts for 84.7% of the influx to the Bosten Lake [46]. The correlation coefficient between the change in the Kaidu River flow and the variation in the Bosten Lake level is 0.45 between 1961–2009 and 0.70 between 1986–2009 [47]. Therefore, undertanding changes in the Kaidu River is vital in the explanation of the changes in the Bosten Lake level. The Kaidu River originates from the center of the Tianshan, extends around the glaciers, and is mainly fed by precipitation and meltwater from snow and glaciers. The long-term average supply from meltwater is 15.2% [45].
Wang et al. [48] observed a declining trend in the Bosten Lake level during 2003–2009 based on ICESat data and claimed that it was probably caused by: (1) increasing water demand from the growing population and irrigation; (2) decreasing runoff recharge in the branches; (3) less precipitation in warm seasons; and (4) a higher temperature in warm seasons and thus a higher evaporation. Qiu et al. [47] checked the relationship between the change in runoff at the Dashankou station in the upper reach of the Kaidu River (protected from anthropogenic activities) and records of precipitation and temperature. Their work shows that the change in runoff has a closer relationship with change in temperature (0.55) than with precipitation (0.34). A warmer and wetter period during 1990–2002 was obviously responsible for the increased runoff in the Kaidu River. Afterwards, the precipitation went back to normal, but the temperature continued to rise. A consequent seriously retreating snowline has been observed, and it has been declared to be the main reason for the fast reducing runoff in the Kaidu River, which has been further decreased by the emerging hydropower stations upstream, according to a local report [49]. The report also pointed out that another problem is the over-exploitation of water resources, including mining, industry development, the expansion of farm land, and well digging. From 1949 to 2012, the population in the basin has increased threefold, and the cultivated land has increased fivefold [50].
Bosten Lake is a good example that shows how glacier melting will impact the local environment and economy. There is a benefit in the short run because of the extra water supply from melting snow and glaciers. This may create a false impression that the environment is improving and its supportive capacity is increasing. As a result, the relevant policies may be implemented more flexibly and the water consumption will rise. There is always a time lag in the response to adaptation. Once the extra supplement passes the peak and begins decreasing again, the increased water usage will seriously harm the local water resource. In the example of Bosten Lake, it only took eight years for the lake level to go from the best on record to the worst on record.

5. Conclusions

Glacier mass change in the Tianshan was estimated with GRACE data and ICESat data. The glaciers are divided into central, northern, and western parts according to spatial distribution. There are three main conclusions.
Firstly, there was a rapid transition from 2009, a dry year, to 2010, a wet year, and this phenomenon can be simultaneously found in the lake levels, snow coverage, precipitation, and total water mass. Furthermore, there is good consistency of spatial coverage in all these factors. The transition originated in the Pamir Plateau and extended eastward along the northern edge of Tianshan but is absent in central Tianshan. The change is likely caused by changes in the westerlies, and the AOI at the start of 2010 is the strongest over the last 65 years.
Secondly, glacier melting is concentrated in the central Tianshan, and the western part of the Tianshan demonstrates very little glacier mass change. After excluding the western and northern parts, which are polluted by the strong interannual variation caused by the varying westerlies, the central region of Tianshan shows a steady changing trend, which is −4.0 ± 0.7 Gt/year during 2003–2014 according to GRACE and −3.4 ± 0.8 Gt/year during 2003–2009 according to ICESat. Our results show a smaller mass loss and have better linearity compared with previous estimates.
Thirdly, we discussed how climate change and anthropogenic activities influence the water level of Bosten Lake. We demonstrate that the impact of climate change on the environment of Bosten Lake varies at different stages. Rising temperature benefited Bosten Lake during 1987–2002 along with the increasing precipitation, but has degraded its condition ever since due to the fast retreating snowline.

Acknowledgments

This research was supported financially by the NNSFC (41331066, and 41474059), the CAS/CAFEA program (KZZD-EW-TZ-19), and Key Research Program of Frontier Sciences CAS: QYZDY-SSW-SYS003.

Author Contributions

S.Y. and W.S. conceived and designed the experiments; S.Y. performed the experiments; Q.W. analyzed the ICESat data; L.C. analyzed the MODIS data; and S.Y. and W.S. wrote the paper.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:
GRACEGravity Recovery and Climate Experiment
MODISmoderate-resolution imaging spectroradiometer
AOIArctic oscillation index
SRTMShuttle Radar Topography Mission
GLIMSGlobal Land Ice Measurements from Space
GPCPGlobal Precipitation Climatology Project
CSRCenter for Space Research
GFZGeoForschungsZentrum
JPLJet Propulsion Laboratory

References

  1. Stocker, T.F.; Qin, D.; Plattner, G.K.; Tignor, M.; Allen, S.K.; Boschung, J.; Nauels, A.; Xia, Y.; Bex, V.; Midgley, P.M. Climate Change 2013: The Physical Science Basis; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014. [Google Scholar]
  2. Jacob, T.; Wahr, J.; Pfeffer, W.T.; Swenson, S. Recent contributions of glaciers and ice caps to sea level rise. Nature 2012, 482, 514–518. [Google Scholar] [CrossRef] [PubMed]
  3. Chen, J.L.; Wilson, C.R.; Blankenship, D.; Tapley, B.D. Accelerated antarctic ice loss from satellite gravity measurements. Nat. Geosci. 2009, 2, 859–862. [Google Scholar] [CrossRef]
  4. Velicogna, I.; Wahr, J. Acceleration of Greenland ice mass loss in spring 2004. Nature 2006, 443, 329–331. [Google Scholar] [CrossRef] [PubMed]
  5. Bolch, T.; Kulkarni, A.; Kaab, A.; Huggel, C.; Paul, F.; Cogley, J.G.; Frey, H.; Kargel, J.S.; Fujita, K.; Scheel, M.; et al. The state and fate of Himalayan glaciers. Science 2012, 336, 310–314. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  6. Farinotti, D.; Longuevergne, L.; Moholdt, G.; Duethmann, D.; Mölg, T.; Bolch, T.; Vorogushyn, S.; Güntner, A. Substantial glacier mass loss in the tien shan over the past 50 years. Nat. Geosci. 2015. [Google Scholar] [CrossRef]
  7. Gardner, A.S.; Moholdt, G.; Cogley, J.G.; Wouters, B.; Arendt, A.A.; Wahr, J.; Berthier, E.; Hock, R.; Pfeffer, W.T.; Kaser, G.; et al. A reconciled estimate of glacier contributions to sea level rise: 2003 to 2009. Science 2013, 340, 852–857. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  8. Matsuo, K.; Heki, K. Time-variable ice loss in Asian high mountains from satellite gravimetry. Earth Planet. Sci. Lett. 2010, 290, 30–36. [Google Scholar] [CrossRef]
  9. Yao, T.; Thompson, L.; Yang, W.; Yu, W.; Gao, Y.; Guo, X.; Yang, X.; Duan, K.; Zhao, H.; Xu, B.; et al. Different glacier status with atmospheric circulations in Tibetan Plateau and surroundings. Nat. Clim. Chang. 2012, 2, 663–667. [Google Scholar] [CrossRef]
  10. Immerzeel, W.W.; van Beek, L.P.; Bierkens, M.F. Climate change will affect the Asian water towers. Science 2010, 328, 1382–1385. [Google Scholar] [CrossRef] [PubMed]
  11. Shi, Y.; Shen, Y.; Kang, E.; Li, D.; Ding, Y.; Zhang, G.; Hu, R. Recent and future climate change in northwest China. Clim. Chang. 2006, 80, 379–393. [Google Scholar] [CrossRef]
  12. Bolch, T.; Buchroithner, M.; Pieczonka, T.; Kunert, A. Planimetric and volumetric glacier changes in the Khumbu Himal, Nepal, since 1962 using Corona, Landsat TM and ASTER data. J. Glaciol. 2008, 54, 592–600. [Google Scholar] [CrossRef]
  13. Andreassen, L.M.; Paul, F.; Kääb, A.; Hausberg, J.E. Landsat-derived glacier inventory for Jotunheimen, Norway, and deduced glacier changes since the 1930s. Cryosphere 2008, 2, 131–145. [Google Scholar] [CrossRef] [Green Version]
  14. Gardelle, J.; Berthier, E.; Arnaud, Y. Slight mass gain of Karakoram glaciers in the early twenty-first century. Nat. Geosci. 2012, 5, 322–325. [Google Scholar] [CrossRef]
  15. Gardelle, J.; Berthier, E.; Arnaud, Y.; Kääb, A. Region-wide glacier mass balances over the Pamir-Karakoram-Himalaya during 1999–2011. Cryosphere 2013, 7, 1263–1286. [Google Scholar] [CrossRef] [Green Version]
  16. Kääb, A.; Berthier, E.; Nuth, C.; Gardelle, J.; Arnaud, Y. Contrasting patterns of early twenty-first-century glacier mass change in the Himalayas. Nature 2012, 488, 495–498. [Google Scholar] [CrossRef] [PubMed]
  17. Bolch, T.; Sørensen, L.S.; Simonssen, S.B.; Mölg, N.; Machguth, H.; Rastner, P.; Paul, F. Mass loss of Greenland’s glaciers and ice caps 2003–2008 revealed from ICESat laser altimetry data. Geophys. Res. Lett. 2013, 40, 875–881. [Google Scholar] [CrossRef] [Green Version]
  18. Neckel, N.; Kropáček, J.; Bolch, T.; Hochschild, V. Glacier mass changes on the Tibetan Plateau 2003–2009 derived from ICESat laser altimetry measurements. Environ. Res. Lett. 2014, 9, 014009. [Google Scholar] [CrossRef]
  19. Yi, S.; Sun, W. Evaluation of glacier changes in high-mountain Asia based on 10 year grace rl05 models. J. Geophys. Res. Solid Earth 2014, 119, 2504–2517. [Google Scholar] [CrossRef]
  20. Tapley, B.D.; Bettadpur, S.; Ries, J.C.; Thompson, P.F.; Watkins, M.M. Grace measurements of mass variability in the earth system. Science 2004, 305, 503–505. [Google Scholar] [CrossRef] [PubMed]
  21. Yi, S.; Wang, Q.; Sun, W. Basin mass dynamic changes in China from GRACE based on a multibasin inversion method. J. Geophys. Res. Solid Earth 2016, 121. [Google Scholar] [CrossRef]
  22. Yi, S.; Sun, W. Characteristics of gravity signal and loading effect in China. Geod. Geodyn. 2015, 6, 280–285. [Google Scholar] [CrossRef]
  23. Zhao, Q.; Wu, W.; Wu, Y. Variations in China’s terrestrial water storage over the past decade using grace data. Geod. Geodyn. 2015, 6, 187–193. [Google Scholar] [CrossRef]
  24. Yi, S.; Sun, W.; Heki, K.; Qian, A. An increase in the rate of global mean sea level rise since 2010. Geophys. Res. Lett. 2015, 42, 3998–4006. [Google Scholar] [CrossRef]
  25. Chen, J.; Wilson, C.; Tapley, B. Contribution of ice sheet and mountain glacier melt to recent sea level rise. Nat. Geosci. 2013, 6, 549–552. [Google Scholar] [CrossRef]
  26. Barthelmes, F.; Köhler, W. International Centre for Global Earth Models (ICGEM). J. Geod. 2012, 86, 932–934. [Google Scholar]
  27. Swenson, S.; Chambers, D.; Wahr, J. Estimating geocenter variations from a combination of grace and ocean model output. J. Geophys. Res. Solid Earth (1978–2012) 2008, 113. [Google Scholar] [CrossRef]
  28. Cheng, M.; Ries, J.C.; Tapley, B.D. Variations of the Earth’s figure axis from satellite laser ranging and GRACE. J. Geophys. Res. Solid Earth (1978–2012) 2011, 116. [Google Scholar] [CrossRef]
  29. Wahr, J.; Molenaar, M.; Bryan, F. Time variability of the Earth’s gravity field: Hydrological and oceanic effects and their possible detection using GRACE. J. Geophys. Res. Solid Earth 1998, 103, 30205–30229. [Google Scholar] [CrossRef]
  30. Swenson, S.; Wahr, J. Post-processing removal of correlated errors in GRACE data. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
  31. Kusche, J.; Schmidt, R.; Petrovic, S.; Rietbroek, R. Decorrelated GRACE time-variable gravity solutions by GFZ, and their validation using a hydrological model. J. Geod. 2009, 83, 903–913. [Google Scholar] [CrossRef]
  32. Hansen, P.C.; O’Leary, D.P. The use of the L-curve in the regularization of discrete ill-posed problems. SIAM J. Sci. Comput. 1993, 14, 1487–1503. [Google Scholar] [CrossRef]
  33. GLIMS: Global Land Ice Measurements from Space. Available online: http://www.glims.org/glimsblurb.html (accessed on 21 September 2016).
  34. Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The shuttle radar topography mission. Rev. Geophys. 2007, 45. [Google Scholar] [CrossRef]
  35. Huss, M. Density assumptions for converting geodetic glacier volume change to mass change. Cryosphere 2013, 7, 877–887. [Google Scholar] [CrossRef]
  36. Global Reservoirs/Lakes (G-REALM). Available online: http://www.pecad.fas.usda.gov/cropexplorer/global_reservoir/ (accessed on 21 September 2016).
  37. Crétaux, J.-F.; Jelinski, W.; Calmant, S.; Kouraev, A.; Vuglinski, V.; Bergé-Nguyen, M.; Gennero, M.-C.; Nino, F.; Rio, R.A.D.; Cazenave, A.; et al. SOLS: A lake database to monitor in the Near Real Time water level and storage variations from remote sensing data. Adv. Space Res. 2011, 47, 1497–1507. [Google Scholar] [CrossRef]
  38. Hall, D.; Salomonson, V.; Riggs, G. Modis/Terra Snow Cover Daily l3 Global 500 m Grid, 5th ed.; National Snow and Ice Data Center: Boulder, CO, USA, 2006. [Google Scholar]
  39. MODIS/Terra Snow Cover Monthly L3 Global 0.05Deg CMG, Version 6. Available online: http://nsidc.org/data/MOD10CM (accessed on 21 September 2016).
  40. Rodell, M.; Houser, P.R.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The global land data assimilation system. Bull. Am. Meteorol. Soc. 2004, 85. [Google Scholar] [CrossRef]
  41. Adler, R.F.; Huffman, G.J.; Chang, A.; Ferraro, R.; Xie, P.P.; Janowiak, J.; Rudolf, B.; Schneider, U.; Curtis, S.; Bolvin, D.; et al. The version-2 global precipitation climatology project (GPCP) monthly precipitation analysis (1979-present). J. Hydrometeorol. 2003, 4, 1147–1167. [Google Scholar] [CrossRef]
  42. PSD Gridded Climate Datasets: Precipitation. Available online: http://www.esrl.noaa.gov/psd/data/gridded/tables/precipitation.html (accessed on 21 September 2016).
  43. Thompson, D.W.; Wallace, J.M. The arctic oscillation signature in the wintertime geopotential height and temperature fields. Geophys. Res. Lett. 1998, 25, 1297–1300. [Google Scholar] [CrossRef]
  44. Daily Arctic Oscillation Index. Available online: http://www.cpc.ncep.noaa.gov/products/precip/CWlink/daily_ao_index/ao_index.html (accessed on 21 September 2016).
  45. Li, Y.-A.; Tan, Y.; Jiang, F. Study on Hydrological Features of the Kaidu River and the Bosten Lake in the Second Half of 20th Century. J. Glaciol. Geocryol. 2003, 25, 215–218. [Google Scholar]
  46. Sun, Z.; Wang, R.; Huang, Q. Comparison of water level changes during the past 20 years between Daihai and Bositen Lakes. J. Arid Land Resour. Environ. 2006, 20, 56–60. [Google Scholar]
  47. Qiu, H.; Zhao, Q.; Zhu, W.; Tao, R.; Qian, H. Analysis of the Bosten lake’s level and its possible mechanism. J. Meteorol. Sci. 2013, 33, 289–295. [Google Scholar]
  48. Wang, X.; Gong, P.; Zhao, Y.; Xu, Y.; Cheng, X.; Niu, Z.; Luo, Z.; Huang, H.; Sun, F.; Li, X. Water-level changes in China’s large lakes determined from ICESat/GLAS data. Remote Sens. Environ. 2013, 132, 131–144. [Google Scholar] [CrossRef]
  49. Saving Bosten Lake. Available online: http://news.ts.cn/content/2014-04/14/content_9549017_all.htm (accessed on 21 September 2016). (In Chinese)
  50. Wang, J.; Chen, Y.-N.; Chen, Z.-S. Quantitative assessment of climate change and human activities impact the inflowing runoff of Bosten Lake. Xinjiang Agric. Sci. 2012, 49, 581–587. [Google Scholar]
Remotesensing 08 00798 g001 550
Figure 1. The negative gravity trend in the Tianshan. The white areas represent the location of glaciers and the red dots represent the footprint of ICESat. The violet patches represent the location of lakes, and their names are annotated. The gray dashed curve marks the scope of lake area.
Figure 1. The negative gravity trend in the Tianshan. The white areas represent the location of glaciers and the red dots represent the footprint of ICESat. The violet patches represent the location of lakes, and their names are annotated. The gray dashed curve marks the scope of lake area.
Remotesensing 08 00798 g001
Remotesensing 08 00798 g002 550
Figure 2. Presentation of results of from the inversion method used in this study: (a) There are nine mascons defined according to the glacier distributions (gray dots), and they are labeled with different colors; (b) The L-curve, which represents the relation between the model complexity and the fit to the data, with the variation in the regularization factor. The values annotated are the exponential item of each factor; (c) The gravity trend in the form of equivalent water height (EWH) observed by the GRACE project, with a Gaussian filter of 300 km; (d) The gravity trend from the inversion model; (e) The recovered mass change by the inversion method. Note the larger color scale; (f) Post-fit residuals between the observation and inversion.
Figure 2. Presentation of results of from the inversion method used in this study: (a) There are nine mascons defined according to the glacier distributions (gray dots), and they are labeled with different colors; (b) The L-curve, which represents the relation between the model complexity and the fit to the data, with the variation in the regularization factor. The values annotated are the exponential item of each factor; (c) The gravity trend in the form of equivalent water height (EWH) observed by the GRACE project, with a Gaussian filter of 300 km; (d) The gravity trend from the inversion model; (e) The recovered mass change by the inversion method. Note the larger color scale; (f) Post-fit residuals between the observation and inversion.
Remotesensing 08 00798 g002
Remotesensing 08 00798 g003 550
Figure 3. (a) Time series of the total mass of all mascons. The dashed ellipse indicates a large jump from 2009 to 2010; (b) Time series of the mass of each mascon with their numbers on the left side. The jumps from 2009 to 2010 are also marked by dashed ellipses. The other series without such jumps are marked by a star on the right side, and their sum is presented in (c). The linearity of the time series is greatly improved in (c).
Figure 3. (a) Time series of the total mass of all mascons. The dashed ellipse indicates a large jump from 2009 to 2010; (b) Time series of the mass of each mascon with their numbers on the left side. The jumps from 2009 to 2010 are also marked by dashed ellipses. The other series without such jumps are marked by a star on the right side, and their sum is presented in (c). The linearity of the time series is greatly improved in (c).
Remotesensing 08 00798 g003
Remotesensing 08 00798 g004 550
Figure 4. (a) Time series of the glacier mass with influences from soil moisture and lake water corrected. The values and uncertainties are based on the nine datasets shown in the bottom plot; (b) Trends of glacier mass from nine datasets (blue) and their mean (red). “CSR_G300+P4M6” means the solution comes from CSR and the smoothing method is a combination of the Gaussian smoothing in 300 km and the deccorelation filter of P4M6.
Figure 4. (a) Time series of the glacier mass with influences from soil moisture and lake water corrected. The values and uncertainties are based on the nine datasets shown in the bottom plot; (b) Trends of glacier mass from nine datasets (blue) and their mean (red). “CSR_G300+P4M6” means the solution comes from CSR and the smoothing method is a combination of the Gaussian smoothing in 300 km and the deccorelation filter of P4M6.
Remotesensing 08 00798 g004
Remotesensing 08 00798 g005 550
Figure 5. Time series of glacier elevation change by ICESat in (a) the western Tianshan and (b) the eastern Tianshan. The trends are fitted in different seasons to reduce the influence from annual variation. The series on land provide references that are not expected to change with time. The footprint count in each sample is shown in the bottom plots.
Figure 5. Time series of glacier elevation change by ICESat in (a) the western Tianshan and (b) the eastern Tianshan. The trends are fitted in different seasons to reduce the influence from annual variation. The series on land provide references that are not expected to change with time. The footprint count in each sample is shown in the bottom plots.
Remotesensing 08 00798 g005
Remotesensing 08 00798 g006 550
Figure 6. Annual and seasonal mean of snow coverage in percentage by MODIS in the Tianshan area and the lake areas (the dashed curves). Spring is from November to January and so forth.
Figure 6. Annual and seasonal mean of snow coverage in percentage by MODIS in the Tianshan area and the lake areas (the dashed curves). Spring is from November to January and so forth.
Remotesensing 08 00798 g006
Remotesensing 08 00798 g007 550
Figure 7. Annual and monthly anomalies in snow coverage in the Tianshan. The average snow coverage over the whole period is deducted.
Figure 7. Annual and monthly anomalies in snow coverage in the Tianshan. The average snow coverage over the whole period is deducted.
Remotesensing 08 00798 g007
Remotesensing 08 00798 g008 550
Figure 8. (a) Time series of lake levels; (b) arctic oscillation index (AOI); (c) Precipitation; (d) Snow coverage; and (e) Total mass in the lake area. The yellow patches represent dry seasons and the green represent wet seasons. In (a), the lake levels are amplified to a comparable scale, and each scaling is shown in the bracket after its name. One-year smoothing means using a one-year running window to smooth the monthly data. The one-year smoothed series in (b) are amplified three times for a better presentation.
Figure 8. (a) Time series of lake levels; (b) arctic oscillation index (AOI); (c) Precipitation; (d) Snow coverage; and (e) Total mass in the lake area. The yellow patches represent dry seasons and the green represent wet seasons. In (a), the lake levels are amplified to a comparable scale, and each scaling is shown in the bracket after its name. One-year smoothing means using a one-year running window to smooth the monthly data. The one-year smoothed series in (b) are amplified three times for a better presentation.
Remotesensing 08 00798 g008
Remotesensing 08 00798 g009 550
Figure 9. Change of the lake level in Bosten Lake over the last 60 years. The time series reference three data sources, Shi et al. [11], LEGOS, and USDA. The declining trend from 2003 to 2010 is fitted in the black dashed line, whose trend is also annotated. The explanations (light red background) and information (light green background) of the change in series are annotated. The environment of the Bosten Lake and three large rivers is shown in the inset.
Figure 9. Change of the lake level in Bosten Lake over the last 60 years. The time series reference three data sources, Shi et al. [11], LEGOS, and USDA. The declining trend from 2003 to 2010 is fitted in the black dashed line, whose trend is also annotated. The explanations (light red background) and information (light green background) of the change in series are annotated. The environment of the Bosten Lake and three large rivers is shown in the inset.
Remotesensing 08 00798 g009
Remotesensing 08 00798 g010 550
Figure 10. Difference in total mass between 2009 and 2010 by nine GRACE datasets. The scope of lake area is indicated by the dashed curve.
Figure 10. Difference in total mass between 2009 and 2010 by nine GRACE datasets. The scope of lake area is indicated by the dashed curve.
Remotesensing 08 00798 g010
Remotesensing 08 00798 g011 550
Figure 11. (a) The difference in precipitation amount between 2008 and 2010; and (b) the difference in snow coverage between 2009 and 2010. The scope of the lake area is indicated by the dashed curve.
Figure 11. (a) The difference in precipitation amount between 2008 and 2010; and (b) the difference in snow coverage between 2009 and 2010. The scope of the lake area is indicated by the dashed curve.
Remotesensing 08 00798 g011
Table
Table 1. Information about the glaciers in each mascon.
Table 1. Information about the glaciers in each mascon.
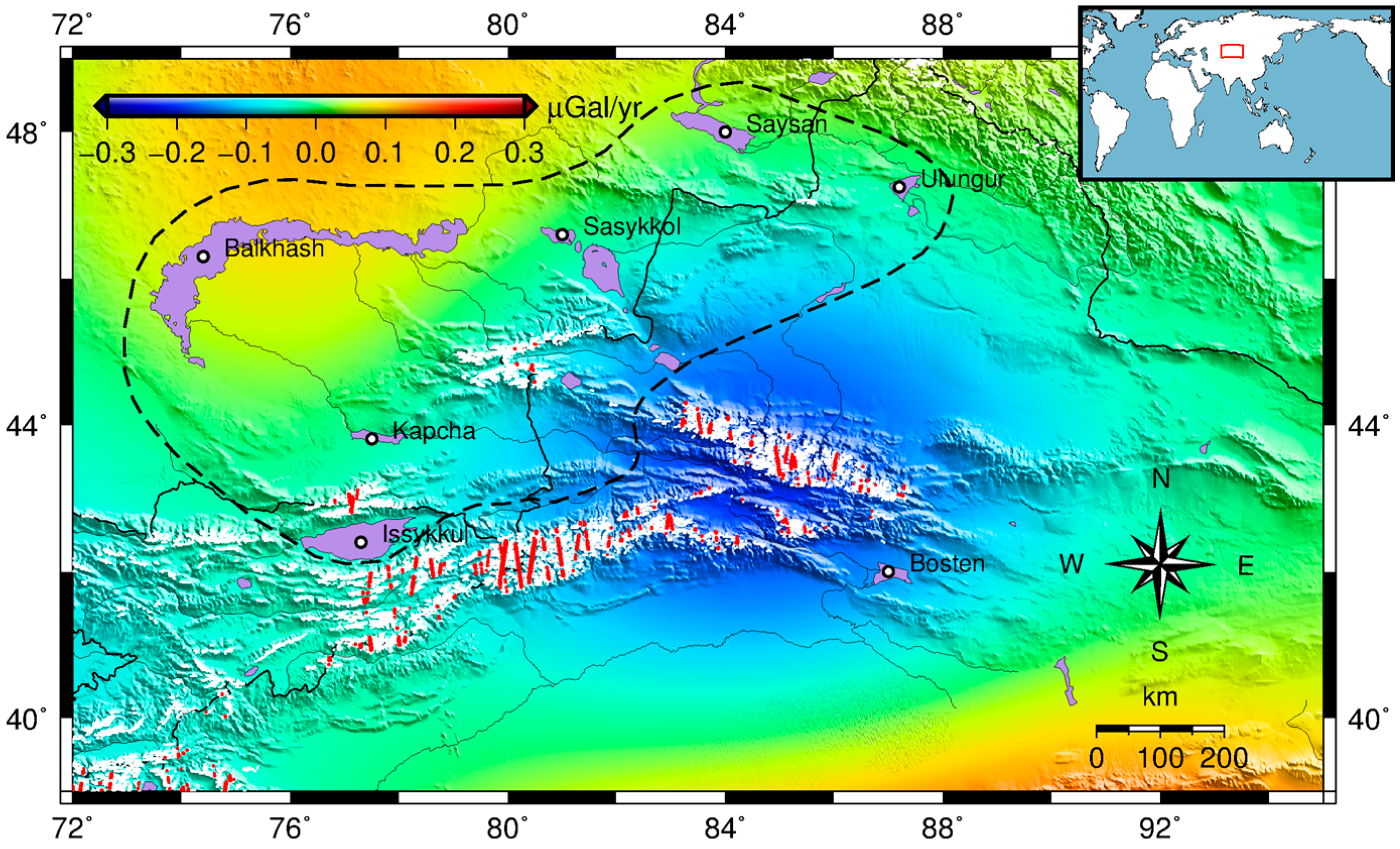
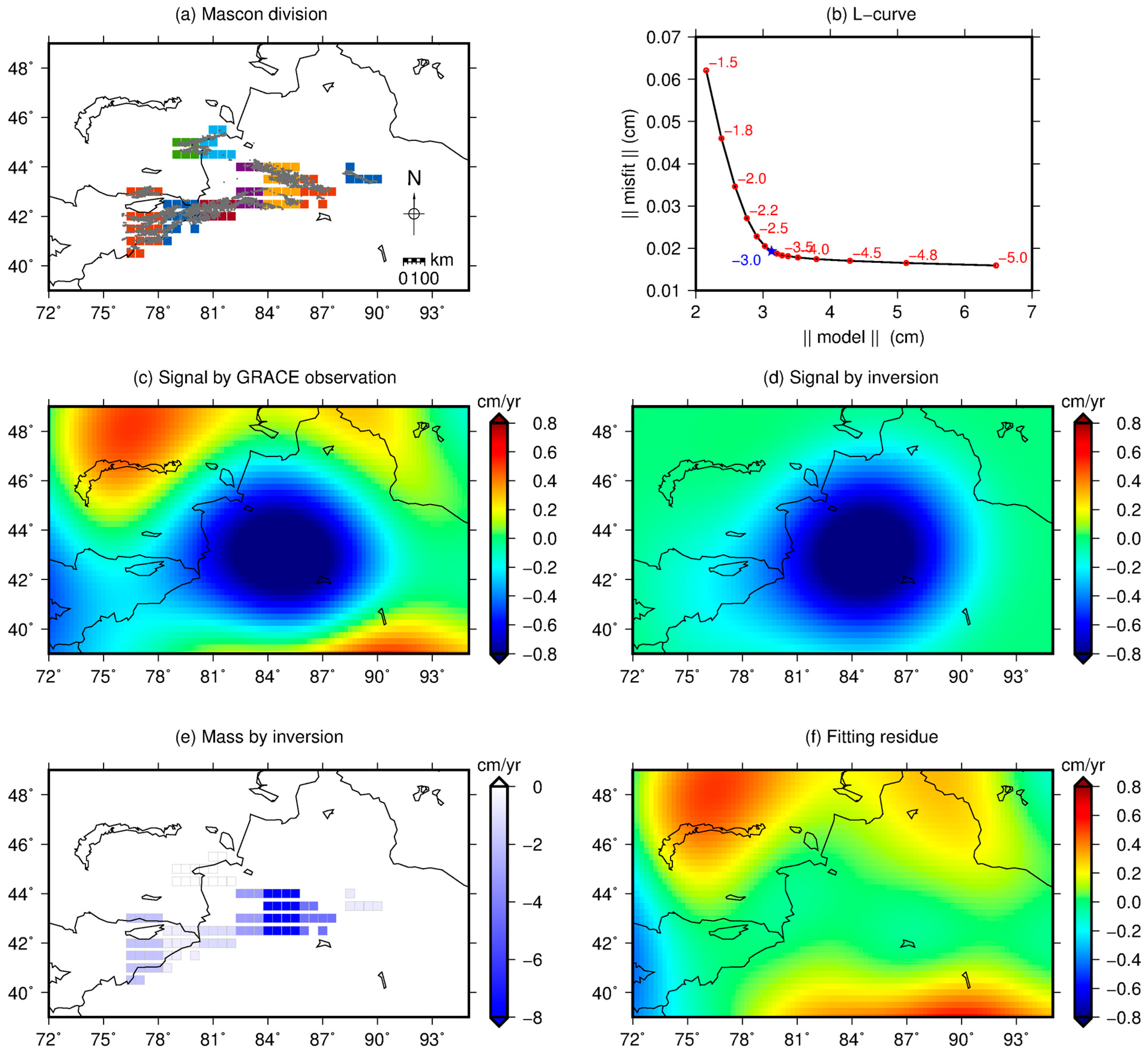
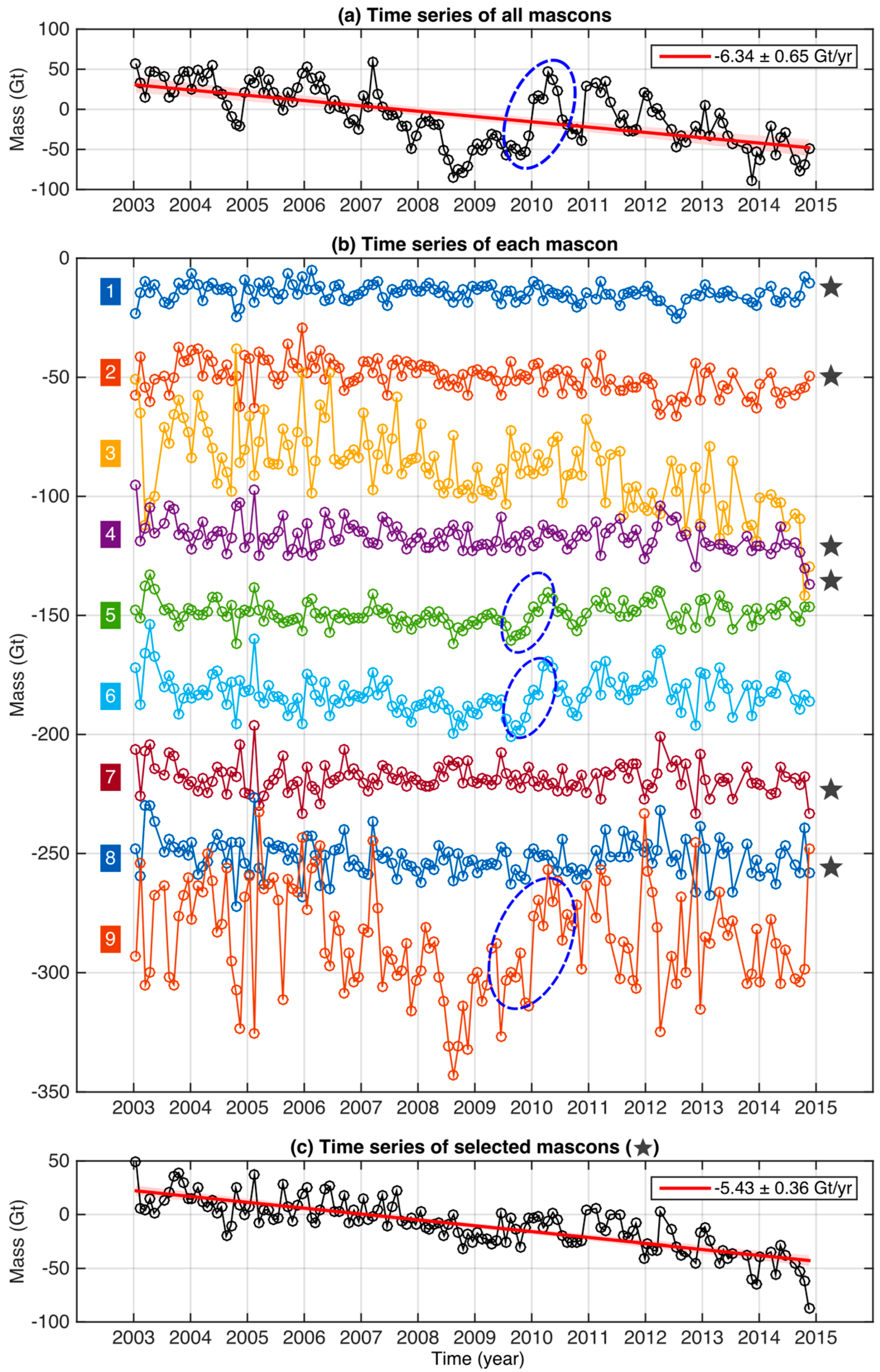
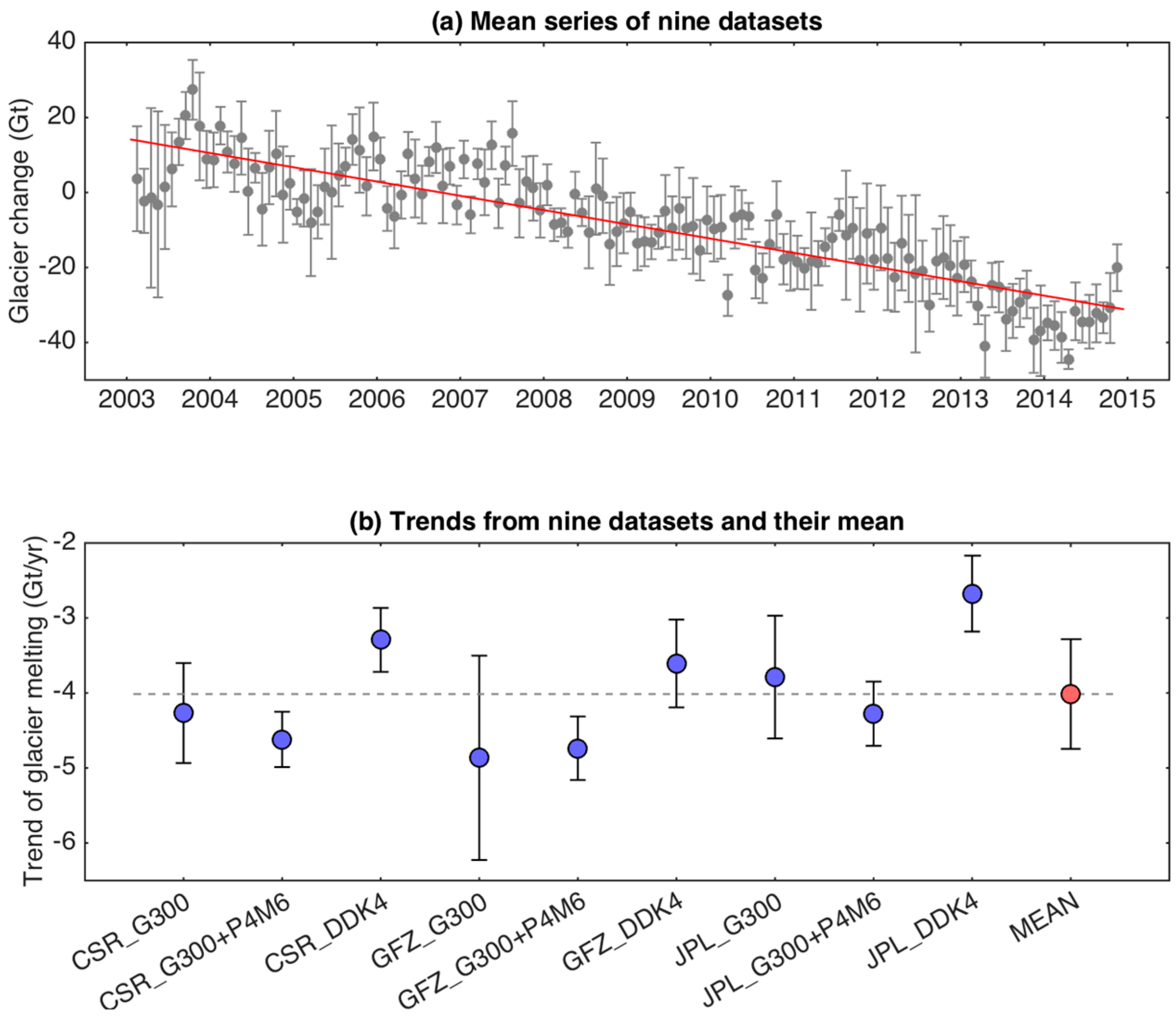
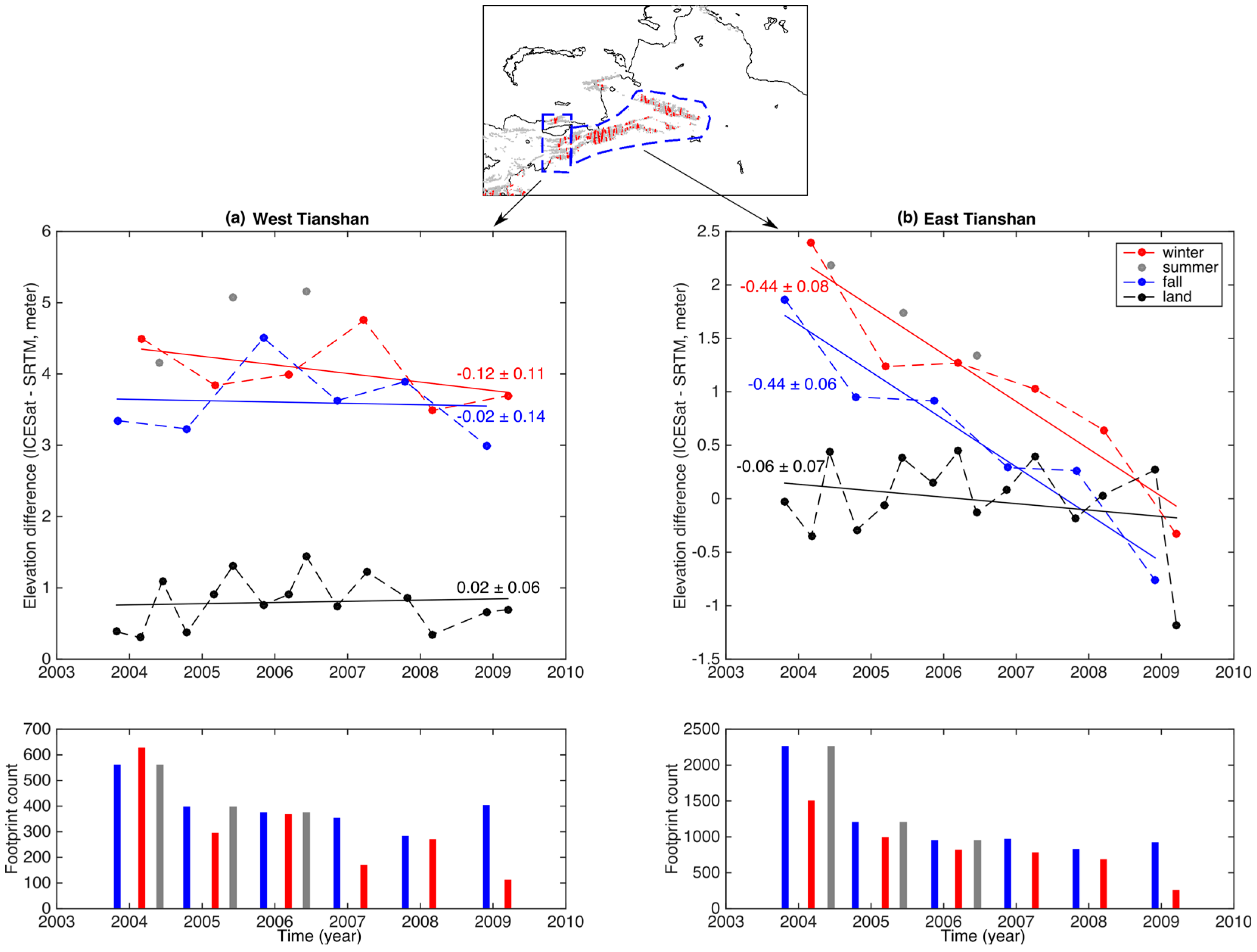
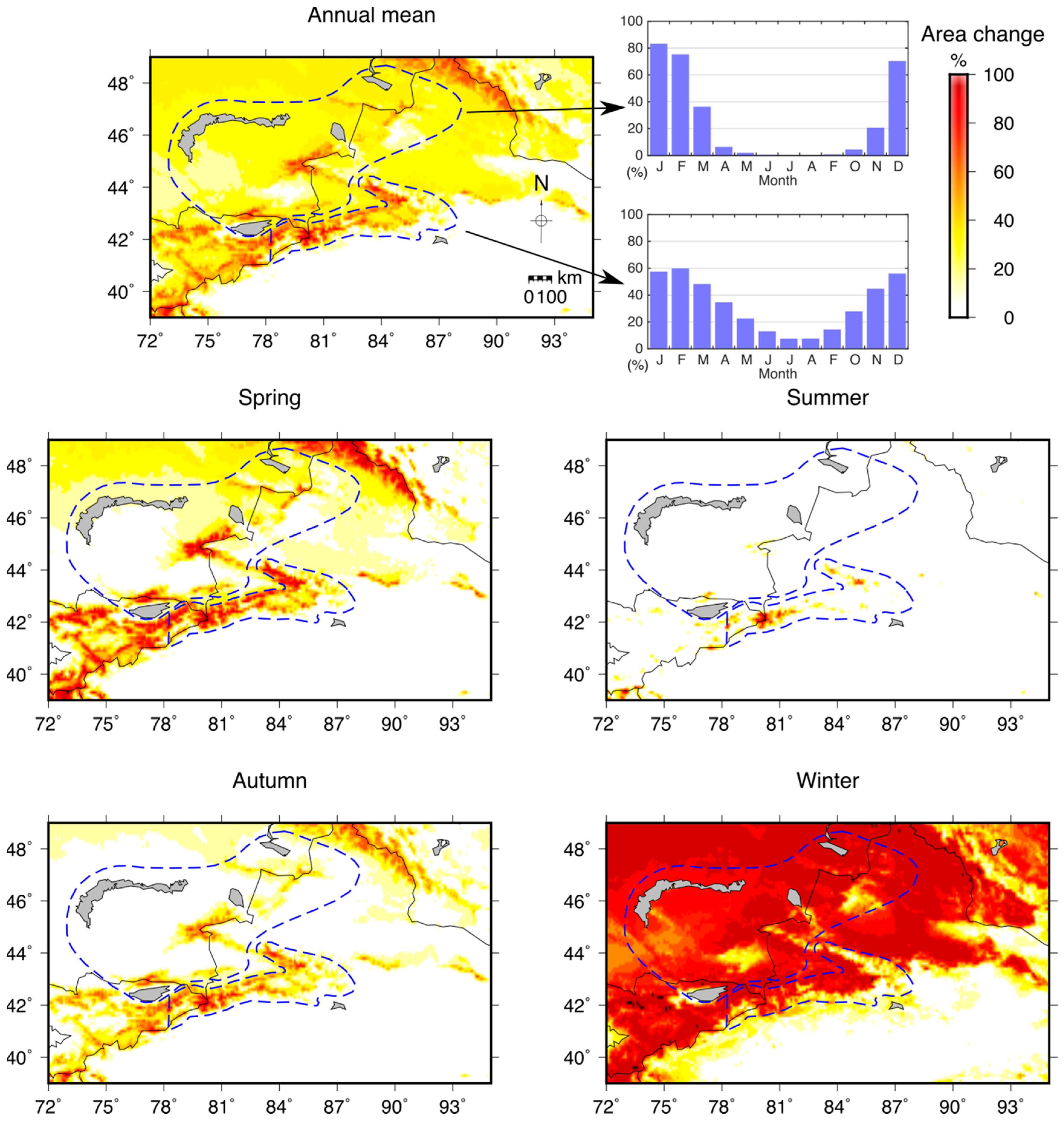
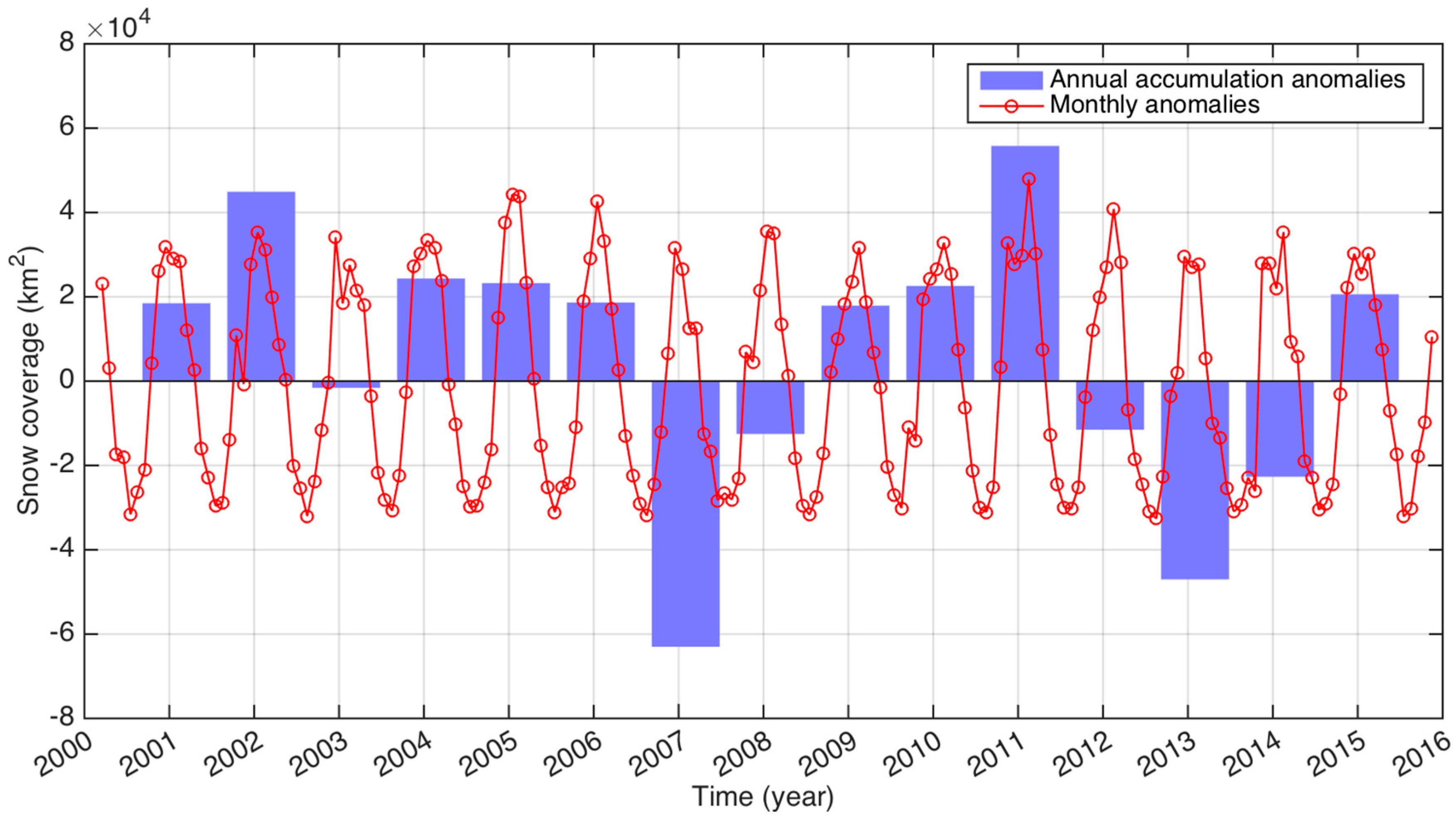
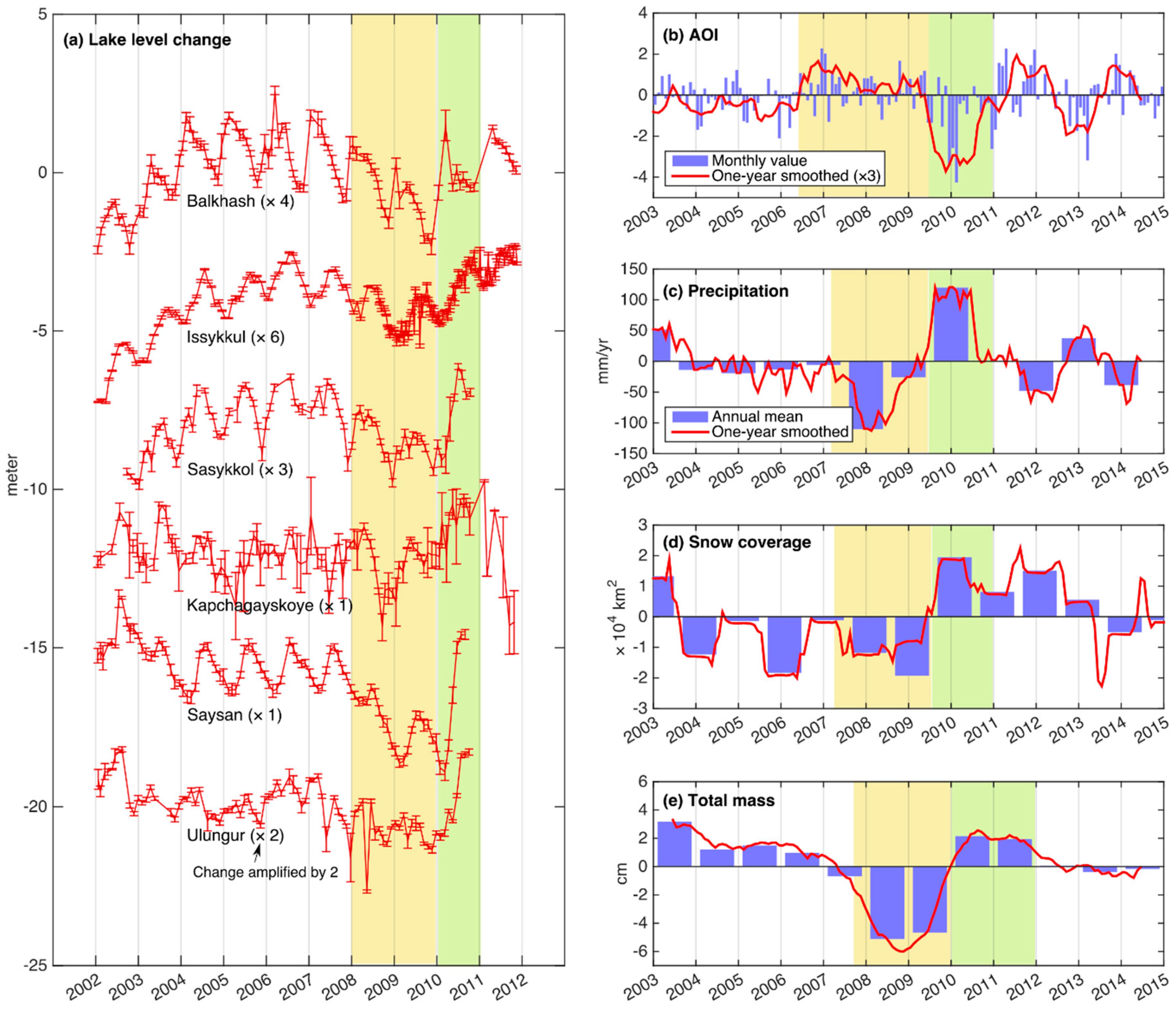
RegionNumber of GlaciersArea (km2)Mean Elevation (m)
1360150.823750
21000304.034015
324261568.114015
41045584.233829
57334.543671
6271111.173754
718093475.324109
813503146.34402
920331608.64310
Table
Table 2. List of all datasets.
Table 2. List of all datasets.
DataTime PeriodSpatial ResolutionTargetAnnotation
GRACE2003–2014~300 kmTotal mass and glaciersInversion method is adopted to estimate the total mass change in the central Tianshan.
ICESat2003–200970 mGlaciersMean elevation is obtained to estimate the total mass change in the central Tianshan.
Altimetry2002–2010/2011Several kilometersLake levelLake level record of the Bosten Lake is extended by site observations.
MODIS2000–20150.05°Snow coverageOnly fraction of coverage is available.
GLDAS2003–20141°Soil moisture and snow volumeThere are four models.
GPCP2003–20142.5°PrecipitationThe dataset is interpolated to a finer resolution of 1° × 1°.
AOI1950–2014N/AWesterliesAOI is an indicator of the westerlies.

Share and Cite

MDPI and ACS Style

Yi, S.; Wang, Q.; Chang, L.; Sun, W. Changes in Mountain Glaciers, Lake Levels, and Snow Coverage in the Tianshan Monitored by GRACE, ICESat, Altimetry, and MODIS. Remote Sens. 2016, 8, 798. https://doi.org/10.3390/rs8100798

AMA Style

Yi S, Wang Q, Chang L, Sun W. Changes in Mountain Glaciers, Lake Levels, and Snow Coverage in the Tianshan Monitored by GRACE, ICESat, Altimetry, and MODIS. Remote Sensing. 2016; 8(10):798. https://doi.org/10.3390/rs8100798

Chicago/Turabian Style

Yi, Shuang, Qiuyu Wang, Le Chang, and Wenke Sun. 2016. "Changes in Mountain Glaciers, Lake Levels, and Snow Coverage in the Tianshan Monitored by GRACE, ICESat, Altimetry, and MODIS" Remote Sensing 8, no. 10: 798. https://doi.org/10.3390/rs8100798

APA Style

Yi, S., Wang, Q., Chang, L., & Sun, W. (2016). Changes in Mountain Glaciers, Lake Levels, and Snow Coverage in the Tianshan Monitored by GRACE, ICESat, Altimetry, and MODIS. Remote Sensing, 8(10), 798. https://doi.org/10.3390/rs8100798

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop