Retrieval of Melt Ponds on Arctic Multiyear Sea Ice in Summer from TerraSAR-X Dual-Polarization Data Using Machine Learning Approaches: A Case Study in the Chukchi Sea with Mid-Incidence Angle Data
Abstract
:1. Introduction
2. Materials
2.1. Airborne SAR Survey Data

2.2. TerraSAR-X Dual-Polarization Data
2.3. Sea Ice Conditions
3. Methodology
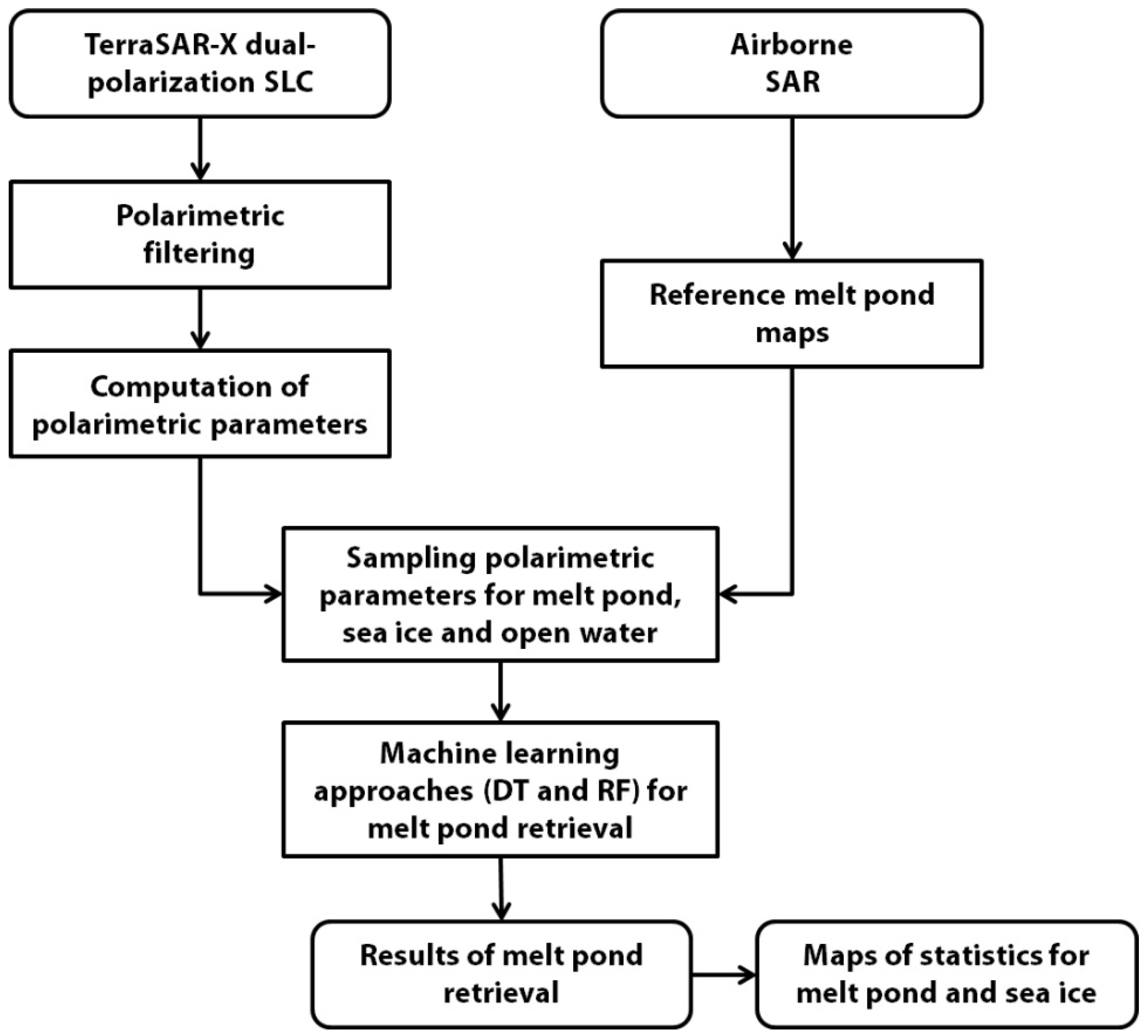
3.1. Construction of the Reference Dataset
3.2. Polarimetric Parameters
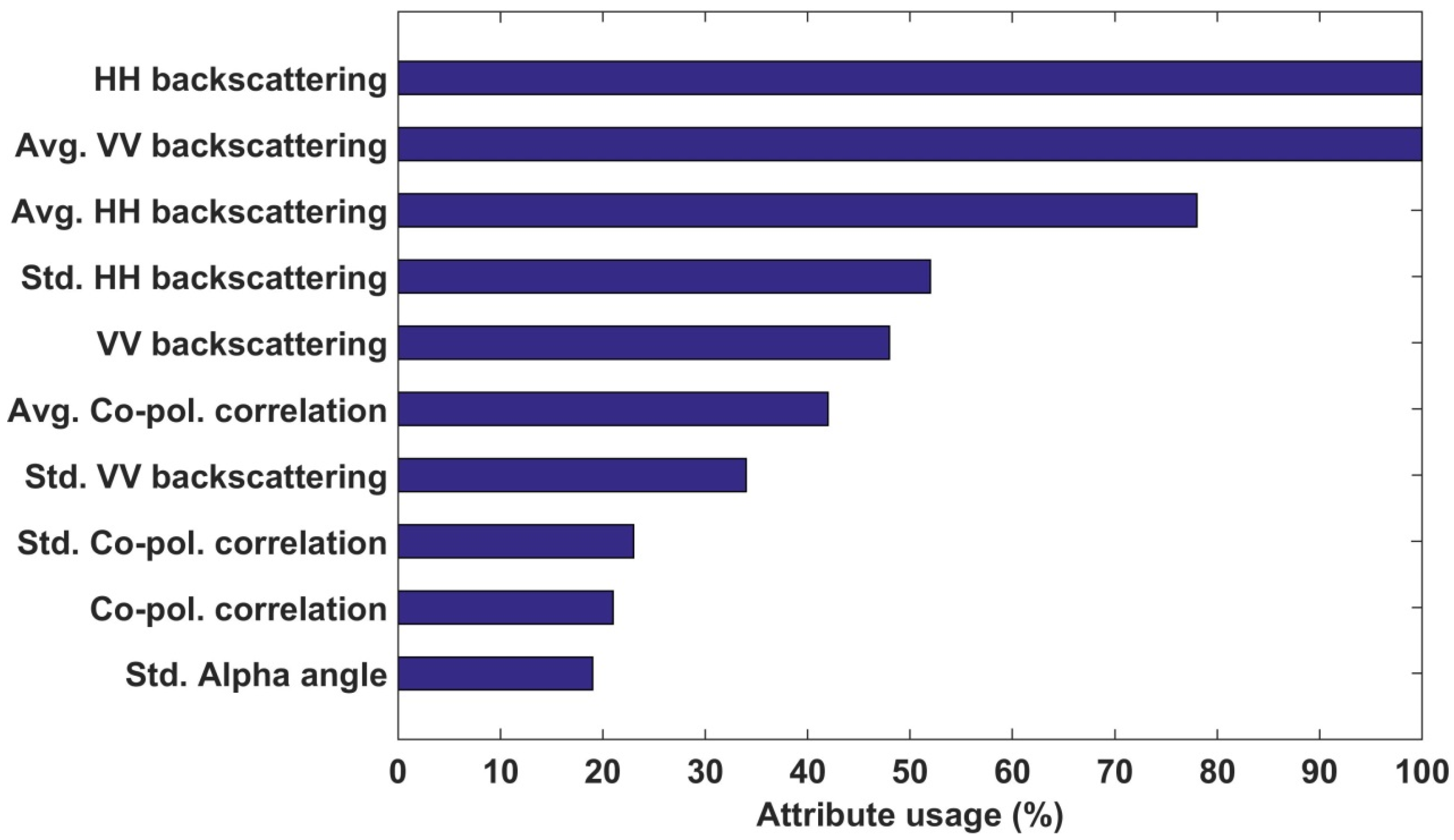
3.3. Machine Learning Approaches for Melt Pond Retrieval
4. Results and Discussion
4.1. Polarimetric Signatures
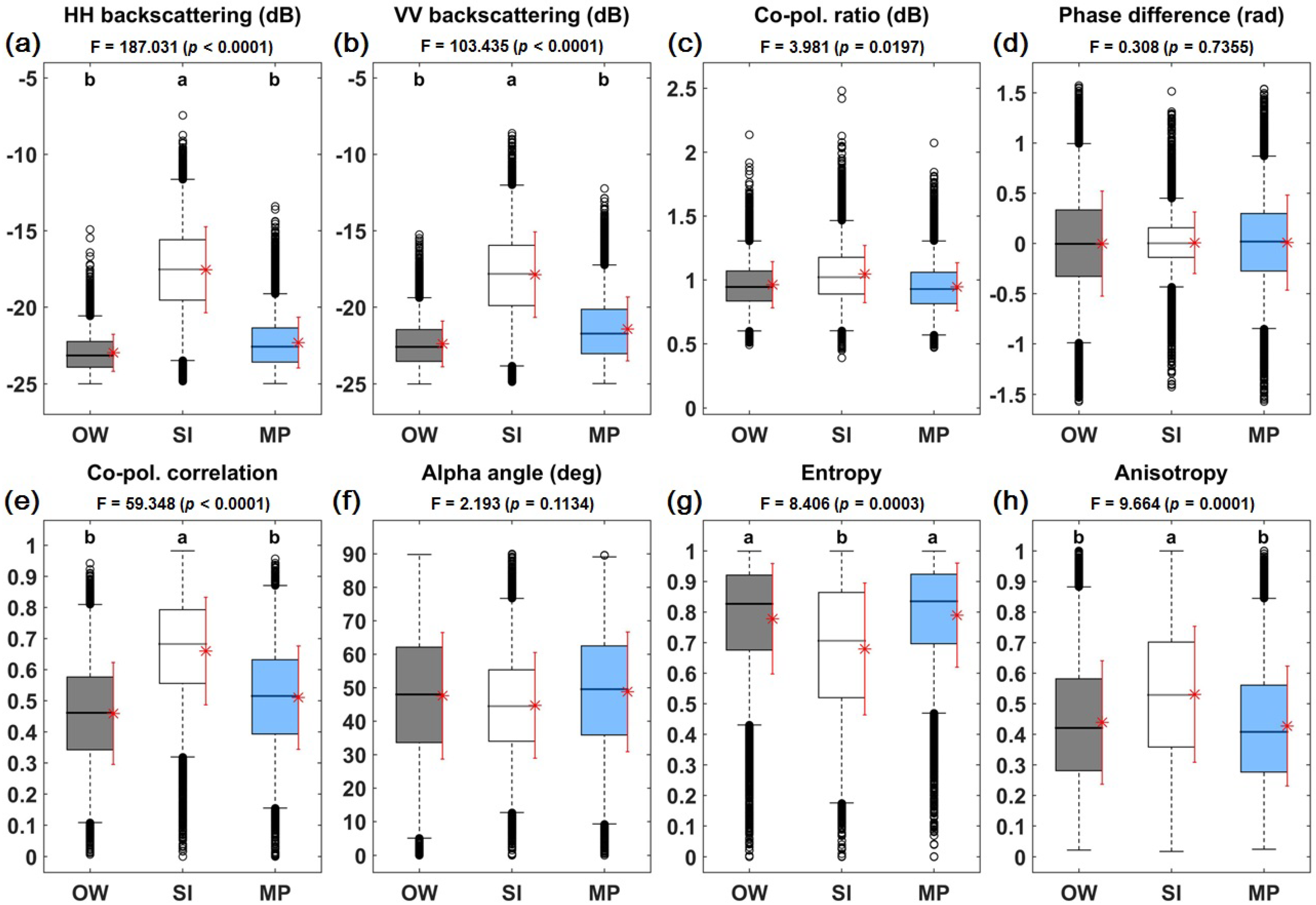
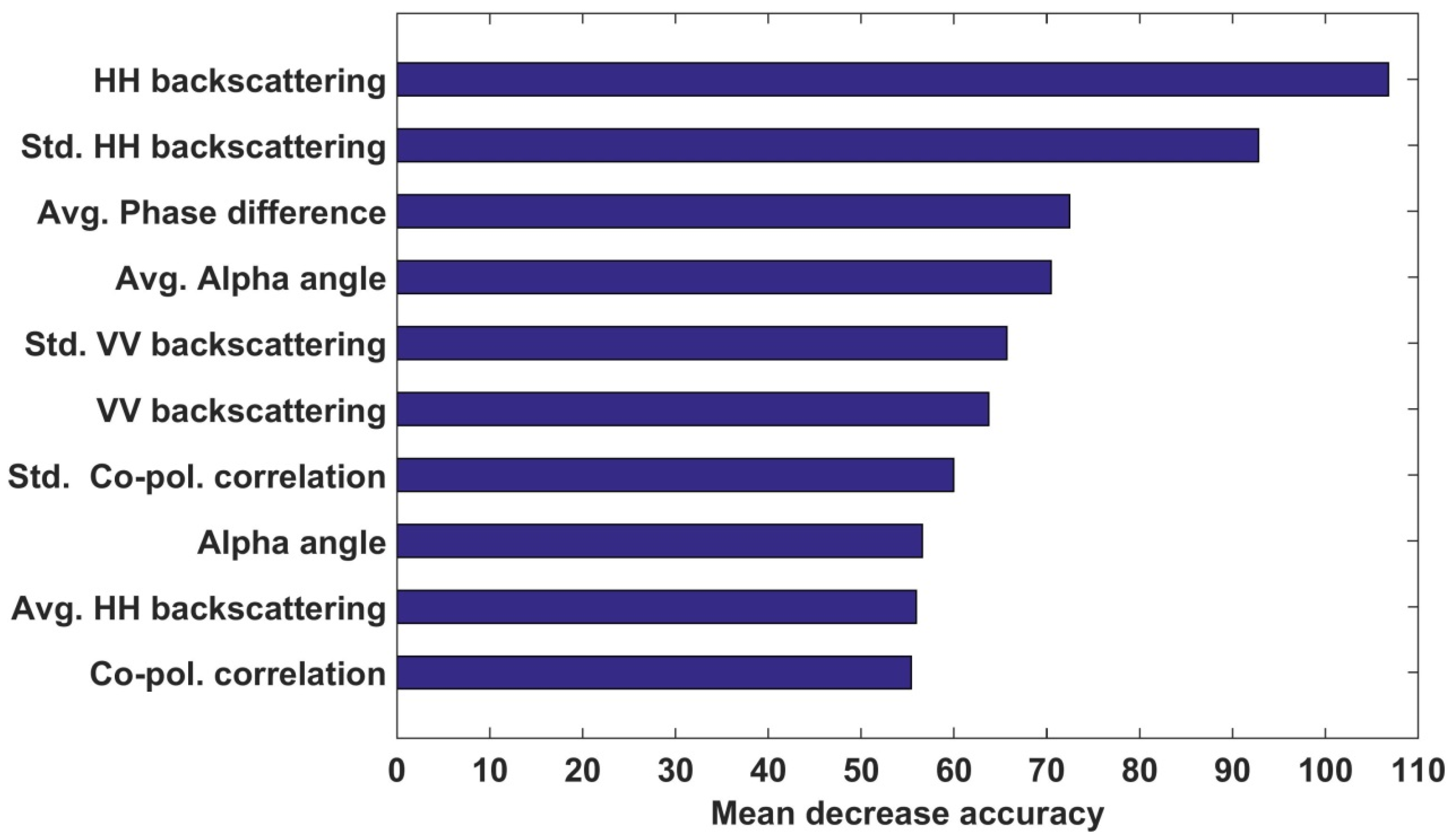
4.2. Performance of Melt Pond Detection Model Using Polarimetric Parameters
| Reference | Open Water | Sea Ice | Melt Pond | Sum | User’s Accuracy |
|---|---|---|---|---|---|
| Classified as | |||||
| Open water | 1865 | 79 | 1197 | 3141 | 59.38% |
| Sea ice | 54 | 2152 | 349 | 2555 | 84.23% |
| Melt pond | 558 | 246 | 931 | 1735 | 53.66% |
| Sum | 2477 | 2477 | 2477 | 7431 | |
| Producer’s accuracy | 75.29% | 86.88% | 37.59% | ||
| Overall accuracy | 66.59% | ||||
| Kappa coefficient | 49.88% | ||||
| Reference | Open Water | Sea Ice | Melt Pond | Sum | User’s Accuracy |
|---|---|---|---|---|---|
| Classified as | |||||
| Open water | 1955 | 50 | 1175 | 3180 | 61.48% |
| Sea ice | 27 | 2222 | 286 | 2535 | 87.65% |
| Melt pond | 495 | 205 | 1016 | 1716 | 59.21% |
| Sum | 2477 | 2477 | 2477 | 7431 | |
| Producer’s accuracy | 78.93% | 89.71% | 41.02% | ||
| Overall accuracy | 69.88% | ||||
| Kappa coefficient | 54.82% | ||||
4.3. Performance of the Melt Pond Detection Model Considering the Texture Features of the Polarimetric Parameters

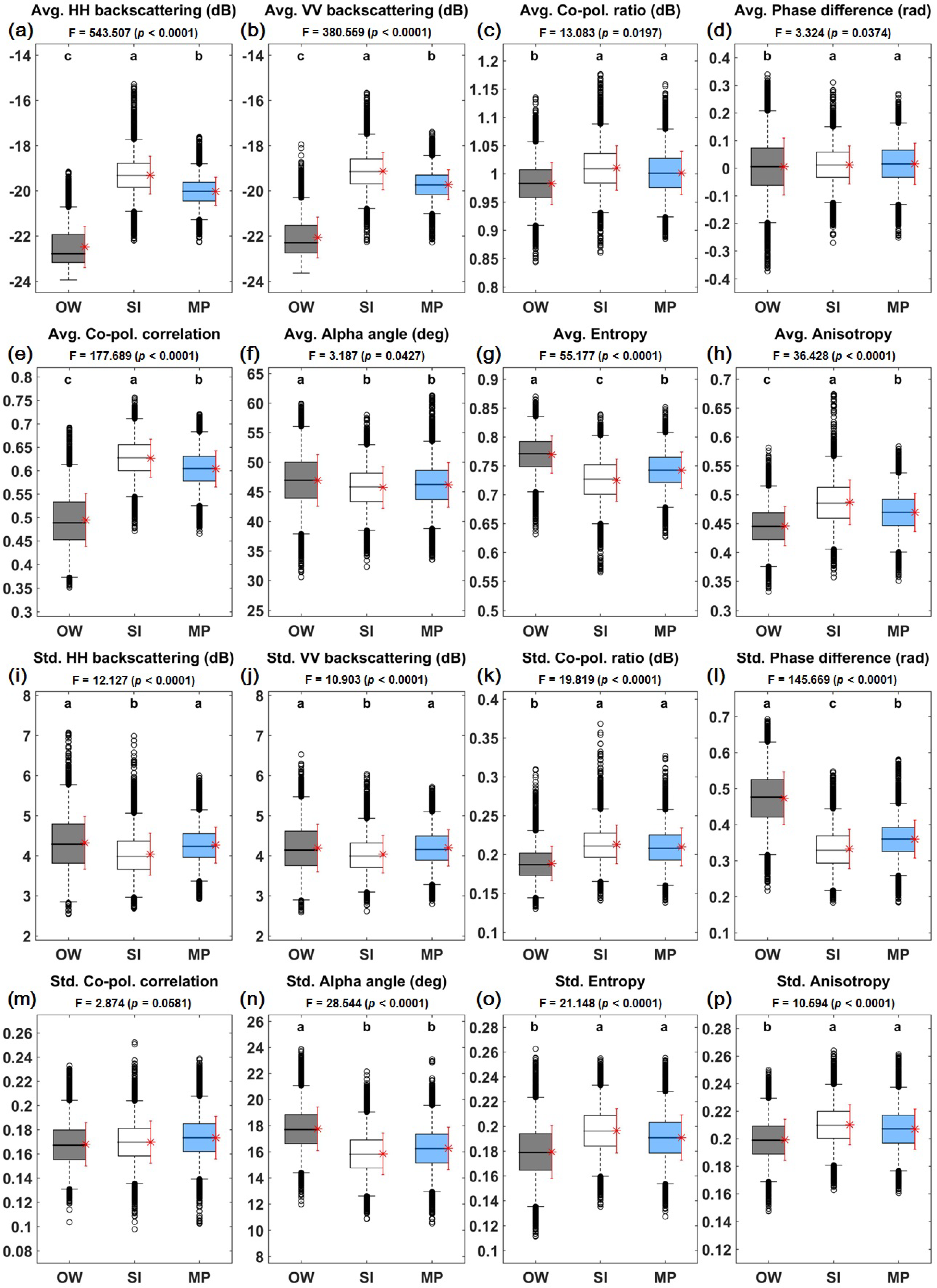
| Reference | Open Water | Sea Ice | Melt Pond | Sum | User’s Accuracy |
|---|---|---|---|---|---|
| Classified as | |||||
| Open water | 2333 | 14 | 210 | 2557 | 91.24% |
| Sea ice | 15 | 2175 | 434 | 2624 | 82.89% |
| Melt pond | 129 | 288 | 1833 | 2250 | 81.47% |
| Sum | 2477 | 2477 | 2477 | 7431 | |
| Producer’s accuracy | 94.19% | 87.81% | 74.0% | ||
| Overall accuracy | 85.33% | ||||
| Kappa coefficient | 78.0% | ||||
| Reference | Open Water | Sea Ice | Melt Pond | Sum | User’s Accuracy |
|---|---|---|---|---|---|
| Classified as | |||||
| Open water | 2366 | 7 | 125 | 2498 | 94.72% |
| Sea ice | 5 | 2280 | 304 | 2589 | 88.06% |
| Melt pond | 106 | 190 | 2048 | 2344 | 87.37% |
| Sum | 2477 | 2477 | 2477 | 7431 | |
| Producer’s accuracy | 95.52% | 92.04% | 82.68% | ||
| Overall accuracy | 90.08% | ||||
| Kappa coefficient | 85.12% | ||||
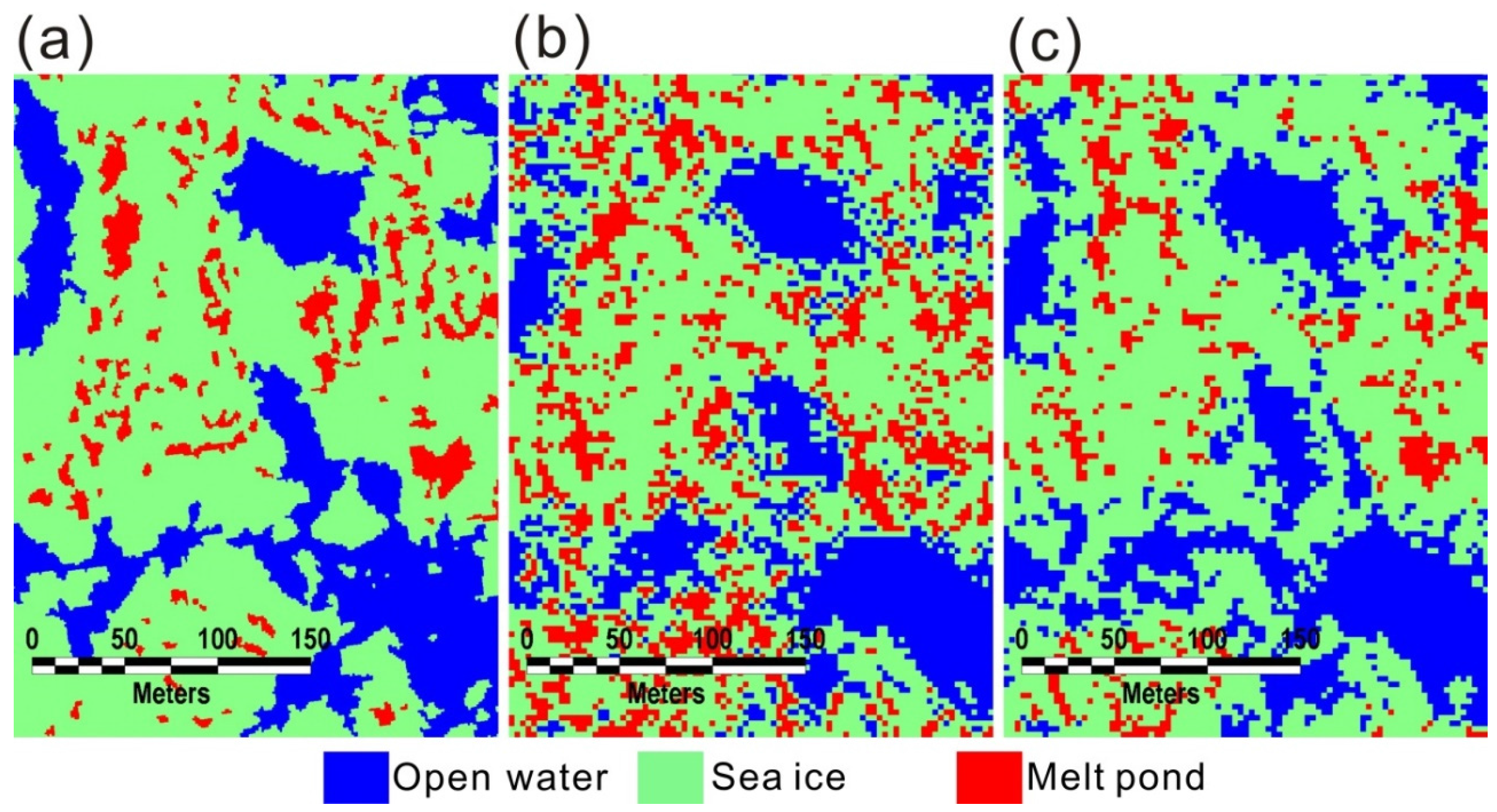
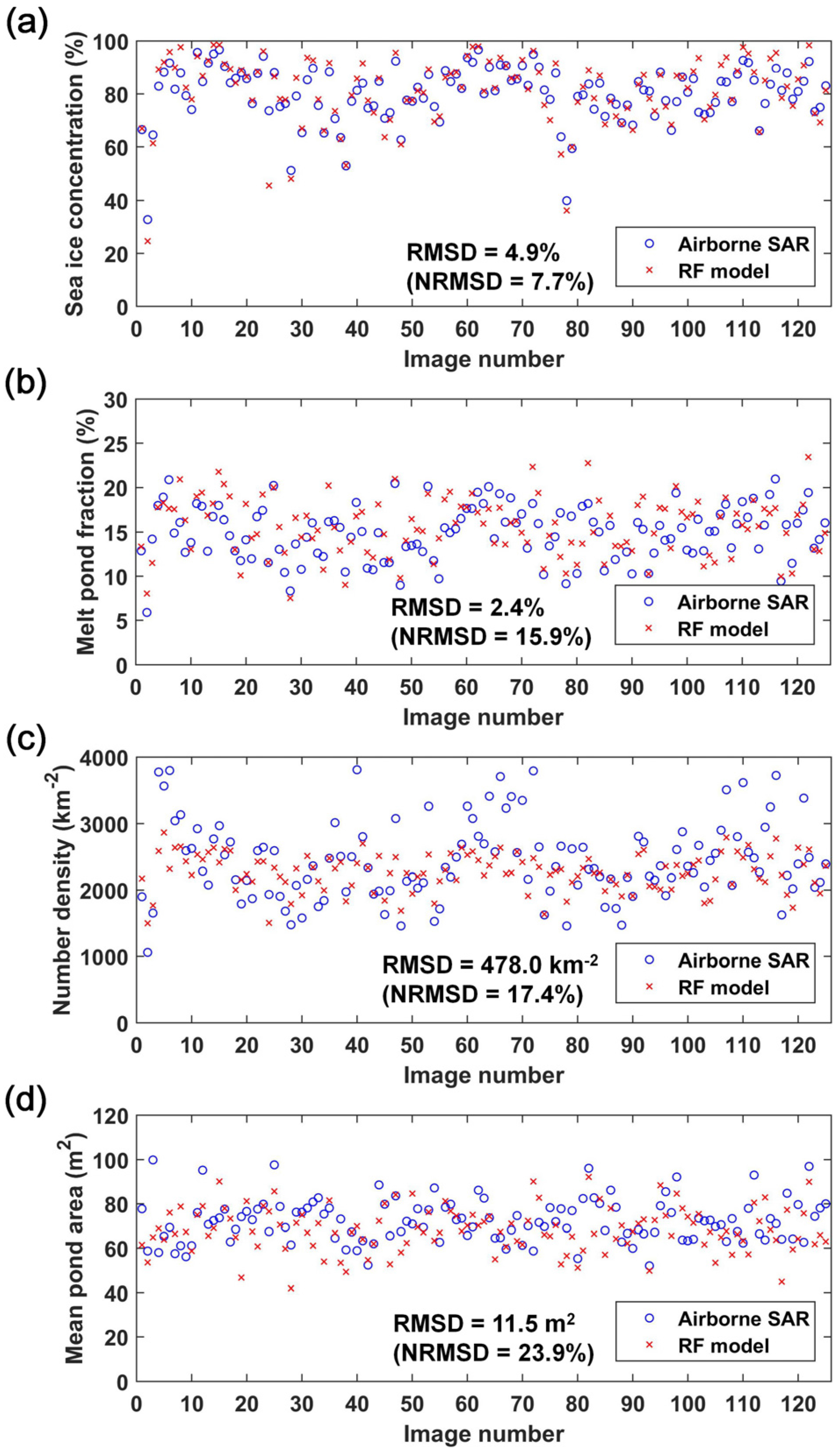
4.4. Retrieved Melt Pond Statistics

5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Cavalieri, D.J.; Parkinson, C.L. Arctic sea ice variability and trends, 1979–2010. Cryosphere 2012, 6, 881–889. [Google Scholar] [CrossRef]
- Comiso, J.C. Large decadal decline of the arctic multiyear ice cover. J. Clim. 2012, 25, 1176–1193. [Google Scholar] [CrossRef]
- Kay, J.E.; Holland, M.M.; Jahn, A. Inter-annual to multi-decadal Arctic sea ice extent trends in a warming world. Geophys. Res. Lett. 2011. [Google Scholar] [CrossRef]
- Screen, J.A.; Deser, C.; Simmonds, I.; Tomas, R. Atmospheric impacts of Arctic sea-ice loss, 1979–2009: Separating forced change from atmospheric internal variability. Clim. Dyn. 2014, 43, 333–344. [Google Scholar] [CrossRef]
- Stroeve, J.C.; Kattsov, V.; Barrett, A.; Serreze, M.; Pavlova, T.; Holland, M.; Meier, W.N. Trends in Arctic sea ice extent from CMIP5, CMIP3 and observations. Geophys. Res. Lett. 2012. [Google Scholar] [CrossRef]
- Vihma, T. Effects of Arctic sea ice decline on weather and climate: A review. Surv. Geophys. 2014, 35, 1175–1214. [Google Scholar] [CrossRef]
- Francis, J.A.; Vavrus, S.J. Evidence linking Arctic amplification to extreme weather in mid-latitudes. Geophys. Res. Lett. 2012. [Google Scholar] [CrossRef]
- Gautier, D.L.; Bird, K.J.; Charpentier, R.R.; Grantz, A.; Houseknecht, D.W.; Klett, T.R.; Moore, T.E.; Pitman, J.K.; Schenk, C.J.; Schuenemeyer, J.H.; et al. Assessment of undiscovered oil and gas in the Arctic. Science 2009, 324, 1175–1179. [Google Scholar] [CrossRef] [PubMed]
- Hansen, B.B.; Grøtan, V.; Aanes, A.; Sæther, B.-E.; Stien, A.; Fuglei, E.; Ims, R.A.; Yoccoz, N.G.; Pedersen, Å.Ø. Climate events synchronize the dynamics of a resident vertebrate community in the high Arctic. Science 2013, 339, 313–315. [Google Scholar] [CrossRef] [PubMed]
- Eicken, H.; Grenfell, T.C.; Perovich, D.K.; Richter-Menge, J.A.; Frey, K. Hydraulic controls of summer Arctic pack ice albedo. J. Geophys. Res. 2004. [Google Scholar] [CrossRef]
- Fetterer, F.; Untersteiner, N. Observations of melt ponds on Arctic sea ice. J. Geophys. Res. 1998, 103, 24821–24835. [Google Scholar] [CrossRef]
- Perovich, D.K.; Grenfell, T.C.; Light, B.; Hobbs, P.V. Seasonal evolution of the albedo of multiyear Arctic sea ice. J. Geophys. Res. 2002, 107, SHE 20-1–SHE 20-13. [Google Scholar] [CrossRef]
- Perovich, D.K.; Richter-Menge, J.A.; Jones, K.F.; Light, B. Sunlight, water, and ice: Extreme Arctic sea ice melt during the summer of 2007. Geophys. Res. Lett. 2008, 35, L11501. [Google Scholar] [CrossRef]
- Perovich, D.K.; Tucker, W.B., III; Ligett, K.A. Aerial observations of the evolution of ice surface conditions during summer. J. Geophys. Res. 2002, 107, 194–198. [Google Scholar]
- Flocco, D.; Feltham, D.L.; Turner, A.K. Incorporation of a physically based melt pond scheme into the sea ice component of a climate model. J. Geophys. Res. 2010, 115, 488–507. [Google Scholar] [CrossRef]
- Schröder, D.; Feltham, D.L.; Flocco, D.; Tsamados, M. September Arctic sea-ice minimum predicted by spring melt-pond fraction. Nat. Clim. Chang. 2014, 4, 353–357. [Google Scholar] [CrossRef]
- Istomina, L.; Heygster, G.; Huntemann, M.; Schwarz, P.; Birnbaum, G.; Scharien, R.; Polashenski, C.; Perovich, D.; Zege, E.; Malinka, A.; et al. Melt pond fraction and spectral sea ice albedo retrieval from MERIS data—Part 1: Validation against in situ, aerial, and ship cruise data. Cryosphere 2015, 9, 1551–1566. [Google Scholar] [CrossRef]
- Markus, T.; Cavalieri, D.J.; Tschudi, M.A.; Ivanoff, A. Comparison of aerial video and Landsat 7 data over ponded sea ice. Remote Sens. Environ. 2003, 86, 458–469. [Google Scholar] [CrossRef]
- Rösel, A.; Kaleschke, L. Comparison of different retrieval techniques for melt ponds on Arctic sea ice from Landsat and MODIS satellite data. Ann. Glaciol. 2011, 52, 185–191. [Google Scholar] [CrossRef]
- Rösel, A.; Kaleschke, L. Exceptional melt pond occurrence in the years 2007 and 2011 on the Arctic sea ice revealed from MODIS satellite data. J. Geophys. Res. 2012, 117, 78–91. [Google Scholar] [CrossRef]
- Rösel, A.; Kaleschke, L.; Birnbaum, G. Melt ponds on Arctic sea ice determined from MODIS satellite data using an artificial neural network. Cryosphere 2012, 6, 431–446. [Google Scholar] [CrossRef]
- Tschudi, M.A.; Maslanik, J.A.; Perovich, D.K. Derivation of melt pond coverage on Arctic sea ice using MODIS observations. Remote Sens. Environ. 2008, 112, 2605–2614. [Google Scholar] [CrossRef]
- Zege, E.; Malinka, A.; Katsev, I.; Prikhach, A.; Heygster, G.; Istomina, L.; Birnbaum, G.; Schwarz, P. Algorithm to retrieve the melt pond fraction and the spectral albedo of Arctic summer ice from satellite optical data. Remote Sens. Environ. 2015, 163, 153–164. [Google Scholar] [CrossRef]
- Liu, J.; Song, M.; Horton, R.M.; Hu, Y. Revisiting the potential of melt pond fraction as a predictor for the seasonal Arctic sea ice extent minimum. Environ. Res. Lett. 2015. [Google Scholar] [CrossRef]
- Lupkes, C.; Gryanik, V.M.; Rösel, A.; Birnbaum, G.; Kaleschke, L. Effect of sea ice morphology during Arctic summer on atmospheric drag coefficients used in climate models. Geophys. Res. Lett. 2013, 40, 446–451. [Google Scholar] [CrossRef]
- Yackel, J.J.; Barber, D.G. Melt ponds on sea ice in the Canadian Archipelago 2. On the use of RADARSAT-1 synthetic aperture radar for geophysical inversion. J. Geophys. Res. 2000, 105, 22061–22070. [Google Scholar] [CrossRef]
- Mäkynen, M.; Kern, S.; Rösel, A.; Pedersen, L.T. On the estimation of melt pond fraction on the Arctic sea ice with ENVISAT WSM images. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7366–7379. [Google Scholar] [CrossRef]
- Kim, D.-J.; Hwang, B.; Chung, K.H.; Lee, S.H.; Jung, H.S.; Moon, W.M. Melt pond mapping with high-resolution SAR: The first view. Proc. IEEE 2013, 101, 748–758. [Google Scholar] [CrossRef]
- Mishra, P.; Singh, D. A statistical-measure-based adaptive land cover classification algorithm by efficient utilization of polarimetric SAR observables. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2889–2900. [Google Scholar] [CrossRef]
- Sawaya, S.; Haack, B.; Idol, T.; Sheoran, A. Land use/cover mapping with quad-polarization radar and derived texture measures near Wad Madani, Sudan. GISci. Remote Sens. 2010, 47, 398–411. [Google Scholar] [CrossRef]
- Sheoran, A.; Haack, B. Classification of California agriculture using quad polarization radar data and Landsat Thematic Mapper data. GISci. Remote Sens. 2013, 50, 50–63. [Google Scholar]
- Scharien, R.K.; Landy, J.; Barber, D.G. First-year sea ice melt pond fraction estimation from dual-polarisation C-band SAR—Part 1: In situ observations. Cryosphere 2014, 8, 2147–2162. [Google Scholar] [CrossRef]
- Scharien, R.K.; Yackel, J.J.; Barber, D.G.; Asplin, M.; Gupta, M.; Isleifson, D. Geophysical controls on C band polarimetric backscatter from melt pond covered Arctic first-year sea ice: Assessment using high-resolution scatterometry. J. Geophys. Res. 2012. [Google Scholar] [CrossRef]
- Scharien, R.K.; Hochheim, K.; Landy, J.; Barber, D.G. First-year sea ice melt pond fraction estimation from dual-polarisation C-band SAR—Part 2: Scaling in situ to Radarsat-2. Cryosphere 2014, 8, 2163–2176. [Google Scholar] [CrossRef]
- Dierking, W.; Wesche, C. C-band radar polarimetry—Useful for detection of icebergs in sea ice? IEEE Trans. Geosci. Remote Sens. 2014, 52, 25–37. [Google Scholar] [CrossRef]
- Gill, J.P.S.; Yackel, J.J. Evaluation of C-band SAR polarimetric parameters for discrimination of first-year sea ice types. Can. J. Remote Sens. 2012, 38, 306–323. [Google Scholar] [CrossRef]
- Barber, D.G.; Yackel, J. The physical, radiative and microwave scattering characteristics of melt ponds on Arctic landfast sea ice. Int. J. Remote Sens. 1999, 20, 2069–2090. [Google Scholar] [CrossRef]
- Breit, H.; Fritz, T.; Balss, U.; Lachaise, M.; Niedermeier, A.; Vonavka, M. TerraSAR-X SAR processing and products. IEEE Trans. Geosci. Remote Sens. 2010, 48, 727–740. [Google Scholar] [CrossRef]
- Werninghaus, R.; Buckreuss, S. The TerraSAR-X mission and system design. IEEE Trans. Geosci. Remote Sens. 2010, 48, 606–614. [Google Scholar] [CrossRef]
- Lee, J.-S.; Grunes, M.R.; de Grandi, G. Polarimetric SAR speckle filtering and its implication for classification. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2363–2373. [Google Scholar]
- Lee, J.-S.; Pottier, E. Polarimetric Radar Imaging: From Basics to Applications; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Cloude, S.R.; Pottier, E. An entropy based classification scheme for land applications of polarimetric SAR. IEEE Trans. Geosci. Remote Sens. 1997, 35, 68–78. [Google Scholar] [CrossRef]
- Niu, X.; Ban, Y. Multi-temporal RADARSAT-2 polarimetric SAR data for urban land-cover classification using an object-based support vector machine and a rule-based approach. Int. J. Remote Sens. 2013, 34, 1–26. [Google Scholar] [CrossRef]
- Lopez-Sanchez, J.M.; Vicente-Guijalba, F.; Ballester-Berman, J.D.; Cloude, S.R. Polarimetric response of rice fields at C-band: Analysis and phenology retrieval. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2977–2993. [Google Scholar] [CrossRef]
- Cloude, S.R. The dual polarization entropy/alpha decomposition: A PALSAR case study. In Proceedings of the 3rd International Workshop on Science and Applications of SAR Polarimetry and Polarimetric Interferometry, Frascati, Italy, 22–26 January 2007.
- Duro, D.C.; Franklin, S.E.; Dubé, M.G. A comparison of pixel-based and object-based image analysis with selected machine learning algorithms for the classification of agricultural landscapes using SPOT-5 HRG imagery. Remote Sens. Environ. 2012, 118, 259–272. [Google Scholar] [CrossRef]
- Ghimire, B.; Rogan, J.; Galiano, V.R.; Panday, P.; Neeti, N. An evaluation of bagging, boosting, and random forests for land-cover classification in Cape Cod, Massachusetts, USA. GISci. Remote Sens. 2012, 49, 623–643. [Google Scholar] [CrossRef]
- Kim, M.; Im, J.; Han, H.; Kim, J.; Lee, S.; Shin, M.; Kim, H.-C. Landfast sea ice monitoring using multisensor fusion in the Antarctic. GISci. Remote Sens. 2015, 52, 239–256. [Google Scholar] [CrossRef]
- Long, J.A.; Lawrence, R.L.; Greenwood, M.C.; Marshall, L.; Miller, P.R. Object-oriented crop classification using multitemporal ETM+ SLC-off imagery and random forest. GISci. Remote Sens. 2013, 50, 418–436. [Google Scholar]
- Maxwell, A.E.; Strager, M.P.; Warner, T.A.; Zégre, N.P.; Yuill, C.B. Comparison of NAIP orthophotography and RapidEye satellite imagery for mapping of mining and mine reclamation. GISci. Remote Sens. 2014, 51, 301–320. [Google Scholar] [CrossRef]
- Qian, Y.; Zhou, W.; Yan, J.; Li, W.; Han, L. Comparing machine learning classifiers for object-based land cover classification using very high resolution imagery. Remote Sens. 2014, 7, 153–168. [Google Scholar] [CrossRef]
- Rhee, J.; Park, S.; Lu, Z. Relationship between land cover patterns and surface temperature in urban areas. GISci. Remote Sens. 2014, 51, 521–536. [Google Scholar] [CrossRef]
- Demir, B.; Bovolo, F.; Bruzzone, L. Updating land-cover maps by classification of image time series: A novel change-detection-driven transfer learning approach. IEEE Trans. Geosci. Remote Sens. 2013, 51, 300–312. [Google Scholar] [CrossRef]
- Tan, B.; Masek, J.G.; Wolfe, R.; Gao, F.; Huang, C.; Vermote, E.F.; Sexton, J.O.; Ederer, G. Improved forest change detection with terrain illumination corrected Landsat images. Remote Sens. Environ. 2013, 136, 469–483. [Google Scholar] [CrossRef]
- Abedi, M.; Norouzi, G.-H.; Bahroudi, A. Support vector machine for multi-classification of mineral prospectivity areas. Comput. Geosci. 2012, 46, 272–283. [Google Scholar] [CrossRef]
- Li, M.; Im, J.; Beier, C. Machine learning approaches for forest classification and change analysis using multi-temporal Landsat TM images over Huntington Wildlife Forest. GISci. Remote Sens. 2013, 50, 361–384. [Google Scholar]
- Lu, D.; Li, G.; Moran, E.; Kuang, W. A comparative analysis of approaches for successional vegetation classification in the Brazilian Amazon. GISci. Remote Sens. 2014, 51, 695–709. [Google Scholar] [CrossRef]
- Xun, L.; Wang, L. An object-based SVM method incorporating optimal segmentation scale estimation using Bhattacharyya Distance for mapping salt cedar (Tamarisk spp.) with QuickBird imagery. GISci. Remote Sens. 2015, 52, 257–273. [Google Scholar] [CrossRef]
- Zhang, C.; Xie, Z.; Selch, D. Fusing lidar and digital aerial photography for object-based forest mapping in the Florida Everglades. GISci. Remote Sens. 2013, 50, 562–573. [Google Scholar]
- Ahmad, S.; Kalra, A.; Stephen, H. Estimating soil moisture using remote sensing data: A machine learning approach. Adv. Water Resour. 2010, 33, 69–80. [Google Scholar] [CrossRef]
- Güneralp, I.; Filippi, A.M.; Hales, B.U. River-flow boundary delineation from digital aerial photography and ancillary images using support vector machines. GISci. Remote Sens. 2013, 50, 1–25. [Google Scholar]
- Kim, Y.H.; Im, J.; Ha, H.K.; Choi, J.K.; Ha, S. Machine learning approaches to coastal water quality monitoring using GOCI satellite data. GISci. Remote Sens. 2014, 51, 158–174. [Google Scholar] [CrossRef]
- Han, H.; Lee, S.; Im, J.; Kim, M.; Lee, M.-I.; Ahn, M.H.; Chung, S.-R. Detection of convective initiation using Meteorological Imager onboard Communication, Ocean, and Meteorological satellite based on machine learning approaches. Remote Sens. 2015, 7, 9184–9204. [Google Scholar] [CrossRef]
- Kühnlein, M.; Appelhans, T.; Thies, B.; Nauss, T. Improving the accuracy of rainfall rates from optical satellite sensors with machine learning—A random forests-based approach applied to MSG SEVIRI. Remote Sens. Environ. 2014, 141, 129–143. [Google Scholar] [CrossRef]
- Quinlan, J.R. Data Mining Tools See5 and C4.5, Version 2.10. Available online: http://www.webcitation.org/6YgqVwnT9 (accessed on 9 September 2015).
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Lawrence, R.L.; Wright, A. Rule-based classification systems using classification and regression tree (CART) analysis. Photogramm. Eng. Remote Sens. 2001, 67, 1137–1142. [Google Scholar]
- Cracknell, M.J.; Reading, A.M. Geological mapping using remote sensing data: A comparison of five machine learning algorithms, their response to variations in the spatial distribution of training data and the use of explicit spatial information. Comput. Geosci. 2014, 63, 22–33. [Google Scholar] [CrossRef]
- Congalton, R.G. A review of assessing the accuracy of classifications of remotely sensed data. Remote Sens. Environ. 1991, 37, 35–46. [Google Scholar] [CrossRef]
- Foody, G.M. Status of land cover classification accuracy assessment. Remote Sens. Environ. 2002, 80, 185–201. [Google Scholar] [CrossRef]
- Stehman, S.V. Selecting and interpreting measures of thematic classification accuracy. Remote Sens. Environ. 1997, 62, 77–89. [Google Scholar] [CrossRef]
- Faul, F.; Erdfelder, E.; Lang, A.-G.; Buchner, A. G*power 3: A flexible statistical power analysis program for the social, behavioral, and biomedical sciences. Behav. Res. Methods 2007, 39, 175–191. [Google Scholar] [CrossRef] [PubMed]
- Deng, H.; Clausi, D.A. Unsupervised segmentation of synthetic aperture radar sea ice imagery using a novel Markov random field model. IEEE Trans. Geosci. Remote Sens. 2005, 43, 528–538. [Google Scholar] [CrossRef]
- Liu, C.Y.; Chao, J.; Gu, W.; Xu, Y.; Xie, F. Estimation of sea ice thickness in the Bohai Sea using a combination of VIS/NIR and SAR images. GISci. Remote Sens. 2015, 52, 115–130. [Google Scholar] [CrossRef]
- Gill, J.P.S.; Yackel, J.J.; Geldsetzer, T.; Fuller, M.C. Sensitivity of C-band synthetic aperture radar polarimetric parameters to snow thickness over landfast smooth first-year sea ice. Remote Sens. Environ. 2015, 166, 34–49. [Google Scholar] [CrossRef]
- Nghiem, S.V.; Kwok, R.; Yueh, S.H.; Drinkwater, M.R. Polarimetric signatures of sea-ice: 1. Theoretical model. J. Geophys. Res. 1995, 100, 13665–13679. [Google Scholar] [CrossRef]
- Pal, M. Random forest classifier for remote sensing classification. Int. J. Remote Sens. 2005, 26, 217–222. [Google Scholar] [CrossRef]
- Geldsetzer, T.; Mead, J.B.; Yackel, J.J.; Scharien, R.K.; Howell, S.E.L. Surface-based polarimetric C-band scatterometer for field measurements of sea ice. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3405–3416. [Google Scholar] [CrossRef]
- Zhang, C.; Xie, Z. Combining object-based texture measures with a neural network for vegetation mapping in the Everglades from hyperspectral imagery. Remote Sens. Environ. 2012, 124, 310–320. [Google Scholar] [CrossRef]
- Andersen, S.; Tonboe, R.; Kaleschke, L.; Heygster, G.; Pedersen, L.T. Intercomparison of passive microwave sea ice concentration retrievals over the high-concentration Arctic sea ice. J. Geophys. Res. 2007. [Google Scholar] [CrossRef]
- Kongoli, C.; Boukabara, S.-A.; Yan, B.; Weng, F.; Ferraro, R. A new sea-ice concentration algorithm based on microwave surface emissivities—Application to AMSU measurements. IEEE Trans. Geosci. Remote Sens. 2011, 49, 175–189. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, H.; Im, J.; Kim, M.; Sim, S.; Kim, J.; Kim, D.-j.; Kang, S.-H. Retrieval of Melt Ponds on Arctic Multiyear Sea Ice in Summer from TerraSAR-X Dual-Polarization Data Using Machine Learning Approaches: A Case Study in the Chukchi Sea with Mid-Incidence Angle Data. Remote Sens. 2016, 8, 57. https://doi.org/10.3390/rs8010057
Han H, Im J, Kim M, Sim S, Kim J, Kim D-j, Kang S-H. Retrieval of Melt Ponds on Arctic Multiyear Sea Ice in Summer from TerraSAR-X Dual-Polarization Data Using Machine Learning Approaches: A Case Study in the Chukchi Sea with Mid-Incidence Angle Data. Remote Sensing. 2016; 8(1):57. https://doi.org/10.3390/rs8010057
Chicago/Turabian StyleHan, Hyangsun, Jungho Im, Miae Kim, Seongmun Sim, Jinwoo Kim, Duk-jin Kim, and Sung-Ho Kang. 2016. "Retrieval of Melt Ponds on Arctic Multiyear Sea Ice in Summer from TerraSAR-X Dual-Polarization Data Using Machine Learning Approaches: A Case Study in the Chukchi Sea with Mid-Incidence Angle Data" Remote Sensing 8, no. 1: 57. https://doi.org/10.3390/rs8010057
APA StyleHan, H., Im, J., Kim, M., Sim, S., Kim, J., Kim, D.-j., & Kang, S.-H. (2016). Retrieval of Melt Ponds on Arctic Multiyear Sea Ice in Summer from TerraSAR-X Dual-Polarization Data Using Machine Learning Approaches: A Case Study in the Chukchi Sea with Mid-Incidence Angle Data. Remote Sensing, 8(1), 57. https://doi.org/10.3390/rs8010057







