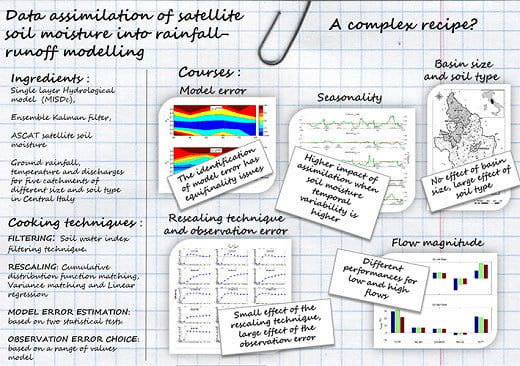
Data Assimilation of Satellite Soil Moisture into Rainfall-Runoff Modelling: A Complex Recipe?
Abstract
:1. Introduction
2. Materials
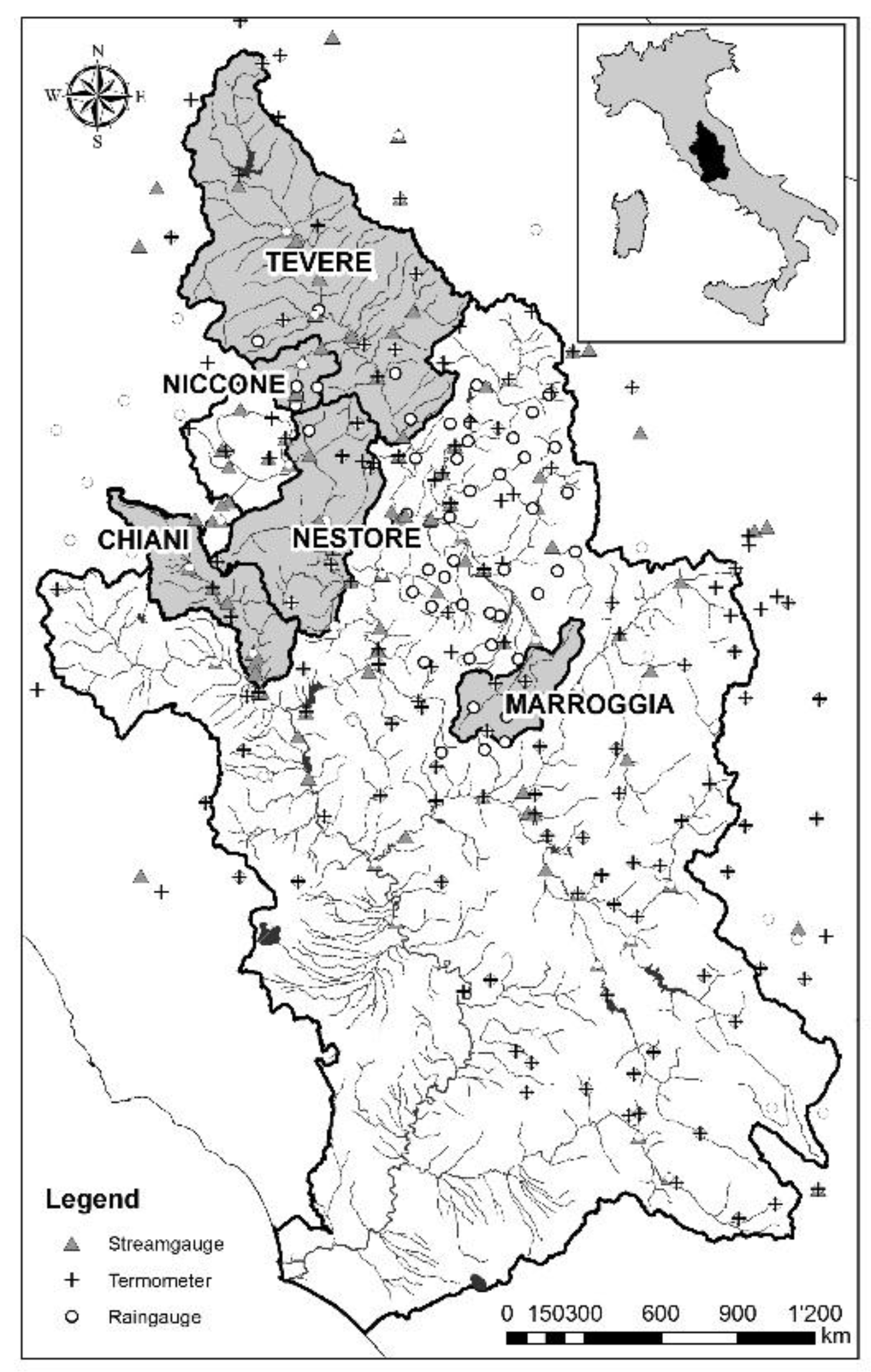
2.1. Study Area
| Catchment | TV-PF | NE-MA | CHI-MO | MA-AZ | NI-MI |
|---|---|---|---|---|---|
| A (km2) | 2040 | 725 | 457 | 258 | 137 |
| P (mm) | 818 | 739 | 724 | 835 | 830 |
| El (m) | 521 | 350 | 404 | 604 | 452 |
| Sl. (%) | 26 | 17 | 19 | 29 | 25 |
| Land Use (%) | |||||
| Woods | 53.6 | 37.7 | 49.5 | 55.7 | 65.1 |
| Croplands | 9.4 | 3.8 | 4.7 | 4.6 | 7.9 |
| Grasslands | 35.2 | 53.5 | 43.8 | 35.8 | 26.6 |
| Urban areas | 1.7 | 5.0 | 2.0 | 3.9 | 0.4 |
| Hydrologic Soil Group—Soil Conservation Service (%) | |||||
| High infiltration rate | 5.0 | 1.7 | 0.6 | 9.4 | 3.2 |
| Moderate infiltration rate | 19.5 | 17.4 | 19.9 | 11.1 | 12.4 |
| Low infiltration rate | 74.4 | 81.0 | 79.4 | 75.6 | 84.4 |
| Very low infiltration rate | 1.0 | 0.0 | 0.1 | 3.9 | 0.0 |
| Parameters of the Rainfall—Runoff Model | |||||
| Wmax (mm) | 497 | 380 | 388 | 327 | 372 |
| Ks (mm/h) | 20.8 | 28.8 | 29 | 40 | 21.8 |
| Kc (mm/h) | 0.87 | 0.84 | 0.66 | 1.03 | 0.89 |
| η (-) | 0.59 | 0.94 | 1.18 | 0.37 | 1.51 |
| (%) | 4 | 4.4 | 2 | 3.3 | 5 |
| α1 (%) | 40 | 40 | 80 | 50 | 80 |
| α2, α3 (%) | 30 | 10 | 30 | 20 | 30 |
| (mm) | 0.75 | 0.5 | 0.25 | 0.75 | 0.25 |
| Satellite Data | |||||
| # SM-OBS4 pixels | 12 | 5 | 1 | 1 | 1 |
| SM-OBS4 noise (%) | 11 | 9.5 | 8 | 13.5 | 9.3 |
| T (days) | 48 | 87 | 67 | 62 | 68 |
2.2. In Situ Data
2.3. Satellite Data
3. Methods
3.1. Hydrological Model
3.2. Ensemble Kalman Filter
3.3. Filtering and Rescaling Techniques
3.4. Model Error Representation and Observation Error
3.5. Performance Indexes
4. Results
4.1. Model Calibration and Validation

| NSc | NSv | NSol | NSa | Effv (%) | Effol (%) | σobs | ||
|---|---|---|---|---|---|---|---|---|
| TV-PF | VM | 0.79 | 39.64 | 35.86 | 0.05 | |||
| LR | 0.80 | 0.65 | 0.67 | 0.80 | 42.33 | 38.72 | 0.05 | |
| CDF | 0.75 | 29.53 | 25.11 | 0.05 | ||||
| NE-MA | VM | 0.91 | 29.30 | 31.56 | 0.20 | |||
| LR | 0.88 | 0.87 | 0.87 | 0.91 | 28.72 | 31.00 | 0.20 | |
| CDF | 0.90 | 23.49 | 25.93 | 0.20 | ||||
| CHI-MOR | VM | 0.87 | 24.64 | 31.66 | 0.09 | |||
| LR | 0.76 | 0.83 | 0.81 | 0.88 | 26.03 | 32.93 | 0.07 | |
| CDF | 0.87 | 21.09 | 28.44 | 0.05 | ||||
| MA-AZ | VM | 0.70 | 2.06 | −13.30 | 0.20 | |||
| LR | 0.77 | 0.69 | 0.74 | 0.71 | 3.67 | −11.44 | 0.20 | |
| CDF | 0.70 | 3.35 | −11.81 | 0.20 | ||||
| NI-MI | VM | 0.79 | 39.58 | 41.67 | 0.03 | |||
| LR | 0.85 | 0.65 | 0.64 | 0.79 | 39.27 | 41.37 | 0.05 | |
| CDF | 0.77 | 34.23 | 36.50 | 0.03 |
| NSv | Errvol (%) | NSol | NSa | Errvol(a) (%) | Effv (%) | Effol (%) | σobs | Nev | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| TV-PF | VM | 0.64 | −2.56 | 52.55 | 50.18 | 0.05 | 16 | ||||
| LS | 0.25 | 26.09 | 0.29 | 0.67 | −5.49 | 56.08 | 53.89 | 0.05 | 16 | ||
| CDF | 0.56 | 2.84 | 41.53 | 38.61 | 0.05 | 16 | |||||
| NE-MA | VM | 0.91 | 14.23 | 37.09 | 38.71 | 0.20 | 16 | ||||
| LS | 0.85 | 19.45 | 0.85 | 0.91 | 15.14 | 36.69 | 38.32 | 0.20 | 16 | ||
| CDF | 0.90 | 16.04 | 32.83 | 34.56 | 0.20 | 16 | |||||
| CHI-MOR | VM | 0.87 | −1.18 | 27.11 | 37.54 | 0.09 | 24 | ||||
| LS | 0.83 | 1.69 | 0.8 | 0.88 | −1.64 | 28.02 | 38.32 | 0.07 | 24 | ||
| CDF | 0.87 | −1.27 | 22.05 | 33.21 | 0.05 | 24 | |||||
| MA-AZ | VM | 0.71 | −7.31 | 7.69 | −34.14 | 0.2 | 17 | ||||
| LS | 0.68 | −0.1 | 0.78 | 0.72 | −6.83 | 10.83 | −29.57 | 0.2 | 17 | ||
| CDF | 0.71 | −5.25 | 8.51 | −32.95 | 0.2 | 17 | |||||
| NI-MI | VM | 0.75 | −9.65 | 55.56 | 57.98 | 0.03 | 30 | ||||
| LS | 0.44 | −3.81 | 0.41 | 0.75 | −12.83 | 54.5 | 56.98 | 0.05 | 30 | ||
| CDF | 0.7 | −9.85 | 46.16 | 49.09 | 0.03 | 30 |
4.2. Ensemble Generation and Data Assimilation Experimental Setup
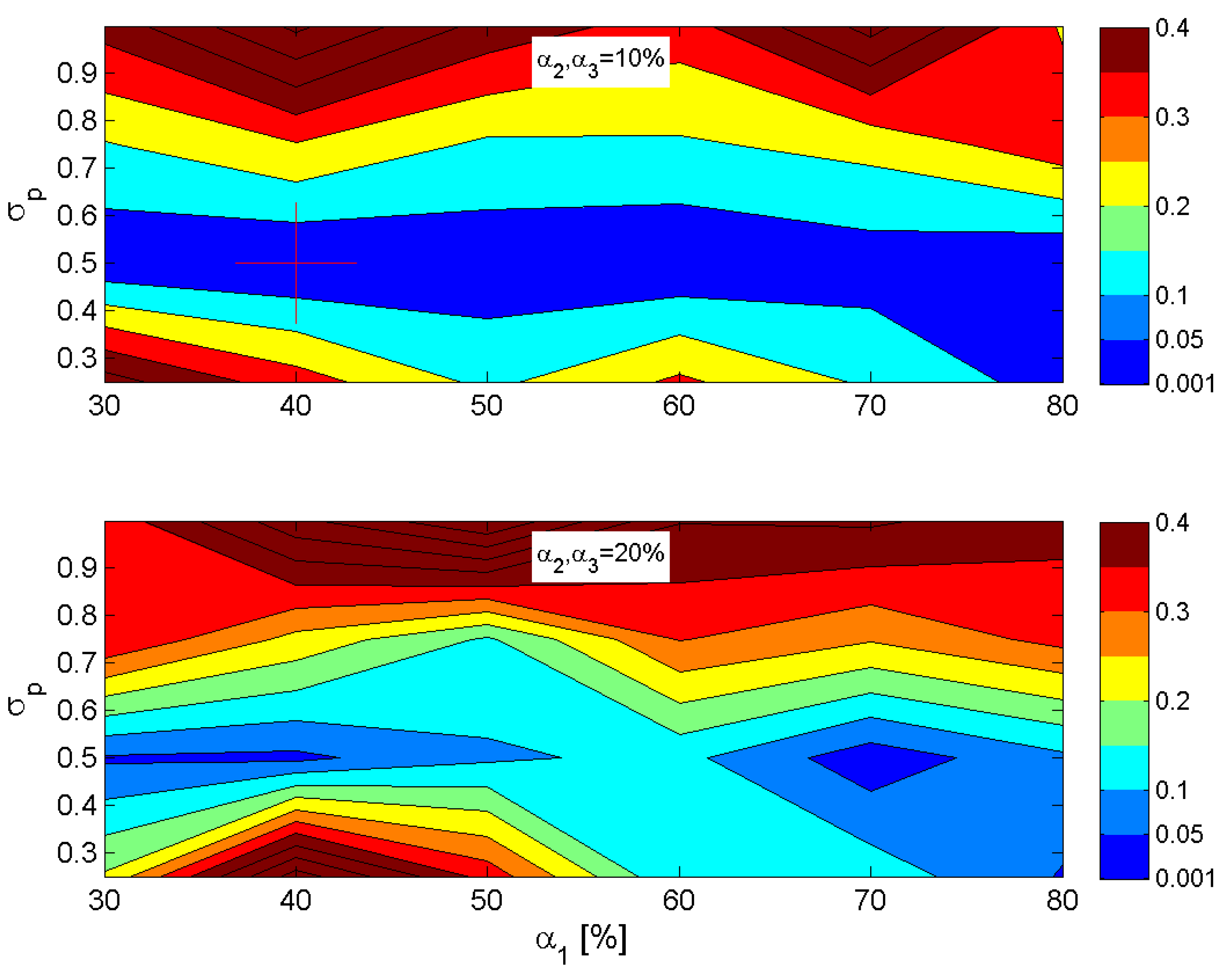
4.3. Data Assimilation Experiment
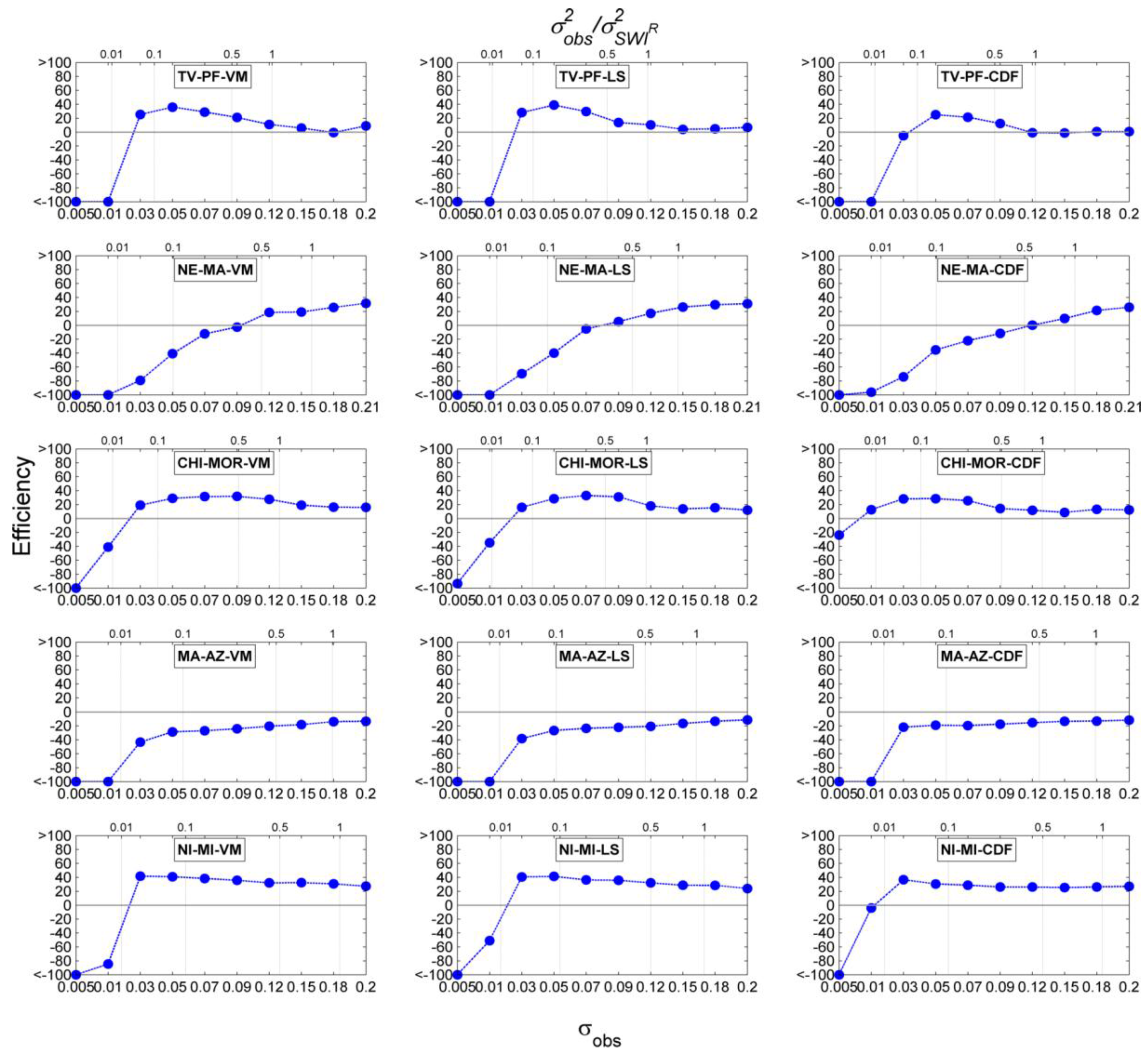
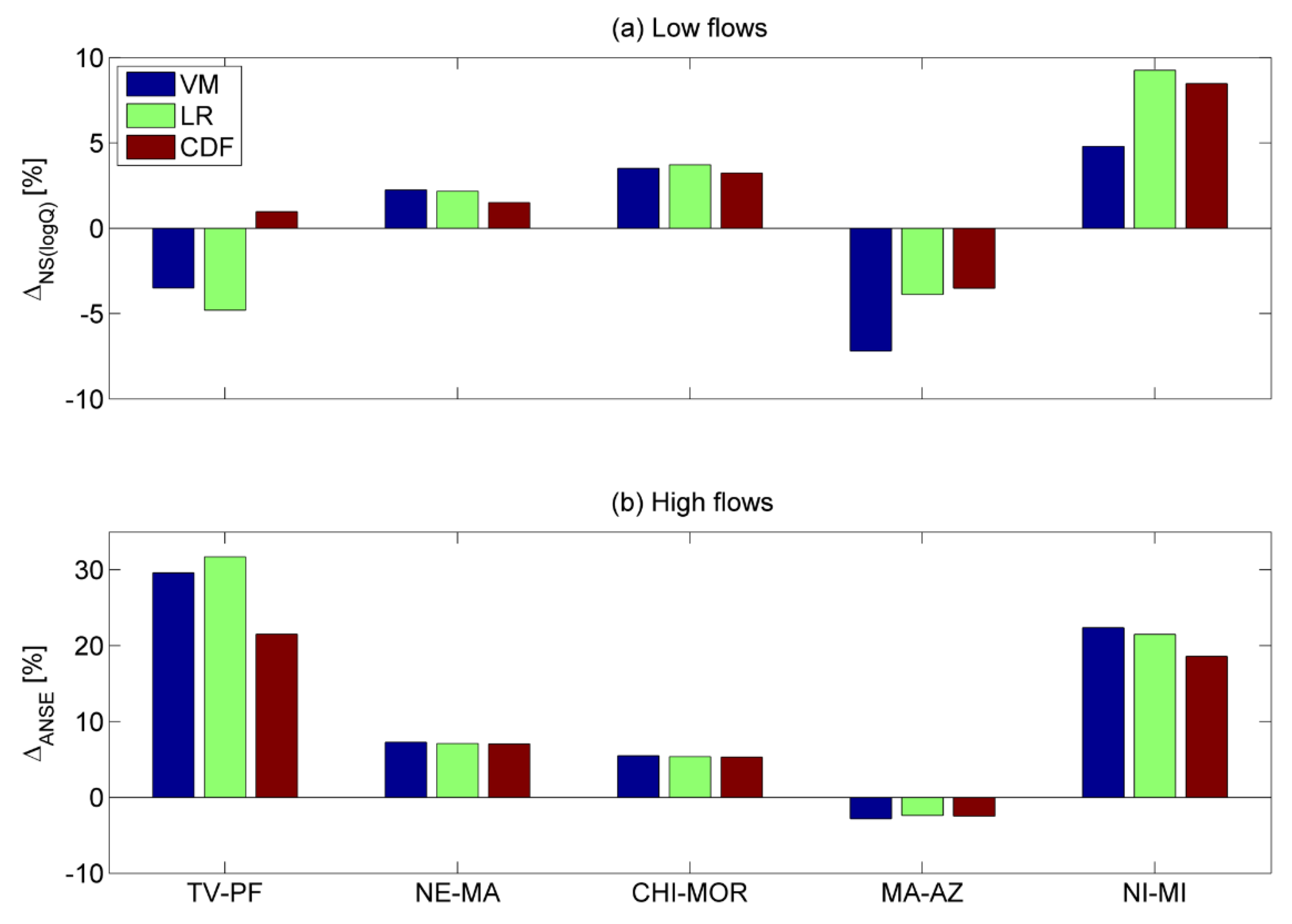
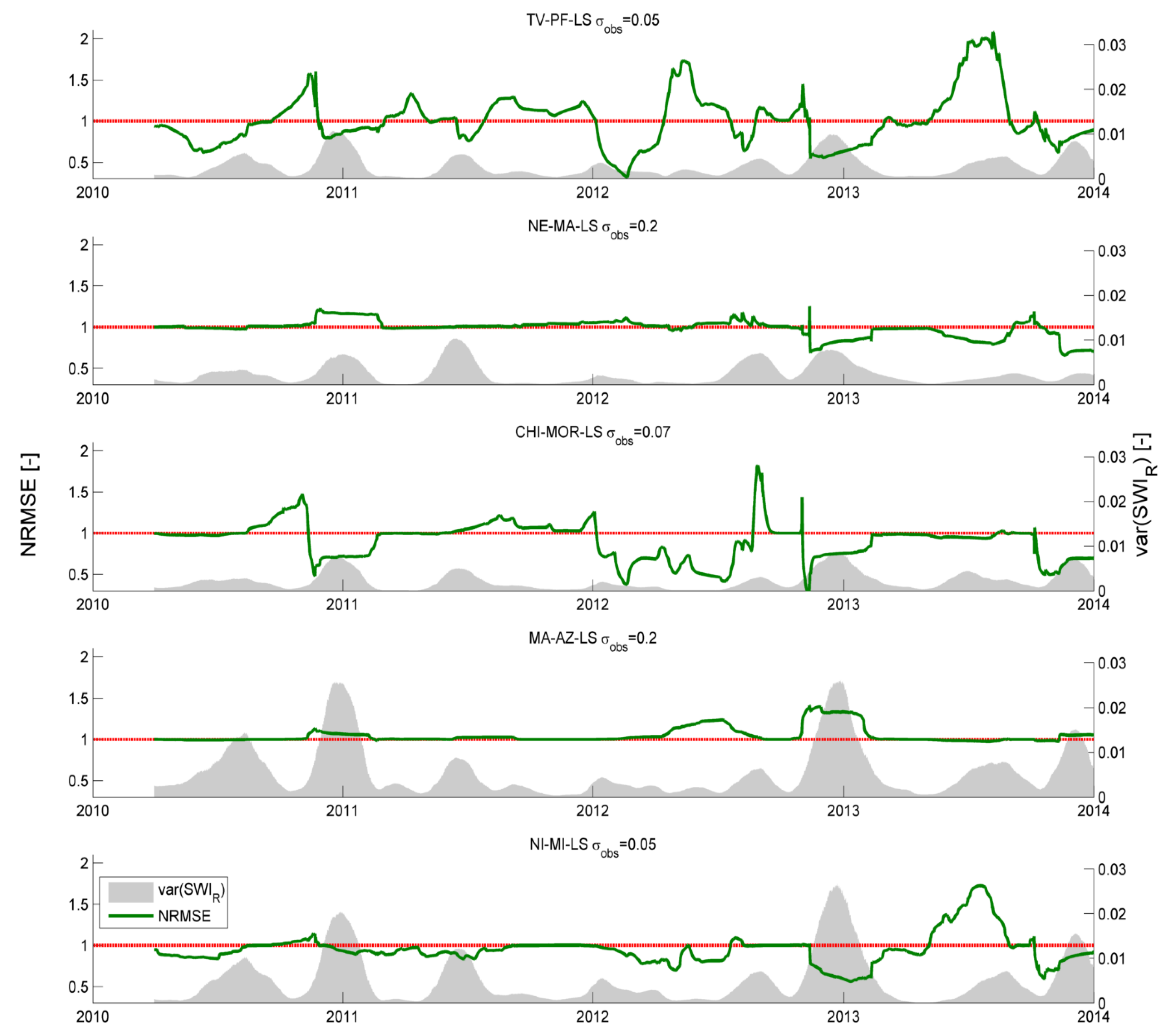
4.5. Discussion
| Factors | What Has Been Done | Findings |
|---|---|---|
| Model error | We performed a sensitivity analysis and calibrated the perturbation of the parameters and of the rainfall for calculating the optimal value of the ensemble statistical indexes | The results are good but we observed a problem of equifinality in which different perturbations lead to same values of the ensemble statistical indexes. |
| Catchment area, topography and soil type | We compared the performance of the assimilation for different catchments characterized by different areas (140–2000 km2) and soil type | We did not observe any effect of the catchment area but catchment specific characteristics may prevent positive results of the DA |
| Rescaling technique | We compared the performance of the assimilation for three different RTs (LR, VM, CDF) | We obtained a uniform pattern of performance of the DA for LR, VM and CDF. We concluded that simple techniques may be equally valid as easier to implement |
| Observation error | We chose different observation errors and tested their optimality in the DA experiments | We obtained that adjacent and similar catchments have very different optimal observation errors, therefore its appropriate choice may strongly depend on a correct model error estimation |
| Flood magnitude | We explored the performance of the DA for low and high flows | We found larger improvements for high flow conditions. |
| Seasonality | We performed a seasonal analysis and compared it against the SM temporal variability | We obtained that DA performance during the year that has a relation with the SM temporal variability. Thus, we advise that this parameter must be taken into consideration when analyzing possible effects of seasonality in the DA of SM. |
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Brocca, L.; Melone, F.; Moramarco, T. On the estimation of antecedent wetness conditions in rainfall–runoff modelling. Hydrol. Process. 2008, 642, 629–642. [Google Scholar] [CrossRef]
- Tramblay, Y.; Bouaicha, R.; Brocca, L.; Dorigo, W.; Bouvier, C.; Camici, S.; Servat, E. Estimation of antecedent wetness conditions for flood modelling in northern Morocco. Hydrol. Earth Syst. Sci. 2012, 16, 4375–4386. [Google Scholar] [CrossRef]
- Coustau, M.; Bouvier, C.; Borrell-Estupina, V.; Jourde, H. Flood modelling with a distributed event-based parsimonious rainfall-runoff model: Case of the karstic Lez river catchment. Nat. Hazard. Earth Syst. Sci. 2012, 12, 1119–1133. [Google Scholar] [CrossRef]
- Van Steenbergen, N.; Willems, P. Increasing river flood preparedness by real-time warning based on wetness state conditions. J. Hydrol. 2013, 489, 227–237. [Google Scholar] [CrossRef]
- Liu, Y.; Gupta, H.V. Uncertainty in hydrologic modeling: Toward an integrated data assimilation framework. Water Resour. Res. 2007, 43, 1–18. [Google Scholar] [CrossRef]
- Tramblay, Y.; Bouvier, C.; Ayral, P.; Marchandise, A. Impact of rainfall spatial distribution on rainfall-runoff modelling efficiency and initial soil moisture conditions estimation. Nat. Hazards Earth Syst. Sci. 2011, 11, 157–170. [Google Scholar] [CrossRef]
- Bárdossy, A.; Das, T. Influence of rainfall observation network on model calibration and application. Hydrol. Earth Syst. Sci. Discuss. 2006, 3, 3691–3726. [Google Scholar] [CrossRef]
- Zehe, E.; Becker, R.; Bárdossy, A.; Plate, E. Uncertainty of simulated catchment runoff response in the presence of threshold processes: Role of initial soil moisture and precipitation. J. Hydrol. 2005, 315, 183–202. [Google Scholar] [CrossRef]
- Grayson, R.; Bloschl, G. Spatial Patterns in Catchment Hydrology: Observations and Modelling, 1st ed.; Cambridge University Press: New York, NY, USA, 2001. [Google Scholar]
- Gupta, H.V.; Sorooshian, S.; Yapo, P.O. Toward improved calibration of hydrologic models: Multiple and noncommensurable measures of information. Water Resour. Res. 1998, 34, 751–763. [Google Scholar] [CrossRef]
- Bartalis, Z.; Wagner, W.; Naeimi, V.; Hasenauer, S.; Scipal, K.; Bonekamp, H.; Figa, J.; Anderson, C. Initial soil moisture retrievals from the METOP-A Advanced Scatterometer (ASCAT). Geophys. Res. Lett. 2007, 34, L20401. [Google Scholar] [CrossRef]
- Owe, M.; de Jeu, R.; Holmes, T. Multisensor historical climatology of satellite-derived global land surface moisture. J. Geophys. Res. 2008, 113, F01002. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Waldteufel, P.; Wigneron, J.-P.; Delwart, S.; Cabot, F.; Boutin, J.; Escorihuela, M.-J.; Font, J.; Reul, N.; Gruhier, C.; et al. The SMOS mission: New tool for monitoring key elements ofthe global water cycle. IEEE Proc. 2010, 98, 666–687. [Google Scholar] [CrossRef]
- Entekhabi, D.; Njoku, E.G.; O’Neill, P.E.; Kellogg, K.H.; Crow, W.T.; Edelstein, W.N.; Entin, J.K.; Goodman, S.D.; Jackson, T.J.; Johnson, J.; et al. The soil moisture active passive (SMAP) mission. IEEE Proc. 2010, 98, 704–716. [Google Scholar] [CrossRef]
- Pauwels, V.R.N.; Hoeben, R.; Verhoest, N.E.C.; De Troch, F.P.; Troch, P.A. Improvement of TOPLATS-based discharge predictions through assimilation of ERS-based remotely sensed soil moisture values. Hydrol. Process. 2002, 16, 995–1013. [Google Scholar] [CrossRef]
- Reichle, R.; McLaughlin, D.B.; Entekhabi, D. Hydrologic data assimilation with the ensemble Kalman filter. Mon. Weather Rev. 2002, 130, 103–114. [Google Scholar] [CrossRef]
- Brocca, L.; Moramarco, T. Assimilation of surface-and root-zone ASCAT soil moisture products into rainfall–runoff modeling. IEEE Trans. Geosci. Remote Sens. 2012, 50, 2542–2555. [Google Scholar] [CrossRef]
- Draper, C.; Mahfouf, J.F.; Calvet, J.C.; Martin, E.; Wagner, W. Assimilation of ASCAT near-surface soil moisture into the SIM hydrological model over France. Hydrol. Earth Syst. Sci. 2011, 15, 3829–3841. [Google Scholar] [CrossRef]
- Matgen, P.; Fenicia, F.; Heitz, S.; Plaza, D.; de Keyser, R.; Pauwels, V.R.N.; Wagner, W.; Savenije, H. Can ASCAT-derived soil wetness indices reduce predictive uncertainty in well-gauged areas? A comparison with in situ observed soil moisture in an assimilation application. Adv. Water Resour. 2012, 44, 49–65. [Google Scholar] [CrossRef]
- Chen, F.; Crow, W.T.; Starks, P.J.; Moriasi, D.N. Improving hydrologic predictions of a catchment model via assimilation of surface soil moisture. Adv. Water Resour. 2011, 34, 526–536. [Google Scholar] [CrossRef]
- Chen, F.; Crow, W.T.; Ryu, D. Dual forcing and state correction via soil moisture assimilation for improved rainfall-runoff modeling. J. Hydrometeorol. 2014, 15, 1832–1848. [Google Scholar] [CrossRef]
- Alvarez-Garreton, C.; Ryu, D.; Western, A.W.; Su, C.-H.; Crow, W.T.; Robertson, D.E.; Leahy, C. Improving operational flood ensemble prediction by the assimilation of satellite soil moisture: Comparison between lumped and semi-distributed schemes. Hydrol. Earth Syst. Sci. 2015, 19, 1659–1676. [Google Scholar] [CrossRef]
- Zhou, Y.; McLaughlin, D.; Entekhabi, D. Assessing the performance of the ensemble kalman filter for land surface data assimilation. Mon. Weather Rev. 2006, 134, 2128–2142. [Google Scholar] [CrossRef]
- Evensen, G. The ensemble Kalman filter for combined state and parameter estimation. IEEE Control Syst. 2009, 83–104. [Google Scholar] [CrossRef]
- Wagner, W.; Lemoine, G.; Rott, H. A method for estimating soil moisture from ERS scatterometer and soil data. Remote Sens. Environ. 1999, 70, 191–207. [Google Scholar] [CrossRef]
- Crow, W.T.; Van Loon, E. Impact of incorrect model error assumptions on the sequential assimilation of remotely sensed surface soil moisture. J. Hydrometeorol. 2006, 7, 421–432. [Google Scholar] [CrossRef]
- Alvarez-Garreton, C.; Ryu, D.; Western, A.W.; Crow, W.; Robertson, D.; States, U. Impact of observation error structure on satellite soil moisture assimilation into a rainfall-runoff model. In Proceedings of the 20th International Congress on Modelling and Simulation, Adelaide, Australia, 1–6 December 2013; pp. 1–6.
- Crow, W.T.; Van Den Berg, M.J. An improved approach for estimating observation and model error parameters in soil moisture data assimilation. Water Resour. Res. 2010, 46, 1–12. [Google Scholar] [CrossRef]
- De Lannoy, G.J.M.; Houser, P.R.; Pauwels, V.R.N.; Verhoest, N.E.C. Assessment of model uncertainty for soil moisture through ensemble verification. J. Geophys. Res. 2006, 111, D10101. [Google Scholar] [CrossRef]
- Dorigo, W.A.; Scipal, K.; Parinussa, R.M.; Liu, Y.Y.; Wagner, W.; de Jeu, R.A.M.; Naeimi, V. Error characterisation of global active and passive microwave soil moisture datasets. Hydrol. Earth Syst. Sci. 2010, 14, 2605–2616. [Google Scholar] [CrossRef]
- Brocca, L.; Hasenauer, S.; Lacava, T.; Melone, F.; Moramarco, T.; Wagner, W.; Dorigo, W.; Matgen, P.; Martínez-Fernández, J.; Llorens, P.; et al. Soil moisture estimation through ASCAT and AMSR-E sensors: An intercomparison and validation study across Europe. Remote Sens. Environ. 2011, 115, 3390–3408. [Google Scholar] [CrossRef]
- Su, C.-H.; Ryu, D.; Western, A.W.; Wagner, W. De-noising of passive and active microwave satellite soil moisture time series. Geophys. Res. Lett. 2013, 40, 3624–3630. [Google Scholar] [CrossRef]
- Reichle, R.H.; Koster, R.D. Assessing the impact of horizontal error correlations in background fields on soil moisture estimation. J. Hydrometeorol. 2003, 4, 1229–1242. [Google Scholar] [CrossRef]
- Lievens, H.; Tomer, S.K.; Al Bitar, A.; De Lannoy, G.J.M.; Drusch, M.; Dumedah, G.; Hendricks Franssen, H.-J.; Kerr, Y.H.; Martens, B.; Pan, M.; et al. SMOS soil moisture assimilation for improved hydrologic simulation in the Murray Darling Basin, Australia. Remote Sens. Environ. 2015, 168, 146–162. [Google Scholar] [CrossRef]
- Koster, R.D.; Guo, Z.; Yang, R.; Dirmeyer, P.A.; Mitchell, K.; Puma, M.J. On the nature of soil moisture in land surface models. J. Clim. 2009, 22, 4322–4335. [Google Scholar] [CrossRef]
- Reichle, R.H.; Koster, R.D. Bias reduction in short records of satellite soil moisture. Geophys. Res. Lett. 2004, 31, L19501. [Google Scholar] [CrossRef]
- Alvarez-Garreton, C.; Ryu, D.; Western, A.W.; Crow, W.T.; Robertson, D.E. The impacts of assimilating satellite soil moisture into a rainfall–runoff model in a semi-arid catchment. J. Hydrol. 2014, 519, 2763–2774. [Google Scholar] [CrossRef]
- Yilmaz, M.T.; Crow, W.T. The optimality of potential rescaling approaches in land data assimilation. J. Hydrometeorol. 2013, 14, 650–660. [Google Scholar] [CrossRef]
- Su, C.; Ryu, D.; Crow, W.T.; Western, A.W. Beyond triple collocation: Applications to soil moisture monitoring. J. Geophys. Res. Atmos. 2014, 119, 6419–6439. [Google Scholar] [CrossRef]
- Brocca, L.; Moramarco, T.; Dorigo, W.; Wagner, W. Assimilation of satellite soil moisture data into rainfall-runoff modelling for several catchments worldwide. In Proceedings of 2013 IEEE Geoscience and Remote Sensing Symposium, Melbourne, Australia, 21–26 July 2013; pp. 2281–2284.
- Djuric, P.; Kotecha, J.; Zhang, J.; Huang, Y.; Ghirmai, T.; Bugallo, M.F.; Miguez, J. Particle filtering. Signal Process. Mag. 2003, 20, 19–38. [Google Scholar] [CrossRef]
- Matgen, P.; Heitz, S.; Hasenauer, S.; Hissler, C.; Brocca, L.; Hoffmann, L.; Wagner, W.; Savenije, H.H.G. On the potential of MetOp ASCAT-derived soil wetness indices as a new aperture for hydrological monitoring and prediction: A field evaluation over Luxembourg. Hydrol. Process. 2012, 26, 2346–2359. [Google Scholar] [CrossRef]
- Corato, G.; Matgen, P.; Fenicia, F.; Schlaffer, S.; Chini, M. Assimilating satellite-derived soil moisture products into a distributed hydrological model. In Proceedings of 2014 IEEE Geoscience and Remote Sensing Symposium, Quebec, QC, Canada, 14 July 2014; pp. 3315–3318.
- Moradkhani, H.; Hsu, K.-L.; Gupta, H.; Sorooshian, S. Uncertainty assessment of hydrologic model states and parameters: Sequential data assimilation using the particle filter. Water Resour. Res. 2005, 41, W05012. [Google Scholar] [CrossRef]
- H-SAF. Available online: http://hsaf.meteoam.it (accessed on 7 September 2015).
- Vachaud, G.; Passerat De Silans, A.; Balabanis, P.; Vauclin, M. Temporal stability of spatially measured soil water probability density function. Soil Sci. Soc. American J. 1985, 49, 822–828. [Google Scholar] [CrossRef]
- Brocca, L.; Melone, F.; Moramarco, T.; Wagner, W.; Hasenauer, S. ASCAT soil wetness index validation through in situ and modeled soil moisture data in central Italy. Remote Sens. Environ. 2010, 114, 2745–2755. [Google Scholar] [CrossRef]
- Melone, F.; Neri, N.; Morbidelli, R.; Saltalippi, C. A conceptual model for flood prediction in basins of moderate size. In Applied Simulation and Modeling; Hamza, M.H., Ed.; IASTED Acta Press: Anaheim, CA, USA, 2001; pp. 461–466. [Google Scholar]
- USDA, SCS. National Engineering Handbook: Hydrology, Section 4; US Department of Agricolture, Soil Conservation Service: Washington, DC, United States, 1985; Chapters 4–10. [Google Scholar]
- Pruitt, W.O.; Doorenbos, J. Background and development of methods to predict reference crop evapotranspiration (ETo). Guidel. Predict. Crop Water Requir. 1977, 24, 108–119. [Google Scholar]
- Brocca, L.; Melone, F.; Moramarco, T.; Morbidelli, R. Antecedent wetness conditions based on ERS scatterometer data. J. Hydrol. 2009, 364, 73–87. [Google Scholar] [CrossRef]
- Melone, F.; Corradini, C.; Singh, V.P. Lag prediction in ungauged basins: An investigation through actual data of the upper Tiber River valley. Hydrol. Process. 2002, 16, 1085–1094. [Google Scholar] [CrossRef]
- Burgers, G.; Jan van Leeuwen, P.; Evensen, G. Analysis scheme in the ensemble kalman filter. Mon. Weather Rev. 1998, 126, 1719–1724. [Google Scholar] [CrossRef]
- Albergel, C.; Rüdiger, C.; Pellarin, T.; Calvet, J.-C.; Fritz, N.; Froissard, F.; Suquia, D.; Petitpa, A.; Piguet, B.; Martin, E. From near-surface to root-zone soil moisture using an exponential filter: An assessment of the method based on in-situ observations and model simulations. Hydrol. Earth Syst. Sci. 2008, 5, 1603–1640. [Google Scholar] [CrossRef]
- Dee, D.P.; Da Silva, A.M. Data assimilation in the presence of forecast bias. Q. J. R. Meteorol. Soc. 1998, 124, 269–295. [Google Scholar] [CrossRef]
- Reichle, R.H.; Crow, W.T.; Keppenne, C.L. An adaptive ensemble Kalman filter for soil moisture data assimilation. Water Resour. Res. 2008, 44, W03423. [Google Scholar] [CrossRef]
- Drusch, M. Observation operators for the direct assimilation of TRMM microwave imager retrieved soil moisture. Geophys. Res. Lett. 2005, 32, L15403. [Google Scholar] [CrossRef]
- Su, C.-H.; Ryu, D. Multi-scale analysis of bias correction of soil moisture. Hydrol. Earth Syst. Sci. 2015, 19, 17–31. [Google Scholar] [CrossRef]
- Tian, Y.; Huffman, G.J.; Adler, R.F.; Tang, L.; Sapiano, M.; Maggioni, V.; Wu, H. Modeling errors in daily precipitation measurements: Additive or multiplicative? Geophys. Res. Lett. 2013, 40, 2060–2065. [Google Scholar] [CrossRef]
- Turner, M.; Walker, J.; Oke, P. Ensemble member generation for sequential data assimilation. Remote Sens. Environ. 2008, 112, 1421–1433. [Google Scholar] [CrossRef]
- Nash, J.; Sutcliffe, J. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Hoffmann, L.; El Idrissi, A.; Pfister, L.; Hingray, B.; Guex, F.; Musy, A.; Humbert, J.; Drogue, G.; Leviandier, T. Development of regionalized hydrological models in an area with short hydrological observation series. River Res. Appl. 2004, 20, 243–254. [Google Scholar] [CrossRef]
- Moramarco, T.; Singh, V.P.; Alta, V.M.; Rouge, B. Simple method for relating local stage and remote discharge. J. Hydrol. Eng. 2001, 6, 78–81. [Google Scholar] [CrossRef]
- Brocca, L.; Melone, F.; Moramarco, T.; Wagner, W.; Naeimi, V.; Bartalis, Z.; Hasenauer, S. Improving runoff prediction through the assimilation of the ASCAT soil moisture product. Hydrol. Earth Syst. Sci. 2010, 14, 1881–1893. [Google Scholar] [CrossRef]
- Albergel, C.; de Rosnay, P.; Gruhier, C.; Muñoz-Sabater, J.; Hasenauer, S.; Isaksen, L.; Kerr, Y.; Wagner, W. Evaluation of remotely sensed and modelled soil moisture products using global ground-based in situ observations. Remote Sens. Environ. 2012, 118, 215–226. [Google Scholar] [CrossRef]
- Massari, C.; Brocca, L.; Barbetta, S.; Papathanasiou, C.; Mimikou, M.; Moramarco, T. Using globally available soil moisture indicators for flood modelling in Mediterranean catchments. Hydrol. Earth Syst. Sci. 2014, 18, 839–853. [Google Scholar] [CrossRef]
- Zwieback, S.; Dorigo, W.; Wagner, W. Temporal error variability of coarse scale soil moisture products-case study in central Spain. In Proceedings of the 2012 IEEE International: Geoscience and Remote Sensing Symposium, Munich, Bavaria, Germany, 22–27 July 2012; pp. 722–725.
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Massari, C.; Brocca, L.; Tarpanelli, A.; Moramarco, T. Data Assimilation of Satellite Soil Moisture into Rainfall-Runoff Modelling: A Complex Recipe? Remote Sens. 2015, 7, 11403-11433. https://doi.org/10.3390/rs70911403
Massari C, Brocca L, Tarpanelli A, Moramarco T. Data Assimilation of Satellite Soil Moisture into Rainfall-Runoff Modelling: A Complex Recipe? Remote Sensing. 2015; 7(9):11403-11433. https://doi.org/10.3390/rs70911403
Chicago/Turabian StyleMassari, Christian, Luca Brocca, Angelica Tarpanelli, and Tommaso Moramarco. 2015. "Data Assimilation of Satellite Soil Moisture into Rainfall-Runoff Modelling: A Complex Recipe?" Remote Sensing 7, no. 9: 11403-11433. https://doi.org/10.3390/rs70911403
APA StyleMassari, C., Brocca, L., Tarpanelli, A., & Moramarco, T. (2015). Data Assimilation of Satellite Soil Moisture into Rainfall-Runoff Modelling: A Complex Recipe? Remote Sensing, 7(9), 11403-11433. https://doi.org/10.3390/rs70911403