Upscaling In Situ Soil Moisture Observations to Pixel Averages with Spatio-Temporal Geostatistics

Abstract

Validation of satellite-based soil moisture products is necessary to provide users with an assessment of their accuracy and reliability and to ensure quality of information. A key step in the validation process is to upscale point-scale, ground-based soil moisture observations to satellite-scale pixel averages. When soil moisture shows high spatial heterogeneity within pixels, a strategy which captures the spatial characteristics is essential for the upscaling process. In addition, temporal variation in soil moisture must be taken into account when measurement times of ground-based and satellite-based observations are not the same. We applied spatio-temporal regression block kriging (STRBK) to upscale in situ soil moisture observations collected as time series at multiple locations to pixel averages. STRBK incorporates auxiliary information such as maps of vegetation and land surface temperature to improve predictions and exploits the spatio-temporal correlation structure of the point-scale soil moisture observations. In addition, STRBK also quantifies the uncertainty associated with the upscaled soil moisture which allows bias detection and significance testing of satellite-based soil moisture products. The approach is illustrated with a real-world application for upscaling in situ soil moisture observations for validating the Polarimetric L-band Multi-beam Radiometer (PLMR) retrieved soil moisture product in the Heihe Water Allied Telemetry Experimental Research experiment (HiWATER). The results show that STRBK yields upscaled soil moisture predictions that are sufficiently accurate for validation purposes. Comparison of the upscaled predictions with PLMR soil moisture observations shows that the root-mean-squared error of the PLMR soil moisture product is about 0.03 m³·m⁻³ and can be used as a high-resolution soil moisture product for watershed-scale soil moisture monitoring.

1. Introduction

Soil moisture is a key variable in controlling the exchange of water and energy fluxes between the hydrosphere, biosphere, and atmosphere [1]. Understanding soil moisture variation in space and time is, therefore, a critical part of many scientific studies and operational applications, such as flood forecasting, weather and climate prediction, and crop growth modeling and monitoring [2]. In practice, soil moisture is generally obtained through in situ measurements, remote sensing technology, or land surface models. In recent years, a series of global-scale and regional-scale remotely sensed surface soil moisture products have become available. However, soil moisture remote sensing retrieval may contain large uncertainties because it involves indirect measurement methods that are prone to all sorts of errors and because of the inherent complexity of the underlying physical processes [3]. Applications highlight the need to validate satellite-based soil-moisture products against ground-based observations, traditionally via in situ measurements.

One significant challenge for the validation of satellite-based soil moisture products with ground-based observations is the disparity in observation scales of ground-based and satellite-based observing systems [4,5]. It is well known that in situ measurements of soil moisture are commonly made at point support (~5² cm²), whereas satellite sensors provide soil moisture estimates for a much larger spatial “block” support (typically > 10² km²). Considering the large within-block spatial variation of point-support soil moisture [6], a large number of ground-based measurements are needed to upscale soil moisture to a satellite-based footprint for validation purposes. In addition, soil moisture varies over time and ground-based measurements are not all taken simultaneously nor at the same time as the satellite-based measurement.

A number of studies have been conducted to validate satellite-based soil moisture products by upscaling in situ measurements [5,7,8,9]. These studies are based on the assumption that in situ measurements have negligible error compared to the satellite-based estimates. Based on this assumption, various strategies have been proposed in the literature for upscaling ground-based soil moisture observations to a larger support, see Vereecken, et al. [10] or Crow, et al. [4] for a review. Specifically, the most direct way is based on statistical sampling theory. The average value of soil moisture in a satellite footprint is estimated by the arithmetic mean of multiple ground-based measurements at randomly selected locations within the footprint. A second strategy is to implement a geostatistical interpolation algorithm, such as block-kriging, that predicts the spatial average while taking spatial autocorrelation into account [11]. A third strategy incorporates intensive field campaigns [12] while a fourth method is based on the results of a distributed land surface model [8,13].

Understanding soil moisture spatial variation is of principal importance for estimating soil moisture at the remote sensing pixel scale. By quantifying its spatial variation through the covariance function (or variogram), kriging produces optimal predictions and associated prediction error variances from incomplete and possibly noisy measurements. Since soil moisture varies not only in space but also in time, upscaling ground-based point observations must also take temporal variation into account. Here, we propose a new upscaling method in the context of spatio-temporal data. To be specific, a geostatistical method that uses spatio-temporal regression block kriging (STRBK) is used to scale up in situ soil moisture spatio-temporal observations. The advantage of upscaling with STRBK is that it corrects time differences between ground-based measurements and satellite-based measurements. It can also make use of a larger set of ground-based measurements, because it is not restricted to a narrow time interval around the time at which the satellite-based measurement was taken. The objective of this study is to improve the reliability of satellite soil-moisture product validation using spatio-temporal geostatistics.

The remainder of this paper is organized as follows. Section 2 describes the study area and presents the data sets used as a basis for upscaling. The methodology for upscaling with STRBK is given in Section 3. Finally, the results of upscaling and the validation of remotely sensed soil moisture products are presented and discussed in Section 4 and Section 5. Conclusions are drawn in Section 6.

2. Study Area and Data Description

In 2012, a number of field campaigns in the context of the HiWATER project [14] were carried out to perform simultaneous airborne, satellite-borne, and ground-based remote-sensing experiments at various scales of the Heihe River Basin (HRB), China. The study area used here is the Yingke-Daman irrigation district (Figure 1), which is an artificial oasis-riparian ecosystem-wetland-desert compound in the middle reaches of the HRB. The district covers 38°50′–38°54′N and 100°19′–100°24′E, and is in a typical semi-arid and arid agricultural region. Cornfields cover most of the area (~75%), but land cover also includes orchards, buildings, roads, and other vegetation. Annual precipitation is approximately 122 mm, while potential evaporation is about 1200–1800 mm per year. Agricultural irrigation is essential for crop growth. Hence, there is a dense network of canals that serve as the irrigation system. The soil moisture pattern is primarily controlled by the artificial irrigation management and the spatial distribution of crops. During the growing season, soil moisture varies from 8 vol % to saturation because of irrigation and precipitation.

To acquire the spatial variation and temporal dynamics of soil moisture during the growing season, we used an airborne Polarimetric L-band (1.4 GHz) Multi-beam Radiometer (PLMR) to measure soil moisture at 700 m resolution [15]. The HiWATER project collected PLMR imagery of the study area on six occasions, always around noon on 30 June, 3 July, 7 July, 10 July, 26 July, and 2 August, 2012. PLMR measures both V and H polarizations using a single receiver with polarization switching at incidence angles of ±7°, ±21.5°, and ±38.5°. Surface soil moisture was retrieved through an L-band microwave emission of the biosphere (L-MEB) model and Levenberg-Marquardt optimization with airborne PLMR radiometer data and Moderate Resolution Imaging Spectroradiometer (MODIS) land surface temperature and leaf area index products [16,17]. Previous studies showed that the L-MEB model can achieve 0.04 m³·m⁻³ accuracy levels for soil moisture retrievals [17]. In addition to remote sensing data, a ground-based Ecological and Hydrological Wireless Sensor Network (EHWSN) was also installed to monitor farmland soil moisture during the HiWATER campaign [18]. Specifically, fifty EHWSN nodes named WATERNET were deployed to measure soil moisture at 0–4 cm depth for validation of the remote sensing product. The spatial distribution of WATERNET is shown in Figure 1. It covers approximately 36 (6 × 6) PLMR pixels. Soil moisture was measured using the frequency-domain reflectometry method and a Hydro Probe II (HP-II) sensor. The laboratory calibration shows that the WATERNET soil moisture instrument error is 0.010 m³·m⁻³ [19]. WATERNET observes soil moisture at 1-minute temporal resolution. The high measurement accuracy and synchronization with satellite and airborne remote sensing overpasses makes WATERNET suitable for validation of the PLMR soil moisture products. In addition, a 1 km × 1 km pixel (the black square in Figure 1), which contains 50 EHWSN nodes jointly named SoilNET, was used as an intensive observation zone to capture small-scale soil moisture variation [20]. SoilNET is an ad hoc network designed by the Jülich Research Center [21]. It measures soil moisture at 0–4 cm depth every 5 min. Laboratory calibration showed that the instrument error of SoilNET is 0.015 m³·m⁻³, which is larger than that of WATERNET.

Figure 1. Soil moisture monitoring network in the Yingke–Daman irrigation district. The triangles and circles show the measurement locations of the WATERNET and SoilNET wireless sensor network, respectively. The background is a 3 m resolution Thermal Airborne Spectrographic Imager (TASI) for land surface Temperature (LST) retrieval.

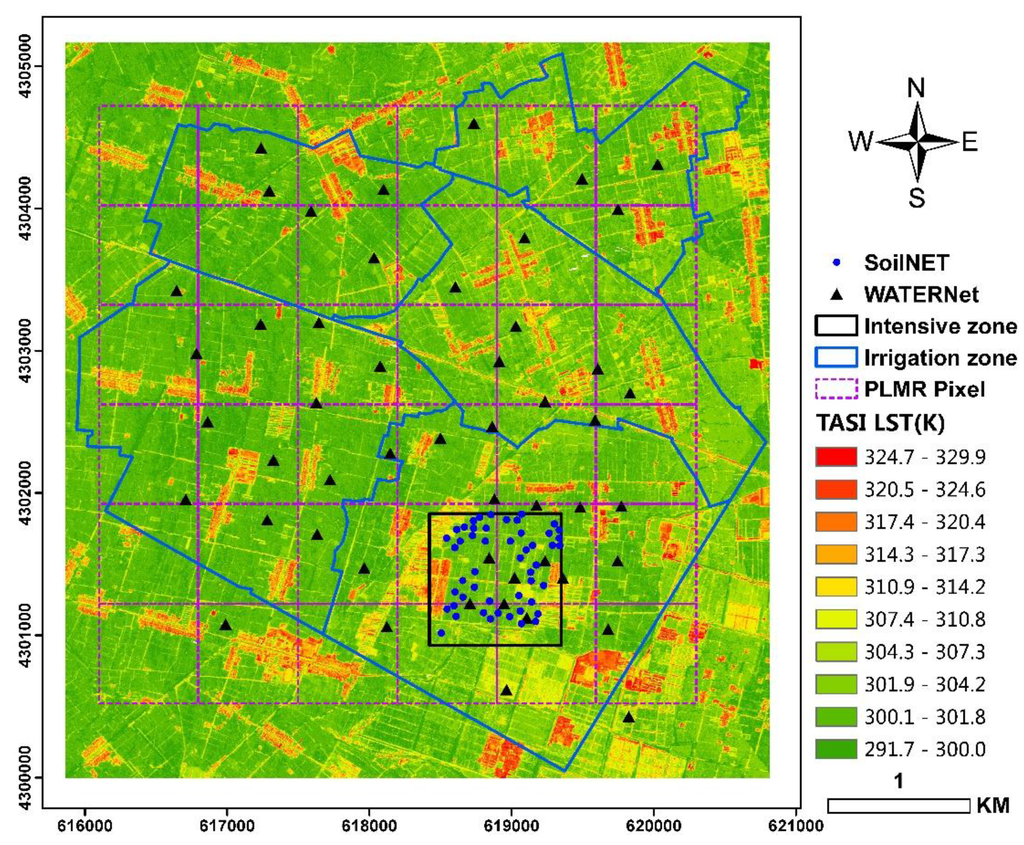
Figure 1. Soil moisture monitoring network in the Yingke–Daman irrigation district. The triangles and circles show the measurement locations of the WATERNET and SoilNET wireless sensor network, respectively. The background is a 3 m resolution Thermal Airborne Spectrographic Imager (TASI) for land surface Temperature (LST) retrieval.

One challenge in upscaling soil moisture arises from the heterogeneity of the soil surface. As indicated by the surface temperature shown in Figure 1, the sparsely located WATERNET nodes are insufficient to capture the spatial variation of soil moisture, especially during irrigation times. Therefore, the spatial upscaling algorithm that relies on in situ observations only yields a crude estimate of pixel-level soil moisture. Because ground-based soil moisture is correlated with soil temperature and land cover type, remote sensing retrievals of these variables provide extra information about the spatial distribution of soil moisture. More specifically, we employed a number of auxiliary variables as reported in Ge, et al. [22], including land surface temperature (LST), normalized difference vegetation index (NDVI) and fractional vegetation cover (FVC), all derived from the Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER). These auxiliary variables have a spatial resolution of 90 m, which is much finer than the target coarse remote sensing product. We only chose two time periods for validation, i.e., 10 July and 2 August, when the weather was clear and the satellite passes were available for the entire study area.

3. Methods

3.1. Upscaling with Spatio-Temporal Regression Block Kriging

3.1.1. Spatio-Temporal Random Field Model

The spatio-temporal variation of soil moisture at point support can be represented by considering a continuous variable $Z=\left\{Z\left(s,t\right)\right|s\in \text{S},t\in T$} that varies within a spatial domain S and time interval T. Let Z be observed at n spatio-temporal observation points (s_i, t_i), i = 1, …, n. The objective of spatio-temporal upscaling is to make a prediction of Z(B), i.e., the average of Z for an unobserved spatio-temporal “block” B, which is defined as a subset of the space-time domain: B ⊂ S × T. For instance, B might be a 1 × 1 square kilometer area integrated over a 24 h period. In order to predict Z(B) we must first define a model for Z.

We assume that the spatio-temporal random field Z is normally distributed and can be decomposed into a deterministic trend m and a stochastic residual R [23,24,25], given by:

$$Z(s,t)=m(s,t)+R(s,t)$$

(1)

where m(s, t) is a deterministic trend that represents variation that can be explained by external environmental “covariates”. R(s, t) is the spatio-temporal correlated stochastic residual, typically representing small-scale, “noisy” variation.

3.1.2. The Trend Component

The simplest way to model the trend component is to assume that it is an unknown constant. However, this is rarely satisfactory in practice, since we often know the driving factors behind the variation in space and time. Alternatively, the trend can be taken as a function of covariates. If we assume linear relationships, then m(s, t) may be written as [23,25]:

$$m(s,t)={\displaystyle \sum _{i=0}^p{\beta }_i{f}_i(s,t)}$$

(2)

where the β_i are unknown regression coefficients, the f_i are covariates that must be exhaustively known over the spatio-temporal domain, and p is the number of covariates. Covariate f₀ is taken as unity, resulting in β₀ representing the intercept.

We assume that the soil moisture trend is temporally constant during a satellite or airborne remote sensing overpass. Therefore, the trend m(s,t) has only spatial components. For this, a linear multiple regression model is established:

$$\begin{array}{cc}{m}_k=X_k{\beta }_k={\beta }_{0k}+{\beta }_{1k}\cdot LS{T}_k+{\beta }_{2k}\cdot NDV{I}_k+{\beta }_{3k}\cdot FV{C}_k,& k=1,2,\mathrm{...},\end{array}K$$

(3)

where subscript k denotes a different satellite overpass time, and K is the total number of overpass times, X_k is a covariates matrix with dimensions $n\times \left(p+1\right)$, and the β_k are parameters to be estimated. LST, NDVI, and FVC are auxiliary environmental variables extracted by taking the block average of the k-th ASTER fly-over.

3.1.3. The Residual Component

The estimated spatio-temporal trend component is subtracted from the point observations to yield values of the spatio-temporal residual R(s,t) at the n observation points. Since the trend component in Equation (1) cannot explain all variation in soil moisture, the residuals of the regression model will have spatio-temporal variation that in addition might be correlated in space and time. This indicates that a spatio-temporal variogram may be estimated from the residuals at the observation locations and used to predict the residuals using kriging.

We model the spatio-temporal semivariance between residuals R(s_i, t_i) and R(s_j, t_j) with the variogram, assuming space-time second-order stationarity:

$$\gamma (h_{ij},{\tau }_{ij})=\gamma (s_i-s_j,t_i-t_j)=0.5\cdot E\left\{{(R(s_i,t_i)-R(s_j,t_j))}^2\right\}$$

(4)

with h_ij = s_i − s_j and τ_ij = t_i − t_j the distance in space and time, respectively, and E denotes the mathematical expectation. In Equation (4), we assume that the semivariance of R at points (s_i, t_i) and (s_j, t_j) only depends on the separation distance (h_ij, τ_ij). This assumption might be difficult to satisfy for the variable Z but are more plausible for the residual variable R. Note that keeping both spatial and temporal distances separate implies that zonal and geometric space-time anisotropies can be accommodated.

The experimental variogram $\widehat{\gamma }\left(h,\text{τ}\right)$ is computed by:

$$\widehat{\gamma }(h,\tau )=\frac{1}{2N(h,\tau )}{\displaystyle \sum _{i=1}^{N(h,\tau )}{(R(s,t)-R(s+h,t+\tau ))}^2}$$

(5)

where $N\left(h,\text{τ}\right)$ is the number of pairs in the spatio-temporal lag. The covariance $\widehat{C}\left(h,\text{τ}\right)$ can be obtained through $\widehat{C}\left(h,\text{τ}\right)=\widehat{\gamma }\left(\infty ,\infty \right)-\widehat{\gamma }\left(h,\text{τ}\right)$ [26].

Once the experimental variogram $\widehat{\gamma }\left(h,\text{τ}\right)$ or covariance $\widehat{C}\left(h, \text{τ}\right)$ has been obtained, a theoretical spatio-temporal variogram or covariance model may be fitted. The choice of spatio-temporal covariance model and estimation of the model parameters are essential prerequisites for prediction and upscaling [27,28]. Here, we adopt a sum-metric model [23,24,25,29] on the spatio-temporal residual. It assumes that the residual R(s, t) consists of three stationary and independent components: a purely spatial process (with constant realizations over time), a purely temporal process (realizations are constant in space), and a spatio-temporal process for which distance in space is made comparable to distance in time by introducing a space-time anisotropy ratio. We also assume spatial isotropy, so that the spatial distance h becomes a scalar h. Thus, the sum-metric covariance structure can be represented by:

$$C(h,\tau )=C_S(h)+C_T(\tau )+C_{ST}\left(\sqrt{h^2+{(\alpha \cdot \tau )}^2}\right)$$

(6)

where $C_S\left(h\right)$ and $C_T\left(\text{τ}\right)$ are the marginal spatial and temporal covariance functions and $C_{ST}$ is the spatio-temporal interaction component. $C_S\left(h\right)+C_T\left(\text{τ}\right)$ accommodates the presence of space-time zonal anisotropy and $C_{ST}\left(\sqrt{h^2+{\left(\alpha ·\text{τ}\right)}^2}\right)$ allows the presence of a space-time geometric anisotropy, represented with the ratio α, which converts units of temporal separation ($\text{τ}$) to spatial separation (h). Once each of the covariance functions is parameterized, the entire sum-metric model typically consists of ten parameters: three nugget, three sill, and three range parameters, and the anisotropy parameter α.

3.1.4. Spatio-Temporal Regression Block Kriging

Spatio-temporal regression kriging (STRK, also known as spatio-temporal kriging with external drift or spatio-temporal universal kriging) is a recently proposed method that has also been applied in regional and global land surface temperature mapping [23,24]. Here, our primary aim is not spatio(-temporal) mapping but spatio-temporal upscaling. Hence, we extend STRK to spatio-temporal regression block kriging (STRBK).

For STRBK, the target variable (i.e., soil moisture) at block B is defined as:

$$Z(B)\equiv {\displaystyle {\int }_{B}Z(s,t)ds}dt/\left|B\right|$$

(7)

where $\left|B\right|$ is the volume of support B. Z(B) is predicted by:

$$\widehat{Z}(B)={\displaystyle \sum _{i=1}^n{\lambda }_i\cdot Z(s_i,t_i)}$$

(8)

The weights ${\text{λ}}_i$ are obtained by solving the following set of equations:

$$\left[\begin{array}{cc}C& X\\ X^{\prime }& 0\end{array}\right]\left[\begin{array}{c}\lambda \\ \mu \end{array}\right]=\left[\begin{array}{c}{c}_B\\ x_B\end{array}\right]$$

(9)

where C is the variance-covariance matrix of the stochastic residuals at observation points as derived from Equation (6), $c_B={\left[c_1\left(B\right),c_2\left(B\right),\dots ,c_n\left(B\right)\right]}^{\text{'}}$ with $c_i\left(B\right)={{\displaystyle \int }}_{B}C\left(s-s_i,t-t_i\right)dsdt/\left|B\right|$ for i = 1, 2, ..., n, $x_B={\left[1,x_1\left(B\right),x_2\left(B\right),\dots ,x_p\left(B\right)\right]}^{\text{'}}$, with $x_j\left(B\right)={\int }_B{x}_j\left(s,t\right)dsdt/\left|B\right|$ for j = 1, 2, ..., p, and μ are Lagrange multipliers introduced to satisfy the unbiasedness constraint [26]. The solution of Equation (9) for λ and μ yields the best linear unbiased prediction (BLUP) $\widehat{Z}\left(B\right)$, which is given by:

$$\begin{array}{l}\widehat{Z}(B)={\lambda }^{\prime }Z(s,t)={c^{\prime }}_B{C}^{-1}(Z(s,t)-X\widehat{\beta })+x_B\widehat{\beta }=\\ \{c_B+X{(X^{\prime }{C}^{-1}X)}^{-1}(x_B-X^{\prime }{C}^{-1}{c}_B){\}}^{\prime }{C}^{-1}Z(s,t),\end{array}$$

(10)

where $\widehat{\beta }$ is the generalized least-squares (GLS) estimate of the trend coefficients. The STRBK variance is given by

$${\widehat{\sigma }}^2(B)=E{[{\lambda }^{\prime }Z(s,t)-Z(B)]}^2={\sigma }_{B,B}^2-{c^{\prime }}_B{C}^{-1}{c}_B+D^{\prime }{(X^{\prime }{C}^{-1}X)}^{-1}D$$

(11)

where $D=x_B-X^{\prime }{C}^{-1}{c}_B$ and ${\text{σ}}_{B,B}^2$ is the within-block covariance. In practice, the integrals above are commonly approximated by discretizing B with a grid and averaging covariance between locations on the grid.

In the case that there is no external trend (i.e., m(s,t) is constant), STRBK reduces to spatio-temporal ordinary block kriging (STOBK). The predictor and the corresponding prediction error variance of STOBK can be easily obtained from Equations (10) and (11) as:

$$\begin{gathered} \widehat{Z}(B)=\{c_B+1{(1^{\prime }{C}^{-\text{1}}1)}^{-1}(1-1^{\prime }{C}^{-\text{1}}{c}_B){\}}^{\prime }{C}^{-1}Z(s,t), \\ {\widehat{\sigma }}^2\left(B\right)={\sigma }_{B,B}^2-{c^{\prime }}_B{C}^{-1}{c}_B+d^{\prime }{\left(1^{\prime }{C}^{-1}1\right)}^{-1}d \end{gathered}$$

(12)

where $d=1-1^{\prime }{C}^{-1}{c}_B$ and 1 is an n-dimensional row vector whose elements are set to unity.

We applied a set of functions in the R package gstat [30] and spacetime [31] to implement STRBK for soil moisture upscaling. The parameters in Equation (6) are estimated simultaneously by using the optim function available in R language for statistical computing [32].

3.2. Accuracy Assessment

The true soil moisture for a given spatio-temporal support (i.e., the average soil moisture for a pixel over several hours period) cannot be measured without error if the space-time support is large. Therefore, it is difficult to assess the accuracy of the upscaling algorithm directly. In this study, an alternative approach was taken and validation was done as follows. First, the independently deployed SoilNET measurements in the intensive zone (see Figure 1) were averaged for a given spatio-temporal support. Second, the 50-SoilNET-averaged values were regarded as the “ground truth”. Third, the WATERNET-based soil moisture was computed using the method presented in Section 3.1.4. Finally, the upscaling strategies were performed to check whether the “ground truth” can be retrieved according to these available soil moisture values. We examined the difference between the “ground truth” and predicted values using the upscaling error, i.e., $\widehat{Z}\left(B\right)-Z\left(B\right)$. Next, the best performing upscaling strategy will be used to validate the accuracy of PLMR soil moisture product. The difference between the PLMR retrievals and predicted values was evaluated by the metrics of mean error (ME), root-mean-squared error (RMSE), and R-square.

4. Results

4.1. Data Summary

In this study, 28 days of WATERNET surface soil moisture observations were obtained from the HiWATER website [15]. Figure 2 shows a multiple time series plot of 50 WATERNET observations from 9 July to 5 August 2012, made with the mvtsplot package in R [33]. From Figure 2, we can conclude that soil moisture has a significant temporal variation, especially when precipitation (16, 21, 30 July) or irrigation occurs. Moreover, unscheduled agriculture irrigation, particularly between 21 and 30 July, also leads to a strong heterogeneity of soil moisture.

Figure 2. Multiple parallel time series plot of 50 WATERNET soil moisture observations. The top-left panel shows the parallel multiple time series of soil moisture. The yellow to red palette represents variation in surface soil moisture. White represents no data. The right panel presents summary statistics of soil moisture for each node. The black dots denote the median while the horizontal lines represent the lower and upper quartiles. The lower panel shows the average moisture time series of the 50 nodes.

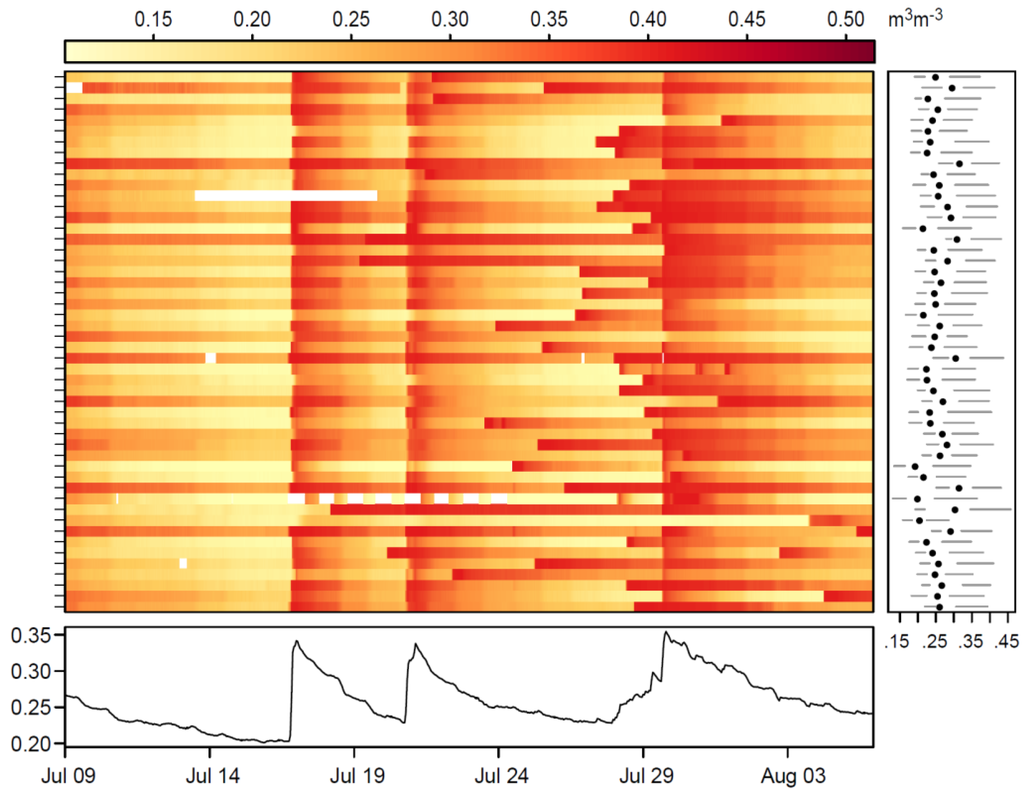
Figure 2. Multiple parallel time series plot of 50 WATERNET soil moisture observations. The top-left panel shows the parallel multiple time series of soil moisture. The yellow to red palette represents variation in surface soil moisture. White represents no data. The right panel presents summary statistics of soil moisture for each node. The black dots denote the median while the horizontal lines represent the lower and upper quartiles. The lower panel shows the average moisture time series of the 50 nodes.

For each of the six flight days, the passing of the PLMR over the study area was around noon. For PLMR soil moisture validation purposes, we only consider observations during three hours before and three hours after satellite or aircraft passes, i.e., from 9:00 to 15:00. Specifically, only two periods, i.e., 10 July and 2 August, were adopted for validation because auxiliary ASTER imagery was available. Figure 2 shows that there was no precipitation or irrigation at these two time periods. Figure 3 shows the LST, NDVI, and FVC products derived from ASTER data at the time of 12:12, 10 July 2012 and 12:18, 2 August 2012, respectively. Since the passing of the aircraft and the ASTER satellite happened almost at the same time, we assumed that the ASTER-derived variables are the same as would have been observed at the time when PLMR passes. Table 1 provides summary statistics of all soil moisture data available at the time of 9:00 to 15:00 on 10 July and 2 August, respectively. As shown in Table 1, soil moisture on 2 August has a higher relative mean value and standard derivation (SD) than that at 10 July. This is due to different irrigation practices within the study area on 2 August (Figure 2).

Table 1. Summary statistics of soil moisture data (m³·m⁻³).

Date	Time Duration		Min	Max	Mean	SD
10 July 2012	9:00–15:00	WATERNET	0.198	0.339	0.256	0.033
		SoilNET	0.221	0.289	0.252	0.027
2 August 2012	9:00–15:00	WATERNET	0.160	0.369	0.274	0.042
		SoilNET	0.237	0.312	0.278	0.034

Table 1. Summary statistics of soil moisture data (m³·m⁻³).

Date	Time Duration		Min	Max	Mean	SD
10 July 2012	9:00–15:00	WATERNET	0.198	0.339	0.256	0.033
		SoilNET	0.221	0.289	0.252	0.027
2 August 2012	9:00–15:00	WATERNET	0.160	0.369	0.274	0.042
		SoilNET	0.237	0.312	0.278	0.034

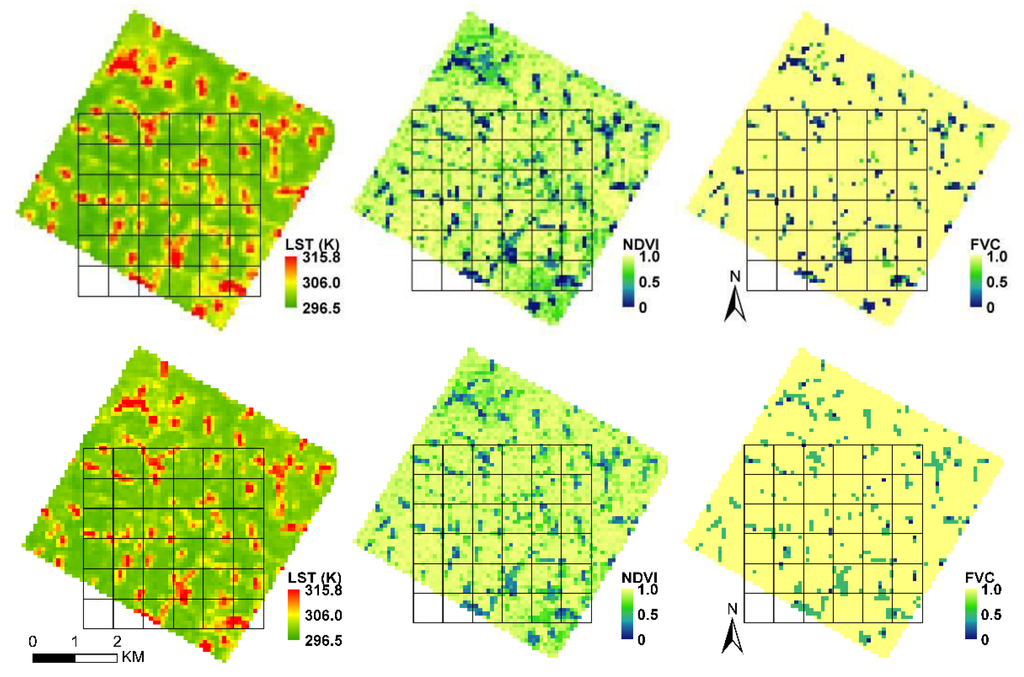
Figure 3. ASTER-derived LST, NDVI, and FVC on 10 July 2012 (top) and 2 August 2012 (bottom). The 6 × 6 grids represent the PLMR pixels coverage.

Figure 3. ASTER-derived LST, NDVI, and FVC on 10 July 2012 (top) and 2 August 2012 (bottom). The 6 × 6 grids represent the PLMR pixels coverage.

4.2. Regression Modeling of Spatial Trends

Results of a correlation analysis revealed that the ASTER LST images were the most significant predictors of soil moisture. The correlation coefficient is around 0.47 in both time periods. The NDVI and FVI have correlation coefficients of 0.36 and 0.14, respectively. The results of linear regression showed that the predictors explain 43% and 47% of the spatial variation of soil moisture for 10 July and 2 August, respectively. The complete list of predictors achieved a precision of ±0.06 m³·m⁻³.

4.3. Variogram Analysis of the Residuals

The left-hand side of Figure 4 shows the residual point sample spatio-temporal variogram. The fitted model (10 variogram parameters described in Section 3.1.3) is shown at the right-hand side of Figure 4. Table 2 summarizes the estimated parameters of the sum-metric variogram model. Note that the marginal spatial component and the spatio-temporal joint component were modeled as Exponential functions. The temporal component on 10 July and 2 August was fitted by pure Nugget function and Exponential function, respectively.

It can be concluded from Figure 4 that the regression residuals have significant correlations both in space and time, and therefore, spatio-temporal kriging of residuals is applicable. However, note that temporal variation is an order of magnitude smaller than spatial variation. The fitted spatio-temporal variogram parameters of the residuals have a significant purely spatial variogram component, while the purely temporal component is absent. This confirms that the temporal variation of soil moisture within six hours is small compared to the spatial variation. Temporal variation of the residual is only contained in the spatio-temporal interaction variogram components. The spatio-temporal anisotropy ratio shows that observation stations with a temporal lag of 1 minute exhibit a similar correlation as stations that are about 1~2 m apart.

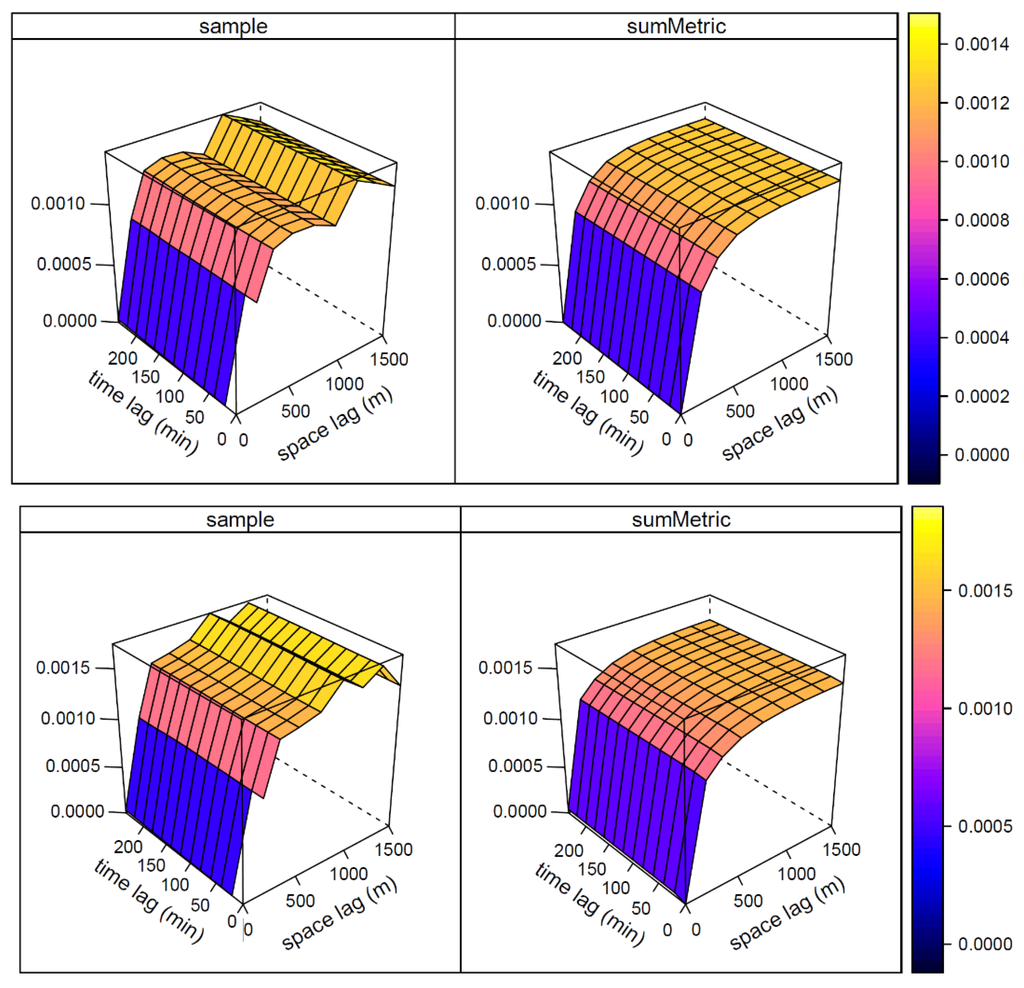
Figure 4. Point sample variogram (left) of residuals from multiple linear regression and the fitted sum-metric model (right) for 10 July (upper), and 2 August 2012 (bottom). Units are (m³·m⁻³)².

Figure 4. Point sample variogram (left) of residuals from multiple linear regression and the fitted sum-metric model (right) for 10 July (upper), and 2 August 2012 (bottom). Units are (m³·m⁻³)².

Table 2. Parameters of the fitted sum-metric variogram model for soil moisture regression residuals.

Date	Component	Model	Nugget	Sill	Range	Anisotropy
10 July	Spatial	Exponential	0	0.00098	201.1 m
	Temporal	Nugget	0	0	0 min
	Spatio-temporal	Exponential	0	0.00029	35.0 m	1.56 m/min
2 August	Spatial	Exponential	0	0.00079	265.3 m
	Temporal	Nugget	0	0.000012	10.0 min
	Spatio-temporal	Exponential	0	0.00068	24.0 m	1.79 m/min

Table 2. Parameters of the fitted sum-metric variogram model for soil moisture regression residuals.

Date	Component	Model	Nugget	Sill	Range	Anisotropy
10 July	Spatial	Exponential	0	0.00098	201.1 m
	Temporal	Nugget	0	0	0 min
	Spatio-temporal	Exponential	0	0.00029	35.0 m	1.56 m/min
2 August	Spatial	Exponential	0	0.00079	265.3 m
	Temporal	Nugget	0	0.000012	10.0 min
	Spatio-temporal	Exponential	0	0.00068	24.0 m	1.79 m/min

4.4. Accuracy Assessment

To assess the STRBK and STOBK upscaling strategies, we first upscaled WATERNET observations to the SoilNET intensive observation zone within three hours before and after satellite or aircraft passes. For comparison, a commonly used upscaling strategy known as ordinary block kriging (BK) algorithm [11] was also adopted. BK is a purely spatial aggregation method that makes no use of covariate information. We only upscaled the soil moisture at the times of satellite or aircraft passes. Table 3 shows the accuracy assessment result of the three upscaling approaches described in Section 3.2. We expect the predictions to be unbiased; if prediction values are unbiased, the upscaling error should be approximately zero. As shown in Table 3, the STRBK upscaling errors smaller than the BK and STOBK.

Table 3. Accuracy assessment of three upscaling strategies with 50-SoilNET-averaged values.

	Upscaling Error (m3·m−3)
	BK	STOBK	STRBK
10 July	0.0016	0.0014	0.0013
2 August	0.0017	0.0017	0.0016

Table 3. Accuracy assessment of three upscaling strategies with 50-SoilNET-averaged values.

	Upscaling Error (m3·m−3)
	BK	STOBK	STRBK
10 July	0.0016	0.0014	0.0013
2 August	0.0017	0.0017	0.0016

Since STRBK upscaling strategy achieves the best performance among these three methods, it was further adopted to upscale in situ soil moisture observations to pixel averages in order to validate the PLMR soil moisture products. The results are shown in Figure 5. It is clearly seen that, with an R-square value of 0.75 and 0.60, the PLMR retrievals have a good consistency with the upscaled soil moisture. The RMSE of 10 July is 0.037 m³·m⁻³ and the ME is 0.016 m³·m⁻³; 2 August yields RMSE = 0.027 m³·m⁻³ with an ME of 0.005 m³·m⁻³. The PLMR product at 10 July is, thus, more accurate than the product of 2 August. The main reason is that the soil moisture is relatively homogeneous during 10 July.

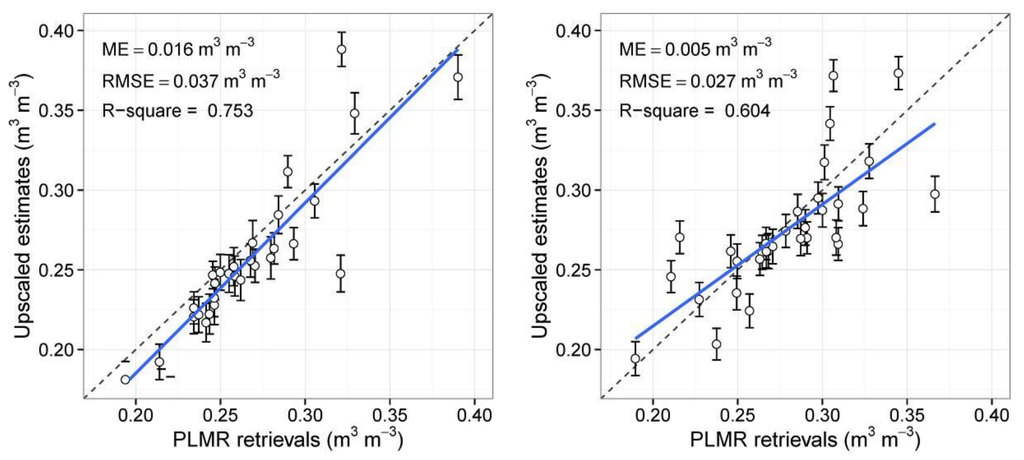
Figure 5. Comparison of the STRBK upscaled predictions with the values of PLMR retrievals on 10 July (left), and 2 August 2012 (right). The blue line is the fitted linear regression, the dashed line is the 1:1 line. The error bars show the 95% prediction intervals, as derived from the block kriging variances.

Figure 5. Comparison of the STRBK upscaled predictions with the values of PLMR retrievals on 10 July (left), and 2 August 2012 (right). The blue line is the fitted linear regression, the dashed line is the 1:1 line. The error bars show the 95% prediction intervals, as derived from the block kriging variances.

5. Discussion

Validation of remote sensing soil moisture products is traditionally carried out by averaging in situ measurements. Given the substantial within-field spatial variation and relatively modest number of ground-based soil moisture observations, this method often fails to achieve acceptable accuracy levels [34]. More accurate results can be obtained by using a geostatistical upscaling method, i.e., BK, which considers the spatial structure in the data. The BK method can be extended to include information derived from environmental covariates and past and future soil moisture. We presented the STRBK approach to scale up point-support observations of soil moisture to block-support averages to be used for validation of remote-sensing based PLMR observations. The main advantages of STRBK are: (1) it is a spatio-temporal upscaling method which can scale up observations to any desired spatio-temporal support; (2) it takes a spatio-temporal trend into account which is treated as a function of environmental covariates; and (3) it uses more observations than a purely spatial upscaling method, and is therefore less sensitive to random measurement errors.

The STRBK upscaling approach starts with trend modeling, which needs appropriate high-resolution covariates to capture the spatio-temporal trend of soil moisture. Previous studies demonstrated that the daily average soil moisture is highly correlated to daily temperature change and vegetation cover. Therefore, land surface parameters derived from 1 km MODIS data have been widely used to model the spatial trend of soil moisture. For example, Qin, et al. [8] proposed a Bayesian linear regression method to upscale in situ soil moisture measurements to a 100 km × 100 km grid box, based on MODIS-derived apparent thermal inertia. In our study, however, the objective was to upscale in situ soil moisture observations to 700 m spatial resolution PLMR pixel averages. MODIS covariates with a spatial resolution of 1 km are too coarse for this purpose. Hence, ASTER-derived land surface parameters with a spatial resolution of 90 m were adopted to model the spatial trend of surface soil moisture. The results of STRBK with high-resolution auxiliary data exhibit more detailed spatial patterns and higher prediction accuracy compared to the STOBK method.

Previous studies have shown the importance of selecting a suitable upscaling approach to evaluate satellite-based soil moisture estimates. For example, Qin, et al. [35] compare four upscaling methods (simple average (SA), BK, model-based (MB), and apparent-thermal-inertia-based (ATI) [8]) by using the unscaled soil moisture to evaluate soil moisture estimated by assimilating microwave signals into a land surface model on the Tibetan Plateau and Mongolia Plateau. They found that the performance of the MB upscaling approach is the most unstable. The BK and SA upscaling methods performed equally well, while ATI upscaling was the most accurate, presumably because it could benefit from high-resolution satellite thermal data. In our study, likewise, by taking advantage of auxiliary information, STRBK upscaling achieves the best performance among the three methods tested (BK, STOBK, and STRBK). However, due to the unavailability of a land surface assimilation model, a comparison of STRBK, MB, and ATI was not carried out in this study. Hence, more investigations are needed to compare the performance of these three upscaling methods.

Despite advantages of STRBK for spatio-temporal upscaling, it is also necessary to consider implementation costs and required accuracy before choosing an appropriate upscaling strategy in routine remote sensing-based soil moisture product validation procedures. The proposed STRBK method depends on the availability of high-resolution optical auxiliary variables, which are available only during clear sky conditions and on specific days. When the auxiliary data are not available, the BK and STOBK approaches can be used. They are easily applied in practice, although their performance will be less.

6. Conclusions

Upscaling ground-based soil moisture observations to satellite or airborne footprint-scale estimates is an essential problem in remote sensing soil moisture product validation. The reliability of the validation is sensitive to the quality of the input observation data and the upscaling strategy. When soil moisture shows high spatio(-temporal) heterogeneity within the footprint, the upscaling strategy can benefit from the spatio-temporal characteristics of point-support soil moisture. In this paper, a new upscaling approach named spatio-temporal regression block kriging was proposed to scale up in situ soil moisture observations to pixel averages. The method incorporates related auxiliary information and makes optimal use of the space-time correlation structure of point-support soil moisture observations. The method was illustrated with a real-world application to scale up soil moisture in the HiWATER experiment for validating PLMR retrieved soil moisture products. Comparison with results obtained using the more common BK upscaling method showed that the proposed approach yields more accurate results. The approach is recommended for upscaling land surface parameters with high spatio-temporal heterogeneity. An important advantage is that it can simultaneously do spatial and temporal aggregation. This was not requested for validation of the PLMR product, because PLMR measures the soil moisture at a time instant, but it would be important for other applications, such as in agricultural, hydrological or climate studies where the average soil moisture over time periods is more relevant than soil moisture at single time points.

It is noted that all analyses and conclusions are based on only two days with coincident overpass time between in situ and PLMR soil moisture observations. The robustness of the proposed method is therefore not yet definitively answered. More investigations and comparisons are needed to evaluate the performance of the proposed method for other seasons and regions with distinct climates and land cover are needed. In addition, due to the absence of an adequate soil map, variations in soil texture were not considered in the analysis of spatial variation of soil moisture. Nevertheless, this study demonstrates that it is critical to select a suitable upscaling approach in routine soil moisture products validation procedures and emphasizes the importance of incorporating covariate information and spatio-temporal variation of soil moisture for the effective validation of coarse-resolution satellite or airborne soil moisture products.