Retrieval of Seasonal Leaf Area Index from Simulated EnMAP Data through Optimized LUT-Based Inversion of the PROSAIL Model
Abstract
:1. Introduction
2. Material & Methods
2.1. Introduction to the Study Area

| Acquisition Date | Sensor | Sun Zenith (°) | Sun Azimuth (°) |
|---|---|---|---|
| 28 April | AVIS-3 | 42 | 132 |
| 8 May | HySpex | 45 | 115 |
| 25 May | AVIS-3 | 39 | 236 |
| 16 June | AVIS-3 | 28 | 146 |
| 12 August | HySpex | 42 | 133 |
| 8 September | AVIS-3 | 45 | 155 |
2.1.1. Data Preprocessing
2.1.2. Data Transfer to EnMAP Scale
2.2. Parameter Retrieval through Look-Up Table Inversion
2.2.1. Input Parameter Setting
| Model | Parameter | Min | Max | Mean | Std. Dev. |
|---|---|---|---|---|---|
| PROSPECT-5b | Leaf chlorophyll content [µg/cm2] | 0 | 90 | 50 | 40 |
| Leaf carotenoid content [µg/cm2] | 0 | 20 | 10 | 7 | |
| Brown pigment content [-] | 0 | 1.5 | 0.2 | 0.8 | |
| Equivalent water thickness [cm] | 0 | 0.05 | 0.02 | 0.025 | |
| Leaf mass per unit leaf area [g/cm2] | 0 | 0.02 | 0.01 | 0.01 | |
| Structure coefficient [-] | 1 | 2.5 | 1.5 | 1 | |
| 4SAIL | Average leaf angle [°] | 30 | 80 | 60 | 20 |
| Leaf area index [m2/m2] | 0 | 7 | 3.5 | 2.5 | |
| Hot spot [-] | 0 | 1 | 0.45 | 0.6 | |
| Soil coefficient [-] | 0 | 1 | 0.5 | 0.5 |
2.2.2. Inversion Sequence
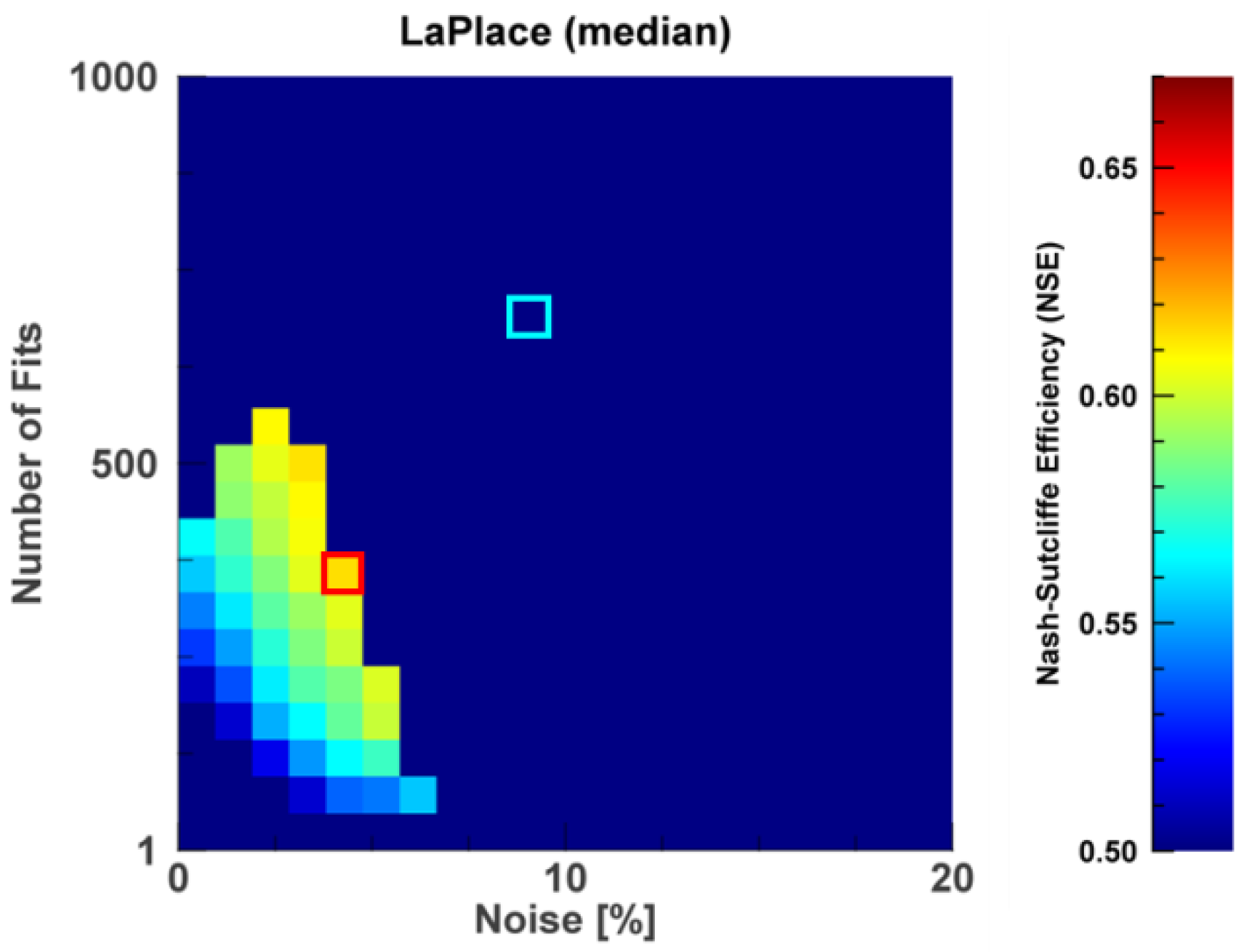
2.3. Selection Criteria
2.3.1. Band Selection
2.3.2. Artificial Noise
- simulated reflectance value for band λ with noise
- simulated reflectance value for band λ
- Gaussian distribution (mean value 0 and standard deviation σ)
- uncertainties within the Gaussian distribution for band λ
2.3.3. Cost Function
- measured reflectance at band λ
- simulated reflectance at band λ
- mean of measured reflectance among all bands
2.3.4. Ill-Posed Problem & Averaging Method
2.4. Design of Retrieval Procedure
3. Results
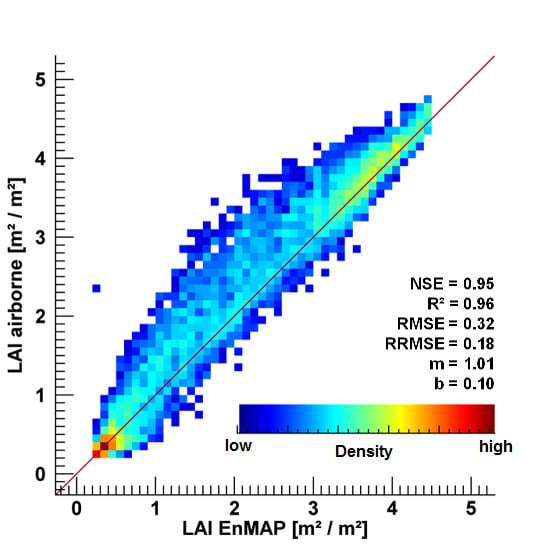
3.1. Validation of the Estimation Quality


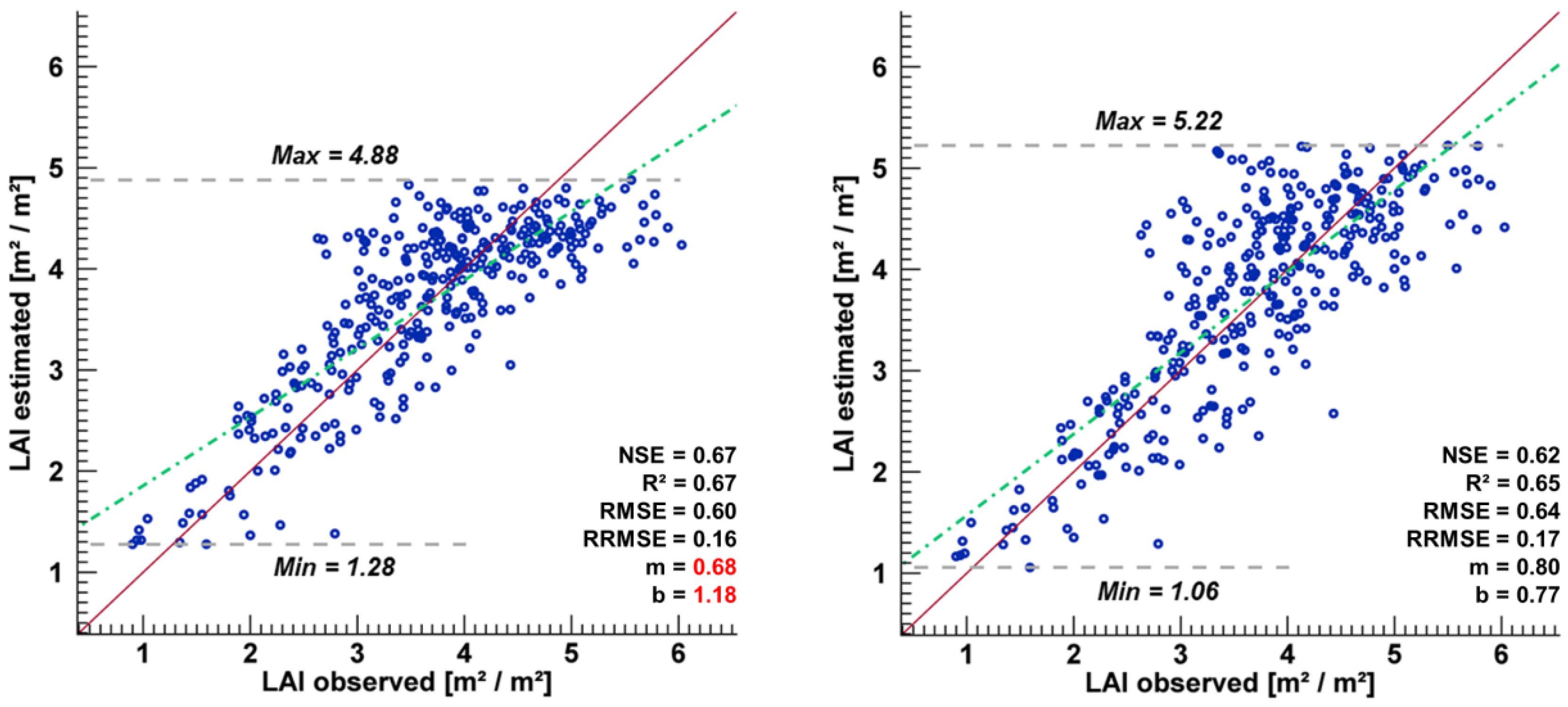

3.2. Transferability to the EnMAP Scale



4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Van Ittersum, M.K.; Cassman, K.G.; Grassini, P.; Wolf, J.; Tittonell, P.; Hochman, Z. Yield gap analysis with local to global relevance—A review. Field Crops Res. 2013, 143, 4–17. [Google Scholar] [CrossRef]
- Kaufmann, H.; Förster, S.; Wulf, H.; Segl, K.; Guanter, L.; Bochow, M.; Heiden, U.; Mueller, A.; Heldens, W.; Schneiderhan, T.; et al. Science Plan of the Environmental Mapping and Analysis Program (EnMAP); Deutsches GeoForschungsZentrum GFZ: Potsdam, Germany, 2012; p. 63. [Google Scholar]
- Govender, M.; Chetty, K.; Bulcock, H. A review of hyperspectral remote sensing and its application in vegetation and water resource studies. Water SA 2007, 33. [Google Scholar] [CrossRef]
- Guanter, L.; Kaufmann, H.; Segl, K.; Foerster, S.; Rogass, C.; Chabrillat, S.; Kuester, T.; Hollstein, A.; Rossner, G.; Chlebek, C.; et al. The EnMAP spaceborne imaging spectroscopy mission for earth observation. Remote Sens. 2015, 7, 8830–8857. [Google Scholar] [CrossRef]
- Duveiller, G.; Weiss, M.; Baret, F.; Defourny, P. Retrieving wheat green area index during the growing season from optical time series measurements based on neural network radiative transfer inversion. Remote Sens. Environ. 2011, 115, 887–896. [Google Scholar] [CrossRef]
- Si, Y.; Schlerf, M.; Zurita-Milla, R.; Skidmore, A.; Wang, T. Mapping spatio-temporal variation of grassland quantity and quality using MERIS data and the prosail model. Remote Sens. Environ. 2012, 121, 415–425. [Google Scholar] [CrossRef]
- Le Maire, G.; Marsden, C.; Verhoef, W.; Ponzoni, F.J.; Seen, D.L.; Bégué, A.; Stape, J.L.; Nouvellon, Y. Leaf area index estimation with MODIS reflectance time series and model inversion during full rotations of eucalyptus plantations. Remote Sens. Environ. 2011, 115, 586–599. [Google Scholar] [CrossRef]
- Richter, K.; Vuolo, F.; D’Urso, G.; Dini, L. Evaluation of different methods for the retrieval of LAI using high resolution airborne data. Proc. SPIE Remote Sens. Agric. Ecosyst. Hydrol. IX 2007. [Google Scholar] [CrossRef]
- Stevens, A.; Udelhoven, T.; Denis, A.; Tychon, B.; Lioy, R.; Hoffmann, L.; van Wesemael, B. Measuring soil organic carbon in croplands at regional scale using airborne imaging spectroscopy. Geoderma 2010, 158, 32–45. [Google Scholar] [CrossRef]
- Oppelt, N.; Mauser, W. Hyperspectral monitoring of physiological parameters of wheat during a vegetation period using AVIS data. Int. J. Remote. Sens. 2004, 25, 145–159. [Google Scholar] [CrossRef]
- Weiss, M.; Troufleau, D.; Baret, F.; Chauki, H.; Prévot, L.; Olioso, A.; Bruguier, N.; Brisson, N. Coupling canopy functioning and radiative transfer models for remote sensing data assimilation. Agric. For. Meteorol. 2001, 108, 113–128. [Google Scholar] [CrossRef]
- Hank, T.; Bach, H.; Mauser, W. Using a remote sening-supported hydro-agroecological model for field-scale simulation of heterogeneous crop growth and yield: Application for wheat in central europe. Remote Sens. 2015, 7, 3934–3965. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Verhoef, W.; Baret, F.; Bacour, C.; Zarco-Tejada, P.J.; Asner, G.P.; Francois, C.; Ustin, S.L. PROSPECT plus SAIL models: A review of use for vegetation characterization. Remote Sens. Environ. 2009, 113, S56–S66. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Baret, F.; Andrieu, B.; Danson, F.M.; Jaggard, K. Extraction of vegetation biophysical parameters by inversion of the PROSPECT + SAIL models on sugar beet canopy reflectance data. Application to TM and AVIRS sensors. Remote Sens. Environ. 1995, 52, 163–172. [Google Scholar] [CrossRef]
- Darvishzadeh, R.; Skidmore, A.; Schlerf, M.; Atzberger, C. Inversion of a radiative transfer model for estimating vegetation LAI and chlorophyll in a heterogeneous grassland. Remote Sens. Environ. 2008, 112, 2592–2604. [Google Scholar] [CrossRef]
- Baret, F.; Buis, S. Estimating canopy characteristics from remote sensing observations: Review of methods and associated problems. In Advances in Land Remote Sensing; Springer: Dordrecht, The Netherlands, 2008; pp. 173–201. [Google Scholar]
- Jacquemoud, S.; Bacour, C.; Poilvé, H.; Frangi, J.P. Comparison of four radiative transfer models to simulate plant canopies reflectance: Direct and inverse mode. Remote Sens. Environ. 2000, 74, 471–481. [Google Scholar] [CrossRef]
- Verhoef, W.; Bach, H. Simulation of hyperspectral and directional radiance images using coupled biophysical and atmospheric radiative transfer models. Remote Sens. Environ. 2003, 87, 23–41. [Google Scholar] [CrossRef]
- Oppelt, N.; Mauser, W. Airborne visible/infrared imaging spectrometer AVIS: Design, characterization and calibration. Sensors 2007, 7, 1934–1953. [Google Scholar] [CrossRef]
- Baumgartner, A.; Gege, P.; Köhler, C.; Lenhard, K.; Schwarzmaier, T. Characterisation methods for the hyperspectral sensor HySpex at DLR’s calibration home base. Proc. SPIE Remote Sens. Agric. Ecosyst. Hydrol. XVI 2012. [Google Scholar] [CrossRef]
- Richter, R.; Schläpfer, D. Atmospheric/Topographic Correction for Airborne Imagery, ATCOR-4 User Guide, Version 4.2; DLR: Wessling, Germany, 2007; p. 125. [Google Scholar]
- Segl, K.; Guanter, L.; Rogass, C.; Kuester, T.; Roessner, S.; Kaufmann, H.; Sang, B.; Mogulsky, V.; Hofer, S. Eetes—The EnMAP end-to-end simulation tool. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 522–530. [Google Scholar] [CrossRef]
- Richter, K.; Atzberger, C.; Vuolo, F.; Weihs, P.; D’Urso, G. Experimental assessment of the Sentinel–2 band setting for RTM–based LAI retrieval of sugar beet and maize. Can. J. Remote Sens. 2009, 35, 230–247. [Google Scholar] [CrossRef]
- Kimes, D.S.; Knyazikhin, Y.; Privette, J.L.; Abuelgasim, A.A.; Gao, F. Inversion methods for physically‐based models. Remote Sens. Rev. 2000, 18, 381–439. [Google Scholar] [CrossRef]
- Darvishzadeh, R.; Atzberger, C.; Skidmore, A.; Schlerf, M. Mapping grassland leaf area index with airborne hyperspectral imagery: A comparison study of statistical approaches and inversion of radiative transfer models. ISPRS J. Photogramm. 2011, 66, 894–906. [Google Scholar] [CrossRef]
- Combal, B.; Baret, F.; Weiss, M.; Trubuil, A.; Macé, D.; Pragnère, A.; Myneni, R.; Knyazikhin, Y.; Wang, L. Retrieval of canopy biophysical variables from bidirectional reflectance: Using prior information to solve the ill-posed inverse problem. Remote Sens. Environ. 2003, 84, 1–15. [Google Scholar] [CrossRef]
- Vuolo, F.; Atzberger, C.; Richter, K.; D’Urso, G.; Dash, J. Retrieval of biophysical vegetation products from rapideye imagery. Proc. ISPRS Tech. Comm. VII Symp. -100 Years ISPRS -Adv. Remote Sens. Sci. 2010, XXXVIII, 281–286. [Google Scholar]
- Durbha, S.S.; King, R.L.; Younan, N.H. Support vector machines regression for retrieval of leaf area index from multiangle imaging spectroradiometer. Remote Sens. Environ. 2007, 107, 348–361. [Google Scholar] [CrossRef]
- Darvishzadeh, R.; Matkan, A.A.; Ahangar, A.D. Inversion of a radiative transfer model for estimation of rice canopy chlorophyll content using a lookup-table approach. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 1222–1230. [Google Scholar] [CrossRef]
- Weiss, M.; Baret, F.; Myneni, R.B.; Pragnère, A.; Knyazikhin, Y. Investigation of a model inversion technique to estimate canopy biophysical variables from spectral and directional reflectance data. Agronomie 2000, 20, 3–22. [Google Scholar] [CrossRef]
- Bacour, C.; Baret, F.; Béal, D.; Weiss, M.; Pavageau, K. Neural network estimation of LAI, fapar, fcover and LAI × CAB, from top of canopy MERIS reflectance data: Principles and validation. Remote Sens. Environ. 2006, 105, 313–325. [Google Scholar] [CrossRef]
- Baret, F.; Hagolle, O.; Geiger, B.; Bicheron, P.; Miras, B.; Huc, M.; Berthelot, B.; Nino, F.; Weiss, M.; Samain, O.; et al. LAI, fapar and fcover cyclopes global products derived from vegetation—Part 1: Principles of the algorithm. Remote Sens. Environ. 2007, 110, 275–286. [Google Scholar] [CrossRef]
- Verger, A.; Baret, F.; Camacho, F. Optimal modalities for radiative transfer-neural network estimation of canopy biophysical characteristics: Evaluation over an agricultural area with Chris/Proba observations. Remote Sens. Environ. 2011, 115, 415–426. [Google Scholar] [CrossRef]
- Meroni, M.; Colombo, R.; Panigada, C. Inversion of a radiative transfer model with hyperspectral observations for LAI mapping in poplar plantations. Remote Sens. Environ. 2004, 92, 195–206. [Google Scholar] [CrossRef]
- Lavergne, T.; Kaminski, T.; Pinty, B.; Taberner, M.; Gobron, N.; Verstraete, M.M.; Vossbeck, M.; Widlowski, J.L.; Giering, R. Application to MISR land products of an RPV model inversion package using adjoint and hessian codes. Remote Sens. Environ. 2007, 107, 362–375. [Google Scholar] [CrossRef]
- Verrelst, J.; Rivera, J.P.; Leonenko, G.; Alonso, L.; Moreno, J. Optimizing LUT-based RTM inversion for semiautomatic mapping of crop biophysical parameters from Sentinel-2 and -3 data: Role of cost functions. Geosci. Remote Sens. IEEE Trans. 2014, 52, 257–269. [Google Scholar] [CrossRef]
- Rivera, J.; Verrelst, J.; Leonenko, G.; Moreno, J. Multiple cost functions and regularization options for improved retrieval of leaf chlorophyll content and LAI through inversion of the PROSAIL model. Remote Sens. 2013, 5, 3280–3304. [Google Scholar] [CrossRef]
- Leonenko, G.; Los, S.; North, P. Statistical distances and their applications to biophysical parameter estimation: Information measures, M-estimates, and minimum contrast methods. Remote Sens. 2013, 5, 1355–1388. [Google Scholar] [CrossRef]
- Wainwright, J.; Mulligan, M. Environmental Modelling: Finding Simplicity in Complexity; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Staudte, R.G.; Sheather, S.J. Robust Estimation and Testing; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Richter, K.; Atzberger, C.; Hank, T.B.; Mauser, W. Derivation of biophysical variables from earth observation data: Validation and statistical measures. J. Appl. Remote Sens. 2012, 6. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Locherer, M.; Hank, T.; Danner, M.; Mauser, W. Retrieval of Seasonal Leaf Area Index from Simulated EnMAP Data through Optimized LUT-Based Inversion of the PROSAIL Model. Remote Sens. 2015, 7, 10321-10346. https://doi.org/10.3390/rs70810321
Locherer M, Hank T, Danner M, Mauser W. Retrieval of Seasonal Leaf Area Index from Simulated EnMAP Data through Optimized LUT-Based Inversion of the PROSAIL Model. Remote Sensing. 2015; 7(8):10321-10346. https://doi.org/10.3390/rs70810321
Chicago/Turabian StyleLocherer, Matthias, Tobias Hank, Martin Danner, and Wolfram Mauser. 2015. "Retrieval of Seasonal Leaf Area Index from Simulated EnMAP Data through Optimized LUT-Based Inversion of the PROSAIL Model" Remote Sensing 7, no. 8: 10321-10346. https://doi.org/10.3390/rs70810321
APA StyleLocherer, M., Hank, T., Danner, M., & Mauser, W. (2015). Retrieval of Seasonal Leaf Area Index from Simulated EnMAP Data through Optimized LUT-Based Inversion of the PROSAIL Model. Remote Sensing, 7(8), 10321-10346. https://doi.org/10.3390/rs70810321