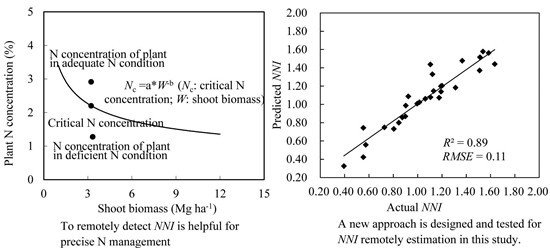
A Comparison of Two Approaches for Estimating the Wheat Nitrogen Nutrition Index Using Remote Sensing
Abstract
:1. Introduction
2. Data and Methods
2.1. Study Sites and Experimental Design
2.2. Data Acquisition
2.2.1. Remote Sensing Data
2.2.2. Crop Biophysical and Biochemical Variables
2.3. Determination of the NNI
2.4. Data Analysis
3. Results and Analyses
3.1. Relationships between the SPAD, LAI, Plant N Concentration and NNI Values
| Index | Name | Formula | Developed by |
|---|---|---|---|
| Nitrogen Indices | |||
| Viopt | Optimal Vegetation Index | (1 + 0.45)((R800)2 + 1)/(R670 + 0.45) | Reyniers et al. [34] |
| RVI I † | Ratio Vegetation Index I | R810/R660 | Zhu et al. [1] |
| RVI II † | Ratio Vegetation Index II | R810/R560 | Xue et al. [35] |
| MCARI/MTVI2 | Combined Index | MCARI/MTVI2 MCARI: (R700 − R670 − 0.2(R700 − R550))(R700/R670) MTVI2:1.5(1.2(R800 − R550) − 2.5(R670 − R550))/sqrt((2R800 + 1)2 − (6R800 − 5sqrt(R670)) − 0.5) | Eitel et al. [36] |
| REIP-LE | Red Edge Inflection Point: Linear Extrapolation Method | Based on the linear extrapolation of two straight lines through two points on the far-red and two points on the NIR flanks of the first derivative reflectance spectrum of the red edge region. The REIP is defined by the wavelength value at the intersection of the straight lines. | Cho and Skidmore [37] |
| DCNI | Double-Peak Canopy Nitrogen Index | (R720 − R700)/(R700 − R670)/(R720 − R670 + 0.03) | Chen et al. [22] |
| Chlorophyll Indices | |||
| MCARI | Modified Chlorophyll Absorption Ratio Index | (R700 − R670 − 0.2(R700 − R550))(R700/R670) | Daughtry et al. [38] |
| TCARI | Transformed Chlorophyll Absorption in Reflectance Index | 3((R700 − R670) − 0.2(R700 − R550)(R700/R670)) | Haboudane et al. [39] |
| TCARI/OSAVI | Combined Index II † | TCARI/OSAVI TCARI: 3((R700 − R670) − 0.2(R700 − R550)(R700/R670)) OSAVI: 1.16(R800 − R670)/(R800 + R670 + 0.16) | Haboudane et al. [40] |
| MTCI | MERIS Terrestrial Chlorophyll Index | (R750 − R710)/(R710 − R680) | Dash and Curran [41] |
| R-M † | Red Model | R750/R720 − 1 | Gitelson et al. [42] |
| CCI | Canopy Chlorophyll Index | D720/D700 | Sims et al. [43] |
| REIP-LI | Red Edge Inflection Point: Linear Interpolation Method | 700 + 40(Rre − R700)/(R740 − R700) Rre: (R670 + R780)/2 | Guyot et al. [44] |
| Index | Name | Formula | Developed by |
|---|---|---|---|
| LAI Indices | |||
| NDVI | Normalized Difference Vegetation Index | (R800 − R670)/(R800 + R670) | Rouse et al. [45] |
| RVI | Ratio Vegetation Index | R800 /R670 | Pearson et al. [46] |
| EVI | Enhanced Vegetation Index | 2.5(R800 − R670)/(R800 + 6R670 − 7.5R470 + 1) | Huete et al. [47] |
| TVI | Triangular Vegetation Index | 0.5(120(R750 − R550) − 200(R670 − R550)) | Broge and Leblanc [48] |
| MSAVI | Modified Soil-Adjusted Vegetation Index | (2R800 + 1 − sqrt((2R800 + 1)2 − 8(R800 − R670)))/2 | Qi et al. [49] |
| OSAVI | Optimization of Soil-Adjusted Vegetation Index | 1.16(R800 − R670)/(R800 + R670 + 0.16) | Rondeaux et al. [50] |
| GNDVI | Green Normalized Difference Vegetation Index | (R800 − R550)/(R800 + R550) | Gitelson et al. [51] |
| MTVI2 | Modified Triangular Vegetation Index 2 | 1.5(1.2(R800 − R550) − 2.5(R670 − R550))/sqrt((2R800 + 1)2 − (6R800 − 5sqrt(R670)) − 0.5) | Haboudance et al. [17] |
| Biomass Indices | |||
| RTVI | Red-Edge Triangular Vegetation Index | (100(R750 − R730) − 10(R750 − R550))sqrt(R700/R670) | Chen et al. [52] |
| Spectral Index | Biomass | LAI | N Concentration | SPAD | NNI |
|---|---|---|---|---|---|
| Data from all growth stages (n = 120) | |||||
| Biomass | 1.00 | ||||
| LAI | 0.93 * | 1.00 | |||
| N concentration | 0.19 | 0.25 * | 1.00 | ||
| SPAD | 0.05 | 0.07 | 0.77 * | 1.00 | |
| NNI | 0.73 * | 0.74 * | 0.80 * | 0.47 * | 1.00 |
| Data from Feekes 4 (n = 60) | |||||
| Biomass | 1.00 | ||||
| LAI | 0.76 * | 1.00 | |||
| N concentration | 0.64 * | 0.73 * | 1.00 | ||
| SPAD | 0.52 * | 0.60 * | 0.70 * | 1.00 | |
| NNI | 0.87 * | 0.81 * | 0.93 * | 0.68 * | 1.00 |
| Data from Feekes 7–8 (n = 60) | |||||
| Biomass | 1.00 | ||||
| LAI | 0.84 * | 1.00 | |||
| N concentration | 0.69 * | 0.87 * | 1.00 | ||
| SPAD | 0.66 * | 0.70 * | 0.80 * | 1.00 | |
| NNI | 0.83 * | 0.92 * | 0.97 * | 0.80 * | 1.00 |
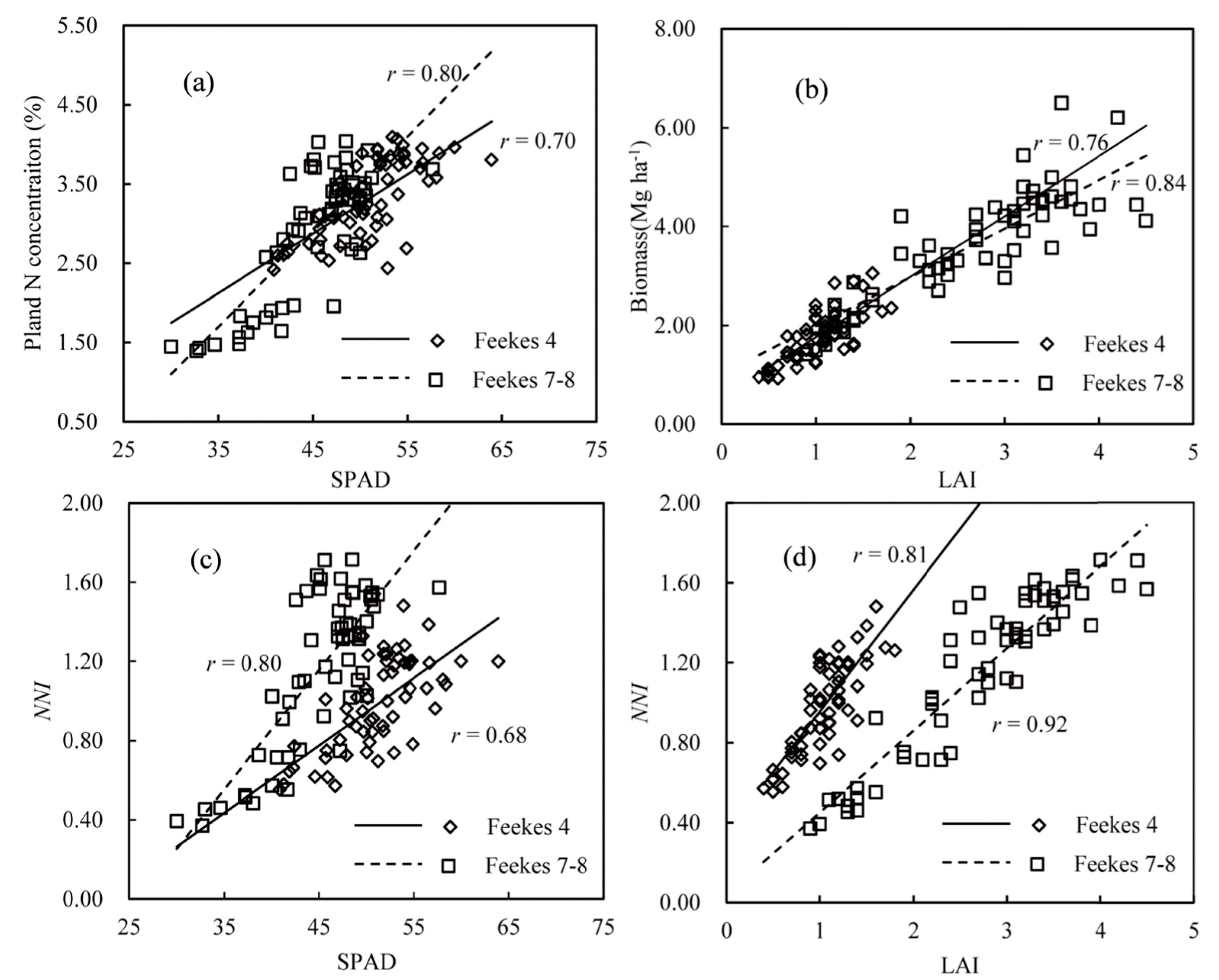
3.2. The NNI Estimation Model Using a Mechanistic Method
| Spectral Index | N Concentration | LAI | ||
|---|---|---|---|---|
| R2 (Model Type) | RMSE (RMSE%) | R2 (Model Type) | RMSE (RMSE%) | |
| Using data from all growth stages (n = 90) | ||||
| Viopt | 0.13 (Log) | 0.67 (21.47%) | 0.90 (Pow) | 0.47 (25.00%) |
| RVI I | 0.09 (Log) | 0.68 (21.79%) | 0.90 (Pow) | 0.53 (28.19%) |
| RVI II | 0.13 (Pow) | 0.68 (21.79%) | 0.90 (Pow) | 0.50 (26.60%) |
| MCARI/MTVI2 | 0.62 (Exp) | 0.46 (14.74%) | 0.26 (Pow) | 0.98 (52.13%) |
| REIP-LE | 0.36 (Pow) | 0.60 (19.23%) | 0.56 (Pow) | 0.75 (39.89%) |
| DCNI | 0.43 (Pow) | 0.59 (18.91%) | 0.41 (Lin) | 0.87 (46.28%) |
| MCARI | − | − | 0.64 (Pow) | 0.76 (40.43%) |
| TCARI | 0.12 (Exp) | 0.70 (22.44%) | 0.15 (Pow) | 1.08 (57.45%) |
| TCARI/OSAVI | 0.37 (Exp) | 0.60 (19.23%) | 0.59 (Pow) | 0.76 (40.43%) |
| MTCI | 0.32 (Pow) | 0.61 (19.55%) | 0.80 (Lin) | 0.56 (29.79%) |
| R-M | 0.17 (Log) | 0.65 (20.83%) | 0.89 (Pow) | 0.50 (26.60%) |
| CCI | 0.31 (Log) | 0.59 (18.91%) | 0.49 (Exp) | 0.85 (45.21%) |
| REIP-LI | 0.32 (Pow) | 0.63 (20.19%) | 0.77 (Exp) | 0.55 (29.26%) |
| Using data from the Feekes 4 growth stage (n = 45) | ||||
| Viopt | 0.55 (Lin) | 0.34 (10.21%) | 0.77 (Pow) | 0.17 (16.19%) |
| RVI I | 0.55 (Log) | 0.35 (10.51%) | 0.76 (Log) | 0.16 (15.24%) |
| RVI II | 0.59 (Log) | 0.33 (9.91%) | 0.80 (Log) | 0.14 (13.23%) |
| MCARI/MTVI2 | 0.61 (Log) | 0.33 (9.91%) | 0.67 (Exp) | 0.21 (20.00%) |
| REIP-LE | 0.48 (Lin) | 0.37 (11.11%) | 0.60 (Pow) | 0.24 (22.86%) |
| DCNI | 0.51 (Log) | 0.37 (11.11%) | 0.42 (Pow) | 0.25 (23.81%) |
| MCARI | 0.20 (Pow) | 0.47 (14.11%) | 0.40 (Pow) | 0.26 (24.76%) |
| TCARI | − | − | 0.25 (Pow) | 0.29 (27.62%) |
| TCARI/OSAVI | 0.59 (Log) | 0.33 (9.91%) | 0.67 (Exp) | 0.20 (19.05%) |
| MTCI | 0.65 (Log) | 0.31 (9.31%) | 0.83 (Pow) | 0.15 (14.29%) |
| R-M | 0.61 (Log) | 0.33 (9.91%) | 0.84 (Pow) | 0.14 (13.33%) |
| CCI | 0.56 (Lin) | 0.35 (10.51%) | 0.45 (Pow) | 0.25 (23.81%) |
| REIP-LI | 0.65 (Lin) | 0.31 (9.31%) | 0.81 (Exp) | 0.20 (19.05%) |
| Using data from the Feekes 7–8 growth stage (n = 45) | ||||
| Viopt | 0.86 (Pow) | 0.36 (12.41%) | 0.84 (Pow) | 0.59 (21.61%) |
| RVI I | 0.78 (Pow) | 0.45 (15.52%) | 0.81 (Pow) | 0.68 (24.91%) |
| RVI II | 0.83 (Pow) | 0.40 (13.79%) | 0.84 (Pow) | 0.65 (23.81%) |
| MCARI/MTVI2 | 0.72 (Pow) | 0.48 (16.55%) | 0.75 (Exp) | 0.71 (26.01%) |
| REIP-LE | 0.76 (Exp) | 0.45 (15.52%) | 0.67 (Pow) | 0.73 (26.74%) |
| DCNI | 0.65 (Pow) | 0.56 (19.31%) | 0.71 (Pow) | 0.79 (28.94%) |
| MCARI | − | − | − | − |
| TCARI | 0.23 (Exp) | 0.75 (25.86%) | 0.31 (Exp) | 0.93 (34.07%) |
| TCARI/OSAVI | 0.67 (Pow) | 0.54 (18.62%) | 0.76 (Exp) | 0.74 (27.11%) |
| MTCI | 0.85 (Exp) | 0.39 (13.45%) | 0.88 (Pow) | 0.61 (22.34%) |
| R-M | 0.84 (Pow) | 0.38 (13.10%) | 0.82 (Pow) | 0.63 (23.08%) |
| CCI | 0.63 (Pow) | 0.51 (17.59%) | 0.53 (Pow) | 0.79 (28.94%) |
| REIP-LI | 0.86 (Exp) | 0.42 (14.48%) | 0.89 (Pow) | 0.62 (22.71%) |
| Spectral Index | Biomass | SPAD | ||
|---|---|---|---|---|
| R2 (Model Type) | RMSE (RMSE%) | R2 (Model Type) | RMSE (RMSE%) | |
| Using data from all growth stages (n = 90) | ||||
| NDVI | 0.86 (Exp) | 0.53 (19.27%) | − | − |
| RVI | 0.85 (Pow) | 0.53 (19.27%) | − | − |
| EVI | 0.82 (Pow) | 0.58 (21.09%) | − | − |
| TVI | 0.79 (Pow) | 0.63 (22.91%) | − | − |
| MSAVI | 0.84 (Pow) | 0.55 (20.00%) | − | − |
| OSAVI | 0.86 (Exp) | 0.52 (18.91%) | − | − |
| GNDVI | 0.86 (Exp) | 0.51 (18.55%) | − | − |
| MTVI2 | 0.85 (Pow) | 0.54 (19.64%) | − | − |
| RTVI | 0.85 (Pow) | 0.53 (19.27%) | − | − |
| Using data from the Feekes 4 growth stage (n = 45) | ||||
| NDVI | 0.78 (Pow) | 0.25 (13.74%) | 0.34 (Pow) | 4.30 (8.42%) |
| RVI | 0.75 (Log) | 0.25 (13.74%) | 0.25 (Pow) | 4.22 (8.26%) |
| EVI | 0.78 (Pow) | 0.26 (14.29%) | 0.32 (Pow) | 4.04 (7.91%) |
| TVI | 0.75 (Pow) | 0.28 (15.38%) | 0.29 (Pow) | 4.13 (8.09%) |
| MSAVI | 0.78 (Pow) | 0.26 (14.29%) | 0.31 (Pow) | 4.06 (7.95%) |
| OSAVI | 0.78 (Pow) | 0.26 (14.29%) | 0.33 (Pow) | 4.00 (7.83%) |
| GNDVI | 0.80 (Pow) | 0.24 (13.19%) | 0.39 (Pow) | 3.83 (7.50%) |
| MTVI2 | 0.78 (Pow) | 0.26 (14.29%) | 0.30 (Pow) | 4.09 (8.01%) |
| RTVI | 0.80 (Pow) | 0.24 (13.19%) | 0.40 (Pow) | 3.82 (7.48%) |
| Using data from the Feekes 7–8 growth stage (n = 45) | ||||
| NDVI | 0.65 (Pow) | 0.65 (17.62%) | 0.60 (Pow) | 3.47 (7.70%) |
| RVI | 0.63 (Pow) | 0.64 (17.34%) | 0.54 (Pow) | 3.75 (8.33%) |
| EVI | 0.66 (Pow) | 0.64 (17.34%) | 0.61 (Pow) | 3.49 (7.75%) |
| TVI | 0.60 (Pow) | 0.68 (18.43%) | 0.55 (Pow) | 3.75 (8.33%) |
| MSAVI | 0.67 (Pow) | 0.63 (17.07%) | 0.62 (Pow) | 3.44 (7.64%) |
| OSAVI | 0.68 (Pow) | 0.63 (17.07%) | 0.63 (Pow) | 3.39 (7.53%) |
| GNDVI | 0.72 (Pow) | 0.61 (16.53%) | 0.68 (Pow) | 3.20 (7.10%) |
| MTVI2 | 0.66 (Pow) | 0.63 (17.07%) | 0.61 (Pow) | 3.50 (7.77%) |
| RTVI | 0.73 (Pow) | 0.59 (15.99%) | 0.66 (Pow) | 3.31 (7.35%) |
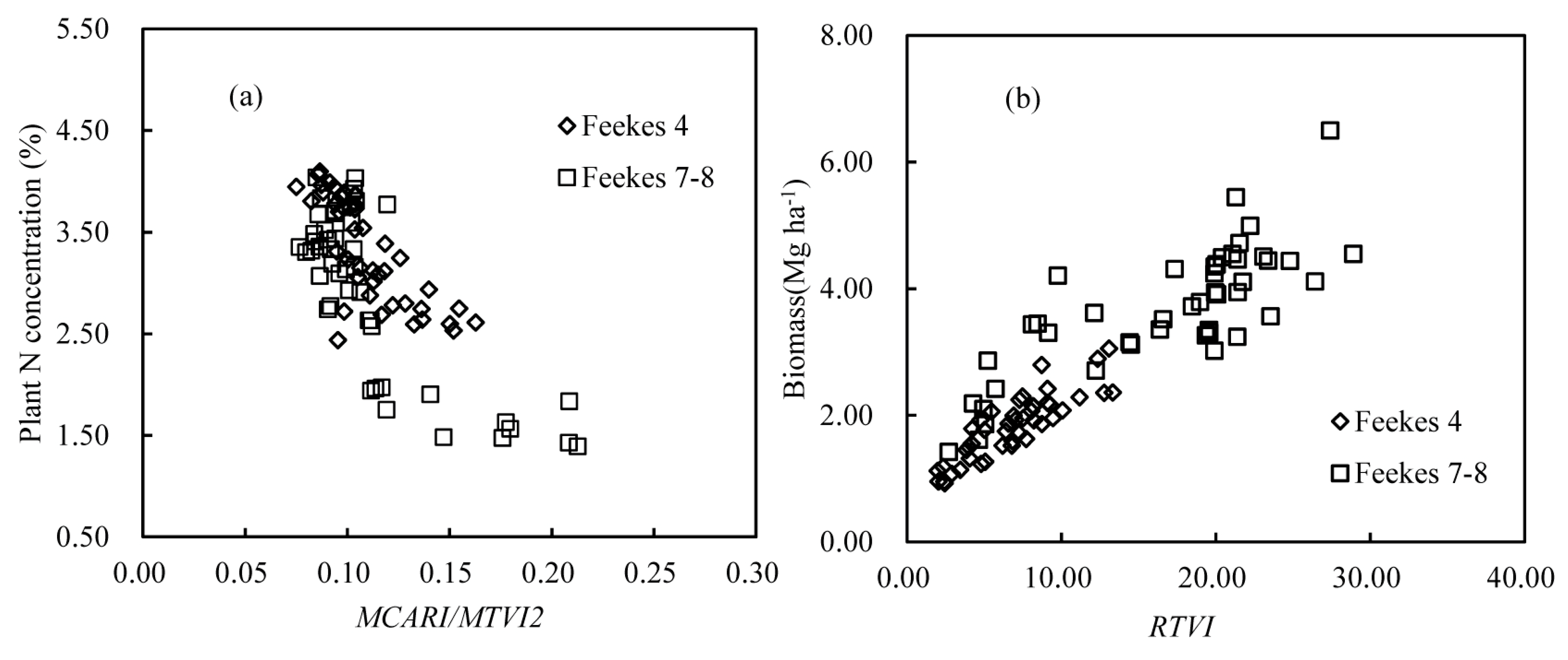
3.3. The NNI Estimation Model Using a Semi-Empirical Method
| Spectral Index | All Growth Stages (n = 90) | Feekes 4 Growth Stage (n = 45) | Feekes 7–8 Growth Stage (n = 45) | |||
|---|---|---|---|---|---|---|
| R2 (Model) | RMSE (RMSE%) | R2 (Model) | RMSE (RMSE%) | R2 (Model) | RMSE (RMSE%) | |
| Viopt | 0.64 (Lin) | 0.20 (18.71%) | 0.76 (Exp) | 0.13 (13.27%) | 0.89 (Pow) | 0.17 (14.78%) |
| RVI I | 0.57 (Log) | 0.22 (20.58%) | 0.75 (Log) | 0.12 (12.24%) | 0.83 (Pow) | 0.20 (17.39%) |
| RVI II | 0.64 (Log) | 0.20 (18.71%) | 0.80 (Pow) | 0.11 (11.22%) | 0.89 (Pow) | 0.17 (14.78%) |
| MCARI/MTVI2 | 0.75 (Pow) | 0.20 (18.71%) | 0.71 (Pow) | 0.14 (14.29%) | 0.80 (Pow) | 0.23 (20.00%) |
| REIP-LE | 0.71 (Pow) | 0.19 (17.77%) | 0.68 (Pow) | 0.18 (18.37%) | 0.78 (Exp) | 0.21 (18.26%) |
| DCNI | 0.68 (Pow) | 0.22 (20.58%) | 0.52 (Lin) | 0.17 (17.35%) | 0.73 (Pow) | 0.26 (22.61%) |
| MCARI | 0.17 (Log) | 0.31 (29.00%) | 0.35 (Pow) | 0.20 (20.41%) | − | − |
| TCARI | − | − | 0.21 (Pow) | 0.22 (22.45%) | 0.28 (Pow) | 0.37 (32.17%) |
| TCARI/OSAVI | 0.73 (Exp) | 0.20 (18.71%) | 0.69 (Exp) | 0.14 (14.29%) | 0.75 (Exp) | 0.24 (20.87%) |
| MTCI | 0.79 (Pow) | 0.17 (15.90%) | 0.84 (Pow) | 0.10 (10.20%) | 0.92 (Pow) | 0.15 (13.04%) |
| R-M | 0.67 (Log) | 0.19 (17.77%) | 0.83 (Pow) | 0.10 (10.20%) | 0.90 (Pow) | 0.16 (13.91%) |
| CCI | 0.60 (Lin) | 0.22 (20.58%) | 0.59 (Exp) | 0.16 (16.33%) | 0.63 (Pow) | 0.27 (23.48%) |
| REIP-LI | 0.80 (Lin) | 0.15 (14.03%) | 0.83 (Exp) | 0.14 (14.29%) | 0.93 (Pow) | 0.14 (12.17%) |
| NDVI | 0.52 (Lin) | 0.24 (22.45%) | 0.78 (Exp) | 0.12 (12.24%) | 0.84 (Exp) | 0.19 (16.52%) |
| RVI | 0.55 (Log) | 0.23 (21.51%) | 0.75 (Log) | 0.12 (12.24%) | 0.82 (Pow) | 0.21 (18.26%) |
| EVI | 0.69 (Lin) | 0.19 (17.77%) | 0.77 (Pow) | 0.12 (12.24%) | 0.93 (Pow) | 0.13 (11.30%) |
| TVI | 0.67 (Lin) | 0.19 (17.77%) | 0.74 (Pow) | 0.13 (13.27%) | 0.88 (Pow) | 0.17 (14.78%) |
| MSAVI | 0.67 (Lin) | 0.19 (17.77%) | 0.77 (Pow) | 0.12 (12.24%) | 0.93 (Pow) | 0.13 (11.30%) |
| OSAVI | 0.61 (Lin) | 0.21 (19.64%) | 0.78 (Pow) | 0.12 (12.24%) | 0.92 (Exp) | 0.14 (12.17%) |
| GNDVI | 0.63 (Lin) | 0.21 (19.64%) | 0.81 (Exp) | 0.11 (11.22%) | 0.89 (Exp) | 0.17 (14.78%) |
| MTVI2 | 0.63 (Lin) | 0.21 (19.64%) | 0.76 (Pow) | 0.12 (12.24%) | 0.91 (Pow) | 0.14 (12.17%) |
| RTVI | 0.70 (Log) | 0.19 (17.77%) | 0.81 (Pow) | 0.11 (11.22%) | 0.93 (Pow) | 0.13 (11.30%) |
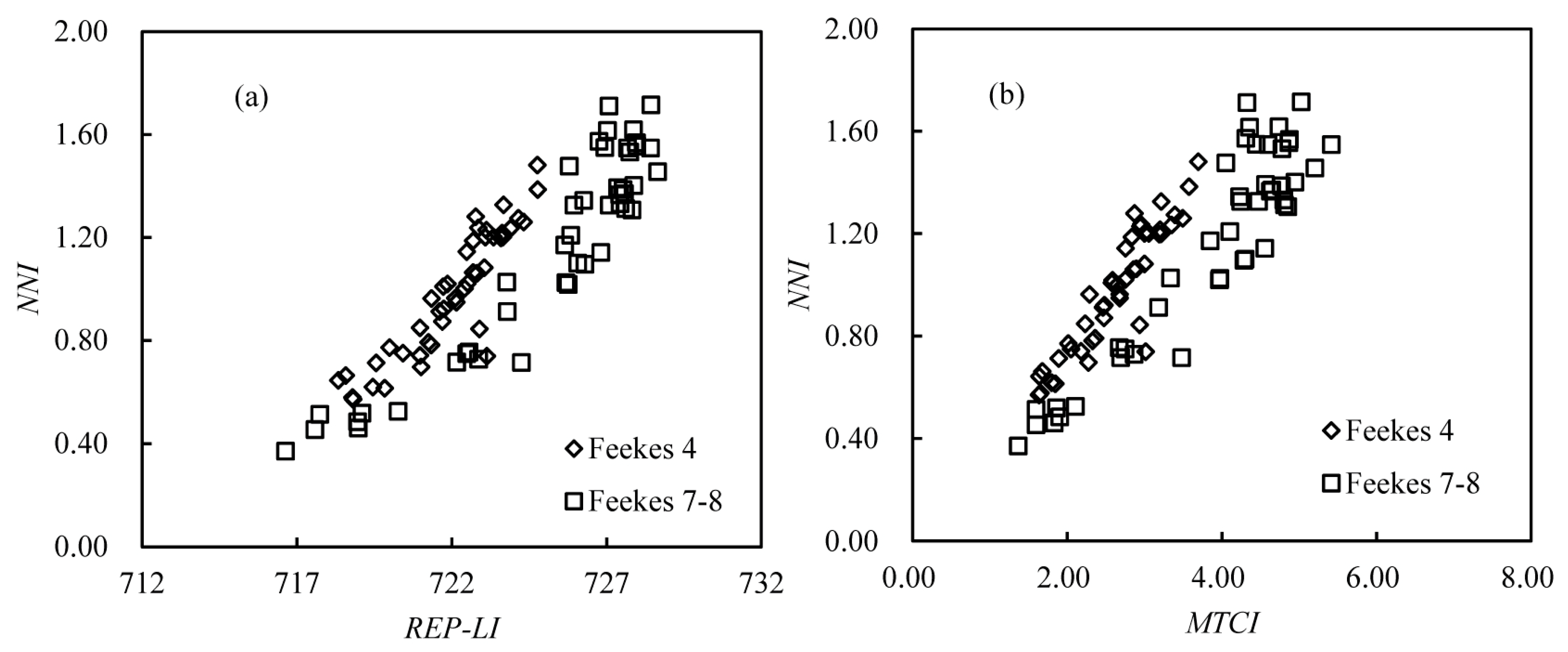
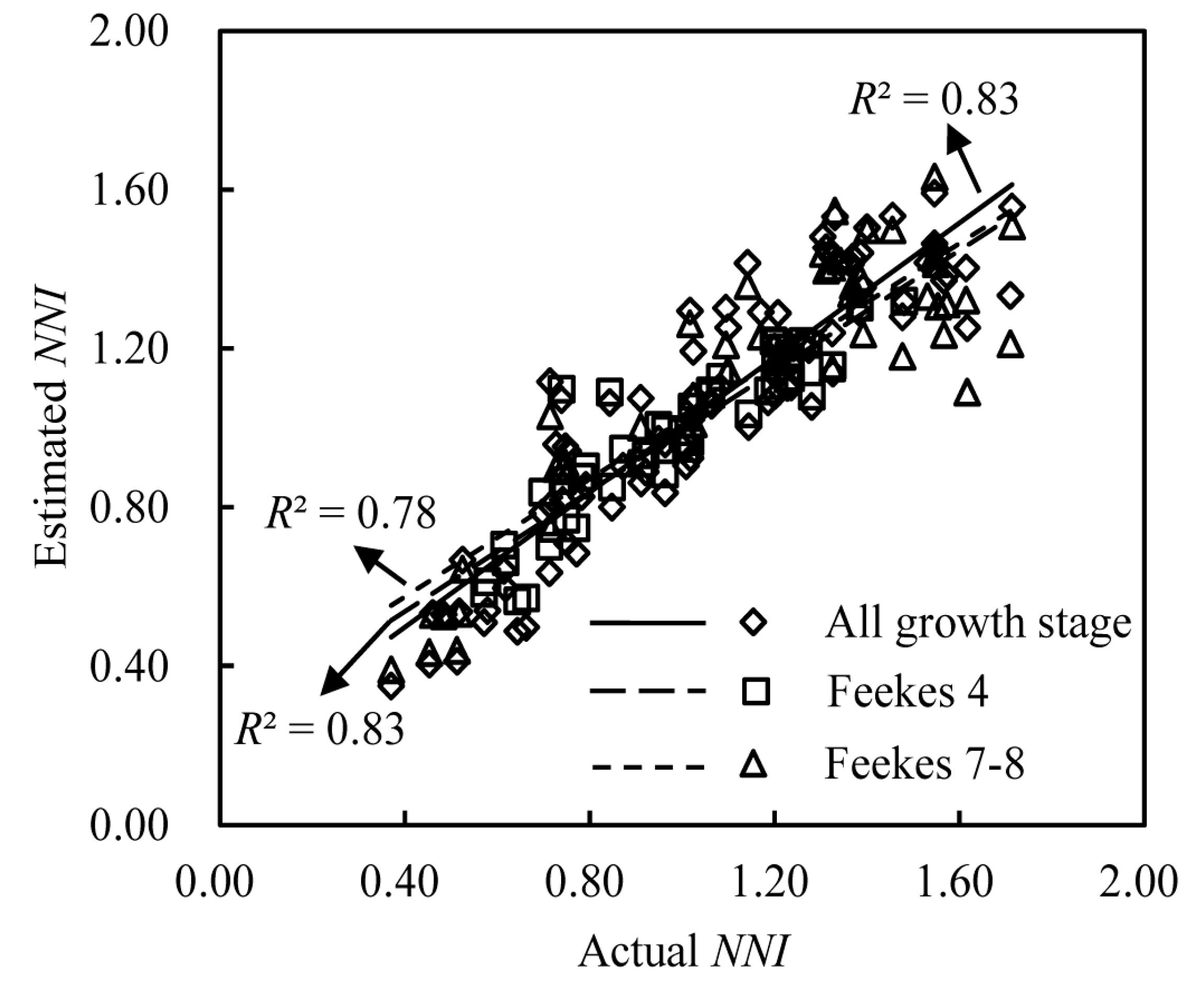
3.4. Validation of the NNI Estimation Models
| Spectral Index Used in Model | Data Used for Model Establishment in Calibration Dataset | Validation by Data from All Growth Stages (n = 30) | Validation by Data from the Feekes 4 Growth Stage (n = 15) | Validation by Data from the Feekes 7–8 Growth Stage (n = 15) | |||
|---|---|---|---|---|---|---|---|
| R2 | RMSE (RMSE%) | R2 | RMSE (RMSE%) | R2 | RMSE (RMSE%) | ||
| MCARI/MTVI2 and RTVI | All data (n = 90) | 0.89 | 0.11 (10.18%) | 0.94 | 0.06 (6.12%) | 0.86 | 0.15 (12.71%) |
| MCARI/MTVI2 and RTVI | Feekes 4 growth stage (n = 45) | 0.88 | 0.12 (11.11%) | 0.94 | 0.05 (5.10%) | 0.86 | 0.16 (13.56%) |
| MCARI/MTVI2 and RTVI | Feekes 7–8 growth stage (n = 45) | 0.85 | 0.13 (12.04%) | 0.93 | 0.06 (6.12%) | 0.82 | 0.17 (14.41%) |
| MTCI | All data (n = 90) | 0.86 | 0.13 (12.03%) | 0.94 | 0.11 (11.22%) | 0.90 | 0.14 (11.86%) |
| MTCI | Feekes 4 growth stage (n = 45) | 0.85 | 0.25 (23.15%) | 0.94 | 0.05 (5.10%) | 0.90 | 0.35 (29.66%) |
| MTCI | Feekes 7–8 growth stage (n = 45) | 0.85 | 0.19 (17.59%) | 0.94 | 0.23 (23.47%) | 0.90 | 0.13 (11.02%) |
| REIP-LI | All data (n = 90) | 0.88 | 0.11 (10.19%) | 0.91 | 0.08 (8.16%) | 0.89 | 0.14 (11.86%) |
| REIP-LI | Feekes 4 growth stage (n = 45) | 0.81 | 0.31 (28.60%) | 0.94 | 0.10 (9.77%) | 0.87 | 0.42 (36.16%) |
| REIP-LI | Feekes 7–8 growth stage (n = 45) | 0.83 | 0.21 (19.44%) | 0.94 | 0.26 (26.53%) | 0.88 | 0.15 (12.71%) |
4. Discussion
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Zhu, Y.; Yao, X.; Tian, Y.C.; Liu, X.J.; Cao, W.X. Analysis of common canopy vegetation indices for indicating leaf nitrogen accumulations in wheat and rice. Int. J. Appl. Earth Obs. 2008, 10, 1–10. [Google Scholar] [CrossRef]
- Mamo, M.; Malzer, G.L.; Mulla, D.J.; Huggins, D.R.; Strock, J. Spatial and temporal variation in economically optimum nitrogen rate for corn. Agron. J. 2003, 95, 958–964. [Google Scholar] [CrossRef]
- Schröder, J.J.; Neeteson, J.J.; Oenema, O.; Struik, P.C. Does the crop or the soil indicate how to save nitrogen in maize production? Reviewing the state of the art. Field Crop Res. 2000, 66, 151–164. [Google Scholar] [CrossRef]
- Dambreville, C.; Morvan, T.; Germon, J.-C. N2O emission in maize-crops fertilized with pig slurry, matured pig manure or ammonium nitrate in Brittany. Agr. Eosyst. Environ. 2008, 123, 201–210. [Google Scholar] [CrossRef]
- Zhao, B.Z.; Zhang, J.B.; Flury, M.; Zhu, A.N.; Jiang, Q.A.; Bi, J.W. Ground water contamination with NO3-N in a wheat-corn cropping system in the north China plain. Pedosphere 2007, 17, 721–731. [Google Scholar] [CrossRef]
- López-Bellido, L.; López-Bellido, R.J.; Redondo, R. Nitrogen efficiency in wheat under rainfed Mediterranean conditions as affected by split nitrogen application. Field Crop Res. 2005, 94, 86–97. [Google Scholar] [CrossRef]
- Justes, E.; Mary, B.; Meynard, J.M.; Machet, J.M.; Thelier-Huché, L. Determination of a critical nitrogen dilution curve for winter wheat crops. Ann. Bot. 1994, 74, 397–407. [Google Scholar] [CrossRef]
- Plénet, D.; Lemaire, G. Relationships between dynamics of nitrogen uptake and dry matter accumulation in maize crops. Determination of critical N concentration. Plant Soil 2000, 216, 65–82. [Google Scholar] [CrossRef]
- Ziadi, N.; Brassard, M.; Bélanger, G.; Cambouris, A.N.; Tremblay, N.; Nolin, M.C.; Claessens, A.; Parent, L.-É. Critical nitrogen curve and nitrogen nutrition index for corn in eastern Canada. Agron. J. 2008, 100, 271–276. [Google Scholar] [CrossRef]
- Ulrich, A. Physiological bases for assessing the nutritional requirements of plants. Annu. Rev. Plant Physiol. 1952, 3, 207–228. [Google Scholar] [CrossRef]
- Lemaire, G.; Gastal, F. N Uptake and distribution in plant canopies. In Diagnosis on the Nitrogen Status in Crops; Lemaire, G., Ed.; Springer-Verlag: Heidelberg, Germany, 1997; pp. 3–43. [Google Scholar]
- Sheehy, J.E.; Dionara, M.J.A.; Mitchell, P.L.; Peng, S.; Cassman, K.G.; Lemaire, G.; Williams, R.L. Critical concentrations: Implications for high-yielding rice (Oryza sativa L.) cultivars in tropics. Field Crop Res. 1998, 59, 31–41. [Google Scholar] [CrossRef]
- Ziadi, N.; Bélanger, G.; Claessens, A.; Lefebvre, L.; Cambouris, A.N.; Tremblay, N.; Nolin, M.C.; Parent, L.-É. Determination of a critical nitrogen dilution curve for sprint wheat. Agron. J. 2010, 102, 241–250. [Google Scholar] [CrossRef]
- Ziadi, N.; Bélanger, G.; Gastal, F.; Claessens, A.; Lemaire, G.; Tremblay, N. Leaf nitrogen concentration as an indicator of corn nitrogen status. Agron. J. 2009, 101, 947–957. [Google Scholar] [CrossRef]
- Lemaire, G.; Marie-Hélène, J.; François, G. Diagnosis tool for plant and crop N status in vegetative stage theory and practices for crop N management. Eur. J. Agron. 2008, 28, 614–624. [Google Scholar] [CrossRef]
- Clevers, J.G.P.W.; Gitelson, A.A. Remote estimation of crop and grass chlorophyll and nitrogen content using red-edge bands on Sentinel-2 and -3. Int. J. Appl. Earth Obs. 2013, 23, 344–351. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Pattey, E.; Zarco-Tejada, P.J.; Strachan, I.B. Hyperspectral vegetation indices and novel algorithms for predicting green LAI of crop canopies: Modeling and validation in the context of precision agriculture. Remote Sens. Environ. 2004, 90, 337–352. [Google Scholar] [CrossRef]
- Thomas, V.; Treitz, P.; Mccaughey, J.H.; Noland, T.; Rich, L. Canopy chlorophyll concentration estimation using hyperspectral and lidar data for a boreal mixedwood forest in northern Ontario, Canada. Int. J. Remote Sens. 2008, 29, 1029–1052. [Google Scholar] [CrossRef]
- Curran, P.J. Remote sensing of foliar chemistry. Remote Sens. Environ. 1989, 30, 271–278. [Google Scholar] [CrossRef]
- Fourty, Th.; Baret, F.; Jacquemoud, S.; Schmuck, G.; Verdebout, J. Leaf optical properties with explicit description of its biochemical composition: Direct and inverse problems. Remote Sens. Environ. 1996, 56, 104–117. [Google Scholar] [CrossRef]
- Kokaly, R.F.; Clark, R.N. Spectroscopic determination of leaf biochemistry using band-depth analysis of absorption features and stepwise multiple linear regression. Remote Sens. Environ. 1999, 67, 267–287. [Google Scholar] [CrossRef]
- Chen, P.; Haboudane, D.; Tremblay, N.; Wang, J.; Vigneault, P.; Li, B. New spectral indicator assessing the efficiency of crop nitrogen treatment in corn and wheat. Remote Sens. Environ. 2010, 114, 1987–1997. [Google Scholar] [CrossRef]
- Boochs, F.; Kupfer, G.; Dockter, K.; Kühbauch, W. Shape of the red-edge as vitality indicator for plants. Int. J. Remote Sens. 1990, 11, 1741–1753. [Google Scholar] [CrossRef]
- Madakadze, I.C.; Madakadze, R.M. Field evaluation of the chlorophyll meter to predict yield and nitrogen concentration of switchgrass. J. Plant Nutr. 1999, 22, 1001–1010. [Google Scholar] [CrossRef]
- Cartelat, A.; Cerovic, Z.G.; Goulas, Y.; Meyer, S.; Lelarge, C.; Prioul, J.L.; Barbottin, A.; Jeuffroy, M.H.; Gate, P.; Agati, G.; et al. Optically assessed contents of leaf polyphenolics and chlorophyll as indicators of nitrogen deficiency in wheat (Triticum aestivum L.). Field Crop Res. 2005, 91, 35–49. [Google Scholar] [CrossRef]
- Hansen, P.M.; Schjoerring, J.K. Reflectance measurement of canopy biomass and nitrogen status in wheat crops using normalized difference vegetation indices and partial least squares regression. Remote Sens. Environ. 2003, 86, 542–553. [Google Scholar] [CrossRef]
- Cilia, C.; Panigada, C.; Rossini, M.; Meroni, M.; Busetto, L.; Amaducci, S.; Boschetti, M.; Picchi, V.; Colombo, R. Nitrogen status assessment for variable rate fertilization in maize through hyperspectral imagery. Remote Sens. 2014, 6, 6549–6565. [Google Scholar] [CrossRef]
- Chen, P. Research on New Hyperspectral Indices for Plant Nitrogen Concentration and Biomass Estimation and Their Applications. Ph.D. Dissertation, China Agricultural University, Beijing, China, 2009. [Google Scholar]
- Mistele, B.; Schmidhalter, U. Estimating the nitrogen nutrition index using spectral canopy reflectance measurements. Eur. J. Agron. 2008, 29, 184–190. [Google Scholar] [CrossRef]
- Liang, H.; Liu, X. Model for calculating corn nitrogen nutrition index using hyper-spectral data. Trans. CSAE 2010, 26, 250–255. (In Chinese) [Google Scholar]
- Miller, T.D. Growth stages of wheat: Identification and understanding improve crop management. Better Crops. 1992, 76, 12–17. [Google Scholar]
- Chen, P.; Zhu, Y. A new method for winter wheat critical nitrogen curve determination. Agron. J. 2013, 105, 1839–1836. [Google Scholar] [CrossRef]
- Lemaire, G.; Meynard, J.M. Use of the Nitrogen Nutrition Index for analysis of agronomical data. In Diagnosis on the Nitrogen Status in Crops; Lemaire, G., Ed.; Springer-Verlag: Heidelberg, Germany, 1997; pp. 45–55. [Google Scholar]
- Reyniers, M.; Walvoort, D.J.J.; de Baardemaaker, J. A linear model to predict with a multi-spectral radiometer the amount of nitrogen in winter wheat. Int. J. Remote Sens. 2006, 27, 4159–4179. [Google Scholar] [CrossRef]
- Xue, L.H.; Cao, W.X.; Luo, W.H.; Dai, T.B.; Zhu, Y. Monitoring leaf nitrogen status in rice with canopy spectral reflectance. Agron. J. 2004, 96, 135–142. [Google Scholar] [CrossRef]
- Eitel, J.U.H.; Long, D.S.; Gessler, P.E.; Smith, A.M.S. Using in situ measurements to evaluate the new RapidEyeTM satellite series for prediction of wheat nitrogen status. Int. J. Remote Sens. 2007, 28, 4183–4190. [Google Scholar] [CrossRef]
- Cho, M.A.; Skidmore, A.K. A new technique for extracting the red edge position from hyperspectral data: The linear extrapolation method. Remote Sens. Environ. 2006, 101, 181–193. [Google Scholar] [CrossRef]
- Daughtry, C.S.T.; Walthall, C.L.; Kim, M.S.; de Colstoun, E.B.; McMurtrey, J.E., III. Estimating corn leaf chlorophyll concentration from leaf and canopy reflectance. Remote Sens. Environ. 2000, 74, 229–239. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Tremblay, N.; Zarco-Tejada, P.J.; Dextraze, L. Integrated narrow-band vegetation indices for prediction of crop chlorophyll content for application to precision agriculture. Remote Sens. Environ. 2002, 81, 416–426. [Google Scholar] [CrossRef]
- Haboudane, D.; Tremblay, N.; Miller, J.R.; Vigneault, P. Remote estimation of crop chlorophyll content using spectral indices derived from hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2008, 46, 423–437. [Google Scholar] [CrossRef]
- Dash, J.; Curran, P.J. The MERIS terrestrial chlorophyll index. Int. J. Remote Sens. 2004, 25, 5003–5013. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Viña, A.; Ciganda, V.; Rundquist, D.C. Remote estimation of canopy chlorophyll content in crops. Geophys. Res. Lett. 2005, 32, L08403. [Google Scholar] [CrossRef]
- Sims, D.A.; Luo, H.Y.; Hastings, S.; Oechel, W.C.; Rahman, A.F.; Gamon, J.A. Parallel adjustments in vegetation greenness and ecosystem CO2 exchange in response to drought in a southern California chaparral ecosystem. Remote Sens. Environ. 2006, 103, 289–303. [Google Scholar] [CrossRef]
- Guyot, G.; Baret, F.; Major, D.J. High spectral resolution: Determination of specral shifts between the red and the near infrared. ISPRS J. Photogramm. 1988, 11, 740–760. [Google Scholar]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W.; Harlan, J.C. Monitoring the Vernal Avancement of Retrogradation (Green Wave Effect) of Natural Vegetation; Type III, Final Report; NASA/GSFC: Greenbelt, MD, USA, 1974; p. 371. [Google Scholar]
- Pearson, R.L.; Miller, L.D. Remote Mapping of Standing Crop Biomass for Estimation of the Productivity of the Short-Grass Prairie, Pawnee National Grasslands, Colorado; ERIM: Ann Arbor, MI, USA, 1972. [Google Scholar]
- Huete, A.; Justice, C.; Liu, H. Development of vegetation and soil indices for MODIS. Remote Sens. Environ. 1994, 49, 224–234. [Google Scholar] [CrossRef]
- Broge, N.H.; Leblanc, E. Comparing prediction power and stability of broadband and hyperspectral vegetation indices for estimation of green leaf area index and canopy chlorophyll density. Remote Sens. Environ. 2001, 76, 156–172. [Google Scholar] [CrossRef]
- Qi, J.; Chehbouni, A.; Huete, A.R.; Kerr, Y.H.; Sorooshian, S. A modified soil adjusted vegetation index. Remote Sens. Environ. 1994, 48, 119–126. [Google Scholar] [CrossRef]
- Rondeaux, G.; Steven, M.; Baret, F. Optimization of soil-adjusted vegetation indices. Remote Sens. Environ. 1996, 55, 95–107. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Kaufman, Y.; Merzlyak, M. Use of a green channel in remote sensing of global vegetation from EOS-MODIS. Remote Sens. Environ. 1996, 58, 289–298. [Google Scholar] [CrossRef]
- Chen, P.; Tremblay, N.; Wang, J.; Vigneault, P.; Huang, W.; Li, B. New index for crop canopy fresh biomass estimation. Spectrosc. Spect. Anal. 2010, 30, 512–517. (In Chinese) [Google Scholar]
- Lemaire, G.; van Oosterom, E.; Sheehy, J.; Jeuffroy, M.H.; Massignam, A.; Rossato, L. Is crop N demand more closely related to dry matter accumulation or leaf area expansion during vegetative growth? Field Crop Res. 2007, 100, 91–106. [Google Scholar] [CrossRef]
- Gitelson, A.A. Wide dynamic range vegetation index for remote quantification of biophysical characteristics of vegetation. J. Plant Physiol. 2004, 161, 165–173. [Google Scholar] [CrossRef] [PubMed]
- Chen, P.; Wang, J.; Huang, W.; Tremblay, N.; Ou, Y.; Zhang, Q. Critical nitrogen curve and remote detection of nitrogen nutrition index for corn in the northwestern plain of Shandong province, China. IEEE J.-STARS 2013, 6, 682–689. [Google Scholar]
- Lukina, E.V.; Freeman, K.W.; Wynn, K.J.; Thomason, W.E.; Mullen, R.W.; Klatt, A.R.; Johnson, G.V.; Elliott, R.L.; Stone, M.L.; Solie, J.B.; et al. Nitrogen fertilization optimization algorithm based on in-season estimates of yield and plant nitrogen uptake. J. Plant Nutr. 2001, 24, 885–898. [Google Scholar] [CrossRef]
- Raun, W.R.; Solie, J.B.; Stone, M.L.; Martin, K.L.; Freeman, K.W.; Mullen, R.W.; Zhang, H.; Schepers, J.S.; Johnson, G.V. Optical sensor based algorithm for crop nitrogen fertilization. Commun. Soil Sci. Plant Anal. 2005, 36, 2759–2781. [Google Scholar] [CrossRef]
- Zhao, C.; Chen, P.; Huang, W.; Wang, J.; Wang, Z.; Jiang, A. Effects of two kinds of variable-rate nitrogen application strategies on the production of winter wheat (Triticum aestivum). N. Z. J. Crop Hort. 2009, 37, 149–155. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, P. A Comparison of Two Approaches for Estimating the Wheat Nitrogen Nutrition Index Using Remote Sensing. Remote Sens. 2015, 7, 4527-4548. https://doi.org/10.3390/rs70404527
Chen P. A Comparison of Two Approaches for Estimating the Wheat Nitrogen Nutrition Index Using Remote Sensing. Remote Sensing. 2015; 7(4):4527-4548. https://doi.org/10.3390/rs70404527
Chicago/Turabian StyleChen, Pengfei. 2015. "A Comparison of Two Approaches for Estimating the Wheat Nitrogen Nutrition Index Using Remote Sensing" Remote Sensing 7, no. 4: 4527-4548. https://doi.org/10.3390/rs70404527
APA StyleChen, P. (2015). A Comparison of Two Approaches for Estimating the Wheat Nitrogen Nutrition Index Using Remote Sensing. Remote Sensing, 7(4), 4527-4548. https://doi.org/10.3390/rs70404527