A Multi-Temporal and Multi-Spectral Method to Estimate Aerosol Optical Thickness over Land, for the Atmospheric Correction of FormoSat-2, LandSat, VENμS and Sentinel-2 Images
Abstract
: The correction of atmospheric effects is one of the preliminary steps required to make quantitative use of time series of high resolution images from optical remote sensing satellites. An accurate atmospheric correction requires good knowledge of the aerosol optical thickness (AOT) and of the aerosol type. As a first step, this study compares the performances of two kinds of AOT estimation methods applied to FormoSat-2 and LandSat time series of images: a multi-spectral method that assumes a constant relationship between surface reflectance measurements and a multi-temporal method that assumes that the surface reflectances are stable with time. In a second step, these methods are combined to obtain more accurate and robust estimates. The estimated AOTs are compared to in situ measurements on several sites of the AERONET (Aerosol Robotic Network). The methods, based on either spectral or temporal criteria, provide accuracies better than 0.07 in most cases, but show degraded accuracies in some special cases, such as the absence of vegetation for the spectral method or a very quick variation of landscape for the temporal method. The combination of both methods in a new spectro-temporal method increases the robustness of the results in all cases.1. Introduction
Optical remote sensing from space in the reflective range of the optical domain is a powerful tool for studying the state and the evolution of land surfaces. However, optical observations from space are significantly disturbed by the atmosphere: clouds, gas molecules and aerosols scatter and absorb the light emitted by the Sun or reflected by the Earth’s surface (e.g., [1,2]). As a result, the operational processing of remote sensing image time series requires preliminary correction steps, such as the detection of clouds and the correction for atmospheric effects. These tasks are particularly difficult above land surfaces, because of two main issues: the identification of cloud-free pixels and, then, the separation of surface and atmospheric effects. The cloud detection problem has already been addressed elsewhere [3,4] and is not within the scope of this article.
Regarding the atmospheric correction, two effects must be taken into account:
The absorption by atmospheric gases (especially water vapor, ozone, oxygen and carbon dioxide): Absorption has a predominant effect within specific absorption bands [5], but the spectral bands for land surface observations are usually designed to avoid strong absorption lines. In these bands, gaseous absorption can be accurately corrected using meteorological analyses and simple analytical models, such as the Simplified Model for Atmospheric Correction (SMAC) [6] or 6S [2].
The scattering by air molecules and aerosols: scattering in the atmosphere is very accurately modeled [7] and can be adequately accounted for, provided the composition of the atmosphere is sufficiently well known. This is the case for the air molecules, but the difficulty lies in the knowledge of the aerosol properties, which are very variable, both in location and time [8].
With good knowledge of the aerosol optical thickness (AOT) and of the aerosol model, and using radiative transfer codes, one can correct for the aerosol effects and convert the satellite top-of-atmosphere (TOA) reflectances into surface reflectances [9].
Several strategies have been developed to estimate the AOT and, sometimes, the aerosol model from remote sensing images. The most popular are multi-spectral (MS) methods, which use empirical relationships between the surface reflectances of several spectral bands [10]. These methods often rely on short wave infrared (SWIR) bands, although a few authors have extended them to space instruments observing only in the visible and the near-infrared (NIR) [11]. These methods are named “dark dense vegetation” or “dark target” approaches [12], and their limitation comes from the necessity to have a sufficient proportion of surface with low reflectances, such as surfaces covered with dense vegetation. This limitation has been overcome thanks to the use of the “deep blue” band (410 nm) of MODIS (Moderate-Resolution Imaging Spectroradiometer) [13], for which the variation of surface reflectances is low compared to the atmospheric contribution, or via the use of polarization brought by POLDER (Polarization and Directionality of Earth Reflectances) instruments [14]. Unfortunately, these two features are not available on the sensors used in this study.
The coming launch of two new missions (VENμS [15] and Sentinel-2 [16]) with a short revisit period, a decametric spatial resolution and a constant viewing angle, has motivated the development of “multi-temporal (MT) methods” [17]. These methods rely on the relative stability of the Earth surface reflectance against time, compared to the high temporal variability of the AOT. Hence, the changes of the reflectances measured on consecutive images can be associated with a change in atmospheric aerosol content and used to estimate the AOT.
Both kinds of methods have pros and cons: the MT approach requires a rather time-stable surface reflectance to discriminate the atmospheric state accurately from land evolutions. Although surface reflectances usually vary slowly with regard to time, a high repetitivity of observations is needed. For this method, a given site must be observed with a constant viewing angle, as otherwise, directional effects might be interpreted as variations of AOT. For this reason, this method is not applicable to the satellites that observe a given site with changing viewing angles (e.g., SPOT, Rapid Eye, etc.). Conversely, MS techniques are not sensitive to temporal variations of surface reflectances, but their accuracy depends on the spectral signature of the observed pixels [18]. Thus, MS hypotheses are not expected to work correctly for all terrains in all seasons, and these methods are often limited to dense vegetation.
In contrast to many aerosol estimation methods ([14,18], etc.), our work aims at estimating aerosol optical thickness mainly to perform an atmospheric correction. For aerosol studies, the accuracy of estimates is essential, and it might be preferable not to provide an estimate if it is likely to be inaccurate. However, in the case of atmospheric correction, it is essential to be able to provide an estimate of the surface reflectance, even when the aerosol estimate is not perfectly accurate, and therefore, an estimate of aerosol content is necessary for all of the cloud-free pixels. We thus tried to maximize the robustness of the aerosol retrieval, i.e., to maximize the number of situations in which an aerosol estimate can be performed.
Our work began with the development of the MT method described in [4] for the VENμS satellite mission, which will offer a two-day repetitivity over 100 sites. In order to apply this technique to the Sentinel-2 mission, which has a longer revisit period of five days with two satellites, and to improve its estimates when the surface reflectance varies quickly, MS criteria have been added to the MT method. As a result, a hybrid method, using both temporal and spectral approaches for retrieving the AOT, has been developed. These methods have been introduced in the Multi-Sensor Atmospheric Correction and Cloud Screening software, developed as a prototype version at the Centre d’Etudes Spatiales de la Biosphère (CESBIO) and as an operational version at the Centre National d’Etudes Spatiales (CNES). They will be used to produce Level 2A products, which, according to Sentinel-2 denomination [16], are ortho-rectified images expressed in surface reflectance. This software is being used within the VENμS satellite ground segment and within the French THEIA land data center ( http://www.theia-land.fr).
After a description of the satellite missions and datasets used in Section 2, this paper details the MT and the MS algorithms and their combination in Section 3 and, then, compares their performances in Section 4.
2. Missions and Datasets
2.1. Missions
VENμS is a joint French-Israeli Earth observation satellite developed by the Centre National d’Etudes Spatiales (CNES) and the Israeli Space Agency (ISA), to be launched in 2016. This satellite is designed to demonstrate the benefits of a very high revisit frequency for land surface monitoring: it will monitor about 100 sites worldwide every two days with a constant viewing angle and with a resolution of 5 m [19]. To achieve this repetitivity, VENμS will be put on a two-day repeat cycle orbit at an altitude of 720 km. VENμS observations will be made with 12 bands in the visible and NIR ranges.
The operational mission Sentinel-2 [16] is being developed by the European Space Agency (ESA) in the frame of the European Union Copernicus program. Its aim is to observe the whole land surface systematically, with a short revisit period of five days. The global acquisitions will be obtained from the nadir at a high resolution (10, 20 to 60 m, depending on the spectral band). The observations will be made with 13 spectral bands, in the visible, NIR and SWIR ranges. Two Sentinel-2 satellites should be launched in 2015 and 2016, respectively. Both of them will fly on a 10-day repeat cycle orbit, but the system made of both satellites will provide a five-day revisit period.
Fortunately, two existing missions, FormoSat-2 and LandSat-5/7, enable one to simulate VENμS and Sentinel-2 products, respectively (Table 1). FormoSat-2 is a mission developed by the National Space Program Office of Taiwan (NSPO), which was launched in 2004. Its orbit has a one-day repeat cycle, which allows observing a given site every day with a constant viewing angle [20]. The Remote Sensing Instrument (RSI) on-board FormoSat-2 provides eight-meter resolution images in four visible and NIR bands. However, for cost reasons, we did not purchase datasets with a repetitivity of one day, but with a repetitivity of three to ten days.
The LandSat program is the longest-running Earth-observation satellite program [21]. It was developed by NASA and USGS. The first LandSat satellite flew in 1972 and was followed by six additional ones. In this study, we used LandSat-5 and 7, launched in 1984 and 1999, respectively. The repeat cycle for these two satellites is 16 days; however, an eight-day repetitivity can be reached combining images from both satellites. The Thematic Mapper (TM) instrument has been installed on-board LandSat-5, while LandSat-7 is equipped with an improved version: the Enhanced Thematic Mapper Plus (ETM+). Both instruments acquire images in the nadir direction in the VNIR, the short wave infrared (SWIR) and the thermal infrared (TIR) ranges, at a resolution of 30 m, except for TIR, for which the resolution is 120 m for LandSat-5 and 60 m for LandSat-7 (see Table 1). In May 2003, the LandSat-7 Scan Line Corrector (SLC) failed, degrading the acquired images from then on. For this reason, we used data acquired before this breakdown, to keep a repetitivity close to that of Sentinel-2. Since April 2013, LandSat-8 data have been available, but have not been involved in this study, because of the reduced repetitivity compared to the period when both LandSat-5 and LandSat-7 were available and working nominally. However, the multi-sensor atmospheric correction and cloud screening (MACCS) spectro-temporal processor is applicable to LandSat-8 and currently used to process surface reflectance products over France at the THEIA Land Data Center.
2.2. Datasets
In order to test our algorithm, several LandSat-5/7 and FormoSat-2 time series were used. FormoSat-2 images were purchased by CNES for the preparation phase of the VENμS mission, over sites of interest for our laboratory. They were orthorectified using the algorithms detailed in [22]. The absolute calibration of the sensor was obtained using the desert sites method [23], which uses stable and uniform desert sites to transfer the calibration of a well-calibrated instrument (such as MODIS) to other optical spaceborne sensors. LandSat orthorectified images were acquired via the United States Geological Survey (USGS). As it is not possible to get dense time series from LandSat-5 and 7 over Europe, we chose several sites in the United States, where LandSat-5 and 7 acquisitions are most frequent. The data from the VNIR and SWIR bands were converted to top-of-atmosphere (TOA) reflectance using the calibration coefficients indicated in their metadata files [24]. The sites have been arbitrarily classified into “green” or “arid” sites. Green sites show NDVI above 0.3 over most natural surfaces, while the arid sites only have an NDVI above 0.3, where irrigated crops are grown or on some sparse forest pixels.
LandSat and FormoSat-2 sites were chosen considering two criteria: first, the existence of one or two AERONET sun-photometers [25] on the image footprint to validate our aerosol content estimates; second, the possibility to test the methods over various types of regions and terrains, in order to assess their robustness with regard to different combinations of viewing geometry (solar and satellite zenith and azimuth angles), climatic conditions and land cover. In addition, in the case of LandSat, we only used images acquired before the SLC breakdown in 2003. For LandSat, the sites containing the American sun-photometers of Boulder, Columbia, Fresno/Corcoran, Howland, Rogers Dry Lake/University of California Los Angeles (UCLA) and Stennis were selected. For FormoSat-2, time series above La Crau/Avignon, Seysses/LeFauga, Ras El Ain and Yaqui AERONET sites were used (Table 2). Although we used very different sites in different climatic zones, the sites we selected never had an aerosol AOT above 0.7 for the remote sensing data acquisition dates and even 0.4 for LandSat time series in stable conditions (the notion of stable conditions is explained in Section 4).
3. Atmospheric Correction
3.1. Performance Requirements for AOT Estimates
The published literature about LandSat-8 or Sentinel-2 mission requirements ([16,26]) does not provide requirements for the accuracy of surface reflectance after atmospheric correction. Defining the needs regarding surface reflectance would be a difficult task, as LandSat and Sentinel-2 data are or will be used for very different applications, such as producing land cover maps, detecting changes, monitoring bio-physical variables, such as the Leaf Area Index (LAI), the fraction of absorbed photosynthetically available radiation (fAPAR) or the plant biomass, providing crop water need estimates, estimating coastal water optical properties, etc.
Vermote and Kotchenova [27] consider that “good” surface reflectances are known with a root mean square error (RMSE) below 0.005 + 0.05 × ρsurf, where ρsurf is the surface reflectance actual value. To build this requirement, the authors did not study user needs for a given application, but computed an error budget, taking into account the calibration, water vapor and ozone content uncertainties and, for aerosols, the “state-of-the-art” performances of AOT estimates. As “state-of-the-art” performances, they used the performances of their own atmospheric correction algorithm applied to the MODIS instrument. This performance does not account for adjacency effects [28], which are not very large at a kilometric resolution, but are much higher at a decametric resolution.
To our knowledge, no study details the needs in terms of accuracy of the various missions addressed by VENμS LandSat and Sentinel-2. To get an order of magnitude of the needs, we studied the errors on surface reflectance due to atmospheric correction errors as a function of the AOT estimate uncertainty and searched the standard deviation of errors on AOT that enable retrieving surface reflectances within the error margin defined by [27].
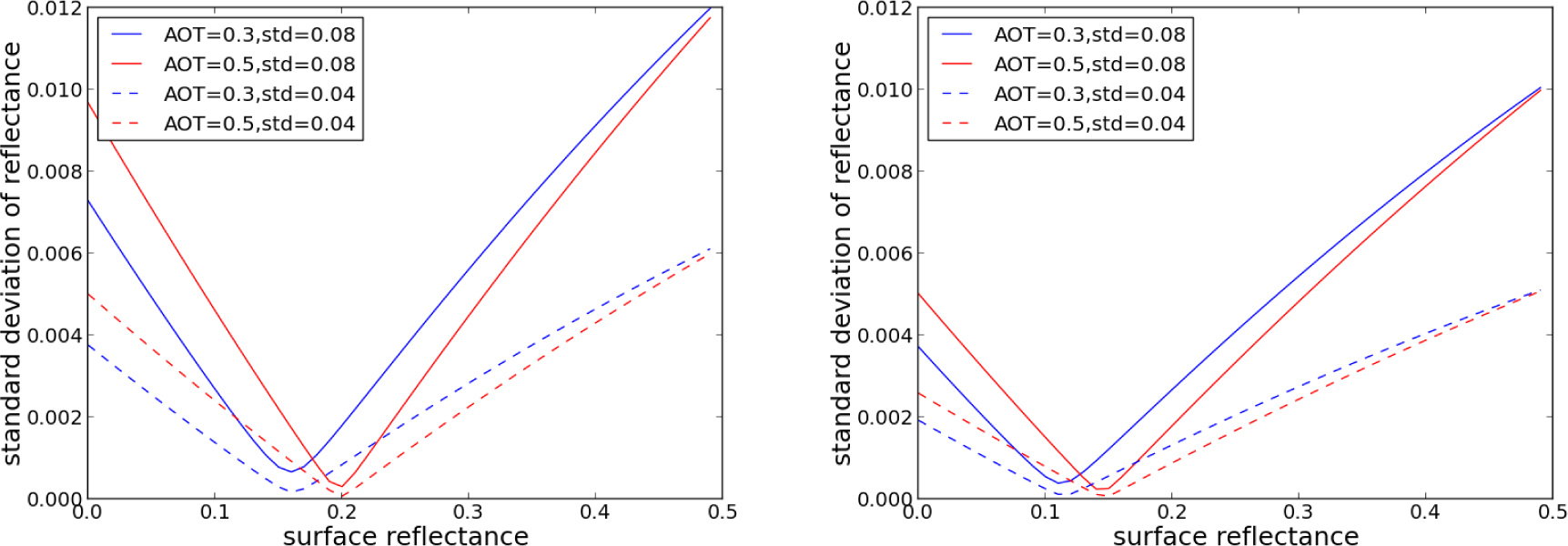
To do that, we used radiative transfer simulations with the successive orders of scattering code [7]: we started from surface reflectances with realistic values between 0 and 0.5, simulated the corresponding values at the top of atmosphere with a known AOT and an added noise to the AOT. Then, an atmospheric correction was performed with the known AOT, but without the noise, to obtain a new value of surface reflectance. The standard deviation of the difference of the input and output surface reflectance values was computed and is shown in Figure 1 for two spectral bands, red and NIR, as a function of surface reflectance, for a nadir viewing instrument and a mean Sun zenith angle of 45 degrees, as well as for two values of the AOT standard deviations, 0.04 and 0.08. The standard deviation is below 0.01 for an optical thickness below 0.5, except for the highest surface reflectances, and it is lower than 0.005 if the AOT standard deviation on AOT is below 0.04. As a result, for the average conditions used for this simulation, we found that a standard deviation of AOT below 0.04 for the low surface reflectances observed for green sites and below 0.08 for the greater surface reflectances observed for arid sites should allow one to meet the requirement developed by Vermote and Kotchenova [27].
3.2. Processing Overview
In the first step, our processor corrects for absorption by atmospheric gas molecules, using the absorption part of the Simplified Model for Atmospheric Correction (SMAC) method [6] and considering ozone, oxygen and water vapor concentrations obtained from either satellite data (ozone) or meteorological data (water vapor, pressure).
A second processing step detects the clouds and their shadows, using the multi-temporal cloud detection (MTCD) method [4]. For this method, the images of a time series must be processed in chronological order. Each time a new image is processed, a cloud-free composite image made of the most recent cloud-free pixels is updated with the newly obtained cloud-free pixels. This composite is used both for the cloud detection and for the multi-temporal method for aerosol detection. For the cloud detection, the current image to process is compared to the composite, and if a large increase of reflectance in the blue band is observed, the pixel is likely to be a cloud. To be finally classified as a cloud, the detection has to be confirmed by several other tests described in [4]. Water and snow (when SWIR bands are available) are also detected and discarded for the AOT estimates, as their reflectances tend to change very quickly with time.
The third step is the AOT estimate. In order to reduce the computational burden and the potential noise existing in the image, the AOT retrievals are not performed at full resolution: FormoSat-2 and LandSat products are subsampled to a coarse resolution, of 100 m and 240 m, respectively. Each estimate is based on a 7 × 7 coarse pixel neighborhood, and the estimate of AOT is computed for one coarse pixel out of three along the lines and columns. The AOT image has finally a resolution of about 300 m for FormoSat-2 and 720 m for LandSat.
Molecular and aerosol scattering effects are modeled using the successive orders of scattering code (SOS, [7,29]), which provides look-up tables (LUT) to convert the TOA reflectances already corrected for gas absorption into surface reflectances. The atmospheric correction function is, in fact, an interpolation within the LUT. The LUTs are parameterized by the viewing geometry, the surface altitude, the AOT and the wavelength. A different LUT is computed for each aerosol model, but in this study, we only used a continental aerosol model, whose characteristics are shown in Table 3.
For both AOT estimation methods (MS or MT), suitable pixels are selected according to various criteria described below. As a result, an AOT estimate is not always available for each pixel in the image. In order to obtain an AOT for each pixel of the image, a final post processing of the image is done to fill the gaps due to the absence of the AOT estimate because of clouds, shadows, water bodies and low NDVI for the multi-spectral method and variation of surface reflectance for the multi-temporal method. A smoothing window (15 × 15 Gaussian filter) is then applied at coarse resolution, and finally, the AOT is interpolated to the full resolution.
In the last step, the atmospheric correction is performed for each pixel in the image using the LUT, as explained in [17]. An adjacency effect correction derived from [28] and a correction of the variations of illumination due to topography [30] have also been implemented, but these parts are not described here for the sake of concision.
3.3. Aerosol Estimate Algorithms
3.3.1. Multitemporal Method
Thanks to the observations with a constant viewing angle provided by the chosen satellite systems, the directional effects on the measured reflectances are minimized [31,32]. For this reason, the variations of TOA reflectances for two cloud-free consecutive images separated by a few days are very likely due to changes in atmospheric aerosol content. The multi-temporal (MT) algorithm described in [17] estimates the AOT based on two assumptions:
the AOT varies faintly with distance;
the surface reflectance varies slowly with time.
As a result, the AOT is assumed constant within a coarse resolution neighborhood of the processed pixel, and surface reflectances are assumed to be the same for the date to be processed and for a recent date Dr used as a reference. The pixels contained in this window are used for the AOT estimate if they are not flagged as cloud, snow or water. Moreover, we discard the pixels for which the NIR (FormoSat-2) or SWIR (LandSat) reflectance has changed too much since the reference date. These bands were chosen because they are less sensitive to AOT variations and more sensitive to surface reflectance variations. A minimum of 40% of useful pixels within the neighborhood is required to compute the AOT estimate.
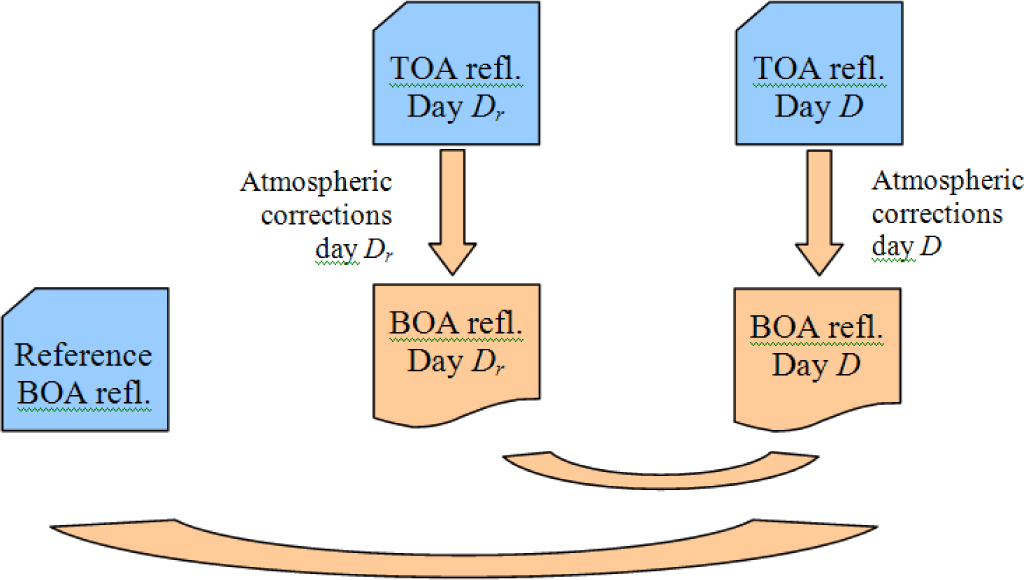
For two successive cloud-free observations acquired at dates D and Dr, the MT algorithm iteratively searches for the AOT of dates D and Dr that minimizes the squared differences between the surface reflectances of D and Dr obtained after atmospheric correction (see Equation (3)). As shown in [17], the resulting AOT estimates are accurate to better than 0.07, except when the AOT is nearly the same for D and Dr. In that case, the TOA reflectances in both dates are similar, and any constant aerosol loading leads to similar surface reflectance values. It is therefore not possible to retrieve the absolute value of AOT, but just to infer that it has not changed. To improve the retrieval when consecutive AOTs are similar, a second equation (Equation (4)) that links the present image surface reflectance to a reference one is computed. This reference image comes from an earlier iteration of the algorithm (Figure 3).
The method cost function is the sum of squares of the errors associated with these equations, and a Levenberg–Marquardt non-linear least mean squares (LMS) algorithm searches the AOT of date D and date Dr that minimize it. The cost function is expressed as:
In Equation (3)atcor is the atmospheric correction function that links TOA reflectances to their corresponding surface reflectance for a given aerosol optical thickness and a given aerosol model, ρTOA(D) is the TOA reflectance for the pixel acquired at date D, ρTOA(Dr) is the TOA reflectance for the composite cloud-free image described above and ρsurf(Dr) is the reference surface reflectance; τ is the AOT for date D, and τr is the AOT for date Dr. Since it was found that reflectances in the blue range have a lower temporal variation, only reflectances of this channel are used in this cost function. The coefficients K1 and K2 weight the contribution of err1 and err2. K2 is set to one, and K1 is proportional to the mean value of the difference of the blue TOA reflectances from dates D and Dr: as said above, the value of err1 will always be close to zero if τ equals τr. For this reason, it is more accurate to increase the weight of err1 when the AOT difference between D and Dr is higher, resulting in a higher difference in the TOA reflectances of D and Dr.
Of course, given these assumptions, the multi-temporal method is less accurate when the repetitivity of observations is reduced or when the vegetation changes quickly. Another drawback of the method is that its sensitivity to aerosol variation decreases and its error increases when the surface reflectance is high. In fact, as shown in [17], there is even a range of reflectances (around 0.25 in the blue) for which an increase of AOT increases the path radiance, but decreases the transmission, such that the TOA reflectance does not depend any more on the AOT (see Figure 2). Fortunately, if this kind of landscape is not ideal for the AOT estimate, the atmospheric correction is not too degraded, since the reflectance does not depend much on the AOT, even if the adjacency effects still depend on the AOT. However, to avoid this case, an additional test was added to select the pixels for which the reflectance is sensitive to the AOT: if the reflectance of a pixel lies in the range where the surface reflectance computed with the atcor function varies by less than 0.01 when the AOT varies by 0.2, then the pixel is not valid to compute AOT.
As said in [17], the MT method does not estimate the aerosol model and must rely on prior knowledge. Early trials showed that estimating the aerosol models added much noise to the time series after atmospheric corrections. These trials were performed using sensors with a very limited number of spectral bands, and it might be useful to try estimating the aerosol model again for sensors with more spectral bands in the visible, such as LandSat-8 or Sentinel-2.
3.3.2. Multispectral Method
Our version of the MS algorithm is based on the dark dense vegetation (DDV) approach (Kaufman and Sendra, 1988 [10]). This method is used, for instance, in the MODIS data processing. It retrieves the AOT above dense vegetation pixels by means of empirical relationships between the surface reflectances in the blue, red and SWIR (around 2 μm) spectrum ranges. For vegetation, these relationships are physically justified by the correlation of the chlorophyll absorption peaks in the blue and red bands and the liquid water absorption in the SWIR [10].
For MODIS, the operational algorithms up to Version 4 [18] assumed that the surface reflectance in the blue (0.47 μm, Channel 3) and the red (0.66 μm, Channel 1) bands were one-quarter and one-half, respectively, of the surface reflectance in the SWIR (2.12 μm, Channel 7). However, several studies suggested that these VIS/SWIR surface ratios depend on the location, season and angles. Levy et al. [33], showed that these values are location dependent during a study along the coast of Virginia. Moreover, Gatebe et al. [34] pointed out that the ratios depend on the viewing geometry, and Remer et al. [35] also found a variation as a function of the season. In order to deal with these issues, these simple relationships were improved for Version 5.2 of the MODIS algorithm, where correlations with the land greenness and the viewing geometry were introduced. Besides, these equations can be extended to brighter pixels, increasing the areas over which the AOT estimation is made [18].
Due to the lack of SWIR channels in FormoSat-2, Version 5.2 for the MODIS algorithm is only applicable to LandSat, and since the channels of both instruments are different (Figure 4), new values of the coefficients must be computed. Moreover, the MODIS band at 1.24 μm, used for the calculation of a greenness parameter, does not exist in LandSat instruments. For these reasons, we decided to build our own multi-spectral relations based on simpler equations.
The relations between the surface reflectance in the blue, red and SWIR channels were determined using LandSat and FormoSat-2 images, for which AERONET measurements are available. We only selected images without clouds or snow and having a low AOT on AERONET records. The uniformity of AOT and the absence of clouds were verified by visual inspection. The TOA reflectances from these images were converted into surface reflectances using the AOT from AERONET measurements (water vapor and AOT at 550 μm) and a small continental aerosol model (the aerosol model has low impact, since only images with a low AOT were selected). Finally, the surface reflectances of the pixels contained in a zone of 20 × 20 km2 around the sun-photometer were extracted and compared. The water pixels have been discarded from the plots. Twenty two images taken from four sites (Sevilleta, Fresno, Columbia, Konza) were used for LandSat. Only two of these sites were also used in the study of the method performance in Section 4. For FormoSat-2, due to the price of the dataset, we could not afford to use a large number of sites, and we used the same sites to compute the coefficients and to validate the AOT, which may result in somewhat optimistic values for the multi-spectral method. Eighteen images were used to obtain FormoSat-2 regression coefficients.
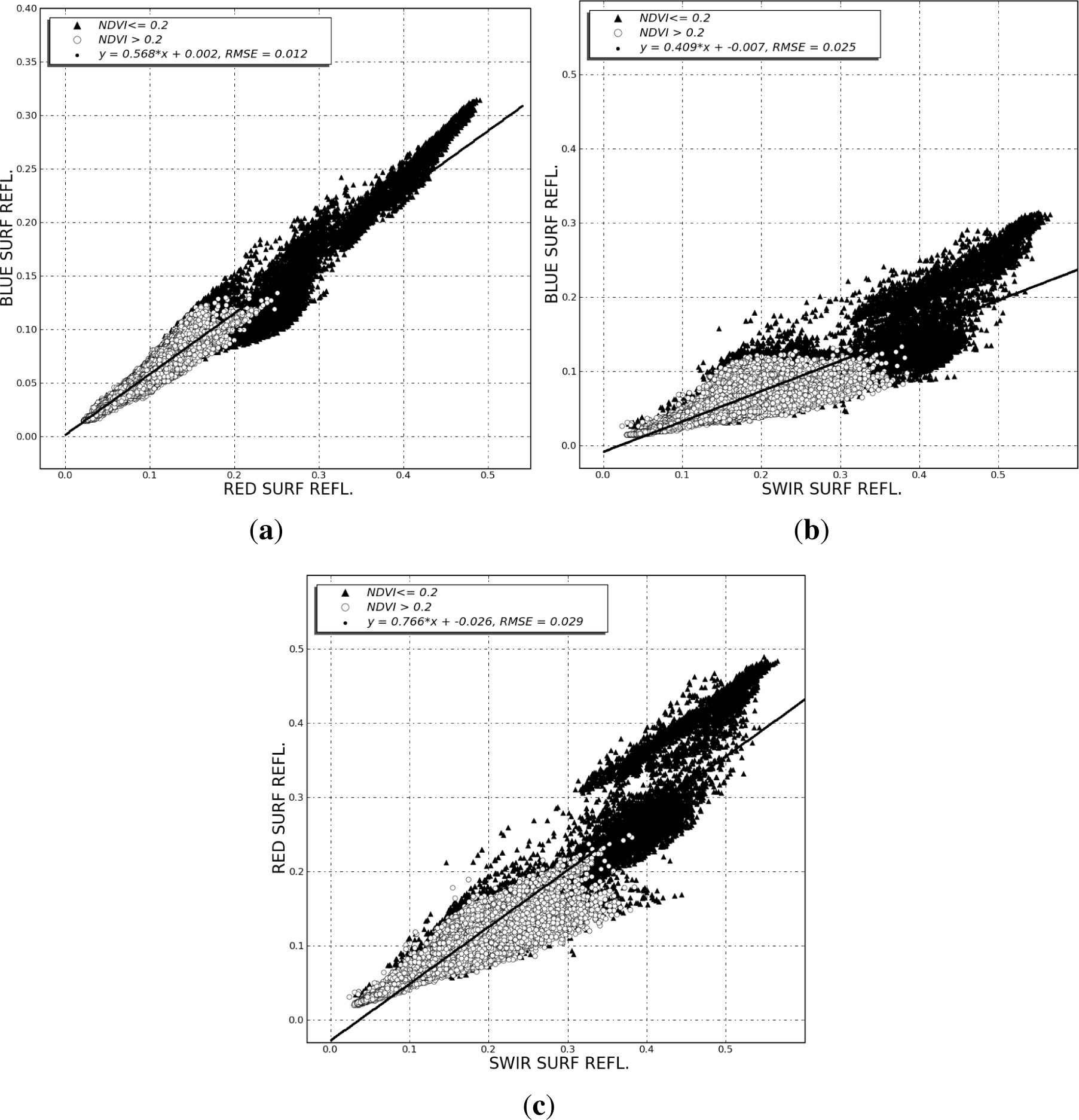
Figure 5 shows the scatter plots obtained by comparing surface reflectances for the following pairs of bands: blue and SWIR bands, red and SWIR bands and blue and red bands. Our first finding is that the scatter (see Table 4) is at least twice as high when a SWIR band is involved than when the blue-red pair is used. The plots also show that the scatter is further reduced when the NDVI is higher, which explains why this method is often named the “dark dense vegetation” method.
Linear regressions were computed after discarding all of the pixels which have an NDVI below 0.2. Although LandSat-5 and 7 bands are very similar, different relationships have been calculated for each satellite. Linear regressions yielded the following results:
LandSat-5:
LandSat-7:
One part of the differences between LandSat-5 and LandSat-7 may be due to the differences between spectral bands, and another part may come from the limited amount of data used in this study to derive the regressions. The coefficients of the equations involving the SWIR bands are not far from those adopted in the initial versions of the MODIS algorithm (slopeblue−SWIR = 0.25, slopered−SWIR = 0.5). The retrieved coefficients are even closer to those obtained by Ju et al. [36], who adopted a method with a constant aerosol model, but which is based on the blue and SWIR 2.2 μm spectral bands (slope blue-SWIR = 0.33).
In the case of FormoSat-2, only a blue-red relationship may be applicable, since this satellite has no band beyond 1 μm.
Table 4 summarizes the RMSE associated with the linear regressions presented.
Due to the higher RMSE observed when a SWIR band is used and to the lack of this channel in FormoSat-2, the blue-red relationships were chosen for the MS method. However, as only one equation is used, retrieving both the AOT and the aerosol model is not possible anymore, and for a given location, a constant aerosol model must be used. The same choice was made by Ju et al. [36], as relying on the SWIR bands to estimate the aerosol model would result in adding more noise to the aerosol estimates due to the higher standard deviation observed in Table 4. Of course, atmospheric correction errors will be observed when the aerosol model used for the AOT estimate is not the right one. For our implementation of the MS method, we used the cost function given in Equation (8). The cost is the sum of squares of the differences between the blue surface reflectances after atmospheric correction and the blue surface reflectance predicted from the red band.
3.3.3. Spectro-Temporal Technique
The hybrid method merges the elementary methods described above. The AOT estimate performed by the hybrid method relies on the minimization of a cost function by an LMS algorithm. The cost function is provided in Equation (10). It combines the MS and the MT equations presented above (Equations (2) and (9)).
3.3.4. Dark Object Method
As indicated above, there are cases when the MT and MS methods used separately can provide wrong estimations (steep variation of reflectances or spectral surface reflectances that do not correspond to the surface reflectance model). To limit these erroneous estimates, two additional constraints have been added and applied to the individual MS and MT methods and also to the hybrid method. The constraints are a lower and upper bound for the AOT estimate: the lower bound is based on the fact that the AOT cannot be negative. The definition of the upper bound is based on the “dark object subtraction” approach (e.g., [37]), which consists of estimating the aerosol optical thickness for dark pixels assuming a fixed value for their surface reflectance in the blue band. To implement the dark object method, we search for the pixels in the image with the minimum reflectance in the blue: to avoid underestimates of the ceiling value, the pixels that lie in the shadow of a cloud or of topography are excluded using the cloud shadow mask and a topographic shadows mask. The method also checks that the selected pixel was also dark in the previous image to avoid undetected cloud shadows. This pixel is assumed to have a surface reflectance of 0.01 (0.03 might be used for more arid sites), and the method searches the necessary AOT to obtain the observed TOA reflectance for that pixel.
Constraints related to upper and lower bounds are added to the cost function. The lower bound constraint has a very large weight, since it is not possible to observe a negative AOT, whereas the upper bound constraint has a low one to allow optical thickness variations within the image: the pixel of minimum reflectance could lie in a zone where the AOT is lower than in other parts of the image. If the image is very large (LandSat or S2), it is possible to divide it into smaller zones and to determine the ceiling value for each zone.
3.3.5. Gap Filling Algorithm
A final AOT value for each pixel is needed to retrieve surface reflectance; however, there are always pixels for which the AOT estimate is not available, since, for instance, clouds, shadows and water pixels are systematically discarded from the AOT estimation. Moreover, the MT and MS methods discard pixels that are not suitable for the estimation, as explained above. A gap filling is therefore necessary.
The gap filling algorithm we implemented works as follows (cf. the example in Figure 7). First, all isolated AOT estimations are removed by a morphological opening (with a small structuring element) because of their lack of reliability, as they are likely to have been computed in an isolated small gap in the cloud cover. The local gap filling algorithm consists of iterating with a neighborhood size that increases from a few hundreds of meters to 20 km: for each neighborhood size, the gaps are filled with the average of the available AOT estimates.
Finally, for data gaps greater than 20 km, usually due to large clouds, the remaining missing data are filled by the average of all AOT values available within the image.
Once the gaps are filled, the AOT image is smoothed with a Gaussian filter and then resampled to the full resolution (using a bilinear interpolation) to be used by the atmospheric correction routine.
4. Results and Discussions
To assess the validity of the estimates obtained by each method, the AOT retrievals at 0.55 μm are compared to AERONET data, after an automatic screening of AERONET data, which are likely corrupted by the presence of clouds. This screening is based on the stability of AOT with time in the AERONET observations, the standard deviation of which must be below 0.02 within an hour around the satellite overpass time. The screening also uses the cloud mask generated for the images, to discard cases when there are more than 10% of clouds in a 20-km neighborhood of the AERONET site. These criteria define the “stable cases” in our study, while the other cases are named “unstable cases”. The image AOT retrievals are averaged on a 20 × 20 km2 neighborhood around the AERONET site. A unique continental aerosol model has been used for all of the sites and all of the dates, although better results could probably be obtained with a proper tuning of the aerosol model.
Table 5 shows the RMS error between our estimated optical thickness and the sun-photometer data for different LandSat and FormoSat time series and for the three different methods. In this table, we only kept the results in stable conditions, for which less than half of the pixels of the neighborhood have been gap filled.
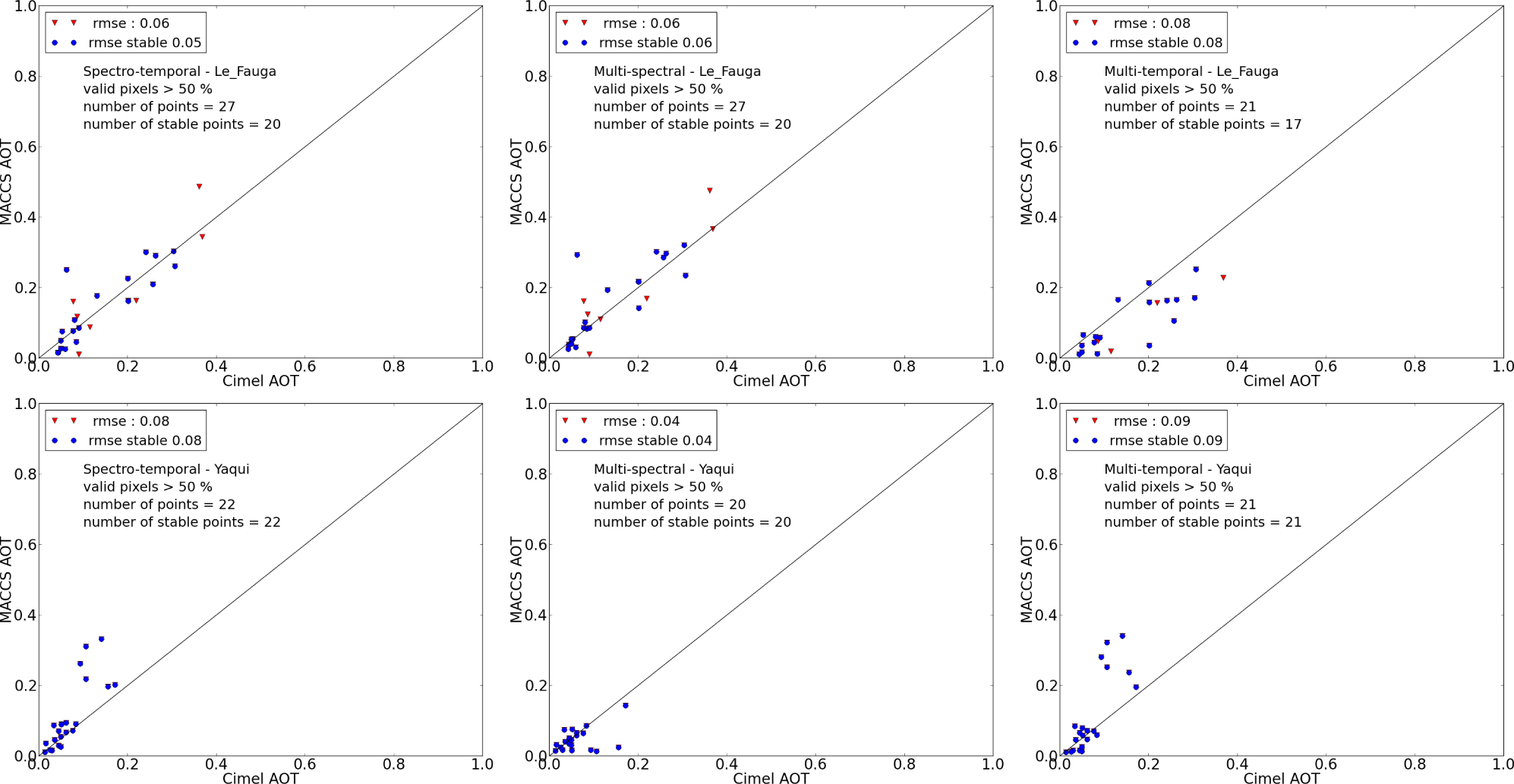
Both methods used individually (MS and MT) provide the same magnitude of RMS errors on AOT estimates, for both satellites (around 0.07 for FormoSat and 0.09 for LandSat). Table 5 details the results obtained for each site and each satellite. The MT method outperforms the MS method for some sites characterized by low cloudiness and, thus, an enhanced repetitivity: Boulder and Rogers for LandSat; Ras-El-Ain for FormoSat-2. When vegetation cover increases, the MS method performs better: this is the case for Columbia and Howland for LandSat and for Avignon, La Crau and Le Fauga for FormoSat-2. Some sites do not show a clear trend, either providing similar results for both MS and MT methods, like Stennis and UCLA, or one method providing a lower RMS error, but a reduced number of valid AOT estimations (Fresno and Corcoran). There is also one case, Howland, where the MT method is not able to provide results, due to the large cloud cover in the region: the MS method only needs one clear date to produce results, while the MT method needs two clear dates separated by less than two months.
The hybrid method usually produces RMS errors very close to the best of the MS or MT method. In a couple of cases (Corcoran, Yaqui), the MS method outperforms the MT and the hybrid method, but a closer look shows that this is due to the fact that the MS method does not provide results for some of the dates corresponding to dry conditions. Some detailed results for a few sites are plotted in Figures 8–10, with all of the points, including the unstable cases. The results obtained for unstable cases are often less accurate than the stable cases, but they are usually not completely wrong. The plots confirm that the MS method produces good results for green sites, while the MT method results have a larger standard deviation for these sites. The results of the hybrid method are quite close to the results of the MS method for these sites. An exception may be seen for the Yaqui site (Figure 8). This site is an irrigated plain in Mexico, which may be classified as a green site during the growing season, but as a very arid site afterwards. Four dates have errors above 0.1, but they all belong to the dry period, in May, when the MS method is not able to obtain an estimate of AOT for these sites. In May, in the whole image, all of the vegetation is quickly drying, and the assumption of stable reflectances is not valid.
Regarding the arid sites, the MT AOT is usually better correlated with the AERONET AOT than the MS AOT, and the MS method is sometimes not able to produce AOT estimates. In that case, getting an atmospheric correction with the MS method would mean relying on the gap filling method only, provided some dense vegetation exists somewhere in the image, and degrading the accuracy of the method in the case of AOT variations within the image. Figures 11 and 12 compare the results for all sites obtained with FormoSat and LandSat. The overall error observed for the hybrid method is lower than that of the multi-temporal method and has the same level as that of the multi-spectral method, but yields a greater number of estimates, showing that the method is more robust to the diversity of the observed conditions. The overall RMS error is 0.06, which is in line with the needs expressed in Section 3.1. For LandSat, the estimates are a little less accurate, but show the same trend with a much greater number of estimates obtained with the hybrid method. The increased noise might be explained by three reasons: first, in our LandSat dataset, the proportion of arid sites is higher and the observed accuracy is lower for these sites; second, given that, for LandSat, the time series areacquired by two different sensors, LandSat 5 and LandSat 7, additional noise due to the differences in spectral bands (see Figure 4) from both LandSat sensors is present (this should not be the case with Sentinel-2); and third, the repetitivity of the LandSat time series is reduced compared to that of FormoSat-2. In terms of bias, a very small bias is observed with FormoSat-2, while the bias is a little greater for LandSat. Part of the bias could be due to the use of an inaccurate aerosol model. It has to be noted that despite the large number of images processed, in the case of LandSat, only low aerosol contents were observed in stable cases.
Finally, the hybrid method yields good results with an accuracy close to the best of the MS and MT method. It shows an increased robustness and provides AOT estimates more frequently in all the kinds of sites and climates that we have tested.
5. Conclusions
A multi-sensor atmospheric correction and cloud screening (MACCS) method was developed in the framework of the preparation of Level 2A processors for the VENμS and SENTINEL-2 satellites, to deliver atmospherically corrected time series of images expressed in surface reflectance. The original part of this method lies in the estimation of the aerosol optical thickness (AOT): our method combines a multi-spectral (MS) assumption that links the surface reflectances of the red and blue bands of the satellite and also assumes that multi-temporal (MT) observations of a given neighborhood separated by a few days should yield similar surface reflectances. Both assumptions were used separately first, in order to compare their respective accuracies, then were hybridated to improve the results.
For the MS method, we decided to implement a simple method to avoid processing a huge amount of data to estimate the relations between spectral bands. During our preliminary analysis, we showed that the correlation of the surface reflectance of the blue and red bands is much higher than the correlation of blue and SWIR bands or red and short wave infrared (SWIR) bands. The “blue-red” relation is also applicable to FormoSat-2, while the blue-SWIR one is not. However, compared to the method implemented with MODIS that uses the blue-SWIR and red-SWIR relations, our MS method is not able to estimate the aerosol model and uses a constant model for a given site, which is a drawback for regions where the aerosol model is subject to large variations.
To assess the performances, we processed hundreds of images from six LandSat and four FormoSat-2 sites. The AOTs derived from our methods were compared to the ground truth provided by the Aerosol Robotic Network (AERONET): we found that both the MT and MS methods provide similar AOT accuracies (around 0.08). As anticipated, the MS method performs always better than the MT method in highly vegetated areas, and the MT method is more accurate when the observations are more frequent. Both methods are less accurate when the surface reflectance in the blue is high, because the sensitivity of TOA reflectance to the aerosol content is reduced.
The combination of MS and MT criteria within the MACCS method enhances the robustness of the retrieval: in most cases, the root mean square (RMS) error of the hybrid method is very close to the minimum of the RMS yielded by each individual method (0.06 for Formosat-2 and 0.08 for LANDSAT). The hybrid method is more robust than the MS method, which often fails above arid surfaces, bare soils and urban areas, and than the MT method when cloud cover is frequent.
Future studies should focus on a way of automatically prescribing the aerosol model, either by implementing an estimate of the aerosol model thanks to the increased number of spectral bands brought by both the VENμS and Sentinel-2 satellites or by using aerosol models provided by meteorological analyses, such as those provided by the Copernicus Atmosphere project [38].
The MACCS method is now used within the French Theia Land Data Center to process time series of LandSat (5, 7, 8) and FormoSat-2, and will be used to process VENμS and Sentinel-2 satellites. The availability of a spectral band at 1.38 μm on LandSat-8 and Sentinel-2 will enable a better discrimination of aerosol layers and of thin cirrus clouds. The increased repetitivity brought by VENμS and Sentinel-2 will also improve the performances of the MT and hybrid methods.
Acknowledgments
The authors would like to thank Carol J. Bruegge, Eric Ceschia, Philippe Goloub, Brent Holben, David Meyer, Doug Moore, Bernard Mougenot, Didier Tanré, Steve Tate and their staff for establishing and maintaining the AERONET sites used in this investigation. We are also grateful to the U.S. Geological Survey for the free distribution of LandSat images. Part of the activity was funded by CNES/TOSCA (Terre Océan Surfaces Continentales Atmosphère) program or by a CNES grant. We would like to thank the anonymous reviewers whose constructive comments helped to improve the quality of the article.
Author Contributions
Olivier Hagolle, Mireille Huc and David Villa-Pascual defined the methods, developed the processor, defined and processed the validation data set and validated the results and wrote the article. Gerard Dedieu was responsible for the study framework in the context of VENμS mission preparation and revised the manuscript.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Fraser, R.S.; Kaufman, Y.J. The relative importance of aerosol scattering and absorption in remote sensing. IEEE Trans. Geosci. Remote Sens. 1985, GE-23, 625–633. [Google Scholar]
- Vermote, E.; Tanré, D.; Deuzé, J.; Herman, M.; Morcette, J.J. Second Simulation of the Satellite Signal in the Solar Spectrum, 6S: An overview. IEEE Trans. Geosci. Remote Sens. 1997, 35, 675–686. [Google Scholar]
- Ackerman, S.A.; Strabala, K.I.; Menzel, W.P.; Frey, R.A.; Moeller, C.C.; Gumley, L.E. Discriminating clear sky from clouds with MODIS. J. Geophys. Res. 1998, 103, 32141–32157. [Google Scholar]
- Hagolle, O.; Huc, M.; Villa Pascual, D.; Dedieu, G. A multi-temporal method for cloud detection, applied to FORMOSAT-2, VENμS, LANDSAT and SENTINEL-2 images. Remote Sens. Environ. 2010, 114, 1747–1755. [Google Scholar]
- Deschamps, P.Y.; Herman, M.; Tanré, D. Modeling of the atmospheric effects and its application to the remote sensing of ocean color. Appl. Opt. 1983, 22, 3751–3758. [Google Scholar]
- Rahman, H.; Dedieu, G. SMAC: A simplified method for the atmospheric correction of satellite measurements in the solar spectrum. Int. J. Remote Sens. 1994, 15, 123–143. [Google Scholar]
- Lenoble, J.; Herman, M.; Deuzé, J.L.; Lafrance, B.; Santer, R.; Tanré, D. A successive order of scattering code for solving the vector equation of transfer in the Earth’s atmosphere with aerosols. J. Quant. Spectrosc. Radiat. Transf. 2007, 107, 479–507. [Google Scholar]
- Dubovik, O.; Holben, B.; Eck, T.F.; Smirnov, A.; Kaufman, Y.J.; King, M.D.; Tanré, D.; Slutsker, I. Variability of absorption and optical properties of key aerosol types observed in worldwide locations. J. Atmos. Sci. 2002, 59, 590–608. [Google Scholar]
- Liang, S.; Fang, H.; Chen, M. Atmospheric correction of Landsat ETM+ land surface imagery. I. Methods. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2490–2498. [Google Scholar]
- Kaufman, Y.J.; Sendra, C. Algorithm for automatic atmospheric corrections to visible and near-IR satellite imagery. Int. J. Remote Sens. 1988, 9, 1357–1381. [Google Scholar]
- Guanter, L.; Gómez-Chova, L.; Moreno, J. Coupled retrieval of aerosol optical thickness, columnar water vapor and surface reflectance maps from ENVISAT/MERIS data over land. Remote Sens. Environ. 2008, 112, 2898–2913. [Google Scholar]
- Levy, R.C.; Mattoo, S.; Munchak, L.A.; Remer, L.A.; Sayer, A.M.; Patadia, F.; Hsu, N.C. The Collection 6 MODIS aerosol products over land and ocean. Atmos. Meas. Tech. 2013, 6, 2989–3034. [Google Scholar]
- Sayer, A.M.; Hsu, N.C.; Bettenhausen, C.; Jeong, M.J. Validation and uncertainty estimates for MODIS Collection 6 “Deep Blue” aerosol data. J. Geophys. Res. 2013, 118, 7864–7872. [Google Scholar]
- Deuzé, J.L.; Bréon, F.M.; Devaux, C.; Goloub, P.; Herman, M.; Lafrance, B.; Maignan, F.; Marchand, A.; Nadal, F.; Perry, G.; et al. Remote sensing of aerosols over land surfaces from POLDER-ADEOS-1 polarized measurements. J. Geophys. Res. 2001, 106, 4913–4926. [Google Scholar]
- Hagolle, O.; Inglada, J.; Dedieu, G.; Huc, M.; Ferrier, P.; Courault, D. VENμS: Towards high quality time series of optical images at high resolution. IEEE Geosci. Remote Sens. Soc. Newsl. 2011, 161, 25–27. [Google Scholar]
- Drusch, M.; del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P.; et al. Sentinel-2: ESA’s optical high-resolution mission for GMES operational services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar]
- Hagolle, O.; Dedieu, G.; Mougenot, B.; Debaecker, V.; Duchemin, B.; Meygret, A. Correction of aerosol effects on multi-temporal images acquired with constant viewing angles: Application to Formosat-2 images. Remote Sens. Environ. 2008, 112, 1689–1701. [Google Scholar]
- Remer, L.A.; Kaufman, Y.J.; Tanré, D.; Mattoo, S.; Chu, D.A.; Martins, J.V.; Li, R.R.; Ichoku, C.; Levy, R.C.; Kleidman, R.G. The MODIS aerosol algorithm, products, and validation. J. Atmos. Sci. 2005, 62, 947–973. [Google Scholar]
- Dedieu, G.; Karnieli, A.; Hagolle, O.; Jeanjean, H.; Cabot, F.; Ferrier, P. The VENμS mission: Earth observation with high spatial and temporal resolution capabilities. Geophys. Res. Abstr. 2007, 9, 06947. [Google Scholar]
- Chern, J.S.; Wu, A.M.; Lin, S.F. Lesson learned from FORMOSAT-2 mission operations. Acta Astronaut. 2006, 59, 344–350. [Google Scholar]
- Williams, D.L.; Goward, S.; Arvidson, T. Landsat: Yesterday, today, and tomorrow. Photogramm. Eng. Remote Sens. 2006, 72, 1171–1178. [Google Scholar]
- Baillarin, S.; Gigord, P.; Hagolle, O. Automatic registration of optical images, a stake for future missions: application to ortho-rectification, time series and mosaic products, Proceedings of the 2008 IEEE International Geoscience and Remote Sensing Symposium (IGARSS 2008), Boston, MA, USA, 7–11 July 2008; 2, pp. II:1112–II:1115.
- Cabot, F.; Hagolle, O.; Henry, P. Relative and multitemporal calibration of AVHRR, SeaWiFS, and VEGETATION using POLDER characterization of desert sites, Proceedings of the 2000 IEEE International Geoscience and Remote Sensing Symposium (IGARSS 2000), Honolulu, Hawai, USA, 24–28 July 2000; pp. 2188–2190.
- Chander, G.; Markham, B.L.; Helder, D.L. Summary of current radiometric calibration coefficients for Landsat MSS, TM, ETM+, and EO-1 ALI sensors. Remote Sens. Environ. 2009, 113, 893–903. [Google Scholar]
- Holben, B.; Vermote, E.; Kaufman, Y.; Tanré, D.; Kalb, V. Aerosol retrieval over land from AVHRR data-application for atmospheric correction. IEEE Trans. Geosci. Remote Sens. 1992, 30, 212–222. [Google Scholar]
- Irons, J.R.; Dwyer, J.L.; Barsi, J.A. The next Landsat satellite: The Landsat Data Continuity Mission. Remote Sens. Environ. 2012, 122, 11–21. [Google Scholar]
- Vermote, E.F.; Kotchenova, S. Atmospheric correction for the monitoring of land surfaces. J. Geophys. Res. 2008. [Google Scholar] [CrossRef]
- Ouaidrari, H.; Vermote, E.F. Operational atmospheric correction of Landsat TM data. Remote Sens. Environ. 1999, 70, 4–15. [Google Scholar]
- Deuzé, J.L.; Herman, M.; Santer, R. Fourier series expansion of the transfer equation in the atmosphere-ocean system. J. Quant. Spectrosc. Radiat. Transf. 1989, 41, 483–494. [Google Scholar]
- Shepherd, J.; Dymond, J. Correcting satellite imagery for the variance of reflectance and illumination with topography. Int. J. Remote Sens. 2003, 24, 3503–3514. [Google Scholar]
- Roujean, J.L.; Leroy, M.; Deschanps, P.Y. A bidirectional reflectance model of the Earth’s surface for the correction of remote sensing data. J. Geophys. Res. 1992, 97, 20455–20468. [Google Scholar]
- Maignan, F.; Bréon, F.M.; Lacaze, R. Bidirectional reflectance of Earth targets: Evaluation of analytical models using a large set of spaceborne measurements with emphasis on the Hot Spot. Remote Sens. Environ. 2004, 90, 210–220. [Google Scholar]
- Levy, R.C.; Remer, L.A.; Martins, J.V.; Kaufman, Y.J.; Plana-Fattori, A.; Redemann, J.; Wenny, B. Evaluation of the MODIS aerosol retrievals over ocean and land during CLAMS. J. Atmos. Sci. 2005, 62, 974–992. [Google Scholar]
- Gatebe, C.K.; King, M.D.; Tsay, S.C.; Ji, Q.; Arnold, G.T.; Li, J.Y. Sensitivity of off-nadir zenith angles to correlation between visible and near-infrared reflectance for use in remote sensing of aerosol over land. IEEE Trans. Geosci. Remote Sens. 2001, 39, 805–819. [Google Scholar]
- Remer, L.; Wald, A.; Kaufman, Y. Angular and seasonal variation of spectral surface reflectance ratios: Implications for the remote sensing of aerosol over land. IEEE Trans. Geosci. Remote Sens. 2001, 39, 275–283. [Google Scholar]
- Ju, J.; Roy, D.P.; Vermote, E.; Masek, J.; Kovalskyy, V. Continental-scale validation of MODIS-based and LEDAPS Landsat ETM+ atmospheric correction methods. Remote Sens. Environ. 2012, 122, 175–184. [Google Scholar]
- Chavez, P.S. Image-based atmospheric corrections-revisited and improved. Photogramm. Eng. Remote Sens. 1996, 62, 1025–1035. [Google Scholar]
- Benedetti, A.; Morcrette, J.J.; Boucher, O.; Dethof, A.; Engelen, R.; Fisher, M.; Flentje, H.; Huneeus, N.; Jones, L.; Kaiser, J.; et al. Aerosol analysis and forecast in the European center for medium-range weather forecasts integrated forecast system: 2. Data assimilation. J. Geophys. Res. 2009. [Google Scholar] [CrossRef]







| Sentinel-2 | LandSat-8 | LandSat-5-7 | VENμS | FormoSat-2 | |
|---|---|---|---|---|---|
| Repetitivity (days) | 5 (2 sat.) | 16 | 8 (2 sat.) | 2 | 1 |
| Swath (km) | 290 | 180 | 180 | 27 | 24 |
| Coverage | All lands | All lands | All lands | 100 sites | few sites |
| SWIR band | Yes | Yes | Yes | No | No |
| Launch | 2015–2016 | 2013 | 1984–1999 | 2016 | 2004 |
| Mission | Site | Years | Path/Row | Latitude | Longitude | Type | AERONET Sites |
|---|---|---|---|---|---|---|---|
| LandSat | Boulder | 2002 | 033/032 | 40°22′N | 104°15′W | arid | Boulder |
| Columbia | 2002 | 017/036 | 34°38′N | 81°14′W | green | Columbia | |
| Fresno | 2002 | 042/035 | 36° 2′N | 119°27′W | arid | Fresno, Corcoran | |
| Howland | 2001 | 011/029 | 44°36′N | 68°48′W | green | Howland | |
| Konza | 2002 | 038/033 | 39°06′N | 96°36′W | green | Konza | |
| Rogers | 2002 | 041/036 | 34°36′N | 118°18′W | arid | Rogers, UCLA | |
| Sevilleta | 2002 | 034/036 | 34°21′N | 106°53′W | arid | Sevilleta | |
| Stennis | 2000 | 022/039 | 30°18′N | 90° 6′W | green | Stennis | |
| Formosat-2 | La Crau | 2006 | — | 43°34′N | 4°50′E | green | Avignon, La Crau |
| Tensift | 2005/2006 | — | 31°39′N | 7°35′W | arid | Ras-El Ain | |
| Toulouse | 2006 | — | 43°27′N | 1°11′E | green | Le Fauga | |
| Yaqui | 2007/2008 | — | 27°14′N | 109°53′W | arid | Yaqui | |
| Model | Radius (μm) | Std | Ref. Index |
|---|---|---|---|
| small continental | 0.2 | 0.4 | 1.44–0.00 i |
| Blue-SWIR | Red-SWIR | Blue-Red | |
|---|---|---|---|
| LandSat-5 | 0.025 | 0.029 | 0.012 |
| Site | Hybrid | MT | MS | Arid |
|---|---|---|---|---|
| Boulder | 0.08 (12) | 0.08 (12) | 0.13 (3) | Yes |
| Columbia | 0.06 (6) | 0.07 (5) | 0.06 (6) | No |
| Corcoran | 0.10 (15) | 0.10 (15) | 0.04 (11) | Yes |
| Fresno | 0.10 (20) | 0.10 (20) | 0.06 (16) | Yes |
| Howland | 0.02 (7) | -.– (0) | 0.02 (7) | No |
| Stennis | 0.07 (7) | 0.07 (6) | 0.07 (7) | No |
| Rogers | 0.08 (18) | 0.08 (18) | -.– (0) | Yes |
| UCLA | 0.06 (5) | 0.06 (5) | 0.06 (5) | Yes |
| Avignon | 0.03 (7) | 0.06 (6) | 0.04 (6) | No |
| La Crau | 0.02 (14) | 0.07 (14) | 0.03 (14) | No |
| Le Fauga | 0.05 (20) | 0.08 (17) | 0.06 (20) | No |
| Yaqui | 0.08 (22) | 0.09 (21) | 0.04 (20) | Yes |
| Ras-El-Ain | 0.09 (16) | 0.07 (15) | 0.13 (6) | Yes |
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hagolle, O.; Huc, M.; Villa Pascual, D.; Dedieu, G. A Multi-Temporal and Multi-Spectral Method to Estimate Aerosol Optical Thickness over Land, for the Atmospheric Correction of FormoSat-2, LandSat, VENμS and Sentinel-2 Images. Remote Sens. 2015, 7, 2668-2691. https://doi.org/10.3390/rs70302668
Hagolle O, Huc M, Villa Pascual D, Dedieu G. A Multi-Temporal and Multi-Spectral Method to Estimate Aerosol Optical Thickness over Land, for the Atmospheric Correction of FormoSat-2, LandSat, VENμS and Sentinel-2 Images. Remote Sensing. 2015; 7(3):2668-2691. https://doi.org/10.3390/rs70302668
Chicago/Turabian StyleHagolle, Olivier, Mireille Huc, David Villa Pascual, and Gerard Dedieu. 2015. "A Multi-Temporal and Multi-Spectral Method to Estimate Aerosol Optical Thickness over Land, for the Atmospheric Correction of FormoSat-2, LandSat, VENμS and Sentinel-2 Images" Remote Sensing 7, no. 3: 2668-2691. https://doi.org/10.3390/rs70302668
APA StyleHagolle, O., Huc, M., Villa Pascual, D., & Dedieu, G. (2015). A Multi-Temporal and Multi-Spectral Method to Estimate Aerosol Optical Thickness over Land, for the Atmospheric Correction of FormoSat-2, LandSat, VENμS and Sentinel-2 Images. Remote Sensing, 7(3), 2668-2691. https://doi.org/10.3390/rs70302668






