Landsat-8 Operational Land Imager (OLI) Radiometric Performance On-Orbit
Abstract
: Expectations of the Operational Land Imager (OLI) radiometric performance onboard Landsat-8 have been met or exceeded. The calibration activities that occurred prior to launch provided calibration parameters that enabled ground processing to produce imagery that met most requirements when data were transmitted to the ground. Since launch, calibration updates have improved the image quality even more, so that all requirements are met. These updates range from detector gain coefficients to reduce striping and banding to alignment parameters to improve the geometric accuracy. This paper concentrates on the on-orbit radiometric performance of the OLI, excepting the radiometric calibration performance. Topics discussed in this paper include: signal-to-noise ratios that are an order of magnitude higher than previous Landsat missions; radiometric uniformity that shows little residual banding and striping, and continues to improve; a dynamic range that limits saturation to extremely high radiance levels; extremely stable detectors; slight nonlinearity that is corrected in ground processing; detectors that are stable and 100% operable; and few image artifacts.1. Introduction
The Landsat-8 spacecraft has been operating successfully on-orbit since it launched on 11 February 2013. The initial checkout of the Landsat-8 observatory proceeded as planned through the end of May 2013 with no significant issues. NASA transferred observatory operations to the USGS for normal operations on 1 June 2013 where it has been operating smoothly since. There are two imagers onboard Landsat-8: the Operational Land Imager (OLI), which is the subject of this paper and the Thermal Infrared Sensor (TIRS) which is covered elsewhere [1]. This paper documents the on-orbit radiometric performance of the OLI and provides insights into how its performance is different from the previous Landsat sensor, the Enhanced Thematic Mapper Plus (ETM+). Users should benefit from the information in terms of understanding the uncertainty in the data they obtain from the ground processing system.
1.1. OLI Design Overview
The OLI is a break from the traditional whiskbroom instruments used on previous Landsats, e.g., the ETM+, onboard Landsat-7. Unlike previous Landsat imagers, which contained, at most, 136 detectors, OLI has 69,160 detectors. This change in design and number of detectors challenges the ground processing system and calibration and validation team.
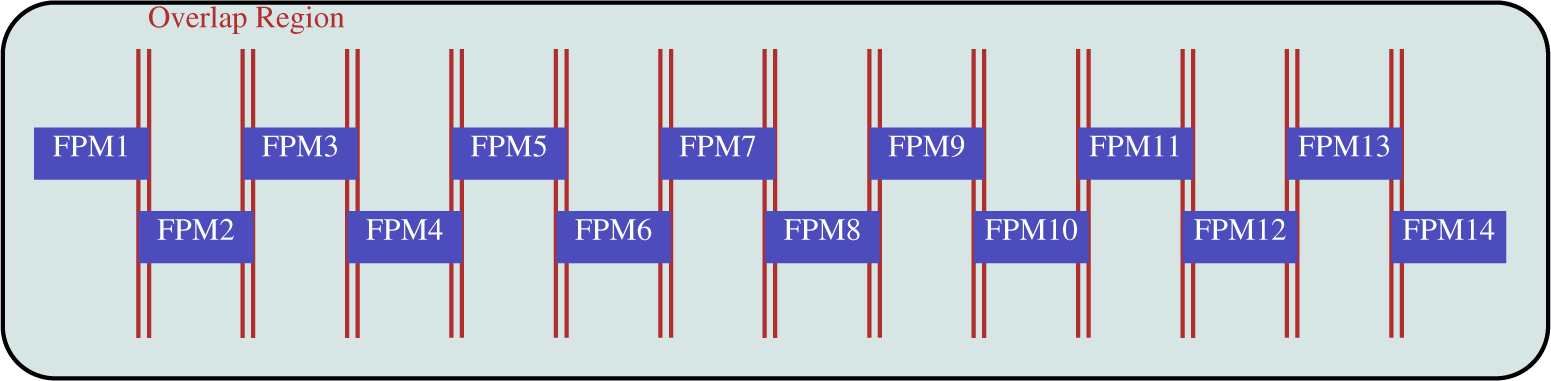
The OLI design is described in detail in [2] and compared to previous Landsat sensors in [3]. A summary of design features relative to the radiometric performance is provided here. The OLI has 9 spectral bands, covering the blue to short wave infrared (SWIR) wavelengths (Table 1). The OLI detectors are separated into 14 Focal Plane Modules (FPMs) that are in a staggered pattern to form the focal plane (Figure 1). Each FPM contains 494 detectors per band. Overlap between the FPMs in the cross track direction assures complete spatial coverage across the 15° field-of-view (FOV). Table 1 also includes the typical (LTypical) and high (LHigh) spectral radiances which are referenced throughout this paper.
The OLI acquires data with 14 bits of radiometric precision, while only transmitting 12 bits to the ground to save bandwidth. For Earth imagery, the spacecraft sends the upper 12 bits of data to maximize the dynamic range. However, for dark shutter collects, the lower 12 bits are transmitted to provide more precise estimates of the dark current level and improve subsequent correction. The Landsat-8 ground processing system converts all data to the equivalent 14 bits, as are all values in this paper when reported in Digital Numbers (DN). Potential truncation errors are accounted for as described in [4].
1.2. Data Types Used for OLI Characterizations
Most on-orbit radiometric characterizations use calibration data collects, as opposed to normal Earth imagery. The collection types and acquisition frequencies are listed in Table 2, along with their common use.
Shutter collects are acquired when the instrument’s shutter is closed, blocking all light from entering the aperture, providing dark levels (biases) for individual detectors. These biases are subtracted from each detector’s response in the ground processing system. This removes variations in detector dark current levels, reducing striping and other pixel-to-pixel non-uniformity issues in the imagery. These normal shutter collects are acquired before daylight imaging begins and after daylight imaging ends, and are about two seconds in duration. An extended shutter collect is acquired about every three months which is 36 min in duration. These longer shutter collects provide a measure of stability over typical contiguous Earth imaging intervals.
The stimulation lamps are used to monitor the detector stability over days. Incandescent lamps excel at showing changes in detector response over relatively short periods of time. There are three sets of stimulation lamps that get used at three different frequencies: daily; bi-monthly; and every six months. These different usages enable differentiation between detector changes and lamp changes [5].
The two solar diffuser panels are reflectance standards characterized prior to launch. Weekly use of the primary diffuser enables detector stability to be monitored and potential changes in calibration to be fed back into the ground processing system. The pristine solar diffuser panel is used every six months as a check on stability of the primary (working) diffuser. Longer, 60 s collects of the working solar diffuser are used to monitor the within-scene detector response stability.
Additionally, a series of solar diffuser collects are acquired about every three months at different detector integration times that is referred to as the Integration Time Sweep (ITS). These collects allow on-orbit assessment of the OLI detector electronics linearity. In an attempt to better characterize the OLI’s full detector-electronic chain linearity, two extended (60 s) diffuser collects were performed during solar eclipses (3 November 2013 and 29 April 2014). Here, the uniform diffuser signal was obtained at a significantly lower radiance level than normal (about 10% and 40%), to allow evaluating and updating relative non-linearities between detectors.
Imaging the moon approximately every 28 days enables an independent measure of the OLI radiometric stability as the moon is an extremely stable source [6]. While the lunar surface is very stable, the viewing geometry varies, so a lunar irradiance model, based on Robotic Lunar Observatory (ROLO) [7] observations accounts for the viewing geometry. The model provides irradiance values that are compared to the OLI response when imaging the moon. The lunar collects are also used to detect and evaluate stray light effects and other artifacts that may exist. The moon is a good source for analysis of these artifacts since it is bright compared to the surrounding space.
A final specialized data collect is the “side slither”, where the spacecraft is yawed 90°, so that the across track direction of the focal plane is now along track. Here each detector in an FPM tracks over nearly identical points on the ground. Performing these side slither maneuvers over uniform regions of the Earth enables individual detector calibration coefficients to be generated that can improve the pixel-to-pixel uniformity. These maneuvers are performed over desert or snow/ice regions about every three months to monitor and potentially improve the pixel-to-pixel uniformity [8].
1.3. Image Assessment System Overview
The primary analysis tool used for this work is the Landsat-8 Image Assessment System (IAS) [9]. The Landsat-8 IAS was built upon the success of the Landsat-7 IAS [10] and Advanced Land Imager Assessment System (ALIAS) [11,12]. Designed to process and store results from large amounts of data, the Landsat-8 IAS is the backbone of the processing system that converts the raw digital signal from the spacecraft to calibrated image product. In addition to generating image products, the IAS runs characterization algorithms and stores information about every detector of every band to the characterization database. This is similar, but more thorough than the IAS implementation of previous Landsat missions because of the large number of detectors in the OLI. Most instrument characteristics and trends described in this paper are extracted from these characterization data.
Using the IAS and other analysis tools, several aspects of the radiometric performance are examined in this paper: noise and signal-to-noise ratio; pixel-to-pixel uniformity; dynamic range; linearity; stability; detector operability; and image artifacts are evaluated.
2. Noise
Noise exists in all instrument measurements and the OLI onboard Landsat-8 is no exception. This section covers electrical noise that corrupts each individual measurement and is considered random in nature. Noise sources include the detectors themselves and the electronics chain up to and including the conversion to DN. The total noise includes contributions from white noise, 1/f noise, and coherent noise (CN). Also covered here is the Signal-to-Noise Ratio (SNR), a general measure of the image quality.
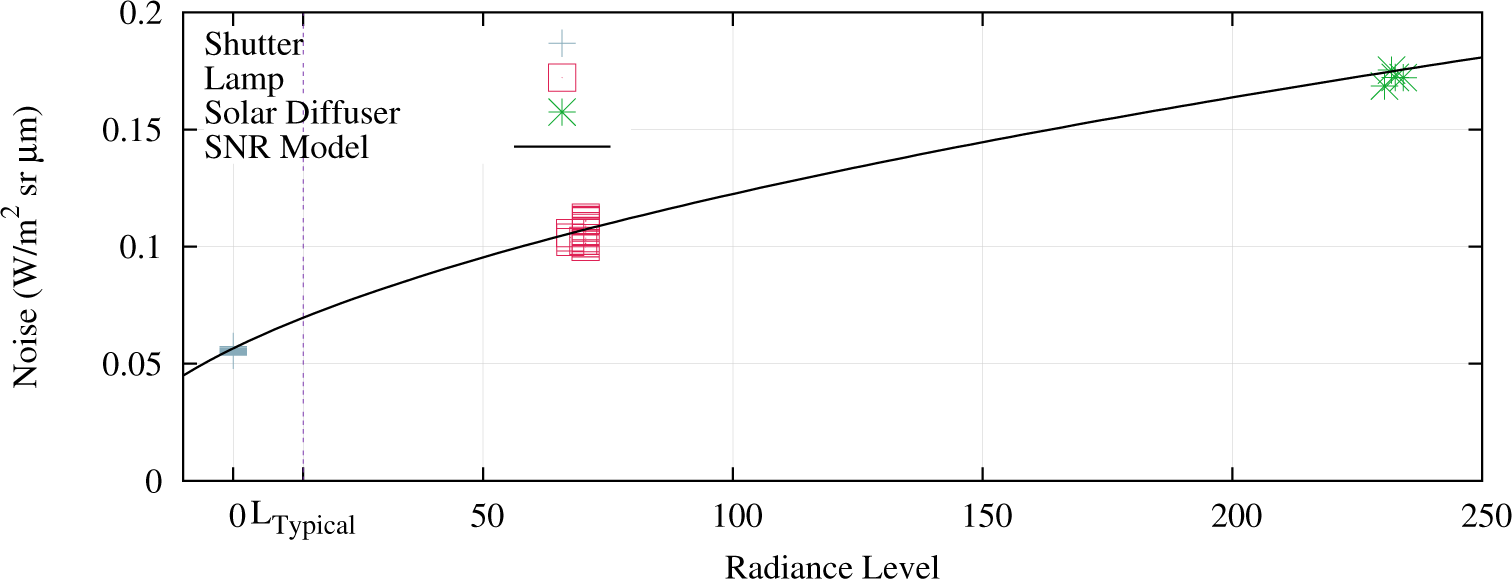
The total sensor noise of the OLI is determined at the dark level of the instrument where all light is blocked by the shutter as well as illumination levels provided by the stimulation lamps and solar diffuser. Normal shutter collects acquired during the month of June 2014 (a total of 945 collects) were used to estimate the 1σ average dark noise in each band (Table 3). These noise levels are converted from DN to radiance units (W/m2srμm) using the band averaged absolute gains. The sensor noise model (Equation (1)) coefficients, were determined using the least squares method for shutter (≈680 collects), lamp (≈630 collects) and diffuser (≈50 collects) 1σ noise levels (Figure 2) and are listed in Table 3 for each spectral band.
These sensor noise model coefficients (a being the signal-independent component and b being the signal-dependent component) relate to an intermediate product inside the ground processing system, and don’t account for the cubic convolution resampling or the product quantization inherent in Landsat-8 16 bit products. The resampler reduces the noise slightly by a factor of 0.8 while the product quantization noise (column 5 of Table 3) adds a small amount of noise. The total product noise (nT) at a given spectral radiance level (L) can be estimated by evaluating Equation (1) at the desired spectral radiance level, and performing a root sum of squares on the reduced sensor noise (nS) and the product quantization noise (ϵq) as shown in Equation (2).
2.1. Signal-to-Noise Ratio
The low noise level of the OLI detectors and long integration time lead to a high SNR that benefits all users of Landsat data. Previous Landsat missions used whiskbroom imagers that had short integration times [3] producing relatively low SNR values. Table 4 compares the on-orbit SNR of OLI to those of the ETM+ onboard the Landsat-7 satellite [13]. The noise model from Equation (1) was evaluated at the typical radiance level (LTypical) listed in Table 1 to determine the SNR values shown in Table 4. These metrics have remained stable within measurement uncertainties throughout the 1.5 years of operations.
2.2. Coherent and 1/f Noise
In addition to using the SNR as a general measure of the OLI noise performance, long duration dark and solar diffuser collects were also collected to further characterize the frequency domain characteristics of the noise. These long collects were also used to investigate other artifacts that impact response drift and CN components.
For OLI the noise floor is defined in Equation (3) as the sum of two noise components: white noise and 1/f noise. The noise floor is determined by smoothing the frequency domain representation of the data from each individual detector with an apodization function to remove any potential CN components while including the 1/f noise in the noise floor.
N is the power spectral density (PSD) of the noise floor in units of DN2/Hz.
nwhite is the white noise magnitude in units of .
fC is the corner frequency of the 1/f noise in Hz.
α is the 1/f noise exponent (typically bound to a value between 0.5 and 3).
Coherent noise components are identified as spikes above the established noise floor. They occur at narrow frequency ranges in which the total power exceeds the visibility threshold. Coherent noise artifacts impact the relative uncertainty of the data and are most visible in flat and low dynamic range scenes. The source of such noise in the raw data stream may originate from the instrument electronics itself or other external electro-magnetic sources. The design of the OLI keeps this noise component contribution at or below a level that is visible.
After one year of operation and the analysis of shutter data and the working solar diffuser data, the OLI exhibits no visible frequency or frequency zone CN in its imagery. Detailed coherent noise characterizations demonstrate that the major coherent noise component is composed of natural occurrences of white-noise extremes in the noise floor.
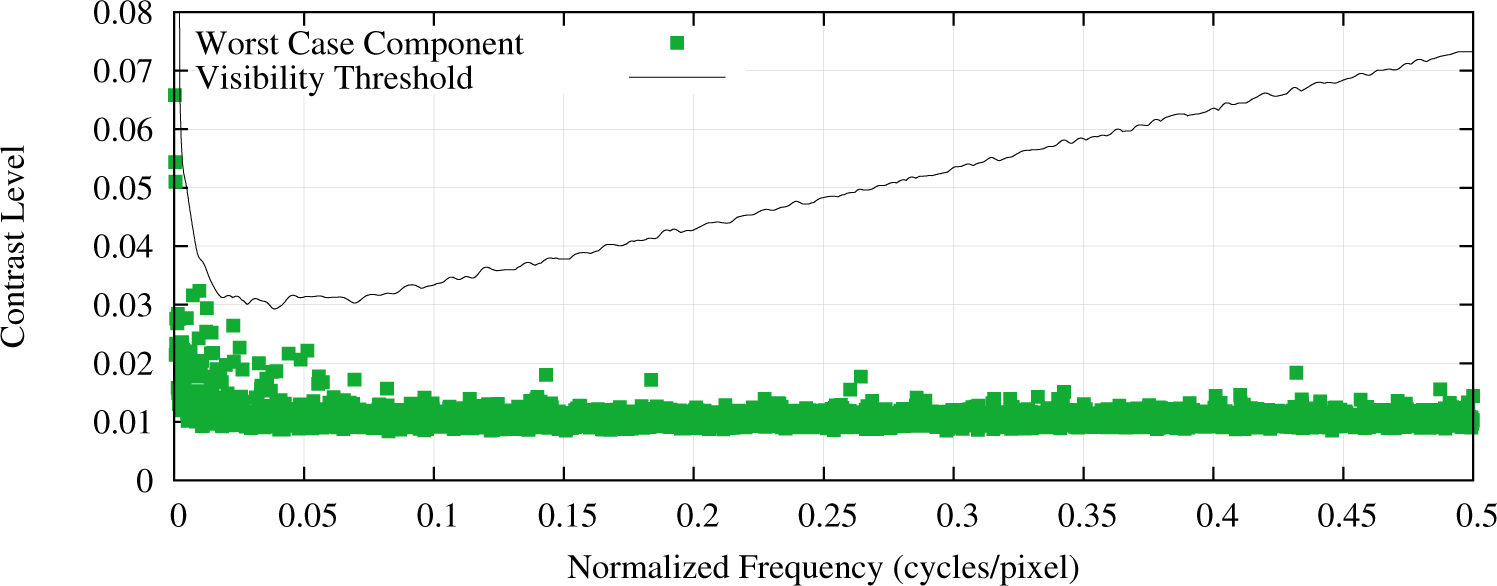
An example of the poorest performing band’s frequency characteristics of OLI noise is shown in Figure 3, representing the worst-case CN components across all detectors in the cirrus band. These data are generated from the analysis of extended shutter and solar diffuser collects. The amplitude shown at each frequency bin is the largest component across all detectors within the band.
The visibility threshold shown in Figure 3 is based upon the baseline artifact visibility threshold (τ) defined in Equation (4) which is defined as a linear function of frequency (f in units of cycles per pixel), approximating the mean human visual contrast sensitivity function [14]. This baseline is adjusted by adding a frequency dependent uncertainty determined by evaluating the variability across all detectors within each band. This general formula applies to all bands.
Coherent noise that results in a visible artifact in the imagery would require multiple detectors having a noise component at a fixed frequency and with noise amplitude that is above the visibility threshold shown in Figure 3. The stability of these frequency domain components of the noise, are better than 0.1% of the contrast level. Since there are no noise components above the visibility threshold, there are no concerns of CN appearing in any imagery at this point of the mission.
3. Radiometric Uniformity
Whereas the SNR defines the noise in the along track (within a detector) direction, the noise in the cross track direction is effectively defined by the uniformity. Many factors contribute to this uniformity, including spectral uniformity of the filters and detectors [15], stability of response and bias, and residual non-linearities in addition to how well the linear portion of each detectors’ radiometric response can be determined. Here the focus is on how the detectors’ relative response was determined and estimate the remaining nonuniformity in the data. The process for determining the relative response has evolved over the mission, so a historical perspective is included. The absolute and relative radiometric calibrations occur simultaneously and relate to uniformity; both are discussed here.
3.1. Pre-Launch Testing
While not directly applicable to the on-orbit performance of the OLI, some pre-launch calibration methodology is included here to provide background of the initial absolute and relative calibration. This calibration was subsequently transferred to the solar diffuser panels which are used for on-orbit assessment.
3.1.1. Yaw Collects
The at-launch absolute and relative gain calibration parameters were generated from the pre-launch yaw scans of the Radiometric Calibration Test Set (Rad-CATS) [2]. The OLI was mounted in the thermal vacuum chamber such that its cross track direction was horizontal and it viewed the large-aperture integrating sphere (the Death Star Sphere (DSS) [2]) through a window in the chamber. The DSS filled the OLI aperture, but was not sufficiently uniform across the full 15° FOV of the OLI for a good detector-to-detector calibration. To improve the effective uniformity of the sphere, the OLI instrument was rotated in the cross track direction while imaging to allow each detector to view the sphere at nearly identical angles and locations (Figure 4). The scans were completed in two sweeps for each band, one for the odd FPMs and one for the even FPMs (because of the offset on the focal plane, the sphere was centered on each line of detectors). The center 1000 frames of the sphere collect were used for each detector to generate the initial gain parameters.
For each FPM, using the appropriate dataset (depending on whether odd or even) the following procedure was performed:
Bias correct and linearize the OLI data.
Find location of center of sphere for a detector in the center of the image (Figure 4b)
Assume linear progression of the sphere across the image. Extrapolate position of center of sphere within the image frame for the whole yaw scan.
Extract 1000 frames of data for each detector around the center position for each detector to calculate an average per-detector sphere signal
Calculate absolute gain (GFPM ) for each FPM and relative gain (ri) for each detector
Qi is the bias-subtracted, linearized digital count (DN) for detector i
L10 is the DSS spectral radiance (W/m2srμm) for the given band
Ndet is the number of detectors within each FPM
Gi is the absolute gain for detector i
The FPM-average gains and relative gains were in the at-launch operational Calibration Parameter File (CPF). They formed the basis for the initial uniformity estimates across the focal plane.
3.1.2. Calibration Transfer to OLI Diffusers
Although the at-launch relative gains came from the integrating sphere calibration, the OLI diffusers were intended to be the primary on-orbit standard for detector relative gains. To use the diffusers as a relative standard, the spatial and angular dependence of their reflectance needs to be known for the illumination and viewing conditions for each OLI detector. Extensive characterization of the OLI diffusers reflectance was performed prior to launch over the range of viewing angles of the OLI detectors (−52.5° to −37.5°) and illuminated on the opposite side at 45° at five locations on the diffuser panel [5]. However, the samples taken do not allow a perfect mapping of the diffuser reflectance for every detector.
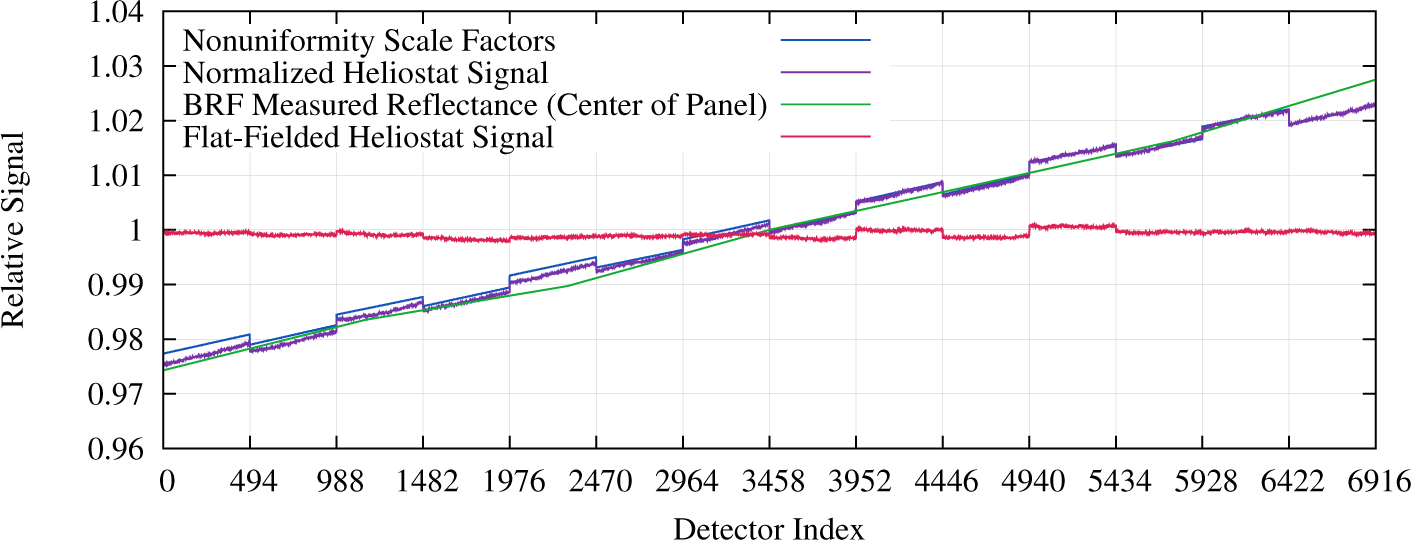
The approach chosen to provide the per-detector diffuser nonuniformity mapping was to use the OLI detectors’ sphere-based calibration when viewing the sun-illuminated diffuser. During CATS testing, the OLI diffuser was deployed and the sunlight was brought in via a heliostat into the side port in the vacuum chamber to illuminate the solar diffuser in its flight configuration. Data from these collects were bias corrected, linearized and converted to radiance using the gains as determined from Equation (5b) and (5c). The diffuser reflectance was shown to be a smooth function of view angle in the pre-launch laboratory characterization. The diffuser’s apparent cross track structure was not as smooth as expected when characterized by the response of the OLI detectors in the heliostat test. To remove per-detector noise, the data from each FPM were fit with a linear function. These fits are the basis for the nonuniformity scale factors in the CPF, which are used to flat-field the on-orbit solar diffuser data for calculation of relative gains. The original data for one heliostat acquisition, FPM fitted functions and center point of the diffuser reflectance are shown in Figure 5 for the NIR band. Figure 5 also shows the heliostat acquisition flat-fielded by the nonuniformity scale factors.
The odd and even FPMs view the diffuser slightly out-of-plane on either side of the principal plane, which may contribute to the odd-even pattern shown in Figure 5 (alternatively this could be caused by odd/even biases in the OLI calibration from the yaw scans). Also note that the measured reflectance is in plane for the center of the diffuser panel and higher and lower number detectors view more and more off-center relative to the center detector (# 3458). For most bands the observed pattern agrees in shape to the panel center measured reflectance to within 0.2%; the coastal aerosol band is the worst case with differences of 0.5%, possibly due to a lower signal and instabilities observed prior to launch.
3.1.3. Primary Sphere Collects
The second round of gains was calculated after launch, in January 2014, based on pre-launch data from the Primary Sphere Collect (PSC) Level-10 collects. Unlike the yaw data, the PSCs were configured to capture images of each FPM separately; each image was a single FPM staring at the DSS where every detector was illuminated. Absolute gains were calculated based on per-FPM data and the DSS radiance using Equation (5a) and (5b). The decision was made to switch to the PSC gains from the yaw gains because the illumination was more uniform within each FPM.
3.2. On-Orbit Characterization
On-orbit, the OLI relative gains are characterized primarily by using the solar diffusers. Using the Earth surface to characterize relative gains is challenging, as most, if not all, surfaces are not uniform or Lambertian enough to be used without additional knowledge. Some methods to make use of relatively large uniform targets are used to assess the uniformity of the OLI as shown in [8] though they are not mature enough to implement yet.
3.2.1. Per-FPM Nonuniformity Determination
As indicated earlier, the solar diffusers were intended to be the primary source of on-orbit OLI relative gain determination. Also, as previously discussed, the diffusers are not perfectly uniform or Lambertian, so each detector measures a slightly different radiance due to viewing the diffuser at different angles. On-orbit, the OLI detectors can be treated as invariant and the diffuser nonuniformity can be recalculated using the directly solar illuminated on-orbit data. The difference between the on-orbit results compared to the pre-launch characterizations is a measure of the uncertainty in the uniformity assessment.
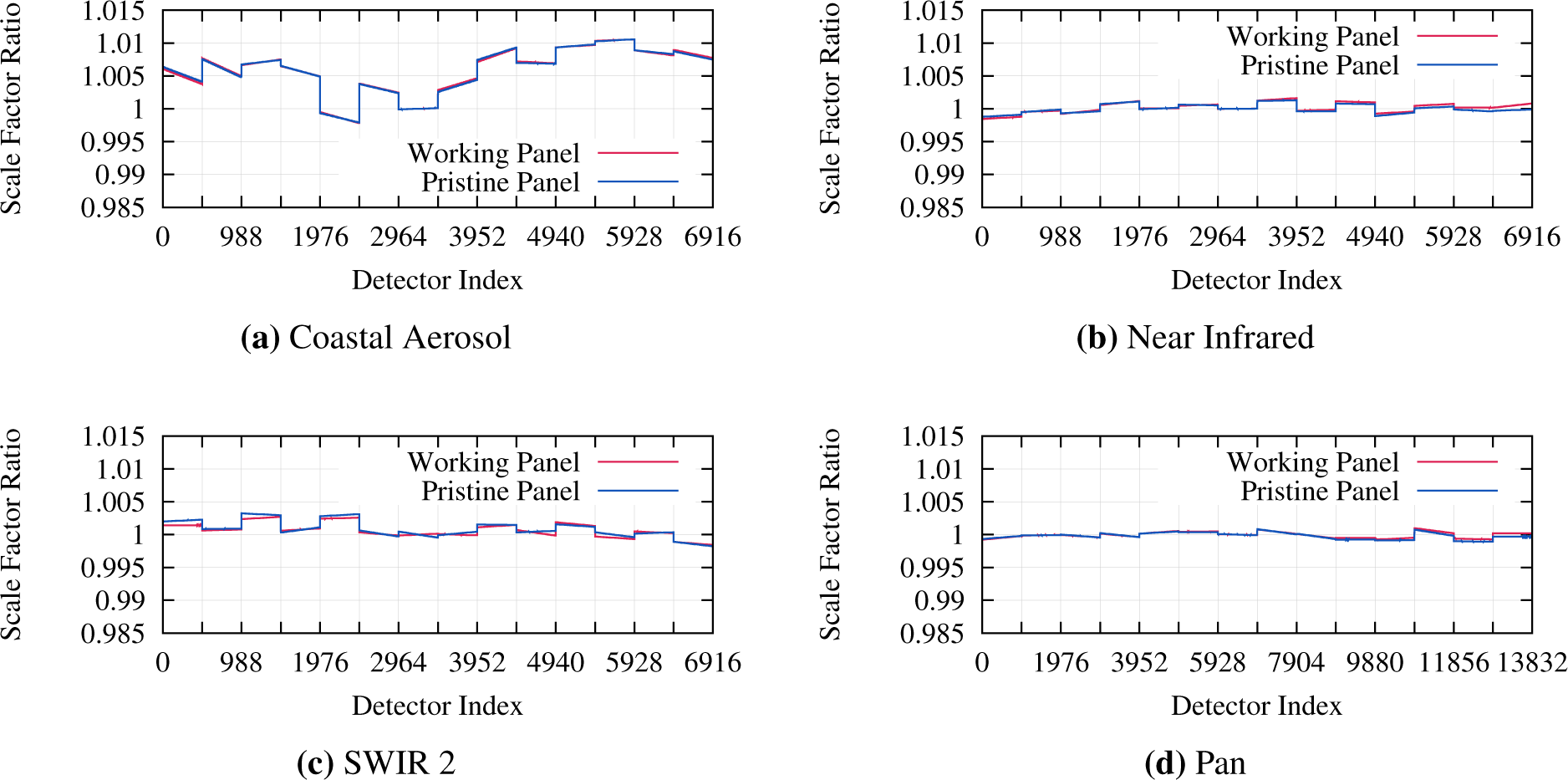
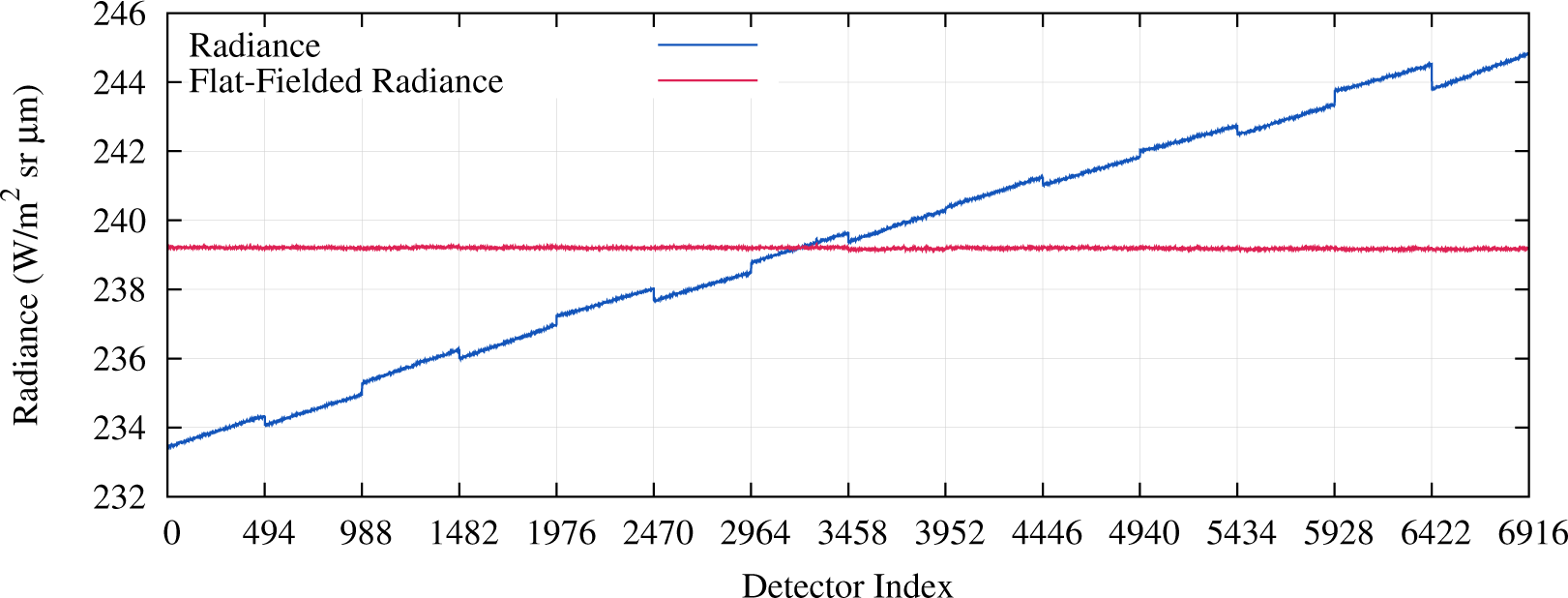
The on-orbit diffuser nonuniformity scale factors were calculated the same way as the pre-launch values, though using the average of the first eight on-orbit collects, rather than pre-launch data. Ratioing the diffuser nonuniformity calculated using the heliostat data to the initial on-orbit data shows very similar patterns for the working diffuser and the pristine diffuser (Figure 6). Some bands, e.g., the pan band, show differences of 0.1% or less and most show differences of 0.2% or less from the pre-launch values. The two shortest wavelength bands, coastal aerosol and blue show the largest changes, in some cases up to 1%. The nature of the apparent change in the coastal aerosol band, i.e., highly FPM dependent and the consistency between the two diffusers suggests that the change is primarily not a change in the diffuser characteristics. More likely causes are (1) uncompensated non-linearity in certain FPM’s causing the discontinuities, as the pre-launch heliostat based signal is about 30% of the on-orbit level in the coastal aerosol band, about 40% in the blue band where it is above 50% in the other bands (seems unlikely) or (2) actual changes in detector gain. The coastal aerosol and blue bands showed the greatest variability (<1%) in pre-launch testing, consistent with gain shifts between pre-launch and on-orbit. Some of the lower frequency variation (across the full FOV) could also be due to heliostat nonuniformity. The on-orbit determined uniformity factors are a pragmatic data-driven method to destripe the imagery consistent with operational imaging. A sample solar diffuser collect and the flattened results are shown in Figure 7.
3.2.2. FPM-to-FPM Discontinuity Adjustment
Some discontinuities in the OLI response across FPM boundaries were apparent in OLI Earth imagery beyond what would be expected based on the differences in view angles between the odd and even FPMs (Figure 8). Because the FPMs are mounted in two rows with the odd and even FPMs offset from each other, the even FPMs have a slightly forward view of the Earth and the odd FPMs have a slightly rearward view of the Earth. For targets with a large directional reflection component, the radiance seen by the odd and even FPMs will be different. This is a generally uncorrectable effect.
However, some of the non-odd/even banding that is visible is likely the result of poor pre-launch characterization. Since the OLI view of the solar diffuser is very out-of-focus, adjacent detectors are effectively seeing the same spot on the panel. At the FPM boundaries, there is a small offset and the odd and even FPM’s view the panel from opposite sides of the principal plane. Typically the reflectance of a diffuser is nearly symmetric around the principal, so it should not be a bad assumption that the reflectance would be equal in the overlap region. To assess the FPM-to-FPM discontinuity, the overlap in the field-of-view between adjacent FPMs is used; inherent in the design of the focal plane, there are about 20 detectors at the edge of each FPM that overlap the edge of the adjacent FPM in the 30m bands (52 detectors overlap in pan band). The radiance measured by the detectors on the east edge of one FPM should be the same radiance measured by the detectors on the west edge of the next FPM.
To assess the discontinuity between the FPMs on the focal plane, the ratio of the edge detectors was calculated for all the 2013 working solar diffuser acquisitions (37 collects). The average ratio was calculated for each adjacent FPM pair and the discontinuity adjustment factor is calculated for each FPM across the array.
LFPM is the solar diffuser radiance for the east edge of FPM j in W/m2srμm
LFPM j+1 is the solar diffuser radiance for the west edge of FPM j + 1 in W/m2srμm
dj is the unitless ratio between adjacent FPM overlap regions
f′(j) is the per-FPM adjustment factor before normalization
f(j) is the per-FPM adjustment factor normalized to maintain the existing scene mean calibration
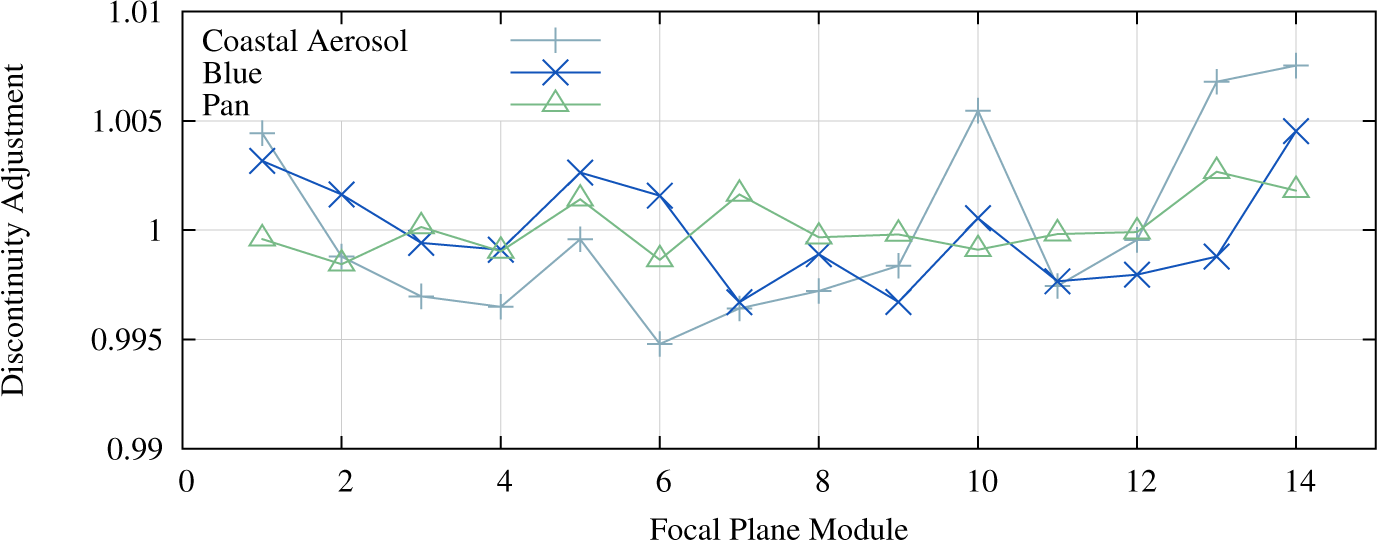
The adjustment factors are normalized to maintain the scene mean radiance. The largest adjustment necessary, as expected based on pre-launch testing, was in the coastal aerosol band, 0.8% (Figure 9).
The results appeared to make visual improvement in the imagery in the coastal aerosol (Figure 10), blue and pan bands so the gains for those bands were adjusted by the discontinuity factors. This correction was implemented to improve the across-track uniformity and did not change the overall absolute radiometric calibration.
3.3. Relative Gain Updates
The initial relative gains in the CPF were generated based on the pre-launch yaw data, as described in Section 3.1.1 and Equations (5a)–(5c). As there was striping visible in very uniform scenes, an effort was made to improve the relative gains based on on-orbit data. The solar diffuser acquisitions were used to estimate new relative gains. Using solar diffuser data flat-fielded with the solar nonuniformity scale factors (Section 3.2.2), new relative gains were calculated:
Li is the per-detector radiance (W/m2srμm)
LFPM is the average radiance over the FPM (W/m2srμm)
νi is the per-detector solar nonuniformity scale factor
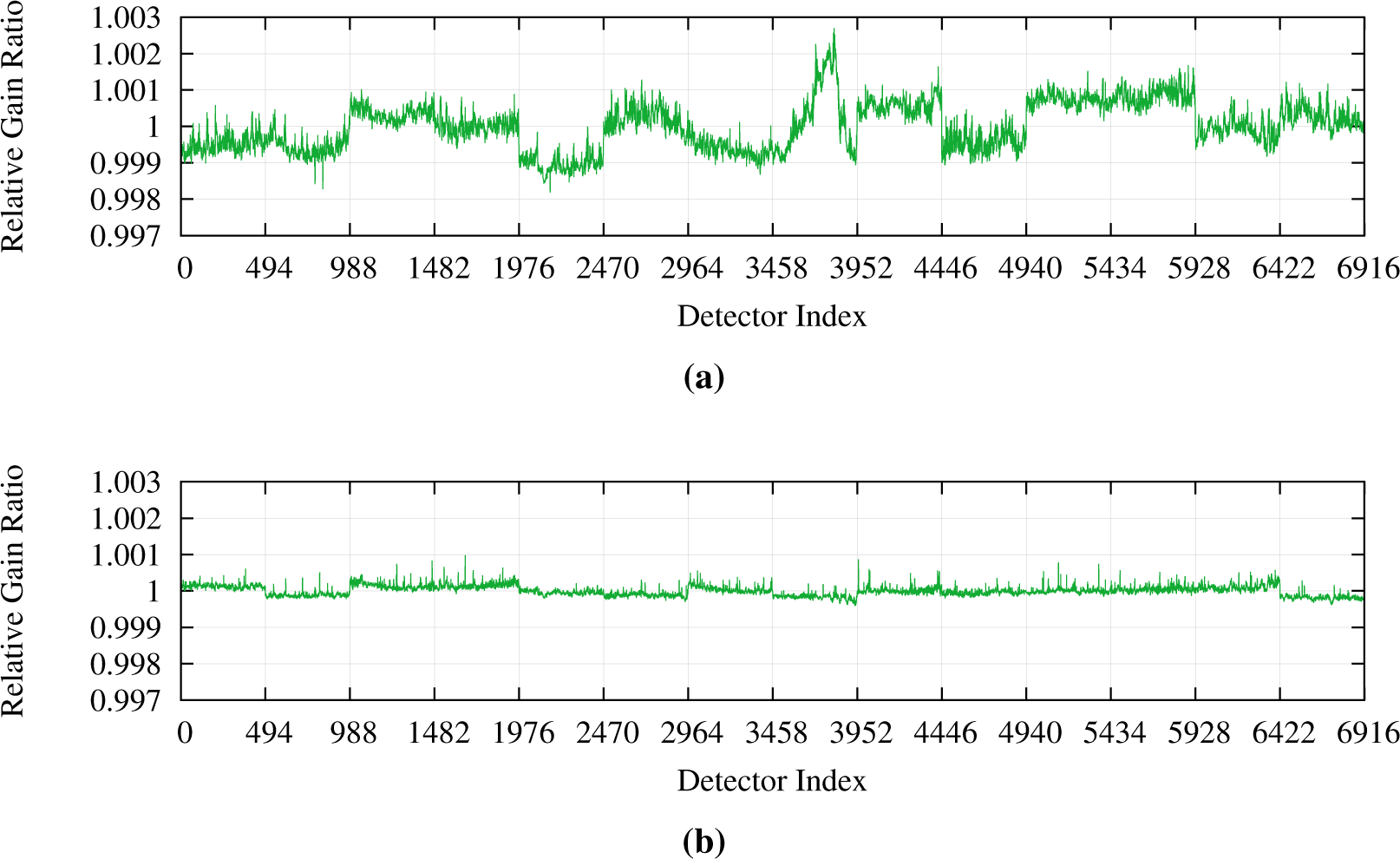
Monitoring of the relative gains continued using the solar diffuser data. After spacecraft safehold event in September 2013, the relative gains appear to jump in many bands (Figure 11). Though it is unclear why this happened, it was not entirely unexpected. The relative gains changed significantly during pre-launch testing after an unintentional power cycle.
However, since the September 2013 safehold event [16], the relative gains have remained stable to within 0.05%, including after the spacecraft safehold in April 2014 [17] except for occasional single detector jumps in the SWIR bands (Figure 12). The relative gains are being updated quarterly based on solar diffuser data from the prior quarter. When a reprocessing of the OLI archive becomes necessary, the CPFs will be updated with the quarterly relative gains based on solar diffuser data from the specific quarter.
3.4. Validation on Earth Scenes
It is difficult to validate the across track uniformity using Earth scenes as none are as uniform as the solar diffuser. A technique has been developed to take advantage of the overlap between the FPMs in a subset of Earth scenes.
3.4.1. Focal Plane Module Overlap Region Statistics
As per the solar diffuser analyses, the field of view of the edge detectors in adjacent FPMs overlaps such that they view the same targets on the Earth’s surface, though at slightly different view angles. The ratios between the detectors’ responses in each of the FPM overlap regions can be used as metrics of the uniformity across the FPM boundaries and indicate the residual relative gain error in each FPM. The advantage of this method is that it can be applied to any Earth scene rather than relying on a solar diffuser, which does not resemble any natural surface. The method can be used to evaluate current relative gains as well as to test the quality of any proposed updates to the relative gains.
Thirty-four Earth scenes were analyzed containing a mix of surface types, clouds and phenological conditions. Ratios were calculated for every pair of FPMs for every frame in each band. The standard deviation of the ratios across the band was used as a filter, to eliminate scenes where the image content wasn’t uniform enough. The resulting subset was generally cloud free and incorporated many different surface types including desert, snow, ice, ocean, and vegetation. After filtering, there were between 22 and 29 Earth scenes for each band.
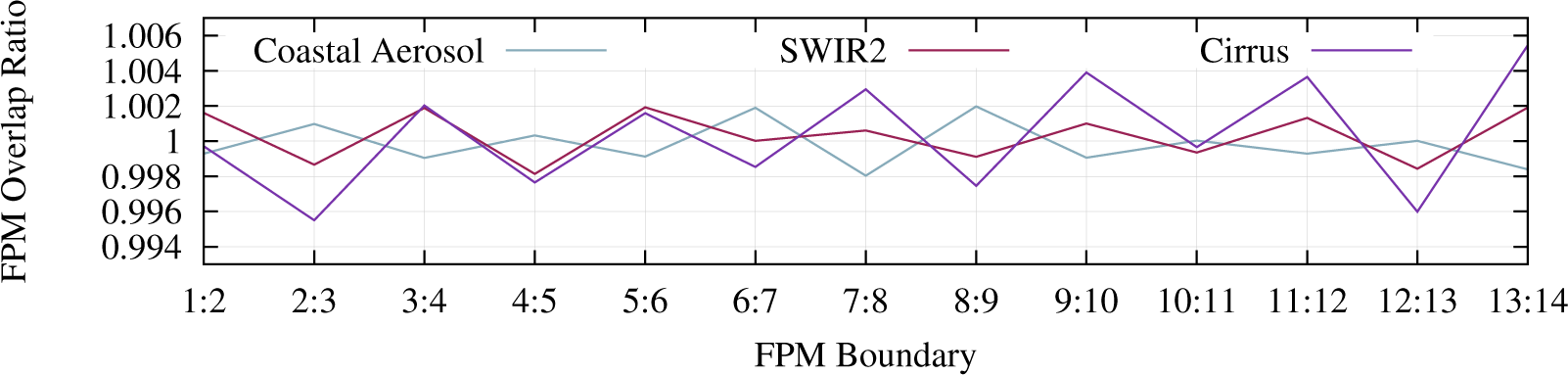
3.4.2. Focal Plane Module Overlap Results
On average, the residual error is less than ±0.2% across all overlap regions, for all bands except the cirrus band. For the cirrus band, the residual error is ±0.4% across all overlap regions (Figure 13). Uncertainty in the derived means in each FPM boundary is on the order of ±0.3% (2σ). The per-FPM results indicate that there is a residual odd/even effect that the current calibration coefficients are not removing. The effect varies by band (Figure 13). Though not strictly an odd/even effect in all the bands, most bands indicate some level of residual odd/even error.
The residual error is likely due to a number of factors, including using the solar diffuser to generate the FPM-to-FPM discontinuity correction and the fact that the diffuser reflectance was assumed to be symmetrical with azimuth angle. As described in Section 3.1.2, the diffuser is viewed slightly out-of-plane between adjacent FPMs, which could cause artificial offsets between adjacent FPMs. This method also needs to be applied to a larger sample of scenes and could allow us to reduce the FPM-to-FPM banding that is currently visible in some images.
With the high level of stability and the low level of non-linearity in OLI, these techniques should be able to derive pixel-to-pixel non uniformity parameters between 0.2% and 0.3%. This is better than the capability of most laboratory characterizations.
4. Dynamic Range
As effectively a 12 bit system, the OLI has a much larger dynamic range than previous Landsat missions, which had a maximum of 8 bits. The increased dynamic range improves noise and quantization performance (discussed in Section 2) and reduces the frequency of a saturated signal. Table 5 shows the approximate maximum spectral radiance levels that each OLI band is capable of sensing (LSat). These are significantly higher than what the ETM+ could measure (columns 5 and 6). While a true Lambertian surface, when illuminated by the sun, will not saturate the OLI sensor, non-Lambertian surfaces such as snow, ice, and clouds can. Certain combinations of sun angles, view angles, and surface features lead to saturated pixels.
The OLI is capable of measuring spectral radiance levels down to the noise floor of the data, listed in Table 3 of Section 2. The OLI response should never drop low enough to saturate at the low end of the dynamic range because the bias level is over 1000 DN for all detectors. Even with a 5σ noise event, the output would be above 990 DN, well on scale. This leads to the full dynamic range of the OLI extending from the noise floor up to Lsat for each spectral band.
4.1. Upper End Saturation
With the much larger dynamic range of OLI, saturation was expected to be a rare occurrence compared to previous Landsat missions. That is certainly the case as through 30 June 2014 only 96,083 scenes (out of 222,897 total scenes acquired) have been acquired where saturation has occurred. In those scenes, an average of about 250 pixels per scene have been saturated, out of over 400 million pixels across all bands in each of those scenes. Table 6 details the number of scenes with saturation and the number of saturated pixels in each spectral band across all scenes from 1 June 2013 through 30 June 2014. While much of this saturation is due to non-Lambertian surfaces, saturation in the SWIR 1 and SWIR 2 bands is typically caused by fires and lava flows. Besides high radiance levels, detectors can also saturate because of high energy particles. This is likely the case for all of the cirrus band saturated pixels as most energy in that spectral band is absorbed by the moisture in the atmosphere.
4.2. Oversaturation
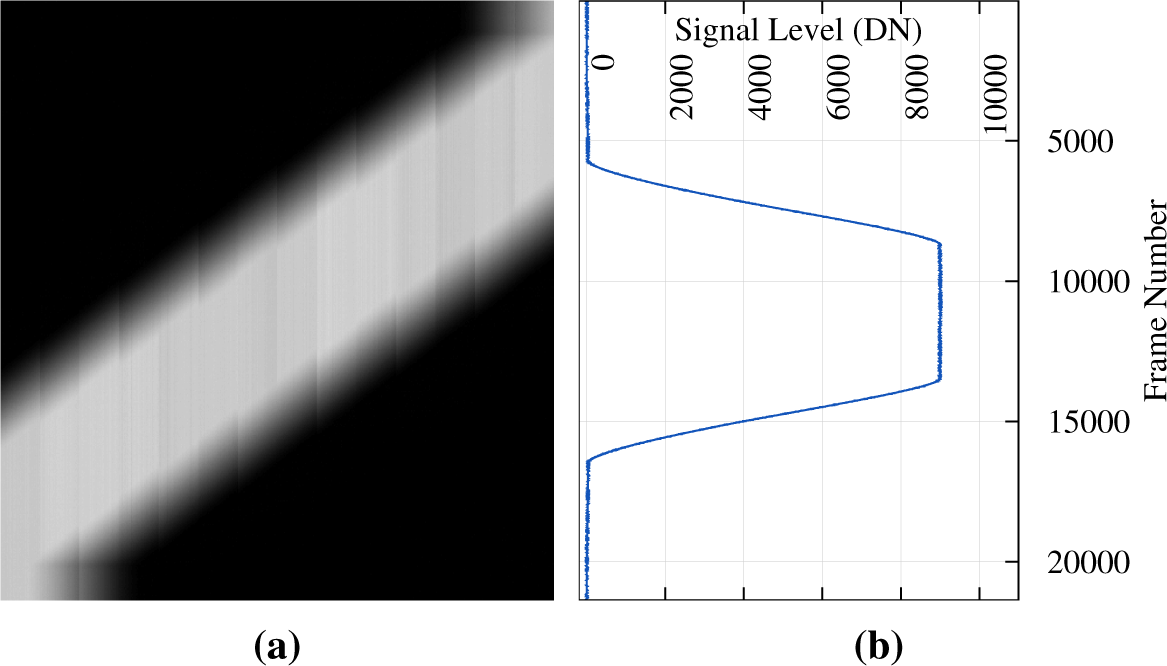
The OLI had never been subjected to radiance levels much higher than its saturation levels prior to launch. Once launched and operating normally, the imager measures whatever radiance levels are reflected by the Earth’s surface. It is possible that a non-Lambertian surface viewed at certain angles could dramatically exceed the saturation levels of the sensor. For example, this occurred while imaging a greenhouse complex in the Novosibirsk region of Russia on 22 September 2013 where the geometry of the greenhouses specularly reflected the sun into the field of view of several OLI detectors. The effect of this specular reflection caused the detectors and associated electronics to output a signal below the bias level of the detectors causing low end saturation (Q = 0 DN) as shown in Figure 14. The detectors immediately returned to operating nominally when viewing radiance levels closer to the saturation levels with no lasting effect. The mechanism for this rare effect isn’t known.
5. Stability
Stability is a measure of how the sensor’s response changes over time. Stability is important to users of Landsat data who are looking for changes on the Earth’s surface; the more stable the sensor, the smaller the detectable changes can be. While the noise and SNR are typically calculated from 2 s intervals, stability is calculated over longer intervals. These longer intervals are comprised of extended shutter collects for bias stability and the longer solar diffuser collects for gain stability. Two timescales are examined here: within scene and between scene. Longer term stability is described elsewhere [5].
Illustrating the uncertainties within a scene, the shortest bias stability timescale examined is on the order of one minute. The standard deviation of each detector is calculated over 60 s of both long solar diffuser collects and extended shutter collects. The average standard deviation per-band is then calculated. These values are normalized to the solar diffuser radiance level and scaled to provide 2σ stability numbers. Table 7 shows the average variation over 60 s of diffuser data for each band, normalized to the solar diffuser radiance level. When trended from launch through mid-April 2014, the stability was constant within 0.003% for all bands.
The stability results for extended shutter collects are comparable to Table 7 within the measurement error. This puts a bound on the uncertainty in Earth imagery due to instrument changes that cannot be corrected by calibration updates.
6. Detector Operability
Since the OLI has such a large number of detectors and the sensor requirements allowed for a small percentage of detectors to be dead or inoperable, a small number of detectors that don’t respond to input radiance was expected. Pre-launch testing showed the OLI exceeded expectations by not having any inoperable detectors. On-orbit analysis confirmed no inoperable detectors after launch as well. Detector operability for OLI is defined as follows:
The detector’s count/radiance (i.e., radiometric gain) slope is greater than 20% of the mean count/radiance slope for the band and not saturated at expected operating temperatures under dark conditions.
The detector’s noise is less than 5 times the mean noise level for the band in which it occurs.
The detector’s dark current remains within ±5 times the RMS noise over the period between dark frame references.
The detector’s actual dynamic response range is greater than 25% of the specified dynamic range: such that the actual dynamic range is greater than or equal to 1.25 times the specified dynamic range.
The sensor requirements for the OLI also allowed for a small number of detectors to be operable, but may have reduced performance, these are labeled as out-of-spec detectors. Out-of-spec detectors are defined as a detectors that fail to meet one or more of the performance requirements stated in the OLI Requirements Document [18]. The applicable requirements are listed here:
Spectral requirements: Evaluated prior to launch.
Detector SNR: Any detector below 80% of the median values shall be considered out of spec.
Streaking: The maximum value of the streaking metric Si (Equation (8)) within a line of radiometrically corrected, including the nonuniformity scale factors described in Section 3.1.2 OLI image data shall not exceed 0.005 for bands 1–7 and 9 and 0.01 for the pan band.
where:, , and are the average radiances of pixel column i, i – 1, and i + 1, respectively.
Saturation Radiances: The OLI shall detect, without saturating, signals up to the LMax as defined in Table 5.
Coherent Noise: Each pixel column in a uniform scene or WRS-sized dark image in any band shall contain CN components with relative amplitude not exceeding the maximum amplitude level.
Only four detectors in the red band (band 4) fail to meet any performance metrics, and those were due to the out-of-band spectral response [15] requirement being violated, which cannot be evaluated on-orbit. On rare occasions many detectors violate some of the performance requirements due to the focal plane temperature deviating from its nominal value. Each case has been attributed to non-nominal operations of the satellite. Table 8 lists each case where the OLI focal plane temperature drifted outside nominal conditions and what caused it.
7. Linearity
For the most part, the OLI detectors respond linearly to incoming radiance, however a small non-linear component remains and is corrected by the Landsat-8 product generation system (LPGS). The linearity correction parameters for the OLI detectors have been calculated from three sources: pre-launch tests, post-launch ITS collections, and special diffuser collections during solar eclipses.
7.1. Pre-Launch Tests
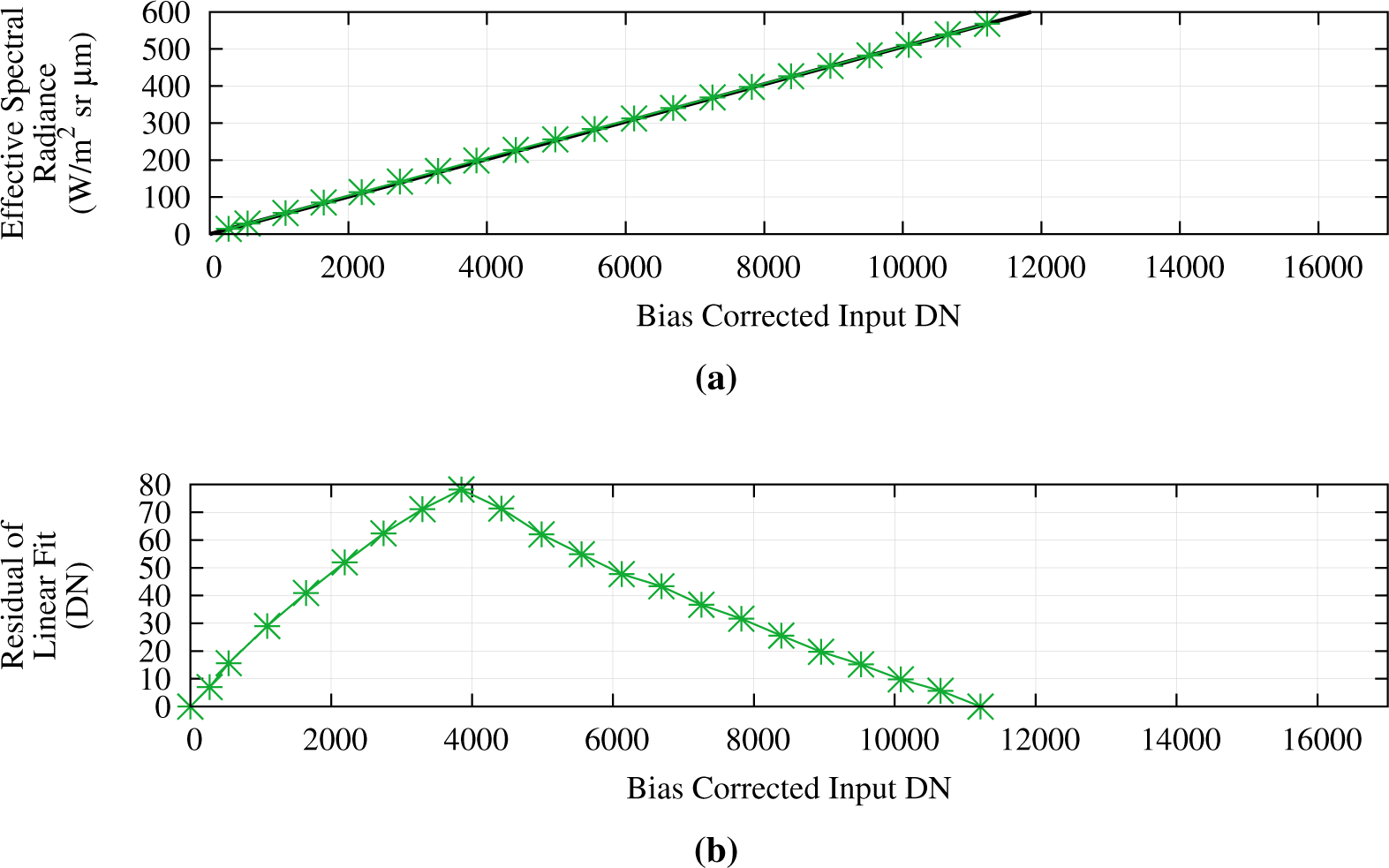
Linearity parameters were calculated from test data prior to launch using a NIST-traceable 40 inch spherical integrating source, also known as DSS, at Ball Aerospace and Technologies Corporation (BATC) manufacturing facility in Boulder, Colorado. Two of the pre-launch calibration tests were relevant for linearity calculation. The PSC used varying radiances from the DSS that covered the dynamic range of each band. The ITS collections held the DSS radiance near the maximum specified radiance (Lmax) for each band, while decreasing the integration time used by the detectors to sample the radiance reflected by the sphere (an example linearity curve based on ITS collections is shown in Figure 15). Shorter integration times were assumed to emulate lower radiances, an assumption that is referred to as reciprocity.
Analysis of both ITS and PSC data showed that both setups had benefits and drawbacks. The ITS collections provided 21 effective radiance levels, but slight errors in reciprocity could be seen at the lowest integration times. The PSC had no reciprocity influences, but data were only acquired at 10 radiance levels for most bands, with up to 19 PSC collections available for the NIR and SWIR bands due to their similar dynamic ranges and the fact that they all used the same band (NIR) for radiance feedback control. An additional difference between the two methods is that the ITS data capture only electronics non-linearities after the detector, whereas the PSC data capture non-linearities for the complete system. The PSC-derived nonlinearity correction parameters performed best for the SWIR 1 and SWIR 2 bands, while the ITS-derived parameters produced the best results for the other bands.
The correction parameters are stored per-detector as a DN-based (post bias subtraction) look-up-table tied to radiance levels the linearity was evaluated, currently a maximum of 34 levels. Linear interpolation between these levels provides the correction at specific DN levels. These pre-launch parameters continue to be evaluated and remain valid for operational use in the Landsat-8 ground system.
7.2. On-Orbit ITS Collections
On-orbit linearity calibrations for OLI are performed using the solar diffuser as the source. When the solar diffuser is fully illuminated by the sun, the integration time for the instrument is then varied to simulate lower radiance levels. One on-orbit ITS collection is performed every three months. Since the on-orbit ITS collects use the solar diffuser, and the diffuser panel has slight nonuniformities, the on-orbit ITS collects are used to verify the measurements made prior to launch. The nonuniformity scale factors described in Section 3.2.1 are used to improve these measurements. The reciprocity effects also reduce the efficacy of the ITS collects on-orbit. However, analysis on-orbit has shown that the linearity has remained constant through transfer to orbit.
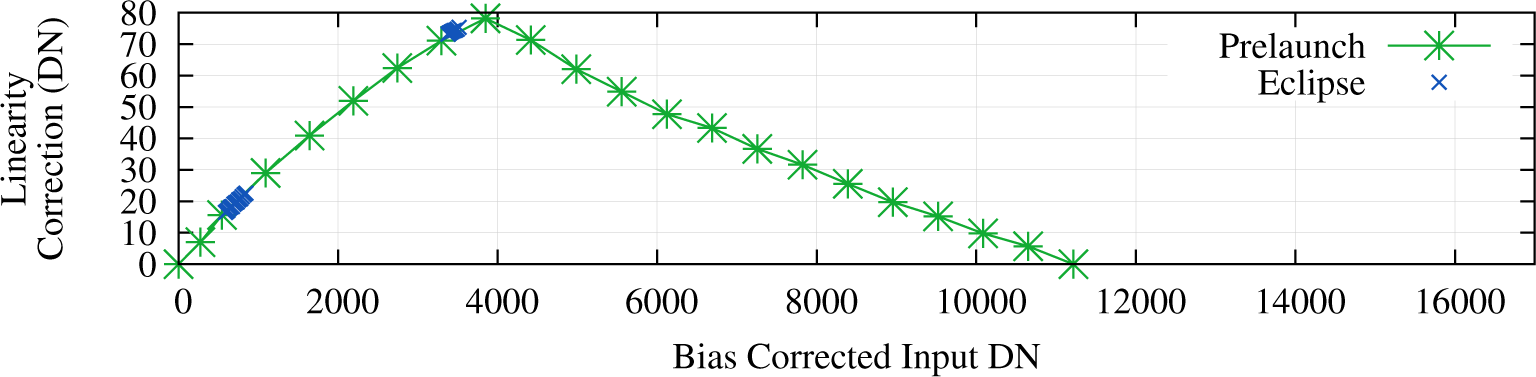
7.3. Eclipse Collections
On 3 November 2013, the opportunity arose to acquire a diffuser collect during a partial solar eclipse. This allowed OLI to view a range of radiances without reciprocity effects of varied integration time. One minute of data was collected during the November eclipse, and a second one minute collect occurred during the eclipse on 29 April 2014. Figure 16 shows updated residuals based on these solar eclipse collects.
Because the absolute spectral radiance on the diffuser during a partial eclipse is not known, the eclipse collections only provide linearity data relative to the mean linearity correction in each FPM. This allows for corrections of residual striping that may be apparent at certain radiance levels. Despite this limitation, the results are very promising over the small portion of the instrument’s dynamic range covered by the eclipse data. Due to safety concerns of the OLI, only 60 s eclipse intervals have been acquired thus far. The linearity corrections calculated from the eclipse data are not currently in use by the ground system.
8. Image Artifacts
Undesired features in imagery that haven’t been covered in other sections are examined here as imaging artifacts. All of these features are quite small, difficult to find in normal Earth imagery, and rarely affect remote sensing applications. They are discussed here to make users aware of potential inaccuracies that come with these artifacts.
8.1. Spectral Cross-talk
Prior to launch, a small amount of electronic crosstalk was seen [15], but it was within requirements and was thought to be due to ground test equipment. Shortly after launch an inspection of ocean scenes off northern or southern coastlines revealed a small artifact in the cirrus band. Analyzing a scene off the north coast of Africa (Figure 17), approximately 0.2% of the SWIR 1 signal leaked into the cirrus band. It appears as a coastline offset from the actual location of the coastline. This artifact varies with each FPM due to the offsets between the spectral bands and results in an apparent coastline being shifted north by about 35 pixels for even FPMs and south (by about 35 pixels) for odd FPMs. This artifact is most prominent in the cirrus band, though theoretically affects the SWIR 1 and SWIR 2 bands as well [15].
8.2. Stray Light
The optical design of the OLI was intended to reduce stray light to a level where it would be virtually undetectable in Earth imagery [19]. Close analysis of imagery acquired while looking at the moon shows virtually no sign of stray light (Figure 18). The SWIR bands, including the cirrus band, show a small effect of stray light off the edge of the moon, but the magnitude is consistent with what was found in the extensive testing done prior to launch. The cirrus band shows a faint ghost to the lower left of the actual moon in Figure 18i. The magnitude of this ghost is difficult to measure as it is below the noise level of the instrument. Initially this artifact was thought to be spectral cross-talk (Section 8.1), however this ghost is smaller and closer to the moon than what would be expected from the cross-talk. The images shown in Figure 18 have been contrast stretched to exaggerate any artifacts, including the noise as described in Section 2. The OLI exhibits only minor imperfections as shown in these lunar images.
8.3. Bright Target Recovery
As discussed in the section on oversaturation, the recovery time after the detectors view a bright target is essentially zero. Previous Landsat missions had a significant recovery time after the detectors imaged extremely bright regions on the ground [13].
8.4. Impulse Noise
In general, impulse noise refers to any non-physical bright, or dark, pixel in imagery which can be caused by transmission error, dust occultation, or single event upsets (SEU). In the case of the OLI, only SEUs are possible. Single event upsets occur when detectors are hit with high energy particles, which transfer their energy to the detectors, causing them to respond as if they had imaged more reflected energy than they actually did. Impulse noise is difficult to reliably detect in normal daylight imagery, so shutter collects are analyzed to characterize impulse noise. Two types of shutter collects are analyzed: the frequent short shutter collects (500 lines or approximately two seconds of data) that are acquired twice per orbit, before and after each imaging interval; and the infrequent extended shutter collects (500,000 lines or approximately 36 min of data) which are acquired four times per year.
In a single extended shutter collect acquired in February 2014, there were close to 9 occurrences of impulse noise every second. This equates to around 200 impulse noise occurrences in each nominal Earth scene across all bands. Impulse noise occurs most frequently in the coastal aerosol and cirrus bands (Figure 19). The differences between the normal shutter collects and extended shutter collects is attributed to the locations where they are acquired. Normal shutter collects are typically acquired near the poles and over open ocean including the South Atlantic Anomaly (SAA) [20], where there is an increased chance of high energy particle hits [13].
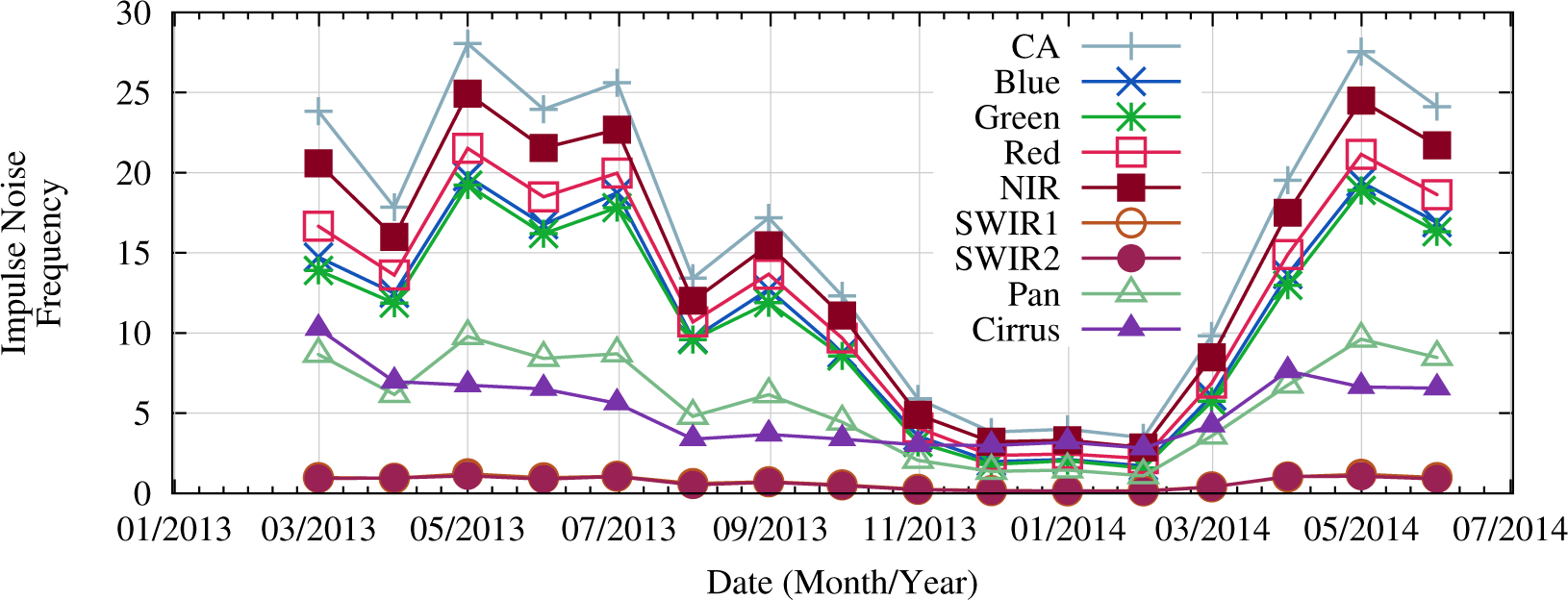
The amount of impulse noise in normal shutter collects varies with seasons (Figure 20). This seasonal variation is believed to be due to operational differences of acquiring shutter collects in different orbital positions as Earth acquisitions change with sun angle. The December 2013 through January 2014 time period show few shutter collects over the South Atlantic Anomaly (SAA) due to this inherently seasonal change in operations. Figure 21 shows every shutter collect acquired from launch through the end of June, 2014 color coded to the amount of impulse noise present in each collect.
9. Summary
With 12 bits of information provided for each OLI detector sample, the noise levels are low and the dynamic range is extremely high. This leads to a high SNR for the OLI that exceeds that of previous Landsat missions by an order of magnitude for typical radiance levels. Noise sources, 1/f and CN, don’t generally affect the overall radiometric accuracy and are low enough and not visible in Earth imagery.
The radiometric uniformity of the image products has improved since launch, but some residual FPM-to-FPM banding and striping can be seen in extremely uniform scenes. The calibration team is continuing to work to improve the image product uniformity, examining the relative gains and non-linearities. While some detectors vary slightly over time, the within-scene and between-scene stability is within 0.25% (2σ), enabling most users to ignore variability within and between scenes.
With a larger dynamic range than previous Landsat missions, saturated pixels are uncommon. Additionally, the recovery after being saturated is essentially eliminated, so fires and specular reflections only affect the pixels that have been directly saturated. There are no inoperable detectors in the OLI. Any artifacts that might exist in the OLI imagery are so small that they typically cannot be seen and won’t affect most applications.
Overall, the OLI has exceeded expectations for Landsat-8 and has raised the bar for future Landsat missions. With the higher radiometric performance, users will be able to extract more information than ever before.
Acknowledgments
Characterizing the radiometric performance of a complex flight instrument and with as many detectors as OLI has takes a great deal of preparation and planning. In order to accomplish this work, many individuals and teams were involved. We would like to identify several individuals and organizations that contributed to this work indirectly, or behind the scenes.
Landsat-8 ground processing system software development team, including Tim Beckmann, Dave Lloyd, Tim Ruggles, Ray Dittmeier, Shar Nelson, David Siver, Tammy Rockvam, and Doug Hollaren.
BATC systems engineering team, including Ed Knight, Geir Kvaran, Brent Canova, Eric Donley, Brian Donley, Khurrum Ansari, Amy Newbury and Jeff Pedelty, NASA on-site representative at BATC.
This work was performed under the Sigma Space/SSAI Contract: NASA contract NNG09HP18C and the SGT Contract: USGS contract G10PC00044.
Any use of trade, firm, or product names is for descriptive purposes only and does not imply endorsement by the U.S. Government.
Author Contributions
Ron Morfitt wrote the first draft with help from several authors, and performed the analysis for the dynamic range, and detector operability. Ron Morfitt, Julia Barsi and Raviv Levy performed the analysis for the noise section, Raviv concentrating on the 1/f noise and CN. Julia, Raviv and Brian Markham provided the analysis on the radiometric uniformity. Lawrence Ong, Ron, Raviv, and Kelly Vanderwerff provided the analysis for the stability section. Pat Scaramuzza performed the linearity analysis. Ron, Pat and Esad Micijevic did the analysis for the image artifacts. All authors reviewed and provided feedback to the final paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Montanaro, M.; Levy, R.; Markham, B. On-orbit radiometric performance of the Landsat 8 thermal infrared sensor. Remote Sens. 2014. [Google Scholar] [CrossRef]
- Knight, E.J.; Kvaran, G. Landsat-8 operational land imager design, characterization, and performance. Remote Sens. 2014. [Google Scholar] [CrossRef]
- Tarde, R.W.; Dittman, M.G.; Kvaran, G.E. Next-generation pushbroom filter radiometers for remote sensing. Proc. SPIE. 2012. [Google Scholar] [CrossRef]
- Vanderwerff, K.; Morfitt, R. Bias estimation for the Landsat 8 operational land imager. Proc. SPIE. 2011. [Google Scholar] [CrossRef]
- Markham, B.; Barsi, J.; Kvaran, G.; Ong, L.; Kaita, E.; Biggar, S.; Czapla-Myers, J.; Mishra, N.; Helder, D. Landsat-8 operational land imager radiometric calibration and stability. Remote Sens. 2014. [Google Scholar] [CrossRef]
- Kieffer, H.H. Photometric stability of the Lunar surface. Icarus 1997, 130, 323–327. [Google Scholar]
- Stone, T.C.; Kieffer, H.H. Absolute irradiance of the moon for on-orbit calibration. Proc. SPIE. 2002, 4814, 211–221. [Google Scholar]
- Pesta, F.; Bhatta, S.; Helder, D.L.; Brinkman, J.; Mishra, N. Radiometric non-uniformity characterization and correction of Landsat 8’s OLI using Earth Imagery-Based Techniques. Remote Sens. 2014. [Google Scholar] [CrossRef]
- Micijevic, E.; Morfitt, R.; Choate, M. Landsat 8 on-orbit characterization and calibration system. Proc. SPIE. 2011. [Google Scholar] [CrossRef]
- Storey, J.C.; Morfitt, R.A.; Thorson, P.R. Image processing on the Landsat 7 image assessment system, Proceedings of the 1999 ASPRS Annual Conference, Portland, OR, USA, 17–21 May 1999; pp. 743–758.
- Markham, B.L.; Chander, G.; Morfitt, R.; Hollaren, D. M.; Nelson, J.; Ong, L.; Mendenhall, J. A. Radiometric processing and calibratoin of EO-1 advanced land imager data, Proceedings of The Pecora 16 Annual Conference, Sioux Falls, SD, USA, 25 October 2005.
- Nelson, J.; Christopherson, J.; Hollaren, D. Advanced Land Imager Assessment System (ALIAS), Proceedings of the PECORA 16, Sioux Falls, SD, USA, 25 October 2005.
- Scaramuzza, P.L.; Markham, B.L.; Barsi, J.A.; Kaita, E. Landsat-7 ETM+ on-orbit reflective-band radiometric characterization. IEEE Trans. Geosci. Remote Sens. 2004, 40, 2796–2809. [Google Scholar]
- Johnson, G.M.; Fairchild, M.D. On contrast sensitivity in an image difference model, Proceedings of the 2002 Society for Imaging Science & Technology, Rochester, NY, USA, April 2002; pp. 18–23.
- Barsi, J.A.; Lee, K.; Markham, B.L.; Kvaran, G.; Pedelty, J.A. The Spectral response of the Landsat-8 operational land imager. Remote Sens. 2014. [Google Scholar] [CrossRef]
- USGS Landsat Mission Headlines, Available online: http://landsat.usgs.gov/mission_headlines2013.php accessed on 8 July 2014.
- USGS Landsat Mission Headlines, Available online: http://landsat.usgs.gov/mission_headlines2014.php accessed on 8 July 2014.
- NASA, Landsat Data Continuity Mission Operational Land Imager Requirements Document–Revision E; NASA Goddard Space Flight Center: Greenbelt, MD, USA, 2009.
- Dabney, P.W.; Levy, R.; Ong, L.; Waluschka, E.; Grochocki, F. Ghosting and stray-light performance assessment of the Landsat Data Continuity Mission’s (LDCM) Operational Land Imager (OLI). Proc. SPIE. 2013. [Google Scholar] [CrossRef]
- International Association of Geomagnetism and Aeronomy. International geomegnetic reference field: The eleventh generation. Geophys. J. Int. 2010, 183, 1216–1230.








| OLI Band # | Band Name | Center Wavelength (nm) | ||
|---|---|---|---|---|
| 1 | Coastal Aerosol | 443 | 40 | 190 |
| 2 | Blue | 482 | 40 | 190 |
| 3 | Green | 561 | 30 | 194 |
| 4 | Red | 655 | 22 | 150 |
| 5 | Near Infrared (NIR) | 865 | 14 | 150 |
| 6 | Short Wave Infrared (SWIR) 1 | 1609 | 4.0 | 32 |
| 7 | SWIR 2 | 2201 | 1.7 | 11 |
| 8 | Panchromatic (Pan) | 590 | 23 | 156 |
| 9 | Cirrus | 1373 | 6.0 | N/A |
| Collect Type | Frequency | Purpose |
|---|---|---|
| Shutter | Twice per orbit | Bias determination and monitoring |
| Stimulation Lamp | Daily | Short term stability monitoring |
| Solar Diffuser | Every 8 days | Relative and absolute calibration and long term stability monitoring |
| Lunar | Every 28 days | Independent monitoring of long term stability |
| Integration time sweep | Every 3 months | Linearity characterization |
| Side slither | Every 6 months | Relative gain determination and evaluation |
| Band Name | Average Dark Noise | Noise Model Coefficients | Product Quantization Noise (∊q) | |
|---|---|---|---|---|
| Coastal Aerosol | 0.11 | 0.012 | 0.00042 | 0.0047 |
| Blue | 0.089 | 0.0082 | 0.000094 | 0.0048 |
| Green | 0.084 | 0.0073 | 0.000089 | 0.0035 |
| Red | 0.083 | 0.0071 | 0.00011 | 0.0039 |
| NIR | 0.056 | 0.0032 | 0.00012 | 0.0028 |
| SWIR 1 | 0.011 | 0.00013 | 0.000026 | 0.00055 |
| SWIR 2 | 0.0034 | 0.000011 | 0.0000091 | 0.00025 |
| Pan | 0.086 | 0.0078 | 0.00069 | 0.0033 |
| Cirrus | 0.025 | 0.00059 | 0.00014 | 0.00070 |
| OLI Band # | Band Name | OLI SNR | ETM+ SNR |
|---|---|---|---|
| 1 | Coastal Aerosol | 237 | – |
| 2 | Blue | 367 | 39 |
| 3 | Green | 304 | 37 |
| 4 | Red | 227 | 26 |
| 5 | NIR | 201 | 34 |
| 6 | SWIR 1 | 267 | 36 |
| 7 | SWIR 2 | 327 | 27 |
| 8 | Pan | 148 | 16 |
| 9 | Cirrus | 160 | – |
| OLI Band # | Band Name | LMax | OLI LSat | ETM+ LSat | |
|---|---|---|---|---|---|
| Low Gain | High Gain | ||||
| 1 | Coastal Aerosol | 555 | 950 | – | – |
| 2 | Blue | 581 | 800 | 300 | 195 |
| 3 | Green | 544 | 760 | 309 | 201 |
| 4 | Red | 462 | 740 | 239 | 156 |
| 5 | NIR | 281 | 500 | 246 | 160 |
| 6 | SWIR 1 | 71.3 | 96 | 48.4 | 31.5 |
| 7 | SWIR 2 | 24.3 | 29 | 16.9 | 11.0 |
| 8 | Pan | 515 | 750 | 249 | 162 |
| 9 | Cirrus | 88.5 | 180 | – | – |
| OLI Band # | Band Name | Number of Scenes | Number of Saturated Pixels |
|---|---|---|---|
| 1 | Coastal Aerosol | 12,833 | 63,175 |
| 2 | Blue | 27,783 | 9,656,828 |
| 3 | Green | 25,824 | 2,642,769 |
| 4 | Red | 17,410 | 223,605 |
| 5 | NIR | 20,394 | 189,741 |
| 6 | SWIR 1 | 60,870 | 1,616,217 |
| 7 | SWIR 2 | 83,759 | 5,605,565 |
| 8 | Pan | 37,937 | 4,445,760 |
| 9 | Cirrus | 221 | 553 |
| OLI Band # | Band Name | 2σ Stability | |
|---|---|---|---|
| Average | Worst Case | ||
| 1 | Coastal Aerosol | 0.19% | 0.20% |
| 2 | Blue | 0.10% | 0.12% |
| 3 | Green | 0.094% | 0.096% |
| 4 | Red | 0.11% | 0.12% |
| 5 | NIR | 0.15% | 0.15% |
| 6 | SWIR 1 | 0.14% | 0.15% |
| 7 | SWIR 2 | 0.14% | 0.15% |
| 8 | Pan | 0.26% | 0.26% |
| 9 | Cirrus | 0.25% | 0.26% |
| Date | Explanation |
|---|---|
| 21 August 2013 | Multi-bit error recovery |
| 6 February 2014 | Multi-bit error recovery |
| 13 February 2014 | Special TIRS lunar stray light scan |
| 19 February 2014 | Multi-bit error recovery |
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morfitt, R.; Barsi, J.; Levy, R.; Markham, B.; Micijevic, E.; Ong, L.; Scaramuzza, P.; Vanderwerff, K. Landsat-8 Operational Land Imager (OLI) Radiometric Performance On-Orbit. Remote Sens. 2015, 7, 2208-2237. https://doi.org/10.3390/rs70202208
Morfitt R, Barsi J, Levy R, Markham B, Micijevic E, Ong L, Scaramuzza P, Vanderwerff K. Landsat-8 Operational Land Imager (OLI) Radiometric Performance On-Orbit. Remote Sensing. 2015; 7(2):2208-2237. https://doi.org/10.3390/rs70202208
Chicago/Turabian StyleMorfitt, Ron, Julia Barsi, Raviv Levy, Brian Markham, Esad Micijevic, Lawrence Ong, Pat Scaramuzza, and Kelly Vanderwerff. 2015. "Landsat-8 Operational Land Imager (OLI) Radiometric Performance On-Orbit" Remote Sensing 7, no. 2: 2208-2237. https://doi.org/10.3390/rs70202208
APA StyleMorfitt, R., Barsi, J., Levy, R., Markham, B., Micijevic, E., Ong, L., Scaramuzza, P., & Vanderwerff, K. (2015). Landsat-8 Operational Land Imager (OLI) Radiometric Performance On-Orbit. Remote Sensing, 7(2), 2208-2237. https://doi.org/10.3390/rs70202208





