A Novel Bias Correction Method for Soil Moisture and Ocean Salinity (SMOS) Soil Moisture: Retrieval Ensembles
Abstract
:1. Introduction
2. Data and Methods
2.1. SMOS Retrieval Algorithm
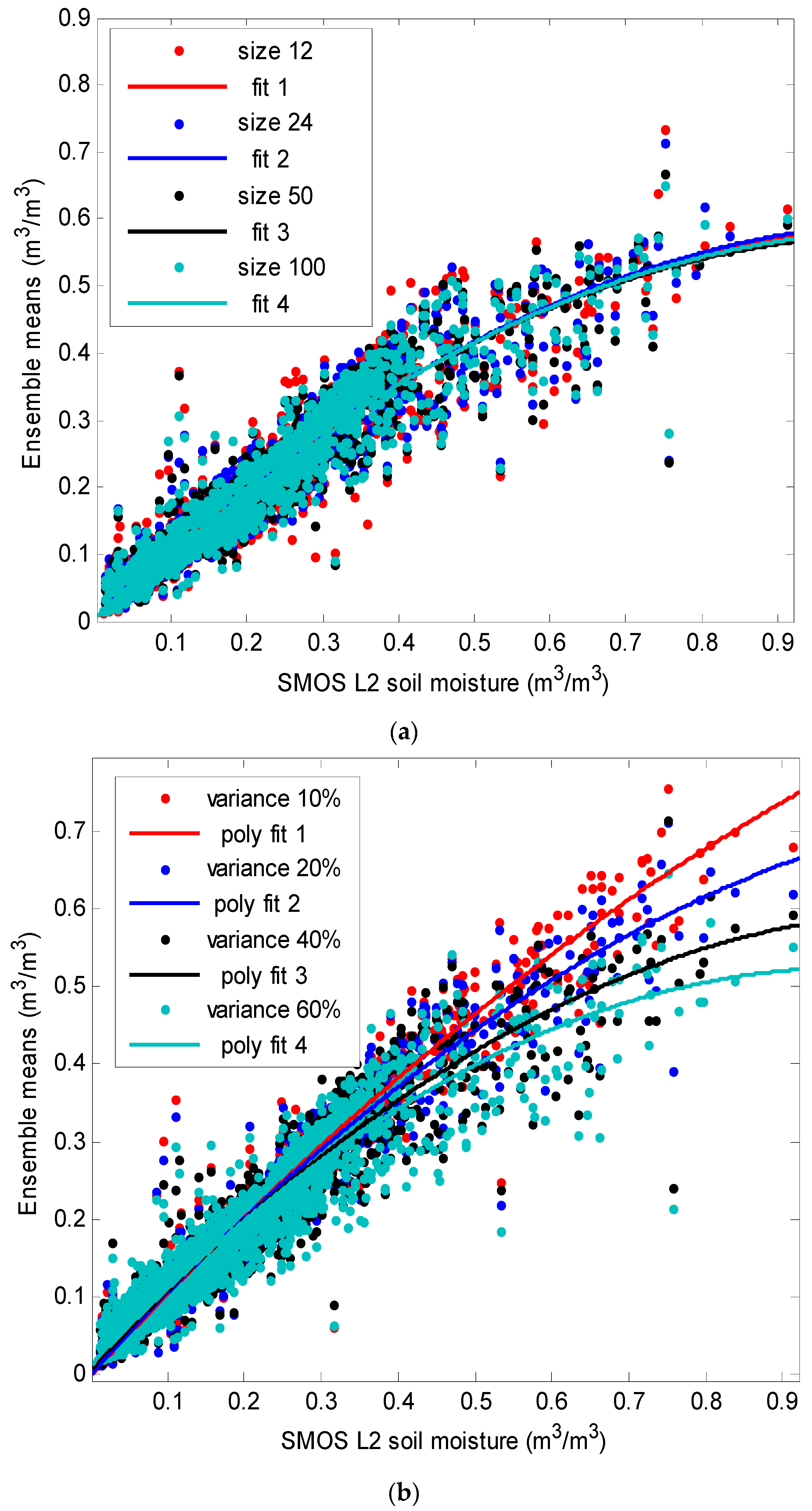
2.2. Retrieval Ensembles
2.2.1. Theoretical Rationale
2.2.2. Experimental Setup for Ensemble Generation
2.3. CDF Matching
3. Results and Discussion
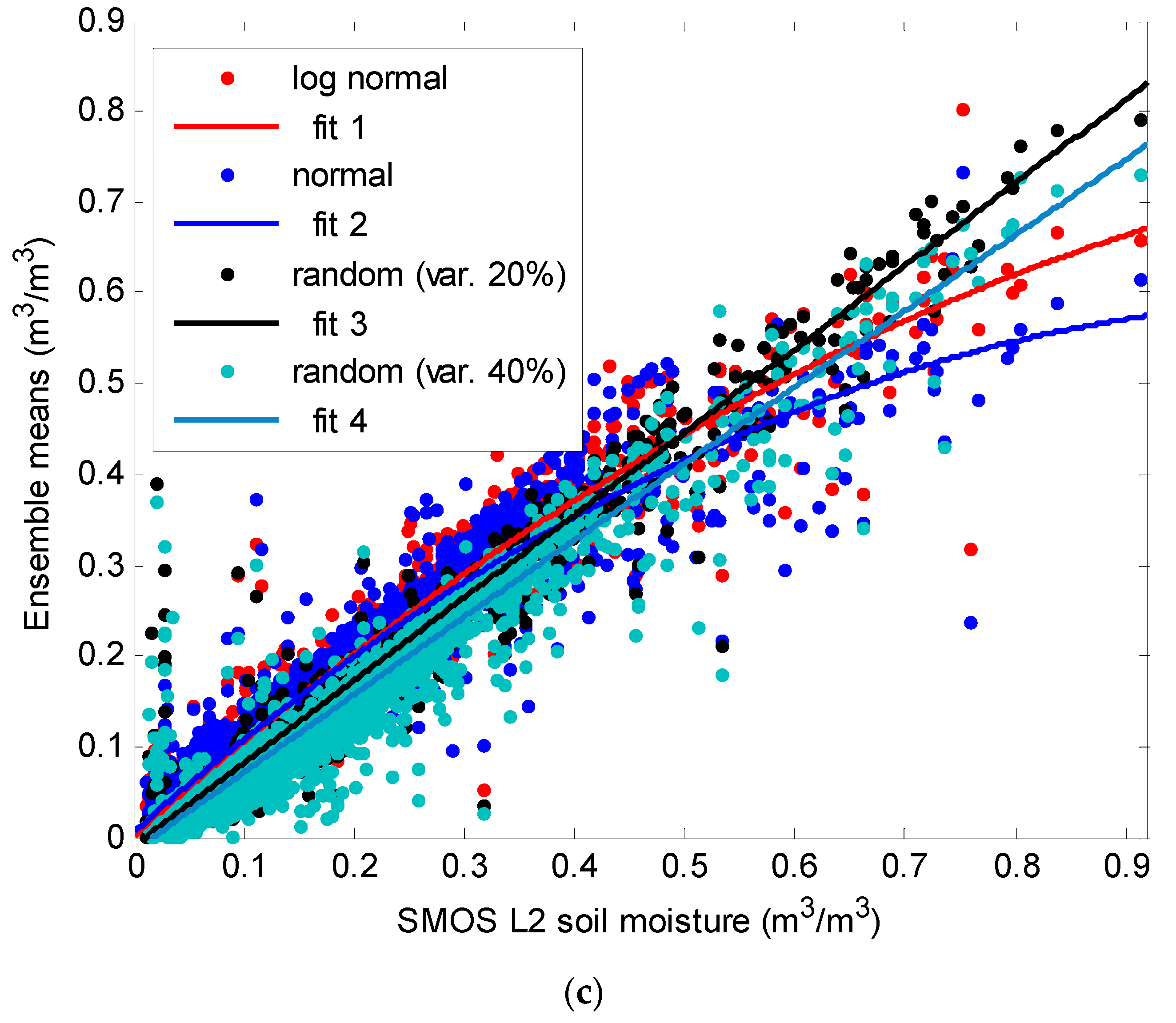
3.1. Rescaling Functions
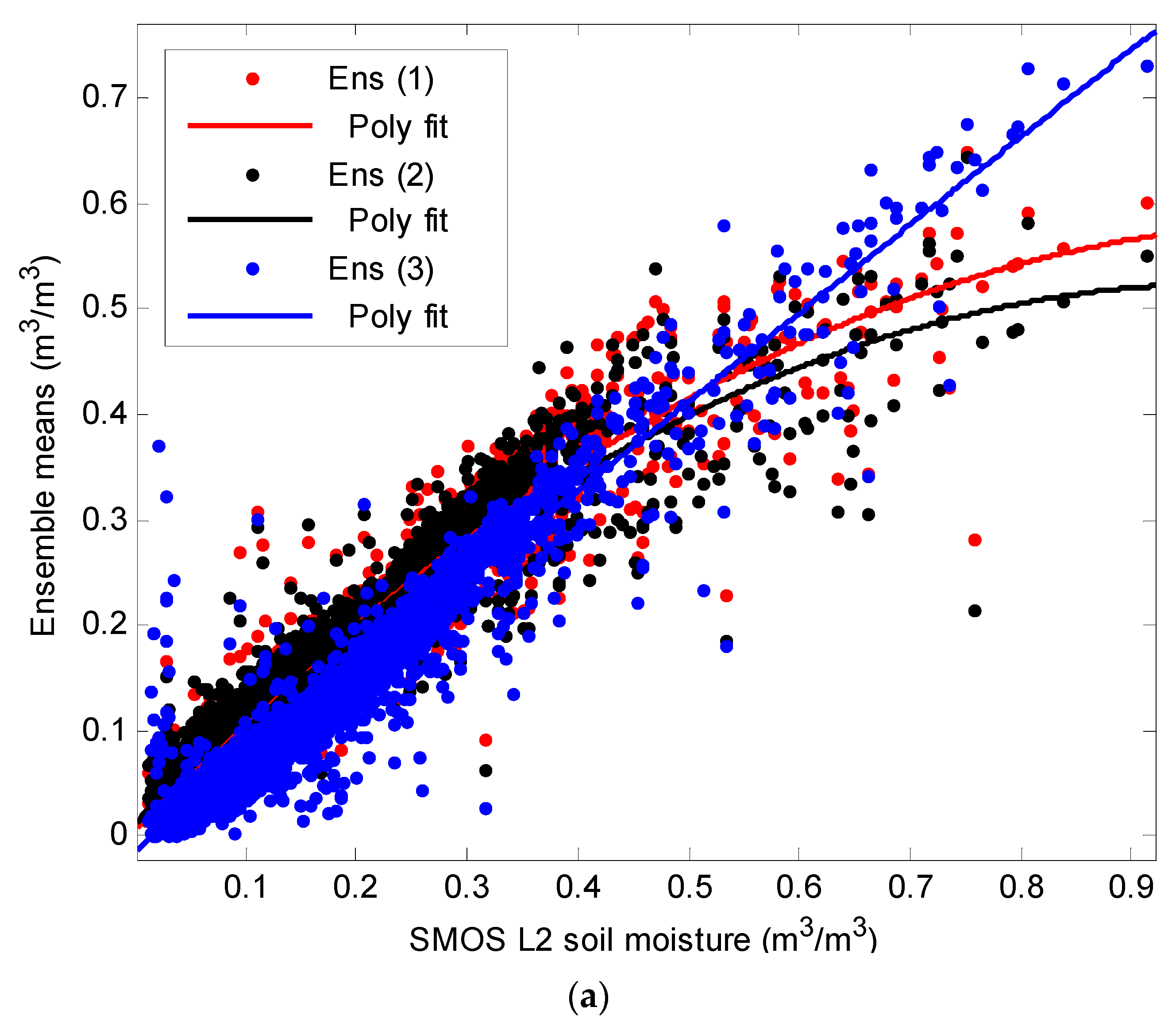
3.2. Point-Scale Validation: CDF Matching vs. Ensemble Rescaling
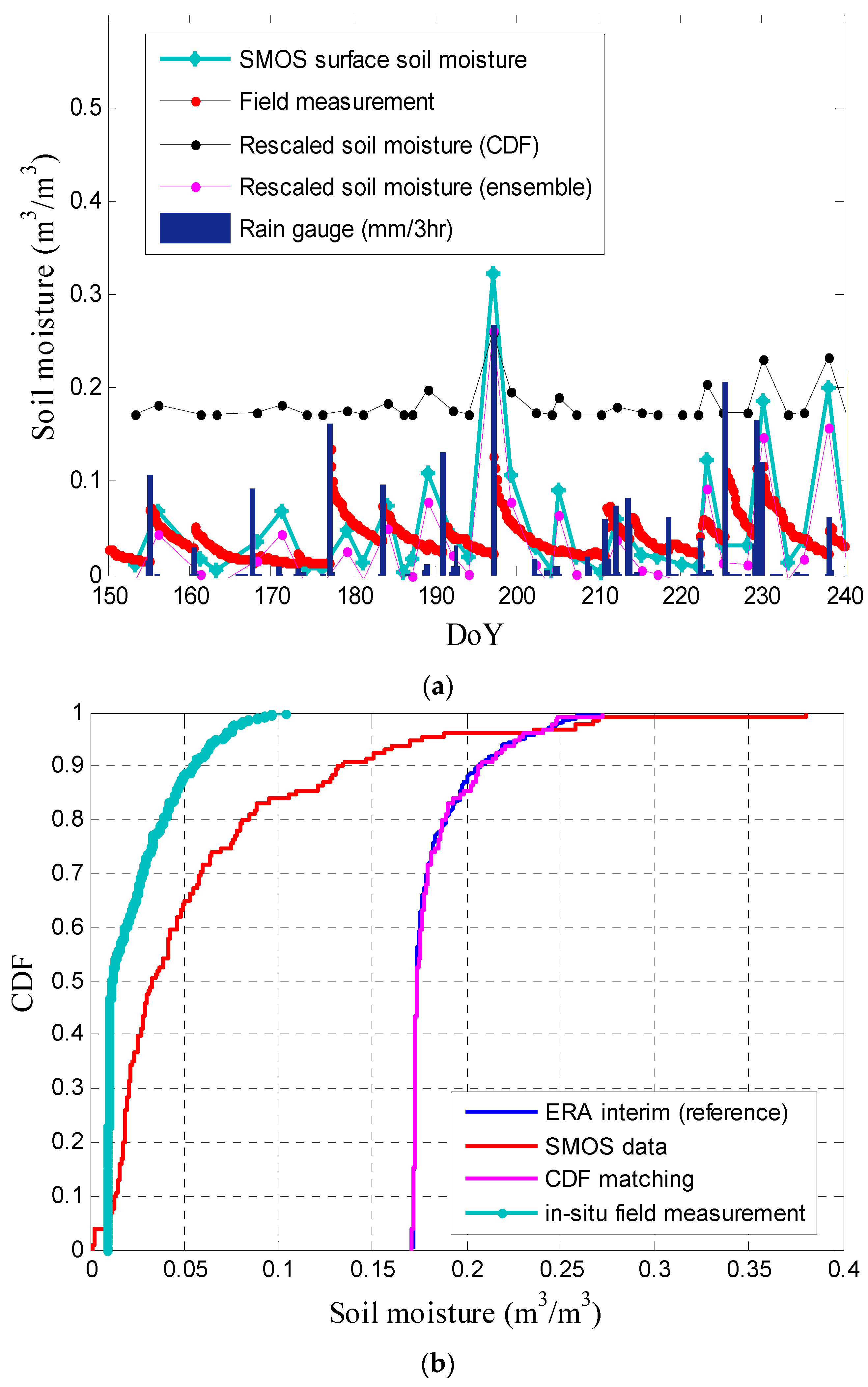
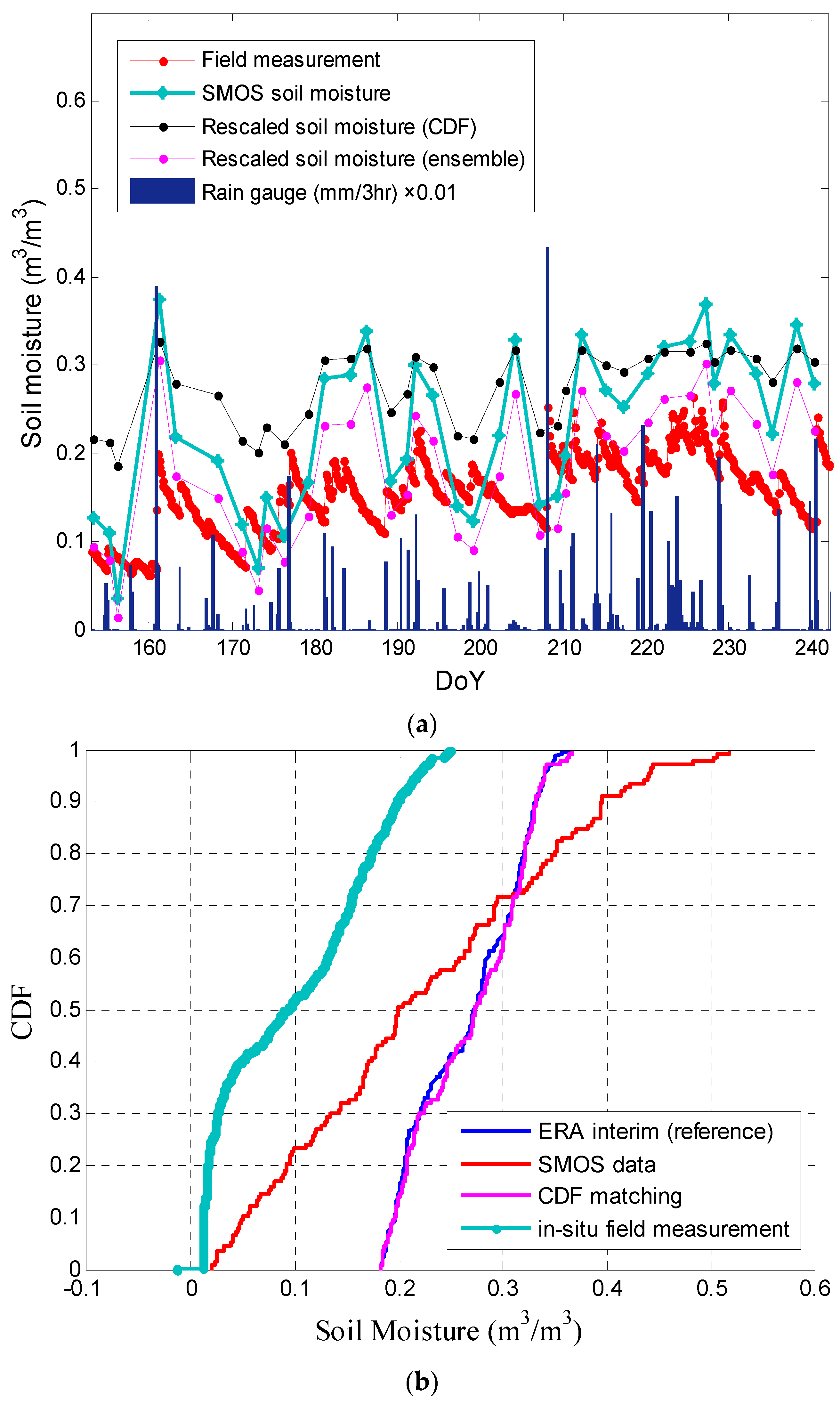
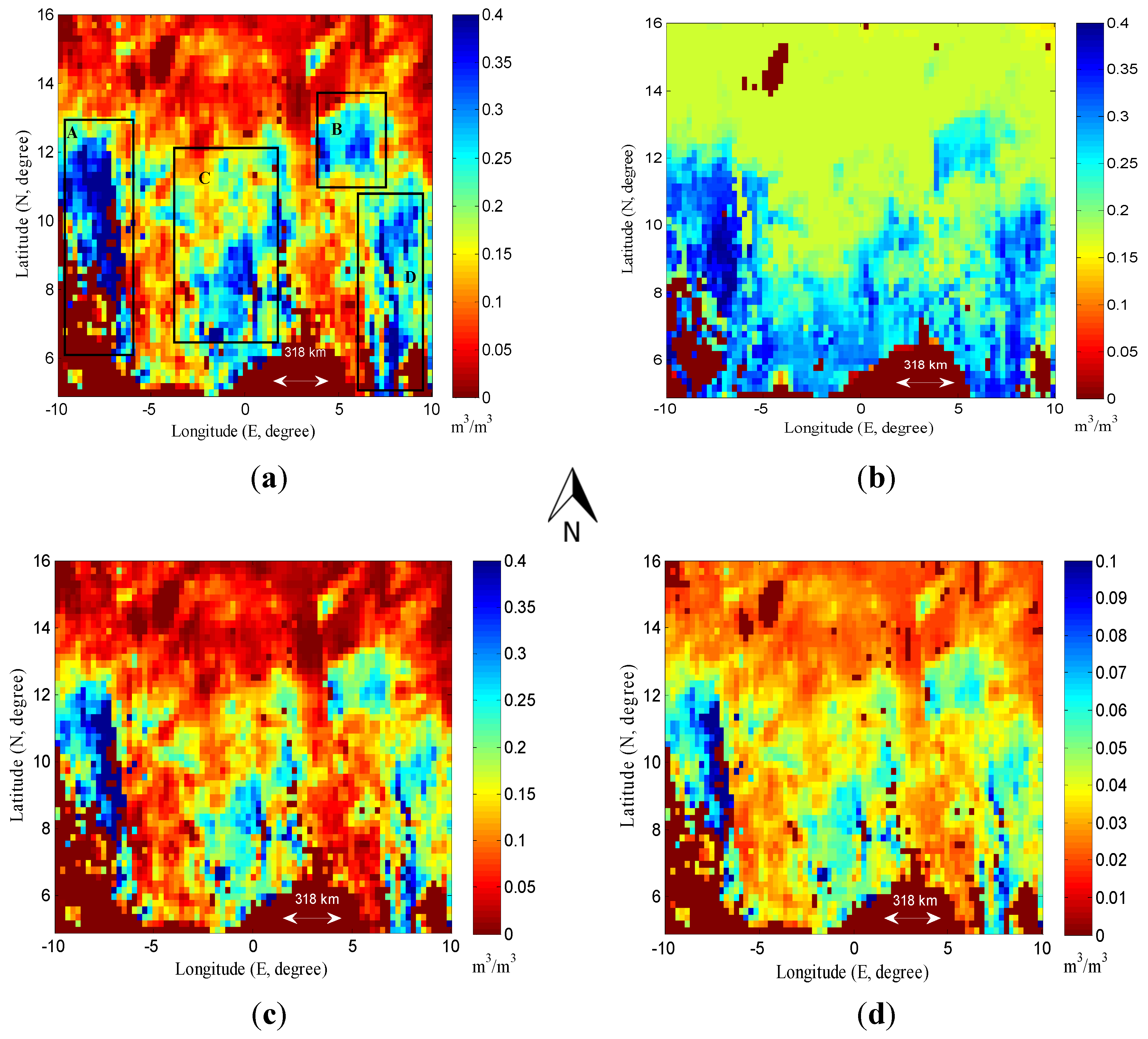
3.3. Spatial Comparison: CDF Matching vs. Ensemble Rescaling
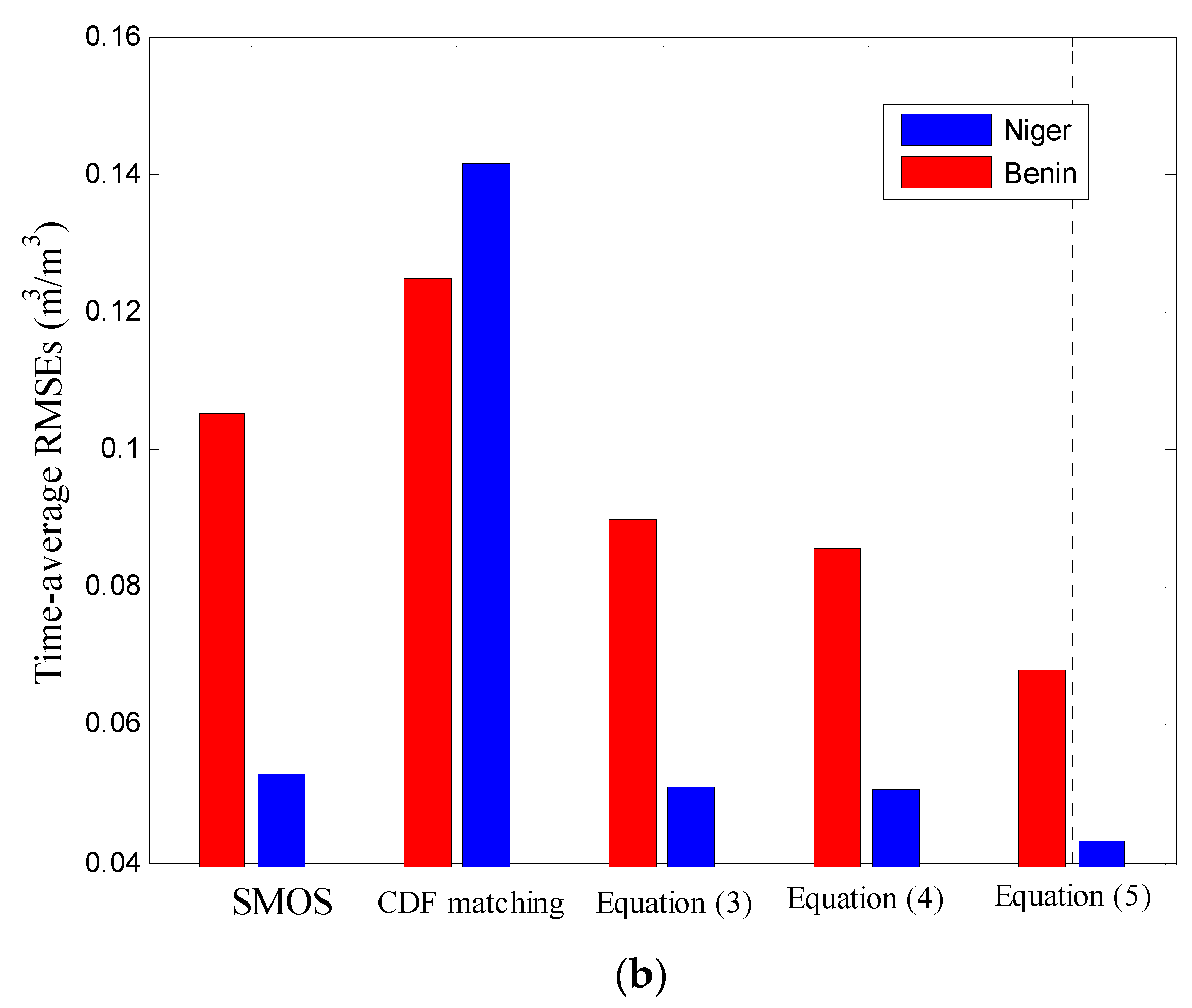
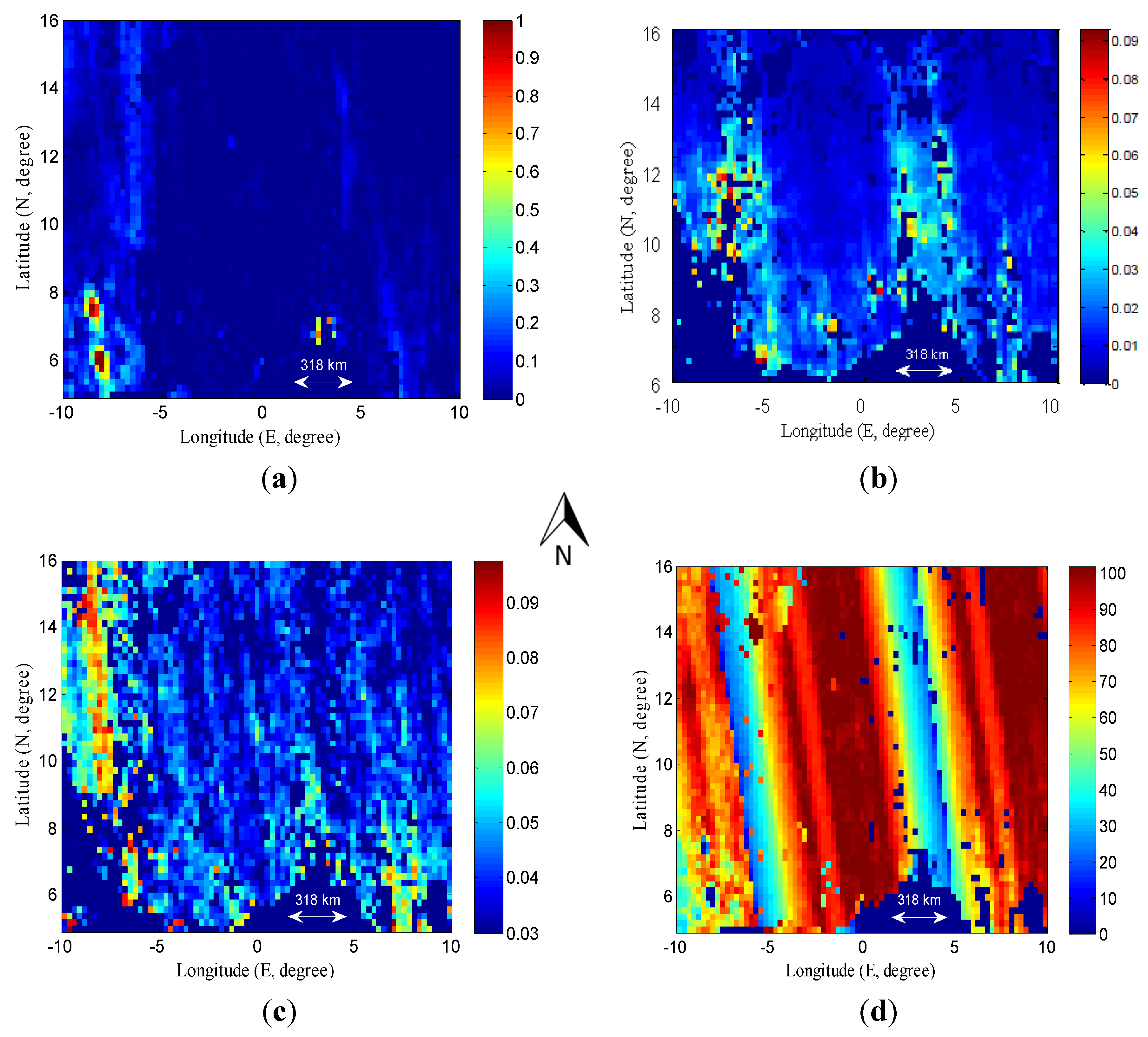
3.4. Spatial Comparison: QC Science Flag vs. Ensemble Rescaling
4. Discussion
5. Conclusions
Supplementary Files
Supplementary File 1Acknowledgments
Author Contributions
Conflicts of Interest
References
- De Rosnay, P.; Muñoz Sabater, J.; Drusch, M.; Albergel, C.; Balsamo, G.; Boussetta, S.; Isaksen, L.; Thépaut, J.-N. Bias correction for SMOS data assimilation in the ECMWF Numerical Weather Prediction System. In Proceedings of the ESA Living Planet Symposium, Edinburgh, UK, 9–13 September 2013.
- Margulis, S.A.; McLaughlin, D.; Entekhabi, D.; Dunne, S. Land data assimilation and estimation of soil moisture using measurements from the Southern Great Plains 1997 Field Experiment. Water Resour. Res. 2002, 38. [Google Scholar] [CrossRef]
- Anderson, J.L. Exploring the need for localization in ensemble data assimilation using a hierarchical ensemble filter. Phys. D: Nonlinear Phenom. 2007, 230, 99–111. [Google Scholar] [CrossRef]
- Gruhier, C.; de Rosnay, P.; Kerr, Y.; Mougin, E.; Ceschia, E.; Calvet, J.-C.; Richaume, P. Evaluation of AMSR-E soil moisture product based on ground measurements over temperate and semi-arid regions. Geophys. Res. Lett. 2008, 35, L10405. [Google Scholar] [CrossRef]
- Reichle, R.H. Data assimilation methods in the Earth sciences. Adv. Water Resour. 2008, 31, 1411–1418. [Google Scholar] [CrossRef]
- Fertig, E.J.; Baek, S.-J.; Hunt, B.R.; Ott, E.; Szunyogh, I.; Aravéquia, J.A.; Kalnay, E.; Li, H.; Liu, J. Observation bias correction with an ensemble Kalman filter. Tellus A 2009, 61, 210–226. [Google Scholar] [CrossRef]
- Reichle, R.H.; Koster, R.D. Bias reduction in short records of satellite soil moisture. Geophys. Res. Lett. 2004, 31, L19501. [Google Scholar] [CrossRef]
- Entekhabi, D.; Yueh, S.; O’Neill, P.; Kellogg, K.; Allen, A; Bindlish, R.; Brown, M.; Chan, S.; Colliander., A; Crow, W.T.; et al. SMAP Handbook; JPL Publication JPL 400–1567; Jet Propulsion Laboratory: Pasadena, CA, USA, 2014; p. 182. [Google Scholar]
- Dee, D.P. Bias and data assimilation. Q. J. R. Meteorol. Soc. 2005, 131, 3323–3343. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S. Variational bias correction of satellite radiance data in the ERA-Interim reanalysis. Q. J. R. Meteorol. Soc. 2009, 135, 1830–1841. [Google Scholar] [CrossRef]
- Draper, C.S.; Mahfouf, J.-F.; Walker, J.P. An EKF assimilation of AMSR-E soil moisture into the ISBA land surface scheme. J. Geophys. Res. 2009, 114, D20104. [Google Scholar] [CrossRef]
- Crow, W.T.; Berg, A.A.; Cosh, M.H.; Loew, A.; Mohanty, B.P.; Panciera, R.; deRosnay, P.; Ryu, D.; Walker, J.P. Upscaling sparse ground-based soil moisture observations for the validation of coarse-resolution satellite soil moisture products. Rev. Geophys. 2012, 50, RG2002. [Google Scholar]
- Reichle, R.H.; Koster, R.D.; Liu, P.; Mahanama, S.P.; Njoku, E.G.; Owe, M. Comparison and assimilation of global soil moisture retrievals from the Advanced Microwave Scanning Radiometer for the Earth Observing System (AMSR-E) and the Scanning Multichannel Microwave Radiometer (SMMR). J. Geophys. Res. 2007, 112, D09108. [Google Scholar] [CrossRef]
- Lee, J.H.; Pellarin, T.; Kerr, Y.H. EnOI optimization of SMOS soil moisture over West Africa. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2015, 8, 1821–1829. [Google Scholar] [CrossRef]
- Drusch, M.; Wood, E.F.; Gao, A.H. Observation operators for the direct assimilation of TRMM microwave imager retrieved soil moisture. Geophys. Res. Lett. 2005, 32, L15403. [Google Scholar] [CrossRef]
- Evensen, G. The Ensemble Kalman Filter: Theoretical formulation, and practical implementation. Ocean Dyn. 2003, 53, 343–367. [Google Scholar] [CrossRef]
- Stroeve, J.; Hamilton, L.C.; Bitz, C.M.; Blanchard-Wrigglesworth, E. Predicting September sea ice: Ensemble skill of the SEARCH Sea Ice Outlook 2008–2013. Geophys. Res. Lett. 2014, 41, 2411–2418. [Google Scholar] [CrossRef]
- Koster, R.D.; Cox, P.M.; Dirmeyer, P.; Guo, Z.; Bonan, G.; Chan, E. Regions of strong coupling between soil moisture and precipitation. Science 2004, 305, 1138–1140. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Li, Z.L.; Li, J.; Li, J.L. Ensemble retrieval of atmospheric temperature profiles from AIRS. Adv. Atmos. Sci. 2014, 31, 559–569. [Google Scholar] [CrossRef]
- Hossain, F.; Anagnostou, E.N. A two-dimensional satellite rainfall error model. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1511–1522. [Google Scholar] [CrossRef]
- Olson, W.S.; Kummerow, C.D.; Yang, S.; Petty, G.W.; Tao, W.; Bell, T.L.; Braun, S.A.; Wang, Y.; Lang, S.E.; Johnson, D.E.; et al. Precipitation and latent heating distributions from satellite passive microwave radiometry. Part I: Improved method and uncertainties. J. Appl. Meteor. Climatol. 2006, 45, 702–720. [Google Scholar] [CrossRef]
- Balsamo, G.; Albergel, C.; Beljaars, A.; Boussetta, S.; Brun, E.; Cloke, H.; Dee, D.; Dutra, E.; Muñoz-Sabater, J.; Pappenberger, F.; et al. ERA-Interim/Land: A global land surface reanalysis data set. Hydrol. Earth Syst. Sci. 2015, 19, 389–407. [Google Scholar] [CrossRef]
- Lee, J.H.; Pellarin, T.; Kerr, Y.H. Inversion of soil hydraulic properties from the DEnKF analysis of SMOS soil moisture over West Africa. Agric. For. Meteorol. 2014, 188, 76–88. [Google Scholar] [CrossRef]
- Delon, C.; Galy-Lacaux, C.; Adon, M.; Liousse, C.; Serça, D.; Diop, B.; Akpo, A. Nitrogen compounds emission and deposition in West African ecosystems: Comparison between wet and dry savanna. Biogeosciences 2012, 9, 385–402. [Google Scholar] [CrossRef]
- Cappelaere, B.; Descroix, L.; Lebel, T.; Boun, N.; Ramier, D.; Laurent, J.-P.; Favreau, G.; Boubkraoui, S.; Boucher, M.; Moussa, I.B.; et al. The AMMA-CATCH experiment in the cultivated Sahelian area of south-west Niger—Investigating water cycle response to a fluctuating climate and changing environment. J. Hydrol. 2009, 375, 34–51. [Google Scholar] [CrossRef]
- Séguis, L.; Boulain, N.; Cappelaere, B.; Cohard, J.M.; Favreau, G.; Galle, S.; Guyot, A.; Hiernaux, P.; Mougin, É.; Peugeot, C.; et al. Contrasted land-surface processes along the West African rainfall gradient. Atmos. Sci. Lett. 2011, 12, 31–37. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Waldteufel, P.; Richaume, P.; Ferrazzoli, P.; Wigneron, J.-P. SMOS LEVEL 2 Processor Soil Moisture Algorithm Theoretical Basis Document (ATBD) v1.3h; SM-ESL (CBSA): Toulouse, France, 2013; p. 141. [Google Scholar]
- Kerr, Y.H.; Waldteufel, P.; Richaume, P.; Wigneron, J.-P.; Ferrazzoli, P.; Mahmoodi, A.; Al Bitar, A.; Cabot, F.; Gruhier, C.; Juglea, S.E.; et al. The SMOS Soil Moisture Retrieval Algorithm. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1384–1403. [Google Scholar] [CrossRef]
- Burgers, G.; Jan van Leeuwen, P.; Evensen, G. Analysis scheme in the Ensemble Kalman Filter. Mon. Weather Rev. 1998, 126, 1719–1724. [Google Scholar] [CrossRef]
- Rodriguez-Fernandez, N.; Richaume, P.; Aires, F.; Prigent, C.; Kerr, Y.; Kolassa, J.; Jimenez, C.; Cabot, F.; Mahmoodi, A. Soil moisture retrieval from SMOS observations using neural networks. In Proceedings of the 2014 IEEE International Geoscience Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014; pp. 2431–2434.
- Holmes, T.R.H.; Drusch, M.; Wigneron, J.P.; de Jeu, R.A.M. A global simulation of microwave emission: Error structures based on output from ECMWF's operational integrated forecast system. IEEE Trans. Geosci. Remote Sens. 2008, 46, 846–856. [Google Scholar] [CrossRef]
- Muñoz-Sabater, J. Incorporation of passive microwave Brightness Temperatures in the ECMWF soil moisture analysis. Remote Sens. 2015, 7, 5758–5784. [Google Scholar] [CrossRef]
- Schlenz, F.; dall’Amico, J.T.; Mauser, W.; Loew, A. Analysis of SMOS brightness temperature and vegetation optical depth data with coupled land surface and radiative transfer models in Southern Germany. Hydrol. Earth Syst. Sci. 2012, 16, 3517–3533. [Google Scholar] [CrossRef]
- Balsamo, G.; Viterbo, P.; Beljaars, A.; van den Hurk, B.; Hirschi, M.; Betts, A.K.; Scipal, K. A revised hydrology for the ECMWF model: Verification from field site to terrestrial water storage and impact in the Integrated Forecast System. J. Hydrometeor. 2009, 10, 623–643. [Google Scholar] [CrossRef]
- Scipal, K.; Drusch, M.; Wagner, W. Assimilation of a ERS scatterometer derived soil moisture index in the ECMWF numerical weather prediction system. Adv. Water Resour. 2008, 31, 1101–1112. [Google Scholar] [CrossRef]
- Chung, D.; Dorigo, W.; Hahn, S.; Melzer, T.; Paulik, C.; Reimer, C.; Vreugdenhil, M.; Wagner, W.; Kidd, R. ECV Production, Fusion of Soil Moisture Products: Algorithm Theoretical Baseline Document, Ver. 2.0. ESA soil moisture CCI; ESA: Vienna, Austria, 2014. [Google Scholar]
- De Jeu, R.A.M.; Wagner, W.W.; Holmes, T.R.H.; Dolman, A.J.; van de Giesen, N.C.; Friesen, J. Global soil moisture patterns observed by space borne microwave radiometers and scatterometers. Surv. Geophys. 2008, 28, 399–420. [Google Scholar] [CrossRef]
- Parinussa, R.M.; Meesters, A.G.C.A.; Liu, Y.Y.; Dorigo, W.; Wagner, W.; de Jeu, R.A.M. Error estimates for near-real-time satellite soil moisture as derived from the Land Parameter Retrieval Model. IEEE Geosci. Remote Sens. Lett. 2011, 8, 779–783. [Google Scholar] [CrossRef]
- Guillod, B.P.; Orlowsky, B.; Miralles, D.G.; Teuling, A.J.; Seneviratne, S.I. Reconciling spatial and temporal soil moisture effects on afternoon rainfall. Nat. Commun. 2015. [Google Scholar] [CrossRef] [PubMed]
- Taylor, C.M.; de Jeu, R.A.M.; Guichard, F.; Harris, P.P.; Dorigo, W.A. Afternoon rain more likely over drier soils. Nature 2012, 489, 423–426. [Google Scholar] [CrossRef] [PubMed]
- Famiglietti, J.S.; Ryu, D.; Berg, A.A.; Rodel, M.; Jackson, T.J. Field observations of soil moisture variability across scales. Water Resour. Res. 2008, 44, W01423. [Google Scholar] [CrossRef]
- Lu, H.; Yang, K.; Koike, T.; Zhao, L.; Qin, J. An improvement of the radiative transfer model component of a land data assimilation system and its validation on different land characteristics. Remote Sens. 2015, 7, 6358–6379. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.H.; Im, J. A Novel Bias Correction Method for Soil Moisture and Ocean Salinity (SMOS) Soil Moisture: Retrieval Ensembles. Remote Sens. 2015, 7, 16045-16061. https://doi.org/10.3390/rs71215824
Lee JH, Im J. A Novel Bias Correction Method for Soil Moisture and Ocean Salinity (SMOS) Soil Moisture: Retrieval Ensembles. Remote Sensing. 2015; 7(12):16045-16061. https://doi.org/10.3390/rs71215824
Chicago/Turabian StyleLee, Ju Hyoung, and Jungho Im. 2015. "A Novel Bias Correction Method for Soil Moisture and Ocean Salinity (SMOS) Soil Moisture: Retrieval Ensembles" Remote Sensing 7, no. 12: 16045-16061. https://doi.org/10.3390/rs71215824
APA StyleLee, J. H., & Im, J. (2015). A Novel Bias Correction Method for Soil Moisture and Ocean Salinity (SMOS) Soil Moisture: Retrieval Ensembles. Remote Sensing, 7(12), 16045-16061. https://doi.org/10.3390/rs71215824





