Evaluation of Sampling Methods for Validation of Remotely Sensed Fractional Vegetation Cover
Abstract
:1. Introduction
2. Generation of Reference Data
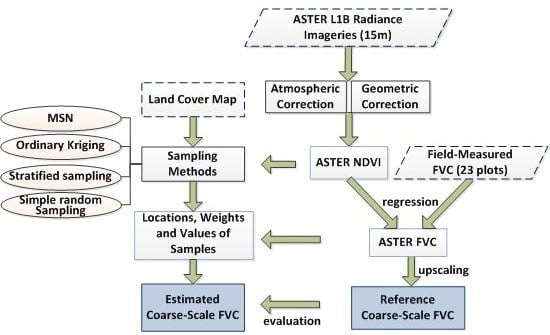
2.1. Framework of Reference Data Generation

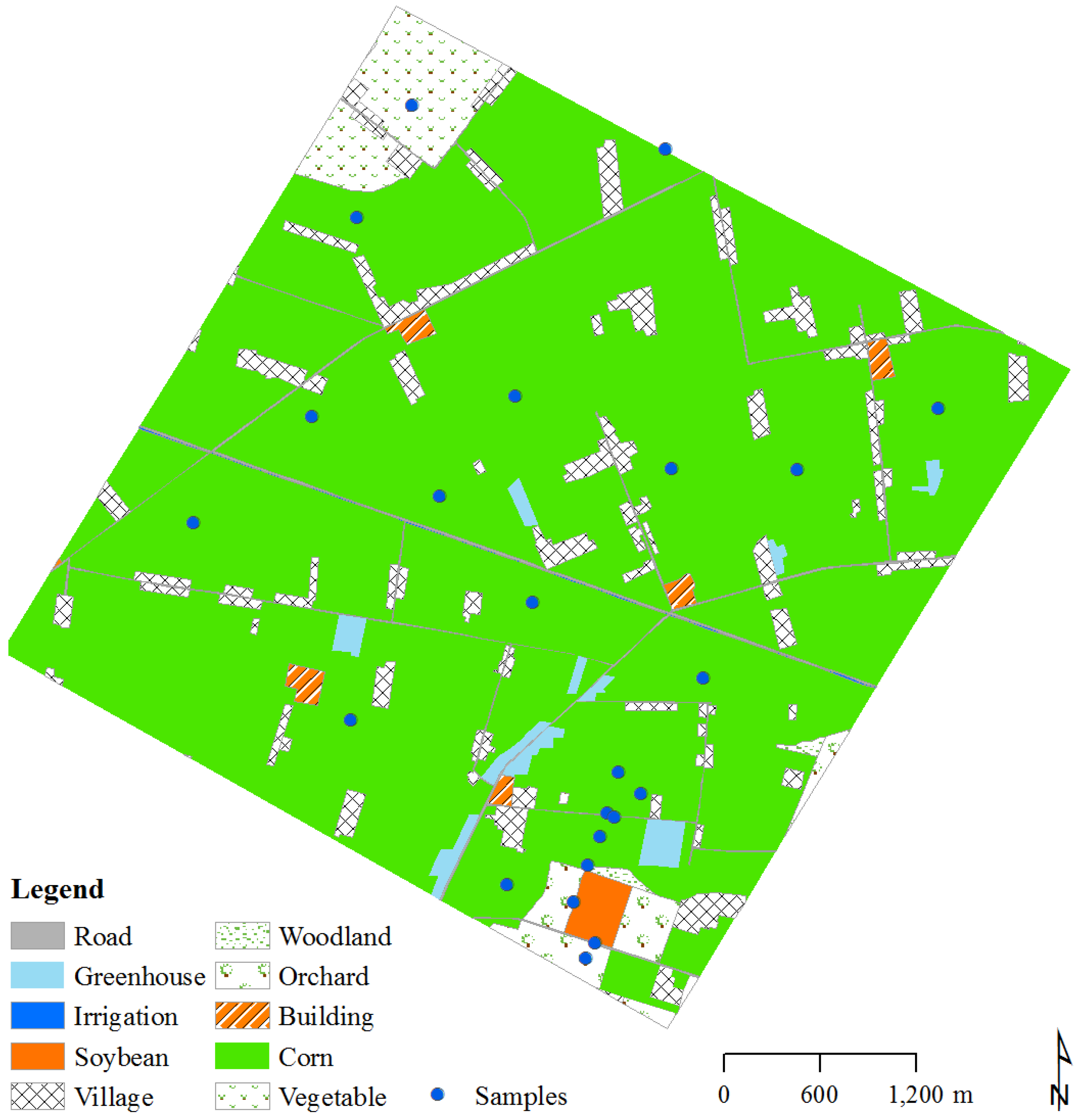
2.2. Study Site and in Situitalic> Data Measurements
2.3. Generation of Reference FVC
| Date | 30 May 2012 | 24 June 2012 | 10 July 2012 | 11 August 2012 | 12 September 2012 | ALL * |
|---|---|---|---|---|---|---|
| R2 | 0.983 | 0.850 | 0.928 | 0.911 | 0.947 | 0.914 |
| k | 1.232 | 1.136 | 0.328 | 0.459 | 1.299 | 0.523 |
| RMSE | 0.020 | 0.020 | 0.016 | 0.031 | 0.010 | 0.072 |
| FVCavg | 0.181 | 0.623 | 0.690 | 0.720 | 0.133 | 0.469 |
| FVCdev | 0.168 | 0.053 | 0.090 | 0.087 | 0.040 | 0.276 |
3. Methodology
3.1. Sampling Methods
3.2. Design of Experiments
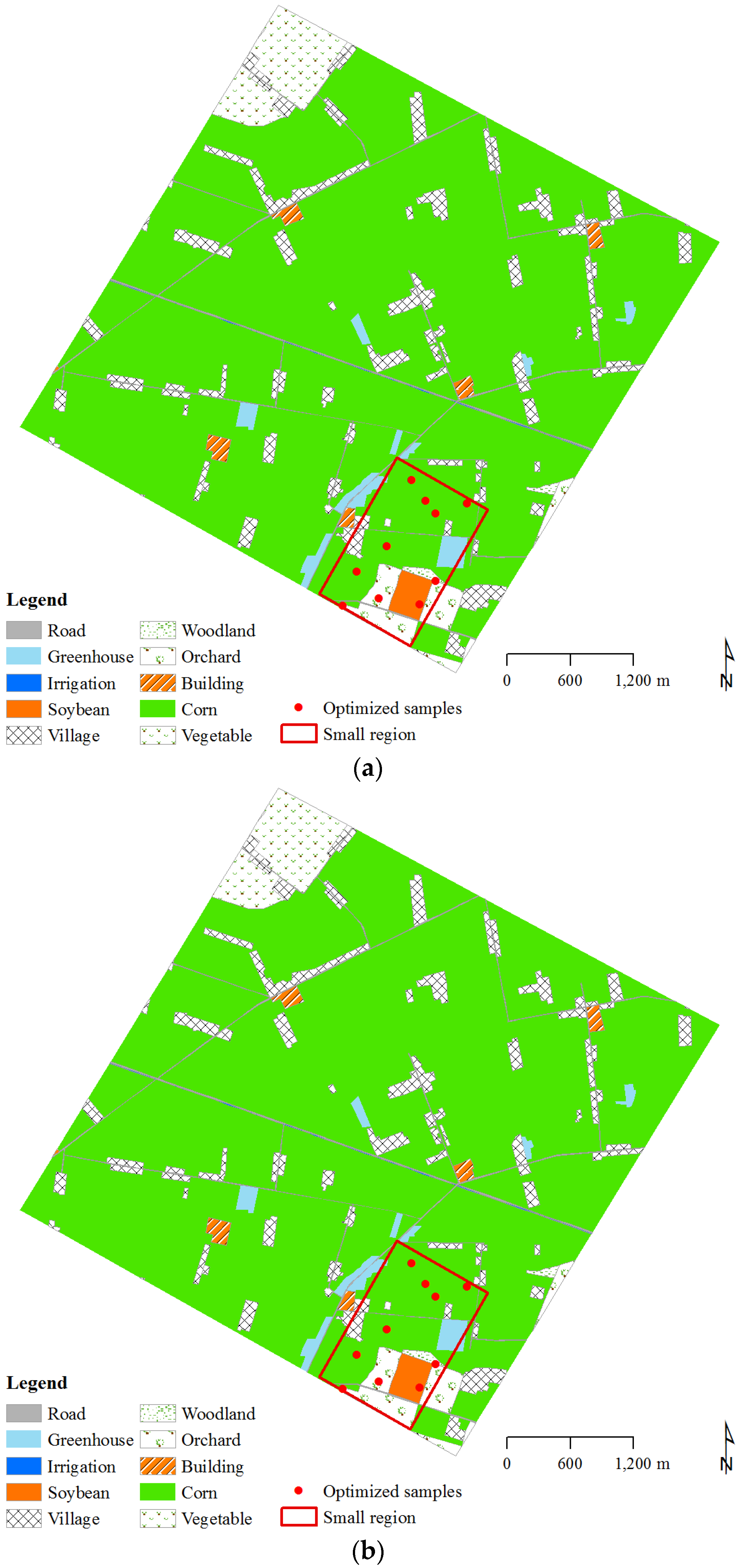
3.2.1. Sparse Sampling (Scene 1)
3.2.2. Dense Sampling (Scene 2)

3.3. Scaling Bias of FVC Estimates
4. Results and Analysis
4.1. Spatial and Temporal Pattern of ASTER FVC
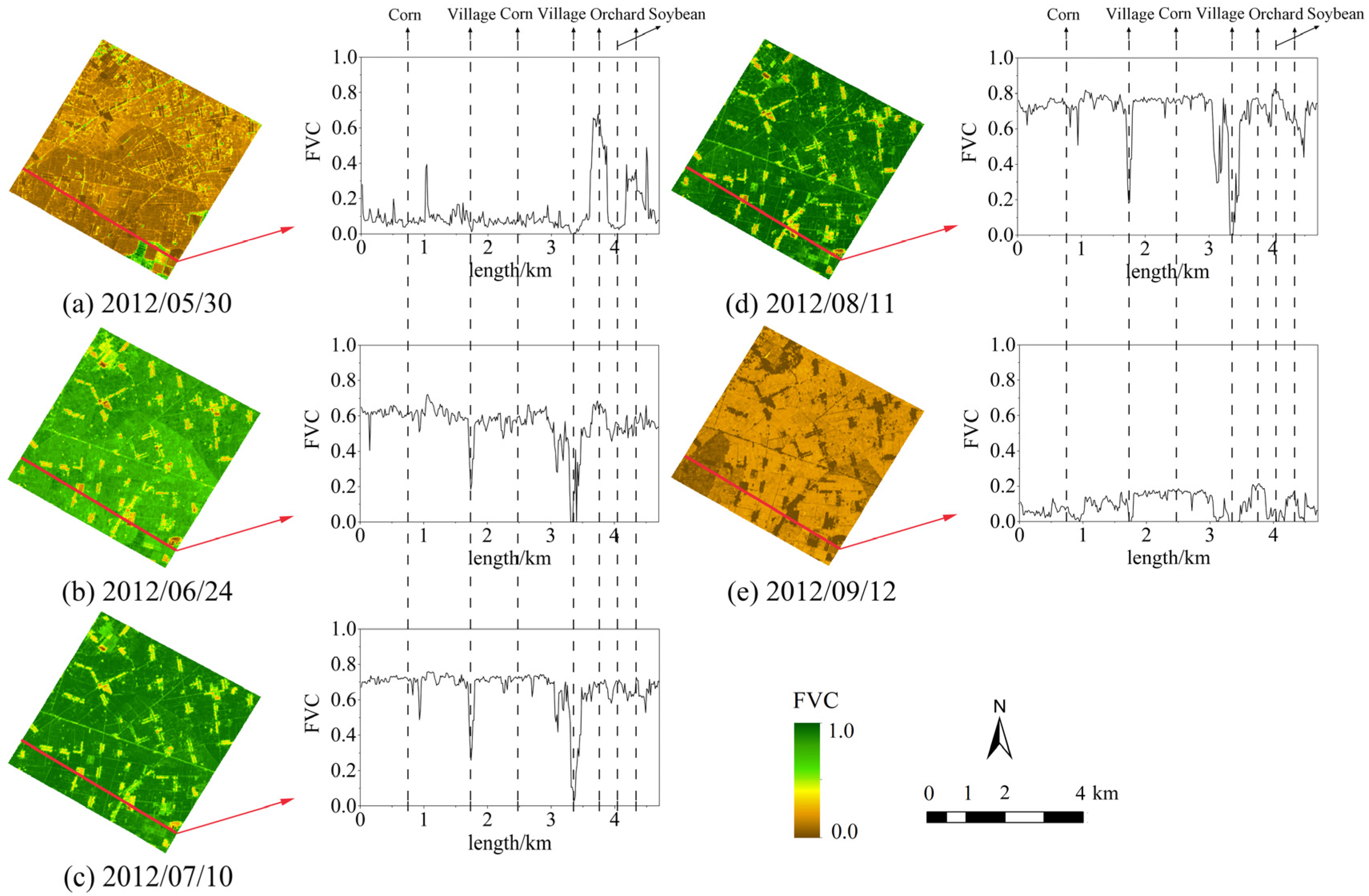
| Date | 30 May 2012 | 24 June 2012 | 10 July 2012 | 11 August 2012 | 12 September 2012 |
|---|---|---|---|---|---|
| Scene 1 | 0.068 | 0.102 | 0.104 | 0.130 | 0.053 |
| Scene 2 | 0.197 | 0.107 | 0.106 | 0.141 | 0.057 |
4.2. Sparsely Distributed Samples
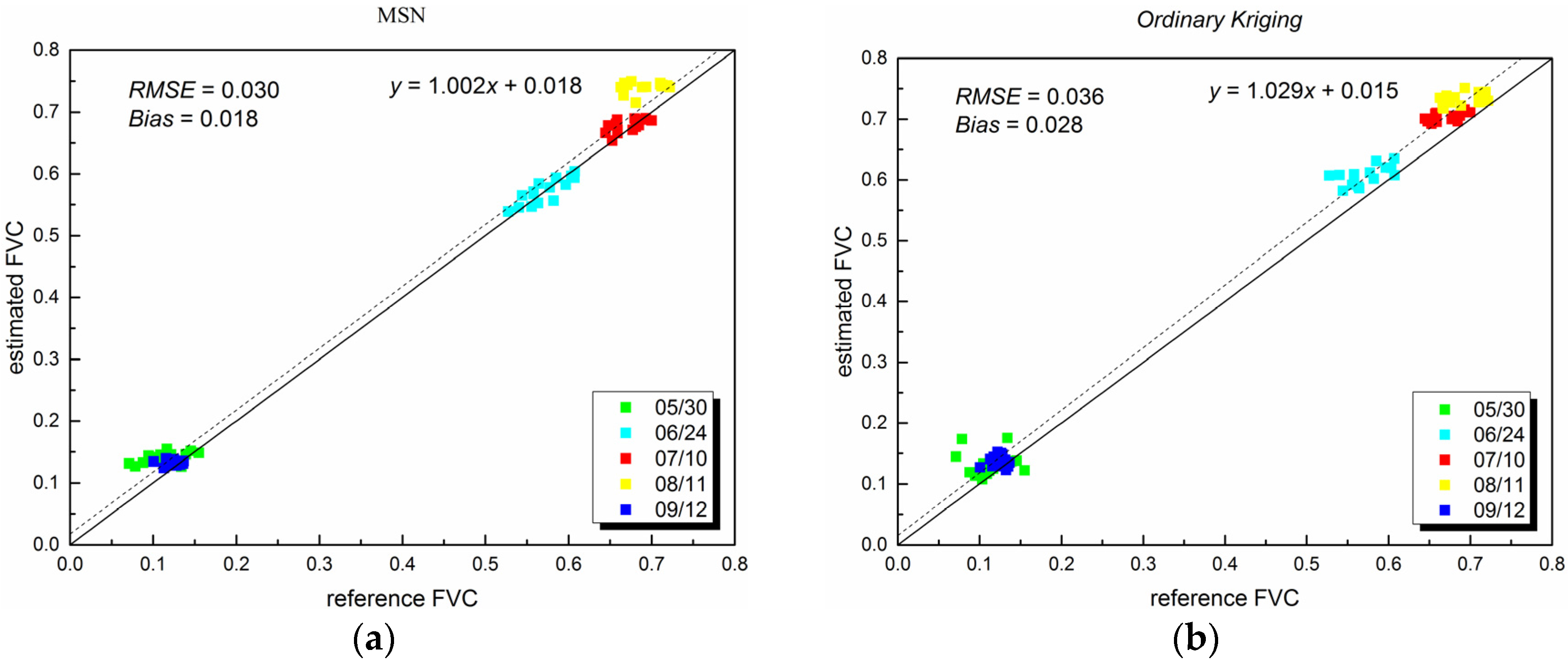
4.3. Densely Distributed Samples

4.4. Evaluation of Sampling Methods with Changing Number of Samples
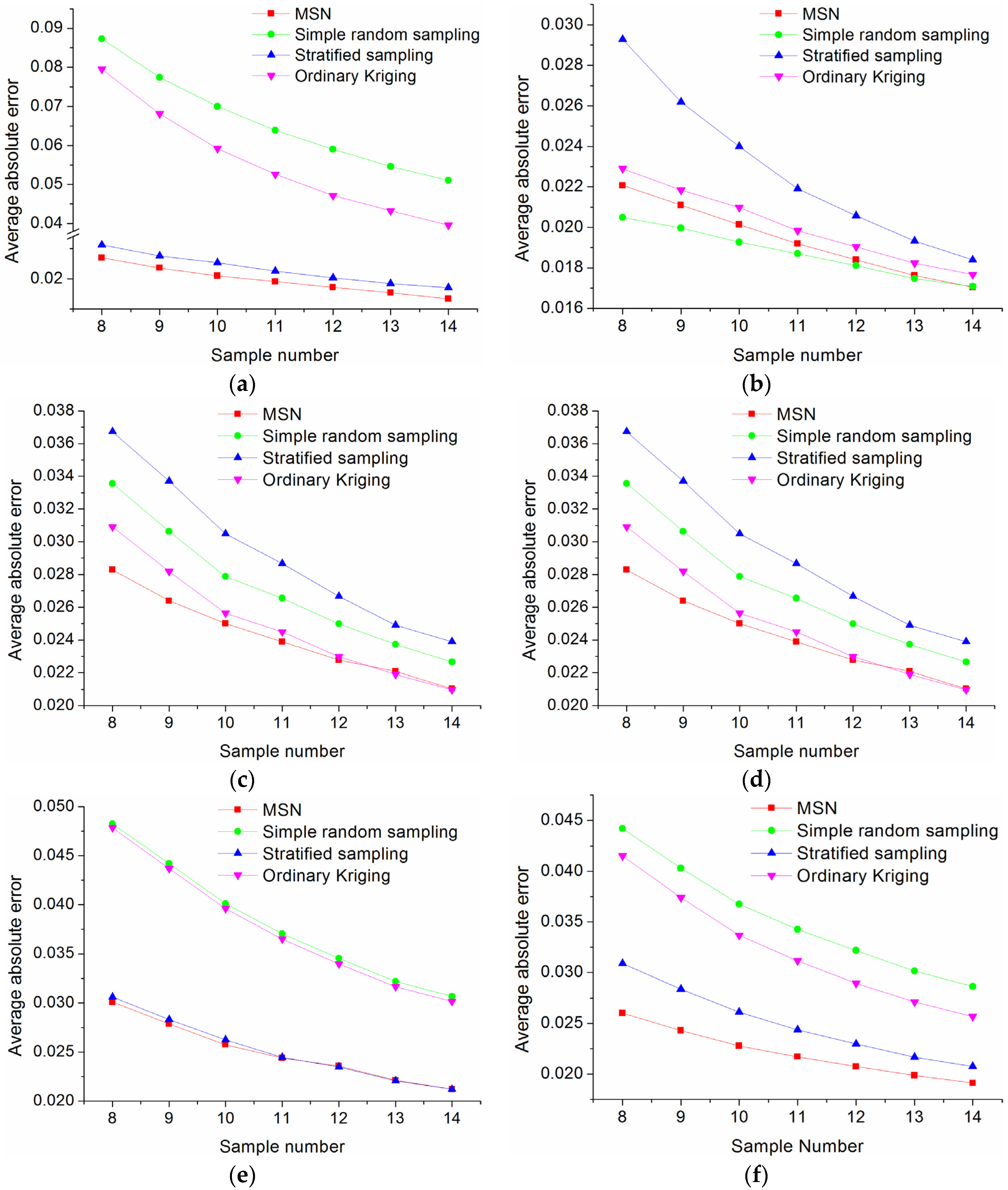
5. Discussions
| Date | 30 May 2012 | 24 June 2012 | 10 July 2012 | 11 August 2012 | 12 September 2012 |
|---|---|---|---|---|---|
| Scene 1 | |||||
| Bias_Pred | −0.004 | 0.000 | 0.006 | 0.011 | −0.005 |
| Bias_Real | 0.009 | 0.008 | 0.030 | 0.023 | 0.007 |
| Scene 2 | |||||
| Bias_Pred | 0.037 | 0.010 | 0.010 | 0.013 | 0.015 |
| Bias_Real | 0.000 | 0.034 | 0.027 | 0.007 | 0.008 |
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ge, Y.; Li, X.; Hu, M.G.; Wang, J.H.; Jin, R.; Wang, J.F.; Zhang, R.H. Technical specification for the validation of remote sensing products. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, XL-2/W1, 13–17. [Google Scholar] [CrossRef]
- Li, X.; Wang, S.G.; Ge, Y.; Jin, R.; Liu, S.M.; Ma, M.G.; Shi, W.Z.; Li, R.X.; Liu, Q.H. Development and experimental verification of key techniques to validate remote sensing products. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, XL-2/W1, 25–30. [Google Scholar] [CrossRef]
- Justice, C.O.; Tucker, C.J. The Sage Handbook of Remote Sensing:Coarse Spatial Resolution Optical Sensors; SAGE Publications Ltd.: London, UK, 2009; pp. 139–151. [Google Scholar]
- Baret, F.; Weiss, M.; Allard, D.; Garrigues, S.; Leroy, M.; Jeanjean, H.; Fernandes, R.; Myneni, R.; Privette, J.; Morisette, J. VALERI: A Network of Sites and a Methodology for the Validation of Medium Spatial Resolution Land Satellite Products. Available online: http://w3.avignon.inra.fr/valeri/documents/VALERI-RSESubmitted.pdf (accessed on 26 August 2015).
- Campbell, J.; Burrows, S.; Gower, S.; Cohen, W. Bigfoot Field Manual; Technical Report, DE2001-13418; NASA STI: Hampton, VA, USA, 1999. [Google Scholar]
- Buermann, W.; Helmlinger, M. SAFARI 2000 LAI and FPAR Measurements at Sua Pan, Botswana, Dry Season 2000; Oak Ridge National Laboratory Distributed Active Archive Cente: Oak Ridge, TN, USA. Available online: http:// daac.ornl.gov/S2K/safari.shtml (accessed on 26 August 2015).
- Morisette, J.T.; Baret, F.; Privette, J.L.; Myneni, R.B.; Nickeson, J.E.; Garrigues, S.; Shabanov, N.V.; Weiss, M.; Fernandes, R.A.; Leblanc, S.G.; et al. Validation of global moderate-resolution LAI products: A framework proposed within the ceos land product validation subgroup. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1804–1817. [Google Scholar] [CrossRef]
- Li, X.; Li, X.; Li, Z.; Ma, M.; Wang, J.; Xiao, Q.; Liu, Q.; Che, T.; Chen, E.; Yan, G.; et al. Watershed allied telemetry experimental research. J. Geophys. Res. Atmos. 2009, 114, D22103. [Google Scholar] [CrossRef]
- Li, X.; Cheng, G.; Liu, S.; Xiao, Q.; Ma, M.; Jin, R.; Che, T.; Liu, Q.; Wang, W.; Qi, Y.; et al. Heihe watershed allied telemetry experimental research (HiWATER): Scientific objectives and experimental design. Bull. Am. Meteorol. Soc. 2013, 94, 1145–1160. [Google Scholar] [CrossRef]
- Mu, X.; Huang, S.; Chen, Y. HiWATER: Dataset of Fractional Vegetation Cover in the Middle Reaches of the Heihe River Basin; Beijing Normal University: Beijing, China; Cold and Arid Regions Environmental and Engineering Research Institute, Chinese Academy of Sciences: Lanzhou, China, 2013. [Google Scholar] [CrossRef]
- Yan, G.; Mu, X.; Liu, Y. Chapter 13—Fractional vegetation cover. In Advanced Remote Sensing; Liang, S., Li, X., Wang, J., Eds.; Academic Press: Boston, MA, USA, 2012; pp. 415–438. [Google Scholar]
- García-Haro, F.J.; Camacho-de Coca, F.; Miralles, J.M. Inter-Comparison of SEVIRI/MSG and MERIS/ENVISAT Biophysical Products over Europe and Africa. In Proceedings of the 2nd MERIS/(A) ATSR User Workshop, Frascati, Italy, 22–26 September 2008.
- Fillol, E.; Baret, F.; Weiss, M.; Dedieu, G.; Demarez, V.; Gouaux, P.; Ducrot, D. Cover fraction estimation from high resolution SPOT HRV & HRG and medium resolution SPOT-VEGETATION sensors. Validation and comparison over South-west France. In Proceedings of the Second International Symposium on Recent Advances in Quantitative Remote Sensing, Torrent (Valencia), Spain, 25–29 September 2006; pp. 659–663.
- Mu, X.; Huang, S.; Ren, H.; Yan, G.; Song, W.; Ruan, G. Validating GEOV1 fractional vegetation cover derived from coarse-resolution remote sensing images over croplands. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 439–446. [Google Scholar] [CrossRef]
- Rooney, D.E. Human Cytogenetic: Constitutional Analysis, 3rd ed.; Oxford University Press: New York, USA, 2001; Volume 1. [Google Scholar]
- Black, T.R. Doing Quantitative Research in the Social Sciences: An Integrated Approach to Research Design, Measurement and Statistics; SAGE: London, UK, 1999; p. 118. [Google Scholar]
- Daniel, J. Sampling Essentials: Practical Guidelines for Making Sampling Choices; SAGE: Los Angeles, CA, USA, 2012; pp. 125–140. [Google Scholar]
- Tobler, W.R. A computer movie simulating urban growth in the detroit region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Cressie, N. Statistics for spatial data. Terra Nova 1992, 4, 613–617. [Google Scholar] [CrossRef]
- Haining, R.P. Spatial Data Analysis: Theory and Practice; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Wang, J.-F.; Stein, A.; Gao, B.-B.; Ge, Y. A review of spatial sampling. Spat. Stat. 2012, 2, 1–14. [Google Scholar] [CrossRef]
- Groenigen, J.W.V.; Stein, A. Constrained optimization of spatial sampling using continuous simulated annealing. J. Environ. Qual. 1998, 27, 1078–1086. [Google Scholar] [CrossRef]
- Brus, D.J.; Heuvelink, G.B.M. Optimization of sample patterns for universal kriging of environmental variables. Geoderma 2007, 138, 86–95. [Google Scholar] [CrossRef]
- Hu, M.-G.; Wang, J.-F. A spatial sampling optimization package using MSN theory. Environ. Model. Softw. 2011, 26, 546–548. [Google Scholar]
- Hu, M.-G.; Wang, J.-F.; Zhao, Y.; Jia, L. A B-SHADE based best linear unbiased estimation tool for biased samples. Environ. Model. Softw. 2013, 48, 93–97. [Google Scholar]
- Wang, G.; Gertner, G.; Anderson, A.B. Sampling design and uncertainty based on spatial variability of spectral variables for mapping vegetation cover. Int. J. Remote Sens. 2005, 26, 3255–3274. [Google Scholar] [CrossRef]
- Brus, D.J.; de Gruijter, J.J. Random sampling or geostatistical modelling? Choosing between design-based and model-based sampling strategies for soil (with discussion). Geoderma 1997, 80, 1–44. [Google Scholar] [CrossRef]
- Groenigen, J.W.V.; Siderius, W.; Stein, A. Constrained optimisation of soil sampling for minimisation of the kriging variance. Geoderma 1999, 87, 239–259. [Google Scholar] [CrossRef]
- Atkinson, P.M.; Lloyd, C.D. Non-stationary variogram models for geostatistical sampling optimisation: An empirical investigation using elevation data. Comput. Geosci. 2007, 33, 1285–1300. [Google Scholar]
- Yeh, H.-C.; Chen, Y.-C.; Wei, C.; Chen, R.-H. Entropy and kriging approach to rainfall network design. Paddy Water Environ. 2011, 9, 343–355. [Google Scholar] [CrossRef]
- Moreno, J. Sentinel-2 and Fluorescence Experiment (sen2flex) Final Report. Available online: http://earth.esa.int/c/document_library/get_file?folderId=21020&name=DLFE-395.pdf (accessed on 26 August 2015).
- Rui, J.; Xin, L.; Baoping, Y.; Xiuhong, L.; Wanmin, L.; Mingguo, M.; Jianwen, G.; Jian, K.; Zhongli, Z.; Shaojie, Z. A nested ecohydrological wireless sensor network for capturing the surface heterogeneity in the midstream areas of the Heihe River Basin, China. IEEE Geosci. Remote Sens. Lett. 2014, 11, 2015–2019. [Google Scholar]
- Ge, Y.; Wang, J.H.; Heuvelink, G.B.M.; Jin, R.; Li, X.; Wang, J.F. Sampling design optimization of a wireless sensor network for monitoring ecohydrological processes in the Babao River Basin, China. Int. J. Geogr. Inf. Sci. 2014, 29, 92–110. [Google Scholar] [CrossRef]
- Wang, J.-F.; Christakos, G.; Hu, M.-G. Modeling spatial means of surfaces with stratified nonhomogeneity. IEEE Trans. Geosci. Remote Sens. 2009, 47, 4167–4174. [Google Scholar] [CrossRef]
- Zhong, B.; Yang, A.; Nie, A.; Yao, Y.; Zhang, H.; Wu, S.; Liu, Q. Finer resolution land-cover mapping using multiple classifiers and multisource remotely sensed data in the heihe river basin. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015. [Google Scholar] [CrossRef]
- Liang, S.; Li, X.; Wang, J. (Eds.) Advanced Remote Sensing: Terrestrial Information Extraction and Applications; Academic Press: Oxford, UK, 2012.
- Liu, Y.; Mu, X.; Wang, H.; Yan, G. A novel method for extracting green fractional vegetation cover from digital images. J. Veg. Sci. 2012, 23, 406–418. [Google Scholar] [CrossRef]
- Zhao, J.; Xie, D.; Mu, X.; Liu, Y.; Yan, G. Accuracy evaluation of the ground-based fractional vegetation cover measurement by using simulated images. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Munich, Germany, 22–27 July 2012; pp. 3347–3350.
- Vermote, E.F.; Tanre, D.; Deuze, J.L.; Herman, M.; Morcette, J.J. Second simulation of the satellite signal in the solar spectrum, 6S: An overview. IEEE Trans. Geosci. Remote Sens. 1997, 35, 675–686. [Google Scholar] [CrossRef]
- Xiao, J.; Moody, A. A comparison of methods for estimating fractional green vegetation cover within a desert-to-upland transition zone in central New Mexico, USA. Remote Sens. Environ. 2005, 98, 237–250. [Google Scholar] [CrossRef]
- Choudhury, B.J.; Ahmed, N.U.; Idso, S.B.; Reginato, R.J.; Daughtry, C.S.T. Relations between evaporation coefficients and vegetation indices studied by model simulations. Remote Sens. Environ. 1994, 50, 1–17. [Google Scholar] [CrossRef]
- Li, F.; Kustas, W.P.; Prueger, J.H.; Neale, C.M.U.; Jackson, T.J. Utility of remote sensing–based two-source energy balance model under low- and high-vegetation cover conditions. J. Hydrometeorol. 2005, 6, 878–891. [Google Scholar] [CrossRef]
- Isaaks, E.H.; Srivastava, R.M. Applied Geostatistics; Oxford University Press: Oxon, UK, 1989. [Google Scholar]
- Wiegand, H.; Kish, L. Survey Sampling; John Wiley & Sons, Inc.: New York, USA, 1968. [Google Scholar]
- Wu, H.; Tang, B.-H.; Li, Z.-L. Impact of nonlinearity and discontinuity on the spatial scaling effects of the leaf area index retrieved from remotely sensed data. Int. J. Remote Sens. 2012, 34, 3503–3519. [Google Scholar] [CrossRef]
- Becker, F.; Li, Z.L. Surface temperature and emissivity at various scales: Definition, measurement and related problems. Remote Sens. Rev. 1995, 12, 225–253. [Google Scholar] [CrossRef]
- Nilson, T. Approximate analytical methods for calculating the reflection functions of leaf canopies in remote sensing applications. In Photon-Vegetation Interactions; Myneni, R., Ross, J., Eds.; Springer: Berlin/Heidelberg, Germany, 1991; pp. 161–190. [Google Scholar]
- Zhang, X.; Yan, G.; Li, Q.; Li, Z.L.; Wan, H.; Guo, Z. Evaluating the fraction of vegetation cover based on NDVI spatial scale correction model. Int. J. Remote Sens. 2006, 27, 5359–5372. [Google Scholar] [CrossRef]
- Jiang, Z.; Huete, A.R.; Chen, J.; Chen, Y.; Li, J.; Yan, G.; Zhang, X. Analysis of NDVI and scaled difference vegetation index retrievals of vegetation fraction. Remote Sens. Environ. 2006, 101, 366–378. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mu, X.; Hu, M.; Song, W.; Ruan, G.; Ge, Y.; Wang, J.; Huang, S.; Yan, G. Evaluation of Sampling Methods for Validation of Remotely Sensed Fractional Vegetation Cover. Remote Sens. 2015, 7, 16164-16182. https://doi.org/10.3390/rs71215817
Mu X, Hu M, Song W, Ruan G, Ge Y, Wang J, Huang S, Yan G. Evaluation of Sampling Methods for Validation of Remotely Sensed Fractional Vegetation Cover. Remote Sensing. 2015; 7(12):16164-16182. https://doi.org/10.3390/rs71215817
Chicago/Turabian StyleMu, Xihan, Maogui Hu, Wanjuan Song, Gaiyan Ruan, Yong Ge, Jinfeng Wang, Shuai Huang, and Guangjian Yan. 2015. "Evaluation of Sampling Methods for Validation of Remotely Sensed Fractional Vegetation Cover" Remote Sensing 7, no. 12: 16164-16182. https://doi.org/10.3390/rs71215817
APA StyleMu, X., Hu, M., Song, W., Ruan, G., Ge, Y., Wang, J., Huang, S., & Yan, G. (2015). Evaluation of Sampling Methods for Validation of Remotely Sensed Fractional Vegetation Cover. Remote Sensing, 7(12), 16164-16182. https://doi.org/10.3390/rs71215817