Estimation of CO2 Sequestration by the Forests in Japan by Discriminating Precise Tree Age Category using Remote Sensing Techniques
Abstract
:1. Introduction
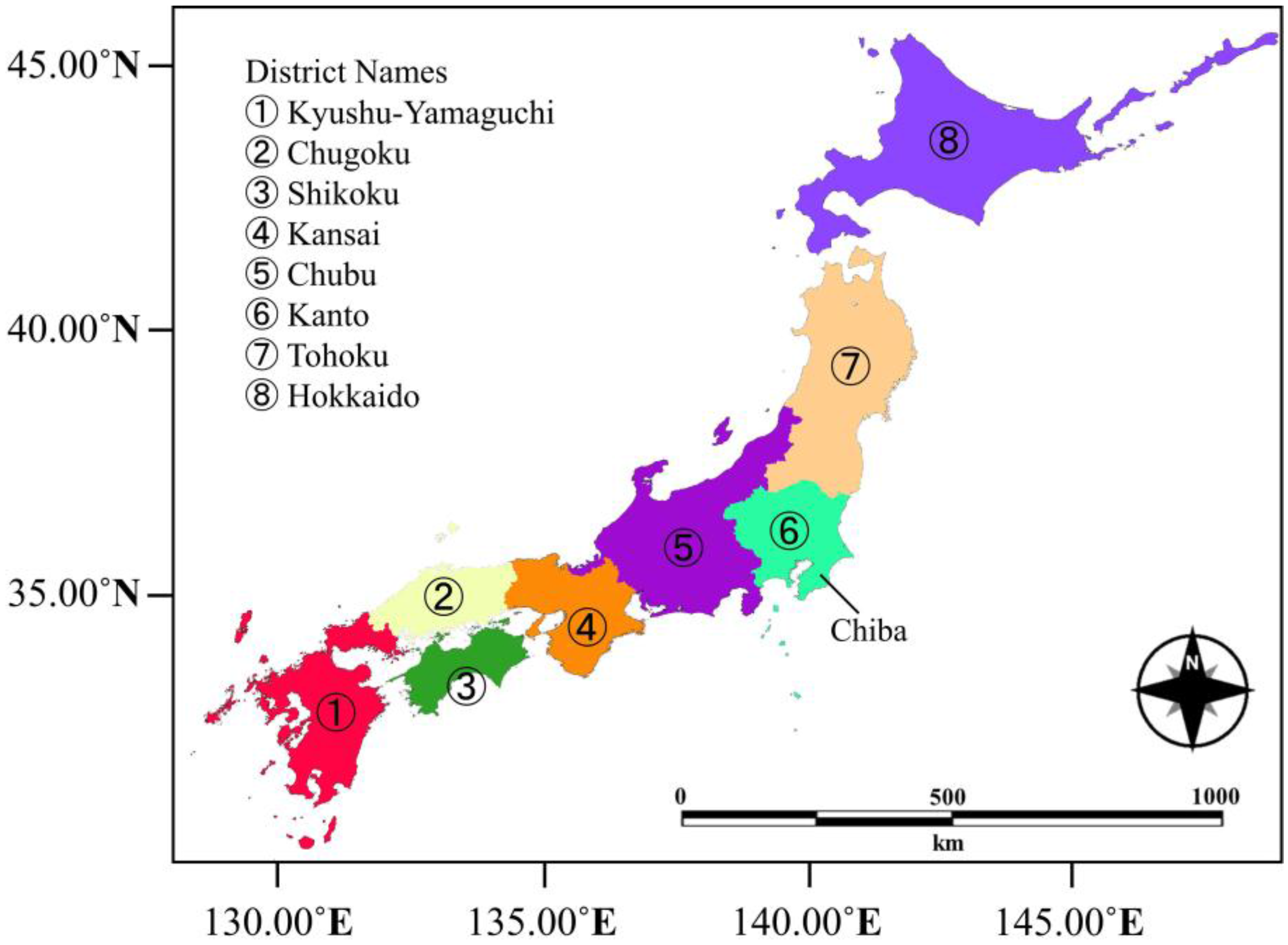
2. Study Area
3. Methods and Data
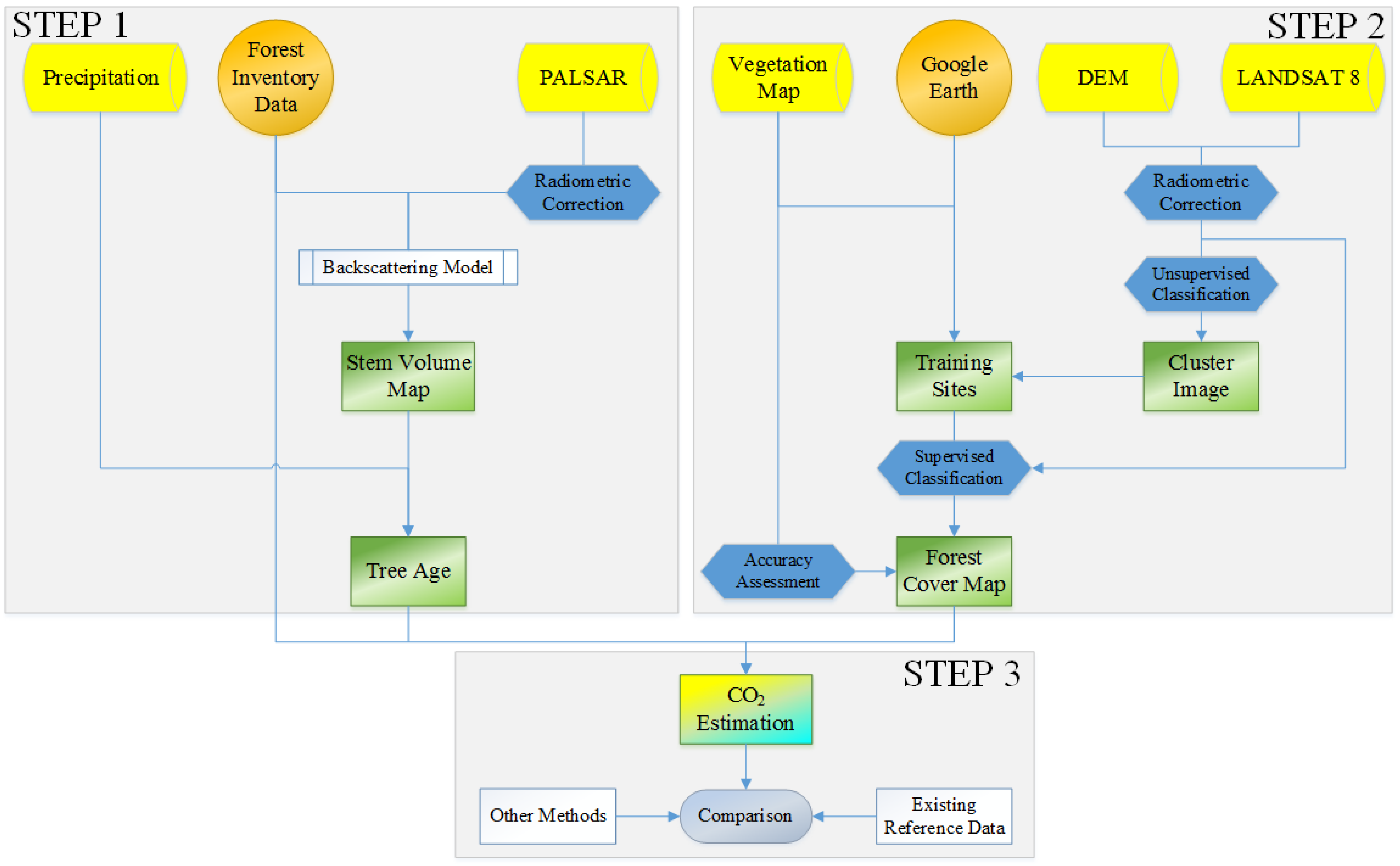
3.1. L-Band PALSAR for Volume Mapping
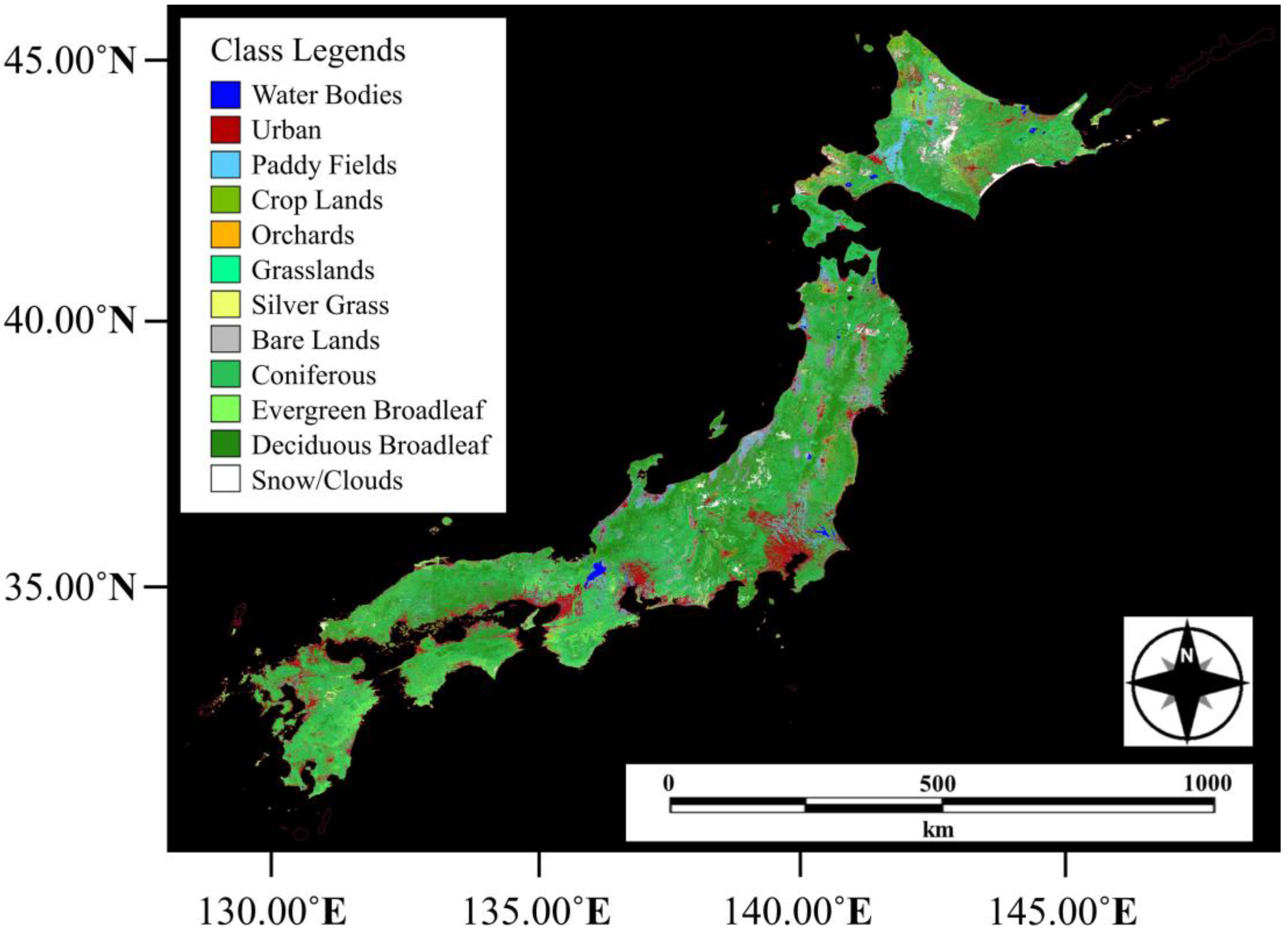
3.2. Land Cover Mapping of Japan
| Landsat OLI Data Sets | Landsat OLI Data Sets | ||||||
|---|---|---|---|---|---|---|---|
| Region | Path | Row | Date | Region | Path | Row | Date |
| Kyushu Yamaguchi | 112 | 36 | 2 May 2014 | Tohoku | 106 | 33 | 8 May 2014 |
| 112 | 37 | 13 April 2013 | 107 | 31 | 29 April 2014 | ||
| 112 | 38 | 13 April 2013 | 107 | 32 | 19 October 2013 | ||
| 113 | 37 | 23 April 2014 | 107 | 33 | 17 September 2013 | ||
| 113 | 38 | 29 October 2013 | 108 | 31 | 20 April 2014 | ||
| Chugoku Shikoku Kansai | 110 | 36 | 17 March 2014 | 108 | 32 | 4 June 2013 | |
| 110 | 37 | 17 March 2014 | 108 | 33 | 4 June 2014 | ||
| 111 | 35 | 24 May 2013 | 108 | 34 | 4 June 2014 | ||
| 111 | 36 | 24 May 2013 | Hokkaido | 105 | 30 | 2 June 2014 | |
| 111 | 37 | 11 May 2014 | 106 | 29 | 25 June 2014 | ||
| 112 | 35 | 19 August 2013 | 106 | 30 | 25 June 2014 | ||
| Chubu | 108 | 35 | 7 August 2013 | 106 | 31 | 28 October 2013 | |
| 108 | 36 | 7 August 2013 | 107 | 29 | 19 October 2013 | ||
| 109 | 35 | 14 August 2013 | 107 | 30 | 19 October 2013 | ||
| 109 | 36 | 14 August 2013 | 108 | 28 | 10 October 2013 | ||
| 109 | 37 | 17 October 2013 | 108 | 29 | 10 October 2013 | ||
| 110 | 35 | 17 May 2013 | 108 | 30 | 10 October 2013 | ||
| Kanto | 107 | 34 | 17 September 2013 | ||||
| 107 | 35 | 17 September 2013 | |||||
| 107 | 36 | 17 September 2013 | |||||
| 109 | 34 | 14 August 2013 | |||||
3.3. Estimating CO2 Sequestration from the Forests of Japan
4. Results
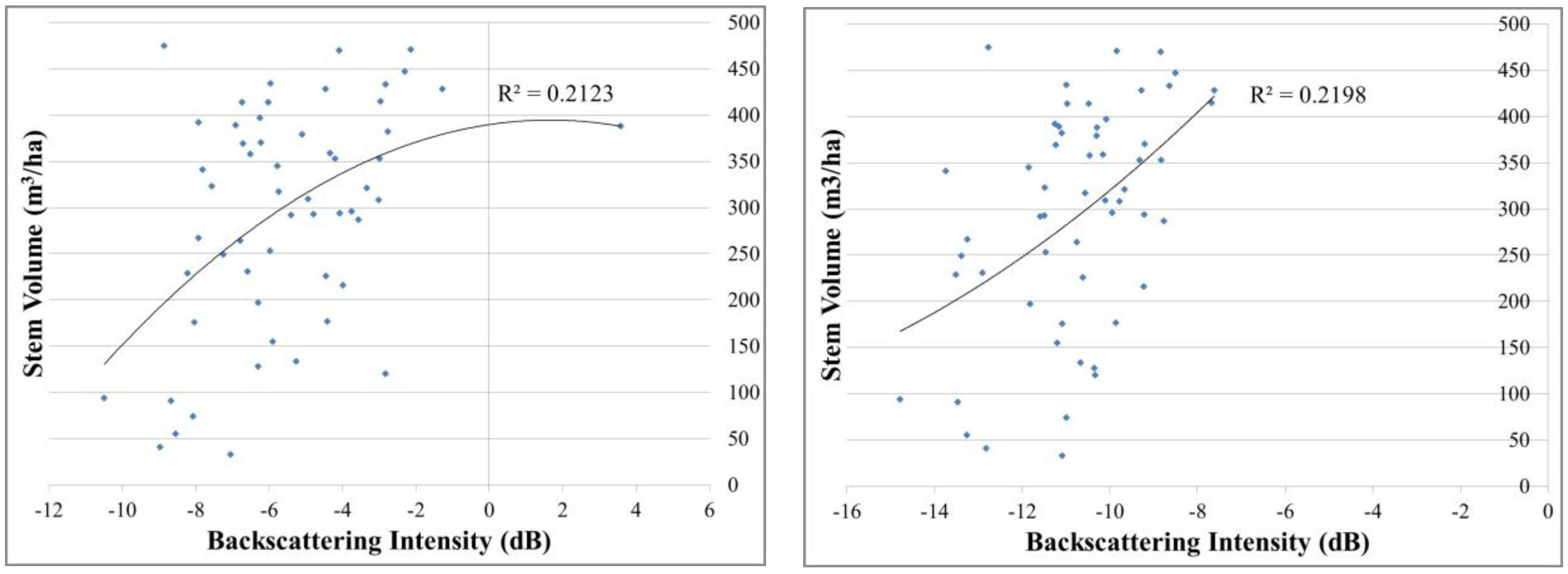
4.1. Stem Volume Modeling and Mapping
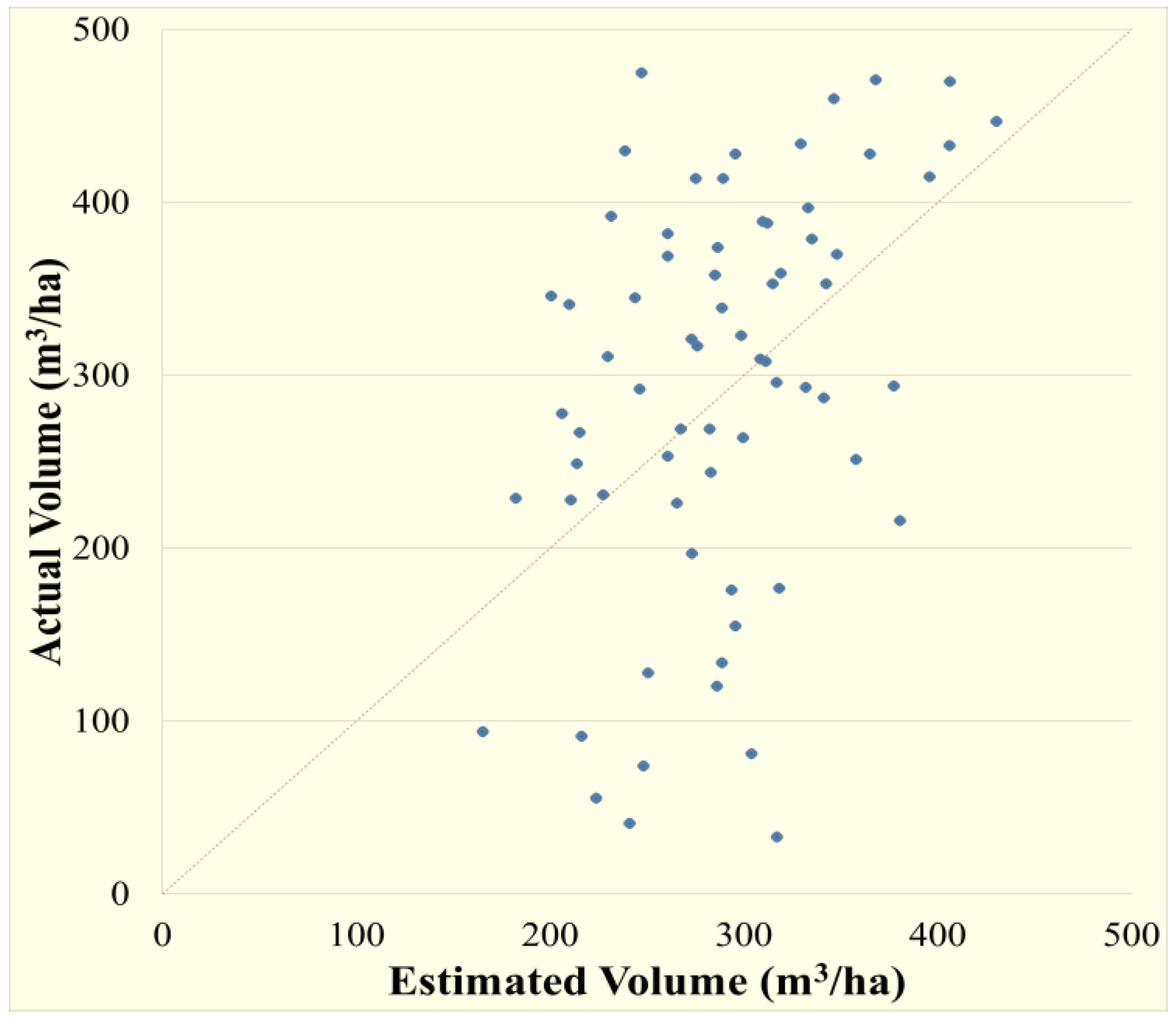

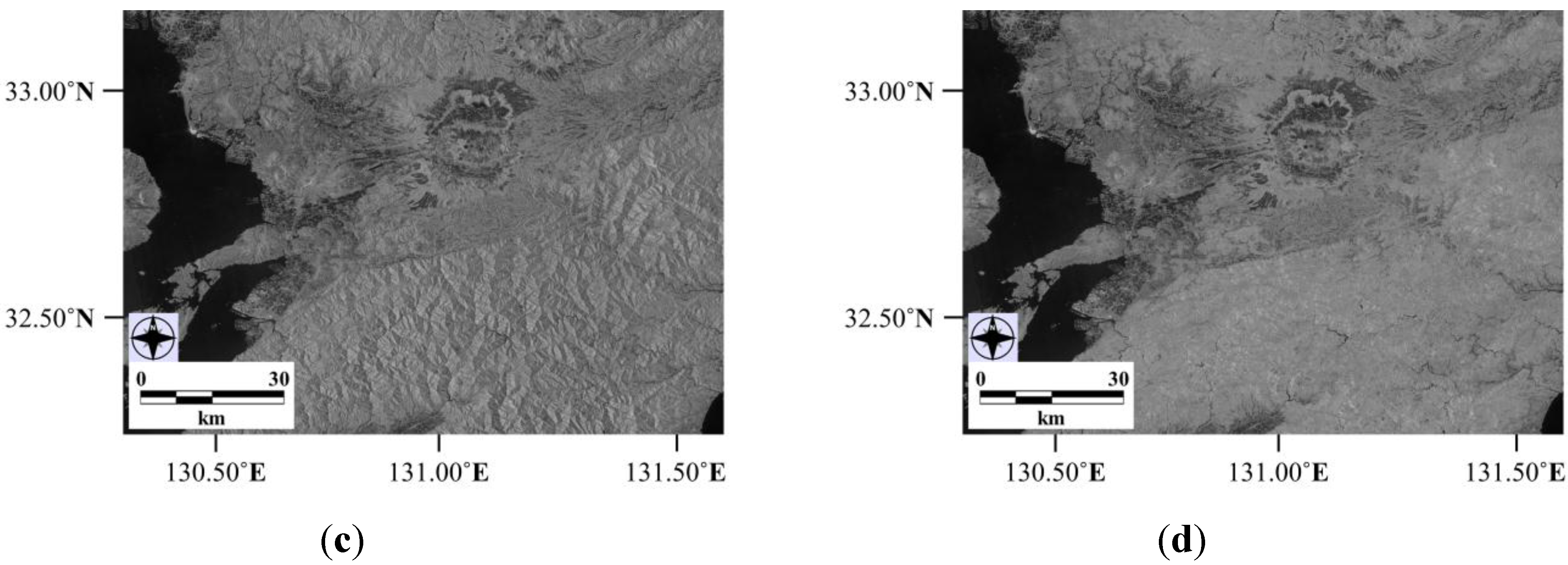
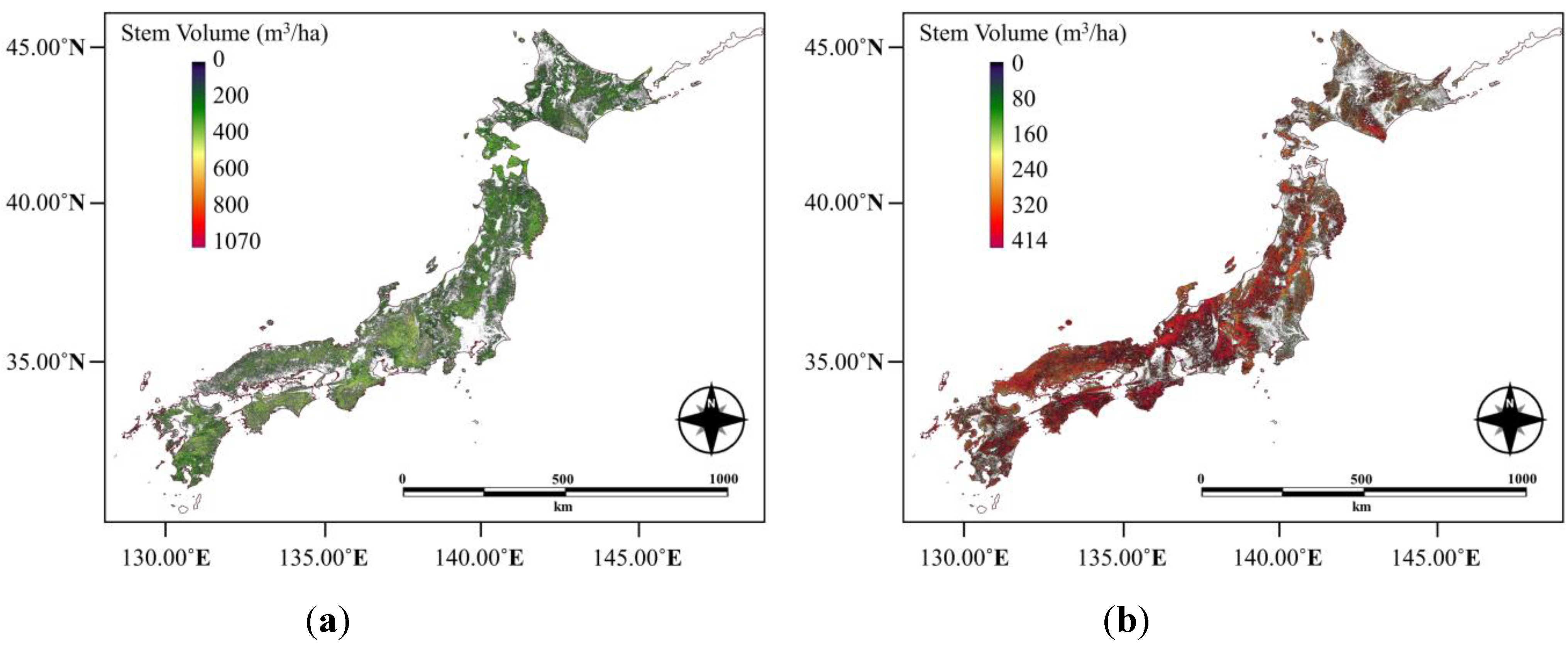
4.2. Land Cover Map and ItsAccuracy
| KIA = 0.65 | Reference | ||||||
|---|---|---|---|---|---|---|---|
| Coniferous | Evergreen Broadleaf | Deciduous Broadleaf | Others | Total | ErrorC | ||
| Classified | Coniferous | 852 | 253 | 149 | 24 | 1278 | 0.3334 |
| Evergreen Broadleaf | 41 | 533 | 113 | 30 | 717 | 0.2566 | |
| Deciduous Broadleaf | 59 | 200 | 680 | 54 | 993 | 0.3152 | |
| Others | 48 | 14 | 58 | 892 | 1012 | 0.1186 | |
| Total | 1000 | 1000 | 1000 | 1000 | 4000 | ||
| ErrorO | 0.1480 | 0.4670 | 0.3200 | 0.1080 | 0.2607 | ||
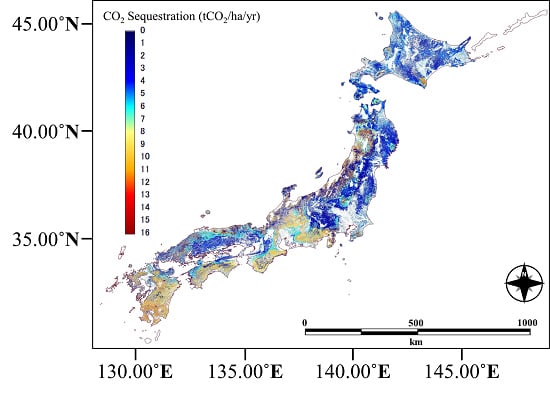
4.3. CO2 Sequestration
4.3.1. CO2 Sequestration by Forest Types and Ages
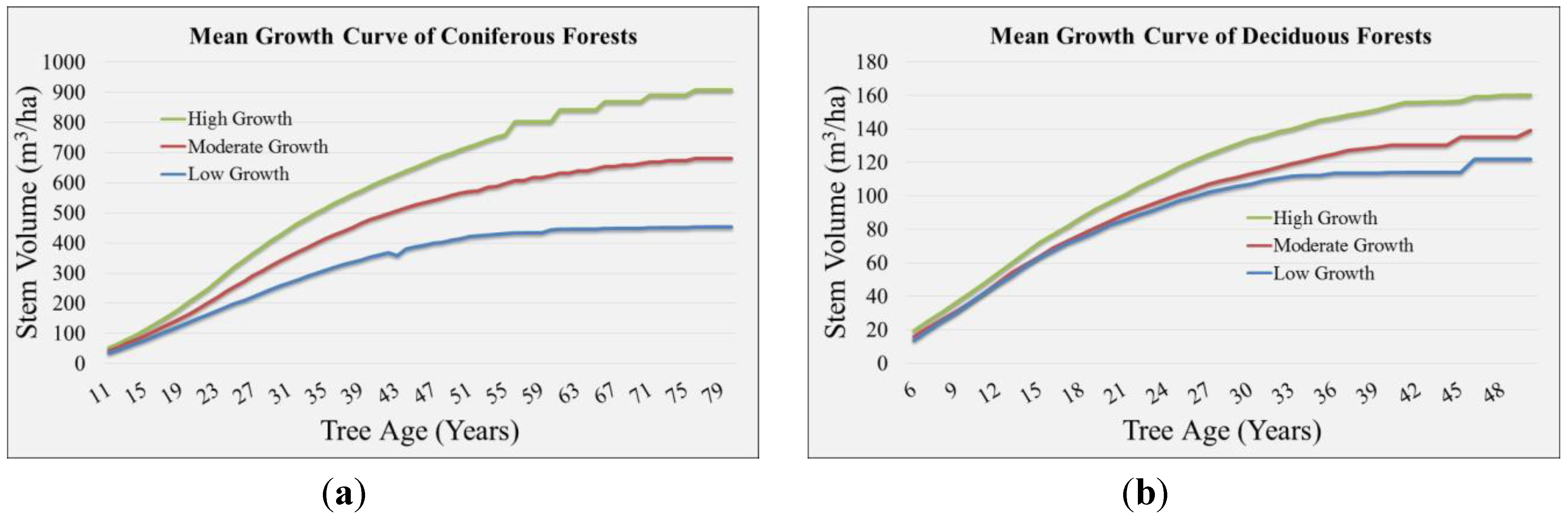
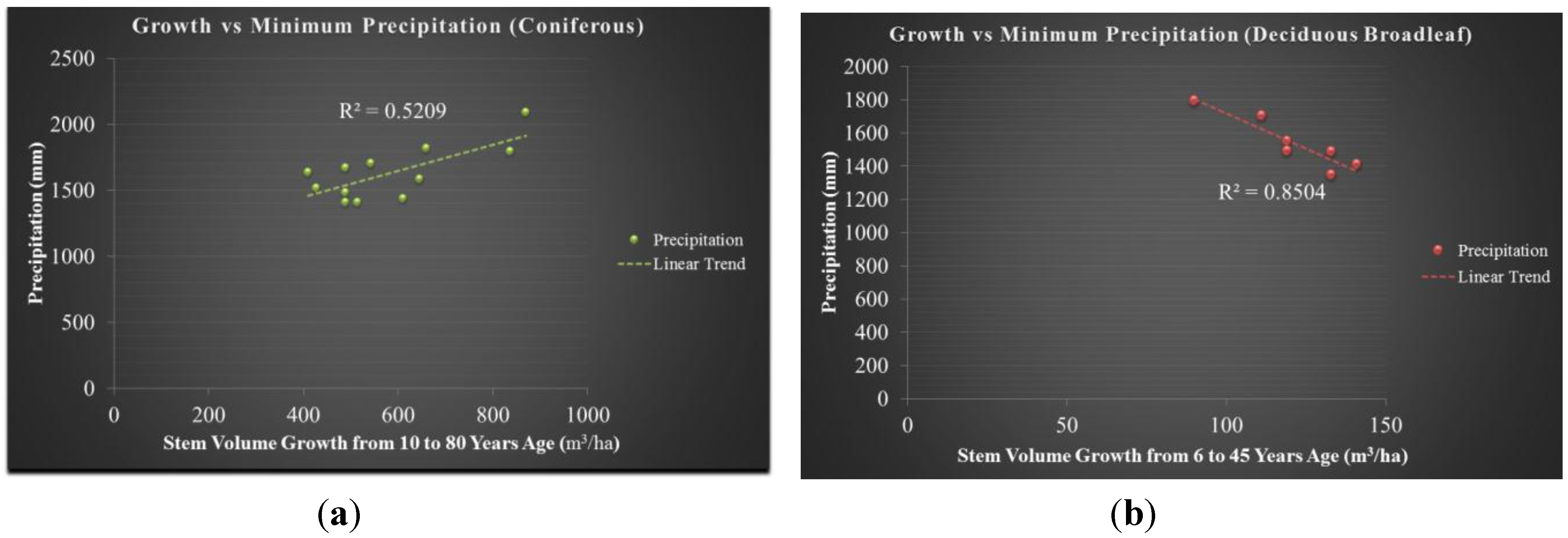
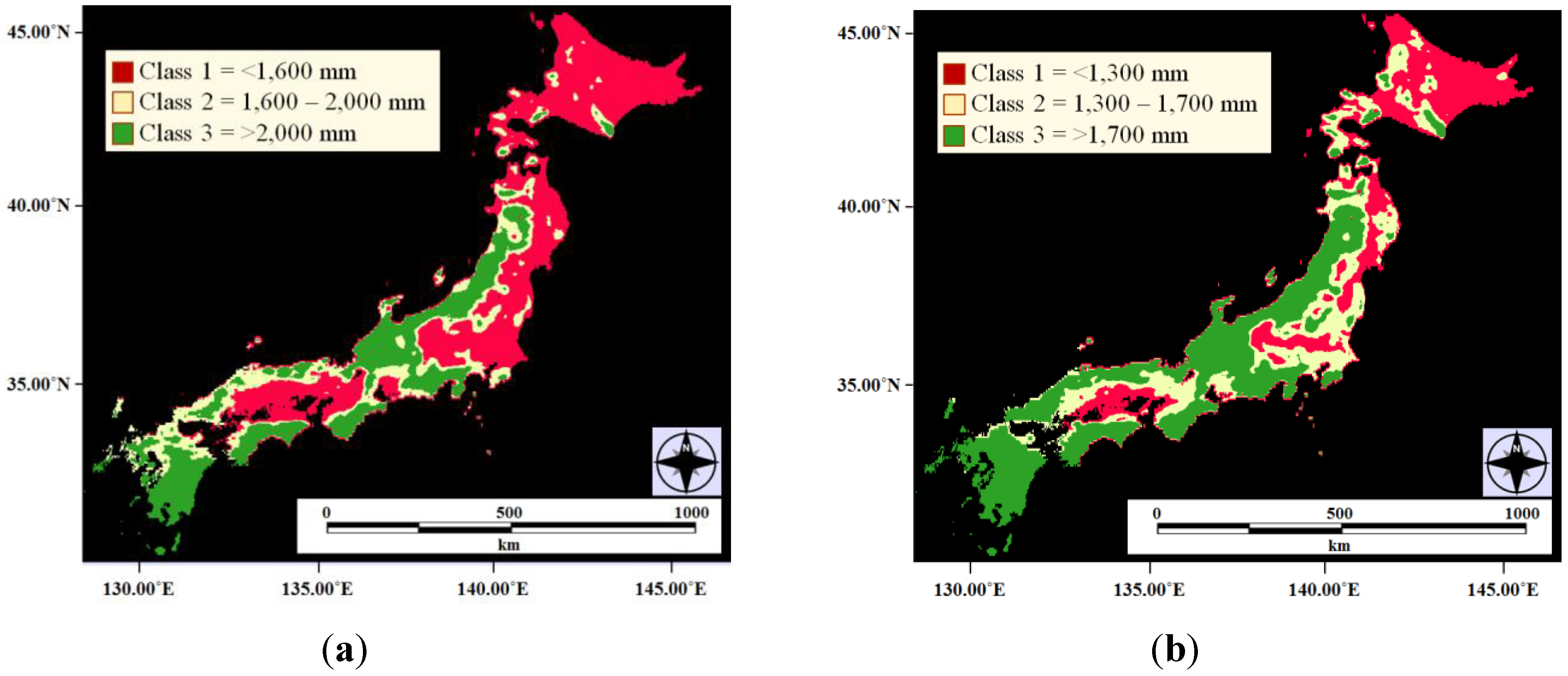
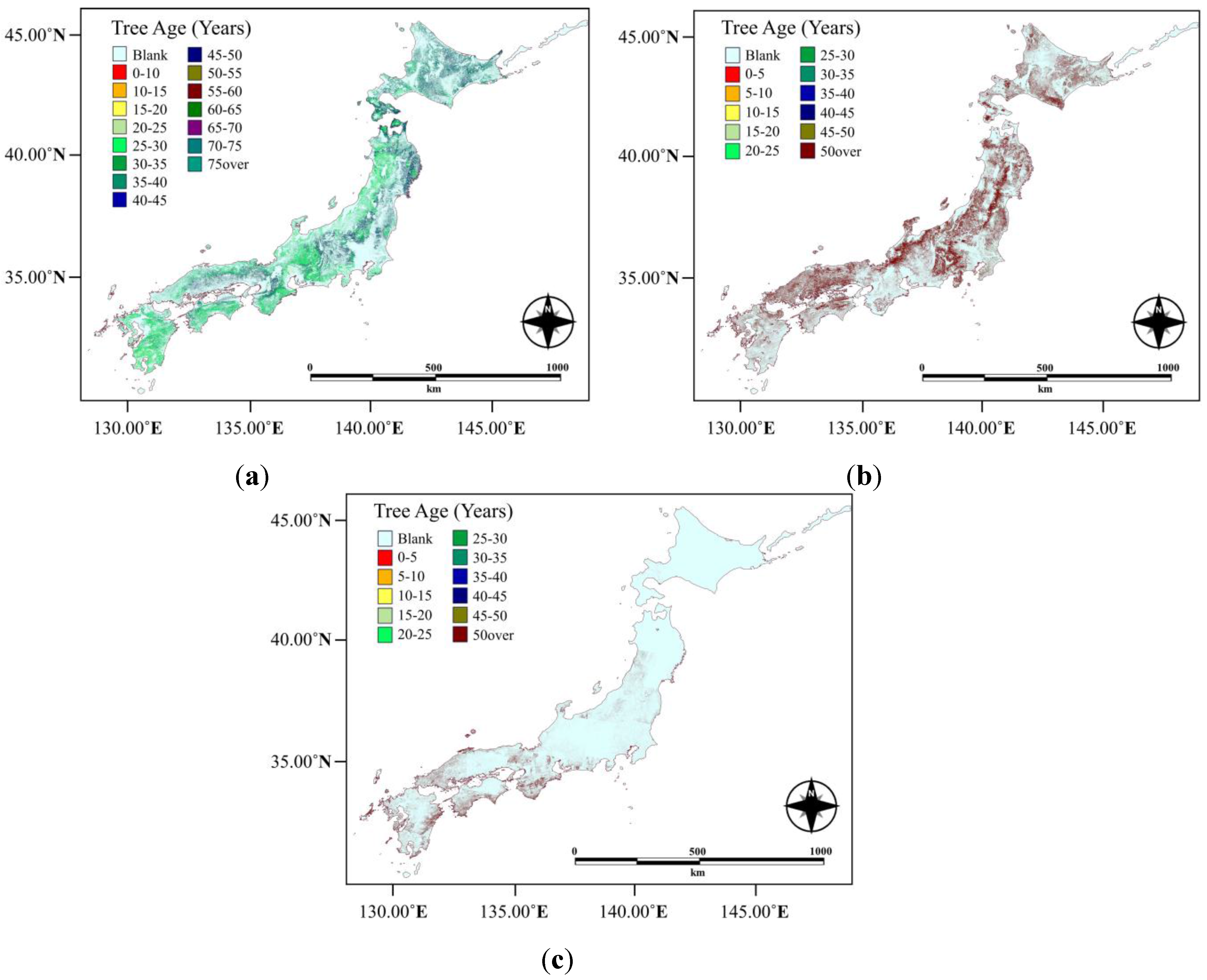
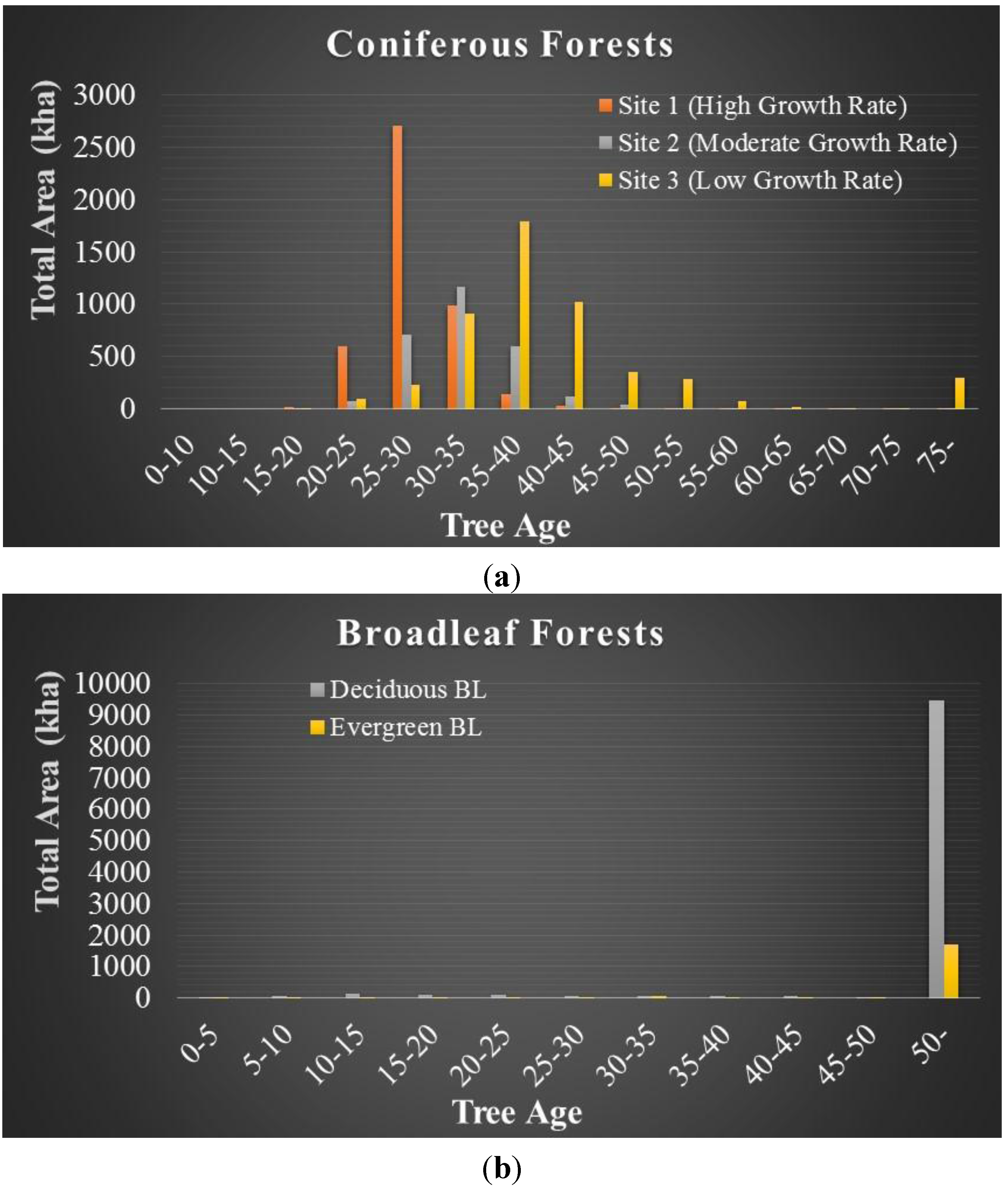
4.3.2. CO2 Sequestration by the Forests of Japan
| Forest Type | Age (years) | t∙CO2/ha/yr | Area (ha) | Total Mt∙CO2 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Site 1 | Site 2 | Site 3 | Site 1 | Site 2 | Site 3 | Site 1 | Site 2 | Site 3 | ||
| Coniferous | 0–5 | 3.38 | 2.56 | 1.70 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5–10 | ||||||||||
| 10–15 | 13.23 | 9.57 | 6.20 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 15–20 | 16.11 | 11.45 | 6.76 | 22,826 | 6,575 | 7,332 | 0.37 | 0.08 | 0.05 | |
| 20–25 | 12.21 | 8.49 | 5.83 | 592,573 | 69,564 | 97,357 | 7.24 | 0.59 | 0.57 | |
| 25–30 | 10.05 | 7.83 | 5.34 | 2,700,597 | 705,043 | 230,650 | 27.15 | 5.52 | 1.23 | |
| 30–35 | 8.16 | 6.74 | 5.21 | 989,309 | 1,168,617 | 904,797 | 8.07 | 7.87 | 4.72 | |
| 35–40 | 6.42 | 5.87 | 4.89 | 137,687 | 600,268 | 1,791,110 | 0.88 | 3.52 | 8.76 | |
| 40–45 | 5.61 | 5.07 | 4.41 | 31,225 | 122,804 | 1,023,606 | 0.18 | 0.62 | 4.51 | |
| 45–50 | 5.41 | 4.63 | 3.78 | 7,835 | 38,352 | 349,890 | 0.04 | 0.18 | 1.32 | |
| 50–55 | 4.84 | 4.20 | 3.30 | 2,179 | 5,265 | 287,697 | 0.01 | 0.02 | 0.95 | |
| 55–60 | 4.08 | 3.61 | 2.91 | 684 | 7,685 | 78,352 | 0.00 | 0.03 | 0.23 | |
| 60–65 | 3.35 | 2.92 | 2.29 | 183 | 877.37 | 15,174 | 0.00 | 0.00 | 0.03 | |
| 65–70 | 2.47 | 1.78 | 1.40 | 1.57 | 1,986 | 9,501 | 0.00 | 0.00 | 0.01 | |
| 70–75 | 2.17 | 1.41 | 1.03 | 0.79 | 190.96 | 9,136 | 0.00 | 0.00 | 0.01 | |
| over 75 | 1.18 | 0.42 | 0.42 | 30.57 | 1,098 | 296,715 | 0.00 | 0.00 | 0.13 | |
| Total | 4,485,131 | 2,728,325 | 5,101,317 | 43.95 | 18.44 | 22.52 | ||||
| Overall | 12,314,773 | 85.0 | ||||||||
| Forest Type | Age (years) | t∙CO2/ha/yr | Area (ha) | Total Mt∙CO2 |
|---|---|---|---|---|
| Deciduous Broadleaf | 0–5 | 2.91 | 38,756 | 0.11 |
| 5–10 | 6.33 | 58,850 | 0.37 | |
| 10–15 | 6.50 | 151,418 | 0.98 | |
| 15–20 | 6.89 | 91,892 | 0.63 | |
| 20–25 | 5.96 | 90,147 | 0.54 | |
| 25–30 | 5.20 | 78,751 | 0.41 | |
| 30–35 | 5.09 | 62,852 | 0.32 | |
| 35–40 | 3.79 | 48,437 | 0.18 | |
| 40–45 | 3.52 | 57,704 | 0.20 | |
| 45–50 | 3.13 | 36,219 | 0.11 | |
| over 50 | 1.87 | 9,475,569 | 17.74 | |
| Total | 10,190,332 | 21.61 | ||
| Forest Type | Age (years) | t∙CO2/ha/yr | Area (ha) | Total Mt∙CO2 |
|---|---|---|---|---|
| Evergreen Broadleaf | 0–5 | 2.46 | 35,540 | 0.09 |
| 5–10 | 6.43 | 33,957 | 0.22 | |
| 10–15 | 6.57 | 15,752 | 0.10 | |
| 15–20 | 6.93 | 17,987 | 0.12 | |
| 20–25 | 6.27 | 20,771 | 0.13 | |
| 25–30 | 5.32 | 23,800 | 0.13 | |
| 30–35 | 5.38 | 68,927 | 0.37 | |
| 35–40 | 3.93 | 31,164 | 0.12 | |
| 40–45 | 3.74 | 36,252 | 0.14 | |
| 45–50 | 3.23 | 41,367 | 0.13 | |
| over 50 | 1.87 | 1,716,706 | 3.21 | |
| Total | 2,042,228 | 4.76 | ||
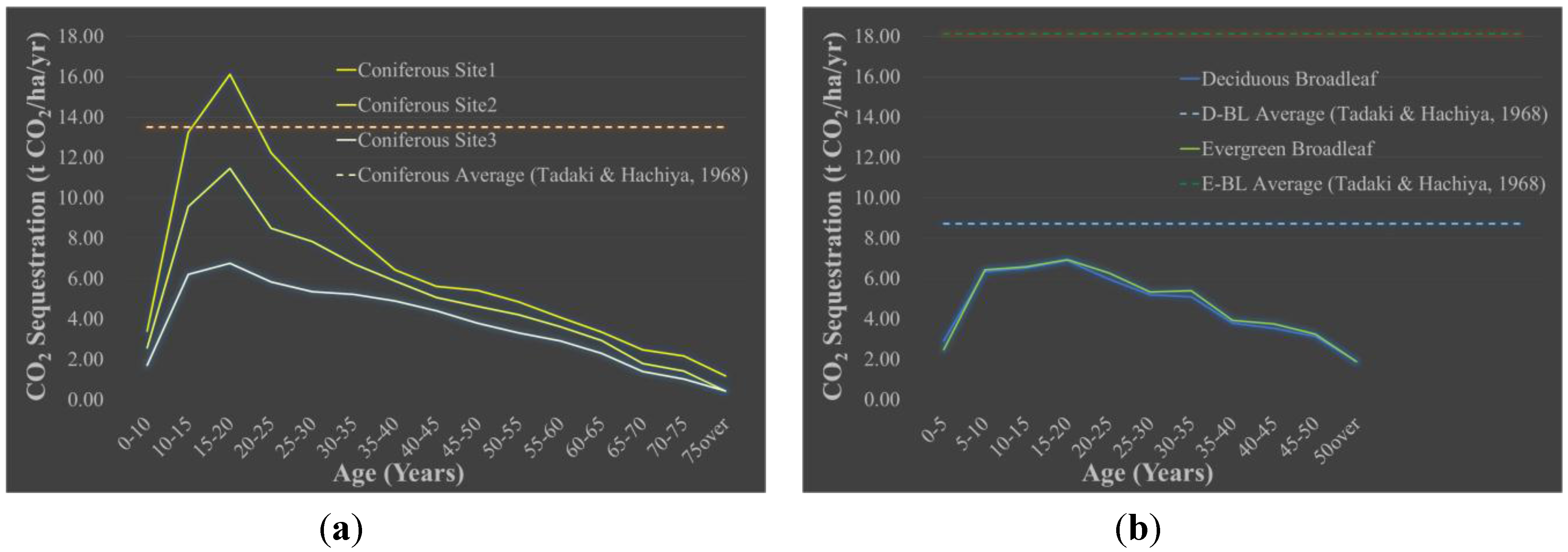
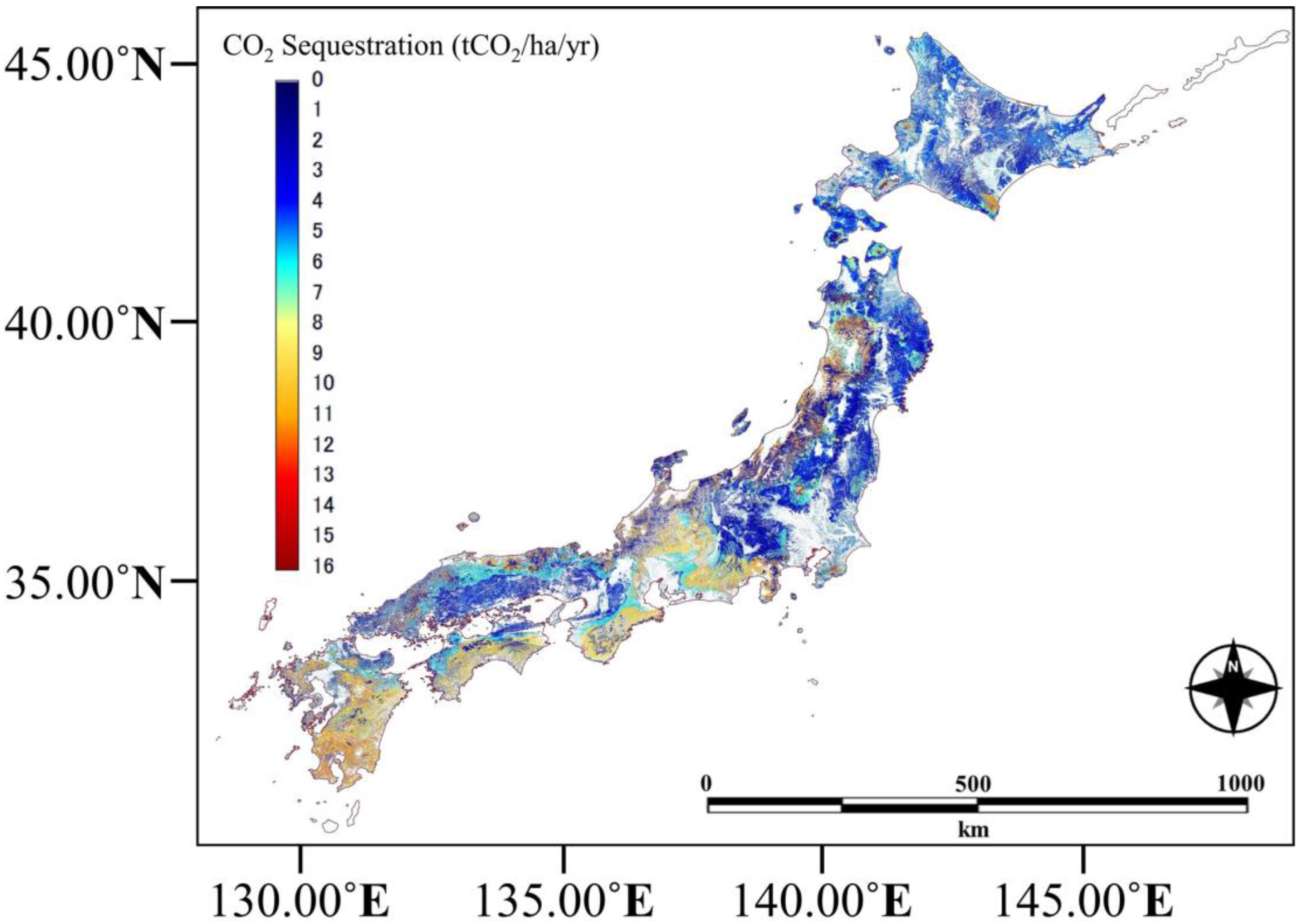
4.4. CO2 Sequestration Estimates and Errors
4.4.1. CO2 Estimates and Potential Errors
- Accuracy of the land cover map (forest cover map)
- Dependency on the backscattering model for stem volume estimation
- Stem volume-age relationship curve
- The sequestration value itself
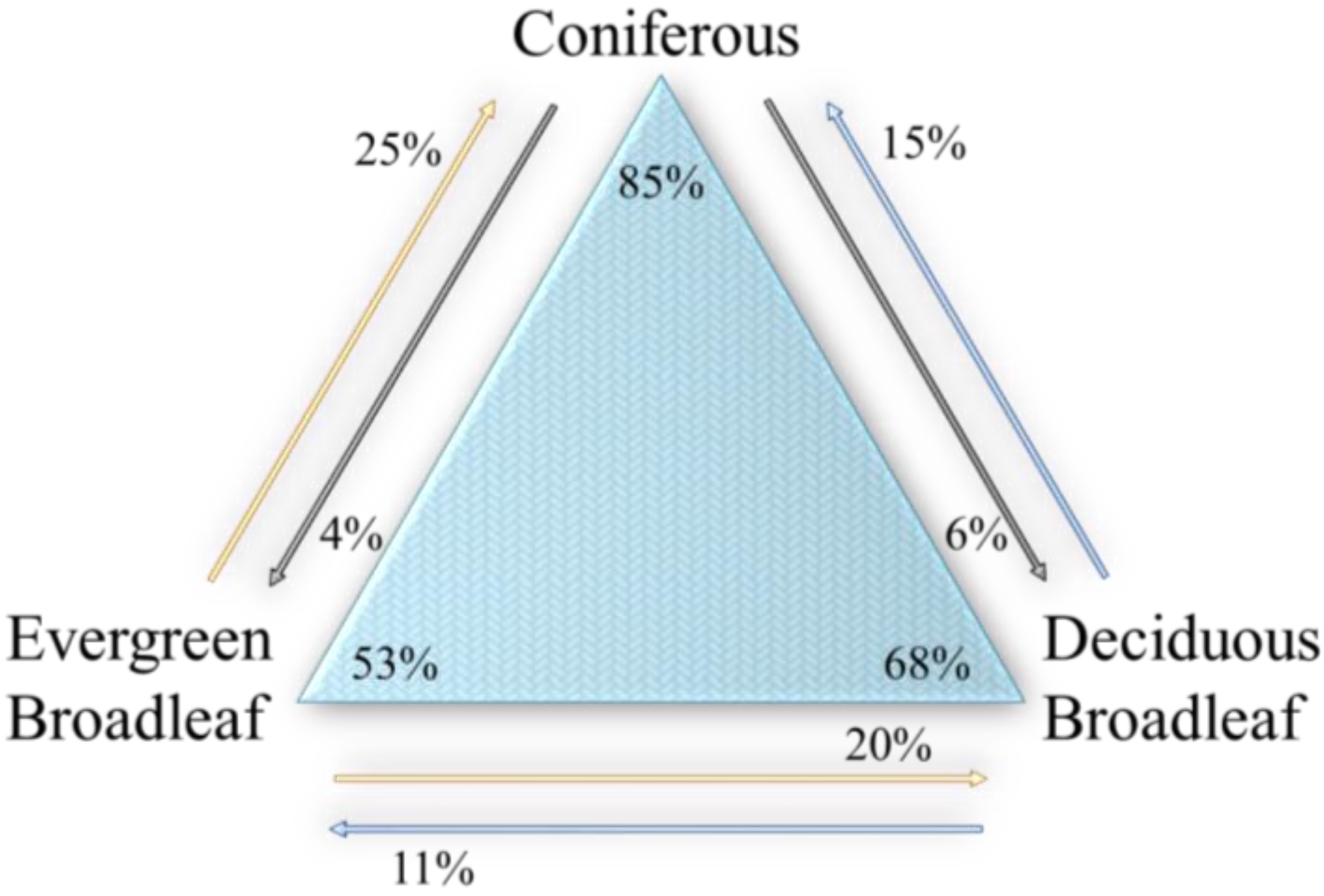
| Coniferous (t∙CO2/ha/yr) | Deciduous Broadleaf (t∙CO2/ha/yr) | Evergreen Broadleaf (t∙CO2/ha/yr) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Site 1 | Site 2 | Site 3 | Min | Max | Min | Max | |||||
| Age (years) | Min | Max | Min | Max | Min | Max | Age (years) | ||||
| 0–5 | 3.26 | 3.49 | 1.95 | 2.75 | 1.23 | 1.84 | 0–5 | 1.72 | 4.16 | 1.56 | 3.44 |
| 5–10 | 5–10 | 3.80 | 9.92 | 3.43 | 10.29 | ||||||
| 10–15 | 11.75 | 18.43 | 8.70 | 11.78 | 5.38 | 8.64 | 10–15 | 5.06 | 8.44 | 5.14 | 8.57 |
| 15–20 | 14.23 | 18.08 | 9.90 | 13.15 | 5.99 | 8.88 | 15–20 | 5.17 | 8.33 | 5.14 | 8.57 |
| 20–25 | 11.13 | 13.23 | 7.70 | 9.49 | 5.29 | 7.31 | 20–25 | 5.08 | 7.20 | 5.32 | 7.60 |
| 25–30 | 9.55 | 10.93 | 7.50 | 8.20 | 4.68 | 5.98 | 25–30 | 3.97 | 5.56 | 4.18 | 5.70 |
| 30–35 | 7.99 | 8.71 | 6.39 | 6.98 | 5.03 | 5.95 | 30–35 | 3.60 | 5.45 | 3.80 | 5.70 |
| 35–40 | 6.30 | 6.71 | 5.63 | 6.61 | 4.55 | 5.27 | 35–40 | 2.12 | 4.81 | 2.28 | 4.94 |
| 40–45 | 5.19 | 5.91 | 4.61 | 5.40 | 3.85 | 4.78 | 40–45 | 1.86 | 4.34 | 1.90 | 4.56 |
| 45–50 | 4.37 | 5.89 | 3.79 | 5.01 | 3.46 | 4.51 | 45–50 | 1.86 | 3.70 | 1.90 | 3.80 |
| 50–55 | 3.44 | 5.75 | 3.23 | 4.94 | 3.02 | 3.78 | 50 over | 0.60 | 3.41 | 1.50 | 3.61 |
| 55–60 | 2.79 | 5.82 | 2.72 | 4.55 | 2.58 | 3.78 | |||||
| 60–65 | 2.08 | 5.28 | 2.01 | 3.65 | 1.71 | 2.93 | |||||
| 65–70 | 1.32 | 4.35 | 1.04 | 2.77 | 0.97 | 1.98 | |||||
| 70–75 | 1.32 | 3.89 | 0.97 | 2.39 | 0.97 | 1.22 | |||||
| 75 over | 0.59 | 2.06 | 0.22 | 0.79 | 0.24 | 0.53 | |||||
4.4.2. Actual CO2 Estimates Considering the Errors
| Error Types | Forest Types | Coniferous | Deciduous Broadleaf | Evergreen Broadleaf | Total CO2 Sequestration | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Unit: Mt∙CO2 | ||||||||||
| Land Cover Mapping | Mintot: 50.94 | Maxtot: 89.67 | Mintot: 20.29 | Maxtot: 25.50 | Mintot: 4.57 | Maxtot: 11.94 | Mintot: 75.80 | Maxtot: 127.11 | ||
| Backscattering Model | (Avgval) Mintot: 65.46 | (Avgval) Maxtot: 99.81 | N/A (21.61) | N/A (4.76) | Mintot: 91.83 | Maxtot: 126.18 | ||||
| Tree Age Curve | N/A | N/A | N/A | N/A | ||||||
| Sequestration Value | Mintot: 78.80 | Maxtot: 90.97 | Mintot: 7.38 | Maxtot: 31.94 | Mintot: 6.55 | Maxtot: 14.78 | Mintot: 92.73 | Maxtot: 137.69 | ||
| Backscattering Model + Sequestration Value | (Minval) Mintot: 64.65 | (Minval) Maxtot: 91.45 | N/A (21.61) | N/A (4.76) | (Minval) Mintot: 91.02 | (Minval) Maxtot: 117.82 | ||||
| (Maxval) Mintot: 75.03 | (Maxval) Maxtot: 110.64 | (Maxval) Mintot: 101.4 | (Maxval) Maxtot: 137.01 | |||||||
5. Discussion
5.1. Stem Volume Empirical Modeling
5.2. Land Cover Mapping of Japan
5.3. Stem Volume Method for CO2 Sequestration Estimates
5.3.1. CO2 Sequestration Values and Trends
5.3.2. Validity of the Method in Comparison
| Methods | Total CO2 Sequestration |
|---|---|
| Conventional (Tadaki and Hachiya [15]) | 308.51 Mt∙CO2 |
| Sasaki and Kim [7] | 73.7 Mt∙CO2 |
| NIES [8] | 77.67 Mt∙CO2 |
| Stem Volume Method (our work) | 111.27 Mt∙CO2 |
6. Concluding Remarks
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hewitt, C.N.; Jackson, A. Handbook of Atmospheric Science: Principles and Applications; Blackwell: Padstow, UK, 2003. [Google Scholar]
- Chiras, D.D. Environmental Science, 7th ed.; Jones and Bartlett: Massachusetts, UK, 2006. [Google Scholar]
- Ministry of Agriculture, Forestry and Fisheries (MAFF) of Japan (2010). Annual Report on Forest and Forestry in Japan (Summary). Available online: http://www.rinya.maff.go.jp/j/kikaku/hakusyo/22hakusho/pdf/22_e.pdf (accessed on 6 August 2015).
- Ministry of Economy, Trade and Industry (METI) of Japan (2005). Kyoto Protocol Target Achievement Plan. Available online: http://www.meti.go.jp/policy/energy_environment/global_warming/study_policy.html (accessed on 6 August 2015). (In Japanese)
- Sanga-Ngoie, K.; Iizuka, K.; Kobayashi, S. Estimating CO2 sequestration by forests in Oita Prefecture, Japan, by combining Landsat ETM+ and ALOS satellite remote sensing data. Remote Sens. 2012, 4, 3544–3570. [Google Scholar] [CrossRef]
- Hiroshima, T.; Nakajima, T. Estimation of sequestered carbon in article-3.4 private planted forests in the first commitment period in Japan. J. For. Res. 2006, 11, 427–437. [Google Scholar] [CrossRef]
- Sasaki, N.; Kim, S. Biomass carbon sinks in Japanese forests: 1966–2012. Forestry 2009, 82, 113–123. [Google Scholar] [CrossRef]
- National Institute for Environmental Studies Japan (NIES), Center for Global Environmental Research (CGER). National Greenhouse Gas Inventory Report of Japan. Available online: http://www.gio.nies.go.jp/aboutghg/nir/2014/NIR-JPN-2014-v3.0.pdf (accessed on 6 August 2015).
- Gibbs, J.K.; Brown, S.; Niles, J.O.; Foley, J.A. Monitoring and estimating tropical forest carbon stocks: Making REDD a reality. Environ. Res. Lett. 2007, 2, 1–13. [Google Scholar] [CrossRef]
- Goetz, S.J.; Prince, S.D.; Goward, S.N.; Thawley, M.M.; Small, J. Satellite remote sensing of primary production: An improved production efficiency modeling approach. Ecol. Model. 1999, 122, 239–255. [Google Scholar] [CrossRef]
- Pachavo, G.; Murwira, A. Remote sensing net primary productivity (NPP) estimation with the aid of GIS modelled shortwave radiation (SWR) in a southern African Savanna. Int. J. Appl. Earth Obs. Geoinf. 2014, 30, 217–226. [Google Scholar] [CrossRef]
- Zheng, G.; Chen, J.J.; Tian, Q.J.; Ju, W.M.; Xia, X.Q. Combining remote sensing imagery and forest age inventory for biomass mapping. J. Environ. Manag. 2007, 85, 616–623. [Google Scholar] [CrossRef] [PubMed]
- Turner, D.P.; Ritts, W.D.; Cohen, W.B.; Gower, S.T.; Running, S.W.; Zhao, M.; Costa, M.H.; Kirschbaum, A.A.; Ham, J.M.; Saleska, S.R.; et al. Evaluation of MODIS NPP and GPP products across multiple biomes. Remote Sens. Environ. 2006, 102, 282–292. [Google Scholar] [CrossRef]
- Turner, D.P.; Guzy, M.; Lefsky, M.A.; Ritts, W.D.; Tuyl, S.V.; Law, B.E. Monitoring forest carbon sequestration with remote sensing and carbon cycle modeling. Environ. Manage. 2004, 33, 457–466. [Google Scholar] [CrossRef] [PubMed]
- Tadaki, Y.; Hachiya, K. Forest Ecosystems and Their Productivity; Ringyo Kagakugijutsu Shinkosho: Tokyo, Japan, 1968. (In Japanese) [Google Scholar]
- Ministry of Agriculture, Forestry and Fisheries (MAFF) of Japan (2010). Function of the Sequestration of Forests/Trees. Available online: http://www.rinya.maff.go.jp/kinki/hyogo/mori-grow/mori-co2.html (accessed on 6 August 2015). (In Japanese)
- Ministry of Environment (MOE) of Japan. Vegetation Distribution of Japan. Available online: http://www.vegetation.biodic.go.jp/zu/index.html (accessed on 9 September 2015). (In Japanese)
- Iizuka, K.; Tateishi, R. Simple relationship analysis between L-band backscattering intensity and the stand characteristics of sugi (Cryptomeria japonica) and hinoki (Chamaecyparis obtusa) trees. Adv. Remote Sens. 2014, 3, 219–234. [Google Scholar] [CrossRef]
- Castel, T.; Beaudoin, A.; Stach, N.; Stussi, N.; Le Toan, T.; Durand, P. Sensitivity of space-borne SAR data to forest parameters over sloping terrain. Theory and experiment. Int. J. Remote Sens. 2001, 22, 2351–2376. [Google Scholar] [CrossRef]
- Dobson, M.C.; Ulaby, F.T.; Le Toan, T.; Beaudoin, A.; Kasischke, E.S.; Christensen, N. Dependence of radar backscatter on coniferous forest biomass. IEEE Trans. Geosci. Remote Sens. 1992, 30, 412–415. [Google Scholar] [CrossRef]
- Harrell, P.; Kasischke, E.S.; Bourgeau-Chavez, L.L.; Haney, E.; Christensen, N.L. Evaluation of approaches to estimating aboveground biomass in southern pine forests using SIR-C data. Remote Sens. Environ. 1997, 59, 223–233. [Google Scholar] [CrossRef]
- Saatchi, S.S.; Moghaddam, M. Estimation of crown and stem water content and biomass of boreal forest using polarimetric SAR imagery. IEEE Trans. Geosci. Remote Sens. 2000, 38, 697–709. [Google Scholar] [CrossRef]
- Sandberg, G.; Ulander, L.M.H.; Fransson, J.E.S.; Holmgren, J.; Le Toan, T. L- and P-Band backscatter intensity for biomass retrieval in hemiboreal forest. Remote Sens. Environ. 2011, 115, 2874–2886. [Google Scholar] [CrossRef]
- Chen, E.; Li, Z.Y.; Ling, F.L.; Lu, Y.; He, Q.S.; Fan, F.Y. Forest volume density estimation capability of ALOS PALSAR data over hilly region. In Proceedings of 4th International Workshop on Science and Applications of SAR Polarimetry and Polarimetric Interferometry (PolInSAR), Frascati, Italy, 26–30 January 2009.
- Small, D. Flattening gamma: Radiometric terrain correction for SAR imagery. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3081–3093. [Google Scholar] [CrossRef]
- Japan Aerospace Exploration Agency (JAXA). PALSAR Calibration Factor Updated. Available online: http://www.eorc.jaxa.jp/en/about/distribution/info/alos/20090109en_3.html (accessed on 6 August 2015).
- Shimada, M. Ortho-Rectification and slope correction of SAR data using DEM and its accuracy evaluation. IEEE J. Sel. Topics Appl. Earth Obs. 2010, 3, 657–671. [Google Scholar] [CrossRef]
- Iizuka, K.; Tateishi, R. Analysis of backscattering characteristics of L-band SAR over the mountainous region of Chiba Japan, using 50 m PALSAR mosaic product. In Proceedings of International Symposium on Remote Sensing, Chiba, Japan, 22–26 April 2013.
- Japan Aerospace and Exploration Agency (JAXA). PALSAR 50 m Orthorectified Mosaic Product. Available online: http://www.eorc.jaxa.jp/ALOS/en/kc_mosaic/kc_mosaic.htm (accessed on 6 August 2015).
- Cartus, O.; Santoro, M.; Kellndorfer, J. Mapping forest aboveground biomass in the northeastern United States with ALOS PALSAR dual-polarization L-band. Remote Sens. Environ. 2012, 124, 466–478. [Google Scholar] [CrossRef]
- Santoro, M.; Beer, C.; Cartus, O.; Schmullius, C.; Shvidenko, A.; McCallum, I.; Wegmüller, U.; Wiesmann, A. Retrieval of growing stock volume in boreal forest using hyper-temporal series of Envisat ASAR ScanSAR backscatter measurements. Remote Sens. Environ. 2011, 115, 490–507. [Google Scholar] [CrossRef]
- Zhou, Z.-S.; Lehmann, E.; Wu, X.; Caccetta, P.; McNeill, S.; Mitchell, A.; Milne, A.; Tapley, I.; Lowell, K. Terrain slope correction and precise registration of SAR data for forest mapping and monitoring. In Proceedings of International Symposium for Remote Sensing of the Environment, Sydney, NSW, Australia, 10–15 April 2011.
- Kobayashi, S.; Sanga-Ngoie, K. The integrated radiometric correction of optical remote sensing imageries. Int. J. Remote Sens. 2008, 29, 5957–5985. [Google Scholar] [CrossRef]
- Li, W.; Du, Z.; Ling, F.; Zhou, D.; Wang, H.; Gui, Y.; Sun, B.; Zhang, X. A comparison of land surface water mapping using the Normalized Difference Water Index from TM, ETM+ and ALI. Remote Sens. 2013, 5, 5530–5549. [Google Scholar] [CrossRef]
- Motohka, T.; Nasahara, K.N.; Oguma, H.; Tsuchida, S. Applicability of green-red vegetation index for remote sensing of vegetation phenology. Remote Sens. 2010, 2, 2369–2387. [Google Scholar] [CrossRef]
- Congalton, R.G.; Green, K. Assessing The Accuracy of Remotely Sensed Data: Principles and Practices, 2nd ed.; CRC/Taylor & Francis: New York, NY, USA, 2009. [Google Scholar]
- Perry, D.A.; Oren, R.; Hart, S.C. Forest Ecosystems, 2nd ed.; The Johns Hopkins University Press: Baltimore, MD, USA, 2008. [Google Scholar]
- Wijaya, A. Evaluation of ALOS-PALSAR mosaic data for estimating stem volume and biomass: A case study from tropical rainforest of central Indonesia. J. Geogr. 2009, 2, 14–21. [Google Scholar]
- Ministry of Environment (MOE) of Japan. National Survey on the Natural Environment. Available online: http://www.biodic.go.jp/english/J-IBIS.html (accessed on 6 August 2015).
- Congalton, R.G.; Mead, R.A. A quantitative method to test for consistency and correctness in photointerpretation. Photogramm. Eng. Remote Sens. 1983, 49, 69–74. [Google Scholar]
- Sasaki, H.; Hayashi, H.; Ise, S. Considerations on the selective logging updating of evergreen broadleaf forests. Tokushima Prefect. For. Res. Cent. Rep. 1989, 27, 22–29. (In Japanese) [Google Scholar]
- Forestry Agency. Aomori Region Sugi Tree Rinbun-Shukaku-Hyou (1962). Available online: http://www.ffpri.affrc.go.jp/labs/shukakushiken/02gyoken/02gyoken_28.pdf (accessed on 6 August 2015). (In Japanese)
- Forestry Agency. Kagoshima Region Sugi Tree Rinbun-Shukaku-Hyou (1965). Available online: http://www.ffpri.affrc.go.jp/labs/shukakushiken/02gyoken/02gyoken_33.pdf (accessed on 6 August 2015). (In Japanese)
- Ulaby, F.T.; Sarabandi, K.; McDonald, K.; Whitt, M.; Dobson, C. Michigan microwave canopy scattering model. Int. J. Remote Sens. 1990, 11, 1223–1253. [Google Scholar] [CrossRef]
- Baghdadi, N.; Le Maire, G.; Bailly, J.S.; Osé, K.; Nouvellon, Y.; Zribi, M.; Lemos, C.; Hakamada, R. Evaluation of ALOS/PALSAR L-band data for the estimation of Eucalyptus plantations aboveground biomass in Brazil. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3802–3811. [Google Scholar] [CrossRef]
- Ulander, L.M.H. Radiometric slope correction of Synthetic-Aperture Radar images. IEEE Trans. Geosci. Remote Sens. 1996, 34, 1115–1122. [Google Scholar] [CrossRef]
- Matsumoto, M. Carbon stock and carbon sequestration by the forests of Japan. Shinrin Kagaku. 2001, 33, 30–36. (In Japanese) [Google Scholar]
- Forestry and Forest Products Research Institute. Guidelines for Implementing REDD-plus ver. 1.1. Available online: http://www.ffpri.affrc.go.jp/reddrdc/en/reference/guideline/REDD+Guidelines_E_ver.1.1_20140327.pdf. (accessed on 6 August 2015).
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iizuka, K.; Tateishi, R. Estimation of CO2 Sequestration by the Forests in Japan by Discriminating Precise Tree Age Category using Remote Sensing Techniques. Remote Sens. 2015, 7, 15082-15113. https://doi.org/10.3390/rs71115082
Iizuka K, Tateishi R. Estimation of CO2 Sequestration by the Forests in Japan by Discriminating Precise Tree Age Category using Remote Sensing Techniques. Remote Sensing. 2015; 7(11):15082-15113. https://doi.org/10.3390/rs71115082
Chicago/Turabian StyleIizuka, Kotaro, and Ryutaro Tateishi. 2015. "Estimation of CO2 Sequestration by the Forests in Japan by Discriminating Precise Tree Age Category using Remote Sensing Techniques" Remote Sensing 7, no. 11: 15082-15113. https://doi.org/10.3390/rs71115082
APA StyleIizuka, K., & Tateishi, R. (2015). Estimation of CO2 Sequestration by the Forests in Japan by Discriminating Precise Tree Age Category using Remote Sensing Techniques. Remote Sensing, 7(11), 15082-15113. https://doi.org/10.3390/rs71115082