Estimation of Evapotranspiration and Crop Coefficients of Tendone Vineyards Using Multi-Sensor Remote Sensing Data in a Mediterranean Environment
Abstract
:1. Introduction
2. Material and Methods
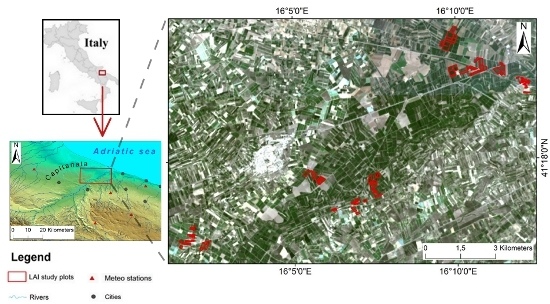
2.1. Study Area and Vineyard Description
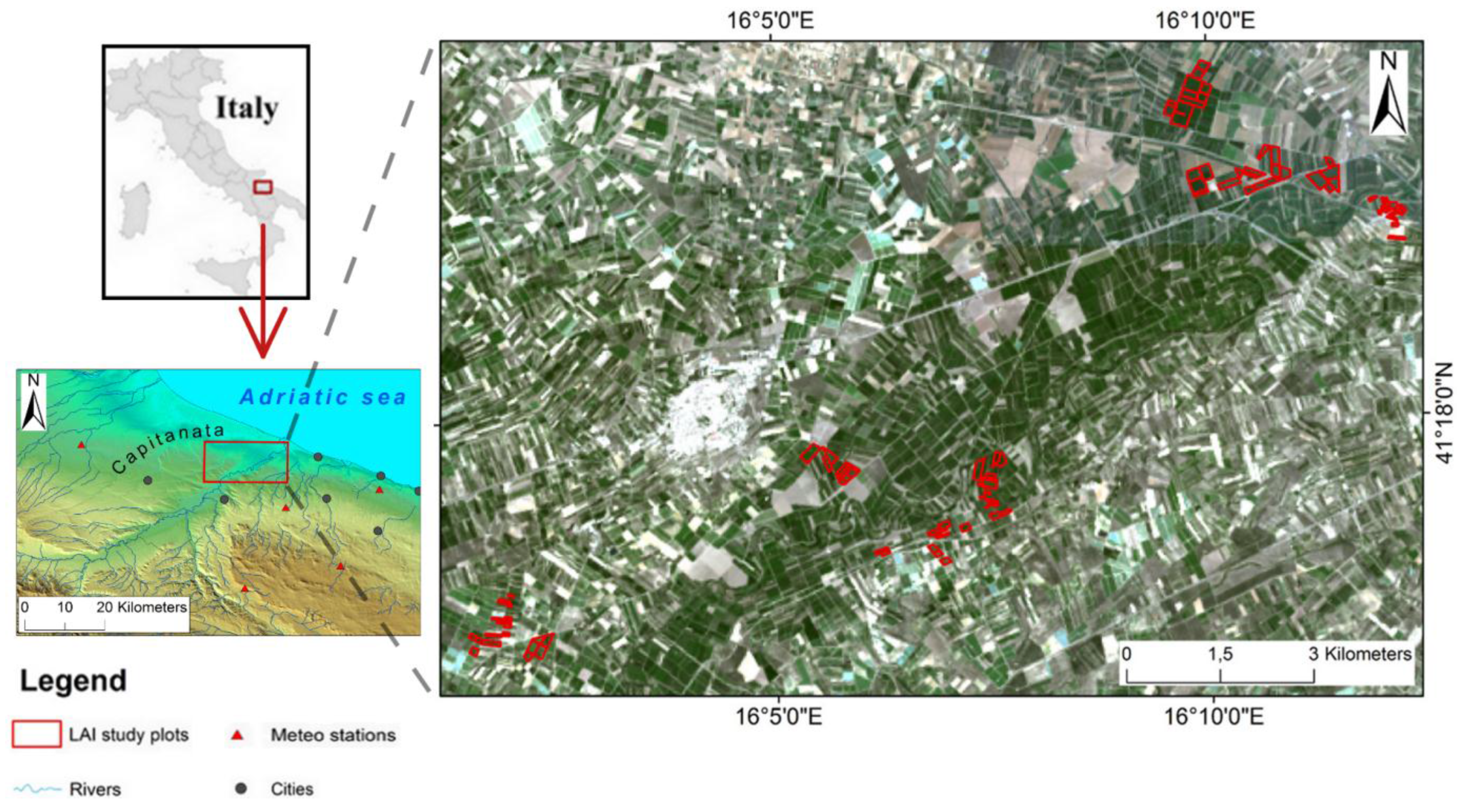

2.2. Dataset
2.2.1. Satellite Images
| Satellite Data | GSD* (m) | Processing Level | Revisit Time | N. of Images | Acquisition Dates |
|---|---|---|---|---|---|
| Landsat 8 OLI | 30 | 1T | 16 day | 14 | from 19/05/2013 to 26/08/2014 |
| RapidEye MSI | 6.5 | 1B | 1 day | 10 | from 10/06/2014 to 29/09/2014 |
2.2.2. Agrometeorological Data and Field Data
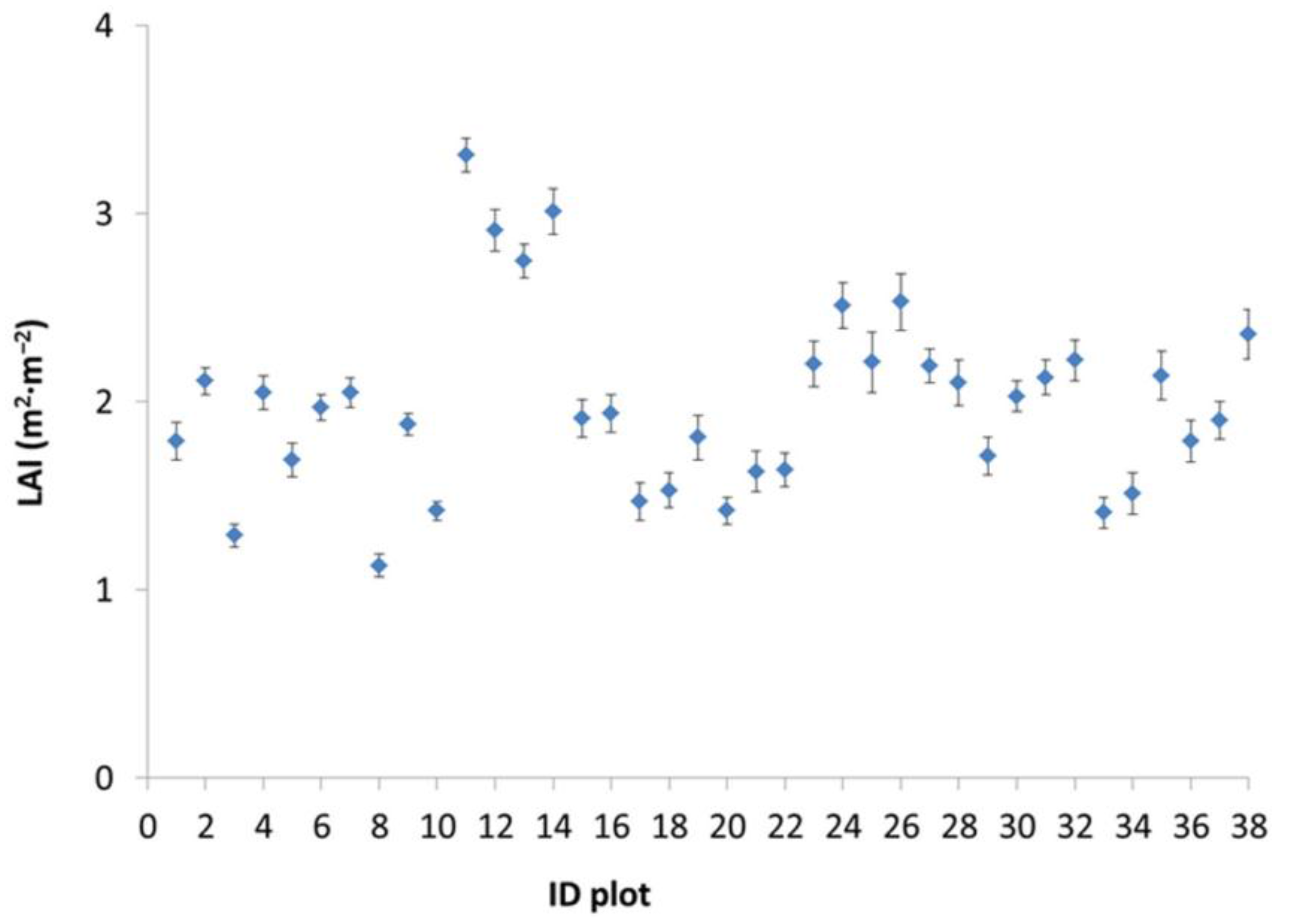
2.2.3. In Situ LAI
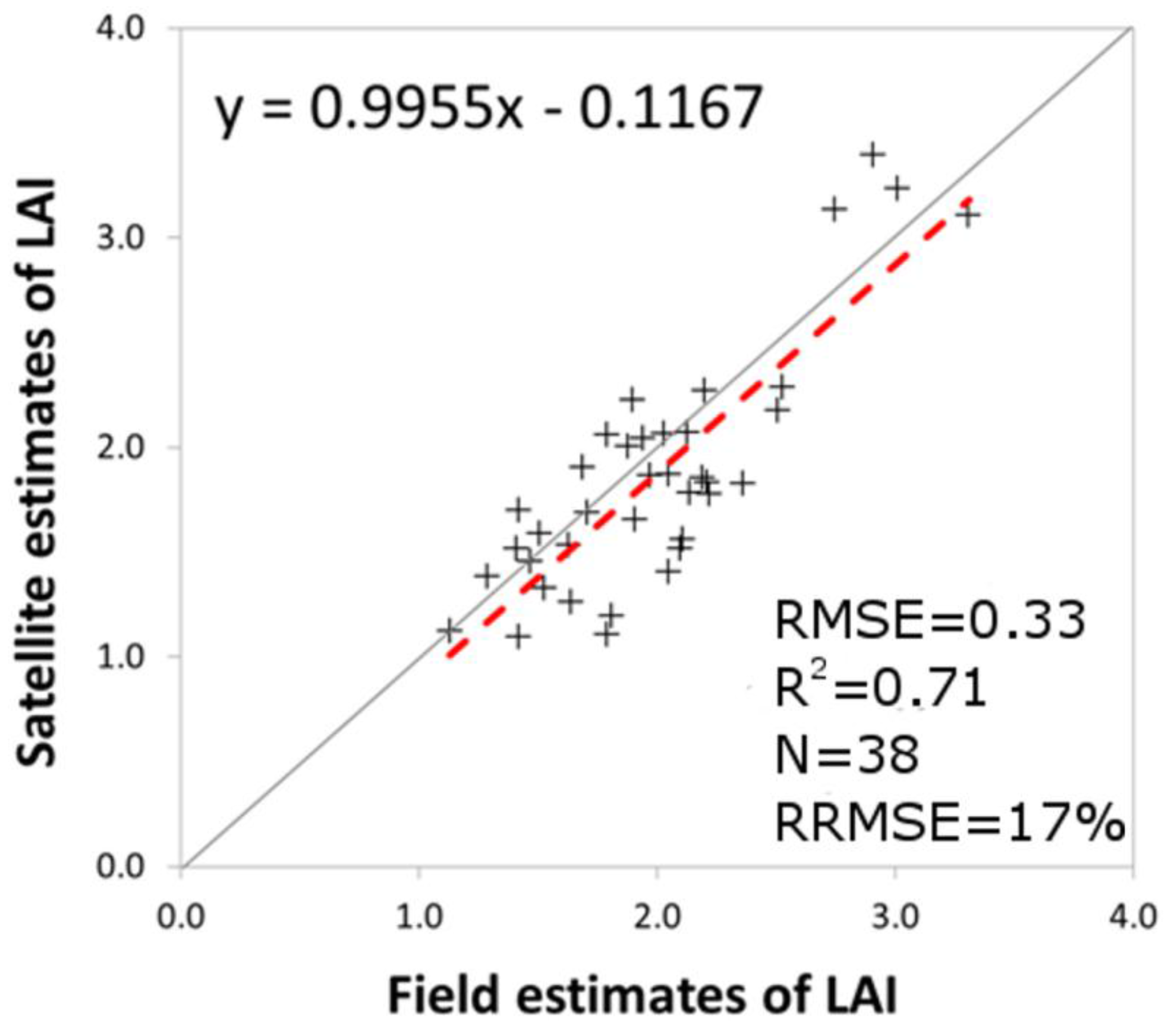
2.3. Methods
Data Processing for Deriving EO-Based Crop Development Maps
3. Results and Discussion
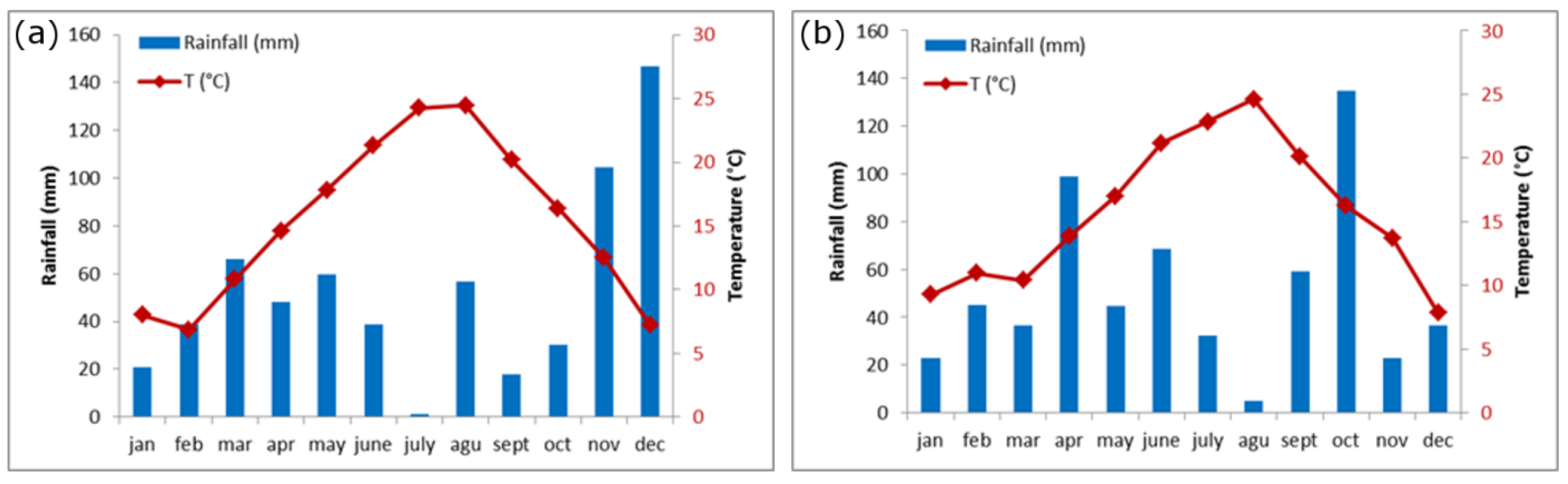
3.1. Weather Conditions, Reference ET, and Phenology
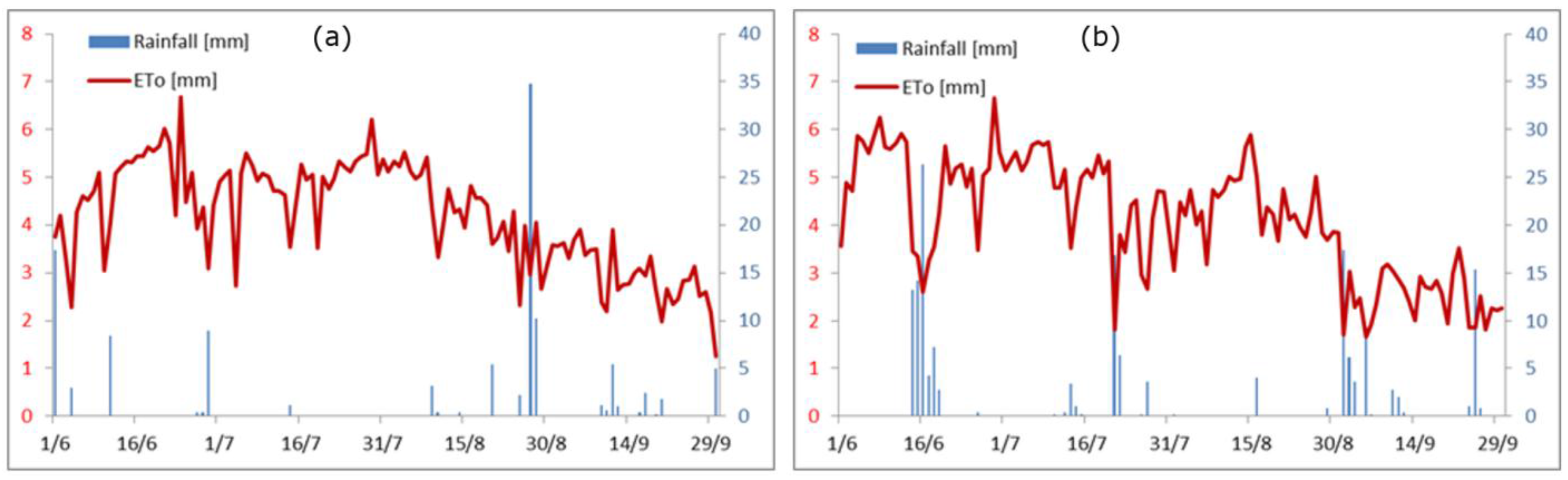
| Phenology * | Time | GDD 2013 | GDD 2014 |
|---|---|---|---|
| Bud break | 1–6 April | 0 | 0 |
| Flowering | 20–30 May | 341 | 279 |
| Veraison | 16–24 July | 981 | 1040 |
| Harvest | 10–15 Sept. | 1747 | 1766 |
| – | 31 October | 2018 | 2128 |
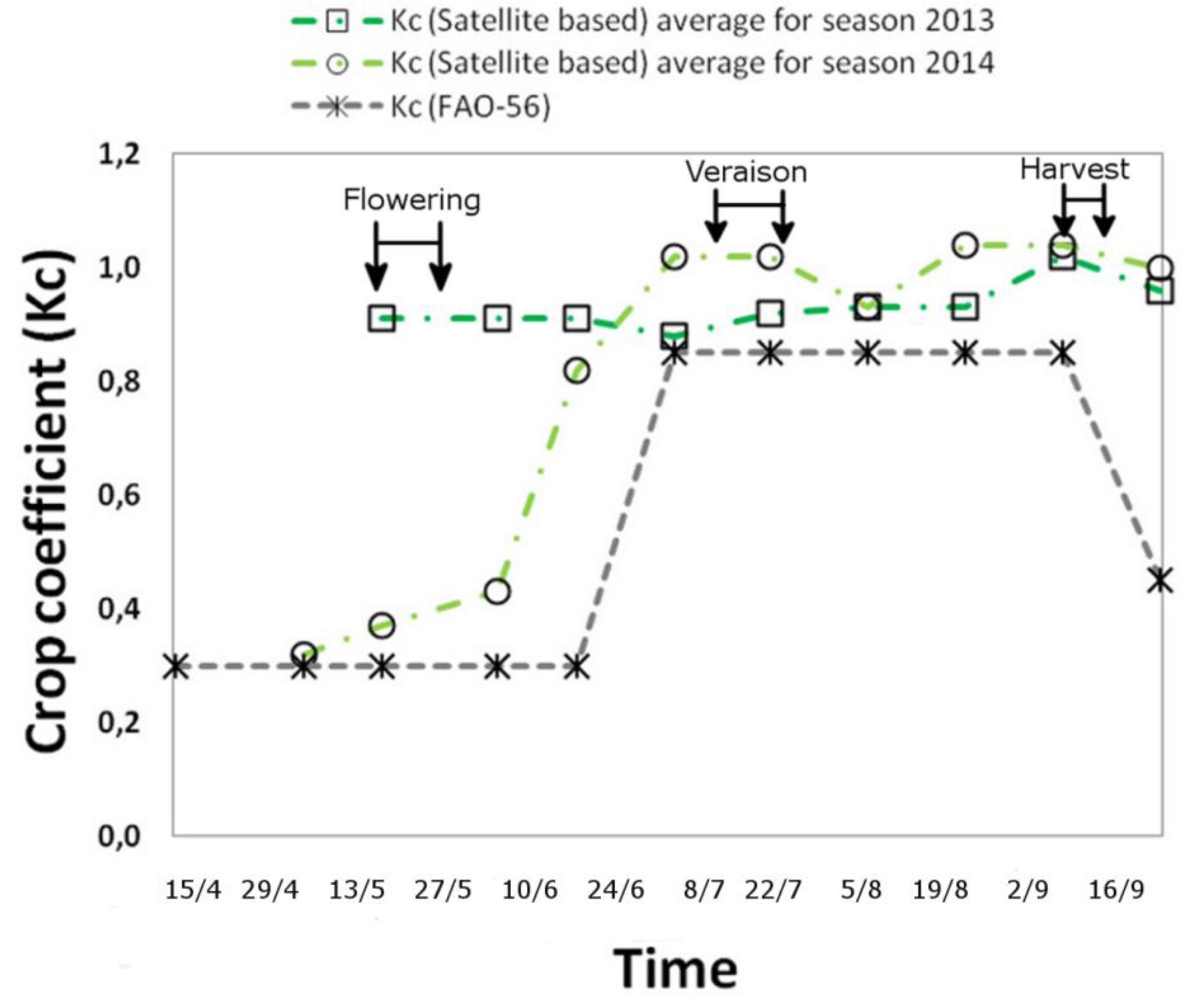
3.2. Temporal Evolution of LAI and Kc
| Kc | 19 May 2013 | 20 June 2013 | 06 July 2013 | 22 July 2013 | 07 August 2013 | 23 August 2013 | 08 Sept 2013 | 24 Sept 2013 |
|---|---|---|---|---|---|---|---|---|
| maximum | 1.14 | 1.14 | 1.14 | 1.19 | 1.19 | 1.18 | 1.23 | 1.19 |
| average | 0.91 | 0.91 | 0.88 | 0.92 | 0.93 | 0.93 | 1.02 | 0.96 |
| minimum | 0.58 | 0.58 | 0.43 | 0.46 | 0.48 | 0.49 | 0.58 | 0.56 |
| Standard deviation | 0.13 | 0.13 | 0.15 | 0.15 | 0.14 | 0.14 | 0.13 | 0.13 |
| Kc | 06 May 2014 | 07 June 2014 | 23 June 2014 | 09 July 2014 | 10 August 2014 | 26 August 2014 |
|---|---|---|---|---|---|---|
| maximum | 0.63 | 0.75 | 1.07 | 1.42 | 1.10 | 1.30 |
| average | 0.32 | 0.43 | 0.82 | 1.02 | 0.93 | 1.04 |
| minimum | 0.14 | 0.17 | 0.53 | 0.68 | 0.56 | 0.63 |
| Standard deviation | 0.08 | 0.10 | 0.11 | 0.16 | 0.10 | 0.12 |
| Kc | Trellis System | Cultivar | Season | Country | References | ||
|---|---|---|---|---|---|---|---|
| Initial | Middle | End | |||||
| – | ~1 | – | Tendone | Italia | 1997 | Italy | Rana et al. [36] |
| 0.2 | 0.9–1.3 | – | Head training system | Thompson seedless | 1998–1999 | California | Williams and Ayars [12] |
| 0.48 | 0.68 | 0.68 | Tendone | – | – | Italy | Lamaddalena and Caliandro [65] |
| 0.4 | 1–1.2 | 1.3 | Open-gable | Superior seedless | 2004–2005 | Israel | Netzer et al. [64] |
| 0.22 | 0.45 | 0.3 | Open-gable | Perlette & Superior seedless | 2005–2006 | Mexico | Er-Raki et al. [28] |
| – | 0.79 | 0.98 | Open-gable* | Red Globe | 2007–2008 | Spain | Moratiel and Martinez-Cob [68] |
| 0.54 | 0.65 | 0.9 | Overhead trellis system* | Crimson seedless | 2008–2009 | Spain | Suvocarev et al. [22] |
| 0.47 | 0.60 | – | Overhead trellis system* | Autumn Royal | 2009 | Spain | |
| 0.2–0.4 | ~0.9–1.2 | 1.2 | Overhead trellis system | Thompson seedless | 2008–2010 | Chile | Villagra et al. [66] |
3.3. Temporal Evolution of Evapotranspiration
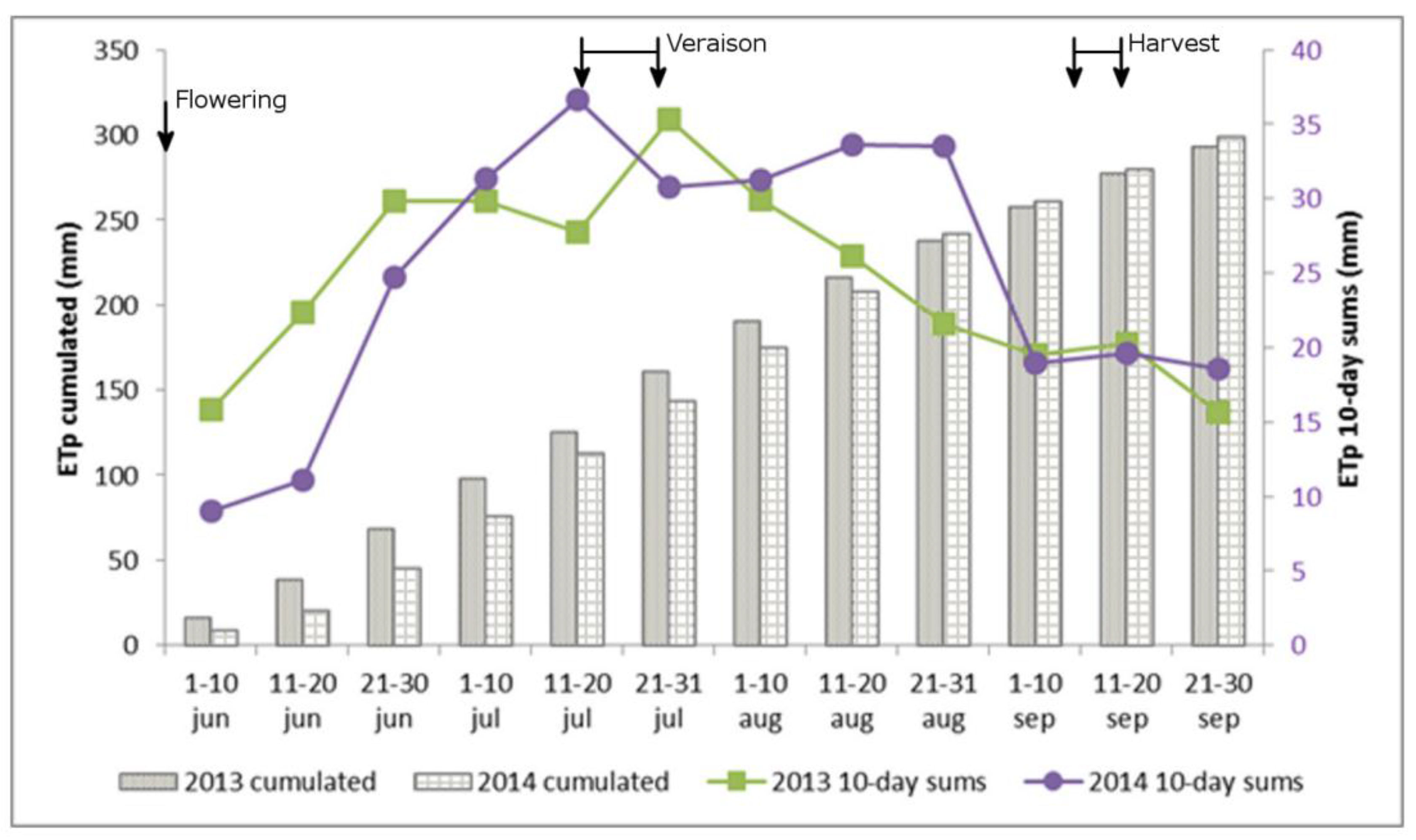
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
List of Symbols and Acronyms
| CLAIR | Clevers’ Leaf Area Index by Reflectance model |
| ET0 | Reference evapotranspiration [mm·d−1] |
| ETp | Crop evapotranspiration [mm·d−1] |
| fcover | Fractional cover [%] |
| GDD | Growing Degree Days [°C] |
| GPS | Global Position System |
| GSD | Ground Sample Distance [m] |
| hc | Crop height [m] (0.12 for reference crop) |
| hc* | Crop height [m] (constant value of 0.4 m in this study) |
| Kc | Crop coefficient [dimensionless] |
| K↓ | Global incoming short-wave radiation flux density [W·m−2] |
| LAI | Leaf area index [m2·m−2] (2.88 for reference crop) |
| LAI* | Leaf area index [m2·m−2] (estimated from satellite) |
| MODTRAN | MODerate resolution atmospheric TRANsmission |
| NDVI | Normalized difference vegetation index [dimensionless] |
| OLI | Operational Land Imager |
| WDVI | Weighted Difference Vegetation Index [dimensionless] |
| P | Actual precipitation [cm·d−1] |
| Pn | Net precipitation [cm·d−1] |
| r | Albedo [dimensionless] (0.23 for reference crop) |
| r* | Albedo [dimensionless] (estimated from satellite) |
| R2 | Coefficient of determination |
| RH | Air humidity [%] |
| RMSE | Root-mean-square error [dimensionless] |
| rsNIR | Spectral reflectance in the near-nfrared channel |
| rsRED | Spectral reflectance in the red channel |
| S | Solar radiation |
| SAVI | Soil Adjusted Vegetation Index [dimensionless] |
| SEL | Standard error of the LAI |
| SIMODIS | SImulation and Management of On-Demand Irrigation System |
| Ta | Air temperature [°C] |
| U | Wind speed [m·s−1] |
| VI | Vegetation Index [dimensionless] |
| a | Crop saturation per unit foliage area [cm·d−1] |
| α* | Extinction coefficient [dimensionless] |
References
- International Organisation of Vine and Wine. Statistical Report on World Viticulture; International Organisation of Vine and Wine: Paris, France, 2013. [Google Scholar]
- De C. Teixeira, A.H.; Bastiaanssen, W.G.M.; Bassoi, L.H. Crop water parameters of irrigated wine and table grapes to support water productivity analysis in the São Francisco river basin, Brazil. Agric. Water Manag. 2007, 94, 31–42. [Google Scholar] [CrossRef]
- Perry, C.; Steduto, P.; Allen, R.G.; Burt, C.M. Increasing productivity in irrigated agriculture: Agronomic constraints and hydrological realities. Agric. Water Manag. 2009, 96, 1517–1524. [Google Scholar] [CrossRef]
- Carrasco-Benavides, M.; Ortega-Farías, S.; Lagos, L.O.; Kleissl, J.; Morales, L.; Poblete-Echeverría, C.; Allen, R.G. Crop coefficients and actual evapotranspiration of a drip-irrigated Merlot vineyard using multispectral satellite images. Irrig. Sci. 2012, 30, 485–497. [Google Scholar] [CrossRef]
- Chaves, M.M.; Zarrouk, O.; Francisco, R.; Costa, J.M.; Santos, T.; Regalado, A.P.; Rodrigues, M.L.; Lopes, C.M. Grapevine under deficit irrigation: Hints from physiological and molecular data. Ann. Bot. 2010, 105, 661–676. [Google Scholar] [CrossRef] [PubMed]
- Williams, L.E.; Grimes, D.W.; Phene, C.J. The effects of applied water at various fractions of measured evapotranspiration on water relations and vegetative growth of Thompson Seedless grapevines. Irrig. Sci. 2010, 28, 221–232. [Google Scholar] [CrossRef]
- Aragüés, R.; Medina, E.T.; Clavería, I.; Martínez-Cob, A.; Faci, J. Regulated deficit irrigation, soil salinization and soil sodification in a table grape vineyard drip-irrigated with moderately saline waters. Agric. Water Manag. 2014, 134, 84–93. [Google Scholar] [CrossRef]
- Faci, J.M.; Blanco, O.; Medina, E.T.; Martínez-Cob, A. Effect of post veraison regulated deficit irrigation in production and berry quality of Autumn Royal and Crimson table grape cultivars. Agric. Water Manag. 2014, 134, 73–83. [Google Scholar] [CrossRef]
- Tarricone, L.; Gentilesco, G.; Di Gennaro, D.; Amendolagine, A.M. Irrigation strategy and vine performance of organic “Italia” table grape grown in Apulia region (Southern Italy). In Proceedings of the 7th International Table Grape Symposium, Mildura, Victoria, Australia, 11–14 November 2014; pp. 97–100.
- García García, J.; Martínez-Cutillas, A.; Romero, P. Financial analysis of wine grape production using regulated deficit irrigation and partial-root zone drying strategies. Irrig. Sci. 2012, 30, 179–188. [Google Scholar] [CrossRef]
- Medrano, H.; Tomás, M.; Martorell, S.; Escalona, J.-M.; Pou, A.; Fuentes, S.; Flexas, J.; Bota, J. Improving water use efficiency of vineyards in semi-arid regions. A review. Agron. Sustain. Dev. 2014, 35, 499–517. [Google Scholar] [CrossRef]
- Williams, L.E.; Ayars, J.E. Grapevine water use and the crop coefficient are linear functions of the shaded area measured beneath the canopy. Agric. For. Meteorol. 2005, 132, 201–211. [Google Scholar] [CrossRef]
- López-Urrea, R.; Montoro, A.; Mañas, F.; López-Fuster, P.; Fereres, E. Evapotranspiration and crop coefficients from lysimeter measurements of mature “Tempranillo” wine grapes. Agric. Water Manag. 2012, 112, 13–20. [Google Scholar] [CrossRef]
- Li, S.; Tong, L.; Li, F.; Zhang, L.; Zhang, B.; Kang, S. Variability in energy partitioning and resistance parameters for a vineyard in northwest China. Agric. Water Manag. 2009, 96, 955–962. [Google Scholar] [CrossRef]
- Li, S.; Kang, S.; Li, F.; Zhang, L.; Zhang, B. Vineyard evaporative fraction based on eddy covariance in an arid desert region of Northwest China. Agric. Water Manag. 2008, 95, 937–948. [Google Scholar] [CrossRef]
- Ortega-Farias, S.; Carrasco, M.; Olioso, A.; Acevedo, C.; Poblete, C. Latent heat flux over Cabernet Sauvignon vineyard using the Shuttleworth and Wallace model. Irrig. Sci. 2007, 25, 161–170. [Google Scholar] [CrossRef]
- Pellegrino, A.; Gozé, E.; Lebon, E.; Wery, J. A model-based diagnosis tool to evaluate the water stress experienced by grapevine in field sites. Eur. J. Agron. 2006, 25, 49–59. [Google Scholar] [CrossRef]
- Zhang, Y.; Kang, S.; Ward, E.J.; Ding, R.; Zhang, X.; Zheng, R. Evapotranspiration components determined by sap flow and microlysimetry techniques of a vineyard in northwest China: Dynamics and influential factors. Agric. Water Manag. 2011, 98, 1207–1214. [Google Scholar] [CrossRef]
- Carrasco-Benavides, M.; Ortega-Farías, S.; Lagos, L.; Kleissl, J.; Morales-Salinas, L.; Kilic, A. Parameterization of the Satellite-Based Model (METRIC) for the Estimation of Instantaneous Surface Energy Balance Components over a Drip-Irrigated Vineyard. Remote Sens. 2014, 6, 11342–11371. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration—Guidelines for Computing Crop Water Requirements—FAO Irrigation and Drainage Paper 56; Food and Agriculture Organization of the United Nations: Rome, Italy, 1998. [Google Scholar]
- Pereira, L.S.; Allen, R.G.; Smith, M.; Raes, D. Crop evapotranspiration estimation with FAO56: Past and future. Agric. Water Manag. 2014, 147, 4–20. [Google Scholar] [CrossRef]
- Suvočarev, K.; Blanco, O.; Faci, J.M.; Medina, E.T.; Martínez-Cob, A. Transpiration of table grape (Vitis vinifera L.) trained on an overhead trellis system under netting. Irrig. Sci. 2013, 31, 1289–1302. [Google Scholar] [CrossRef] [Green Version]
- Kamble, B.; Kilic, A.; Hubbard, K. Estimating crop coefficients using remote sensing-based vegetation index. Remote Sens. 2013, 5, 1588–1602. [Google Scholar] [CrossRef]
- Moriondo, M.; Jones, G.V.; Bois, B.; Dibari, C.; Ferrise, R.; Trombi, G.; Bindi, M. Projected shifts of wine regions in response to climate change. Clim. Chang. 2013, 119, 825–839. [Google Scholar] [CrossRef]
- Moriondo, M.; Ferrise, R.; Trombi, G.; Brilli, L.; Dibari, C.; Bindi, M. Modelling olive trees and grapevines in a changing climate. Environ. Model. Softw. 2015, 72, 387–401. [Google Scholar] [CrossRef]
- Campos, I.; Neale, C.M.U.; Calera, A.; Balbontín, C.; González-Piqueras, J. Assessing satellite-based basal crop coefficients for irrigated grapes (Vitis vinifera L.). Agric. Water Manag. 2010, 98, 45–54. [Google Scholar] [CrossRef]
- Galleguillos, M.; Jacob, F.; Prévot, L.; French, A.; Lagacherie, P. Comparison of two temperature differencing methods to estimate daily evapotranspiration over a Mediterranean vineyard watershed from ASTER data. Remote Sens. Environ. 2011, 115, 1326–1340. [Google Scholar] [CrossRef]
- Er-Raki, S.; Rodriguez, J.C.; Garatuza-Payan, J.; Watts, C.J.; Chehbouni, A. Determination of crop evapotranspiration of table grapes in a semi-arid region of Northwest Mexico using multi-spectral vegetation index. Agric. Water Manag. 2013, 122, 12–19. [Google Scholar] [CrossRef]
- D’Urso, G.; Richter, K.; Calera, A.; Osann, M.A.; Escadafal, R.; Garatuza-Pajan, J.; Hanich, L.; Perdigão, A.; Tapia, J.B.; Vuolo, F. Earth Observation products for operational irrigation management in the context of the PLEIADeS project. Agric. Water Manag. 2010, 98, 271–282. [Google Scholar] [CrossRef]
- Glenn, E.P.; Huete, A.R.; Nagler, P.L.; Nelson, S.G. Relationship between remotely-sensed vegetation indices, canopy attributes and plant physiological processes: What vegetation indices can and cannot tell us about the landscape. Sensors 2008, 8, 2136–2160. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Howell, T.A.; Jensen, M.E. Evapotranspiration information reporting: I. Factors governing measurement accuracy. Agric. Water Manag. 2011, 98, 899–920. [Google Scholar] [CrossRef]
- Er-Raki, S.; Chehbouni, A.; Guemouria, N.; Duchemin, B.; Ezzahar, J.; Hadria, R. Combining FAO-56 model and ground-based remote sensing to estimate water consumptions of wheat crops in a semi-arid region. Agric. Water Manag. 2007, 87, 41–54. [Google Scholar] [CrossRef]
- Er-Raki, S.; Chehbouni, A.; Duchemin, B. Combining satellite remote sensing data with the FAO-56 dual approach for water use mapping in irrigated wheat fields of a semi-arid region. Remote Sens. 2010, 2, 375–387. [Google Scholar] [CrossRef]
- Duchemin, B.; Hadria, R.; Erraki, S.; Boulet, G.; Maisongrande, P.; Chehbouni, A.; Escadafal, R.; Ezzahar, J.; Hoedjes, J.C.B.; Kharrou, M.H.; et al. Monitoring wheat phenology and irrigation in Central Morocco: On the use of relationships between evapotranspiration, crops coefficients, leaf area index and remotely-sensed vegetation indices. Agric. Water Manag. 2006, 79, 1–27. [Google Scholar] [CrossRef]
- Consoli, S.; Barbagallo, S. Estimating Water Requirements of an Irrigated Mediterranean Vineyard Using a Satellite-Based Approach. J. Irrig. Drain. Eng. 2012, 138, 896–904. [Google Scholar] [CrossRef]
- Rana, G.; Katerji, N.; Introna, M.; Hammami, A. Microclimate and plant water relationship of the “overhead” table grape vineyard managed with three different covering techniques. Sci. Hortic. (Amsterdam) 2004, 102, 105–120. [Google Scholar] [CrossRef]
- Justice, C.; Townshend, J. Special issue on the moderate resolution imaging spectroradiometer (MODIS): A new generation of land surface monitoring. Remote Sens. Environ. 2002, 83, 1–2. [Google Scholar] [CrossRef]
- Fandiño, M.; Cancela, J.J.; Rey, B.J.; Martínez, E.M.; Rosa, R.G.; Pereira, L.S. Using the dual-Kc approach to model evapotranspiration of Albariño vineyards (Vitis vinifera L. cv. Albariño) with consideration of active ground cover. Agric. Water Manag. 2012, 112, 75–87. [Google Scholar] [CrossRef]
- Vuolo, F.; D’Urso, G.; De Michele, C.; Bianchi, B.; Cutting, M. Satellite-based Irrigation Advisory Services: A common tool for different experiences from Europe to Australia. Agric. Water Manag. 2015, 147, 82–95. [Google Scholar] [CrossRef]
- ISTAT 6 Censimento Generale dell’Agricoltura. Available online: http://dati-censimentoagricoltura.istat.it/ (accessed on 3 July 2015).
- Vanino, S.; Nino, P.; De Michele, C.; Bolognesi, S.F.; Pulighe, G. Earth Observation for Improving Irrigation Water Management: A Case-study from Apulia Region in Italy. Agric. Agric. Sci. Procedia 2015, 4, 99–107. [Google Scholar] [CrossRef]
- Benedetti, A.; Teresa, M.; Abate, D.; Napoli, R. The Soils of Italy; Edoardo, A.C., Costantini, C.D., Eds.; Springer: Dordrecht, Netherlands, 2013. [Google Scholar]
- Winkler, A.J.; Cook, J.A.; Kliewer, W.M.; Lider, L.A. General Viticulture, 2nd ed.; University of California Press: Oakland, CA, USA, 1974. [Google Scholar]
- LI-COR. LAI-2000 Plant Canopy Analyzer Instruction Manual 1992. Available online: http://www.licor.com/env/products/leaf_area/LAI-2200/ (accessed on 3 July 2015).
- D’Urso, G. Simulation and Management of on-Demand Irrigation Systems: A Combined Agrohydrological and Remote Sensing Approach. PhD Thesis, Wageningen Agricultural University, Wageningen, Netherlands, 2001. [Google Scholar]
- Minacapilli, M.; Iovino, M.; D’Urso, G. A distributed agro-hydrological model for irrigation water demand assessment. Agric. Water Manag. 2008, 95, 123–132. [Google Scholar] [CrossRef]
- Minacapilli, M.; Agnese, C.; Blanda, F.; Cammalleri, C.; Ciraolo, G.; D’Urso, G.; Iovino, M.; Pumo, D.; Provenzano, G.; Rallo, G. Estimation of actual evapotranspiration of Mediterranean perennial crops by means of remote-sensing based surface energy balance models. Hydrol. Earth Syst. Sci. 2009, 13, 1061–1074. [Google Scholar] [CrossRef]
- Braden, H. Ein Energiehaushalts- und Verdunstungsmodell for Wasser und Stoffhaushaltsuntersuchungen landwirtschaftlich genutzer Einzugsgebiete. M. Dtsch. Bodenkd. Geselschaft 1985, 42, 294–299. [Google Scholar]
- FAO. Irrigation Scheduling: From Theory to Practice. In Water Reports 8, Proceedings of the ICID/FAO Workshop on Irrigation Scheduling, Rome, Italy, 12–13 September 1995; Food and Agriculture Organization of the United Nations: Rome, Italy, 1996. [Google Scholar]
- Akdim, N.; Alfieri, S.; Habib, A.; Choukri, A.; Cheruiyot, E.; Labbassi, K.; Menenti, M. Monitoring of Irrigation Schemes by Remote Sensing: Phenology versus Retrieval of Biophysical Variables. Remote Sens. 2014, 6, 5815–5851. [Google Scholar] [CrossRef]
- De Vries, C.; Danaher, T.; Denham, R.; Scarth, P.; Phinn, S. An operational radiometric calibration procedure for the Landsat sensors based on pseudo-invariant target sites. Remote Sens. Environ. 2007, 107, 414–429. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.; Pérez-Cabello, F.; Lasanta, T. Assessment of radiometric correction techniques in analyzing vegetation variability and change using time series of Landsat images. Remote Sens. Environ. 2008, 112, 3916–3934. [Google Scholar] [CrossRef]
- Richter, R. Atmospheric Correction Methodology for Imaging Spectrometer Data. In The Digital Airborne Spectrometer Experiment (DAISEX); Wooding, M., Harris, R.A., Eds.; European Space Agency: Noordwijk, The Netherlands, 2001. [Google Scholar]
- Bréda, N.J.J. Ground-based measurements of leaf area index: A review of methods, instruments and current controversies. J. Exp. Bot. 2003, 54, 2403–2417. [Google Scholar] [PubMed]
- Clevers, J.G.P.W. The application of a weighted infrared-red vegetation index for estimating leaf area index by correcting for soil moisture. Remote Sens. Environ. 1989, 29, 25–37. [Google Scholar] [CrossRef]
- Vuolo, F.; Neugebauer, N.; Bolognesi, S.F.; Atzberger, C.; D’Urso, G. Estimation of leaf area index using DEIMOS-1 data: Application and transferability of a semi-empirical relationship between two agricultural areas. Remote Sens. 2013, 5, 1274–1291. [Google Scholar] [CrossRef]
- Clevers, J.G.P.W. The derivation of a simplified reflectance model for the estimation of leaf area index. Remote Sens. Environ. 1988, 25, 53–69. [Google Scholar] [CrossRef]
- Jones, G.V.; Duff, A.A.; Hall, A.; Myers, J.W. Spatial Analysis of Climate in Winegrape Growing Regions in the Western United States. Am. J. Enol. Vitic. 2010, 61, 313–326. [Google Scholar]
- Ramos, M.C.; Martínez-Casasnovas, J.A. Effects of precipitation patterns and temperature trends on soil water available for vineyards in a Mediterranean climate area. Agric. Water Manag. 2010, 97, 1495–1505. [Google Scholar] [CrossRef]
- Williams, L.E. Interaction of applied water amounts and leaf removal in the fruiting zone on grapevine water relations and productivity of Merlot. Irrig. Sci. 2012, 30, 363–375. [Google Scholar] [CrossRef]
- Poblete-Echeverría, C.A.; Ortega-Farias, S.O. Evaluation of single and dual crop coefficients over a drip-irrigated Merlot vineyard (Vitis vinifera L.) using combined measurements of sap flow sensors and an eddy covariance system. Aust. J. Grape Wine Res. 2013, 19, 249–260. [Google Scholar] [CrossRef]
- Tomasi, D.; Jones, G.V.; Giust, M.; Lovat, L.; Gaiotti, F. Grapevine Phenology and Climate Change: Relationships and Trends in the Veneto Region of Italy for 1964–2009. Am. J. Enol. Vitic. 2011, 62, 329–339. [Google Scholar] [CrossRef]
- Baronti, S.; Vaccari, F.P.; Miglietta, F.; Calzolari, C.; Lugato, E.; Orlandini, S. Impact of biochar application on plant water relations in Vitis vinifera(L.). Eur. J. Agron. 2014, 53, 38–44. [Google Scholar] [CrossRef]
- Netzer, Y.; Yao, C.; Shenker, M.; Bravdo, B.A.; Schwartz, A. Water use and the development of seasonal crop coefficients for Superior Seedless grapevines trained to an open-gable trellis system. Irrig. Sci. 2009, 27, 109–120. [Google Scholar] [CrossRef]
- Lamaddalena, N.; Caliandro, A. Riorientamenti Produttivi del Territorio Agricolo Pugliese per uno Sviluppo Rurale Sostenibile: Promozione di Servizi Orientati allo Sviluppo Agricolo—Azione 3; Regione Puglia & CIHEAM Istituto agronomico mediterraneo di Bari: Valenzano, Italy, 2008. [Google Scholar]
- Villagra, P.; García de Cortázar, V.; Ferreyra, R.; Aspillaga, C.; Zuñiga, C.; Ortega-Farias, S.; Selles, G. Estimation of water requirements and Kc values of “Thompson Seedless” table grapes grown in the overhead trellis system, using the Eddy covariance metho. Chil. J. Agric. Res. 2014, 74, 213–218. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S. Estimating crop coefficients from fraction of ground cover and height. Irrig. Sci. 2009, 28, 17–34. [Google Scholar] [CrossRef]
- Moratiel, R.; Martínez-Cob, A. Evapotranspiration of grapevine trained to a gable trellis system under netting and black plastic mulching. Irrig. Sci. 2012, 30, 167–178. [Google Scholar] [CrossRef]
- De Azevedo, P.V.; Soares, J.M.; Da Silva, V.P.R.; Da Silva, B.B.; Nascimento, T. Evapotranspiration of “Superior” grapevines under intermittent irrigation. Agric. Water Manag. 2008, 95, 301–308. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vanino, S.; Pulighe, G.; Nino, P.; De Michele, C.; Bolognesi, S.F.; D’Urso, G. Estimation of Evapotranspiration and Crop Coefficients of Tendone Vineyards Using Multi-Sensor Remote Sensing Data in a Mediterranean Environment. Remote Sens. 2015, 7, 14708-14730. https://doi.org/10.3390/rs71114708
Vanino S, Pulighe G, Nino P, De Michele C, Bolognesi SF, D’Urso G. Estimation of Evapotranspiration and Crop Coefficients of Tendone Vineyards Using Multi-Sensor Remote Sensing Data in a Mediterranean Environment. Remote Sensing. 2015; 7(11):14708-14730. https://doi.org/10.3390/rs71114708
Chicago/Turabian StyleVanino, Silvia, Giuseppe Pulighe, Pasquale Nino, Carlo De Michele, Salvatore Falanga Bolognesi, and Guido D’Urso. 2015. "Estimation of Evapotranspiration and Crop Coefficients of Tendone Vineyards Using Multi-Sensor Remote Sensing Data in a Mediterranean Environment" Remote Sensing 7, no. 11: 14708-14730. https://doi.org/10.3390/rs71114708
APA StyleVanino, S., Pulighe, G., Nino, P., De Michele, C., Bolognesi, S. F., & D’Urso, G. (2015). Estimation of Evapotranspiration and Crop Coefficients of Tendone Vineyards Using Multi-Sensor Remote Sensing Data in a Mediterranean Environment. Remote Sensing, 7(11), 14708-14730. https://doi.org/10.3390/rs71114708