The Utility of AISA Eagle Hyperspectral Data and Random Forest Classifier for Flower Mapping
Abstract
:1. Introduction
2. Experimental Section
2.1. Study Area
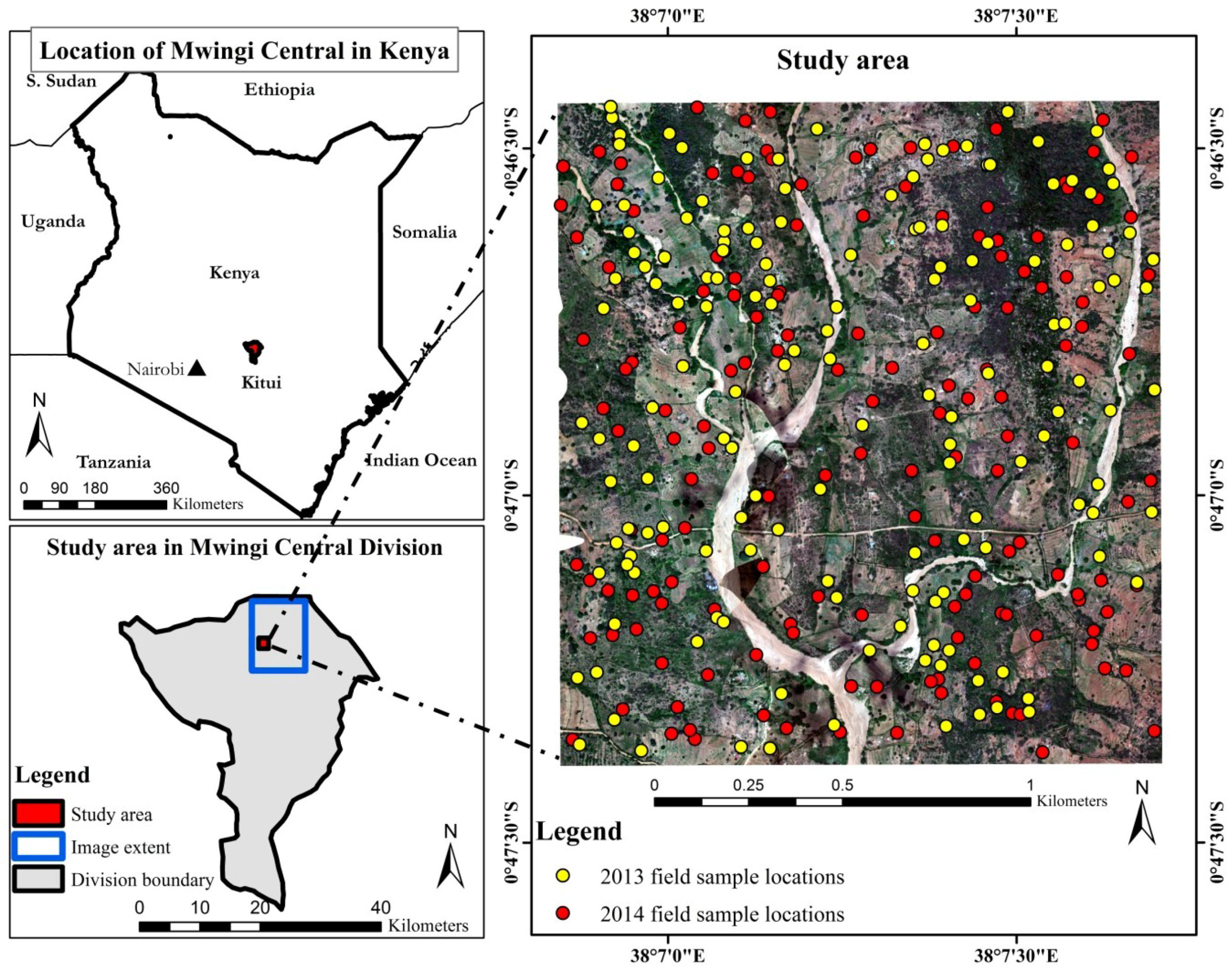
2.2. Image Acquisition and Pre-Processing
2.3. Field Data Collection
| Class | Code | 2013 | 2014 | ||||
|---|---|---|---|---|---|---|---|
| Training | Validation | Total | Training | Validation | Total | ||
| Yellow flowering trees | YF | 135 | 58 | 193 | 58 | 25 | 83 |
| White flowering trees | WF | 135 | 58 | 193 | 81 | 35 | 116 |
| Green (non-flowering) trees | GT | 133 | 57 | 190 | 116 | 50 | 166 |
| Shrubs | SR | 138 | 59 | 197 | 116 | 50 | 166 |
| Forbs (with white flowers) | FB | 128 | 55 | 183 | 81 | 35 | 116 |
| Cropland (maize and sorghum) | CL | NA | NA | NA | 58 | 25 | 83 |
| Brown (chlorophyll-inactive leaves) trees | BT | NA | NA | NA | 58 | 25 | 83 |
| Total | 669 | 287 | 956 | 568 | 245 | 813 | |
2.4. Random Forest Classification Algorithm
2.5. Variable Selection
2.6. Accuracy Assessment
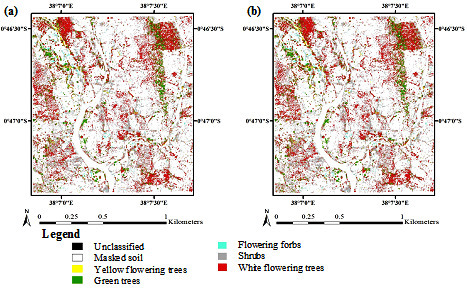
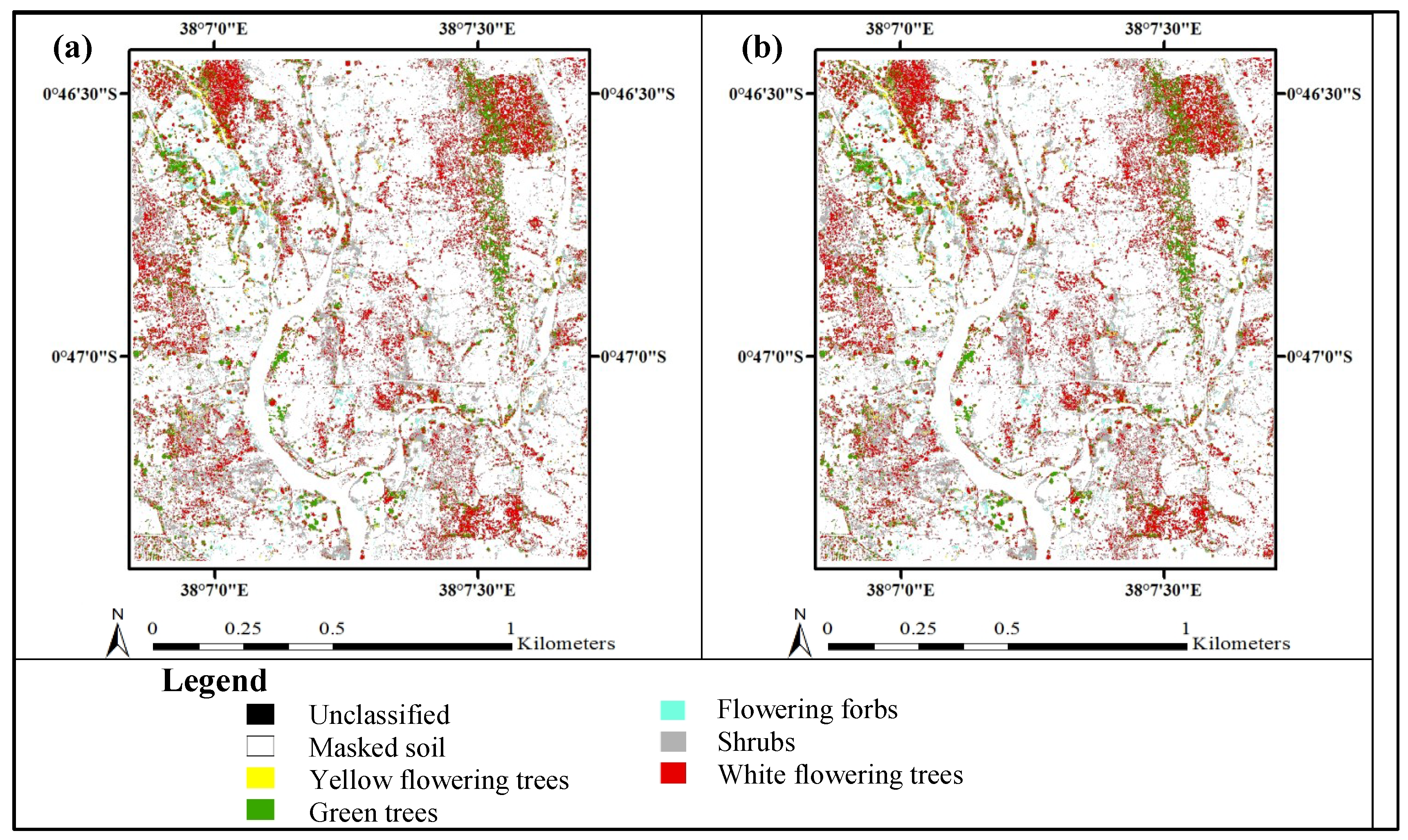
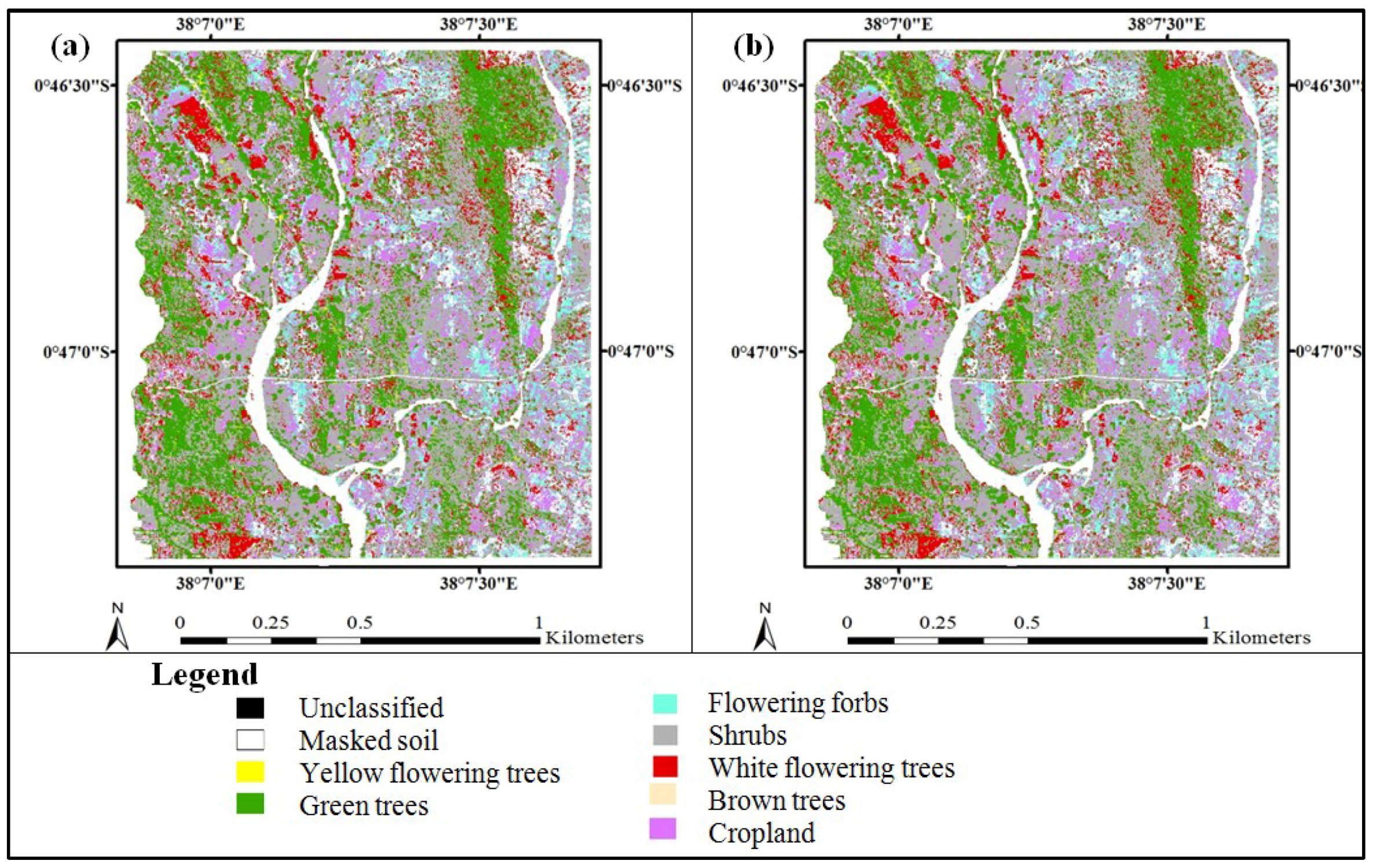
3. Results
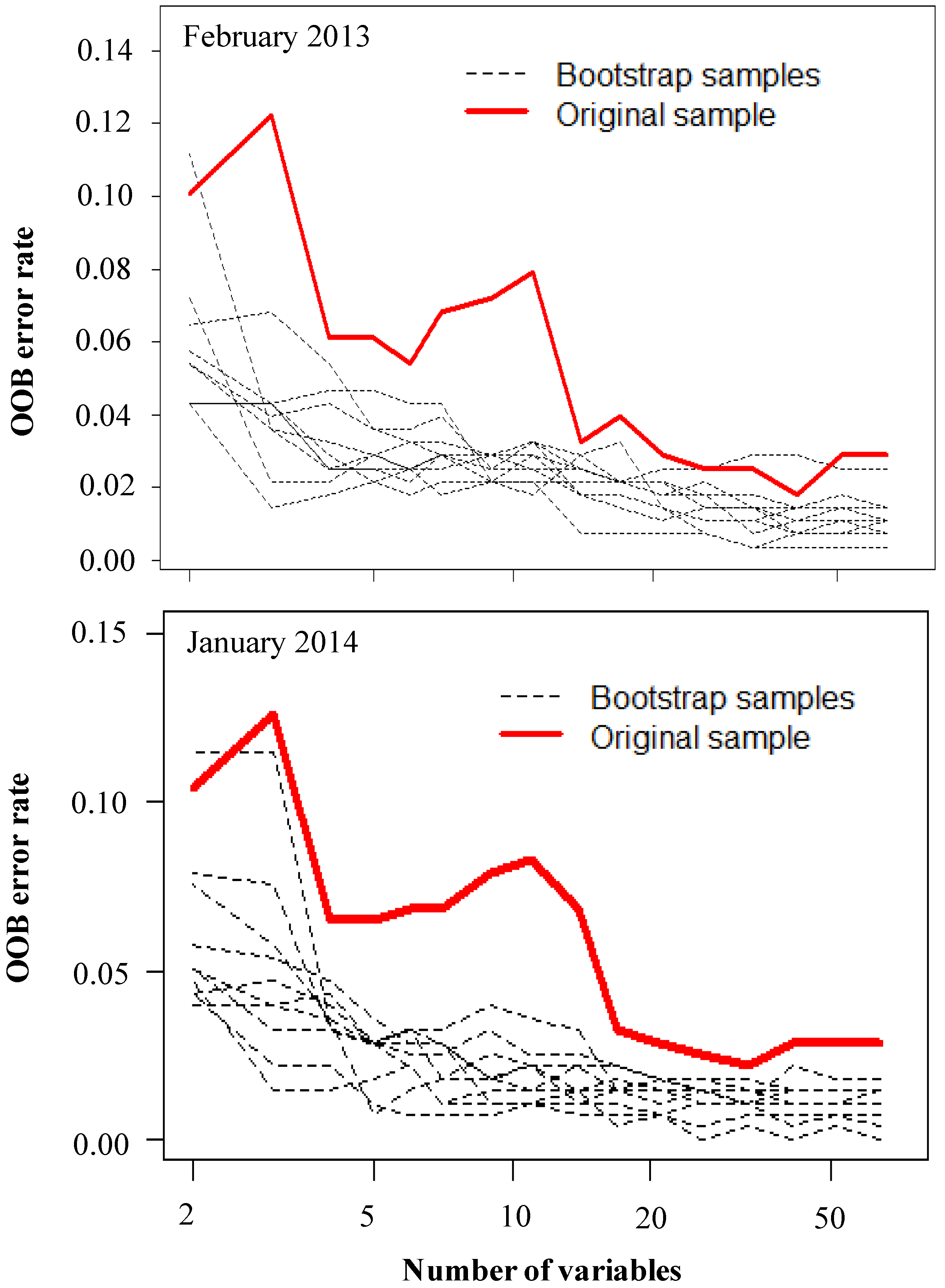
3.1. Optimization of Random Forest Classification Models
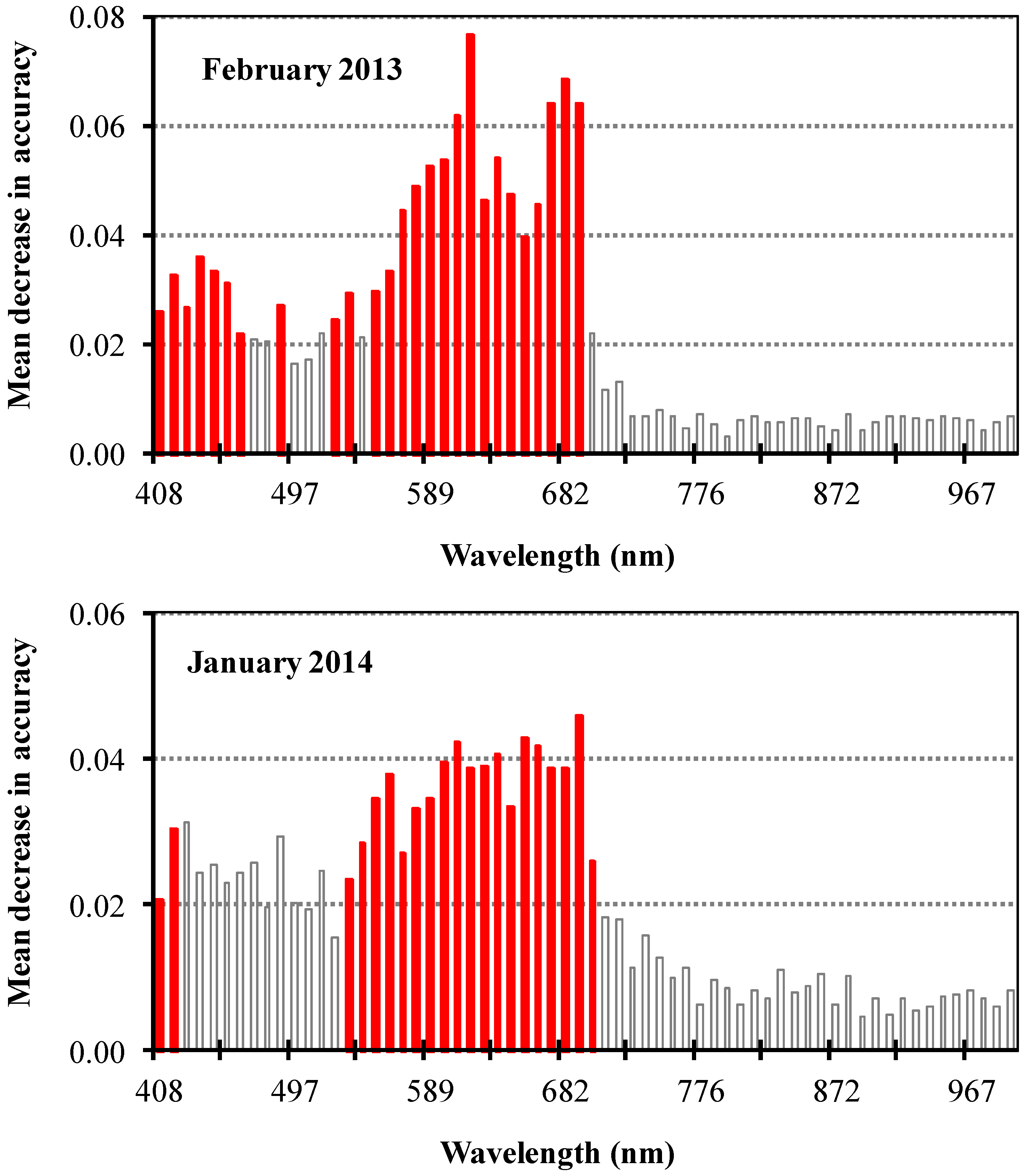
3.2. Spectral Band Selection
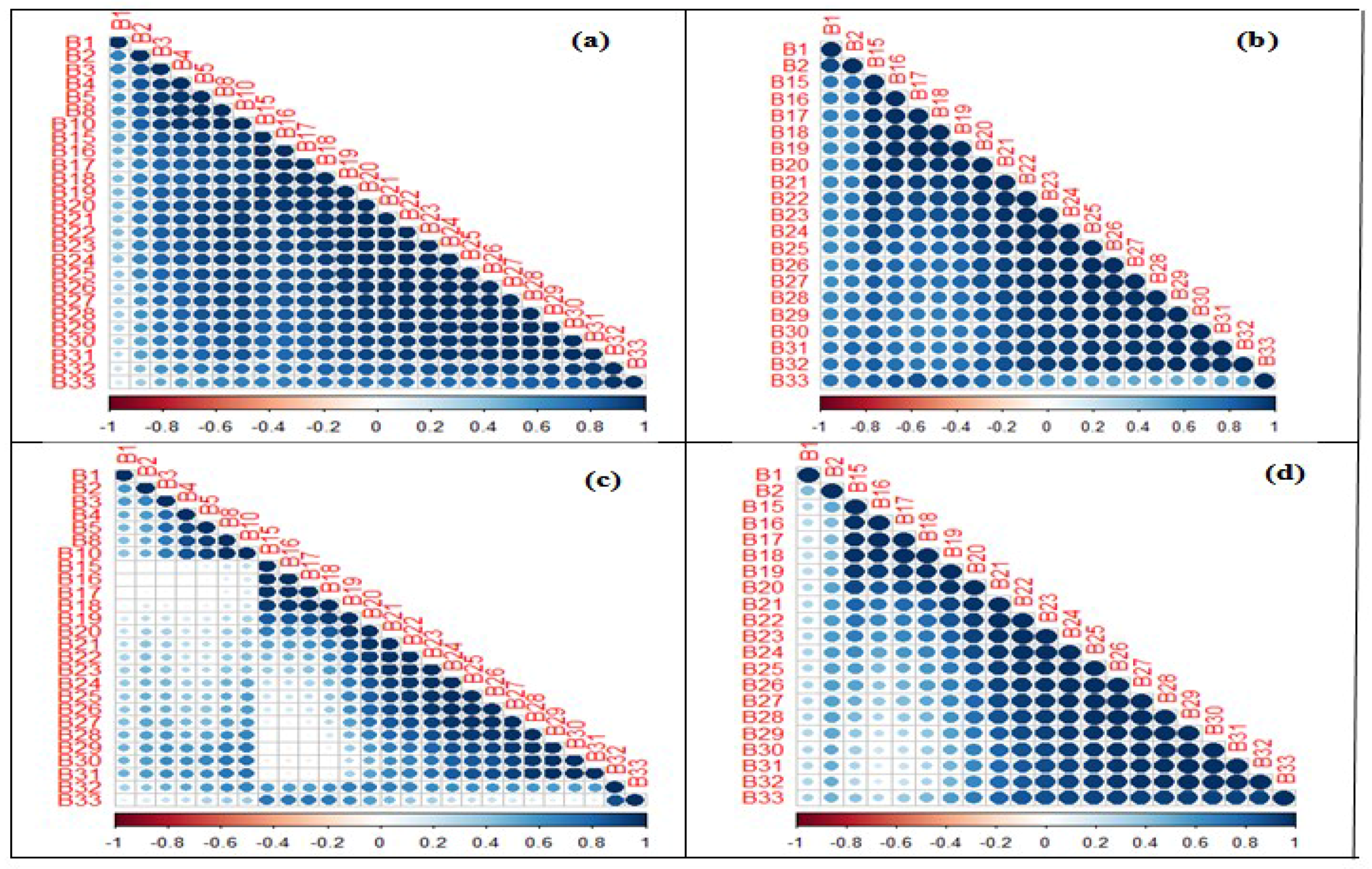
3.3. Accuracy Assessment
| Ground Truth | |||||||
|---|---|---|---|---|---|---|---|
| (a) Classified | WF | YF | GT | SHR | FB | Total | UA |
| Using all (n= 64) AISA Eagle wavebands | |||||||
| WF | 46 | 02 | 01 | 01 | 03 | 53 | 86.79 |
| YF | 02 | 50 | 01 | 00 | 02 | 55 | 90.91 |
| GT | 05 | 03 | 54 | 02 | 00 | 64 | 84.38 |
| SHR | 02 | 01 | 01 | 54 | 01 | 59 | 91.53 |
| FB | 03 | 02 | 00 | 02 | 49 | 56 | 87.50 |
| Total | 58 | 58 | 57 | 59 | 55 | 287 | |
| PA (%) | 76.67 | 83.33 | 90.00 | 90.00 | 89.09 | ||
| OA (%) | 88.15 | ||||||
| QD (%) | 03.00 | ||||||
| AD (%) | 09.00 | ||||||
| (b) | Using the most important (n = 26) AISA Eagle wavebands | ||||||
| WF | 44 | 03 | 02 | 02 | 03 | 54 | 81.48 |
| YF | 03 | 49 | 02 | 01 | 03 | 58 | 84.48 |
| GT | 04 | 02 | 52 | 02 | 00 | 60 | 86.67 |
| SHR | 03 | 02 | 01 | 53 | 01 | 60 | 88.33 |
| FB | 04 | 02 | 00 | 01 | 48 | 55 | 87.27 |
| Total | 58 | 58 | 58 | 58 | 55 | 287 | |
| PA (%) | 73.33 | 81.67 | 86.67 | 88.33 | 87.27 | ||
| OA (%) | 85.71 | ||||||
| QD (%) | 01.00 | ||||||
| AD (%) | 13.00 | ||||||
| Ground Truth | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| (a) Classified | WF | YF | GT | SHR | CR | BT | FB | Total | UA |
| Using all (n= 64) AISA Eagle wavebands | |||||||||
| WF | 18 | 01 | 01 | 01 | 01 | 01 | 01 | 24 | 75.00 |
| YF | 02 | 27 | 02 | 02 | 01 | 00 | 02 | 36 | 75.00 |
| GT | 02 | 02 | 44 | 01 | 00 | 01 | 00 | 50 | 88.00 |
| SHR | 01 | 01 | 01 | 43 | 00 | 01 | 00 | 47 | 91.49 |
| CR | 01 | 02 | 00 | 01 | 21 | 00 | 02 | 27 | 77.78 |
| BT | 01 | 00 | 02 | 01 | 00 | 22 | 00 | 26 | 84.62 |
| FB | 00 | 02 | 00 | 01 | 02 | 00 | 30 | 35 | 85.71 |
| Total | 25 | 35 | 50 | 50 | 25 | 25 | 35 | 245 | |
| PA (%) | 72.00 | 77.14 | 88.00 | 86.00 | 84.00 | 88.00 | 85.71 | ||
| OA (%) | 83.67 | ||||||||
| QD (%) | 02.00 | ||||||||
| AD (%) | 15.00 | ||||||||
| (b) | WF | YF | GT | SHR | CR | BT | FB | Total | UA |
| Using the most important (n = 21) AISA Eagle wavebands | |||||||||
| WF | 18 | 01 | 01 | 01 | 01 | 02 | 02 | 26 | 69.23 |
| YF | 02 | 26 | 02 | 03 | 02 | 00 | 03 | 38 | 68.42 |
| GT | 02 | 02 | 43 | 01 | 00 | 01 | 00 | 49 | 87.76 |
| SHR | 01 | 02 | 02 | 42 | 00 | 01 | 00 | 48 | 87.50 |
| CR | 01 | 02 | 00 | 01 | 20 | 00 | 02 | 26 | 76.92 |
| BT | 01 | 00 | 02 | 01 | 00 | 21 | 00 | 25 | 84.00 |
| FB | 00 | 02 | 00 | 01 | 02 | 00 | 28 | 33 | 84.85 |
| Total | 25 | 35 | 50 | 50 | 25 | 25 | 35 | 245 | |
| PA (%) | 72.00 | 74.29 | 86.00 | 84.00 | 80.00 | 84.00 | 80.00 | ||
| OA (%) | 80.82 | ||||||||
| QD (%) | 02.00 | ||||||||
| AD (%) | 17.00 | ||||||||
| Ground Truth | |||||||
|---|---|---|---|---|---|---|---|
| (a) Classified | WF | YF | GT | SHR | FB | Total | UA |
| Using all (n= 64) AISA Eagle wavebands | |||||||
| WF | 08 | 10 | 15 | 07 | 06 | 46 | 17.39 |
| YF | 06 | 12 | 11 | 08 | 06 | 43 | 27.91 |
| GT | 04 | 04 | 19 | 13 | 04 | 44 | 43.18 |
| SHR | 03 | 05 | 03 | 20 | 05 | 36 | 55.56 |
| FB | 04 | 04 | 02 | 02 | 14 | 26 | 53.85 |
| Total | 25 | 35 | 50 | 50 | 35 | 195 | |
| PA (%) | 13.33 | 20.00 | 31.67 | 33.33 | 40.00 | ||
| OA (%) | 37.44 | ||||||
| QD (%) | 18.00 | ||||||
| AD (%) | 45.00 | ||||||
| (b) | Using the most important (n = 21) AISA Eagle wavebands | ||||||
| WF | 05 | 12 | 17 | 09 | 10 | 53 | 09.43 |
| YF | 06 | 09 | 13 | 10 | 07 | 45 | 20.00 |
| GT | 04 | 06 | 14 | 16 | 04 | 44 | 31.82 |
| SHR | 06 | 05 | 04 | 13 | 06 | 34 | 38.24 |
| FB | 04 | 03 | 02 | 02 | 08 | 19 | 42.11 |
| Total | 25 | 35 | 50 | 50 | 35 | 195 | |
| PA (%) | 08.33 | 15.00 | 23.33 | 21.67 | 22.86 | ||
| OA (%) | 25.13 | ||||||
| QD (%) | 19.00 | ||||||
| AD (%) | 55.00 | ||||||
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Sammataro, D.; Weiss, M. Comparison of productivity of colonies of honey bees, Apis mellifera, supplemented with sucrose or high fructose corn syrup. J. Insect Sci. 2013, 13. [Google Scholar] [CrossRef] [PubMed]
- Sponsler, D.B.; Johnson, R.M. Honey bee success predicted by landscape composition in Ohio, USA. PeerJ 2015, 3. [Google Scholar] [CrossRef] [PubMed]
- Raina, S.K.; Kioko, E.; Zethner, O.; Wren, S. Forest habitat conservation in Africa using commercially important insects. Annu. Rev. Entomol. 2011, 56, 465–485. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Shen, M.; Zhu, X.; Tang, Y. Indicator of flower status derived from in situ hyperspectral measurement in an alpine meadow on the Tibetan Plateau. Ecol. Indic. 2009, 9, 818–823. [Google Scholar] [CrossRef]
- Decourtye, A.; Mader, E.; Desneux, N. Landscape enhancement of floral resources for honey bees in agro-ecosystems. Apidologie 2010, 41, 264–277. [Google Scholar] [CrossRef]
- Fitter, A.; Fitter, R. Rapid changes in flowering time in British plants. Science 2002, 296, 1689–1691. [Google Scholar] [CrossRef] [PubMed]
- Houle, G. Spring-flowering herbaceous plant species of the deciduous forests of eastern Canada and 20th century climate warming. Can. J. For. Res. 2007, 37, 505–512. [Google Scholar] [CrossRef]
- Landmann, T.; Piiroinen, R.; Makori, D.M.; Abdel-Rahman, E.M.; Makau, S.; Pellikka, P.; Raina, S.K. Application of hyperspectral remote sensing for flower mapping in African savannas. Remote Sens. Environ. 2015, 166, 50–60. [Google Scholar] [CrossRef]
- Kumar, L.; Dury, S.J.; Schmidt, K.; Skidmore, A. Imaging spectrometry and vegetation science. In Image Spectrometry; van der Meer, F.D., de Jong, S.M., Eds.; Kluwer Academic Publishers: London, UK, 2003; pp. 111–156. [Google Scholar]
- Lillesand, T.M.; Kiefer, R.W. Remote Sensing and Image Interpretation, 4th ed.; John Wiley & Sons Inc.: New York, NY, USA, 2001. [Google Scholar]
- Naidoo, L.; Cho, M.; Mathieu, R.; Asner, G. Classification of savanna tree species, in the Greater Kruger National Park region, by integrating hyperspectral and LiDAR data in a Random Forest data mining environment. ISPRS J. Photogramm. Remote Sens. 2012, 69, 167–179. [Google Scholar] [CrossRef]
- Cho, M.A.; Mathieu, R.; Asner, G.P.; Naidoo, L.; van Aardt, J.; Ramoelo, A.; Debba, P.; Wessels, K.; Main, R.; Smit, I.P. Mapping tree species composition in South African savannas using an integrated airborne spectral and LiDAR system. Remote Sens. Environ. 2012, 125, 214–226. [Google Scholar] [CrossRef]
- Giurfa, M.; Nunez, J.; Chittka, L.; Menzel, R. Colour preferences of flower-naive honeybees. J. Comp. Physiol. 1995, 177, 247–259. [Google Scholar] [CrossRef]
- Cnaani, J.; Thomson, J.D.; Papaj, D.R. Flower choice and learning in foraging bumblebees: Effects of variation in nectar volume and concentration. Ethology 2006, 112, 278–285. [Google Scholar] [CrossRef]
- Weng, Q. Advances in Environmental Remote Sensing: Sensors, Algorithms, and Applications; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Thenkabail, P.S.; Lyon, J.G.; Huete, A. Hyperspectral Remote Sensing of Vegetation; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Christian, B.; Krishnayya, N. Classification of tropical trees growing in a sanctuary using Hyperion (EO-1) and SAM algorithm. Curr. Sci. 2009, 96, 1601–1607. [Google Scholar]
- Féret, J.; Asner, G.P. Tree species discrimination in tropical forests using airborne imaging spectroscopy. IEEE Trans. Geosci. Remote Sens. 2013, 51, 73–84. [Google Scholar] [CrossRef]
- Prospere, K.; McLaren, K.; Wilson, B. Plant species discrimination in a tropical wetland using in situ hyperspectral data. Remote Sens. 2014, 6, 8494–8523. [Google Scholar] [CrossRef]
- Plaza, A.; Benediktsson, J.A.; Boardman, J.W.; Brazile, J.; Bruzzone, L.; Camps-Valls, G.; Chanussot, J.; Fauvel, M.; Gamba, P.; Gualtieri, A. Recent advances in techniques for hyperspectral image processing. Remote Sens. Environ. 2009, 113, S110–S122. [Google Scholar] [CrossRef]
- Ham, J.; Chen, Y.; Crawford, M.; Ghosh, J. Investigation of the random forest framework for classification of hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2005, 43, 492–501. [Google Scholar] [CrossRef]
- Lawrence, R.L.; Wood, S.D.; Sheley, R.L. Mapping invasive plants using hyperspectral imagery and Breiman Cutler classifications (randomForest). Remote Sens. Environ. 2006, 100, 356–362. [Google Scholar] [CrossRef]
- Chan, J.C.W.; Paelinckx, D. Evaluation of Random Forest and Adaboost tree-based ensemble classification and spectral band selection for ecotope mapping using airborne hyperspectral imagery. Remote Sens. Environ. 2008, 112, 2999–3011. [Google Scholar] [CrossRef]
- Waske, B.; Benediktsson, J.A.; Ãrnason, K.; Sveinsson, J.R. Mapping of hyperspectral AVIRIS data using machine-learning algorithms. Can. J. Remote Sens. 2009, 35, 106–116. [Google Scholar] [CrossRef]
- Ramoelo, A.; Skidmore, A.; Cho, M.; Mathieu, R.; Heitkönig, I.; Dudeni-Tlhone, N.; Schlerf, M.; Prins, H. Non-linear partial least square regression increases the estimation accuracy of grass nitrogen and phosphorus using in situ hyperspectral and environmental data. ISPRS J. Photogramm. Remote Sens. 2013, 82, 27–40. [Google Scholar] [CrossRef]
- Abdel-Rahman, E.M.; Mutanga, O.; Adam, E.; Ismail, R. Detecting Sirex noctilio grey-attacked and lightning-struck pine trees using airborne hyperspectral data, random forest and support vector machines classifiers. ISPRS J. Photogramm. Remote Sens. 2014, 88, 48–59. [Google Scholar] [CrossRef]
- Ngugi, R.K. Use of Indigenous and Contemporary Knowledge on Climate and Drought Forecasting Information in Mwingi District, Kenya; A Report to UNDP; College of Agriculture and Veterinary Science, University of Nairobi: Nairobi, Kenya, 1999. [Google Scholar]
- Raina, S.; Kimbu, D. Variations in races of the honeybee Apis mellifera (Hymenoptera: Apidae) in Kenya. Int. J. Trop. Insect Sci. 2005, 25, 281–291. [Google Scholar] [CrossRef]
- Delaplane, K.S. Honey Bees and Beekeeping; A Report of Cooperative Extension; College of Agricultural and Environmental Sciences, College of Family and Consumer Sciences, The University of Georgia: Athens, GA, USA, 2010. [Google Scholar]
- Williams, G.R.; Tarpy, D.R.; Vanengelsdorp, D.; Chauzat, M.P.; Cox-Foster, D.L.; Delaplane, K.S.; Neumann, P.; Pettis, J.S.; Rogers, R.E.; Shutler, D. Colony collapse disorder in context. Bioessays 2010, 32, 845–846. [Google Scholar] [CrossRef] [PubMed]
- Fening, K.O.; Kioko, E.N.; Raina, S.K.; Mueke, J.M. Monitoring wild silkmoth, Gonometa postica Walker, abundance, host plant diversity and distribution in Imba and Mumoni woodlands in Mwingi, Kenya. Int. J. Biodivers. Sci. Manage. 2008, 4, 104–111. [Google Scholar] [CrossRef]
- Muya, B.I. Determinants of Adoption of Modern Technologies in Beekeeping Projects: The Case of Women Groups in Kajiado County, Kenya. Master’s Thesis, University of Nairobi, Nairobi, Kenya, 2014. [Google Scholar]
- Gao, B.C.; Montes, M.J.; Davis, C.O.; Goetz, A.F. Atmospheric correction algorithms for hyperspectral remote sensing data of land and ocean. Remote Sens. Environ. 2009, 113, S17–S24. [Google Scholar] [CrossRef]
- Richter, R.; Schläpfer, D. Geo-atmospheric processing of airborne imaging spectrometry data. Part 2: Atmospheric/topographic correction. Int. J. Remote Sens. 2002, 23, 2631–2649. [Google Scholar] [CrossRef]
- Guanter, L.; Richter, R.; Kaufmann, H. On the application of the MODTRAN4 atmospheric radiative transfer code to optical remote sensing. Int. J. Remote Sens. 2009, 30, 1407–1427. [Google Scholar] [CrossRef]
- Mannschatz, T.; Pflug, B.; Borg, E.; Feger, K.-H.; Dietrich, P. Uncertainties of LAI estimation from satellite imaging due to atmospheric correction. Remote Sens. Environ. 2014, 153, 24–39. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Liaw, A.; Weiner, M. Classification and regression by randomForest. R News. 2002, 2, 18–22. [Google Scholar]
- Statnikov, A.; Wang, L.; Aliferis, C.F. A comprehensive comparison of random forests and support vector machines for microarray-based cancer classification. BMC Bioinf. 2008, 9, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Prasad, A.; Iverson, L.; Liaw, A. Newer classification and regression tree techniques: Bagging and random forests for ecological prediction. Ecosystems 2006, 9, 181–199. [Google Scholar] [CrossRef]
- Guo, L.; Chehata, N.; Mallet, C.; Boukir, S. Relevance of airborne lidar and multispectral image data for urban scene classification using Random Forests. ISPRS J. Photogramm. Remote Sens. 2011, 66, 56–66. [Google Scholar] [CrossRef]
- Qi, Y. Random forest for bioinformatics. In Ensemble Machine Learning: Methods and Applications; Zhang, C., Ma, Y., Eds.; Springer: Berlin, Germany, 2012; pp. 307–323. [Google Scholar]
- R Development Core Team. R: A Language and Environment for Statistical Computing, R Foundation for Statistical Computing. Available online: http://www.R-project.org (accessed on 20 April 2015).
- Diaz-Uriarte, R. Package “varSelRF”. Available online: http://ligarto.org/rdiaz/Software/Software.html (accessed on 20 April 2015).
- Efron, B.; Tibshirani, R. Improvements on cross-validation: The .632+ bootstrap method. J. Am. Stat. Assoc. 1997, 92, 548–560. [Google Scholar]
- Diaz-Uriarte, R.; Alvarez de Andres, S. Gene selection and classification of microarray data using random forest. BMC Bioinf. 2006, 7, 1–13. [Google Scholar]
- Deng, H.; Runger, G. Feature selection via regularized trees. In Proceedings of the 2012 International Joint Conference on Neural Networks (IJCNN), Brisbane, QLD, Australia, 10–15 June 2012.
- Adam, E.; Mutanga, O.; Ismail, R. Determining the susceptibility of Eucalyptus nitens forests to Coryphodema tristis (cossid moth) occurrence in Mpumalanga, South Africa. Int. J. Geogr. Inf. Sci. 2013, 27, 1924–1938. [Google Scholar] [CrossRef]
- Cohen, J.A. Coefficient of agreement for nominal scales. Educ. Psychol. Meas. 1960, 20, 37–46. [Google Scholar] [CrossRef]
- Congalton, R.G.; Green, K. Assessing the Accuracy of Remotely Sensed Data: Principles and Practices; Lewis Publishers: Boca Raton, FL, USA, 1999. [Google Scholar]
- Pontius, R.G.; Millones, M. Death to Kappa: Birth of quantity disagreement and allocation disagreement for accuracy assessment. Int. J. Remote Sens. 2011, 32, 4407–4429. [Google Scholar] [CrossRef]
- Foody, G.M. Thematic map comparison: Evaluating the statistical significance of differences in classification accuracy. Photogramm. Eng. Remote Sens. 2004, 70, 627–633. [Google Scholar] [CrossRef]
- Abdel-Rahman, E.M.; Ahmed, F.B.; Ismail, R. Random forest regression and spectral band selection for estimating sugarcane leaf nitrogen concentration using EO-1 Hyperion hyperspectral data. Int. J. Remote Sens. 2013, 34, 712–728. [Google Scholar] [CrossRef]
- Ge, S.; Everitt, J.; Carruthers, R.; Gong, P.; Anderson, G. Hyperspectral characteristics of canopy components and structure for phenological assessment of an invasive weed. Environ. Monit. Assess. 2006, 120, 109–126. [Google Scholar] [CrossRef] [PubMed]
- Filella, I.; Penuelas, J. The red edge position and shape as indicators of plant chlorophyll content, biomass and hydric status. Int. J. Remote Sens. 1994, 15, 1459–1470. [Google Scholar] [CrossRef]
- Anderson, J.R.; Hardy, E.E.; Roach, J.T.; Witmer, R.E. A Land Use and Land Cover Classification System for Use with Remote Sensor Data; US Government Printing Office: Washington, DC, USA, 1976; Volume 964. [Google Scholar]
- Olofsson, P.; Foody, G.M.; Stehman, S.V.; Woodcock, C.E. Making better use of accuracy data in land change studies: Estimating accuracy and area and quantifying uncertainty using stratified estimation. Remote Sens. Environ. 2013, 129, 122–131. [Google Scholar] [CrossRef]
- Petropoulos, G.P.; Manevski, K.; Carlson, T.N. Hyperspectral remote sensing with emphasis on land cover mapping: From ground to satellite observations. In Scale Issues in Remote Sensing; Weng, Q., Ed.; John Wiley & Sons Inc.: Oxford, UK, 2014; pp. 285–320. [Google Scholar]
- De Jong, S.M.; Hornstra, T.; Maas, H.G. An integrated spatial and spectral approach to the classification of Mediterranean land cover types: The SSC method. Int. J. Appl. Earth Obs. Geoinf. 2001, 3, 176–183. [Google Scholar] [CrossRef]
- Ouyang, Z.T.; Zhang, M.Q.; Xie, X.; Shen, Q.; Guo, H.Q.; Zhao, B. A comparison of pixel-based and object-oriented approaches to VHR imagery for mapping saltmarsh plants. Ecol. Inform. 2011, 6, 136–146. [Google Scholar] [CrossRef]
- Piiroinen, R.; Heiskanen, J.; Mõttus, M.; Pellikka, P. Classification of crops across heterogeneous agricultural landscape in Kenya using AisaEAGLE imaging spectroscopy data. Int. J. Appl. Earth Obs. Geoinf. 2015, 39, 1–8. [Google Scholar] [CrossRef]
- Dormann, C.F.; Elith, J.; Bacher, S.; Buchmann, C.; Carl, G.; Carré, G.; Marquéz, J.R.G.; Gruber, B.; Lafourcade, B.; Leitão, P.J. Collinearity: A review of methods to deal with it and a simulation study evaluating their performance. Ecography 2013, 36, 27–46. [Google Scholar] [CrossRef]
- Dongock, N.; Tchoumboue, J.; Youmbi, E.; Zapfack, L.; Mapongmentsem, P.; Tchuenguem, F. Predominant melliferous plants of the western Sudano Guinean zone of Cameroon. AJEST 2011, 5, 443–447. [Google Scholar]
- Abou-Shaara, H. Continuous management of varroa mite in honey bee, Apis. mellifera, colonies. Acarina 2014, 22, 149–156. [Google Scholar]
- Tashev, A.; Pancheva, E. The Melliferous plants of the Bulgarian flora—Conservation importance. For. Ideas 2011, 17, 228–237. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdel-Rahman, E.M.; Makori, D.M.; Landmann, T.; Piiroinen, R.; Gasim, S.; Pellikka, P.; Raina, S.K. The Utility of AISA Eagle Hyperspectral Data and Random Forest Classifier for Flower Mapping. Remote Sens. 2015, 7, 13298-13318. https://doi.org/10.3390/rs71013298
Abdel-Rahman EM, Makori DM, Landmann T, Piiroinen R, Gasim S, Pellikka P, Raina SK. The Utility of AISA Eagle Hyperspectral Data and Random Forest Classifier for Flower Mapping. Remote Sensing. 2015; 7(10):13298-13318. https://doi.org/10.3390/rs71013298
Chicago/Turabian StyleAbdel-Rahman, Elfatih M., David M. Makori, Tobias Landmann, Rami Piiroinen, Seif Gasim, Petri Pellikka, and Suresh K. Raina. 2015. "The Utility of AISA Eagle Hyperspectral Data and Random Forest Classifier for Flower Mapping" Remote Sensing 7, no. 10: 13298-13318. https://doi.org/10.3390/rs71013298
APA StyleAbdel-Rahman, E. M., Makori, D. M., Landmann, T., Piiroinen, R., Gasim, S., Pellikka, P., & Raina, S. K. (2015). The Utility of AISA Eagle Hyperspectral Data and Random Forest Classifier for Flower Mapping. Remote Sensing, 7(10), 13298-13318. https://doi.org/10.3390/rs71013298