Defining the Spatial Resolution Requirements for Crop Identification Using Optical Remote Sensing
Abstract
: The past decades have seen an increasing demand for operational monitoring of crop conditions and food production at local to global scales. To properly use satellite Earth observation for such agricultural monitoring, high temporal revisit frequency over vast geographic areas is necessary. However, this often limits the spatial resolution that can be used. The challenge of discriminating pixels that correspond to a particular crop type, a prerequisite for crop specific agricultural monitoring, remains daunting when the signal encoded in pixels stems from several land uses (mixed pixels), e.g., over heterogeneous landscapes where individual fields are often smaller than individual pixels. The question of determining the optimal pixel sizes for an application such as crop identification is therefore naturally inclined towards finding the coarsest acceptable pixel sizes, so as to potentially benefit from what instruments with coarser pixels can offer. To answer this question, this study builds upon and extends a conceptual framework to quantitatively define pixel size requirements for crop identification via image classification. This tool can be modulated using different parameterizations to explore trade-offs between pixel size and pixel purity when addressing the question of crop identification. Results over contrasting landscapes in Central Asia demonstrate that the task of finding the optimum pixel size does not have a “one-size-fits-all” solution. The resulting values for pixel size and purity that are suitable for crop identification proved to be specific to a given landscape, and for each crop they differed across different landscapes. Over the same time series, different crops were not identifiable simultaneously in the season and these requirements further changed over the years, reflecting the different agro-ecological conditions the crops are growing in. Results indicate that sensors like MODIS (250 m) could be suitable for identifying major crop classes in the study sites, whilst sensors like Landsat (30 m) should be considered for object-based classification. The proposed framework is generic and can be applied to any agricultural landscape, thereby potentially serving to guide recommendations for designing dedicated EO missions that can satisfy the requirements in terms of pixel size to identify and discriminate crop types.1. Introduction
Agriculture is mankind’s primary source of food production and plays the key role for cereal supply to humanity. One of the future challenges will be to feed a constantly growing population, which is expected to reach more than nine billion by 2050 [1]. This will lead to an increasing demand for food, which only can be met by boosting agricultural production [2]. Critically the potential to expand cropland is limited and changes in the climate system can further exaggerate the future pressure on freshwater resources, e.g., through reshaping the pattern of water availability [3]. These trends suggest an increasing demand for dependable, accurate and comprehensive agricultural intelligence on crop production. Agricultural production monitoring can support decision-making and prioritization efforts towards ameliorating vulnerable parts of agricultural systems. The value of satellite Earth observation (EO) data in agricultural monitoring is well recognized [4] and a variety of methods have been developed in the last decades to provide agricultural production related statistics [5,6]. However, spatially explicit monitoring of agricultural production requires routinely updated information on the total surface under cultivation, and sometimes the spatial distribution of crops as input [4,7]. This underlines the need for developing accurate and effective methods to map and monitor the distribution of agricultural lands and crop types (crop mapping).
Monitoring crop conditions and food production from local to global scales is at the heart of many modern economic, geostrategic and humanitarian concerns. Remote sensing is a valuable resource in monitoring agricultural production because it provides variables that are strongly linked with the two main components of crop production, namely crop acreage and yield [8]. Mapping the spatial distribution of crops in an accurate and timely manner is a fundamental input for agricultural production monitoring (and for derived application such as producing early warnings of harvest shortfalls), especially for systems relying on satellite EO to monitor agricultural resources [4,7]. The traditional way to retrieve such crop maps is by classifying an image, or a series of images, using one of the widely known classifier concepts and algorithms that are currently available [9]. Examples include statistical (parametric) methods like maximum likelihood classifier (MLC) [10,11] or non-parametric “machine learners” like random forest (RF) and support vector machines (SVM) [12–14].
The concept of crop mapping can have different interpretations depending on the application. Some require delineating accurately where all crops are located over the entire area of interest. This is necessary for producing accurate crop specific masks [15], or it can be a prerequisite for acreage estimations [16]. Object-based image analysis based on high-resolution images has shown great potential for this task [17]. Other applications, like crop monitoring, do not require a spatially exhaustive classification that includes the delineation of other (non-crop) land uses or natural land cover. Past studies have shown how only an adequate cropland mask is needed to considerably improve either classification accuracy and acreage estimations [18] or yield estimations [19,20]. Research has further shown how focusing on a population of crop specific time series by choosing only those pixels falling adequately into the agricultural fields allows the correct characterization of the crop behavior even in highly heterogeneous landscapes [21,22]. Since this paper targets crop-monitoring applications, the interest is geared towards this notion of crop identification for subsequent crop-specific monitoring rather than exhaustive crop mapping.
Image masking is a crucial step to restrict the analysis to a subset of a region’s pixels or time series rather than using all of the pixels in the scene. Several techniques for creating cropland masks were proposed where all sufficiently “cropped” pixels were included in the mask regardless of crop type, so the signal remained non-crop specific [18]. Yet, the challenge of discriminating pixels that correspond to a particular crop type within such cropland masks remains daunting when the signal encoded in pixels stem from several land uses (mixed pixels), e.g., over heterogeneous landscapes were individual fields are often smaller than individual pixels. Depending on the degree of mixing (or purity) this can result in large differences in classification accuracy [23], which means that pixels characterized by different purities might not be equally reliable for discriminating the classes under investigation [24].
But what type of remote sensing data, with respect to spatial resolution, should be used as classification input? Monitoring agriculture at regional to global scales with remote sensing requires the use of sensors that can provide information over large geographic extends with a sufficiently large swath. The data also requires the capacity to provide crop specific information with an adequate spatial resolution for proper crop classification. Up to now, a good candidate that can satisfy these requirements has been AWiFS, which has been used to generate some of the Cropland Data Layer products in the United States [25]. Undoubtedly, the new and upcoming satellite EO systems, such as RapidEye, Landsat-8 and Sentinel-2, provide new opportunities for agricultural applications. Although they may not entirely satisfy by themselves the requirements for crop growth monitoring, which typically needs higher temporal resolution than what they can provide individually [26], they should be capable of handling crop identification over a wide scale if used in a synchronized way. Despite the rise of such systems with relatively high revisit, coarser sensors such as MODIS, PROBA-V and Sentinel-3/OLCI (and MERIS for the past) should not be discarded. Not only do they provide added information with the higher repetitivity, but also those such as MODIS and MERIS will retain much importance as a source of long-term historical record, e.g., as archives of crop specific time series for the past years that can be very valuable for agricultural monitoring, and which the new systems will not achieve for decades to come [22,27].
The necessity for a continued exploitation of coarser spatial resolution data, plus the growing interest in exploiting multi-scale data synergistically, drive the reasoning for the subject of this paper: to explore the spatial resolution requirements for the specific task of crop identification and proper crop discrimination via image classification. Although defining suitable pixel sizes for remote sensing applications has a long tradition of research [28–33], numerous authors have pointed out how spatial resolution is a complex concept that depends on the instrument’s spatial response [31,34–37]. Although smaller pixels are preferred to assure a good delineation and to reduce the amount of mixed pixels, increasing the spatial resolution may lead to oversampling, resulting in increased within-feature or class variability. Such variation can lead to error in feature identification [23,38,39], and better classification accuracies may sometimes be attained using coarser pixel sizes [28]. On the other side, classification quality can deteriorate when selecting pixel sizes that are too coarse since this can result in excessively mixed pixels when the heterogeneity of the land cover class in one pixel increases [23,40]. However, it has been questioned if selecting one single spatial resolution is appropriate for a single remotely sensed image [38,41,42]. Furthermore, [43] and [31] illustrated how, for a given application like crop area estimation, the spatial resolution and purity requirement differs considerably over different landscapes.
To analyze the spatial resolution requirements for crop identification and proper crop discrimination, this study builds upon and extents a conceptual framework established in a previous work of [31]. That framework is based on simulating how agricultural landscapes, and more specifically the fields covered by one crop of interest, are seen by instruments with increasingly coarser resolving power. The concept of crop specific pixel purity, defined as the degree of homogeneity of the signal encoded in a pixel with respect to the target crop type, is used to analyze how mixed the pixels can be (as they become coarser) without undermining their capacity to describe the desired surface properties. In [31], the authors used this approach to restrict the analysis to a subset of a region’s pixels and to identify the maximum tolerable pixel size for both crop growth monitoring and crop area estimation, respectively.
In the present paper, we propose to revisit this framework and steer it towards answering the question: “What is the spatial resolution requirement for crop identification within a given landscape?” The proposed tool provides a comprehensive understanding of how crop identification via classification of satellite image time series depends on both pixel size and pixel purity. These properties are analyzed both for (i) a specific crop found across different landscapes and (ii) different crops within the same landscape. Minimum and maximum tolerable pixel sizes and corresponding pixel purities were analyzed with respect to whether a supervised or an unsupervised classification approach is used. Some further analyses, which are critical for operational monitoring, include an exploration of how the suitable pixel size changes along the crop growing-period of a given year, and whether results are stable by repeating the approach on the same site for different years.
2. Study Site and Data Description
Although the methodology developed in this study is generic, and thus applicable to any agricultural landscape, the demonstration is focused on four contrasting agricultural landscapes in Central Asia. They are located between the Amu-Darya and Syr-Darya rivers and are characterized by vast agricultural systems, which were extensively developed under the aegis of the former Soviet Union during the second half of the 20th century [44]. The climate is arid, continental and dry, with 100–250 mm precipitation per year falling mainly in winter. Thus agriculture is limited to irrigated lands [45]. Each test site is 30 km × 30 km. Figure 1 shows subsets of the imagery and the corresponding crop specific masks, respectively of the four sites.
The first site is located in the Khorezm region (KHO) in the north-western part of Uzbekistan. The agricultural landscape appears fragmented due to a comparatively high diversity of crops (e.g., cotton, rice, sorghum, maize, winter wheat and fruit trees). Cover fraction (Cf) of agricultural fields (e.g., the fraction of the sites covered by agricultural fields) is the highest among the four test sites (Table 1 [46]). The second site is situated in the autonomous region of Karakalpakstan (KKP), in the north-western part of Uzbekistan. Crop diversity is high, including: cotton, winter wheat, rice, maize, sorghum, watermelons, and alfalfa. Crop pattern in KKP is very heterogeneous, with more regularly shaped fields in the south-western part, whilst in the north-eastern direction the landscapes becomes increasingly more fragmented with smaller and more irregularly shaped fields. The third site is located in the Kyzl-Orda district (KYZ) in southern Kazakhstan, and was chosen to have an example with more regularly shaped field structures. Only two crops are dominating the agricultural landscape: rice and alfalfa. Large and regular shaped agricultural fields of approx. 2–3 ha each characterize this landscape, where the same crop is grown on adjacent fields, that are aggregated to blocks which together exceed the area of between 500 × 500 m and 1000 × 1000 m (25–100 ha). Fergana Valley (FER), in the eastern part of Uzbekistan, has comparatively large and regular shaped fields, and a variety of crops including rice, cotton, winter wheat, and fruit trees are cultivated. In all sites excepting KYZ, multiple cropping is sometimes practiced, e.g., a double cropping sequences with a second major NDVI peak in summer due to the growth of a summer crop, after harvest of winter wheat. In this study, such land use type will be labelled: “wheat-other”.
2.1. Satellite Imagery
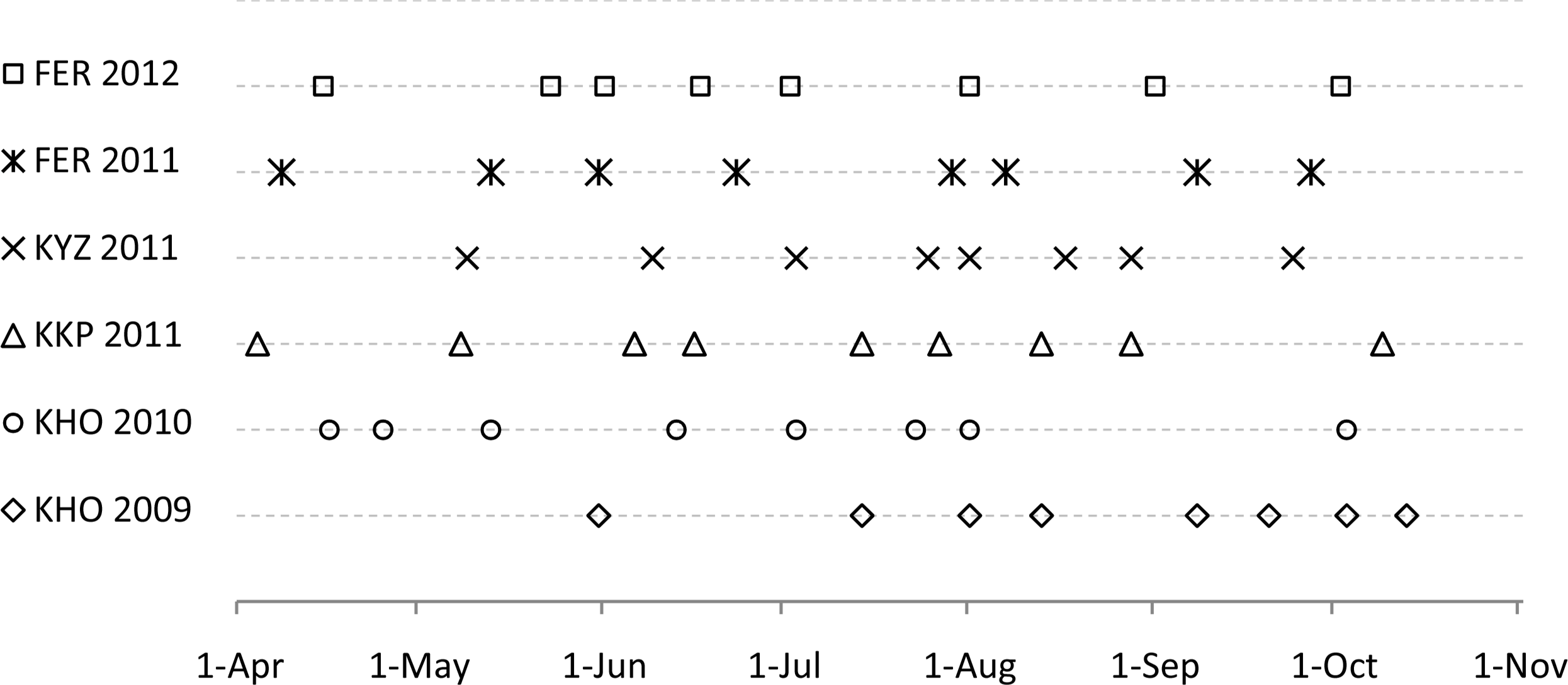
Images from the RapidEye mission [47] with a ground sampling distance (GSD) of 6.5 m, were available for each site. These images have five spectral bands: blue (440–510 nm), green (520–590 nm), red (630–685 nm), red edge (690–730 nm), and near infrared (NIR, 760–850 nm). Images were atmospherically corrected using the ATCOR-2 module [48], and geometrically corrected and co-registered with ground control points, resulting in RMSEs of <6.5 m. For the analysis, eight top-of-canopy (TOC) reflectance images are available. They are well distributed along the season, approx. between day-of-year (DoY) 80 and DoY 280, in order to provide the necessary phenological information for crop discrimination. RapidEye images were available for KHO in 2009 and 2010, for FER in 2011 and 2012, and for KKP and KYZ in 2011. Thus, at least in KHO and FER, the analysis could be repeated in two consecutive years (Figure 2).
An experimental variogram of the NDVI was calculated for every site and acquisition date. Then, modelled variograms were derived by fitting exponential models over each variogram curve, and the mean length scales Dc (e.g., the square root of the variogram integral range) of [49] were extracted for each site (Table 1). Dc was shown to be suitable to assess if an image is large enough to characterize the spatial structures within the landscape: [49] propose that an image is large enough if the integral range of the variogram is smaller than 5% of the image surface, e.g., the corresponding Dc for a 30 × 30 km image is below 6.7 km. To test if this hypothesis is fulfilled the maximum of all Dc values for the NDVI along the season was calculated, confirming that the subsets could be considered as large enough.
2.2. Crop Masks
Crop specific masks are necessary to identify the target objects (agricultural fields cultivated with a certain crop) in the scene, and later for calculating the purity of coarser pixels with regard to specific crops. For the study sites access to vector databases of the agricultural fields including information on crops was either non-existent or restricted. However, crop masks were available from previous studies for the years 2009, 2011 and 2012 [50], and for 2010 [51]. These masks were created using supervised object-based image classification applied to a set of high-resolution time series of RapidEye images acquired over the growing seasons. The overall accuracies of the crop masks were more than reasonable (>93% in most cases) and assumed to have negligible error for the purpose of this study. Sorghum and maize were merged into the class “sorghum/maize” because they could not be distinguished from each other. The resulting proportions of crops in the sites, and the median field sizes cultivated by certain crops, are summarized in Table 2.
3. Methodology
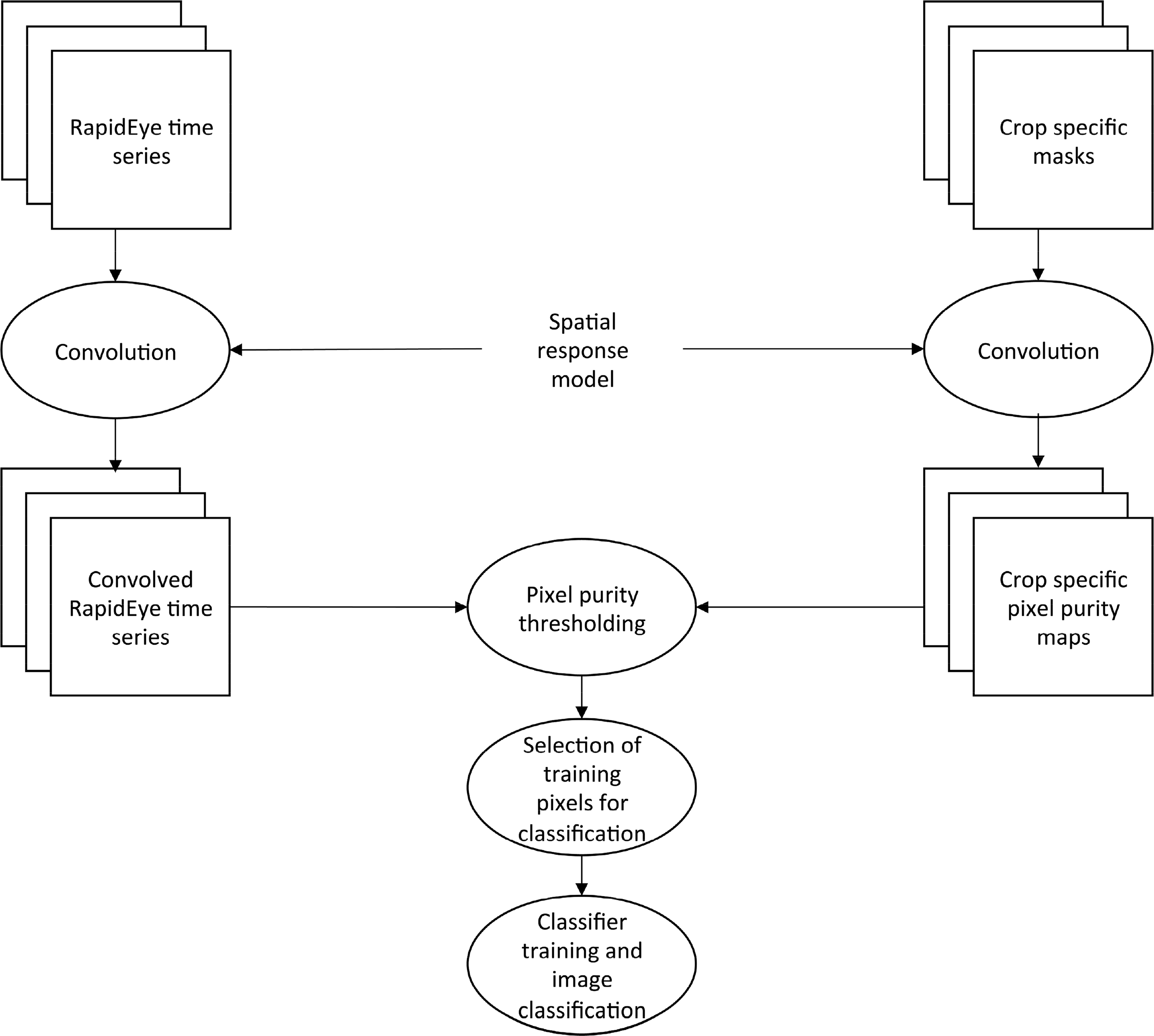
The methodology is based on the same conceptual framework designed by [31]. It relies on using high spatial resolution images and corresponding crop masks to generate various sets of pixel populations over which a classification algorithm can be applied. The pixel populations are characterized by increasingly coarser pixel sizes and with a range of different crop specific purity thresholds. The difference here is that for each pixel population several crop classes are considered for classification, whilst [31] used pixel purity with regard to only a single crop. The necessary processing steps to simulate coarser imagery and to define suitable pixel sizes for crop identification are henceforth described. The general flowchart in Figure 3 may guide the reader throughout the following descriptions.
3.1. Selecting Target Pixel Population by Aggregation and Thresholding
To simulate coarser pixel sizes, a spatial response model is convolved over the original RapidEye images. The spatial response model [36] of an imaging instrument with coarser GSD consists of a point spread function that characterizes both optical (PSFopt) and detector (PSFdet) components of a generic sensor:
The PSFnet is scaled to a range of sizes between 6.5 m and 748.5 m, in increments of 6.5 m, in order to simulate a continuum of coarser images. A bi-dimensional convolution of the spatial response model, PSFnet at each scale over the RapidEye time series, followed by a sub-sampling operation, results in simulated images at a given coarser pixel size. It has to be noted that the PSFnet used in this study is not intended to mimic the exact response of a particular sensor, but has intentionally been defined to be generic.
The convolution of the same PSFnet over the high resolution crop masks result in crop specific purity maps at each scale, which map the pixel purity with respect to the spatial structures represented in the high resolution crop masks [31]. This allows controlling the degree at which the footprints of coarser pixels coincide with the target structures (e.g., fields belonging to certain crops). At each spatial resolution pixel populations can be selected based on thresholds on the pixel purity, here denoted π (for the sake of consistency the terms used by [31] were applied, and purity is symbolized with π, and pixels size is equal to the GSD, symbolized with ν). A threshold can be chosen to separate the aggregated binary crop masks into two sets: target pixels and non-target pixels. The threshold can vary from 0, where all pixels in the images are selected as target, to 1, where only completely pure pixels are selected. The sets of selected target pixels, or pixel populations, vary with respect to their GSD (ν) and to the minimum acceptable purity threshold that defines them (π). This method goes beyond former approaches for image masking by allowing for a detailed assessment of the effect of pixel size and purity on crop classification.
3.2. Image Classification
The second step consists of applying classification procedures to the selected pixel populations. Two classification algorithms were tested: one supervised machine-learning techniques (RF), and one unsupervised algorithm (K-means). Each classifier was applied to classify the five RapidEye bands and the normalized difference vegetation index (NDVI), which was calculated for the entire time series data at each spatial scale, and all crop classes present in the corresponding study sites were included in the legend.
For the supervised classifier, independent training and testing data sets were generated from each selected pixel populations following an equalized random sampling design to obtain approximately the same number of pixels for each class. The target size of both the training and testing sets was initially set to 400 randomly selected pixels per class. A smaller number of pixels could be selected (e.g., with coarser pixel sizes), but the analysis was ultimately halted when the number of pixels in any class dropped below 20. The implementation of Breiman’s RF [12] within the randomForest package [52] in the R programming environment was used. The number of trees T at which an optimal accuracy level is achieved varies with the number of samples and features, and with the variability of feature values. The number of trees commonly recommended is 500 [53]. The second free parameter relevant for accurate classifications is the number of features mtry to split the nodes [53]. The number of features at each node was set to , where f is the total number of predictor variables within the corresponding input dataset.
The purpose of using the unsupervised K-means [9] here is to evaluate to what extent crop specific signals can be detected in NDVI signatures at different spatial scales (and for different purities) in the absence of training data. In this regard, the unsupervised technique extracts temporal classes defined by their characteristics in the time series data to identify natural groupings of pixels with similar NDVI properties, corresponding to key phenological stages (green-up, peak, senescence) in the NDVI time series [54]. The K-means clustering [9] was chosen to evaluate the suitability of unsupervised crop identification. The version used is implemented in the stats package [55] in R. A range of cluster numbers was tested {10,15,20,25}, and the number that achieved highest values for the evaluation criteria was selected. The K-means algorithm was repeated 20 times, thereby creating different random seeds for the initial clustering. From the 20 model runs, the model with the lowest resulting sum of squared distances between the samples and their corresponding cluster centers was taken for the suitability evaluation of the unsupervised clustering. Each cluster containing at least 50% of the samples of a class i were assigned to this class.
To obtain robust performance estimates and to reduce possible bias in the results because of different distributional properties of the test and training sets the draws of training and validation data were repeated 10 times, and the parameters defined above were averaged over the 10 independent runs of models from both algorithms, RF and K-means.
3.3. Characterizing Classification Performance
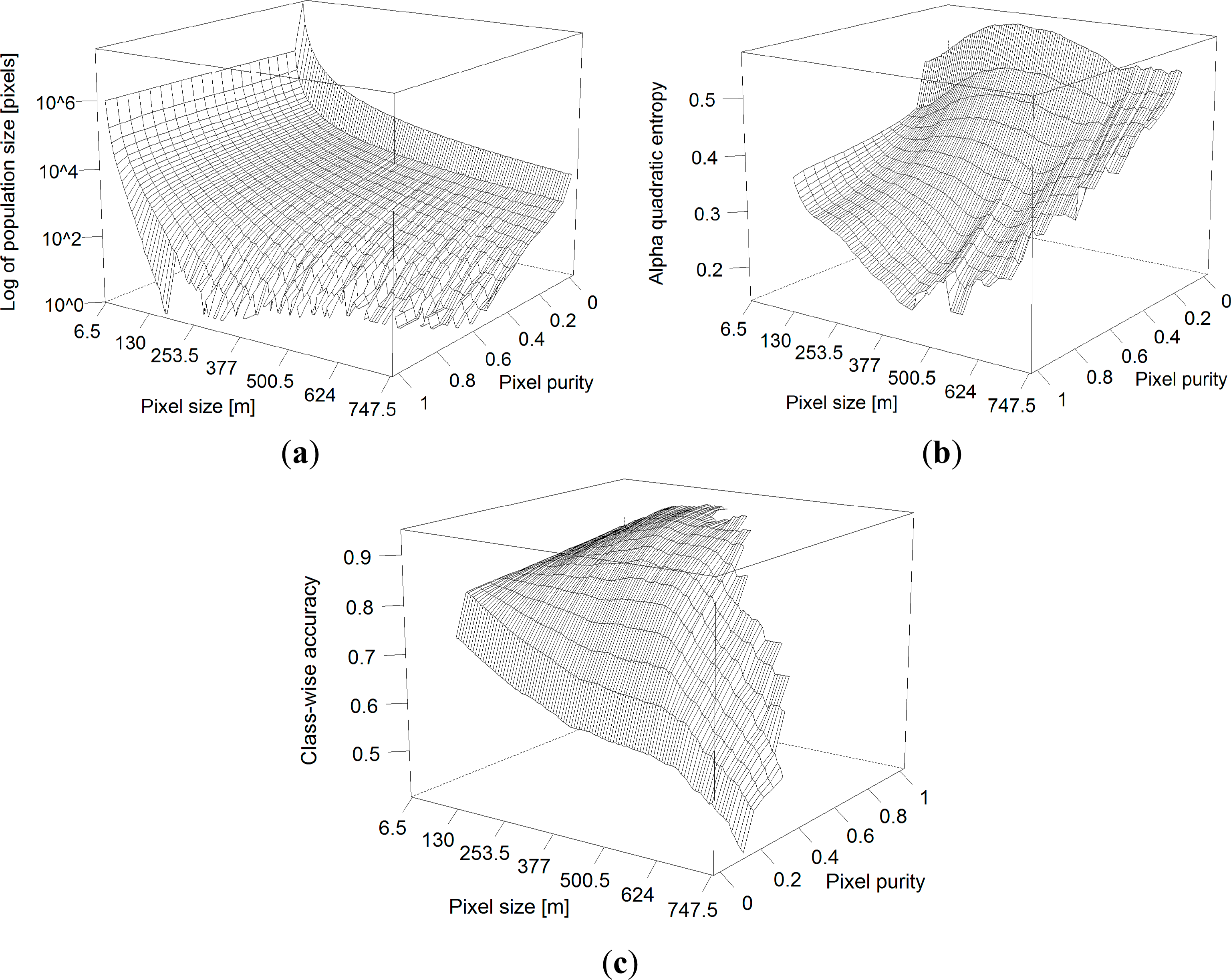
Pixel size and pixel purity can be considered as two dimensions of a ν − π space. For each selected pixel population in this ν − π space, information regarding the classification performance (e.g., overall accuracy) can be summarized as a surface mapped along the pixel ν − π dimensions (e.g., Figure 4). The standard protocol in remote sensing for evaluating the accuracy stems from quantitative metrics derived from the confusion matrix [56]. Yet, different metrics evaluate different components of accuracy because they are based on different statistical assumptions on the input data [57] and such measures should be selected based on the requirements of the study [58]. Consequently, seeking to optimize or compare classifier algorithm performance (or defining suitable pixel sizes with only one metric) may lead to a non-optimal result when viewed from another point of view or quantified with a different metric that is sensitive to different features concerning accuracy [59,60]. Regarding this, the user might be interested in restricting the application of coarser pixel sizes on the basis of the most restrictive metric, among several metrics tested. Hence, to evaluate crop identification performance, the following parameters were calculated for each combination of π and ν (their 3-D representation is shown in Figure 4).
3.3.1. Number of Available Reference Pixels per Class (Ni)
The number of available reference pixels Ni of a given class i gives the total available size of pixel populations in the ν − π dimensions that can be used for training and testing the classifier. In general Ni decreases with both π and ν (Figure 4a). The rate of decrease differs for different crops depending on the total area of the crop in the test site, mean field sizes, and the aggregation pattern of field with the same crop. In supervised crop classification a minimum number of pixels per crop class can be desirable to assure the generalizability of the classifier model to the unseen dataset, and to reduce the influence of (random) variability in the training data on the classification result.
3.3.2. α-Quadratic Entropy (AQE)
Measures of classification uncertainty like entropy assess the spatial variation of the classification quality on a per-case (e.g., per-pixel) basis, and can be used to supplement the global summary provided by standard accuracy statements like overall accuracy [59]. It can be characterized as a quantitative measure of doubt when a classification decision is made in a hard way. Beneath the final (“hard”) class label, non-parametric algorithms such as RF can generate for each classified case x (agricultural field or pixel) a “soft” output in form of a vector p(x) = (p1, ..,. pi, ..., pn) that contains the probabilities that a pixel is classified into a class i, n being the total number of classes. Entropy measures were shown to be indicative of the spatial distribution of error and to be a useful complement to traditional accuracy measures like overall accuracy [61]. Each of the elements in p(x) can be interpreted as a degree of belief or posterior probability that a pixel actually belongs to i. From this vector, the α-quadratic entropy [62] for a given pixel (x) can be calculated as a measure of uncertainty, which is defined as:
3.3.3. Classification Accuracy (ACC and CAi)
A set of confusion matrices [56] was computed on the hard result of the test sets defined along the ν − π dimensions. The overall accuracy (ACC) is defined as the total proportion of correctly classified pixels per total number of test pixels. It is one of the most common measures of classification performance in remote sensing [59], and is defined as:
For each class i under investigation the general Fβ -measure of [63] was adopted as class-wise measure of accuracy. This measure combines precision pri (which gives the proportion of samples which truly have class i among all samples which were classified as class i) and recall tpi (the true positive rate (TPR) which gives the proportion of samples classified into class i among all samples which truly have class i). The former determined the error of omission (false exclusion), the latter the error of commission (false inclusion). Here a special case of the Fβ-measure, F0.5 was chosen that is defined as:
3.4. Definition of Constraints for Crop Identification
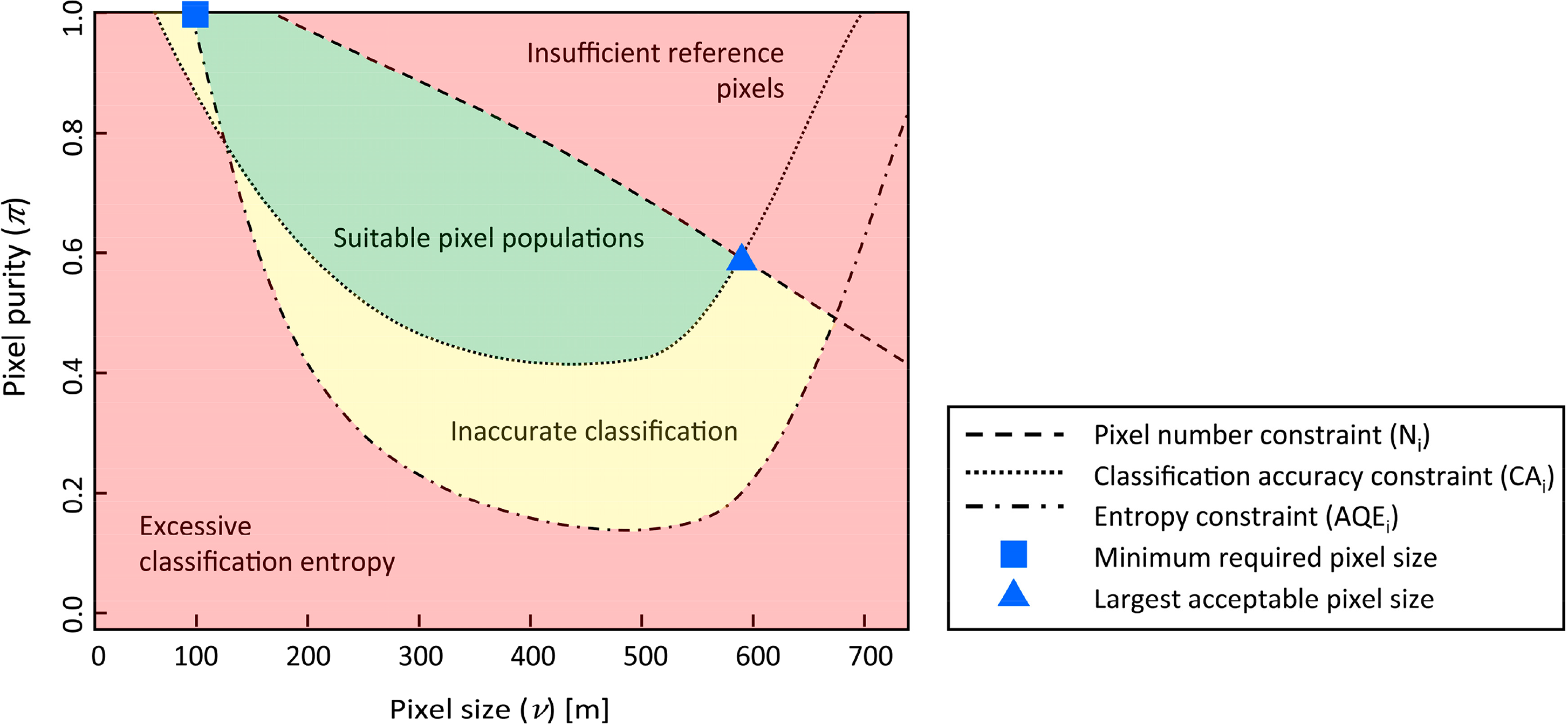
The final step to determine the suitable spatial resolution for crop identification is to isolate the (ν, π) combinations for which the classification performance is good enough. This is accomplished by defining acceptable thresholds for the parameters defined above. Such thresholds will be used to slice the surfaces with a plane parallel to the ν − π space, thereby defining a frontier in this ν − π space dividing pixel populations that are above or below the acceptable threshold for a given surface. As an example, if an application requires a minimum overall accuracy of 75%, the surface CAi is sliced by a plane passing by the value CAi = 0.75. When the intersection of CAi and the plane is projected onto the 2-D space ν − π, it separates this domain into the region where selected pixel populations have classification accuracy higher than 75% and the region where the accuracy of the remaining population will be lower than 75%. The coordinates (ν, π) along the division boundary satisfy the imposed condition CAi = 0.75. By drawing limits on the different parameters, according to the thresholds defined in Table 3, the parameter surfaces were sliced and the intersection points of these slices in ν − π space were used to identify the position of the coarsest acceptable pixel sizes (νmax) and the corresponding minimum required pixel purities π, respectively.
Figure 5 shows an example of the experimental boundaries used to define suitable pixel populations for crop identification. In this example the intersection of the pixel number constraint (Ni) and CAi determine the position of νmax in the ν − π space. As can be seen from this figure, a theoretical minimum pixel size (νmin) can also be defined when the application of finer pixels is restricted, e.g., due to excessive entropy (AQEi) or insufficient accuracy (CAi).
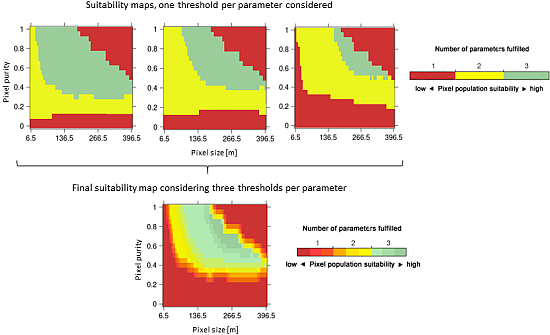
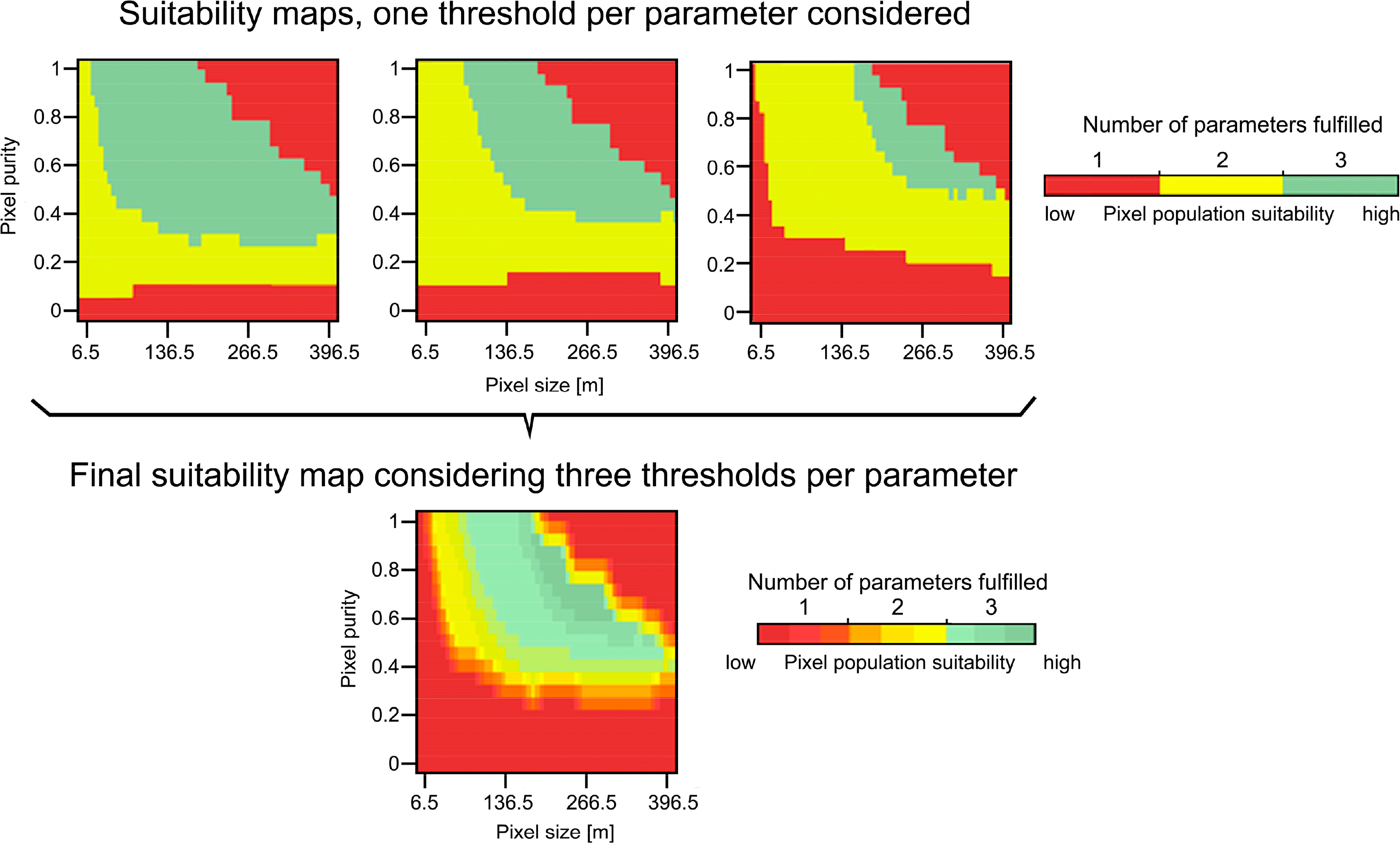
Users will have different requirements for selecting their pixel population of interest, e.g., it might be acceptable to have crop classes identified at different levels of accuracy as long as the classes of interest are sufficiently accurately identified. Hence, a range of thresholds was applied to the parameters. Increasing the severity of the thresholds for the parameters (e.g., 0.75, 0.80, and 0.85 for CAi) to define these experimental boundaries results in having less and less suitable pixel populations left for crop identification that can fulfill the stricter thresholds. Figure 6 demonstrates this effect: first, higher thresholds are successively selected for each parameter at the same time, according to the parameterization defined in Table 3. Green colors indicate that all parameters (CAi, AQEi, and Ni) are fulfilled and the pixel population can be considers adequate (“suitable”) for crop identification. Then, combining these three maps yields a “suitability” map (bottom map in Figure 6), which shows the degree of suitability of pixel populations for crop identification considering several thresholds at the same time. In these maps, shades of a given color means that a specific number of parameters is fulfilled, that is, they satisfy at least the minimum threshold set for them in Table 3. However, they do so at different levels: for instance, shades of green means that all three parameters are fulfilled, but not necessarily under the strictest thresholds defined in Table 3. Only dark green color indicates that all parameters are fulfilled under the strictest values.
4. Results
4.1. How Do Pixel Size and Purity Requirements Differ per Crop for Each Site?
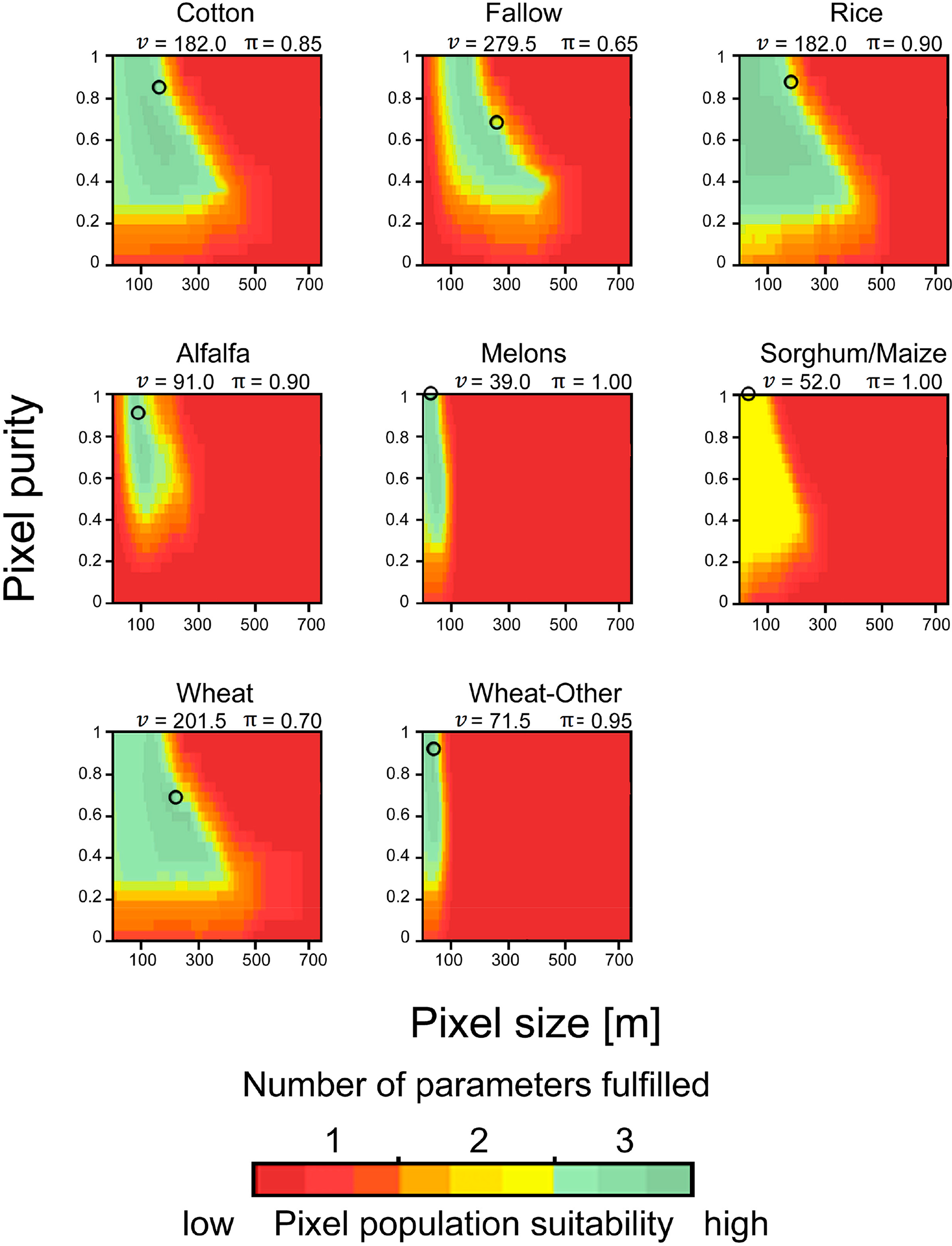
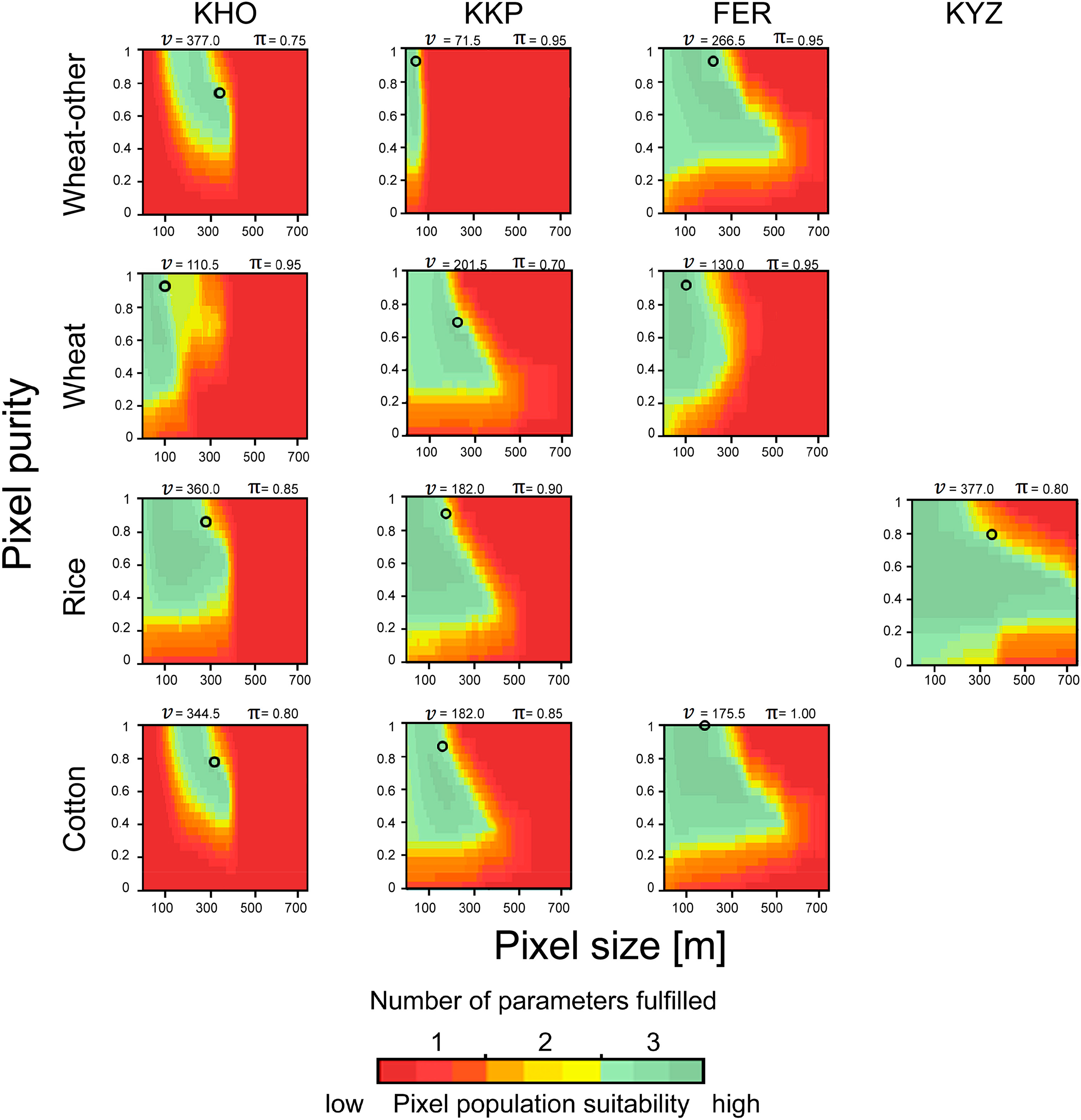
The performance of crop identification as a function of pixel size and pixel purity has been found to vary within a landscape and across landscapes. From the suitability map in KKP (Figure 7) class-specific differences regarding the spatial resolution requirement for the identification become apparent. For example, νmax for rice was 429.0 m, whilst νmax for wheat-other was 91.0 m. Also the minimum required pixel sizes (νmin) varied. For instance, cotton could be identified using very small pixels (νmin = 6.5 m), whilst other crop classes like alfalfa-1y and fallow fields required relatively coarse values for νmin (65.0 m and 78.0 m, respectively). Sorghum/maize could not effectively be identified because more than two thresholds were generally exceeded (CAi and AQEi).
Further, there are differences in the minimum required pixel purity for νmax and νmin. For the identification of rice fields comparatively low pixel purity for νmax was needed (π = 0.35 in KKP), compared with the corresponding purities of other crops (e.g., π = 0.75 for alfalfa-1y). The position in the ν − π space maximising classification performance according to the class-wise accuracy CAi was assessed for each case. Inspecting Figure 7 it can be seen that this position did not necessarily coincide with the highest degree of the corresponding pixel populations’ suitability (e.g., dark green colors in the suitability maps), which means that the “best” position in ν − π of different accuracy metrics are not necessarily identical. Another characteristic is the need for relatively coarse pixels to achieve maximum classification accuracy (e.g., 182.0 m were required to achieve highest CAi for rice fields while finer pixel sizes were equally suitable).
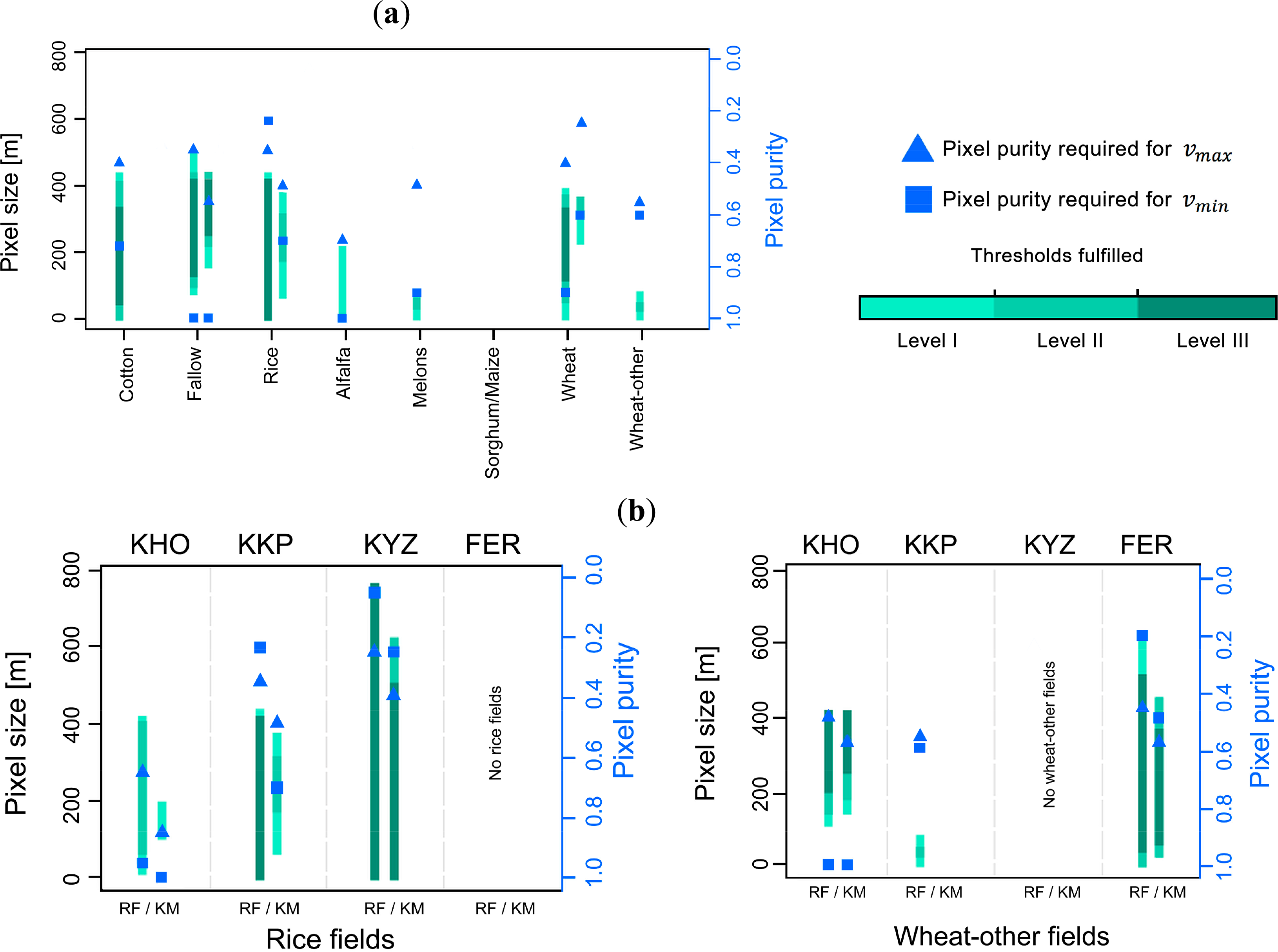
When looking at a specific type of crop, the requirements for its identification differed among the four landscapes (Figure 8). For instance, the identification of cotton in KHO required a minimum pixel size of νmin = 117.0 m, whilst in FER νmin could be 6.5 m. Wheat-other could be identified over a large range of pixel sizes in FER (νmin = 6.5 m, νmax = 611.0 m), whilst its identification in KKP was restricted to a rather narrow range of pixel sizes (32.5–91.0 m).
4.2. How Does Changing from Supervised to Unsupervised Classification Influence the Pixel Population Suitability?
The application of the unsupervised classification achieved results that are comparable to the supervised approach only for some crop classes. Figure 9 reveals that the most notable difference to the supervised approach is that in general coarser pixels were required to effectively identify crops (e.g., νmin = 91.5 m for rice, compared to 6.5 m using RF). Using coarser pixels is supposed to reduce within class variance [23], which could facilitate the unsupervised crop identification as long as the effect of pixel mixing does not become dominating. In KYZ only rice fields could be identified (νmax = 604.5 m, compared to 745.5 m using RF).
This is most probably because of the indistinct NDVI profiles of alfalfa and fallow fields, which are characterized by heterogeneous patterns due to several irregularly scheduled cuttings throughout the season. In contrast, all crops except for winter wheat fields could be identified in the FER landscape and with highest degree of suitability (not shown in Figure 9), e.g., all criteria defined in Table 3 could be fulfilled with accuracies of more than 0.85 (CAi), albeit the range of suitable pixel sizes differed from crop to crop. Similar to KYZ, νmax of the crop classes was smaller for the unsupervised approach (e.g., νmax = 422.5 m for wheat-other, compared to 611.0 m using RF).
4.3. How Does Pixel Population Suitability Evolve along the Season?
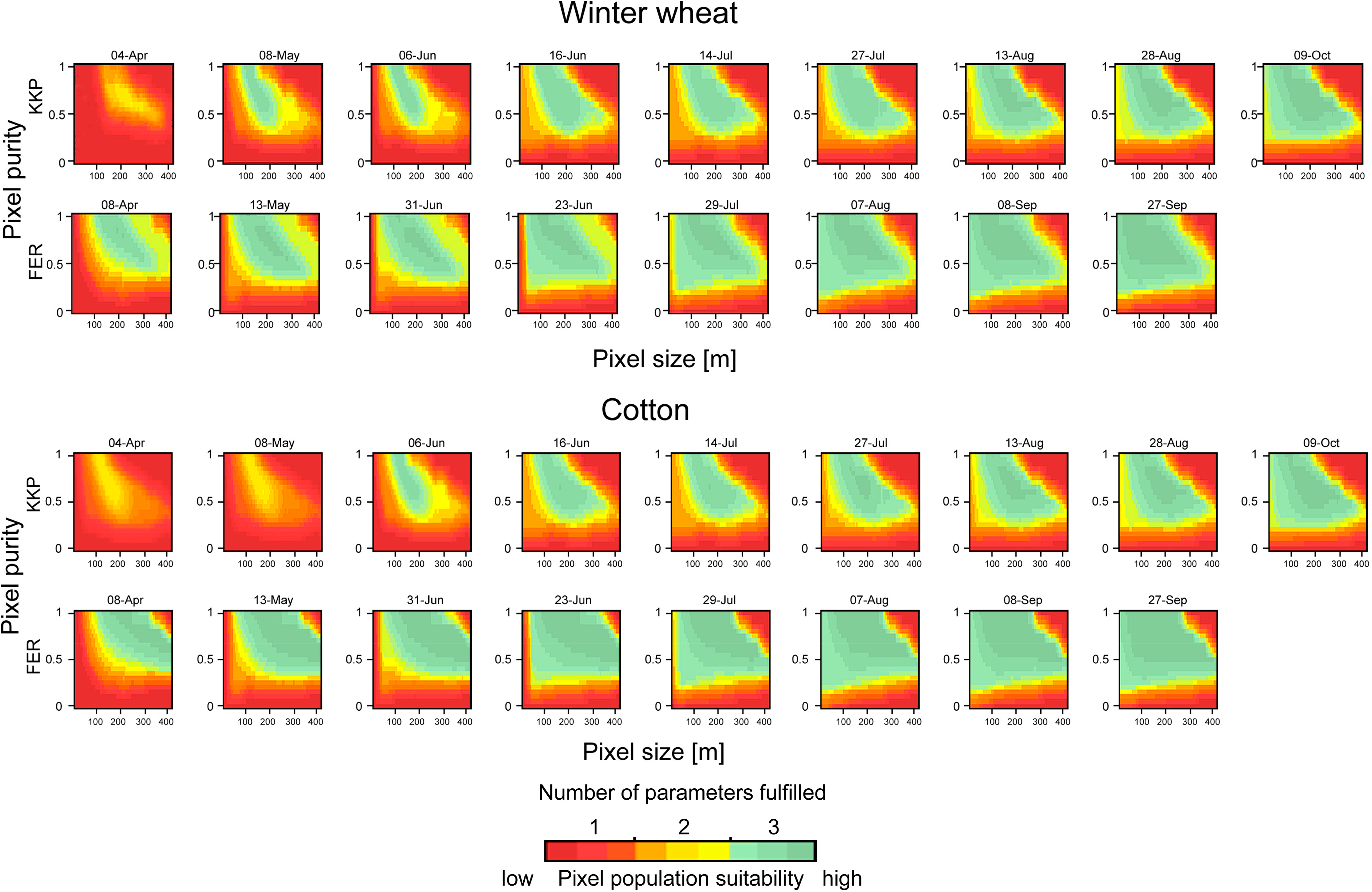
In order to test if the suitability of pixel populations changes along the season and to what extent, the observation length (e.g., the number of images in the time series) was increased by incrementally adding images along the season, one-by-one. Then, for each incremental step, the pixel suitability for individual crops was calculated. The focus here is on two classes that can be found in KKP and FER, namely cotton and winter wheat. These two sites were selected for this experiment, because RapidEye images are available earliest in the season (beginning of April, see Figure 2), which allows for a finer assessment of early estimation in the early phase of the growing season. In KKP one additional image from 7 June was available for this analysis.
Figure 10 demonstrates for these two classes how adding images enhances the suitability of the pixel populations in ν − π space for crop identification. In KKP the identification of cotton was not possible based only on the first two acquisitions. As of 7 June cotton could be identified but this was restricted to a rather small range of pixel sizes (νmin = 162.5, νmax = 266.5 m). Adding images till 14 July enabled the use of pixels with a wider range of resolutions (νmin = 45.5, νmax = 383.5 m) and purities, respectively. Adding an image after 27 July had no significant effect on the suitability of the pixel populations. Winter wheat fields in KKP could be identified as of 9 May, starting with pixel sizes ranging from νmin = 117.0 m to νmax = 247.0 m, and adding more and more images improved the values for νmin, which were shifted towards 13.0 m, whilst νmax was further shifted towards 429.0 m. Compared to KKP, crops in FER could be identified using a larger range of pixel sizes (e.g., winter wheat) or earlier in the season, e.g., cotton identification in FER was possible two months earlier than in KKP.
4.4. Can the Defined Pixel Size Requirements be Transferred to Another Year?
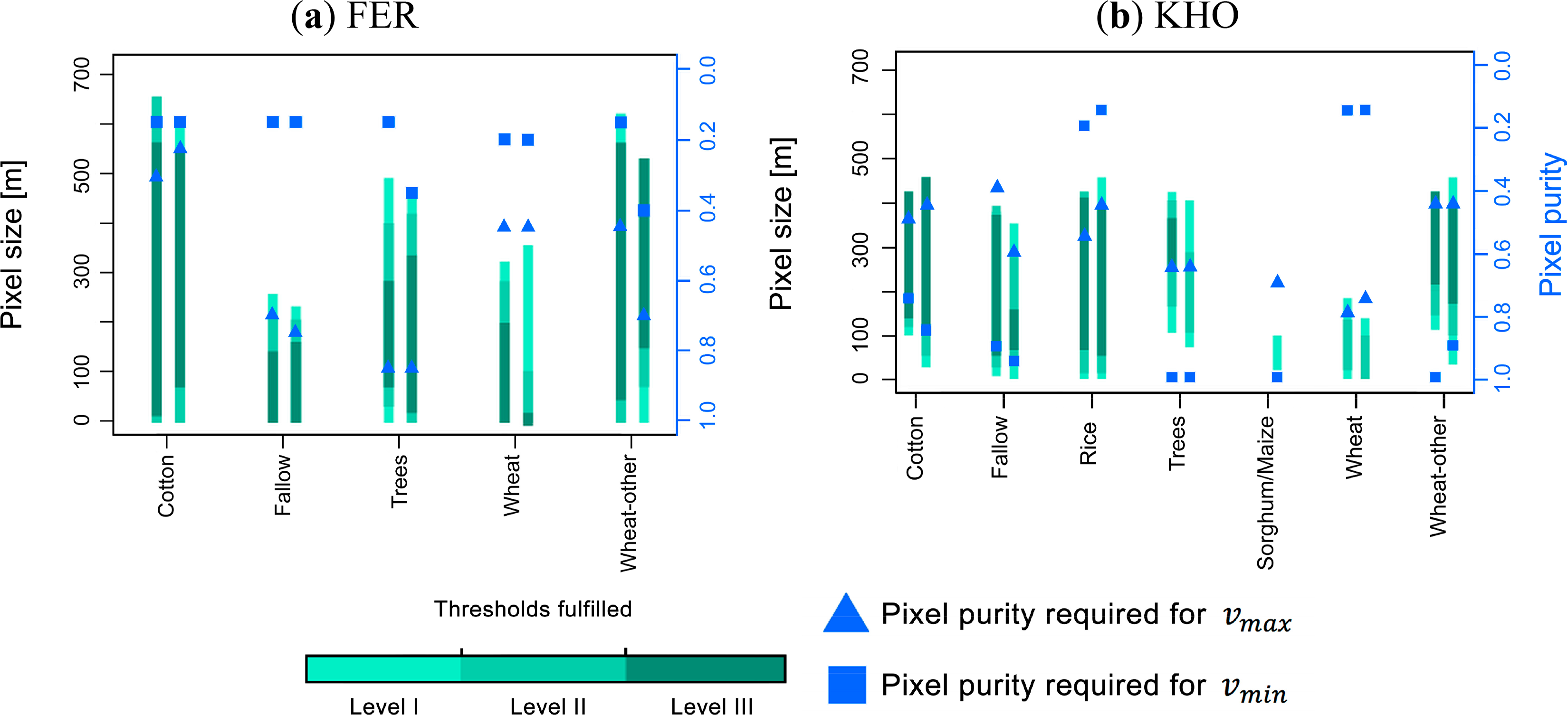
To answer this question, the experiments were repeated on RapidEye data sets from another year in two sites, KHO (2010) and FER (2012), because no RapidEye data was available for another year in KKP or KYZ. Figure 11 shows the ranges of suitable pixel sizes for each crop in KHO and FER, respectively in two consecutive years.
In general, the requirements for crop identification in FER did not significantly change. However, νmax tended to be coarser in 2011 than in 2012 for most classes. The identification of fallow fields in 2012 was limited to a comparatively small range of pixel sizes (νmin = 6.5 m, νmax = 202.0 m), compared to 2011 (νmin = 6.5 m, νmax = 260.5 m). The cover fraction (Cf) of fallow fields was almost four times higher in 2011 (Table 2) and found on larger fields (on average). This means that it was easier to have coarser pixels fall within target fields and thus conferring higher acceptable pixel sizes for the crop identification. The same could be found for winter wheat (νmax in 2011 was 331.5 m, νmax in 2012 was 364.0 m), which covered a larger fraction of the landscape in 2012 (Cf = 0.09) than in 2011 (Cf = 0.05). The cover fractions of wheat-other fields decreased in 2012 (Cf = 0.27) compared to 2011 (Cf = 0.32), which was reflected in a change of νmax for that crop type from 656.5 m to 539.5 m. In general higher classification performances could be achieved over a wider range of pixel sizes in 2011, indicated by the length of the dark green bars in Figure 11. Compared to νmax, differences of νmin between the two years were marginal.
In KHO the situation was different. Overall, there was a tendency that νmin of most crops was coarser in 2009. For instance, the values of νmin for cotton decreased from 104.0 m (in 2009) to 26.0 m (in 2010), and νmin of wheat–other was 39.0 m in 2010 (compared to 117.0 m in 2009). The cover fraction of wheat-other in 2009 (Cf = 0.27) was lower compared to 2010 (Cf = 0.30), but there was no such obvious difference in the values for νmax of this class. Likewise, the purity requirements for νmax tended to be higher in 2009.
5. Discussion
As demonstrated by the results in Central Asia, the conceptual framework developed in this paper allows a quantification of the potential trade-offs between pixel size and pixel purity when addressing the question of crop identification. The result is an improvement of the framework proposed by [31] with a more dedicated objective and that has been tested robustly with more realistic conditions, i.e., time series of images instead of individual images.
The various experiments over Central Asia demonstrate that the task of finding the optimum pixel size for crop identification does not have a “one-size-fits-all” solution. Landscape heterogeneity, including the size of surface features and the properties of their neighborhood, are known to be important factors determining classification accuracy [40,64]. The proposed framework reacted to the specific landscape pattern situations in the four study sites, e.g., as characterized by the mean fields sizes and cover fractions of the individual crops. When the crops were grown on larger and more regular fields (such as FER and KHO), or when the cover fraction was high coarser pixel sizes could be tolerated for crop identification. Crops covering small parts of the landscape like sorghum/maize or melons in KKP could only be detected using small pixel sizes, if they could be detected at all. However, landscape heterogeneity with respect to the spatial pattern also seemed to influence the choice of pixel sizes. For instance, while the mean field sizes in KYZ and KKP are comparable, the former’s fields are more regular in shape, less variable in size, and the same crops are found on blocks of fields that together can aggregate to more than 100 ha in size. Due to this spatial aggregation pattern, it is easier to have coarser pixels fall within target fields and thus conferring higher acceptable pixel sizes for crop identification, resulting in notably higher values in KYZ (747.5 m) than in KKP (429.0 m).
Satellites with coarser spatial resolutions tend to have finer temporal, spectral or radiometric resolutions. The question of determining the optimal pixel size for an application such as crop identification is therefore naturally inclined towards finding the coarsest acceptable pixel sizes (νmax) so as to potentially benefit from what instruments with coarser pixels can offer (including a tendency to have a longer archive). However, the experiments proposed in this paper also highlight the importance of defining the finest acceptable pixel size (νmin). In some cases (depending on crop, landscape and timing), the finest pixel sizes used (νmin = 6.5 m) was not deemed suitable while coarser pixel sizes were. This has previously been observed in other studies [28]. The reason why coarser pixels achieved higher accuracies than smaller pixels could be the interplay of increasing error-rates of smaller but purer pixels (which become more abundant when pixels become smaller), caused by increasing within-class variability [23] and decreasing error of mixed pixels (which become less abundant when pixels become smaller). In such a situation it might be better to have coarser pixels, thereby reducing this variance and counterbalancing the effect of pure-pixel heterogeneity within smaller pixels. An even better solution would be to consider image segmentation [17] of high spatial resolution time series to obtain image-objects that minimize the variance but that are not constrained by the rectangular nature of the pixels. Analyzing the optimal size of (multi-date) image objects for crop identification could be an interesting extension of the proposed conceptual framework, but such questions are beyond the scope of this current paper.
The discussion of pixel size must not eclipse that of pixel purity. The optimal pixel purity (i.e., the one yielding the most accurate classifications) is not necessarily equal to 1 in various cases. This emphasizes how tolerating some signal contamination may be beneficial in the case of crop identification. Although this may seem counter-intuitive, since mixed pixels will certainly be more difficult to classify, perhaps such effect is counter-balanced to a certain extent by the larger number of sample pixels that are available for classification training when some degree of impurity is tolerated. A larger sample size for classification training may better represent the diversity of the spectral response of the target class within the landscape [24]. This point raises another issue regarding the representativity of the selected pixel population: does selecting a population of purer time series engender a bias caused by focusing on the larger features in a given landscape? In some cases, agro-management of the larger fields may be considerably different from that of the smaller fields. Controlling for such bias could be done by adding a dedicated constraint in the analysis of the pixel size-pixel purity trade-off in a future version of the framework. Regarding minimum purity, it must be acknowledged that under the parameterization chosen in these experiments, they can reach quite low values (of the order of 0.3) and still remain “suitable” in some cases. This somewhat illustrates the capacity to detect sub-pixel features using coarse spatial resolution time series. In case of rice, this could be explained by the distinct NDVI signature of rice fields, which are flooded in spring (resulting in negative NDVI values). In the four studied landscapes, the surroundings of the fields are characterized by bare soils or sparse vegetation, hence lower purities might not necessarily lead to mixing with other vegetation signals. However, these purity values may still be excessively low, perhaps suggesting the thresholds on the classification performance metrics AQEi and CAi defined in level I (see Table 3) were too relaxed to portray realistic conditions in the lower part of the purity spectrum. From the suitability maps it can be seen that selecting level-III thresholds resulted in higher purity values (of the order of 0.4) and for some users selecting higher thresholds (e.g., ACC > 0.9) might better meet the requirements imposed by specific applications.
An originality of this research includes the suitability maps in the ν − π space that combine the information from the different classification performance metrics. In this case, the balance between the metrics was evenly weighted and defined by a predefined set of thresholds. This balance could be fine-tuned for different applications that may require either giving more weight to one metric, defining more threshold levels for a given metric, or incorporating a different combination of metrics. The proportion of orange and yellow hues in the suitability maps provide insight on how the combined use of several metrics changes results with respect to using single metrics separately. In general, it must also be stressed that the estimations provided in this study are only valid within the framework defined by the chosen parameterization. The parameters were set with the same values in each landscape in order to illustrate how the method responds to different spatial landscape patterns, but a dedicated analysis for each landscape should probably be thought with thresholds tailored to the specific conditions of that particular landscape.
The timing of crop identification along the season can be of particular interest for operational monitoring activities. The definition of what combination of pixel size and purity is suitable for crop identification was found to change along the season, and differently according to the studied landscapes. In the FER landscape, winter wheat fields could be identified within a wider range of pixel sizes and much earlier in the season, as compared to the KKP landscape. The differences between the two crops, wheat and cotton, was much smaller than the difference between the landscapes. One reason could be the higher contrast between the target crop and its surroundings on the FER landscape in April (when summer crops were not yet sown but winter wheat stems were already elongated and fully covered the fields) than on the KKP landscape (when winter wheat had not already grown significantly and bare soil that covered the latent summer seeds had comparable reflectance to winter wheat fields, resulting in a low signal response to vegetation due to the little amount of biomass). This difference can be explained by the earlier irrigation water availability and onset of the vegetation period, respectively in FER than in the downstream regions of the Amu Darya where the KKP site is located and where the start of the vegetation season is estimated to be approximately 30 days later [65]. Another reason could be differences in crop development at different phenology stages.
Changes in spatial requirements over consecutive years could also be explained by differences in agricultural practices or seasonal water balance. One possible explanation for this in KHO could be the sharply reduced irrigation water supply in 2009, compared to 2010. To illustrate this: the average water intake from the Amu Darya into the KHO irrigation system through the Tuyamujun reservoir in the period 2000–2011 was 3859 Mm3 [66]. However, in 2009 water intake was reduced to 3660 Mm3. In 2010 the water intake was above the 11-year average (4902 Mm3). It was illustrated by [61] how in water sparse areas crops only had a low biomass and did not produce a large NDVI response, which led to increasing classification entropy. Reduced water supply could also cause bare or salty patches within agricultural fields, which would enhance class confusion when smaller pixels fall within such patches within a field. In this regard using coarser pixel sizes would reduce some of the variance within the pixels. In the FER landscape no such pronounced differences were observed between the two years. Water intake from the Toktogul reservoir into Fergana Valley was slightly above the 11-year average (3940 Mm3) in 2011 and 2012, respectively, but the difference between the two years was negligible: 4216 and 4476 Mm3. These findings indicate that coarser spatial resolution sensors, like MODIS (250 m) or Sentinel-3 (300 m), could be suitable for identification of major crop classes under normal weather conditions, while for years suffering from drier than normal conditions, a finer resolution (e.g., 100 m) might be required. Another potential explanation could be differences in fertilization, but no such data was available for this study.
A series of additional improvements could still be mentioned. To solidify or dismiss results uncovered in this research, the analysis could be extended to additional landscapes or envisage the impact of varying class legends on the definition of pixel suitability. Possible candidate sites might be found in the USA, with relatively large field sizes [67], or sites in China with field sizes reported <2 ha [31]. Other vegetation indices like EVI could be tested instead of NDVI, although these two indices were shown to perform equally well in crop classification [67].
By design, all crops present in the study site were to be classified, but aggregating crop classes or selecting a different class legend could impact the definition of suitable pixel sizes, as was demonstrated by [32]. For instance, in the KHO landscape the experiments were halted at 429 m due to an insufficient number of training pixels for class sorghum/maize, and merging or dismissing minor classes might lead to the definition of coarser values for νmax. The inclusion of more acquisition dates could be considered to better approximate the revisit frequency of sensors that have coarser GSD like MODIS or Sentinel-3. Furthermore, a fine diagnostic tailored to a specific instrument could be envisaged if the specific sensor spatial response can be reasonably approximated. A final remark is that the analysis need not be restricted to optical data and the framework could be extended by further evaluating region specific requirements regarding the type of data (optical, radar, or hyper-spectral) to find out which is best suited for specific landscapes.
6. Conclusions
A framework was proposed to quantitatively define pixel size requirements for crop identification via image classification. This tool can be modulated using different parameterizations to explore the trade-offs between pixel size and pixel purity. This was demonstrated by applying it to different agricultural landscapes in Central Asia. From these specific results, several conclusions could be drawn regarding the pixel size and purity requirements for crop identification that are applicable in a more general context. First, the EO data requirements for each crop class investigated were specific within a given landscape, and for each crop they differed over different landscapes. Second, unsupervised crop identification was shown to perform reasonably well, which may be a valuable alternative to supervised approaches when collecting training data is not necessarily feasible (e.g., in an operational near-real time monitoring context when priority must be given to analysis). However, the unsupervised approach tested here could detect fewer crop classes compared with the supervised method, especially when crops have comparable NDVI signatures. Finally, the requirements also changed along the season and over the years, which indicates that the application of existing satellite sensors might not be equally suitable for crop identification in different agricultural landscapes in a multi-year perspective. The findings indicate that selecting coarser spatial resolution sensors, like MODIS (250 m) or Sentinel-3 (300 m), could be suitable for identification of major crop classes with overall accuracies of >0.85. The use of Landsat (30 m) should be considered for object-based classification rather than pixel-based crop identification. In general, pixel purities of 0.4–0.5 sufficed to identify major crop types. Crops in different landscapes were not identified simultaneously in the season, reflecting the different agro-ecological conditions the crops are growing in (e.g., timing of irrigation water availability). This proposed framework can serve to guide recommendations for designing dedicated EO missions that can satisfy the requirements in terms of pixel size to identify and discriminate crop types. In a world with increasingly diverse geospatial data sources (in terms of combinations of spatial and temporal resolutions), the tool can also help users to choose the different data sources that meet the requirements imposed by their applications.
Acknowledgments
This publication was funded by the German Research Foundation (DFG) and the University of Wuerzburg in the funding programme Open Access Publishing. This work was undertaken at the University of Würzburg, Department of Remote Sensing, within the CAWa project funded by the German Federal Foreign Office, and the German-Uzbek Khorezm project. We thank the German Aerospace Agency (DLR) for providing data from the RapidEye Science Archive (RESA). SPOT 5 images were made available through the Spot Image project Planet Action. The German National Academic Foundation funded this research by way of a PhD grant to the first author. The authors would also like to thank the Deutsche Gesellschaft für Internationale Zusammenarbeit (GIZ) for supporting the field studies in Uzbekistan and Kazakhstan. We gratefully acknowledge the valuable comments of Raul Lopez Lozano from the Joint Research Centre (JRC), Italy on this manuscript. The authors also thank the three anonymous reviewers for their valuable comments, which helped to improve this manuscript.
Author Contributions
Fabian Löw and Grégory Duveiller conceived and designed the experiments; Fabian Löw performed the experiments and analyzed the data; Fabian Löw and Grégory Duveiller wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- United Nations, World Urbanization Prospects—The 2014 Revision; United Nations: New York, NY, USA, 2014; p. 32.
- Foley, J.A.; Ramankutty, N.; Brauman, K.A; Cassidy, E.S.; Gerber, J.S.; Johnston, M.; Mueller, N.D.; O’Connell, C.; Ray, D.K.; West, P.C.; et al. Solutions for a cultivated planet. Nature 2011, 478, 337–342. [Google Scholar]
- Pachauri, R.K.; Reisinger, A. Climate Change 2007: Synthesis Report. Contribution of Working Groups I, II and III to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2008; p. 104. [Google Scholar]
- Ozdogan, M.; Yang, Y.; Allez, G.; Cervantes, C. Remote sensing of irrigated agriculture: Opportunities and challenges. Remote Sens 2010, 2, 2274–2304. [Google Scholar]
- Carfagna, E.; Gallego, J.F. Using remote sensing for agricultural statistics. Int. Stat. Rev 2005, 73, 389–404. [Google Scholar]
- Gallego, J.F.; Delince, J.; Rueda, C. Crop area estimates through remote sensing: Stability of the regression correction. Int. J. Remote Sens 1993, 14, 3433–3445. [Google Scholar]
- Atzberger, C. Advances in remote sensing of agriculture: Context description, existing operational monitoring systems and major information needs. Remote Sens 2013, 5, 949–981. [Google Scholar]
- Justice, C.; Becker-Reshef, I. Report from the Workshop on Developing a Strategy for Global Agricultural Monitoring in the Framework of Group on Earth Observations (GEO); University of Maryland: College Park, MD, USA, 2007; p. 67. [Google Scholar]
- Tso, B.; Mather, P.M. Classification Methods for Remotely Sensed Data, 2nd ed; CRC Press Taylor & Francis Group: Boca Raton, FL, USA/London, UK/New York, NY, USA, 2009. [Google Scholar]
- Murakami, T.; Ogawa, S.; Ishitsuka, N.; Kumagai, K.; Saito, G. Crop discrimination with multitemporal SPOT/HRV data in the Saga Plains, Japan. Int. J. Remote Sens 2001, 22, 1335–1348. [Google Scholar]
- Yang, C.; Everitt, J.H.; Fletcher, R.S.; Murden, D. Using high resolution QuickBird imagery for crop identification and area estimation. Geocarto Int 2007, 22, 219–233. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar]
- Loosvelt, L.; Peters, J.; Skriver, H. Impact of reducing polarimetric SAR input on the uncertainty of crop classifications based on the random forests algorithm. IEEE Trans. Geosci. Remote Sens 2012, 50, 4185–4200. [Google Scholar]
- Waske, B.; Braun, M. Classifier ensembles for land cover mapping using multitemporal SAR imagery. ISPRS J. Photogramm. Remote Sens 2009, 64, 450–457. [Google Scholar]
- Peña-Barragán, J.M.; Ngugi, M.K.; Plant, R.E.; Six, J. Object-based crop identification using multiple vegetation indices, textural features and crop phenology. Remote Sens. Environ 2011, 115, 1301–1316. [Google Scholar]
- Gallego, J.F. Remote sensing and land cover area estimation. Int. J. Remote Sens 2004, 25, 3019–3047. [Google Scholar]
- Blaschke, T. Object based image analysis for remote sensing. ISPRS J. Photogramm. Remote Sens 2010, 65, 2–16. [Google Scholar]
- Fritz, S.; Massart, M.; Savin, I.; Gallego, J.F.; Rembold, F. The use of MODIS data to derive acreage estimations for larger fields: A case study in the south-western Rostov region of Russia. Int. J. Appl. Earth Obs. Geoinf 2008, 10, 453–466. [Google Scholar]
- Genovese, G.; Vignolles, C.; Nègre, T.; Passera, G. A methodology for a combined use of normalised difference vegetation index and CORINE land cover data for crop yield monitoring and forecasting. A case study on Spain. Agronomie 2001, 21, 91–111. [Google Scholar]
- Kastens, J.H.; Kastens, T.L.; Kastens, D.L.A.; Price, K.P.; Martinko, E.A.; Lee, R.-Y. Image masking for crop yield forecasting using AVHRR NDVI time series imagery. Remote Sens. Environ 2005, 99, 341–356. [Google Scholar]
- Duveiller, G.; Baret, F.; Defourny, P. Crop specific green area index retrieval from MODIS data at regional scale by controlling pixel-target adequacy. Remote Sens. Environ 2011, 115, 2686–2701. [Google Scholar]
- Duveiller, G.; Baret, F.; Defourny, P. Remotely sensed green area index for winter wheat crop monitoring: 10-Year assessment at regional scale over a fragmented landscape. Agric. For. Meteorol 2012, 166–167, 156–168. [Google Scholar]
- Hsieh, P.; Lee, L.C.; Chen, N. Effect of spatial resolution on classification errors of pure and mixed pixels in remote sensing. IEEE Trans. Geosci. Remote Sens 2001, 39, 2657–2663. [Google Scholar]
- Foody, G.M. Incorporating mixed pixels in the training, allocation and testing stages of supervised classifications. Pattern Recognit. Lett 1996, 17, 1389–1398. [Google Scholar]
- Johnson, D.M.; Mueller, R. The 2009 cropland data layer. Photogramm. Eng. Remote Sens 2010, 76, 1201–1205. [Google Scholar]
- Duveiller, G.; López-Lozano, R.; Seguini, L.; Bojanowski, J.S.; Baruth, B. Optical remote sensing requirements for operational crop monitoring and yield forecasting in Europe. In Proceedings of the Sentinel-3 OLCI/SLSTR and MERIS/(A)ATSR Workshop, Frascati, Italy, 15–19 October 2012.
- Brown, J.C.; Kastens, J.H.; Coutinho, A.C.; Victoria, D.D.C.; Bishop, C.R. Classifying multiyear agricultural land use data from Mato Grosso using time-series MODIS vegetation index data. Remote Sens. Environ 2013, 130, 39–50. [Google Scholar]
- McCloy, K.R.; Bøcher, P.K. Optimizing image resolution to maximize the accuracy of hard classification. Photogramm. Eng. Remote Sens 2007, 73, 893–903. [Google Scholar]
- Pax-Lenney, M.; Woodcock, C.E. The effect of spatial resolution on the ability to monitor the status of agricultural lands. Remote Sens. Environ 1997, 61, 210–220. [Google Scholar]
- Atkinson, P.M.; Curran, P. Choosing an appropriate spatial resolution for remote sensing investigations. Photogramme. Eng. Remote Sens 1997, 63, 1345–1351. [Google Scholar]
- Duveiller, G.; Defourny, P. A conceptual framework to define the spatial resolution requirements for agricultural monitoring using remote sensing. Remote Sens. Environ 2010, 114, 2637–2650. [Google Scholar]
- Marceau, D.J.; Howarth, P.J.; Gratton, D.J. Remote sensing and the measurement of geographical entities in a forested environment. 1: The scale and spatial aggregation problem. Remote Sens. Environ 1994, 49, 93–104. [Google Scholar]
- Woodcock, C.E.; Strahler, A.H. The factor of scale in remote sensing. Remote Sens. Environ 1987, 21, 311–332. [Google Scholar]
- Cracknell, A.P. Synergy in remote sensing—What’s in a pixel? Int. J. Remote Sens 1998, 19, 2025–2047. [Google Scholar]
- Fisher, P. The pixel: A snare and a delusion. Int. J. Remote Sens 1997, 18, 679–685. [Google Scholar]
- Schowengerdt, R.A. Remote Sensing: Models and Methods for Image Processing, 3rd ed; Academic Press: San Diego, CA, USA, 2007; p. 515. [Google Scholar]
- Townshend, J.R.G. The spatial resolving power of earth resources satellites. Prog. Phys. Geogr 1981, 5, 32–55. [Google Scholar]
- Atkinson, P.M.; Aplin, P. Spatial variation in land cover and choice of spatial resolution for remote sensing. Int. J. Remote Sens 2004, 25, 3687–3702. [Google Scholar]
- Cushnie, J.L. The interactive effect of spatial resolution and degree of internal variability within land-cover types on classification accuracies. Int. J. Remote Sens 1987, 8, 15–29. [Google Scholar]
- Smith, J.H.; Stehman, S.V.; Wickham, J.D.; Yang, L. Effects of landscape characteristics on land-cover class accuracy. Remote Sens. Environ 2003, 84, 342–349. [Google Scholar]
- Aplin, P. On scales and dynamics in observing the environment. Int. J. Remote Sens 2006, 27, 2123–2140. [Google Scholar]
- Ju, J.; Gopal, S.; Kolaczyk, E.D. On the choice of spatial and categorical scale in remote sensing land cover classification. Remote Sens. Environ 2005, 96, 62–77. [Google Scholar]
- Ozdogan, M.; Woodcock, C.E. Resolution dependent errors in remote sensing of cultivated areas. Remote Sens. Environ 2006, 103, 203–217. [Google Scholar]
- Saiko, T.A.; Zonn, I.S. Irrigation expansion and dynamics of desertification in the Circum-Aral region of Central Asia. Appl. Geogr 2000, 20, 349–367. [Google Scholar]
- Siegfried, T.; Bernauer, T.; Guiennet, R.; Sellars, S.; Robertson, A.W.; Mankin, J.; Bauer-Gottwein, P.; Yakovlev, A. Will climate change exacerbate water stress in Central Asia? Clim. Chang 2012, 112, 881–899. [Google Scholar]
- Garrigues, S.; Allard, D.; Baret, F.; Weiss, M. Influence of landscape spatial heterogeneity on the non-linear estimation of leaf area index from moderate spatial resolution remote sensing data. Remote Sens. Environ 2006, 105, 286–298. [Google Scholar]
- Tyc, G.; Tulip, J.; Schulten, D.; Krischke, M.; Oxford, M. The RapidEye mission design. Acta Astronaut 2005, 56, 213–219. [Google Scholar]
- Richter, R. Atmospheric/Topographic Correction for Satellite Imagery. ATCOR-2/3 User Guide 7.1; German Areospace Center: Wessling, Germany, 2011. [Google Scholar]
- Garrigues, S.; Allard, D.; Baret, F.; Weiss, M. Quantifying spatial heterogeneity at the landscape scale using variogram models. Remote Sens. Environ 2006, 103, 81–96. [Google Scholar]
- Löw, F.; Schorcht, G.; Michel, U.; Dech, S.; Conrad, C. Per-field crop classification in irrigated agricultural regions in middle Asia using random forest and support vector machine ensemble. Proc. SPIE 2012, 8538. [Google Scholar] [CrossRef]
- Conrad, C.; Machwitz, M.; Schorcht, G.; Löw, F.; Fritsch, S.; Dech, S. Potentials of RapidEye time series for improved classification of crop rotations in heterogeneous agricultural landscapes: Experiences from irrigation systems in Central Asia. Proc. SPIE 2011, 8174. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and Regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Random Forests—Leo Breiman and Adele Cutler. Available online: http://www.stat.berkeley.edu/~breiman/RandomForests/cc_home.htm (accessed on 8 September 2014).
- Chen, X.; Tateishi, R.; Wang, C. Development of a 1-km landcover dataset of China using AVHRR data. ISPRS J. Photogramm. Remote Sens 1999, 54, 305–316. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing. Available online: http://www.R-project.org/ (accessed on 15 September 2014).
- Congalton, R.G. A review of assessing the accuracy of classifications of remotely sensed data. Remote Sens. Environ. 1991, 37, 35–46. [Google Scholar]
- Stehman, S.V. Comparing thematic maps based on map value. Int. J. Remote Sens 1999, 20, 2347–2366. [Google Scholar]
- Stehman, S.V. Selecting and interpreting measures of thematic classification accuracy. Remote Sens. Environ. 1997, 62, 77–89. [Google Scholar]
- Foody, G.M. Status of land cover classification accuracy assessment. Remote Sens. Environ 2002, 80, 185–201. [Google Scholar]
- Provost, F.; Fawcett, T. Analysis and visualization of classifier performance: Comparison under imprecise class and cost distributions. In Proceedings of the Third International Conference on Knowledge Discovery and Data Mining, Newport Beach, CA, USA, 14–17 August 1997; pp. 43–48.
- Löw, F.; Michel, U.; Dech, S.; Conrad, C. Impact of feature selection on the accuracy and spatial uncertainty of per-field crop classification using Support Vector Machines. ISPRS J. Photogramm. Remote Sens 2013, 85, 102–119. [Google Scholar]
- Pal, N.R.; Bezdek, J.C. Measuring fuzzy uncertainty. IEEE Trans. Fuzzy Syst 1994, 2, 107–118. [Google Scholar]
- Van Rijsbergen, C.J. Information Retrieval, 2nd ed; Butterworth-Heinemann Ltd: London, UK, 1979; p. 224. [Google Scholar]
- Van Oort, P.A.J.; Bregt, A.K.; de Bruin, S.; de Wit, A.J.W.; Stein, A. Spatial variability in classification accuracy of agricultural crops in the Dutch national land-cover database. Int. J. Geogr. Inf. Sci 2004, 18, 611–626. [Google Scholar]
- Bohovic, R.; Klein, D.; Conrad, C. Phenological patterns in Central Asia: Monitoring vegetation dynamics using remote sensing at different scales. Proceedings of the EARSeL Remote Sensing and Geoinformation not only for Scientific Cooperation, Prague, Czech, 30 May– 2 June 2011; pp. 289–297.
- CA Water Info. Available online: http://www.cawater-info.net/index_e.htm (accessed on 8 September 2014).
- Wardlow, B.D.; Egbert, S.L. A comparison of MODIS 250-m EVI and NDVI data for crop mapping: A case study for southwest Kansas. Int. J. Remote Sens 2010, 31, 805–830. [Google Scholar]
| Study Site | Scene Center (Lat, Lon) | Total Number of Fields | Mean, Median and Standard Deviation of Field Size (ha) | Cover Fraction | Max Dc | Moran’s I Index |
|---|---|---|---|---|---|---|
| Khorezm (KHO) | 60°35′19E, 41°31′12N | 22,247 | 4.31, 3.21, 2.07 | 0.59 | 2.3 | 0.149 |
| Karakalpakstan (KKP) | 59°33′48E, 42°42′37N | 21,205 | 2.19, 1.71, 1.86 | 0.32 | 2.8 | 0.143 |
| Kyzl-Orda (KYZ) | 64°55′55E, 44°58′71N | 14,561 | 2.45, 2.14, 1.62 | 0.25 | 1.7 | 0.348 |
| Fergana (FER) | 71°45′00E, 40°32′33N | 12,670 | 6.74, 5.47, 2.25 | 0.57 | 2.4 | 0.042 |
| KHO 2009 | KHO 2010 | KKP 2011 | KYZ 2011 | FER 2011 | FER 2012 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Crop | Cf | MFS (ha) | Crop | Cf | MFS (ha) | Crop | Cf | MFS (ha) | Crop | Cf | MFS (ha) | Crop | Cf | MFS (ha) | Crop | Cf | MFS (ha) |
| C | 0.34 | 5.05 ± 1.83 | C | 0.35 | 5.03 ± 1.93 | C | 0.12 | 2.50 ± 1.68 | F | 0.28 | 2.56 ± 1.62 | WO | 0.32 | 7.83 ± 2.81 | WO | 0.27 | 7.54 ± 2.75 |
| WO | 0.27 | 4.49 ± 1.95 | WO | 0.30 | 4.60 ± 2.17 | F | 0.48 | 2.15 ± 1.86 | R | 0.52 | 2.36 ± 1.36 | F | 0.04 | 4.68 ± 2.45 | F | 0.01 | 4.27 ± 2.53 |
| T | 0.23 | 4.22 ± 2.11 | T | 0.19 | 4.45 ± 2.15 | R | 0.07 | 2.11 ± 1.68 | A1 | 0.10 | 2.36 ± 1.80 | W | 0.05 | 6.49 ± 2.84 | W | 0.09 | 8.45 ± 2.66 |
| W | 0.01 | 5.14 ± 1.78 | W | 0.01 | 4.14 ± 2.10 | S | 0.02 | 1.60 ± 1.53 | A3 | 0.10 | 2.67 ± 1.48 | C | 0.42 | 7.72 ± 2.71 | C | 0.44 | 7.40 ± 2.70 |
| R | 0.07 | 4.15 ± 2.25 | R | 0.13 | 4.10 ± 1.75 | W | 0.22 | 2.39 ± 1.83 | T | 0.19 | 4.70 ± 2.42 | T | 0.19 | 4.70 ± 2.78 | |||
| S | 0.01 | 5.88 ± 2.86 | S | 0.01 | 3.60 ± 2.18 | A1 | 0.07 | 2.29 ± 1.67 | |||||||||
| FA | 0.07 | 2.70 ± 1.82 | FA | 0.01 | 3.20 ± 1.9 | M | 0.03 | 1.40 ± 1.16 | |||||||||
| WO | 0.01 | 1.62 ± 1.45 | |||||||||||||||
| OA: 94.4 | OA: 87.4 | OA: 94.60 | OA: 93.90 | OA: 96.10 | OA: 95.6 | ||||||||||||
| Criterion | Symbol | Level I | Level II | Level III |
|---|---|---|---|---|
| Number of available reference pixels per class | Ni | >50 | >75 | >100 |
| Classification accuracy | ACC/CAi | >0.75 | >0.80 | >0.85 |
| α-Quadratic classification entropy | AQE/AQEi | <0.55 | <0.50 | <0.45 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Löw, F.; Duveiller, G. Defining the Spatial Resolution Requirements for Crop Identification Using Optical Remote Sensing. Remote Sens. 2014, 6, 9034-9063. https://doi.org/10.3390/rs6099034
Löw F, Duveiller G. Defining the Spatial Resolution Requirements for Crop Identification Using Optical Remote Sensing. Remote Sensing. 2014; 6(9):9034-9063. https://doi.org/10.3390/rs6099034
Chicago/Turabian StyleLöw, Fabian, and Grégory Duveiller. 2014. "Defining the Spatial Resolution Requirements for Crop Identification Using Optical Remote Sensing" Remote Sensing 6, no. 9: 9034-9063. https://doi.org/10.3390/rs6099034
APA StyleLöw, F., & Duveiller, G. (2014). Defining the Spatial Resolution Requirements for Crop Identification Using Optical Remote Sensing. Remote Sensing, 6(9), 9034-9063. https://doi.org/10.3390/rs6099034