Characterizing Spatio-Temporal Dynamics of Urbanization in China Using Time Series of DMSP/OLS Night Light Data
Abstract
: Stable nighttime light (NTL) data, derived from the Defense Meteorological Satellite Program’s Operational Linescan System (DMSP/OLS), are typically considered a proxy measure of the dynamics of human settlements and have been extensively used to quantitative estimates of demographic variables, economic activity, and land-use change in previous studies at both regional and global scales. The utility of DMSP data for characterizing spatio-temporal trends in urban development at a local scale, however, has received less attention. In this study, we utilize a time series of DMSP data to examine the spatio-temporal characteristics of urban development in 285 Chinese cities from 1992 to 2009, at both the local and national levels. We compare linear models and piecewise linear models to identify the turning points of nighttime lights and calculate the trends in nighttime light growth at the pixel level. An unsupervised classification is applied to identify the patterns in the nighttime light time series quantitatively. Our results indicate that nighttime light brightness in most areas of China exhibit a positive, multi-stage process over the last two decades; however, the average trends in nighttime light growth differ significantly. Through the piecewise linear model, we identify the saturation of nighttime light brightness in the urban center and significant increases in suburban areas. The maps of turning points indicate the greater the distance to the city center or sub-center, the later the turning point occurs. Six patterns derived from the classification illustrate the various characteristics of the nighttime light time series from the local to the national level. The results portray spatially explicit patterns and conspicuous temporal trends of urbanization dynamics for individual Chinese cities from 1992 to 2009.1. Introduction
Over the past few decades, there has been increasing interest among policy makers and researchers in the spatio-temporal changes of urban areas. The world is experiencing rapid urbanization, accompanied by economic and population growth. The share of the world’s urban population has grown to over one-half, and this urban population is projected to grow by more than two billion people by 2050 [1]. The effects of urbanization, such as increasing human activity and impervious surfaces, may contribute to water and air contamination and climate change [2,3]. In addition, vegetation deterioration and biodiversity reduction are usually associated with the land-cover changes that accompany urbanization [4–6].
Because urbanization is associated with many crucial issues, various data and methods have been applied to investigate the spatio-temporal dynamics of urbanization. Socio-economic data, such as Gross Domestic Product (GDP) and demographics, are most frequently utilized to assess urbanization; however, the shortcomings of these indicators include their inconsistency over time, their lacking of distribution information, and their costliness to survey. These problem are worse in many developing countries, especially war-torn countries, where standard statistical sources are difficult to collect or unavailable. Consequently, developing alternatives for studying urbanization presents an urgent challenge for the scientific community.
Satellite sensors provide a convenient way to inspect land-use changes. However, monitoring urbanization dynamics using remote sensing is difficult due to the spectrally diverse land cover types present in urban areas [7]. The nighttime light images acquired from the Defense Meteorological Satellite Program’s Operational Linescan System (DMSP/OLS) provide a unique proxy for monitoring urbanization dynamics. The DMSP/OLS dates to the 1970s [8] but was not widely noticed until 1992 when the images became available in digital format. Since then, DMSP/OLS data have been utilized in numerous studies of urbanization that examine maps of city lights [9], urban areas [10,11], greenhouse gases [12], economic activity [13,14], population [15,16], electric power consumption [17], light pollution [18], gas flares [19], and in-use steel stock [20].
Most previous studies evaluate the correlation between nighttime light and urbanization indicators at various levels; however, only a few studies have investigated the multi-temporal characteristics of urban dynamics [21–24]. The development of an urban area is usually a multi-stage process during which a rural area changes into an urban area and suburbs develop around the downtown area. Each stage involves its own pattern of land-use change, public infrastructure, and economic and population growth. Identifying these patterns could improve our understanding of the dynamics of urbanization. The correlation between nighttime light and urbanization suggests that long-term DMSP/OLS data could be employed to identify the spatio-temporal pattern of urbanization, as well as to detect when the urbanization process accelerated, slowed or reached equilibrium.
The objectives of this study are to identify the spatio-temporal characteristics of urbanization and to quantify these trends and patterns of urbanization in 285 Chinese cities by analyzing DMSP data at the pixel level. First, we estimate linear and piecewise regressions on multi-temporal DMSP/OLS data for Chinese cities from 1992 to 2009 and determine the best-fitting model for each pixel. Second, we employ an unsupervised classification method for the regressionn results to identify patterns within the nighttime light data. Finally, we analyze the regression and classification results for nighttime light at the local and national levels to reveal the characteristics of urbanization for these 285 Chinese cities.
2. Data and Methods
2.1. Multi-Temporal DMSP/OLS NTL Dataset
The DMSP-OLS nighttime light time series data were obtained from the website of the National Geophysical Data Center (NGDC) of the National Oceanic and Atmospheric Administration (NOAA), which initially collected global cloud cover and cloud top temperature data. The satellites sensors have a unique capability [25,26] to detect low-light moonlit clouds. In addition, the satellites are also sensitive to light emitted from cities, gas flares, fires, and fishing boats. An archive of cloud-free NTL data exists, from which the annual time series is produced from all available DSMP-OLS smooth resolution data since 1992.
The version 4 time series of stable light span from −180 to 180 degrees longitude and −65 to 75 degrees latitude with a spatial resolution of 30 arc-seconds. The images are composed of the annual average brightness level digital number (DN), which ranges from 0 to 63 with sunlit, glare and moonlit data excluded. There are five sensors collecting NTL data from 1992 to 2009: F10 (1992–1994), F12 (1994–1999), F14 (1997–2003), F15 (2000–2007), and F16 (2004–2009). Due to differences in satellite orbits and sensor degradation, measurements of NTL brightness could differ significantly even when the ground has not changed [22]. To minimize sensor errors, we estimate a second order regression model [19] to intercalibrate the yearly NTL data to match the F12 1999 data range. There are two separate annual composites of different sensors for most years, and we utilize the best-fitting composite for each year: 1992–1994 (F10), 1995–1997 (F12), 1998 (F14), 1999 (F12), 2000–2002 (F15), 2003 (F14), 2004 (F15), 2005 (F16), 2006 (F15), and 2007–2009 (F16). We exclude areas with DN < 12 in 2009, which are determined to be undeveloped areas by comparing them with Landsat images [23,26]. Furthermore, we extract NTL data for 285 Chinese cities utilizing their administrative boundaries in the same geo-reference system (Figure 1).
2.2. Regression Analysis of NTL Data
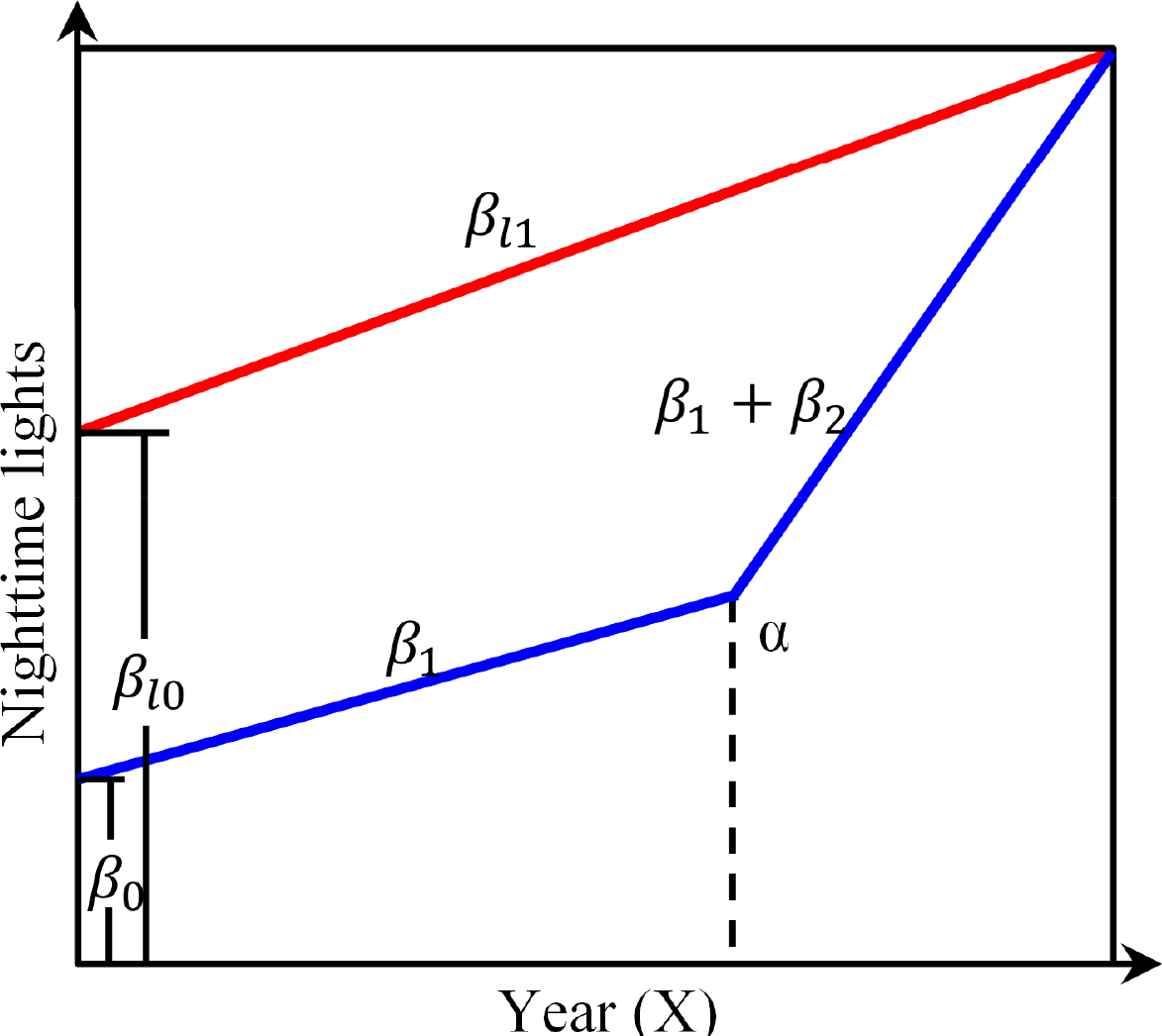
Piecewise, or segmented, regression is widely used in trend analysis to monitor the turning points in a time series [27,28]. Piecewise linear model, which is good at change detection compare to linear model, is one kind of piecewise regression model that the relations in the intervals are obtained by linear regression. To detect the most significant change in nighttime lights, we employ unweighted sliding-average smooth data with a smooth width of 3 years to reduce the noise produced by data acquisition and preprocessing. Then, we estimate a piecewise linear regression (Figure 2) to fit NTL time series at pixel level with two line segments connected at the turning point:
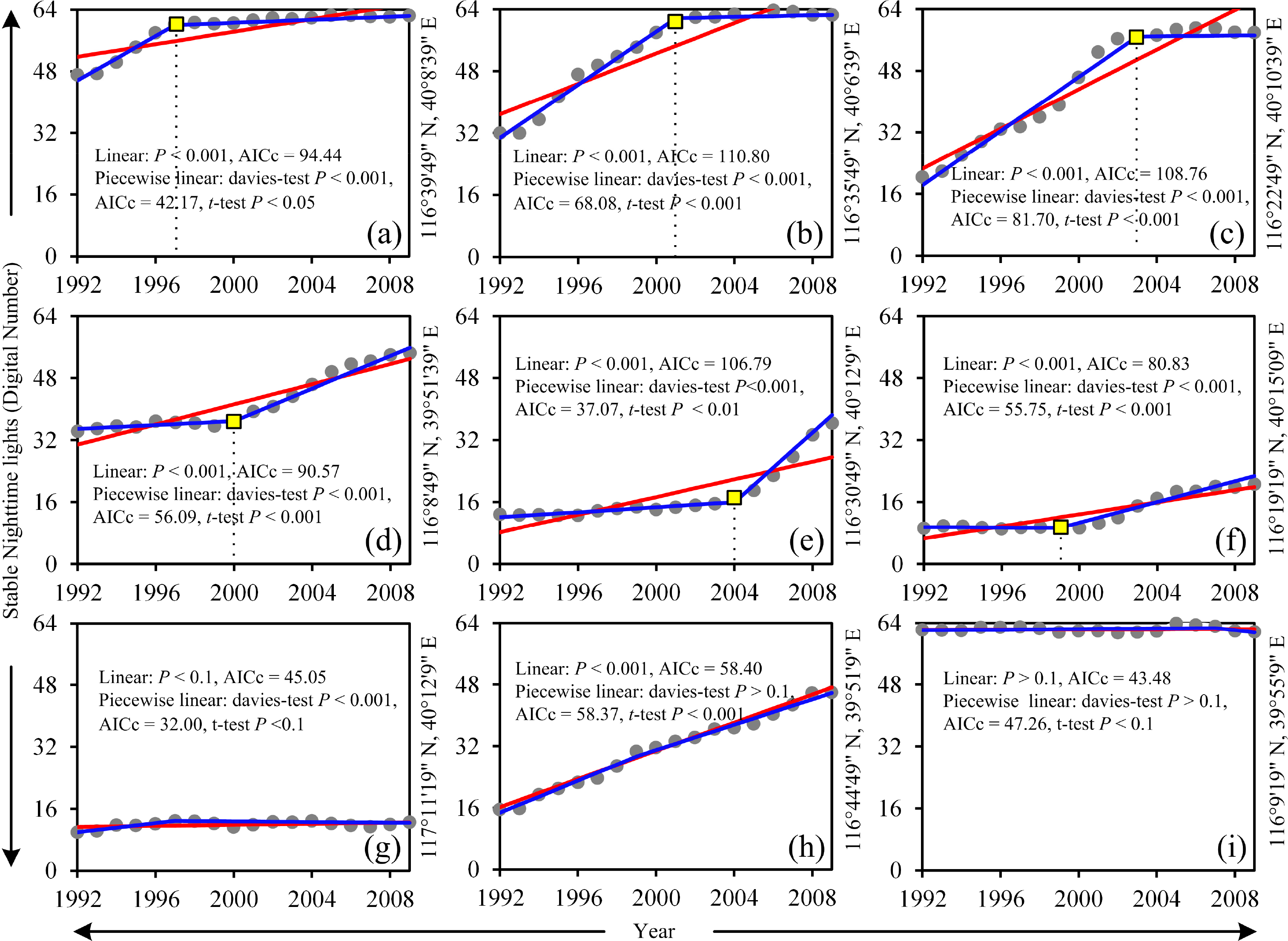
It is noteworthy that the turning point is not prevailing for all urban development processes. Some regions display increasing urbanization with a constant growth rate or no significant alterations over time. Therefore, we compare the linear models with piecewise linear models to identify the best-fitting model. A Davies test [29] identifies the constantly developing regions by examining where there are no conspicuous changes in urban dynamics. However, applying the Davies test on unchanged regions is problematic. Although the area displays no significant alteration, errors from satellite sensors and data preprocessing may produce a false turning point. Therefore, Welch’s t-test is employed to recognize unchanged regions by determining whether two sets of DN values divided by the turning point differ significantly. In addition, the statistical significance of the linear model is tested using the t-statistic. All significance tests are performed under a 95% confidence level. We also employ the corrected Akaike information criterion (AICc) to quantify the information loss in both piecewise linear model and linear model. The model with the minimum AICc is considered the best fit. Through the Davies test, Welch’s t-test, and AICc, we identify best-fitting model for each pixel. Figure 3 displays the typical trends in the NTL data and regression results. According to our strategy Figure 3a–f are identified as piecewise linear model, while Figure 3g–i are identified as linear model. Although NTL data are available from 1992 to 2009, turning points are identified from 1994 to 2007 to insure statistical significance on both sides of the turning point.
2.3. Classification and Trend Analysis of NTL Data
Although the regression analysis recognizes the turning point of urbanization at the pixel level, one cannot distinguish among the urbanization patterns of cities or city regions from these regression results. Therefore, we follow an unsupervised classification procedure to recognize the patterns of urbanization and statistically quantify the long-term average trend of NTL in Chinese cities.
The ISODATA clustering algorithm [30] identifies the classes by iteratively computing the clusters center through the minimum Euclidean distance. We transform the β1, β2 and DN values for 1992 into values that range from 0 to 1 to input into the ISODATA because these three variables potentially capture the long-term trend of NTL from 1992 to 2009. First, we set the maximum number of clusters to a high value, 10, to minimize information loss. Then, according to the dendrogram of attribute distances among classes and an empirical understanding of the data, we discard noisy classes. Of the 10, 6 classes remain. Based on the cluster results, maximum likelihood classification was utilized to assign each pixel to one of the 6 classes.
Nighttime light brightness may vary with urban development. To identify trends in urbanization, we obtain the average trend in nighttime light growth of an urban area by the sum of the slope of lit pixels divided by the total number of lit pixels located in the urban area. For comparison, we also calculate this variation at the national level. The slope of lit pixels is acquired from the best-fitting model.
3. Results and Discussion
3.1. Long-Term Trends at the National Level
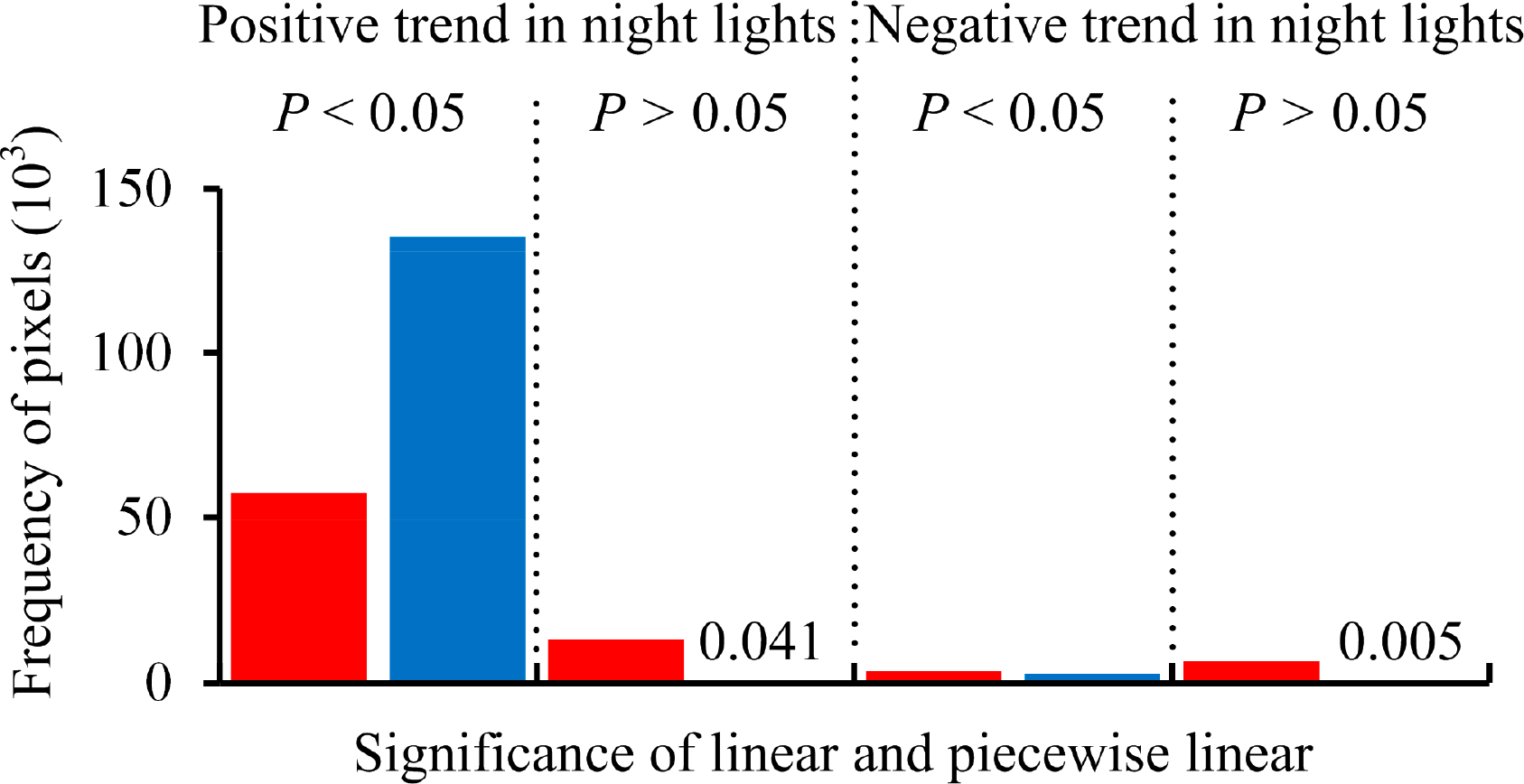
Previous studies indicate that China has been experiencing rapid urbanization since the 1990s [23,31]. Figure 4 presents the summary of statistical significance of long-term trends in NTL for all 285 Chinese cities for the period 1992–2009. As displayed in Figure 4, significant increases in nighttime light brightness are identified in 88% of pixels and turning points are identified in 70% of them by the piecewise linear model. Significantly decreased night light brightness was recognized in only 2% of pixels, including 1% identified by the linear model and 1% identified by the piecewise linear model. Most insignificant areas are identified by the linear model (6% of pixels increased and 3% decreased) rather than the piecewise linear model because night light brightness in these areas generally exhibited gentle slopes (−0.5 to 0.5) without significant changes. These results imply that most areas in China experienced increasing urbanization over the last two decades, and the existence of turning points indicates the multi-stage characteristic of urbanization. In the following subsections, we first examine the spatio-temporal distribution of turning points, and then analyze the patterns and trends of urban dynamics based on the best-fitting models of multi-temporal NTL data.
3.2. Spatio-Temporal Distribution of Turning Points
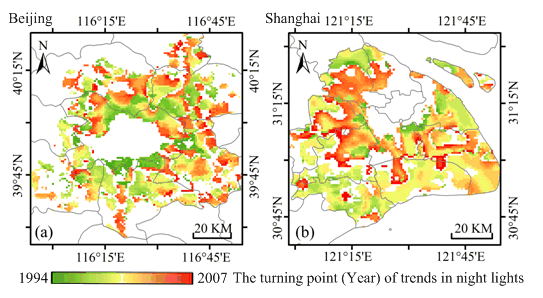
Empirically, turning points in urbanization occur when population density and economic activity reach critical points. For example, villages or towns may change into urban areas when industry is established as occurred in Shenzheng. Some regions develop faster than neighboring regions do, and the speed of urbanization slows in the urbanized areas. To recognize the temporal trend and spatial distribution of turning points, we mapped the turning point, left slope and right slope of the piecewise linear model and slope of the linear model respectively for 285 Chinese cities. Figure 5 illustrates these parameters for three major Chinese cities: Beijing, Shanghai and Guangzhou. As indicated in Figure 5, nearly all city centers are identified by the linear model. Generally, these areas were characterized by intense development, high population density and economic activity before 1992; therefore, the nighttime light brightness of these areas remained high and suggested no significant changes from 1992 to 2009. There exists a ring around the center in many cities that follows the piecewise linear model. Turning points usually occur earlier in the inner ring and later in the outer ring of cities, such as Beijing (Figure 5a) and Shanghai (Figure 5b). However, some cities exhibit no explicit structure, including Guangzhou (Figure 5c). By examining the piecewise slopes, we recognize that the nighttime light in these areas first develops quickly (the red areas in Figure 5d–f) then reach a saturation point when nighttime light brightness suggest no significant changes (the blue and yellow areas in Figure 5g–i). In the outskirts of cities, turning points occur in two different patterns. First, in the ring zones around sub-centers, such as those surrounding the city center, nighttime light brightness stabilized after the turning point. Second, the remaining suburban areas first suggest no statistically significant trend; however, after the turning point, they exhibit remarkable increases in light brightness. As depicted in Figure 5a–c, the years in which turning points occur are associated with the distance to the city center. Generally, the greater the distance to the city center or sub-center, the later the turning point occurs. Moreover, the slopes of the linear models (Figure 5j–l) first increase and then decrease as the distance to the city center or sub-center increases.
These results of nighttime lights may indicate the spatio-temporal distribution of turning points in urban development. According to the maps of piecewise slopes (Figure 5d–i), the spatial distribution of the two major types of turning points, deceleration and acceleration, could be identified. The former usually occurs in the city center and sub-center, while the latter usually occurs in suburban areas. The maps of turning points (Figure 5a–c) allow us to detect the spatial trends of the turning points. In addition, the maps of linear slopes (Figure 5j–l) depict nighttime light in areas without turning points. It is quite noticeable that the decrease in brightness in Fangshan (light blue areas in Figure 5j) may be related to gas flares reduction. Sinopec Beijing Yanshan Company upgraded the recycling systems and shut down 8 gas flares due to environmental concerns and energy efficiency during 1996 to 2004. The nighttime light brightness in Fangshan first sharply decreased then increased in recent years (Figure 5a,d,g) reflected this event. A previous study [32] show the decreases in brightness occurring in economically developed regions may associate with renovation of lighting system. Shanghai changed the street lighting type from incandescent lamp to high pressure sodium lamp, and upgraded the lighting system for energy conservation reasons since 2005. Street lights are dimed by intelligent control system after 11 p.m. These facts may lead to the noticeable and extensive decrease in brightness after the turning points in Shanghai (Figure 5h).
3.3. Patterns of Nighttime Light Time Series
Previous subsection provides an intuitional way to observe the urban dynamics; however, statistically quantify the patterns may enable us to better understand the differentiation of urbanization between Chinese cities. To analyze the patterns of nighttime light for 285 Chinese cities, we obtain 6 classes following an unsupervised classification procedure. Three classes exhibit convex shapes and three exhibit concave long-term trend shapes for nighttime light brightness. Therefore, we define the convex classes as saturated patterns A to C because they saturated after the turning points, and define the concave classes as accelerated patterns D to F because they accelerated after the turning points. Generally, pattern A areas were already brightly lit in 1992, and reached saturation later with gently increasing slopes (Figure 3a). Pattern B areas rapidly reached saturation from lower light levels in 1992 (Figure 3b). Pattern C areas exhibited even lower light levels in 1992 and reached saturation with sharply increase (Figure 3c). Pattern D areas first exhibit the same brightness as pattern C, but light brightness did not increase until the turning point (Figure 3d). Areas characterized by patterns E and F emitted dim light in 1992; however, after their turning points, brightness in pattern E increased sharply (Figure 3e) but increased at a very low rate in pattern F (Figure 3f). Figure A1 shows the spatial distribution of six patterns across 285 Chinese cities.
To inspect the temporal variation in nighttime lights patterns, we partition each pattern by the year in which turning points occur (Figure 6). As indicated in Figure 6a, the long-term trend of total frequency of turning points at the national level reach a local peak in 1996 and global peak in 2000, which implies that 1996 and 2000 are pivotal years in Chinese urbanization. The two major patterns indicate reverse trends (Figure 6a): the saturated patterns are slightly concentrated in the early and recent years, while the accelerated types center on the year 2000. The stacked percentage histogram (Figure 6b) illustrates the distribution of patterns from 1994 to 2007. As illustrated in Figure 6b, there are fewer saturated patterns than accelerated patterns except during 2006 and 2007. At first, patterns A and B each represented 20% of turning points in 1994, which decreased to minimums of 4% and 6% in 2000, respectively, and increased to 12% by 2005. Pattern C exhibits a similar trend before 2002 but experienced subsequent rapid increases and reached more than 46% in 2007. Spanning the range from 40% to 3% of turning points pattern D show reverse trend of pattern C. Pattern E increases from less than 1% of turning points to approximately 20% and then exhibits no significant changes until 2007, which then sharply decreased to 13%. Pattern F includes the most pixels of the six patterns and exhibits a unimodal distribution, which reached a maximum of 45% in 2001. These results indicate that neither the saturated patterns nor the accelerated patterns maintain stable proportions, which implies imbalances in Chinese urbanization. In 1996, the saturated patterns outnumbered accelerated patterns for the first time; however, from that time until 2000, the accelerated pattern increased sharply, and the turning points reached their maximum frequency, which indicates that Chinese cities had greatly expanded [33]. This pattern is likely correlated with the economic and technological development zones established in many Chinese cities in the 1990s [34,35]. From 2000 to 2007, significant increases were observed for pattern C that indicates significant expansion of city centers. Table A1 lists the statistical summary of six patterns for 285 Chinese cities.
Figure 7 displays the six patterns for some typical cities. Accelerated patterns in many cities increased around 2000, which was observed in Beijing, Shanghai, Changzhou, and Changsha. However, Beijing exhibits considerably different saturation patterns from Shanghai; an insufficient area of Shanghai reached saturation before 2000 compare this city to Beijing. In Guangzhou, the proportions of saturated and accelerated patterns remain steady, which implies balanced urbanization. Some coastal regions, such as the Pearl River Delta, experienced rapid development under free and open economic conditions since the 1990s. In Dongguan, for instance, saturated patterns are dominant and exhibit a bimodal distribution, which likely indicates that this city underwent rapid urbanization and most city regions eventually reached saturation. Over the last two decades, many factories were established in Yangtze River Delta, which significantly extended the boundaries of cities. In Changzhou for example, the prevalence of accelerated patterns from 1998 to 2004 correlates with the numerous new factories and enterprises established. Some cities exhibit a trend towards decreased frequency. In Daqing, for instance, this decrease is most likely associated with a local recession within the petroleum industry. In some cities, such as Putian and Changsha, saturated and accelerated patterns concentrate in different periods, which imply imbalanced urbanization. Medium and small cities sometimes lack one or more patterns and always exhibit an imbalanced distribution of patterns. In Liaocheng, for example, patterns D and E are missing, and saturated patterns strongly concentrate in 1996. These results imply that the investigation of nighttime lights patterns potentially reveals the characteristics of cities at different stages of urbanization.
3.4. Average Trend in Nighttime Light Growth
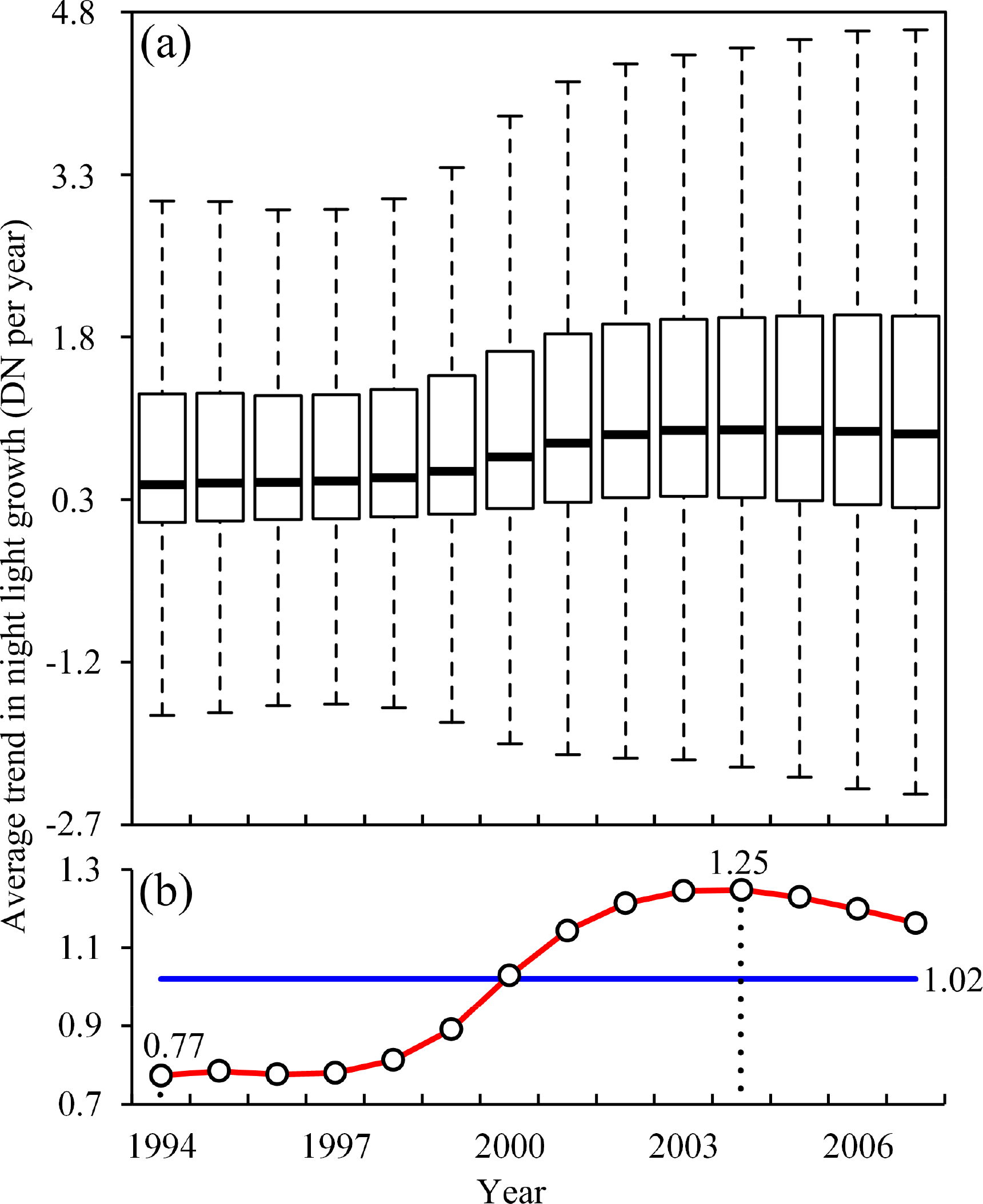
The NTL patterns show characteristics of Chinese cities in the urbanization process, study the trends in nighttime light could reveal how the urbanization process is affected by those characteristics. Figure 8 displays the average trend in nighttime light growth in China. The whiskers of the boxplot (Figure 8a) represent the data within the 1.5 interquartile range of the first and third quartiles, and the data beyond this range are excluded. As indicated in Figure 8a, nighttime light brightness in over 75% of Chinese regions increased from 1994 to 2007 as evidenced by all third quartiles above zero. The increased interquartile range over time likely implies that the imbalance in night light in Chinese cities intensified. Figure 8b compares the average trend obtained from the linear model to the combination of linear and piecewise linear models. The DN value grows at a constant rate of 1.02 per year according to the linear model; however, when the piecewise linear model is considered, the average trend fluctuates and intersects with the horizontal line at 2000. The average trend in night light growth implies that the speed of urbanization in China accelerated since 1994 and slightly slowed after reaching a maximum in 2004.
Figure 9 illustrates the average trend in night light growth in a selection of Chinese cities. Major cities exhibit stable growth of night light brightness between 0.8 and 1.6 DN per year such as Beijing, Shanghai and Guangzhou (Figure 9a). Nighttime light experienced significant growth between 1998 and 2002 in Wuxi, Suzhou, and Changzhou (Figure 9b), which potentially reflects the recent rapid development of the Yangtze River Delta. Some cities exhibit stable increased rates of nighttime light growth, such as Chuzhou, Baotou, and Fangchenggang (Figure 9c). The nighttime light growth in some cities first slightly increases and then sharply decreases at some point. Jinhua, Shaoxing, and Changsha, for instance, exhibit a significantly negative trend after 2003. In Huangshan, Nanchang, and Jiaxing, the growth of night light brightness first increased and then fell around 2002. A few cities exhibit a negative trend in the growth of nighttime light, such as Chaozhou, Dongguan and Wenzhou, which decreased from more than 2.4 DN per year in 1994 to less than 0.8 DN per year in 2007. These results suggest diverse trends in night light growth that correspond to diverse trends in the urbanization of Chinese cities, which implies the unbalanced development of Chinese cities; however most cities exhibit increasing growth rate of NTL brightness indicate Chinese cities experienced continuing development over the last two decades.
4. Conclusions
Urbanization is a global transformation of human society that involves population migration, economic activity and land-use change. Due to night light brightness is verified associate with features of urbanization in many studies [36], nighttime light images derived from DMSP/OLS provide a unique proxy for urbanization.
In this paper, we utilize time series of DMSP data to investigate the urban dynamics of 285 Chinese cities from 1992 to 2009 at the pixel level. Rather than examining the relationship between nighttime light and urban variables, we utilize nighttime light as a proxy for urban dynamics to examine the patterns and trends of urbanization at local and national levels. Linear and piecewise linear models are estimated and compared for NTL data, and AICc and Welch’s t-test are employed to identify the best-fitting model. To quantify the patterns of urbanization statistically, we apply an unsupervised classification procedure utilizing three variables: the DN value in 1992 and the left and right slopes of the piecewise linear model to generate six distinct patterns. Moreover, we calculated the average trend in nighttime light growth for the local and national levels.
Our study suggests that the long-term nighttime light brightness of most areas follows the piecewise linear function, although some follow the linear function. 88% of lit pixels in China, of which 70% follow the piecewise linear function, show increasing brightness over the last two decades. We identify the turning point of the nighttime light time series according to the piecewise linear model. The spatio-temporal distribution of turning points are identified by the left and right slopes and turning point of the piecewise linear model and slope of the linear model. The maps of these parameters show NTL saturation in an urban center and growth in suburban areas; in addition, the greater the distance to the city center or sub-center, the later the turning point occurs. The yearly variation in the six night light patterns at city level reveals the diverse characteristics of cities at different stages of urbanization. These patterns at national level implies that the urbanization of Chinese cities focused on established city areas in 1996, and Chinese cities expanded remarkably around 2000, while city centers have expanded significantly in recent years. The local nighttime light growth data suggest that Chinese cities exhibit varying trends in urbanization. However, the national trend implies that Chinese urbanization accelerated since 1994 until it decreased slightly after 2004. In addition, most areas experienced positive rates of nighttime light growth, which implies that most Chinese cities experienced consistent urban development during the last two decades. It is noteworthy that the problem of saturation in urban centers [37] and overglow effects [26] in DMSP data may blur the long-term trend and spatial distribution of urban changes. Therefore, further research should consider these problems, and improve the accuracy of DMSP data. The newly available nighttime lights products derived from Visible Infrared Imaging Radiometer Suite (VIIRS), which provide a more reliable way for investigating urbanization compare to DMSP [38,39], should be applied in further research.
Acknowledgments
This research has been funded by the National Natural Science Foundation of China (No. 41371379 and No. 41171307), Key Programs of the Chinese Academy of Sciences (No. KZZD-EW-07) and National Key Technology R&D Program (No. 2011BAH24B10). We would like to gratefully thank the anonymous reviewers for their insightful and helpful comments to improve the manuscript.
Author Contributions
Tao Xu collected and processed the data, performed analysis and wrote the paper. Ting Ma and Chenghu Zhou conceived and designed the study and methods. Yuke Zhou contributed to analysis and interpretation of the data.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix

| City Name | The Proportion of Urbanization Patterns (%) | Total Frequency | |||||
|---|---|---|---|---|---|---|---|
| Saturated A | Saturated B | Saturated C | Accelerated D | Accelerated E | Accelerated F | ||
| Beijing | 12.15 | 17.94 | 19.91 | 22.59 | 5.91 | 21.51 | 5384 |
| Tianjin | 8.52 | 11.13 | 10.43 | 17.35 | 16.77 | 35.81 | 5177 |
| Shijiazhuang | 25.00 | 29.61 | 24.67 | 16.45 | 0.00 | 4.28 | 304 |
| Tangshan | 6.39 | 5.81 | 3.24 | 15.35 | 12.64 | 56.57 | 2254 |
| Qinhuangdao | 22.37 | 20.09 | 0.46 | 42.92 | 4.57 | 9.59 | 219 |
| Handan | 33.00 | 22.11 | 0.33 | 41.58 | 0.00 | 2.97 | 303 |
| Xingtai | 42.65 | 35.29 | 19.12 | 2.94 | 0.00 | 0.00 | 68 |
| Baoding | 36.36 | 43.94 | 10.61 | 3.03 | 0.00 | 6.06 | 66 |
| Zhangjiakou | 13.00 | 10.00 | 0.00 | 24.67 | 24.33 | 28.00 | 300 |
| Chengde | 3.08 | 4.79 | 2.05 | 28.42 | 18.49 | 43.15 | 292 |
| Cangzhou | 6.49 | 22.08 | 36.36 | 3.90 | 14.29 | 16.88 | 77 |
| Langfang | 4.29 | 4.63 | 17.32 | 7.03 | 11.15 | 55.57 | 583 |
| Hengshui | 7.26 | 10.68 | 17.52 | 4.27 | 3.42 | 56.84 | 234 |
| Taiyuan | 20.30 | 13.08 | 9.67 | 25.61 | 8.86 | 22.48 | 734 |
| Datong | 12.60 | 24.88 | 9.52 | 21.35 | 13.52 | 18.13 | 651 |
| Yangquan | 3.55 | 23.08 | 0.00 | 65.09 | 0.00 | 8.28 | 169 |
| Changzhi | 10.38 | 14.15 | 0.94 | 25.00 | 0.47 | 49.06 | 212 |
| Jincheng | 37.93 | 31.03 | 10.34 | 20.69 | 0.00 | 0.00 | 29 |
| Shuozhou | 2.83 | 3.91 | 0.65 | 20.65 | 18.48 | 53.48 | 460 |
| Jinzhong | 6.82 | 4.75 | 2.08 | 19.29 | 15.13 | 51.93 | 337 |
| Yuncheng | 3.52 | 9.15 | 19.72 | 1.41 | 17.61 | 48.59 | 284 |
| Xinzhou | 3.95 | 5.92 | 7.89 | 11.18 | 19.08 | 51.97 | 152 |
| Linfen | 14.01 | 7.01 | 21.02 | 14.65 | 1.27 | 42.04 | 157 |
| Lvliang | 2.11 | 9.15 | 4.23 | 28.17 | 10.56 | 45.77 | 142 |
| Hohhot | 8.18 | 5.92 | 5.69 | 18.13 | 16.94 | 45.14 | 844 |
| Baotou | 7.97 | 7.50 | 1.22 | 25.12 | 20.06 | 38.14 | 1067 |
| Wuhai | 3.15 | 13.96 | 4.28 | 26.13 | 26.58 | 25.90 | 444 |
| Chifeng | 4.47 | 4.71 | 0.00 | 25.56 | 31.51 | 33.75 | 403 |
| Tongliao | 7.41 | 5.70 | 0.00 | 15.10 | 21.37 | 50.43 | 351 |
| Hulunbeier | 6.47 | 5.18 | 0.00 | 21.04 | 45.95 | 21.36 | 309 |
| Bayannao’er | 4.53 | 4.53 | 0.00 | 11.70 | 48.30 | 30.94 | 265 |
| Ulanqab | 5.88 | 7.84 | 0.00 | 18.63 | 40.20 | 27.45 | 102 |
| Shenyang | 11.36 | 8.92 | 5.19 | 30.66 | 19.00 | 24.87 | 2332 |
| Dalian | 19.08 | 14.84 | 7.87 | 12.87 | 17.49 | 27.86 | 1321 |
| Anshan | 21.41 | 21.65 | 9.41 | 34.82 | 2.35 | 10.35 | 425 |
| Fushun | 28.37 | 13.48 | 0.00 | 48.58 | 0.71 | 8.87 | 282 |
| Benxi | 13.97 | 9.32 | 1.64 | 32.33 | 8.77 | 33.97 | 365 |
| Dandong | 14.59 | 10.81 | 1.08 | 35.14 | 4.86 | 33.51 | 185 |
| Jinzhou | 28.78 | 12.95 | 3.60 | 30.94 | 10.79 | 12.95 | 139 |
| Yingkou | 11.55 | 7.57 | 3.98 | 20.72 | 38.65 | 17.53 | 251 |
| Fuxin | 14.71 | 12.75 | 7.35 | 43.14 | 0.00 | 22.06 | 204 |
| Liaoyang | 14.90 | 8.86 | 0.43 | 44.71 | 5.62 | 25.49 | 463 |
| Panjin | 50.00 | 16.25 | 5.00 | 16.88 | 1.25 | 10.63 | 160 |
| Tieling | 20.65 | 13.04 | 1.09 | 35.87 | 0.00 | 29.35 | 92 |
| Chaoyang | 7.03 | 6.07 | 0.00 | 17.25 | 33.55 | 36.10 | 313 |
| Huludao | 12.39 | 12.83 | 5.31 | 30.53 | 7.96 | 30.97 | 226 |
| Changchun | 12.85 | 7.65 | 6.47 | 10.33 | 29.18 | 33.52 | 1268 |
| Jilin | 22.42 | 12.93 | 3.03 | 28.08 | 9.29 | 24.24 | 495 |
| Siping | 16.13 | 9.68 | 8.87 | 36.29 | 3.23 | 25.81 | 124 |
| Liaoyuan | 13.39 | 4.46 | 0.00 | 34.82 | 9.82 | 37.50 | 112 |
| Tonghua | 4.35 | 14.49 | 6.76 | 26.09 | 13.04 | 35.27 | 207 |
| Baishan | 5.52 | 8.97 | 2.07 | 30.00 | 8.28 | 45.17 | 290 |
| Songyuan | 17.35 | 12.06 | 0.88 | 26.18 | 11.47 | 32.06 | 340 |
| Baicheng | 14.81 | 5.56 | 1.85 | 12.96 | 22.22 | 42.59 | 54 |
| Harbin | 9.44 | 8.14 | 10.03 | 14.93 | 15.87 | 41.59 | 1695 |
| Qiqihar | 8.52 | 4.42 | 2.84 | 25.24 | 5.99 | 53.00 | 317 |
| Jixi | 11.81 | 19.69 | 0.79 | 59.84 | 0.00 | 7.87 | 127 |
| Hegang | 23.28 | 17.24 | 0.00 | 26.72 | 0.00 | 32.76 | 116 |
| Shuangyashan | 6.61 | 3.31 | 0.83 | 17.77 | 11.16 | 60.33 | 242 |
| Daqing | 16.36 | 14.77 | 8.42 | 27.02 | 6.67 | 26.75 | 1828 |
| Yichun | 1.51 | 6.40 | 7.16 | 18.83 | 23.16 | 42.94 | 531 |
| Jiamusi | 13.82 | 4.07 | 3.25 | 24.39 | 0.00 | 54.47 | 123 |
| Qitaihe | 8.03 | 13.87 | 9.85 | 31.75 | 4.38 | 32.12 | 274 |
| Mudanjiang | 20.00 | 11.43 | 0.00 | 29.52 | 2.86 | 36.19 | 105 |
| Heihe | 10.48 | 3.81 | 0.00 | 15.24 | 0.95 | 69.52 | 105 |
| Suihua | 10.14 | 10.14 | 0.00 | 20.29 | 21.01 | 38.41 | 138 |
| Shanghai | 7.33 | 18.38 | 24.23 | 19.39 | 16.51 | 14.15 | 4663 |
| Nanjing | 6.83 | 10.14 | 9.71 | 22.22 | 14.21 | 36.90 | 2534 |
| Wuxi | 6.00 | 5.57 | 4.33 | 36.67 | 33.95 | 13.48 | 1617 |
| Xuzhou | 4.70 | 6.54 | 8.14 | 12.84 | 23.97 | 43.81 | 872 |
| Changzhou | 3.51 | 3.95 | 5.21 | 13.49 | 43.64 | 30.20 | 2053 |
| Suzhou | 3.73 | 6.22 | 6.52 | 8.01 | 53.56 | 21.95 | 2009 |
| Nantong | 1.92 | 5.57 | 5.14 | 7.86 | 35.23 | 44.27 | 1615 |
| Lianyungang | 4.90 | 12.05 | 14.88 | 5.46 | 34.09 | 28.63 | 531 |
| Huai’an | 4.34 | 7.17 | 15.85 | 5.28 | 28.68 | 38.68 | 530 |
| Yancheng | 2.67 | 5.15 | 7.44 | 2.86 | 32.44 | 49.43 | 524 |
| Yangzhou | 4.64 | 4.85 | 4.54 | 6.60 | 33.64 | 45.72 | 969 |
| Zhenjiang | 2.30 | 3.93 | 4.31 | 15.15 | 21.48 | 52.83 | 1043 |
| Taizhou | 2.33 | 4.92 | 43.26 | 2.07 | 21.50 | 25.91 | 386 |
| Suqian | 1.15 | 3.65 | 10.00 | 0.77 | 37.69 | 46.73 | 520 |
| Hangzhou | 5.63 | 7.91 | 27.08 | 7.94 | 26.22 | 25.21 | 2681 |
| Ningbo | 3.05 | 9.02 | 25.88 | 1.25 | 24.22 | 36.57 | 1441 |
| Wenzhou | 5.34 | 6.45 | 58.56 | 0.00 | 5.71 | 23.94 | 543 |
| Jiaxing | 2.85 | 3.51 | 17.01 | 1.65 | 24.26 | 50.71 | 911 |
| Huzhou | 1.08 | 3.55 | 34.00 | 4.95 | 12.36 | 44.05 | 647 |
| Shaoxing | 0.00 | 14.86 | 47.97 | 6.08 | 18.24 | 12.84 | 148 |
| Jinhua | 0.00 | 7.23 | 30.35 | 1.16 | 5.20 | 56.07 | 346 |
| Quzhou | 0.50 | 13.37 | 18.81 | 6.44 | 4.95 | 55.94 | 202 |
| Zhoushan | 0.25 | 4.48 | 18.41 | 1.24 | 16.42 | 59.20 | 402 |
| Taizhou | 0.84 | 7.74 | 55.27 | 0.42 | 1.41 | 34.32 | 711 |
| Lishui | 0.00 | 4.31 | 9.48 | 0.00 | 40.09 | 46.12 | 232 |
| Hefei | 11.22 | 15.27 | 11.22 | 10.98 | 31.50 | 19.81 | 419 |
| Wuhu | 1.91 | 13.38 | 14.33 | 7.96 | 40.76 | 21.66 | 314 |
| Bengbu | 3.98 | 9.95 | 14.43 | 7.96 | 7.96 | 55.72 | 201 |
| Huainan | 2.93 | 5.86 | 7.11 | 28.45 | 14.23 | 41.42 | 239 |
| Maanshan | 2.55 | 23.57 | 7.01 | 32.48 | 17.20 | 17.20 | 157 |
| Huaibei | 1.10 | 14.29 | 5.49 | 34.07 | 13.19 | 31.87 | 182 |
| Tongling | 0.00 | 7.79 | 3.90 | 50.65 | 5.19 | 32.47 | 77 |
| Anqing | 7.89 | 12.28 | 28.07 | 6.14 | 8.77 | 36.84 | 114 |
| Huangshan | 0.00 | 7.84 | 18.30 | 2.61 | 19.61 | 51.63 | 153 |
| Chuzhou | 2.88 | 4.94 | 0.82 | 7.00 | 38.68 | 45.68 | 243 |
| Fuyang | 0.00 | 8.19 | 21.98 | 1.72 | 13.79 | 54.31 | 232 |
| Suzhou | 0.00 | 0.78 | 1.18 | 15.69 | 19.22 | 63.14 | 255 |
| Lu’an | 0.00 | 7.36 | 10.82 | 2.60 | 16.45 | 62.77 | 231 |
| Bozhou | 2.03 | 3.38 | 19.59 | 4.05 | 10.14 | 60.81 | 148 |
| Chizhou | 0.00 | 2.03 | 0.00 | 10.14 | 74.32 | 13.51 | 148 |
| Xuancheng | 0.00 | 0.78 | 1.56 | 12.50 | 25.78 | 59.38 | 128 |
| Fuzhou(Fujian) | 15.51 | 20.90 | 39.55 | 1.57 | 3.37 | 19.10 | 445 |
| Xiamen | 8.04 | 7.18 | 15.41 | 7.37 | 37.22 | 24.78 | 1045 |
| Putian | 0.99 | 6.06 | 17.04 | 5.35 | 30.56 | 40.00 | 710 |
| Sanming | 2.63 | 12.28 | 10.53 | 11.40 | 0.88 | 62.28 | 114 |
| Quanzhou | 8.37 | 10.59 | 50.49 | 0.00 | 12.56 | 17.98 | 406 |
| Zhangzhou | 12.56 | 14.07 | 23.62 | 17.59 | 3.02 | 29.15 | 199 |
| Nanping | 0.00 | 12.50 | 17.19 | 10.94 | 0.00 | 59.38 | 64 |
| Longyan | 4.82 | 11.65 | 28.51 | 2.01 | 6.43 | 46.59 | 249 |
| Ningde | 0.00 | 1.35 | 33.78 | 0.00 | 14.86 | 50.00 | 74 |
| Nanchang | 2.39 | 13.15 | 8.37 | 29.08 | 22.71 | 24.30 | 251 |
| Jingdezhen | 1.30 | 27.27 | 10.39 | 2.60 | 0.00 | 58.44 | 77 |
| Pingxiang | 0.00 | 14.29 | 65.71 | 0.00 | 0.00 | 20.00 | 35 |
| Jiujiang | 2.76 | 2.76 | 15.17 | 11.03 | 0.00 | 68.28 | 145 |
| Xinyu | 0.58 | 3.49 | 2.33 | 12.79 | 30.23 | 50.58 | 172 |
| Yingtan | 1.67 | 10.00 | 16.67 | 5.00 | 8.33 | 58.33 | 60 |
| Ganzhou | 2.55 | 5.61 | 11.22 | 12.24 | 21.94 | 46.43 | 196 |
| Ji’an | 0.00 | 4.85 | 13.94 | 12.12 | 9.09 | 60.00 | 165 |
| Yichun | 0.00 | 10.71 | 28.57 | 7.14 | 10.71 | 42.86 | 56 |
| Fuzhou(Jiangxi) | 0.00 | 2.37 | 9.47 | 2.37 | 27.22 | 58.58 | 169 |
| Shangrao | 0.00 | 4.48 | 0.00 | 8.96 | 14.93 | 71.64 | 67 |
| Jinan | 7.67 | 8.38 | 5.61 | 18.18 | 24.05 | 36.11 | 1551 |
| Qingdao | 13.94 | 13.22 | 25.64 | 3.36 | 23.30 | 20.55 | 983 |
| Zibo | 11.74 | 15.14 | 2.88 | 41.09 | 7.52 | 21.63 | 971 |
| Zaozhuang | 1.18 | 5.31 | 0.74 | 19.62 | 15.78 | 57.37 | 678 |
| Dongying | 9.11 | 20.24 | 34.40 | 6.07 | 7.08 | 23.10 | 593 |
| Yantai | 9.59 | 8.14 | 15.36 | 6.91 | 28.25 | 31.75 | 970 |
| Weifang | 4.00 | 4.88 | 5.11 | 17.54 | 24.64 | 43.84 | 901 |
| Jining | 4.73 | 6.08 | 12.16 | 7.66 | 11.94 | 57.43 | 444 |
| Taian | 2.76 | 6.67 | 29.66 | 0.00 | 9.66 | 51.26 | 435 |
| Weihai | 3.17 | 9.33 | 14.44 | 0.00 | 24.30 | 48.77 | 568 |
| Rizhao | 2.65 | 7.01 | 8.52 | 1.52 | 40.15 | 40.15 | 528 |
| Laiwu | 4.10 | 6.35 | 6.35 | 28.69 | 12.30 | 42.21 | 488 |
| Linyi | 3.12 | 5.28 | 6.64 | 8.24 | 24.56 | 52.16 | 1250 |
| Dezhou | 5.38 | 6.73 | 27.80 | 0.00 | 20.18 | 39.91 | 223 |
| Liaocheng | 8.46 | 9.06 | 37.46 | 0.00 | 1.51 | 43.50 | 331 |
| Binzhou | 2.58 | 4.92 | 0.70 | 24.36 | 20.37 | 47.07 | 427 |
| Heze | 1.29 | 7.12 | 16.18 | 4.53 | 12.94 | 57.93 | 309 |
| Zhengzhou | 5.44 | 8.82 | 15.60 | 9.00 | 35.56 | 25.58 | 1122 |
| Kaifeng | 12.02 | 14.90 | 16.35 | 8.65 | 18.27 | 29.81 | 208 |
| Luoyang | 10.48 | 15.49 | 13.67 | 23.01 | 14.81 | 22.55 | 439 |
| Pingdingshan | 9.03 | 10.32 | 2.58 | 35.16 | 12.90 | 30.00 | 310 |
| Anyang | 16.34 | 16.34 | 14.38 | 18.95 | 0.00 | 33.99 | 153 |
| Hebi | 5.00 | 18.33 | 0.00 | 24.17 | 6.67 | 45.83 | 120 |
| Xinxiang | 10.00 | 20.00 | 13.64 | 37.27 | 12.73 | 6.36 | 110 |
| Jiaozuo | 5.21 | 13.27 | 9.00 | 56.87 | 1.42 | 14.22 | 211 |
| Puyang | 29.84 | 20.97 | 5.65 | 12.90 | 0.81 | 29.84 | 124 |
| Xuchang | 2.99 | 16.42 | 29.85 | 19.40 | 14.93 | 16.42 | 67 |
| Luohe | 4.22 | 13.92 | 26.58 | 1.69 | 10.97 | 42.62 | 237 |
| Sanmenxia | 23.44 | 21.88 | 15.63 | 1.56 | 10.94 | 26.56 | 64 |
| Nanyang | 4.02 | 8.67 | 16.41 | 9.60 | 11.76 | 49.54 | 323 |
| Shangluo | 0.00 | 0.81 | 0.00 | 14.63 | 43.09 | 41.46 | 123 |
| Xinyang | 0.36 | 5.73 | 1.79 | 12.54 | 32.97 | 46.59 | 279 |
| Zhoukou | 3.08 | 26.15 | 24.62 | 13.85 | 16.92 | 15.38 | 65 |
| Zhumadian | 0.00 | 12.90 | 18.71 | 1.29 | 8.39 | 58.71 | 155 |
| Wuhan | 2.25 | 8.77 | 17.31 | 17.27 | 12.28 | 42.13 | 2224 |
| Huangshi | 8.22 | 35.62 | 38.36 | 15.07 | 0.00 | 2.74 | 73 |
| Shiyan | 3.70 | 16.67 | 7.41 | 20.37 | 8.33 | 43.52 | 108 |
| Yichang | 0.00 | 9.09 | 32.03 | 1.73 | 0.00 | 57.14 | 231 |
| Xiangfan | 2.56 | 24.18 | 14.65 | 16.85 | 9.89 | 31.87 | 273 |
| Ezhou | 1.51 | 4.02 | 9.05 | 22.11 | 0.00 | 63.32 | 199 |
| Jingmen | 0.99 | 4.95 | 45.54 | 0.00 | 0.00 | 48.51 | 101 |
| Xiaogan | 0.00 | 1.20 | 10.84 | 9.64 | 10.84 | 67.47 | 83 |
| Jingzhou | 3.75 | 15.00 | 20.00 | 11.25 | 2.50 | 47.50 | 80 |
| Huanggang | 0.00 | 14.81 | 50.62 | 1.23 | 0.00 | 33.33 | 81 |
| Xianning | 0.00 | 12.04 | 2.78 | 18.52 | 25.00 | 41.67 | 108 |
| Suizhou | 0.00 | 4.04 | 3.03 | 6.06 | 3.03 | 83.84 | 99 |
| Changsha | 10.68 | 21.92 | 26.85 | 7.67 | 20.00 | 12.88 | 365 |
| Zhuzhou | 6.56 | 15.85 | 7.65 | 31.15 | 7.10 | 31.69 | 183 |
| Xiangtan | 0.00 | 7.34 | 35.59 | 13.56 | 0.00 | 43.50 | 177 |
| Hengyang | 4.24 | 5.93 | 1.69 | 28.81 | 1.69 | 57.63 | 118 |
| Shaoyang | 0.00 | 3.75 | 1.25 | 28.75 | 11.25 | 55.00 | 80 |
| Yueyang | 1.26 | 12.58 | 24.53 | 8.18 | 1.26 | 52.20 | 159 |
| Changde | 1.50 | 8.61 | 49.06 | 0.00 | 0.00 | 40.82 | 267 |
| Zhangjiajie | 0.00 | 2.20 | 35.16 | 0.00 | 0.00 | 62.64 | 91 |
| Yiyang | 0.00 | 2.83 | 56.60 | 0.94 | 0.00 | 39.62 | 106 |
| Chenzhou | 0.00 | 10.58 | 35.58 | 0.00 | 0.00 | 53.85 | 104 |
| Yongzhou | 0.00 | 6.67 | 17.33 | 24.00 | 1.33 | 50.67 | 75 |
| Huaihua | 3.95 | 18.42 | 9.21 | 2.63 | 6.58 | 59.21 | 76 |
| Loudi | 0.00 | 13.54 | 30.21 | 6.25 | 0.00 | 50.00 | 96 |
| Guangzhou | 20.13 | 17.76 | 23.04 | 11.48 | 12.33 | 15.25 | 2708 |
| Shaoguan | 1.19 | 5.06 | 5.06 | 18.15 | 14.29 | 56.25 | 336 |
| Shenzhen | 50.23 | 23.75 | 18.14 | 3.15 | 2.57 | 2.16 | 1714 |
| Zhuhai | 8.80 | 4.80 | 5.92 | 21.92 | 14.08 | 44.48 | 625 |
| Shantou | 5.89 | 10.46 | 49.85 | 3.25 | 5.58 | 24.97 | 985 |
| Foshan | 17.18 | 23.25 | 20.13 | 10.66 | 15.87 | 12.91 | 3144 |
| Jiangmen | 8.15 | 8.06 | 19.70 | 8.42 | 6.71 | 48.97 | 1117 |
| Zhanjiang | 7.92 | 12.38 | 4.46 | 3.47 | 4.95 | 66.83 | 202 |
| Maoming | 16.80 | 11.48 | 27.46 | 20.49 | 0.00 | 23.77 | 244 |
| Zhaoqing | 2.78 | 6.60 | 6.25 | 7.64 | 7.29 | 69.44 | 288 |
| Huizhou | 5.08 | 8.08 | 5.87 | 26.39 | 9.80 | 44.78 | 1398 |
| Meizhou | 12.00 | 18.67 | 50.67 | 0.00 | 0.00 | 18.67 | 75 |
| Shanwei | 4.35 | 2.90 | 11.59 | 12.32 | 13.04 | 55.80 | 138 |
| Heyuan | 1.56 | 3.12 | 0.62 | 9.35 | 49.22 | 36.14 | 321 |
| Yangjiang | 7.69 | 15.38 | 25.00 | 0.00 | 0.00 | 51.92 | 52 |
| Qingyuan | 1.76 | 2.14 | 0.00 | 11.59 | 44.21 | 40.30 | 794 |
| Dongguan | 27.66 | 29.28 | 35.78 | 2.65 | 2.42 | 2.20 | 2722 |
| Zhongshan | 15.79 | 21.42 | 34.24 | 10.81 | 7.18 | 10.55 | 1545 |
| Chaozhou | 30.88 | 20.59 | 45.59 | 0.00 | 0.00 | 2.94 | 68 |
| Jieyang | 11.61 | 12.26 | 72.26 | 0.65 | 0.65 | 2.58 | 155 |
| Yunfu | 1.71 | 5.98 | 6.84 | 12.82 | 1.71 | 70.94 | 117 |
| Nanning | 7.68 | 4.69 | 12.76 | 7.28 | 30.81 | 36.79 | 1003 |
| Liuzhou | 10.36 | 7.71 | 3.61 | 21.20 | 19.04 | 38.07 | 415 |
| Guilin | 25.97 | 13.81 | 11.60 | 16.02 | 0.55 | 32.04 | 181 |
| Wuzhou | 2.99 | 2.99 | 3.73 | 27.61 | 16.42 | 46.27 | 134 |
| Beihai | 3.52 | 0.00 | 0.00 | 5.63 | 2.82 | 88.03 | 142 |
| Fangchenggang | 0.00 | 4.41 | 0.00 | 13.24 | 35.29 | 47.06 | 136 |
| Qinzhou | 2.82 | 1.06 | 1.41 | 8.45 | 26.41 | 59.86 | 284 |
| Guigang | 2.49 | 3.60 | 1.39 | 14.68 | 15.24 | 62.60 | 361 |
| Yulin | 1.54 | 5.38 | 8.08 | 5.77 | 19.62 | 59.62 | 260 |
| Baise | 2.00 | 9.00 | 39.00 | 0.00 | 0.00 | 50.00 | 100 |
| Hezhou | 0.00 | 18.42 | 36.84 | 21.05 | 0.00 | 23.68 | 38 |
| Hechi | 0.00 | 9.26 | 20.37 | 5.56 | 16.67 | 48.15 | 54 |
| Laibin | 0.00 | 1.07 | 2.40 | 4.27 | 9.60 | 82.67 | 375 |
| Chongzuo | 0.00 | 0.00 | 0.00 | 4.30 | 43.01 | 52.69 | 93 |
| Haikou | 0.73 | 4.36 | 28.36 | 9.82 | 11.64 | 45.09 | 275 |
| Sanya | 0.00 | 0.77 | 8.21 | 7.18 | 24.87 | 58.97 | 390 |
| Chongqing | 6.40 | 7.39 | 19.75 | 5.41 | 12.32 | 48.73 | 2922 |
| Chengdu | 8.38 | 7.54 | 10.52 | 9.42 | 25.03 | 39.11 | 1910 |
| Zigong | 0.00 | 15.87 | 23.81 | 28.57 | 0.00 | 31.75 | 63 |
| Panzhihua | 6.72 | 17.23 | 23.95 | 14.29 | 5.88 | 31.93 | 238 |
| Luzhou | 0.00 | 10.94 | 35.16 | 0.00 | 0.78 | 53.13 | 128 |
| Deyang | 3.71 | 3.47 | 0.99 | 13.37 | 6.19 | 72.28 | 404 |
| Mianyang | 3.89 | 9.73 | 39.66 | 2.68 | 0.00 | 44.04 | 411 |
| Guangyuan | 0.00 | 7.83 | 0.00 | 16.27 | 9.04 | 66.87 | 166 |
| Suining | 2.21 | 5.52 | 0.55 | 14.92 | 19.34 | 57.46 | 181 |
| Neijiang | 0.00 | 0.00 | 17.39 | 13.04 | 0.00 | 69.57 | 23 |
| Leshan | 0.00 | 3.73 | 20.90 | 0.00 | 0.00 | 75.37 | 134 |
| Nanchong | 0.87 | 1.74 | 11.30 | 6.09 | 0.00 | 80.00 | 115 |
| Meishan | 0.00 | 0.00 | 11.57 | 17.36 | 1.65 | 69.42 | 121 |
| Yibin | 0.00 | 9.65 | 32.46 | 10.53 | 0.00 | 47.37 | 114 |
| Guang’an | 0.00 | 0.00 | 74.42 | 0.00 | 0.00 | 25.58 | 86 |
| Dazhou | 8.51 | 23.40 | 12.77 | 25.53 | 0.00 | 29.79 | 47 |
| Ya’an | 0.00 | 0.00 | 55.00 | 0.00 | 0.00 | 45.00 | 20 |
| Bazhong | 0.00 | 0.00 | 61.29 | 0.00 | 0.00 | 38.71 | 62 |
| Ziyang | 0.00 | 4.65 | 0.00 | 33.72 | 1.16 | 60.47 | 86 |
| Guiyang | 8.17 | 6.48 | 16.90 | 11.97 | 8.03 | 48.45 | 710 |
| Liupanshui | 0.92 | 13.76 | 21.10 | 22.94 | 0.00 | 41.28 | 109 |
| Zunyi | 0.00 | 12.66 | 45.57 | 11.39 | 0.00 | 30.38 | 79 |
| Anshun | 1.05 | 13.68 | 22.11 | 5.26 | 20.00 | 37.89 | 95 |
| Kunming | 9.83 | 12.90 | 18.43 | 9.83 | 14.62 | 34.40 | 814 |
| Qujing | 6.81 | 13.09 | 21.47 | 0.52 | 14.14 | 43.98 | 191 |
| Yuxi | 4.03 | 6.38 | 34.23 | 0.00 | 16.11 | 39.26 | 298 |
| Baoshan | 0.00 | 4.65 | 16.86 | 0.58 | 11.63 | 66.28 | 172 |
| Zhaotong | 0.00 | 7.69 | 14.42 | 1.92 | 30.77 | 45.19 | 104 |
| Lijiang | 0.00 | 0.00 | 54.55 | 0.00 | 20.20 | 25.25 | 99 |
| Puer | 1.37 | 5.48 | 4.11 | 12.33 | 15.07 | 61.64 | 73 |
| Lincang | 0.00 | 0.00 | 69.64 | 0.00 | 1.79 | 28.57 | 56 |
| Lhasa | 8.02 | 17.90 | 37.04 | 1.23 | 15.43 | 20.37 | 162 |
| Xi’an | 6.80 | 6.89 | 4.45 | 15.75 | 19.22 | 46.89 | 2045 |
| Tongchuan | 0.00 | 6.01 | 20.22 | 16.94 | 7.65 | 49.18 | 183 |
| Baoji | 5.59 | 9.12 | 1.18 | 27.06 | 12.06 | 45.00 | 340 |
| Xianyang | 7.24 | 7.44 | 20.94 | 20.94 | 10.18 | 33.27 | 511 |
| Weinan | 7.46 | 6.97 | 2.49 | 14.93 | 29.85 | 38.31 | 201 |
| Yan’an | 0.00 | 2.67 | 36.53 | 2.13 | 3.47 | 55.20 | 375 |
| Hanzhong | 13.74 | 11.45 | 0.00 | 16.03 | 16.79 | 41.98 | 131 |
| Yulin | 0.00 | 1.91 | 11.07 | 1.15 | 47.33 | 38.55 | 262 |
| Ankang | 1.69 | 6.21 | 6.21 | 11.30 | 3.95 | 70.62 | 177 |
| Shangqiu | 2.96 | 5.93 | 21.85 | 3.70 | 10.37 | 55.19 | 270 |
| Lanzhou | 21.47 | 18.08 | 13.56 | 22.60 | 3.67 | 20.62 | 354 |
| Jiayuguan | 10.82 | 10.31 | 6.19 | 16.49 | 29.90 | 26.29 | 194 |
| Jinchang | 15.96 | 9.57 | 0.00 | 35.11 | 12.77 | 26.60 | 94 |
| Baiyin | 7.45 | 12.77 | 0.00 | 44.15 | 7.45 | 28.19 | 188 |
| Tianshui | 8.47 | 11.86 | 9.32 | 22.88 | 0.00 | 47.46 | 118 |
| Wuwei | 2.38 | 13.10 | 28.57 | 3.57 | 2.38 | 50.00 | 84 |
| Zhangye | 2.97 | 10.89 | 18.81 | 14.85 | 6.93 | 45.54 | 101 |
| Pingliang | 0.00 | 5.07 | 8.70 | 15.22 | 14.49 | 56.52 | 138 |
| Jiuquan | 1.13 | 5.08 | 2.82 | 7.34 | 27.12 | 56.50 | 177 |
| Qingyang | 0.00 | 0.00 | 2.27 | 4.55 | 18.75 | 74.43 | 176 |
| Dingxi | 0.00 | 2.04 | 2.04 | 42.86 | 0.00 | 53.06 | 49 |
| Longnan | 0.00 | 0.00 | 0.00 | 25.00 | 41.67 | 33.33 | 36 |
| Xining | 14.86 | 12.69 | 17.34 | 16.72 | 10.84 | 27.55 | 323 |
| Yinchuan | 13.57 | 8.00 | 7.83 | 21.91 | 11.30 | 37.39 | 575 |
| Shizuishan | 11.18 | 7.89 | 0.00 | 32.89 | 12.50 | 35.53 | 152 |
| Wuzhong | 0.00 | 13.79 | 18.39 | 8.05 | 31.03 | 28.74 | 87 |
| Guyuan | 0.00 | 4.39 | 2.63 | 10.53 | 24.56 | 57.89 | 114 |
| Zhongwei | 0.00 | 3.24 | 0.54 | 14.59 | 46.49 | 35.14 | 185 |
| Urumqi | 16.29 | 15.50 | 12.14 | 22.20 | 3.35 | 30.51 | 626 |
| Karamay | 6.76 | 9.85 | 11.78 | 18.73 | 26.83 | 26.06 | 518 |
References
- Heilig, G.K. World Urbanization Prospects the 2011 Revision; U.S. Department of Economic and Social Affairs (DESA), Population Division, Population Estimates and Projections Section: New York, NY, USA, 2012. [Google Scholar]
- Grimm, N.B.; Faeth, S.H.; Golubiewski, N.E.; Redman, C.L.; Wu, J.; Bai, X.; Briggs, J.M. Global change and the ecology of cities. Science 2008, 319, 756–760. [Google Scholar]
- Grimmond, S. Urbanization and global environmental change: local effects of urban warming. Geogr. J 2007, 173, 83–88. [Google Scholar]
- Falcucci, A.; Maiorano, L.; Boitani, L. Changes in land-use/land-cover patterns in Italy and their implications for biodiversity conservation. Landsc. Ecol 2007, 22, 617–631. [Google Scholar]
- Alberti, M. The effects of urban patterns on ecosystem function. Int. Reg. Sci. Rev 2005, 28, 168–192. [Google Scholar]
- Hahs, A.K.; McDonnell, M.J.; McCarthy, M.A.; Vesk, P.A.; Corlett, R.T.; Norton, B.A.; Clemants, S.E.; Duncan, R.P.; Thompson, K.; Schwartz, M.W. A global synthesis of plant extinction rates in urban areas. Ecol. Lett 2009, 12, 1165–1173. [Google Scholar]
- Imhoff, M.L.; Lawrence, W.T.; Elvidge, C.D.; Paul, T.; Levine, E.; Privalsky, M.V.; Brown, V. Using nighttime DMSP/OLS images of city lights to estimate the impact of urban land use on soil resources in the United States. Remote Sens. Environ 1997, 59, 105–117. [Google Scholar]
- Croft, T.A. Nighttime images of the earth from space. Sci. Am 1978, 239, 86–98. [Google Scholar]
- Elvidge, C.D.; Baugh, K.E.; Kihn, E.A.; Kroehl, H.W.; Davis, E.R. Mapping city lights with nighttime data from the DMSP operational linescan system. Photogramm. Eng. Remote Sens 1997, 63, 727–734. [Google Scholar]
- Imhoff, M.L.; Lawrence, W.T.; Stutzer, D.C.; Elvidge, C.D. A technique for using composite DMSP/OLS “city lights” satellite data to map urban area. Remote Sens. Environ 1997, 61, 361–370. [Google Scholar]
- Small, C.; Pozzi, F.; Elvidge, C. Spatial analysis of global urban extent from DMSP-OLS night lights. Remote Sens. Environ 2005, 96, 277–291. [Google Scholar]
- Doll, C.N.H.; Muller, J.P.; Elvidge, C.D. Night-time imagery as a tool for global mapping of socioeconomic parameters and greenhouse gas emissions. Ambio 2000, 29, 157–162. [Google Scholar]
- Doll, C.N.H.; Muller, J.-P.; Morley, J.G. Mapping regional economic activity from night-time light satellite imagery. Ecol. Econ 2006, 57, 75–92. [Google Scholar]
- Ghosh, T.; Powell, R.L.; Elvidge, C.D.; Baugh, K.E.; Sutton, P.C.; Anderson, S. Shedding light on the global distribution of economic activity. Open. Geogr. J 2010, 3, 148–161. [Google Scholar]
- Sutton, P.; Roberts, D.; Elvidge, C.; Baugh, K. Census from Heaven: An estimate of the global human population using night-time satellite imagery. Int. J. Remote Sens 2001, 22, 3061–3076. [Google Scholar]
- Zhuo, L.; Ichinose, T.; Zheng, J.; Chen, J.; Shi, P.J.; Li, X. Modelling the population density of China at the pixel level based on DMSP/OLS non-radiance-calibrated night-time light images. Int. J. Remote Sens 2009, 30, 1003–1018. [Google Scholar]
- Chand, T.R.K.; Badarinath, K.V.S.; Elvidge, C.D.; Tuttle, B.T. Spatial characterization of electrical power consumption patterns over India using temporal DMSP-OLS night-time satellite data. Int. J. Remote Sens 2009, 30, 647–661. [Google Scholar]
- Han, P.; Huang, J.; Li, R.; Wang, L.; Hu, Y.; Wang, J.; Huang, W. Monitoring trends in light pollution in China based on nighttime satellite imagery. Remote Sens 2014, 6, 5541–5558. [Google Scholar]
- Elvidge, C.D.; Ziskin, D.; Baugh, K.E.; Tuttle, B.T.; Ghosh, T.; Pack, D.W.; Erwin, E.H.; Zhizhin, M. A fifteen year record of global natural gas flaring derived from satellite data. Energies 2009, 2, 595–622. [Google Scholar]
- Liang, H.; Tanikawa, H.; Matsuno, Y.; Dong, L. Modeling in-use steel stock in China’s buildings and civil engineering infrastructure using time-series of DMSP/OLS nighttime lights. Remote Sens 2014, 6, 4780–4800. [Google Scholar]
- Pandey, B.; Joshi, P.K.; Seto, K.C. Monitoring urbanization dynamics in India using DMSP/OLS night time lights and SPOT-VGT data. Int. J. Appl. Earth Obs. Geoinf 2013, 23, 49–61. [Google Scholar]
- Zhang, Q.; Seto, K.C. Mapping urbanization dynamics at regional and global scales using multi-temporal DMSP/OLS nighttime light data. Remote Sens. Environ 2011, 115, 2320–2329. [Google Scholar]
- Ma, T.; Zhou, C.; Pei, T.; Haynie, S.; Fan, J. Quantitative estimation of urbanization dynamics using time series of DMSP/OLS nighttime light data: A comparative case study from China’s cities. Remote Sens. Environ 2012, 124, 99–107. [Google Scholar]
- Frolking, S.; Milliman, T.; Seto, K.C.; Friedl, M.A. A global fingerprint of macro-scale changes in urban structure from 1999 to 2009. Environ. Res. Lett 2013, 8, 024004. [Google Scholar]
- Elvidge, C.D.; Imhoff, M.L.; Baugh, K.E.; Hobson, V.R.; Nelson, I.; Safran, J.; Dietz, J.B.; Tuttle, B.T. Night-time lights of the world: 1994–1995. ISPRS J. Photogramm. Remote Sens 2001, 56, 81–99. [Google Scholar]
- Small, C.; Elvidge, C.D.; Balk, D.; Montgomery, M. Spatial scaling of stable night lights. Remote Sens. Environ 2011, 115, 269–280. [Google Scholar]
- Verbesselt, J.; Hyndman, R.; Newnham, G.; Culvenor, D. Detecting trend and seasonal changes in satellite image time series. Remote Sens. Environ 2010, 114, 106–115. [Google Scholar]
- Sun, J.; Wang, X.; Chen, A.; Ma, Y.; Cui, M.; Piao, S. NDVI indicated characteristics of vegetation cover change in China’s metropolises over the last three decades. Environ. Monit. Assess 2011, 179, 1–14. [Google Scholar]
- Muggeo, V.M. Segmented: An R package to fit regression models with broken-line relationships. R News 2008, 8, 20–25. [Google Scholar]
- Ball, G.H.; Hall, D.J. ISODATA, A Novel Method of Data Analysis and Pattern Classification; Stanford Research Institute: Stanford, CA, USA, 1965. [Google Scholar]
- Zhang, K.H.; Song, S. Rural–urban migration and urbanization in China: Evidence from time-series and cross-section analyses. China Econ. Rev. 2003, 14, 386–400. [Google Scholar]
- Bennie, J.; Davies, T.W.; Duffy, J.P.; Inger, R.; Gaston, K.J. Contrasting trends in light pollution across Europe based on satellite observed night time lights. Sci. Rep 2014, 4. [Google Scholar] [CrossRef]
- Tian, G.; Liu, J.; Xie, Y.; Yang, Z.; Zhuang, D.; Niu, Z. Analysis of spatio-temporal dynamic pattern and driving forces of urban land in China in 1990s using TM images and GIS. Cities 2005, 22, 400–410. [Google Scholar]
- Démurger, S.; Sachs, J.D.; Woo, W.T.; Bao, S.; Chang, G.; Mellinger, A. Geography, economic policy, and regional development in China. Asian Econ. Pap 2002, 1, 146–197. [Google Scholar]
- Wong, S.W.; Tang, B.S. Challenges to the sustainability of ‘development zones’: A case study of Guangzhou Development District, China. Cities 2005, 22, 303–316. [Google Scholar]
- Ghosh, T.; Anderson, S.; Elvidge, C.; Sutton, P. Using nighttime satellite imagery as a proxy measure of human well-being. Sustainability 2013, 5, 4988–5019. [Google Scholar]
- Elvidge, C.D.; Baugh, K.E.; Dietz, J.B.; Bland, T.; Sutton, P.C.; Kroehl, H.W. Radiance calibration of DMSP-OLS low-light imaging data of human settlements. Remote Sens. Environ 1999, 68, 77–88. [Google Scholar]
- Shi, K.; Yu, B.; Huang, Y.; Hu, Y.; Yin, B.; Chen, Z.; Chen, L.; Wu, J. Evaluating the ability of NPP-VIIRS nighttime light data to estimate the gross domestic product and the electric power consumption of China at multiple scales: A comparison with DMSP-OLS data. Remote Sens 2014, 6, 1705–1724. [Google Scholar]
- Coscieme, L.; Pulselli, F.M.; Bastianoni, S.; Elvidge, C.D.; Anderson, S.; Sutton, P.C. A thermodynamic geography: Night-time satellite imagery as a proxy measure of emergy. Ambio 2013. [Google Scholar] [CrossRef]




© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Xu, T.; Ma, T.; Zhou, C.; Zhou, Y. Characterizing Spatio-Temporal Dynamics of Urbanization in China Using Time Series of DMSP/OLS Night Light Data. Remote Sens. 2014, 6, 7708-7731. https://doi.org/10.3390/rs6087708
Xu T, Ma T, Zhou C, Zhou Y. Characterizing Spatio-Temporal Dynamics of Urbanization in China Using Time Series of DMSP/OLS Night Light Data. Remote Sensing. 2014; 6(8):7708-7731. https://doi.org/10.3390/rs6087708
Chicago/Turabian StyleXu, Tao, Ting Ma, Chenghu Zhou, and Yuke Zhou. 2014. "Characterizing Spatio-Temporal Dynamics of Urbanization in China Using Time Series of DMSP/OLS Night Light Data" Remote Sensing 6, no. 8: 7708-7731. https://doi.org/10.3390/rs6087708
APA StyleXu, T., Ma, T., Zhou, C., & Zhou, Y. (2014). Characterizing Spatio-Temporal Dynamics of Urbanization in China Using Time Series of DMSP/OLS Night Light Data. Remote Sensing, 6(8), 7708-7731. https://doi.org/10.3390/rs6087708