Next Article in Journal
Remote Sensing Assessment of Forest Disturbance across Complex Mountainous Terrain: The Pattern and Severity of Impacts of Tropical Cyclone Yasi on Australian Rainforests
Next Article in Special Issue
Open Access Data in Polar and Cryospheric Remote Sensing
Previous Article in Journal
A Bayesian Based Method to Generate a Synergetic Land-Cover Map from Existing Land-Cover Products
Previous Article in Special Issue
Investigating High-Resolution AMSR2 Sea Ice Concentrations during the February 2013 Fracture Event in the Beaufort Sea
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 6
Issue 6
10.3390/rs6065614
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Estimation of Mass Balance of the Grosser Aletschgletscher, Swiss Alps, from ICESat Laser Altimetry Data and Digital Elevation Models

by
Jan Kropáček
1,2,*,
Niklas Neckel
2 and
Andreas Bauder
3
1
Institute for Cartography, TU-Dresden, Helmholzstr. 10., 01062 Dresden, Germany
2
Institute of Geography, University of Tuebingen, Rümelinstr. 19–23, 72070 Tübingen, Germany
3
Laboratory of Hydraulics, Hydrology and Glaciology, ETH Zurich, Wolfgang-Pauli-Str. 27, 8093 Zürich, Switzerland
*
Author to whom correspondence should be addressed.
Remote Sens. 2014, 6(6), 5614-5632; https://doi.org/10.3390/rs6065614
Submission received: 19 November 2013 / Revised: 30 May 2014 / Accepted: 30 May 2014 / Published: 17 June 2014
(This article belongs to the Special Issue Cryospheric Remote Sensing)
Browse Figures
Versions Notes

Abstract

:
Traditional glaciological mass balance measurements of mountain glaciers are a demanding and cost intensive task. In this study, we combine data from the Ice Cloud and Elevation Satellite (ICESat) acquired between 2003 and 2009 with air and space borne Digital Elevation Models (DEMs) in order to derive surface elevation changes of the Grosser Aletschgletscher in the Swiss Alps. Three different areas of the glacier are covered by one nominal ICESat track, allowing us to investigate the performance of the approach under different conditions in terms of ICESat data coverage, and surface characteristics. In order to test the sensitivity of the derived trend in surface lowering, several variables were tested. Employing correction for perennial snow accumulation, footprint selection and adequate reference DEM, we estimated a mean mass balance of −0.92 ± 0.18 m w.e. a−1. for the whole glacier in the studied time period. The resulting mass balance was validated by a comparison with another geodetic approach based on the subtraction of two DEMs for the years 1999 and 2009. It appears that the processing parameters need to be selected depending on the amount of available ICESat measurements, quality of the elevation reference and character of the glacier surface.

1. Introduction

Worldwide rapid retreat of mountain glaciers has been reported by numerous authors for the past few decades (e.g., [1,2]). Glacier fluctuations are regarded as a good indicator for climate variability. This holds true especially for changes in ice volume rather than in glacier extent as glacier area changes tend to show a delayed signal to a changing climate [3]. Precise estimates of glacier volume changes are still challenging and, especially for inaccessible mountain glaciers, remote sensing is a promising data source. In this study, we used data from the Ice Cloud and Elevation Satellite (ICESat) to derive surface elevation changes and volume changes of the Grosser Aletschgletscher in the Swiss Alps. This is the first time that ICESat data was used to estimate changes in geometry of a glacier in the European Alps.
The ICESat mission, which was primarily dedicated for the observation of polar ice sheets, provides precise elevation measurements along nadir tracks acquired between 2003 and 2009. The major obstacle in deriving a time series of elevation changes between consecutive ICESat tracks is that the individual repeated tracks do not match exactly but can be horizontally separated by several hundred meters. This is especially the case in mid-latitudes between 59°S and 59°N for which ICESat’s precision spacecraft pointing control was not used [4]. In order to circumvent this problem, several methods have been developed lately, however they have mostly been of value for the large polar ice sheets and ice caps [5–9]. Compared to mid-latitude mountain glaciers, polar ice sheets and ice caps feature an enormous size, good data coverage in terms of satellite orbits, and relatively homogeneous surface characteristics and slope. Due to these characteristics, several methods of analysis exist. One method makes use of crossover points between ascending and descending satellite tracks (e.g., [10]). This method yields accurate results at the cost of sample density. However, the number of crossovers decreases as the distance to the equator decreases and no crossovers exist over the Grosser Aletschgletscher. Another method compares overlapping repeat tracks by projecting a younger profile onto an older one [6,7]. For this method, the tracks must be spatially close which is a limiting factor for the amount of available data. A third method uses the average slope derived from neighboring ICESat tracks in pre-defined boxes (e.g., [5,7]) to account for the cross-track slope. This method is restricted to a relatively gentle and homogeneous surface structure and is therefore not suitable for the mountainous topography in our study area. However, three recent studies proved the suitability of ICESat data in also deriving elevation changes for mountain glaciers [11–13]. Similar to them, we used a DEM as reference surface on which we compare the acquired ICESat data. In these studies [11–13], ICESat measurements are integrated over a large number of glaciers of different orientation and elevation in order to derive a statistically valid region wide mass balance estimate. Although slightly different approaches were applied by these authors, the results in the overlapping areas are in good agreement. In contrast to these studies, we aim at the derivation of detailed elevation changes for a single mountain glacier. Therefore, in this study, several data processing approaches and various reference DEMs were investigated in terms of their influence on the derived trend in elevation change and on the resulting mass balance. A number of ICESat footprints were re-measured by DGPS and serve as ground truth for the derived surface elevation changes.

2. Study Area and Data

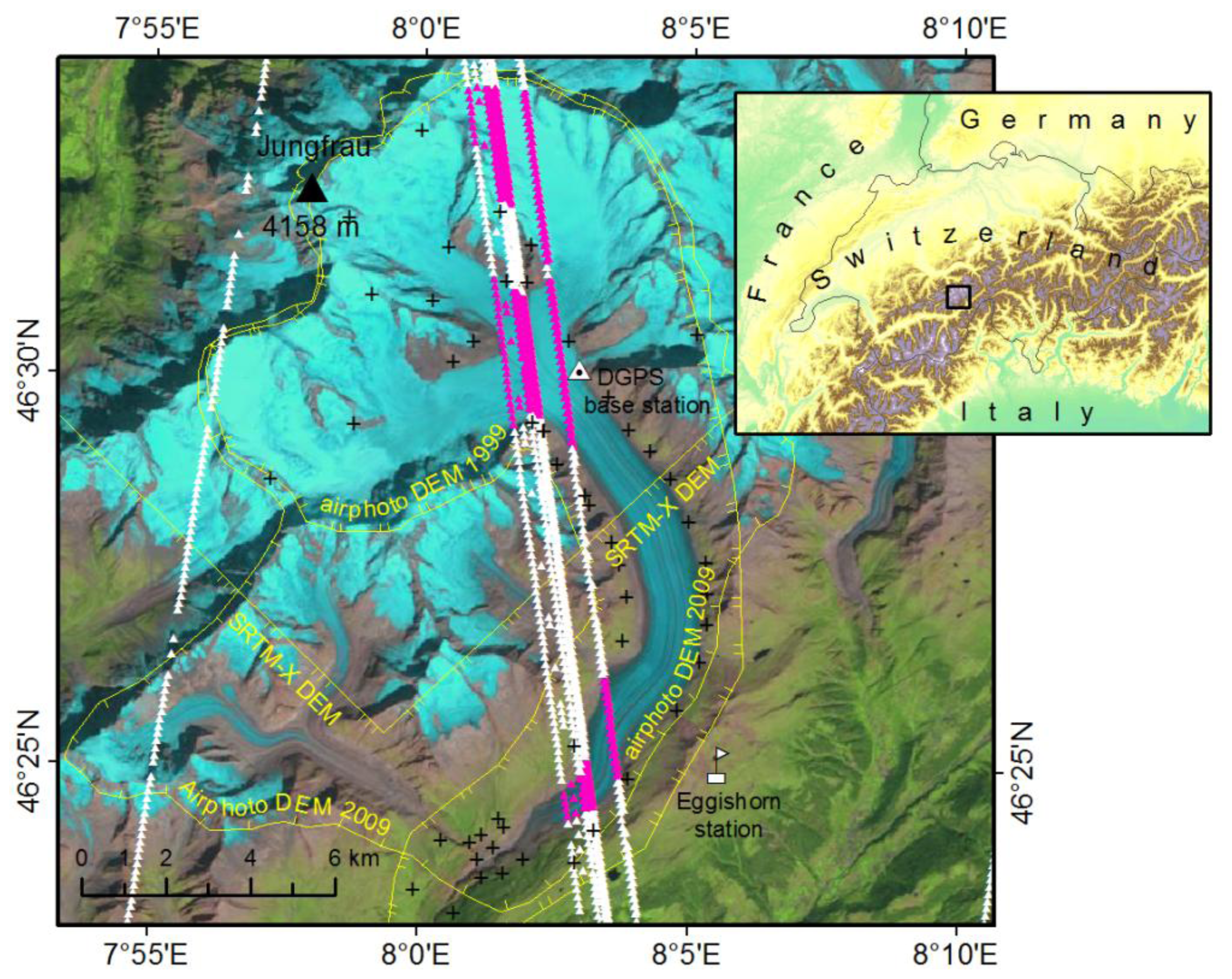
2.1. Study Area

The Grosser Aletschgletscher located in the Bernese Alps in the central part of Switzerland is the longest (22.6 km) and largest (83.0 km2) glacier in the Swiss Alps (Figure 1) [14]. It features a rich archive of glaciological records and climate data dating back to 1841 when the first ablation measurements on this glacier were carried out [15]. The accumulation area, which is located on the southern slopes of the main mountain range, is marked by the two prominent summits of Jungfrau and Mönch. The main tongue is formed by the confluence of three tributaries (Grosser Aletschfirn, Jungfraufirn and Ewig Schneefeld) at the so-called Konkordiaplatz. The Grosser Aletschgletscher reaches an ice thickness of 890 m in its central part [16]. The glacier has been losing volume since the Little Ice Age [14] with a considerably increased speed since the late 1980s [14,17]. Its mean annual mass balance in the period from 1880–1999 has been estimated as −0.42 m w.e. a−1 which corresponds to more than 50 m mean thickness loss [14]. A mass balance monitoring program was set up in the 1960s in the framework of a hydropower project but the data was too sparse to obtain an area-averaged mass balance [18]. Point based surface mass balance has been measured on one site in the accumulation area at the Jungfernfirn since 1920 [18].

2.2. Data

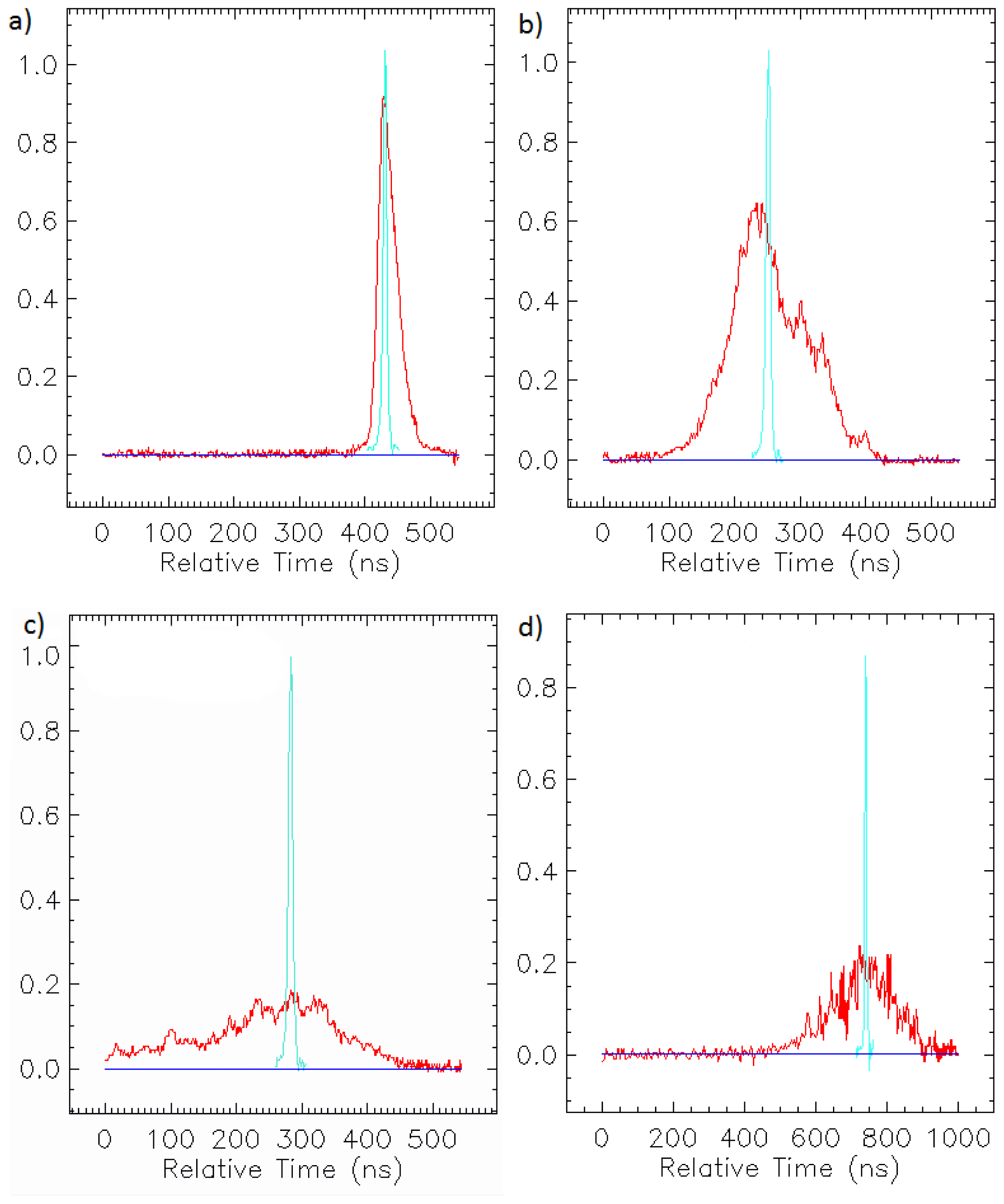
2.2.1. ICESat/GLASS Data

NASA’s Ice Cloud and Elevation Satellite (ICESat) mission provides accurate along-track elevation measurements derived from the two-way travel time of the emitted laser pulse. Measurements are acquired in nadir every 172 m with a footprint diameter of 70 m [19]. The instrument was operational in the period 2003–2009. The launch of ICESat-2 with an improved instrument is planned for early 2016 [20]. Data acquisitions were carried out every 3–6 months during 18 one-month campaigns. In the ideal case of no cloud cover, each campaign typically resulted in one repeat-pass track for a nominal track. In this study, we used the ICESat/GLAS product L2 Global Land Surface Altimetry Data, release 33 [21] denoted as GLA14, provided by the National Snow & Ice Data Center (NSIDC). It contains information on land surface elevation, geolocation, reflectance as well as geodetic atmospheric and instrument corrections.
The Grosser Aletschgletscher is crossed by one nominal ICESat track which yields 14 ground tracks out of which one track provides only sparse measurements. The ground tracks run parallel in a stripe of 1.37 km width and cross the glacier in three separate areas (Figure 2). The first area with a mean elevation of 3400 m a.s.l. called Ewig Schneefeld, denoted here as A1, belongs to the accumulation area of the glacier. The second area (A2) which is located in the relative flat glacier confluence called Konkordiaplatz belongs to the ablation area of the glacier. This area with a mean elevation of 2800 m a.s.l. is crossed by a number of crevasses and by distinct medial moraines. The third area (A3) is located close to the terminus at a mean elevation of 2100 m a.s.l., some 1600 meters lower than the highest ICESat measurements of area A1. These three areas (A1, A2 and A3) which represent different units in terms of slope, surface roughness and glacier dynamics were treated separately.

2.2.2. SRTM DEM

The Shuttle Radar Topography Mission (SRTM) conducted during 11 days in February 2000 provided data for two high resolution digital elevation models [22,23] acquired at C- and X-band. The data was interferometrically processed by the National Aeronautics and Space Administration (NASA) and the German Aerospace Center (DLR), respectively. The homogeneous freely available DEMs cover the entire land mass of the Earth between latitudes 60N and 57S. However, the SRTM-X DEM was acquired with a swath width of 45 km leading to larger data gaps [22]. Due to the gaps between the acquisition stripes, the SRTM-X DEM is only available for area A3. In this study, we use the SRTM-C DEM version 3 which is available via the U.S. Geological Survey (USGS) with a grid posting of three arc seconds and the SRTM-X DEM which is available via the German Aerospace Center (DLR) with a grid posting of one arc second. The vertical accuracy of the SRTM-C DEM as specified in the mission requirements is ± 16 m at 90% confidence [22]. It has been repeatedly confirmed that these requirements were met [24–26]. A mean and standard deviation of 0.60 ± 3.46 m between ICESat and SRTM C elevations were found by [27] in a low relief area with sparse tree cover in the Western United States. However, Gorokhovich and Voustianiouk [26] showed that the error of the SRTM values have a strong correlation with slope and aspect, particularly for slope values >10°.

2.2.3. ASTER GDEM

The Advanced Spaceborne Thermal Emission and Reflection Radiometer Global Digital Elevation Model (ASTER GDEM) covers the land mass of the World between 83°N and 83°S with a resolution of 30 m. It was produced by feature matching techniques using optical stereo-pairs acquired by nadir- and backward-looking infrared cameras of the ASTER instrument onboard the Terra Satellite between 2000 and 2010. Multiple stereo pairs were processed for each point. The vertical accuracy is a function of the number of used stereo pairs and is specified as 17 m at the 95% confidence level [28]. For the Grosser Aletschgletscher, between four and 19 stereo-images were employed. A visual comparison of a shaded relief calculated from GDEM version 2 with high resolution DEMs revealed that the GDEM over Grosser Aletschgletscher contains a high level of noise (Figure 3) which corresponds to the findings of [29]. To account for the noise, we used a smoothed version obtained by a 5 × 5 low pass filter besides the original dataset.

2.2.4. Airphoto DEM

Two DEMs were derived from aerial photographs from 2009 and 1999 [14] by means of digital stereo-photogrammetry whereas the former was used further as an elevation reference for the ICESat data processing. A two-phase procedure with automatic terrain extraction and manual post-processing for blunder elimination was applied. As a ground control, 50 permanently marked geodetic points were used (Figure 1). The resulting DEMs cover the glacier and its immediate surroundings and have a spatial resolution of 25 m. The expected accuracy is in the order of <0.3 m which was confirmed by a cross validation using independent check points outside the glacier.

2.2.5. Glacier Outlines

Glacier outlines from 1998 are available via the Global Land Ice Measurements from Space (GLIMS) database [30] and were used for the selection of ICESat footprints on the glacier. The glacier outline was provided to GLIMS by F. Paul who used a band ratio of Landsat Thematic Mapper data for the delineation of the ice body.

3. Methods

To ensure that the ICESat elevation measurements are comparable between the non-identical tracks on the tilted and irregular shaped glacier surface, this method, similarly to [11–13], makes use of a static elevation reference. Therefore, the surface elevation for each ICESat point was extracted from existing DEM data using bilinear interpolation of the four closest cells in the DEM following [25]. The elevation difference between both datasets (ICESat-DEM) is further denoted as ΔH.
First of all, the DEMs had to be checked for horizontal shifts with respect to the ICESat profiles. Following [31], all values of ΔH in off-glacier regions were normalized by the local slope inclination and were plotted against the terrain aspect. The horizontal shift was estimated by the amplitude of a fitted sinusoid and then removed by an adjustment of the reference coordinates of the DEMs (Table 1). The Airphoto DEM did not provide enough ΔH values for the fitting as it is limited mainly to the glacier area. Its shift with respect to the ICESat measurements could be derived by calculating the displacement between the Airphoto DEM and the adjusted SRTM-C DEM (Table 1).
Since the ICESat data is referenced to the TOPEX/Poseidon ellipsoid [19], the ICESat measurements were converted to WGS-84 heights following [32,33]. In the next step, the ellipsoidal elevations were recalculated to heights above the EGM2008 geoid using information on geoidal heights contained in the GLA14 records. Then, the ICESat points were filtered based on the distance to the reference DEM. The threshold of 100 m appears to effectively sort out all measurements affected by clouds. In order to sort out short tracks with too high variation of ΔH which can provide no meaningful elevation information, a threshold for the in-track standard deviation of ΔH was set to 20 m. Since the vertical error of ICESat elevations increases with the incidence angle between the laser vector and the surface normal [27,34], an upper limit of terrain slope of 10° suggested by [34] was applied to account for the effect of the inaccuracy induced by the Gaussian fitting of the wide waveforms (see Figure 4b). Further, the effect of the slope threshold on the resultant trend was investigated. The effect of terrain slope and surface roughness is illustrated by waveforms recorded over different surfaces (Figure 4). Furthermore, the impact of smoothing of the ΔH values along the track and the elimination of outliers on the derived surface lowering trend was explored. Outliers were replaced by the average of two neighboring values, and for the smoothing, a running mean was applied. To exclude the influence of a systematic bias in the ICESat data (differences between the lasers used during different ICESat campaigns, instrument drift, etc.), off-glacier measurements from the surrounding area were checked for a possible trend.
In order to estimate trends in surface elevation change, assuming a linear trend of surface lowering of the glacier, a linear function was fitted through all ΔH values per ICESat track and area. This way, the trend is independent of the absolute elevation of the reference. The statistical significance of the estimated trends was checked with an f-test and the error of the regression was shown by its standard deviation. Irregularities in glacier surface changes caused by variation in albedo, debris cover and glacier flow together with processing artifacts of the DEM introduce a noise to the derived values of ΔH. However, the variation of ΔH along the tracks can also indicate the quality of the reference data set. A low variation indicates a good match between the ICESat profiles and their vertical projection on the DEM. Various DEMs were used as a reference and were compared in terms of variation of ΔH for all three areas.
Seasonal snow cover introduces a variation into the time series of glacier elevations measured by ICESat. For testing of the snow pack correction of ICESat elevations, we used snow depths for days of ICESat flyovers measured at Eggishorn Station (2495 m a.s.l.) which is located 1.7 km to the SE from the lower part of the glacier (Figure 1). The multi-seasonal ICESat measurements were corrected for snow pack depth by subtraction of the snow depth measured at the station. 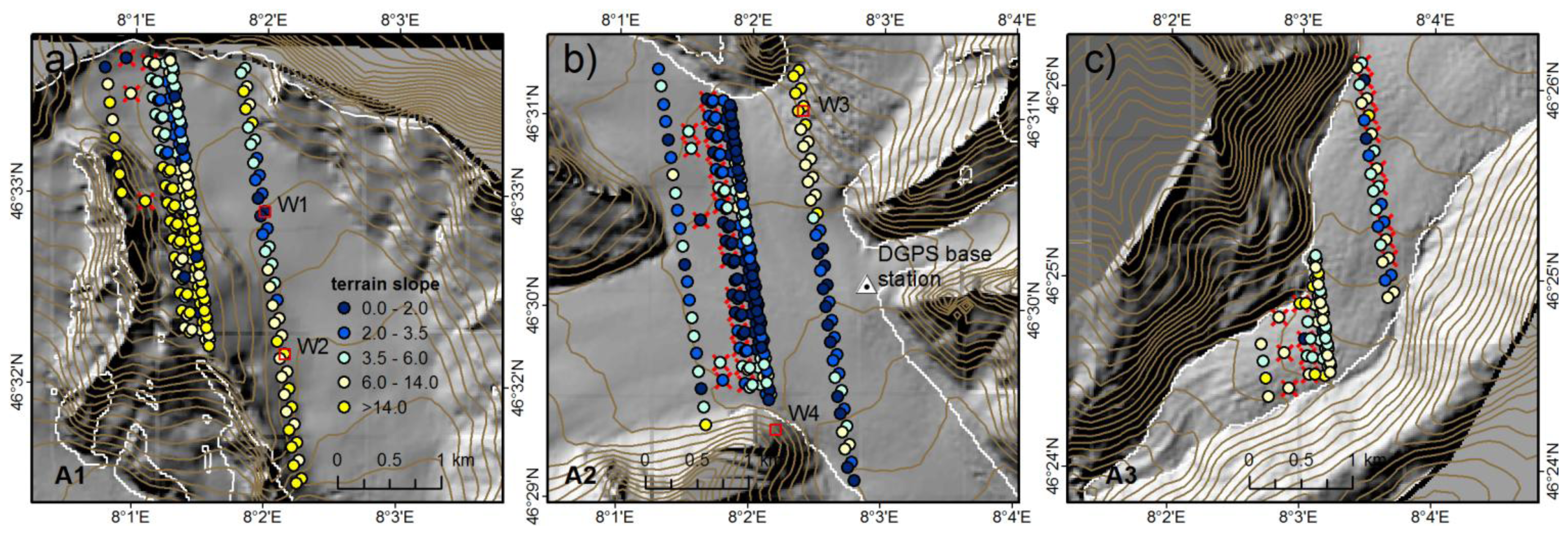The resulting trend was compared to the trend derived from measurements acquired after the ablation period (i.e., autumn trends).

4. Results

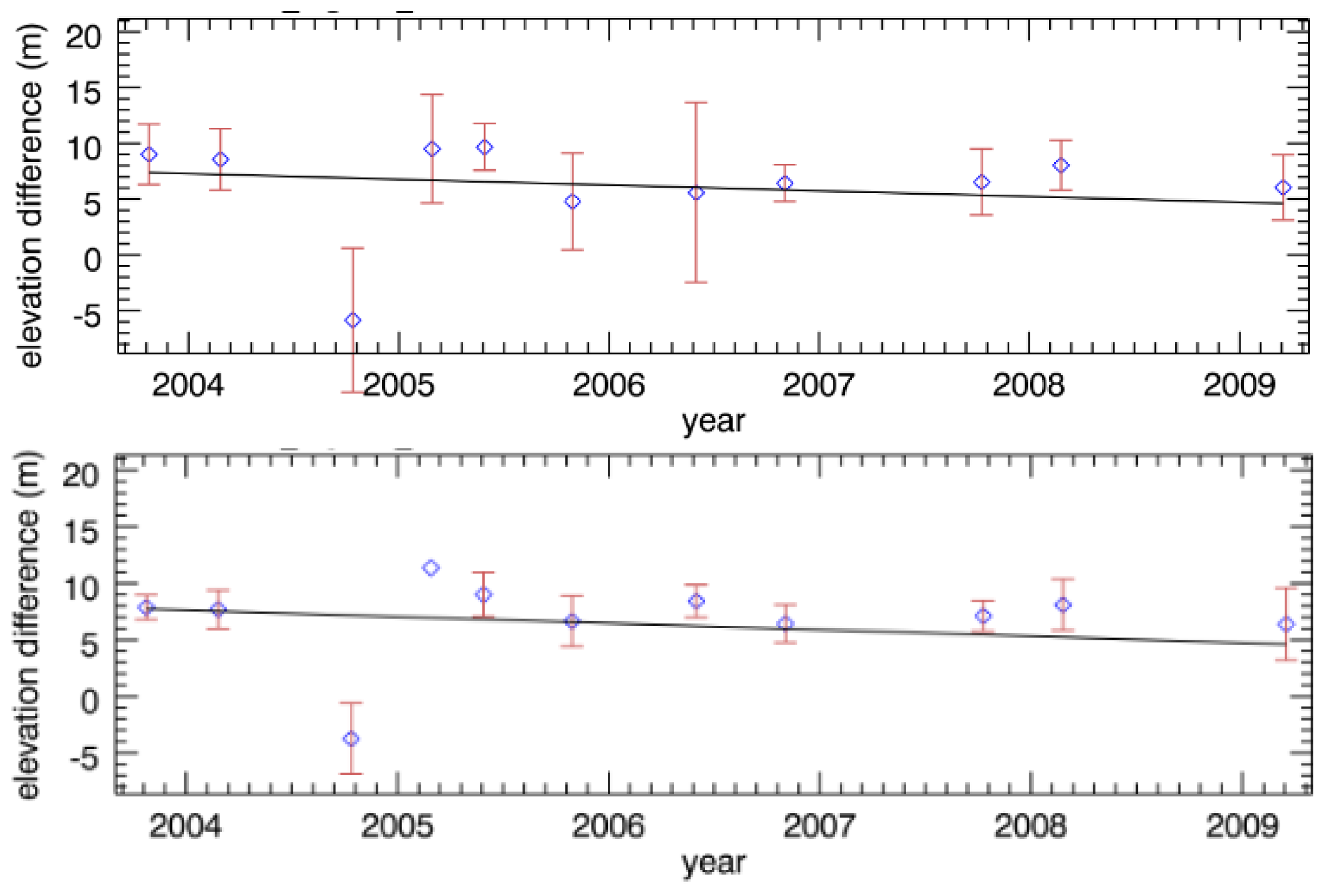
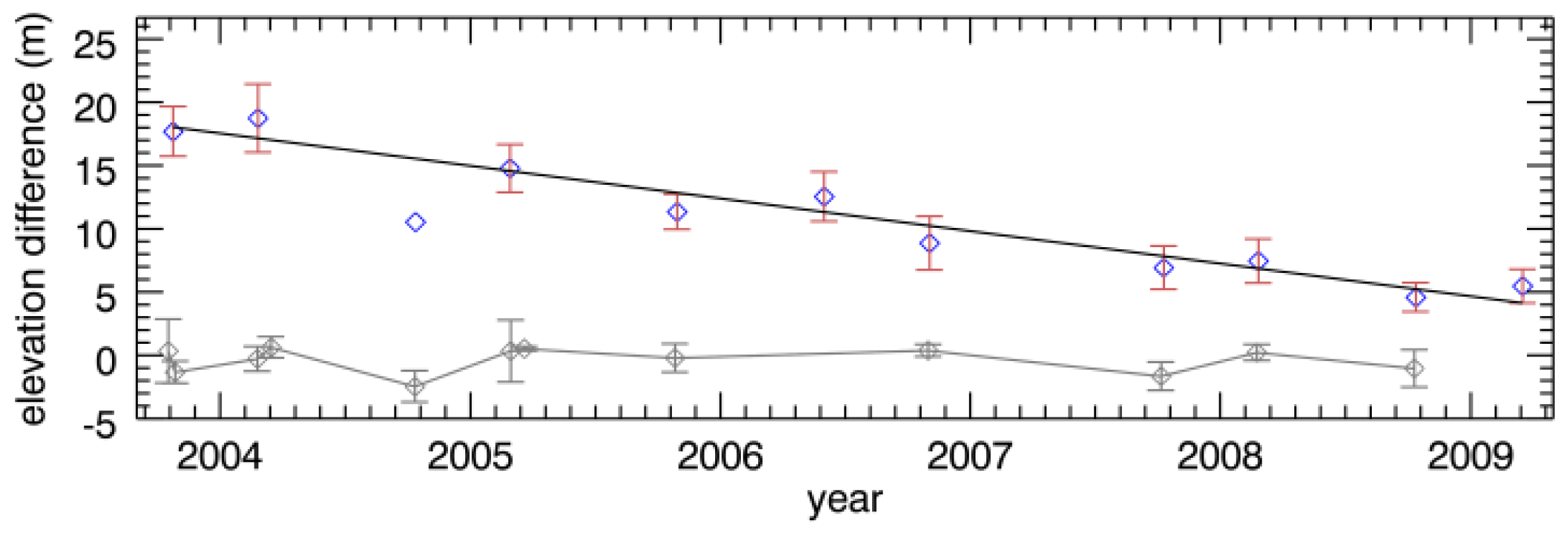
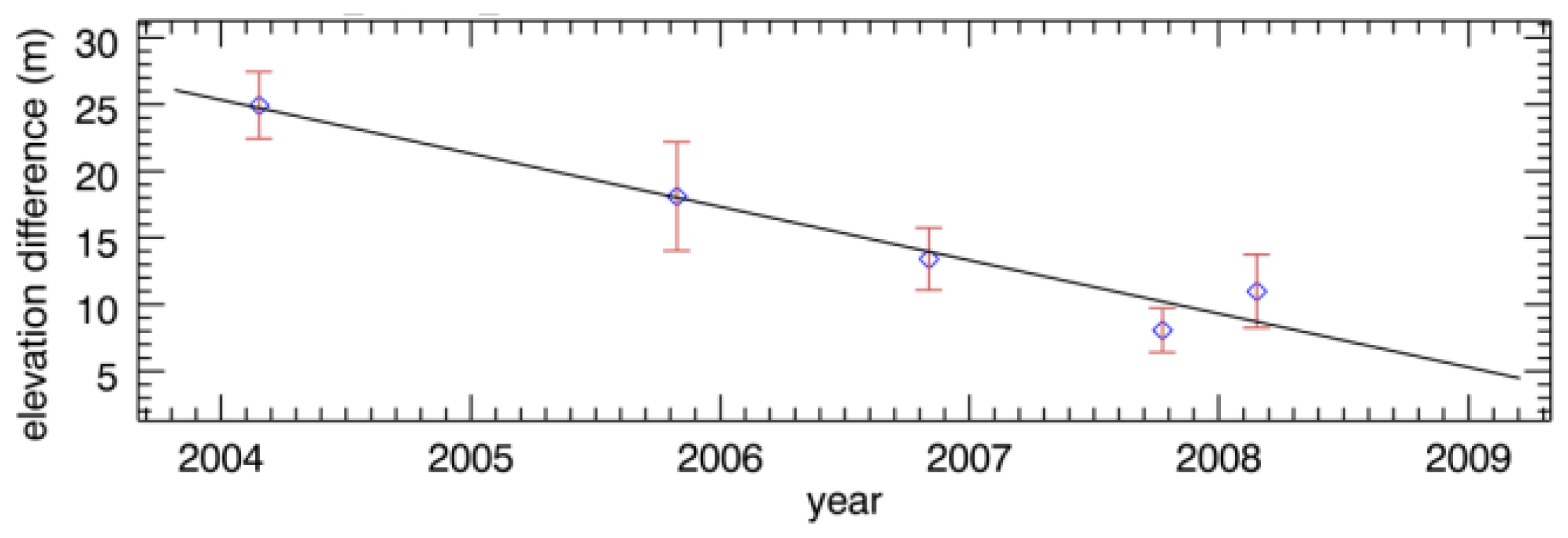
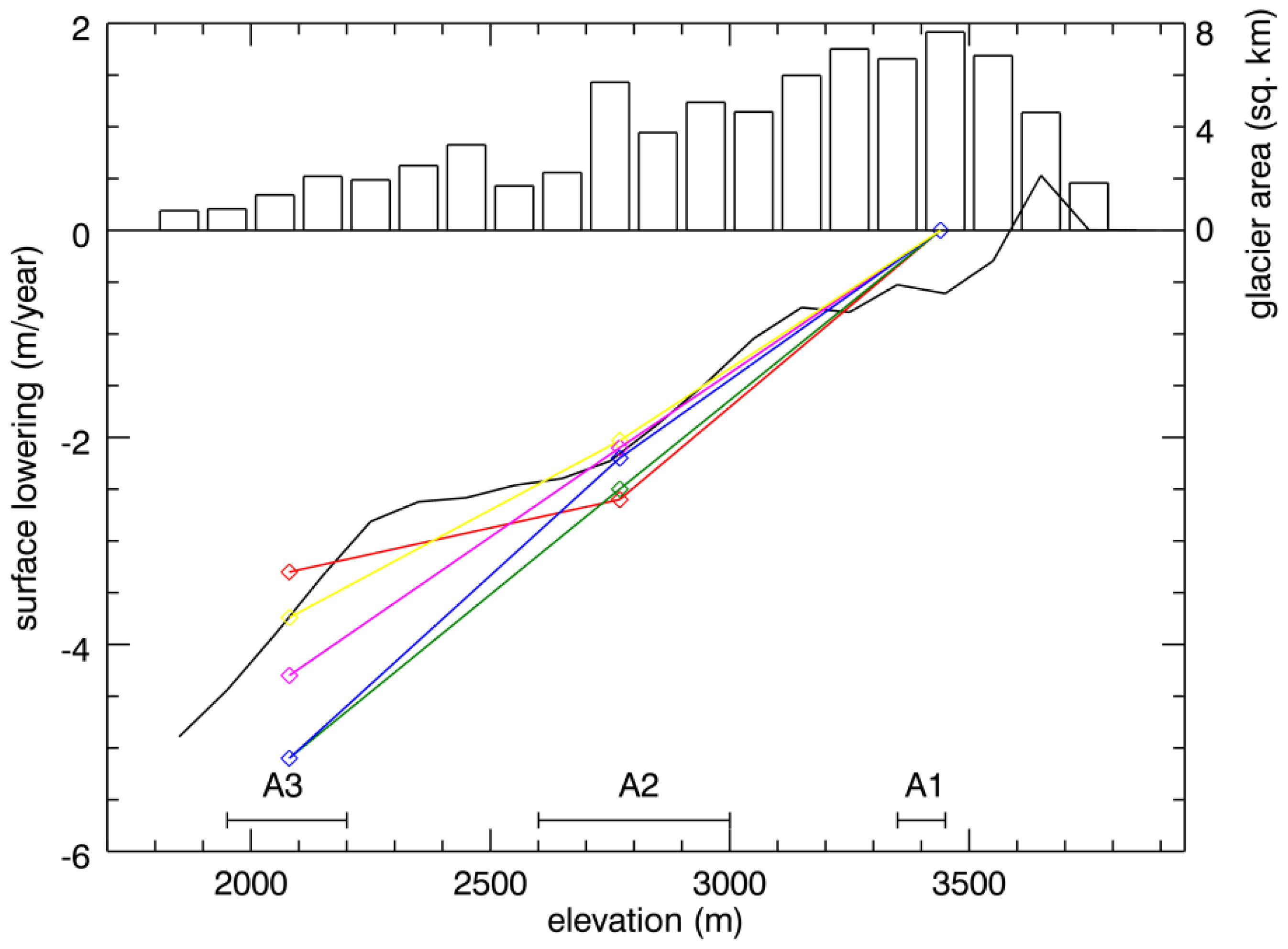
4.1. Trends in the Surface Lowering

The surface lowering of the Grosser Aletschgletscher observed from ICESat elevations appears to be nearly zero in the accumulation area (A1) (Figure 5). The lowering in the upper part of the ablation area (A2) is 2.2 m/a and it increases towards the terminus (area A3) where it approximately doubles (Table 2). This is a common pattern observed at alpine glaciers in the last decade [14,18]. The analysis of ΔH for the surrounding area not covered by the glacier did not produce any statistically significant trend (Figure 6), which is in an agreement with [11–13], and it confirms that the use of different lasers for the ICESat campaigns or a possible instrument drift did not affect the trends extracted on the glacier.
In area A1, no elevation changes could be detected by ICESat because the derived low trends are not statistically significant (Table 2). The in-track variation in ΔH over this area appears to be high. The application of a slope threshold of 5° led to a strong reduction of measurements (Figure 5). The best results in terms of ΔH variations are achieved when using the Airphoto DEM. When comparing the two global DEMs, the SRTM DEM outperforms the ASTER GDEM which confirms the superiority of the InSAR technique in snow covered areas due to a lack of features for stereo-processing.
The trend in surface lowering derived for A2 (Figure 6) based on the Airphoto DEM (2.6 ± 0.10 m/a) is equal to the one based on the DGPS measurements (Table 2). Very similar results were also achieved using the SRTM-C DEM. The trends derived using the ASTER GDEM slightly underestimate the rates of the surface lowering. The smoothing reduces the variation of ΔH but does not affect the trend significantly. The estimation of surface lowering in this area benefits from long intersections of ICESat tracks with the glacier surface (Figure 2). The smooth surface topography leads generally to a relatively low variation of ΔH (Figure 6).
The use of the DEMs provided by space borne platforms led to similar results in case of A3. Both, the trend and the variations in ΔH are almost identical when comparing the SRTM-X DEM with the SRTM-C DEM. Nevertheless, they differ from the results which use the Airphoto DEM as elevation reference (−3.3 ± 0.36) (Figure 7). This difference is probably due to changes of the surface geometry between different acquisition dates taking into account the high dynamics of the retreating glacier terminus. A number of ICESat measurements acquired in winter were sorted out due to erroneous elevations caused by the presence of low clouds (Figure 2).
It appeared that different approaches in data processing of the ICESat data as listed in Table 3 have only a limited effect on the resulting mass balance. The difference is in all cases within 6% (Table 3). When looking at the differences in surface lowering (Table 3), it can be seen that the listed processing approaches affects also the error ranges and the statistical significance. For instance, the application of the slope threshold of 10° has little effect on the surface lowering but it leads to an increase of the statistical significance of the trend and to a narrowing of the error range in A2. In this area, this threshold leads to cancelation of the points over the highly dynamic inflow of Ewig Schneefeld, where the surface velocity reaches 90 cm/day [35] which is likely the reason for this improvement. A weak contrary effect can be observed for A3. In A1, the f-value more than doubles but the trend remains non-significant. The correction for snow pack depth using the in-situ data results in an increase in the statistical significance of the derived trend in surface lowering for A2. The effect is less strong in A3. The trend in both A2 and A3 stays almost unaffected. Finally, the selection of autumn measurements led to a change in trend of 18.9% in A3 resulting in a trend value of 2.6 m/a, which diverges substantially from the value obtained by the DEM subtraction. This is connected to a high increase in the error range and a substantial decrease in the statistical significance. Only small changes were observed for area A2 in which the flat surface and abundance of measurements ensure a robust result. The high variations in A1 between the tested approaches are caused by the fluctuation of the non-significant trend near zero. The results for A1 were shown for completeness. The smoothing of the ΔH values along the tracks did not significantly affect the trend in both regions, A2 and A3. However, its effect on the error ranges and the statistical significance is contradictory.

4.2. Estimation of Mass Balance

Since no surface lowering was detected for the accumulation area, the interpolation of the trend was limited entirely to the ablation area using solely the surface lowering tends in the areas A2 and A3. The trend was interpolated in elevation bands of 100 m by piecewise linear interpolation in an altitude range from 1800 to 3000 m a.s.l., the upper one being an approximate position of the equilibrium line. The volume change was then obtained by multiplication of these trends by the area delimited by the elevation range of each band and summing up of the products. The volume to mass conversion was then calculated assuming an ice density of 850 ± 60 kg·m−3 following [36]. The utilization of the Airphoto DEM as elevation reference produced a total mass balance of −0.92 ± 0.18 m w.e. a−1 using the snow corrected multi-seasonal data and a slope threshold of 10°. The use of the different DEMs resulted in a range of mass balances from −0.90 ± 0.17 m to −1.04 ± 0.19 m w.e. a−1 (Table 4). The error of the mass balance was quantified as a combination of the following contributions: error of derived trends, uncertainty of the glacier outlines and the error of the ice density. Following [11,12], the accuracy of the glacier area delimited by the GLIMS outlines was estimated to be 10%.

4.3. Validation

In order to get a high accuracy elevation reference for comparison with the DEMs, elevations of ICESat footprints were measured in-situ by Differential Global Positioning System (DGPS) during a four day field campaign in July 2012. Elevations of 57% of the footprint center points in area A2 were obtained in static mode with a relative accuracy in the order of centimeters. To provide a comparison with the DEMs, the DGPS measurements were used as elevation reference and values of ΔH were calculated for each point. The resulting surface lowering (Table 2) is almost identical to the surface lowering obtained when using the Airphoto DEM. The ΔH has considerably lower standard deviation in comparison to the use of all the DEMs. This shows that an analysis of ICESat data of flat areas well sampled by ICESat measurements leads to a highly accurate result when using a good quality DEM.
To validate the calculated mass balance, we applied another geodetic method based on the subtraction of two DEMs produced by aerial stereo-photogrammetry. For this purpose, the Airphoto DEMs for the years 2009 and 1999 were co-registered, re-sampled to the same spatial resolution (25 m) and subtracted from each other under the mask for the whole glacier area. The obtained volume was converted to mass balance using again the assumption about the ice density of 850 ± 60 kg·m−3. The thickness change was then calculated in elevation bands of 100 m and plotted against elevation (Figure 8). This plot shows a non-linearity between surface lowering and altitude around 2200 m a.s.l. This non-linearity is not captured by the ICESat data due to the gaps in data coverage along the elevation range. Another non-linearity occurs in the accumulation area which could be due to difficulties of optical stereoscopy over snow covered areas. The error estimation of the DEM subtraction employed the uncertainty of the elevation difference of the two DEMs, error of the ice density and the uncertainty of the glacier outlines. The uncertainty of the elevation difference of the two DEMs was calculated after [37] using statistics of an off-glacier area calculated from each 20th pixel in the sample in order to account for the autocorrelation inherent to the stereoscopically derived DEMs. The resulting mass balance (−1.02 ± 0.34 m w.e. a−1) is in a good agreement with the values calculated from the ICESat measurements using different DEMs (Table 4). The lowest and highest difference is for the SRTM-C (2%) and GDEM ASTER without smoothing (12%), respectively. It should be noted that the two above mentioned nonlinearities which divert from the lowering rates derived from ICESat measurements compensate each other which contributes to this good agreement. It also has to be noted that different methods of mass balance estimation do not lead to identical results and that great care has to be taken when comparing them [38].
Further, we checked the representativeness of the sparse ICESat sampling distribution using simu-laser approach proposed by [39]. The simu-laser elevation changes were extracted at the locations of the ICESat footprints in the areas A2 and A3 from the difference image calculated from the two airphoto DEMs. These differences were averaged over the studied areas to obtain surface lowering (Figure 8). These values were then converted to mass balance applying the same method as for the ICESat measurements. The resulting mass balance 0.81 m w.e. a−1 is only 3% higher with respect to the subtraction of the two DEMs if this subtraction is limited to the ablation area. The resulting lower value of the mass balance is due to the above mentioned non-linearity around the altitude 2200 m a.s.l. This good agreement shows that the ICESat sampling is representative and it supports the validity of the approach.

5. Discussion

The ICESat coverage of the Grosser Aletschgletscher allowed us to test the derivation of the trend of surface lowering under different conditions. Ground DGPS measurements on Konkordiaplatz provided an accurate elevation reference which validates the results achieved by various DEMs. Even though there is a certain variation of ΔH present when using the DGPS data, it is lower than in the case of the DEMs. This residual variation can be attributed to terrain undulations in the ICESat footprints and probably also to the effects of the horizontal component of glacier movements. The trend for Konkordiaplatz based on DGPS is equal to the one for the Airphoto DEM and very close to the one for the SRTM-C DEM.
The available DEMs that were used for the analysis differ in terms of detail level, amount of noise and spatial coverage. The use of the Airphoto DEM for the elevation reference provided results comparable with the ground truth measurements. When comparing the global DEMs, the use of the SRTM-C DEM as elevation reference provides a more robust estimate of ΔH for all three areas than the ASTER GDEM which provides the worse results, especially in the snow-covered accumulation area. The different penetration depth of the C-band signal into firn and ice discussed by several authors [11,40,41] did not affect the results since the accumulation area was treated separately. The penetration depth of C-band signal during the SRTM data acquisition can be estimated as a difference between ΔH values for C- and X-band in the area A3 (Table 2). The resulting value of 3.0 m seems to be a realistic estimate of the C-band signal penetration. The spatially limited SRTM-X DEM does not seem to provide a better result than the SRTM-C DEM.
Although the snow cover depth of alpine glaciers, especially in the accumulation area, can be highly variable [42], the use of in-situ snow depth measurements led to suppression of a seasonal signal in the data. This allowed us to take multi-seasonal ICESat measurements which can be essential in areas with only few ICESat tracks. Multi-seasonal data was similarly used by [12,13]. The representativeness of snow depth measurement from a close meteorological station is biased by the spatial irregularity of precipitation, the redistribution of snow cover by wind and a depth gradient with elevation. Regardless, in our case, the application of the snow correction leads to a higher statistical significance of the derived trends.
A recent study of [34] showed that ICESat measurements tend to be inaccurate for slope values higher than 10°. The comparison of waveforms over various glacier surfaces in terms of slope and roughness in Figure 4 showed that higher slope and higher roughness results in a wider and more complex waveform which can in turn lead to an error in elevation estimation. The application of a threshold for terrain slope seems to be an effective approach in areas with complex topography as was shown for area A1. It leads to a reduction of error ranges and to an increase of statistical significance even over the relatively flat surface of Konkordiaplatz. However, this approach did not bring any improvements in area A3. Moreover, a trade-off between this positive effect and the reduction of number of measurements has to be considered.
Unfortunately, there are no glaciological mass balance measurements for the studied period that could be used for a comparison. However, the mass balance derived from the combination of ICESat data with the SRTM-C DEM matches well to the results of another geodetic method based on the subtraction of two DEMs from the years 1999 and 2009 (Table 4) and to a detailed reconstruction of mass balance by [43]. Certain underestimation of trends derived from ICESat measurements for areas A2 and A3 and a non-linearity of the surface lowering with altitude revealed by the DEM subtraction lead to an underestimation of the mass balance due to the sparse ICESat sampling (Figure 8). This suggests that proper attention has to be paid to the distribution of ICESat data over the elevation range when considering this method for a single glacier. The differences of the trend in surface lowering in area A3 (Table 2) are difficult to explain. As this area is close to the terminus, a high variability of the surface shape can be assumed between the different DEMs acquired at different times. It is evident from Figure 8 that the ICESat-derived trend in ΔH using the Airphoto DEM as an elevation reference is the best match to the subtraction of DEMs. Nevertheless, the impact of these differences on the resulting mass balance is rather small.

6. Conclusions

In this study, the mass balance of the Grosser Aletschgletscher in the Swiss Alps was estimated from ICESat laser altimetry combined with a digital elevation model (DEM). This is the first time that the mass balance of a single mountain glacier was estimated using ICESat measurements. The mass balance differs only 9.8% when comparing with the result of another geodetic approach based on the subtraction of two DEMs produced by aerial stereo-photogrammetry. Depending on the DEM used as an elevation reference, an annual mass balance between −0.90 ± 0.17 m w.e. a−1 and −1.02 ± 0.34 m w.e. a−1 was estimated for the period 2003–2009. Various processing approaches were tested including a threshold for terrain slope, snowpack correction, selection of autumn measurements and along-track smoothing of ICESat-DEM elevation differences. Comparison of the various approaches resulted in differences in mass balance in the range from 0.4% to 5.8%, comparing to the other geodetic approach. It was shown that even the use of global DEMs as elevation reference can lead to a good estimate of surface lowering. The use of the SRTM-C and ASTER-GDEM results in differences of 3.8% and 15.3% from the surface lowering based on Differential Global Positioning System measurements as an elevation reference. However, the use of a higher quality DEM provides better results in terms of variation of ICESat-DEM elevation differences which in turn leads to a higher significance of the estimated trends and to a more accurate mass balance. Global availability of a detailed high quality DEM in the future will indeed improve the accuracy of the derived mass balance of mountain glaciers. In this context, there are high expectations for the global DEM derived from data of the TanDEM-X mission and for the ICESat-2 mission. The results of the Grosser Aletschgletscher indicate that, for a single glacier, surface lowering can be realistically assessed by interpolation across the elevation range, if the ICESat measurements are favorably distributed over the glacier surface. However, the actual surface lowering may locally differ due to non-linearities caused by glacier geometry. This approach indeed cannot compete with a glaciological approach in terms of accuracy; it appears however that it can lead to a realistic estimate of mass balance of a single glacier. As there is only a small fraction of mountain glaciers covered by mass balance measurements worldwide, ICESat data in combination with a DEM can help to fill this gap.

Acknowledgments

This work was supported by the German Research Foundation (DFG) Priority Programme 1372, “Tibetan Plateau: Formation–Climate–Ecosystems” within the DynRG-TiP (“Dynamic Response of Glaciers on the Tibetan Plateau to Climate Change”) project under the code BU 949/20-3, and by the German Federal Ministry of Education and Research (BMBF) Programme “Central Asia–Monsoon Dynamics and Geo-Ecosystems” (CAME) within the WET project (“Variability and Trends in Water Balance Components of Benchmark Drainage Basins on the Tibetan Plateau”) under the code 03G0804D. We acknowledge support by Open Access Publishing Fund of the University of Tuebingen. ICESat data was provided by NSIDC, SRTM-C DEM was obtained from the USGS and the SRTM-X DEM was provided by the DLR. ASTER GDEM is a product of METI and NASA. The field measurements of the snow depth were provided by the Institute for Snow and Avalanche Research in Davos, Switzerland. The Landsat scene was provided by the USGS. Thanks to B. Schröter for support during the field survey.

Conflicts of Interest

The authors declare no conflict of interest.
  • Author ContributionsThe authors contributed to the reported research and writing of this paper as follows Jan Kropáček: 60%, 65%, Niklas Neckel: 25%, 25%, Andreas Bauder: 15%, 10%.

References and Notes

  1. WGMS, Global Glacier Changes: Facts and Figures; Zemp, M.; Roer, I.; Kääb, A.; Hoelzle, M.; Paul, F.; Haeberli, W. (Eds.) World Glacier Monitoring Service: Zurich, Switzerland, 2008.
  2. WGMS, Fluctuations of Glaciers 2005–2010; Volume X, Zemp, M.; Frey, H.; Gärtner-Roer, I.; Nussbaumer, S.U.; Hoelzle, M.; Paul, F.; Haeberli, W. (Eds.) World Glacier Monitoring Service: Zurich, Switzerland, 2012.
  3. Oerlemans, J. Glaciers and Climate Change; CRC Press: Rotterdam, The Netherlands, 2001. [Google Scholar]
  4. NSIDC. Available online: http://nsidc.org/data/icesat/orbit_grnd_trck.html (accessed on 24 October 2013).
  5. Howat, I.M.; Smith, B.E.; Joughin, I.; Scambos, T.A. Rates of southeast Greenland ice volume loss from combined ICESat and ASTER observations. Geophys. Res. Lett 2008. [Google Scholar] [CrossRef]
  6. Slobbe, D.; Lindenbergh, R.; Ditmar, P. Estimation of volume change rates of Greenland’s ice sheet from ICESat data using overlapping footprints. Remote Sens. Environ 2008, 112, 4204–4213. [Google Scholar]
  7. Moholdt, G.; Nuth, C.; Hagen, J.O.; Kohler, J. Recent elevation changes of Svalbard glaciers derived from ICESat laser altimetry. Remote Sens. Environ 2010, 114, 2756–2767. [Google Scholar]
  8. Rinne, E.J.; Shepherd, A.; Palmer, S.; van den Broeke, M.R.; Muir, A.; Ettema, J.; Wingham, D. On the recent elevation changes at the Flade Isblink Ice Cap, northern Greenland. J. Geophys. Res.: Earth Surface 2011. [Google Scholar] [CrossRef]
  9. Sørensen, L.S.; Simonsen, S.B.; Nielsen, K.; Lucas-Picher, P.; Spada, G.; Adalgeirsdottir, G.; Forsberg, R.; Hvidberg, C.S. Mass balance of the Greenland ice sheet (2003–2008) from ICESat data—The impact of interpolation, sampling and firn density. Cryosphere 2011, 5, 173–186. [Google Scholar]
  10. Brenner, A.C.; DiMarzio, J.P.; Zwally, H.J. Precision and accuracy of satellite radar and LASER altimeter data over the continental ice SHEETS. IEEE Trans. Geosci. Remote Sens 2007, 45, 321–331. [Google Scholar]
  11. Kääb, A.; Berthier, E.; Nuth, C.; Gardelle, J.; Arnaud, Y. Contrasting patterns of early twenty-first-century glacier mass change in the Himalayas. Nature 2012, 488, 495–498. [Google Scholar]
  12. Gardner, A.S.; Moholdt, G.; Cogley, J.G.; Wouters, B.; Arendt, A.A.; Wahr, J.; Berthier, E.; Hock, R.; Pfeffer, W.T.; Kaser, G.; et al. A reconciled estimate of glacier contributions to sea level rise: 2003 to 2009. Science 2013, 340, 852–857. [Google Scholar]
  13. Neckel, N.; Kropáček, J.; Bolch, T.; Hochschild, V. Glacier mass changes on the Tibetan Plateau 2003–2009 derived from ICESat laser altimetry measurements. Environ. Res. Lett 2014. [Google Scholar] [CrossRef]
  14. Bauder, A.; Funk, M.; Huss, M. Ice-volume changes of selected glaciers in the Swiss Alps since the end of the 19th century. Ann. Glaciol 2007, 46, 145–149. [Google Scholar]
  15. Holzhauser, H. Die bewegte Vergangenheit des Grossen Aletschgletschers. Blätter aus der Walliser Geschichte 2009, 41, 103–121. [Google Scholar]
  16. Thyssen, F.; Ahmad, M. Ergebnisse seismischer Messungen auf dem Aletschgletscher. Polarforschung, Bremerhaven, Alfred Wegener Institute for Polar and Marine Research & German Society of Polar Research 1969, 39, 283–293. [Google Scholar]
  17. Huss, M.; Hock, R.; Bauder, A.; Funk, M. 100-year mass changes in the Swiss Alps linked to the Atlantic Multidecadal Oscillation. Geophys. Res. Lett 2010. [Google Scholar] [CrossRef]
  18. Huss, M.; Bauder, A.; Funk, M.; Hock, R. Determination of the seasonal mass balance of four Alpine glaciers since 1865. J. Geophys. Res.: Earth Surface 2008. [Google Scholar] [CrossRef]
  19. Schutz, B.E.; Zwally, H.J.; Shuman, C.A.; Hancock, D.; Di Marzio, J.P. Overview of the ICESat mission. Geophys. Res. Lett 2005. [Google Scholar] [CrossRef]
  20. Abdalati, W.; Zwally, H.J.; Bindschadler, R.; Csatho, B.; Farrell, S.L.; Fricker, H.A.; Harding, D.; Kwok, R.; Lefsky, M.; Markus, T.; et al. The ICESat-2 laser altimetry mission. Proc. IEEE 2010, 98, 735–751. [Google Scholar]
  21. Zwally, H.J.; Schutz, R.; Bentley, C.; Bufton, J.; Herring, T.; Minster, J.; Spinhirne, J.; Thomas, R. GLAS/ICESat L2 Global Land Surface Altimetry Data, Version 33; National Snow and Ice Data Center: Boulder, CO, USA, 2003. [Google Scholar]
  22. Rabus, B.; Eineder, M.; Roth, A.; Bamler, R. The shuttle radar topography mission, a new class of digital elevation models acquired by spaceborne radar. ISPRS J. Photogramm. Remote Sens 2003, 57, 241–262. [Google Scholar]
  23. Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The shuttle radar topography mission. Rev. Geophys 2007. [Google Scholar] [CrossRef]
  24. Sun, G.; Ranson, K.J.; Kharuk, V.I.; Kovacs, K. Validation of surface height from shuttle radar topography mission using shuttle laser altimeter. Remote Sens. Environ 2003, 88, 401–411. [Google Scholar]
  25. Hoffman, D.; Walter, J. How complementary are SRTM-X and -C band digital elevation models? Photogramm. Eng. Remote Sens 2006, 72, 261–268. [Google Scholar]
  26. Gorokhovich, Y.; Voustianiouk, A. Accuracy assessment of the processed SRTM-based elevation data by CGIAR using field data from USA and Thailand and its relation to the terrain characteristics. Remote Sens. Environ 2006, 104, 409–415. [Google Scholar]
  27. Carabajal, C.C.; Harding, D.J. ICESat validation of SRTM C-band digital elevation models. Geophys. Res. Lett 2005. [Google Scholar] [CrossRef]
  28. Tachikawa, T.; Kaku, M.; Iwasaki, A.; Gesch, D.; Oimoen, M.; Zhang, Z.; Danielson, J.; Krieger, T.; Curtis, B.; Haase, J.; et al. ASTER Global Digital Elevation Model Version 2—Summary of Validation Results. Available online: http://www.ersdac.or.jp/GDEM/ver2Validation/ (accessed on 1 November 2013).
  29. Frey, H.; Paul, F. On the suitability of the SRTM DEM and ASTER GDEM for the compilation of topographic parameters in glacier inventories. Int. J. Appl. Earth Observ. Geoinf 2011. [Google Scholar] [CrossRef]
  30. Armstrong, R.; Raup, B.; Khalsa, S.; Barry, B.; Kargel, J.; Helm, C.; Kieffer, H. GLIMS Glacier Database; National Snow and Ice Data Center: Boulder, CO, USA, 2005. [Google Scholar]
  31. Nuth, C.; Kääb, A. Co-registration and bias corrections of satellite elevation data sets for quantifying glacier thickness change. Cryosphere 2011, 5, 271–290. [Google Scholar]
  32. Bhang, K.J.; Schwartz, F.W.; Braun, A. Verification of the vertical error in C-band SRTM DEM using ICESat and Landsat-7, Otter Tail County, MN. IEEE Trans. Geosci. Remote Sens 2007, 45, 36–44. [Google Scholar]
  33. Wesche, C.; Riedel, S.; Steinhage, D. Precise surface topography of the grounded ice ridges at the Ekströmisen, Antarctica, based on several geophysical data sets. ISPRS J. Photogramm. Remote Sens 2009, 64, 381–386. [Google Scholar]
  34. Hilbert, C.; Schmullius, C. Influence of surface topography on ICESat/GLAS forest height estimation and waveform shape. Remote Sens 2012, 4, 2210–2235. [Google Scholar]
  35. Schubert, A.; Faes, A.; Kääb, A.; Meier, E. Glacier surface velocity estimation using repeat TerraSAR-X images: Wavelet- vs. correlation-based image matching. ISPRS J. Photogramm. Remote Sens 2013, 82, 49–62. [Google Scholar]
  36. Huss, M. Density assumptions for converting geodetic glacier volume change to mass change. Cryosphere 2013, 7, 877–887. [Google Scholar]
  37. Koblet, T.; Gärtner-Roer, I.; Zemp, M.; Jansson, P.; Thee, P.; Haeberli, W.; Holmlund, P. Reanalysis of multi-temporal aerial images of Storglaciären, Sweden (1959–99)—Part 1: Determination of length, area, and volume changes. Cryosphere 2010, 4, 333–343. [Google Scholar]
  38. Fischer, A. Comparison of direct and geodetic mass balances on a multi-annual scale. Cryosphere 2011, 5, 107–124. [Google Scholar]
  39. Berthier, E.; Schiefer, E.; Clarke, G.K.C.; Menounos, B.; Rémy, F. Contribution of Alaskan glaciers to sea-level rise derived from satellite imagery. Nature Geosc 2010. [Google Scholar] [CrossRef] [Green Version]
  40. Rignot, E.; Echelmeyer, K.A.; Krabill, W. Penetration depth of interferometric synthetic-aperture radar signals in snow and ice. Geophys. Res. Lett 2001, 28, 501–504. [Google Scholar]
  41. Gardelle, J.; Berthier, E.; Arnaud, Y. Impact of resolution and radar penetration on glacier elevation changes computed from DEM differencing. J. Glaciol 2012, 58, 419–422. [Google Scholar]
  42. Machguth, H.; Paul, F.; Hoelzle, M. Strong spatial variability of snow accumulation observed with helicopter-borne GPR on two adjacent Alpine glaciers. Geophys. Res. Lett 2006. [Google Scholar] [CrossRef]
  43. Farinotti, D.; Usselmann, S.; Huss, M.; Bauder, A.; Funk, M. Runoff evolution in the Swiss Alps: Projections for selected high-alpine catchments based on ENSEMBLES scenarios. Hydrol. Process 2012, 26, 1909–1924. [Google Scholar]
Remotesensing 06 05614f1 1024
Figure 1. Ground tracks of ICESat cross the surface of Grosser Aletschgletscher in three separate places: Ewig Schneefeld (A1), Konkordiaplatz (A2) and the lower part close to the terminus (A3). ICESat measurements on the glacier are highlighted in violet. Outlines of the DEMs with only partial coverage of the area are in yellow. The points used as ground control for the airphoto DEMs are shown as black crosses. In the background is a Landsat TM image from 28 August 2011.
Figure 1. Ground tracks of ICESat cross the surface of Grosser Aletschgletscher in three separate places: Ewig Schneefeld (A1), Konkordiaplatz (A2) and the lower part close to the terminus (A3). ICESat measurements on the glacier are highlighted in violet. Outlines of the DEMs with only partial coverage of the area are in yellow. The points used as ground control for the airphoto DEMs are shown as black crosses. In the background is a Landsat TM image from 28 August 2011.
Remotesensing 06 05614f1
Remotesensing 06 05614f2 1024
Figure 2. Terrain slope at ICESat points in the three areas A1 (a), A2 (b) and A3 (c) on the Grosser Aletschgletscher. Red crosses indicate canceled points with erroneous elevations due to cloud cover. Glacier outlines are from the Global Land Ice Measurements from Space (GLIMS) dataset. The red squares mark the points for which the waveforms are shown in below.
Figure 2. Terrain slope at ICESat points in the three areas A1 (a), A2 (b) and A3 (c) on the Grosser Aletschgletscher. Red crosses indicate canceled points with erroneous elevations due to cloud cover. Glacier outlines are from the Global Land Ice Measurements from Space (GLIMS) dataset. The red squares mark the points for which the waveforms are shown in below.
Remotesensing 06 05614f2
Remotesensing 06 05614f3 1024
Figure 3. The area A2 (Konkordiaplatz) on different DEMs shown as shaded relief. (a) The SRTM-C DEM features a smooth surface with little detail. Artifacts are clearly visible on the glacier surface in the case of the ASTER GDEM (b) while the Airphoto DEM (c) has a smooth surface with a distinct medial moraine.
Figure 3. The area A2 (Konkordiaplatz) on different DEMs shown as shaded relief. (a) The SRTM-C DEM features a smooth surface with little detail. Artifacts are clearly visible on the glacier surface in the case of the ASTER GDEM (b) while the Airphoto DEM (c) has a smooth surface with a distinct medial moraine.
Remotesensing 06 05614f3
Remotesensing 06 05614f4 1024
Figure 4. Waveforms of ICESat pulses recorded on 24 October 2003 over (a) flat glacier surface in A1 (slope = 1.7°), (b) steeper glacier surface (slope = 14.9°), (c) rough glacier surface marked by a number of crevasses that form between Ewig Schneefeld and Konkordiaplatz and (d) steep off-glacier slope south of Konkordiaplatz. The raw waveform is in red and the fit is in blue. One hundred ns corresponds to 15.1 m of the elevation difference. Positions of the points labeled as W1, W2, W3 and W4, respectively, are shown in Figure 2.
Figure 4. Waveforms of ICESat pulses recorded on 24 October 2003 over (a) flat glacier surface in A1 (slope = 1.7°), (b) steeper glacier surface (slope = 14.9°), (c) rough glacier surface marked by a number of crevasses that form between Ewig Schneefeld and Konkordiaplatz and (d) steep off-glacier slope south of Konkordiaplatz. The raw waveform is in red and the fit is in blue. One hundred ns corresponds to 15.1 m of the elevation difference. Positions of the points labeled as W1, W2, W3 and W4, respectively, are shown in Figure 2.
Remotesensing 06 05614f4
Remotesensing 06 05614f5 1024
Figure 5. Linear trend of the surface lowering in area A1 fitted through multi-seasonal ICESat data. Snow corrections and a threshold for the local terrain slope of 10° (above) and 5° (below) were applied to reduce the high in-track variation of ΔH.
Figure 5. Linear trend of the surface lowering in area A1 fitted through multi-seasonal ICESat data. Snow corrections and a threshold for the local terrain slope of 10° (above) and 5° (below) were applied to reduce the high in-track variation of ΔH.
Remotesensing 06 05614f5
Remotesensing 06 05614f6 1024
Figure 6. Linear trend of the surface lowering in area A2 fitted through multi-seasonal ICESat data using the Airphoto DEM as elevation reference. A terrain slope threshold of 10° and snow pack corrections were applied. Values of mean ΔH for off-glacier area (in grey) do not show a statistically significant trend.
Figure 6. Linear trend of the surface lowering in area A2 fitted through multi-seasonal ICESat data using the Airphoto DEM as elevation reference. A terrain slope threshold of 10° and snow pack corrections were applied. Values of mean ΔH for off-glacier area (in grey) do not show a statistically significant trend.
Remotesensing 06 05614f6
Remotesensing 06 05614f7 1024
Figure 7. Linear trend of the surface lowering in area A3 fitted through multi-seasonal ICESat data using the Airphoto DEM as elevation reference. A terrain slope threshold of 10° and snow pack corrections were applied.
Figure 7. Linear trend of the surface lowering in area A3 fitted through multi-seasonal ICESat data using the Airphoto DEM as elevation reference. A terrain slope threshold of 10° and snow pack corrections were applied.
Remotesensing 06 05614f7
Remotesensing 06 05614f8 1024
Figure 8. Glacier hypsometry (upper panel) and surface lowering in elevation bands of 100 m derived from the subtraction of two Airphoto DEMs (black line) and surface lowering from ICESat measurements using the Airphoto DEM (red), SRTM-C DEM (green), the ASTER GDEM original (blue) and the ASTER GDEM smoothed version (magenta) as elevation reference and from SIMU-Laser (wellow). The subtraction of the two DEMs and the ICESat measurements cover slightly different periods: 1999–2009 and 2003–2009, respectively. The elevation ranges covered with the ICESat data (A1, A2 and A3) are marked by horizontal lines in the lower part of the image.
Figure 8. Glacier hypsometry (upper panel) and surface lowering in elevation bands of 100 m derived from the subtraction of two Airphoto DEMs (black line) and surface lowering from ICESat measurements using the Airphoto DEM (red), SRTM-C DEM (green), the ASTER GDEM original (blue) and the ASTER GDEM smoothed version (magenta) as elevation reference and from SIMU-Laser (wellow). The subtraction of the two DEMs and the ICESat measurements cover slightly different periods: 1999–2009 and 2003–2009, respectively. The elevation ranges covered with the ICESat data (A1, A2 and A3) are marked by horizontal lines in the lower part of the image.
Remotesensing 06 05614f8
Table
Table 1. Horizontal shifts of the reference DEMs with respect to the ICESat measurements which had to be removed before the extraction of ΔH values.
Table 1. Horizontal shifts of the reference DEMs with respect to the ICESat measurements which had to be removed before the extraction of ΔH values.
DEMHorizontal Shift (m)Azimuth of the Shift (deg.)
SRTM-C70.8124.2
SRTM-X40.072.1
Airphoto DEM55.1−106.3
ASTER GDEM17.1200.6
Table
Table 2. Mean surface lowering for areas A1, A2 and A3 using different DEMs as elevation reference. The snow pack correction and the threshold of the terrain slope were applied. F-values in italics indicate a statistically non-significant trend.
Table 2. Mean surface lowering for areas A1, A2 and A3 using different DEMs as elevation reference. The snow pack correction and the threshold of the terrain slope were applied. F-values in italics indicate a statistically non-significant trend.
Elevation ReferenceAreaMean ΔH (m)σ of ΔH (m)Mean Surface Lowering (m/a)f-ValueCanceled Points (%)Canceled Tracks (No)
SRTM-CA18.14.7−0.2 ± 0.320.4155.81
ASTER GDEM originalA1−13.412.90.2 ± 1.050.0276.12
ASTER GDEM smoothedA1−12.710.20.1 ± 0.670.0458.91
Airphoto DEMA15.53.9−0.0 ± 0.300.0254.31
SRTM-CA2−6.12.8−2.5 ± 0.13380.614.91
ASTER GDEM originalA2−3.84.2−2.2 ± 0.20125.933.21
ASTER GDEM smoothedA2−3.33.5−2.1 ± 0.15183.815.91
Airphoto DEMA210.71.9−2.6 ± 0.10759.816.81
DGPSA215.00.9−2.6 ± 0.08788.57.51
SRTM-CA3−25.64.4−5.1 ± 0.35209.0628.22
ASTER GDEM originalA3−18.24.6−4.3 ± 0.5268.3256.42
ASTER GDEM smoothedA3−17.14−5.1 ± 0.34217.4430.82
Airphoto DEMA3173.8−3.3 ± 0.3684.7739.72
SRTM-XA3−22.64.4−5.3 ± 0.39189.2333.32
Table
Table 3. The effect of various approaches in the processing of ICESat data on the trend in ΔH, the error range, the statistical significance and the resulting mass balance are expressed in percentages. The calculation is based on the Airphoto DEM for 2009.
Table 3. The effect of various approaches in the processing of ICESat data on the trend in ΔH, the error range, the statistical significance and the resulting mass balance are expressed in percentages. The calculation is based on the Airphoto DEM for 2009.
Tested ChangeAreaSurface LoweringSigmaf-ValueMass Balance
threshold for terrain slope 10°A150.0%0.0%120.5%1.74%
A23.2%−30.8%119.7%
A30.0%9.1%−15.1%
snow pack correctionA1−15.7%2.6%−33.3%0.44%
A2−1.9%22.2%−33.7%
A33.0%5.6%−5.3%
selection of autumn measurementsA1−70.6%34.2%−95.2%−5.8%
A26.8%7.7%0.3%
A3−18.9%63.6%−75.4%
smoothing of ΔH profilesA158.8%−15.8%237.3%−4.8%
A2−0.4%−23.1%71.0%
A30.9%60.6%−59.1%
Table
Table 4. Mass balance of the Grosser Aletschgletscher estimated from ICESat measurements for the period 2003–2009 using different DEMs as elevation reference and from the subtraction of the DEMs for the years 1999 and 2009.
Table 4. Mass balance of the Grosser Aletschgletscher estimated from ICESat measurements for the period 2003–2009 using different DEMs as elevation reference and from the subtraction of the DEMs for the years 1999 and 2009.
DEMMass Balance (m w.e. a−1)
Airphoto DEM−0.92 ± 0.18
SRTM-C−1.04 ± 0.19
GDEM ASTER original−0.90 ± 0.17
GDEM ASTER smoothed−0.94 ± 0.18
subtraction of DEMs−1.02 ± 0.34

Share and Cite

MDPI and ACS Style

Kropáček, J.; Neckel, N.; Bauder, A. Estimation of Mass Balance of the Grosser Aletschgletscher, Swiss Alps, from ICESat Laser Altimetry Data and Digital Elevation Models. Remote Sens. 2014, 6, 5614-5632. https://doi.org/10.3390/rs6065614

AMA Style

Kropáček J, Neckel N, Bauder A. Estimation of Mass Balance of the Grosser Aletschgletscher, Swiss Alps, from ICESat Laser Altimetry Data and Digital Elevation Models. Remote Sensing. 2014; 6(6):5614-5632. https://doi.org/10.3390/rs6065614

Chicago/Turabian Style

Kropáček, Jan, Niklas Neckel, and Andreas Bauder. 2014. "Estimation of Mass Balance of the Grosser Aletschgletscher, Swiss Alps, from ICESat Laser Altimetry Data and Digital Elevation Models" Remote Sensing 6, no. 6: 5614-5632. https://doi.org/10.3390/rs6065614

Article Metrics

Back to TopTop