An Assessment of Polynomial Regression Techniques for the Relative Radiometric Normalization (RRN) of High-Resolution Multi-Temporal Airborne Thermal Infrared (TIR) Imagery
Abstract
:1. Introduction
2. Methods
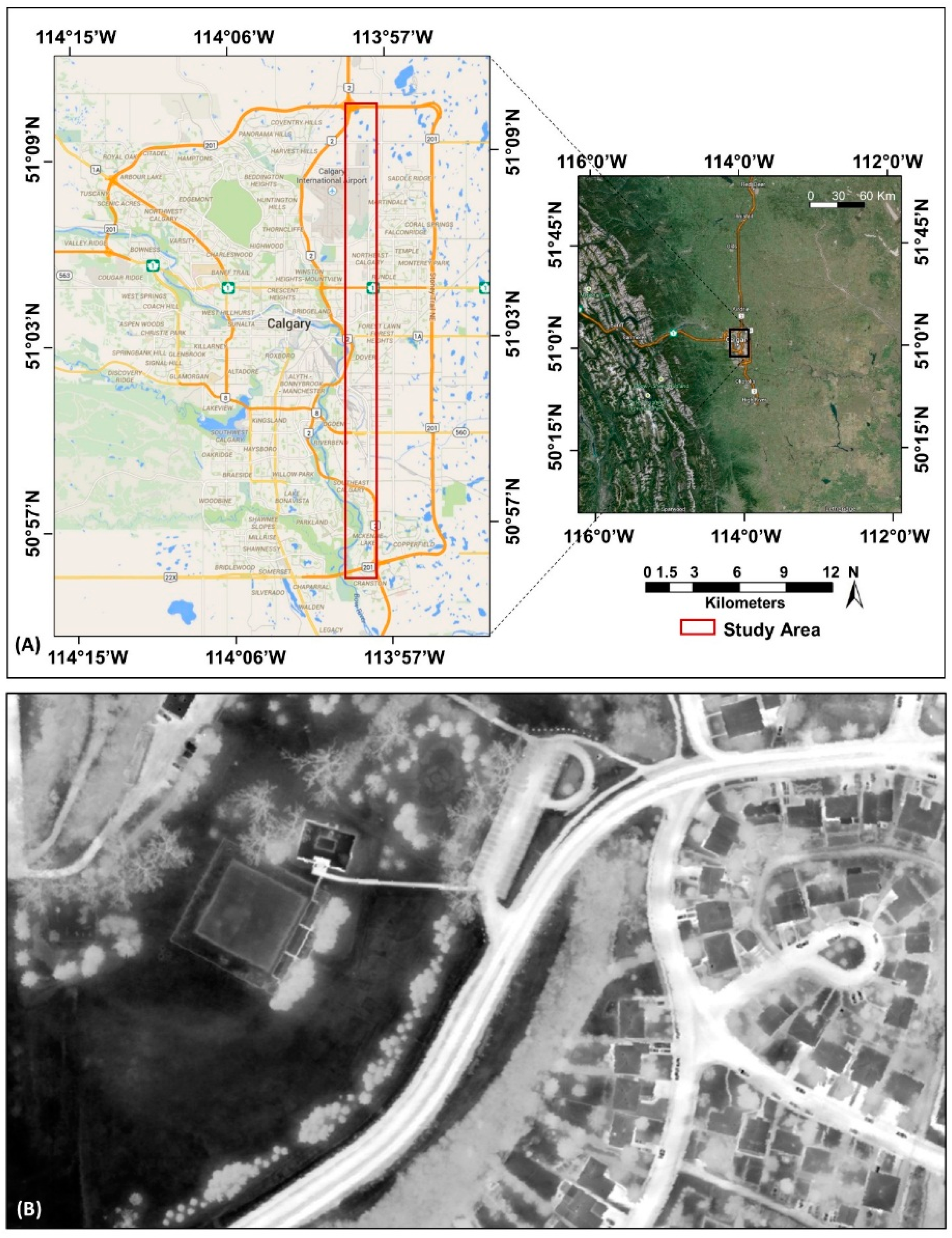
2.1. Study Area and Dataset
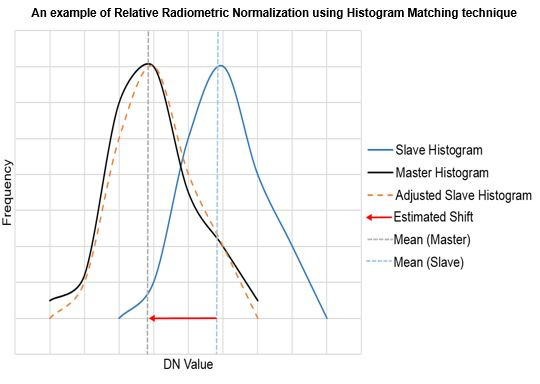
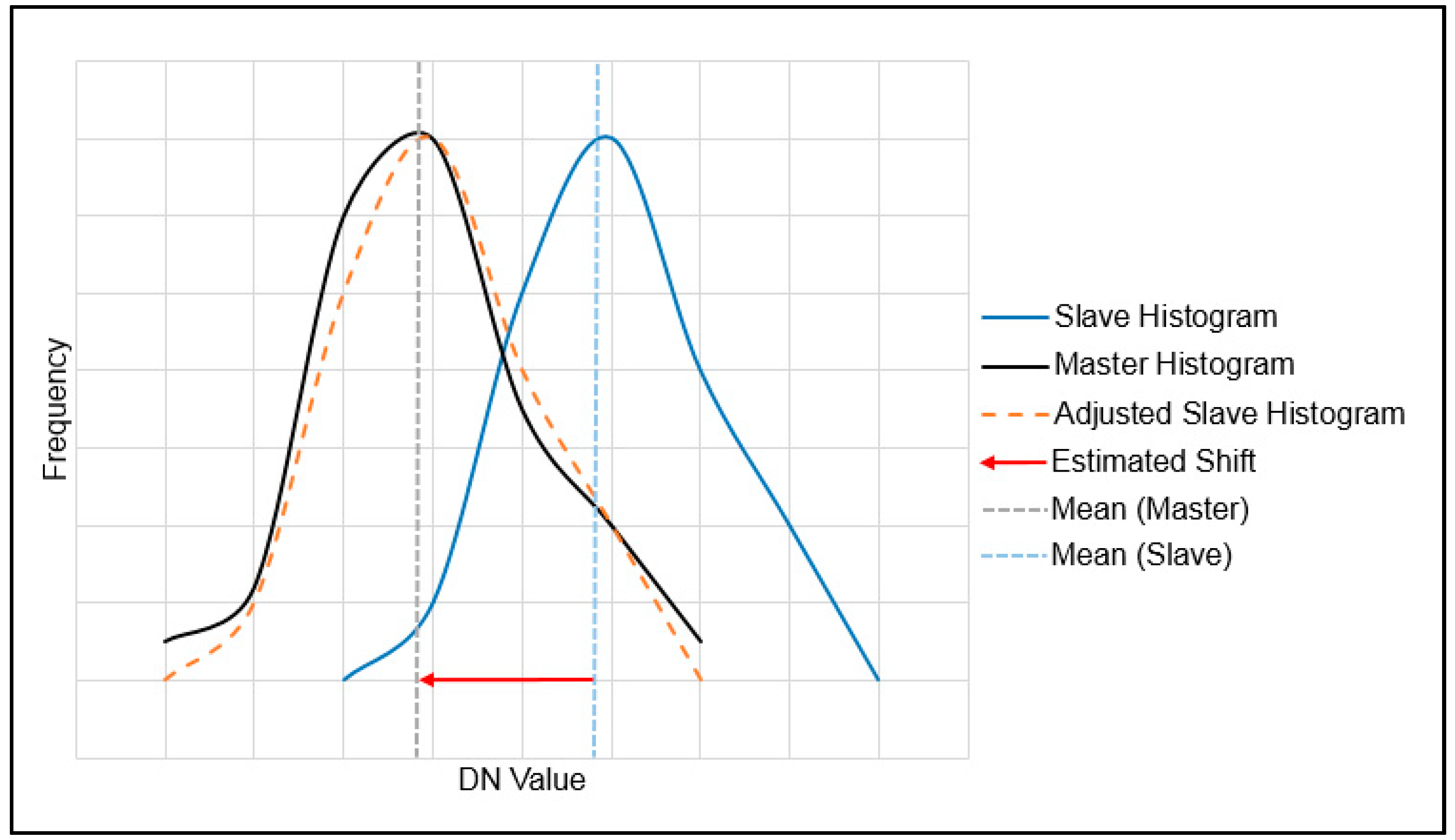
2.2. Relative Radiometric Normalization
2.2.1. Histogram Matching
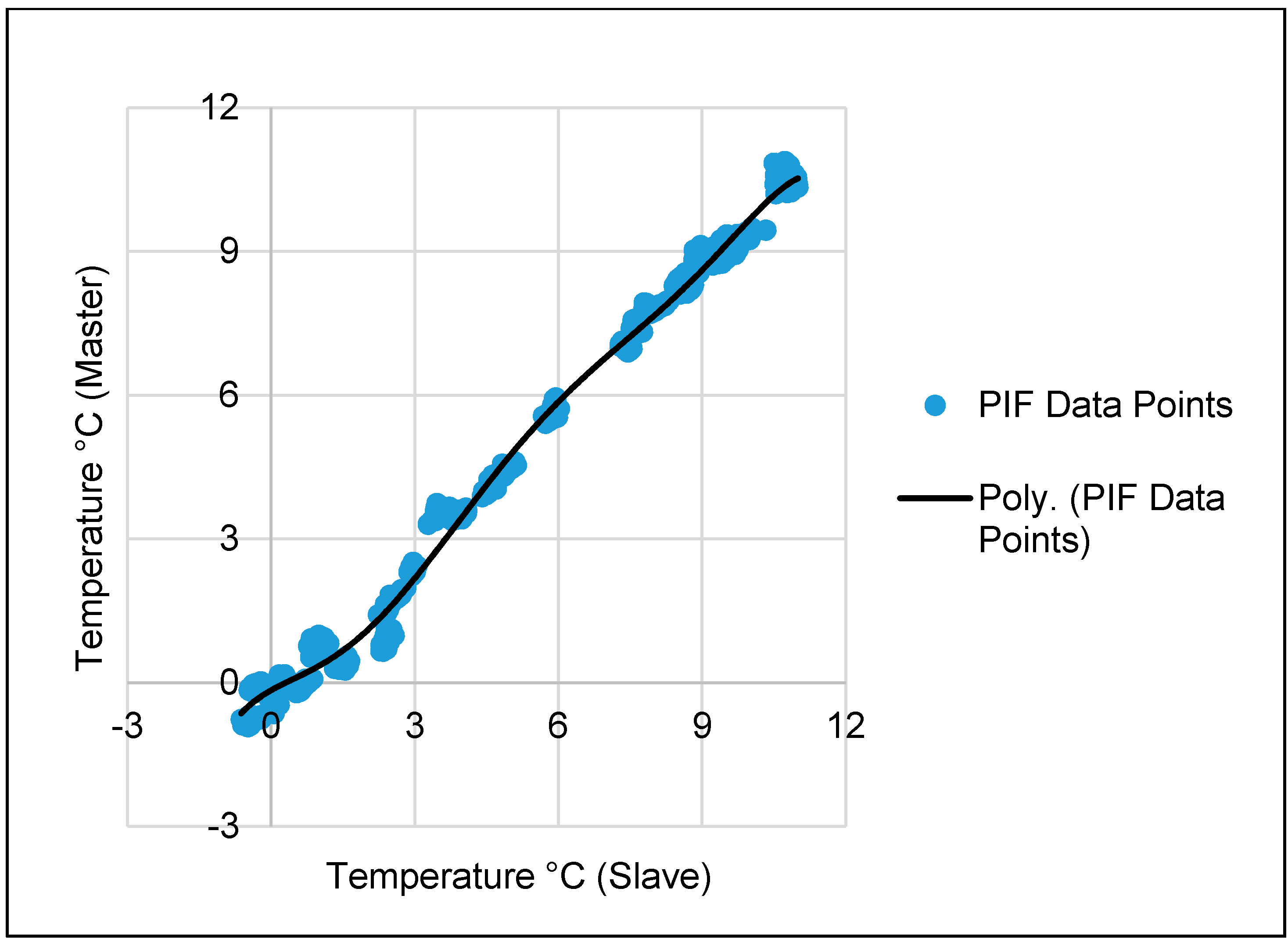
2.2.2. Pseudo-Invariant Feature (PIF)-Based Polynomial Regression (PIF_Poly)
2.2.3. No-Change Stratified Random Sample (NCSRS)-Based Linear Regressions
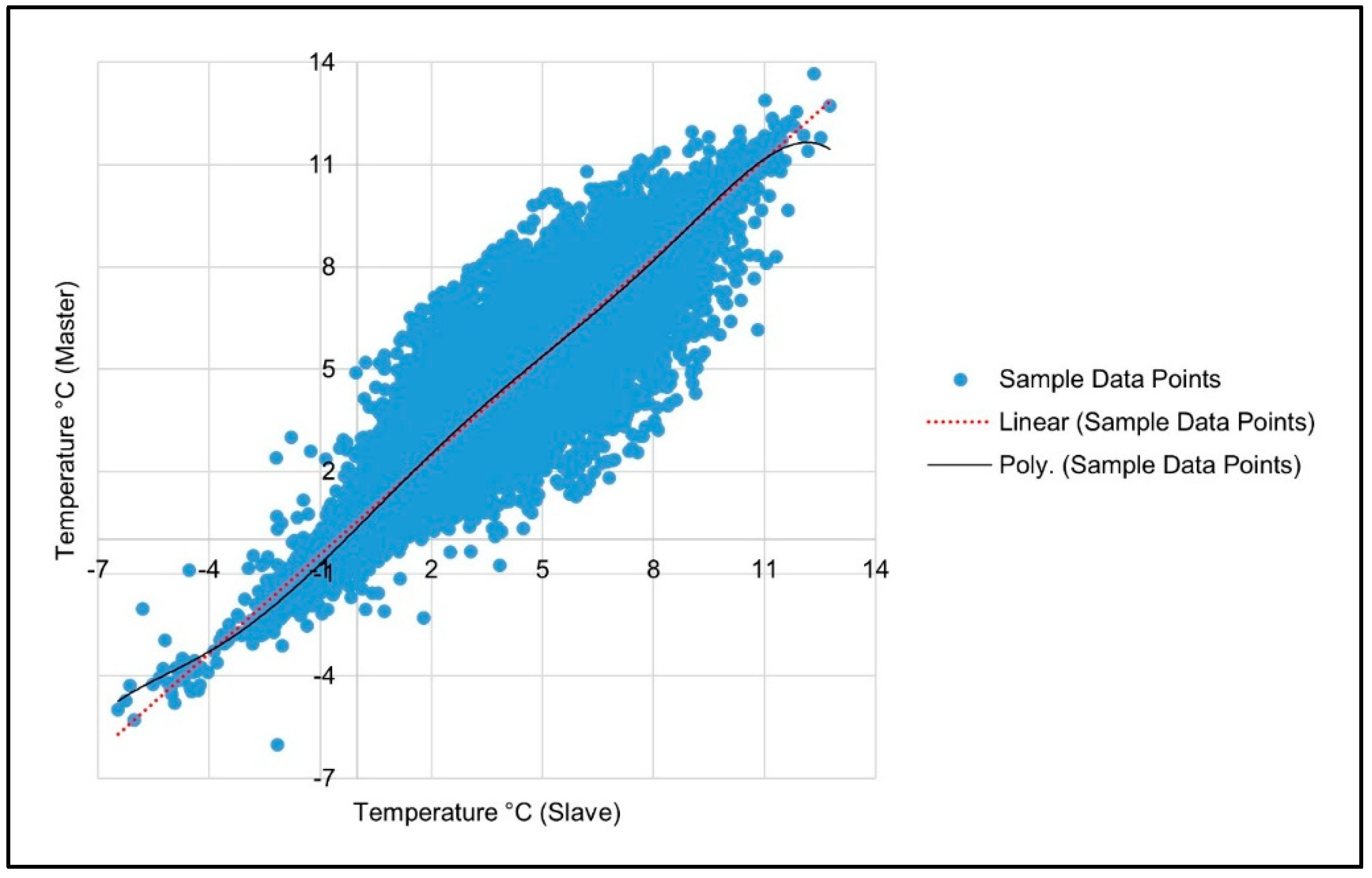
2.2.4. No-Change Stratified Random Sample (NCSRS)-Based Polynomial Regression
2.3. Validation of the Results Using Root Mean Square Error (RMSE)
3. Results and Discussions
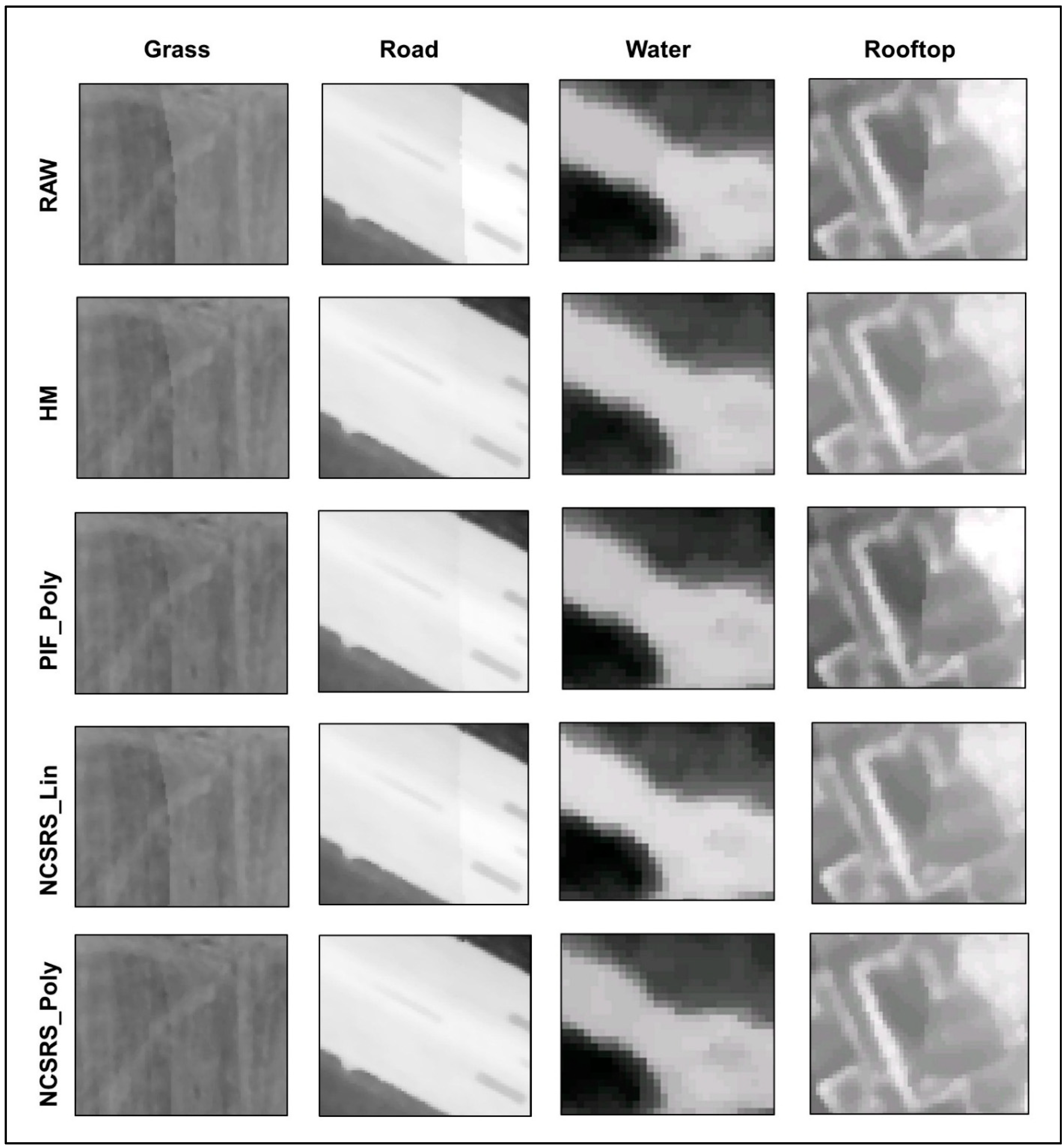
3.1. Visual Assessments
- ▪
- HM appears to perform very well for road and water, but performs only moderately well for grass and rooftop.
- ▪
- PIF_Poly performs well for road and water and moderately well for grass, but it does not perform well for rooftop.
- ▪
- NCSRS_Lin performs very well for water and moderately well for road, grass and rooftop.
- ▪
- NCSRS_Poly performs very well for road and water and well for grass and rooftop. Though subjective, we further suggest that grass and rooftop visually appear best modeled by this method.
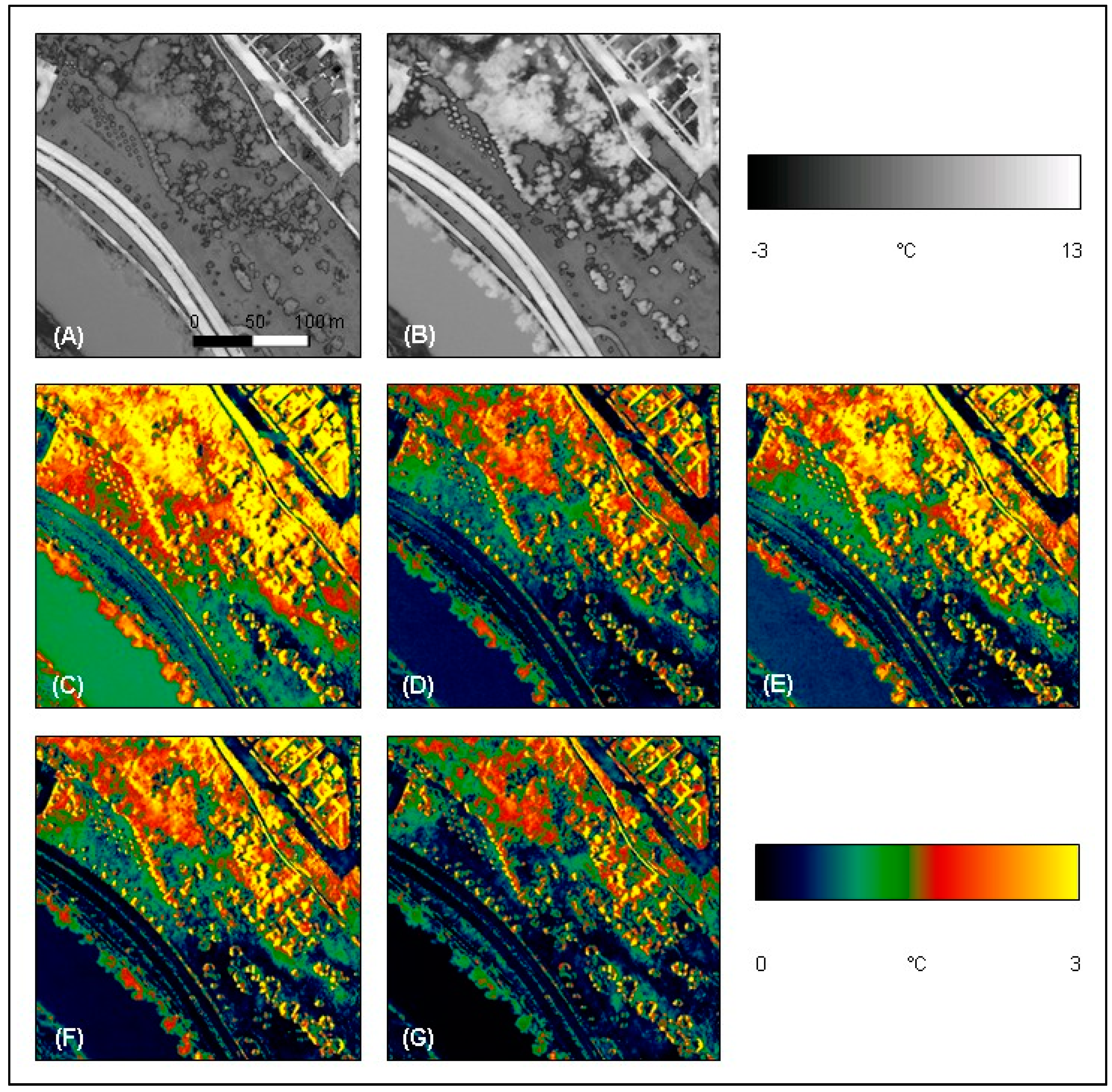
3.2. Statistical Analysis
| Land Cover Type | RMSE (°C) | ||||
|---|---|---|---|---|---|
| Slave | HM | PIF_Poly | NCSRS_Lin | NCSRS_Poly | |
| Grass | 0.420 | 0.236 | 0.227 | 0.193 | 0.163 |
| Road | 0.201 | 0.097 | 0.128 | 0.122 | 0.123 |
| Rooftop | 0.586 | 0.436 | 0.452 | 0.371 | 0.322 |
| Water | 0.216 | 0.106 | 0.108 | 0.130 | 0.113 |
| Overall * | 0.356 | 0.194 | 0.210 | 0.173 | 0.159 |
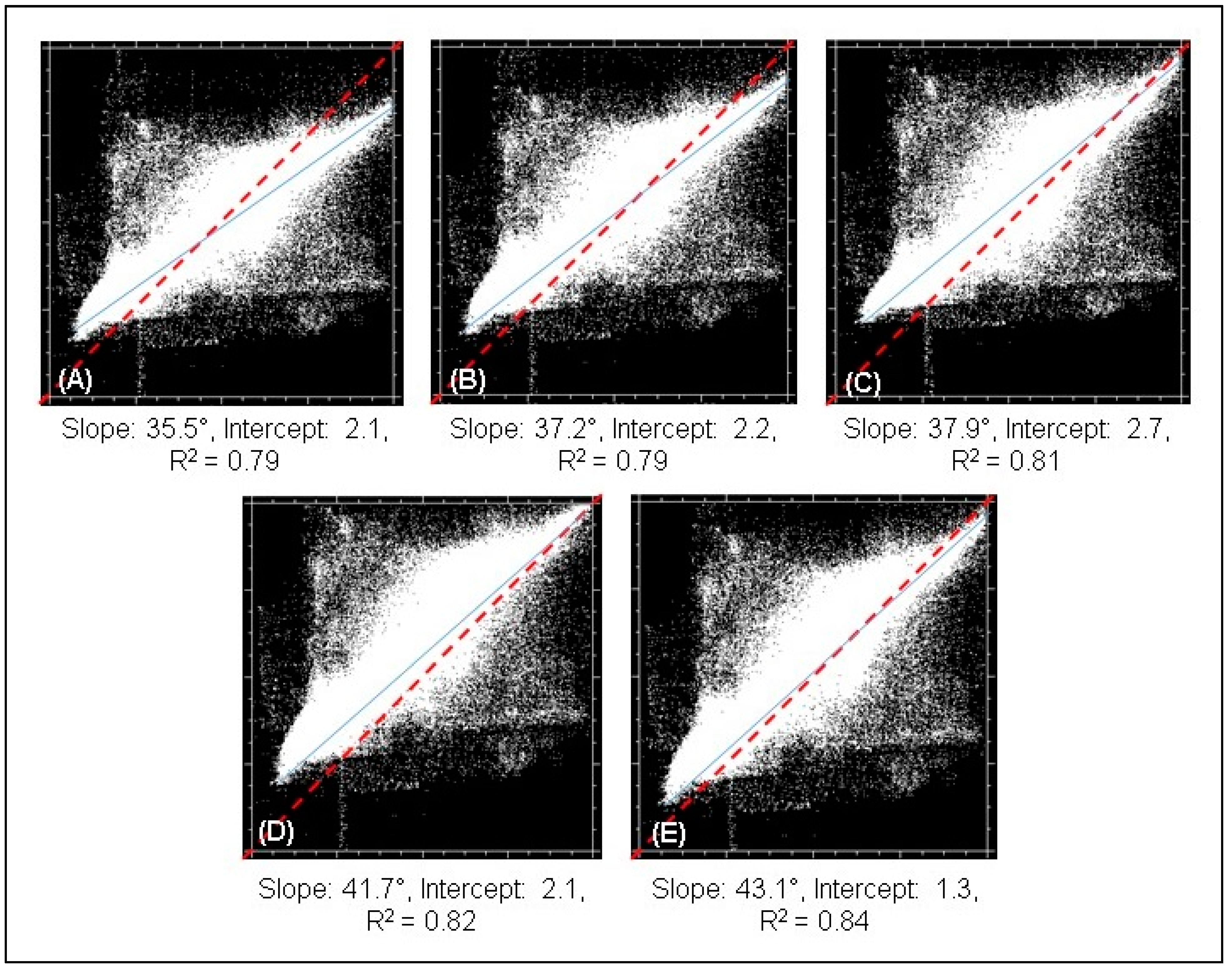
3.2.1. A Comparison of Automatic vs Manual Methods
3.2.2. An Assessment of Computation Time
| RRN Method | Computing Time (min) |
|---|---|
| Histogram Matching | 2.14 |
| PIF_Poly | 4.7 * |
| NCSRS_Lin | 1.4 |
| NCSRS_Poly | 4.7 |
3.2.3. A Comparison of Linear vs Polynomial Methods
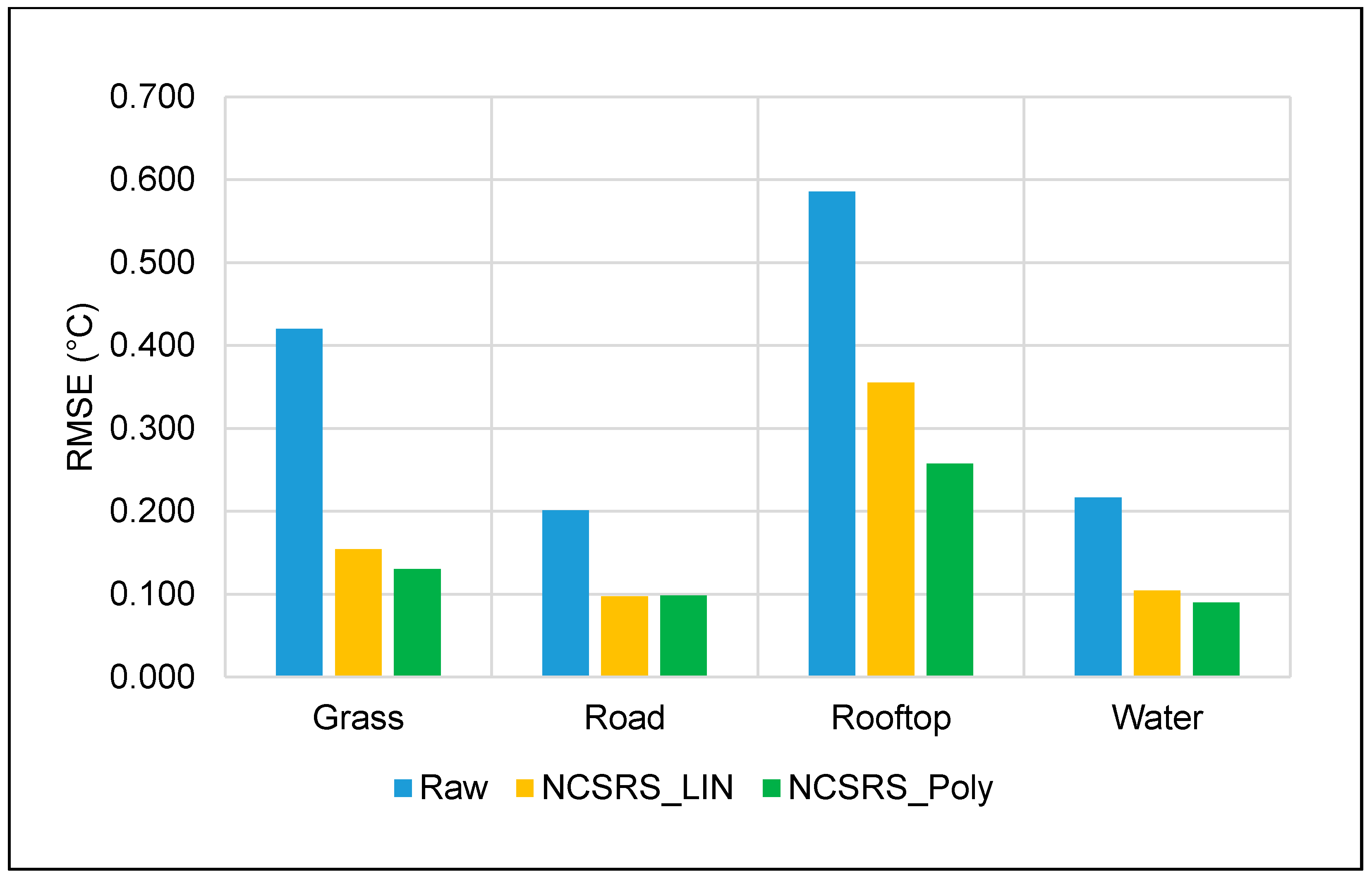
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Voogt, J.A.; Oke, T.R. Complete urban surface temperatures. J. Appl. Meteorol. 1997, 36, 1117–1132. [Google Scholar] [CrossRef]
- Rahman, M.M.; Hay, G.J.; Couloigner, I.; Hemachandran, B.; Tam, A. Geographic object-based mosaicing (OBM) of high-resolution thermal airborne imagery (TABI-1800) to improve the interpretation of urban image objects. IEEE Geosci. Remote Sens. Lett. 2013, 10, 918–922. [Google Scholar] [CrossRef]
- Rahman, M.M.; Hay, G.J.; Couloigner, I.; Hemachandran, B. Transforming image-objects into multiscale fields: A GEOBIA approach to mitigate urban microclimatic variability within H-Res thermal infrared airborne flight lines. Remote Sens. 2014, 6, 9435–9457. [Google Scholar] [CrossRef]
- Hill, J.; Sturm, B. Radiometric correction of multitemporal thematic mapper data for use in agricultural land-cover classification and vegetation monitoring. Int. J. Remote Sens. 1991, 12, 1471–1491. [Google Scholar] [CrossRef]
- Du, Y.; Teillet, P.M.; Cihlar, J. Radiometric normalization of multitemporal high-resolution satellite images with quality control for landcover change detection. Remote Sens. Environ. 2002, 82, 123–134. [Google Scholar] [CrossRef]
- Hall, F.G; Sterbel, D.E.; Nickeson, J.E.; Goetz, S.J. Radiometric rectification: Toward a common radiometric response among multidate, multisensory images. Remote Sens. Environ. 1991, 35, 11–27. [Google Scholar] [CrossRef]
- Chen, X.; Vierling, L.; Deering, D. A simple and effective radiometric correction method to improve landscape change detection across sensors and across time. Remote Sens. Environ. 2005, 98, 63–79. [Google Scholar] [CrossRef]
- Canty, M.J.; Nielsen, A.A.; Schmidt, M. Automatic radiometric normalization of multitemporal satellite imagery. Remote Sens. Environ. 2004, 91, 441–451. [Google Scholar] [CrossRef]
- Fernandes, R.; Leblance, S.G. Parametric (modified least squares) and non-parametric (Theil-Sen) linear regressions for predicting biophysical parameters in the presence of measurement errors. Remote Sens. Environ. 2005, 95, 303–316. [Google Scholar] [CrossRef]
- Xing, Y.; Jiang, Q.G.; Qiao, Z.P.; Li, W.Q. Study of relative radiometric normalization based on multitemporal ASTER images. Adv. Mater. Res. 2010, 108, 190–194. [Google Scholar] [CrossRef]
- Warner, T.A.; Chen, X. Normalization of Landsat thermal imagery for the effects of solar heating and topography. Int. J. Remote Sens. 2001, 22, 773–788. [Google Scholar] [CrossRef]
- Scheidt, S.; Ramsey, M.; Lancaster, N. Radiometric normalization and image mosaic generation of ASTER thermal infrared data: An application to extensive sand sheets and dune fields. Remote Sens. Environ. 2003, 112, 920–933. [Google Scholar] [CrossRef]
- Rahman, M.M; Hay, G.J.; Couloigner, I.; Hemachandran, B.; Bailin, J.A. A comparison of four radiometric normalization techniques for mosaicing H-res multi-temporal thermal infrared flight lines of a complex urban scene. ISPRSJ. Photogramm. Remote Sens. 2014. accepted. [Google Scholar]
- Theil, H.A. Rank-Invariant Method of Linear and Polynomial Regression Analysis. Available online: http://link.springer.com/chapter/10.1007/978-94-011-2546-8_20 (accessed on 10 September 2014).
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Peng, H.; Wang, S.; Wang, X. Consistency and asymptotic distribution of the Theil-Sen estimator. J. Stat. Plan. Infer. 2008, 138, 1836–1850. [Google Scholar] [CrossRef]
- Kahle, A.B.; Gillespie, A.R.; Goetz, A.F. Thermal inertia imaging: A new geologic mapping tool. Geophys. Res. Lett. 1976, 3, 26–28. [Google Scholar] [CrossRef]
- Jensen, J.R. Remote Sensing of the Environment: An Earth Resource Perspective, 2nd ed; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2007. [Google Scholar]
- Oke, T.R. Canyon geometry and the nocturnal urban heat island: Comparison of scale model and field observations. J. Climatol. 1981, 1, 237–254. [Google Scholar] [CrossRef]
- Chudnovsky, A.; Ben-Dor, E.; Saaroni, H. Diurnal thermal behavior of selected urban objects using remote sensing measurements. Energ. Build. 2004, 36, 1063–1074. [Google Scholar] [CrossRef]
- Richards, J.A. Remote Sensing Digital Image Analysis; Springer: NewYork, NY, USA, 1999. [Google Scholar]
- Schott, J.R.; Salvaggio, C.; Vochok, W.J. Radiometric scene normalization using pseudo-invariant features. Remote Sens. Environ. 1988, 26, 1–16. [Google Scholar] [CrossRef]
- Salvaggio, C. Radiometric scene normalization utilizing statistically invariant features. In Proceedings of Workshop Atmospheric Correction of Landsat Imagery, Torrance, CA, USA, 29 June–1 July 1993.
- Bao, N.; Lechner, A.M.; Fletcher, A.; Mellor, A.; Mulligan, D.; Bai, Z. Comparison of relative radiometric normalization methods using pseudo-invariant features for change detection studies in rural and urban landscapes. J. Appl. Remote Sens. 2012, 6. [Google Scholar] [CrossRef]
- Elvidge, C.D.; Yuan, D.; Ridgeway, D.W.; Lunetta, R.S. Relative radiometric normalization of Landsat Multispectral Scanner (MSS) data using an automatic scattergram-controlled regression. Photogmm. Eng. Remote Sens. 1995, 61, 1255–1260. [Google Scholar]
- de Carvalho, O.A.; Júnior; Guimarães, R.F.; Silva, N.C.; Gillespie, A.R.; Gomes, R.A.T.; Silva, C.R.; de Carvalho, A.P.F. Radiometric normalization of temporal images combining automatic detection of pseudo-invariant features from the distance and similarity spectral measures, density scatterplot analysis, and robust regression. Remote Sens. 2013, 5, 2763–2794. [Google Scholar] [CrossRef]
- Hu, C.M.; Ping, T. Automatic algorithm for relative radiometric normalization of data obtained from Landsat TM and HJ-1A/B charge-coupled device sensors. J. Appl. Remote Sens. 2012, 6. [Google Scholar] [CrossRef]
- Friedl, M.A.; Davis, F.W. Sources of variation in radiometric surface temperature over a tallgrass prairie. Remote Sens. Environ. 1994, 48, 1–17. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mustafizur Rahman, M.; Hay, G.J.; Couloigner, I.; Hemachandran, B.; Bailin, J. An Assessment of Polynomial Regression Techniques for the Relative Radiometric Normalization (RRN) of High-Resolution Multi-Temporal Airborne Thermal Infrared (TIR) Imagery. Remote Sens. 2014, 6, 11810-11828. https://doi.org/10.3390/rs61211810
Mustafizur Rahman M, Hay GJ, Couloigner I, Hemachandran B, Bailin J. An Assessment of Polynomial Regression Techniques for the Relative Radiometric Normalization (RRN) of High-Resolution Multi-Temporal Airborne Thermal Infrared (TIR) Imagery. Remote Sensing. 2014; 6(12):11810-11828. https://doi.org/10.3390/rs61211810
Chicago/Turabian StyleMustafizur Rahman, Mir, Geoffrey J. Hay, Isabelle Couloigner, Bharanidharan Hemachandran, and Jeremy Bailin. 2014. "An Assessment of Polynomial Regression Techniques for the Relative Radiometric Normalization (RRN) of High-Resolution Multi-Temporal Airborne Thermal Infrared (TIR) Imagery" Remote Sensing 6, no. 12: 11810-11828. https://doi.org/10.3390/rs61211810
APA StyleMustafizur Rahman, M., Hay, G. J., Couloigner, I., Hemachandran, B., & Bailin, J. (2014). An Assessment of Polynomial Regression Techniques for the Relative Radiometric Normalization (RRN) of High-Resolution Multi-Temporal Airborne Thermal Infrared (TIR) Imagery. Remote Sensing, 6(12), 11810-11828. https://doi.org/10.3390/rs61211810