1. Introduction
Traditional line scanners used on space-borne platforms (e.g., MODIS and ETM+) contain a handful of detectors that collect data of a scene in the cross-track direction as the satellite flies over in the along-track direction [
3,
4]. Minimal effort is required to perform a relative calibration of their data as the simplicity of their focal plane design minimizes non-uniformities in the raw data [
5]. However, these sensors require moving parts, which have the potential to fail on-orbit, and exhibit relatively low signal-to-noise ratios (SNR) compared to modern pushbroom systems. The focal plane design of pushbroom-style architectures is advantageous as it eliminates the need for cross-track motion when collecting data. As a result, the need for moving parts is reduced and SNR is enhanced due to longer dwell times [
6]. To take full advantage of these potential benefits, much more effort is required to perform a relative calibration as pushbroom sensors typically contain tens-of-thousands (if not hundreds-of-thousands) of detectors arranged on several focal plane modules (FPMs) that are staggered across the focal plane [
7].
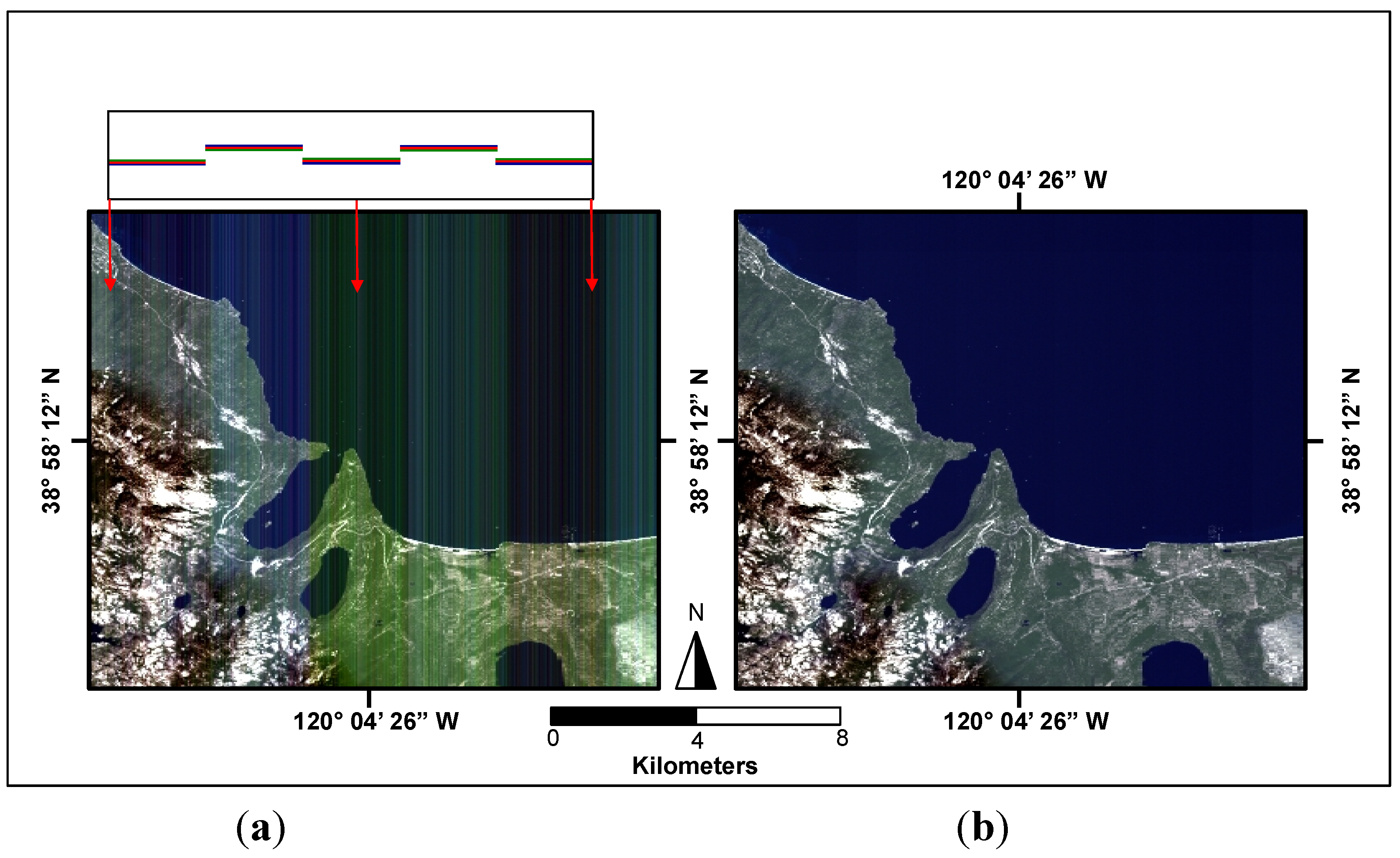
Figure 1 shows a generic focal plane design for a pushbroom sensor and the raw data (simulated in this case) that is collected from this type of system. Each detector on the focal plane will have a unique radiometric response due to the doping process used to fabricate the detector arrays, variability in electronic gains and biases, and lens fall-off. As a result, banding and streaking will be apparent in the raw data and must be corrected, so as to take full advantage of the enhanced SNR exhibited by these modern imaging systems.
Figure 1a shows the raw simulated image data prior to calibration while
Figure 1b shows the processed data after flat-fielding.
Figure 1.
Focal plane design of a typical pushbroom sensor used to simulate data of Lake Tahoe, California with all non-uniformity effects applied (i.e., per detector gains, biases, spectral response functions, nonlinearities, noise, etc.) (a) Shows the raw data and (b) shows data after flat-fielding.
Figure 1.
Focal plane design of a typical pushbroom sensor used to simulate data of Lake Tahoe, California with all non-uniformity effects applied (i.e., per detector gains, biases, spectral response functions, nonlinearities, noise, etc.) (a) Shows the raw data and (b) shows data after flat-fielding.
The nine-band Operational Land Imager (OLI) and the dual band Thermal Infrared Sensor (TIRS) are the latest sensors in the Landsat series and, in a departure from traditional sensor design, use pushbroom-style architectures. They were launched onboard Landsat 8 (formerly LDCM) on 11 February 2013. OLI is equipped with dual full-aperture solar diffusers and multi-bulbed tungsten lamp assemblies that are used for on-orbit detector-to-detector radiometric calibration. The primary solar diffuser is deployed every eight days to determine flat-fielding coefficients and the pristine diffuser every six months to monitor the primary diffuser’s degradation. Tungsten lamp assemblies will provide an additional source of calibration coefficients; a working lamp set will be used daily, a reference lamp set monthly, and a pristine lamp set every six months [
8]. TIRS is equipped with a scene select mechanism that is deployed regularly to view deep space and its onboard blackbody to enable an on-orbit detector-to-detector radiometric calibration [
9].
To perform a relative calibration as illustrated in
Figure 1, a governing calibration equation relating radiance at the focal plane to digital counts for each detector must be defined. For each detector within an array,
where
DNi is the raw detector response in digital counts for detector
i,
fi(L) is the radiometric response function of the detector
i to the incident radiance,
Gi is the gain for detector
i,
Bi is the bias measured in the absence of light for detector
i,
n is the total number of detectors in the array, and
Q[] indicates the quantization process. Although detectors may have a nonlinear radiometric response, these effects are not directly addressed in this work. Additionally, the bit-depth of most modern sensors is at least 12-bit so Equation (1) can be simplified to,
To perform a relative calibration on-orbit, per-detector biases from Equation (2) can be obtained by imaging deep space or by closing the shutter. Then by sampling a uniform bright source (Lf), per-detector gains can be derived for each detector,
The gains from Equation (3) can be divided by the average gain across the entire array to derive the relative gains that get applied during the flat-field correction.
A flat-field correction can then be obtained in image data by applying Equation (5) for each detector i.
Note that this procedure must be applied for all arrays on the focal plane. For satellite systems equipped with a solar diffuser, a uniform bright source (
Lf) can be achieved by introducing the solar-diffuser into the field-of-view (FOV) of the sensor to flood the focal plane with diffuse, reflected sunlight. However, diffuser panels can degrade over time causing a non-uniform illumination of the focal plane. This is evident with Terra’s MODIS (The Moderate Resolution Imaging Spectroradiometer) sensor where an anomaly forcing its solar diffuser door to remain open has led to an accelerated degradation of its solar diffuser [
10]. As a result, the proper performance of the Terra MODIS solar diffuser stability monitor is critical to a well-calibrated system. The OLI is equipped with a pristine diffuser that may be used to monitor the primary diffuser’s degradation but the need for a vicarious method to flat-field the data is desirable for systems not equipped with on-board calibrators.
The side slither calibration technique is an on-orbit maneuver that has been used to flat-field image data for the QuickBird and RapidEye pushbroom systems [
1,
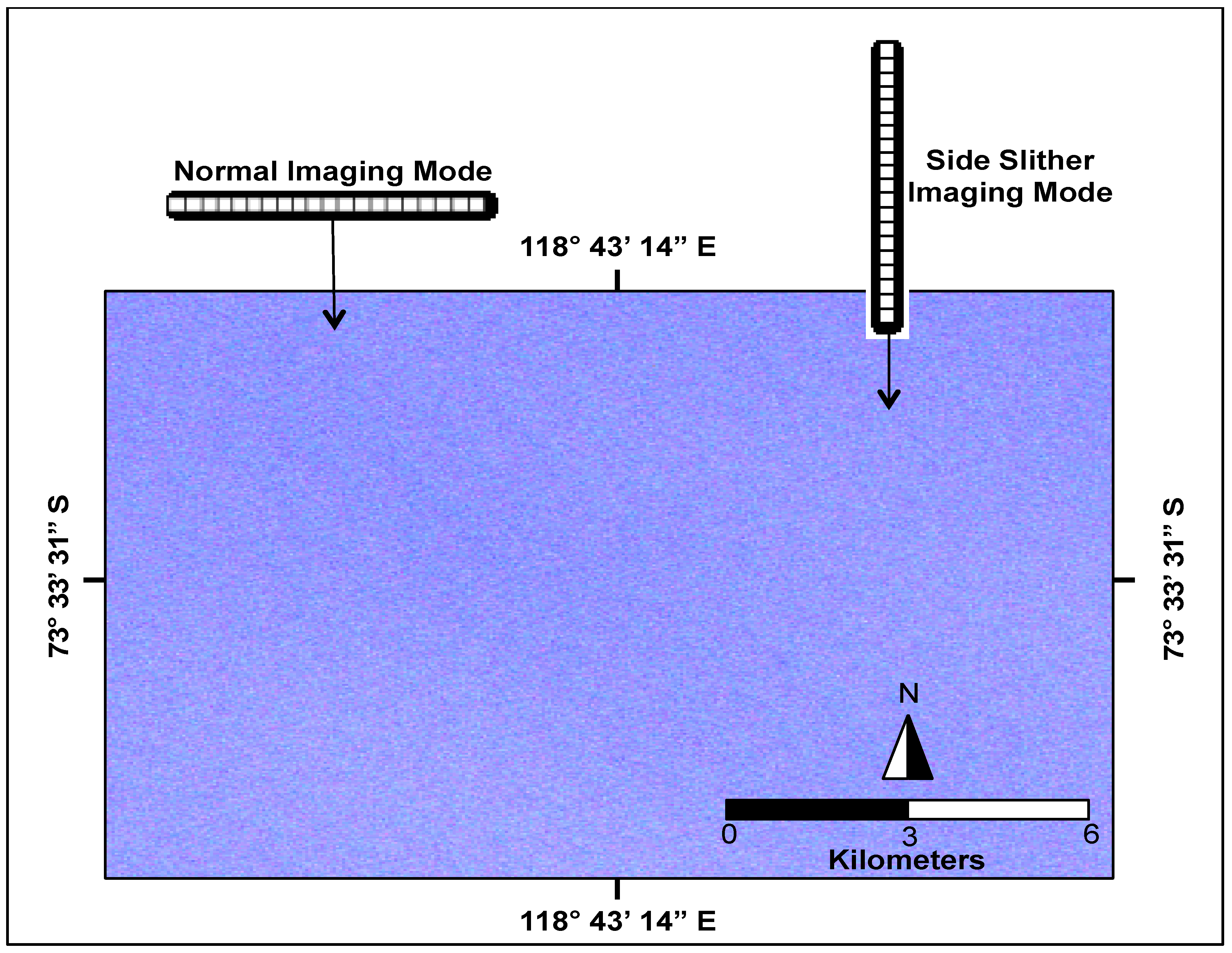
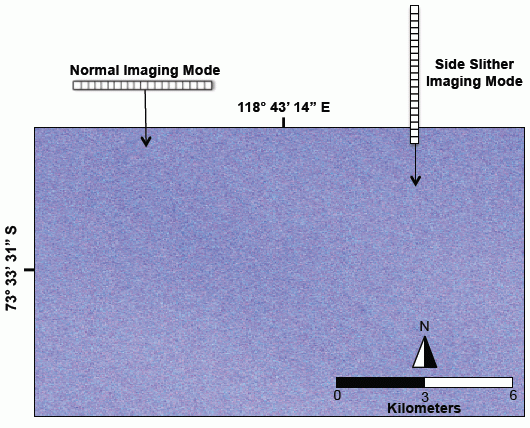
2]. The Earth’s surface exhibits excessive variability to enable a relative calibration in normal imaging mode with wide FOV pushbroom instruments. However, a 90-degree yaw maneuver can be applied to the spacecraft (thus the focal plane) forcing each detector to image a similar spot on the ground. This concept is illustrated in
Figure 2 which shows an ideal linear array imaging over Dome Concordia (Dome C), Antarctica in both normal imaging mode (left) and in side slither imaging mode (right).
When the satellite is yawed 90 degrees, each detector on the idealized focal plane array will scan over the same area on the ground. This is a favorable scenario for relative calibration, as each detector should receive the same illumination. However, pushbroom-style imaging systems with wide fields-of-view (e.g., Landsat sensors) are not perfect linear arrays but more closely resemble the array illustrated in
Figure 1.
Figure 2.
Illustration of a perfect linear array imaging over Dome Concordia, Antarctica in both normal imaging mode and side slither mode.
Figure 2.
Illustration of a perfect linear array imaging over Dome Concordia, Antarctica in both normal imaging mode and side slither mode.
This article presents the results of simulated studies designed to investigate the potential to use the side slither maneuver to perform a relative calibration for pushbroom-style imaging systems such as Landsat 8 (i.e., systems with a wide field-of-view). While this technique has been previously applied to other systems, the sources of potential errors in the flat-field process have not been convincingly identified. This work uses simulation and modeling to identify sources that will introduce errors into the calibration process, to assist in developing metrics to evaluate the efficacy of the side slither maneuver, and to provide recommendations for future side slither missions.
Section 2 introduces techniques that enable an enhanced side slither calibration to be performed. Illustrations of how side slither data are obtained, how it can be interpreted, and how it is processed to calculate relative gains are presented. Preprocessing techniques intended to minimize scene-induced error are then presented and a simulated case study designed to identify uniform regions on Earth suitable for the side slither maneuver is introduced. In
Section 3, potential issues associated with performing a relative calibration using side slither are identified and on-orbit modifications to the technique suggested. Additionally, a qualitative characterization of how to identify uniform regions that are suitable for the maneuver is provided. The site identification study is revisited and re-designed for sensors with a wide field-of-view. Finally, a summary of the side slither recommendations made for Landsat 8 during its commissioning phase is presented.
2. The Side Slither Maneuver
Before describing the processing chain that can be applied to effectively flat-field an image using the side slither maneuver, a basic knowledge of the data is required. To develop an understanding of the difference between data collected in normal imaging mode and side slither mode, simulation and modeling can be utilized. The DIRSIG (Digital Imaging and Remote Sensing Image Generation) model was used to support this work. DIRSIG is a well-developed physics-based model created at the Rochester Institute of Technology to simulate the spectral radiance images produced by sensors that observe the reflective and emitted energy from the Earth’s surface [
11]. DIRSIG supports scenes developed from complex geometries or can use radiance data directly as input to describe the synthetic landscape. Recent enhancements to DIRSIG support the development of a sophisticated data-driven sensor model [
12]. If the user is able to make lab measurements, DIRSIG accepts line-of-sight measurements to define the focal plane layout, platform jitter, and can handle inputs of gains, biases, relative spectral response functions, noise,
etc. on a per-detector basis [
13,
14,
15].
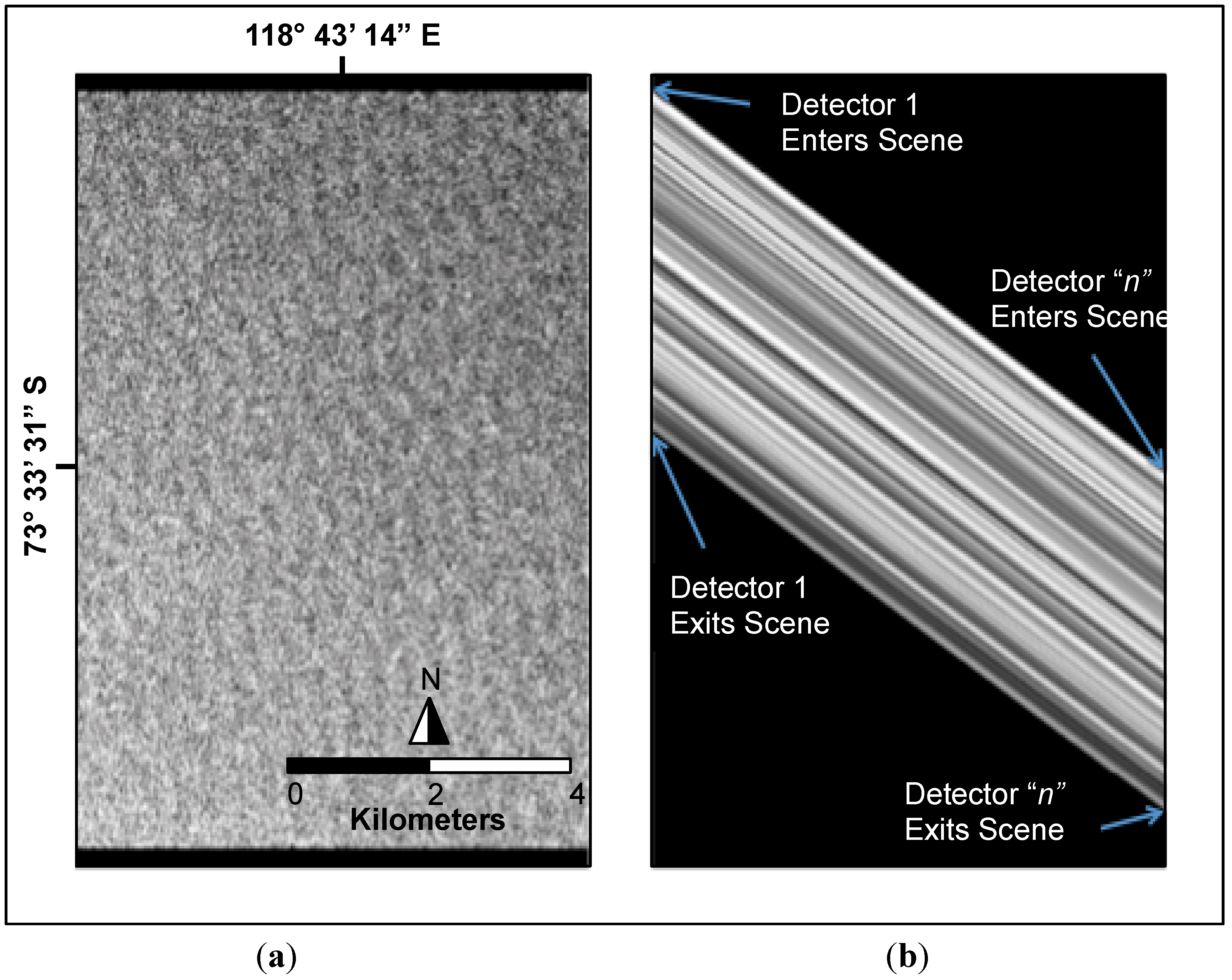
To generate the simulated data shown in
Figure 3, Landsat 7 radiance data of the Dome C (from
Figure 2) was provided directly as input to the DIRSIG model and imaged using a simple linear array in both normal and side slither imaging modes.
Figure 3a shows the data that results from imaging in normal mode while
Figure 3b shows the corresponding side slither data (Note: for simplicity the Earth beyond the Dome C “scene” was treated as a black background in these initial DIRSIG simulations).
To develop our knowledge of how the side slither data shown in
Figure 3b is obtained, and how it can potentially be used for calibration, we refer again to
Figure 2. By treating the Earth outside the scene of interest as a black background, each detector of the linear array will image black prior to entering the uniform region when imaging in side slither mode. This is shown in
Figure 3b where the first few rows of the image are black. When the first detector enters the scene, the array images all black except for the first detector (first column in
Figure 3b). As subsequent detectors image over the uniform region, more image data is introduced into each column from left to right. Approximately halfway down
Figure 3b, the first detector leaves the uniform region as indicated by the introduction of black data in the first column. As subsequent detectors leave the uniform region, black data is introduced to the corresponding columns until finally all detectors image black. The last few rows of
Figure 3b indicate that all detectors are imaging outside of the uniform region.
Figure 3.
DIRSIG simulated grayscale images collected over Dome Concordia, Antarctica in both (a) normal mode and (b) side slither mode.
Figure 3.
DIRSIG simulated grayscale images collected over Dome Concordia, Antarctica in both (a) normal mode and (b) side slither mode.
2.1. Basic Processing
The techniques described in [
1] and [
2] describe how side slither data should be shifted prior to processing the relative gains. In this paper, a
horizontal correction is defined as a shifting of the columns in the side slither data so the linear features in the data are oriented horizontally. A horizontal correction is performed prior to calculating relative gains to simplify the data processing.
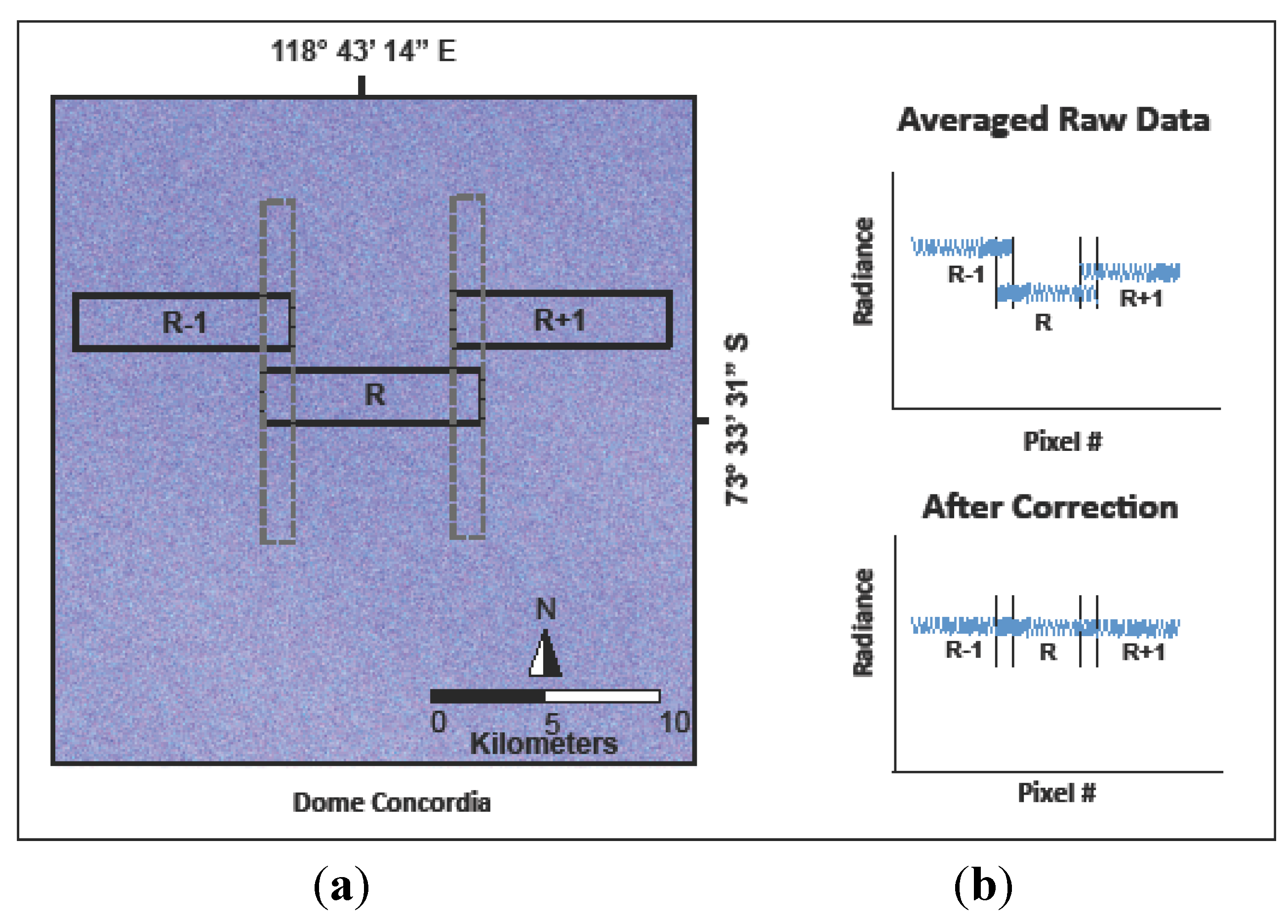
Figure 4 illustrates the horizontal correction process where each subsequent column
i of the raw side slither data (left) is shifted up.
So (according to Equation (6)) the first column of the data is left alone, the second column is shifted up one row, the third column is shifted up two rows, and so on.
Figure 4(center) shows the result of this nominal horizontal correction process. Notice that the linear features in the data are not perfectly horizontal. This is likely due to the focal plane read-out clock cycle being out of synch when the array is oriented in the direction of motion, a perfect 90-degree side slither is not achieved, or a combination of the two.
Figure 4(right) shows the side slither data after an enhanced horizontal correction has been applied, where the slopes of the lines in
Figure 4(center) were determined and used to further shift the data. Note that in the enhanced correction, only integer shifts of the data are applied to avoid the resampling of data.
Figure 4.
Illustration of the horizontal correction process where raw Thermal Infrared Sensor (TIRS) side slither data (left) was corrected using a nominal correction (center) and an enhanced correction (right).
Figure 4.
Illustration of the horizontal correction process where raw Thermal Infrared Sensor (TIRS) side slither data (left) was corrected using a nominal correction (center) and an enhanced correction (right).
The enhanced correction is a manual process, as conducted in this research, but potentially significant to an accurate relative calibration.
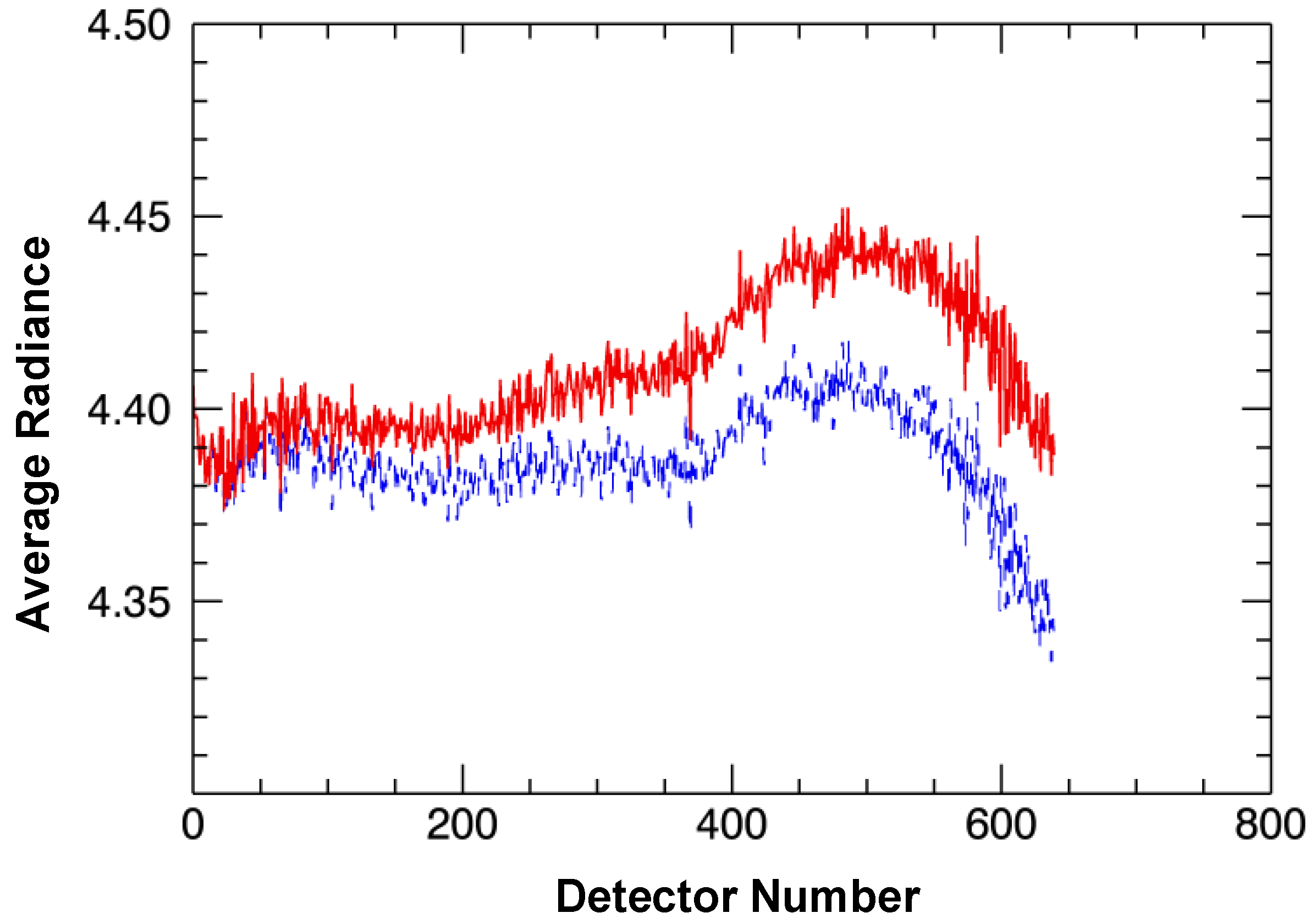
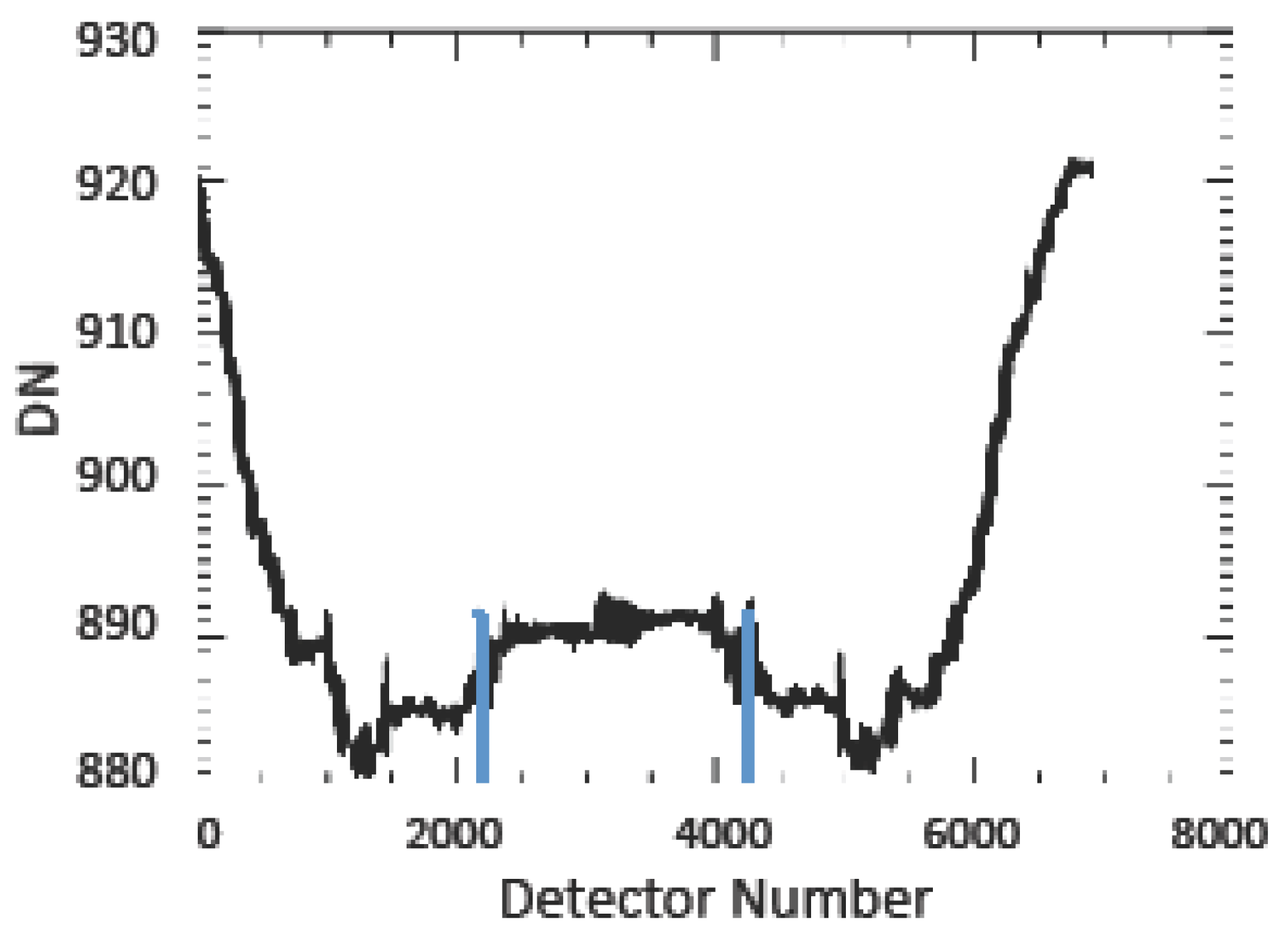
Figure 5 shows the column averages of the side slither data from
Figure 4. The red (solid) curve in
Figure 5 corresponds to the column average for each detector calculated from the side slither data when a basic horizontal correction is applied,
i.e.,
Figure 4 (center). The blue (dashed) curve corresponds to the column averages when the enhanced horizontal correction is applied,
Figure 4(right). The two curves differ by as much as 1.5 percent in this example illustrating the importance of an accurate horizontal correction. If the relative gains are calculated using the data from
Figure 4(center) then in-scene variability will be introduced to the relative gains simply due to poor data manipulation causing a low frequency gradient to appear in the final corrected image data. This will be further illustrated in
Section 3.
Once a suitable horizontal correction is achieved (e.g., the blue-dashed curve of
Figure 5) the column averages can be normalized by their mean to determine the relative gain coefficients for each detector, recall Equation (4). Using Equation (5), the gain coefficients can then be applied to the bias-subtracted data (illustrated in
Figure 1) to perform the flat-field.
Figure 5.
Column averages obtained from the horizontally corrected data of
Figure 4. The red solid curve shows the column averages obtained from the nominal horizontal correction (
Figure 4(center)) while the blue dashed curve shows the column averages obtained from the enhanced correction (
Figure 4(right)).
Figure 5.
Column averages obtained from the horizontally corrected data of
Figure 4. The red solid curve shows the column averages obtained from the nominal horizontal correction (
Figure 4(center)) while the blue dashed curve shows the column averages obtained from the enhanced correction (
Figure 4(right)).
2.2. Enhanced Automated Processing: Finding Regions of Lowest Variability in Data
Previous work suggests a visual inspection to determine which region of the side slither data to use when deriving relative gains [
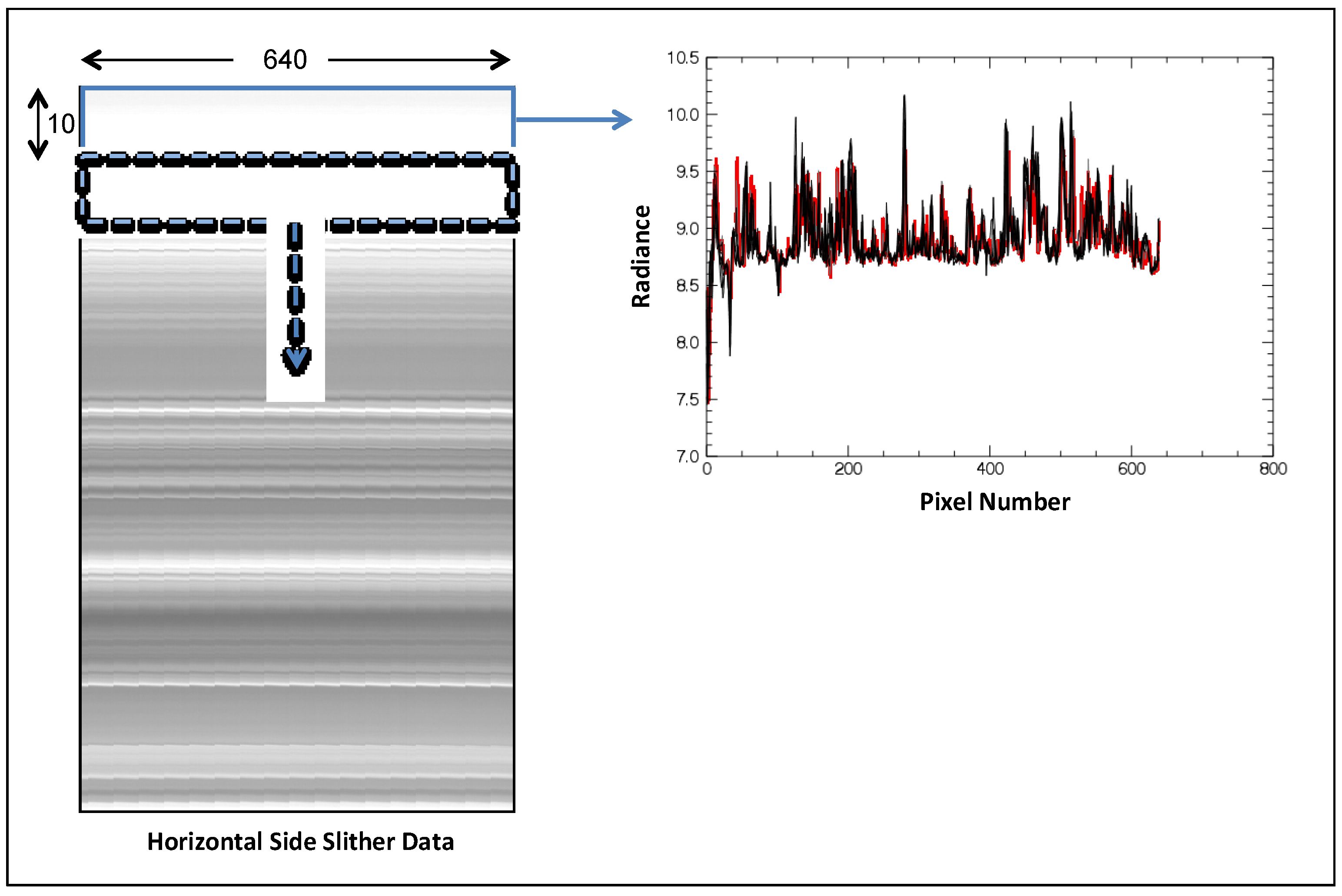
2]. This section describes a simple methodology for identifying regions of lowest variability in the side slither data. By automatically identifying regions in the data that have minimal variability introduced by the scene, the derived relative gains can be calculated from data that reflect the instrument’s behavior, not in-scene (or human-induced) variability. This concept is illustrated with an example where the regions of minimal variability are identified in an actual TIRS side slither dataset.
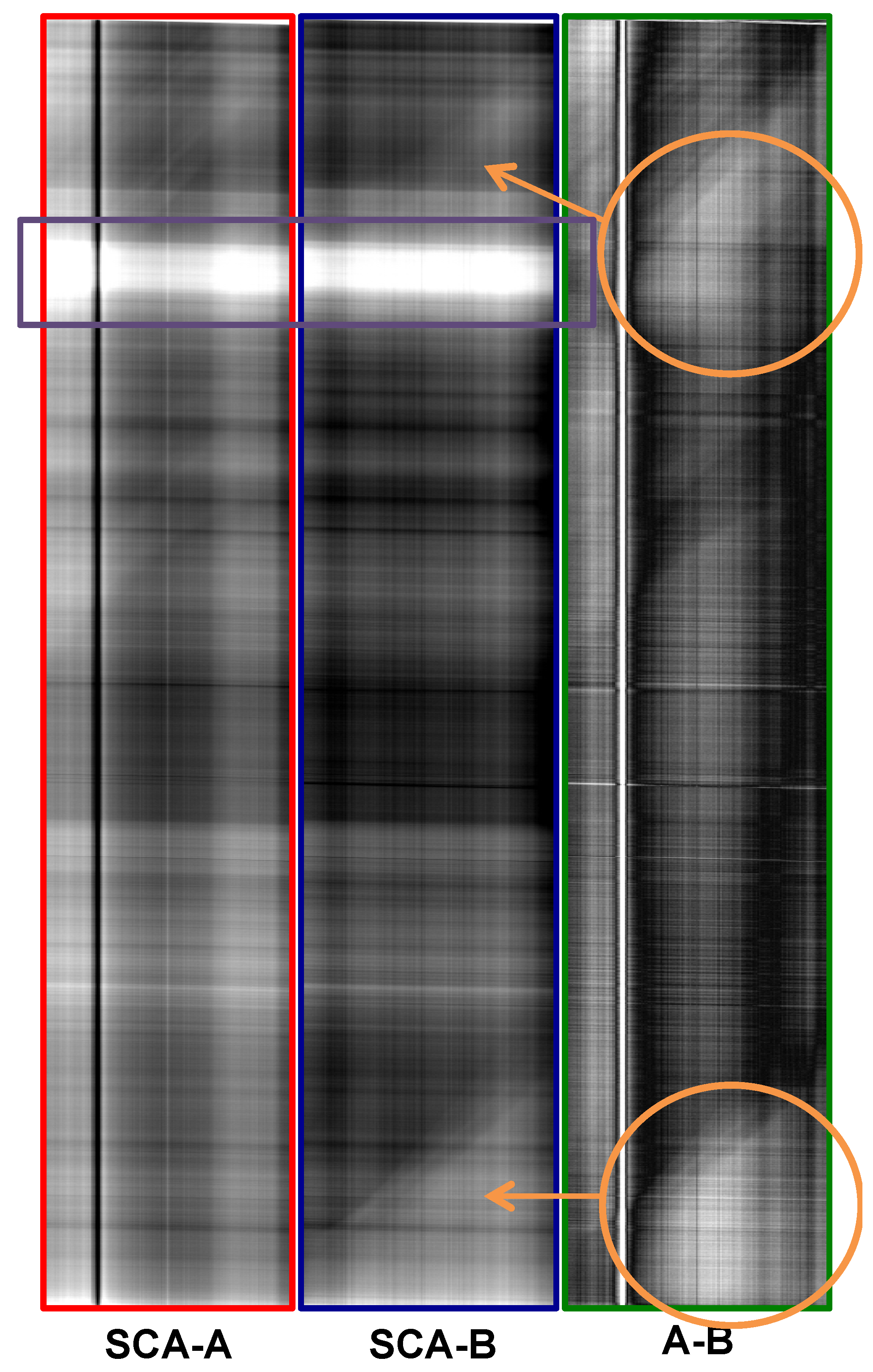
Figure 6 shows side slither data collected with SCA-A (sensor-chip assembly “A”) on the TIRS instrument after an enhanced horizontal correction has been applied. To determine regions of lowest scene-induced variability in this TIRS side slither data, the horizontal data of
Figure 6 can be segmented into smaller regions and the variability calculated within each region. The TIRS sensor has 640 cross-track detectors in each array so the data was arbitrarily segmented into regions of size 10 × 640 for this study. The typical side slither collect contains several thousand frames (
i.e., rows) of data so hundreds (perhaps thousands) of 10 × 640 regions may be characterized in this process.
To characterize the variability within each region, the column mean vector
x is first calculated (red curve in
Figure 6). Next, the deviations of each row vector from the column mean (black curves in
Figure 6) are calculated and summed to describe the variability associated with the region. Finally, the region(s) with the minimum variability (or close to the minimum variability) can be used to calculate the relative gains, as these regions represent portions of the scene that introduce minimal in-scene variability. Mathematically, this concept is written.
where
i is the row number within a region,
xi is the
ith row vector in a region,
x is the mean column vector within a region,
j is the region number, and
n is the total number of regions being characterized. Qualitatively, regions where the radiance curves for each row vary the least from their corresponding column mean will be identified as low variability regions. Since several hundreds of regions will be characterized, the user can be selective as to how many regions to use in the final processing of relative gains. Once the regions are identified, the relative gains can be calculated in these regions according to Equation (5).
Figure 6.
Illustration of automated processing method to find regions of lowest variability in the side slither data.
Figure 6.
Illustration of automated processing method to find regions of lowest variability in the side slither data.
2.3. Site Identification
To determine worldwide sites that are favorable to support a side slither maneuver for Landsat 8, Gerace
et al. 2012 [
16] conducted a modeling effort focused on identifying uniform regions whose brightness values span the dynamic range of the OLI bands yet introduce minimal variability to the calculated relative gains. Sites of this nature are favorable for side slither as they can help identify potential detector nonlinearities while reducing pixel-to-pixel variability.
Basnet 2010 [
17] conducted a statistical analysis with Landsat 5 data to identify potential worldwide pseudo-invariant calibration sites (PICS). Sites labeled as pseudo-invariant exhibited temporally and spatially stable brightness values in the data indicating that they were typically cloud free and that their landscape did not vary significantly. Sites of this nature are favorable for side slither missions as the potential risk of adverse weather is reduced in these regions. Gerace
et al. 2012 [
16] used these scenes for the side slither analysis by acquiring Landsat 5 images from Earth Explorer [
18] and using their corresponding radiance data as input to the DIRSIG model.
For the initial modeling effort described in [
16], a sensor model that did not include non-uniformity effects was developed to simulate the two center arrays of Landsat 8’s OLI sensor. Non-uniformity effects were excluded from this preliminary sensor model to determine the variability introduced by just the test site to properly assess its potential utility for side slither calibration. The sensor model was then used to image the Landsat radiance data in side slither mode and the variability in the corresponding relative gain coefficients was observed.
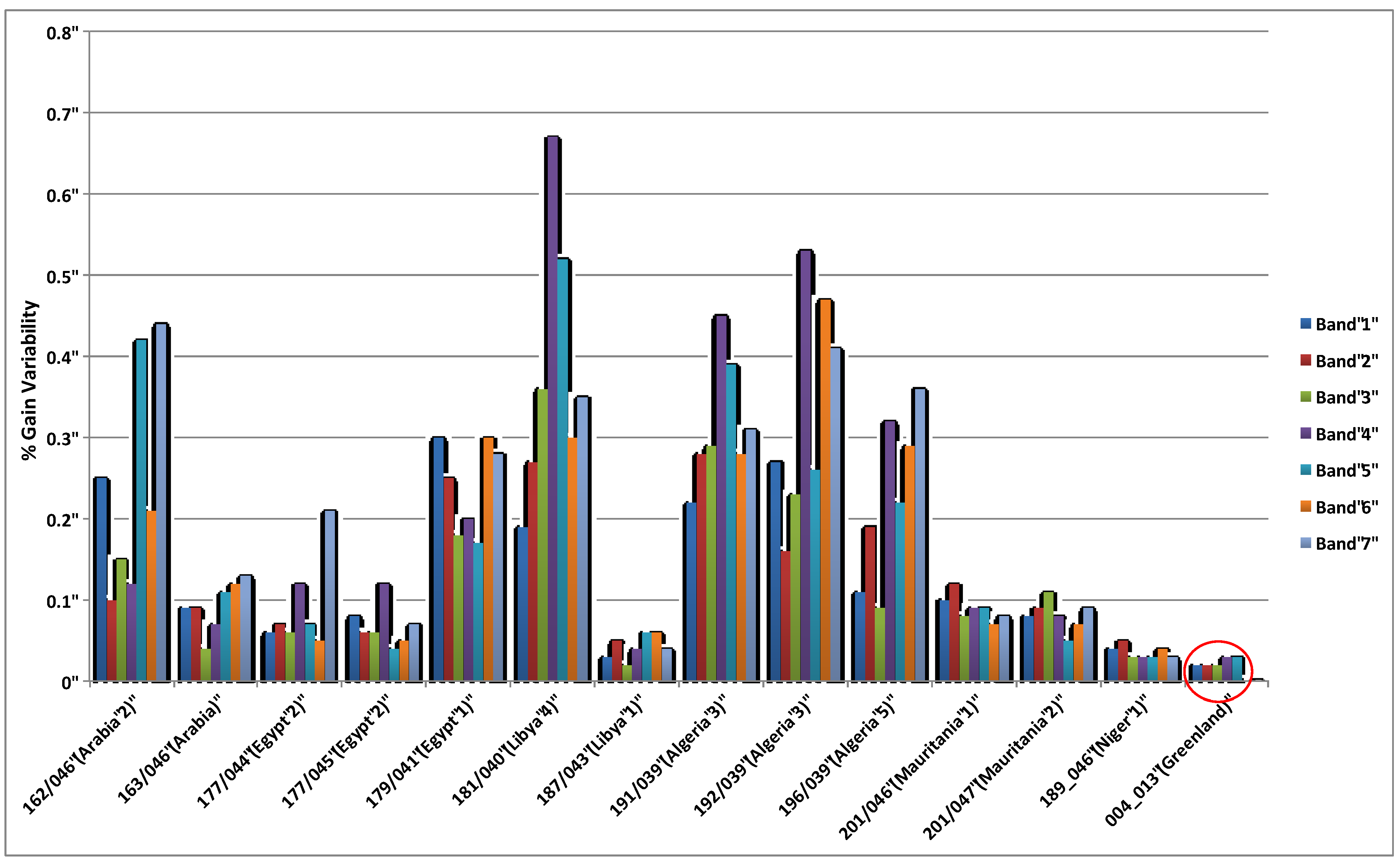
Figure 7 shows the within-array variability introduced to the process by each of the sites with the maximum acceptable target error (0.05%) highlighted as a dashed (red) line. Note that this error target was chosen since it is an order of magnitude smaller than OLI’s pixel-to-pixel uniformity requirement (0.5%).
Figure 7.
Within-array gain variability introduced by the sites listed in Table 1 for the first seven bands of the Operational Land Imager (OLI). The red dashed indicates the maximum acceptable target error of 0.0005 or 0.05%.
Figure 7.
Within-array gain variability introduced by the sites listed in Table 1 for the first seven bands of the Operational Land Imager (OLI). The red dashed indicates the maximum acceptable target error of 0.0005 or 0.05%.
The variability described in
Figure 7 represents the standard deviation divided by the mean of the relative gains (calculated using Equation (5))
within an array. Encouragingly, many of the sites studied in [
16] introduce gain variability that is just at, or below, the threshold of 0.05% when the 2-array sensor model is used.
4. Conclusions, Future Work, and Recommendations
While previous work [
1,
2] demonstrates the potential to use side slither to flat-field image data for sensors with a narrow field-of-view, this work uses simulation and modeling to investigate potential issues with the maneuver when applied to sensors (such as those onboard Landsat 8) with a wide field-of-view. The modeling efforts performed in this work led to several significant conclusions.
Section 2.1 shows a proper horizontal correction should be applied to avoid introducing low-frequency artifacts into the corrected image data. In
Section 2.2, an automated processing technique designed to find region(s) of lowest variability in the side slither data was introduced. This simple method was devised to ensure that the most uniform regions in the data were being used to derive relative gains.
Section 2.3 and
Section 3.3 described a methodology that was conceived to identify and characterize sites around the globe that may be suitable for the side slither maneuver.
In
Section 3, potential issues that may arise when imaging in side slither mode were presented. The most notable and most likely to negatively impact the data is the concept of “smearing”, which occurs when arrays are not aligned exactly 90 degrees to significant features in the landscape. There are two methods to avoid this unwanted effect; avoid any features by choosing the most uniform regions on Earth (see
Figure 16) or performing multiple side slithers over a chosen region to align all the arrays properly. Failure to employ one of these methods will likely lead to banding in the corrected image data, recall
Figure 11(bottom).
Future modeling efforts to characterize the utility of the calibration sites presented here for side slither calibration will focus on the incorporation of BRDF effects. All studies performed in this work used existing Landsat data or simulated data with Lambertian materials (e.g., the Libya 4 scene in
Figure 10). Although the effects due to the terrain (and in some cases the relevant atmospheric paths) were present in the simulations performed in this work, the impact of material BRDFs on side slither calibration was not conducted. Recent enhancements to the DIRSIG model, however, have made the incorporation of BRDF effects possible for the large-scale landscapes required for a comprehensive analysis of the side slither maneuver.
Much of the work presented here has been recommended to, and employed by, the Landsat Calibration and Validation team. Several side slither maneuvers were conducted during the commissioning phase of Landsat 8, including successful maneuvers over Niger and Greenland. The side slither maneuver continues to be part of normal operations where once a quarter, the maneuver is performed over the most suitable available sites from
Figure 16.