Forest Stand Size-Species Models Using Spatial Analyses of Remotely Sensed Data
Abstract
: Regression models to predict stand size classes (sawtimber and saplings) and categories of species (hardwood and softwood) from fractal dimensions (FD) and Moran’s I derived from Landsat Thematic Mapper (TM) data were developed. Three study areas (Oakmulgee National Forest, Bankhead National Forest, and Talladega National Forest) were randomly selected and used to develop the prediction models, while one study area, Chattahoochee National Forest, was saved for validation. This study has shown that these spatial analytical indices (FD and Moran’s I) can distinguish between different forest trunk size classes and different categories of species (hardwood and softwood) using Landsat TM data. The results of this study also revealed that there is a linear relationship between each one of the spatial indices and the percentages of sawtimber–saplings size classes and hardwood–softwood categories of species. Given the high number of factors causing errors in the remotely sensed data as well as the Forest Inventory Analysis (FIA) data sets and compared to other studies in the research literature, the sawtimber–saplings models and hardwood–softwood models were reasonable in terms of significance and the levels of explained variance for both spatial indices FD and Moran’s I. The mean absolute percentage errors associated with the stand size classes prediction models and categories of species prediction models that take topographical elevation into consideration ranged from 4.4% to 19.8% and from 12.1% to 18.9%, respectively, while the root mean square errors ranged from 10% to 14% and from 11% to 13%, respectively.1. Introduction
There are many situations where knowledge of forest species diversity and distribution of stand characteristics are needed. Estimation of biomass, carbon sequestration, primary productivity, nutrient export, and quantities for clearing prior to construction are only a few examples where characteristics of forested areas are essential. Forests can encompass very large areas so that ground-based evaluations can be very expensive and time consuming. For this reason the use of remotely sensed data has become increasingly common.
Several sources of remotely sensed data are currently available that might be useful for forest characterization purposes. The data can be from satellite or aircraft platforms, and can be from either passive or active instruments. Recently, the focus has been on the use of laser altimetry, e.g., Light Detection and Ranging (LiDaR) data to gain three dimensional images of forest structure [1–5]. Although LiDaR has been found to be very effective in describing forest attributes such as canopy height and structure [4,5], as well as species identification [6], it still possesses significant weaknesses—it is not universally available, it is expensive to acquire, particularly over large footprints, and it cannot determine some important attributes directly [2].
Consequently, a large amount of research has been performed using airborne- or satellite-mounted radar to estimate forest parameters (e.g., Harrell et al. [7]; Ranson and Sun [8]; Fransson and Israelsson [9]; Perko et al. [10]; Robinson et al. [11]). Research has shown the forest height data can be well detected using synthetic aperture radar (SAR) signals and that these data can then be used to improve models of forest structure [10] or to directly compute total above ground biomass [11]. SAR also possesses the advantage that long wavelength signals can penetrate clouds and are not dependent on daylight observations [12]. A number of SAR systems have been operational in the past, including the European Remote Sensing (ERS) 1-2, the Japanese Earth Resources Satellite (JERS) and Envisat. Currently, the main operational instruments available are within the Canadian Radar Satellite (RADARSAT) program.
Concurrently, a significant amount of research has also been performed on forest biomass estimation using passive instruments, particularly radiometric data (e.g., Curran et al. [13]; Anderson et al. [14]; Hame et al. [15]; Martin et al. [16]; Nelson et al. [17]; Foody and Cutler [18]; Dong et al. [19]; Giree et al. [20]). Studies that employ passive radiometric data (e.g., Landsat Thematic Mapper (TM), NOAA Advanced Very High Resolution Radiometer (AVHRR), or the Moderate Resolution Imaging Spectroradiometer (MODIS)) usually focus on the estimation of indirect measurement of biomass or canopy coverage such as the Leaf Area Index (LAI) or Normalized Difference Vegetation Index (NDVI) [19,21–24]. On the other hand, Foody and Cutler [25,26] employed a variety of Neural Network analyses to classify species and determine biodiversity indices directly from Landsat TM data. Recent authors (e.g., Rocchini et al. [27,28]) have analyzed the relationship between variations in the spectral response between bands in radiometric data and species diversity. In a comparison of the effectiveness of different data sources to determine forest biodiversity indices, Hyyppa et al. [29] asserted that, despite the promise shown by radar applications, radiometric data still possess the greatest usefulness in this regard. Similar conclusions were later given by Boyd and Danson [30]. However, as a rule, the full capabilities of passive spectrometer data to characterize forest structure directly have not been fully exploited.
Radiometric data are much more easily accessible and cost effective than active radar data. Thus, it would be of great benefit if passive radiometer data could be employed to characterize forest structure such as stand density, trunk size, etc. directly. This paper seeks to formulate a general model of forest attributes based on passive radiometric data that would be applicable over a range of forest species and structural characteristics.
2. Methods and Materials
In a previous paper by Al-Hamdan et al. [31], the authors compared several passive radiometric data sets, including Landsat TM, IKONOS, and MODIS, and concluded that, based on the spectral and spatial resolution of the data, Landsat TM data were better suited for determination of forest attributes. Subsequently, Al-Hamdan et al. [32] showed that individual forest attributes such as stand density and breast diameter could be extracted from Landsat data for a single site. This paper presents a generalized model that is formulated and verified over a range of forest characteristics.
Landsat TM images were obtained covering a range of US National Forests, i.e., areas where species diversity and stand characteristics are well documented. Spatial analysis techniques (fractals and Moran’s I) were used to characterize these images in terms of image complexity and roughness associated with forests. One of the advantages of fractal and spatial autocorrelation techniques over other spatial indices used in landscape ecology such as contagion, dominance, and interspersion is that it can be applied directly to unclassified images [33]. The Landsat data were composed of leaf-on scenes since forest canopies reflect energy more efficiently than do bare tree trunks and stems. For a given tree species, the reflectance values recorded by sensors is a function of exposed projection area (canopy closure). Furthermore, many studies have shown that there is a strong correlation between the crown width and the diameter at breast height for different species in different regions [31,34–43].
2.1. Study Areas and Data Sets
In order to examine the issues listed above and to be consistent with Al-Hamdan et al. [31,32], Landsat TM images were obtained that covered four U.S. national forest areas wherein the forest stand characteristics (trunk size, species, age, etc.) are known with a good degree of precision and spatial detail. Topographic data were also obtained from the United States Geological Survey (USGS) geographic data sets in order to be used in the analysis. The Forest Inventory and Analysis (FIA) data were obtained from the U.S. Forest Service for Talladega National Forest (AL), Oakmulgee National Forest (AL), Bankhead National Forest (AL), and Chattahoochee National Forest (GA). Figure 1 shows the locations of the study areas. There are three size classes within the forest data sets: sawtimber, poletimber, and saplings. The diameter at breast height (DBH) values for those classes are greater than 9 inches (22.9 cm), 5 to 9 inches (12.7 to 22.9 cm), and 1 to 5 inches (2.5 to 12.7 cm), respectively. Significant species includes longleaf-slash pine, shortleaf-loblolly and white oak, red oak, hickory, sweetgum, ash, and yellow-poplar.
Table 1 summarizes the characteristics of the Landsat data used in this study, which were acquired in the summers of 1999 and 2000. Landsat TM images have seven bands and each band characterizes ground features in different spectral regions. The spatial resolution of the Landsat TM images is 30 m except for Band 6 that is 120 m. For consistency purposes, the data recorded in Band 6 were excluded from these analyses. Figure 2 shows pseudo natural color composite images of the study areas using bands 5, 4, and 3.
2.2. Methodology and Data Processing
The methodology employed in this study is described in Al-Hamdan et al. [31,32]. Two spatial analysis methods were used to analyze the Landsat images: fractals and Moran’s I. To compute the fractal dimension (FD), the isarithm method was used [33,44]. Each pixel brightness value (reflected energy representation) is classified as being either above or below assumed contour brightness values for each step size. Neighboring pixels along rows or columns are then compared to determine whether the pairs are both above or both below the assumed value; if they are not the same, then an isarithm contour is drawn between them. A linear regression is then performed between contour length and step size as the following:
As a flat surface grows more complex, the maximum FD increases from a value of 2.0 and approaches 3.0 as the surface begins to become more three dimensional [33,45]. The final FD of the surface is taken as the average of the FD values for those isarithms having a coefficient of determination (R2) greater than or equal to 0.9 [46,47]. Based on a review of the research literature of studies that used fractal analysis and Landsat TM data [45,48], the number of steps were set to 6 (i.e., 1, 2, 4, 8, 16, 32 pixel intervals) and the isarithm interval to 2 for all calculations in this study.
Moran’s I [49] is a measure of the spatial autocorrelation of the pixel brightness values of a raster image and reflects the differing spatial structures of the smooth and rough surfaces [46]. It can vary from +1.0 for perfect positive autocorrelation (a clumped pattern) to −1.0 for perfect negative autocorrelation (a checker board pattern) [33,46]. Moran’s I is calculated from the following formula:
I(d) is Moran’s spatial autocorrelation at distance d;
wi,j is the weight at distance d, so that
wi,j = 1 if point j is within distance d of point i, otherwise wi,j = 0;
zi = deviation (i.e., zi = xi − xmean for variable x); and
W = the sum of all the weights where i ≠ j.
Samples were collected randomly from the images for each forest area, obtaining equal coverage of all parts of the forests [31]. Sample size was chosen to be 100 × 100 pixels based on a review of the research literature [50,51]. As shown in Figure 3 the total numbers of collected samples were 36, 52, 32, and 31 for Talladega National Forest (AL), Oakmulgee National Forest (AL), Bankhead National Forest (AL), and Chattahoochee National Forest (GA), respectively. The FD and Moran’s I values were calculated for all bands of the Landsat TM coverage except the thermal infrared band (Band 6), which has a different spatial resolution. The Image Characterization and Modeling System (ICAMS) [48] module was used to calculate the spatial indices as described in Al-Hamdan et al. [31]. The averages of FD and Moran’s I for each sample were calculated using the results of all Landsat TM bands except Band 6, which was excluded due to its different spatial resolution as discussed previously.
The concept of spatial complexity indices to extract forest structure attributes is based on the relationship between forest canopy characteristics and trunk diameter DBH [31,32,34–43]. As crown width increases, stand diameter increases and stand density (trunks/unit area) decreases. The goal is to obtain a relationship between DBH and FD or I, such that the spatial indices can then be used to estimate the stand attributes. Al-Hamdan et al. [31] have demonstrated the mechanism by which crown complexity or roughness measures can be characterized by fractals or spatial correlation depending on the mixture of large and small trees and the resulting homogeneity or heterogeneity of the forest canopy surface. For each sample, the forest stand data were extracted, including percent of each size class present (sawtimber, poletimber, saplings), percent of each category of species (hardwood and softwood), age and elevation using the national forests vector GIS data obtained from the Forest Service and the digital elevations GIS data obtained from the Earth Resources Observation Systems (EROS) Data Center. The computed FD and I were then related to the stand variables using linear regression as reported for the Oakmulgee forest by Al-Hamdan et al. [32]. Table 2 lists summary statistics of all the in situ and computed variables for each study area, and Table 3 lists the FD and Moran’s I values at the minimum and maximum percentages of each stand size class and category of species among all study areas. The computed FD is shown for each sample in Figure 3, as well.
3. Preliminary Results
To examine the modeling, the relationship between stand characteristics and spatial indices were examined for each forest individually and without the influence of elevation. The results of this analysis are given in Table 4 for each variable for each forest, including the Oakmulgee, which was previously given in Al-Hamdan et al. [32].
Table 4 shows that all of the regression slopes were significantly different than 0 (α = 0.05) with the exception of three cases. These same three cases (Talladega I vs. Poletimber %; Bankhead FD vs. Poletimber %; Bankhead I vs. Poletimber %) also showed relatively low coefficient of determination (R2) values. In addition, the correlation coefficient (r) values for poletimber are not significant at the 0.05 level in the cases of FD and I for Talladega National Forest. In all other cases a significant linear relationship does appear to exist between the variables. Thus, it appears that the spatial indices may not be able to clearly distinguish poletimber in all cases, but that they can detect larger trunk sizes (sawtimber) and smaller diameters (saplings) effectively.
The difficulty in identifying poletimber is in line with Al-Hamdan et al. [32]. Large crown trees (sawtimber) and smaller trees (saplings) will produce consistent FD and I across multiple canopies with the sawtimber corresponding to a complex surface (high FD) and the saplings associated with a homogeneous surface (low FD). On the other hand, uneven mid-sized canopies (i.e., poletimber) will result in surface whose complexity is bounded by the sawtimber from above and the saplings from below and thus will not demonstrate sufficient variability to define a relationship between the variables as shown for the Oakmulgee by Al-Hamdan et al. [32]. This phenomenon can be seen in Table 3 where the variation of the indices with the sawtimber and saplings percentages are seen to be substantial, while very little variation is associated with the poletimber coverage.
The mean elevation of each sample was then added to the data and multiple linear regression was employed to clarify how the terrain or the topographical characteristics affect the spatial indices that potentially will be used to estimate the stand characteristics. The results of this analysis are shown in Table 5 and can be spatially visualized in Figure 3 where the FD values are shown with the topographic background.
A comparison of Tables 4 and 5 reveals that sample topography plays an important role in several instances. It particularly served to strengthen the relationship between the spatial indices and the poletimber fraction in three of the four forests with the most striking example being Talladega. The topographic variation of each forest as shown in Table 2 can be summarized as follows: Talladega: Mean Elevation = 338.02 m; Std. Dev. = 94.68 m; Oakmulgee: Mean = 130.63 m; Std. Dev. = 22.67 m; Bankhead: Mean = 236.46 m; Std. Dev. = 23.28 m; Chattahoochee: Mean = 378.0 m; Std. Dev. = 29.89 m.
The role of topographic relief in spectral reflectance of forested areas has been well documented in the literature [52–54]. The rough terrain introduces radiometric distortion of the recorded signal (i.e., anisotropy) because in some locations the area of interest might even be in complete shadow, dramatically affecting the brightness values of the pixels involved [55]. Anisotropy of remote sensing data can have an effect on the analysis of canopy structure from remote sensing data [56]. This means that the topographically induced illumination variation produces the anomaly that two objects having the same reflectance properties will not have the same brightness level because of their different orientation to the sun’s position.
The effects topographic relief has on measurements of fractals and spatial autocorrelation are significant. Since the isarithm method draws a line between values above and below a given brightness value assigned to the isarithm, then topographic boundaries, particularly breaks in slope and aspect, affect the isarithm and the spatial autocorrelation matrix. It is not surprising that the greatest topographic effect would be in the Talladega forest which demonstrated by far the greatest topographic relief. Figure 3 demonstrates how the FD follows with the topography for the Talladega Forest, as well as the other forests to a lesser extent.
4. Further Interpretation of Forest Attributes’ Regressions
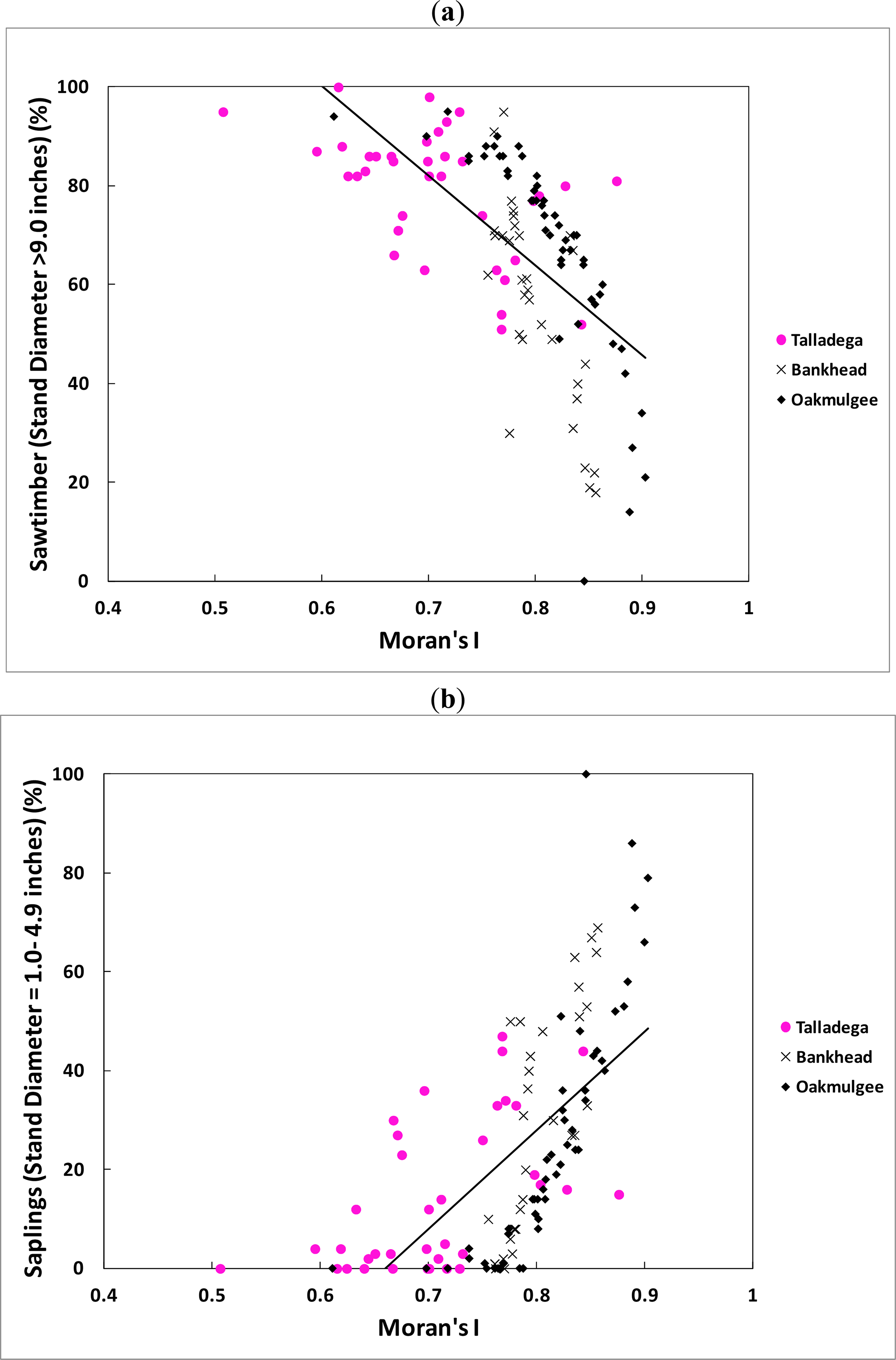
All the regressions showed that the fractal dimension (FD) increased (positive slopes) and the Moran’s I decreased (negative slopes) as the sawtimber (DBH > 22.9 cm) percentage increased. The regressions also showed that FD decreased (negative slopes) and Moran’s I increased (positive slopes) as the saplings (DBH = 2.5–12.7 cm) percentage increased. These results are consistent with the discussion given above in regard to the relationship between the spatial indices, the crown dimensions and the stand characteristics.
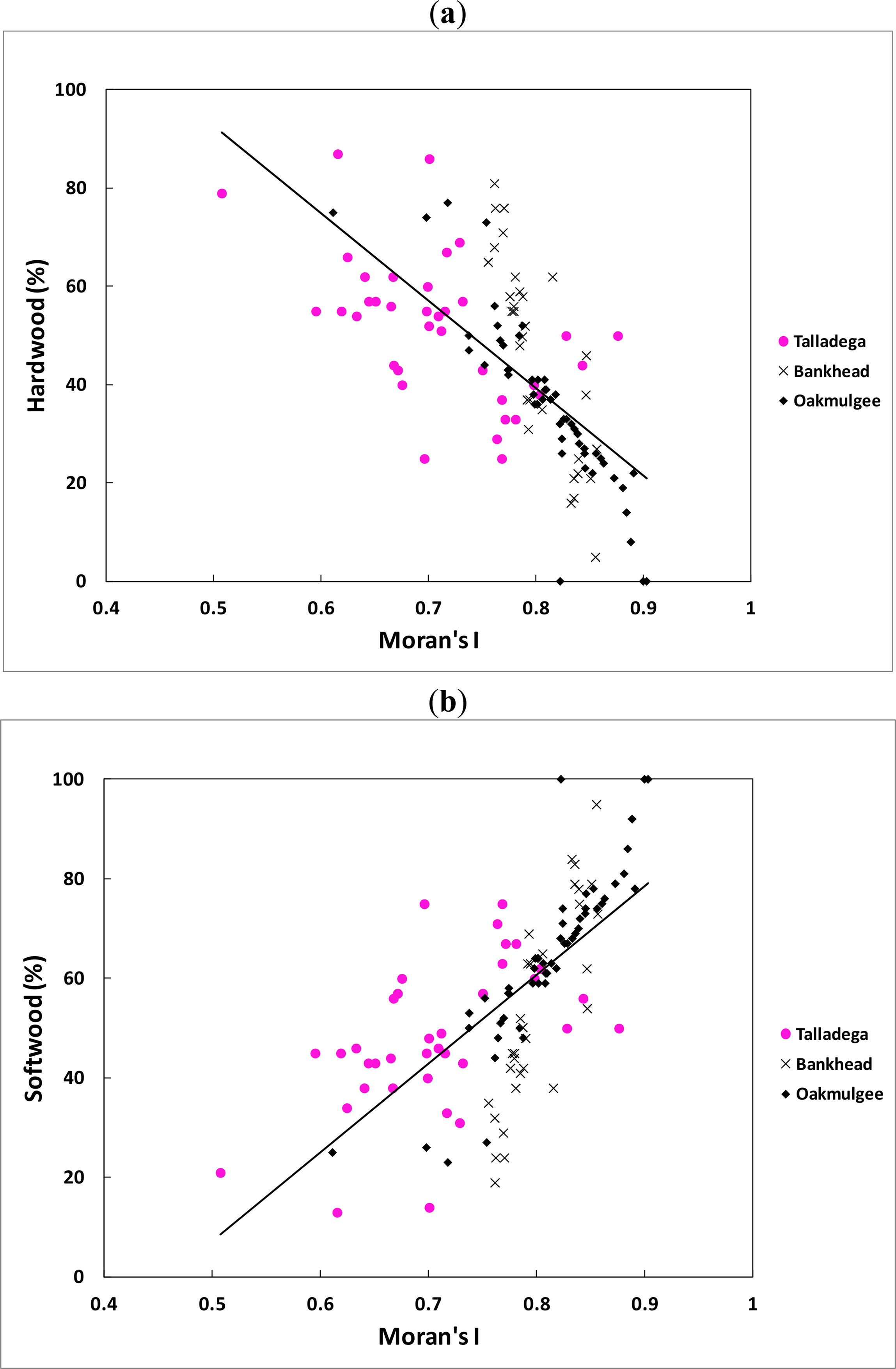
All the regressions showed an increase (positive slopes) in fractal dimension (FD) and a decrease (negative slopes) in Moran’s I as the hardwood percentages increased while all the regressions showed a decrease (negative slopes) in fractal dimension (FD) and an increase (positive slopes) in Moran’s I as the softwood percentages increased. The explanation for this result is as given above because softwood trees (for example, pine trees) are mostly with small crowns, while hardwood trees (such as oak trees) likely have large crowns. As a matter of fact, the category of species case had even stronger correlations with the average spatial indices than the Diameter at Breast Height (DBH) case. This can be due to the fact that remote sensing data do not measure DBH directly, but they measure crown reflectivity by satellite sensors. Thus, for a given tree species, the reflectance value recorded by satellite sensors is a function of exposed projection area (canopy closure). The strong relationship between the spatial indices and both categories of species therefore offers an alternative method of estimating stand density parameters.
5. Prediction Models of Stand Size Classes and Categories of Species
The purpose of this exercise is to develop a general remotely sensed based model that can be applied over a range of forest attributes. To that end, the data from three of the forests were combined to form the general model leaving one for validation purposes. The stand size classes (sawtimber, saplings), categories of species (hardwood, softwood) and elevation data were used in the analysis. Due to the relatively weak performance of the individual forest models in predicting poletimber percentages, and for the physical reasoning discussed above, it was decided to omit that stand size class. However, if acceptable predictions of the other two stand size classes (i.e., sawtimber and saplings) can be gained, then the percent of poletimber occurring in a given forest would just be 100 minus the sum of the other two classes’ percentages.
In this analysis the independent and dependent variables were switched making the size class percentage as the independent variable of the relationship. Thus, the regression described in this section is the inverse of that described in the previous section.
Before proceeding with regression, it must be determined if the data sets could have come from the same population (i.e., they are not significantly different). To that end, two-way ANOVA tests were conducted using the average spatial indices as the dependent factor and the size class percentage as the independent factor. These ANOVA tests were conducted for each size class (sawtimber and saplings). In each test, the same size classes in all study areas were compared to each other (i.e., sawtimber to sawtimber, and saplings to saplings). If it is found that tree data sets of similar size classes come from the same populations, the regression analysis could be run for the combined data from all the study areas for each size class. The results of the ANOVA tests showed that the same size classes in all study areas came from the same population (i.e., not significantly different) at the 0.05 significance level. P values were 0.077 and 0.075, for the size classes of sawtimber and saplings, respectively.
For modeling purposes, three study areas were randomly selected and used to create the prediction model. The three study areas selected were Oakmulgee National Forest, Bankhead National Forest, and Talladega National Forest, while one study area, Chattahoochee National Forest, was saved for validation. The prediction model was developed by performing linear regression between either FD or Moran’s I and the percentage of the size class. To validate the regression model the predicted values of the developed model were compared with the original Forest Inventory Analysis (FIA) data for Chattahoochee National Forest to see how well they were correlated.
In making predictions from regression equations, it is important to ensure that the underlying assumptions of regression are maintained. The independent variables must be random, independent of each other, and the residuals of the regression equation should be normally distributed. In all cases, the samples were acquired in a manner to ensure randomness and mutual independence to the extent possible. However, issues did arise with the normality assumption. Analyses revealed that, due to the small magnitude of some samples (i.e., percentages approached 0), distortion was introduced into the residuals as the boundary was approached. While this distortion could have been removed by merely eliminating those samples, Miller [57] has indicated that the effect of non-normality of residuals on the regression model is minimal for large samples and decreases rapidly as the sample size increases beyond 10. Since sample sizes in this study are all larger than 30, it is considered that the non-normality of residuals is not a significant factor.
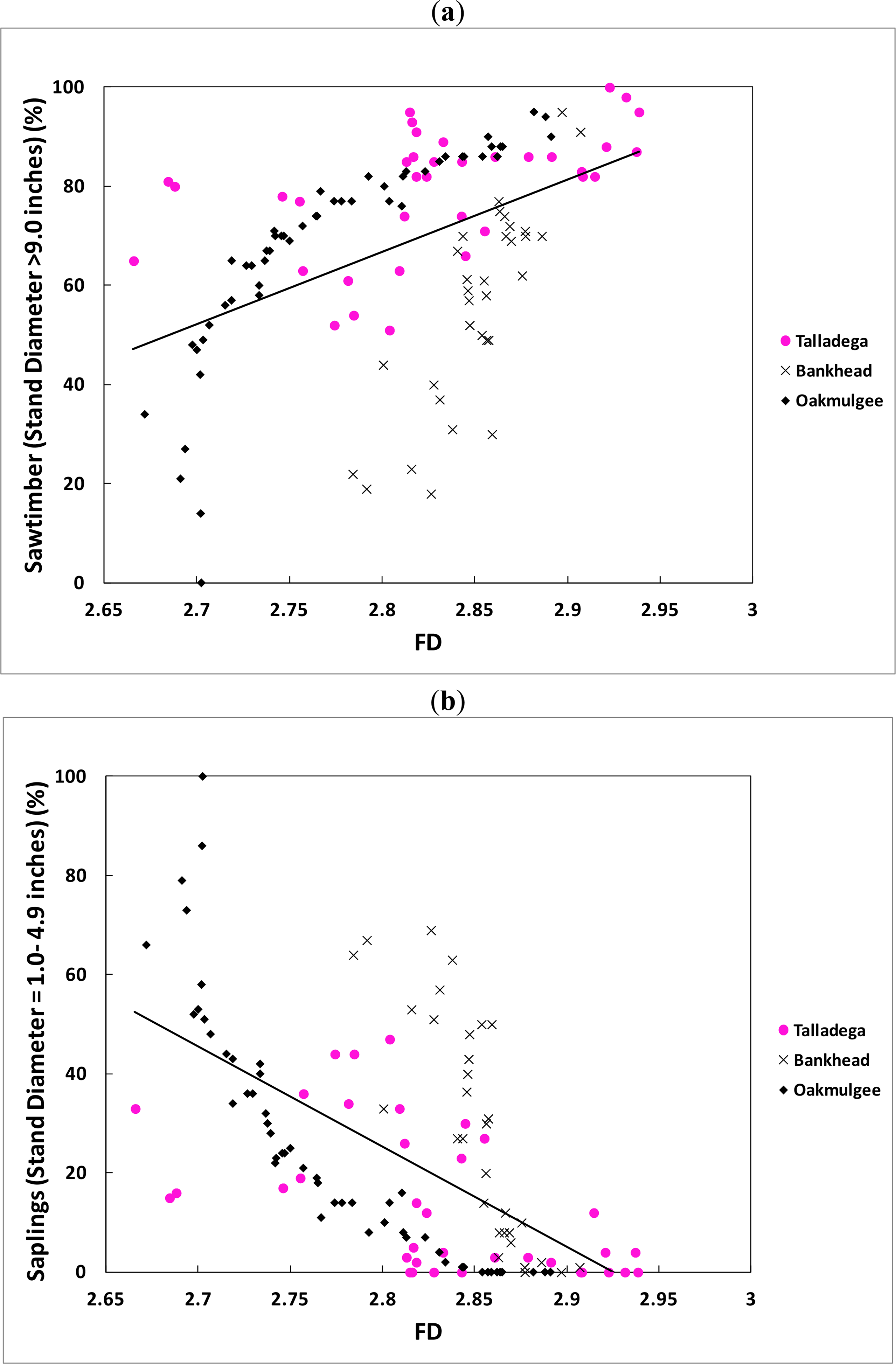
The stand size classes prediction equations with the regression statistics are summarized in Table 6 and the data are plotted in Figures 4 and 5. Table 6 shows the regression results for both the with and without elevation cases since it was shown above that elevation can play a significant role as a mask that covers the effect of the canopy characteristics in cases of uneven topography as in the Talladega case.
Table 6 illustrates that the models to predict the percentages of saplings size class demonstrated steeper slopes than did the models to predict the percentages of sawtimber size class using both spatial indices (i.e., fractal dimension and Moran’s I. For example, a 3.7% increase in FD from 2.7 to 2.8, would cause a percentage change in sawtimber and saplings of 27.9% and 44.4% respectively. Also, a 6.7% increase in Moran’s I from 0.75 to 0.85, would cause a percentage change in sawtimber and saplings of 12.4% and 55.5% respectively. Al-Hamdan et al. [31,32] also demonstrated that if continuous small crown trees are covering two adjacent remotely sensed pixels of a similar area, the integration of the brightness levels within each pixel (i.e., pixel value) will be similar in magnitude and the result is two homogeneous surfaces. Thus, these results appear to indicate that the spatial indices are more sensitive to the homogenous surfaces created by small size trees than they are to the heterogeneous surfaces created by large size trees.
The categories of species prediction equations and associated regression statistics are shown in Table 7 and the data are plotted in Figures 6 and 7. Table 7 shows that the categories of species equations followed the same general pattern as the stand size equations. This is not surprising in light of the results for the individual forests given previously. As before, the R2 values were generally higher in the categories of species equations for the combined data than was the case for the stand characteristics equations.
6. Discussion
The fractal dimension (independent variable) can only vary from 2.0 to 3.0 for a surface. In practice, for a remotely sensed image, the fractal dimension varies from 2.5 for homogeneous surfaces, like water bodies, to 3.0 for very heterogeneous surfaces [45]. When the fractal dimension approaches 2.5, the forest being measured is dominated by trees of saplings size class and, as the surface becomes more complex (FD ≈ 3.0), the forest is dominated by trees of sawtimber size class [32]. In the case of Moran’s I, it ranges, in practice, from 0.5 to 1.0 in a remotely sensed image. When Moran’s I approaches 1.0, this means that the forest being measured is dominated by trees of saplings size class. Thus, as a practical matter, in cases where the forest is dominated by one class, the FD or I will approach the bounds and the prediction model will not be as effective (i.e., the indices will show little variation). Therefore, the developed prediction models work best for forests with a mixture of different tree sizes and species.
In the stand size cases, the regression model using Moran’s I as the chief independent variable is stronger (in terms of R2) overall than the model that utilizes the fractal dimension as the chief independent variable. Furthermore, the addition of elevation appears to have very little value in the fractal based model, while it adds substantially to the Moran’s I model. Overall, one might conclude at this stage that Moran’s I is a more robust indicator of forest growth characteristics than the fractal dimension as the R2 values were generally higher for that model.
The R2 values obtained in these fits were comparable to those found in previous studies. R2 values such as 0.53 [58], 0.61 [59], 0.65 [58], and 0.78 [60] are reported in the literature for studies of some Forest Stand Characteristics like basal area and biomass using RADAR and LIDAR data rather than passive remote sensing data (Lansat TM) [61]. Watts [62] sought to determine forest productivity and carbon dynamics in southeastern Ohio from remotely sensed data. The adjusted R2 value of 0.40 in his model is similar to those found by Cook et al. [63], who developed values of 0.27, 0.39, and 0.42 when relating forest productivity indices to TM and bio-geographical data in Tennessee, Illinois, and New York, respectively. Taking all these results into account, and given the wide variety of sources of error that remotely sensed and forest GIS data can encounter as will be discussed in a later section, the adjusted R2 values in the models of this study shown in Tables 6 and 7 are reasonable.
7. Models Validation
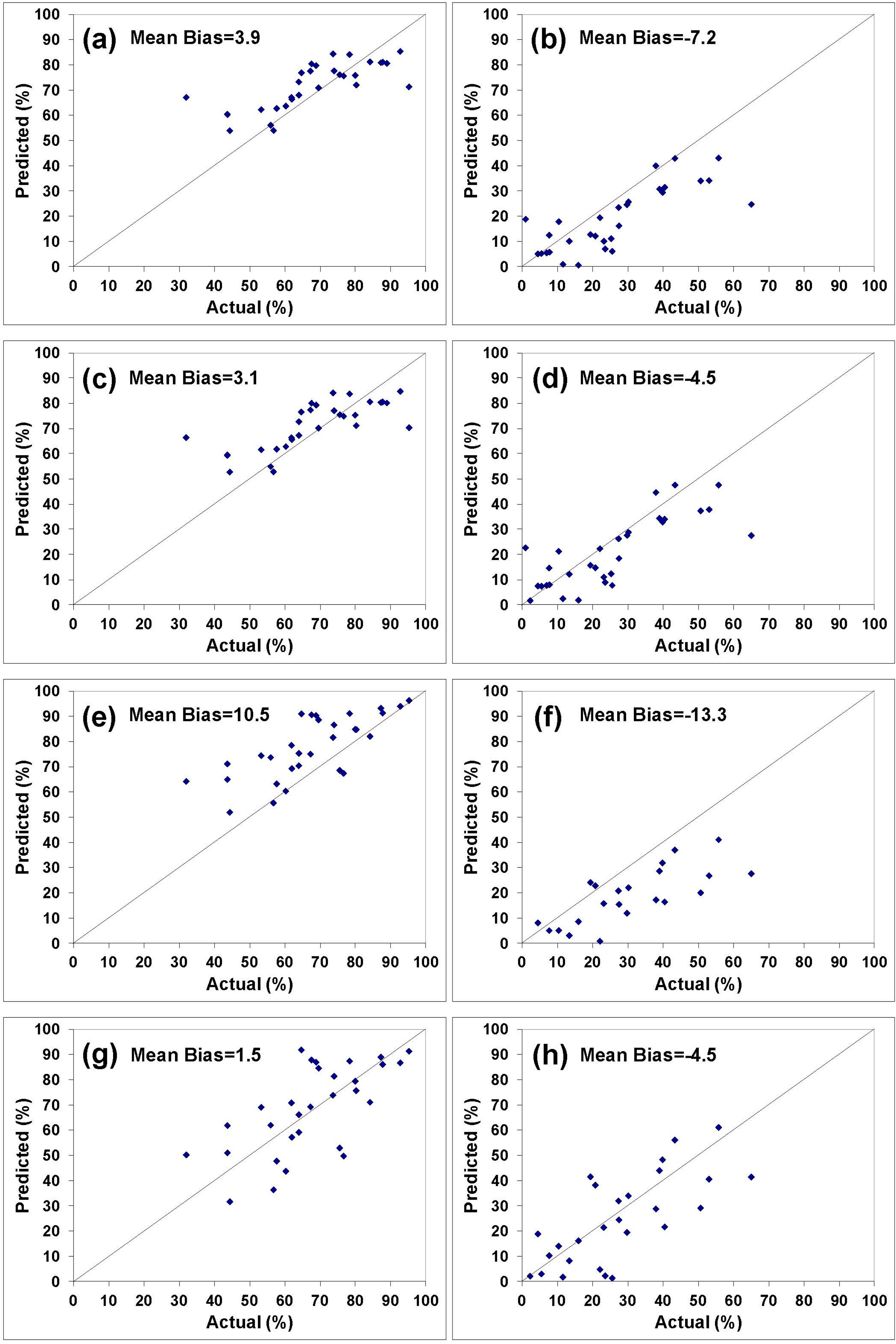
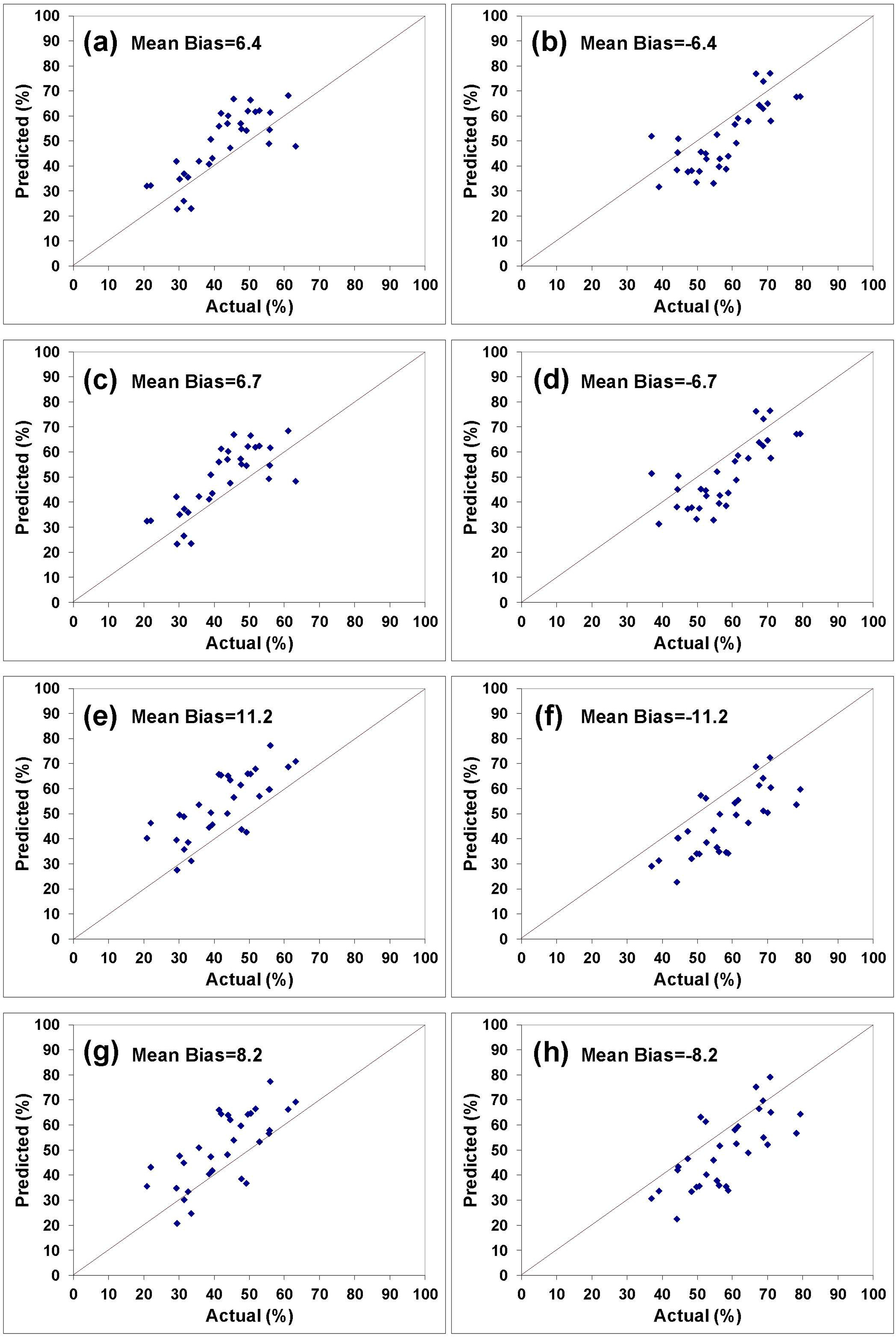
To validate the developed models, they were used to predict the percentages of stand size classes and categories of species in Chattahoochee National Forest, a data set not used in their development. The validation results are shown in Figures 8 and 9 and Tables 8 and 9. A number of measures of model prediction and error were used to illustrate the models’ overall effectiveness.
The mean absolute percentage error (MAPE), the root mean square error (RMSE), Pearson’s correlation coefficient (r), and R21:1 that measures the relationship between the predicted values and a perfect fit to the observed data (i.e., a 1:1 line through the origin) are the most commonly used statistics in the validation of satellite estimates [64]. The MAPE measures the average absolute difference between the estimated and observed values compared to the observed values. The RMSE also measures the average error magnitude but gives greater weight to the larger errors. The r measures the degree of correspondence between the estimated and observed distributions and it is independent of absolute or conditional bias; it should therefore be used along with other measures when validating satellite estimates [64].
These measures were the models’ evaluation criteria and calculated to test the ability of the models to predict the percentages of stand size classes (or categories of species) or to judge the models’ prediction capability. These statistics were calculated using the models’ predicted values and the actual FIA values of all samples and the results of these measures are summarized in Tables 8 and 9.
Error statistics should be viewed in light of the observed mean percentages of each size class in the Chattahoochee National Forest (i.e., sawtimber (68%) and saplings (25%)) and/or their variance (i.e., sawtimber (241) and saplings (290)). For example, as shown in Table 8 for the stand size classes prediction models, the mean absolute error percentages ranged from 4.4% relative to the observed data for the (FD + Elevation)-based sawtimber class to 51.4% for the I-based sapling class. More importantly, the RMSE varied from 10 relative to a variance of 241 of the observed data for the (FD + Elevation)-based sawtimber class to 17 relative to a variance of 290 for the I-based sapling class.
All these statistical measures demonstrated that the FD-based equations outperformed the Moran’s I-based predictors by a wide margin, and were, in fact, quite accurate. Adding elevation to the models as an explanatory variable generally improved the predictions in terms of reducing the prediction errors. The MPE and RMSE were lowered and the r and R21:1 were increased after adding the elevation as an independent variable in all cases. The significant effect of terrain was discussed previously in terms of its role in sometimes masking surface spectral effects.
The improvement of the FD-based models over the I-based ones is interesting but not entirely inconsistent with the previous regressions. While it is true that the stand size regression models based on Moran’s I resulted in a better fit to the combined data than did those based on fractals in terms of R2, the reverse was true of the categories of species models. The relationship of the categories of species to the crown diameters has been discussed earlier and it was shown that this relationship is indirectly related to the stand class sizes. In fact, the categories of species equations have demonstrated better fits to the data in terms of the coefficient of determination (R2) all the way through the analyses, and the FD-based equations have nearly always been superior. In addition, the analyses of the individual forests given in the Preliminary Results section revealed that the FD-based regressions were slightly superior in terms of R2 to the I-based regressions even in the stand class cases. Thus, it appears that the FD-based approach has demonstrated superiority in the vast majority of the cases.
8. Sources of Error
Error is introduced into the analyses from four basic sources: errors in the remotely sensed images, errors in the analysis of the images, uncertainty in the relationships between the remotely sensed indices (FD and I) and the in situ data, and finally, errors in the in situ data themselves. In this case, the Landsat images obtained from the EROS data center were geometrically corrected but were not processed for radiometric errors (i.e., dropped lines) or atmospherically corrected. However, no radiometric issues were encountered when working with the images, and previous authors [45,48,65] have demonstrated that atmospheric interference has negligible effect on the spatial indices.
The second source of error is associated with the estimation of the spatial indices. As discussed previously, the FD were computed by the isarithm method which is essentially a regression technique. As only regressions with a 0.90 or higher R2 values were accepted, that effectively defines the error in that particular index. The Moran’s I is a straightforward spatial autocorrelation index, so that its value is itself a measure of uncertainty. The I value varied from 0.51 to 0.90.
The third source of uncertainty in the study is the error associated with the estimation of forest stand characteristics and categories of species from the spatial indices. These errors and uncertainties have been shown and thoroughly discussed in the previous sections.
Finally, the National Forest Service inventory data are not perfect. FIA’s primary objective is to determine the extent, condition, volume, growth, and depletions of timber on the nation’s forestland. FIA is required to collect data on 20 percent of the plots annually within each state [66]. The inventories are based on photo interpretation and field surveys. Aerial photos are used to classify basic land covers and then to break forested areas into subclasses according to type, volume per acre, stand size, stand density, ownership, and/or stand age. Then, ground plots are measured to adjust the aerial photo sample for changes since its acquisition date, to correct any misclassification, and to obtain estimates that cannot be made from the aerial photography. The photo classifications of these ground plots, together with the area estimates from the aerial photo sample, are used to assign area expansion factors to all ground plots which are used to expand values observed on the plot from a per acre basis to a population basis. For all plots, several observations are recorded for each sample tree, including its diameter, species, and other measurements that enable the prediction of the tree’s volume, growth rate, and quality. These tree measurements form the basis of the data on the tree records in the FIA Data Base.
The inventories must meet national accuracy standards. For example, a state with five million acres of timberland would have a maximum allowable sampling error of 1.3 percent, a geographic unit within that state with one million acres of timberland would have a 3.0 percent maximum allowable sampling error, and a county within that state with 100 thousand acres would have a 9.5 percent maximum allowable sampling error at the 67 percent confidence level.
To summarize, it is believed that errors associated with the Landsat images themselves were negligible, errors attached to the computation of the spatial indices were 10% or less, uncertainties in the relationships between the spatial indices and the forest characteristics ranged from 3% to 20% and errors in the in situ data were less than 10%.
One final comment is in order here. Our previous study by Al-Hamdan et al. [31] showed that the spatial indices are much more distinguishable in the Landsat TM visible bands than they are in the TM infrared bands. That result could be attributed to the fact that green leaves absorb visible red and blue light, and relate less to middle infrared light. It also could be attributed to the fact that the signal strength in visible bands is much stronger than it is in middle infrared bands. Therefore, spectral responses from the vegetation chlorophyll have a bigger influence on the spatial analytical techniques in the visible bands than is the case in the infrared bands. However, since the contribution of atmospheric molecular and aerosol scattering is higher in the visible channels than it is in the near and middle infrared channels [67], visible bands should be used with caution and be carefully atmospherically corrected. It is possible, however, that the developed models in this study might have been more accurate if the average spatial indices of only the visible bands had been used to study the tree size classes, categories of species, and elevation, rather than using the average spatial indices of all bands. That is open for further investigation to verify and is recommended for future research.
9. Summary
This study has shown that the spatial analytical indices of remotely sensed data (i.e., FD and Moran’s I) can distinguish between different forest trunk size classes and different categories of species (hardwood and softwood) based on the percentage of trees in the size class or category of species. The results of this study also revealed that there is a linear relationship between each one of the spatial indices and the percentages of sawtimber and saplings size classes, and hardwood and softwood categories of species. However, there is not such a linear relationship between the spatial indices and poletimber size class percentages. That led to the process of developing models to predict the relative percentages of sawtimber and saplings, which are needed to estimate the flow resistance coefficients in forested flood plain areas. Other models to predict the relative percentages of hardwood and softwood were also developed.
Three out of four data sets were selected for model development and the fourth one was left for validation purposes. Given the high number of factors causing errors in the remotely sensed data as well as the Forest Inventory Analysis (FIA) data sets and compared to other studies in the research literature, the sawtimber–saplings models and hardwood–softwood models were reasonable in terms of significance and the levels of explained variance for both spatial indices FD and Moran’s I. The models were validated on the remaining data set and the results were reasonable in terms of the error measurements and prediction performance measures for both FD and Moran’s I-based models. The mean absolute percentage errors associated with the stand size classes prediction models and categories of species prediction models that take topographical elevation into consideration ranged from 2.9% to 19.8% and from 12.1% to 18.9%, respectively; while the root mean square errors ranged from 10% to 14% and from 11% to 13%, respectively.
Acknowledgments
This project was supported by a grant from the U.S. Department of Transportation “Applications of remote sensing and related spatial technologies to environmental assessments in transportation.” The assistance of the project manager, Roger King of Mississippi State University, and the USDOT program director, K. Thirumalai is gratefully acknowledged. The authors would also like to thank Nina Lam of Louisiana State University and Charles Emerson of Western Michigan University for their assistance.
Author Contributions
Mohammad Al-Hamdan performed the remotely sensed data processing and spatial analyses, statistical analysis, overall analysis and manuscript writing. James Cruise contributed to the statistical analysis, overall analysis and manuscript writing. Douglas Rickman and Dale Quattrochi contributed to the overall analysis and manuscript writing.
Conflicts and Interest
The authors declare no conflict of interest.
References
- Lefsky, M.A.; Cohen, W.B.; Parker, G.G.; Harding, D.J. Lidar remote sensing for ecosystem studies. Bioscience 2002, 52, 19–30. [Google Scholar]
- Dubayah, R.O.; Drake, J.B. Lidar remote sensing for forestry. J. Forest 2000, 98, 44–46. [Google Scholar]
- Lim, K.; Treitz, P.; Wulder, M.; St-Onge, B.; Flood, M. LiDAR remote sensing of forest structure. Prog. Phys. Geog 2003, 27, 88–106. [Google Scholar]
- Hyyppä, J.; Yu, X.; Hyyppä, H.; Vastaranta, M.; Holopainen, M.; Kukko, A.; Kaartinen, H.; Jaakkola, A.; Vaaja, M.; Koskinen, J.; et al. Advances in forest inventory using airborne laser scanning. Remote Sens 2012, 4, 1190–1207. [Google Scholar]
- Lindberg, E.; Hollaus, M. Comparison of methods for estimation of stem volume, stem number and basal area from airborne laser scanning data in a hemi-boreal forest. Remote Sens 2012, 4, 1004–1023. [Google Scholar]
- Vaughn, N.R.; Moskal, L.M.; Turnblom, E.C. Tree species detection accuracies using discrete point Lidar and airborne waveform Lidar. Remote Sens 2012, 4, 377–403. [Google Scholar]
- Harrell, P.A.; Bourgeau-Chavez, L.L.; Kasischke, E.S.; French, N.H.; Christensen, N.L. Sensitivity of ERS-1 and JERS-1 radar data to biomass and stand structure in Alaskan boreal forest. Remote Sens. Environ 1995, 54, 247–260. [Google Scholar]
- Ranson, K.J; Sun, G. An evaluation of AIRSAR and SIRC/X-SAR images for mapping northern forest attributes in Maine, USA. Remote Sens. Environ 1997, 59, 203–222. [Google Scholar]
- Fransson, J.S.; Israelsson, H. Estimation of stemvolume in boreal forests using ERS-1 C- and JERS-1 L-band SAR data. Int. J. Remote Sens 1999, 20, 123–137. [Google Scholar]
- Perko, R.; Raggam, H.; Deutscher, J.; Gutjahr, K.; Schardt, M. Forest assessment using high resolution SAR data in X-Band. Remote Sens 2011, 3, 792–815. [Google Scholar]
- Robinson, C.; Saatchi, S.; Neumann, M.; Gillespie, T. Impacts of spatial variability on aboveground biomass estimation from L-band radar in a temperate forest. Remote Sens 2013, 5, 1001–1023. [Google Scholar]
- Van, Z.J.; Kim, Y. Synthetic Aperture Radar Polarimetry; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Curran, P.J.; Dungan, J.L.; Gholz, H.L. Seasonal LAI in slash pine estimated with Landsat TM. Remote Sens. Environ 1992, 39, 3–13. [Google Scholar]
- Anderson, G.L.; Hanson, J.D.; Haas, R.J. Evaluating Landsat Thematic Mapper derived vegetation indices for estimating above-ground biomass on semiarid rangelands. Remote Sens. Environ 1993, 45, 165–175. [Google Scholar]
- Hame, T.; Salli, A.; Andersson, K.; Lohi, A. A new methodology for the estimation of biomass of conifer-dominated boreal forest using NOAA AVHRR Data. Int. J. Remote Sens 1997, 18, 3211–3247. [Google Scholar]
- Martin, M.E.; Newman, S.D.; Aber, J.D.; Congalton, R.G. Determining forest species composition using high spectral resolution remote sensing data. Remote Sens. Environ 1998, 65, 249–254. [Google Scholar]
- Nelson, R.F.; Kimes, D.S.; Salas, W.A.; Routhier, M. Secondary forest age and tropical forest biomass estimation using thematic mapper imagery. BioScience 2000, 50, 419–431. [Google Scholar]
- Foody, G.M.; Boyd, D.S.; Cutler, M.J. Predictive relations of tropical forest biomass from Landsat TM data and their transferability between regions. Remote Sens. Environ 2003, 85, 463–474. [Google Scholar]
- Dong, J.; Kaufmann, R.; Myneni, R.; Tucker, C.; Kauppi, P.; Liski, J.; Buermann, W.; Alexeyev, V.; Hughes, M.K. Remote sensing estimates of boreal and temperate forest woody biomass: Carbon pools, sources, and sinks. Remote Sens. Environ 2003, 84, 393–410. [Google Scholar]
- Giree, N.; Stehman, S.V.; Potapov, P.; Hansen, M.C. A sample-based forest monitoring strategy using Landsat, AVHRR and Modis Data to estimate gross forest cover loss in Malaysia between 1990 and 2005. Remote Sens 2013, 5, 1842–1855. [Google Scholar]
- Bauer, M.E.; Burk, T.E.; Ek, A.R.; Coppin, P.R.; Lime, S.D.; Walsh, T.A.; Walters, D.K.; Befort, W.; Heinzen, D.F. Satellite inventory of Minnesota forest resources. Photogramm. Eng. Remote Sens 1994, 60, 287–298. [Google Scholar]
- Fiorella, M.; Ripple, W.J. Analysis of conifer forest regeneration using Landsat Thematic Mapper data. Photogramm. Eng. Remote Sens 1993, 59, 1383–1388. [Google Scholar]
- Hunt, E.R.; Rock, B.N. Detection of changes in leaf water content using near and middle-infrared reflectance. Remote Sens. Environ 1989, 30, 43–54. [Google Scholar]
- Schlerf, M.; Atzberger, C.; Hill, J. Remote sensing of forest biophysical variables using HyMap imaging spectrometer data. Remote Sens. Environ 2005, 95, 177–194. [Google Scholar]
- Foody, G.M.; Cutler, M.J. Tree biodiversity in protected and logged Bornean tropical rain forests and its measurement by satellite remote sensing. J. Biogeogr 2003, 30, 1053–1066. [Google Scholar]
- Foody, G.M.; Cutler, M.J. Mapping the species richness and composition of tropical forests from remotely sensed data with neural networks. Ecol. Model 2006, 195, 37–42. [Google Scholar]
- Rocchini, D.; Ricotta, C.; Chiarucci, A. Using satellite imagery to assess plant species richness: The role of multispectral systems. Appl. Veg. Sci 2007, 10, 325–332. [Google Scholar]
- Rocchini, D.; Balkenhol, N.; Carter, G.A.; Foody, G.M.; Gillespie, T.W.; He, K.S.; Kark, S.; Levin, N.; Lucas, K.; Luoto, M.; et al. Remotely sensed spectral heterogeneity as a proxy of species diversity: Recent advances and open challenges. Ecol. Inform 2010, 5, 318–329. [Google Scholar]
- Hyyppa, J.; Hyyppa, H.; Inkinen, M.; Engdahl, M.; Linko, S.; Shu, Y-H. Accuracy comparison of various remote sensing data sources in the retrieval of forest stand attributes. Forest Ecol. Manag 2000, 128, 109–120. [Google Scholar]
- Boyd, D.S.; Danson, F.M. Satellite remote sensing of forest resources: Three decades of research development. Prog. Phys. Geog 2005, 29, 1–26. [Google Scholar]
- Al-Hamdan, M.; Cruise, J.; Rickman, D.; Quattrochi, D. Effects of spatial and spectral resolutions on fractal dimensions in forested landscapes. Remote Sens 2010, 2, 611–640. [Google Scholar]
- Al-Hamdan, M.Z.; Cruise, J.F.; Rickman, D.L.; Quattrochi, D.A. Characterization of forested landscapes from remotely sensed data using fractals and spatial autocorrelation. Adv. Civil. Eng 2012, 2012. Article ID 945613. [Google Scholar] [CrossRef]
- Lam, N.S.-N.; Qiu, H.L.; Quattrochi, D.A.; Emerson, C.W. An evaluation of fractal methods for characterizing image complexity. Cartogr. Geogr. Inf. Sci 2002, 29, 25–35. [Google Scholar]
- Bragg, D.C. A local basal area adjustment for crown width prediction. North. J. Appl. For 2001, 18, 22–28. [Google Scholar]
- Oladi, D. Developing a Framework and Methodology for Plantation Assessment Using Remotely Sensed Data. Ph.D. Thesis, University of New Brunswick, New Brunswick, Canada,. 1996. [Google Scholar]
- Steinman, J.; Gauvin, J.; Hunt, T.; Tardif, R. Documentation on the Growth Phase Model; Edmondstone Applied Forestry Technology Group: University of Moncton, Edmundston, NB, Canada, 1993. [Google Scholar]
- Farr, W.A.; Demars, D.J.; Dealy, J.E. Height and crown width related to diameter for open-grown western hemlock and Sitka spruce. Can. J. For. Res 1989, 19, 1203–1207. [Google Scholar]
- Sprinz, P.T.; Burkhart, H.E. Relationships between tree crown, stem, and stand characteristics in unthinned loblolly pine plantation. Can. J. For. Res 1987, 17, 534–538. [Google Scholar]
- Roberts, E.G.; Ross, R.D. Crown area of free-growing loblolly pine and its apparent independence of age and site. J. Forest 1965, 63, 462–463. [Google Scholar]
- Wile, B.C. Crown Size and Stem Diameter in Red Spruce And Balsam Fir, Forestry Pub. 1056, Canada Department of Forestry; Forestry Research Branch: Ottawa, ON, Canada, 1964. [Google Scholar]
- Smith, J.H.; Baily, G.R. Influence of stocking and stand density on crown widths of Douglas fir and lodgepole pine. Commonw. Forest. Rev 1964, 43, 243–246. [Google Scholar]
- Vezina, P.E. More about the Crown Competition Factor; Contribution No. 505; Department of Forestry, Forest Research Branch: Ottawa, ON, Canada, 1963. [Google Scholar]
- Minor, C.O. Stem-crown diameter relations in southern pine. J. Forest 1951, 49, 490–493. [Google Scholar]
- Goodchild, M.F. Fractals and the accuracy of geographical measures. Math. Geol 1980, 12, 85–98. [Google Scholar]
- Quattrochi, D.A.; Emerson, C.W.; Lam, N.S.-N.; Qiu, H.L. Fractal characterization of multitemporal remote sensing data. In Modeling Scale in Geographic Information Science; Tate, N.J., Atkinson, P.M., Eds.; John Wiley & Sons, Ltd: Hoboken, NJ, USA, 2001. [Google Scholar]
- Emerson, C.W.; Lam, N.S.-N.; Quattrochi, D.A. Multiscale fractal analysis of image texture and pattern. Photogramm. Eng. Remote Sens 1999, 65, 51–61. [Google Scholar]
- Jaggi, S.; Quattrochi, D.A.; Lam, N.S.-N. Implementation and operation of three fractal measurement algorithms for analysis of remote sensing data. Comput. Geosci 1993, 19, 745–767. [Google Scholar]
- Lam, N.S.-N.; Quattarochi, D.A.; Qiu, H.-L.; Zhao, W. Environmental assessment and monitoring with image characterization and modeling system using multi-scale remote sensing data. Appl. Geogr. Studies 1998, 2, 77–93. [Google Scholar]
- Cliff, A.D.; Ord, J.K. Spatial Autocorrelation; Pion Limited: London, UK, 1973. [Google Scholar]
- Myint, S.W. Fractal approaches in texture analysis and classification of remotely sensed data: Comparisons with spatial autocorrelation techniques and simple descriptive statistics. Int. J. Remote Sens 2003, 24, 1925–1947. [Google Scholar]
- Zhao, W. Multiscale Analysis for Characterization of Remotely Sensed Images. Ph.D. Dissertation, Louisiana State University, Baton Rouge, LA, USA. 2001. [Google Scholar]
- Lu, D. Estimation of Forest Stand Parameters and Application in Classification and Change Detection of Forest Cover Types in the Brazilian Amazon Basin. Ph.D. Dissertation, Indiana State University, Evansville, IN, USA,. 2001. [Google Scholar]
- Justice, C.O.; Wharton, S.W.; Holben, B.N. Applications of digital terrain data to quantify and reduce the topographic effect on Landsat data. Int. J. Remote Sens 1981, 2, 213–230. [Google Scholar]
- Teillet, P.M.; Guindon, B.; Goodenough, D.G. On the slope-aspect correction of multispectral scanner data. Can. J. Remote Sens 1982, 8, 84–96. [Google Scholar]
- Jensen, J.R. Introductory Digital Image Processing: A Remote Sensing Perspective; Prentice Hall: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Miller, R.G., Jr. Beyond ANOVA, Basics of Applied Statistics; John Wiley and Sons, Inc: New York, NY, USA, 1986. [Google Scholar]
- Widlowski, J.-L.; Pinty, B.; Gobron, N.; Verstraete, M.M.; Diner, D.J.; Davis, A.B. Canopy structure parameters derived from multi-angular remote sensing data for terrestrial carbon studies. Clim. Change 2004, 67, 403–415. [Google Scholar]
- Nelson, R.; Karbill, W.; Tonelli, J. Estimating forest biomass and volume using airborne laser data. Remote Sens. Environ 1988, 24, 247–267. [Google Scholar]
- Hyyppa, J.; Hallikainen, M. Applicability of airborne profile radar to forest inventory. Remote Sens. Environ 1996, 57, 39–57. [Google Scholar]
- Nilsson, M. Estimation of tree heights and stand volume using an airborne lidar system. Remote Sens. Environ 1996, 56, 1–7. [Google Scholar]
- Lefsky, M.A. Lidar Remote Sensing of Canopy Height Profiles: Application to Spatial and Temporal Trends in Canopy Structure. Ph.D. Dissertation, The University of Virginia Charlottesville, VA, USA. 1997. [Google Scholar]
- Watts, S.E. Determining Forest Productivity and Carbon Dyanamics in Southeastern Ohio from Remotely-Sensed Data; Ph.D. Dissertation,; The Ohio State University: Columbus, OH, USA, 2001. [Google Scholar]
- Cook, E.A.; Iverson, L.R.; Graham, R.L. Estimating forest productivity with thematic mapper and biogeographical data. Remote Sens. Environ 1989, 28, 1–17. [Google Scholar]
- Ebert, E.E. Verifying Satellite Precipitation Estimates for Weather and Hydrological Applications. In Proceedings of 1st International Precipitation Working Group (IPWG) Workshop, Madrid, Spain, 23–27 September 2002.
- Emerson, C.W.; Lam, N.S.-N.; Quattrochi, D.A. A comparison of local variance, fractal dimension, and Moran’s I as aids to multispectral image classification. Int. J. Remote Sens 2005, 26, 1575–1588. [Google Scholar]
- Miles, P.D.; Brand, G.J.; Alerich, C.L.; Bednar, L.F.; Woudenberg, S.W.; Glover, J.F.; Ezell, E.N. The Forest Inventory and Analysis Database Description and Users Manual Version 1.0, General Technical Report NC-218; U.S. Dept. of Agriculture Forest Service, North Central Research Station: St. Paul, MN, USA, 2001. [Google Scholar]
- Arino, O.; Vermote, O.; Spaventa, V. Operational atmospheric correction of Landsat tm imagery. Earth Obs. Quart 1997, 57, 32–35. [Google Scholar]




| Area of Study | Landscape Characteristics | Data Type | Resolution (m) | Bands | Spectral Characteristics (µm) | Date |
|---|---|---|---|---|---|---|
| Talladega National Forest, AL, USA | Forest | Landsat TM | 30 | 1–5, 7 | 0.45–2.35 | June 7, 2000 |
| Oakmulgee National Forest, AL, USA | Forest | Landsat TM | 30 | 1–5, 7 | 0.45–2.35 | Sep. 16, 1999 |
| Bankhead National Forest, AL, USA | Forest | Landsat TM | 30 | 1–5, 7 | 0.45–2.35 | Aug. 31, 1999 |
| Chatahoochee National Forest, GA, USA | Forest | Landsat TM | 30 | 1–5, 7 | 0.45–2.35 | June 7, 2000 |
| Study Area | Statistic | Sawtimber (%) | Poletimber (%) | Saplings (%) | Hardwood (%) | Softwood (%) | Elevation (m) | FD | Moran’s I |
|---|---|---|---|---|---|---|---|---|---|
| Talladega | Min | 51 | 0 | 0 | 25 | 13 | 210 | 2.666 | 0.507 |
| Max | 100 | 18 | 47 | 87 | 75 | 538 | 2.939 | 0.876 | |
| Mean | 79.3 | 6.4 | 14.2 | 51.9 | 48.1 | 338.0 | 2.829 | 0.706 | |
| SD | 12.8 | 4.7 | 15.1 | 15.1 | 15.1 | 94.7 | 0.07 | 0.08 | |
| CV | 0.16 | 0.73 | 1.06 | 0.29 | 0.31 | 0.28 | 0.02 | 0.11 | |
| Oakmulgee | Min | 0 | 0 | 0 | 0 | 23 | 60 | 2.672 | 0.611 |
| Max | 95 | 14 | 100 | 77 | 100 | 170 | 2.891 | 0.903 | |
| Mean | 68.2 | 6.0 | 25.7 | 35.9 | 64.1 | 130.6 | 2.773 | 0.810 | |
| SD | 20.9 | 4.8 | 24.9 | 17.2 | 17.2 | 22.7 | 0.06 | 0.05 | |
| CV | 0.31 | 0.80 | 0.97 | 0.48 | 0.27 | 0.17 | 0.02 | 0.07 | |
| Bankhead | Min | 18 | 0 | 0 | 5 | 19 | 180 | 2.784 | 0.755 |
| Max | 95 | 30 | 69 | 81 | 95 | 278 | 2.907 | 0.856 | |
| Mean | 56.0 | 14.8 | 29.1 | 46.5 | 53.5 | 236.5 | 2.851 | 0.800 | |
| SD | 20.3 | 9.7 | 23.0 | 20.1 | 20.1 | 23.3 | 0.03 | 0.03 | |
| CV | 0.36 | 0.65 | 0.79 | 0.43 | 0.38 | 0.10 | 0.01 | 0.04 | |
| Chattahoochee | Min | 31.9 | 0 | 0.9 | 20.8 | 36.9 | 315 | 2.712 | 0.587 |
| Max | 95.2 | 12.8 | 65 | 63.1 | 79.2 | 444 | 2.929 | 0.866 | |
| Mean | 68.1 | 6.6 | 25.3 | 42.4 | 57.6 | 378.0 | 2.836 | 0.720 | |
| SD | 15.5 | 3.5 | 17.0 | 11.0 | 11.0 | 29.9 | 0.06 | 0.07 | |
| CV | 0.23 | 0.53 | 0.67 | 0.26 | 0.19 | 0.08 | 0.02 | 0.10 | |
| Min/Max Percentage of Stand Size Class or Category of Species | FD | Moran’s I |
|---|---|---|
| Minimum Sawtimber (0%) | 2.7025 | 0.8457 |
| Maximum Sawtimber (100%) | 2.9226 | 0.6153 |
| Minimum Poletimber (0%) | 2.8119 | 0.7499 |
| Maximum Poletimber (30%) | 2.8772 | 0.7618 |
| Minimum Saplings (0%) | 2.9385 | 0.5074 |
| Maximum Saplings (100%) | 2.7025 | 0.8457 |
| Minimum Hardwood (0%) | 2.7035 | 0.8225 |
| Maximum Hardwood (87%) | 2.9226 | 0.6153 |
| Minimum Softwood (13%) | 2.9226 | 0.6153 |
| Maximum Softwood (100%) | 2.7035 | 0.8225 |
| Relation | Talladega (R2, p) | Oakmulgee (R2, p) | Bankhead (R2, p) | Chattahoochee (R2, p) |
|---|---|---|---|---|
| FD vs. Sawtimber | 0.229, 0.002 | 0.701, <0.001 | 0.666, <0.001 | 0.551, <0.001 |
| FD vs. Poletimber | 0.105, 0.03 | 0.711, <0.001 | 0.004, 0.297 | 0.277, 0.001 |
| FD vs. Saplings | 0.268, 0.001 | 0.751, <0.001 | 0.640, <0.001 | 0.627, <0.001 |
| I vs. Sawtimber | 0.239, 0.001 | 0.627, <0.001 | 0.552, <0.001 | 0.551, <0.001 |
| I vs. Poletimber | 0.107, 0.107 | 0.484, <0.001 | 0.064, 0.087 | 0.241, 0.003 |
| I vs. Saplings | 0.277, 0.001 | 0.639, <0.001 | 0.619, <0.001 | 0.616, <0.001 |
| FD vs. Hardwood | 0.336, <0.001 | 0.836, <0.001 | 0.649, <0.001 | 0.579, <0.001 |
| FD vs. Softwood | 0.336, <0.001 | 0.836, <0.001 | 0.649, <0.001 | 0.579, <0.001 |
| I vs. Hardwood | 0.271, 0.001 | 0.797, <0.001 | 0.709, <0.001 | 0.529, <0.001 |
| I vs. Softwood | 0.271, 0.001 | 0.797, <0.001 | 0.709, <0.001 | 0.529, <0.001 |
| Relation | Talladega | Oakmulgee | Bankhead | Chattahoochee |
|---|---|---|---|---|
| FD vs. Sawtimber + Elevation | 0.55 | 0.699 | 0.669 | 0.658 |
| FD vs. Poletimber + Elevation | 0.513 | 0.712 | 0.042 | 0.515 |
| FD vs. Saplings + Elevation | 0.562 | 0.75 | 0.632 | 0.624 |
| I vs. Sawtimber + Elevation | 0.616 | 0.619 | 0.568 | 0.567 |
| I vs. Poletimber + Elevation | 0.58 | 0.474 | 0.111 | 0.457 |
| I vs. Saplings + Elevation | 0.626 | 0.632 | 0.618 | 0.611 |
| FD vs. Hardwood + Elevation | 0.627 | 0.84 | 0.668 | 0.588 |
| FD vs. Softwood + Elevation | 0.627 | 0.84 | 0.668 | 0.588 |
| I vs. Hardwood + Elevation | 0.625 | 0.793 | 0.743 | 0.534 |
| I vs. Softwood + Elevation | 0.625 | 0.793 | 0.743 | 0.534 |
| Stand Size Class Prediction Model * | R2 | Adjusted R2 |
|---|---|---|
| Sawtimber (%) = −340.51 + 145.45 * FD | 0.224 | 0.217 |
| Sawtimber (%) = −352.01 + 149.97 * FD − 0.0054 * Elevation | 0.224 | 0.211 |
| Saplings (%) = 593.02 − 202.73 * FD | 0.360 | 0.354 |
| Saplings (%) = 635.34 − 219.37 * FD + 0.02 * Elevation | 0.366 | 0.355 |
| Sawtimber (%) = 209.48 − 181.88 * I | 0.423 | 0.418 |
| Sawtimber (%) = 297.75 − 270.35 * I − 0.0886 * Elevation | 0.525 | 0.516 |
| Saplings (%) = −131.6696 + 199.51* I | 0.421 | 0.416 |
| Saplings (%) = −219.08 + 287.13 * I + 0.0878 * Elevation | 0.504 | 0.495 |
*Sawtimber: Diameter at Breast Height (DBH) > 22.9 cm, Poletimber: DBH = 12.7 to 22.9 cm, and Saplings: DBH = 2.5 to 12.7 cm; Poletimber (%) = 100 − (Sawtimber (%) + Saplings (%))
| Category of Species Prediction Model | R2 | Adjusted R2 |
|---|---|---|
| Hardwood (%) = −546.266 + 209.834 * FD | 0.561 | 0.557 |
| Hardwood (%) = −540.85 + 207.71 * FD + 0.0026 * Elevation | 0.561 | 0.554 |
| Softwood (%) = 646.266 − 209.834 * FD | 0.561 | 0.557 |
| Softwood (%) = 640.85 − 207.71 * FD − 0.0026 * Elevation | 0.561 | 0.554 |
| Hardwood (%) = 181.733 − 178.064 * I | 0.489 | 0.484 |
| Hardwood (%) = 211.22 − 207.62 * I − 0.0296 * Elevation | 0.502 | 0.494 |
| Softwood (%) = −81.733 + 178.064 * I | 0.489 | 0.484 |
| Softwood (%) = −111.218 + 207.62 * I + 0.0296 * Elevation | 0.502 | 0.494 |
| Stand Size Class Prediction Model * | Predicted Average (%) | Actual Average (%) | MAPE (%) | RMSE ** | r | R21:1*** |
|---|---|---|---|---|---|---|
| Sawtimber (%) = −340.51 + 145.45 * FD | 72 | 68 | 5.9 | 11 | 0.75 | 0.478 |
| Sawtimber (%) = −352.01 + 149.97 * FD − 0.0054 * Elevation | 71 | 68 | 4.4 | 10 | 0.75 | 0.496 |
| Saplings (%) = 593.02 − 202.73 * FD | 18 | 25 | 27.7 | 12 | 0.80 | 0.455 |
| Saplings (%) = 635.34 − 219.37 * FD + 0.02 * Elevation | 21 | 25 | 15.8 | 11 | 0.79 | 0.547 |
| Sawtimber (%) = 209.48 − 181.88* I | 78 | 68 | 14.7 | 15 | 0.74 | 0.089 |
| Sawtimber (%) = 297.75 − 270.35 * I − 0.0886 * Elevation | 72 | 68 | 5.9 | 13 | 0.67 | 0.221 |
| Saplings (%) = −131.6696 + 199.51 * I | 12 | 25 | 51.4 | 17 | 0.79 | 0.059 |
| Saplings (%) = −219.08 + 287.13 * I + 0.0878 * Elevation | 20 | 25 | 19.8 | 14 | 0.74 | 0.399 |
*Sawtimber Diameter at Breast Height (DBH) > 22.9 cm, Poletimber. DBH = 12.7 to 22.9 cm, and Saplings: DBH = 2.5 to 12.7 cm, Poletimber (%) = 100 − (Sawtimber (%) + Saplings (%));**Variance of Sawtimber = 241; Variance of Saplings = 290;***R21:1 measures fit around a 1:1 line through the origin.
| Category of Species Prediction Model | Predicted Average (%) | Actual Average (%) | MAPE (%) | RMSE * | r | R21:1** |
|---|---|---|---|---|---|---|
| Hardwood (%) = −546.266 + 209.834 * FD | 48.8 | 42.4 | 14.1 | 11 | 0.77 | 0.565 |
| Hardwood (%) = −540.85 + 207.71 * FD + 0.0026 * Elevation | 49.1 | 42.4 | 16.5 | 11 | 0.77 | 0.564 |
| Softwood (%) = 646.266 − 209.834 * FD | 51.3 | 57.6 | 10.4 | 11 | 0.77 | 0.591 |
| Softwood (%) = 640.85 − 207.71 * FD − 0.0026 * Elevation | 50.9 | 57.6 | 12.1 | 11 | 0.77 | 0.594 |
| Hardwood (%) = 181.733 − 178.064 * I | 53.5 | 42.4 | 25.9 | 14 | 0.74 | 0.428 |
| Hardwood (%) = 211.22 − 207.62 * I − 0.0296 * Elevation | 50.6 | 42.4 | 18.9 | 13 | 0.71 | 0.472 |
| Softwood (%) = −81.733 + 178.064 * I | 46.4 | 57.6 | 19.1 | 14 | 0.74 | 0.544 |
| Softwood (%) = −111.218 + 207.62 * I + 0.0296 * Elevation | 49.5 | 57.6 | 13.9 | 13 | 0.71 | 0.504 |
*Variance of Hardwood = 121; Variance of Softwood = 121;**R21:1 measures fit around a 1:1 line through the origin.
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Hamdan, M.; Cruise, J.; Rickman, D.; Quattrochi, D. Forest Stand Size-Species Models Using Spatial Analyses of Remotely Sensed Data. Remote Sens. 2014, 6, 9802-9828. https://doi.org/10.3390/rs6109802
Al-Hamdan M, Cruise J, Rickman D, Quattrochi D. Forest Stand Size-Species Models Using Spatial Analyses of Remotely Sensed Data. Remote Sensing. 2014; 6(10):9802-9828. https://doi.org/10.3390/rs6109802
Chicago/Turabian StyleAl-Hamdan, Mohammad, James Cruise, Douglas Rickman, and Dale Quattrochi. 2014. "Forest Stand Size-Species Models Using Spatial Analyses of Remotely Sensed Data" Remote Sensing 6, no. 10: 9802-9828. https://doi.org/10.3390/rs6109802
APA StyleAl-Hamdan, M., Cruise, J., Rickman, D., & Quattrochi, D. (2014). Forest Stand Size-Species Models Using Spatial Analyses of Remotely Sensed Data. Remote Sensing, 6(10), 9802-9828. https://doi.org/10.3390/rs6109802




