Quantifying Forest Spatial Pattern Trends at Multiple Extents: An Approach to Detect Significant Changes at Different Scales
Abstract
: We propose a procedure to detect significant changes in forest spatial patterns and relevant scales. Our approach consists of four sequential steps. First, based on a series of multi-temporal forest maps, a set of geographic windows of increasing extents are extracted. Second, for each extent and date, specific stochastic simulations that replicate real-world spatial pattern characteristics are run. Third, by computing pattern metrics on both simulated and real maps, their empirical distributions and confidence intervals are derived. Finally, multi-temporal scalograms are built for each metric. Based on cover maps (1954, 2011) with a resolution of 10 m we analyze forest pattern changes in a central Apennines (Italy) reserve at multiple spatial extents (128, 256 and 512 pixels). We identify three types of multi-temporal scalograms, depending on pattern metric behaviors, describing different dynamics of natural reforestation process. The statistical distribution and variability of pattern metrics at multiple extents offers a new and powerful tool to detect forest variations over time. Similar procedures can (i) help to identify significant changes in spatial patterns and provide the bases to relate them to landscape processes; (ii) minimize the bias when comparing pattern metrics at a single extent and (iii) be extended to other landscapes and scales.1. Introduction
Forest ecosystems have played a major role in human history, and periodic deforestation has accompanied population growth and development throughout the world for thousands of years [1]. Although tropical forests are affected by intensive deforestation because of the dependence of local populations on land-based economic activities, harvesting practices, of vital importance in the postwar economy, have recently become moderate in temperate forests [1]. In particular, the current distribution of temperate forests in several hilly and mountainous landscapes of Europe derive from centuries of extensive forest exploitation followed by the abandonment of traditional agricultural practices [2–4]. In this context, the analysis of forest spatial pattern through time and, in particular, the study of the process of natural regrowth is of primary importance in ecological research because forest distributions could affect many ecosystem functions at multiple scales [4].
The most common approach for analyzing changes in forest spatial patterns over time is the mere comparison of pattern metrics extracted from areas of fixed size defined by administrative or natural limits [5,6]. However, such an approach could be problematic for at least three principal issues: (i) the arbitrary choice of the extent of the analyzed area [7]; (ii) the lack of specific scale breaks (thresholds) to identify significant changes in landscape structure and function [8]; and (iii) the negligence, or, in the worst cases, the absence of an analysis of statistical significance when comparing categorical maps [9]. Indeed, forests, like other ecological systems, are characterized by a hierarchical spatial structure [10–14] where specific patterns and processes may take place at certain “characteristic” spatial extents (scale effect) [15]. This means that, for example, different forest dynamics can be most effectively studied at a particular characteristic extent. Thus, identifying this characteristic extent provides a key to further understand the processes that occur in a specific ecological system. It follows that limiting the analysis of forest distribution to a single spatial extent could introduce potential bias or misleading conclusions in pattern analysis [16,17]. Furthermore, the majority of pattern metrics, commonly used to quantify and monitor forest spatial distribution, are scale-dependent, and their scale sensitivity has been demonstrated (see Šímová and Gdulová [7] for a review) for both empirical [18–22] and simulated landscapes [16,18,23]. In fact, the limitations and pitfalls introduced as a result of the use of landscape metrics to compare landscapes with different map sizes are well documented (see Sitzia et al. [24] for examples), and there is a critical need for further research addressing the influence of spatial extent on pattern analysis over time. An accurate knowledge of metric scaling relations could be given by empirical scalograms in which variations of pattern metrics are plotted directly against scale [25,26]. In this context, we believe that multi-temporal scalograms could help in both cases: Relate the observed patterns to underlying ecological processes and correctly extrapolate the recorded information across scales. Finally, although the observed spatial patterns are the realization of specific spatial processes [27], it is of great importance to understand whether the observed differences between two patterns could have arisen purely by chance or whether a specific process has promoted this differences [9]. Nevertheless, the attribution of statistical significance to differences in forest pattern over time is still one of the most important and complex challenges to be faced [27]. The statistical comparison of two different landscapes is quite difficult to perform because field studies usually address only one or a few landscapes so that no simple test is available for making statistical inferences [9,15,27]. One possible way to compare and test the statistical significance of pattern metric values between two maps is the use of computer-generated simulations (e.g., Neutral Landscape Models) to reproduce a set of maps with spatial characteristics (composition and configuration) that are similar to real-world characteristics [27–31]. Among the neutral landscape models [9,31], the Modified Random Cluster Method (MRC) [32] is able to correctly represent forest aggregation (or fragmentation) caused by human land use pressure [33]. By varying simulation parameters (the proportion of forest cover pi and the degree of aggregation H), it is possible to obtain different levels of habitat aggregation and patchiness [32]. In view of the above, we are strongly confident that such statistical methods, if extended to multi-temporal analysis, could offer a consistent framework for assessing forest pattern changes over time and sound information necessary for relating them to landscape processes.
Based on consideration of the aforementioned points, we propose and test a procedure in this study to quantify the spatial pattern of forests over time at multiple spatial extents with statistically robust methods. As an application, we focus on forest cover dynamics in hilly landscapes. We analyze the spatial pattern of temperate forest patches in a Man and Biosphere Reserve (MAB-UNESCO) in central Italy as a representative example of landscape transformation occurring during the past 60 years in sub-Mediterranean hilly landscapes. In particular, we attempt to clarify the following questions by implementing the proposed procedure: (i) how did the forest pattern vary on the compared dates in relationship to various spatial extents? (ii) do specific scale breaks exist that indicate consistent changes in landscape structure and function? (iii) are the differences in the spatial pattern of forests over time statistically significant? To address this issue appropriately, we first used a set of pattern metrics to describe the forest spatial dynamics over time and across various extents and then assessed the statistical significance of any possible differences by comparing the metric values of real and simulated landscapes. An analysis at multiple spatial scales might help to better define the characteristic extents at which it is possible to focus on specific aspects of forest dynamics (e.g., forest loss or gain; forest fragmentation or coalescence of forest patches). The assessment of the statistical significance of forest pattern differences over time and across scales could also offer sound information to relate the observed spatial pattern to the specific underlying ecologic processes and to better understand the specificities of the study case, thus allowing for the application in other cases.
2. Materials and Methods
2.1. Study Area
The Collemeluccio-Montedimezzo Man and Biosphere Reserve (MAB-UNESCO) in Central Italy was selected for analysis (Figure 1). This MAB reserve was chosen because the recent historic changes occurring in this area offer a good example of the pattern of landscape transformation in all sub-Mediterranean hilly landscapes. Since the end of the Second World War, many socio-economic changes have occurred in Europe, where the abandonment of traditional rural activities has produced marked changes in the distribution of temperate forests [34–36]. The reserve and its buffer zone covers approximately 25,000 ha and currently consists of a hilly and mountain landscape dominated by broadleaved natural forests (60% of the area) and other semi-natural vegetation types, such as shrubs and meadows (20% of the area), along with agricultural land and pastures (20% of the area). Altitudes range from 380 m a.s.l., (the Verrino fluvial plain) to 1730 m a.s.l. (Mt. Capraro), and the climate is temperate [37]. The main potential natural vegetation (sensu Zerbe [38] and Ricotta et al. [39]) is a broadleaved temperate forest [36,37].
2.2. Forest Cover Maps
To assess changes in forest distribution, we used existing large-scale (1:8000) forest cover maps of the MAB reserve for the years 1954 and 2011. The 2011 forest cover map was derived by applying a manual classification process (manual segmentation and photointerpretation supported by field data performed in summer 2011) to panchromatic digital orthophotos (flight AGEA05) relative to the Collemeluccio-Monte di Mezzo Reserve. For the preparation of the 1954 map, a series of greyscale aerial photographs (flight GAI) were acquired, georeferenced and digitized within a Geographic Information System. The 1954 aerial photos were scanned in 8-bit TIFF images with a resolution of 600 dpi and orthorectified using OrthoEngine software (PCI Geomatica) with a 10 m Digital Elevation Model (DEM). For each data frame, 30 ground control points were used for the orthorectification process, and the resulting Root Mean Square Error (RMSE) was less than 4 m. A manual classification process was applied to produce the 1954 forest cover map. Next, both forest cover maps (1954 and 2011) were rasterized with a spatial resolution of 10 m. To make the maps comparable, we set the minimum mapping unit to 0.5 ha by applying a majority filter.
2.3. Data Analysis
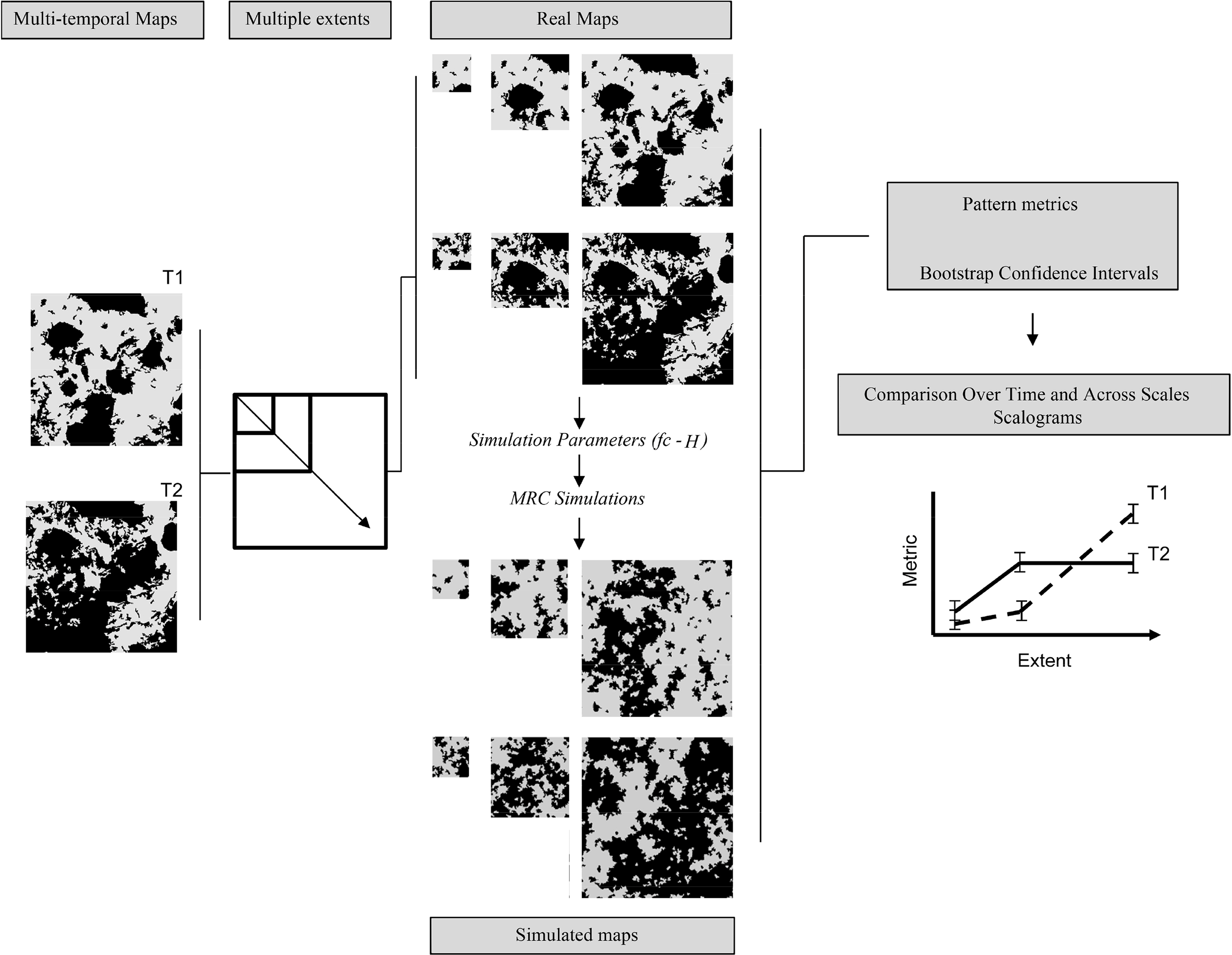
We quantified the spatial pattern of forests over time at multiple spatial extents using real and simulated maps and detected significant changes in forest spatial pattern relaying on bootstrapping procedures [29] to perform significance testing. The general framework is outlined in Figure 2.
2.4. Multi-Scale Analysis
To perform the multi-scale (extent) analysis over time, we selected from both forest maps (1954 and 2011), a set of three representative geographic windows of different dimensions. As suggested by Wu [22], we delineated a first window extent of 128 × 128 pixels (small) and diagonally expanded it starting from the upper left corner to the bottom right corner of the original area with the following increasing dimensions: 256 × 256 (medium) and 512 × 512 pixels (large). It is important to note that also the window direction can influence the result of a pattern metric analysis, since landscapes are commonly anisotropic [20]. However, we overcome this issue by using neutral simulations (as described below) able to reproduce isotropic landscapes. The analyzed extents correspond to 163.84 ha, 655.36 ha and 2621.44 ha, respectively (Figure 1). The selected widow dimensions are comparable with those commonly used for local and regional forest analysis at landscape scale [40]. As suggested by O’Neil et al. [19], the chosen extents are at least two times larger than the largest patch area in the year 1954 (see Figure 1). To frame the landscape transformation patterns in an ecologically significant manner, the wider window was entirely included in one homogeneous environmental type [36], i.e., in one potential natural vegetation type [38,39], thus, in an area where in absence of human interventions or hazard events the vegetation would evolve in one potential natural type (see Zerbe [38] and Ricotta et al. [39] for details). Note that in our case the analysis on larger windows would include in the extent, areas with different and heterogeneous environmental characteristics (geology, morphology, soils and climate) and, thus, forest dynamics must be interpreted accounting of the presence of extra environmental heterogeneity.
2.5. Spatial Pattern Analysis
To analyze the spatial pattern of forests over time and across extents, we selected a set of eight pattern metrics that had been previously reported as ecologically meaningful and that have proven useful for describing and comparing the spatial structure of forests [41,42]. The selected metrics are adequate for describing forest patch size (MPS = Mean Patch Size), forest subdivision (NP = Number of Patches, PD = Patch Density), forest spatial geometry (LSI = Landscape Shape Index, ED = Edge Density TE = Total Edge), and connectivity (AI = Aggregation Index, CLUMPY = Clumpiness Index). The landscape pattern analysis software FRAGSTATS 4.0 [43] was used to calculate the metrics. The description of the pattern metrics used in the study (based on McGarigal and Marks [44]), along with their respective variation range, are provided in Table 1.
The scaling behavior of the Number of Patches [21–23], the Total Edge [18,21,22] and the Shape Index [22,23] is well documented, whereas the relation between Mean Patch Size and the extent has been found to be unpredictable [22]. However, current information about the response of Edge Density, Aggregation, Clumpiness and Patch Density to changing scales is highly controversial (see Table 1 for details). Several studies have reported that Edge Density, Patch Density [16] Aggregation and Clumpiness [20] were insensitive or weakly sensitive to the spatial extent of the analysis, whereas several others have stated that they could show different types of scaling behaviors [21–23].
2.6. Map Simulations and Inference
In the real world, replications of a given landscape are often difficult to obtain because each single landscape shows a specific degree of land cover proportion and spatial autocorrelation [30]. To overcome the limited number of replications in natural landscapes, it is possible to rely upon simulations based on computer-generated models that serve to reproduce an expected pattern that shares statistical properties with an empirical pattern of interest [30]. Among the spatial models developed in ecology, Neutral Landscape Models (NLMs) can produce an expected pattern in the absence of specific landscape processes [45]. In this study, we used the Modified Random Cluster Method (MRC) implemented in the software SIMMAP 2.0 [32] to generate categorical (thematic) landscape spatial patterns in raster format (grid-based data). MRC is a stochastic simulation procedure that, through the variation of simulation parameters (the proportion of forest cover, fc, and the initial probability, p, which controls the degree of spatial autocorrelation), provides a wide range of simulated landscapes with intermediate levels of spatial dependence and in which the fragmentation and abundance of land-cover classes can be systematically and independently controlled (see, for details, Saura and Martínez-Millán [32]).
First, for each year and extent, we simulated 15 maps (see Appendix A) that adequately characterized the mean values for the metrics considered [46]. We ran specific simulations for each extent and date, using their corresponding actual fc and p values as input. Because the initial probability p is not an explicit spatial pattern metric, we iteratively generated landscapes with different levels of p and then chose those simulated landscapes in which the level of autocorrelation, measured as Contagion H [47], was similar (based on a 99% confidence interval) to those of the observed real landscapes. Thus, by computing selected pattern metrics (Table 1) on both real and simulated landscapes, their empirical distributions (sensu Fortin et al. [29]) for each date and extent were derived. The empirical distributions, which are functions of the parameters used to generate the landscapes (fc and p), are often non-Gaussian but they provide the basis for determining confidence intervals [30]. Since pattern metrics are not statistics per se, that is their distributions are not derived analytically, to statistically compare them randomizations, resampling techniques or bootstrapping procedures are needed [48]. To compare real map pattern indices at different scales and time a bootstrap procedure (Bias-Corrected and accelerated bootstrap) was applied. By bootstrapping pattern metric values of each set of simulated MRC maps (three window sizes and two time periods) we derived the arithmetic mean and the 99% confidence intervals necessary to perform the significance testing [23,30,48]. If the confidence intervals (e.g., 99%) of a given spatial metric between different extents or time periods overlap, it can be stated that there are no significant differences between the compared landscapes. In order to better interpret the magnitude of the observed temporal processes, we measure the effect size of forest pattern change by computing the weighted average of the standardized difference (based on pooled variance measures) between mean metric values (for small medium and large windows) in 1954 and 2011 landscapes (that is, Hedges’ g [49]). The effect size is positive when the metric value of the 2011 maps is greater than that of the 1954 ones and is negative when the metric value decrease in the recent time period. The magnitude of the effect size indicates which pattern metric has changed more than the others. We used a resampling procedure based on 10000 bootstrap samples (with replacement) to generate the mean effect size and 99% confidence intervals. All the analyses were performed in the R statistical computing program [50] by using the BootES package [51]. Then, for each metric, we built a multi-temporal scalogram by representing real map values (three map extents 128 × 128, 256 × 256 and 512 × 512 pixels and two temporal periods 1954 and 2011) and the 99% confidence intervals (obtained by bootstrapping procedures on metric values of simulated MRC maps). Each multi-temporal scalogram reported the response curve of one pattern metric to changing extents on both the compared time periods (1954 and 2011).
3. Results
3.1. Pattern Metrics across Extents
The analysis of the multi-temporal scalograms underlined the existence of many significant differences between the compared extents of analysis and pinpointed specific behaviors of pattern metrics for each date (Figure 3; Table 2). Note that although the changes in the 2011 response curves were strongly linear, the 1954 curves appear to show a scale break (sensu Wu et al. [25]). For most of the metrics measured on the 1954 maps, an abrupt variation in the response curve at medium scale is evident.
In the more recent landscape (2011), significant differences across all three compared extents were found for six of the eight metrics (except for ED and CLUMPY). In particular, ED significantly decreased between the small and the large extent as well as the medium and the large extent. The clumpiness index significantly increased from the smallest and the largest extents as well as between the medium and the large extents. The MPS, TE, NP, LSI and AI showed significant increases across the considered extents, whereas PD showed a significant decrease. The 1954 scalograms showed significant differences across all the extents for four of the analyzed parameters (TE, NP, SI and ED). All these metrics increased as the extent expanded. Mean Patch Size (MPS) significantly increased between small and medium extents as well as between small and large extents. The Aggregation Index (AI) significantly increased between the small and the medium extent, but no significant changes were evident between medium and large extents. Both patch density (PD) and Clumpiness Index (CLUMPY) tended to decrease across extents, but no significant changes were evident.
3.2. Pattern Metrics over Time
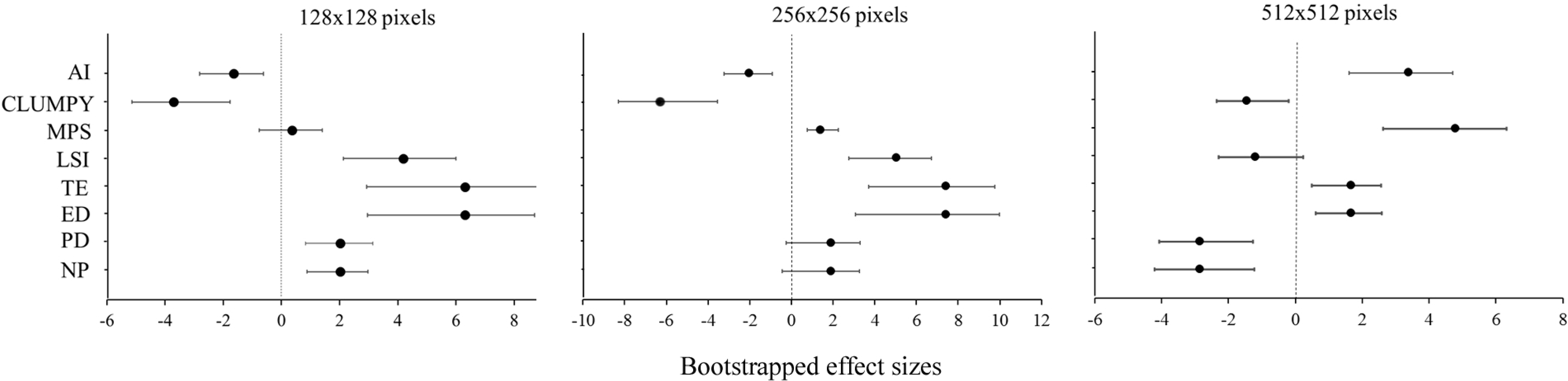
Comparing the maps for 1954 and 2011 (Figure 1), we found significant temporal changes in both the abundance and the spatial distribution of forests. Although the effect size varied between pattern metrics and scales (Figure 4). The magnitude of the effect sizes for each metric varies in correspondence of the different scales and tends to be higher on small and medium extents. For medium and small scales we found that TE and ED are the most sensitive metrics with an effect size substantially higher than that of the other metrics (Figure 4). For large extents, the most sensitive parameters are MPS and AI (Figure 4). Overall we found that all the significant changes on pattern metrics over time are relevant. The analysis of the multi-temporal scalograms (Figure 3) showed a strong influence of the spatial extent on forest pattern, and a specific response curve for the compared dates was also evident. The observed scaling relationships over time were schematically summarized in three main types of multi-temporal scalograms: Type A, where pattern metric curves for the compared data did not intersect and did not converge with each other; Type B, in which scalograms intersected each other and diverged; and Type C, with metric curves that converged but did not intersect.
Type A metrics tend to increase over time regardless of the extent of analysis. Total Edge (TE) and Mean Patch Size (MPS), increased between 1954 and 2011 across all extents, and belonged to this group. However, note that the MPS values at the smallest extent were not significantly distant from each other (99% confidence interval overlap between them). The scalograms of Type B intersected each other; furthermore, depending on the chosen extent of analysis, opposite temporal changes in the spatial metrics emerged. Interestingly, most of the metrics belong to this Type B group: Number of Patches (NP), Patch Density (PD), Aggregation Index (AI) and Shape Index (SI). For example, the curves describing Number of Patches (NP) and Patch Density (PD) relative to the years 2011 and 1954 intersected each other after the medium extent. Thus, the analysis of forest pattern at medium and small extents showed significant increments in the number and density of forest patches. In contrast, at the largest extent, a significant decrease in the number and density of patches between 1954 and 2011 was found. SI showed similar behavior, but the decline in the 2011 map was not significant at the largest extent. For the Aggregation Index at smaller extents, the 1954 curve was higher than the 2011 curve, whereas the 1954 curve dropped below the 2011 curve at the largest extent. Specifically, the AI values decreased significantly between 1954 and 2011 at smaller extents but significantly increased at the largest extent. In the Type C scalograms, the 1954 and 2011 curves tended to converge but maintained significant distances at all the investigated spatial extents and did not intersect. Type C curves included ED and CLUMPY. In particular, CLUMPY significantly increased over time as ED significantly decreased.
4. Discussion
The observed increase in forest cover over the past 60 years, along with the significant changes in forest spatial pattern and the effect sizes analysis, suggest that the analyzed area has undergone an intense process of natural recolonization that began after World War II and that is still in progress. The phenomenon that we observed could be considered reforestation (sensu Sitzia et al. [24]), i.e., the natural reestablishment of a forested landscape on disused agricultural lands following farm abandonment in regions where the potential natural vegetation (sensu Zerbe [38]) is a forest.
The statistical comparison of pattern metrics at different window sizes over time allows the recognition of the characteristic extent, highlighted by the scale breaks, at which specific patterns of the ongoing process of reforestation are more evident. For the compared dates, significant variations in many metric values were found to correspond with different map extents. The multi-temporal scalograms of type A summarize the behavior of metrics (MPS and TE) that describe similar temporal changes in forest pattern regardless of the extent of analysis. Even if such parameters can be sensitive to the map boundary effect [21,52], they unambiguously depict the ongoing landscape process of forest regrowth in our case. The increase in patch size and edge length over time suggests that forest regrowth has occurred evenly over the entire landscape. At small extents, the absence of significant differences in patch size in association with an increase in the total edge length depicts a landscape with many small patches that, most likely, are the new nuclei of young forests [34]. In the multi-temporal scalograms of type B, the curves intersect each other due to the presence of a scale break at the medium extent for the 1954 scalograms. The curves of type B include parameters such as NP, PD, AI and LSI that describe opposite temporal trends in the pattern of forests depending on the extent of analysis. Such findings serve as a warning to researchers and planners. If these parameters are used over time, it is strongly recommended to analyze them at multiple scales to avoid misleading or partial conclusions. In our case, the parameters of type B describe different aspects of the forest regrowth process. At small and medium extents, the general increase in the number of patches and their spatial density over time describe the ongoing process of natural recolonization. Indeed, the establishment of several new forest nuclei is characteristic of the natural colonization of abandoned lands in Mediterranean ecosystems [34]. In contrast, the observed decrease at larger extents in NP, PD and SI describes the expansion and the coalescence of several secondary forest patches into larger ones [31,34,35,53]. Similar behavior is also evident for the AI index. At smaller extents, decreasing values of AI pinpoint the typical disaggregated pattern that characterizes the initial stages of natural forest regrowth [34]. In contrast, at the larger extent, the significant decline in forest pattern aggregation over time highlights the process of coalescence of forest patches and the consequent increase in forest connectivity. In the scalograms of type C, the 1954 and 2011 curves are significantly distant but tend to converge at the largest extent. The growth of ED over time and the reduction of CLUMPY values clearly indicate a more dispersed distribution of present-day forests relative to past forests. The convergence of ED values in association with a significant increase in forest cover-from 35% (1954) to 62% (2011)-is most likely related to the parabolic distribution of the index as a function of forest cover [54,55]. In particular, ED values increase as forest cover expands and peak when the proportion of forest reaches 50% of the landscape extent. For this reason, markedly different landscapes exhibit very similar ED values. On the other hand, the significant decrease in CLUMPY values over time and across all the extents reveals an increase in forest dispersion. Most likely, the process of natural forest recolonization in abandoned lands occurs in a stochastic manner [34].
Overall, the observed differences in the scaling behaviors over the compared time periods are most likely related to the various ways in which humans exploited landscape resources in the compared years. In 1954, for example, land-based economic activities (such as grazing and agriculture) had forced forests into areas in which productivity was low [36] promoting the development of an anisotropic pattern. Instead, the more recent process of natural reforestation has been driving the entire landscape toward a more natural and homogeneous pattern [35]. Forest regrowth on abandoned lands occurs in a stochastic manner [34], with patches that expand isotropically (in all directions) and tend to be uniformly distributed over the entire landscape (statistically stationary). In such situations, pattern metrics manifest predictable and simple scaling relations. Note that the obtained results are strongly dependent on the specific type of landscape, which, in our case, is characterized by a homogeneous underlying environmental structure [36] (geology, morphology, climate, soil). Indeed, we are observing the natural reestablishment of a forested landscape in regions where the potential natural vegetation (sensu Zerbe [38]) is a temperate forest. Different results should emerge in landscapes with high environmental heterogeneity, in which, by tuning the extent of analysis, specific scalograms and metric behaviors could emerge.
Many of the understandings and conclusions obtained in this study have been facilitated by the proposed statistical framework. The chosen modeling procedure, which incorporates the temporal variation in landscape composition (forest cover) and configuration (spatial autocorrelation) occurring in real landscapes [16,19] offers useful insights to address the influence of spatial extent on pattern variation over time. In particular, the utilization of the observed proportions of forest (fc) and the values of spatial autocorrelation (H) as input parameters for the stochastic simulation procedures allows an adequate description of the process of forest regrowth and, at the same time, has yielded a robust statistical and defendable framework. In particular, the application of the MRC algorithm allows the following approaches: (i) modeling a plausible set of maps, with different levels of forest proportion and patchiness, that adequately describes the spatial pattern of forests through time and across scales; (ii) generating a set of landscape replications that recognizes the most relevant real landscape information; (iii) defining the landscape expectations, allowing the statistical comparison of patterns through time and across scales; and (iv) avoiding the effects of the window direction of analysis.
5. Conclusions
Although many authors have stressed the importance and limitations of employing pattern metrics for comparing landscapes [56], the use of these metrics for characterizing and monitoring forest distribution over time continues to be highly popular [57,58]. We proposed and tested a procedure to detect significant changes in forest spatial patterns and relevant scales. This approach enriches the set of the existing methods for multi-scale/multi-temporal landscape studies by including the statistical analysis of the observed differences. As a demonstration, we analyzed the change in the spatial pattern of temperate forests in a Mediterranean hilly landscape over the last 60 years across different extents.
Our results highlight that if landscape pattern is analyzed at a single extent that does not match the scale at which a given phenomenon occurs (e.g., reforestation), the results are incomplete and obscure the effective landscape variation over time. For example, we found that different patterns of the ongoing process of natural reforestation emerged (e.g., nucleation and coalescence of the existing patches in a unique bigger one) at different spatial extents.
The proposed multi-temporal analysis, which incorporates the effects of scale on pattern metrics and the statistical significance of the differences in metric values, have helped to relate the changes in pattern parameters to landscape processes. It overcame and minimized the potential bias introduced in traditional studies that simply resort to the comparison of pattern metrics at a single extent, ignoring information about the distribution and variability of the pattern metrics.
Even if the obtained results are strongly dependent on both the specific type of landscape and the chosen spatio-temporal scales, analogous methods could be used for the study of pattern changes and statistical expectations across a large ensemble of landscapes. In any case, consistent scale breaks could be expected in strongly human-shaped landscapes, where anthropogenic driving forces lead to the juxtaposition of different ecosystems (natural, semi-natural and artificial), whereas linear scaling relations should emerge in more natural landscapes.
From a practical point of view, the obtained results offer scientifically sound bases for orienting decisions in various fields, such as forest management and monitoring. For example, the correct choice of the spatial extent might help to better define conservation measures oriented to increase landscape connectivity values [59]. Furthermore, the proposed approach could allow for the examination of the long-term effects of the extent of the protected area on forest distribution and other conservation features, which is essential for assessing their effectiveness [60,61].
We believe that similar procedures, designed to perform statistically robust multi-temporal and multi-scale analyses, could become a standard method for the comparison of categorical maps, especially if the investigated landscapes, are samples extracted from areas of fixed size and shape [6]. Such procedures are particularly necessary in the consideration of change detection and when uncertainties about the scale and pattern metric values exist and could provide relevant indications regarding the changes in landscape structure over time and all the ecological and cultural consequences linked to this issue.
Acknowledgments
We gratefully acknowledge the editor and three anonymous referees for valuable comments on the original version of the manuscript. The work was partially supported by the CUIA (Consorzio Universitario Italiano per Argentina) in the framework of the project “Conservation and sustainable management of highly fragmented landscapes”.
Author Contributions
Conceived and designed the experiments, analyzed the data and wrote the manuscript: Ludovico Frate, Maria Laura Carranza. Produced data and reviewed the drafts: Michele Minotti, Carmen Giancola, Paolo Di Martino. Discussed main topics and reviewed the text: Santiago Saura.
Conflicts of Interest
The authors declare no conflict of interest.
References
- FAO, State of the World’s Forests 2012; Food and Agriculture Organization of the United Nations: Rome, Italy, 2012.
- MacDonald, D.; Crabtree, J.R.; Wiesinger, G.; Dax, T.; Stamou, N.; Fleury, P.; Gutierrez Lazpita, J.; Gibon, A. Agricultural abandonment in mountain areas of Europe: Environmental consequences and policy response. J. Environ. Manag 2000, 59, 47–69. [Google Scholar]
- Antrop, M. Landscape change and the urbanization process in Europe. Landsc. Urban Plan 2004, 67, 9–26. [Google Scholar]
- Rudel, T.K.; Coomes, O.T.; Moran, E.; Achard, F.; Angelsen, A.; Xu, J.; Lambin, E. Forest transitions: Towards a global understanding of land use change. Glob. Environ. Chang 2005, 15, 23–31. [Google Scholar]
- Turner, M.G.; Gardner, R.H.; O’Neill, R.V. Landscape Ecology in Theory and Practice; Springer: New York, NY, USA, 2001. [Google Scholar]
- Castilla, G.; Linke, J.; McLane, A.J.; McDermid, G.J. Quantifying bias in pattern indices extracted from spatially offset landscape samples. Can. J. For. Res 2011, 41, 2090–2096. [Google Scholar]
- Šímová, P.; Gdulová, K. Landscape indices behaviour: A review of scale effects. Appl. Geogr 2012, 34, 385–394. [Google Scholar]
- Li, H.; Wu, J. Landscape pattern analysis: Key issues and challenges. In Key Topics in Landscape Ecology; Wu, J., Hobbs, R.J., Eds.; Cambridge University Press: New York, NY, USA, 2007; pp. 39–59. [Google Scholar]
- Remmel, T.K.; Fortin, M.J. Categorical, class-focused map patterns: Characterization and comparison. Landsc. Ecol 2013, 28, 1587–1599. [Google Scholar]
- O’Neill, R.V.; DeAngelis, D.L.; Waide, J.B.; Allen, T.F.H. A Hierarchical Concept of Ecosystems; Princeton University Press: Princeton, NJ, USA, 1986. [Google Scholar]
- Urban, D.L.; O’Neill, R.V.; Shugart, H.H. Landscape ecology: A hierarchical perspective can help scientists understand spatial patterns. BioScience 1987, 37, 119–127. [Google Scholar]
- Wu, J. Hierarchy and scaling: Extrapolating information along a scaling ladder. Can. J. Remote Sens 1999, 25, 367–380. [Google Scholar]
- Zurlini, G.; Riitters, K.H.; Zaccarelli, N.; Petrosillo, I.; Jones, K.B.; Rossi, L. Disturbance patterns in a socio-ecological system at multiple scales. Ecol. Complex 2006, 3, 119–128. [Google Scholar]
- Diaz-Varela, E.R.; Marey-Pérez, M.F.; Álvarez-Álvarez, P. Use of simulated and real data to identify heterogeneity domains in scale-divergent forest landscapes. For. Ecol. Manag 2009, 258, 2490–2500. [Google Scholar]
- Li, H.; Wu, J. Concepts of scale and scaling. In Scaling and Uncertain Analysis in Ecology: Methods and Applications; Wu, J., Jones, K.B., Li, H., Loucks, O.L., Eds.; Spinger: Dordrecht, The Netherlands, 2006; pp. 3–15. [Google Scholar]
- Saura, S.; Martínez-Millán, J. Sensitivity of lanscape pattern metrics to map spatial extent. Photogramm. Eng. Remote Sens 2001, 67, 1027–1036. [Google Scholar]
- Gergel, S.E. New direction in landscape pattern analysis and linkages with remote sensing. In Understanding Forest Disturbance and Spatial Pattern: Remote Sensing and GIS Approaches; Wulder, M.A., Franklin, S.E., Eds.; Taylor and Francis: Boca Raton, FL, USA, 2007; pp. 173–208. [Google Scholar]
- Turner, M.G.; O’Neill, R.V.; Gardner, R.H.; Milne, B.T. Effects of changing spatial scale on the analysis of landscape pattern. Landsc. Ecol 1989, 3, 153–162. [Google Scholar]
- O’Neill, R.V.; Hunsaker, C.T.; Timmins, S.P.; Jackson, B.L.; Jones, K.B.; Riitters, K.H.; Wickham, J.D. Scale problems in reporting landscape pattern at the regional scale. Landsc. Ecol 1996, 11, 169–180. [Google Scholar]
- Wu, J.; Shen, W.J.; Sun, W.Z.; Tueller, P.T. Empirical patterns of the effects of changing scale on landscape metrics. Landsc. Ecol 2002, 17, 761–782. [Google Scholar]
- Baldwin, D.J.B.; Weaver, K; Schnekenburger, F.; Perera, A.H. Sensitivity of landscape pattern indices to input data characteristics on real landscapes: Implications for their use in natural disturbances emulation. Landsc. Ecol 2004, 19, 255–271. [Google Scholar]
- Wu, J. Effects of changing scale on landscape pattern analysis: Scaling relations. Landsc. Ecol 2004, 19, 125–138. [Google Scholar]
- Shen, W.; Jenerette, G.D.; Wu, J.; Gardner, R.H. Evaluating empirical scaling realtions of pattern metrics with simulated landscapes. Ecography 2004, 27, 459–469. [Google Scholar]
- Sitzia, T.; Semenzato, P.; Trentanovi, G. Natural reforestation is changing spatial patterns of rural mountain and hill landscapes: A global overview. For. Ecol. Manag 2010, 259, 1354–1362. [Google Scholar]
- Wu, J.; Jelinski, D.E.; Luck, M.; Tueller, P.T. Multiscale analysis of landscape heterogeneity: Scale variance and pattern metrics. Geogr. Inf. Sci 2000, 6, 6–19. [Google Scholar]
- Wu, J. Scale and scaling: A cross-disciplinary perspective. In Key Topics in Landscape Ecology; Wu, J., Hobbs, R.J., Eds.; Cambridge University Press: New York, NY, USA, 2007; pp. 115–137. [Google Scholar]
- Boots, B.; Csillag, F. Categorical maps, comparisons, and confidence. J. Geogr. Syst 2006, 8, 109–118. [Google Scholar]
- Keitt, T.H. Spectral representation of neutral landscapes. Landsc. Ecol 2000, 15, 479–493. [Google Scholar]
- Fortin, M.J.; Boots, B; Csillag, F. On the role of spatial stochastic models in understanding landscape indices in ecology. Oikos 2003, 102, 203–212. [Google Scholar]
- Remmel, T.K.; Csillag, F. When are two landscape pattern indices significantly different? J. Geogr. Syst 2003, 5, 331–351. [Google Scholar]
- Frate, L.; Carranza, M.L. Quantifying landscape-scale patterns of temperate forests over time by means of neutral simulation models. Int. J. Geo-Inf 2013, 2, 94–109. [Google Scholar]
- Saura, S.; Martínez-Millán, J. Landscape patterns simulation with a modified random cluster methods. Landsc. Ecol 2000, 15, 661–678. [Google Scholar]
- Li, X.; He, H.S.; Wang, X.; Bu, R.; Hu, Y; Chang, Y. Evaluating the effectiveness of neutral landscape models to represent a real landscape. Landsc. Urban Plan 2004, 69, 137–148. [Google Scholar]
- Rocchini, D.; Perry, G.L.W.; Salerno, M.; Maccherini, S; Chiarucci, A. Landscape change and the dynamics of open formations in a natural reserve. Landsc. Urban Plan 2006, 77, 167–177. [Google Scholar]
- Geri, F.; Rocchini, D.; Chiarucci, A. Landscape metrics and topographical determinants of large-scale forest dynamics in a Mediterranean landscape. Landsc. Urban Plan 2010, 95, 46–53. [Google Scholar]
- Acosta, A.; Carranza, M.L.; Giancola, M. Landscape change and ecosystem classification in a municipal district of a small city (Isernia, Central Italy). Environ. Monit. Assess 2005, 108, 323–335. [Google Scholar]
- Blasi, C. La Vegetazione d’Italia; Palombi Editore: Rome, Italy, 2003. [Google Scholar]
- Zerbe, S. Potential natural vegetation: Validity and applicability in landscape planning and nature conservation. Appl. Veg. Sci 1998, 1, 165–172. [Google Scholar]
- Ricotta, C.; Carranza, M.L.; Avena, G.C.; Blasi, C. Are potential natural vegetation distribution a meaningful alternative to neutral landscape models? Appl. Veg. Sci 2002, 5, 271–275. [Google Scholar]
- Gomez-Sanz, V.; Bunce, R.G.H.; Elana-Rossello, R. Landscape assessment and monitoring. In Forest Landscape and Global Change: Challenges for Research and Management; Azevedo, J.C., Perera, A.H., Pinto, M.A., Eds.; Springer Science + Business Media: New York, NY, USA, 2008; pp. 199–226. [Google Scholar]
- Haines-Young, R.; Chopping, M. Quantifying landscape structure: A review of landscape indices and their application to forested landscapes. Prog. Phys. Geogr 1996, 20, 418–445. [Google Scholar]
- McGarigal, K.; Cushman, S.; Reagan, C. Quantifying Terrestrial Habitat Loss and Fragmentation: A Protocol; USDA General Technical Report; USDA, Rocky Mountain Region: Golden, CO, USA, 2005. [Google Scholar]
- FRAGSTATS v4. Spatial Pattern Analysis Program for Categorical and Continuous Maps, 2012. Available online: http://www.umass.edu/landeco/research/fragstats/fragstats.html (accessed on 20 February 2014).
- McGarigal, K.; Marks, B.J. FRAGSTATS: Spatial Pattern Analysis Program for Quantifying Landscape Structure; General Technical Report PNW-GTR-351; USDA, Forest Service, Pacific Northwest Research Station: Portland, OR, USA, 1995. [Google Scholar]
- Gardner, R.H.; Milne, B.T.; Turner, M.G.; O’Neill, R.V. Neutral models for the analysis of broad-scale landscape pattern. Landsc. Ecol 1987, 1, 19–28. [Google Scholar]
- Gardner, R.H.; Urban, D.L. Neutral models for testing landscape hypotheses. Landscape Ecol 2007, 22, 15–29. [Google Scholar]
- Li, H.; Reynolds, J.F. A new contagion index to quantify spatial patterns of landscapes. Landsc. Ecol 1993, 8, 155–162. [Google Scholar]
- Fortin, M.J.; Jacquez, G.M.; Shipley, B. Computer-intensive methods. In Encyclopedia of Environmetrics, 2nd ed.; El-Shaarawi, A.H., Piegorsch, W.W., Eds.; Wiley: Chichester, UK, 2012; pp. 399–402. [Google Scholar]
- Hedges, L.V. Distribution theory for Glass’s estimator of effect size and related estimators. J. Educ. Behav. Statist 1981, 6, 107–128. [Google Scholar]
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2014. Available online: http://www.R-project.org/ (accessed on 25 July 2014).
- Kirby, K.N.; Gerlanc, D. BootES: An R package for bootstrap confidence intervals on effect sizes. Behav. Res. Methods 2013, 45, 905–927. [Google Scholar]
- Greenberg, J.D.; Gergel, S.E.; Turner, M.G. Understanding landscape metrics II: The effects of changes in scale. In Learning Landscape Ecology: A Practical Guides to Concepts and Techniques; Gergel, S.E., Turner, M.G., Eds.; Springer-Verlag: New York, NY, USA, 2002; pp. 101–111. [Google Scholar]
- Bracchetti, L.; Carotenuto, L.; Catorci, A. Land-cover changes in a remote area of central Apennines (Italy) and management directions. Landsc. Urban Plan 2012, 104, 157–170. [Google Scholar]
- Neel, M.C.; McGarigal, K.; Cushman, S.A. Behavior of class-level landscape metrics across gradients of class aggregation and area. Landsc. Ecol 2004, 19, 435–455. [Google Scholar]
- Long, J.A.; Nelson, T.A.; Wulder, M.A. Characterizing forest fragmentation: Distinguish change in composition and configuration. Appl. Geogr 2010, 30, 426–435. [Google Scholar]
- Li, H.; Wu, J. Use and misuse of landscape indices. Landsc. Ecol 2004, 19, 389–399. [Google Scholar]
- Turner, M.G.; Pearson, S.M.; Bolstad, P.; Wear, D.N. Effects of land-cover change on spatial pattern of forest communities in the Southern Appalachian Mountains (USA). Landsc. Ecol 2003, 18, 449–464. [Google Scholar]
- Batistella, M.; Robeson, S.; Moran, E.F. Settlement design, forest fragmentation, and landscape change in Rondonia, Amazonia. Photogramm. Eng. Remote Sens 2003, 69, 805–812. [Google Scholar]
- Pascual-Hortal, L.; Saura, S. Impact of spatial scale on the identification of critical habitat patches for the maintenance of landscape connectivity. Landsc. Urban Plan 2007, 83, 176–186. [Google Scholar]
- Diaz-Varela, E.R.; Marey-Pérez, M.F.; Rigueiro-Rodriguez, A.; Álvarez-Álvarez, P. Landscape metrics for characterization of forest landscapes in a sustainable management framework: Potential application and prevention of misuse. Ann. For. Sci 2009, 66. [Google Scholar] [CrossRef]
- Townsend, P.A.; Lookingbill, T.R.; Kingdon, C.C.; Gardner, R.H. Spatial pattern analysis for monitoring protected areas. Remote Sens. Environ 2009, 113, 1410–1420. [Google Scholar]


| Landscape Metrics | Description | Range | Scaling Relation | References |
|---|---|---|---|---|
| Number of Patches (NP) | The number of forest patches | ≥1 | ▲ | (Baldwin et al. [21]; Shen et al. [23]; Wu [22]) |
| Patch Density (PD) | The number of forest patches per unit area (patches/ha) | >0 | ? ▼ | (Shen et al. [23]; Wu [22]) (Saura and Martínez-Millán [16]; Baldwin et al. [21]) |
| Mean Patch Size (MPS) | The average area of all forest patches in the landscape (ha) | >0 | ? | (Shen et al. [23]; Wu [22]) |
| Total Edge (TE) | The sum of the lengths of all forest edges in the landscape (m) | ≥0 | ▲ | (Turner et al. [18]; Baldwin et al. [21]; Shen et al. [23]; Wu [22]) |
| Edge Density (ED) | The total length of all forest edges per ha (m/ha) | ≥0 | ? = | (Shen et al. [23]; Wu [22]) (Saura and Martínez-Millán [16]) (Baldwin et al. [21]) |
| Landscape Shape Index (LSI) | Equals 0.25 times the sum of the entire forest boundary divided by the square root of the total landscape area | ≥1 | ▲▼ | (Shen et al. [23]; Wu [22]) |
| Aggregation Index (AI) | Equals the number of like adjacencies involving the corresponding class (gii), divided by the maximum possible number of like adjacencies involving the corresponding class (max-gii), which is achieved when the class is maximally clumped into a single, compact patch (%) | 0 ≤ AI ≤ 100 | ▼ ? | For the aggregation metrics (sensu McGarigal and Marks [44]) Baldwin et al. [21] reported a general decreasing function, while Wu et al. [20] reported unpredictable function |
| Clumpiness Index (CLUMPY) | Equals the proportional deviation of the proportion of like adjacencies (Gi) involving the corresponding class (Pi) from that expected under a spatially random distribution (%) | 1≤ CLU ≤ +1 |
| Landscape Metrics | 1954 | 2011 | ||||||
|---|---|---|---|---|---|---|---|---|
| Window Size | Real Value | Upper CI | Lower CI | Window Size | Real Value | Upper CI | Lower CI | |
| Number of Patches (NP) | 128 a | 5 * | 5.26 | 3.26 | 128 a | 7 * | 9.8 | 6.93 |
| 256 b | 13 * | 15.73 | 11.73 | 256 b | 19 * | 20.42 | 16.79 | |
| 512 c | 53 * | 63.08 | 49.29 | 512 c | 35 * | 38.00 | 33.78 | |
| Patch Density (PD) | 128 a | 3.03 * | 3.23 | 1.99 | 128 a | 4.24 * | 6.06 | 4.19 |
| 256 a | 1.98 * | 2.42 | 1.79 | 256 b | 2.89 * | 3.15 | 2.56 | |
| 512 a | 2.08 * | 2.41 | 1.90 | 512 c | 1.33 * | 1.45 | 1.29 | |
| Mean Patch Size (MPS) | 128 a | 5.95 ns | 9.71 | 5.61 | 128 a | 10.07 ns | 10.94 | 7.19 |
| 256 b | 15.53 * | 16.92 | 13.88 | 256 b | 19.33 * | 22.05 | 18.27 | |
| 512 b | 17.53 * | 18.97 | 14.97 | 512 c | 46.74 * | 43.83 | 49.75 | |
| Total Edge (TE) | 128 a | 6000 * | 7226 | 5871 | 128 a | 18,200 * | 19,414 | 16,953 |
| 256 b | 30,760 * | 33,638 | 28,944 | 256 b | 64,180 * | 68,893 | 62,195 | |
| 512 c | 153,680 * | 165,624 | 141,188 | 512 c | 191,730 * | 207,541 | 190,012 | |
| Edge Density (ED) | 128 a | 36.34 * | 44.11 | 35.84 | 128 a | 110.22 * | 118.50 | 103.47 |
| 256 b | 46.75 * | 51.33 | 44.17 | 256 a | 97.55 * | 105.12 | 94.902 | |
| 512 c | 58.51 * | 63.18 | 53.86 | 512 b | 72.99 * | 79.158 | 72.487 | |
| Landscape Shape Index (LSI) | 128 a | 3.37 * | 3.73 | 3.07 | 128 a | 6.04 * | 6.39 | 5.64 |
| 256 b | 5.97 * | 6.41 | 5.56 | 256 b | 9.03 * | 9.66 | 8.91 | |
| 512 c | 13.37 ns | 14.21 | 12.07 | 512 c | 12.72 ns | 13.63 | 12.55 | |
| Aggregation Index (AI) | 128 a | 95.53 * | 96.01 | 95.53 | 128 a | 93.93 * | 94.39 | 93.01 |
| 256 b | 96.47 * | 96.72 | 96.47 | 256 b | 95.78 * | 95.79 | 95.41 | |
| 512 ab | 95.92 * | 96.35 | 95.63 | 512 c | 97.10 * | 97.14 | 96.86 | |
| Clumpiness Index (CLUMPY) | 128 ab | 0.9455 * | 0.9515 | 0.9376 | 128 a | 0.8949 * | 0.9043 | 0.8784 |
| 256 a | 0.9491 * | 0.9526 | 0.9451 | 256 ab | 0.9045 * | 0.9049 | 0.8962 | |
| 512 b | 0.9369 * | 0.9434 | 0.9327 | 512 c | 0.9230 * | 0.9237 | 0.9166 | |
a,b,cUppercase letters indicate significant differences among scales.*Asterisks indicate significant differences and ns, no significant differences, among time periods.
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Frate, L.; Saura, S.; Minotti, M.; Di Martino, P.; Giancola, C.; Carranza, M.L. Quantifying Forest Spatial Pattern Trends at Multiple Extents: An Approach to Detect Significant Changes at Different Scales. Remote Sens. 2014, 6, 9298-9315. https://doi.org/10.3390/rs6109298
Frate L, Saura S, Minotti M, Di Martino P, Giancola C, Carranza ML. Quantifying Forest Spatial Pattern Trends at Multiple Extents: An Approach to Detect Significant Changes at Different Scales. Remote Sensing. 2014; 6(10):9298-9315. https://doi.org/10.3390/rs6109298
Chicago/Turabian StyleFrate, Ludovico, Santiago Saura, Michele Minotti, Paolo Di Martino, Carmen Giancola, and Maria Laura Carranza. 2014. "Quantifying Forest Spatial Pattern Trends at Multiple Extents: An Approach to Detect Significant Changes at Different Scales" Remote Sensing 6, no. 10: 9298-9315. https://doi.org/10.3390/rs6109298
APA StyleFrate, L., Saura, S., Minotti, M., Di Martino, P., Giancola, C., & Carranza, M. L. (2014). Quantifying Forest Spatial Pattern Trends at Multiple Extents: An Approach to Detect Significant Changes at Different Scales. Remote Sensing, 6(10), 9298-9315. https://doi.org/10.3390/rs6109298






