An Empirical Assessment of Temporal Decorrelation Using the Uninhabited Aerial Vehicle Synthetic Aperture Radar over Forested Landscapes

Abstract

We present an empirical assessment of the impact of temporal decorrelation on interferometric coherence measured over a forested landscape. A series of repeat-pass interferometric radar images with a zero spatial baseline were collected with UAVSAR (Uninhabited Aerial Vehicle Synthetic Aperture Radar), a fully polarimetric airborne L-band radar system. The dataset provided temporal separations of 45 minutes, 2, 7 and 9 days. Coincident airborne lidar and weather data were collected. We theoretically demonstrate that UAVSAR measurement accuracy enables accurate quantification of temporal decorrelation. Data analysis revealed precipitation events to be the main driver of temporal decorrelation over the acquisition period. The experiment also shows temporal decorrelation increases with canopy height, and this pattern was found consistent across forest types and polarization.

1. Introduction

Interferometric Synthetic Aperture Radar (InSAR) has been used to produce digital elevation models (DEM) of the Earth for several decades [1–3], and has matured to produce global elevation datasets [4]. In radar interferometry, two radar acquisitions are combined to obtain coherence (i.e., similarity between the acquisitions) and phase difference between these acquisitions [5,6]. When obtained from slightly different vantage points, this phase difference (or phase center) can be used to estimate the elevation of the target (e.g. surface topography). In most cases, DEMs derived from interferometry use two antennas that are mounted on an aircraft or spaceborne platform, acquiring data simultaneously. But early work has shown that a single sensor repeating nearly the same flight track can also be used to produce DEM’s [3]. It was soon realized that the interferometric coherence decreases with time between radar acquisitions because of intrinsic changes in surface reflectivity that increase phase noise [5] and reduce elevation measurement accuracy [3,7–9]. Such phenomena are a major unknown in the design of InSAR systems [5] and are still not well understood.

Recent advances that exploit the complementarity between radar interferometry and polarimetric diversity now enable estimates of forest canopy height [10–13]. The height of the phase center within a forest canopy depends on the structural parameters of the canopy as well as the incident and received signal polarization. The so-called Polarimetric interferometric Synthetic Aperture Radar (PolinSAR) technique uses a simplified radar scattering model to invert canopy height or other structural parameters given a set of coherence and phase observations at various polarization configurations. Over short repeat-pass time (i.e., scale of minutes to a few hours), temporal decorrelation over forest usually may be neglected [14,11] but is otherwise significant at longer time scales [7,9]. The motion of leaves and branches caused by wind as well as variations in moisture content (for example from precipitation events) reduce the observed interferometric correlation as do phenological changes of leaf emergence, growth, senescense and fall [7,8]. In [14], it has been shown, using a physical model, that temporal decorrelation depends on the structural parameters of forests, such as canopy height, and changes with polarization. Because the observed coherence becomes dominated by temporal changes rather than the forest volume, it may inhibit estimation of canopy height. The impact of temporal decorrelation has been partially addressed in the PolinSAR model [12,13]. In order to assess DEM accuracy and compensate for its impact in the PolinSAR model, it is necessary to quantify the contribution of temporal decorrelation on InSAR coherence.

In this paper we empirically measure the impact of vegetation structure and type, weather, and sensor configuration on temporal decorrelation of L-band interferometric coherence. Measurements of were acquired during a UAVSAR (Uninhabited Aerial vehicle Synthetic Aperture Radar) experiment specifically designed to assess temporal decorrelation. UAVSAR is an airborne L-band fully polarimetric SAR that enables accurate repeat-pass interferometry [15]. The remainder of this paper is structured as follows. First, we describe the data collection strategy and parameters of the experiment. Next we develop a theoretical treatment of coherence and demonstrate, using this derivation, that UAVSAR performance enables accurate measurements of temporal decorrelation. We then analyze the dependence of InSAR coherence on forest type, canopy height, repeat-pass time interval, weather and polarization using UAVSAR data and conclude with a discussion of our major findings.

2. Data Collection Strategy

The UAVSAR campaign was designed specifically to identify factors that impact InSAR coherence and quantify temporal decorrelation. UAVSAR data were acquired in the Réserve Faunique des Laurentides (Québec, Canada), located between Québec City and Saguenay (47.7°N, −71.3°W) in Eastern Canada, in August 2009. The site is characterized by a 1,000-m elevational gradient with a transition from deciduous temperate to boreal coniferous forest, and includes mature forests in conservation units, as well as managed stands in forest extraction zones. Thus, this site enables the study of temporal decorrelation across broad gradients in forest composition, structure and successional stage.

In general, repeat-pass InSAR coherence estimated over forested areas is dominated by volume decorrelation, temporal decorrelation and thermal noise decorrelation [4]. For an arbitrary spatial and temporal baseline, the volume and temporal decorrelation can be of the same magnitude. To isolate the impact of temporal decorrelation from the volume decorrelation, we performed a set of UAVSAR flights with nominal zero spatial baselines. The UAVSAR system is designed to fly within 5 m of the planned flight track [16]. The residual motion of the platform leads to local deviations of the baseline along the flight trajectory. In the next section, we show UAVSAR’s zero-baseline repeat-pass InSAR acquisitions are sufficiently accurate to ensure that the InSAR coherence measurement is dominated by temporal rather than other system and volume effects.

To measure temporal decorrelation, UAVSAR data were collected several times repeating the same flight track (i.e., zero baseline) to obtain a set of temporal intervals from minutes up to days. Flights were performed twice on 5, 7 and 14 August 2009. This strategy provided temporal periods of 45 min, 2 days, 7 days and 9 days by combining all possible pairs and generating radar interferograms.

3. Accuracy of Temporal Coherence Measurement

In this section, we estimate the expected accuracy of the temporal decorrelation measurement δ_τ using the UAVSAR system. The observed InSAR coherence can be expressed as the product of noise γ_snr, geometric γ_g, volume γ_v and temporal coherences γ_t such that [7]:

$${\gamma }_{\text{m}}={\gamma }_{\text{snr}}{\gamma }_{\text{g}}{\gamma }_{\text{v}}{\gamma }_{\text{t}}.$$

(1)

Given estimates for the other coherence terms, measurements of temporal coherence γ̃_t can be obtained from:

$${\tilde{\gamma }}_t=\frac{{\gamma }_m}{{\gamma }_{\mathit{snr}}{\gamma }_g{\gamma }_v}$$

(2)

In order to obtain the error stemming from the various decorrelation sources, we differentiate Equation (2) to obtain:

$$\mathrm{\Delta }{\tilde{\gamma }}_t=\frac{\partial {\tilde{\gamma }}_t}{\partial {\gamma }_{\mathit{snr}}}\mathrm{\Delta }{\gamma }_{\mathit{snr}}+\frac{\partial {\tilde{\gamma }}_t}{\partial {\gamma }_g}\mathrm{\Delta }{\gamma }_g+\frac{\partial {\tilde{\gamma }}_t}{\partial {\gamma }_v}\mathrm{\Delta }{\gamma }_v=-{\tilde{\gamma }}_t\left[\frac{\mathrm{\Delta }{\gamma }_{\mathit{snr}}}{{\gamma }_{\mathit{snr}}}+\frac{\mathrm{\Delta }{\gamma }_g}{{\gamma }_g}+\frac{\mathrm{\Delta }{\gamma }_v}{{\gamma }_v}\right].$$

(3)

We obtain the individual relative error terms from differentiation of published definitions for γ_snr, γ_v and γ_g. The SNR correlation γ_snr with SNR being the signal-to-noise ratio in linear units as given by [5,7]:

$${\gamma }_{\mathit{snr}}=\frac{\mathit{SNR}}{\mathit{SNR}+1}.$$

(4)

Differentiating with respect to SNR, we obtain:

$$\frac{\mathrm{\Delta }{\gamma }_{\mathit{snr}}}{{\gamma }_{\mathit{snr}}}=\frac{\mathrm{\Delta }\mathit{SNR}}{{\mathit{SNR}}^2}{\gamma }_{\mathit{snr}}.$$

(5)

For volumetric coherence, we set an upperbound using a uniform scattering model with [17]:

$${\gamma }_v-\mathit{sinc}(\frac{k_{z}h}{2}),$$

(6)

where h and k_z are the canopy height and the vertical wavenumber respectively. Assuming a flat Earth, the latter is given by [5,6]:

$${\text{k}}_{\text{z}}=\frac{\partial \varphi }{\partial \text{z}}=\frac{2\pi {\text{pb}}_{\perp }}{\lambda \rho \text{sin}\theta }=\frac{4\pi {\text{b}}_{\perp }}{\lambda {\text{h}}_{\text{p}}\text{tan}\theta }$$

(7)

where b_⊥ is the perpendicular baseline, λ is the signal wavelength, π = 2 for repeat-pass observations, θ the look angle and h_p the platform altitude. Differentiating, we obtain:

$$\frac{\partial {\gamma }_{\text{v}}}{\partial \text{h}}=\frac{1}{\text{h}}\left[\text{cos}\left(\frac{{\text{k}}_{\text{z}}\text{h}}{2}\right)-{\gamma }_{\text{v}}\right]$$

(8)

and therefore

$$\frac{\mathrm{\Delta }{\gamma }_{\text{v}}}{{\gamma }_{\text{v}}}=\frac{\mathrm{\Delta }\text{h}}{\text{h}}\left[\frac{{\text{k}}_{\text{z}}\text{h}}{2\text{tan}\left(\frac{{\text{k}}_{\text{z}}\text{h}}{2}\right)}-1\right].$$

(9)

Finally, the geometric coherence γ_f for a flat surface is given by [5,7]

$${\gamma }_{\text{f}}=1-\frac{2{\text{b}}_{\perp }\mathrm{\Delta }\rho \text{cos}\theta }{\lambda {\text{h}}_{\text{p}}\text{tan}\theta },$$

(10)

where Δ_ρ is the range resolution. Correcting for geometric decorrelation using filtering [17,18] results in

$${\gamma }_{\text{g}}=1-\left(\frac{1-{\gamma }_{\text{f}}}{{\gamma }_{\text{f}}}\right)\left(\frac{\text{tan}\theta }{\text{tan}\left(\theta -{\tau }_{\rho }\right)}-1\right),$$

(11)

where τ_ρ is the terrain slope in the range direction. Differentiating equation (11) with respect to τ_ρ leads to:

$$\frac{\mathrm{\Delta }{\gamma }_{\text{g}}}{{\gamma }_{\text{g}}}=-\left(\frac{1-{\gamma }_{\text{f}}}{{\gamma }_{\text{g}}{\gamma }_{\text{f}}}\right)\frac{2\mathrm{\Delta }{\tau }_{\rho }}{\text{sin}\left(2\left(\theta -{\tau }_{\rho }\right)\right)}.$$

(12)

From Equations (5), (9) and (12), we obtain the relative error in our measurement of temporal decorrelation δ_τ (δ_τ=1−γ̃_t):

$$\frac{\mathrm{\Delta }{\tilde{\gamma }}_t}{{\tilde{\gamma }}_t}=\left|\frac{\mathrm{\Delta }\mathit{SNR}}{{\mathit{SNR}}^2}{\gamma }_{\mathit{snr}}\right|+\left|\frac{\mathrm{\Delta }h}{h}\left[\frac{k_{z}h}{2\text{tan}\left(\frac{k_{Z}h}{2}\right)}-1\right]\right|+\left|\left(\frac{1-{\gamma }_{\text{f}}}{{\gamma }_{\text{g}}{\gamma }_{\text{f}}}\right)\frac{2\mathrm{\Delta }{\tau }_{\rho }}{\text{sin}\left(2\left(\theta -{\tau }_{\rho }\right)\right)}\right|.$$

(13)

Therefore, for the UAVSAR system with a SNR better than 25 dB, maximum baseline of 2.5 m, wavelength of 0.24 m, range resolution of 1.66 m and a platform height of 12.5 km, one obtains an upper bound relative error $\frac{\mathrm{\Delta }{\gamma }_t}{{\gamma }_t}<0.0056$ over forests with canopy height varying between 0 and 30 m and a mean of 15 m, typical of the Reserve Faunique des Laurentides and surrounding parks. At a look angle of 35°, UAVSAR coherence factors are, γ_v = 0.9979, γ_g = 0.9989, γ_snr = 0.99685, which combined contribute less than 1% decorrelation, and are negligible with respect to the observed coherences γ_m, as discussed below. Therefore, we can assume γ̃ ≈ γ_m.

4. Ancillary Data

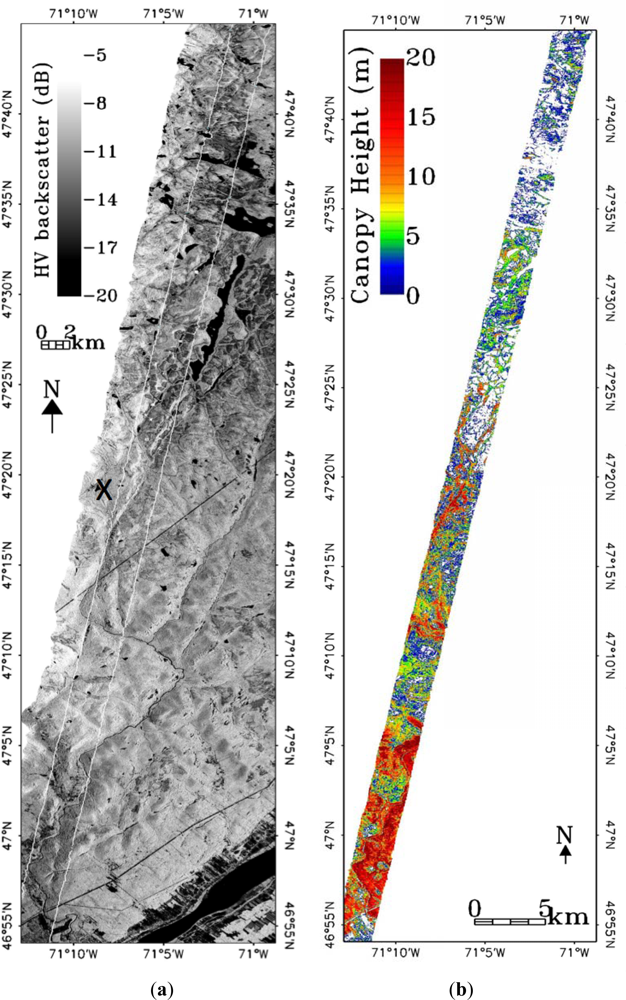
During the UAVSAR campaign, we collected airborne lidar data using the Laser Vegetation Imaging System (LVIS) [19,20] as well as weather data (precipitation and wind). LVIS data provide spatially dense lidar shots covering a 2.5 km wide × 100 km long strip within the UAVSAR data (UAVSAR data has a swath width of approximately 20–23 km with an incidence angle variation of 25°–60°). The LVIS footprint is about 20 m in diameter covering 16 UAVSAR pixels (5 by 5 m). Our analysis focuses on the region covered by the LVIS data (Figure 1) which coincides with a UAVSAR look angle around 35°.

We used the publically distributed LVIS relative height RH75 to represent canopy height. RH75 is a waveform metric defined as the height above the ground at which the waveform cumulative measured energy reaches 75% of the total energy [19]. RH100 is commonly used to represent “canopy height” using LVIS data but is actually the highest return in the waveform footprint (i.e., it is a measurement of the tallest tree). Because a single LVIS footprint encompasses multiple UAVSAR pixels, the use of RH100 to understand canopy height effects is problematic. A better measure is related to the average canopy height within the footprint, say as determined from the dominant or co-dominant trees, as this would capture sub-footprint variation in canopy height within an LVIS shot commensurate with UAVSAR pixel size. RH75 has been shown to be more representative of the average height of the canopy surface within footprints and is also well-correlated to basal-area weighted height (Lorey’s height) at the plot level [21]. Additionally, RH75 is less sensitive than RH100 to geolocation error and horizontal heterogeneity of forest canopies [22].

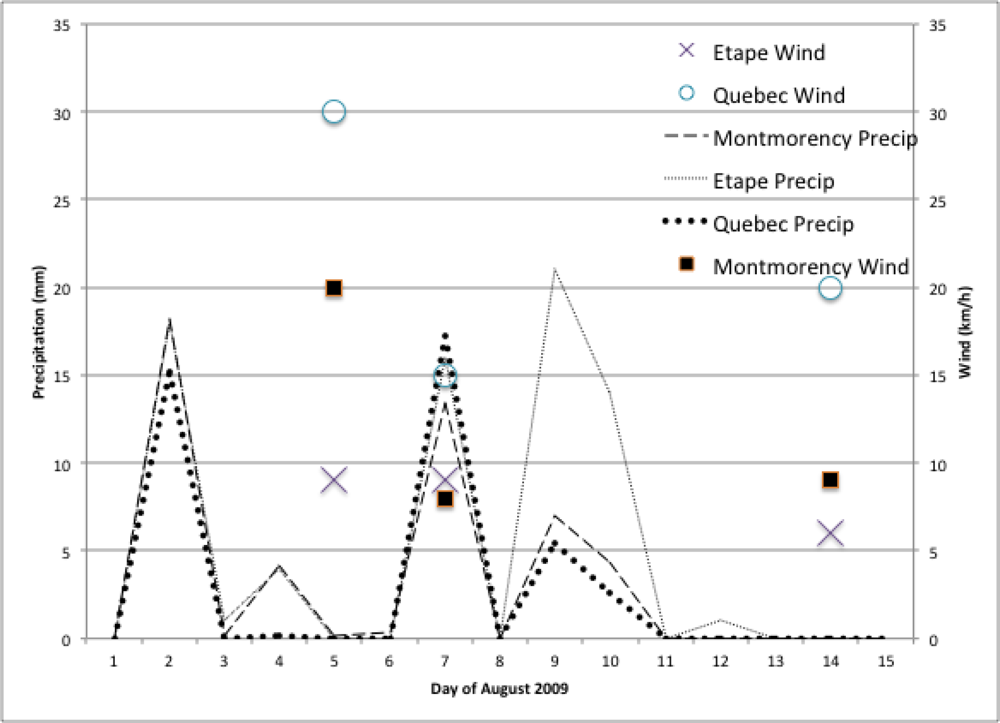
We used weather data from Environment Canada’s National Climate Data and Information Archive covering the UAVSAR acquisition period. Figure 2 shows the recorded precipitation starting from 1 August 2009 and wind speed at the time of the radar data acquisitions.

We used the forest map from Natural Resources Canada (canadaforests.nrcan.gs.ca) and a Landsat scene to identify regions of coniferous boreal and mixed deciduous forests. Forest pixels were selected with RH75 greater than 2 m and UAVSAR HV backscatter above −20 dB. While the first criteria indicated the presence of a canopy the latter threshold removed smaller patches (pixels) of bare ground and water.

5. Analysis of Temporal Decorrelation

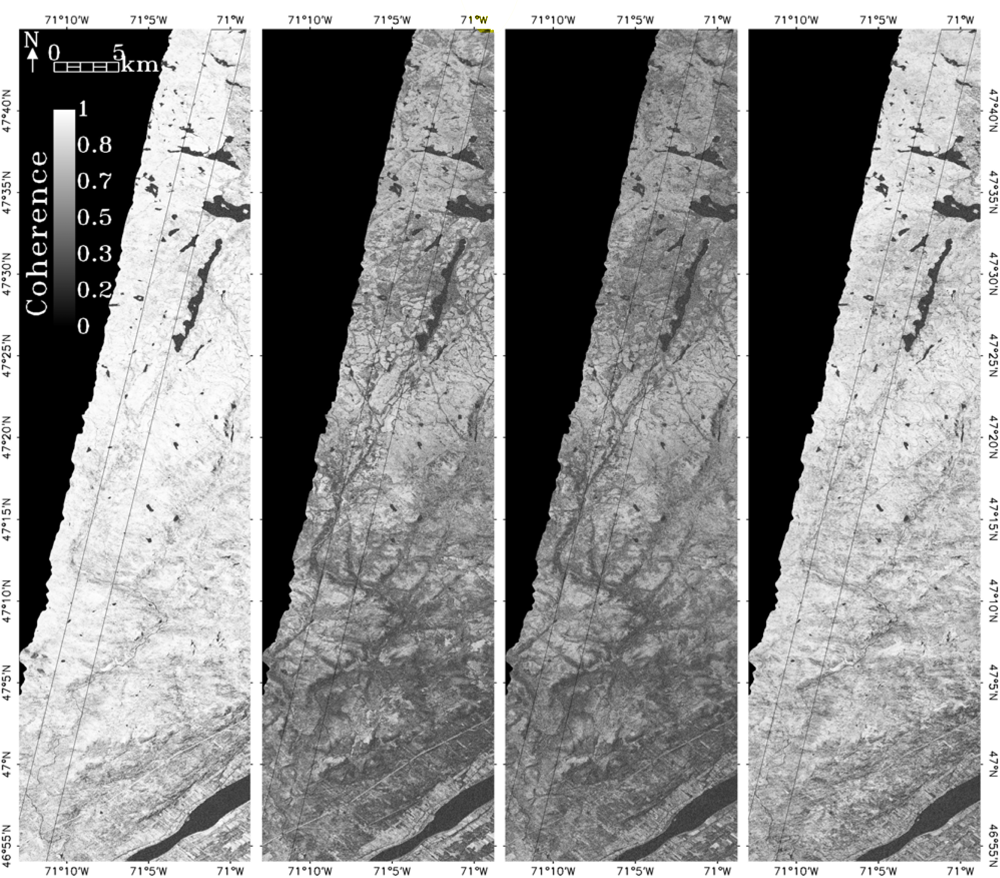
We analyzed the zero baseline InSAR coherence (Equation (1)) as a function of time, weather, canopy height, forest type as well as polarization. The InSAR HH coherence images are shown in Figure 3 for the 45 min, 2-, 7- and 9-day time intervals. Overall, the highest coherences were observed for the 45 min and 9-day intervals.

5.1. Weather

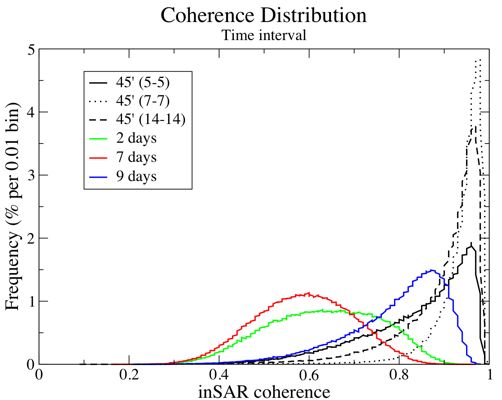
Variations in precipitation and wind induce changes in the complex radar backscattering properties of the canopy and the underlying ground. These changes result in a modification of the InSAR coherence, which could significantly impact the measurement accuracy of canopy height retrieval using repeat pass InSAR [7–9,12–14]. Figure 2 shows the precipitation and wind speed recorded during the UAVSAR campaign. A day prior to the first acquisition on 5 August, 4 mm of rain was recorded within the Reserve, causing the canopy and soil to be moist at the time of the acquisition. On 7 August, both the canopy and ground were saturated with water as a large rain event occurred during the flight. The last acquisition was the driest with no rain during the previous days.

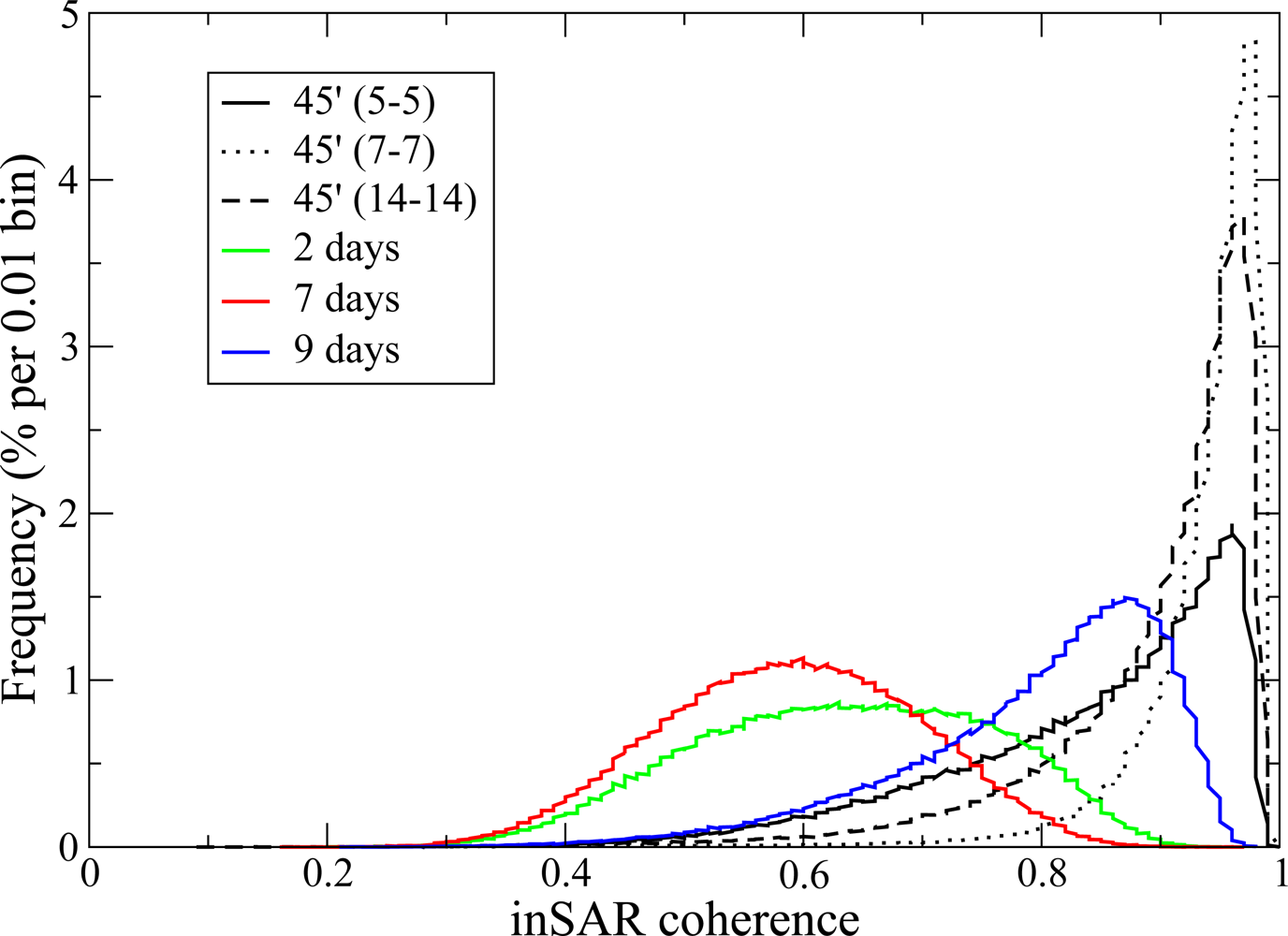
Figure 4 shows the frequency distribution of HH temporal coherence γ̃_t as a function of temporal baseline for all forest pixels within the UAVSAR image. The largest observed InSAR coherence occurs for same day InSAR pairs while the lowest coherence is measured from the 7-day temporal baseline. Not surprisingly, any interferogram using the August 7th acquisition produces low coherence. The 9-day temporal baseline interferogram produced with the August 5th and August 14th acquisitions has higher coherence than the 2-day August 5th and 7th interferogram. The large precipitation event that occurred during the acquisition of August 7th is the main factor responsible for the decrease in measured coherence.

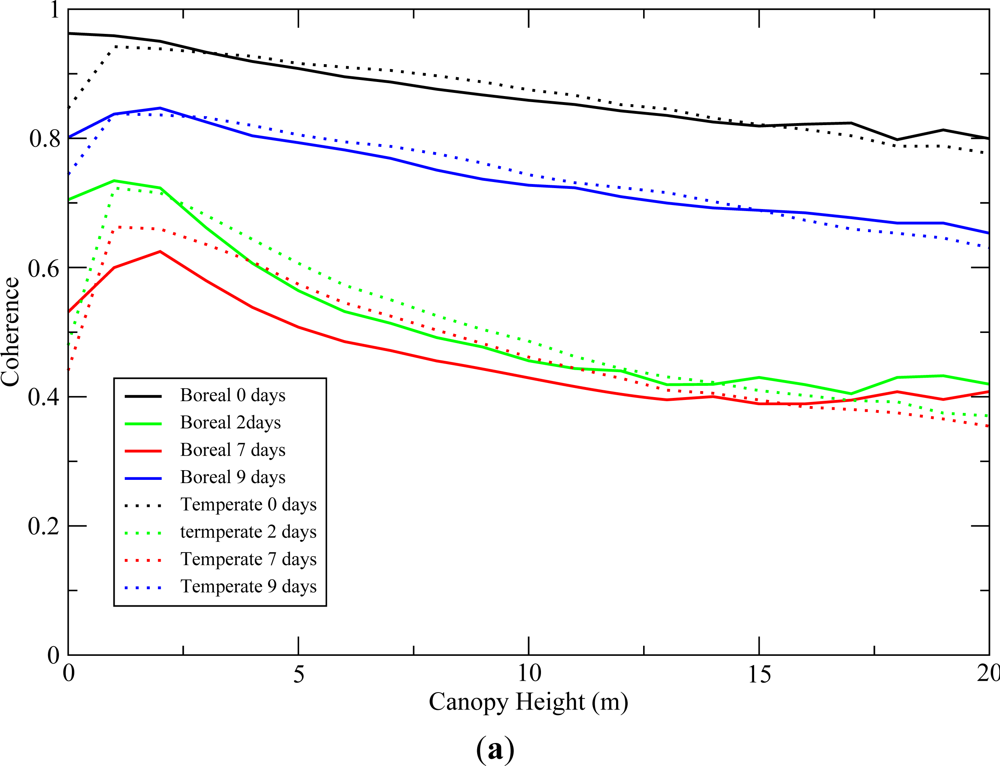
5.2. Canopy Height

The canopy height estimates from LVIS (RH75) were used to investigate potential relationships between canopy structure and temporal decorrelation δ_τ. The canopy structure per se is not expected to affect coherence. However, the impact of certain environmental phenomena, such as wind and interception of precipitation will vary as a function of canopy height [14]. We aggregated UAVSAR coherence pixels to 20 m to compare with the LVIS canopy height estimates to investigate this effect. Figure 5(a) shows the mean coherence as a function of canopy height for all time intervals for both temperate and boreal forests. It shows that changes in target characteristics due to precipitation (e.g., moisture content, surface water, resulting displacement of leaves and branches) are the most significant drivers of temporal decorrelation. In addition, temporal decorrelation δ_τ increases with canopy height, i.e., decrease in γ̃_t as in Figure 5(a). This trend is observed across all time intervals and forest types and is consistent with our model for the impact of wind. There is, however, a significant variability in the observed coherence within a canopy height class with standard deviations of about 0.08.

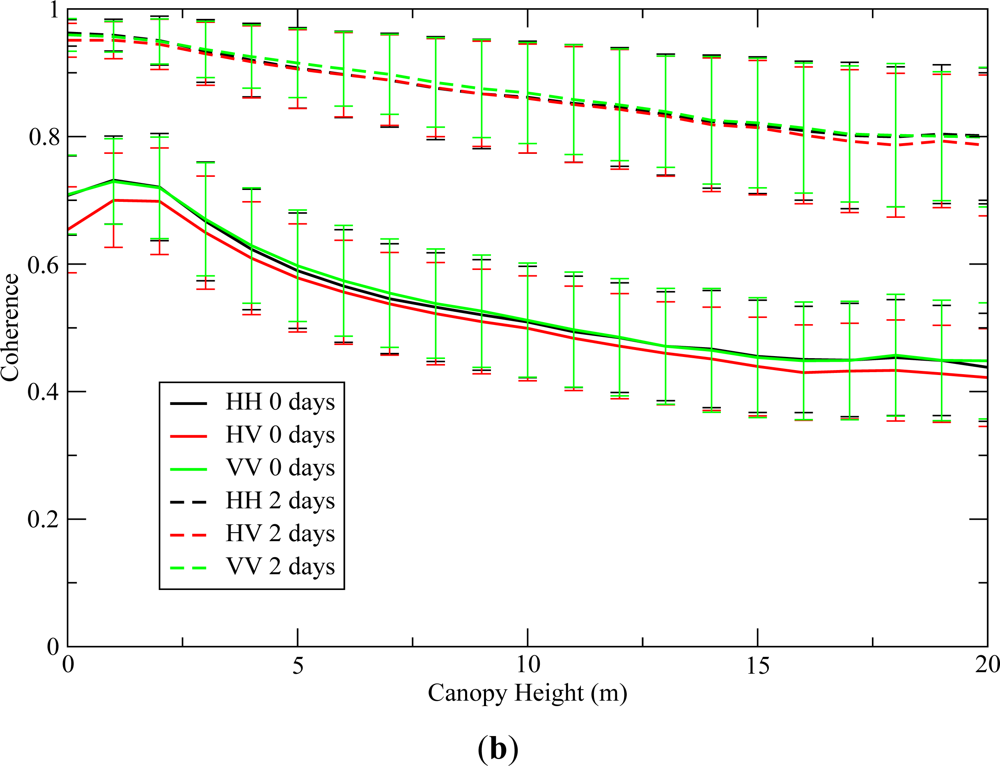
5.3. Polarization

The dependence of coherence on polarization is shown in Figure 5(b) for the 45 min and 2 day periods. Standard deviation (∼0.08) is only shown on Figure 5(b) but also apply to Figure 5(a). Temporal decorrelation trends and levels for a given time interval are similar at all polarizations.

6. Conclusions

The impact of temporal decorrelation in repeat-pass interferometry has been repeatedly observed during the historical development of repeat-pass radar interferometry (e.g., [3,7,9]). However, there has not been sufficient data to identify and understand the drivers of this decorrelation. The lack of a quantitative comprehension of these effects has limited the application of repeat-pass InSAR for canopy height derivation. To address this issue, we analyzed the dependence of InSAR temporal coherence on forest type, canopy height, repeat-pass time interval, weather and polarization using UAVSAR data. We formulated the expected measurement accuracy for the UAVSAR system and found it was adequate (i.e., γ_t ≈ γ_m) for measurement of temporal decorrelation.

Our experiment has shown that for our study area the main drivers of decorrelation were related to precipitation and canopy height. The main decrease in coherence was observed when interferograms were produced from radar acquisitions collected with different weather conditions, especially recent precipitation events. The range of InSAR coherence measurements for any given InSAR pair was large and shows a relationship to canopy height. InSAR coherence decreased by about 10% to 20% over the range of canopy heights (∼20 m), even at short repeat time intervals regardless of polarization diversity and forest type. The standard deviation of coherence measurement over a given copy height class was around 0.08.

In interferometry applications related to measurement of ground topography, temporal decorrelation increases phase noise and therefore ground measurement error [5]. Although this effect cannot be compensated for, estimates of temporal decorrelation can be used to estimate elevation measurement accuracy through analytic expressions [6]. PolinSAR has shown great potential for measurement of canopy heights. However, repeat-pass methods for canopies, in contrast to bare earth, must contend with the pliant and dynamic nature of trees; leaves and branches change on short time scales as a result of their interaction with the weather. By quantifying the magnitudes of these decorrelations and exploring their causes, our work may potentially be used to improve PolinSAR canopy height estimates [12,13].