Estimating Biophysical Parameters of Individual Trees in an Urban Environment Using Small Footprint Discrete-Return Imaging Lidar
Abstract
:1. Introduction
2. Biomass Estimation Using Airborne Lidar
3. Methodology
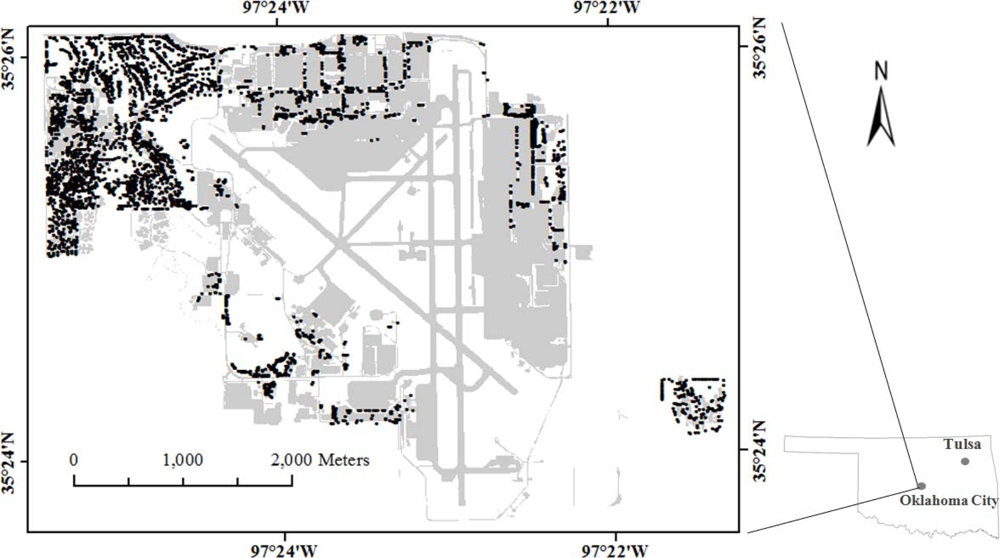
3.1. Study Area
3.2. Lidar Data
3.3. High-Resolution Satellite Image
3.4. Field Measurement
3.5. Variables Predicted
4. Results and Discussion
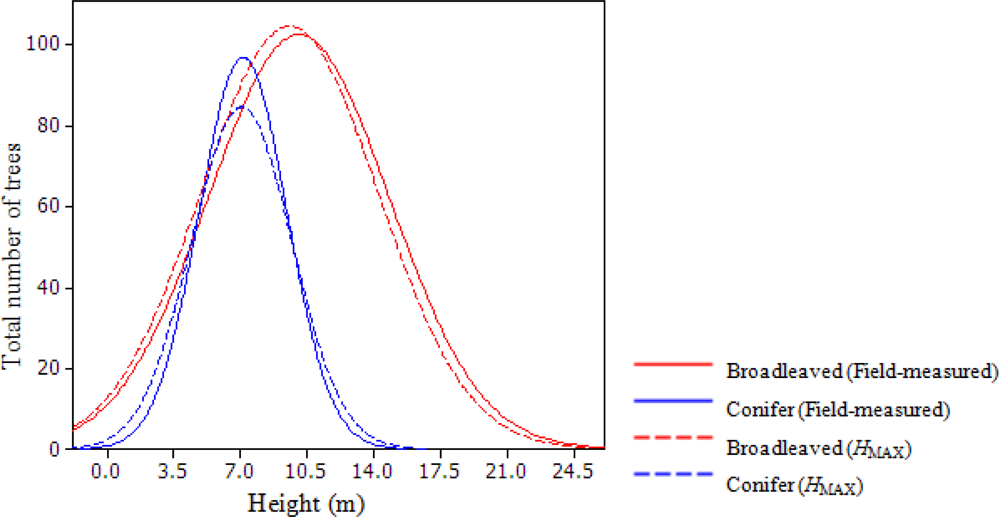
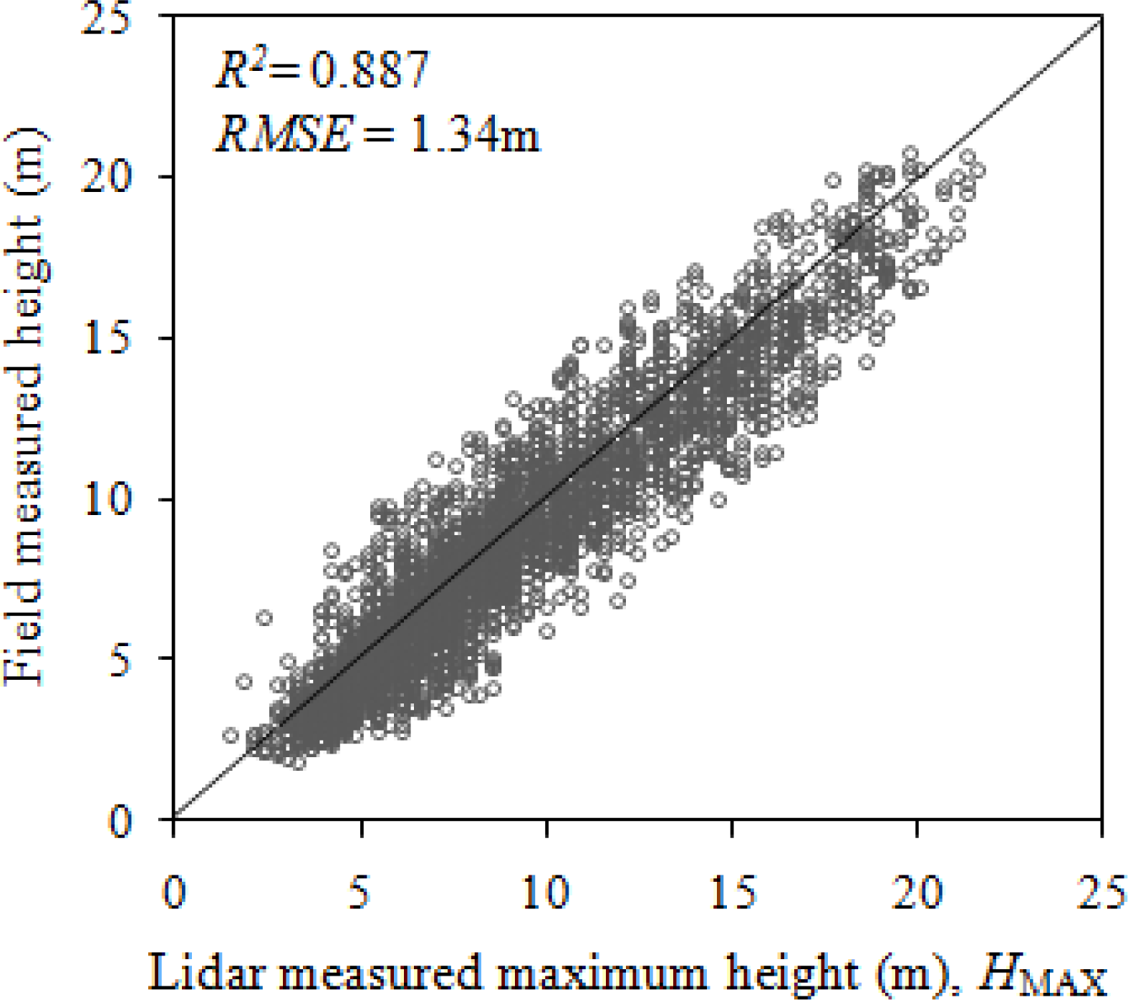
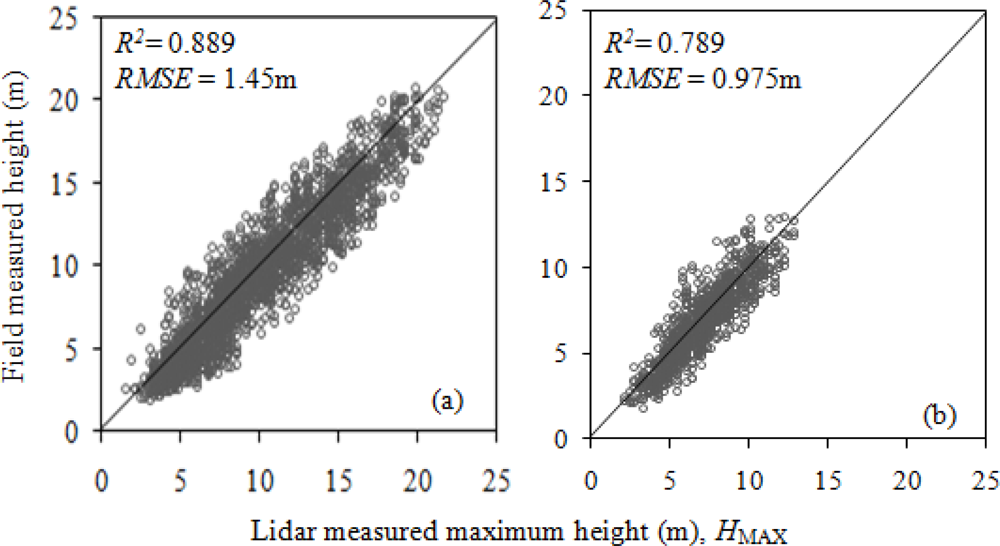
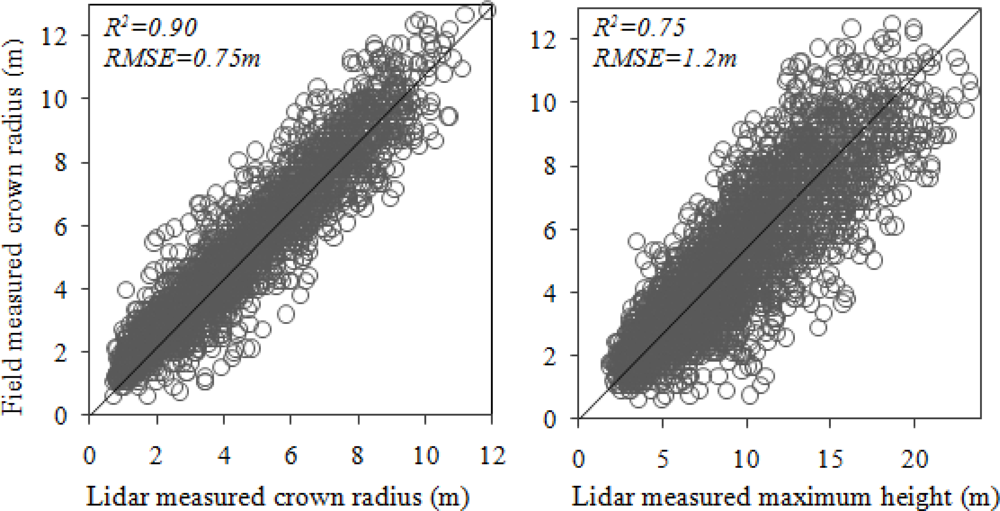
4.1. Relationship between Tree Height and HMAX
4.2. Diameter at Breast Height
4.3 Crown Radius
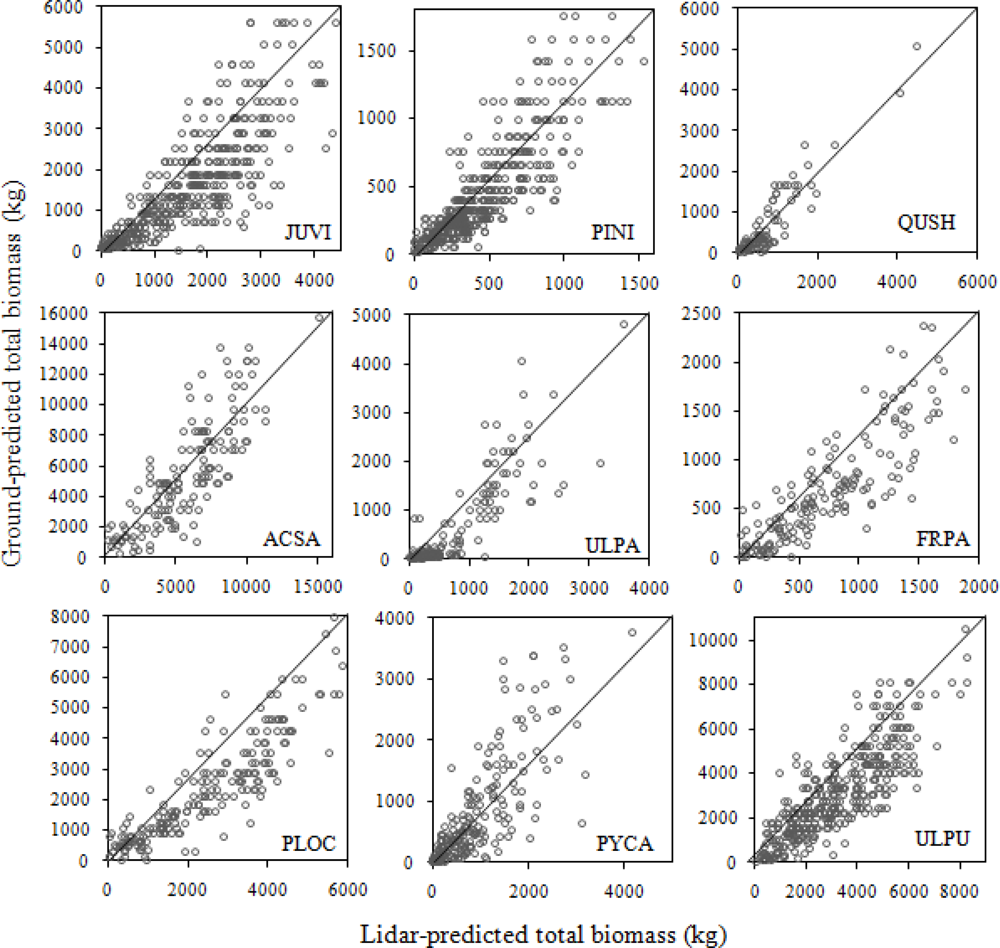
4.4. Aboveground Biomass
5. Conclusions
Acknowledgments
References
- McPherson, E.G.; Nowak, D.; Heisler, G.; Grimmond, S.; Souch, C.; Grant, R.; Rowntree, R. Quantifying urban forest structure, function, and value: The Chicago Urban Forest Climate Project. Urban Ecosystems 1997, 1, 49–61. [Google Scholar]
- Bolund, P.; Hunhammar, S. Ecosystem services in urban areas. Ecol. Econ 1999, 29, 293–301. [Google Scholar]
- Nowak, D.J.; Crane, D.E. Carbon storage and sequestration by urban trees in the USA. Environ. Pollut 2002, 116, 381–389. [Google Scholar]
- Myeong, S.; Nowak, D.; Duggin, M. A temporal analysis of urban forest carbon storage using remote sensing. Remote Sens. Environ 2006, 101, 277–282. [Google Scholar]
- Pataki, D.E.; Alig, R.J.; Fung, A.S.; Golubiewski, N.E.; Kennedy, C.A.; Mcpherson, E.G.; Nowak, D.J.; Pouyat, R.V.; Lankao, P.R. Urban ecosystems and the North American carbon cycle. Global Change Biol 2006, 12, 2092–2102. [Google Scholar]
- Miller, R.W. Urban Forestry: Planning and Managing Urban Greenspaces; Prentice Hall: Upper Saddle River, NJ, USA, 1996; p. 480. [Google Scholar]
- Duryea, M.L.; Malavasi, M.M. Tree Growth in the Urban Forest; Forestry Report R8-FR; USDA Forest Service, Southern Region: Atlanta, GA, USA, 1995; p. 53. [Google Scholar]
- McHale, M.; Burke, I.; Lefsky, M.; Peper, P.; McPherson, E. Urban forest biomass estimates: Is it important to use allometric relationships developed specifically for urban trees? Urban Ecosystems 2009, 12, 95–113. [Google Scholar]
- Wood, J.P. Tree Inventories and GIS in Urban Forestry. M.Sc. Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA. 1999. Available online: http://scholar.lib.vt.edu/theses/available/etd-012499-141520 (accessed on 1 November 2011).
- Boyd, D.S.; Danson, F.M. Satellite remote sensing of forest resources: Three decades of research development. Prog. Phys. Geog 2005, 29, 1–26. [Google Scholar]
- Lu, D. The potential and challenge of remote sensing-based biomass estimation. Int. J. Remote Sens 2006, 27, 1297–1328. [Google Scholar]
- Nelson, R.F.; Kimes, D.S.; Salas, W.A.; Routhier, M. Secondary forest age and tropical forest biomass estimation using thematic mapper imagery. Bioscience 2000, 50, 419–431. [Google Scholar]
- Schlerf, M.; Atzberger, C.; Hill, J. Remote sensing of forest biophysical variables using HyMap imaging spectrometer data. Remote Sens. Environ 2005, 95, 177–194. [Google Scholar]
- Chubey, M.; Franklin, S.; Wulder, M. Object-based analysis of IKONOS-2 imagery for extraction of forest inventory parameters. Photogramm. Eng. Remote Sensing 2006, 72, 383–394. [Google Scholar]
- Wulder, M. Optical remote-sensing techniques for the assessment of forest inventory and biophysical parameters. Prog. Phys. Geog 1998, 22, 449–476. [Google Scholar]
- Lutz, D.; Washington-Allen, R.; Shugart, H. Remote sensing of boreal forest biophysical and inventory parameters: A review. Can. J. Remote Sens 2009, 34, S286–S313. [Google Scholar]
- Dean, T.J.; Cao, Q.V.; Roberts, S.D.; Evans, D.L. Measuring heights to crown base and crown median with LiDAR in a mature, even-aged loblolly pine stand. For. Ecol. Manage 2008, 257, 126–133. [Google Scholar]
- Bortolot, Z.J.; Wynne, R.H. Estimating forest biomass using small footprint LiDAR data: An individual tree-based approach that incorporates training data. ISPRS J. Photogramm 2005, 59, 342–360. [Google Scholar]
- Brandtberg, T.; Warner, T.A.; Landenberger, R.E.; McGraw, J.B. Detection and analysis of individual leaf-off tree crowns in small footprint, high sampling density lidar data from the eastern deciduous forest in North America. Remote Sens. Environ 2003, 85, 290–303. [Google Scholar]
- Hyyppä, H.J.; Hyyppä, J.M. Effects of stand size on the accuracy of remote sensing-based forest inventory. IEEE Trans. Geosci. Remote Sens 2001, 39, 2613–2621. [Google Scholar]
- Popescu, S.C.; Wynne, R.H. Seeing the trees in the forest: Using lidar and multispectral data fusion with local filtering and variable window size for estimating tree height. Photogramm. Eng. Remote Sensing 2004, 70, 589–604. [Google Scholar]
- Todd, K.W.; Csillag, F.; Atkinson, P.M. Three-dimensional mapping of light transmittance and foilage distribution using lidar. Can. J. Remote Sens 2003, 29, 544–555. [Google Scholar]
- Boudreau, J.; Nelson, R.F.; Margolis, H.A.; Beaudoin, A.; Guindon, L.; Kimes, D.S. Regional aboveground forest biomass using airborne and spaceborne LiDAR in Québec. Remote Sens. Environ 2008, 112, 3876–3890. [Google Scholar]
- Nelson, R.; Krabill, W.; Tonelli, J. Estimating forest biomass and volume using airborne laser data. Remote Sens. Environ 1988, 24, 247–267. [Google Scholar]
- Hyyppä, J.; Inkinen, M. Detecting and estimating attributes for single trees using laser scanner. Photogramm. J. Finland 1999, 16, 27–42. [Google Scholar]
- Means, J.E.; Acker, S.A.; Fitt, B.J.; Renslow, M.; Emerson, L.; Hendrix, C.J. Predicting forest stand characteristics with airborne scanning lidar. Photogramm. Eng. Remote Sensing 2000, 66, 1367–1371. [Google Scholar]
- Naesset, E. Predicting forest stand characteristics with airborne scanning laser using a practical two-stage procedure and field data. Remote Sens. Environ 2002, 80, 88–99. [Google Scholar]
- Naesset, E.; Bjerknes, K.O. Estimating tree heights and number of stems in young forest stands using airborne laser scanner. Remote Sens. Environ 2001, 78, 328–340. [Google Scholar]
- Naesset, E.; Okland, T. Estimating tree height and tree crown properties using airborne scanning laser in a boreal nature reserve. Remote Sens. Environ 2002, 79, 105–115. [Google Scholar]
- Magnussen, S.; Boudewyn, P. Derivations of stand heights from airborne laser scanner data with canopy-based quantile estimators. Can. J. For. Res 1998, 28, 1016–1031. [Google Scholar]
- van Aardt, J.A.N.; Wynne, R.H.; Oderwald, R.G. Forest volume and biomass estimation using small-footprint lidar-distributional parameters on a per-segment basis. For. Sci 2006, 52, 636–649. [Google Scholar]
- Tesfamichael, S.G.; van Aardt, J.A.N.; Ahmed, F. Estimating plot-level tree height and volume of Eucalyptus grandis plantations using small-footprint, discrete return lidar data. Prog. Phys. Geog 2010, 34, 515–540. [Google Scholar]
- Popescu, S.C.; Wynne, R.H. Esimating plot-level forest biophysical parameters using small-footprint airborne lidar measurements. Comput. Electron. Agric 2002, 37, 71–95. [Google Scholar]
- Popescu, S.C.; Wynne, R.H.; Scrivani, J.A. Fusion of small-footprint lidar and multispectral data to estimate plot-level volume and biomass in deciduous and pine forests in Virginia, USA. For. Sci 2004, 50, 551–565. [Google Scholar]
- Bortolot, Z.J. Using tree clusters to derive forest properties from small footprint lidar data. Photogramm. Eng. Remote Sensing 2006, 72, 1379–1388. [Google Scholar]
- Persson, A.; Holmgren, J.; Soderman, U. Detecting and measuring individual trees using an airborne laser scanner. Photogramm. Eng. Remote Sensing 2002, 68, 925–932. [Google Scholar]
- Roberts, S.D.; Dean, T.J.; Evans, D.L.; McCombs, J.W.; Harrington, R.L.; Glass, P.A. Estimating individual tree leaf area in loblolly pine plantations using LiDAR-derived measurements of height and crown dimensions. For. Ecol. Manage 2005, 213, 54–70. [Google Scholar]
- Chen, Q.; Gong, P.; Baldocchi, D.; Tian, Y.Q. Estimating basal area and stem volume for individual trees from lidar data. Photogramm. Eng. Remote Sensing 2007, 73, 1355–1365. [Google Scholar]
- Hyyppä, J.; Kelle, O.; Lehikoinen, M.; Inkinen, M. A segmentation-based method to retrieve stem volume estimates from 3-D tree height models produced by laser scanners. IEEE Trans. Geosci. Remote Sens 2001, 39, 969–975. [Google Scholar]
- Popescu, S.C.; Wynne, R.H.; Nelson, R.F. Measuring individual tree crown diameter with lidar and assessing its influence on estimating forest volume and biomass. Can. J. Remote Sens 2003, 29, 564–577. [Google Scholar]
- Næsset, E.; Gobakken, T. Estimation of above- and below-ground biomass across regions of the boreal forest zone using airborne laser. Remote Sens. Environ 2008, 112, 3079–3090. [Google Scholar]
- Hudak, A.T.; Lefsky, M.A.; Cohen, W.B.; Berterretche, M. Integration of lidar and Landsat ETM+ data for estimating and mapping forest canopy height. Remote Sens. Environ 2002, 82, 397–416. [Google Scholar]
- Holmgren, J.; Persson, A.; Soderman, U. Species identification of individual trees by combining high resolution lidar data with multi-spectral images. Int. J. Remote Sens 2008, 29, 1537–1552. [Google Scholar]
- Dalponte, M.; Bruzzone, L.; Gianelle, D. Fusion of hyperspectral and lidar remote sensing data for classification of complex forest areas. IEEE Trans. Geosci. Remote Sens 2008, 46, 1416–1427. [Google Scholar]
- St-Onge, B.; Hu, Y.; Vega, C. Mapping the height and above-ground biomass of a mixed forest using lidar and stereo Ikonos images. Int. J. Remote Sens 2008, 29, 1277–1294. [Google Scholar]
- van Aardt, J.A.; Wynne, R.H.; Scrivani, J.A. Lidar-based mapping of forest volume and biomass by taxonomic group using structurally homogenous segments. Photogramm. Eng. Remote Sensing 2008, 74, 1033–1044. [Google Scholar]
- Naesset, E.; Gobakken, T. Estimating forest growth using canopy metrics derived from airborne laser scanner data. Remote Sens. Environ 2005, 96, 453–465. [Google Scholar]
- Popescu, S.C. Estimating biomass of individual pine trees using airborne lidar. Biomass Bioenergy 2007, 31, 646–655. [Google Scholar]
- Naesset, E. Practical large-scale forest stand inventory using a small-footprint airborne scanning laser. Scand. J. For. Res 2004, 19, 164–179. [Google Scholar]
- Nelson, R.; Short, A.; Valenti, M. Measuring biomass and carbon in Delaware using an airborne profiling lidar. Scand. J. For. Res 2004, 19, 500–511. [Google Scholar]
- Nelson, R.; Parker, G.; Horn, M. A portable airborne laser system for forest inventory. Photogramm. Eng. Remote Sensing 2003, 69, 267–273. [Google Scholar]
- Nelson, R.F.; Hyde, P.; Johnson, P.; Emessiene, B.; Imhoff, M.L.; Campbell, R.; Edwards, W. Investigating RaDAR-lidar synergy in a North Carolina pine forest. Remote Sens. Environ 2007, 110, 98–108. [Google Scholar]
- Hyde, P.; Nelson, R.; Kimes, D.; Levine, E. Exploring lidar-RaDAR synergy—Predicting aboveground biomass in a southwestern ponderosa pine forest using lidar, SAR and InSAR. Remote Sens. Environ 2007, 106, 28–38. [Google Scholar]
- Hall, S.A.; Burke, I.C.; Box, D.O.; Kaufmann, M.R.; Stoker, J.M. Estimating stand structure using discrete-return lidar: an example from low density, fire prone ponderosa pine forests. For. Ecol. Manage 2005, 208, 189–209. [Google Scholar]
- Banskota, A.; Wynne, R.H.; Johnson, P.; Emessiene, B. Synergistic use of very-high-frequency radar and discrete-return lidar for estimating biomass in temperate hardwood and mixed forests. Ann. Forest Sci 2011, 68, 347–356. [Google Scholar]
- Nelson, R. Modeling forest canopy heights: The effects of canopy shape. Remote Sens. Environ 1997, 60, 327–334. [Google Scholar]
- Jenkins, J.C.; Chojnacky, D.C.; Heath, L.S.; Birdsey, R.A. National-scale biomass estimators for United States tree species. For. Sci 2003, 49, 12–35. [Google Scholar]
- Naesset, E. Estimating timber volume of forest stands using airborne laser scanner data. Remote Sens. Environ 1997, 61, 246–253. [Google Scholar]
- Gary, H. The vertical distribution of needles and branchwood in thinned and unthinned 80-year-old lodgepole pine. Northwest Sci 1978, 52, 303–309. [Google Scholar]
- Peichl, M.; Arain, M.A. Allometry and partitioning of above- and belowground tree biomass in an age-sequence of white pine forests. For. Ecol. Manage 2007, 253, 68–80. [Google Scholar]
- TAFB. Tinker Air Force Base Fact Sheet. 2011. Available online: http://www.tinker.af.mil/library/factsheets/factsheet.asp?id=9404 (accessed on 1 November 2011).
- Otey, J.K. GIS Applications in Urban Tree Inventory; Master Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA; 2007. [Google Scholar]
- Palenichka, R.M.; Zaremba, M.B. Multiscale isotropic matched filtering for individual tree detection in LiDAR images. IEEE Trans. Geosci. Remote Sens 2007, 45, 3944–3956. [Google Scholar]
- Rouse, J.; Haas, R.; Schell, J.; Deering, D.; Harlan, J. Monitoring the Vernal Advancement of Retrogradation of Natural Vegetation; Final Report; NASA/Goddard Space Flight Centre: Greenbelt, MD, USA, 1974. [Google Scholar]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ 1988, 25, 295–309. [Google Scholar]
- Qi, J.; Chehbouni, A.; Huete, A.R.; Kerr, Y.H.; Sorooshian, S. A modified soil adjusted vegetation index. Remote Sens. Environ 1994, 48, 119–126. [Google Scholar]
- Baret, F.; Guyot, G. Potentials and limits of vegetation indices for LAI and APAR assessment. Remote Sens. Environ 1991, 35, 161–173. [Google Scholar]
- Avery, T.E.; Burkhart, H.E. Forest Measurements, 5th ed.; McGraw-Hill: Boston, MA, USA, 2002; p. 456. [Google Scholar]
- Pillsbury, N.; Reimer, J.; Thompson, R. Tree Volume Equations for Fifteen Urban Species in California; California Polytechnic State University, Urban Forest Ecosystems Institute: San Louis Obispo, CA, USA, 1995; p. 56. [Google Scholar]
- Snowdon, P.; Eamus, D.; Gibbons, P.; Khanna, P.; Keith, H.; Raison, R.; Kirschbaum, M. Synthesis of Allometrics, Review of Root Biomass, and Design of Future Woody Biomass Sampling Strategies; The Australian Greenhouse Office: Canberra, ACT, Australia, 2001. [Google Scholar]
- Ter-Mikaelian, M.T.; Korzukhin, M.D. Biomass equations for sixty-five North American tree species. For. Ecol. Manage 1997, 97, 1–24. [Google Scholar]
- West, P.W. Tree and Forest Measurement; Springer: Berlin/Heidelberg, Germany, 2004; p. 167. [Google Scholar]
- Norris, M.D.; Blair, J.M.; Johnson, L.C.; McKane, R.B. Assessing changes in biomass, productivity, and C and N stores following Juniperus virginiana forest expansion into tallgrass prairie. Can. J. For. Res 2001, 31, 1940–1946. [Google Scholar]
- Clark, A, III; Phillips, D.R.; Frederick, D.J. Weight, Volume, and Physical Properties of Major Hardwood Species in the Piedmont; Southeastern Forest Experiment Station, North Carolina State University: Raleigh, NC, USA, 1986; p. 88. [Google Scholar]
- Schlaegel, B. Green Ash Volume and Weight Tables; Res. Pap. SO-206.; US Department of Agriculture, Forest Service, Southern Forest Experiment Station: New Orleans, LA, USA, 1984. [Google Scholar]
- Brenneman, B.B.; Frederick, D.J.; Gardner, W.E.; Schoenhofen, L.H.; Marsh, P.L. Biomass of Species and Stands of West Virginia Hardwoods. Proceedings of Central Hardwood Forest Conference II, West LaFayette, Indiana, USA, 14–16 November 1978; pp. 159–178.
- Jenkins, J.; Chojnacky, D.; Heath, L.; Birdsey, R. Comprehensive Database of Diameter-Based Biomass Regressions for North American Tree Species; NE-319; United States Forest Service, Northeastern Research Station: New Town Square, PS, USA, 2004; p. 45. [Google Scholar]
- Johnson, A.; Gerhold, H. Carbon storage by utility-compatible trees. J. Arboricul 2001, 27, 57–68. [Google Scholar]
- Hocking, R.R. Methods and Applications of Linear Models: Regression and the Analysis of Variance, 2nd ed.; John Wiley & Sons, Inc: Hoboken, NJ, USA, 2005; p. 776. [Google Scholar]
- Montgomery, D.; Peck, E. Introduction to Linear Regression Analysis, 4th ed.; Wiley: New York, NY, USA, 2006; p. 640. [Google Scholar]
- Rozeboom, W. Estimation of cross-validated multiple correlation: A clarification. Psychol. Bull 1978, 85, 1348–1351. [Google Scholar]
- Allen, D. The relationship between variable selection and data agumentation and a method for prediction. Technometrics 1974, 16, 125–127. [Google Scholar]
- Kleinbaum, D.; Kupper, L.; Nizam, A.; Muller, K. Applied Regression Analysis and Other Multivariable Methods, 4th ed.; Thompson Higher Education: Belmont, CA, USA, 2007; p. 928. [Google Scholar]
- Hopkinson, C.; Chasmer, L.; Sass, G.; Creed, I.; Sitar, M.; Kalbfleisch, W.; Treitz, P. Vegetation class dependent errors in lidar ground elevation and canopy height estimates in a boreal wetland environment. Can. J. Remote Sens 2005, 31, 191–206. [Google Scholar]
- Hyyppä, J.; Pyysalo, U.; Hyyppä, H.; Samberg, A. Elevation Accuracy of Laser Scanning-Derived Digital Terrain and Target Models in Forest Environment. Proceedings of EARSeL-SIG-Workshop LIDAR, Dresden, Germany, 16–17 June 2000; pp. 14–17.
- Heurich, M.; Persson, A.; Holmgren, J.; Kennel, E. Detecting and Measuring Individual Trees with Laser Scanning in Mixed Mountain Forest of Central Europe Using an Algorithm Developed for Swedish Boreal Forest Conditions. Proceedings of the ISPRS Working Group VIII/2 “Laser-Scanners for Forest and Landscape Assessment”, Freiburg, Germany, 3–6 October 2004; 36, pp. 307–312.
- Falkowski, M.; Smith, A.; Gessler, P.; Hudak, A.; Vierling, L.; Evans, J. The influence of conifer forest canopy cover on the accuracy of two individual tree measurement algorithms using lidar data. Can. J. Remote Sens 2008, 34, S338–S350. [Google Scholar]
- Clark, M.L.; Clark, D.B.; Roberts, D.A. Small-footprint lidar estimation of sub-canopy elevation and tree height in a tropical rain forest landscape. Remote Sens. Environ 2004, 91, 68–89. [Google Scholar]
- Kwak, D.-A.; Lee, W.-K.; Lee, J.-H.; Biging, G.; Gong, P. Detection of individual trees and estimation of tree height using LiDAR data. J. Forest Res.-Jpn 2007, 12, 425–434. [Google Scholar]
- Omasa, K.; Hosoi, F.; Uenishi, T.; Shimizu, Y.; Akiyama, Y. Three-dimensional modeling of an urban park and trees by combined airborne and portable on-ground scanning LIDAR remote sensing. Environ. Model. Assess 2008, 13, 473–481. [Google Scholar]
- Zheng, D.; Rademacher, J.; Chen, J.; Crow, T.; Bresee, M.; Le Moine, J.; Ryu, S.-R. Estimating aboveground biomass using Landsat 7 ETM+ data across a managed landscape in northern Wisconsin, USA. Remote Sens. Environ 2004, 93, 402–411. [Google Scholar]
- Hall, R.J.; Skakun, R.S.; Arsenault, E.J.; Case, B.S. Modeling forest stand structure attributes using Landsat ETM+ data: Application to mapping of aboveground biomass and stand volume. For. Ecol. Manage 2006, 225, 378–390. [Google Scholar]
- Heiskanen, J. Estimating aboveground tree biomass and leaf area index in a mountain birch forest using ASTER satellite data. Int. J. Remote Sens 2006, 27, 1135–1158. [Google Scholar]
- Smith, M.-L.; Ollinger, S.V.; Martin, M.E.; Aber, J.D.; Hallett, R.A.; Goodale, C.L. Direct estimation of aboveground forest productivity through hyperspectral remote sensing of canopy nitrogen. Ecol. Appl 2002, 12, 1286–1302. [Google Scholar]
- Blackard, J.A.; Finco, M.V.; Helmer, E.H.; Holden, G.R.; Hoppus, M.L.; Jacobs, D.M.; Lister, A.J.; Moisen, G.G.; Nelson, M.D.; Riemann, R.; et al. Mapping U.S. forest biomass using nationwide forest inventory data and moderate resolution information. Remote Sens. Environ 2008, 112, 1658–1677. [Google Scholar]
- Leboeuf, A.; Beaudoin, A.; Fournier, R.A.; Guindon, L.; Luther, J.E.; Lambert, M.C. A shadow fraction method for mapping biomass of northern boreal black spruce forests using QuickBird imagery. Remote Sens. Environ 2007, 110, 488–500. [Google Scholar]
- Gonzalez, P.; Asner, G.P.; Battles, J.J.; Lefsky, M.A.; Waring, K.M.; Palace, M. Forest carbon densities and uncertainties from Lidar, QuickBird, and field measurements in California. Remote Sens. Environ 2010, 114, 1561–1575. [Google Scholar]
- Kayitakire, F.; Hamel, C.; Defourny, P. Retrieving forest structure variables based on image texture analysis and IKONOS-2 imagery. Remote Sens. Environ 2006, 102, 390–401. [Google Scholar]
- Ouma, Y.; Tateishi, R. Optimization of second-order grey-level texture in high-resolution imagery for statistical estimation of above-ground biomass. J. Environ. Inform 2006, 8, 70–85. [Google Scholar]

| Study | Variable | RMSE* | Remarks | ||
|---|---|---|---|---|---|
| Dec† | Con† | Mixed | |||
| Naesset [49] | Volume | - | 0.2§ | - | Pine /Spruce |
| van Aardt et al. [46] | Volume | 56.0 | 8.2 | 28.0 | 3-class volume |
| Næsset and Gobakken [41] | Biomass | - | 0.2§ | - | Coniferous boreal |
| Popescu [48] | Biomass | - | 16.7 | - | Individual loblolly pines |
| Nelson et al. [52] | Biomass | - | 33.9 | - | Loblolly pine |
| Hyde et al. [53] | Biomass | - | 24.8 | - | Pondorosa pine |
| Hall et al. [54] | Biomass | - | 35.8 | - | Ponderosa pine |
| Foliage | - | 2.1 | - | ||
| Bortolot and Wynne [18] | Biomass | - | 13.7 | - | Loblolly pine |
| Popescu et al. [34] | Biomass | 44.0 | 29.0 | - | |
| Height Distribution Statistics1 | Density Measures | ||
|---|---|---|---|
| HMEAN | Mean height | NC | Number of crown returns |
| HVAR | Variance of height | NT | Number of total returns |
| HMIN | Minimum height | NP | Point density (NC /NT) |
| HMAX | Maximum height | NCD | NC /CA |
| HR | Range of height (HMAX – HMIN) | NTD | NT /CA |
| HSTD | Standard deviation of height | NX | (Number of crown returns in x% of HR)/ CA (x = <20, 40, 80, 90, 95, >95) |
| HMODE | Most frequent height of crown returns | ||
| HCV | Coefficient of variation of height | ||
| HSE | Standard error of mean of height | Crown Dimension2 | |
| HKUR | Kurtosis of height | CA | Area of crown projected onto XY plane |
| HSKW | Skewness of height | CP | Perimeter of crown projected onto XY plane |
| HQX | x % Quantile of height (x = 5, 10, 25, 50, 75, 90, and 95) | ||
| Bands | Wavelength (nm) |
|---|---|
| Panchromatic | 450–900 |
| Band 1 (Blue) | 450–520 |
| Band 2 (Green) | 520–600 |
| Band 3 (Red) | 630–690 |
| Band 4 (Near Infrared) | 780–900 |
| BandXMIN, BandXMEAN, BandXMAX, BandXSTD | Minimum, mean, maximum and standard deviation of spectral value of Band X, where X = 1 to 4 |
| NDVIMIN, NDVIMEAN, NDVIMAX, NDVISTD | Minimum, mean, maximum and standard deviation of normalized difference vegetation index (NDVI) computed as [64]: |
| SAVIMIN, SAVIMEAN, SAVIMAX, SAVISTD | Minimum, mean, maximum and standard deviation of soil-adjusted vegetation index (SAVI) computed as [65]: |
| MSAVIMIN, MSAVIMEAN, MSAVIMAX, MSAVISTD | Minimum, mean, maximum and standard deviation of modified soil-adjusted vegetation index (MSAVI) computed as [66]: |
| Species | Total Trees | Height Class (m) | |||||
|---|---|---|---|---|---|---|---|
| <6 | 6–9 | 9–12 | 12–15 | 15–18 | >18 | ||
| Conifers | |||||||
| Juniperus virginiana | 475 | 156 | 208 | 102 | 8 | 1 | 0 |
| Pinus nigra | 461 | 143 | 223 | 77 | 16 | 2 | 0 |
| Others conifer (10 species) | 182 | 60 | 96 | 21 | 5 | 0 | 0 |
| Broadleaf Species | |||||||
| Ulmus pumila | 387 | 12 | 73 | 111 | 110 | 53 | 28 |
| Pyrus calleryana | 280 | 116 | 132 | 30 | 2 | 0 | 0 |
| Platanus occidentalis | 212 | 4 | 9 | 23 | 37 | 43 | 96 |
| Fraxinus pennsylvannica | 184 | 17 | 43 | 49 | 46 | 26 | 3 |
| Ulmus parvifolia | 172 | 44 | 76 | 39 | 11 | 2 | 0 |
| Acer saccharinum | 163 | 1 | 8 | 16 | 50 | 55 | 33 |
| Quercus shumardii | 118 | 33 | 49 | 22 | 10 | 3 | 1 |
| Other broadleaf species (53) | 928 | 313 | 272 | 151 | 122 | 52 | 18 |
| Species | Diameter at Breast Height (cm) | Crown Radius (m) | ||||||
|---|---|---|---|---|---|---|---|---|
| Mean | Std† | Min | Max | Mean | Std† | Min | Max | |
| Conifers | ||||||||
| Juniperus virginiana | 30.9 | 14.4 | 5.1 | 68.6 | 11.9 | 4.0 | 2.5 | 24.5 |
| Pinus nigra | 31.9 | 11.8 | 7.6 | 66.0 | 11.7 | 3.7 | 3.5 | 25.0 |
| Others conifers (10 species) | 25.9 | 11.5 | 7.6 | 66.0 | 9.7 | 3.1 | 3.5 | 23.0 |
| Broadleaf species | ||||||||
| Ulmus pumila | 60.7 | 19.7 | 0.0 | 139.7 | 23.3 | 7.4 | 0.0 | 47.0 |
| Pyrus calleryana | 20.9 | 10.0 | 7.6 | 48.3 | 9.7 | 4.4 | 3.5 | 25.0 |
| Platanus occidentalis | 54.0 | 19.4 | 10.2 | 124.5 | 24.9 | 7.3 | 7.0 | 44.0 |
| Fraxinus pennsylvannica | 43.4 | 20.4 | 2.5 | 96.5 | 18.5 | 7.1 | 2.0 | 35.0 |
| Ulmus parvifolia | 26.0 | 18.4 | 7.6 | 111.8 | 13.9 | 5.8 | 4.5 | 34.0 |
| Acer saccharinum | 64.3 | 21.2 | 17.8 | 119.4 | 25.5 | 6.6 | 8.0 | 41.0 |
| Quercus shumardii | 25.0 | 16.0 | 5.1 | 86.4 | 11.9 | 4.0 | 2.5 | 24.5 |
| Other broadleaf species (53) | 31.3 | 22.9 | 0.0 | 200.7 | 14.8 | 7.7 | 0.0 | 44.5 |
| Species§ | Biomass Equation# | R2 | dbh Range (cm) | N | Locality | Source |
|---|---|---|---|---|---|---|
| JUVI | Ln (Y, kg)= −0.912+2.322 Ln (dbh, cm) | 0.98 | 13–37 | 12 | Kansas, Oklahoma | [73] |
| ULPU | (Y, lb) = 2.17565 (dbh, in) 2.4962 | 0.98 | 6–70 | 15 | Piedmont (SE USA) | [74] |
| FRPE | Ln(Y, lb) = −1.104+0.88814 ln((dbh, in)2(H, ft)) | 0.91 | 2–77 | 70 | West-central Mississipi | [75] |
| ULPA | (Y, lb) = 2.17565 (dbh, in)2.4962 | 0.98 | 6–70 | 15 | Piedmont (SE USA) | [74] |
| ACSA | log10(Y, lb) = log10(2.4439)+ 2.5735 log10(dbh, in) | 0.98 | 5–50 | 119 | W. Virginia | [76] |
| QUSH | Ln(Y, kg)= −2.0127 + 2.4342 Ln(dbh, cm) | 0.99 | <73 | 485 | - | [77] |
| PYCA | (Y, kg) =0.0029 ((dbh, cm)2(H, m))1.4607 | 0.89 | 4.0–11.0 | 6 | Pennsylvania, Ohio | [78] |
| PINI | Ln (Y, kg) = −2.5356+ 2.4349 Ln (dbh, cm) | 0.99 | <180 | 331 | - | [77] |
| PLOC | (Y, lb) = 1.57573 (dbh, in) 2.5801 | 0.98 | 12.3–60.7 | 14 | Piedmont (SE USA) | [74] |
| Speciesa | N | Crown-Size Metrics | Height Metrics | ||||
|---|---|---|---|---|---|---|---|
| Metricsb | R2 | RMSE | Metricsb | R2 | RMSE | ||
| All trees | 3,505 | CP | 0.818 | 9.1 | HMEAN | 0.723 | 11.2 |
| Broadleaf species | 2,414 | CP | 0.843 | 9.5 | HMEAN | 0.761 | 11.8 |
| ULPU | 378 | CP | 0.738 | 9.7 | HMAX | 0.603 | 12.0 |
| PYCA | 273 | CP | 0.706 | 5.1 | HQ75 | 0.620 | 5.8 |
| PLOC | 207 | CP | 0.830 | 7.7 | HQ95 | 0.820 | 8.7 |
| FRPA | 175 | CP | 0.794 | 8.8 | HMAX | 0.701 | 10.6 |
| ULPA | 167 | CP | 0.888 | 5.8 | HQ75 | 0.855 | 6.6 |
| ACSA | 160 | CP | 0.715 | 11.2 | HQ75 | 0.643 | 12.5 |
| QUSH | 114 | CP | 0.911 | 4.5 | HMAX | 0.851 | 5.8 |
| Conifers | 1,093 | CP | 0.739 | 6.6 | HMEAN | 0.541 | 8.8 |
| JUVI | 475 | CP | 0.673 | 8.2 | HMEAN | 0.510 | 10.1 |
| PINI | 461 | CP | 0.691 | 6.6 | HMEAN | 0.572 | 7.7 |
| Speciesa | N | Modelb | R2 | R2adj | R2predc | RMSE |
|---|---|---|---|---|---|---|
| All trees | 3,517 | Y= 0.30898 + 0.74960 × HMEAN | 0.771 | 0.770 | 0.770 | 1.1 |
| All broadleaf species | 2,414 | Y= 0.21928 + 0.76909 × HMEAN | 0.779 | 0.778 | 0.778 | 1.2 |
| ULPU | 378 | Y= 0.71799 + 0.59987 × HQ95 | 0.643 | 0.642 | 0.639 | 1.3 |
| PYCA | 272 | Y= −0.36681 + 0.76381 × HMED | 0.733 | 0.732 | 0.729 | 0.7 |
| PLOC | 205 | Y= 0.84456 + 0.42798 × HMAX | 0.770 | 0.768 | 0.766 | 1.0 |
| FRPA | 178 | Y= −0.24987 + 0.67583 × HQ75 | 0.730 | 0.729 | 0.724 | 1.1 |
| ULPA | 167 | Y= 0.70168 + 0.58483 × HQ90 | 0.818 | 0.817 | 0.813 | 0.7 |
| ACSA | 160 | Y= 0.39968 + 0.56739 × HQ90 | 0.589 | 0.587 | 0.580 | 1.3 |
| QUSH | 114 | Y= −0.05268 + 0.50024 × HMAX | 0.810 | 0.809 | 0.804 | 0.7 |
| All conifers | 1,092 | Y= 1.19172 + 0.38139 × HQ90 | 0.460 | 0.459 | 0.458 | 0.8 |
| JUVI | 449 | Y= 1.28095 + 0.33242 × HMAX | 0.530 | 0.529 | 0.525 | 0.8 |
| PINI | 440 | Y= 1.05681 + 0.39898 × HQ90 | 0.531 | 0.530 | 0.527 | 0.7 |
| R2 | R2adj | MSE | R2preda | PRESS | Best Modelb, c | |
|---|---|---|---|---|---|---|
| All trees (n = 2,425) | ||||||
| Lidar only | 0.665 | 0.665 | 1093.1 | 0.663 | 2907146469 | Y = −828.1762 + 18.135676 CA + 242.3016 HQ5 |
| Quickbird only | 0.405 | 0.404 | 1456.9 | 0.403 | 5156216255 | Y = 1261.291+0.00617 MSAVIMAX − 0005016 MSAVIMEAN − 17.67353 * Band4STDEV |
| Broadleaf trees (n = 1,489) | ||||||
| Lidar only | 0.634 | 0.633 | 1303.3 | 0.632 | 2538508726 | Y = −808.7527 + 18.106044 CA + 264.14317 HQ5 |
| Quickbird only | 0.432 | 0.430 | 1625.5 | 0.428 | 3945573886 | Y = 9421.6382 − 0.002867 MSAVIMIN − 5.64675 Band2MEAN − 12.89806 Band4MIN − 31.22805 Band4STD |
| Conifers (n = 897) | ||||||
| Lidar only | 0.453 | 0.451 | 680.2 | 0.447 | 417899538 | Y = −84.97512 + 25.5688 CA − 306.7143 N>90 + 144.889 N40-60 |
| Quickbird only | 0.336 | 0.333 | 750.1 | 0.328 | 507518718 | Y = −1045.448 + 0.003535 MSAVIMAX + 1925.2053 SAVIMAX + 4.552205 Band4MAX − 13.70097 Band4STDEV |
| Speciesa | N | R2 | R2adj | MSE | R2predb | Modelc |
|---|---|---|---|---|---|---|
| Broadleaf species | ||||||
| ULPU | 377 | 0.702 | 0.699 | 1098.9 | 0.694 | Y = −932.5395 + 16.3418 CA+ 161.10597 HVAR + 263.449 HQ5 |
| PYCA | 274 | 0.697 | 0.695 | 450.1 | 0.688 | Y = −345.3206 + 34.9041 CA+ 1808.5412 HSE |
| PLOC | 210 | 0.803 | 0.800 | 780.7 | 0.792 | Y = 1517.2267 + 9.46736 CA+ 158.7919 HVAR − 79.73756 HCV |
| FRPA | 175 | 0.783 | 0.779 | 259.2 | 0.767 | Y = −351.1855 + 4.197 CA+ 67.9569 HVAR + 89.8835 HQ5 |
| ULPA | 171 | 0.841 | 0.839 | 354.3 | 0.833 | Y = −171.942 + 19.2475 CA – 0.5355 NT |
| ACSA | 158 | 0.706 | 0.701 | 1964.1 | 0.687 | Y = −3674.714 + 24.5642 CA + 286.0985 HVAR + 593.973 HQ5 |
| QUSH | 115 | 0.838 | 0.833 | 330.1 | 0.771 | Y = −569.97 + 1.9247 NC + 141.973 HVAR + 198.2907 HQ5 |
| Conifers | ||||||
| JUVI | 459 | 0.684 | 0.683 | 737.1 | 0.678 | Y = −660.1173 + 44.694116 CA + 327.94367 HMIN |
| PINI | 449 | 0.715 | 0.713 | 197.6 | 0.708 | Y = −284.7497 + 12.792 CA + 1043.889 HSE + 77.7504 HQ5 |
Share and Cite
Shrestha, R.; Wynne, R.H. Estimating Biophysical Parameters of Individual Trees in an Urban Environment Using Small Footprint Discrete-Return Imaging Lidar. Remote Sens. 2012, 4, 484-508. https://doi.org/10.3390/rs4020484
Shrestha R, Wynne RH. Estimating Biophysical Parameters of Individual Trees in an Urban Environment Using Small Footprint Discrete-Return Imaging Lidar. Remote Sensing. 2012; 4(2):484-508. https://doi.org/10.3390/rs4020484
Chicago/Turabian StyleShrestha, Rupesh, and Randolph H. Wynne. 2012. "Estimating Biophysical Parameters of Individual Trees in an Urban Environment Using Small Footprint Discrete-Return Imaging Lidar" Remote Sensing 4, no. 2: 484-508. https://doi.org/10.3390/rs4020484
APA StyleShrestha, R., & Wynne, R. H. (2012). Estimating Biophysical Parameters of Individual Trees in an Urban Environment Using Small Footprint Discrete-Return Imaging Lidar. Remote Sensing, 4(2), 484-508. https://doi.org/10.3390/rs4020484






