1. Introduction
We consider the problem of collecting data from widespread stationary data sources such as ground-based environmental sensors. Such ground-based sensors can gather data unavailable to those on aircraft or satellites; for example, continuous proximal surveillance of flora [
1] or fauna [
2], or measurements that require physical interaction such as watershed runoff [
3]. The sensors may be far from cellular networks, have insufficient power or size to use long-range radio, and collect too much data to upload via satellite. We use a fixed-wing unmanned aircraft (UA) to fly over the sensors and collect the data via short-range radio [
4]. Since the sensors may continuously generate data over long periods, the UA may need to ferry the data to a collection site over repeated tours. The goal is to discover tours that minimise costs such as delays, UA operating costs, or sensor energy. We break the problem down into three layers:
Tour Design: If sensor locations are known, in what order should the UA visit them? Otherwise, what search pattern should the UA follow in order to locate them?
Trajectory Optimisation: What sequence of waypoints should be given to the autopilot in order to ensure that all waiting data are collected and performance goals are met?
Vehicle Control: How should the waypoints be translated into control surface and engine commands in order to follow the waypoint plan? What commands should be sent to the communication system?
Before the aircraft gains experience with the quirks of the radio field, the high-level planner must choose an initial trajectory. Even when node locations are precisely known, choosing an order to visit them is NP-hard and surprisingly subtle [
5]. We will focus on the case in which approximate node location information is available as when, for example, the sensors have been deployed from an aircraft.
The trajectory flown by the aircraft depends on the set of waypoints passed to the autopilot, weather, aircraft dynamics, and the control models within the autopilot. Some autopilots generate smooth shortest-path trajectories for some of the time, but at other times unexpectedly add loops and detours. Similarly, communication system performance is a complex function that depends on radio protocols, antenna patterns, noise, and interference. We assume autopilot and communication systems to be black boxes and make no assumptions about their specific functionality. Only aggregate performance of the ferry system is reported to the learner.
The focus of this paper is the trajectory optimisation layer. The goal may be to minimise trajectory length under some constraints such as collecting D bytes of data from each sensor node, or to transmit the data at lower energy cost, extending the trajectory without exceeding the aircraft’s range. Thus the task is to solve a constrained optimisation through direct sampling of trajectories.
As an example, a simple trajectory that we will use as a reference has the UA circle the assumed—possibly incorrect—location of each sensor node until it has collected all waiting data, and then proceed to the next node in the tour. As we will show, we can do significantly better than this.
If accurate models of the radio field and flight dynamics are available, then the maximum data transfer for any control policy may be computed, and standard techniques of optimal control may be used. But we are concerned with the case in which an accurate radio model is not available. Data rate is an irregular nonlinear function with a high-dimensional domain—all six degrees of freedom of the aircraft—and thus a sufficiently accurate model is time-consuming to create and use. For this reason, prior work has used various simplified radio models, all of which assume that sensor locations are known. In
Visit models, the ferry automatically exchanges all data upon visiting a node [
5–
8].
Communication radius models assume a mechanism for complete data transfer below a threshold distance, possibly by permitting the ferry to hover [
9–
14]. A learning variant on a communication radius model is described by Sugihara and Gupta [
15]: route planning assumes a communication radius, but data may also be transmitted (at the same rate) opportunistically, allowing planned tours to be shortened if possible.
Variable rate models allow data rate to change with communication range: Henkel and Brown [
16] present theoretical results using a distance-dependent rate model, Carfang
et al. [
17] compare planning results using the communication radius model with those that assume smooth and stepped variable rate models, which approximate the behaviour of 802.11g hardware. Stachura
et al. [
18] make a slightly different assumption about the nature of signal degradation in their investigation of a mobile tracking problem: the probability of packet transmission varies linearly with distance according to a model fit from data. Jiang and Swindlehurst [
19] use a more sophisticated communication model in addressing a different but related problem: the UAV serves mobile nodes. Their ferry is equipped with a beamforming antenna, and a detailed system model is used to plan trajectories that maximise the signal-to-noise ratio (SNR) to each node.
The lifetime of a sensor network may depend on the energy reserves of the nodes, so minimising the energy cost per bit (ECPB) for data transmission to the UA is valuable. The unpredictable SNR of real systems makes computing ECPB difficult, but when some model of SNR is available the data-ferry approach can be highly effective for reducing radio energy requirements. Jun
et al. [
20] compare ferry-assisted networks with hopping networks in simulation and find that a ferry can reduce node energy consumption by up to 95% (further gains would be possible if their configuration space were broader). Tekdas
et al. [
13] reach a similar conclusion on a real toy network in which wheeled robots represent ferries. Anastasi
et al. [
21] consider energy requirements per message sent including the overhead associated with turning a node’s radio on in order to search for a fixed-trajectory ferry. Similarly, Ma and Yang [
12] optimise the lifetime of nodes by choosing between multi-hop node-to-node routing and changing the ferry’s route and speed. Sugihara
et al. [
22] examine optimal solutions under the trade-off between energy use and latency given a fixed ferry trajectory, and Ciullo
et al. [
23] decrease a node’s transmit power as its data load rises, which allows high-data nodes to conserve energy and low-data nodes to require less of a detour on the part of the ferry, which moves in straight lines and stops while collecting data. Bölöni and Turgut [
24] allow nodes to learn whether or not to transmit to the ferry at a power that varies with range—if the node expects the ferry to come closer later, then it should not waste energy transmitting now. Taylor
et al. [
25] take a different approach in which the ferry’s radio field provides both data transmission and power for simple sensor nodes in a structural monitoring application. Anastasi
et al. [
26] provide a recent review covering not just data ferries but many other techniques of energy minimisation in sensor networks.
When modelling a system, simplifying assumptions are necessary, but any inaccuracies will hamper planning. The difficulty of generating and maintaining sufficiently accurate models under possibly changing conditions motivates our question: Can an autonomous aircraft learn to optimise its flight path, in a reasonable time, directly on a radio field? The goal is to provide a UA with approximate information about the geometry of a sensor network, and to have it improve its performance rapidly and autonomously. We focus on minimising sampling costs. Computational costs are comparatively minor and will not be discussed.
The contributions are as follows:
We demonstrate the feasibility of a general reinforcement learning approach for rapid discovery of good trajectories in the absence of a system model, including incorrect information on sensor node locations and radio antenna patterns.
We compare two trajectory encodings that are well-suited to the task of interfacing between reinforcement learning algorithms and off-the-shelf commercial autopilots. We show that one can produce superior results for fixed low data requirements while the other can reliably service high-data or variable-data nodes, and that both quickly learn to outperform a handcoded reference.
As an additional example of the role of learning in unmodeled environments, we show how the general approach can maximise network lifetime by learning a policy to minimise the energy used by the nodes for radio transmission.
The reinforcement learning approach developed in this paper requires significant adaptations of existing techniques in order to make a general learning framework appropriate to the data ferry problem. These are described and evaluated in detail. Through a series of scenarios we show that this learning framework can provide significantly shorter ferry trajectories (from 7% up to and beyond a factor of 3 shorter depending on the scenario). When sensor energy conservation is a goal, the learning framework can produce trajectories within the limits of ferry endurance that conserve 25%–60% of the sensor communication energy. More important than these particular results is the development of a general framework for rapid in-situ optimisation of ferry-serviced sensor networks.
Section 2 provides an overview intended to put our choice of subproblem in context. Section 3 develops the radio model used for the simulations. Section 4 describes how waypoints are interpreted by our simulated autopilots. Section 5 reviews the learning algorithm and explores two applications: waypoint placement and minimisation of sensor radio transmission energy. Simulations that show what improvements can be gained are shown in Section 6. In Section 7 we summarise what this work contributes and discuss its relationship to other layers of the data ferrying problem. Section 8 concludes with the broader implications of the work.
2. Data Ferrying: Problem Overview
The concept of data ferries is widely applicable, and consequently the variety of considerations is large. This section is not meant to be exhaustive, but to give a sense of the breadth of the problem space and to provide context for our choices within this space.
2.1. Sensors
Some ground-based sensors do not move once deployed. Some move without control; for example, sensors deployed on ice floes, floating in bodies of water, in flood plains, or attached to wildlife. Data ferries are sometimes used to provide connectivity for fully mobile nodes such as military ground forces. In this paper we assume stationary sensors in environments that are unchanging on the timescale of a few dozens of tours.
Sensor energy is generally supplied by battery, although some sensors harvest energy from the environment. We do not model sensor energy levels explicitly, but assume that radio transmission may consume a significant portion of a node’s energy reserves.
The kind of sensor data, expected sensor lifetime, and network latency all contribute to the required data storage (buffer) capability of sensors. We assume that storage and buffers suffice for the application and do not model buffer state.
2.2. Ferries
A ferry moves between sensors and possibly base stations, retrieving and transmitting data. Ferry mobility hardware is diverse. The ferry may be attached to a vehicle such as a bus or commercial aircraft and thus follow a regular route with few concessions to data collection. Ferries may have a prescribed mobility pattern designed for a specific sensor deployment, or may change trajectories in response to new information. Our ferries are special-purpose vehicles whose trajectories may be manipulated with no consideration for non-ferrying tasks, and whose range and refuelling requirements are assumed to be appropriate for the application. Watts
et al. [
27] review currently available platforms.
Our hardware, unmanned fixed-wing aircraft, is constrained by some range, maximum and minimum speeds, and turning radii, but this is not the only possible choice, and other choices are amenable to our approach given appropriate trajectory representations and cost functions. Helicopters and quadrotors can hold a position at some cost in energy; ground vehicles can hold a position without an energy cost, as can buoyant vehicles in calm weather. Some vehicles can be controlled precisely; others, such as our fixed-wing aircraft with their off-the-shelf autopilots, cannot, which imposes further constraints on trajectory shapes and the accuracy with which they can be realised.
2.3. Radios
The selection of radio hardware and standards constrains trajectory choice. For example, available data transmission rates and association times affect the ability of the ferry to sense and respond to its radio environment. Beam pattern controls range and signal isolation. A steerable antenna can offer a greater advantage at the cost of complexity and weight.
If only one sensor transmits data at any given time, interference from other sensors is eliminated. But this may not always be possible, for example when searching for sensors or comparing signal strengths, using multiple ferries, or in the presence of sources that are not part of the sensor network. In the first two cases, enhanced protocols can mitigate multi-source interference.
All of these variations could be accommodated, but here we have chosen to ignore protocol details and ties to specific hardware, and instead focus on a simple model that creates a sufficiently complex radio environment to explore a versatile model-free learning approach.
2.4. Problem “Size”
The notion of problem size can take many useful forms. There may be one sensor or thousands, served by one ferry or by many. The ferry may need to retrieve bytes or gigabytes. The longevity of a sensor network is another useful measure of size: in some cases a single collection run is anticipated, and in others the network’s lifetime and the number of collection runs may be indefinite. Here we assume a single ferry, up to a few dozens of sensor nodes, a single base station, a broad range of data requirements, and a network that is designed to collect data continuously and be polled by the ferry at least dozens of times.
2.5. Knowledge
Often the locations of the sensors will be approximately known—the location of a measurement is usually important—but the accuracy requirement may be inadequate for optimal trajectory planning. It is possible that each sensor knows its own location but this information is not available to the ferry until contact, and in the case of mobile sensors or noisy GPS this information may not be static. Other times sensors may not know their positions, and it is up to the ferry to provide approximate location information. In other cases sensors may be known only to lie somewhere in an area, necessitating a search.
When using radio or other propagating-wave communication system, knowledge of the shape of the radio field is likely approximate, and may change over time due to sensor mobility or environmental effects. The interaction of radio waves with terrain leads to reflections, occlusions, and self-interference, and the existence of other radio sources causes further difficulties. Therefore, while accurate knowledge of the radio field can allow effective trajectory planning, the ability to accommodate vague or incorrect information is important.
We assume that the aircraft knows the identities of sensor nodes, and that it knows enough about their positions to fly to within radio communication range of them. This information could be discovered by a preliminary search pattern, inventory, and initial tour generation phase, but that phase of learning is outside the scope of this paper.
2.6. Objectives
Trajectories can be optimised in terms of standard network performance measures and various other measures relevant to data-ferry networking.
Bandwidth is the average rate of arrival of data at the hub. If this is not the same as the total of data production rates of the sensors, then they must discard data, which may be appropriate for some tasks. Latency, the delay between a sensor taking a measurement and the measurement arriving at a base station, is sensitive to the ferry’s trajectory. We consider only the latency minimisation that comes with reducing tour length.
Other objectives are possible: sensor radio energy use (considered in Section 5.4), spatial costs to the ferry such as difficult terrain or hazardous flight conditions, or value-of-information metrics used for event reconstruction. These objectives can be accommodated using this paper’s approach, but we do not investigate them here.
Two ways of classifying optimisation criteria will be especially useful:
Hard vs. Soft Constraints: A hard constraint is a property of the solution that either exists or does not exist. In this paper, the notable hard constraint is that trajectories must collect the required quantity of data. In contrast, for a soft constraint a more extreme value is always preferred. For example, shorter trajectories are generally preferred.
Global vs. Local: The tour length is a global criterion, since each action affects others and thus impacts the whole tour. Other objectives are spatially localised; for example, radio energy used at any given sensor depends only on decisions made in the vicinity of that sensor.
The first distinction is important because of the difficulty inherent in model-free learning algorithms: fulfillment of hard constraints is not guaranteed, but must be learned quickly or ensured by a non-learning component. The second distinction has a bearing on the scalability of the problem: the speed of optimisation of global objectives depends on the number of nodes or trajectory parameters, whereas the optimisation of local-flavoured objectives can be largely independent of the number of nodes.
3. Radio Environment Model
Our goal is to evaluate the ability and limitations of model-free optimisation in a complex, unknown radio environment. To this end we introduce a radio model that incorporates several complicating factors that are rarely considered: variable-rate transmission, point noise sources, and anisotropic antenna patterns. This model extends that introduced in our previous work [
28] only by adding dipole antennas to the nodes.
The signal to noise ratio at node
a from node
b is given by
where
P (
a, b) is the power received by node
a from node
b,
N is background noise from electronics and environment, and
ni are other transmitters or noise sources. The power between
a and
b is normally computed as
for reference transmit power
P0,a, reference distance
d0 = 1, distance between transmitter and receiver |
Xa –
Xb|, and propagation decay ∊. However, antenna shape and radio interactions with nearby objects make most antennas directional, so the orientations of the antennas affect power. We model the aircraft’s antenna as a short dipole with a factor of 1.5 gain (1.76 dBi) oriented on the dorsal-ventral axis of the aircraft, and approximate the resulting radio pattern as a torus. We model the nodes’ fields similarly with random fixed orientations, so we adjust the power computation in
Equation (2) to:
where
ξxy is the angle between antenna
x’s pole and the direction to
y, and depends on the relative position of transmitter from aircraft (∈ ℝ
3), the aircraft’s heading, roll, and pitch (∈ ℝ
3), and the transmitter’s orientation, although the latter is assumed not to change. Here we consider only constant-altitude trajectories with zero pitch and yaw relative to the direction of travel.
In order to evaluate
Equation (3) we require the UA’s position and orientation. A full dynamical simulation of the aircraft is unnecessarily complex for our purposes, so we assume that course and heading ϕ are the same (yaw = 0), pitch = 0, and roll
, which varies between 0 for a straight course and ±54° for our maximum turning rate of
ϕ̇ ≃ 0.347 rad/s (
i.e., the UA flies a complete circle in 20s).
We use the Shannon–Hartley law to compute the data transmission rate between transmitter
a and receiver
b:
This assumes that data rate varies continuously. The hardware may use discrete rates that are chosen according to current SNR conditions, but Carfang
et al. [
17] indicate that the difference in trajectories and performance outcomes between continuously variable and the 9 discrete rates of 802.11 g may be small for this type of problem.
This model ignores many characteristics of a real radio environment such as occlusion, reflection, higher-order directionality, and multipath propagation. Moreover, the sensor nodes all transmit simultaneously and interfere at the UA—we do not simulate obvious protocol modifications that would allow other sensor nodes to cease transmission and thereby reduce interference with the active node. However, in part due to the latter omission, the model produces fields that have irregularities similar to those that occur in real radio environments, and thus it meets our aim of having a complex simulation environment within which we can test whether the aircraft can learn in situ.
4. Policy, Autopilot, Trajectory
The aircraft is directed to follow some trajectory by the autopilot. The design of the policy representation is driven on one hand by the learning algorithms that we will see in Section 5, which require a representation for which it is easy to generate variations and that can be manipulated at low computational cost. The other factor dictating the design of the policy representation is the autopilot, which generally cannot accurately track arbitrary trajectories, but which can easily work with waypoints. Thus the autopilot realises trajectories and the policy representation serves as the interface between the learner and the autopilot, allowing the latter to remain ignorant of the former’s internals.
4.1. Reference
The non-learning
Reference autopilot is taken from Carfang
et al. [
17]. It is provided with estimates of the sensor nodes’ locations (although these can be difficult to discover [
29]), which it assumes to be correct. For each node, the UA receives data only from that node while flying at constant speed
v towards the tangent of a circle of minimum turning radius about the node’s nominal location. It then circles the target node at the maximum turning rate
ω until
D bytes are received, and then proceeds to the next node (this is an improvement on the Reference used in [
28], in which the aircraft flew toward a waypoint and then circled so that the waypoint was on the circle’s perimeter rather than at its center). This produces the Reference trajectory.
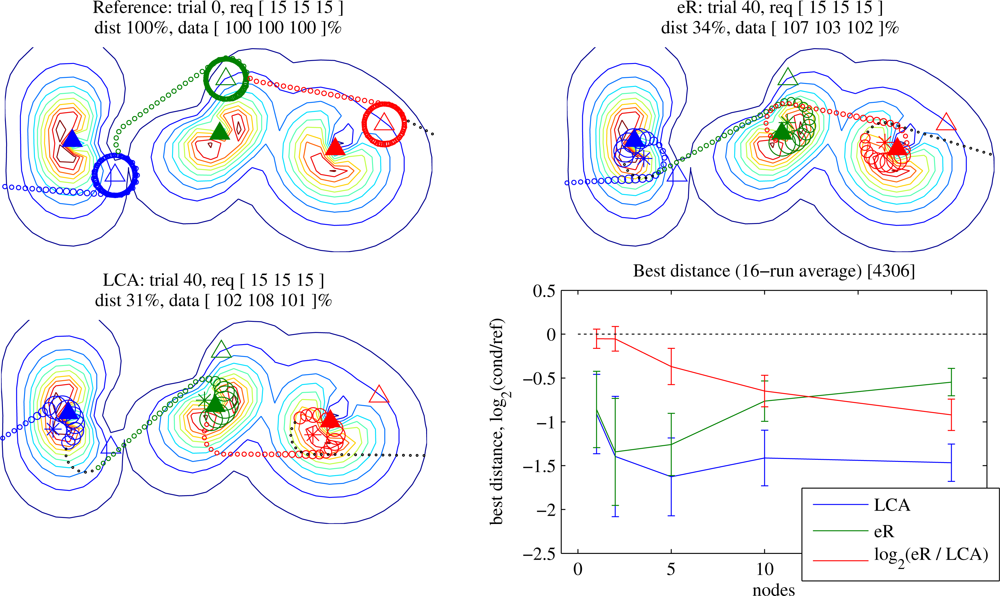
Figure 1 (left) shows an example of a trajectory generated by the reference autopilot.
4.2. Waypoints
The learning
Waypoints autopilot flies directly towards each waypoint in the sequence supplied by the planner, adjusting its heading for the next waypoint at its maximal turning rate
ω as soon as it has passed the current one. We define “passing” a waypoint as being within the UA’s turning circle of it:
(see
Figure 1 (middle)). We initialise trajectories of “
n waypoints per node” with a waypoint at the nominal location of each node (not including the start and end points) and
n – 1 waypoints evenly spaced along each tour segment. The UA collects data
opportunistically: at each timestep, of the nodes that still have data to be uploaded, communication is to the node with the highest observed SNR—a suboptimal greedy algorithm, but one that performs well in practice. We have assumed that the protocol overhead of monitoring the SNR and associating to each node is relatively small.
Under the conditions for which it was designed, the Waypoints autopilot can discover excellent trajectories (see Section 5), but it has three weaknesses due to the fact that it has no inbuilt mechanism for lingering in the vicinity of a node in order to fulfill larger data requirements.
While learning proceeds quickly, often producing trajectories that recover all the data in a few dozen training circuits, the requirement for an initial training time during which not all data are collected limits the domains in which the technique is applicable.
As the data requirement grows or a node’s SNR becomes too low due to interference or power constraints, it becomes more and more difficult to learn waypoint placements that generate the loops required to collect all the data.
If the data requirement or radio background change much from flight to flight, the learned Waypoints trajectory will no longer be appropriate.
4.3. Data-Loops
The learning
Data-loops autopilot is an attempt to combine the advantages of the Reference and the Waypoints autopilots, obviating the need to learn the hard constraint on data requirement (
Figure 1 (right)). It assigns one waypoint to each node—we will assume that node identities and approximate locations are known during tour initialisation, although the assignment could instead occur on the fly as nodes are discovered. The aircraft collects data from any node opportunistically while flying towards the tangent of a minimum-turning-radius circle about the waypoint, and then if necessary circles the waypoint exchanging data only with the assigned node until it has collected sufficient data. Note that the true node location and the waypoint location may differ, and as we will see, usually they will.
5. Trajectory Learning
The optimal waypoint placement solves:
where
d is the total distance flown by the ferry aircraft on the time interval [0,
T] under waypoint policy
π(
θ) (defined in Section 5.1),
Rj is the radio transmission rate to node
j, and
Dj is node
j’s data requirement. The models for radio (Section 3) and autopilot (Section 4) underlie
Equation (5), but it is difficult to anticipate
Rj at a given aircraft position. Besides, due to the unpredictable nature of the autopilot, it is difficult to anticipate the aircraft’s position through time in response to a set of waypoints. Thus knowing a set of waypoints does not allow us to anticipate how far the aircraft will fly or whether a given trajectory will satisfy the constraints.
This paper compares two solutions to this difficulty. For the
Waypoints planner we will rewrite the constraints of
Equation (5) as costs for the optimiser to minimise through experience. For
Data-loops we alter the behaviour of the underlying autopilot to guarantee that the data constraints are satisfied.
Since
Equation (5) cannot be solved directly given the available knowledge, we use a parameter optimiser based on a Policy Gradient Reinforcement Learning (PGRL) algorithm. For waypoint placement we use a simplified version that reduces to Simultaneous Perturbation Stochastic Approximation (SPSA) [
30,
31]. Because the policies do not react to state, it is not strictly correct to refer to this simplified version as “reinforcement learning”: the policies are open-loop, and a non-learning trajectory-tracking controller (the autopilot) closes the control loop. This is not uncommon in the PGRL literature [
32–
34] but Kohl and Stone [
32] referred to it as “a degenerate form of standard policy gradient reinforcement learning”. The simplification is desirable because it allows a reduced policy space and thus faster learning. More importantly, the PGRL framework makes it easy to reintroduce state dependence at the policy level, as we will do when minimising sensor transmission power requirements in Section 5.4.
In [
35] we showed that the Waypoints learner can quickly discover trajectories that outperform a similar handcoded reference if the data requirement does not grow too large. We will apply the same learning algorithm to the Data-loops representation. We review the learning technique in Sections 5.1 and 5.2. In [
28] we developed a local credit assignment (LCA) decomposition that improves the optimiser’s scalability during the local-flavoured phases of the optimisation; we review this and discuss its relationship to the Data-loops policy representation in Section 5.3. To show the versatility of the learning approach, Section 5.4 has the ferry learn a communication policy that prolongs sensor lifetime by minimising the radio transmission power used.
5.1. Baseline Gradient Estimation
In PGRL, a stochastic policy
π(
s,
u;
θ) = Pr(
u|
s;
θ) defines the probability of choosing action
u in state
s with the policy’s parameter vector
θ ∈ ℝ
n. The expectation of discounted rewards averaged over all states
s and actions
u under a policy
π(
θ) is called the expected return
J:
where
r is the reward received at each time step,
γ ≤ 1 is a “temporal discount” that places higher value on rewards received sooner than on those received in the more distant future (this will be discussed further in Section 5.3), and
γΣ normalises the temporal discount weights and satisfies
. We will use the common abbreviation
J(
θ) =
J(
π(
s,
u;
θ)). The key component of PGRL is estimating the gradient of the expected reward:
.
We break the task down into distinct “trials”. Each consists of a complete execution of π(θ) over a bounded time interval—the aircraft flying a complete tour τ—followed by receipt of reward r at the end. During a trial, the policy defines a probability distribution over the action chosen at any point. Assume that the controller makes some finite number H of decisions uk at times tk, k ∈1 … H during a trial; discretizing time in this manner makes it possible to compute the probability of a trajectory under a policy as the product of the probabilities of each (independent) decision at each time tk. So
.
To optimise
θ, we estimate the gradient using stochastic optimisation’s “likelihood-ratio trick” [
36] or reinforcement learning’s “episodic REINFORCE” (eR) [
37] with non-discounted reward. Each element ∇
θi of the gradient is estimated as:
in which
bi is a “reward baseline” for element
θi, computed as the inter-trial weighted mean of rewards, using the per-trial weight
, and 〈 · 〉 is the average over some number
N of trajectories.
μΣ∇ is the mean over trials of the ∑∇
θi terms. This term does not appear in [
33] but is included here in order to reduce the variance of the “characteristic eligibility”, as we found it further improves the gradient estimation process. The gist of
Equation (7) is that when action
u performed in state
s produces a better-than-average reward, the policy parameters
θ should be adjusted to make future production of the high-reward response more probable, and
vice versa. The equation may be arrived at in several ways; for derivations see the above references or [
33]. We will revisit the temporal discount factor
γ in Section 5.3; unless otherwise noted we use γ = 1.
Once we have computed a policy gradient estimate
for episode
e, we take a step of some length
α in that direction,
thus altering the policy. The gradient estimation and update may be repeated until a design requirement is met, until the policy converges to a local optimum, or forever—to adapt to an environment that changes slowly over time. If
α decreases over time and the environment is static, the algorithm is guaranteed to find a locally optimal policy eventually. The theoretical guarantee of convergence to a locally optimal policy is only available if
α decreases over time. That guarantee is useful, but does not directly apply to learners operating in a changing environment, although we will revisit it for energy conservation in Section 6.5.
5.2. Learning Waypoint Placement
We consider a sequence of nodes that need to be visited in some order {
a, b1, …,
bn,
c} that was determined by a higher-level planner [
5,
11]. We will assume that the aircraft must fly a trajectory that starts at
a and ends at
c and allows exchange of
Dj bytes of data with each of the
n sensor nodes
b1 to
bn. Thus we seek the shortest path
a →
c subject to the constraint that for each sensor node
j, ∫
Rj(
t)
dt ≥
Dj, in which the data rate
Rj(
t) is measured in flight, or simulated as described in Section 3.
5.2.1. Policy
Both
Waypoints and
Data-loops policies are implemented as sequences of constant-altitude waypoints that are fed to the autopilot. So for
m waypoints, the policy’s parameter vector
θ = [
x1 y1 x2 y2 …
xm ym]
T. In order to be used by
Equation (7) the controller adds noise such that Pr(
τ|
θ) can be computed. In a real system, actuator noise or autopilot error
E can be used for this purpose if ∇
θ log Pr(
u +
E |
θ) can be computed, but in our simulations we simply add zero-mean Gaussian noise
(0, Σ), Σ =
I, directly to the waypoint locations at the beginning of each tour:
Recall that this policy’s output does not depend on state
s, but see Section 5.4.1 for an example of a policy that does respond to
s.
5.2.2. Reward
When a system model is not available, constraints cannot be guaranteed. For the Waypoints planner we seek to fulfill them by trial and error through the gradient estimation process. Hence instead of solving
Equation (5), we maximise the expected return (
Equation (6)) for a reward function chosen to favour solutions that also solve
Equation (5). Rewards (or their negatives, costs) are assigned so that solutions that better satisfy the design objectives have higher reward (lower cost). The constraints in
Equation (5) differ from the corresponding summands of the reward in that the former merely state requirements while the latter create a function at whose maximum the constraints are satisfied.
For our waypoint-placement problem, we seek the shortest tour subject to the constraint of allowing exchange of
Dj bytes of data with each sensor
bj, so we define a reward function that aggressively punishes data underrun while placing a more modest cost on trajectory length:
where
d is the trajectory path length,
η = 10, 000 is a weighting term chosen so that violation of a hard constraint (data underrun) dominates the costs,
mj is the data quantity collected from sensor node
j,
Dj is the data requirement on sensor
j, and
μ is an optional small safety margin that helps to ensure that all data are collected even in the presence of policy noise. When the constraint is satisfied—or for the guaranteed collection of the Data-loops planner—the second term disappears and only trajectory length affects reward.
5.3. Local Credit Assignment for Data Ferries
When reward is received at the end of an episode, we encounter a version of RL’s credit assignment problem: noise was added to the policy’s output at several points and that noise had some effect on the reward, but we have little information as to which variations to the policy output were responsible for the observed outcome. As the number of parameters increases, this difficulty worsens, leading to increased noise in the gradient estimate, and therefore to increased learning time.
The reward function (
Equation (11)) is made up of 1 +
n summands—a cost for the optimisation criterion
d and a cost designed to create a suitable reward gradient for each of the
n constraints. The policy is made up of some numbers of parameters that define the locations of waypoints, so each policy parameter can influence some subset of the
n + 1 reward summands. The members of the subset are no more predictable than are the trajectory and radio interactions, but they are observable. Can the effect of exploration noise on reward be credited to the relevant policy parameters? Can this be used to speed learning as problem size increases?
Below we develop an approach based on such a reward decomposition. We introduce an estimate of the relationship between policy parameters and nodes, which allows us to compute a policy gradient for each data constraint term. This allows the policy updates to be directly based on individual constraint-violation-based gradient estimates, rather than through the indirect mechanism by which constraint violations dominate the monolithic reward gradient.
5.3.1. Components of the Reward
The reward function is designed to drive the learner towards good solutions that satisfy the constraints. In our current example, the UA must collect as much waiting data as possible from each of the
n nodes while remaining as short as possible—leading to 1 +
n terms. Other terms could be included in the optimisation function: for this explanation, let us consider those two types and introduce one more:
While slight gains can be achieved by treating local contributions to trajectory length, here we will focus on the latter two types of constraint due to their local flavour.
5.3.2. Local Credit Assignment (LCA)
In reinforcement learning, when an action
u is taken at time
tu and a reward
r is received at future time
tr, the action is assigned
credit for the reward based on an estimate of how important the action was in producing the reward. In eR, this takes the form of optionally putting greater weight on rewards received early in the episode than on those received later, modulated by the term
γtk, 0 <
γ ≤ 1 in
Equation (7). The Policy Gradient Theorem (PGT) [
38] and G(PO)MD [
39] take a more sophisticated approach by using the separation in time between
tu and
tr to assign credit in proportion to
γ tr−tu,
tu <
tr (the full estimator will appear shortly as
Equation (12)). There is generally no correct choice for
γ because the assumption that the effect of a decision decays exponentially with time is just an approximation, usually based on the programmer’s intuition and experience with the problem. But when we know the temporal link between a policy decision that causes action
u and a reward
r, we can usurp this mechanism and use it to assign credit correctly.
Reward (
Equation (11)) is a sum of functions of total trajectory length and the data underrun for each node. Since the data requirement constraint for each node can be satisfied by disjoint regions in the trajectory, the value of each reward summand is available only after completion of a trial. LCA aims to redistribute the final reward such that credit for exploration-induced changes in each local-flavoured summand is attributed only to the exploration noise added to the relevant policy parameters. To this end we define a more general credit assignment function that credits action
utd for reward
rtr as
γ(
tr–
td)·
rtr, where
γ(·) is a function that encodes causal knowledge about the timescale of the effect of
utd.
Under the Policy Gradient Theorem, the following estimator is used to compute the gradient for policy parameter
i:
where 0 <
γ ≤ 1 is a scalar temporal credit discount base that determines how much credit to give to an action chosen at
tu for reward at
tr. Because our policies are open-loop, the moment
tu at which an action is “chosen” may be defined arbitrarily. We sacrifice the conventional notion of causality in exchange for symmetry, and define the time of choice
tu for a given waypoint to be the moment at which the aircraft passes the “chosen” waypoint. Thus “actions” affect not just the future as in the PGT, but also “the past”—points in the trajectory that occur leading up to the waypoint. We modify
Equation (12) as follows to produce the LCA estimator:
We have changed
γ from a scalar to an arbitrary function that assigns credit at time step
k for policy parameter (or waypoint)
i, and re-inserted the variance-reducing term
μΣ∇ from
Equation (7). Since
rj is computed at the end of a trial, we introduce
ρjk in order to distribute the reward received from summand
j at time
tk. Finally, the indices of the reward summation can span the whole trajectory since
γik will modulate reward through time.
Redistributing reward requires that we determine the effect of each waypoint on each reward summand, which requires that we answer the following two questions:
Question (I) may easily be answered—approximately. When the trajectory is well-approximated by line segments, each point in the trajectory between waypoints wi and wi+1 is affected only by those two waypoints. (With higher-order splines such as NURBS, the number of control points affecting each time step would be greater, but still generally a small constant.)
x(
tk) =
xk is the aircraft’s position at time
tk. To compute the effect of exploration noise at waypoint
wi (or, equivalently,
θi ∈ ℝ
2) on the aircraft’s location at time
tk we must look at three cases: that in which the aircraft has passed waypoint
wi–1 and is now steering towards waypoint
wi, that in which the aircraft is orbiting
wi, and that in which it has passed
wi and is en route to
wi+1. We define the parameter-point credit relating the current point on the trajectory to
wi as:
where
d(·, ·) is the distance between the (GPS) positions of its arguments. This gives the parameters that define
wi 0% of the credit for the aircraft’s position at
wi–1, increasing linearly to 100% as the aircraft approaches
wi, and decreasing linearly as the aircraft recedes towards the next waypoint, and ∀
tk Σ
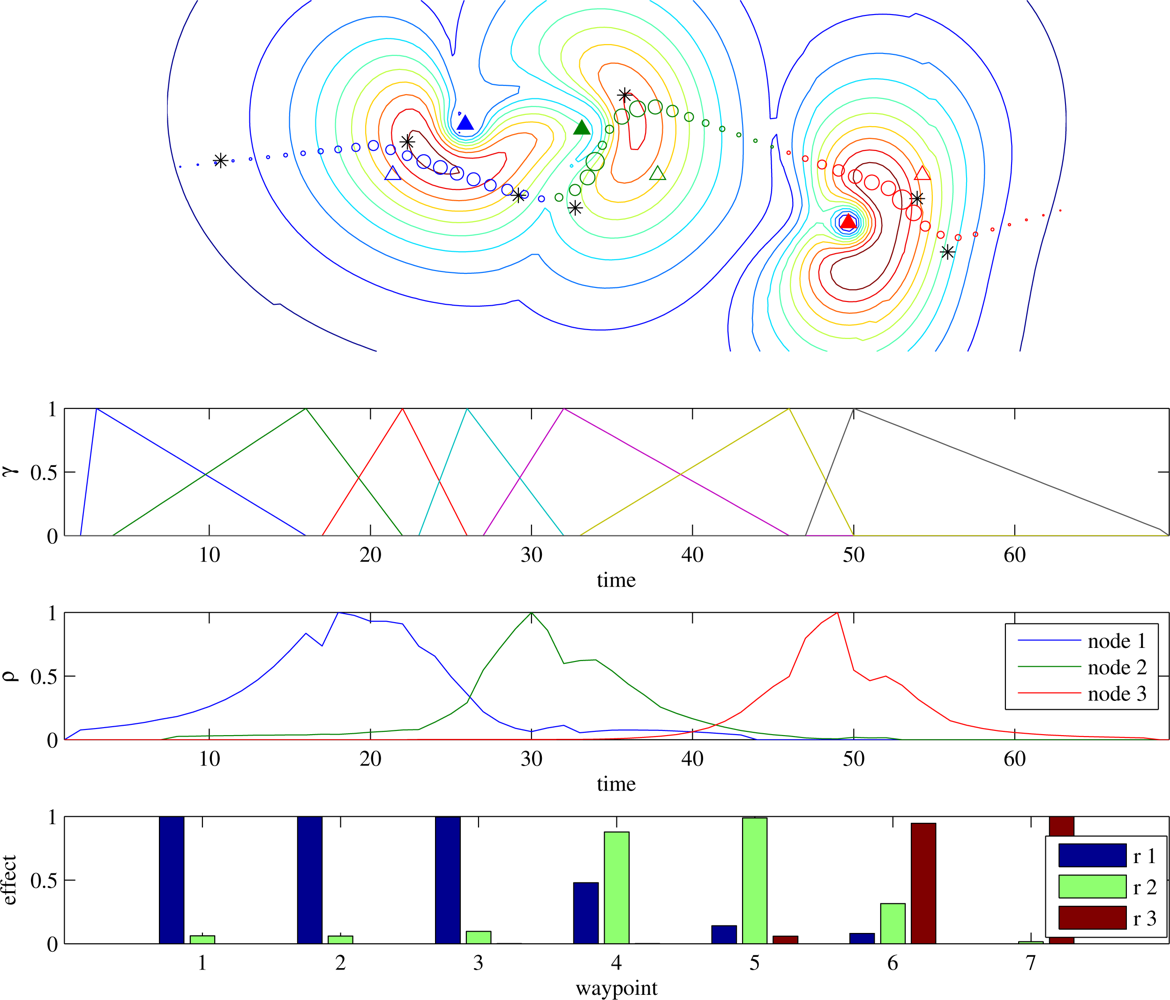
i∈waypoints γik = 1. An example of the computation of
γ is illustrated in
Figure 2.
This is exact for trajectories made up of constant-velocity line segments, but our assumption of unknown autopilot control policies and UA flight dynamics make it impossible to compute
γ exactly. Therefore
Equation (14) is an approximation. Future work will investigate learning a better approximation to the true form of
γ from data, but for now our objective is to show the value of this problem decomposition, which we can do even when
γ is approximate.
Question (II) addresses the following problem: each reward summand can only be computed at the end of the trajectory, but in order to assign credit we must decide which points along the trajectory contributed to the eventual reward. For our current example, the reward is of two types:
The
underrun reward summand rj for each node
nj is affected by some number of steps along the trajectory. Those points
k on the trajectory that can most affect
rj—those with the highest data transfer rate—should be given the greatest weight in
ρjk, so we assign a contribution to point
x(
tk) =
xk for reward summand
rj proportional to the maximum observed transfer rate from the UA at
xk to node
nj. We
L∞-normalise the contributions so that nodes with a relatively low maximum transfer rate are not ignored:
An example of
ρ vs. time is depicted in
Figure 2, along with the product
γρT—the effect of each waypoint on each node’s reward used in
Equation (13). The gradient due to each underrun summand is computed separately via
Equation (13).
The reward function treats the
tour length reward summand as a global property of the trajectory, but it too can be decomposed by considering the portion of the trajectory length due to each waypoint. The mechanism of LCA is overkill for this term:
ρt =
vΔ
t, and therefore
Equation (13) reduces nearly to
Equation (12): the waypoints still define the same
γik described in
Equation (14) rather than the decaying exponential assumed by
Equation (12). For this reason we will refer to this variant as
LCA-length.
5.3.3. Combining the Gradient Estimates
In the example above, we have shown how to compute three different gradient estimates:
The original reward function (
Equation (11)) balances underrun and length penalties by ensuring through
η that whenever there is underrun, the policy gradient with respect to reward is steepest in the direction that will most reduce the hard constraint. But with the LCA decomposition, length and individual underrun penalties are each computed from their own reward terms, producing separate policy gradient vectors. This allows us to balance optimisation of the hard constraints against the soft not through the indirect mechanism of the monolithic reward function but rather by ensuring that hard-constraint gradients dominate the policy update.
We create a new policy update for
Equation (8) by combining the LCA-based gradient estimates
and
in a way that ensures that wherever a hard constraint is violated (a data underrun occurs and
is nonzero), that update vector dominates the total update, otherwise only the LCA-length update vector
is used. Due to sampling a rough reward space, the gradient estimates’ magnitudes are somewhat arbitrary, so before adding them it is first desirable to scale their values. We use:
where
δu controls the relative weight of each underrun gradient
guj relative to that computed from trajectory length. Careful tuning is unnecessary as long as
δu ≫ 1, which ensures that the gradient update calculated from underrun dominates whenever it exists. We will use
δu = 5 in our examples. The global eR gradient estimate is redundant and does not need to be included.
For purposes of comparison, we perform one final L∞-normalisation step on this combined gradient estimate in order to ensure that when comparing LCA to eR the gradient-ascent steps have the same magnitude.
5.4. Learning to Reduce Sensor Energy Expenditure
The data-ferrying approach allows sensors to communicate with distal base stations without the need for high-powered radios, but the energy that nodes spend in communicating with the ferry is still non-negligible [
13,
20]. Recall the data rate from Section 3:
The derivative of
is negative whenever
which is true except at
P = 0, so lower power always results in a lower energy cost per bit. However, lower transmission rates require longer trajectories. So here we ask: given a predefined trade-off between ferry trajectory length and node energy savings, when should a sensor transmit, and at what power?
This question is made difficult by our standard assumption that the SNR between transmitter and aircraft is hard to predict. Again, a model-free learning approach seems appropriate. For this experiment, we assume that at each time step a sensor can transmit with any power P ∊ [0, Pmax], that it occasionally sends short probe packets at P = Pmax, and that the aircraft’s radio can use these packets to measure the current maximum SNR and provide instructions to the node. We assume that these packets are too brief to transmit sensor data or use significant power, so we do not model them explicitly.
5.4.1. Policy
The
power policy is a learned function that controls the power a node uses to transmit given a reported SNR, given in dB. Our desired behaviour is to transmit at a target power
Ptarget ≤
Pmax whenever the probed SNR is greater than some threshold
RT. In order to apply reinforcement learning, exploration noise must be added to
Ptarget. Therefore the actual transmission power
Pnow for each time step is drawn from a Gaussian whose mean is taken from a sigmoid of height
Ptarget:
where
s = SNR
probed. With this we define our policy:
with
When SNR
probed =
RT, the mean transmission power is 50% of
Ptarget, going to 100% as SNR
probed increases above
RT and vice versa, thus implementing the desired behaviour with exploration. The sigmoid’s width is controlled by
ϕ, and Gaussian exploration is controlled by
σ. For example, when
Ptarget =
Pmax and
RT is small, if σ is small then the policy mimics the full-power Data-loops policy.
The policy’s derivatives are:
Unlike the waypoint-placement policy, this one is closed-loop: sensing packets detect SNR, which informs the choice of action (transmission power) at each time step. Thus we use the full capabilities of the episodic REINFORCE algorithm of Section 5.1. This policy and the waypoint-placement one run in parallel, using the same flights to estimate their gradients.
5.4.2. Reward
Since lower power necessitates longer trajectories and we would like to be able to explore without incurring data underruns, we investigate only Data-loops trajectories. The most energy-efficient transmit power leads to infinite-length trajectories, so we add a constraint: we seek the policy that requires the least transmission power subject to an approximate maximum desired tour length
dmax, representing the endurance limit of the aircraft. We choose the following reward function, which describes these constraints:
where
Pjk is the transmission power of node
j at timestep
k,
ϱ controls the sensitivity of the soft maximum distance penalty, and
φj is a weighting for the value of energy for node
j. There is no penalty for trajectory lengths
d <
dmax.
5.4.3. An “LCA” Decomposition?
LCA is effective for linking the satisfaction of local-flavoured constraints such as data underrun to waypoints that are not explicitly tied to nodes—that the satisfaction of the constraints is a well-defined local property of portions of the trajectory makes local credit assignment meaningful. But for the power policy under the Data-loops planner, parameters and rewards both correspond to nodes rather than to waypoints, so the mechanism by which LCA assigns per-node reward to influential waypoints is unnecessary.
Our simpler approach uses a pseudo-local breakdown of
Equation (16), estimating the reward gradient for each node’s policy separately, computing the reward for node
j as:
The first term, the total nonlinear length penalty divided evenly between the
n nodes, makes this decomposition simplistic. It nonetheless yields a small but consistent performance and scalability gain, and will be used to produce per-node gradient estimates throughout Section 6.5.
6. Experiments
The first four subsections investigate factors that affect trajectory length with the transmitters at full power. Our previous work showed that under certain conditions the Waypoints trajectory planner can quickly outperform Reference. Here we confirm those results and compare them to results for the Data-loops planner.
We define acceptable trajectories to be those that collect the required D bytes of data, regardless of trajectory length. The reference and Data-loops autopilots always produce acceptable trajectories, while the Waypoints autopilot may take some number of trials before discovering one. The learning autopilots are judged by three criteria: the fraction of the trajectories that are acceptable when testing on randomly-generated problems, the length of the trajectory as a fraction of the reference trajectory, and how many trials (samples) the agent required in order to learn the presented solution. Computational cost is not considered since these algorithms take negligible time compared to flying the aircraft.
Section 6.5 explores the simultaneous optimisation of trajectory length and node energy using the Data-loops planner. Energy use and trajectory length balance each other as specified by
Equation (16), so the main performance criterion is the composite measure defined by reward.
Parameters: The aircraft flies at a constant speed
v = 1 at altitude
z = 3, with a maximum turning rate of
ω = 20°/
s, which yields a turning radius
. We use bandwidth
β = 1, and background noise
N = 2. For the Waypoints trajectory, we use safety factor
μ = 1 (
Equation (11)). Unless otherwise noted, gradient estimates are computed after 4 trials, which as we found generally produces fast learning for this problem [
28]. These generic parameters do not qualitatively affect the results, and can be replaced by appropriate values for any given hardware.
6.1. Waypoints vs. Data-loops
When the SNR is high enough and the data requirement low enough that the ferry does not need to repeatedly loop around a sensor, Waypoints quickly learns trajectories that are significantly shorter than Reference. Pearre and Brown [
35] explored the performance that the Waypoints learner could achieve, and those results will be confirmed here (the Reference planner used here is improved compared to [
35], but the difference turns out to be small). How does Data-loops compare?
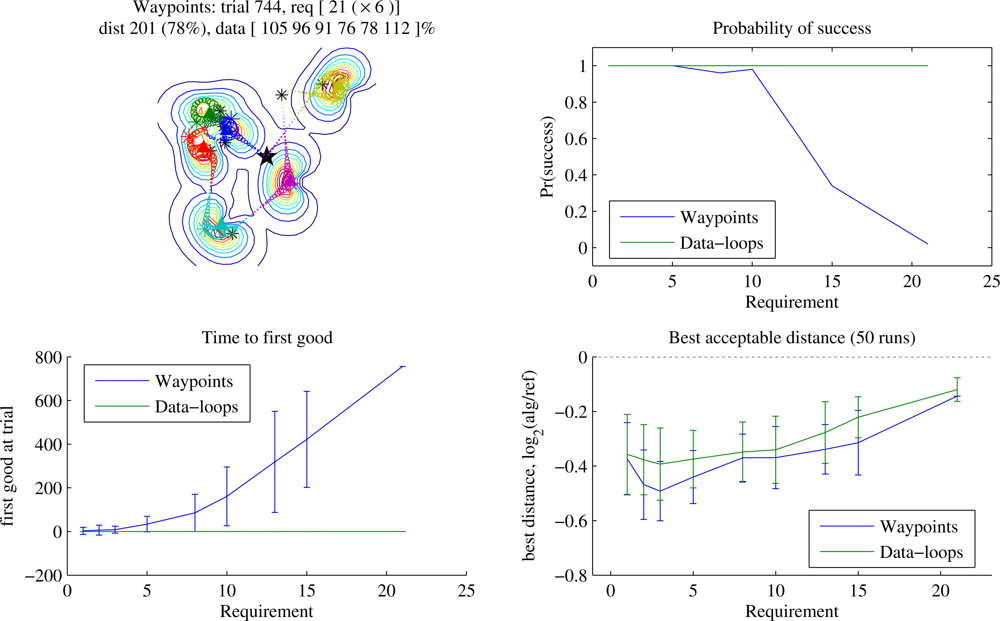
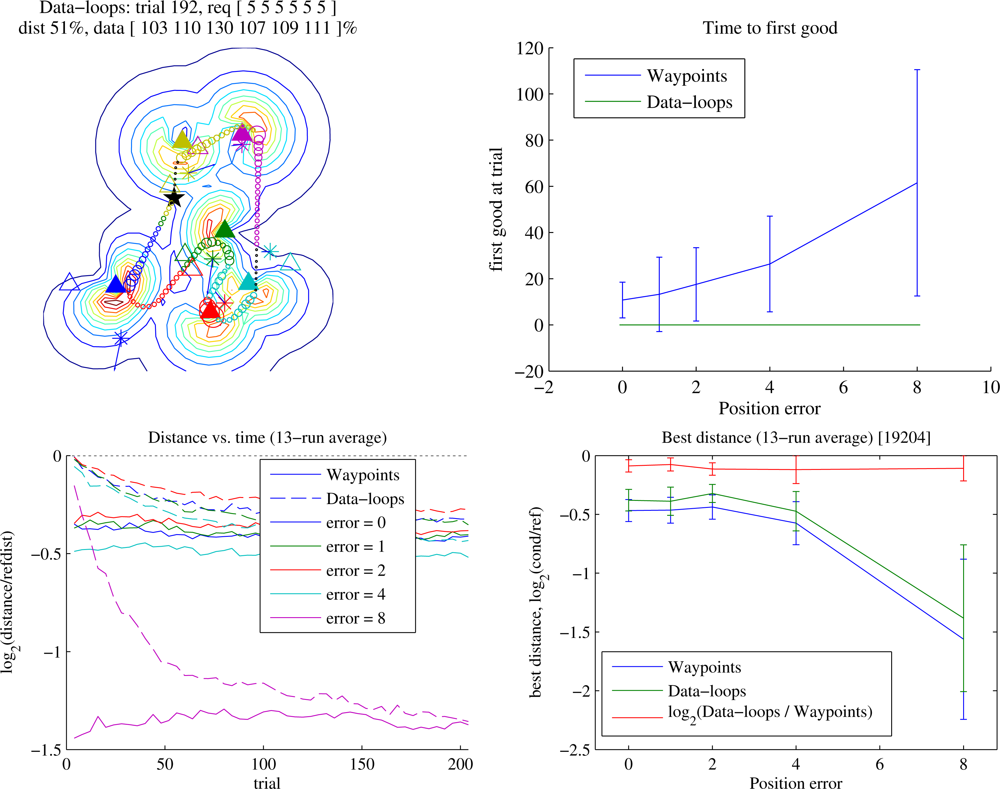
Figure 3 shows how solution quality varies for different data requirements. In this test case (details given in the caption) Waypoints reliably learns to outperform Reference when the data requirement is below about 10, but as the requirement overwhelms the available transmission time, the learning time grows and the probability of success diminishes. Beyond a certain point, Waypoints cannot discover a trajectory to solve the problem. In contrast, Data-loops always does so, with the caveat that we measure retrieval of a certain quantity of data rather than data generated at a certain rate (bandwidth is
including time taken to deliver the data to the base and recharge or refuel, which we do not consider here). Trajectories ranged approximately from 2
−0.2 ≃ 90% to 2
−0.5 ≃ 70% of the length of Reference depending on the data requirement and the autopilot, and the best trajectories found by Waypoints were usually about 4% shorter than the best found by Data-loops. As the data requirement rises towards infinity in this moderately sparse scenario, Waypoints fails, and Data-loops tends to find trajectories about 7% shorter than Reference, although as sensor density increases the learner’s advantage increases (not shown).
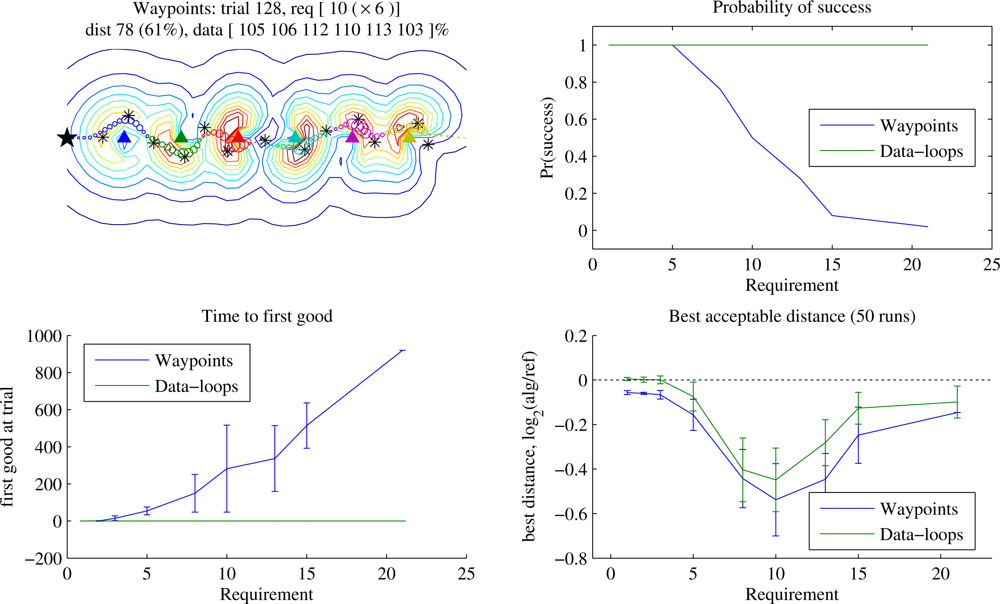
Figure 4 shows the same experiment for a linear deployment. Once again, when data quantities are small the Waypoints learner eventually beats Data-loops by a few percent. More interesting is the distinctive shape of the graph of best acceptable distance: the greatest gains for both trajectory planners were to be found at a data requirement of around 12. At this requirement the Reference planner is beginning to incorporate full loops to collect enough data from a sensor, but the learners are often able to refine the waypoint positions and eliminate those loops. With the 2-dimensional deployment of
Figure 3, the more highly variable radio field can require the Reference autopilot to require loops at any point, eliminating the distinctive shape. Here, as the data requirement goes to infinity, the gain of Data-loops over Reference approaches ∼ 4%. Greater field complexity can increase the separation between locations of waypoint and node for prolonged orbiting, so this number depends on radio source density.
We anticipate that in most cases the immediate guarantee of complete collection combined with the ability to collect larger and variable quantities of data will be reason to prefer Data-loops. However, examined in this context of static problems, when some initial learning time is feasible and data quantities are small, a Waypoints-style encoding may be superior.
6.2. eR vs. LCA
LCA was developed in order to reduce the number of samples required before discovery of an acceptable (zero-underrun) trajectory. Pearre and Brown [
28] explore that benefit, and here we review the result. Data-loop trajectories are guaranteed to have no underrun, but as explained in Section 5.3 a simplified LCA can also be used to improve the gradient estimate for trajectory length. Here we explore how learning speed scales with the number of nodes for both Waypoints and Data-loops trajectories.
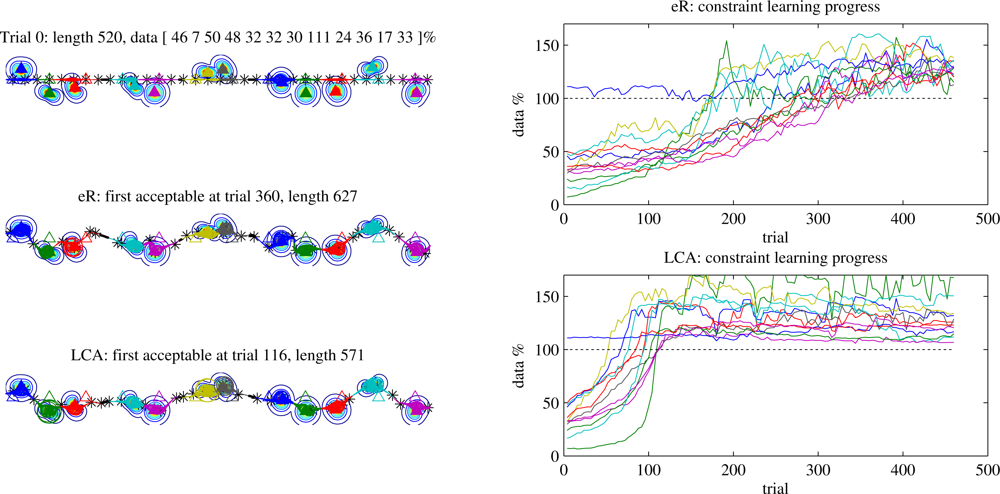
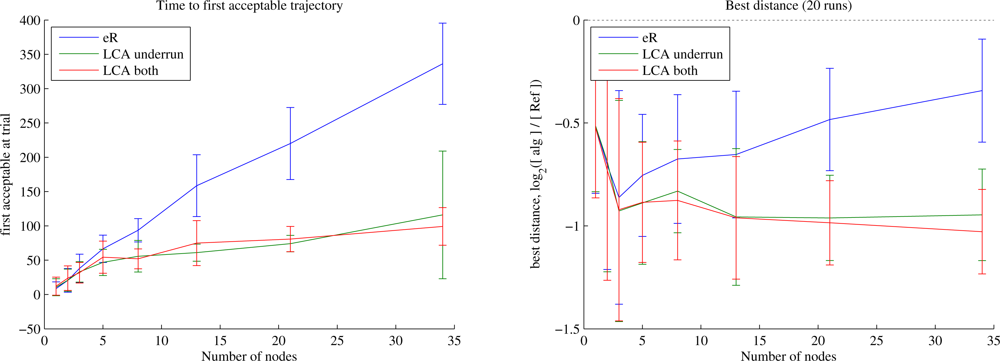
Figure 5 shows an example of learning histories for Waypoints trajectories for a 12-node problem in which the sensors lie at unknown locations near a line, imitating deployment by parachute from an aircraft (Section 6.3 will explore position error more fully). The trace of the data requirement fulfillment for each node (on the right) shows that under eR the trajectory’s performance near any given node can stay the same or get worse as long as the average improves, while under LCA this effect mostly disappears. More concretely, LCA allows more rapid convergence to a better trajectory.
Figure 6 shows that LCA improves scalability of the learning system for Waypoints trajectories. eR requires a number of trials roughly linear in the number of nodes, whereas with LCA the learning time grows much more slowly. Perhaps more surprising is the difference in first good trajectory length between eR and LCA. When some nodes but not others have underrun, the locality of the LCA update allows optimisation for length on whichever waypoints bear no responsibility for underrun. This effect is most significant at higher data requirements when the learner is required to spend significant time optimising the trajectory in the vicinity of each node, and almost disappears at low requirements (not shown). When using LCA for both underrun and distance, the first good trajectory tends to be slightly shorter than for LCA-underrun only, but the difference is only significant under a narrow range of conditions. We weight the LCA updates for underrun more heavily than those for length (as described in the caption), which ensures that wherever there is an underrun, its gradient will dominate the policy update. What happens after the first acceptable trajectory is found? The behaviour remains similar to that when using the zero-underrun trajectories generated by Data-loops, as discussed below.
Figure 7 shows how learning rate scales for Data-loops trajectories. We have shown a quasi-linear sensor layout: the assumed sensor positions lie near a line, and the actual positions are displaced by 8 in a uniformly random direction from where the UA believes it to lie. Because time to first good is 0 for Data-loops, we show the quality of the trajectory after 40 trials (initial quality is nearly identical to that of Reference, so initially
). While the quality of the trajectory achieved by eR after 40 trials improves over Reference less as the number of nodes increases, LCA-length achieves consistently good performance even for large problems, in this case generally finding trajectories 2
−1.5 ≃ 0.35 times the length of Reference within 40 trials. This improvement sounds vastly greater than reported above, but as we will discuss in the next section, when the Reference planner is given incorrect information, the advantage of the learners can be arbitrarily large.
6.3. Position Error
When sensor locations are not known precisely, learning allows recovery from error in the position information.
Figure 8 shows results of learning with incorrect sensor location information. As the position error increases, Reference must fly ever-increasing numbers of loops in order to collect the required data, but the learners compensate for the misinformation by modifying the trajectory.
Here the Waypoints planner is at an additional disadvantage: since the initial waypoint positions lead to an inferior trajectory, more learning iterations may be required before the aircraft eliminates underrun. In contrast, the Data-loops planner, with its collection guarantee, avoids that issue at the cost of potentially very long trajectories: initially it performs identically to Reference, and through learning quickly it discovers similar solutions to the no-position-error case.
No Position Error
Interestingly, even when the Reference planner is given perfect knowledge of node positions, it is reliably and quickly outperformed by the Data-loops planner despite the similarity between them (
Figure 8, bottom right). This is due to three reasons:
Radio field irregularity: The radio fields are messy (and assumed to be difficult to model). The circular orbit with the highest average data rate is not generally centered on the node’s actual location. At high (i.e., loop-dominated) data requirements, the best trajectories were those in which the waypoint positions differed from true node positions by roughly 1.5.
Wasted partial orbits: The circular orbit with the highest average data rate is suboptimal when the data transfer completes before the loop completes. This effect is most pronounced at lower data requirements, in which achieving the highest possible data rate is less important than shortening the trajectory. In this case, the waypoint may be moved, resulting in a lower transmission rate that is still sufficient for complete data transfer.
Opportunistic communication: During execution of a Reference trajectory, the aircraft communicates with the node towards which it is flying. In contrast, the Data-loops planner allows communication with nodes that offer higher SNR.
6.4. Antenna Patterns
The learner finds trajectories that place the aircraft in a position and orientation that allow high SNR with each of the target nodes. High-gain antennas, when oriented appropriately, allow transmission at a higher rate or at longer range. Perhaps more importantly, if an antenna’s null can be aimed appropriately, then it can reduce interference from other antennas or from multipath. A steerable antenna would provide great benefit at the cost of hardware and controller complexity (even the smallest commercially-available units can easily exceed the payload of a lightweight UA).
How do antenna patterns affect the quality of the trajectories found? We have assumed that both the aircraft and the nodes use short dipole antennas as represented by
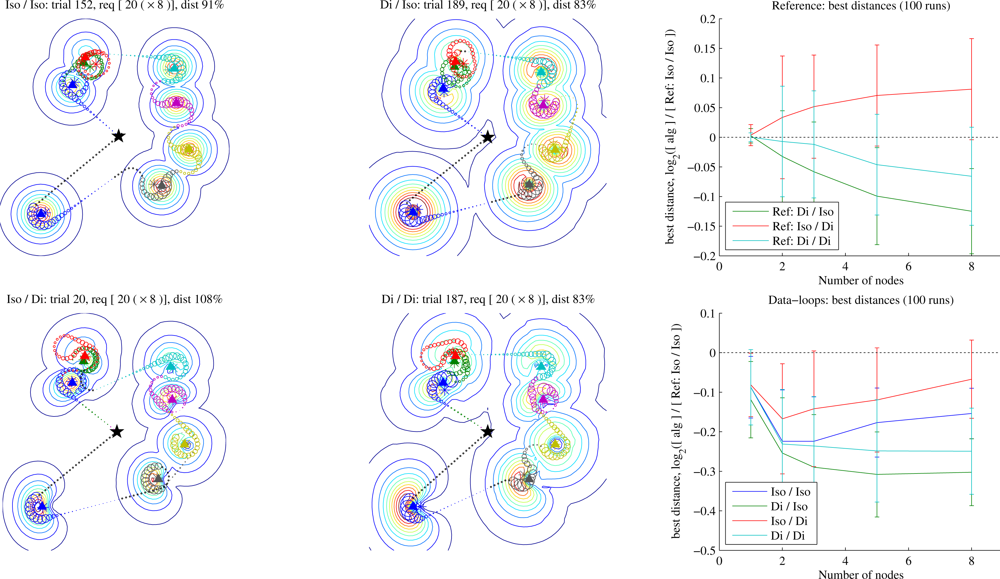
Equation (3) (directivity = 1.5, gain = 1.76 dBi). Here we compare the dipoles to equally efficient isotropic antennas operating at the same power, in both aircraft and nodes. We place some number of nodes randomly on a 20 × 20 field, and each node has a data requirement of 20. We show Data-loops trajectories here, although with Waypoints the results are similar whenever the latter can find an acceptable trajectory.
Results are shown in
Figure 9. The dipole is not an especially high-gain antenna, yet equipping the aircraft with a dipole offers a large improvement over an isotropic antenna, especially in a noisier environment. We observed this effect both for learned and for reference trajectories, and whether the nodes use dipoles or isotropic antennas. However, equipping the nodes with dipoles had the opposite effect: regardless of the UA’s equipment and the trajectories flown (reference or learned), it was able to discover shorter trajectories when the nodes had isotropic antennas. The best combination was a dipole on the aircraft combined with isotropics on the nodes, especially as the sensor density increased. It should be noted, however, that while we observed this trend over a range of conditions, we did not test across every possible configuration. For example, it is possible that a more manoeuvrable UA could better take advantage of directional node antennas.
More important than the preceding observation is the confirmation that the learner adapts to the antenna characteristics it experiences. It would take full advantage of any real-world antenna pattern such as would be expected in the presence of fuselage, landing gear, and other mechanical elements of the aircraft, or systematic noise sources on the aircraft (e.g., due to the onboard computer).
We use the dipole antenna model for both aircraft and nodes throughout the paper: our objective is to compare a learning approach to handcoded heuristics in complex environments, and the dipole radio pattern of our nodes serves as a proxy for the complex structure of real radio fields.
We leave for future work investigation of more directional antennas, laterally asymmetric patterns, steerable antennas, patterns based on real-world measurements, and aircraft movement models designed to take advantage of directional node antennas.
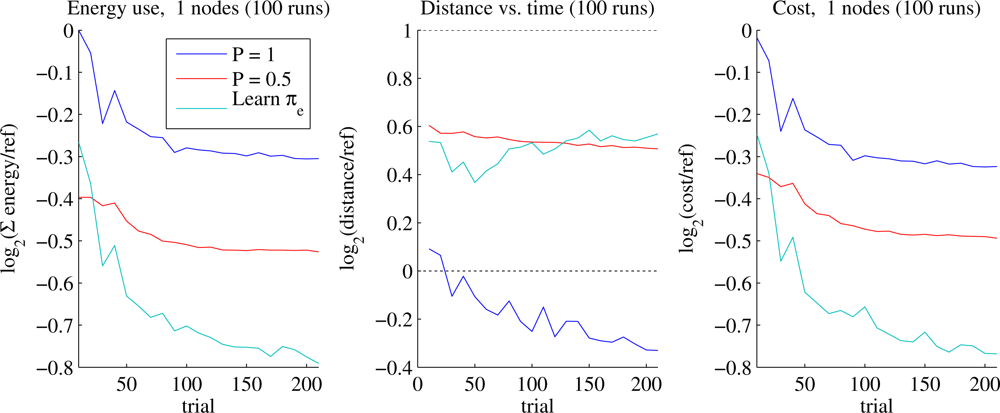
6.5. Node Energy Conservation
Our primary baseline for comparison is the Reference planner. The learner can find significantly shorter trajectories, but here we allow the learner to instead increase the trajectory length up to a certain point if that allows the sensors to use less energy in transmitting data to the aircraft (Section 5.4). In our test cases, we allow trajectories twice the length of each problem’s Reference trajectory (
dmax = 2
dref in
Equation (17)), after which the distance penalty grows with exponent
ϱ = 3.
The same trials are used to compute gradients for both waypoint position and node energy policies. For this scenario we found it helpful to increase the number of trials per policy update to 10—this need may be greatly alleviated by parameter tuning or by the importance-sampling re-weighting procedure described by Tang and Abbeel [
40], which we leave as future work. Also, in order to mitigate abrupt changes in the trajectory due to waypoints moving, we reinstated the common learning practice of decreasing the waypoint exploration and learning rates (we used a factor of 0.99
trial) and the power policy learning rate (0.995
trial).
In addition to our standard Reference, we provide two baselines that learn waypoint placement but do not modify radio power. The first transmits at full power (
Pnow =
Pmax), mimicking the behaviour of Data-loops but learning waypoint placement in response to the energy-sensitive reward function (
Equation (17)) rather than
Equation (11). The second,
Half-power, differs only in that it follows the simple heuristic of transmitting at half power (
Pnow = 0.5 ·
Pmax) independent of SNR.
Figure 10 shows performance of concurrent learning of both waypoint placement and energy policy on a single node with no position error. Within 50 trials the learner requires about 65% of the radio transmission energy required by Reference at 30% greater flight distance, and achieves about a 10% energy savings over Half-power. We stop learning after 200 trials, by which time the energy requirement has decreased to 57% of Reference at 50% greater distance, saving about 20% energy over Half-power at similar trajectory length. Performance for different data requirements was analogous.
The best reward may occur when the trajectory is slightly longer than the soft “limit”, since the learner balances the length cost against the energy cost. However, the learned policies yield trajectories significantly shorter than
dmax, especially with few nodes. This is an artifact resulting from the way we define
dmax in
Equation (17). Changes to the power policy may cause the Data-loops autopilot to add whole loops, and overshooting
dmax carries a larger penalty than undershooting it by the same distance. With more nodes, each loop is a smaller fraction of
dmax so policies can more closely approach
dmax without overshooting, realising greater average energy savings for these comparisons.
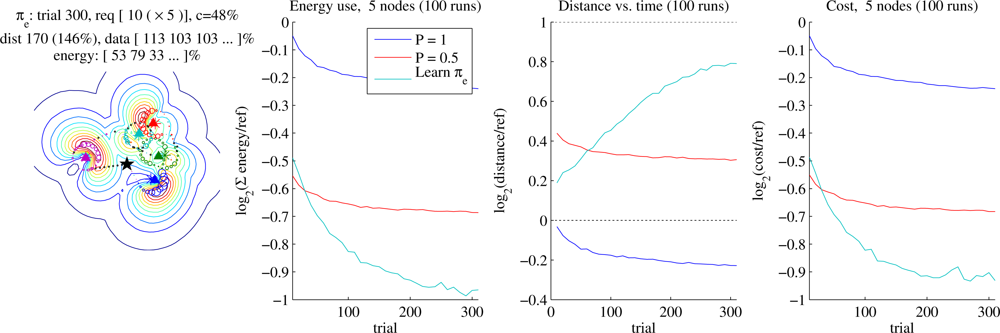
Figure 11 shows the same experiment for problems of five nodes deployed uniformly randomly in a 15 × 15 field (an example configuration is shown on the left of the figure). By 200 trials the nodes require, on average, 50% of the energy of Reference and 75% of the energy required by Half-power, while not exceeding the soft trajectory limit.
Finally, we misinform the aircraft about the nodes’ locations: sensor placement is distance 3 (approximately the aircraft’s turning circle) from where the aircraft believes the sensors to be. Results are shown in
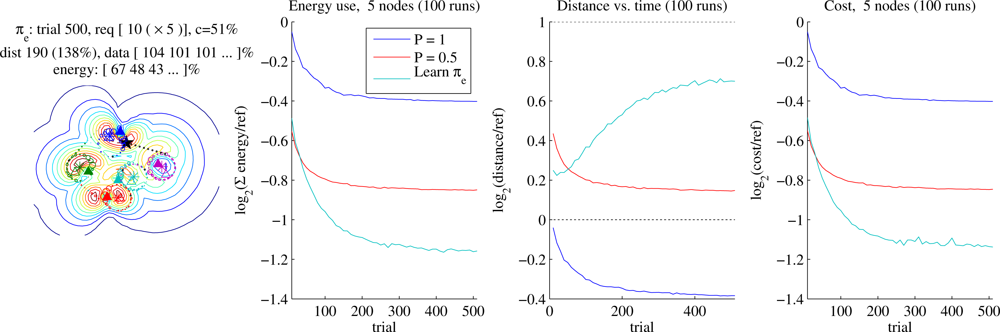
Figure 12. Here the advantage of learning both waypoint-placement and power policies over non-learning or waypoint-placement-only policies increases, with the full learner requiring the nodes to use only 40% of the energy demanded by Reference, about half the energy of our Data-loops with full power, and again about 75% of the energy required by Half-power. As position error increases further and the number of nodes increases, the advantage of this combined learning approach over our reference grows arbitrarily.
7. Discussion
We have applied a model-free policy learning approach to two simple trajectory representations, comparing results to a handcoded reference. The representations were chosen for the ease with which they interface with a black-box autopilot. The Data-loops representation is guaranteed to collect all data from each sensor on every pass, while the Waypoints representation can lead to shorter flights and hence lower network latency when data requirements are low. Given an initial trajectory based on reasonable guesses as to the nodes’ locations, the convergence to a good solution is rapid. Trajectories significantly superior to those of the Reference are found after only dozens of passes.
With a näive approach, the time required to learn policies scales roughly with the number of policy parameters. Some of these problems lend themselves to local decompositions, leading to faster solutions. In particular, the Local Credit Assignment (LCA) decomposition disassembles a global reward and assigns credit based on an approximation of the policy parameters’ responsibilities for their portions of the reward, leading to an asymptotic improvement in learning time and making solution of large ferrying problems feasible.
The learning approach was adopted in order to allow for irregular radio fields that can be hard to model, and the benefit of learners is especially pronounced when the sensor nodes’ locations are not known precisely. Learning trajectory planners never need to know the nodes’ precise locations, since rather than making assumptions about how location is likely to affect performance, they optimise directly on observed performance. Even with perfect location information, the learner can generally surpass a handcoded reference, but as information about sensor locations becomes increasingly degraded, the benefit of the learning approach increases arbitrarily over methods that assume perfect location information.
We have also shown that in the presence of even a few radio noise sources, the aircraft can benefit greatly from the use of a directional antenna, whereas the nodes should use a less directional pattern. At moderately high sensor densities, the simple selection of a dipole antenna in the UA and isotropics on the ground led to trajectories 15% shorter than those possible with the converse choice at the same power, and further improvements are anticipated with higher-gain antennas or more noise sources. We leave as future work an investigation of further synergies between aircraft and ground antenna patterns.
Finally, we showed that the methods used above readily adapt to the task of minimising the energy that sensors must consume in order to transmit data to the aircraft. If we allow the ferry’s trajectory length to double, we can see nearly a factor-of-two reduction in transmission power. If radio transmission is a significant portion of sensors’ energy use, this could greatly extend network lifetime.
Our emphasis has been on showing feasibility of the learning approach for this problem, so much leeway remains for improving learning speed and reducing the number of flights required, for example by careful tuning of learning rates and exploration noise, or by allowing the gradient estimator to re-weight and re-use past exploratory trajectories, which may allow a high-quality gradient estimate to be obtained with fewer trials. However, while learning may be fast enough for deployment in the field for long-term sensor monitoring tasks such as hydrological, seismic, or wildlife monitoring, little would be gained in short-term time-critical monitoring tasks such as wildfire tracking.
The autopilot and radio models used here are simplistic. For instance, it is likely that the sensors would interfere with each other and not transmit continuously (unless the network were extended to use multiple ferries) nor would the data volume be constant across tours, and the directionality of node antennas may be far more pronounced than this model’s field irregularities reproduce. However, since this approach assumes nothing about these variations, we are confident that for any reasonable UA system, trajectories can be significantly optimised using the techniques in this paper.
We know of no other studies investigating UA ferry trajectory planning through unknown radio fields. Each of the papers reviewed in Section 1 assumes a radio transmission model appropriate to the problem investigated therein, whereas this work is based on the premise that such a model is not readily available to the planner, and shows that fast trajectory optimisation is possible despite that lack.
8. Conclusions
We have shown that when an accurate radio environment model is not available, reinforcement learning is feasible for planning trajectories for unmanned aircraft (UA) serving as data ferries. Good trajectories are quickly learned by a policy gradient learning algorithm that treats the aircraft dynamics and radio field idiosyncrasies as black boxes, obviating a complex system identification problem. The UA can learn in situ while it is doing useful work, and can exploit actual environmental quirks. Under our assumptions, reference trajectory lengths can be improved by 10%–30% even with perfect sensor location information, and by 65% or more as the information available to the planner is degraded. With a different objective function, the same technique can be used to extend sensor lifetime by minimising the energy used for communication: if the aircraft can double its flight time, nodes can reduce their radio energy requirements by 50% or more.
Significant challenges remain to be addressed. For example, we have treated the learning task as episodic, only allowing policy updates between flights, whereas adaptation could occur during flight, such as while an aircraft orbits a waypoint, allowing faster learning. Another factor to be considered in future work is planning in the presence of wind: how should the waypoint-placement and energy policies change in response to a changing wind vector? The policy learning techniques explored here may be applicable to learning optimal data retrieval policies for event reconstruction, gathering a fraction of the available data from each of many sensors in order to optimise the trade-off between completeness of information and event reporting latency. Finally, while none of the methods presented herein precludes the use of multiple aircraft, explicit extensions to multi-aircraft sensor networks, including UA-enabled multi-hop relay networks, may provide valuable capabilities.