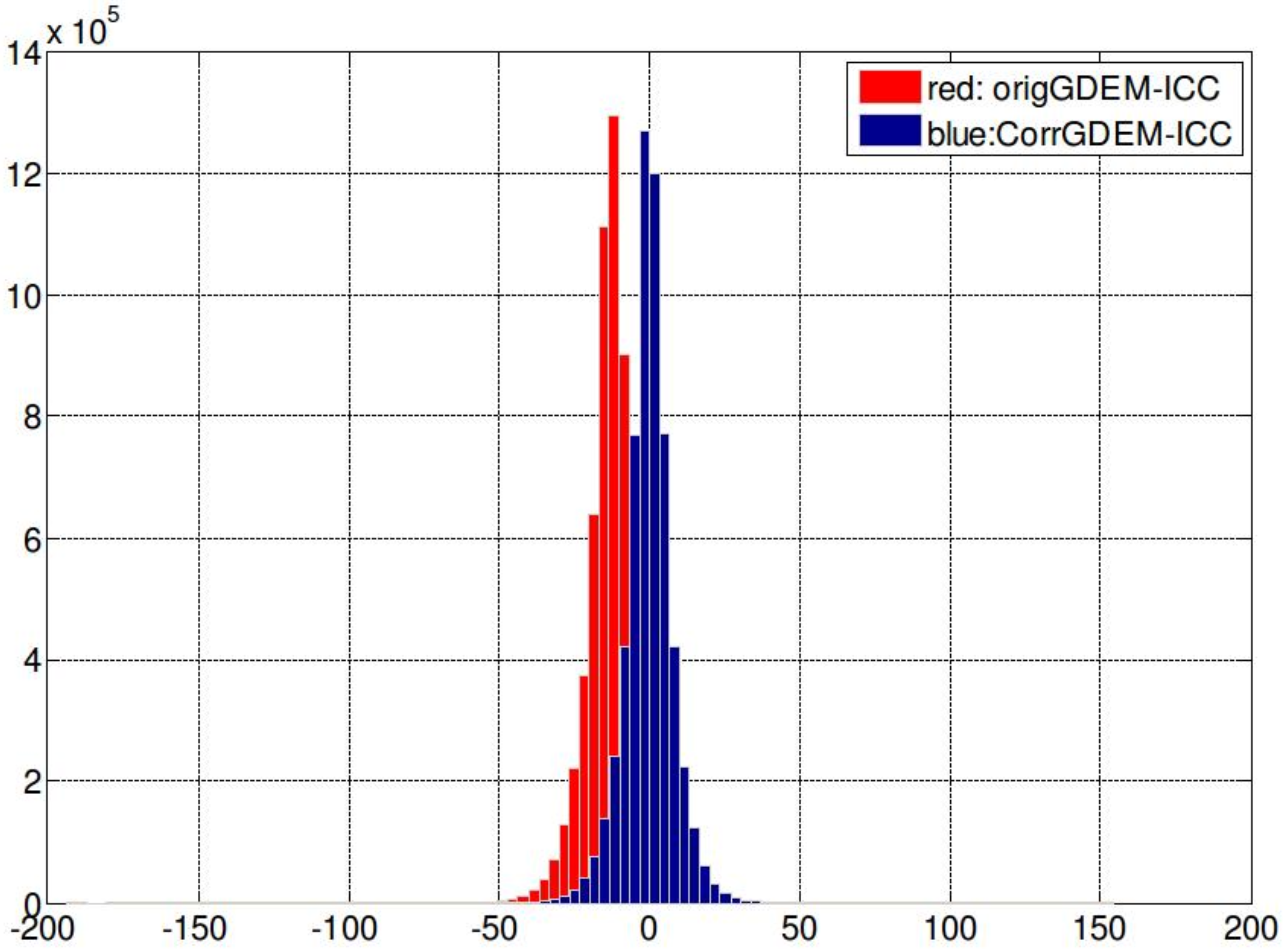
2.1. Correction of the Height Errors Using ICESat Laser Altimetry Points:
The focus is on the refinement of the elevation data by reducing the ASTER GDEM bias based on a correction layer, which is provided from the ICESat laser altimetry data. For that, a correction height layer is provided according to the height deviation of the ASTER GDEM points from the corresponding ICESat points.
As first step, the ICESat point clouds corresponding to the test area are extracted from the dataset repository. In order to use the ICESat points as Ground Control Points (GCPs) to be applied on evaluation and correction of the DEMs, the erroneous points caused by clouds, outliers, underlying slopes or vegetation should be eliminated first. Based on the criteria proposed by Huber
et al. [
3], the points containing errors are filtered to reach a vertical accuracy of nearly 1 m compared to the reference data. Accordingly, the ICESat waveform laser points are filtered by selecting appropriate thresholds for different parameters as follows: (1) number of peaks as a criterion to distinguish bare soil and forest areas, (2) received energy from signal begin to signal end, and (3) the signal width (in meter), which is the distance between signal begin and signal end.
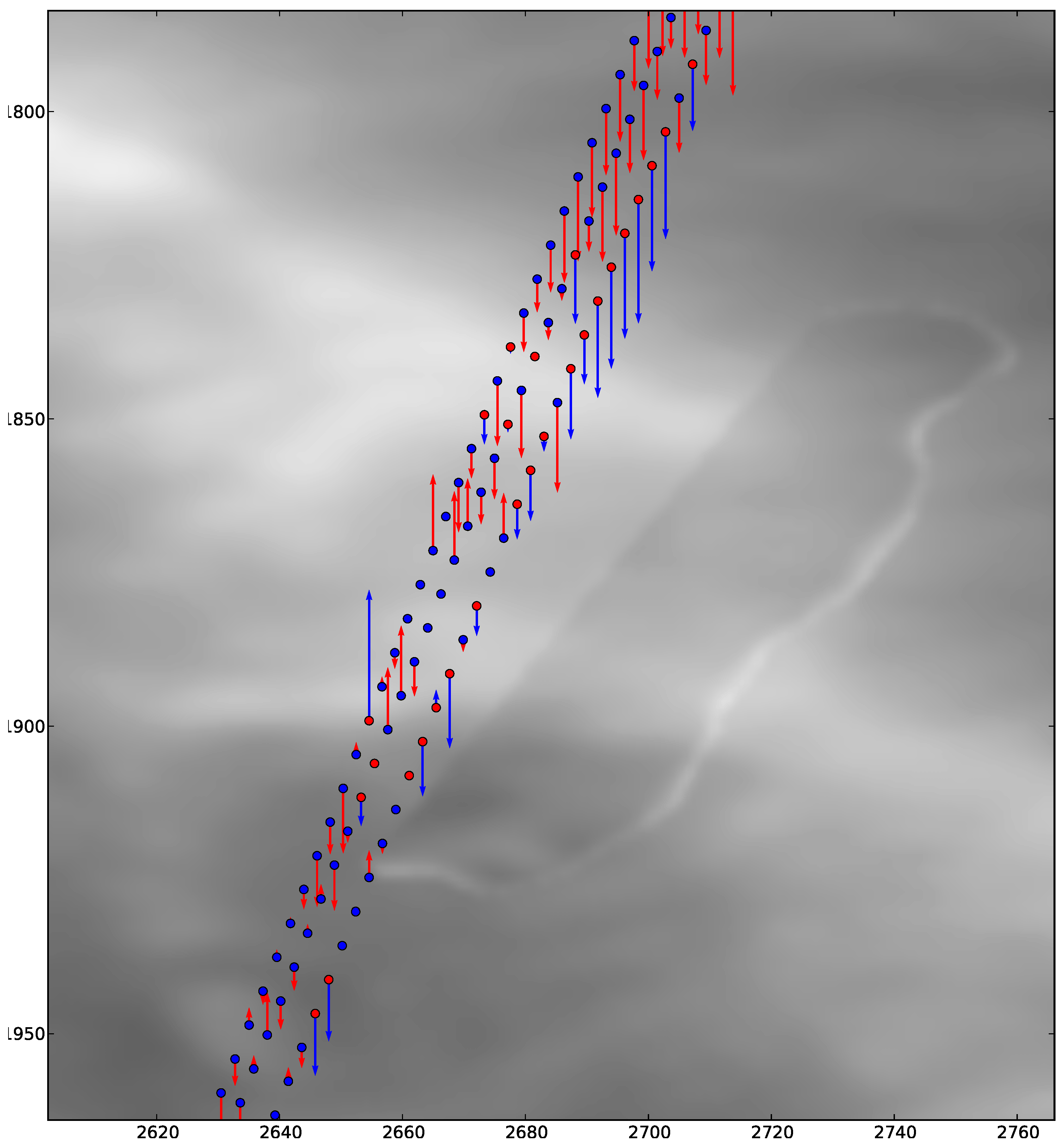
Figure 1 represents the locations of the ICESat laser altimetry data over a sample of ASTER GDEM data. It additionally shows the direction and magnitude of the height deviation of the GDEM regarding the ICESat points. The direction of the vertical arrows proves that the ASTER GDEM is located generally below the correct elevation. The original laser points located in the region are refined using the parameters recommended by Huber
et al. [
3] as follows: Points with less than 6 peaks, received energy lower than 10 fJ (femtojoule), and a signal width smaller than 25 m are selected. The ICESat points that are not satisfying all the predefined criteria are eliminated from the dataset. They are visualized as blue arrows in
Figure 1.
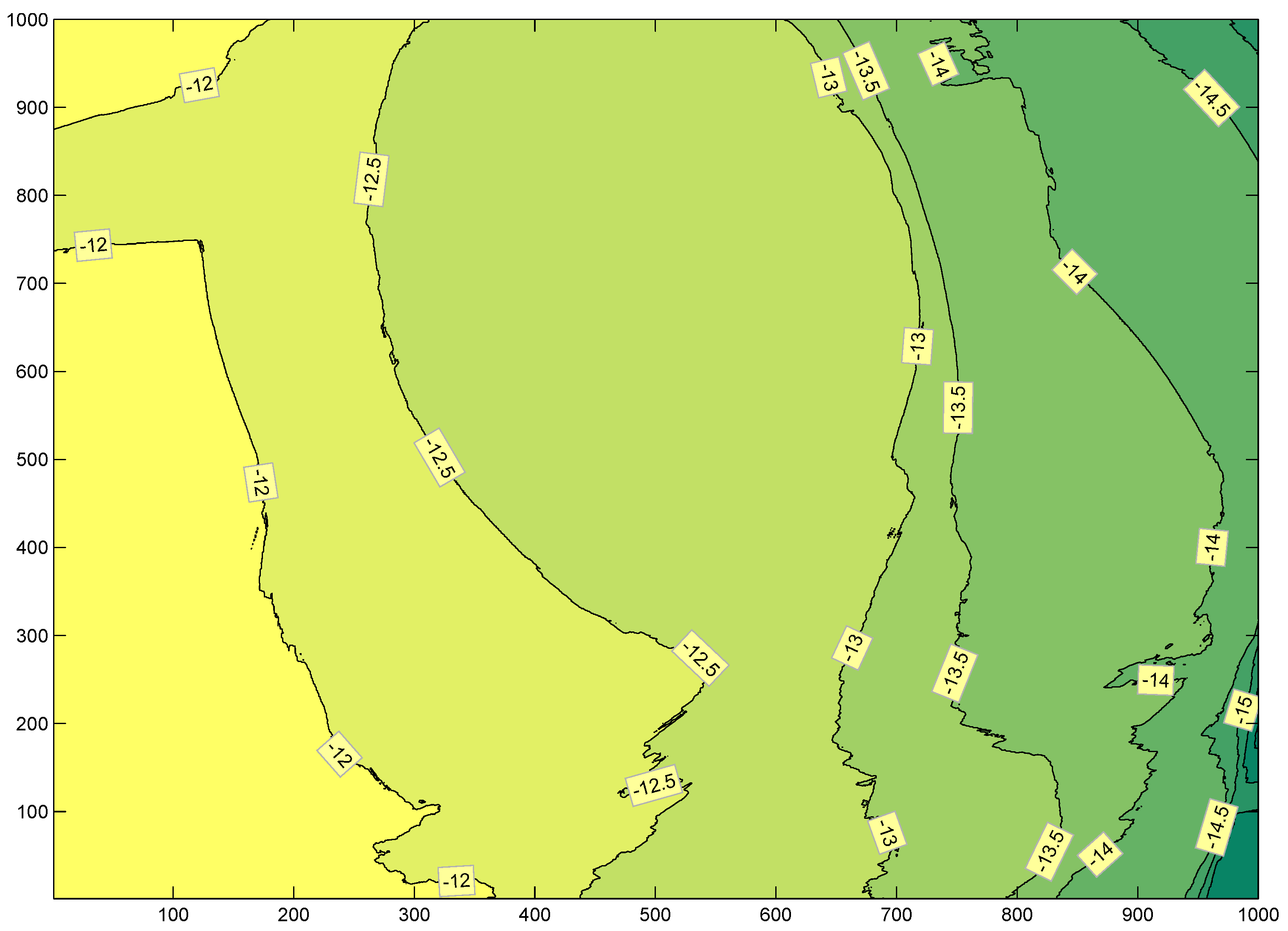
After selecting the corresponding ICESat points and their correction, in order to obtain high accuracy points, analogous ASTER GDEM points are extracted using interpolation. An additional criterion is utilized to reject the ICESat laser points that are not consistent with the GDEM points considering them as outliers. In this step, the aim is to obtain the vertical offsets related to each ASTER GDEM point to reduce the negative bias of the ASTER GDEM. For that purpose the difference between the selected ICESat points and their corresponding ASTER GDEM points are measured. A correction height layer is provided by interpolation of the height differences within the test area (
cf. Figure 2).
In practice, in order to increase the quality of the correction layer and to be able to apply the algorithm more globally, an area much larger than the test area is analyzed for extracting ICESat points as well as the corresponding GDEM points. This procedure has two benefits: (1) since the ICESat points are not as dense as the GDEM points, selecting a larger area allows to more precisely measure the height offset for the corresponding area, and (2) extracting the ICESat points for a larger area and applying the correction layer only on the test region provides a smooth transition on overlapping areas between neighboring scenes. For the interpolation of the height differences over the entire scene, an ordinary Moving Average method is employed. It assigns the values to the grid nodes by averaging the data within a search ellipse around each node.
Figure 1.
ICESat points located on the ASTER GDEM, corresponding to an area of 6 km × 5.1 km plus vector arrows showing the vertical errors of each point. Refined ICESat points to get points located only on the ground surface (red arrows) as well as eliminated points (blue arrows) are visualized.
Figure 1.
ICESat points located on the ASTER GDEM, corresponding to an area of 6 km × 5.1 km plus vector arrows showing the vertical errors of each point. Refined ICESat points to get points located only on the ground surface (red arrows) as well as eliminated points (blue arrows) are visualized.
2.2. Segment-Based Artifacts and Anomalies Detection and Elimination:
In this step, an algorithm is proposed to detect and remove artifacts and anomalies as outliers from the ASTER GDEM based on a segmentation. The algorithm to extract and eliminate the artifacts and anomalies from the ASTER GDEM using segmentation technique has been reported in an earlier work of the authors [
7].
Figure 2.
Elevation correction layer corresponding to an area of about 30 km × 30 km. The values on the X and Y axis represent the pixel coordinates.
Figure 2.
Elevation correction layer corresponding to an area of about 30 km × 30 km. The values on the X and Y axis represent the pixel coordinates.
In order to extract the outliers effectively, their types and specifications are identified first. The specifications of the common errors existing in the released ASTER GDEM, which are detailed in ASTER GDEM validation report [
2], are summarized as follows:
“Pits” occur as small negative elevation anomalies, which vary from a few meters to about 100 m in height.
Figure 3 illustrates an example of the area containing the “pit” artifacts and their association with stack number boundaries (
cf. Figure 3(B)). Stack numbers correspond to the number of image pairs that are using to generate DEM.
Figure 3.
Example of “pit” artifacts;
(A) shaded relief,
(B) clear relation to the stack (scene) number boundaries,
(C) appearance in ASTER GDEM represented as gray scale image (originally appeared in [
8]).
Figure 3.
Example of “pit” artifacts;
(A) shaded relief,
(B) clear relation to the stack (scene) number boundaries,
(C) appearance in ASTER GDEM represented as gray scale image (originally appeared in [
8]).
“Bumps” appear as positive elevation anomaly artifact; their magnitude can range from just few meters to more than 100 m in height (
cf. Figure 4).
Figure 4.
Example of “bump” artifacts;
(A) shaded relief,
(B) clear relation to the stack number boundaries,
(C) appearance in ASTER GDEM image (originally appeared in [
8]).
Figure 4.
Example of “bump” artifacts;
(A) shaded relief,
(B) clear relation to the stack number boundaries,
(C) appearance in ASTER GDEM image (originally appeared in [
8]).
“Mole runs” are curvilinear anomalies above the ground, which are less common than pits and bumps and occur in relatively flat terrains. The corresponding magnitude of “mole runs” is much less than for the two previous anomalies and it ranges from barely perceptible to a few meters, and rarely more than 10 m (
cf. Figure 5). Due to their linear behavior, they can be easily recognized in a shaded DEM.
Figure 5.
Example of “mole-run” artifacts;
(A) shaded relief,
(B) clear relation to the stack number boundaries,
(C) less obvious in ASTER GDEM image (originally appeared in [
8]).
Figure 5.
Example of “mole-run” artifacts;
(A) shaded relief,
(B) clear relation to the stack number boundaries,
(C) less obvious in ASTER GDEM image (originally appeared in [
8]).
The artifacts and anomalies produced by small and different stack numbers are apparent in almost all ASTER GDEM tiles. In addition, the effects of residual clouds have been already eliminated in Version 1 of the ASTER GDEM by replacing the elevation with −9999 values [
2]. Here, an algorithm based on image reconstruction using geodesic morphological dilation [
9,
10] is employed to extract the regional extrema, which is later used for eliminating the “pits” and “bumps”. Geodesic dilation from gray-scale mathematical morphology differs to basic dilation where an image and a structuring element are involved in the filtering process. In geodesic dilation the dilated image is additionally “masked” with a predefined “mask” image. Equation (
1) shows the geodesic dilation of image J (marker) using mask I. In most applications, the marker image is defined by a height offset to the mask image, which generally represents the original DEM.
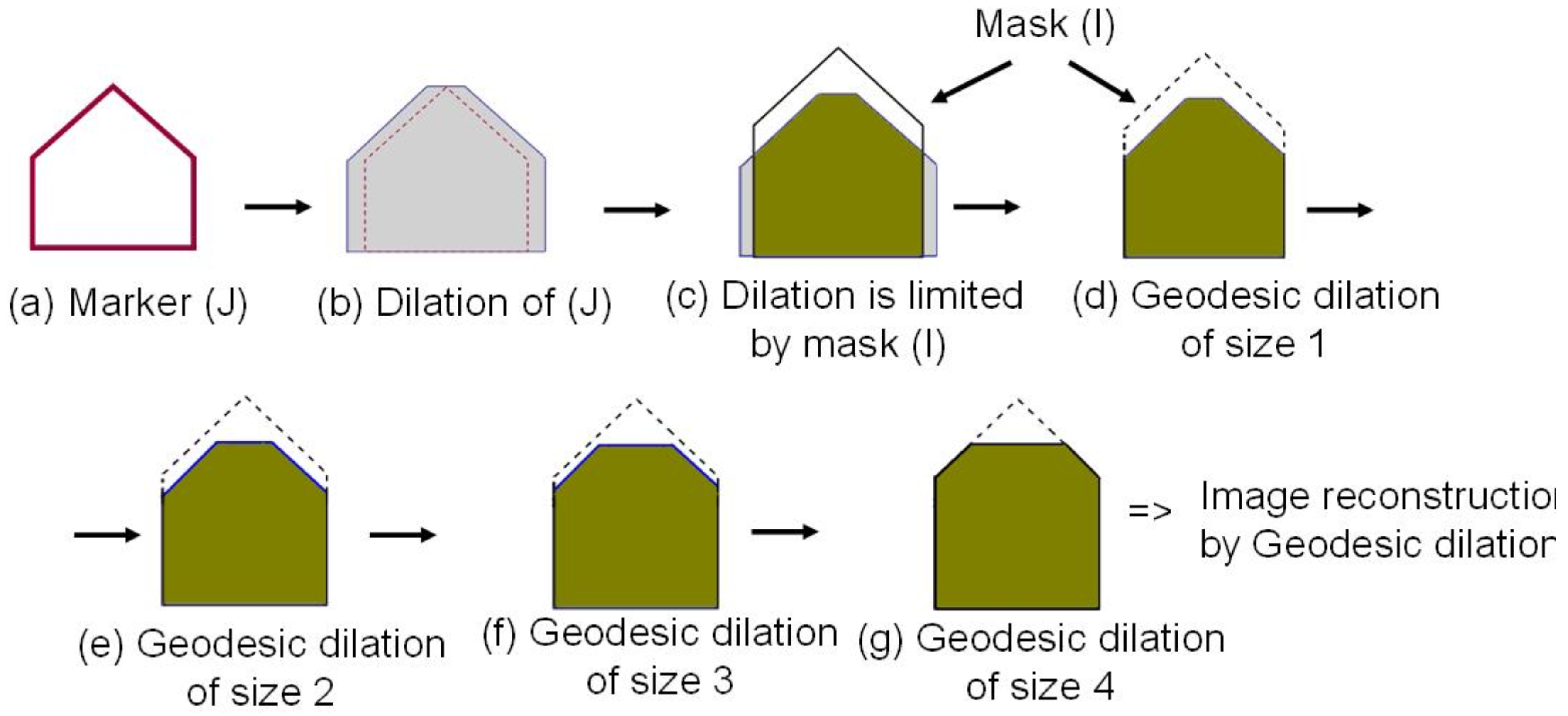
Figure 6 illustrates the difference between geodesic and basic image dilation as well as reconstruction based on geodesic dilation in a profile view of a simple building with gable roof. The input image (a), here called marker, is enlarged by dilation,
i.e., the gray region in (b), and limited by the mask image (I). The result of geodesic dilation is shown in (d) with a dashed line around it depicting the mask image. If this process,
i.e., dilation and limitation by mask, is iteratively continued, it stops after four iterations reaching stability. The result provided by this step is called reconstruction of marker (J) by mask (I) using geodesic dilation (
cf. Figure 6(g)). The number of iterations,
i.e.,
n in Equation (
2), to create reconstructed image varies from one sample to another. In the example presented in
Figure 6 the reconstruction procedure stops after four iterations.
Figure 6.
Geodesic dilation.
Figure 6.
Geodesic dilation.
Accordingly, geodesic dilation (
) and image reconstruction are defined as
Equation (
2) defines the morphological reconstruction of the marker image (J) based on geodesic dilation (
) (
cf. Equation (
1)) if the iterative geodesic dilations reaches to stability. The basic dilation (
δ) of marker and point-wise minimum (∧) between dilated image and mask (I) is employed iteratively until stability. Looking at the reconstructed image of the example depicted in
Figure 6 shows that the upper part of the object,
i.e., the difference between marker and mask is suppressed during image reconstruction. Therefore, the result of gray scale reconstruction depends on the height offset between the marker and the mask images and accordingly, different height offset suppress different parts of the object. More information regarding the segmentation of the DEMs by gray scale reconstruction using geodesic dilation can be found in [
11] where similar algorithms are employed for extracting 3D objects as well as the ridge lines from high resolution LIDAR DSM. In a segmentation algorithm based on geodesic reconstruction, selecting an appropriate “marker” image plays the main role and has a direct effect on the quality of the final reconstructed image. A “marker” image with a small offset, e.g., few meters, from the “mask” can suppress mainly local maxima regions similar to artifacts above the ground.
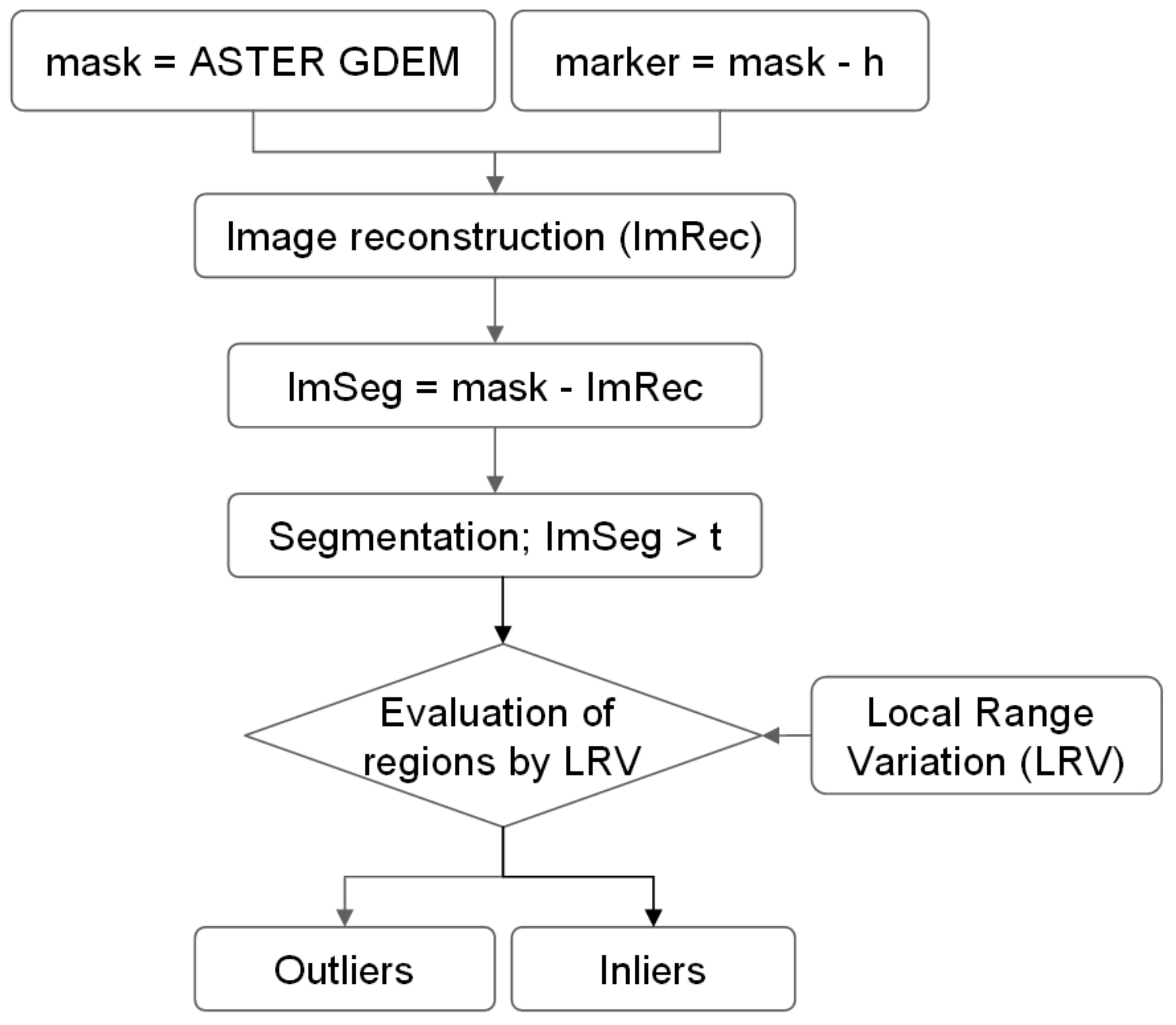
The proposed outlier extraction algorithm regarding the positive artifacts and anomalies is represented in
Figure 7. The first step for segmentation based outlier detection is to generate the “marker” image as a second input image. The first input image is the original ASTER GDEM as “mask” image. The marker is generated by subtraction of an offset value h from the ASTER GDEM:
where
is the “mask” image employed to extract the “positive” outliers. Since the artifacts are in most cases located far beyond the ground elevation level with low height variation of their internal pixels, a single offset value (h) of about “25 m” generates an appropriate marker image for segmentation of the outliers for ASTER GDEM. This is a basic assumption for the outlier elimination algorithm. It means if an outlier region contains low inclination on most parts of its boundary to the neighboring ground pixels, the algorithm might fail to detect it.
Figure 7.
Proposed workflow for extracting positive outliers.
Figure 7.
Proposed workflow for extracting positive outliers.
Figure 8 shows a small ASTER GDEM tile with 420 × 550 pixels which is used as “mask” in this algorithm. After providing the second input image (“marker”), the image reconstruction ImRec is determined accordingly. For segmentation purpose, the reconstructed image is subtracted from the original DEM. The result is a normalized DEM similar to normalized Digital Surface Model (nDSM) where the regions which are about h meter higher than their neighborhood are highlighted. Similar results can be achieved by morphological “tophat” filtering [
12,
13], but the operation based on geodesic dilation is better suited because of its independence from the size of the objects to be filtered. Therefore, there is no need to tune the size of the structuring element.
Figure 8.
ASTER GDEM sample data corresponding to an area of 24 km × 39 km.
Figure 8.
ASTER GDEM sample data corresponding to an area of 24 km × 39 km.
The segmentation procedure is implemented using thresholding and the labeled regions are provided by means of connected components analysis. A geometric feature descriptor is created which highlights the height variation on each pixel regarding its adjacency to evaluate the labeled regions. A feature called Local Range Variation (LRV) is created by subtracting the maximum and minimum values in every 3×3 windows over the image (
cf. Figure 9). All the boundary pixels of the detected regions are evaluated by the LRV descriptor. The regions having certain height jumps on their boundary pixels will be evaluated as outliers (positive artifacts). In practice, the LRV values of the boundary of each region are extracted and if the majority (here 90%) of LRV values are above the threshold (here above 25 m), the region is classified as outlier and corresponding pixels are eliminated from the original data set.
The pixel values corresponding to the LRV are additionally utilized to determine the values that are taken by
h (offset from DSM) for automatic generation of the marker image in each iteration. Accordingly the process begins by choosing the maximum value of LRV as initial offset
h for marker generation. For an efficient extraction of all outliers, ten offsets are determined by dividing the difference between maximum and minimum LRV into ten equal intervals. The iteration begins with maximum value and the provided segments based on proposed algorithm are evaluated accordingly. Procedure continues by selecting the next
h and evaluating the new segments which are not evaluated in previous step until no more new segments are produced. A similar process is utilized to eliminate the negative outliers but in this case, the complementary image of the ASTER GDEM is selected as “mask” and therefore:
where
is used to extract the negative outliers and is created by inverting the original GDEM. Classified outlier regions in this step are then integrated and corresponding pixels are eliminated from the original ASTER GDEM.
Figure 10 illustrates the final detected outliers from the example ASTER GDEM image.
Figure 9.
Local Range Variation (LRV) feature descriptor.
Figure 9.
Local Range Variation (LRV) feature descriptor.
Figure 10.
Final detected positive and negative outliers.
Figure 10.
Final detected positive and negative outliers.
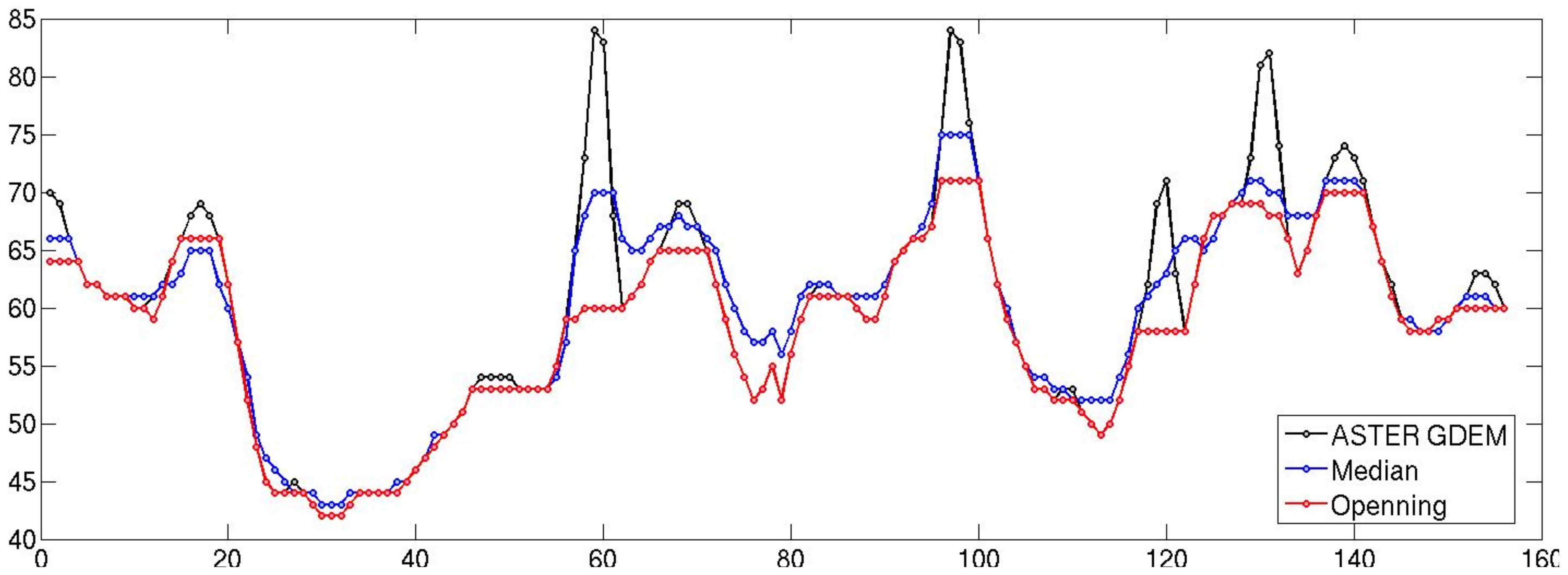
The segment-based algorithm is employed to eliminate the area-shaped artifacts such as “pits” and “bumps”. An additional filtering is integrated to reduce the “mole-runs” errors. Since the “mole-runs” appear as curvilinear and positive height errors, a morphological opening filter is utilized to eliminate them. A disk shaped structuring element with the radius of 7 pixels is selected to suppress curvilinear elevated errors (
cf. Figure 11). Median filter is a well-known filtering method of this category, which replaces the value of a pixel by the median of gray values in the neighborhood (
cf. Figure 11).
Figure 11.
Removal of the curvilinear height errors of “mole-run”. (a) ASTER GDEM; (b) Median filter using a neighborhood image size of 7 × 7; (c) Morphology Opening using a disc shape of radius length of 3 pixels.
Figure 11.
Removal of the curvilinear height errors of “mole-run”. (a) ASTER GDEM; (b) Median filter using a neighborhood image size of 7 × 7; (c) Morphology Opening using a disc shape of radius length of 3 pixels.
Figure 11 represents the corresponding results by applying median filter and morphological opening on original ASTER GDEM. For the median filter, a neighborhood image size of 7 × 7 is selected for this example which depends on the width of the linear errors to be suppressed. A similar size of structuring element is used for morphological opening to be comparable with the result of median filter. In this work, a disc shaped structuring element with the radius of 3 is employed. To assess the quality of the employed filters for eliminating the mole-runs, a profile plot is provided (
cf. Figure 12). In this figure, the black line corresponds to the original ASTER GDEM points where the locations of the several mole-runs as positive peaks are visualized. Median filter (blue line) suppresses parts of the peaks as well as smoothing the other terrain parts. Since the aim is to suppress the sharp peaks with low interference with the other pixels, image opening using an appropriate structuring size creates a better result (
cf. Figure 12, red line).
Figure 12.
Profiles from images represented in
Figure 11, showing that the median filter does not suppress properly the mole-runs errors
Figure 12.
Profiles from images represented in
Figure 11, showing that the median filter does not suppress properly the mole-runs errors
2.3. Correction of the Height Errors of Water Body Regions:
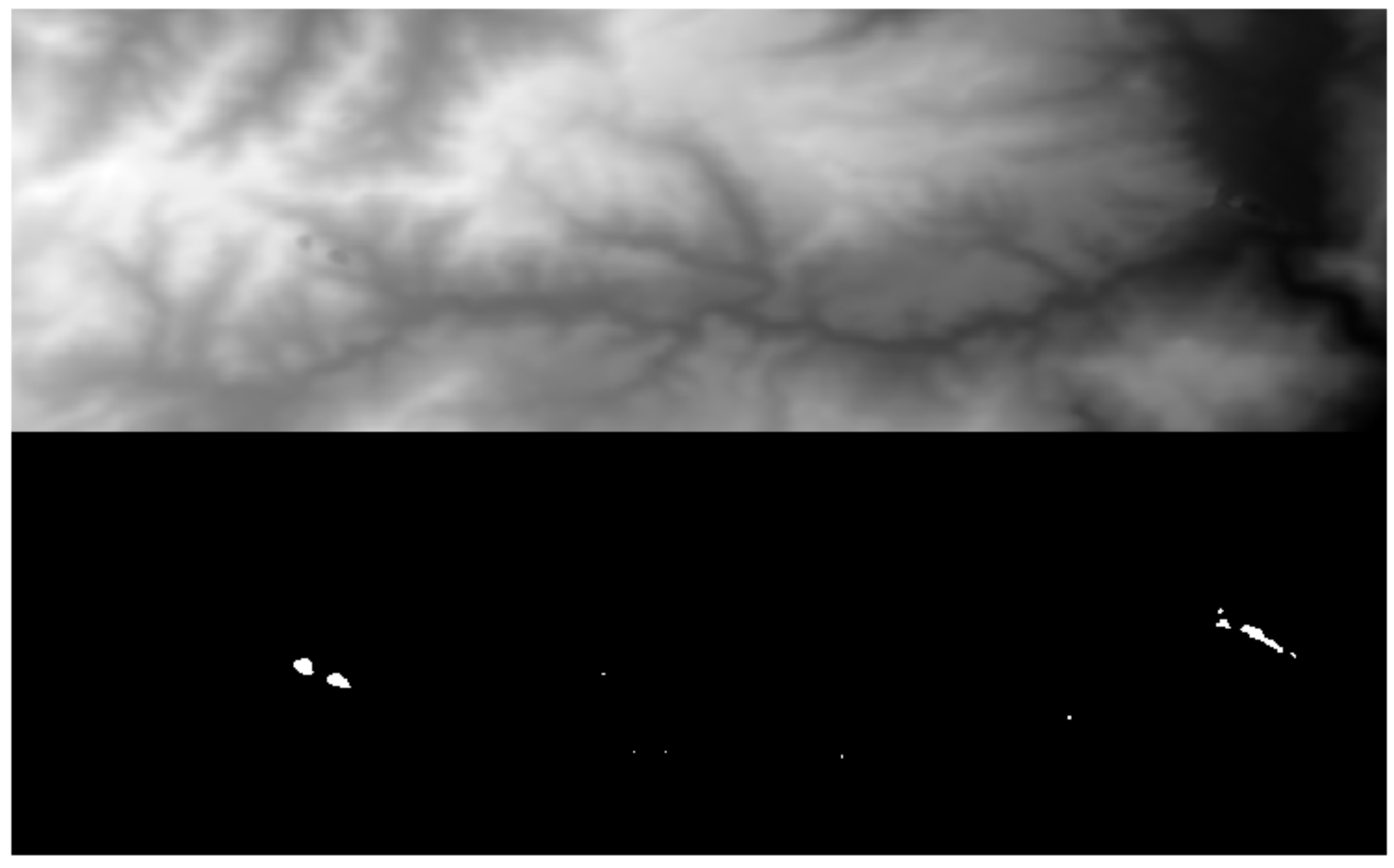
A further criterion is considered for the final classification into outlier and inliers regions. During production of the ASTER GDEM, the pixels inside inland water bodies are not filtered and, therefore, they contain random errors. In this step, a water mask binary image is provided as a sort of quality layer that warns the user about the lower quality of height points inside water body areas. In addition, the water mask layer can directly be used to filter out all the height points inside the water. In order to provide high quality water mask, the vector map containing the boundary points of the shoreline regions in different resolutions are automatically extracted from the ”Global Self-consistent, Hierarchical, High-resolution Shoreline Database“ (GSHHS) which is is freely available to download [
14]. GSHHS is combined from two main databases World Data Bank II (WDB) and World Vector Shoreline (WVS). The shorelines are provided as closed polygons and are free of intersections or other artifacts caused by data inaccuracies [
15].
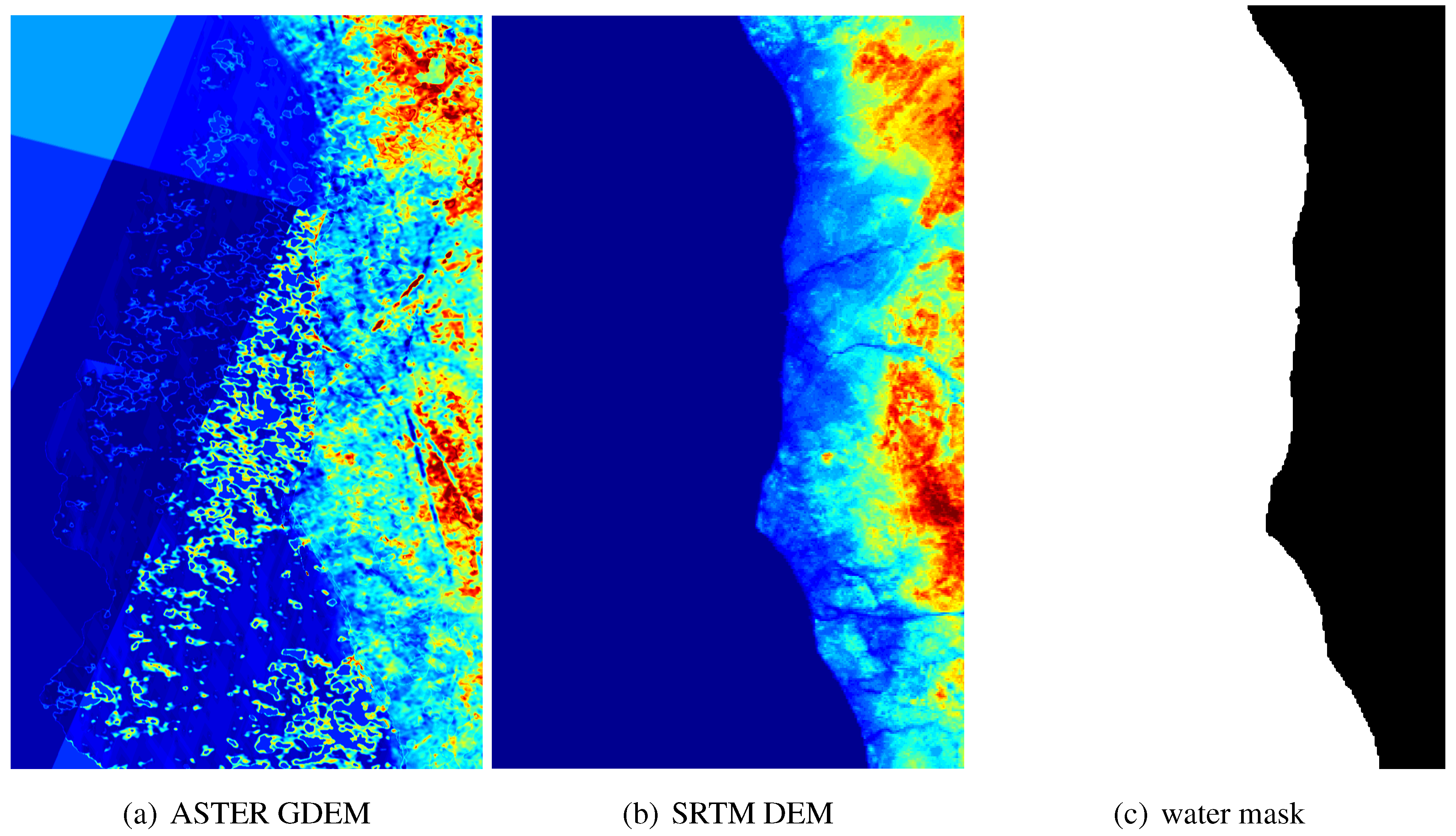
Figure 13(a) shows a small tile of ASTER GDEM corresponding to an area containing a water region with low elevation quality. Comparing to the SRTM image
cf. Figure 13(b)), the different blue tones in the water region illustrated that the water region is a merged result of smaller DEMs created from different numbers of stereo scenes (stack numbers). Particularly, such effects occur when the merged DEMs have been generated using a small numbers of stereo scenes. In such situation the quality of SRTM DEM (
cf. Figure 13(b)) for the region with small stack numbers are much higher than the ASTER GDEM (
cf. Figure 13(a)).
Accordingly, the height values inside the water regions in ASTER GDEM are flattened using the water mask created from the GSHHS data set (
cf. Figure 13(c)). After extracting the corresponding water regions, the median value of the associated heights of the boundary region is inserted for the pixels in the related water region. It should be mentioned that, the median of the heights is not applied for rivers. Hence, the difference between the maximum and minimum heights of the boundary pixels are measured. If the difference is less than a predefined value, e.g., 2 m, the median of the heights of the boundary pixels is used as replacement, otherwise the pixels in the region remain intact.
Figure 13.
ASTER GDEM, SRTM, and water mask provided by GSHHS data (3 km × 1.4 km).
Figure 13.
ASTER GDEM, SRTM, and water mask provided by GSHHS data (3 km × 1.4 km).
An additional check is required to guarantee that the new water level is not higher than the surrounding ground pixels. In case of a higher water level, the median of the lowest 10% of the boundary pixels is considered as water elevation. In the final step, the gaps provided by all the different outliers are filled by applying a spatial interpolation procedure. In this paper, Inverse Distance Weighting (IDW) interpolation [
16] is utilized.