Comparison of the Noise Robustness of FVC Retrieval Algorithms Based on Linear Mixture Models

Abstract

The fraction of vegetation cover (FVC) is often estimated by unmixing a linear mixture model (LMM) to assess the horizontal spread of vegetation within a pixel based on a remotely sensed reflectance spectrum. The LMM-based algorithm produces results that can vary to a certain degree, depending on the model assumptions. For example, the robustness of the results depends on the presence of errors in the measured reflectance spectra. The objective of this study was to derive a factor that could be used to assess the robustness of LMM-based algorithms under a two-endmember assumption. The factor was derived from the analytical relationship between FVC values determined according to several previously described algorithms. The factor depended on the target spectra, endmember spectra, and choice of the spectral vegetation index. Numerical simulations were conducted to demonstrate the dependence and usefulness of the technique in terms of robustness against the measurement noise.

1. Introduction

The spatio-temporal distribution of biophysical parameters on land surfaces has been retrieved from remotely sensed surface reflectances [1,2]. The fraction of vegetation cover (FVC) is the fraction of the horizontally projected area occupied by green vegetation, which is estimated to quantify the horizontal spread of vegetation on the subpixel level. FVC provides useful information for monitoring changes in the forest [3] or land use [4], and it guides policy development decisions [5]. FVC estimates at the continental and larger scale have been used as input parameters to describe surface processes in climate models [6,7].

Several types of algorithm have been introduced and developed for estimating FVC from multispectral and hyperspectral data. Among them, techniques based on linear mixture models (LMM) have been employed most frequently [8,9,10,11,12,13] The framework of these models was proposed by [14] and extracts useful information in terms of the fractional abundances of spectra corresponding to pure components (endmembers) within a certain area. The LMM algorithms have been developed in several studies [15,16] to analyze surface materials or minerals [17,18], classify [19,20], and inform other environmental studies [21]. FVC retrieval techniques have been facilitated by unmixing an LMM to compute the weights of vegetation endmembers [22]. Subsequently, numerical inversion of a radiative transfer model [23,24] and signal processing approaches, including neural networks [25,26], have been applied to FVC estimation.

This study focuses on an LMM-based algorithm that shows some variation in the retrieved FVCs owing to differences in the model assumptions and constraints on the retrieval algorithms [27,28]. This study is performed as a series of investigations [28,29] about the three LMM-based FVC algorithms, which are widely used in practical applications. In these studies, a two-endmember LMM assuming two multispectral bands was used throughout to facilitate analytical derivations. Previous studies have investigated the relationship among the three types of LMM-based FVC algorithms under a two-endmember assumption [28]. Here, the relationship between FVC values derived from different algorithms is expressed analytically. Errors in the calculated FVC, which were propagated from errors in the reflectance spectra, are investigated [29], and the relationships among errors propagated in different algorithms are described. The results show that the relationships are described by an asymmetric ellipse with coefficients that depend on the target spectrum, assumed endmember spectra, and vegetation indices (VIs) used as constraints. Although the relationship was derived analytically and demonstrated numerically, a technique for deterministically judging the robustness of the algorithms against errors in the reflectance spectra has not been previously addressed. This study attempts development of such a technique.

The objective of this study was to introduce a technique for comparing different LMM-based algorithms for FVC. Using an analytical approach, we derived a factor that deterministically compares the relative robustness of two algorithms. Note that sources of error can arise from various intervening factors, such as poor radiometric calibration and atmospheric contamination [30,31]. As a result, errors in the reflectance spectra eventually propagate into FVC estimations [32,33,34]. An assessment of the algorithm robustness toward these errors can be performed based on intensive parameter studies of reflectance models. An advantage of analytical approaches is that they provide deterministic information without uncertainty (without parametric studies.)

2. LMM-Based Algorithms

The LMM approach represents a target spectrum as a linear combination of the endmember spectra [35]. The weights of the endmember spectra are the fractional abundances of endmember components in a target field. After extracting the endmember from satellite data or measurements, spectral unmixing may be conducted to retrieve the fractional abundance of each endmember by minimizing distance metrics, such as the Euclidean norm, between the modeled and the target spectra. The algorithms can vary, depending on the choice of endmember variables and constraints assumed in the algorithms. The standard algorithm uses reflectance as an endmember variable, and constraints are provided by distance metrics defined on the reflectance spectra.

In this study, we considered three variants of the LMM-based algorithm under the two-endmember assumption. The choice of endmember variable (endmember model) and constraints on the algorithms are summarized in

Table 1. Assumed endmember variables and constraints in the three LMM-based algorithms.

Type of algorithm	Endmember model	Constraint
Reflectance-based LMM	reflectance spectrum	reflectance spectrum
VI-based LMM	VI	VI
Isoline-based LMM	reflectance spectrum	VI

. Below, we briefly introduce the three algorithms for the two-band case, as assumed in previous studies [28,29].

2.1. Algorithm-1: Reflectance-Based LMM

The reflectance-based LMM [22], denoted algorithm-1 in this study, uses reflectance as an endmember variable and the Euclidian norm as the distance measure on the reflectance spectra (Table 1). Algorithm-1 defines the FVC as a function of three spectra, the target spectrum, ${\mathit{\rho }}_t=({\rho }_{t,r},{\rho }_{t,n})$, vegetation endmember spectrum, ${\mathit{\rho }}_v=({\rho }_{v,r},{\rho }_{v,n})$, and non-vegetation endmember spectrum, ${\mathit{\rho }}_s=({\rho }_{s,r},{\rho }_{s,n})$, which are used to define two-dimensional vectors in the red and NIR reflectance subspace. According to this algorithm, the FVC can be written as

$${\widehat{\omega }}_1=\frac{\mathit{d}·({\mathit{\rho }}_t-{\mathit{\rho }}_s)}{\mathit{d}·\mathit{d}}$$

(1)

where $\mathit{d}$ is the vector from ${\mathit{\rho }}_s$ to ${\mathit{\rho }}_v$ defined by

$$\begin{array}{c}\hfill \mathit{d}={\mathit{\rho }}_v-{\mathit{\rho }}_s\end{array}$$

(2)

2.2. Algorithm-2: VI-Based LMM

The endmember spectra can be selected according to other variables, such as the VI. In the second variant of the LMM-based algorithm (algorithm-2), the VI for a target pixel is modeled as a linear sum of the endmember VIs [36] (the VI-based LMM in Table 1). In this study, we employed three VIs, NDVI [37], SAVI [38], and EVI2 [39], as examples. The FVC estimation is written as a function of the three VIs (the target spectrum, $v_t$, vegetation endmember, $v_v$, and non-vegetation endmember, $v_s$)

$$\begin{array}{c}\hfill {\widehat{\omega }}_2=\frac{v_t-v_s}{v_v-v_s}\end{array}$$

(3)

where v (two-band VI) is a function of ρ, and the VI coefficients are

$$\begin{array}{c}\hfill v=\frac{{\mathit{c}}_1·\mathit{\rho }+r_1}{{\mathit{c}}_2·\mathit{\rho }+r_2}\end{array}$$

(4)

with the definition of ${\mathit{c}}_i$ given by

$$\begin{array}{c}\hfill {\mathit{c}}_i=(p_i,q_i)(i=1,2)\end{array}$$

(5)

The coefficients $p_i$, $q_i$, and $r_i$ depend on the choice of VI, as summarized in

Table 2. Coefficients of the two-band VIs ($p_i$, $q_i$, and $r_i$) used as examples in this study.

	${\mathit{p}}_1$	${\mathit{q}}_1$	${\mathit{r}}_1$	${\mathit{p}}_2$	${\mathit{q}}_2$	${\mathit{r}}_2$
NDVI	$-1$	1	0	1	1	0
SAVI	$-(1+L)$	$1+L$	0	1	1	L
EVI2	$-2.5$	$2.5$	0	$2.4$	1	1

.

2.3. Algorithm-3: Isoline-Based LMM

The third algorithm (Isoline-based LMM, algorithm-3) is essentially a combination of algorithm-1 and -2. In the third algorithm, the reflectance spectrum is modeled as in algorithm-1, using VI as a constraint [40], similar to algorithm-2 (Table 1). The FVC of this algorithm is represented by

$$\begin{array}{c}\hfill {\widehat{\omega }}_3=\frac{({\mathit{c}}_1-v_t{\mathit{c}}_2)·{\mathit{\rho }}_s+r_1-v_t{r}_2}{(v_t{\mathit{c}}_2-{\mathit{c}}_1)·\mathit{d}}\end{array}$$

(6)

3. Error Propagation in FVC

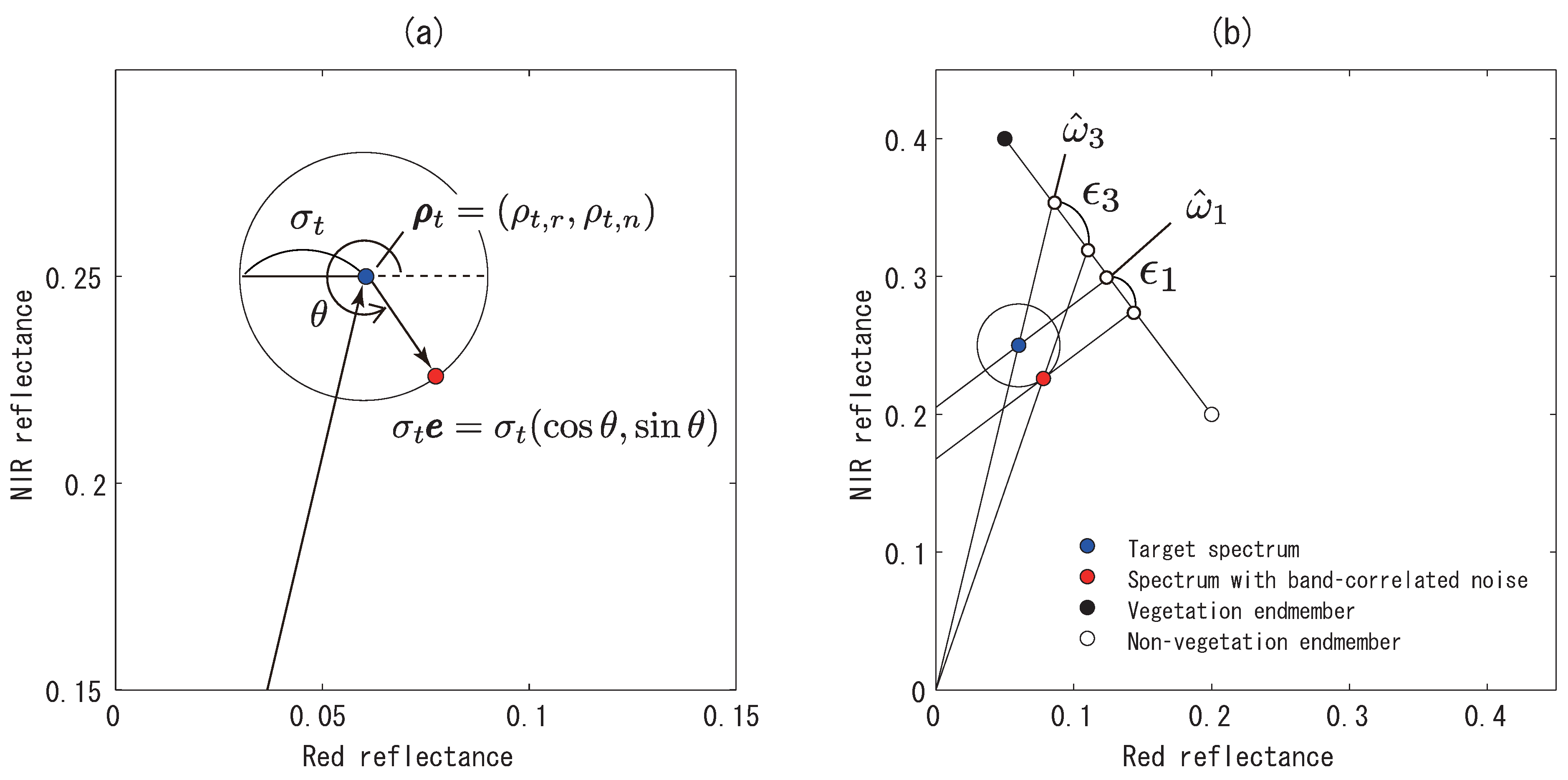
3.1. Measurement Errors in the Reflectance Spectra and Propagated Errors in the FVC

Biased errors in the spectral measurements are modeled as band-correlated noise in the red-NIR reflectance space [29]. The magnitude of the noise spectrum is represented by ${\sigma }_t$, and the direction of the band correlation in the error is represented by the directional vector (unit vector) in the red-NIR reflectance space, $\mathit{e}=(cos\theta ,sin\theta )$. Hence, the band-correlated noise is assumed to be the product of those variables, ${\sigma }_t\mathit{e}(\theta )$.

Errors propagated in the FVC retrieval by LMM-based algorithms are computed from ${\sigma }_t\mathit{e}(\theta )$ as an input noise. The errors are determined by four types of input variables: (i) band-correlated noise (${\sigma }_t\mathit{e}(\theta )$), (ii) target spectrum (${\mathit{\rho }}_t$), (iii) endmember spectrum assumed in the LMM-based algorithms (${\mathit{\rho }}_v$ and ${\mathit{\rho }}_s$), and (iv) choice of VI. Below, these parameters comprise the input data. Figure 1 illustrates the input noise and the band-correlated errors propagated in the FVC based on algorithm-1 and -3, as examples. The blue dot in Figure 1(a) indicates the target spectrum, and the red dot indicates the band-correlated noise, which is a distance ${\sigma }_t$ from the target spectrum. The circle around the blue dot indicates the positions of the noisy target reflectance spectrum, which includes band-correlated noise, determined by the directional parameter θ in the vector $\mathit{e}$. Figure 1(b) illustrates the FVC retrieval processes for the target spectrum (blue dot) and the biased spectrum (red dot) using algorithm-1 and -3 with the NDVI constraints. We then obtain the error propagated in the FVC as the FVC difference between the target spectrum and the biased spectrum, represented by ${ϵ}_1$ and ${ϵ}_3$ for algorithm-1 and -3, respectively (Figure 1(b)). As described in Figure 1, the amplitudes of the propagated error in the FVC differ by algorithm.

The errors propagated in the FVC by each of the three algorithms were derived previously [29]. The errors in algorithm-1 are represented in terms of the band-correlated noise and the endmember spectra (independent of the target spectrum) as

$$\begin{array}{c}\hfill {ϵ}_1=\frac{{\sigma }_t}{\mathit{d}·\mathit{d}}\mathit{d}·\mathit{e}\end{array}$$

(7)

The errors propagated in the FVC by algorithm-2 are a function of the input data, expressed as

$$\begin{array}{c}\hfill {ϵ}_2=\frac{{\sigma }_t\mathit{a}·\mathit{e}}{{\sigma }_t\mathit{b}·\mathit{e}+\varphi }\end{array}$$

(8)

where

$$\begin{array}{cc}\hfill \varphi & =(v_v-v_s){({\mathit{c}}_2·{\mathit{\rho }}_t+r_2)}^2\hfill \end{array}$$

(9a)

$$\begin{array}{cc}\hfill \mathit{a}& =({\mathit{c}}_2·{\mathit{\rho }}_t+r_2){\mathit{c}}_1-({\mathit{c}}_1·{\mathit{\rho }}_t+r_1){\mathit{c}}_2\hfill \end{array}$$

(9b)

$$\begin{array}{cc}\hfill \mathit{b}& =(v_v-v_s)({\mathit{c}}_2·{\mathit{\rho }}_t+r_2){\mathit{c}}_2\hfill \end{array}$$

(9c)

The errors propagated by algorithm-3 also depend on an input data set according to

$$\begin{array}{c}\hfill {ϵ}_3=\frac{{\sigma }_t\mathit{s}·\mathit{e}}{{\sigma }_t\mathit{t}·\mathit{e}+\psi }\end{array}$$

(10)

where

$$\begin{array}{cc}\hfill \psi & ={[{\mathit{c}}_1·{\mathit{\rho }}_t+r_1+\eta ({\mathit{c}}_2·{\mathit{\rho }}_t+r_2)]}^2\hfill \end{array}$$

(11a)

$$\begin{array}{cc}\hfill \mathit{s}& =\zeta [({\mathit{c}}_1·{\mathit{\rho }}_t+r_1){\mathit{c}}_2-({\mathit{c}}_2·{\mathit{\rho }}_t+r_2){\mathit{c}}_1]\hfill \end{array}$$

(11b)

$$\begin{array}{cc}\hfill \mathit{t}& =({\mathit{c}}_1+\eta {\mathit{c}}_2)[{\mathit{c}}_1·{\mathit{\rho }}_t+r_1+\eta ({\mathit{c}}_2·{\mathit{\rho }}_t+r_2)]\hfill \end{array}$$

(11c)

and where

$$\begin{array}{cc}\hfill \eta & =-\frac{\mathit{d}·{\mathit{c}}_1}{\mathit{d}·{\mathit{c}}_2}\hfill \end{array}$$

(12a)

$$\begin{array}{cc}\hfill \zeta & =\frac{[({\mathit{c}}_1·{\mathit{\rho }}_s+r_1){\mathit{c}}_2-({\mathit{c}}_2·{\mathit{\rho }}_s+r_2){\mathit{c}}_1]·{\mathit{\rho }}_v+(r_2{\mathit{c}}_1-r_1{\mathit{c}}_2)·{\mathit{\rho }}_s}{{({\mathit{c}}_2·\mathit{d})}^2}\hfill \end{array}$$

(12b)

The relationship among those errors can be determined by varying the parameter θ in $\mathit{e}$ (Equations (7), (8), and (10)). For example, the relationship between ${ϵ}_1$ and ${ϵ}_2$ is shown in Figure 2 as a function of θ. In this example, the target spectrum and the vegetation and non-vegetation endmember spectra are set to (0.1,0.2), (0.05,0.4), and (0.2,0.2), respectively (Figure 2(a)). The magnitude of the input error is 0.01, and NDVI is used as the endmember model in algorithm-2. The relationship among these variables becomes an asymmetric ellipse (Figure 2(b)).

In a previous study, we derived the relationships among the errors propagated in the three FVC retrieval algorithms under a two endmember assumption [29]. Because the variable θ was eliminated during the derivation process, the expression describing the relationship was independent of θ. In the next subsection, we summarize the relationships among the errors associated with the three algorithms.

3.2. Relationships Among the Errors Propagated in the FVC

The relationships among the propagated errors (${ϵ}_1$, ${ϵ}_2$, ${ϵ}_3$, ${ϵ}_2^{\prime }$ and ${ϵ}_3^{\prime }$, the definitions of which are provided in [29]) were derived for all pairs. Figure 3 illustrates a schematic diagram describing the relationships among the propagated errors. The relationships are indicated by bidirectional arrows with different colors, which are labeled according to the corresponding figure numbers in the results section, discussed in detail below. The corresponding sections and equations derived in [29] are also indicated in the figure. Proceeding with the explanation, we define a set S of the propagated errors according to

$$\begin{array}{c}\hfill S=\{{ϵ}_1,{ϵ}_2,{ϵ}_3,{ϵ}_2^{\prime },{ϵ}_3^{\prime }\}\end{array}$$

(13)

A pair of any two choices in S is represented by x and y. The relationship between x and y, except for the pairs ${ϵ}_2$ and ${ϵ}_3$, and ${ϵ}_2^{\prime }$ and ${ϵ}_3^{\prime }$, can be represented by [29]

$$\begin{array}{c}\hfill \sum _{i=0}^2\sum _{j=0}^2{p}_{i,j}{x}^i{y}^i=0\end{array}$$

(14)

where the definitions of the coefficients $p_{i,j}$ are summarized in [29]. Equation (14) represents an asymmetric ellipse, as shown in Figure 2.

The relationship between ${ϵ}_2$ and ${ϵ}_3$ (or between ${ϵ}_2^{\prime }$ and ${ϵ}_3^{\prime }$), denoted by a green bidirectional arrow as shown in Figure 3, becomes

$$\begin{array}{c}\hfill {ϵ}_3=\frac{{\gamma }_1{ϵ}_2}{1-{\gamma }_2{ϵ}_2}\end{array}$$

(15)

where

$$\begin{array}{cc}\hfill {\gamma }_1& =\frac{{(1-\nu {\widehat{\omega }}_3)}^2}{1-\nu }\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill {\gamma }_2& =\frac{\nu }{\nu -1}\hfill \end{array}$$

(17)

and

$$\begin{array}{c}\hfill \nu =\frac{(v_v-v_s{\mathit{c}}_2)·\mathit{d}}{(v_v{\mathit{c}}_2-{\mathit{c}}_1)·\mathit{d}}\end{array}$$

(18)

Figure 4 shows a plot of Equation (15) under the same conditions (except non-vegetation endmember spectrum) as were applied in the simulation illustrated in Figure 2. Note that NDVI were chosen as the variables or constraints in both algorithms. The relationship shown in Figure 4(b) is one-to-one.

In general, Equation (14) describes an asymmetric ellipse rotated to a certain degree and centered at the origin (Figure 2(b)). The shape and degree of rotation (the inclination of major axis) depend on the coefficients $p_{i,j}$. Similarly, the shape and rotation (or slope of the relationship) in Equation (15) depend on the coefficients ${\gamma }_i$.

These figures suggest an important observation: the robustness properties of the algorithms may be directly compared by deriving the rotational angle of the major axis of the ellipse. For example, if the major axis is more aligned with the X-axis than with the Y-axis (the rotational angle is less than $\pi /4$), the average propagated error along the X-axis exceeds that along the Y-axis. This indicates that the algorithm applied to the Y-axis is more robust than that applied to the X-axis.

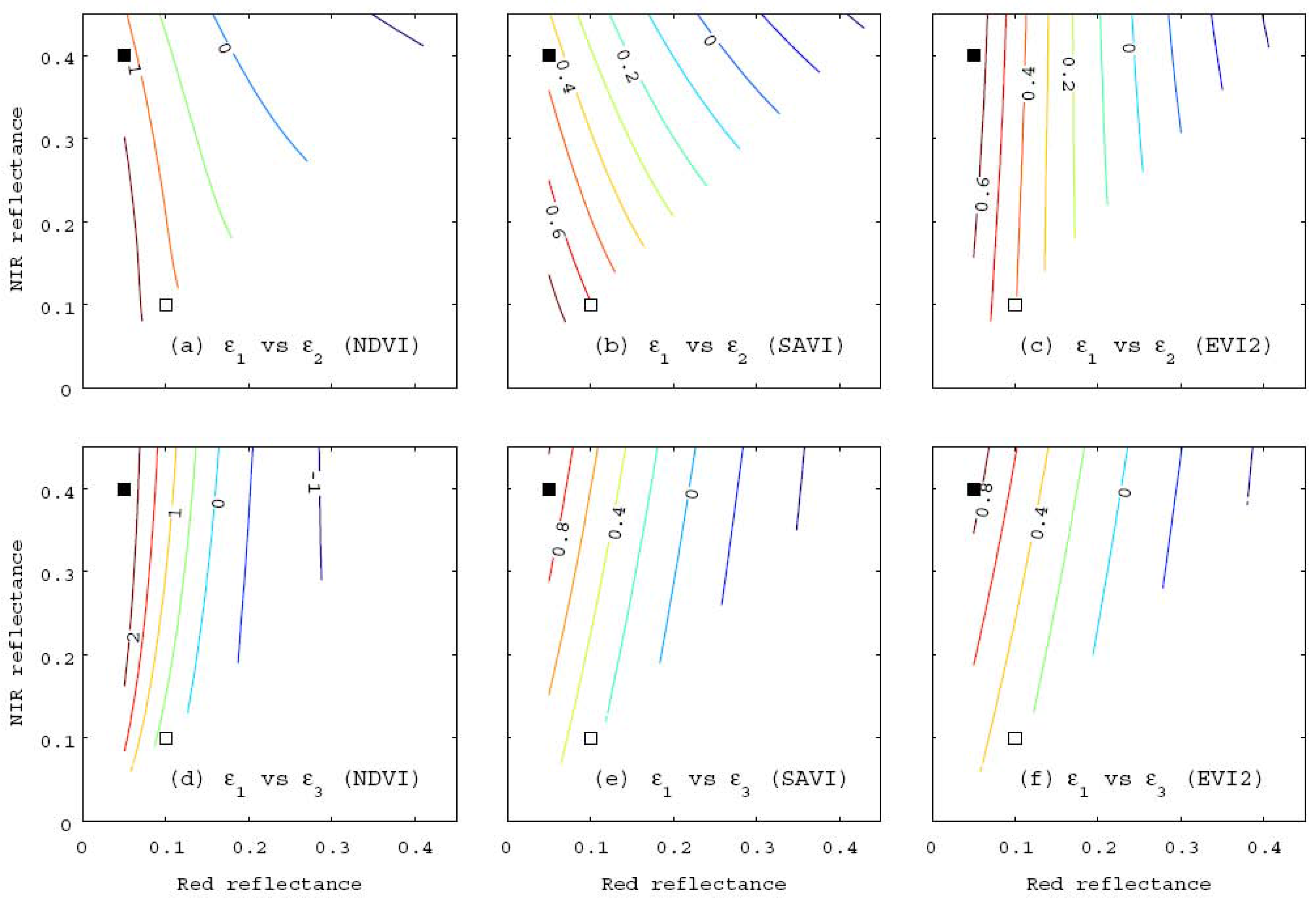
4. Comparison of the Propagated Errors

An elliptical relationship is obtained by varying the angle θ of the band-correlated noise. Thus, a point on the ellipse corresponds to a certain value of θ, which is implicitly included in Equation (14). Figure 5 shows a cross plot of ${ϵ}_1$ and ${ϵ}_2$ for θ between 0 and $2\pi$. In the figure, the values of θ are indicated by the intersections with the lines of ${ϵ}_1={ϵ}_2$ and ${ϵ}_1=-{ϵ}_2$. The red dots between $\theta =96$ and 233, and 274 and 53, indicate the range of θ in which the absolute value of ${ϵ}_1$ is smaller than that of ${ϵ}_2$. This suggests that algorithm-1 is more robust under conditions in which errors are present in the target reflectance spectrum. On the other hand, the blue dots indicate the ranges in which algorithm-2 is more robust.

Note that the parameter θ depends on the type of noise present. For example, an increase in the aerosol optical thickness increases the red reflectance but decreases the NIR reflectance [41], whereas the soil brightness beneath the vegetation canopy tends to shift the reflectance along the one-to-one line [42]. Although each effect influences the target spectrum in a different way, the robustness in the presence of noise can be compared by averaging the relative robustness over the parameter range θ. To do so, we use the slope of the major axis in the asymmetric ellipse (Equation (14)) as a robustness factor in a comparison of the two algorithms. When the slope of the major axis in the ellipse (red line in Figure 6(a)) is greater than one, the average absolute value of ${ϵ}_1$ is less than that of ${ϵ}_2$. In contrast, if the slope of the ellipse is less than one (Figure 6(b)), the average absolute value of ${ϵ}_1$ is larger than that of ${ϵ}_2$, indicating that algorithm-1 is less robust than algorithm-2. We next discuss a derivation of the rotation angle of the ellipse.

The inclination of the ellipse results from the cross terms in Equation (14). Among the cross terms, the term with coefficient $p_{1,1}$ provides the most significant contribution. To indicate this fact, we plot the ellipse by setting $p_{1,1}$ equal to zero (Figure 7(a)). As is clearly shown in the figure, the ellipse is no longer inclined. The inclination angle ${\theta }_0$ (illustrated in Figure 7(b)) can then be approximated by transforming (rotating) the coordinates.

4.1. Derivation of the Angle

Let us define a new coordinate system $(x^{\prime },y^{\prime })$ obtained by rotating the original coordinate system by ${\theta }_0$ in the counterclockwise direction (Figure 7(b)). The geometric transformation is represented by

$$\begin{array}{c}\hfill \left[\begin{array}{c}x\\ y\end{array}\right]=\left[\begin{array}{cc}cos{\theta }_0& -sin{\theta }_0\\ sin{\theta }_0& cos{\theta }_0\end{array}\right]\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]\end{array}$$

(19)

Substituting Equation (19) into Equation (14), we obtain the following expression for the ellipse in the new coordinate system,

$$\begin{array}{c}\hfill \sum _{i^{\prime }=0}^4\sum _{j^{\prime }=0}^4{\mu }_{i^{\prime },j^{\prime }}{(x^{\prime })}^{i^{\prime }}{(y^{\prime })}^{j^{\prime }}=0,(i^{\prime }+j^{\prime }\le 4)\end{array}$$

(20)

where the definitions of ${\mu }_{i^{\prime },j^{\prime }}$ are summarized in Appendix A.

Because the major axis is now aligned with the $X^{\prime }$-axis, the coefficient of the first-order cross term, ${\mu }_{1,1}$, must be close to zero,

$$\begin{array}{cc}\hfill {\mu }_{1,1}& =2sin{\theta }_{0}cos{\theta }_0(p_{0,2}-p_{2,0})+({cos}^2{\theta }_0-{sin}^2{\theta }_0)p_{1,1}\approx 0\hfill \end{array}$$

(21)

Solving the above equation for ${\theta }_0$, we obtain

$$\begin{array}{c}\hfill {\theta }_0\approx \frac{1}{2}{tan}^{-1}\frac{p_{1,1}}{p_{2,0}-p_{0,2}}\end{array}$$

(22)

Note that the coefficients, $p_{2,0}$, $p_{0,2}$, and $p_{1,1}$ depend on three factors: the target spectrum, the endmember spectra, and the choice of VI. Also, note that the term $p_{0,2}$, which depends on ${\sigma }_t$, is negligibly small compared to the other terms [29]. This indicates that ${\sigma }_t$ does not affect ${\theta }_0$. Finally, the slope of the major axis is approximated by $tan{\theta }_0$. If $tan{\theta }_0$ exceeds 1, the error propagated along the Y-axis is larger than that propagated along the X-axis.

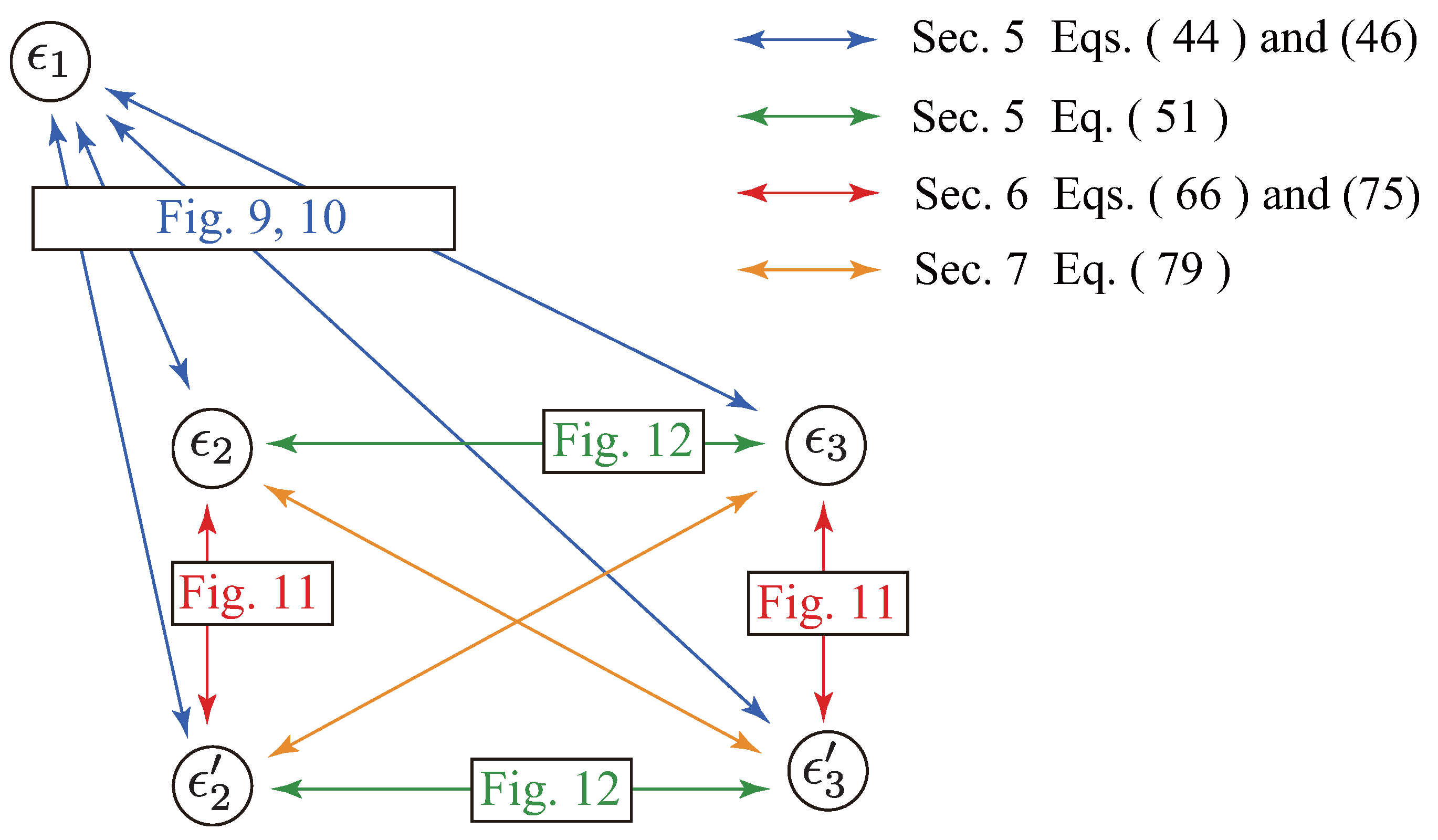
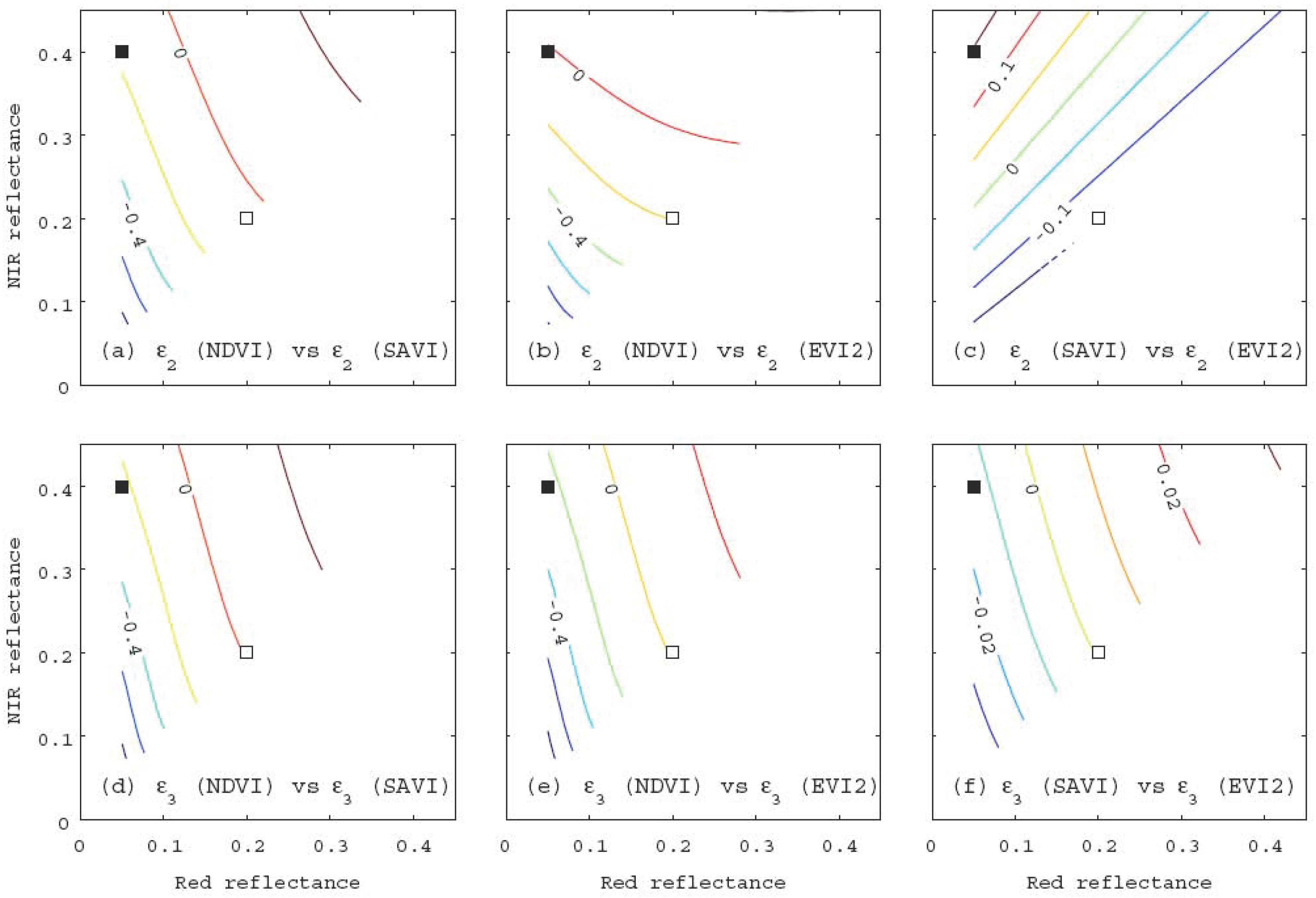
5. Comparison between Algorithms-2 and -3 under Identical VI Conditions

The relationship between the FVC errors associated with algorithm-2 and -3, assuming identical VI, is more straightforward than the relationship described above, because the relationship is one-to-one (Equation (15)). The robustness factors may be compared using the derivative of the relationship. The derivative of ${ϵ}_3$ with respect to ${ϵ}_2$ is

$$\begin{array}{c}\hfill \frac{\partial {ϵ}_3}{\partial {ϵ}_2}=\frac{{\gamma }_1}{{(1-{\gamma }_2{ϵ}_2)}^2}\end{array}$$

(23)

Note that ${ϵ}_2$ is a function of the directional parameter θ.

The robustness properties should be compared based on the average over the range of the directional parameter θ. The average derivative (represented by α) can be approximated according to the average value of ${ϵ}_2$ ($\overline{{ϵ}_2}$)

$$\begin{array}{c}\hfill \alpha \approx \frac{{\gamma }_1}{{(1-{\gamma }_2{\overline{ϵ}}_2)}^2}\end{array}$$

(24)

Applying the definition of ${\overline{ϵ}}_2$ shows that α is negligibly smaller than unity. Thus, in the context of the above equation, ${\overline{ϵ}}_2$ is considered to be

$$\begin{array}{c}\hfill {\overline{ϵ}}_2={\int }_0^{2\pi }{ϵ}_2(\theta )d\theta \approx 0\end{array}$$

(25)

As a result, Approximation (24) becomes

$$\begin{array}{c}\hfill \alpha \approx {\gamma }_1\end{array}$$

(26)

Note that the average slope (α) depends on the target spectrum, endmember spectra, and choice of VI (independent of the magnitude of the input error). Also note that $\nu <0$ [28] and ${\gamma }_1>0$. As a result, α becomes positive. When α is larger than one, the absolute value of ${ϵ}_2$ is less than ${ϵ}_3$, meaning that algorithm-2 is more robust than algorithm-3 in terms of the propagated error in the FVC.

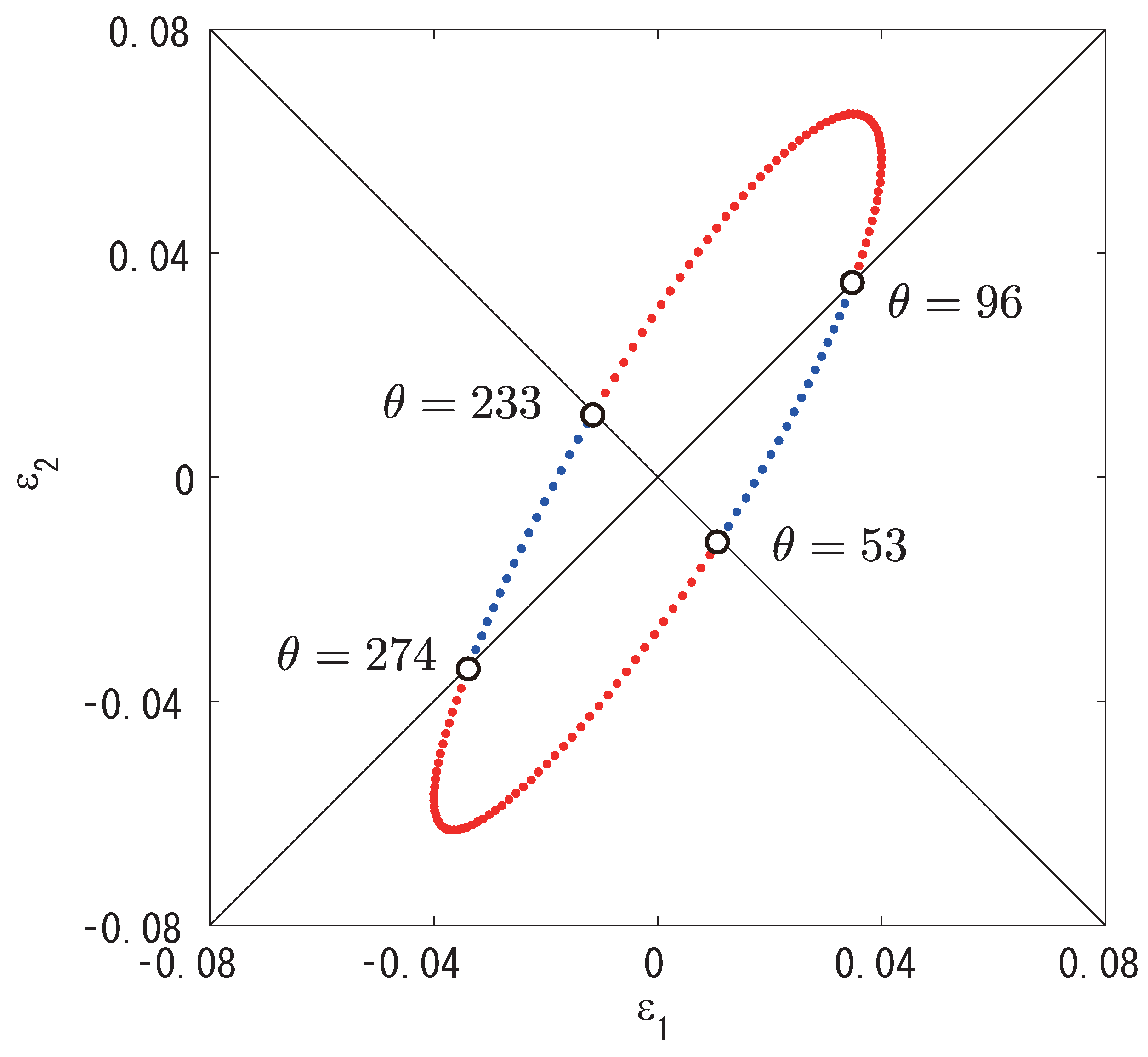
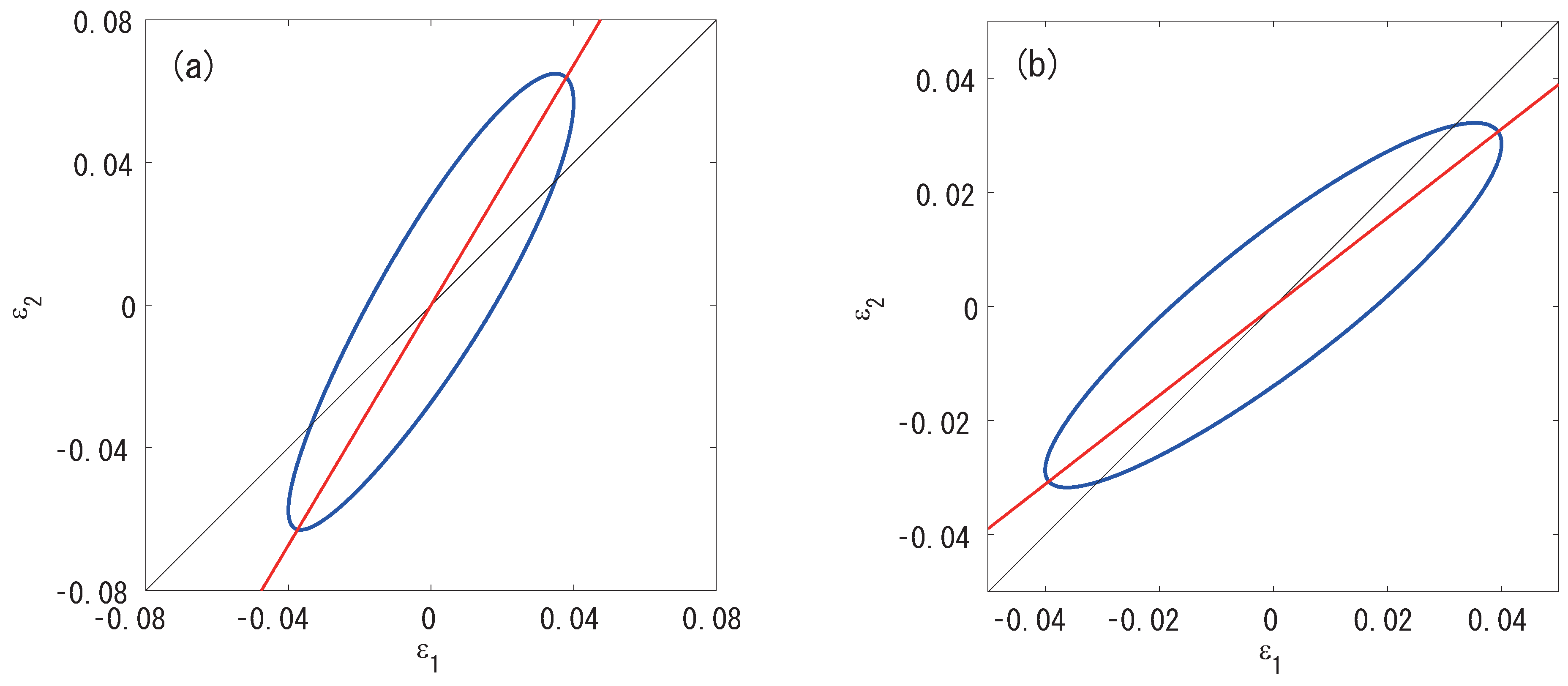
6. Numerical Demonstrations

The robustness factors of the LMM-based algorithms were compared for various errors in the target spectrum. Numerical simulations were conducted to compute the robustness factor ($tan{\theta }_0$ in Equation (22) or α in Equation (26)) for various sets of endmember spectra and VI values over a range of target spectra. The coefficients in Equations (22) and (26) were determined according to three types of input data: (i) target spectrum, (ii) vegetation and non-vegetation endmember spectra, and (iii) two-band VI used in the endmember model or the constraint. The target spectra assumed in the demonstration are shown in Figure 8. For the endmember spectra, we prepared two pairs of spectra, EM1 and EM2. Although the vegetation endmembers of both pairs were identical, the spectra of the non-vegetation endmembers were different. The bright and dark soils were modeled using EM1 and EM2, respectively (

Table 3. Two sets of endmember spectra (EM1 and EM2) used for the numerical demonstration.

Class	Vegetation		Non-vegetation
Band	Red	NIR	Red	NIR
EM1	0.05	0.4	0.2	0.2
EM2	0.05	0.4	0.1	0.1

). The two-band VI was selected from three VIs: NDVI, SAVI, and EVI2. The magnitude of the noise spectrum was assumed to be 0.01 throughout the demonstration (although it did not significantly influence the robustness comparisons.)

The robustness factors, $tan{\theta }_0$ and α, were computed for various combinations of the input parameters. The results are summarized in four sets of figures (Figure 9, Figure 10, Figure 11, and Figure 12.) The factors are plotted as contour maps on the logarithmic scale ($ln(tan{\theta }_0)$ or $ln(\alpha )$) as a function of the red and NIR reflectance. The FVC errors propagated in the algorithms were compared, pairwise, and are indicated in the figures as “A vs. B”. In the figures, the region corresponding to positive values indicates the subspace in which the error “A” is smaller than the error “B”. Additionally, the algorithm corresponding to the error “A” is more robust than the error “B”.

Figure 9 compares algorithm-1 and -2 (upper three panels), and algorithm-1 and -3 (lower three panels) for the endmember pair EM1 with the three VIs. In general, ${ϵ}_1$ is independent of the target spectrum. Therefore, variations in $tan{\theta }_0$ are caused by the variations in ${ϵ}_2$. In the figures, the contour lines for $ln(tan{\theta }_0)=0$ are proximal to the lines spanned by the two-endmember spectra. This suggests that, for the target spectra located on the left-hand sides of the lines spanned by the endmember spectra, algorithm-1 is more robust than the other two algorithms.

Figure 10 shows a comparison similar to that shown in Figure 9, with different endmember spectra, EM2. Recall that EM2 is a darker non-vegetation endmember spectrum than EM1. In the figures, the positive value regions increased in size (relative to the regions in the previous figures), indicating that algorithm-1 is more robust than the other two algorithms over a wider range of the target spectra. This also indicates that algorithm-1 is more robust than the others for darker non-vegetation spectra.

In summary, algorithm robustness depends on the endmember spectra assumed in the algorithm. Even when assuming identical endmember spectra, the robustness properties of two algorithms can vary with the measured target spectrum. In general, the brightness of the target spectrum and the position of its reflectance spectra relative to the endmember spectra are important factors.

Figure 11 shows an intra-algorithm comparison (for different VIs) of algorithm-2 and -3 using EM1. Although the contour lines showed similar patterns, the use of SAVI or EVI2 for ${ϵ}_2$ (upper-right figure) resulted in different patterns, and the mechanism remains unclear. The line spanned by the endmember spectra was no longer the discriminator of robustness in this case.

Figure 12 plots the values of α to compare algorithm-2 and -3 for a given VI with two sets of endmember spectra. The upper three panels show the results using EM1, and the lower three panels present results using EM2. In general, when the VI of the target spectrum is high, algorithm-2 is more robust (hence, a better choice) to noise in the target reflectance spectrum. Interestingly, the contour patterns were similar, and were comparable to the pattern considered to be an exception, as shown in Figure 11 (upper right panel). We also note that the differences in the non-vegetation spectra did not significantly influence the patterns of the contour lines, whereas the magnitude of α varied significantly.

7. Conclusions

This study derived the robustness factors necessary for comparing LMM-based FVC algorithms. The derivations relied on analytical expressions for the relationships between the errors propagated in FVC, introduced previously [29]. Based on our derivations, the relative robustness between the two algorithms can be judged by a single factor, ${\theta }_0$ (or α). This approach is significant in that the robustness of different algorithms can be compared deterministically (statistical approaches are not necessary) using only prior knowledge of a target field and the endmember spectra assumed in the algorithms. Also note that parameter studies and iterative approaches are not involved in comparison processes. These factors provide important information for discussions of the optimum algorithm under two-endmember and two-band assumptions.

Although the range of practical applications to which the results of this study may be applied is somewhat limited due to the assumptions made on the LMM (number of bands and endmember species), the findings and the essence of the theoretical development contribute to a better understanding of the FVC retrieval algorithms in terms of robustness to noise. Further studies are required to expand the techniques to achieve broader applicability.