Determining Regional Actual Evapotranspiration of Irrigated Crops and Natural Vegetation in the São Francisco River Basin (Brazil) Using Remote Sensing and Penman-Monteith Equation

Abstract

To achieve sustainable development and to ensure water availability in hydrological basins, water managers need tools to determine the actual evapotranspiration (ET) on a large scale. Field energy balances from irrigated and natural ecosystems together with a net of agro-meteorological stations were used to develop two models for ET quantification at basin scale, based on the Penman-Monteith equation. The first model (PM1) uses the resistances to the latent heat fluxes estimated from satellite measurements, while the second one (PM2) is based on the ratio of ET to the reference evapotranspiration (ET₀) and its relation to remote sensing parameters. The models were applied in the Low-Middle São Francisco river basin in Brazil and, after comparison against field results, showed good agreements with PM1 and PM2 explaining, respectively, 79% and 89% of the variances and mean square errors (RMSE) of 0.44 and 0.34 mm d⁻¹. Even though the PM1 model was not chosen for ET calculations, the equation for surface resistance (r_s) was applied to infer the soil moisture conditions in a simplified vegetation classification. The maximum values of r_s were for natural vegetation—caatinga (average of 1,937 s m⁻¹). Wine grape and mango orchard presented similar values around 130 s m⁻¹, while table grape presented the lowest ones, averaging 74 s m⁻¹. Petrolina and Juazeiro, in Pernambuco (PE) and Bahia (BA) states, respectively, were highlighted with the biggest irrigated areas. The highest increments are for vineyards and mango orchards. For the first crop the maximum increment was verified between 2003 and 2004 in Petrolina-PE, when the cultivated area increased 151%. In the case of mango orchards the most significant period was from 2005 to 2006 in Juazeiro-BA (129%). As the best performance was for PM2, it was selected and used to analyse the regional ET at daily and annual scales, making use of Landsat images and a geographic information system for different soil moisture conditions. Considering the daily rates of the regional ET, pixels with values lower than 1.0 mm d⁻¹ occurred outside the rainy season, representing the caatinga species. Values from 1.0 to 5.0 mm d⁻¹ during the driest conditions of the year coincided with irrigated crops, being the highest values for table grapes. The highest accumulated ET values during 2006 were for mango orchards, being around 500–1,300 mm yr⁻¹. Vineyards presented lower values, ranging from 450–800 mm yr⁻¹, while in caatinga they were between 200 and 400 mm yr⁻¹. It could be concluded that irrigated mango orchards and vineyards in that year consumed more water than caatinga by factors of 3 and 2, respectively. The mango orchards and vineyard areas, representing 19.4 and 8.2% of the total irrigated area, respectively, resulting in a total evaporative depletion of 0.22 km³ yr⁻¹ in the growing regions comprised of the agro-meteorological stations.

1. Introduction

Disputes over shared water resources are raising local, national, and even international tensions. Rising conflicts are expected as populations expand, economies grow, and the competition for limited water supplies intensifies [1]. Basin-level dialogs among different users to negotiate and agree on the allocation of water resources are required. The success of any dialog depends on the knowledge base and the general trust in data sources, such as the actual evapotranspiration (ET) of each land use type. Experimentally, the calculation of ET can be made accurately using the Bowen ratio (BR) method, eddy covariance (EC) techniques, and scintillometers. The BR method has been applied in agricultural crops and natural vegetation [2,3,4,5]. Examples of EC measurements can also be found [6,7,8,9,10,11,12,13,14]. However, the spatial variability is significant and extrapolation of energy balance data directly from flux tower to a surrounding landscape environment can lead to inaccurate regional estimates. Aiming to increase the spatial scales, ET was obtained by means of scintillometers across a path length of several kilometers [15,16], but these field methods cannot provide a fair sample of a whole biome [17]. Remote sensing, excluding the need of quantifying other complex hydrological processes, is an excellent means for determining and mapping the spatial and temporal structure of the energy balance components, including ET, at basin scale.

Vegetative indexes remotely obtained, together with agro-meteorological data, can be used to extrapolate ET values from local to regional scales. Hydrological models are in general too complex and costly for this extrapolation because of the difficulty in obtaining data sets in different hydrological uniform sub-areas and due to this deficiency, these models can yield unreliable results [18]. Oversimplification of land surface complexity may cause hydrological models to be biased and if species-specific algorithms were needed to scale tower data to larger areas, detailed, species-level vegetation maps of each river stretch would be necessary [19]. With the technological advances in satellites, electronic equipment and informatics in the 21st century, several remote sensing methods for regional ET calculations have been reviewed and improved [20,21,22,23,24,25,26,27,28]. Research on obtaining crop coefficients for applications in water management have also been carried out [29,30,31,32,33,34,35,36,37].

Several remote sensing algorithms have been developed. The energy balance methods have several advantages. The Surface Energy Balance Algorithm for Land—SEBAL [38], the Surface Energy Balance Index—S-SEBI [39] and the Surface Energy Balance System—SEBS [40], taking into account the crop conditions can be applied to various ecosystems without the need of crop classification. The identification of fruit trees from satellite data is not straightforward [41]. Unresolved problems for identifying different fruit crops in the semi-arid region of the São Francisco river basin in Brazil were reported [42]. It is considered easier to determine ET based on thermal infrared imagery, rather than through the procedures of crop classification [43]. However, the disadvantage of the energy balance methods is the need to identify extreme conditions, which is not required for the Two-Source Model—TSM [44], Dual-Temperature Difference—DTD [45] and Disaggregated Atmosphere Land Exchange Inverse model—DisALEXI [46]. The aerodynamic resistance-surface energy balance approach—RSEB [47] failed because small errors in the radiative temperature translate into large errors in the sensible heat fluxes, and then into estimates of ET.

One of the problems in relation to the applicability of the energy balance models, aimed at the end users, is the need of background knowledge in radiation physics involved inside these algorithms. The suitability of applying the Penman-Monteith (PM) equation by the surface conductance algorithm has been shown by using remotely-sensed vegetation indices (leaf area index and NDVI) together with weather data [23]. The big advantages of the PM equation are the applicability and the low sensitivity to input data and parameters. Its use is also highlighted by the METRIC model, which applies the reference evapotranspiration (ET₀) throughout the ratio ET/ET₀ to extrapolate instantaneous values of ET to larger time scales [48].

ET remote sensing methods have been useful for studies that were carried out involving net depletion of river flows, administering water rights, crop water requirements and irrigation management in the Western US states [49]. The effectiveness of using very high resolution visible and thermal infrared images in an Israeli vineyard for scheduling irrigation was demonstrated [50]. Thermal infrared measurements have enabled growers to produce maps of relative water stress in orchards [51]. With the use of ET and biomass production maps, crop water productivity was analyzed in the semi-arid conditions of Brazil [37]. However, the remote surface temperature and vegetation cover must be at high enough resolutions, where different land surface conditions can be distinguished, important for the validation of ET estimated by land surface models [52]. Procedures for the validation of remote sensing models have been carried out [53,54,55,56,57,58,59,60]. The research primarily involved comparing energy balance measurements from satellites with those of tower-based systems. Data from flux stations increase the confidence in remote sensing techniques, however, the success of the applicability of satellite images in quantifying water consumption is conditioned by the availability of biophysically realistic models, which are simple enough for implementation [23].

The intensification of agriculture in the Low-Middle São Francisco river basin, Brazil, with mainly fruit crops, has caused large land use changes, with the replacement of the natural vegetation (caatinga) by large irrigated areas. Water scarcity in some areas and periods of the year has been a problem and the drainage of irrigated agriculture may affect the water quality. With the reduction of the amount of good quality water, conflicts among users tend to rise. To avoid both water scarcity and water excess, one must have efficient tools to quantify ET at the basin scale. Field energy balance measurements in this region have been done in vineyards [5], mango orchard [13] and natural vegetation [14]; however, the results from these specific flux towers are only first estimations of ET in a region containing different ecosystems.

The energy balance methods using satellite measurements have the advantage that, while taking into account the crop growing conditions, they do not require a crop classification. However, for some of them, identification of extreme conditions is necessary [38,39,40] which can be difficult during the rainy seasons. The SEBAL algorithm was calibrated and validated with field measurements in surfaces with hydrological contrast in the semi-arid region of the São Francisco river basin [27]. Although the model performed well, the difficulty lies in its assumption of zero ET for dry pixels, which is difficult during the rainy season, because the regional moisture status is homogeneous in the mixed ecosystems of irrigated crops and natural vegetation.

Considering the simplicity of application, and its needing neither crop classification nor extreme conditions, two models based on the PM equation were developed and validated with field data from four flux stations involving irrigated crops and natural vegetation, in the semi-arid conditions of the Low-Middle São Francisco river basin [5,13,14]. The modeling involved the net radiation and soil heat fluxes, the resistances to water fluxes, and interpolated weather data. Remote sensing parameters from Landsat images, together with field energy balance experiments and a net of agro-meteorological stations were used. The two simple observation models, when used with satellites and a net of agro-meteorological stations, will be appropriate for implementation at basin scale for ET monitoring. After validation, a first application of the one selected was done for regional and incremental ET analyses at daily and annual scales, which are useful for decision-making policies in conditions of quick land and water use changes.

2. Material and Methods

2.1. Modeling Evapotranspiration

2.1.1. General Equations

The physical process, whereby water flows from evaporating surfaces into the atmosphere, is referred to as actual evapotranspiration (ET). This water flux occurs via canopies through stomata as actual transpiration and directly from the soil surface as actual evaporation. Stomata are small openings on the plant leaf through which gases and water vapor pass. The vaporization occurs within the leaf, in the intercellular spaces, and the vapor exchange with the atmosphere is controlled by the stomatal aperture, which can be open and closed, depending on the pressure of the guard cell. Nearly all soil water taken up by roots is lost by transpiration and a negligible fraction is used within the plant. Not only the type of crop, but also the crop development, environment, cultural management and irrigation system should be considered when assessing transpiration.

For modeling ET, distinctions are made between reference crop evapotranspiration (ET₀) and actual evapotranspiration (ET). ET₀ is the evapotranspiration rate from a reference surface, not short of water, which can be a hypothetical grass surface with specific characteristics, while ET involves all conditions of any vegetated surface. Agro-meteorological parameters, vegetation characteristics, management and environmental aspects affect ET. Other factors to be considered are ground cover, plant density, plant architecture, microclimate and soil moisture. Considering irrigated crops, cultivation practices and the type of irrigation system, can alter the microclimate, affecting the canopy characteristics and the moisture content of the soil and the plants. The effect of soil moisture on water fluxes is primarily conditioned by the magnitude of the water deficit and the type of soil. On the other hand, too much water will result in water logging, which might damage the root and limit root water uptake by inhibiting respiration [61].

Evapotranspiration is an energy consuming process, referred to as the latent heat flux (λE). ET can be derived from the latent heat of vaporization (λ), density of water and λE. As a first approximation, an ET of 1 mm d⁻¹ is equivalent to a λE of 28 W m⁻², being therefore the chain between the water and energy balances. All energy fluxes should be considered when deriving the energy balance equation, which for a given surface can be written as:

$$R_n-\lambda E-H-G=0$$

(1)

where R_n is the net radiation, H is the sensible heat flux and G is the soil heat flux. All terms in Equation 1 can be expressed in W m⁻² or MJ m⁻² d⁻¹, being either positive or negative. Positive R_n means energy flux to the surface and positive G, λE and H indicate fluxes of energy from the surface. Equation 1 states that the R_n is redistributed over H, λE and G, considering only vertical fluxes and ignoring the net rate at which energy is being transferred horizontally, by advection; however, this term can be significant near the edges of crops or natural vegetation [62]. Therefore it is accurate only when applied to large, extensive surfaces. Other energy terms, such as heat stored or released in the canopies, or the energy used in metabolic activities, are not considered. These last terms account only for a small fraction of the daily R_n and can be neglected in hydrological studies.

The atmosphere warms up when R_n is positive. Heating of the atmosphere occurs from the land surface, thus the surface temperature (T₀) during daylight hours exceeds the air temperature (T_a). H is the rate of heat loss to the air by convection and conduction, due to a temperature difference, being expressed by the following equation for heat transport [63]:

$$\mathrm{H}=\frac{{\mathsf{\rho }}_{\mathrm{a}}{\mathrm{c}}_{\mathrm{p}}({\mathrm{T}}_0-{\mathrm{T}}_{\mathrm{a}})}{{\mathrm{r}}_{\mathrm{a}\mathrm{h}}}$$

(2)

where ρ_a is air density (kg m⁻³), c_p is air specific heat at constant pressure (J kg⁻¹ K⁻¹), T₀ and T_a are in K; and r_ah is the aerodynamic resistance to heat transport in the boundary above the land surface (s m⁻¹) applicable to the same two heights.

λE can be determined as:

$$\mathsf{\lambda }\mathrm{E}=\frac{{\mathsf{\rho }}_{\mathrm{a}}{\mathrm{c}}_{\mathrm{p}}}{\mathsf{\gamma }}\left[\frac{{\mathrm{e}}_{\mathrm{s}}({\mathrm{T}}_0)-{\mathrm{e}}_{\mathrm{a}}}{{\mathrm{r}}_{\mathrm{a}\mathrm{v}}+{\mathrm{r}}_{\mathrm{s}}}\right]$$

(3)

where γ is the psychrometric constant (kPa °C⁻¹); e_a is the actual water vapor pressure of the air (kPa) at the reference height above the surface (z); r_s and r_av are respectively the surface and aerodynamic resistances (s m⁻¹) to the latent heat flux; and e_s(T₀) is the saturated water vapor pressure (kPa) at T₀.

These fundamental equations constitute the base for regional ET modeling approaches, which use remotely-sensed radiances. The transfer equations for H (Equation 2) and for λE (Equation 3) were combined [64] into the surface energy balance (Equation 1), and the world wide accepted combination equation for open water evaporation was developed. The combination equation was modified into a version that can be applied to the vegetated surfaces by inserting a canopy resistance [65], eliminating T₀ from Equations 1–3.

Considering r_ah and r_av nearly equal in practice, and replaced by r_a for both heat and vapor flux transports, the PM equation to predict ET from vegetated surfaces [61] became:

$$\mathsf{\lambda }\mathrm{E}=\frac{\Delta {\text{(R}}_{\text{n}}\text{-G) }+{\mathsf{\rho }}_{\text{a}}{\text{c}}_{\text{p}}{\text{D/r}}_{\text{a}}}{\Delta +\mathsf{\gamma }\text{(1 }+{\text{ r}}_{\text{s}}{\text{/r}}_{\text{a}}\text{)}}$$

(4)

where Δ (kPa °C⁻¹) is the slope of the saturated vapor pressure curve and D (kPa) is the vapor pressure deficit in the air near the vegetated surfaces.

The difficulties of using Equation 4, especially at the regional scale, are considered to be the estimations of r_a and r_s [66]. Differences in crop height and leaf area index (LAI) determine crop roughness and thereby r_a. Crop rooting characteristics, root water uptake and LAI influence the value of r_s. With the availability of the evapotranspiration resistances, ET can be derived from agro-meteorological data by means of Equation 4, providing a good approach because it combines the main drivers of water fluxes; provides an energy constraint on the water fluxes; and modeled ET are not overly sensitive to any of the inputs [23]. The magnitude of r_s is mainly governed by environmental entities and soil moisture status [67,68]. Where the vegetation does not completely cover the soil, r_s includes the effects of the soil evaporation. With field values of λE, R_n, G, r_a and microclimatic data, r_s can be estimated inverting Equation 4 [5,13,14], and together with remote sensing parameters, the ET at the regional scale can be obtained. On the other hand, Equation 4 applied to the reference crop allows the modeling of the ratio ET/ET₀ with satellite variables. The next section describes the steps for modeling by using the PM equation in these two ways.

2.1.2. Penman-Monteith models

Table 1 summarizes the steps for modeling the regional ET by the two models based on the PM equation. For the first model (PM1), the radiation balance was done with locally calibrated equations and satellite values of R_n, G and the evapotranspiration resistances together with weather data, while for the second one (PM2), the only remote sensing parameters are the surface albedo (α₀), the surface temperature (T₀) and the Normalized Difference Vegetation Index (NDVI). For both models, the ratio ET/ET₀ is applied to grids of ET₀ at instantaneous and daily time scales.

Table 1. Summary of the regression analyses.

Parameter	Equation	a	b	R2
α0	α0 = aαp + b	0.70	0.06	0.96
T0	T0 = aTsat + b	1.11	−31.89	0.95
εa	εa = a(−lnsw)b	0.94	0.10	0.75
ε0	ε0 = alnNDVI + b	0.06	1.00	0.90
G/Rn	G/Rn = aexp(bα0)	3.98	−25.47	0.90
z0m	z0m = exp [(aNDVI/α0) + b]	0.24	−2.12	0.92
rs	rs = exp[a(T0/α0)(1 − NDVI) + b]	0.04	2.72	0.93
ra	ra = azoh−1 + b	0.22	29.5	0.78
ET/ET0	ET/ET0 = exp{a + b[T0/( α0NDVI)]}	1.90	−0.008	0.91

Table 1. Summary of the regression analyses.

Parameter	Equation	a	b	R2
α0	α0 = aαp + b	0.70	0.06	0.96
T0	T0 = aTsat + b	1.11	−31.89	0.95
εa	εa = a(−lnsw)b	0.94	0.10	0.75
ε0	ε0 = alnNDVI + b	0.06	1.00	0.90
G/Rn	G/Rn = aexp(bα0)	3.98	−25.47	0.90
z0m	z0m = exp [(aNDVI/α0) + b]	0.24	−2.12	0.92
rs	rs = exp[a(T0/α0)(1 − NDVI) + b]	0.04	2.72	0.93
ra	ra = azoh−1 + b	0.22	29.5	0.78
ET/ET0	ET/ET0 = exp{a + b[T0/( α0NDVI)]}	1.90	−0.008	0.91

Figure 1 shows the radiation balance for obtaining R_n with the parameterizations of Table 1, necessary for the PM1 model.

Figure 1. Schematic flowchart for the regional radiation balance for PM1 model.

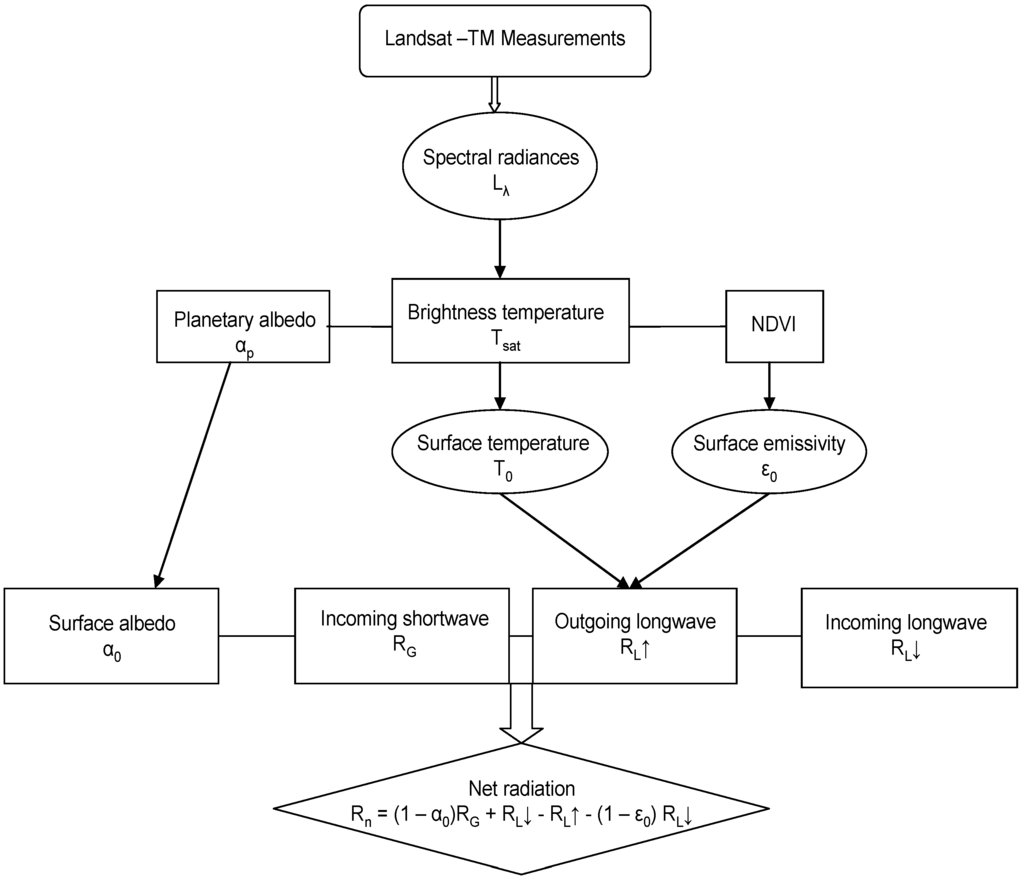
Figure 1. Schematic flowchart for the regional radiation balance for PM1 model.

Simple regression equations were used for atmospheric correction to obtain the regional values of α₀ and T₀ by using field and satellite measurements. The satellite measured radiances are affected by the atmospheric interaction in the radiative transfer path, being part of the incident global solar radiation (R_G) scattered back before it reaches the earth surface. A simplified linear relationship between α₀ measured by pyranometers in the field and the planetary albedo by Landsat satellite (α_p) has been applied [69]. From the field energy balance experiments, the aerodynamic surface temperature (T₀) was calculated from Equation 2 while the radiometric surface temperature was obtained from the Landsat band 6 (T_sat). Other than for a thin surface, a difference arises between radiometric and aerodynamic surface temperatures [70]. Excellent agreement was found between aerodynamic surface and canopy radiometric temperatures for a dense, fully closed wheat crop [71], however, for sparse or composite vegetation, the differences increase [72]. The satellite thermal radiation was therefore corrected for both atmospheric emission and the difference between radiometric and surface temperature by applying a regression equation with field and satellite values (Table 1).

Considering that the field measurements involved contrasting hydrological surfaces with different values for α₀; for the use of the Equation 2 for estimating T₀, microclimatic measurements with stability corrections were applied to r_a in flux profile relationships. Since EC systems directly provide u_*, with good agreements of H when comparing field and satellite values [27], it is assumed that the two key first regressions from Table 1 have good accuracy in the semi-arid region of the Low-Middle São Francisco river basin.

In the regional radiation balance (Figure 1), the net short wave radiation available at the earth surface depends on R_G and α₀.

Measured R_L↓ over natural vegetation (caatinga)—in combination with microclimatic data of air temperature (T_a)—accorded the inspection of the apparent emissivity of the atmosphere (ε_a). The regional values of R_L↓ were then estimated from the Stefan Boltzman equation by using the relation of ε_a with the atmospheric transmissivity (τ_sw) together with grids of T_a from the net of agro-meteorological stations. τ_sw was, in turn, calculated by the ratio of the grid of R_G measured by the net of pyrometers and the solar radiation at the top of the atmosphere (R_a) [27]. For R_L↑, the Stefan Boltzman equation was applied using images of T₀ and the correlation of field values of surface emissivity (ε₀) and satellite measurements of NDVI [73], this last parameter being obtained from the infrared and red regions of the Landsat images.

The regional values of R_n resulted from the balance of all short and long wave radiations (Figure 1). The term G in large scale was acquired by an exponential relation of field values of the ratio G/R_n and α₀, assuming that both ratios are dependent on the type and architecture of the vegetation and soil moisture conditions and that the exponential relation was the best found for comparing the two ratios involving natural vegetation and irrigated crops (R² = 0.96) under several hydrological conditions in semi-arid region of Brazil (Table 1).

The behavior of z_0m in natural vegetation and irrigated crops was described for the semi-arid conditions of the Low-Middle São Francisco river basin [14]. To estimate this roughness parameter at the regional scale from remote sensing measurements, a simplified expression based on α₀ from field measurements and NDVI from satellite images, with locally calibrated regression coefficients shown in Table 1 was used. The inclusion of α₀ helps to distinguish between vegetation having different architecture but similar values of NDVI [48]. For example table grape may present the same NDVI values as mango orchard, but substantially lower LAI. The coefficient of determination is rather encouraging for describing a difficult land surface parameter by some simplified remote sensing variables.

For the PM1 model, r_a was estimated from the roughness length for heat transport (z_0h), which in turn was considered as a function of z_0m (z_0h = 0.1 z_0m) [61]. This relation is very useful, as there is no unique relationship between surface roughness characteristics such as the geometry of the roughness elements and z_0h [74,75]. The low determination coefficient in Table 1 is not a problem, because Equation 4 is insensitive to r_a, especially when r_a << r_s and at daily timescales [23]. Finally, to complete the resistance terms in the PM equation, the field values of r_s were correlated with the field values of T₀, α₀ and satellite measurements of NDVI. For PM2 model, the instantaneous ET/ET₀ field values were also modeled with field values of T₀ and α₀ together with satellite data of NDVI (Table 1).

Figure 2 presents the schematic overview to convert spectral radiance into ET by using the satellite parameters and the grids of daily ET₀ when applying the PM2 model.

Figure 2. Schematic flowchart for calculating the actual evapotranspiration when applying the PM2 model.

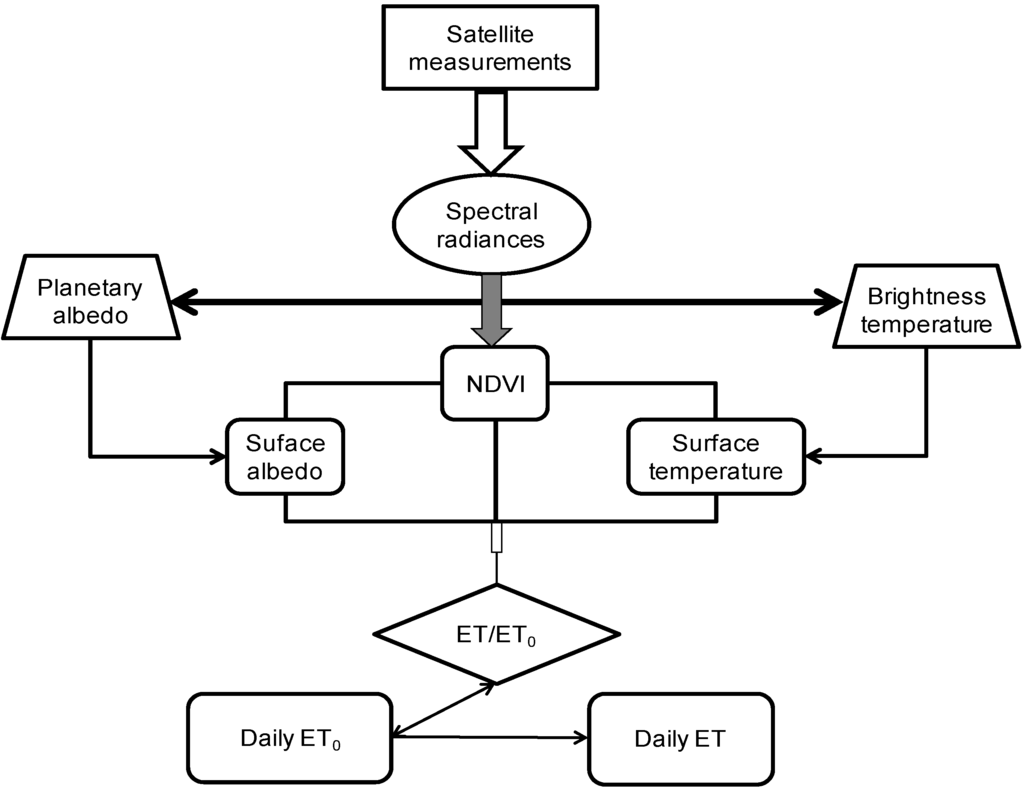
Figure 2. Schematic flowchart for calculating the actual evapotranspiration when applying the PM2 model.

After converting the spectral radiances and the atmospheric corrections, the images of NDVI, α₀ and T₀ are the only input parameters for estimating the instantaneous values of the ratio ET/ET₀ without the need of the regional radiation balance shown in Figure 1. The instantaneous values of this ratio are multiplied by the daily grids of ET₀ to estimate the regional ET for 24 hours.

Both, r_s and ET/ET₀ values are related to the soil moisture conditions and so are the remote sensing vegetation indicators such as NDVI, α₀ and T₀. Based on this principle, two models were proposed. The relationship between vegetation indices with soil moisture and ET rates have been reported in the semi-arid region of Brazil [14,27]. The relations for modeling the regional ET in a mixture of natural vegetation and irrigated crops are depicted in Figure 3.

For the first model based on direct application of Equation 4 (PM1), the images of R_n, G, r_s and r_a, are used together with the interpolated weather data from the net of agro-meteorological stations (Table 1; Figure 1, Figure 3a and Figure 3b). The regional values of λE are acquired and transformed into millimeters of water (ET). After the determination of ET at the regional scale, the instantaneous ratio of ET/ET₀ is calculated with grids of ET₀ for these same spatial and time scales. The second model (PM2) is based on the modeling of ET/ET₀ at the satellite overpass time (subscript sat) at the regional scale (Table 1 and Figure 3c). The instantaneous images of ET/ET₀ obtained by both models are then multiplied by the grids of ET₀ for 24 hours.

The satellite overpass time values of ET/ET₀ and those for 24 hours in irrigated mango orchard and caatinga were compared (Figure 3d). The slope is close to one, supporting the assumption that instantaneous and daily ratios can be considered equal. A factor of 1.18 for the evaporative fraction [EF = λE/(R_n − G)] was necessary to extrapolate the latent heat fluxes from satellite overpass to daily time scale based on field and satellite measurements in the semi-arid conditions of the Low-Middle São Francisco river basin, Brazil [14,37].

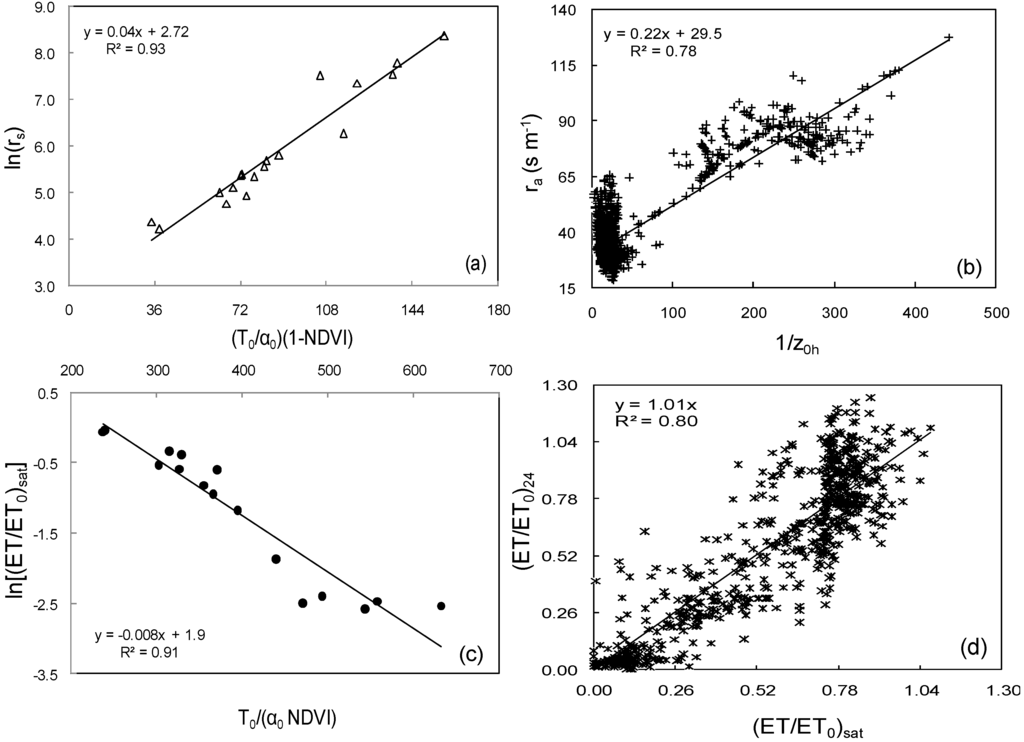
Figure 3. Relations for the evapotranspiration resistances and ET/ET₀ ratio. (a) Surface resistance (r_s); (b) aerodynamic resistance (r_a); (c) satellite overpass time value of ET/ET₀ (subscript sat). (d) daily values of ET/ET₀ (subscript 24). T₀: surface temperature; α₀: surface albedo; NDVI: Normalized Difference Vegetation Index; z_0h: roughness length for heat transport.

Figure 3. Relations for the evapotranspiration resistances and ET/ET₀ ratio. (a) Surface resistance (r_s); (b) aerodynamic resistance (r_a); (c) satellite overpass time value of ET/ET₀ (subscript sat). (d) daily values of ET/ET₀ (subscript 24). T₀: surface temperature; α₀: surface albedo; NDVI: Normalized Difference Vegetation Index; z_0h: roughness length for heat transport.

The coefficients of determination in Figure 3a and Figure 3c are very good (R² > 0.90). The lower value for r_a (Figure 3b) is not a big problem since, according to some sensitivity analysis errors in λE estimations, changes in the magnitudes of this resistance do not cause large errors, because it appears in both the numerator and the denominator of the PM equation [23,76].

2.2. Field and Remote Sensing Parameterizations

2.2.1. Field Parameters

The transfer of heat and water vapor from the evaporating surface into the air above the canopy is determined by r_a, which was estimated using flux profile relationships (FP) in vineyards and EC measurements in mango orchard and natural vegetation. The atmospheric surface-layer similarity theory was applied in both situations to estimate the roughness elements related to mechanically generated turbulence. The universal functions and the integrated stability functions of temperature (Ψ_h) and momentum (Ψ_m) were applied [77]. This resistance accounts for the drag force between land and atmosphere in Equation 4. Its determination requires the surface roughness for heat transfer (z_0h) and friction velocity (u_*) to be specified:

$${\mathrm{r}}_{\mathrm{a}}=\frac{\ln \left[\frac{\mathrm{z}-\mathrm{d}}{{\mathrm{z}}_{0\mathrm{h}}}\right]-{\mathsf{\text{ψ}}}_{\mathrm{h}}(\frac{\mathrm{z}-\mathrm{d}}{\mathrm{L}})}{\mathrm{k}{\mathrm{u}}_{*}}$$

(5)

where z (m) is the measurement height, d (m) is the displacement height, k is the von Karman’s constant (0.41), ψ_h is the stability correction due to buoyancy and L is the Obukhov length.

For vineyards u_* was calculated by using two levels of wind speed measurements [5], while for mango orchard and caatinga the EC measurements directly provided this roughness parameter [13,14]. The value for z_0h was then considered to be 10% of the roughness length for moment transfer (z_0m).

With field measurements of wind speed over the vegetation the z_0m was obtained by:

$${\mathrm{z}}_{0\mathrm{m}}=\frac{\mathrm{z}-\mathrm{d}}{\exp (\frac{\mathrm{k}\mathrm{u}(\mathrm{z})}{{\mathrm{u}}_{*}}+{\text{Ψ}}_{\mathrm{m}}(\frac{\mathrm{z}-\mathrm{d}}{\mathrm{L}}))}$$

(6)

where u(z) is the wind speed at the first level (z = z₁) in vineyards or at the height of the sonic anemometer above mango orchard or caatinga and ψ_m is the stability function for momentum.

Microclimatic data of air temperature (T_a) and relative humidity (RH) were used together with R_n, λE and G to estimate r_s inverting Equation 4.

The aerodynamic temperature (T₀) was calculated from Equation 2 [27,63] with field data of r_a, T_a and H:

$${\mathrm{T}}_0={\mathrm{T}}_{\mathrm{a}}+\frac{{\mathrm{r}}_{\mathrm{a}}\mathrm{H}}{{\mathsf{\rho }}_{\mathrm{a}}{\mathrm{c}}_{\mathrm{p}}}$$

(7)

In the two models based on Equation 4, for vegetation in general (PM1) and for grass, taking it as a reference surface (PM2), all the input field parameters were α₀, T₀, R_n, G, r_s and r_a together microclimatic data and the ratio ET/ET₀ (Table 1). The field measurements were then correlated with remote sensing parameters described in the next section.

2.2.2. Remote Sensing Parameters

In the regional radiation balance (Figure 1), α₀ is acquired from satellite-measured spectral radiances for each narrow band, followed by mathematical expressions for spectral integration and atmospheric correction. Regional R_G in the present research was computed using interpolated measurements from seven pyrometers, which were calibrated periodically with a new sensor (Kipp & Zonnen, Delft, the Netherlands), kept for this calibration.

The planetary albedo for each Landsat satellite band (${\mathsf{\alpha }}_{{\mathrm{p}}_{\mathrm{b}}}$) is calculated as:

$${\mathsf{\alpha }}_{{\mathrm{p}}_{\mathrm{b}}}=\frac{{\mathrm{L}}_{\mathrm{b}}\mathsf{\pi }{\mathrm{d}}^2}{{\mathrm{R}}_{{\mathrm{a}}_{\mathrm{b}}}\cos \mathsf{\phi }}$$

(8)

where L_b is the spectral radiance for wavelengths of the band b (W m⁻² sr⁻¹ µm⁻¹), d is the relative earth-sun distance; ${{\mathrm{R}}_{\mathrm{a}}}_{\mathrm{b}}$ is the mean solar irradiance at the top of the atmosphere (or atmospheric irradiance) for each band (W m⁻² µm⁻¹) and φ the solar zenith angle. The broadband planetary albedo (α_p) is obtained as the total sum of the different narrow-band ${\mathsf{\alpha }}_{{\mathrm{p}}_{\mathrm{b}}}$ values according to weights for each band (w_b).

$${\mathsf{\alpha }}_{\mathrm{p}}=\sum {\mathrm{w}}_{\mathrm{b}}{\mathsf{\alpha }}_{\mathrm{p}\mathrm{b}}$$

(9)

The weights for the different bands are computed as the ratio of the amount of incoming shortwave radiation from the sun at the top of the atmosphere in a particular band and the sum for all the bands. The bands 1 to 5 and 7 provide data for the visible and near infrared bands used for α₀ calculations. Values of w_b for the Landsat satellites are given in Table 2:

Table 2. Weighting coefficients (w_b) for Landsat images

Satellite	Band 1	Band 2	Band 3	Band 4	Band 5	Band 6	Band 7
Landsat 5	0.293	0.274	0.233	0.157	0.033	-	0.011
Landsat 7	0.293	0.274	0.231	0.156	0.034	-	0.012

Table 2. Weighting coefficients (w_b) for Landsat images

Satellite	Band 1	Band 2	Band 3	Band 4	Band 5	Band 6	Band 7
Landsat 5	0.293	0.274	0.233	0.157	0.033	-	0.011
Landsat 7	0.293	0.274	0.231	0.156	0.034	-	0.012

The spectral radiance in band 6 (L₆) of Landsat is converted into a radiation temperature applicable at the top of the atmosphere (T_sat) by inversion of Plank’s law in the 10.4–12.5 µm bandwidth:

$${\mathrm{T}}_{\mathrm{s}\mathrm{a}\mathrm{t}}=\frac{{\mathrm{K}}_2}{\ln (\frac{{\mathrm{K}}_1}{{\mathrm{L}}_6+1})}$$

(10)

where T_sat is the brightness temperature (K); L₆ is the uncorrected thermal radiance from the land surface; and K₁ (607.76 and 666.09 for Landsat 5 and 7, respectively) and K₂ (1,260.56 and 1,282.71 for Landsat 5 and 7, respectively) are conversion coefficients given in mW cm² sr⁻¹μm⁻¹ and W m² sr⁻¹μm⁻¹ for Landsat 5 and Landsat 7, respectively.

Another important satellite parameter for ET modeling is the Normalized Difference Vegetation Index (NDVI) which is an indicator related to the land cover:

$$\mathrm{N}\mathrm{D}\mathrm{V}\mathrm{I}=\frac{{\mathsf{\alpha }}_{{\mathrm{p}}_{(\mathrm{N}\mathrm{I}\mathrm{R})}}-{\mathsf{\alpha }}_{{\mathrm{p}}_{(\mathrm{R}\mathrm{E}\mathrm{D})}}}{{\mathsf{\alpha }}_{{\mathrm{p}}_{(\mathrm{N}\mathrm{I}\mathrm{R})}}+{\mathsf{\alpha }}_{{\mathrm{p}}_{(\mathrm{R}\mathrm{E}\mathrm{D})}}}$$

(11)

where ${\mathsf{\alpha }}_{{\mathrm{p}}_{(\mathrm{N}\mathrm{I}\mathrm{R})}}$ and ${\mathsf{\alpha }}_{{\mathrm{p}}_{(\mathrm{R}\mathrm{E}\mathrm{D})}}$ represent the planetary albedo over the ranges of wavelengths in the near infrared (NIR) and red (RED) regions of the solar spectrum, respectively.

2.3. Study Region, Field Experiments and Agro-Meteorological Stations

The São Francisco river basin encompasses several Brazilian states with a size of 636,920 km². It is divided into four physiographic regions: The Upper, the Middle, the Low-Middle and the Lower São Francisco sub basins. The upstream region has an average annual precipitation of more than 2,000 mm. In the semi-arid and arid zones of the states of Bahia and Pernambuco, the rainfall drops to less than 350 mm yr⁻¹. Near the mouth of the river, oceanic influence gradually increases rainfall again to about 1,300 mm yr⁻¹. More than 50% of the territory of the basin is located in the semi-arid region of Brazil in the northeastern part of the country. Disturbed currents of South, North, East and West influence the climatology of this region. Excluding the places of high altitude, all areas in the Low-Middle sub-basin present annual averaged air temperatures higher than 24 °C, even higher than 26 °C in the depressions at 200 to 250 m of altitude. The average maximum air temperature for this sub basin is 33 °C and the average minimum is 19 °C. The averaged monthly values are in the range from 17 °C to 29 °C [78].

The experimental data set involving vineyards, mango orchards and natural vegetation, together with satellite images and agro-meteorological stations, were used for modeling and analyzing ET in the growing regions of the Low-Middle São Francisco river basin. Figure 4 shows the details of the entire basin, sub-basins, field experiments and agro-meteorological stations.

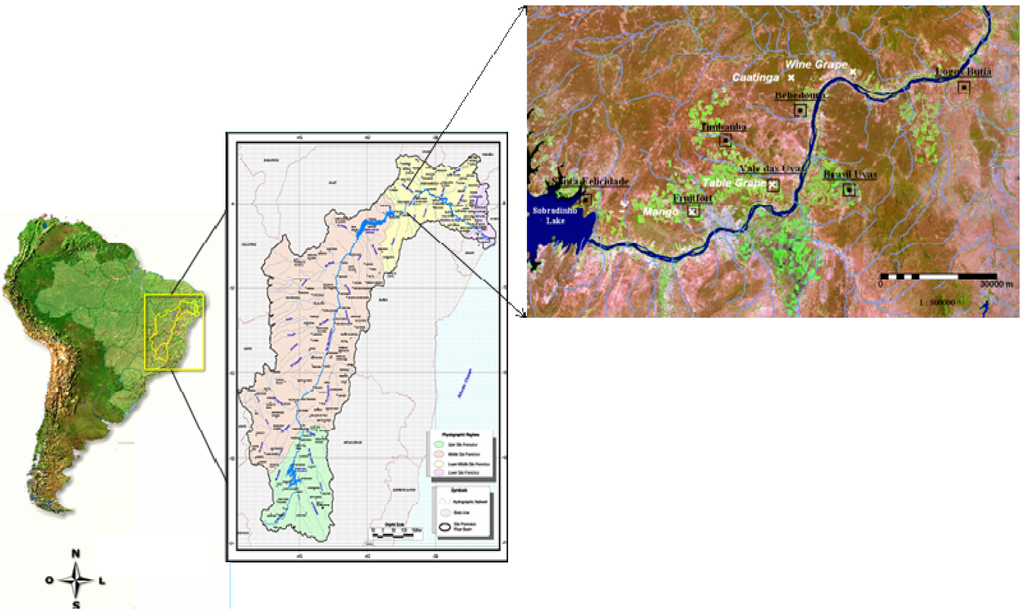
Figure 4. The São Francisco river basin and the semi-arid region studied. The agro-meteorological stations (black) and the flux towers (white) on irrigated fruit crops (wine grape, table grape, mango orchard) and natural vegetation (caatinga) are indicated on the right side.

Figure 4. The São Francisco river basin and the semi-arid region studied. The agro-meteorological stations (black) and the flux towers (white) on irrigated fruit crops (wine grape, table grape, mango orchard) and natural vegetation (caatinga) are indicated on the right side.

The four field experiments involved measurements of solar radiation, energy and water balances as well as microclimate conditions. Table 3 shows the coordinates, the methods of measurements, size of the plots and irrigation systems.

Table 3. Field energy balance experiments used for modeling actual evapotranspiration in the Low-Middle São Francisco river basin.

Vegetation	Location (latitude, longitude)	Area (ha)	Irrigation system	Method of measurements
Wine grape	9°02′24.53″S; 40°11′13.49″W	4.13	Drip	Bowen ratio
Table grape	9°18′40.84″S; 40°22′29.47″W	5.13	Micro sprinkler	Bowen ratio
Mango	9°22′32.20″S; 40°33′54.23″W	11.92	Micro sprinkler	Eddy covariance
Caatinga	9°03′30.71″S; 40°19′45.21″W	N/A	Not irrigated	Eddy covariance

Table 3. Field energy balance experiments used for modeling actual evapotranspiration in the Low-Middle São Francisco river basin.

Vegetation	Location (latitude, longitude)	Area (ha)	Irrigation system	Method of measurements
Wine grape	9°02′24.53″S; 40°11′13.49″W	4.13	Drip	Bowen ratio
Table grape	9°18′40.84″S; 40°22′29.47″W	5.13	Micro sprinkler	Bowen ratio
Mango	9°22′32.20″S; 40°33′54.23″W	11.92	Micro sprinkler	Eddy covariance
Caatinga	9°03′30.71″S; 40°19′45.21″W	N/A	Not irrigated	Eddy covariance

The measurements covered two growing seasons of irrigated fruit crops—wine grape, table grape, mango orchard and two years with different rainfall conditions in natural vegetation—caatinga.

2.4. Field and Satellite Data

2.4.1. Field Measurements

The weather data were taken from seven automatic agro-meteorological stations shown in black in Figure 4. The geographic positions are described in Table 4. They were equipped with pyranometers, anemometers, net radiometers, sensors for air temperature and relative humidity, rain gauges, and soil heat flux plates. The data were available for every 30 minutes and used for the regional calculation of the radiation balance terms (Figure 1) and ET₀ by FAO Penman-Monteith method [61] allowing the acquirement of daily and annual ET [28,37,48].

Table 4. Agro-meteorological stations used for the regional radiation balance and reference evapotranspiration calculations.

Station	Latitude	Longitude	State
Fruitfort	09°22′22.99″S	40°33′40.47″W	Pernambuco
Vale das Uvas	09°18′50.93″S	40°22′22.98″W	Pernambuco
Bebedouro	09°08′12.35″S	40°18′31.51″W	Pernambuco
Timbaúba	09°12′28.75″S	40°29′05.21″W	Pernambuco
Santa Felicidade	09°20′40.24″S	40°48′59.42″W	Bahia
Brasil Uvas	09°19′26.71″S	40°11′48.67″W	Bahia
Logos Butiá	09°05′01.79″S	39°55′28.78″W	Bahia

Table 4. Agro-meteorological stations used for the regional radiation balance and reference evapotranspiration calculations.

Station	Latitude	Longitude	State
Fruitfort	09°22′22.99″S	40°33′40.47″W	Pernambuco
Vale das Uvas	09°18′50.93″S	40°22′22.98″W	Pernambuco
Bebedouro	09°08′12.35″S	40°18′31.51″W	Pernambuco
Timbaúba	09°12′28.75″S	40°29′05.21″W	Pernambuco
Santa Felicidade	09°20′40.24″S	40°48′59.42″W	Bahia
Brasil Uvas	09°19′26.71″S	40°11′48.67″W	Bahia
Logos Butiá	09°05′01.79″S	39°55′28.78″W	Bahia

The BR method was used to estimate the partition of the net available energy into sensible and latent heat fluxes in vineyards, while in mango orchard and natural vegetation (caatinga) this was done by EC measurements [5,13,14].

In both vineyards (wine grape and table grape), the sensors were installed at the centre of the plots shown in Figure 4 and described in Table 3. The wine grape was trained vertically at a height of 1.6 m with the plants spaced at 1.2 m × 3.5 m, while the table grape was spaced at 3.5 m × 4.0 m with an overhead horizontal trellis system of 1.8 m. The gradients of air temperature and vapor pressure were calculated by wet and dry thermocouples of copper/constantan at 0.5 and 1.5 m above the canopies. The surface albedo (α₀ = R_R/R_G) was measured through incident (R_G) and reflected (R_R) global solar radiation acquired with pyranometers faced up and down (model Eppley, number 19,579, Rhode Island, RI, USA). The net radiation (R_n) was measured over the canopies with two net radiometers (model NR-Lite, Kipp & Zonnen, Delft, the Netherlands). All radiation sensors were placed at 1 m above the canopies. The soil heat flux (G) was obtained with four heat flux plates (HFT3-L, REBS, Radiation and Energy Balance Systems, Seattle, WA and Hukseflux, Delft, the Netherlands) at 2 cm soil depth and 0.5 m from the plants. Wind speed was measured with anemometers (R. M., Young wind Sentry, 03101, MI, USA) at two levels, i.e., 1.0 and 2.0 m above the canopies. Air temperature and relative humidity at 0.5 m from the leaves were obtained with probes from Vaisala (model HMP 35A, Helsinki, Finland) and Sky (SKH 2013, Sky instruments LTD, Llandrindod Wells, UK).

In the vineyards, λE and H were calculated by using the Bowen ratio, as a function of the gradients of air temperature and vapor pressure above the canopies. Missing or erroneous ET data from BR system were filled by using the relation of λE with the available energy (R_n − G) for specific periods of time. As the vineyards are inside large irrigated farms, with several plots with the same crop, the BR method is considered accurate with H representing only 12 and 18% of R_n for table and wine grapes, respectively [5,14].

The EC system (EC) in mango orchard determined H and λE by a three-axis sonic anemometer (Model CSAT3, Campbell Scientific, Logan, UT, USA) and a krypton hygrometer (Model KH20, Campbell Scientific, Logan, UT, USA), respectively. The trees were spaced in a regular square pattern at 10 m × 10 m, with an average height of 5.5 m. The sensors were set at 3 m above the crown of a tree with a sampling frequency of 16 Hz. Corrections to water flux due to density fluctuations introduced by the fluxes of sensible and latent heat flux [79], oxygen absorption [80] and frequency losses [81] were applied. R_n was acquired with one net radiometer (model NR-Lite, Kipp & Zonnen, Delft, the Netherlands) at a height of 2.5 m above the canopy. At this same height the surface albedo was measured with pyranometers faced up and down (model Eppley, number 19579, RI, USA). The soil heat flux (G) was acquired with two heat flux plates (model HFT3-L, REBS, Radiation and Energy Balance Systems, Seattle, WA, USA) at 2 cm soil depth and bellow the projected tree crown at 100 cm from the trunk. Air temperature and relative humidity near the leaves were measured with a probe (SKH 2013, Sky instruments LTD, Llandrindod Wells, UK) installed at the same height of the radiation sensors [13,14].

The EC system over caatinga was installed at 11 m height above the ground. The natural vegetation is a mixture of species with a mean height of 8 m. The system consisted of a sonic anemometer from the same manufacturer as for mango orchard and a gas analyzer (LI7500, LI-COR, Lincoln, NE, USA) with the same sampling frequency, datalogger and corrections as for mango orchard. All components of short and long wave radiation were measured with pyranometers and pyrgeometers facing up and down (Kipp & Zonnen, Delft, the Netherlands) at a height of 10 m from the ground. R_n was acquired with a net radiometer at the same height of the other radiation sensors and G was measured with one flux plate at 2 cm soil depth. Both the net radiometer and the flux plates were from the same manufacturer as for mango orchard. Microclimatic measurements of air temperature and relative humidity were taken above the vegetation with a probe from Vaisala (model HMP 45C-L, Helsinki, Finland) at the same height of the radiation sensors.

The data quality from EC systems, in mango orchard and caatinga, was verified by studying the energy balance closure: fluxes (λE + H) and available energy (R_n − G) were compared at a daily time scale, being 88%, with a RMSE of 1.7 MJ m⁻² d⁻¹, evidenced the good quality of the dataset. The gaps in ET data from the EC systems, mainly during the rainy periods for the krypton data in mango orchard, were filled by the equation resulting from the energy closure. A closure error of 10 to 30% seems to occur frequently with EC—based latent heat flux estimates. A summary paper of 22 flux sites indicated a general lack, with a mean imbalance in the order of 20% [82]. Available energy systematically exceeding measured fluxes have been published [83,84,85]. The lack of energy balance closure can also be associated with measurement errors in R_n and G, but not completely explained by this uncertainty, because EC systems have their own sources of error [83]. Further to systematic biases in the instrumentation, the general hypothesis about this lack can be explained by sampling errors related to different footprints, neglected energy sinks, loss of low and/or high frequency contributions to the turbulent heat flux and advection of scalars [86].

2.4.2. Remote Sensing Measurements

The regional radiation balance calculations were done from Landsat Thematic Mapper (TM) and Enhanced Thematic Mapper (ETM+). The cloud free satellite images used are in Table 5.

Table 5. Landsat satellite data during the period from September 2001 to January 2007 and the experiments used for calibrations and validations.

Date	DOY	Satellite	Field experiments
10 September 2001	253	Landsat 7	Wine grape
04 October 2001	277	Landsat 5	Wine grape
06 July 2003	187	Landsat 5	Table grape, Caatinga
24 September 2003	267	Landsat 5	Table grape, Caatinga
12 October 2004	286	Landsat 5	Mango orchard, Caatinga
14 November 2004	328	Landsat 5	Mango orchard, Caatinga
15 October 2005	288	Landsat 5	Mango orchard, Caatinga
16 November 2005	320	Landsat 5	Mango orchard, Caatinga
30 July 2006	211	Landsat 5	Mango orchard, Caatinga
22 January 2007	022	Landsat 5	Mango orchard, Caatinga

* DOY: Day of the year

Table 5. Landsat satellite data during the period from September 2001 to January 2007 and the experiments used for calibrations and validations.

Date	DOY	Satellite	Field experiments
10 September 2001	253	Landsat 7	Wine grape
04 October 2001	277	Landsat 5	Wine grape
06 July 2003	187	Landsat 5	Table grape, Caatinga
24 September 2003	267	Landsat 5	Table grape, Caatinga
12 October 2004	286	Landsat 5	Mango orchard, Caatinga
14 November 2004	328	Landsat 5	Mango orchard, Caatinga
15 October 2005	288	Landsat 5	Mango orchard, Caatinga
16 November 2005	320	Landsat 5	Mango orchard, Caatinga
30 July 2006	211	Landsat 5	Mango orchard, Caatinga
22 January 2007	022	Landsat 5	Mango orchard, Caatinga

* DOY: Day of the year

The Landsat satellites have a 16-day overpass at around 09:30 hours local time but only a maximum of two images per year were free of clouds. They were used together with the results of field experiments and interpolated weather data from the network of seven agro-meteorological stations (Table 3, Table 4 and Table 5).

Landsat 5 Thematic Mapper (TM) and Landsat 7 Enhanced Thematic Mapper (ETM+) are sun-synchronous, near-polar satellites that provide spectral radiance measurements in narrow bands. The bands 1 to 5 and 7 give data for the visible and near infrared bands. The pixel size for these bands is 30 m by 30 m. The band 6 provides data for long wave (thermal) radiation, with a pixel size of 60 m by 60 m for Landsat 7 and 120 m by 120 m for Landsat 5. Both Landsat satellites have a swath width of 185 km and an orbit of 705 km (about 435 miles) above the earth.

For Landsat 5 and 7 the spectral radiance for each band (L_b) is computed as [78]:

$${\mathrm{L}}_{\mathrm{b}}=\left[\frac{{\mathrm{L}}_{\mathrm{M}\mathrm{A}\mathrm{X}}-{\mathrm{L}}_{\mathrm{M}\mathrm{I}\mathrm{N}}}{\mathrm{Q}\mathrm{C}\mathrm{A}{\mathrm{L}}_{\mathrm{M}\mathrm{A}\mathrm{X}}-\mathrm{Q}\mathrm{C}\mathrm{A}{\mathrm{L}}_{\mathrm{M}\mathrm{I}\mathrm{N}}}\right]\left(\mathrm{D}\mathrm{N}-\mathrm{Q}\mathrm{C}\mathrm{A}{\mathrm{L}}_{\mathrm{M}\mathrm{I}\mathrm{N}}\right)+{\mathrm{L}}_{\mathrm{M}\mathrm{I}\mathrm{N}}$$

(12)

where DN is the digital number of each pixel, L_MAX and L_MIN are calibration constants, QCAL_MAX and QCAL_MIN are the highest and lowest range of values for rescaled radiance in DN. The units for L_b are W m⁻² sr⁻¹ μm⁻¹.

For Landsat 5, QCAL_MAX = 255 and QCAL_MIN = 0. For Landsat 7 with header file data on gains and biases, a simpler equation for L_b is given:

$${\mathrm{L}}_{\mathrm{b}}=\left(\mathrm{G}\mathrm{a}\mathrm{i}\mathrm{n} \mathrm{x} \mathrm{D}\mathrm{N}\right)+\mathrm{B}\mathrm{i}\mathrm{a}\mathrm{s}$$

(13)

where Gain and Bias refer to the values given in the header file.

3. Results and Discussion

3.1. Model Validations

To test the validity of the equations involving the PM1 and PM2 models, field and remote sensing parameterizations were used. They have been applied to all 10 different Landsat images throughout the equations from Table 1 and Figure 1 and Figure 2. The ET results were validated with field measurements from BR and EC systems in the contrasting hydrological ecosystems of irrigated crops and natural vegetation in the Brazilian semi-arid conditions. Figure 5 shows the scatter plots for the daily ET which resulted from the two models. The satellite values were taken from the Landsat pixels where the flux towers were installed, representing an area of 900 m².

Figure 5. Relationships between satellite and field measurements of daily actual evapotranspiration. (a) using the modeled evapotranspiration resistances (PM1). (b) using the modeled ET/ET₀ ratio (PM2).

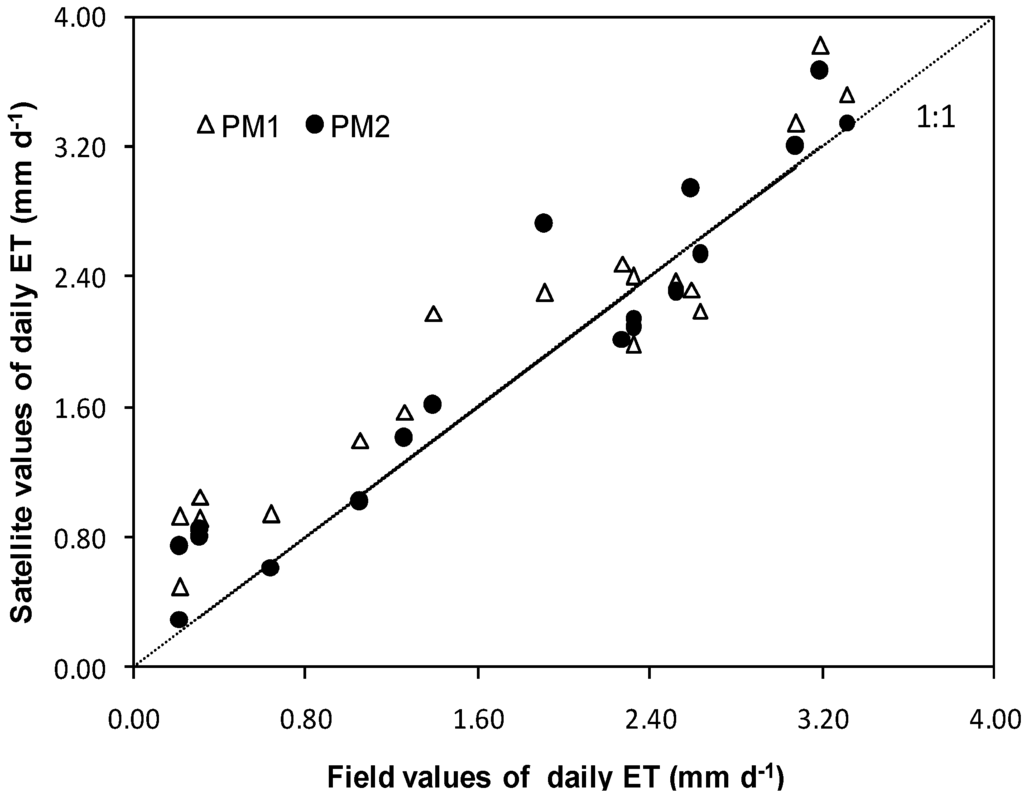
Figure 5. Relationships between satellite and field measurements of daily actual evapotranspiration. (a) using the modeled evapotranspiration resistances (PM1). (b) using the modeled ET/ET₀ ratio (PM2).

The results showed good agreement for both models, but better for PM2 (R² = 0.79 and 0.89 and a root mean square error—RMSE of 0.44 and 0.34 mm d⁻¹, for PM1 and PM2, respectively). While this last model fitted more the line 1:1, explaining 89% of the variance, the PM1 model, explaining 79% of the variance, overestimated the field values for the low ET rates of natural vegetation.

The lower regression coefficient and higher RMSE for the PM1 model can be due to the fact that the weather data from the agro-meteorological stations are not representative of the microclimatic conditions of the caatinga. One can see in Figure 5 that better results of PM1 is for higher values of ET, corresponding to irrigated crops, independently of their microclimate, as the agro-meteorological stations are inside of irrigated areas. Actual projects in the Low-Middle São Francisco river basin foresee the installation of new stations in the region, which will cover more areas inside the natural vegetation.

To verify the influence of instantaneous radiation and energy balance components determination (Figure 1 and Table 1) on the instantaneous values of λE from Equation 4, the scatter plots of these components involved in the processes were constructed (Figure 6).

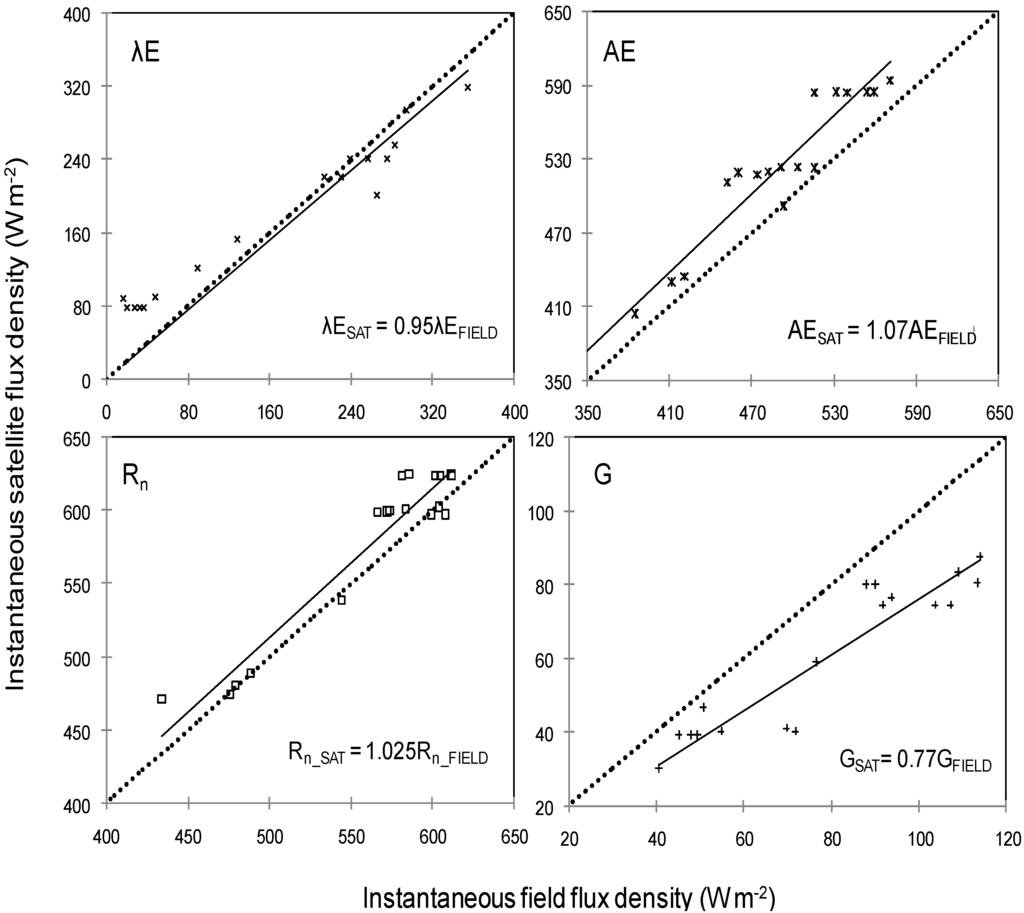
Figure 6. Relationships between instantaneous radiation and energy balance components from satellite (subscript SAT) and from field measurements (subscript FIELD): λE—latent heat flux; AE—Available energy; R_n—net radiation; G—soil heat flux.

Figure 6. Relationships between instantaneous radiation and energy balance components from satellite (subscript SAT) and from field measurements (subscript FIELD): λE—latent heat flux; AE—Available energy; R_n—net radiation; G—soil heat flux.

Reasonable agreement was found for λE, with a coefficient of determination of R² = 0.78, a RMSE of 39.7 W m⁻², and an average deviation of 5%. The differences occurred typically for the lower values because the weather data used in Equation 4 are from agro-meteorological stations inside of irrigated areas. This is confirmed by the good correlation shown in the scatter plot of the available energy (AE), with a R² = 0.91 and a RMSE of 38.6 W m⁻². In general the AE satellite values overestimated the field values a little, which was due to an overestimation in R_n. Despite this overestimation, excellent agreement was found for R_n, with an R² of 0.92 and a RMSE of only 21.8 W m⁻². This overestimation could be related to the low coefficient of determination for ε_a together with an underestimation in α₀ (Table 1). The largest differences from the line 1:1 were found for G, however still with good statistical results (R² = 0.85 and RMSE of 21.7 W m⁻²). The biggest distances were verified for higher values, representative of caatinga where G was measured with just one flux plate.

In the case of PM2, all the calculations for obtaining R_n and G are not necessary (Table 1 and Figure 1). The ratio ET/ET₀ is directly modeled with only three remote sensing parameters, which are related to vegetation. In addition, there is a small difference between the instantaneous and daily values of ET/ET₀ (Figure 3d). The interpolated values of ET₀ by a Geographic Information System (GIS) yield a better characterization of the spatial climatic variation and, in case of the satellite without thermal bands, one can incorporate grids of T_a instead of images of T₀ in applying the equation for ET/ET₀ estimation from Table 1, with different regression coefficients, even with lower accuracy. Although T_a being affected by each surface, the inclusion of α₀ and NDVI can reduce the errors, because these last remote sensing parameters are characteristics of the different kind of vegetation and moisture status. When T_a was used instead T₀ in the relation for ET/ET₀ in Table 1 the coefficients became a = 2.3 and b = −0.011 with a R² of 0.82. These last statistical results showed the suitability for using grids of T_a in the case of a satellite with high spatial resolution but without a thermal band. The possibility of using interpolated weather data, including T_a, together with remotely vegetative indexes available from MODIS images, has been demonstrated for ET regionalization in Australia [23].

Another advantage of the PM2 model is that it can be applied without the need to identify the extreme conditions, being also suitable for the rainy periods. The local calibrated SEBAL algorithm was tested in the Low-Middle São Francisco river basin [27] with good agreement between field and Landsat measurements of daily ET (R² of 0.91 and RMSE of 0.38 mm d⁻¹). However, to consider the necessary extreme conditions, EC towers were used for flux measurements in hydrological contrasting surfaces in the study region, to not consider ET null during the rainy season. The disadvantage is that EC systems are costly and operationally difficult, as compared with the parameterizations of the PM2 model, which needs only three satellite parameters and permanent agro-meteorological stations, which would also be useful for other important crop management applications such as ET-based irrigation scheduling.

Considering the better performance and simplicity of PM2, it was chosen and tested whether it is sufficiently robust and accurate for the task of ET determination at different spatial scales in the Low-Middle São Francisco river basin. In addition, the relation for r_s depicted in Table 1 and Figure 3a was used for the classification of irrigated areas and natural vegetation. Furthermore both parameters r_s and ET/ET₀ can be useful to infer soil water conditions. Because of the reasons explained for using the modeled ratio ET/ET₀ together with grids of daily ET₀, it was concluded that this approach has considerable potential for estimating ET at different time and spatial scales in hydrological basins with the availability of agro-meteorological stations. The challenges faced to make the model applicable in other river basins are the implementation of a net of agro-meteorological stations to combine weather data with satellites measurements at different spatial and temporal resolutions and to test the algorithm over a more diverse range of ecosystems.

3.2. Land Use Change

Even with PM1 model not being chosen for ET calculations, the equation for r_s shown in Table 1 and in Figure 3a was applied to infer the soil moisture conditions for a simplified vegetation classification. The satellite images of the study region were layered with the shapes of the main fruit growing regions in the Pernambuco (Petrolina, Lagoa Grande and Santa Maria da Boa Vista) and Bahia (Juazeiro and Casa Nova) states, involved by the net of agro-meteorological stations to identify the main direction of the quick land use change, highlighting the best possibility for the irrigation expansion.

Figure 7 shows the satellite overpass images of r_s representative for the dry (Figure 7a) and for the rainy (Figure 7b) periods in the semi-arid region comprised of the net of agro-meteorological stations.

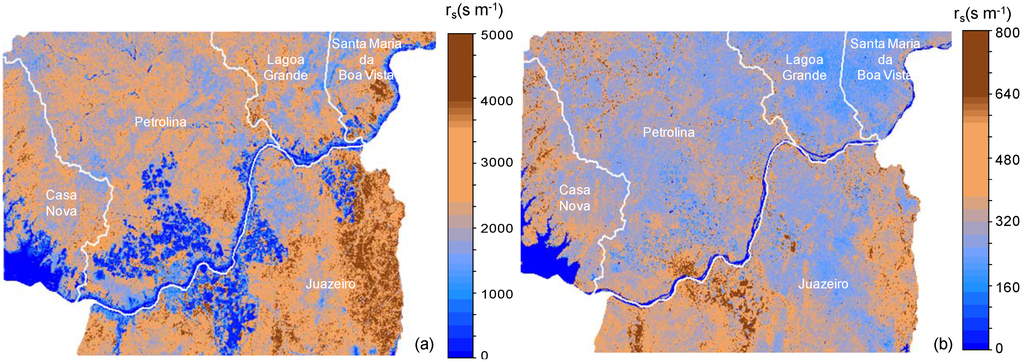
Figure 7. Images of the satellite overpass surface resistance for the region comprised of the net of agro-meteorological stations in the Low-Middle São Francisco river basin. (a) October 2005. (b) January 2007.

Figure 7. Images of the satellite overpass surface resistance for the region comprised of the net of agro-meteorological stations in the Low-Middle São Francisco river basin. (a) October 2005. (b) January 2007.

One can see that during the first period, the irrigated crops with much lower values than those for natural vegetation are strongly highlighted by the blue areas. In general, caatinga shows r_s values higher than 800 s m⁻¹ during this dry period of the year. Inside the wet period there is more homogeneity in the whole area and both, irrigated and not irrigated vegetated areas, present values lower than 800 s m⁻¹. The relation of r_s with soil moisture shows the suitability of estimating this last important water variable in semi-arid regions which involve a mixture of ecosystems. According to the location of the field experiments shown in Figure 4, the maximum values are for caatinga (average of 1,937 s m⁻¹). Wine grape and mango orchard present similar values around 130 s m⁻¹, while table grapes present the lowest ones, averaging 74 s m⁻¹ [14].

Considering that the quick land use change by the replacement of natural vegetation with irrigated crops can cause environmental problems, it becomes very important to make a historical picture at the growing regions level about this replacement. Figure 8 presents the evolution of the irrigated areas during the period from 2002 to 2006 for the growing regions involved in the net of agro-meteorological stations, by using the classified satellite data. The total irrigated areas were calculated by summing the number of pixels with r_s values lower than 800 s m⁻¹ and multiplying this number by the area of each pixel. Images of 2001 and 2003 were interpolated to give the situation for 2002 and the image of 2006 gave the situation for this year (Table 4).

Although Petrolina-PE and Juazeiro-BA present the biggest irrigated areas, the increments throughout the years (2002–2006) are lower (213 and 171%) than those for Santa Maria-PE (275%) and for Lagoa Grande-PE (260%). The municipality of Casa Nova-BA showed an intermediary value of 198% being the best option for irrigation expansion.

Figure 8. Evolution of irrigated growing areas comprised of the net of agro-meteorological stations, in the Low-Middle São Francisco river basin.

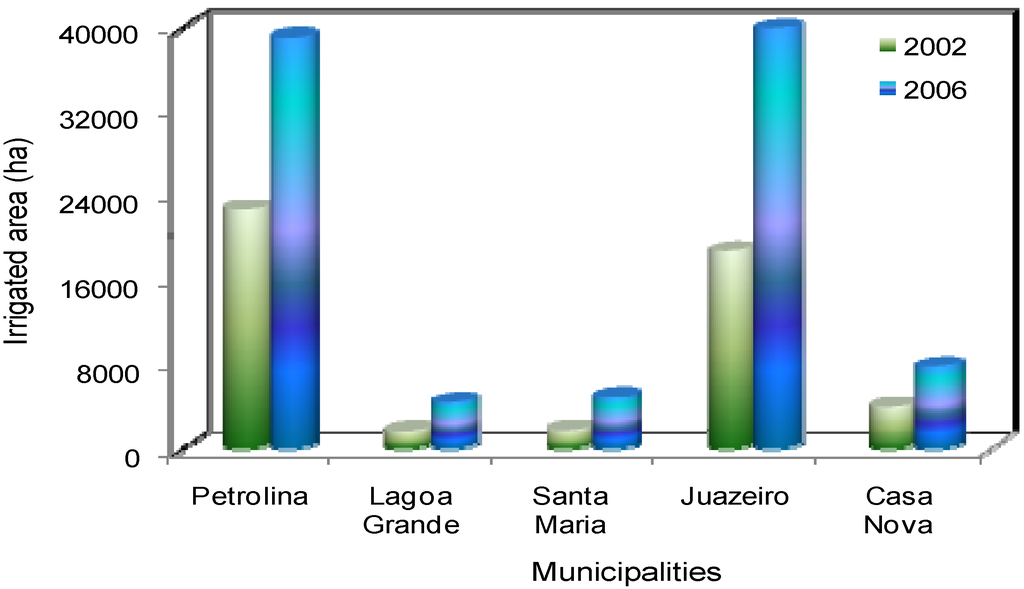
Figure 8. Evolution of irrigated growing areas comprised of the net of agro-meteorological stations, in the Low-Middle São Francisco river basin.

The most important commercially irrigated crops in the semi-arid region of Brazil are vineyards and mango orchards, being the main responsible vegetation for the quick land use change, growing mainly in Petrolina-PE and Juazeiro-BA. Figure 9a shows the evolution of the areas with the first crop, while Figure 9b depicts the increment for the second crop in the growing regions of Petrolina-PE and Juazeiro-BA based on the data from Brazilian Institute for Geography and Statistics (IBGE).

Figure 9. Evolution of cultivated areas with vineyards and mango orchards for the centers of development Petrolina-PE/Juazeiro-BA in the Low-Middle São Francisco river basin.

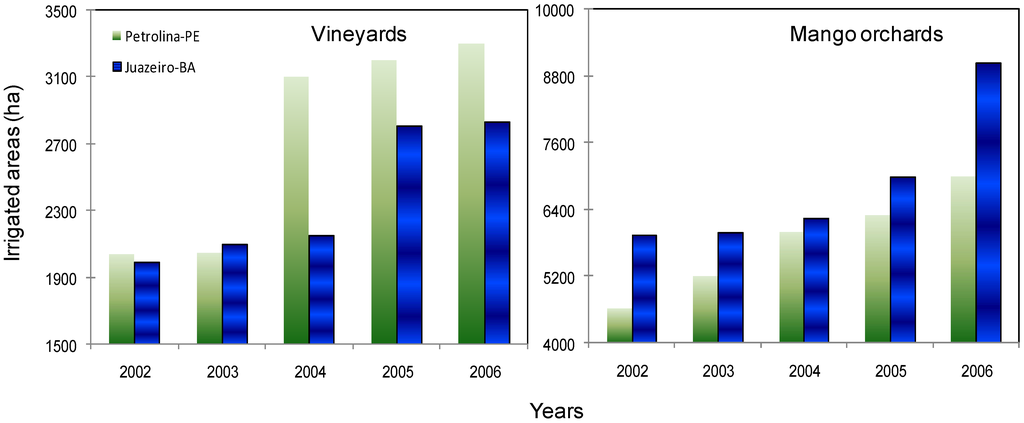
Figure 9. Evolution of cultivated areas with vineyards and mango orchards for the centers of development Petrolina-PE/Juazeiro-BA in the Low-Middle São Francisco river basin.

In the case of Petrolina-PE, the larger increase is for vineyards, while in Juazeiro-BA the biggest area is for mango orchards. The highest increment for the first crop was verified between 2003 and 2004 in Petrolina-PE, when the cultivated area increased 151%. In the case of mango orchards the most significant period was from 2005 to 2006 in Juazeiro-BA (129%). The agricultural water usage in both growing regions is highly productive. These cities have increased in terms of exports, and are good examples of converting marginal savannah land into a booming rural development; however the irrigation management requires full attention to tools for analysis of the regional ET for planning the expansion of irrigated areas.

3.3. Regional Evapotranspiration

As PM2 model uses the ratio ET/ET₀, the values of this ratio were also investigated for the same periods of the year as for r_s (Figure 10).

Figure 10. Images of the satellite overpass ET/ET₀ for the region comprised of the net of agro-meteorological stations in the Low-Middle São Francisco river basin. (a) October 2005. (b) January 2007.

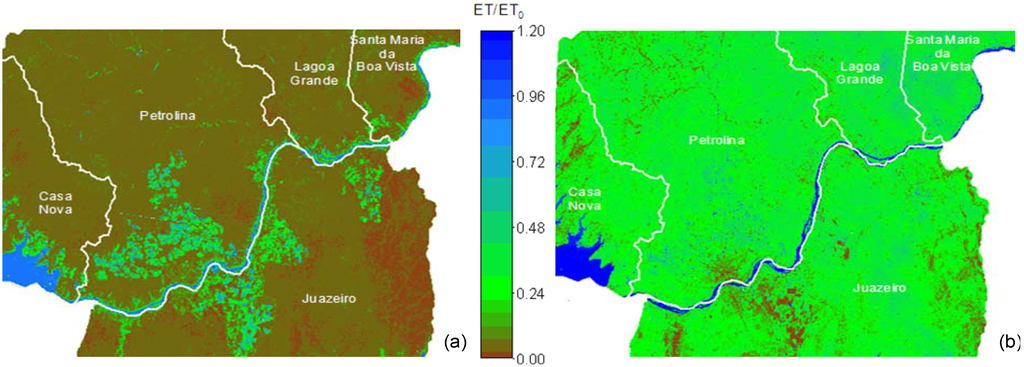
Figure 10. Images of the satellite overpass ET/ET₀ for the region comprised of the net of agro-meteorological stations in the Low-Middle São Francisco river basin. (a) October 2005. (b) January 2007.

The same effects of the soil moisture conditions are evidenced as in the case of r_s. During the dry conditions (Figure 10a), the ET/ET₀ values for irrigated crops are near 1.00 because the water supply reduces the heat losses to the atmosphere while for caatinga this ratio ranges from 0.00 to 0.20, as it converts the biggest part of the available energy into H during this period of the year. Inside the wet season (Figure 10b), the moisture conditions are more homogeneous, making the values for caatinga in some cases around 0.50, similar to those for irrigated crops. During this season, a higher portion of the available energy in natural vegetation is converted into λE and, in most commercial farms, the irrigation is stopped while the rainfall keeps the soil uniformly wet for all ecosystems. For complete growing seasons, crops with micro sprinkler system in general present mean values of ET/ET₀ around 0.90, while for drip irrigated systems they are around 0.75–0.80. Considering the period of the year, involving different soil moisture conditions, the average value for caatinga is 0.30 [78].

The variation of the modeled ET/ET₀ ratio with these extreme seasonal moisture conditions and the similarity with field values is encouraging to simulate timing and magnitude of ET, capturing the strong contrast between the four sites depicted in Figure 4. The ratio can also be a good option as an input parameter for the soil moisture estimations at the regional scale, similar to the EF reported in the international literature. Values of EF for irrigated cotton and perennial vegetation (vineyards and orchards) were found varying from 0.40, when the crops started to be irrigated, to 0.70–0.90 during the irrigation season in the Gediz basin (Turkey) [87]. A grazing steppe in central Mongolia presented seasonal values of EF following the variation in leaf areas and rainfall events during the dry-wet cycles [88]. For a tropical watershed in the Kenyan Rift Valley with natural meadows, the values of EF were 0.70 during the wet season and 0.10 during the dry season [89]. The behavior of ET/ET₀ for irrigated crops and natural vegetation in different soil moisture conditions of the actual study was thus similar to the behavior of EF reported in the literature.

The daily values of ET involving different periods of the year (before, just after, and during the rainy season) in the study region are presented in Figure 11.

Figure 11. Daily actual evapotranspiration (ET) for the region comprised of the net of agro-meteorological stations in the Low-Middle São Francisco river basin. (a) wet season in January 2007. (b) end of the rainy season in July of 2006. (c) dry season in October 2005.

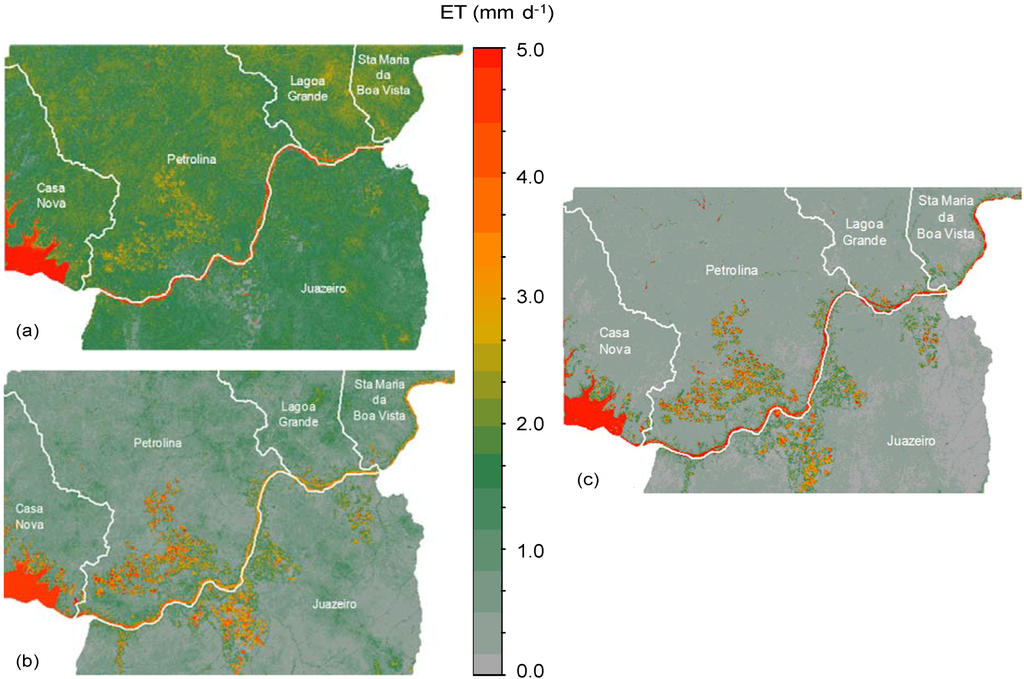
Figure 11. Daily actual evapotranspiration (ET) for the region comprised of the net of agro-meteorological stations in the Low-Middle São Francisco river basin. (a) wet season in January 2007. (b) end of the rainy season in July of 2006. (c) dry season in October 2005.

During the rainy period (Figure 11a), a large area comprised of the net of agro-meteorological stations presents similar values of ET, with the exception of water bodies. Intermediate values in natural vegetation occur just after the rainy season (Figure 11b), because antecedent precipitation during January to April provides sufficient water storage in the caatinga root zone still keeping the bushes wet and green, despite the quick rise of the atmospheric demand in the second half of the year. As a consequence of the higher portions of the available energy converted into H, during the driest period of the year (Figure 11c), the natural vegetation presents low values of ET, while the irrigated fields show the highest ones. In general, irrigation intervals are short (daily irrigation), and the water supply is uniform, reducing the heat losses to the atmosphere. According to Figure 11, the effect of the soil moisture in the magnitude of the ET rates is strong. Pixels with values lower than 1.0 mm d⁻¹ occur during the dry season representing the caatinga species. Values from 1.0 to 5.0 mm d⁻¹ under the driest conditions of the year coincide with irrigated crops, being the highest values for table grapes [78].

The ET/ET₀ maps for the dry period of 2005 (October) and for the wet period of 2007 (January) were calibrated with field data of irrigated mango orchard and caatinga for the same DOY of 2006 to be used together with the image of July of this last year (Table 5). The average ET/ET₀ values from these three images, representative of different soil moisture conditions were multiplied by the grid of the total ET₀ of 2006 giving the map of the annual ET (Figure 12).

Figure 12. Total annual actual evapotranspiration for 2006 for the region comprised of the net of agro-meteorological stations in the Low-Middle São Francisco river basin.

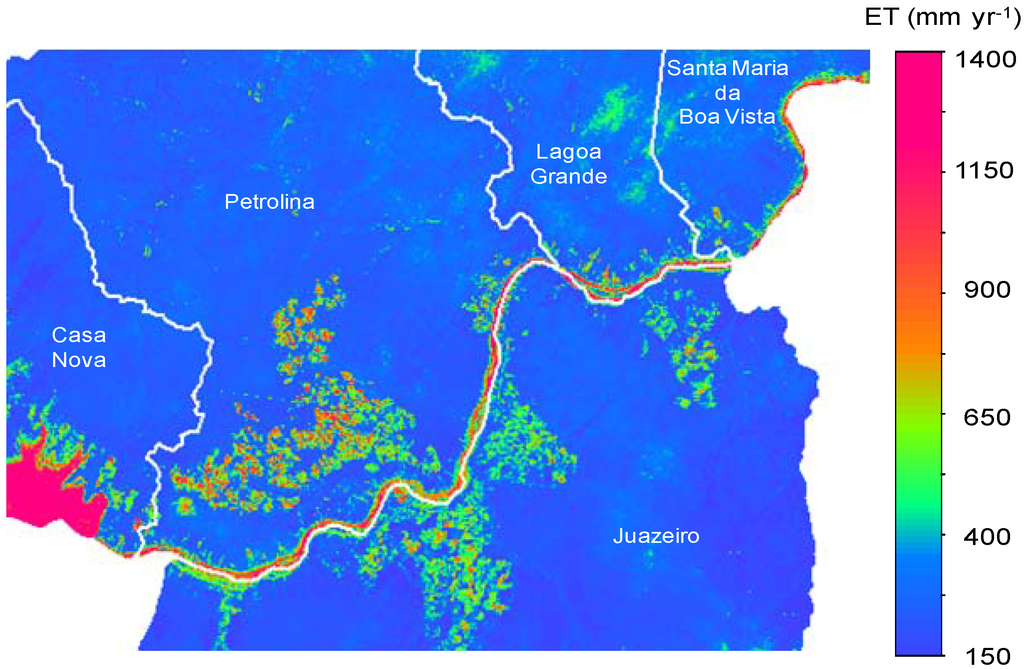
Figure 12. Total annual actual evapotranspiration for 2006 for the region comprised of the net of agro-meteorological stations in the Low-Middle São Francisco river basin.

According to the location of the field experiments depicted in Figure 4, the highest accumulated regional ET values in 2006 (Figure 12) are for mango orchards, being around 500–1,300 mm yr⁻¹. Vineyards presented lower values, ranging from 450 to 800 mm yr^-1, while in caatinga they were between 200 and 400 mm yr⁻¹. Considering that mango orchards are cultivated during the whole year and the cultivation of table grapes are restricted to the dry seasons, it can be concluded that irrigated mango orchards and vineyards consumed more water per area than caatinga by factors of 3 and 2, respectively.

The classification of the Landsat images into irrigated areas and natural vegetation based on the r_s values of Figure 7a allowed highlighting the incremental ET due to irrigation, in each growing region involved in the net of agro-meteorological stations. Summary statistics of land use and the regional ET for 2006 are shown in Table 6.

Table 6. Total (A_T), irrigated (A_I) and not irrigated (AN_I) areas together with the annual actual evapotranspiration (ET) for irrigated crops (I) and natural vegetation (NV) in the growing regions comprised of the net of agro-meteorological stations in 2006.

Growing regions	AT (ha)	AI (ha)	ANI (ha)	ETI (km3 yr−1)	ETNV (km3 yr−1)
Petrolina-PE	455,854	39,094	416,770	0.23	1.07
Lagoa Grande-PE	185,219	4,363	180,856	0.02	0.54
Santa Maria da Boa Vista-PE	297,780	4,793	292,987	0.03	0.88
Juazeiro-BA	638,962	39,906	599,056	0.18	1.37
Casa Nova-BA	965,751	7,831	965,751	0.04	2.30

Table 6. Total (A_T), irrigated (A_I) and not irrigated (AN_I) areas together with the annual actual evapotranspiration (ET) for irrigated crops (I) and natural vegetation (NV) in the growing regions comprised of the net of agro-meteorological stations in 2006.

Growing regions	AT (ha)	AI (ha)	ANI (ha)	ETI (km3 yr−1)	ETNV (km3 yr−1)
Petrolina-PE	455,854	39,094	416,770	0.23	1.07
Lagoa Grande-PE	185,219	4,363	180,856	0.02	0.54
Santa Maria da Boa Vista-PE	297,780	4,793	292,987	0.03	0.88
Juazeiro-BA	638,962	39,906	599,056	0.18	1.37
Casa Nova-BA	965,751	7,831	965,751	0.04	2.30

Petrolina and Juazeiro, in Pernambuco (PE) and Bahia (BA) states, respectively, are highlighted with the biggest irrigated areas. Even with the first growing region presenting a smaller value than that for the second, higher ET rates are verified which could be due to more irrigation water excess conditions in conjunction with greater evaporative demand. The growing region of Casa Nova-BA has the biggest area, with natural vegetation presenting the highest ET rates for this kind of vegetation, which is an indication of the best option for irrigation expansion in the Low-Middle São Francisco river basin, once adopting rational criteria for water resource management.

As the main irrigated crops for all the growing regions in the Low-Middle São Francisco river basin are vineyards and mango orchards, another summary of statistics for 2006 involving the growing regions are given in Table 7. The daily ET rates for grapes (GR) were taken from [5], while for mangoes (MG) these rates were from [13].

Table 7. Area of the main irrigated crops and annual actual evapotranspiration in the growing regions comprised of the net of agro-meteorological stations in 2006.

Growing regions	AGR (ha)	AMG (ha)	ETGR (m3 yr−1)	ETMG (m3 yr−1)
Petrolina-PE	3,300	7,000	4,697,550	4,336,200
Lagoa Grande- PE	760	140	1,081,860	998,640
Santa Maria da Boa Vista-PE	620	600	882,570	814,680
Juazeiro-BA	2,830	9,043	4,028,505	3,718,620
Casa Nova-BA	350	1,825	498,225	459,900

Table 7. Area of the main irrigated crops and annual actual evapotranspiration in the growing regions comprised of the net of agro-meteorological stations in 2006.

Growing regions	AGR (ha)	AMG (ha)	ETGR (m3 yr−1)	ETMG (m3 yr−1)
Petrolina-PE	3,300	7,000	4,697,550	4,336,200
Lagoa Grande- PE	760	140	1,081,860	998,640
Santa Maria da Boa Vista-PE	620	600	882,570	814,680
Juazeiro-BA	2,830	9,043	4,028,505	3,718,620
Casa Nova-BA	350	1,825	498,225	459,900

Even though mangoes represent a bigger cropped area than for grapes, considering all growing regions comprised of the agro-meteorological stations and a continuous cultivation throughout the year for both crops, the annual mango orchards water consumption is a little lower than for vineyards. These cropped areas represent 19.4 and 8.2% of the total irrigated area, respectively, resulting in a total evaporative depletion of 0.22 km³ yr⁻¹. The incremental ET from irrigated crops in the Low Middle São Francisco river basin was reported as being 2.2 mm d⁻¹ on average [78]. Considering all growing regions from Table 6 and Table 7, the additional volume of water used was around 0.77 mm yr⁻¹ in 2006. The latter volume represents the net depletion, the difference between diversion and return flow that is truly consumed and no longer available for downstream urban and environmental users.

Although the modeled seasonal and spatial patterns of ET are generally reasonable and consistent, for transferring the PM2 model to another Brazilian basin, probably local calibrations and validations are necessary for the coefficients of the equations relating ET/ET₀ with remote sensing parameters (Table 1). Further testing of the algorithm in different areas and climatic conditions with a net of agro-meteorological stations and satellite images, is important for making the model applicable in the São Francisco centers of development.

4. Conclusions

Field radiation and energy balances in natural vegetation and irrigated crops, together with agro-meteorological stations and Landsat images, were used to develop and validate two models based on the Penman-Monteith equation for regional evapotranspiration acquirement in the Low-Middle São Francisco river basin, Brazil. The images covered a period from 2001 to 2007. The first model (PM1) was based on the resistances to evapotranspiration, while the second uses the estimated ratio of the actual to the reference evapotranspiration (PM2). The PM1 model presented a regression coefficient of 0.79 and a root mean square error of 0.44 mm d⁻¹, whereas for the best results of the PM2 model, the correspondent values were 0.89 and 0.34 mm d⁻¹. The second model fitted more the line 1:1, explaining 89% of the variance and the first model explained 79% of the variance. The lower performance of PM1 model could be due to the fact that the weather data from the agro-meteorological stations are not representative of the dry microclimatic conditions of the natural vegetation.

Even with the PM1 model not being chosen for ET calculations, the equation for surface resistance was applied to infer the soil moisture conditions for a simplified vegetation classification. The maximum values of surface resistance were for natural vegetation—caatinga (average of 1,937 s m⁻¹). Wine grape and mango orchard presented similar values around 130 s m⁻¹, while table grape presented the lowest ones, averaging 74 s m⁻¹. Petrolina and Juazeiro, in Pernambuco (PE) and Bahia (BA) states, respectively, were highlighted with the biggest irrigated areas.

The most important commercially irrigated crops in the semi-arid region of Brazil are vineyards and mango orchards, being the main responsible vegetation for the quick land use change, growing mainly in Petrolina-PE and Juazeiro-BA. In the case of Petrolina-PE, the larger increase is for vineyards, while in Juazeiro-BA the biggest area is for mango orchards. The highest increment for the first crop was verified between 2003 and 2004 in Petrolina-PE, when the cultivated area increased 151%. In the case of mango orchards the most significant period was from 2005 to 2006 in Juazeiro-BA (129%).

After having been identified as the best performance, the PM2 model was used to analyze the evapotranspiration from irrigated crops and natural vegetation. Considering the daily rates of the regional evapotranspiration, pixels with values lower than 1.0 mm d⁻¹ occurred outside the rainy season, representing the caatinga species. Values from 1.0 to 5.0 mm d^-1 during the driest conditions of the year coincided with irrigated crops, being the highest values for table grapes. The highest accumulated ET values during 2006 were for mango orchards, being around 500–1,300 mm yr⁻¹. Vineyards presented lower values, ranging from 450–800 mm yr⁻¹, while in the natural vegetation (caatinga) they were between 200 and 400 mm yr⁻¹. It could be concluded that irrigated mango orchards and vineyards consumed more water than caatinga by factors of 3 and 2, respectively.

Petrolina and Juazeiro in the semi-arid regions of Pernambuco and Bahia states presented the highest evapotranspiration rates, mainly as a consequence of land use change with the replacement of natural vegetation by vineyards and mango orchards. Analyzing land use together with the regional evapotranspiration for 2006 the regional evapotranspiration rates for these growing regions were 0.23 and 0.18 km³ yr⁻¹. Although the first growing region presented higher rates than the second, the irrigated area was lower: this could be a combined effect of irrigation water excess together with greater evaporative demand. The mango orchards and vineyard areas, representing 19.4 and 8.2% of the total irrigated area respectively, resulted in a total evaporative depletion of 0.22 km³ yr⁻¹ in the growing region covered by the agro-meteorological stations.

The separation of irrigated crops was possible by a simplified classification with logical functions applied to the surface resistance values. The incremental ET in the Low Middle São Francisco river basin was reported as being 2.2 mm d⁻¹ on average [78]. Considering all growing regions analyzed, the additional volume of water used was around 0.77 mm yr⁻¹ in 2006. The latter volume represents the net depletion, the difference between diversion and return flow that is truly consumed and no longer available for downstream urban and environmental users.

The results were rather encouraging given the complex mixture of the ecosystems in the semi-arid conditions, considering that only maps of NDVI, surface albedo and surface temperature together with interpolated data of reference evapotranspiration are necessary, without the need of crop classification, which is not straightforward in fruit crops. However, if the satellite does not have a thermal band, there is also the possibility of using grids of air temperature together with remote sensing parameters instead of surface temperature obtained from satellite measurements.

The actual condition of the evolution of the irrigated areas over the natural vegetation is an indication of the importance of having efficient tools for rational water resources management as water conflicts are imminent. With the use of remote sensing together with a net of agro-meteorological stations, one can make an historical evaluation of the evapotranspiration at the regional scale in the semi-arid areas of Brazil. The tools tested and presented here can be operationally tested and implemented to monitor the increase of irrigated agriculture, subsidizing ways to avoid environmental damage in hydrological basins with increasing land use change.