Geostationary Orbital Targets Imaging Based on Ground-Based Multiple-Input Multiple-Output Radar

Highlights

What are the main findings?

• A three-dimensional imaging method for geostationary orbit (GEO) targets is proposed based on ground-based radar, which synthesizes a large equivalent aperture on the Earth’s surface via sequential transmitting and simultaneously receiving MIMO radar.
• A Three-Dimensional Target-Oriented (TDTO) coordinate system is established to obtain a front-view, three-dimensional image of the GEO target, with its origin at the Earth’s center and its X-axis pointing towards the target.

What are the implications of the main findings?

• The proposed method overcomes the problem that there is no relative motion between ground-based radars and targets in geosynchronous orbits, which causes imaging failure, and obtains a three-dimensional image of the target.
• The established TDTO coordinate system can obtain a front-view, three-dimensional image of the target.

Abstract

Compared with the Earth’s surface, geostationary orbital (GEO) targets are relatively static, which makes it difficult to obtain two-dimensional radar images when the radar is ground-based without movement. This paper proposes an imaging method for GEO targets based on ground-based Multiple-Input Multiple-Output (MIMO) radar. It combines multiple ground-based radars distributed across the Earth’s surface to image GEO targets. When the virtual aperture of the MIMO radar is planar, three-dimensional imaging results can be obtained. First, the ground-based MIMO radar imaging scenario for GEO targets is introduced, and an analysis of the azimuth resolution is performed. Subsequently, a Three-Dimensional Target-Oriented (TDTO) coordinate system is established. The back-projection (BP) algorithm is then employed to reconstruct the target image. Finally, simulations are conducted and analyzed, including cases of a single-point target, multiple scatterers of a satellite model, and full-wave radar echo simulation using CST. The results show that when the center frequency is 35 GHz, and the baseline length is 1500 km, azimuth resolution of the imaging is better than 0.1 m.

1. Introduction

A geostationary Earth orbit (GEO) is a type of geosynchronous orbit with an orbital inclination of 0 degrees, characterized by a stationary sub-satellite point such that its ground track is a single point. GEO orbital targets are situated approximately 35,768 km above the Earth’s equator, synchronized with the Earth’s rotation. This configuration results in a stationary position relative to the Earth, enabling continuous coverage over a vast area. Due to their high application value, GEO targets are extensively utilized across military, civilian, and commercial domains, garnering significant strategic interest worldwide [1,2]. If high-resolution imaging of GEO targets can be acquired, information such as the satellite structure, the equipment carrier type and size, etc., can then be obtained, and further analysis of its frequency, imaging ability, and undertaken tasks can be implemented.

Compared to optical imaging, radar imaging has the advantage of imaging capability in all-weather conditions and at all times of the day. In radar imaging, high range resolution is typically achieved through the pulse compression of wideband signals, while cross-range resolution is obtained via the aperture formed by the antenna. Imaging radar can be further categorized into Synthetic Aperture Radar (SAR) [3,4] and Inverse Synthetic Aperture Radar (ISAR) [1,5,6,7]. SAR primarily relies on the motion of the radar platform to form a synthetic aperture, whereas ISAR mainly utilizes the motion of the target. Additionally, radars can be classified based on the deployment platform, primarily into ground-based and space-based radars [8]. Due to the constraint of the radar power–aperture product, the signal-to-noise ratio in space-based ISAR imaging systems is relatively low, leading to poor imaging quality. Ground-based radar systems are capable of detecting space targets and performing ISAR imaging with relative motion. A two-dimensional ISAR image represents the projection of the target onto the range-Doppler imaging plane. Consequently, when the imaging plane changes significantly, the two-dimensional ISAR images of the same target can vary considerably. In contrast, three-dimensional (3D) ISAR imaging can extract more comprehensive information such as the spatial structure, size, shape, and motion posture of the target. Based on different imaging principles, 3D ISAR imaging methods can primarily be categorized into two categories: one combines ISAR imaging techniques with interferometric techniques [9], and the other is based on time sequences of one-dimensional range profiles or two-dimensional ISAR images [10].

On the other hand, the Ground-Based Synthetic Aperture Radar (GB-SAR) is a SAR system deployed on the Earth’s surface. GB-SAR offers unique advantages such as high precision, continuity, and capability for long-term monitoring [11,12,13,14,15], making it a core tool in fields like landslide detection, slope stability monitoring, mining area subsidence, and the deformation monitoring of large-scale structures. Reference [2] first proposed the use of GB-SAR for imaging space targets and analyzed the influence of the imaging aperture on parameters such as azimuth resolution. However, since the observed target is located far from the GEO, a relatively large power-to-aperture product is usually required for observation. Radars meeting this requirement are often too bulky and difficult to move, making it challenging to form a synthetic aperture in practice.

Multiple-Input Multiple-Output (MIMO) radar can form a virtual aperture through different combinations of transmitting and receiving antennas, enabling the imaging of observed targets without requiring physical movement of the antenna array [16,17,18]. Currently, operational radars exist that can detect GEO targets. If multiple such systems were coherently combined to synthesize a very large virtual aperture, this distributed network would gain the capability to generate images of GEO targets.

Frequency division multiplexing (FDM) and time division multiplexing (TDM) are two modes of the MIMO radar. In the FDM mode, all transmitting antennas emit signals simultaneously, but each antenna’s carrier frequency is offset by a small amount, making the signals orthogonal in the frequency domain [19]. Its advantages include a high data rate, high unambiguous velocity, and efficient utilization of time resources. The drawbacks, however, lie in the complexity of waveform design and processing, high hardware requirements, and the difficulty of direct adaptation based on existing hardware. In TDM mode, multiple transmitting antennas operate sequentially in different time slots [20]. At any given moment, only one transmitting antenna is active, and all receiving antennas capture echoes solely from that specific transmitter. Since the signals are separated in time, they are inherently orthogonal. The TDM mode offers several advantages: it avoids complex waveform design, enjoys low hardware complexity, and can be implemented by upgrading existing hardware with synchronization commands for time, phase, and spatial alignment.

For relatively stationary targets like those in the GEO, the target can be considered motionless during a short time period. The TDM mode can meet the time resolution requirements. Therefore, to maximize the utilization of the power and frequency resources of each radar, the sequential transmitting and simultaneously receiving MIMO mode is a reasonable choice.

Similarly to Synthetic Aperture Radar (SAR) imaging algorithms, MIMO radar imaging algorithms can also be classified into frequency-domain techniques and time-domain techniques. Xiaodong Zhuge first applied the three-dimensional Range Migration Algorithm (RMA) to near-field MIMO radar imaging. By combining the transmitting wave vector and receiving wave vector, a complete target spatial spectrum was obtained, achieving high-quality imaging results [21]. However, the topology of the MIMO radar must satisfy specific conditions for the RMA to be used effectively in imaging [18,22].

The back-projection (BP) imaging algorithm utilizes the delay-and-sum principle to achieve the focusing process. It is adaptable to arbitrary array topologies, easily extendable to three dimensions, and its application is not limited by near-field or far-field conditions, leading to its widespread use in near-field MIMO radar imaging. Frank Gumbmann combined the MIMO array design with digital beamforming technology [23], investigating the application of millimeter-wave 3D imaging in Non-Destructive Testing. Xiaodong Zhuge designed an ultra-wideband 3D imaging system based on MIMO-SAR for concealed weapon detection [24]. By integrating the characteristics of ultra-wideband signals with sparse array design techniques, this approach can reduce the number of array elements while suppressing grating lobe levels. The pixel-by-pixel coherent processing in BP imaging incurs a substantial computational burden. This high computational cost hinders its application in scenarios requiring high real-time performance.

Currently, some fast BP algorithms, such as Fast Back-Projection (FBP) and Fast Factorized Back-Projection (FFBP) [25], are attracting increasing attention from researchers. To suppress grating and sidelobes in back-projection imaging, several aperture-domain suppression algorithms have been proposed, such as the Coherence Factor (CF) [26,27], Phase Coherence Factor (PCF), and aperture cross-correlation, which have proven to be effective in suppressing these undesired components. CF is defined as the ratio of the coherent power sum to the non-coherent power sum in the aperture domain data. At the main lobe, the amplitudes of the coherent and non-coherent sums are similar, so the CF value is close to 1; whereas grating/sidelobes have a lower coherence, making the coherent power sum less than the non-coherent power sum, thus resulting in CF values less than 1. The basic idea of the PCF algorithm is that the phase distribution in the aperture domain data is consistent at the main lobe but relatively disordered at the grating/sidelobes.

This paper proposes a novel ground-based distributed MIMO radar imaging paradigm to overcome the challenge that conventional radar cannot image stationary GEO targets due to the lack of relative motion. Specifically, a “sequential transmission, simultaneous reception” operational mode is adopted to achieve high-resolution, three-dimensional imaging through global networking.

The core contributions of this work are as follows: 1. Scenario Definition and Modeling: This study is the first to systematically define the “ground-based distributed MIMO radar GEO imaging” scenario. Based on the constraints imposed by the Earth’s curvature, the observable range is derived, quantifying the theoretical performance bounds of the system. 2. Imaging Framework Construction: A dedicated Three-Dimensional Target-Oriented (TDTO) coordinate system is established to uniformly describe the geometric relationships among globally distributed radars, the target, and the Earth. Combined with the back-projection (BP) algorithm, a complete processing chain is formed. 3. Feasibility Verification: Through systematic experiments ranging from point targets to full-wave satellite simulations, this work provides numerical validation of the theoretical feasibility of achieving 0.1 m resolution three-dimensional imaging.

The remainder of this paper is organized as follows: Section 2 introduces the ground-based MIMO radar imaging scenario for GEO targets and then analyzes the azimuth resolution. Section 3 establishes a Three-Dimensional Target-Oriented coordinate system for the ground-based radar imaging of GEO targets, and the BP imaging algorithm is used to image the target. Section 4 presents the simulation results and analysis, including point targets and satellite models. Beyond validating the ideal imaging performance, this section further investigates the influence of key system parameters (e.g., baseline length and element spacing) on imaging quality and evaluates the system’s sensitivity to practical non-idealities such as synchronization errors and ionospheric effects. Finally, Section 5 concludes this paper.

2. Azimuth Resolution of GEO Targets

Figure 1 depicts an imaging scenario involving a ground-based radar and a GEO satellite target. P is a point target on the geostationary orbit, and the red line indicates the transmission path of the electromagnetic wave from the transmitting antenna to target P, while the blue line indicates the path of the electromagnetic wave scattered from target P back to the receiving antenna of the GB radar. Assuming that the Earth is an ideal sphere, a cross-sectional view passing through the Earth’s center, the North Pole, and target P is depicted in Figure 2.

In Figure 2, the center of the sphere is denoted as O, and P is the GEO target. The line connecting O and P intersects with the Earth’s surface at point Q. In this 2D plane, the two tangents to the Earth drawn from target P contact the Earth at points T1 and T2, respectively. Therefore, the observable arc on the Earth’s surface for target P is defined as the segment T1-Q-T2. The distance OQ is equal to the Earth’s radius, while the distance OP equals the sum of the Earth’s radius and the geostationary orbit altitude. Based on this geometry, the angle T₁PO, denoted as $\theta$ in Figure 2, can be expressed as

$$\theta =\arcsin \left({\displaystyle \frac{\left|\overrightarrow{O{T}_1}\right|}{\left|\overrightarrow{OP}\right|}}\right)$$

(1)

The value of $\theta$ is calculated to be 8.696°; therefore, the angle $\phi$ is 81.304°. This indicates that the maximum observable range for GEO targets from the Earth’s surface is (−81.304°, 81.304°). Due to this geometric symmetry, the observation angle for radars distributed along the latitudinal direction (equator) is also constrained. Taking the target’s sub-satellite point as the center, the maximum observable range along the equatorial plane is also (−81.304°, 81.304°).

However, due to the elevation angle constraints of the radar, it is impossible for the radar to be deployed near point T₁. Suppose one end of the radar array is located at S₁, and S₁ is an arbitrary point on the arc segment Q-T₁, as depicted in Figure 3. In the triangle PS₁O, the relationship between angles ${\phi }_2$ and ${\theta }_2$ can be derived using the Law of Sines and the Law of Cosines as follows.

With angle ${\phi }_2$ known, the length of side PS₁ can be obtained using the Law of Cosines.

$$\left|\overrightarrow{P{S}_1}\right|=\sqrt{{\left|\overrightarrow{O{S}_1}\right|}^2+{\left|\overrightarrow{OP}\right|}^2-2\left|\overrightarrow{O{S}_1}\right|\left|\overrightarrow{OP}\right|\cos {\phi }_2}$$

(2)

Among these, the length of $O{S}_1$ is the Earth’s radius. Then, according to the Law of Sines,

$${\displaystyle \frac{\sin {\theta }_2}{\left|\overrightarrow{O{S}_1}\right|}}={\displaystyle \frac{\sin {\phi }_2}{\left|\overrightarrow{P{S}_1}\right|}}$$

(3)

Then, the angle ${\theta }_2$ can be calculated using Equation (3).

With angle ${\theta }_2$ known, then, according to the Law of Sines

$${\displaystyle \frac{\sin {\theta }_2}{\left|\overrightarrow{O{S}_1}\right|}}={\displaystyle \frac{\sin \left({\theta }_2+{\phi }_2\right)}{\left|\overrightarrow{OP}\right|}}$$

(4)

Then, the angle ${\theta }_2$ can be calculated using Equation (4).

Following the determination of the ground baseline-to-target observation angles, the corresponding imaging range and azimuth resolution are derived and presented below.

The range resolution of the MIMO radar is determined by the bandwidth of the transmitting signal and is expressed as

$${\rho }_r={\displaystyle \frac{c}{2B}}$$

(5)

where $B$ denotes the signal bandwidth in frequency; $c$ is the speed of light in free space. In the case of a rectangular window function, the theoretical resolution derived above must be scaled by a factor of 0.886. Equation (5) clearly demonstrates an inverse proportionality between range resolution and signal bandwidth in frequency. Specifically, an increase in signal bandwidth causes a corresponding decrease in range resolution values, thereby enhancing the range resolution capability of the system.

According to Reference [2], the azimuth resolution in SAR imaging is given by

$${\rho }_y={\displaystyle \frac{0.886\lambda }{4\sin \left({\Theta }_R/2\right)\cos \gamma }}$$

(6)

where ${\Theta }_R$ represents the observation angle formed by the synthetic aperture with respect to the target, and $\gamma$ is the longitudinal angular difference between the target’s sub-satellite point and the array.

For MIMO arrays, the boundary between the near-field and far-field is defined as the range where the maximum two-way path difference between the target and the array center versus the array edges is less than $\lambda /4$ [28]. Ground-based radar imaging of GEO targets operates in the near-field regime. And the PCA (phase center approximation) method, which assumes far-field conditions, does not apply for analyzing the performance of such MIMO arrays. Therefore, we conduct the analysis from the perspective of wavenumber support. This method is applicable to the near-field resolution analysis of SAR and MIMO arrays.

Take two-dimensional imaging as an example. In Figure 4, the reference line is a straight line perpendicular to line OP in Figure 3. At any given point on Earth, the observation angle relative to the GEO target is defined as the angle between the local line of sight to the target and a defined reference direction. Assume the number of array elements is N, and the transmitted signal is a stepped-frequency signal $f_k$, where $k=0,1,2,\cdots K-1$. The angle between the target and the n-th antenna element is ${\theta }_n$, where $n=0,1,2,\cdots ,N$. According to the two-way echo characteristics of SAR, the spatial spectrum of the target can be obtained as follows:

$${\Omega }_{SAR}^{2D}=\left\{k=\left(\begin{array}{c}{k}_x\\ k_y\end{array}\right)\right.\left|\left.\begin{array}{c}{k}_x={\displaystyle \frac{4\pi f_k}{c}}\cos {\theta }_n,k_y={\displaystyle \frac{4\pi f_k}{c}}\sin {\theta }_n\\ k=0,1,\cdots K-1;n=1,2,\cdots ,N\end{array}\right\}\right.$$

(7)

In SAR, the spatial spectrum of the target exhibits an annular “arc-segment” shape, with an inner arc radius of $4\pi f_0/c$ and an outer arc radius of $4\pi f_{K-1}/c$.

In MIMO arrays, the spatial wavenumber vector of the target is composed of the sum of the transmitting and receiving wavenumber vectors. That is, the two-dimensional spatial spectrum of the MIMO array target is expressed as

$${\Omega }_{MIMO}^{2D}=\left\{k=\left(\begin{array}{c}{k}_x\\ k_y\end{array}\right)\right.\left|\left.\begin{array}{c}{k}_x={\displaystyle \frac{2\pi f_k}{c}}\left(\cos {\theta }_{r,n}+\cos {\theta }_{t,m}\right),k_y={\displaystyle \frac{2\pi f_k}{c}}\left(\sin {\theta }_{r,n}+\sin {\theta }_{t,m}\right)\\ k=0,1,\cdots K-1;n=1,2,\cdots ,N;m=1,2,\cdots ,M;\end{array}\right\}\right.$$

(8)

Here, ${\theta }_{r,n}$ is the angle between the line connecting the target and the n-th transmitting antenna and the reference line, and ${\theta }_{t,m}$ is the angle between the line connecting the target and the m-th receiving antenna and the reference line. The spatial spectrum of the MIMO array can be regarded as a combination of M (number of transmitting antennas) spatial spectra, expressed as

$${\Omega }_{MIMO}^{2D}={\displaystyle \underset{m=1}{\overset{M}{\cup }}\left\{k_m=\left(\begin{array}{c}{k}_x\\ k_y\end{array}\right)\right.\left|\left.\begin{array}{c}{k}_x=\frac{2\pi f_k}{c}\left(\cos {\theta }_{r,n}+\cos {\theta }_{t,m}\right),k_y=\frac{2\pi f_k}{c}\left(\sin {\theta }_{r,n}+\sin {\theta }_{t,m}\right)\\ k=0,1,\cdots K-1;n=1,2,\cdots ,N;\end{array}\right\}\right.}$$

(9)

Different MIMO array configurations exhibit significant variations in the spatial spectrum shape of a target. To facilitate the analysis, the Ends-Transmitting and Multiple-Receiving array configuration is taken as an example. As shown in Figure 5, two transmitting antennas are located at both ends of the antenna array, while N receiving antennas are situated in the middle of the array, remarked as Ends-Transmitting and Multiple-Receiving. It can be observed that the spatial spectrum consists of two parts with a gap between them. To achieve better imaging performance, the gap between the two spatial spectrum segments can be eliminated through array design. The ideal array design should ensure that the spatial spectrum segments neither overlap nor have gaps. Generally, under near-field conditions, a MIMO array cannot guarantee non-overlapping spatial spectra for targets at all positions.

If only a single transmitter in the array is employed, and the scattered signal is received by N receiving antennas, the array is remarked as One-Transmitting and Multiple-Receiving. The corresponding spatial spectrum for this configuration is illustrated in Figure 6.

After obtaining the spatial spectral support region of the target, the imaging resolution can be analyzed. The spatial spectral support region determines the imaging resolution of the target. Generally, a larger spatial spectral support region results in a higher imaging resolution.

According to the Rayleigh criterion [29], the following relationship is obtained:

$$\left\{\begin{array}{c}{\rho }_x=2\pi /\left[\max \left(k_x\right)-\min \left(k_x\right)\right]\\ {\rho }_y=2\pi /\left[\max \left(k_y\right)-\min \left(k_y\right)\right]\end{array}\right.$$

(10)

By selecting the center frequency and combining Equation (8) with Equation (9), the imaging resolution in SAR mode can be derived:

$$\begin{array}{l}{\rho }_{x,SAR}=2\pi /\left(2k_c\left(\underset{n}{\max \left(\cos {\theta }_n\right)-}\underset{n}{\min \left(\cos {\theta }_n\right)}\right)\right)\\ {\rho }_{y,SAR}=c/2B\end{array}$$

(11)

where ${\rho }_{x,SAR}$ is the azimuth resolution in SAR mode, and ${\rho }_{y,SAR}$ is the range resolution in SAR mode.

The imaging resolution in MIMO mode is given by

$$\begin{array}{l}{\rho }_{x,MIMO}=2\pi /\left(2k_c\left(\underset{n}{\max \left(\cos {\theta }_{r,n}\right)-}\underset{m}{\min \left(\cos {\theta }_{t,m}\right)}\right)\right)\\ {\rho }_{y,MIMO}=c/2B\end{array}$$

(12)

where ${\rho }_{x,MIMO}$ is the azimuth resolution in MIMO mode, and ${\rho }_{y,MIMO}$ is the range resolution in MIMO mode.

In practice, the above expression must be multiplied by the corresponding window function factor.

Assuming a point target is located at P in Figure 1, the relationship between the theoretical target resolution and the ground baseline length for the Ends-Transmitting and Multiple-Receiving and One-Transmitting and Multiple-Receiving array configurations are shown in Figure 7. For the Ends-Transmitting and Multiple-Receiving array configuration, the two transmitting antennas are positioned at the ends of the array. Consequently, the baseline length is defined as the distance between these two transmitting antennas. For the One-Transmitting and Multiple-Receiving array configuration, the transmitting antenna is fixed at a single location. Here, the baseline length refers to the ground baseline length of the receiving antenna array.

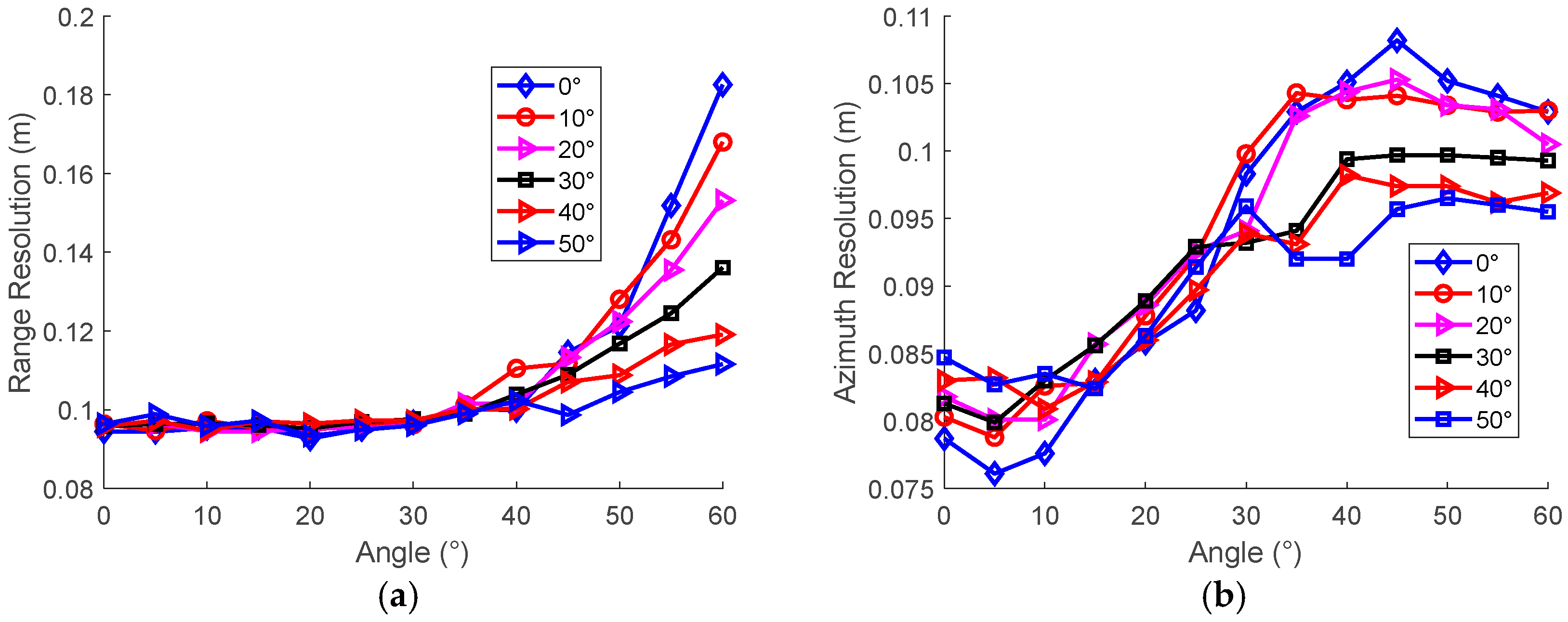
In Figure 7, the value of the theoretical azimuth resolution decreases as the baseline length increases from 800 km to 4000 km. For the Ends-Transmitting and Multiple-Receiving array configuration, when the transmitting signal center frequency is 10 GHz, the theoretical resolution corresponding to baseline length of 1000 km, 2000 km, and 3000 km is 0.47 m, 0.24 m, and 0.16 m, respectively. When the center frequency is 15 GHz, the azimuth resolution corresponding to same baseline length is 0.32 m, 0.16 m, and 0.11 m, respectively. When the center frequency is 35 GHz, the corresponding resolution further improves to 0.14 m, 0.07 m, and 0.05 m, respectively.

For the One-Transmitting and Multiple-Receiving array configuration, the absence of half the wavenumber support results in a degraded resolution under identical aperture lengths. Specifically, when the center frequency is 10 GHz, the theoretical resolution corresponding to three baseline lengths is 0.95 m, 0.48 m, and 0.32 m, respectively. When the center frequency is 15 GHz, the theoretical resolution is 0.63 m, 0.32 m, and 0.21 m, respectively. When the center frequency is 35 GHz, the theoretical resolution is 0.27 m, 0.14 m, and 0.09 m, respectively.

The impact on the azimuth resolution of angle $\gamma$ is analyzed. For the One-Transmitting and Multiple-Receiving array configuration, when the center frequency is 35 GHz, and the baseline length is 1500 km, the theoretical azimuth varies with angel $\gamma$, as depicted in Figure 8. The azimuth resolution degrades as $\gamma$ increases from 0° to 70°.

Note that the theoretical resolution values in Figure 7 and Figure 8 do not account for azimuth windowing or processing techniques such as CF weighting. The above analysis demonstrates that, when the center frequency is 35 GHz and baseline length is 2000 km, the Ends-Transmitting and Multiple-Receiving array’s theoretical azimuth resolution is 0.07 m, while the One-transmitting and Multiple-Receiving array is 0.14 m. These results confirm the theoretical feasibility of imaging GEO targets using ground-based MIMO radar.

Figure 9 shows a cross-sectional view of the equatorial plane, where O represents the Earth’s center (and also the center of the geostationary orbit). Point A lies on the Earth’s surface. The lines tangent from A to the Earth intersect the geostationary orbit at points B and C, respectively. The arc BC corresponds to the spatial coverage observable by a radar located at A. With OA equal to the Earth’s radius and OB equal to the geostationary orbital radius, the central angle ∠BOC is calculated as $2\delta$ = 162.608°, which defines the spatial coverage from point A.

If a linear array is deployed along the equator with endpoints A and D, the tangent lines from D intersect the orbit at points E and F. The combined spatial coverage of the array is the intersection of individual coverages, i.e., arc EC. Let the angular extent of the array baseline relative to the Earth’s center be $\eta$; then, the observable angular range is $2\delta -\eta$. For a baseline length of 1500 km, the resulting spatial coverage is calculated as 149.1793°.

When the radar is not located on the equator, suppose its latitude is $\beta$. The tangent plane through this point intersects the equatorial plane along a line at a distance of $R/\cos \beta$ from O. The spatial coverage can be computed similarly. Figure 10 illustrates the spatial coverage of a single radar at different latitudes.

As shown in Figure 10, even at high latitudes (e.g., =60°), the spatial coverage remains large (144.5123°). The intersection of coverage areas from all antennas in an array still yields a substantial observable range.

3. Three-Dimensional Imaging of GEO Targets

For the three-dimensional imaging of GEO targets, coordinate system synchronization is essential for ensuring geometric accuracy. The Earth-Centered, Earth-Fixed (ECEF) [30,31] coordinate system provides an effective synchronization framework that unifies the coordinate representations of geostationary targets, target scattering point models, and ground-based radar arrays, ensuring all entities are modeled within a consistent spatiotemporal reference. The ECEF system originates at the Earth’s center of mass, with its X-axis pointing toward the intersection of the prime meridian and the equator, the Y-axis lying in the equatorial plane perpendicular to the X-axis and directed toward the 90° east longitude, and the Z-axis orthogonal to the equatorial plane, pointing toward the North Pole.

However, in the ECEF coordinate system, when the longitude of a GEO target’s sub-satellite point significantly deviates from 0°, the imaging area of the target is also far from the X-axis. Using the ECEF system as the imaging coordinate system directly would cause variations in the azimuth and range directions, leading to perspective distortion in the imagery and complicating the interpretation of results.

To obtain a front-view 3D image of the target, we establish a Three-Dimensional Target-Oriented coordinate system (TDTO). Its X-axis is defined by the vector from the Earth’s center to the target, the XY-plane coincides with the equatorial plane, the Z-axis is perpendicular to the XY-plane pointing toward the North Pole, and the Y-axis lies in the equatorial plane perpendicular to the X-axis, forming a right-handed system. The established TDTO coordinate system is depicted in Figure 11.

Figure 11 depicted the TDTO coordinate system for the MIMO radar imaging of GEO targets. This unified coordinate system establishes an accurate geometric foundation for subsequent radar echo modeling. Its relationship to the ECEF coordinate system is defined as follows: the origin and Z-axis orientation remain unchanged, while the XY-plane is rotated by a specific angle about the Z-axis.

The coordinates of ground-based radar are generally expressed in terms of longitude, latitude, and height coordinates. These parameters can be converted to ECEF coordinates through the WGS84 ellipsoid model, with specific conversion methods detailed in Reference [31]. After converting radar coordinates into the ECEF coordinate system, the subsequent step involves transforming both the radar and GEO target coordinates from the ECEF coordinate system to the TDTO coordinate system.

Assuming the coordinates of point P in the ECEF coordinate system is (x′, y′, z′), then its coordinates (x, y, z) in the TDTO coordinate system satisfy the following rotational relationship:

$$\left(\begin{array}{c}x\\ y\\ z\end{array}\right)=R\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ z^{\prime }\end{array}\right)$$

(13)

When the target’s sub-satellite point longitude is $\gamma$ (east longitude), the rotation angle of the ECEF coordinate system relative to the TDTO coordinate system is $\gamma$, and the corresponding rotation matrix $R$ is given by

$$R=\left(\begin{array}{ccc}\cos \gamma & \sin \gamma & 1\\ -\sin \gamma & \cos \gamma & 1\\ 1& 1& 1\end{array}\right)$$

(14)

The rotation matrix R is utilized to convert the coordinates of all transmitting and receiving antennas in the MIMO radar distributed across the Earth’s surface into the TDTO coordinate system.

In the TDTO coordinate system, the range direction of the target imaging is defined along the X-axis, the azimuth direction is along the Y-axis, and the height direction is along the Z-axis.

During the transmitting and receiving time of ground-based MIMO radar, the target is assumed to be stationary, meaning its coordinate position remains unchanged. The coordinate of the m-th transmitting antenna is denoted as $r_{m,T}=\left(x_{m,T},y_{m,T},z_{m,T}\right)$, where the subscript $T$ indicates the transmitting antenna, the subscript m is the index of the antenna $m\left(m=1,2,\cdots M\right)$, and $M$ is the total number of transmitting antennas. The coordinate of the n-th receiving antenna is denoted as $r_{n,R}=\left(x_{n,R},y_{n,R},z_{n,R}\right)$, where the subscript R indicates the receiving antenna, the subscript n is the index of the antenna $n\left(n=1,2,\cdots N\right)$, and $N$ is the total number of receiving antennas. $r=\left(x,y,z\right)$ represents the coordinates of a specific scattering point P on the GEO target.

The distance from the m-th transmitting antenna to point P can be expressed as

$$R_T^{\left(m\right)}=‖r_{m,T}-r‖=\sqrt{{\left(x_{m,T}-x\right)}^2+{\left(y_{m,T}-y\right)}^2+{\left(z_{m,T}-z\right)}^2}$$

(15)

The distance from point P to the n-th receiving antenna can be expressed as

$$R_R^{\left(n\right)}=‖r_{n,R}-r‖=\sqrt{{\left(x_{n,R}-x\right)}^2+{\left(y_{n,R}-y\right)}^2+{\left(z_{n,R}-z\right)}^2}$$

(16)

The transmitting antenna sequentially emits radar signals, while all receiving antennas synchronously capture scattered signals from the target.

The linear frequency-modulated (LFM) waveform transmitted by the ground-based radar is expressed as

$$p\left(t\right)=rect\left({\displaystyle \frac{t}{T_p}}\right)\exp \left[j2\pi \left(f_{c}t+{\displaystyle \frac{1}{2}}K{t}^2\right)\right]$$

(17)

where $rect\left(·\right)$ is the rectangular window function, $t$ represents the fast time, $T_p$ denotes the pulse width, $j=\sqrt{-1}$ is the imaginary unit, $f_c$ corresponds to the center frequency, and $K$ indicates the chirp rate.

Given that the target position is known a priori, the radar antenna main beam can be pre-pointed toward the target, satisfying the spatial synchronization condition. Assuming that all radars share identical parameters, minor frequency discrepancies and jitter among their frequency sources are negligible, thereby meeting the frequency synchronization requirement. Each radar employs satellite-based time synchronization to achieve temporal alignment. Disregarding antenna modulation effects, when the m-th transmitting antenna emits a signal, the echo signal from point P received by the n-th receiving antenna is expressed as

$$s_{m,n}^{\prime }\left(t\right)=\sigma rect\left({\displaystyle \frac{t-{\tau }_{m,n}}{T_p}}\right)\exp \left\{j2\pi \left[f_c\left(t-{\tau }_{m,n}\right)+{\displaystyle \frac{1}{2}}K{\left(t-{\tau }_{m,n}\right)}^2\right]\right\}$$

(18)

Here, $\sigma$ denotes the backscattering coefficient of the point; ${\tau }_{m,n}=\left(R_T^{\left(m\right)}+R_R^{\left(n\right)}\right)/c$ represents the two-way echo delay of the point.

Equation (18) corresponds to the echo from point P. Since the radar illumination area covers the entire target, the total target echo constitutes the superposition of echoes from all scattering points within this region. Therefore, the received echo can be expressed as

$$s{s}_{m,n}\left(t\right)={\displaystyle \underset{D}{\iiint }\sigma \left(x,y,z\right)}rect\left({\displaystyle \frac{t-{\tau }_{m,n}}{T_p}}\right)\exp \left\{j2\pi \left[f_c\left(t-{\tau }_{m,n}\right)+{\displaystyle \frac{1}{2}}K{\left(t-{\tau }_{m,n}\right)}^2\right]\right\}dxdydz$$

(19)

where $D$ denotes the area illuminated by the radar electromagnetic wave, and $\sigma \left(x,y,z\right)$ represents the backscattering coefficient of scattering point $\left(x,y,z\right)$.

Assuming dechirp processing is employed for pulse compression, where the transmitted signal $p\left(t\right)$ serves as the reference signal, the received echo undergoes sequential processing including dechirp, video phase compensation, and inverse Fourier transform. Finally, the one-dimensional range profile of the target is obtained and denoted as $r_{m,n}\left(f_{\Delta }\right)$.

Based on the back-projection (BP) imaging theory, the imaging area is discretized into grids in the TDTO coordinate system. The numbers of grids along the X-axes, Y-axes, and Z-axes are defined as $N_x$, $N_y$, and $N_z$, respectively, resulting in a total of $N_x\times N_y\times N_z$ grids, where each grid corresponds to a single pixel.

The imaging is processed sequentially by the transmitting antenna. When the m-th antenna transmits, the one-dimensional range profiles $r_{m,n}\left(f_{\Delta }\right)$ from $N$ receiving antennas are coherently summed with appropriate time delays, thereby obtaining the back-projection result $z_{mn}\left(f_{\Delta }\right)$ under this specific transmitting antenna:

$$z_{mq}\left(f_{\Delta }\right)={\displaystyle \sum _{n=1}^N{r}_{m,n}\left(f_{\Delta }+{\tau }_{m,n}-{\tilde{\tau }}_{m,n}\right)}$$

(20)

For each of the $M$ transmitting antennas in sequence, the back-projection result from N receiving antennas is computed. The final value $I\left(x_q\right)$ at pixel $x_q$ is the coherent sum of these $M$ individual results.

$$I\left(x_q\right)={\displaystyle \sum _{m=1}^M{z}_{mq}\left(f_{\Delta }\right)={\displaystyle \sum _{m=1}^M{\displaystyle \sum _{n=1}^N{r}_{m,n}}}\left(f_{\Delta }+{\tau }_{m,n}-{\tilde{\tau }}_{m,n}\right)}$$

(21)

To further suppress sidelobes and noise in the imaging results, a weighting coefficient is introduced, and the above expression is modified as follows:

$$I\left(x_q\right)=w\left(x_q\right){\displaystyle \sum _{m=1}^M{\displaystyle \sum _{n=1}^N{r}_{m,n}}}\left(f_{\Delta }+{\tau }_{m,n}-{\tilde{\tau }}_{m,n}\right)$$

(22)

where $w\left(x_q\right)$ represents the CF weighting value at pixel point $x_q$ for the scenario, with M transmitting antennas operating sequentially and N receiving antennas operating simultaneously, given by

$$w\left(x_q\right)={\displaystyle \frac{{‖{\displaystyle \sum _{m=1}^M{\displaystyle \sum _{n=1}^N{r}_{m,n}}}\left(f_{\Delta }+{\tau }_{m,n}-{\tilde{\tau }}_{m,n}\right)‖}^2}{MN{\displaystyle \sum _{m=1}^M{\displaystyle \sum _{n=1}^N{‖r_{m,n}\left(f_{\Delta }+{\tau }_{m,n}-{\tilde{\tau }}_{m,n}\right)‖}^2}}}}$$

(23)

The imaging result $I\left(x_q\right)$ at each location is obtained by iterating through every position $x_q$ within the imaging grid. The final output $I\left(x_q\right)$ is a three-dimensional matrix, whose dimensions are $N_x$, $N_y$ and $N_z$, respectively.

4. Simulation Results

This section presents imaging simulations for both point targets and satellite targets. The point target imaging result is primarily used to validate imaging parameters such as resolution. Satellite target imaging results are used to verify the feasibility and applicability of the algorithm. Imaging verification is then performed using two distinct types of data: echoes synthesized from an ideal 3D point-scatterer model and target data acquired from CST electromagnetic simulations.

4.1. Imaging Results of Point Target

The 3D imaging scenario is illustrated in Figure 12. The center of the antenna array coincides with the target’s sub-satellite point. A total of 100 transmitting antennas is uniformly distributed along a longitudinal line, with a baseline length of 1500 km, while 100 receiving antennas are uniformly distributed along the equator, with an identical baseline length of 1500 km. Each antenna transmits sequentially, with all receiving antennas receiving signals simultaneously, forming a 100 × 100 MIMO array configuration. The target and radar parameters are summarized in

Table 1. Three-dimensional imaging simulation parameters.

Parameter	Type
Center Frequency	35 GHz
Bandwidth	2 GHz
Transmit Arc Length	1500 km
Receive Arc Length	1500 km
Number of Transmit Antennas	100
Number of Receive Antennas	100
Target Center Position	(4.2 × 107, 0, 0) m

.

The transmit antenna array length is 1500 km, and the corresponding Earth observation angle is 13.43°. According to Equation (3), the angular span of the ground-based array relative to the GEO target is only 2.38°. Although the system employs a long baseline of 1500 km, the angular extent of the array as viewed from the GEO target does not exceed 3°. This small angular span indicates that baseline decorrelation effects are negligible in this configuration.

4.1.1. Effect of Range Windowing and Imaging CF Weighting

As derived from previous analysis, when the transmitting signal bandwidth is 2 GHz, the theoretical range resolution under a rectangular window is 0.886·$c/2B$= 6.64 cm. However, the rectangular window introduces significant sidelobes. To suppress range sidelobes, windowing is typically applied during range pulse compression. After applying a Hamming window, the main lobe broadens to 1.77 × $c/2B$= 13.3 cm.

The target center is set at (4.2 × 10⁷, 0, 0) m, and the imaging region is defined relative to this center, covering a volume of (−2, 2) m × (−2, 2) m × (−2, 2) m.

For comparison, Figure 13a shows the 3D imaging result with a rectangular range window and without CF weighting, while Figure 13b presents the result with a Hamming range window and CF weighting applied. Both results are obtained under the same simulation conditions. Profiles taken at the maximum value of the target point are used to determine the range and azimuth resolutions, as shown in Figure 14. The measured resolutions and theoretical values are summarized in

Table 2. Theoretical and measured resolutions of point targets.

	Range	Azimuth
Theoretical Resolution (m)	0.0664 (Rectangular window) 0.0912 (Hamming window)	0.1809
Measured Resolution (m)	0.0666 (Rectangular window) 0.0968 (Hamming window, CF)	0.1787 0.0824 (CF)

. Due to the symmetry of the target and the transceiver array layout, the azimuth and elevation results are identical. Thus, only the azimuth results are presented here.

As can be observed from Table 2, in the range direction, the theoretical resolution is 6.64 cm with the rectangular window, while the measured resolution is 6.66 cm. When the Hamming window is applied, the theoretical resolution becomes 9.12 cm, and the measured resolution is 9.68 cm. In the azimuth direction, the theoretical resolution is 18.08 cm, and the measured resolution is 17.87 cm. These results indicate that the simulation closely matches the theoretical resolution values. Furthermore, when CF weighting is applied, the resulting azimuth resolution is 8.24 cm, which is comparable to the range resolution achieved with the Hamming window. Therefore, in subsequent simulations, the Hamming window for range processing and CF weighting for imaging are adopted.

4.1.2. Resolution Variation with Azimuth Angle

The antenna array configuration is the same as in Section 4.1.1, with the latitudes of array centers being 0°, 10°, 20°, 30°, 40°, and 50°, respectively. Resolutions at different azimuth angles were simulated, and the range resolution and azimuth resolutions are depicted in Figure 15.

Note that the X-axis of the TDTO coordinate system is always pointing towards the center of the target. When the target is directly aligned with the center of the array, the azimuth and range directions generated by the array are perpendicular. However, when the target deviates from the center of the array, the azimuth and range directions are no longer perpendicular. At this time, the range direction remains pointing from the geocenter towards the target, while the azimuth direction is perpendicular to the range direction but not necessarily perpendicular to the distribution of the antenna array. Therefore, as shown in Figure 15, when the deviation angle is not large, the resolution in the range direction does not differ significantly from that when directly aligned, while the azimuth direction exhibits periodic changes with changes in the angle, but the value of azimuth resolution changes slightly. Simulation results show that when the point target is not aligned in the same azimuth as the array center, it can still be imaged while maintaining good azimuth and range resolutions.

4.1.3. Resolution Variation with Transmitting and Receiving Antenna Spacing

Assuming that receiving antennas are distributed along the equator with One-Transmitting and Multiple-Receiving array configuration, the receiving antenna baseline length is set to 2000 km, 1500 km, and 1000 km, respectively. For each fixed baseline length, the number of receiving antennas is set to 10, 20, 30, 40, 50, and 60, respectively. As the number of receiving antennas increases, the spacing between them gradually decreases. Cross-sectional profiles are extracted from the imaging results in the range and azimuth direction, respectively, and the resolution is derived from these profiles. The range and azimuth resolution for the different numbers of antennas are shown in Figure 16.

As can be seen from Figure 16a, the range resolution is largely invariant to changes in antenna spacing or baseline length, in accordance with theoretical expectations. In contrast, Figure 16b indicates that the azimuth resolution is significantly influenced by the array baseline length but only marginally affected by the number of antenna elements for a constant baseline length. The resolution is approximately 6.1 cm for a baseline length of 2000 km, 8.2 cm for 1500 km, and 12.3 cm for 1000 km, respectively.

4.1.4. Resolution Variation with Baseline Length

The receiving antenna spacing is set to 40 km, 30 km, and 20 km, with the corresponding numbers of receiving antennas set to 10, 20, 30, 40, 50, and 60, respectively. As the number of receiving antennas increases, the resulting aperture length of the receiving array gradually expands. Following the same procedure as in Section 4.1.2, range and azimuth resolution are depicted in Figure 17.

In Figure 17, the range resolution remains unchanged with the variation in antenna spacing or baseline length, whereas the azimuth resolution decreases with the increasing baseline length. Azimuth resolution is primarily determined by the transmitting signal frequency and the ground-based baseline length. When the transmitting signal center frequency is 35 GHz, the baseline length is 1500 km, with the One-Transmitting and Multiple-Receiving array configuration, the azimuth resolution is approximately 0.08 m, which is better than 0.1 m.

The point target simulation results demonstrate that the range and azimuth resolution obtained from imaging are consistent with the theoretical results. Furthermore, when the baseline length is 1500 km, the azimuth resolution is better than 0.1 m.

4.1.5. Analysis of the Impact of Synchronization Errors

Based on References [32,33,34], synchronization error plays a crucial role in MIMO-distributed coherent radar imaging. Synchronization is categorized into spatial, temporal, frequency, and phase synchronization. The distributed coherent radar system has relatively low requirements for frequency and phase synchronization, which are easier to satisfy, whereas it imposes extremely stringent demands on time synchronization.

Reference [34] demonstrates that time synchronization over 13,134 km of fiber can be maintained with a TDEV under 32 ps/10 s and a total uncertainty below 89.6 ps. We next analyze the impact of the synchronization error on MIMO radar imaging.

In the simulation, time synchronization errors with standard deviations of 0.01, 0.02, 0.03, 0.04, and 0.05 ns are introduced randomly into the received signals. Imaging is then conducted on point targets to generate azimuth profiles, from which the Peak Sidelobe Ratio (PSLR) is extracted. To ensure statistical robustness, the entire process is repeated 10 times for each error level. The resulting PSLR values are presented in Figure 18. The simulation covers three frequency bands: Ka-band (9–11 GHz), Ku-band (15–17 GHz), and X-band (34–36 GHz). To achieve a consistent azimuth resolution across bands, the corresponding synthetic aperture lengths are set to 1500 km, 3000 km, and 4800 km, respectively.

Figure 19 presents some imaging results, where the first, second, and third rows correspond to the Ka-band, Ku-band, and X-band, respectively. The first column shows the imaging results with a time synchronization error of 10 ps, the second column with 30 ps, and the third column with 50 ps.

The simulation results indicate that the proposed imaging algorithm exhibits relative sensitivity to time synchronization errors. For the Ka-band, acceptable imaging quality is achieved only when the time synchronization error remains below 0.01 ns. As the error exceeds 0.02 ns, significant azimuthal defocusing occurs, as illustrated in Figure 19b, where the azimuthal sidelobe rises to −1.84 dB. With a further increase in error to 0.05 ns, the PSLR deteriorates to −0.85 dB. Figure 19c shows complete azimuthal defocusing, where the peak response is displaced from the true target location.

In the Ku-band, the target can be accurately focused with a time synchronization error standard deviation of 0.02 ns, yielding a PSLR of −13.08 dB. However, azimuthal defocusing emerges when the error exceeds 0.03 ns, with the PSLR degrading to −5.32 dB. These results demonstrate that the imaging performance degrades markedly when the time synchronization error surpasses 50 ps. Consequently, applying this method in practical distributed radar scenarios imposes stringent synchronization requirements, highlighting the need for further research into improving its robustness to such errors.

4.1.6. Analysis of the Impact and Suppression of Grating Lobes

In the ground-based MIMO radar imaging of GEO targets, azimuth resolution depends on the equivalent array length, with longer arrays yielding finer resolution. However, the limited number of available ground-based radars leads to large inter-element spacing, resulting in spatially sparse arrays. Such arrays tend to produce high grating lobes during imaging, which manifest as strong false targets near the true target position over a certain azimuth span.

To illustrate this effect, Figure 20 presents azimuth profiles simulated for antenna counts of 100, 50, 40, 30, 20, and 10, with a fixed baseline length of 1500 km. The imaging area is extended to 30 × 30 m to encompass typical satellite dimensions. Results show that as the number of antennas decreases—and thus the element spacing increases—grating lobes emerge in the azimuth dimension. To suppress grating lobes, the spacing between antennas cannot be excessively large, which requires a greater number of antennas and thus conflicts with the azimuth resolution.

An alternative approach to grating lobe suppression involves optimizing the spatial layout of antennas. In previous simulations, antennas are uniformly distributed along the baseline, resulting in approximately uniform observation angles to the target. By deviating from uniform spacing, grating lobes can be mitigated. Figure 21 presents the azimuth profile of a 10-element array configured in a Fibonacci distribution under the same imaging conditions as Figure 20f. The azimuth grating lobes for equally spaced and Fibonacci-distributed arrays are compared in Figure 22a and Figure 22b, respectively. The results show that array optimization effectively suppresses grating lobe levels. In practice, optimization algorithms such as particle swarm optimization (PSO) are commonly used to design antenna layouts to minimize grating lobes and further improve imaging quality.

4.1.7. Analysis of the Impact and Ionospheric Errors

In long-baseline MIMO systems, the transmitting and receiving antennas are widely separated, causing the ionospheric penetration points along the electromagnetic wave propagation paths to differ significantly. This leads to variations in the total electron content (TEC) for each path, introducing additional phase errors that degrade imaging quality. To analyze the impact of ionospheric errors on imaging performance, this section introduces ionospheric phase errors into the echo signals based on the International Reference Ionosphere (IRI) model and TEC spatial variation characteristics, followed by imaging simulations.

The ionosphere-induced phase error can be expressed as [35]

$$\Delta \varphi =-{\displaystyle \frac{4\pi K}{cf}}\cdot TE{C}_{path}$$

(24)

where $K=40.28 {\mathrm{m}}^3/{\mathrm{s}}^2$ is the ionospheric constant, $f$ is the signal frequency, and $TE{C}_{path}$ is the total electron content along the path. For long-baseline systems, the TEC values for the transmitting and receiving paths differ. If the TEC errors are not compensated for, the imaging quality will be impaired.

To quantify this effect, relevant studies have shown that the compensation method can control the TEC residual errors to below 2 TECU [36,37]. Accordingly, in the echo simulation of this paper, random TEC phase errors are added separately to the receiving signal. The simulation parameters are set as follows: center frequency of 35 GHz, baseline length of 1500 km, and a One-Transmitting–Multiple-Receiving array configuration. A total of six groups of TEC phase error conditions is designed in the experiment, with the error range from 0 to 10 TECU. The influence of errors is analyzed by observing the PLSR in the azimuth direction of the point target, and the corresponding experimental results are presented in Figure 23. Experimental results show that, as the TEC error increases from 0 to 10 TECU, the PSLR degrades by approximately 6 dB.

4.2. Imaging Results of Satellites Scatter Points

Geostationary Operational Environmental Satellite (GOES) scatter points are simulated in this section, and simulation parameters are the same as Section 4.1. The GOES model consists of about 30,000 points, as shown in Figure 24. The satellite consists of a main body, solar cell arrays, and a rod antenna. The main body size is 5 m × 4.5 m × 4 m, the solar panel is 3.4 m × 5.9 m, the length of the rod antenna is 9.8 m. All scattering points are assumed to have constant and identical scattering coefficients. Imaging results are depicted in Figure 25.

Figure 25a presents the result of three-dimensional imaging on a certain isosurface, which reflects the three-dimensional structure of the target. The components of the target can be clearly seen in the three-dimensional structure. Figure 25b–d are the projections of the three-dimensional imaging results on the range–azimuth plane, range–elevation plane, and azimuth–elevation plane, respectively, from which distinct scattering center features can be observed. By measuring the distance of the target, the main body size is measured as 4.6 m × 4.2 m × 3.9 m, the solar panel is measured as 3.5 m × 6.6 m, and the length of the rod antenna is measured as 9.7 m. The size measured from the imaging results are consistent with the simulated target size. Simulation results indicate that when the array length is 1500 km, three-dimensional imaging results of scattering point targets can be obtained.

Four imaging scenarios are simulated with different array centers and target azimuth angles. In scenario 1, the array center is located on the equator, while the target is aligned in the same azimuth of the center; in scenario 2, the array center is located at 30° north latitude, while the target is aligned in the same azimuth of the center; in scenario 3, the array center is located on the equator, while the target is located at 30° in the azimuth of the center; and in scenario 4, the array center is located at 30° north latitude, while the target is located at 30° in the azimuth of the center. The simulation results are depicted in Figure 26, Figure 27, Figure 28, and Figure 29, respectively.

In the TDTO coordinate system, the imaging results of the target can be obtained. When the target is located at different positions relative to the antenna array, its three-dimensional imaging consistently reflects its true three-dimensional structure. At the same time, due to differences in observation angles, the solar panels exhibit significant variations in the imaging. The azimuth–elevation projection of the target remains consistent, whereas the range–elevation and range–azimuth projections show considerable differences due to varying observation angles. Simulation results demonstrate that this method is capable of achieving three-dimensional imaging of targets at different locations.

4.3. Imaging Results of Radar Echo Simulation Using CST

The Tracking and Data Relay Satellite (TDRS) is a geosynchronous orbit communication satellite system. Serving as a central hub for space communication, it provides near-continuous data relay and telemetry, tracking, and command services between low-Earth orbit spacecraft and ground stations. When the solar panels of the satellite are fully extended, the satellite measures approximately 21 m in total length and 13.1 m in total width, including solar panels and two 4.5 m-diameter parabolic antennas. Firstly, the radar echo of the TDRS is simulated in CST Studio Suite 2022, based on its imported CAD model and defined surface material properties. The simulation parameters are the same as in Table 1. The array consists of 100 transmitting antennas with uniform angular spacing in elevation and 100 receiving antennas with uniform angular spacing in azimuth. The simulation frequency ranges from 34 GHz to 36 GHz. Then, the BP algorithm is used to image the target. Figure 30 shows the 3D model of the TDRS satellite, and Figure 31, Figure 32 and Figure 33 present its corresponding 3D imaging results.

Figure 31a presents the result of three-dimensional imaging on a certain isosurface, which reflects the three-dimensional structure of the target. Solar panels on both sides and two parabolic antennas are clearly seen in the three-dimensional structure; the measured antenna diameter is about 4.5 m. Figure 31b–d are the projections of the three-dimensional imaging results on the range–azimuth plane, range–elevation plane, and azimuth–elevation plane, respectively, from which distinct scattering center features can be observed. The TDRS model has dimensions of approximately 21 m in length and 13.4 m in width, closely matching its actual size. Simulation results indicate that when the array length is 1500 km, the three-dimensional imaging results of scattering point targets can be obtained.

Figure 31 and Figure 32 are the CST simulation results for the aforementioned scenario 1. Specifically, Figure 31 shows the radar transmitting signals at a frequency of 34–36 GHz, while Figure 32 depicts the radar operating at a frequency of 15–17 GHz. Figure 33 illustrates the radar in the aforementioned scenario 2, operating at a frequency of 34–36 GHz.

From the comparison results in Figure 31 and Figure 32, it can be observed that, as the radar operating frequency increases, the azimuth and elevation image resolutions improve, and the target outline becomes clearer. From the simulation results in Figure 31 and Figure 33, which correspond to the previous results of Figure 26 and Figure 27, respectively, it can be seen that the CST simulation results are capable of achieving three-dimensional imaging of the target.

The simulation results validate that the proposed method can effectively reconstruct both the global geometry and key components of the target, demonstrating its feasibility for 3D imaging of space objects.

5. Conclusions

There is no relative motion between ground-based radars and targets in geosynchronous orbits, which causes imaging failure. This paper overcomes the aperture limitation by deploying multiple radars in a MIMO configuration, effectively synthesizing a large aperture across the Earth’s surface. MIMO azimuth resolution is analyzed from the perspective of wavenumber support. When the center frequency is 35 GHz and the baseline length 2000 km, the Ends-Transmitting and Multiple-Receiving array theoretical azimuth resolution is 0.07 m, while the One-Transmitting and Multiple-Receiving array is 0.14 m. The TDTO coordinate system is established based on radar distribution and target location, which can obtain front-view three-dimensional imaging of the target. Back-projection and Coherence Factor weighting are used to image the target. The point target simulation results demonstrate that the range and azimuth resolution obtained from imaging are consistent with the theoretical results. When the baseline length is 1500 km, the azimuth resolution is better than 0.1 m. GOES satellite scatter points and TDRS satellite radar echo simulation using CST are also simulated, and results demonstrate that the proposed method can effectively image the target’s overall structure and key components, verifying its feasibility for the 3D imaging of space objects, while azimuth resolution primarily depends on the baseline length rather than antenna array spacing. However, large spacing introduces grating lobes that degrade the imaging performance. Future work should address grating lobe suppression through both signal processing techniques for sparse arrays and array configuration optimization.