The Assimilation of CFOSAT Wave Heights Using Statistical Background Errors

Highlights

What are the main findings?

• CFOSAT altimetry wave height measurements are assimilated into an operational wave forecast model
• Background errors and correlation lengths are quantified with spatial variation in the assimilation process

What are the implications of the main findings?

• Such assimilation does generally improve the forecast for wave heights based on validation with both buoys and alternative altimetry observations
• Distributed correlation length is a preferred method over the traditional constant correlation length

Abstract

This paper discusses the assimilation of significant wave height (Hs) observations from the China France Oceanography SATellite (CFOSAT) into the Global Deterministic Wave Prediction System developed by Environment and Climate Change Canada. We focus on the quantification of background errors in an effort to address the conventional, simplified, homogeneous assumptions made in previous studies using Optimal Interpolation (OI) to generate Hs analysis. A map of Best Correlation Length, L, is generated to count for the inhomogeneity in the wave field. This map was calculated from pairs of Hs forecasts of two grid points shifted in space and time from which a look-up table is derived and used to infer the spatial extent of correlations within the wave field. The wave spectra are then updated from Hs analysis using a frequency shift scheme. Results reveal significant spatial variance in the distribution of L, with notably high values located in the eastern tropical Pacific Ocean, a pattern that is expected due to the persistent swells dominating in this region. Experiments are conducted with spatially varying correlation lengths and a set correlation length of eight grid points in the analysis step. Forecasts from these analyses are validated independently with the Global Telecommunications System buoys and the Copernicus Marine Environment Monitoring Service (CMEMS) altimetry wave height observations. It is found that the proposed statistical method generally outperforms the conventional method with lower standard deviation and bias for both Hs and peak period forecasts. The conventional method has more drastic corrections on Hs forecasts, but such corrections are not robust, particularly in regions with relatively short spatial correlation length scales. Based on the analysis of the CMEMS comparison, the globally varying correlation length produces a positive increment of the Hs forecast, which is globally associated with forecast error reduction lasting up to 24 h into the forecast.

1. Introduction

Timely wave forecasts are an essential marine service for a wide range of operational activities, such as recreational and commercial navigation and coastal hazard management. The Global Deterministic Wave Prediction System (GDWPS) is an operational wave forecast system developed by Environment and Climate Change Canada (ECCC) to replace the regional system, which often had poor performance in forecasting swells on the west coast of Canada [1]. The GDWPS is continuously under development to improve forecasts, e.g., in regions exposed to far-generated swells.

Data assimilation is a well-developed tool for numerical weather forecasts, yet its application in wave modelling was stagnant, partly because of a lack of globally distributed observations. Improvements in wave models have been primarily driven by improvements in their forcing fields rather than initial conditions. Early studies have shown that an improved initial condition leads to limited forecast improvement before wind forcing wipes out the memory of the initial condition [2]. Over time, space-based observations have increased, and wave model complexity has increased, providing an opportunity to reconsider data assimilation as a means of improving wave forecasts.

Launched in 2018, The China France Oceanography SATellite (CFOSAT) carries the SWIM (Surface Waves Investigation and Monitoring) instrument to enable the observation of directional spectral wave parameters from the off-nadir beams with a diversity of incidence and azimuth angles over a wide wavelength range of 70–500 m [3]. CFOSAT also carries an instrument to measure wind at the same time. These unique features make CFOSAT products the perfect candidates to test data assimilation as a method for improving wave forecasts. The assimilation of CFOSAT products, especially the off-nadir spectrum parameters, has the potential to improve the source and dissipation terms of the wave model [4].

Hs assimilation is crucial, as the wave energy is derived from Hs; hence, the application of this assimilation is the foundation for 2D spectrum assimilation. Most of the current global operational wave data assimilation systems are based on Hs [2,5,6].

The assimilation of Hs is unique compared to data assimilation in other earth systems, as it has to be followed by an a posteriori analysis of the wave spectra in order to update the initial conditions for the forecasts. For this reason, a more sophisticated data assimilation method does not necessarily lead to a better initial condition. In this paper, we used the classical optimal interpolation (OI), which is the most commonly used method in similar studies [7,8,9]. We explored the benefit of assimilating only CFOSAT nadir-significant wave height (Hs) observations into the operational GDWPS of ECCC. The assessment of 2D spectra assimilation will be discussed in a following paper.

One innovation of this paper is its explicit quantification of background error. Such quantification is challenging in data assimilation [10,11] and even more so in wave data assimilation [12] due to multiple factors.

Compared to atmospheric observations, wave observations (e.g., from buoys, altimetry, or scatterometry) are both spatially and temporally sparse, making it difficult to estimate error structures due to the limited variability across scales. Wave models are often coupled with atmospheric and ocean models; therefore, errors in wind forcing or currents can propagate into wave predictions, making it challenging to isolate wave-specific background errors.

Unlike atmospheric models, the presence of landmasses significantly affects wave propagation, which involves more local nonlinear interactions such as refraction, diffraction, reflection, and shallow bathymetry. The interruption caused by land creates disconnected regions where wave fields cannot propagate freely, leading to sharp gradients in error statistics in the coastal area. Standard covariance modelling, which assumes smooth spatial correlations, breaks down near coastlines. These factors introduce greater scale variability in the wave field, an issue that has not been sufficiently addressed in previous studies.

In OI, the quantification of background error boils down to the identification of the correlation length scale L, which defines the spatial error correlation between two wave systems at different locations. Considering the inhomogeneity of the wave field, the value of L should have some spatial (and temporal, which is beyond the scope of this paper) variability. In practice, L is often assumed to be a global constant value, via an ad hoc estimate, given the difficulty of calculating a distributed L field [2,12].

Greenslade and Young [13] found that L varies considerably over the globe, with larger L at low latitudes and smaller L at high latitudes. Aouf et al. [14] proposed an empirical equation to describe L based on the latitudes of the analysis and the observations. The rationale of this method is that the wave statuses in low, mid, and high latitudes usually have unique features forced by the wind field that have distinctive latitude features. In reality, L is not always proportional to latitudes given the impact of swells/planetary waves as well as the coastline, sea ice etc. In this paper, a statistical method is proposed to identify the correlation length solely from model forecasts where the background errors are replaced with forecast errors from different forecast lead times at different locations. The goal is to obtain an objective estimate of the correlation length based on the analysis location, which is free from assumptive errors.

The remainder of this paper is structured as follows. Section 2 provides a detailed description of the wave forecasting system and the observation dataset. It also outlines the implementation of the Optimal Interpolation (OI) method, with particular emphasis on the quantification of correlation length. Section 3 presents the results, followed by a comprehensive discussion in Section 4. Finally, Section 5 concludes the study with a summary of key findings.

2. Materials and Methods

2.1. GDWPS

The WaveWatch III^® (hereafter WW3) version 7.0 [15]-based Global Deterministic Wave Prediction System (GDWPS) became operational at the Meteorological Service of Canada (MSC) of ECCC in 2017 [1]. The GDWPS has a spectral resolution of 36 direction bins (10° each) and 36 logarithmically spaced frequency bins starting at 0.035 Hz with a frequency increment factor of 1.10 until 0.984 Hz. A parametric tail is fitted for higher frequencies.

In GDWPS, wave fields are computed by solving the linear balance equation for the spectral wave action density. Parameterizations for wind input and dissipation are computed using the Ardhuin et al. [16] source term package (ST4), in which BETAMAX is set to 1.297, TAUWSHELTER is set to 0.955, and SWELLF is set to 0.818. Nonlinear wave–wave interactions are computed using the discrete interaction approximation [17]. The Joint North Sea Wave Project (JONSWAP) parameterization is used for bottom friction [18], and the Battjes and Janssen [19] scheme is chosen for depth-induced wave breaking. The propagation scheme is set to the third-order Ultimate Quickest with the Tolman [20] averaging technique. The ice concentration is treated as a mask over a specific grid cell, where ice is treated as absent when the ice concentration is less than 25% and non-penetrable for waves when it is higher than 75%. Between those two thresholds, wave propagation is attenuated proportionally. Further study about wave–ice interaction is being conducted at ECCC. Current documentation and information about open data products of the GDWPS can be accessed at https://eccc-msc.github.io/open-data/msc-data/nwp_gdwps/readme_gdwps_en/ (accessed on 5 January 2026).

The domain of GDWPS covers 80°S–86°N on a regular spherical latitude–longitude grid with a spacing of 0.25° × 0.25°. It is driven by hourly 10 m winds from the operational Global Deterministic Prediction System (GDPS) [21] and 3-hourly ice forecasts from the Global Ice-Ocean Prediction System [22]. To account for the wind weakening at the coastline due to the increased land surface friction, the forcing fields are first mapped to the wave grid using the atmospheric model land–sea interface by spreading wind speeds from ocean points onto the land points adjacent to the land–sea interface to avoid bias in wind speeds along the coastline [23]. The interpolation of the wind speeds is then performed to produce the forcing fields. The correction is particularly useful in high latitude regions where the grid spacing of the atmospheric and wave models differs significantly.

In this study, two experiment configurations are used. The control experiment, which is also referred to as open loop or OL, is that of the operational system. It relies on a pseudo-analysis to generate an initial condition by forcing a wave model with hourly winds and 3 h ice fields derived from the Incremental Analysis Update produced in the data assimilation process of the atmospheric model. The pseudo-analysis is executed four times a day for 6 h, centred at 00, 06, 12, and 18 UTC. Each pseudo-analysis retrieves initial conditions by reading a restart file written at the end of the previous pseudo-analysis. Before initiating a forecast cycle, an additional three hours (−2 h, −1 h, and 00 h) are run to mitigate potential initial-condition shocks introduced by the newly analyzed wind forcing (https://collaboration.cmc.ec.gc.ca/cmc/CMOI/product_guide/docs/tech_specifications/tech_specifications_GDWPS_e.pdf (accessed on 5 January 2026)). The forecasts from this configuration serve as the benchmark in the validation of the wave height assimilations.

In the second configuration, wave assimilation is conducted hourly using the same forcing and configuration as the control run. The significant wave height observations are assimilated hourly within the 6 h pseudo-analysis window to produce a real wave analysis, which is stored in the restart file as a new initial condition. The wave forecast based on these new initial conditions is then compared to that from the control run.

For efficiency, only the forecasts covering 48 h issued every 36 h were chosen for evaluation. The 48 h length covers lead times within which DA impacts forecasts. Limiting new forecasts to every 36 h allows us to cover a longer time period and thus sample more weather situations without vast increases in computation cost.

An example of this configuration is shown in Figure 1. For the 48 h forecast initialized at 00Z, the initial condition derived from the analysis traces back to the end of hour 21 from the 18Z analysis cycle, with an additional three hours of spin-up (22 h, 23 h, and 00 h) to smooth the transition to the new wind forcing. This approach arguably diminishes the impact of the updated initial condition from Hs assimilation, as the nominal 1 h forecast effectively corresponds to a 4 h forecast. Nevertheless, this configuration aligns with the operational GDWPS and enables a direct comparison between the two systems.

Figure 1. Diagram of GDWPS analysis and forecast cycle (beige refers to analysis cycles and blue refers to forecast cycle, downward arrows mark the time of assimilation, horizontal arrows refer to the propagation of model forecasts).

2.2. CFOSAT L2P

Among the various Hs datasets extracted from CFOSAT SWIM, the Level 2 Plus (L2P) near-real-time (NRT) 1 Hz Nadir product is chosen for assimilation due to the secondary calibration this product has. The generation of L2P involves two stages, namely cross-calibration and absolute calibration [3]. The cross-calibration is performed by comparing CFOSAT against Jason-3 at their crossover points from 1 November 2018 to 26 February 2019. The bias between these two satellites was calculated for Hs to be between 1 and 6 m. A linear regression of bias–Hs was retrieved and then applied to the CFOSAT Hs. The absolute calibration was performed in a similar method, except the reference was an in situ measurement from buoys [24].

The L2P product was first converted from its original data format, which records a single track, to the standard grid file used by ECCC. The track of Hs was aggregated to the same grid as GDWPS, and the quality control flag was interpolated using the nearest-neighbour method.

A quality control flag was used to filter the L2P Hs before it was overlaid on top of the land/sea and sea ice mask of GDWPS. Initial tests revealed that the nearshore values of the L2P Hs are often unrealistic compared to the corresponding Hs retrievals nearby. Hence, a secondary mask, which served as a buffer, was used to extend the land mask by two grid points into the sea; L2P Hs values that fell into this buffer were not considered in the assimilation. A potential drawback of this method is that it might impact the validation with buoys, which are often located nearshore. However, such an impact is minor compared to the impact of assimilating an unrealistic wave observation. Furthermore, the assimilation was only applied to grid cells where the difference between background and observed Hs was less than 5 m to minimize the impact of potential abnormal observation retrievals.

On average, each L2P track file covers a time span of roughly 90 min. The time stamp of each observation along the satellite track was matched against the valid time of the GDWPS. Observations within ±30 min of the GDWPS hourly data were kept for the assimilation.

Note that CFOSAT products were only used in the assimilation and were excluded from the CMEMS altimetry products used for validation purposes.

2.3. Optimal Interpolation

Optimal Interpolation (OI) has been the de facto method to calculate Hs for analysis in similar studies [8]. As part of the first step to update the initial condition, it handles the spatial correlations between the background Hs and relatively sparse altimetry observations efficiently.

In the classic OI, the Hs analysis $X_a$ at a given grid point is a linear combination of the background Hs $X_b$ and the innovations contributed by the surrounding observations:

$$X_a=X_b+{\sum }_{i=1}^N{W_i(X}_o^i-X_b^i)$$

(1)

where $X_o^i$ and $X_b^i$ are the observed and background Hs at the grid point location, respectively. N is the total number of surrounding observations chosen to contribute to the Hs analysis. $W_i$ is the weight assigned to each of the observations so that the root-mean-square-error between the analyzed Hs and the true Hs is minimized. The observation operator is neglected here, as it reduces to a unity matrix, since the observed variable is the same as the modelled variable. Hence, the matrix of W can be solved as follows:

$$\mathit{W}=[W_{1,}{W}_2,\dots ,W_N]=\mathit{P}{(\mathit{P}+\mathit{R})}^{-1}$$

(2)

where $\mathit{P}$ and $\mathit{R}$ are the N × N background error correlation and observation error correlation matrices, respectively. It is common to assume that altimetry observation errors are uncorrelated spatially; in this case, $\mathit{R}$ becomes a diagonal matrix with elements expressed as follows [2]:

$$R_{ii}=({{\sigma }_o^i/{\sigma }_b^i)}^2$$

(3)

where ${\sigma }_o^i/{\sigma }_b^i$ is the ratio between observation scatter and background scatter. In this study, ${\sigma }_o^i$ is set to 0.2 and ${\sigma }_b^i$ is set to 0.1, empirically.

The quantification of $\mathit{P}$ is less straightforward due to the inhomogeneity of the wave field. Analytically, the correlation between Hs at location k and location j can be calculated via

$$P_{kj}={\sigma }_b^k{\sigma }_b^j{\rho }_{kj}$$

(4)

where ${\sigma }_b^k$ and ${\sigma }_b^j$ are the background scatters at different locations. ${\rho }_{kj}$ is the spatial error correlation equation. In practice, $P_{kj}$ can be calculated through the following empirical equation [13]:

$$P_{kj}={(1+{\displaystyle \frac{D_{kj}}{L}})}^a\mathrm{e}\mathrm{x}\mathrm{p}[-c{({\displaystyle \frac{D_{kj}}{L}})}^b]$$

(5)

where $D_{kj}$ represents the distance between two grid points k and j. a, b, and c are constants whose values are established empirically. L is the optimal correlation length scale, meaning the two grid points are considered uncorrelated when their distance exceeds L. Hence, the value of L decides how far an observation can contribute to its surrounding analysis. Wang [12] argued that the analyzed Hs is more sensitive to L than to the constants a, b, and c. In this study, a simple Gaussian scenario of Equation (5) was chosen with a = 0, b = 1, and c = 1. The determination of L is discussed in the following subsection.

2.4. Background Error

Typically, L is assumed to be constant both spatially and temporally, implying a homogeneous wave field. In reality, wave field homogeneity is rarely observed. Fetches driven by inhomogeneous wind fields, wave dispersion, wave refraction, and the interaction between different wave trains [25] all contribute to the inhomogeneity of the wave field. A direct calculation of the global background error field is challenging, partly due to the limited coverage of wave observations. Parrish and Derber [26] suggested that background error can be calculated from the difference between a pair of forecasts at different lead times that are both valid at the same time, i.e., the forecasts for the same valid time but issued from different times. Based on this assumption, the background error time series B at the given grid point was calculated. We used a time difference of 36 h such that

$$\mathit{B}(\mathrm{1,2},\dots ,T)\approx ⟨{SWH}^{36}-{SWH}^0⟩$$

(6)

where T is the length of the time series, and ${SWH}^{36}$ and ${SWH}^0$ are the 36 h and nowcast significant wave height time series from GDWPS, respectively. The correlation is then calculated between this grid point and all its nearby grid points. Supposing that the distance between grid point $j$ and grid point $k$ is $D$, $P_{kj}\left(D\right)$ can be calculated from the correlation of $\mathit{B}$ between two locations with

$$P_{kj}\left(D\right)=corr({\mathit{B}}_{\mathit{j}},{\mathit{B}}_{\mathit{j}+\mathit{D}})$$

(7)

where ${\mathit{B}}_{\mathit{j}}$ and ${\mathit{B}}_{\mathit{j}+\mathit{D}}$ are the background error time series at $j$ and $k,$ respectively.

This method was first proposed by Parrish & Derber (1992) [26] in the U.S.A., but given its operational implementation and refinement at Environment Canada [27,28], it is sometimes referred to as “the Canadian method” [10]. At Environment Canada, the operational 4D-Var uses the differences between a series of 48 h and 24 h atmospheric forecasts to calculate background error covariances, which are mostly constant in time as they are computed for each month by interpolating between a set of summer and winter covariances [28]. The application of such a statistical method is relatively rare in wave modelling. Greenslade and Young [13] compared this method against an empirical method that only depended on latitude in the quantification of the spatial scale of the background error in global wave models. Admittedly, since their background error correlation computation was based on very coarse 20° by 20° boxes (even though the wave model has a resolution of 1°), they found that this method is not superior to the simple latitude-dependent method.

Bannister [10] argued that the need for specific forecast lengths is not necessary, as longer forecasts are usually chosen to eliminate errors in modelling the diurnal cycle. In this paper, 00 h–36 h was chosen mainly because the GDWPS experiments only issued forecasts every 36 h, and it was expected that the benefits of Hs assimilation would be more visible for wave forecasts in the shorter term. Nevertheless, a sensitivity study over different lengths would be an interesting subject in the future.

Figure 2 shows the curve fitting between $P_{kj}\left(D\right)$ and $D$. The background error was estimated from the GDWPS hourly forecast from early August 2021 to early June 2022. The grid was resampled to 1° by 1° to reduce data volume. Note that the unit of distance D is set to the number of grid cells instead of kilometres. This setting facilitates the calculation of $P_{kj}$, although it would lead to a larger zonal spatial scale at low latitudes than at high latitudes [2]. Based on this fitting, the best value for L is set to 8 (rounded to the closest integer). Equation (5) then reduces to Equation (8). L = 8 is set as the searching radius in OI; hence, the assimilation experiment based on this method is designated as R8.

$$P_{kj}=\exp \left[-{\displaystyle \frac{D}{8}}\right]$$

(8)

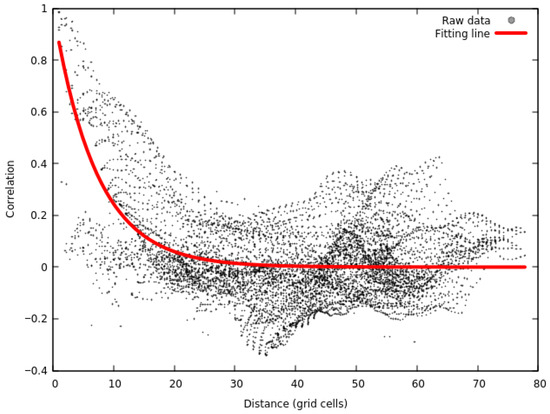
Figure 2. Curve fitting for distance-based error correlation function $P_{kj}\left(D\right)$.

A constant global L, regardless of its retrieval method, does not address the inhomogeneity of the Hs field. To address this issue, a map of the distributed L value is generated by the following steps: (a) perform the curve fitting on each 0.25° grid cell; (b) determine the significance level for the correlation coefficient, which in this study was set as 0.6; (c) on each grid cell, calculate the minimum value of L so that the correlation coefficient reaches the threshold set in Step (b); (d) generate the map of L.

Figure 3 shows the result of the L distribution based on the original 0.25° grid of the WW3 model. The unit of L is the number of grid points. The assimilation experiment based on this map is hereafter referred to as BCL (Best Correlation Length).

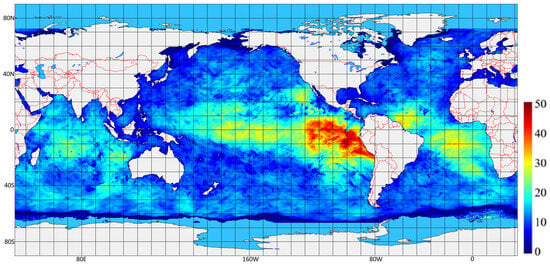
Figure 3. Distributed L in unit of number of (0.25°) grid numbers.

In online assimilation, each grid point is assigned an individual L value drawn from this L map. For research purposes, DA assimilation was carried out within the period when L was retrieved, and the potential seasonal/annual variations in L were not considered here due to the length of the study period. For a more robust result of the L map, one can repeat this method over several years and average the results, taking into account seasonal variability.

In general, the major spatial patterns shown in Figure 3 agree well with similar studies [13,29]. Our approach allows for the inclusion of additional details that capture spatial variabilities potentially associated with global ocean circulation patterns, especially in the equatorial region. In Figure 3, L has some distinctive patterns, especially in the Pacific and Atlantic Oceans. In the Pacific Ocean, there is a patch of high L values extending from the Philippines to Ecuador. In the East Philippines, the width of this patch is merely a few hundred kilometres, while it expands from California to Chile upon reaching the American continents. The value of L in this patch also increases from west to east. L values are around 20 grid points near the Philippines and can reach more than 50 grid points in the eastern Pacific Ocean, the largest values globally. For the rest of the Pacific, L values are roughly between 4 and 12. This patch seems to pass through South America and continues to develop in the South Atlantic, with a weaker signal (L = 25~35), but it covers almost all of the southeast Atlantic. The irregular shape of this patch indicates that L is not linearly related to latitudes, even though the tropical region generally has higher L values.

The rest of the Atlantic has similar values to the outskirts of the Pacific, which are not covered by the jet. The Indian Ocean does not have such distinctive patterns. The north and east Indian Ocean tend to have higher L values (~25) compared to the south and west Indian Ocean, where L tends to be below 10. In general, the Southern Ocean has lower L values (below 8), which is likely due to the strong winds in this region. Compared to other oceans, the Southern Ocean has more complex bathymetry. Variations in seafloor depth and features like ridges and troughs can create local patterns of currents and eddies, which prevent the development of large correlation lengths.

2.5. Spectral Update

Significant wave height is an a posteriori parameter that only reflects the total energy of the wave. The 2D wave spectrum, which is the actual state vector that propagates in the dynamic model, must be updated in the initial condition to reflect the impact of data assimilation. The state vector is only updated indirectly; this is a key difference between Hs assimilation and spectrum assimilation. The key issue in the conversion from the Hs update to the spectrum update is the reconstruction of the wave spectra. Traditionally, this was performed with a diagnostic spectrum shape from Hs [18,30]. However, these unimodal spectrum shapes usually fail to address the different properties of individual wave components, i.e., wind waves and swells [31].

In this paper, the reconstruction scheme proposed by Saulter et al. [32] is adopted, in which the wind, sea, and swell components are updated separately. To separate the wind waves from swells, a relative wind speed ${WS}_r$ is calculated using

$${WS}_r=\alpha WS\times cos(WnD-WD)$$

(9)

where $\alpha$ is the wind wave cutoff coefficient. $WS$ is the 10 m wind speed, $WnD$ is the wind direction and $WD$ is the componential wave direction. If ${WS}_r$ is larger than the componential wave velocity, then the component is considered a wind wave. In this case, the wind wave energy is integrated over frequency space, and the significant wave height for wind sea (Hw) is retrieved. Otherwise, it is considered a swell, and the significant wave height for the swell (Hs) is retrieved. Finally, the total wave height $H_t$ is calculated from the combined wave energy of both wind waves and swells. With these, the wind wave energy contribution ratio $c$ is calculated using

$$c={({\displaystyle \frac{H_w}{H_t}})}^2$$

(10)

When c > 0.7, the spectrum is considered wind-sea dominant, and the whole wave energy is updated following:

$$E_a(f,\theta )=c_w^2{E}_b(\alpha f,\theta )$$

(11)

where the update factor $c_w$ is calculated only when the analyzed Hs is larger than the background significant wave height for swells:

$$c_w^2={\displaystyle \frac{{SWH}^2-H_s^2}{H_w^2}}$$

(12)

$$\alpha =c_w^{-2/3}$$

(13)

When c ≤ 0.7, the spectrum is considered swell dominant and the updated wave energy $E_a$ is calculated by applying an analyzed Hs-related bulk factor to the background wave energy $E_b$:

$$E_a(f,\theta )={\left({\displaystyle \frac{SWH}{H_t}}\right)}^2{E}_b(f,\theta )$$

(14)

Equation (13) is based on the relationship between significant wave height and peak period for growing wind-seas. The non-dimensional version of the significant wave height can be expressed with the 3/2 power of the non-dimensional version of the peak period. This is known as the three-second power law for wind waves of a simple spectrum [33].

The frequency shift is followed by the interpolation of the wave energy bins to the inherent frequency-direction space of WW3. In this study, the swell parts of a wind-wave dominant spectrum are also updated, but without a frequency shift. The final updated spectra are a combination of both the updated wind waves and updated swells.

It is worth noting that the frequency shifting method is still an empirical method, even though it is more sophisticated than most other spectral update methods. The energy contribution threshold between wind waves and swells is often set subjectively, and the frequency shift is applied not necessarily to wind waves [34]. Toba’s equation only applies during the stage of growing wind-seas; it might not perform well for abating winds and seas. It also only shifts frequency when the Hs analysis is larger than the background Hs, which is not always the case. That being said, this method does outperform other methods without frequency shifts based on our tests. It is hence selected as the de facto method until the spectrum observations are assimilated directly in the future.

3. Results

3.1. Hs Increments

Figure 4 shows the Hs forecast differences or increments between the control open loop (hereby referred to as OL) and assimilation experiments, where BCL refers to the distribution of BCL and R8 refers to the universal length R = 8 grids all over the globe. The forecasts were issued at 00 h of 30 September 2021, after two months of hourly Hs assimilation. Figure 4a shows the nowcast of OL at 00 h. Figure 4c shows the Hs difference between OL and the nowcast from BCL, and Figure 4e shows the Hs difference between OL and the nowcast from R8. The right column shows the same contents but for the 48 h forecasts.

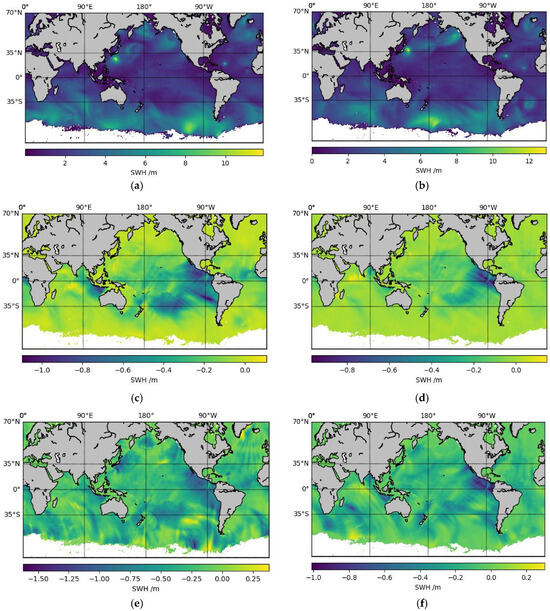
Figure 4. Significant wave height Hs forecast differences between Open Loop (OL) and assimilation experiment BCL (the middle row) and R8 (the lower row) at 00 h (left column) and 48 h forecast (right column). (a) L1: nowcast at 2021093000_00h; (b) R1: forecast at 2021093000_48h; (c) L2: OL minus BCL at 2021093000_000h; (d): R2: OL minus BCL at 2021093000_048h; (e) L3: OL minus R8 at 2021093000_000h; (f) R3: OL minus R8 at 2021093000_048h.

The widespread negative values in Figure 4c show that BCL assimilation increases Hs globally compared to OL. Such an increase is particularly significant in the mid-low latitude Pacific Ocean, while it is very small in high latitude oceans. The maximum difference between OL and BCL can be as high as −1.1 m. After 48 h, the domain of larger increment shrinks significantly to the mid-east Pacific (see Figure 4d), aligning with the high values of L in the BCL map. However, the peak increment in Figure 4d can still reach up to −1.0 m, representing a 0.1 m reduction from the maximum increment 48 h before.

Like BCL, R8 also increases the Hs forecast almost everywhere compared to OL. At 00 h, the major increments are also located in the mid-east Pacific but have a much smaller domain compared to BCL. Another two locations with major increments are south of Japan and in the Southern Ocean (Figure 4e), where there are storm events in development (Figure 4a), which cannot be seen in BCL (Figure 4c). Globally, the difference between OL and R8 can reach up to −1.7 m, which is much larger than BCL. At 48 h, the increment diminishes significantly globally, with the largest increments still in the mid-east Pacific and larger increments elsewhere compared to BCL (see Figure 4f). The maximum difference between OL and R8 is −1.1 m, decreasing by 0.6 m in 48 h. Although the two aforementioned storms are still ongoing, the impact from the previous assimilation seems to have disappeared completely.

The persistence of increments in the mid-east Pacific is likely due to the swell’s dominance in this region, as these have a longer memory compared to wind waves. Globally, R8 leads to more increments than BCL, although it is less robust compared to BCL. The analysis of R8 is affected more by local winds, and the analysis of BCL is affected more by geo-locations.

3.2. Forecast Scores

The forecasts of Hs and peak period TP from the two assimilation experiments were compared against wave buoy observations from the Global Telecommunications System (GTS) (https://community.wmo.int/en/activity-areas/global-telecommunication-system-gts (accessed on 5 January 2026)) using the operational EMET verification system developed at ECCC. The location of the buoys that passed quality control in EMET can be found in Figure 5. In EMET, the buoys are matched to the model data using the nearest-neighbour method. EMET takes the time of observation, rounded to the nearest whole hour, as the valid date to match with the valid date of the model without interpolation. If more than one observation lies within 30 min of the top of the hour, only the observation nearest in time to the top of the hour is retained, thus producing a unique time series for each wave buoy.

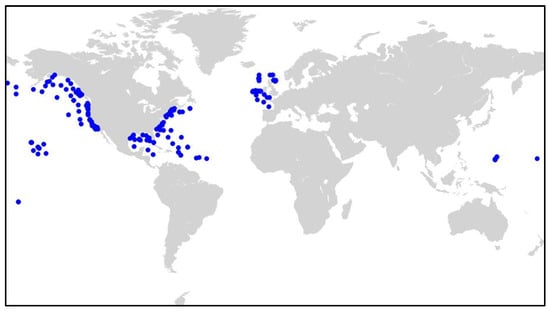
Figure 5. Buoy network used in EMET score calculation.

Figure 6 shows the bias and standard deviation (stdev) for the Hs and TP forecasts up to 48 h. A detailed comparison between R8 and BCL is provided in Table 1. Figure 6a shows the bias in the Hs forecast for all models compared to the buoys. Compared to BCL and OL, R8 has a more significant impact on bias. However, it seems to overcorrect the bias of Hs for the first few hours. At 00 h, BCL reduces the bias of OL from −5.8 × 10⁻² m to −3.9 × 10⁻² m while R8 corrects it to 4.6 × 10⁻² m. OL tends to underestimate Hs, and forecasts from data assimilation will eventually converge to OL. The positive correction of R8 brings a significant reduction to the bias and absolute bias in the forecast, but it diminishes dramatically in later hours. The correction brought by BCL assimilation, although mild, shows sufficient robustness in longer forecasts. At the end of 48 h, there is still roughly a 13% improvement compared to OL.

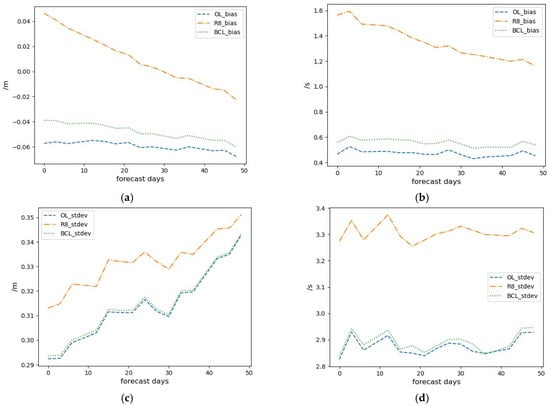
Figure 6. Buoy verification results for Hs and TP forecasts up to 48 h (a): Hs bias; (b): TP bias; (c): Hs stdev; (d): TP stdev.

Table 1. Compare R8 with BCL with statistics.

Statistic	Model	00 h	03 h	06 h
Hs_bias(m)	R8	0.046	0.041	0.034
	BCL	−0.039	−0.039	−0.042
Hs_STDEV(m)	R8	0.313	0.315	0.323
	BCL	0.294	0.294	0.300
Tp_bias(s)	R8	1.564	1.594	1.491
	BCL	0.558	0.608	0.576
Tp_STDEV(s)	R8	3.274	3.352	3.279
	BCL	2.840	2.942	2.881

Neither R8 nor BCL reduce the bias in the peak period forecast (Figure 6b). This is not uncommon, considering the extremely volatile nature of TP, which is difficult to model and very sensitive to changes in initial conditions. However, the degradation of TP from BCL is minimal compared to R8. At 00 h, BCL increases TP bias from 0.47 s to 0.56 s, representing a 20% degradation. At 48 h, this degradation shrinks to 12%. R8 bias is 1.56 s at 00 h, which represents 330% degradation; at the end of 48 h, there is still a 260% degradation.

The standard deviations for both Hs (Figure 6c) and TP (Figure 6d) have similar patterns to the TP bias. R8 has significant degradation in both cases, yet the impact of BCL is very minimal, especially for the standard deviation of Hs, in which BCL has almost a neutral impact.

Table 1 compares BCL to R8 in terms of the scores for the first 6 h forecasts. The better performance is in bold. It verifies the overcorrection of Hs bias from R8, as the absolute bias from BCL at both 00 h and 03 h is smaller than that from R8. Only starting from 06 h, the forecast from R8 assimilation starts to outperform BCL for Hs bias. For all other indicators, including TP bias, Hs, and TP STDEV, BCL outperforms R8.

3.3. CMEMS Validation

Wave buoys are often deployed nearshore and do not offer a truly global representation. It is therefore necessary to verify these results with alternative satellites which have a global footprint. In this study, the global L3 altimetry Hs product (https://doi.org/10.48670/moi-00179 (accessed on 5 January 2026)) from Copernicus Marine Environment Monitoring Service (CMEMS) was used. The following altimetry missions were used for verification: Cryosat-2, Jason-3, SARAL-Altika, Sentinel-3a, Sentinel-3b, Sentinel-6a and HaiYang-2B. None of the satellite observations used for verification were used in the data assimilation process.

Note that GDWPS was calibrated against selected buoys but was not bias-corrected relative to CMEMS, as CMEMS retrievals themselves may contain systematic biases, and such a correction is impractical in an operational forecasting context. In contrast to wave models, ECMWF applies bias correction to altimetry observations prior to assimilating them into the ERA6 wave reanalysis.

Considering the computation cost to obtain the data density required for the results to be statistically meaningful, both L3 track files and model outputs were aggregated to 2-degree by 2-degree blocks during the verification [1]. Matches between the along-track satellite observations and model values were also binned into forecast days (as opposed to lead hours). This spatial and temporal aggregation helped to reduce the length of the signal needed, as many of the altimeters have a return period of order 10 days. In this context, it would take roughly two months for a global coverage of CMEMS track files.

Figure 7 shows the bias of 1-day forecasts from various models with and without previous assimilation. Figure 7a,b, and c show the difference between OL and CMEMS, R8 and CMEMS, and BCL and CMEMS, respectively. The positive bias in red means that the model overestimates Hs, and the negative bias in blue means that the model underestimates Hs compared to CMEMS. The three models have some similar spatial patterns, for example, overestimation in the southern oceans (south of 23.5°S) and underestimation in the tropical oceans (23.5°N−23.5°S).

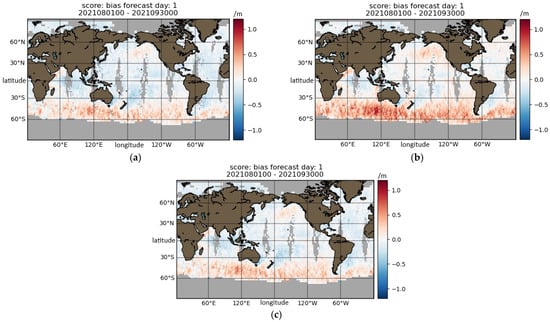
Figure 7. 0–24 h Hs bias (model-CMEMS) of three models: (a) OL minus CMEMS; (b) R8 minus CMEMS; (c) BCL minus CMEMS.

R8 has a higher Hs forecast globally compared to OL. It mitigates the underestimation in the tropical oceans, but at the cost of worsening the overestimation in the southern oceans. OL overestimates Hs in the northeast Pacific Ocean but underestimates it in the northwest Pacific Ocean and the northern Atlantic Ocean. With R8, Hs is overestimated in all three regions, indicating a positive overcorrection. Compared to R8, the correction from BCL is more moderate, and it is capable of reducing both the underestimation in the tropical oceans with lighter blue and the overestimation in the southern oceans with lighter red observed when comparing Figure 6c against Figure 6a.

To further investigate the performance of R8 versus BCL, a block-to-block comparison was performed over three different parts of the global oceans based on latitudes, namely the northern oceans (23.5°N–66°N), the tropical oceans (23.5°N−23.5°S), and the southern oceans (23.5°S–66°S). For the 3 months of the study period, the probability distribution (PD) of the 1-day forecast from the models (beige) was compared against CMEMS Hs observations (blue). The overlay of two models is marked in grey. The PD results are shown in Figure 8, and their statistics are listed in Table 2, where the better performances are in bold.

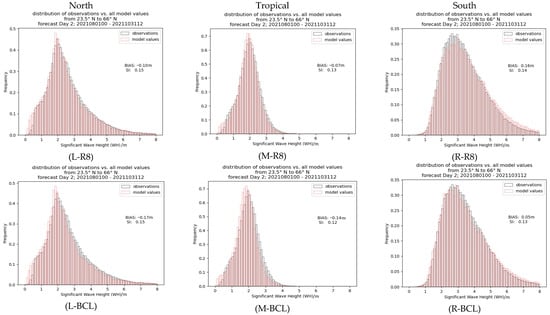
Figure 8. Latitude-based Probability Distributions of CMEMS Hs observations from 2021-09-30-00h to 2021-10-31-12h (black) compared to the most recent model forecasts (red) from R8 and BCL. (L-R8): R8 in North Ocean; (M-R8): R8 in Tropical Ocean; (R-R8): R8 in South Ocean; (L-BCL): BCL in North Ocean; (M-BCL): BCL in Tropical Ocean; (R-BCL): BCL in South Ocean.

Table 2. Statistics of R8 and BCL compared to CMEMS.

		R8	BCL
North	Bias (m)	−0.10	−0.17
	SI (-)	0.15	0.15
Tropics	Bias (m)	−0.07	−0.14
	SI (-)	0.13	0.12
South	Bias (m)	0.16	0.05
	SI (-)	0.14	0.13

In Figure 8, the left panel shows the results for northern oceans (L-R8 and L-BCL), the middle panel shows the results for tropical oceans (M-R8 and M-BCL), and finally, the right panel shows the results for southern oceans (R-R8 and R-BCL).

In the northern oceans, the BCL forecast has better variation than R8 but a worse mean value. BCL slightly underestimates Hs with a right-shifted PD compared to CMEMS (see L-BCL), which is less obvious in R8 (see L-R8). The better mean of R8 is in accordance with Figure 6a, and the worse variation is in accordance with Figure 6c. This is reasonable considering that most of the GTS buoys used in this study are located in the northern oceans.

In the southern oceans, BCL significantly outperforms R8 in terms of both bias and scatter index (SI) (see Table 2). R8 underestimates medium and low Hs and overestimates high Hs (see R-R8). This indicates that the constant L of the eight grid points is probably too short in the southern oceans, even though this region is wind-wave dominant.

According to Table 2, in both northern and tropical oceans, Compared to BCL, R8 has a lower bias but not necessarily a lower scatter index. Although BCL provides slightly better SI in the tropics, the variable L values offered by BCL are probably too large in this area.

Compared to the tropical and southern oceans, the wave propagation is more likely to be affected by coastlines in the northern oceans due to the larger landmass here. The identification of L is therefore more complicated here.

4. Discussion

This paper evaluates the impact of CFOSAT wave height assimilation on wave forecasts using GDWPS. A statistical method is proposed to quantify the background error. To account for the inhomogeneity of the wave field, a BCL map is generated. This map reveals that there is a high correlation length zone located in the mid-east Pacific Ocean. Although the correlation lengths are much higher in tropical oceans than in high-latitude oceans, they are not linearly related to the latitudes. Based upon buoy and satellite validations, this new method, BCL, overall outperforms the traditional method, which is based on a constant global correlation length (R8).

Compared to R8, the propagation of the increment of Hs in BCL is more robust, despite the initial increment of the former having a larger magnitude. The increment of the 48 h forecast in BCL still retains a similar spatial pattern to the initial condition, indicating a better carry-over of the assimilation of swells in BCL. The 48 h increment in R8 has a very minimal memory of the spatial patterns of 00 h. This means it is more sensitive to the background wave condition and wind forcing.

Based upon buoy validation, both BCL and R8 can reduce the bias in Hs forecast from the open loop for at least 48 h. The BCL forecast has a smaller absolute bias than R8 for up to 6 h. While neither model can reduce the bias in the forecast of the peak period, TP, the deterioration from R8 is much worse than that of BCL. BCL has a very minimal impact on the standard deviation of both Hs and TP, while they deteriorate significantly in R8. The failure to improve the TP forecast is not uncommon, considering the volatile nature of TP. There are ongoing efforts to replace TP with the mean period for a more reliable assessment of model performance in the future.

The global bias maps of the Hs forecasts, which are based on CMEMS satellite observations, show that R8 brings a positive increment to the Hs forecast on a global scale. In the northern oceans, it often overcorrects the negative bias in the Hs forecast from the open loop. In the southern oceans, it worsens the overestimation of Hs, which is not the case for BCL. Statistics of PDs reveal that BCL is far superior to R8 in the southern oceans. In the northern oceans, BCL has a better standard variation, while R8 has a better mean value. BCL slightly underperforms compared to R8 in the tropical oceans, which implies that BCL might overestimate correlation lengths in the tropics. A potential solution is to relax the significance threshold in the generation of the BCL map.

5. Conclusions

Overall, CFOSAT Hs is considered suitable for assimilation into wave forecasting systems. Given the distinct distribution of BCL, it would be valuable to investigate its correlation with global physical constraints such as wind forcing, ocean currents, and bathymetry. This study demonstrates that a statistical approach can effectively estimate background errors for the wave field, which could potentially enhance other data assimilation frameworks, such as 4D-Var or EnKF, when applied to wave data assimilation. In addition to further refinement of the current system, direct assimilation of two-dimensional spectra is under development to fully exploit CFOSAT observations. BCL will also be evaluated using additional altimetry observations in preparation for future operational wave assimilation.