UAV Remote Sensing of Submerged Marine Heritage: The Tirpitz Wreck Site, Håkøya, Norway

Highlights

What are the main findings?

• UAV-based through-surface photogrammetry successfully produced accurate (<10 cm) reconstructions of shallow submerged structures.
• Bathymetric estimation in shallow (<10 m) water using structure from motion applied to through-surface UAV data was effective compared to spectral ratio methods, such as the Stumpf model.

What is the implication of the main finding?

• Low-cost, easily implementable UAV systems can be used effectively to document underwater cultural heritage in shallow, clear water, providing a practical alternative to surveys using divers or vessels.
• This highlights the potential of SfM for shallow-water bathymetry in situations where the sea floor is optically heterogeneous.

Abstract

This study evaluates the use of UAV-based photogrammetry to document shallow submerged cultural heritage, focusing on the Tirpitz wreck salvage site near Håkøya, Norway. Using a DJI Phantom 4 Multispectral drone, we acquired RGB and multispectral imagery over structures located at depths of up to 5–10 m. Structure-from-motion (SfM) processing enabled the three-dimensional reconstruction of submerged features, including a 52 × 10 m wharf and adjacent debris piles, with an accuracy of the order of 10 cm. Our data represents the first and only accurate mapping of the site yet carried out, with an absolute position uncertainty estimated to be no greater than 3 m. Volumes of imaged debris could be estimated, using a background subtraction method to allow for variable bathymetry, at around 350 m³. Bathymetric data for the sea floor could be derived effectively from an SfM point cloud, though less effectively applying the Stumpf model to the multispectral data as a result of significant spectral variation in the sea floor reflectance. Our results show that UAV-based through-surface SfM is a viable, low-cost method for reconstructing submerged heritage with high spatial accuracy. These findings support the integration of UAV-based remote sensing into heritage and environmental monitoring frameworks for shallow aquatic environments.

1. Introduction

The use of UAVs (unmanned/uncrewed/unoccupied aerial vehicles, or, in popular usage, ‘drones’) as platforms for collecting scientifically valid data has increased enormously over the last few years in many fields of study, including marine environments [1,2,3]. UAV platforms, and the unmanned aerial systems (UASs) of which they form a part, provide a number of advantages compared with satellite remote sensing data, including an increased flexibility of operation and the potential for centimetric spatial resolution, though with some disadvantages, including the need for higher technical skill on the part of the operator and a more restrictive legislative environment [4]. UAVs provide a platform from which different types of sensors can be deployed, though the commonest such sensor remains the three-band-colour digital camera (‘RGB imager’). Multispectral imagers, typically also providing one or more spectral bands in the near-infrared part of the spectrum, are also often carried via UAVs.

In general, the digital images acquired from such systems, viewing downwards towards the earth’s surface, can be analysed quantitatively using the methods of multispectral image classification [5,6,7] to classify different surface materials on the basis of their spectral signature (characteristic variation of reflectance with wavelength). Such methods have been very extensively developed and refined for digital RGB and multispectral imagery acquired from spaceborne, airborne, and handheld platforms [8,9,10], although object-based classification, again well established for satellite-borne imagery, finds its way into the analysis of data collected from UAV platforms [11].

The flexibility of image collection from UAVs has also led to their increasing popularity for generating three-dimensional datasets in which the spatial coordinates of imaged objects are deduced from the different geometrical perspectives present in overlapping images acquired from different viewpoints, using the structure-from-motion technique [12,13,14]. This can be used qualitatively to visualise objects as they would be seen from vantage points not physically realised, and quantitatively for the mensuration of remote objects.

UAV-based imaging at a very high spatial resolution is routinely possible for objects located within the aerial space. A search of the Web of Science database (https://www.webofscience.com/wos/woscc/basic-search accessed 15 July 2025) at the time of writing (July 2025) showed 1080 documents with author-supplied keywords including both ‘UAV’ and ‘photogrammetry’, dating from 1998. However, the UAV-based imaging of objects located below a water surface is a much less well-established technique. A similar Web of Science search for the terms ‘UAV’ and ‘bathymetry’ located 54 documents, with the earliest being dated to 2013, and a search for ‘UAV’ and ‘two-media’ found only six documents, dating from 2014 onwards. Photogrammetric bathymetry from a UAV platform was demonstrated in 2016 [15], and some of the technical difficulties have been explored since then [1,16,17]. Recent publications suggest that two-medium imaging and geometric reconstruction can be achieved to depths of up to 5–10 m and with spatial resolutions approaching 10 cm [18,19], although no systematic investigation of this potential, and of the factors affecting performance, has yet been reported to the best of the authors’ knowledge.

One of the most challenging aspects of two-media photogrammetry is that of refraction at the air–water interface. The two-medium problem in photogrammetry has been identified and addressed since three-quarters of a century ago [20]. The usual SfM process for reconstructing three-dimensional geometry assumes a rectilinear propagation of light from the target object to the imaging device [21,22], whereas refraction at the interface introduces nonlinearity to the propagation. The deleterious effect on imaging quality is known to increase with depth [21]. The rigorous modification of the ray-tracing procedures employed in SfM geometrical reconstruction is complicated (although the physics is well understood) and slows an already computationally intense process [16,23], so there is a clear interest in testing whether simpler methods of approximately correcting for refractive effects can be successful [24].

This study investigates the feasibility of using UAV-based imaging, including SfM, to document shallow submerged cultural heritage features. The study location is the historic Tirpitz wreck salvage site near Håkøya, Norway. Our aim is to test whether centimetric-scale reconstructions of submerged structures are possible using off-the-shelf UAV hardware and standard processing software and to explore the implications of such techniques for archaeological and environmental monitoring. After demonstrating that successful two-medium retrievals are possible, we pay particular attention to the scope for determining 2- and 3-dimensional geometries of materials lying on the sea floor, and we also consider the scope offered by UAV multispectral imagery for extracting bathymetric data for the sea floor itself.

Our analytical approach prioritises the understanding and validation of the data processing chain over computational efficiency. We, therefore, adopt a ‘tiered’ approach combining GIS-based spatial processing with lower-level image analysis and numerical tools that allow us to interrogate individual steps in isolation before integrating them into a unified workflow. This gives us greater confidence in the robustness of our results. However, we emphasise that the final workflow is not dependent on the use of these latter tools and can be implemented in standard GIS software such as QGIS. It is also our aim to generate documentary evidence of the wreck site.

2. Materials and Methods

2.1. Study Site

The study site is located off the southern shore of Håkøya Island in Troms County, Norway, at approximately 69.647°N, 18.806°E (Figure 1). The site was the last location of the second-world-war German battleship Tirpitz, deployed to Norway in 1942 and finally sunk at anchor by Royal Air Force bombers on 12 November 1944, following earlier attempts by the Royal Navy, the Soviet Red Army Air Force, and the RAF (Figure 2). During the subsequent salvage (1947 to 1958), many pollutants were released, and commercially worthless material was dumped on the seabed. The site continues to be of significance and to attract political debate. As a second-world-war shipwreck site, it is representative of the main category of submerged cultural heritage in northern Norway, with vessels built over 100 years ago automatically protected by the Norwegian Cultural Heritage Act. The ship itself has been removed, but the site remains popular with divers. An attempt to protect the site under the Cultural Heritage Act, based in part on the threat from the widespread unauthorised removal of artefacts and as a political initiative to provide a more balanced representation of WWII heritage, was abandoned in 2016 as a result of opposition from the diving community and others. For these reasons, the site is unusually attractive as a location in which to investigate the possibilities offered via robotic investigation. It has been the focus of the Tirpitz Site Project of the Arctic Legacy of War programme [25], https://en.uit.no/project/Arcticlow accessed 15 December 2025) of the UiT Arctic University of Norway since 2023. However, it appears that no detailed mapping of the site has been undertaken. While this statement is difficult to substantiate formally since a lack of documentation is not usually something commented upon, we note that the report ‘Tirpitz ved Tromsø: Krigshistorie og opphogging Rapport’ [Tirpitz near Tromsø: war history and scrapping report] 02/00848 of the Tromsø kommune in 2002 mentions existing investigations and documentation limited to environmental surveys.

The principal visible manifestations of the site, and the objects of this study, are piles of salvage debris and the remains of a wharf that was constructed as part of the salvage operation. These lie in shallow water at a nominal depth of around 5 m. At low tide, the wharf structure can be partially exposed above the surface.

2.2. UAV Platform and Data Acquisition

We deployed a DJI Phantom 4 Multispectral UAV, equipped with both RGB and multispectral sensors. The multispectral sensor has five bands, at 450 ± 16 nm, 560 ± 16 nm, 650 ± 16 nm, 730 ± 16 nm, and 840 ± 26 nm (blue, green, red, red edge, and near-infrared, respectively), with a 1600 × 1300 pixel resolution and a ground sample distance of 0.43 milliradians. The RGB camera has wider coverage (5472 × 4104 pixel resolution) and a finer resolution (0.23 milliradians).

We determined that the optimal time of year for acquiring data would be after the return of sunlight at this arctic location, but before the spring algal bloom [26]. In consultation with members of the local diving community, who have dived on the site for several decades, late March was chosen for the initial survey and data collection took place on 28 March 2023. The flying altitude was around 60–70 m, giving pixel resolutions of around 3 cm (multispectral) and 1.6 cm (RGB). Flight paths were programmed to maintain a constant orientation of solar illumination and shadows, in order to simplify image processing. The image overlap was set to 80%. UAV operations were coordinated with local Air Traffic Control due to the site’s proximity to Tromsø airport, and the UAV was maintained in line of sight, and personally observed, throughout the operations. Although data collection took place around low tide, the wharf was fully submerged.

2.3. Image Preprocessing

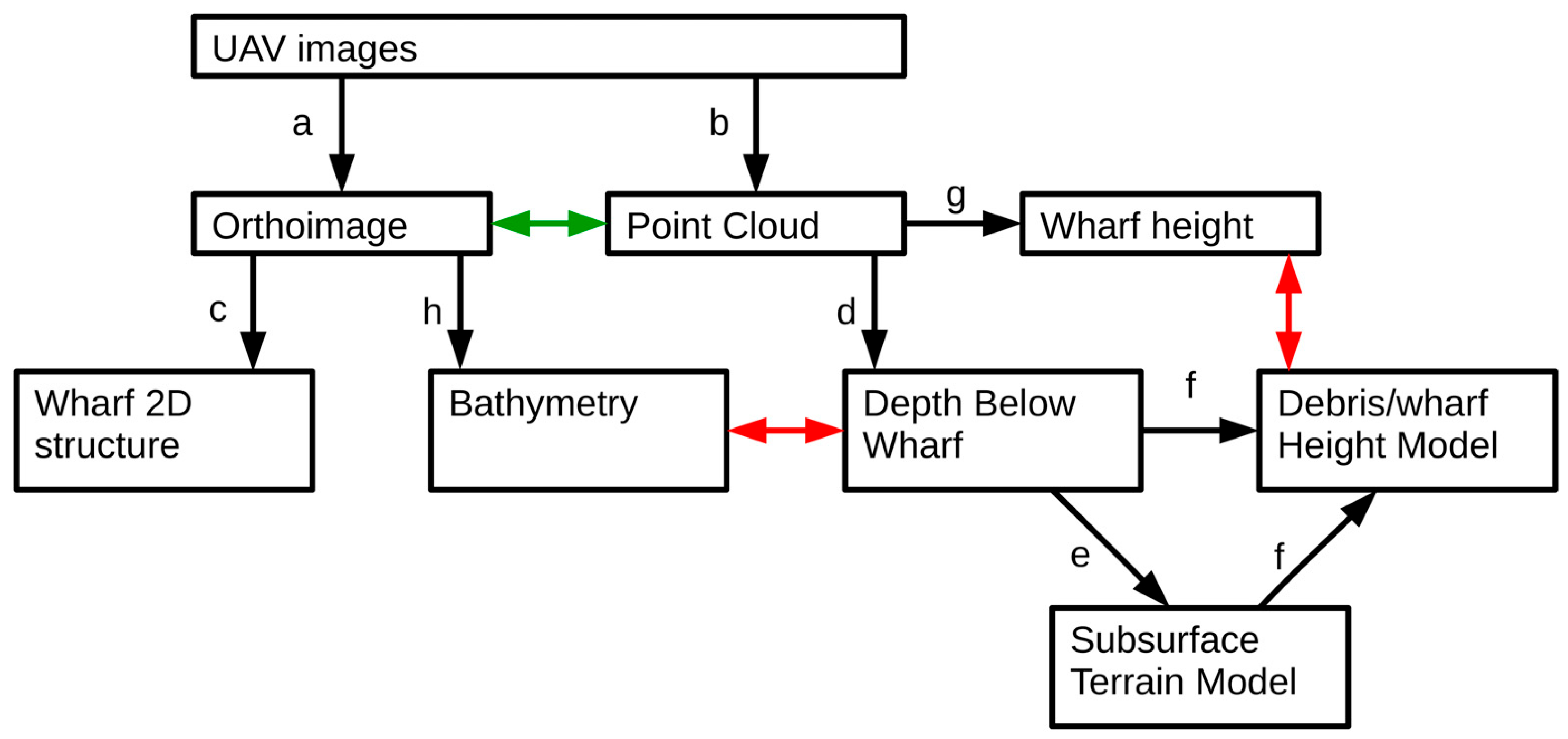
In this section, and subsequently, bold letters in parentheses, (a) to (h), are used to identify steps in the data processing summarised in Figure 3.

A total of 976 images were collected. Preprocessing was conducted using the Pix4D software (https://www.pix4d.com/ accessed 15 December 2025), version 4.9.0, without any special precautions or refraction correction for the two-medium imaging of submerged objects (this is discussed in Section 2.4). We followed the standard processing procedures with default values, including filtering the images for quality, assessing the quality of alignment and frame overlap, and producing dense point clouds, orthomosaics, and DEMs. For the multispectral images, radiometric calibration to reflectance was also carried out, using preflight images of calibration targets. Two sets of images were analysed: one covering the entire site (828 images) and another focused on the wharf (148 images). 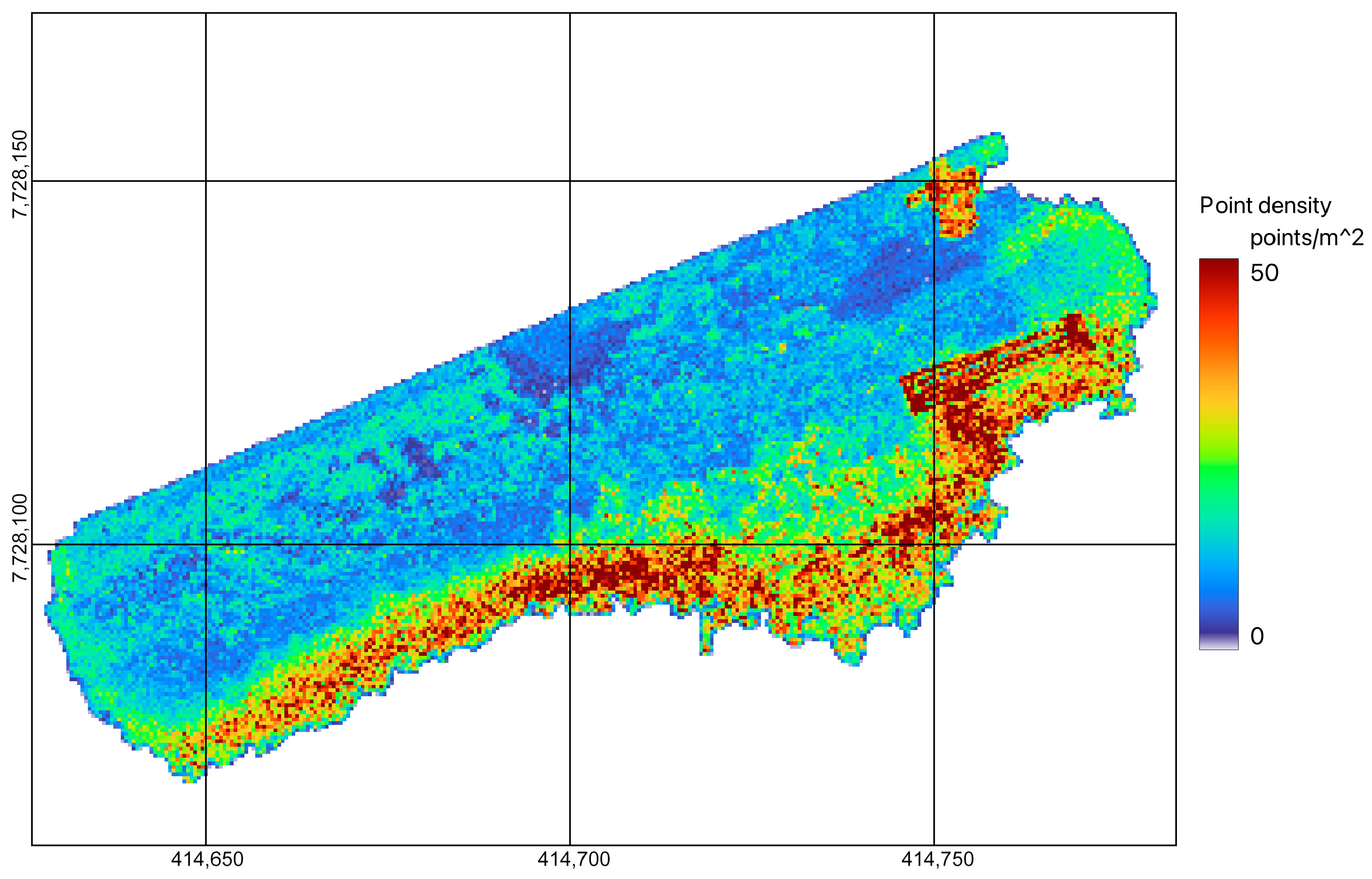This resulted in two principal data products: a 5-band georeferenced multispectral orthomosaic (a), with a pixel size of 2.2 cm, clipped to the area of interest defined by the wharf and the debris piles, and a point cloud (b) of 494,176 georeferenced points at an average density of around 16 points per square metre (calculated from area of convex hull). Point densities around the debris piles and wharf were typically above 25 per square metre (Figure 4). The point cloud was visualised within the Pix4D software, giving the first indication of the success of the SfM processing and the quality of the data (Figure 5).

2.4. Refraction Model

As noted above, one serious concern regarding two-medium imaging is whether refraction effects at the surface are large enough to invalidate the assumptions made in applying normal ray-tracing methods for three-dimensional reconstruction from images. Here, we consider the potential influence of refraction on geometrical reconstruction by developing a simple model, following [18,24] and assuming that photogrammetric image processing does not otherwise allow for the effects of refraction at the water–air interface. To obtain a quantitative understanding of the effect of refraction, we consider the case where a point object is imaged just twice, at angles of φ₁ and φ₂ to the vertical. The object is assumed to be located at depth d below the water surface, and its apparent position (defined as the intersection of the imaging rays in air) is located at depth d′ below the surface and displaced by horizontal distance x (Figure 6). The refractive index of water relative to air is n.

A straightforward application of Snell’s law of refraction shows that

$${\displaystyle \frac{x}{d}}={\displaystyle \frac{\frac{cos{\varphi }_1}{\sqrt{n^2-{sin}^2{\varphi }_1}}-\frac{cos{\varphi }_2}{\sqrt{n^2-{sin}^2{\varphi }_2}}}{cot{\varphi }_1-cot{\varphi }_2}}$$

(1)

and that

$${\displaystyle \frac{d^{\prime }}{d}}={\displaystyle \frac{x}{d}}cot\varphi -{\displaystyle \frac{cos\varphi }{\sqrt{n^2-{sin}^2\varphi }}}$$

(2)

where φ can denote either φ₁ or φ₂. As is well known, when values of |φ| are sufficiently small, (2) is approximated as

$${\displaystyle \frac{d^{\prime }}{d}}\approx {\displaystyle \frac{1}{n}}$$

(3)

Equations (1) and (2) are plotted in Figure 7, for a nominal refractive index n = 1.33. The figure shows that, for example, for viewing angles up to about 30˚ from the nadir, the assumption that the imaged point is not displaced horizontally and that Equation (3) is valid is accurate to about 0.05 d. It is thus reasonable to assume that the reconstruction of a point cloud for a submerged object will be successful for images acquired reasonably close to vertical observation and that the only correction that would need to be applied would be to compensate for the effect of Equation (3) on the position of submerged points. This optimistic conclusion forms the basis of the UAV-based studies described below.

2.5. Bathymetric Analysis

It is well known that multispectral data from shallow water can be used to estimate the depth of the water column to the sea floor, as a consequence of the different absorption coefficients in water for light of different wavelengths. Although Lyzenga’s [27] approach is closely based on Beer’s law of absorption, the ‘Stumpf model’ [28] is usually preferred since it requires fewer parameters to be tuned and is less sensitive to variations in bottom reflectance. According to the latter model, the depth z is estimated by a function

$$z=m_1{\displaystyle \frac{ln\left(n{r}_1\right)}{ln\left(n{r}_2\right)}}+m_0,$$

(4)

where r₁ and r₂ are the measured reflectances at two different wavelengths, while m₀, m₁ and n are tuneable parameters to fit suitable calibration data. The parameter n also performs the role of ensuring that neither of the logarithm terms is negative; i.e., it must satisfy

$$n>max(r_1^{-1},r_2^{-1}).$$

(5)

2.6. Data Processing

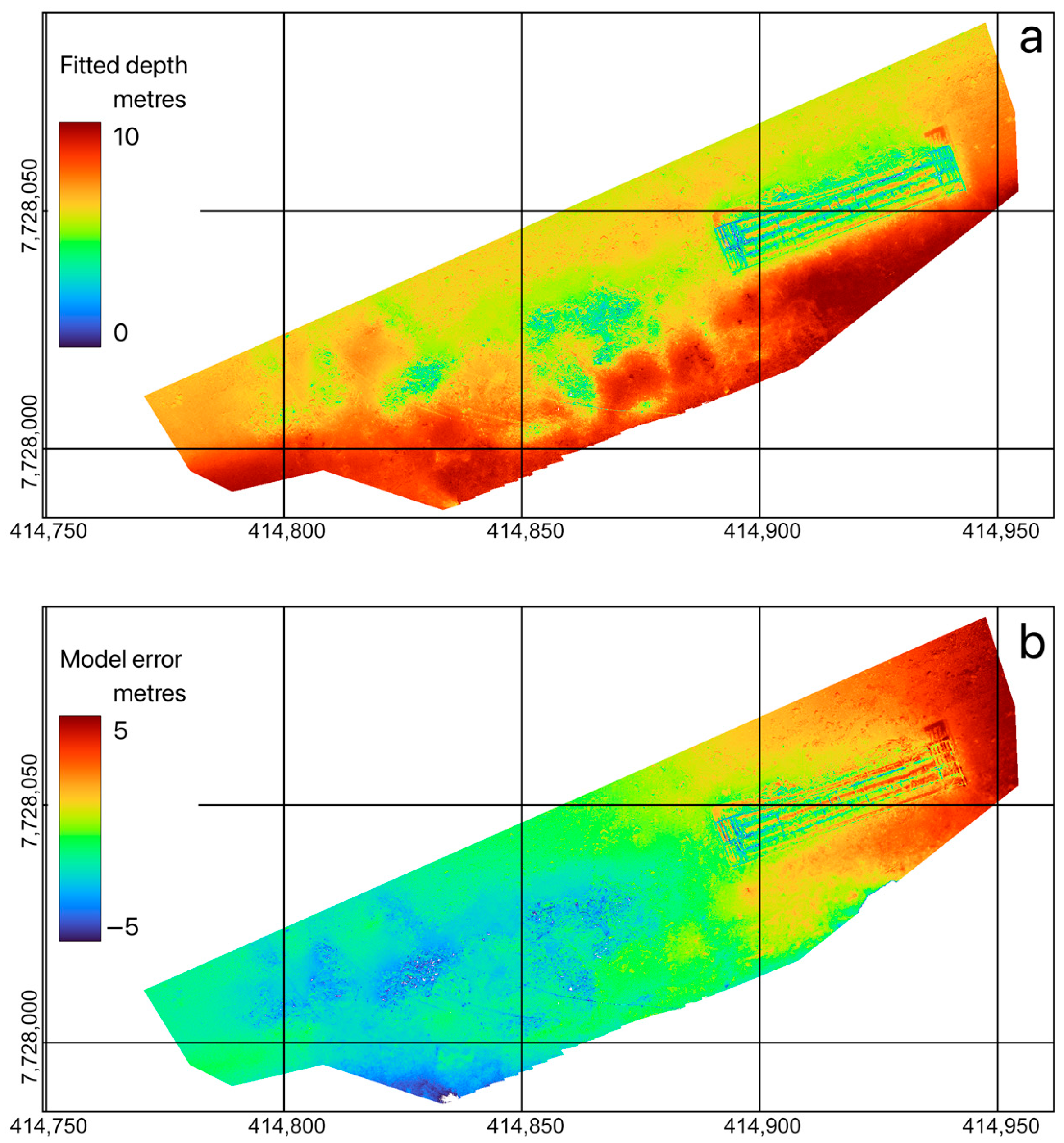
Data products (point-cloud and orthomosaic) were inspected visually for quality, and it was observed with satisfaction that the SfM processing had succeeded despite the through-surface imaging geometry (Figure 5 and Figure 8), although the infrared (band 5) channel of the multispectral orthomosaic displayed some irregularities in calibration across the mosaic. Inspection of the orthomosaic showed no instances of sun-glint, and visualisation of the point cloud (Figure 5) confirmed the fidelity of the 3D structure.

The two-dimensional georeferenced geometry of the wharf structure was determined by viewing and digitising the orthomosaic using QGIS (c). Estimates of three-dimensional geometry were made from the point-cloud data. The principal data product from which 3D geometry was determined was a map of the ‘depth below wharf’ (DBW). This was generated from the point-cloud data by manually determining the z-coordinate of the highest point on the (submerged) wharf and then subtracting this from all other z-coordinates, followed by multiplication by a factor of 1.33 to account for refraction (Equation (3)). The data were then gridded to a raster data product at a pixel size of 0.25 m, using the XYZ2DEM plugin (https://imagej.net/ij/plugins/xyz2dem-importer.html, accessed 15 July 2025) in the ImageJ (v. 2.16.0/1.54p) processing environment [29,30]. This process, which uses Delaunay triangulation as an intermediate step, followed by linear interpolation, will undoubtedly introduce errors around the wharf with its relatively open structure but, elsewhere, will map the solid surface (d). We note that an equivalent functionality is provided via the GDAL grid operation, accessible through QGIS.

To estimate the volume of debris material lying above the sea floor, we constructed the equivalent of a digital terrain model to represent the bottom topography, using the ‘rolling-ball’ background subtraction method [31] in ImageJ (e). This was chosen in preference to multispectral classification of the point cloud because of spectral variability, partly as a result of depth variations, noted in the imagery of the sea floor (see also results, Section 3.3). We used a radius of 20 m, chosen empirically but with regard to the observed size of the debris piles (e.g., Figure 11), for the rolling ball. Again, we note that an equivalent functionality to this method of surface fitting could be achieved within the QGIS environment, for example, using a combination of focal minimum filtering, followed by smoothing.

Subtraction from the DBW data was performed in QGIS, followed by smoothing with a Gaussian kernel with a 1-metre standard deviation. This generated a data product showing the height above the sea floor (f). As noted above, this was expected to be less reliable for the wharf structure than the debris piles, so a second method of estimating the 3D characteristics of the former was employed (g). This approach capitalises on the open structure of the wharf, meaning that several points in the point cloud can be expected to be found at approximately the same planimetric (x-y) coordinates, similar to the imaging of an open vegetation canopy [32]. In fact, as observed in Figure 4, the point-cloud densities around the wharf structure exceeded 50 m⁻². We thus gridded the point-cloud data, and we calculated the range between the minimum and maximum z-coordinates (again, with a factor of 1.33 for refraction), to estimate the height above the sea floor in the wharf structure. This step, implemented using GNU Octave, also allowed a straightforward estimate of point-cloud noise to be made from areas not forming part of the wharf structure (result noted in Section 3.2).

The bathymetric variation across the study site was most directly determined from the DBW data product. However, we also tested the extent to which the Stumpf model, applied to the multispectral orthomosaic, could be tuned to accurately represent variations in the bottom topography. Successful retrieval using this method would represent an approximately 10-fold improvement in the linear spatial resolution of the bathymetric model. The Stumpf model, while less sensitive to variations in bottom reflectance, is not immune to them, especially when they arise from different spectral characteristics. Since the debris piles were clearly spectrally different from the sea floor (e.g., Figure 11), we chose to fit the model of Equation (4) to the DBW data, following manual masking to remove areas of debris and the wharf structure. We extracted DBW values and reflectances in all five spectral bands of the multispectral orthomosaic. Model fitting was performed in GNU Octave, considering all possible pairwise combinations of the multispectral data and choosing the combination that gave the best model fit (h).

Table 1. Coordinates (WGS84, UTM zone 34 N) of the representative points identified in Figure 8.

Point Number	X/m	Y/m
1	414,890.54	7,728,046.29
2	414,939.66	7,728,063.75
3	414,943.14	7,728,054.56
4	414,894.20	7,728,037.08
5	414,893.23	7,728,039.40
6	414,892.39	7,728,041.53
7	414,892.26	7,728,041.88
8	414,891.40	7,728,044.02
9	414,940.51	7,728,061.44
10	414,941.30	7,728,059.31
11	414,942.27	7,728,056.78
12	414,939.32	7,728,053.72
13	414,935.77	7,728,062.37
14	414,894.67	7,728,047.67
15	414,897.17	7,728,040.67

shows the coordinates of some points representative of the overall geometry, manually digitised in QGIS (Figure 8). The corresponding dimensions are sketched in Figure 9. The estimated accuracy of this manual digitisation is around 0.05 m. Many dimensions can be determined. For example, the wharf can be measured as approximately 52 m long and 10 m wide. It is divided into four equally spaced sections longitudinally. Approximately 4 m at each end of the wharf has lateral reinforcements spaced around one metre apart, while the main length of the wharf has lateral reinforcements around two metres apart. The width of the structural members is between about 0.15 and 0.25 m.

3. Results

3.1. Wharf Planimetric Geometry

Figure 8 shows an extract of the multispectral composite detailing the wharf structure. Fifteen points, representative of the overall geometry, were manually digitised. Their coordinates are listed in Table 1, and the corresponding dimensions are sketched in Figure 9. The estimated accuracy of this manual digitisation is around 0.05 m, based on the appearance in the orthomosaic of parts of the wharf structure that are clearly approximately linear. Many dimensions can be determined. For example, the wharf can be measured as approximately 52 m long and 10 m wide. It is divided into four equally spaced sections longitudinally. Approximately 4 m at each end of the wharf has lateral reinforcements spaced around one metre apart, while the main length of the wharf has lateral reinforcements around two metres apart. The width of the structural members is between about 0.15 and 0.25 m. Since no previous measurements of the wharf’s dimensions are known to us, we are unable to verify their accuracy.

The absolute accuracy of the geographical locations noted in Table 1 cannot be determined properly since we are unaware of any remotely comparable mapping of the area. However, we can compare some of the coordinates with recent high-resolution Maxar imagery accessible through Google Earth. Two images are useful in this respect, from 20 April 2022 and 20 July 2022. Manual digitisation of some of the points reported in Table 1 shows that the apparent coordinates within the Maxar images vary by around 1 metre between images, while the difference between the coordinates reported in Table 1 and those in either of the Maxar images is consistent to around 0.5 m. We also performed a comparison against aerial orthophotos from 2024 found at https://www.norgeibilder.no and https://norgeskart.no (accessed on 15 December 2025). Although coordinates could be extracted for these photos with a precision of only 1 m, we did not find any discrepancies from our estimated coordinates exceeding 3 m. We thus propose that the absolute uncertainty in our coordinates is, at most, 3 m.

3.2. Depth Below Wharf, Debris Volume, and Wharf Height

The ‘depth below wharf’ dataset derived from the point-cloud data is visualised in Figure 10. As noted before, this has a spatial resolution of 0.25 m, and values range from 0 to around 15 m. The presence of the wharf structure is very obvious, while the debris piles are more indistinct.

The smoothed ‘object height model’, resulting from the subtraction of the estimated sea-floor background from the DBW, is visualised as a contour map in Figure 11. We identified more or less discrete debris piles and estimated their volumes through a local integration of the object height model (

Table 2. Estimated volumes of the debris piles identified in Figure 11.

Pile	Volume (m3)
A	102
B	65
C	90
D	120
E	53
F	53
G	38
H	96
J	61
K	52
L	24

). The total estimated volume of debris within the evaluated area is 701 m³. We estimated the uncertainty in the height estimates as around 5 cm, based on the modal standard deviation of heights within 1 m² cells within the point cloud. This is around 10% of the average height of a debris pile, and we thus also estimate the uncertainty of our volume estimate as around 10%.

From Table 2 and Figure 11, it can be inferred that typical, more or less discrete piles of debris reach around one metre above the sea floor, with volumes of a few tens of cubic metres and, hence, base areas of the order of 100 square metres. When the packing fraction (the ratio of the volume of solid material to the total pile volume) of a randomly arranged debris pile is estimated as ~0.5 [33], the total volume of solid debris would be around 350 m³, and when the density of this solid material as 7000 kg m⁻³ is estimated under the assumption that it is predominantly steel, the total mass of material would be around 2400 tonnes. We note that these are minimum estimates since there may well be more debris material not covered via the multispectral imagery.

The wharf height above the sea floor, estimated through both the rolling-ball seafloor removal and estimation similar to that for vegetation canopy height (range of point-cloud height values within a single 1 m² grid cell) ranged from around 1 metre to a maximum of 2.65 metres.

3.3. Bathymetry

As noted earlier, the best bathymetric product from our data is the depth-below-wharf (DBW) dataset shown in Figure 10. However, we also investigated the extent to which bathymetric variation in the sea floor could be extracted from the multispectral composite. Testing all possible pairwise band combinations showed that the strongest statistical relationship of the form represented in Equation (4) was found for bands 1 and 3 (i.e., blue and red). The optimum selected model had parameters of m₀ = 0.6615, m₁ = 4.5597, and n = 2000. It was fitted after approximately 40% of the data points were rejected, which evidently did not fit the distribution. Figure 12 shows the depth map constructed using this model and its difference from the DBW map of Figure 10. The inspection of Figure 12 shows that the Stumpf model performed reasonably well in the part of the image lying to the west of the wharf (the RMS error here is typically around 0.25 m) but increasingly poorly to the east, where the systematic errors increase to 4–5 m. This points to a spatial gradient in the spectral reflectance characteristics of the sea floor.

4. Discussion

The principal aim of this study was to investigate whether UAV-based SfM and multispectral imaging are capable of providing better-than-decimetric-resolution reconstructions of submerged structures in shallow water. Despite the challenges posed by refraction, the results were positive and strongly suggest that this approach is viable for documenting and monitoring submerged heritage. Since the existing literature in this area is not extensive, this is a significant finding, especially to the extent that it shows that off-the-shelf hardware and software can be adequate to the task.

The spatially coherent structure of the wharf, the visible parts of which were submerged to a maximum depth of around 5 m, proved relatively simple to quantify, with an accuracy of around 5 cm (implied by both dispersion in the heights represented in the point cloud and also by the physical integrity of the objects reconsructed from the pount cloud, as visualised in Figure 5). This is comparable to the few other reported accuracies for UAV-based two-medium SfM in shallow water. The open structure of the wharf allowed it to be analysed in a manner similar to that for a vegetation canopy, with relatively complete three-dimensional imaging of the geometry. Although our investigation did not include any validation activity, it would be relatively straightforward to confirm the dimensions of the wharf structure using in situ measurements made by divers. This is one of the proposed public engagement activities described below.

The reconstructed three-dimensional geometry also proved effective for quantifying the less ordered material that composed the debris piles. In distinction to the wharf, the piles could be characterised as having a closed structure, with little to no visibility through them. The vegetation canopy analogy was inappropriate in this case, and instead, we treated the problem of shape characterisation as similar to that of determining both a Digital Surface Model (DSM, directly deduced from the UAV data) and a Digital Terrain Model (DTM, representing the sea floor). The approach used here to estimate the DTM is a background subtraction based on a simple rolling-ball algorithm and could undoubtedly be improved on through the use of a more sophisticated approach [34], though the evident and expected smoothness of the seafloor geometry encourages us to believe that the approach is unlikely to be seriously inaccurate. The estimated accuracy of heights in the point cloud is very similar to that of the horizontal accuracy, around 5 cm. We can note that the estimated mass contained in the debris piles identified in this study, around 1900 tonnes, would constitute around 5% of the mass of the entire Tirpitz.

Bathymetry using the multispectral imagery showed some promise but requires further validation and correction for variations in seafloor reflectance. When the SfM method succeeds in imaging the bottom surface, which it has done in the present instance to a depth of at least 10 m, this would seem to be a much more reliable method of determining bathymetry.

Perhaps the least satisfactory result from this investigation is the residual uncertainty in planimetric coordinates. We estimate this as not greater than 3 m, which is not likely to be sufficiently precise for future archaeological studies. We are, however, much more confident in the relative planimetric positions, and any lateral offset in the coordinates we have estimated could be reduced through surveying, for example, through a terrestrial RTK measurement of the wharf when exposed due to the tide.

Through-surface imaging is not the only, or necessarily the most obvious, means of characterising the structure of submerged objects. Robotic equipment operating purely underwater (Autonomous Underwater Vehicles, or AUVs) can use SONAR, LiDAR, or conventional photography to capture information that can, in principle, be integrated with that obtained from through-surface imaging, though accurately locating the underwater data and co-registering them with the aerially acquired data proves challenging. The concept of an Internet of Underwater Things (IoUT) has recently been proposed [35] as a framework linking the underwater part of data collection, and UAVs will have a role to play in maintaining the connectivity of this network [36]. There are useful synergies between aerial and underwater detection systems [37], though difficulties remain for both the communication and navigation of AUVs [38]. As part of the Tirpitz Site Project, we are currently investigating the use of an AUV for data collection and for identifying some of the objects comprising the debris piles.

Environmental conditions were selected with care to perform the data collection for this project. We note in particular the sea state, sun geometry, and water turbidity, as well as the state of the tide. Neither the work reported here nor any work reported elsewhere in the literature has yet provided a comprehensive understanding of optimum environmental conditions. However, we can note that some useful environmental data is potentially encoded in the measurements themselves. For example, spectral variation in the optical absorption coefficient in the water column contains information about water turbidity, and hence, for example, algal blooms or glacial runoff, while sun-glint conveys information about the sea and wind state. These will be explored in future work.

Other aims for the future development of this work include UAV platform upgrades, integration with underwater robotic data, and the deployment of geolocated seabed markers to improve registration and support long-term monitoring. Broader goals include the development of a spatial transect for pollutant monitoring and a web-based GIS platform [39] for community engagement.

5. Conclusions

The principal aim of this research was to investigate the potential of two-media structure-from-motion and multispectral imagery for shallow submerged structures, using off-the-shelf components and processing software. This was shown to be successful, achieving accuracies of a few centimetres at depths of up to 5–10 m. The specific characteristics of the Tirpitz wreck site were determined with high precision in this study: we were able to measure both the two-dimensional projected form of the wharf and its three-dimensional structure, as well as that of the piles of debris nearby. The volume of these debris piles is estimated at around 350 m³, with a somewhat less confident estimate of their mass at around 2400 tonnes. The Tirpitz salvage site offers a challenging but informative testbed for the remote sensing of underwater cultural heritage. Our results support a further exploration of hybrid aerial–underwater sensing frameworks and community-engaged monitoring initiatives.